Условия равновесия техническая механика – Условия равновесия системы сил

Содержание

Условия равновесия системы сил | Лекции и примеры решения задач механики

Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия: R=0, M_O=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

∑x_i =0, ∑M_ix=0;
∑y_i =0, ∑M_iy=0; (1.20)
∑z_i =0, ∑M_iz=0.

Формы условий равновесия

Первая форма

Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:

∑x_i=0;
∑y_i=0; (1.21)
∑M_O=0,

причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это

первая форма уравнений равновесия.

Вторая форма

Уравнения равновесия могут быть записаны иначе:

∑x_i =0;
∑M_A=0; (1.22)
∑M_B=0.

Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.

Третья форма

∑M_A=0;
∑M_B=0; (1.23)
∑M_C=0.

Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.

Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.

Другие условия равновесия

При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):

∑x_i =0;
∑M_O=0. (1.24)

Рисунок 1.26

Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:

∑z_i =0;
∑M_ix=0; (1.25)
∑M_iy=0.

Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:

∑x_i =0;
∑y_i =0; (1.26)
∑z_i =0

и два уравнения для плоской системы:

∑x_i =0;
∑y_i =0. (1.27)

В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.

>> Равновесие системы сходящихся сил

isopromat.ru

техническая механика

1. Аксиомы статики

-две равные по модулю силы, приложенные к абсолютно твёрдому телу, направленные по одной прямой в противоположные стороны взаимно уравновешиваются.

-не нарушая механического состояния абсолютно твёрдого тела, к нему можно приложить или отбросить от него уровновешанную систему сил => всякую силу, действующую на абсолютно твёрдое тело можно перенести вдоль линии действия в любую т. Тела, не нарушая при этом его мех-ое состояние.

2.Равнодействующая двух сил, приложенных в одной точке

равнодействующая 2ух сил, приложенная к одной точке, приложенная в этой же точке и является диагональю параллелограмма, построенных на этих силах.

3.Связи, реакции связей

Связи–это тела, ограничивающие движение заданного тела. Реакции связи – это силы, действующие со стороны связей.

Принцип освобождение связей – не изменяя равновесия тела каждую связь можно отбросить заменив её реакцией.

4.Наиболее часто встречающиеся виды связей

1) Гибкая нить(связь осуществляемая веревкой, тросом и тд.)

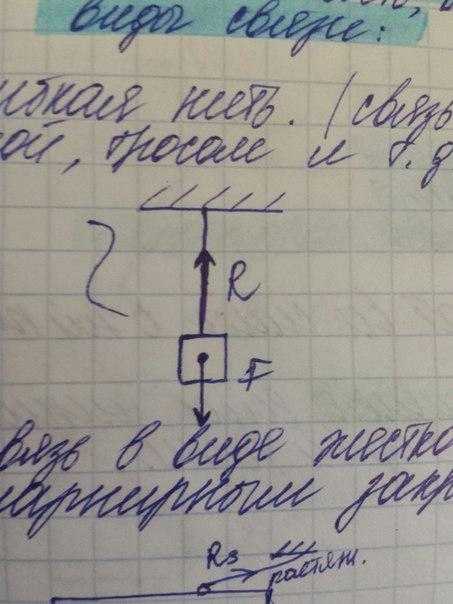
2) связь в виде жёсткого прямого стержня с шарнирным закреплением концов

3) идеально гладкая плоскость

4) связь в виде контакта цилиндрической или шаровой поверхности

5) связь, осуществляемая опорой или ребром двугранного угла.

5.Опорные устройства балочных систем и их реакции

1) шарнирно -подвижная опора –возникает вертикальная опорная реакция

2) неподвижная опора

3)жёсткая опора

Примеры задач:

6.Система сходящихся сил. Геометрическое и аналитическое условия равновесия

1)-все силы находятся в одной плоскости;

— линии действия всех ил пересекаются в одной точке –сходящиеся точка 2)геом-ое усл. равновесие с.с.с: при построение силовой многогранник замыкается. Для определённых равнодействующих систем сходящихся сил или необходимо построить силовой многоугольник. Система сходящихся сил находится в равновесии если их равнодействующая равно 0.

7.Проекция силы на ось

Проек-ия силы на ось – отрезок, соединяющий точки пересечения перпендикуляров, опущенных из начала и конца вектора силы на ось.

1)проекция вектора на ось равна произведению модуля силы вектора на косинус угла между направлением вектора (силы) и осью.

2) проекция вектора положительна, если направление вектора и оси совпадает.

3) отрицательна, если напра-ие вектора и оси противоположно.

8.Пара сил

Пара сил – это две равные параллельные противоположные силы.

Пара сил стремиться вращать тело.

9.Момент силы относительно точки. Плечо силы

Момент пары сил – произведение одной из силы на кратчайшие расстояние между линиями действия сил.

Момент пары сил положено считать положительным, если пара стремиться повернуть тело по ходу часовой стрелки.

Плечо силы –это кратчайшие расстояние между линиями действиями сил(кН-м; Н-м)

10.Условие равновесия плоской системы произвольно расположенных сил

Св-ва пары сил:

1) момент пары не зависит от пары плоскости;

2) можно как угодно менять модули сил и плечо пары, лишь бы момент оставался неизменным.

Действия пары сил полностью опр-тся её моментом и направ-нием вращения, поэтому, если имеется несколько пар сил их можно заменить одной эквивалентной парой. Для этого достаточно произвести простое алгебраическое правило:

Система пар находится в равновесие, если момент результирующей пары равно 0, или сумма момента всех пар действующая на тела равно нулю:

Момент силы относительно точки равен произведению модуля силы равен на кратчайшие расстояния от точки до линии действия силы.

Момент отношения силы равно 0, если точка находится на линии действия силы.

11.Уравнения равновесия

1)Сумма моментов всех сил относительно двух взятых произвольно точек равно 0. Сумма моментов всех сил на перпендикулярную ось х не перпендикулярна a, b не равна 0.

2) Сумма проекции всех сил на две взаимно перпендикулярной оси равна 0. Сумма момента всех сил относительно любой взятой произвольной точки равна 0.

3) Сумма момента всех сил относительно трёх произвольно взятых точек, не лежащих на одной прямой, равна 0.

12. Определение опорных реакций в балках, фермах.

Определение опорных реакций в балках — вертикальная составляющая реакции в балке равна сумме сил, приложенных к балке.

Ферма – геометрически не изменяемая стержневая система остающаяся такой же при замене всех её жестких узлов, шарнирами.

Балки— стержневая система состоящая из прямолинейных элементов, жестко или в некоторых углах шарнирно соединенных между собой. Рамы являются статически неопределимыми системами.

13.Определение усилий в стержнях фермы методом сквозных сечений

– определяются опорные реакции, если они ранее не были определены;

– ферма разрезается на две части сечением, которое проходит через стержни, усилия в которых необходимо определить; при этом должно разрезаться не более трех стержней, усилие в которых неизвестны;

– рассматривается равновесие одной из двух частей фермы; действие отброшенной части заменяется реакциями перерезанных стержней, которые направляются вдоль стержней от узлов; изображаются активные силы, действующие на рассматриваемую часть фермы;

– составляются уравнения равновесия так, чтобы в каждое уравнение входило одно неизвестное усилие. Обычно составляются уравнения моментов сил относительно точек, где пересекаются линии действия двух неизвестных усилий. Если же на расчетной схеме два стержня параллельны, то составляется уравнение проекций сил на ось, перпендикулярную к этим стержням;

– решая каждое из составленных уравнений равновесия, находят искомые усилия в стержнях.

14. Определение усилий в двух сходящихся стержнях

15.Классификация нагрузок

16. Центр тяжести плоских фигур. Статический момент площади

Центр тяжести тела — центр параллельных сил действующих сил на все части тела.

Статический момент площади – взятое по всему сечению сумма произведений элементарных площадей на расстояния от х центра тяжести до оси.

17. Профили стандартного проката

К стандартным профилям проката относятся уголок, швеллер, балка, которые сохраняют свои качества в различных видах конструкций, их применяют в строительной сфере.

-Современный равнополочный уголок – это стальное изделие, полученное методом фасонного проката; используется при связках, укреплении конструкций, а также обводке; В основе уголка может лежать разная сталь, чёрный металл.

— Неравнополочный стальной уголок – это сортовой металлопрокат, в поперечном сечении которого явно угадывается буква «Г»

— Балка двутавровая – это металлическая балка, которая имеет в своем сечении вид буквы «Н».

— Швеллер (техника) — металлические балки (гнутые профили), в сечении напоминающие букву «П». Полки швеллера находятся по одну сторону от стенки (в отличие от зетовых профилей, в которых полки лежат по разные стороны от стенки).

18.Устойчивое, неустойчивое, безразличное равновесие

-Равновесие тела называют устойчивым, если при отклонении от него возникают силы, возвращающие тело в положение равновесия.

-Равновесие тела называют неустойчивым, если при самом незначительном отклонении от него равнодействующая действующих на тело сил вызывает дальнейшее отклонение тела от положения равновесия.

— Равновесие, при котором смещение тела в любом направлении не вызывает изменения действующих на него сил и равновесие тела сохраняется, называют безразличным

19. Момент опрокидывающий, момент устойчивости, коэффициент устойчивости

20.Упругие и пластические деформации

-если тело после снятия нагрузки полностью восстановит форму и первоначальные размеры, то деформация возникающая при действии нагрузки наз-тся упругой.

— Пластической деформацией называется такая, при которой после прекра-щения действия нагрузки тело не восстанавливает своей первоначальной фор-мы и размеров. Пластической деформации всегда предшествует упругая.

21. Нагрузки и их классификации

В зависимости от продолжительности действия нагрузок следует различать постоянные и временные (длительные , кратковременные , особые ) нагрузки.

К постоянным нагрузкам следует относить:

а) вес частей сооружений, в том числе вес несущих и ограждающих строительных конструкций;

б) вес и давление грунтов (насыпей, засыпок), горное давление;

в) гидростатическое давление.

К длительным нагрузкам следует относить:

а) вес временных перегородок, подливок и подбетонок под оборудование;

б) вес стационарного оборудования: станков, аппаратов, моторов, емкостей, трубопроводов с арматурой, опорными частями и изоляцией, ленточных конвейеров, постоянных подъемных машин с их канатами и направляющими, а также вес жидкостей и твердых тел, заполняющих оборудование;

в) давление газов, жидкостей и сыпучих тел в емкостях и трубопроводах, избыточное давление и разрежение воздуха, возникающее при вентиляции шахт;

г) нагрузки на перекрытия от складируемых материалов и стеллажного оборудования в складских помещениях, холодильниках, зернохранилищах, книгохранилищах, архивах и подобных помещениях;

д) температурные технологические воздействия от стационарного оборудования;

е) вес слоя воды на плоских водонаполненных покрытиях;

ж) вес отложений производственной пыли, если не предусмотрены соответствующие мероприятия по ее удалению;

з) пониженные нагрузки, перечисленные в 4.1;

и) воздействия, обусловленные деформациями основания, не сопровождающимися коренным изменением структуры грунта, а также оттаиванием вечномерзлых грунтов;

к) воздействия, обусловленные изменением влажности, усадкой и ползучестью материалов.

К кратковременным нагрузкам следует относить:

а) нагрузки от оборудования, возникающие в пускоостановочном, переходном и испытательном режимах, а также при его перестановке или замене;

б) вес людей, ремонтных материалов в зонах обслуживания и ремонта оборудования;

в) нагрузки от людей, животных, оборудования на перекрытия жилых, общественных и сельскохозяйственных зданий с полными нормативными значениями, кроме нагрузок, указанных в 5.4, а, б, г, д;

г) нагрузки от подвижного подъемно-транспортного оборудования (погрузчиков, электрокаров, кранов-штабелеров, тельферов, а также от мостовых и подвесных кранов с полным нормативным значением), включая вес транспортируемых грузов;

д) нагрузки от транспортных средств;

е) климатические (снеговые, ветровые, температурные и гололедные) нагрузки.

К особым нагрузкам следует относить:

а) сейсмические воздействия;

б) взрывные воздействия;

в) нагрузки, вызываемые резкими нарушениями технологического процесса, временной неисправностью или поломкой оборудования;

г) воздействия, обусловленные деформациями основания, сопровождающимися коренным изменением структуры грунта (например, при замачивании просадочных грунтов) или оседанием его в районах горных выработок и в карстовых;

д) нагрузки, обусловленные пожаром;

е) нагрузки от столкновений транспортных средств с частями сооружения. Расчетные значения особых нагрузок устанавливаются в соответствующих нормативных документах или в задании на проектирование.

22. Метод сечений. Внутренние силовые факторы, возникающие в сечении бруса

1) Для расчетов элементов конструкции на прочность необходимо знать внутренние силы упругости, возникающие в результате приложения внешних сил в разных точках и частях конструкции. Способы определения этих внутренних сил с помощью науки сопротивление материалов включают такой прием, как метод сечений.

2)Рассечем брус (рис. 1) поперечным сечением а-а и рассмотрим равновесие его левой части. Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а-а, будут главный вектор Fгл, приложенный в центре тяжести сечения, и главный момент Мгл = Ми, уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.

Разложим главный вектор на составляющую N, направленную вдоль оси бруса, и составляющую Q, перпендикулярную этой оси и лежащую в плоскости сечения. Эти составляющие главного вектора и главный момент называют внутренними силовыми факторами, действующими в сечении бруса. Составляющую N называют продольной силой, составляющую Q –поперечной силой, пару сил с моментом Ми – изгибающим моментом.

23. Напряжения: полное, касательное. Единицы измерения

24. Осевое растяжение и сжатие

25.Продольная сила. Величина, знак, эпюра продольных сил

26.Нормальные напряжения, возникающие в поперечных сечениях бруса при осевом растяжении и сжатии

27. Продольные и поперечные деформации, возникающие при осевом растяжении и сжатии

установлено, что поперечные деформации при растяжении и сжатии прямо пропорциональны продольным деформациям. По аналогии с продольной деформацией введем понятие относительной поперечной деформации. Коэффициент Пуассона является безразмерной величиной, и характеризует упругие свойства материала. При растяжении и сжатии этот коэффициент принимается одинаковым.

28. Закон Гука. Модуль продольной упругости.

закон Гука формулируется следующим образом: механическое напряжение в упруго деформированном теле прямо пропорционально относительной деформации этого телах

Величина характеризующая зависимость механического напряжения в материале от рода последнего и от внешних условий, называется модулем упругости. Модуль упругости измеряется механическим напряжением, которое должно возникнуть в материале при относительной упругой деформации, равной единице.

29. Механические испытания материалов.

МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ — определение механич. св-в материалов и изделий. Для определения механических свойств материалов специальные образцы или готовые изделия испытывают в соответствии с требованиями ГОСТов. В зависимости от характера действия приложенных к образцу или изделию сил (нагрузок) различают деформации сжатия, растяжения, изгиба, сдвига (среза), кручения .

30. Диаграммы растяжения и сжатия для пластических и хрупких материалов.

По механическим свойствам материалы могут быть разделены на две основные группы: пластичные и хрупкие. У первых разрушению предшествует возникновение значительных остаточных деформаций; вторые разрушаются при весьма малых остаточных деформациях. Пластичными материалами в обычных условиях являются малоуглеродиста 03; сталь, медь; хрупкими — некоторые специальные сорта стали, чугун.

31. Понятие о наклепе

Наклёп – это совокупность структурных изменений и связанных с ними св-в при холодной пластичной деформации. Различают два вида наклёпа: фазовый и деформационный. (упрочнение металлов и сплавов вследствие изменения их структуры и фазового состава в процессе пластической деформации при температуре ниже температуры рекристаллизации. Наклёп сопровождается выходом на поверхность образца дефектов кристаллической решётки, увеличением прочности и твёрдости и снижением пластичности, ударной вязкости, сопротивления металлов деформации противоположного знака (эффект Баушингера).)

32.Нормативные и расчетные нагрузки и сопротивления

Основным параметром, определяющим прочностные свойства различных материалов, считается нормативное сопротивление материала R_n (может обозначаться как R_н), Па (кгс/см²). Величина нормативного сопротивления представляет собой значение контрольной или браковочной характеристики данного материала, определяемое соответствующими ГОСТами. Величина нормативного сопротивления определяется путем статистической обработки большого числа опытных данных. При этом обеспеченность значений нормативных сопротивлений материалов должна составлять не менее 0,95, т. е. чтобы не менее чем в 95% случаев материал имел прочность, равную или большую, чем R_n.

33.Условия прочности по предельным состояниям и допускаемым напряжениям

В качестве предельных напряжений для указанных трех групп материалов при статическом нагружении принимают следующие механические характеристики:

для пластичных материалов (разрушению их предшествует возникновение больших пластических деформаций) — физический , или условный предел текучести, практически одинаковый при растяжении и сжатии;

для хрупкопластичных материалов (разрушение их происходит при сравнительно небольших пластических деформациях)— условный предел текучести, значение которого при растяжении и сжатии различно: < ,

для хрупких материалов (разрушение их происходит при очень малых пластических деформациях) — предел прочности, значение которого при растяжении и сжатии различно: , <

Основные факторы, влияющие на выбор требуемого коэффициента запаса прочности, следующие:

а) точность определения действующих нагрузок и применяемых методов расчета;

б) степень однородности применяемого материала, его чувствительность к недостаткам механической обработки и изученность свойств;

в) ответственность детали.

34.Срез и смятие

Срез и смятие: внутренние силовые факторы и геометрические характеристики прочности (условная площадь при срезе и смятии). Условия прочности при срезе и смятии. Расчеты на срез и смятие заклепочных штифтовых и шпоночных соединений.

35.Геометрические характеристики плоских сечений. Моменты инерции, моменты сопротивлений

1.Простейшая геометрическая характеристика плоской фигуры – её площадь. От площади поперечного сечения зависят прочность и жесткость стержня при осевом растяжении и сжатии.

2.Момент инерции при параллельном переносе осей

Оси, проходящие через центр тяжести плоской фигуры, называют центральными осями. Момент инерции относительно центральной оси называется центральным моментом инерции.

36.Зависимость между моментами инерции относительно параллельных осей

При вычислении моментов инерции для сложных фигур следует запомнить одно правило: значения для моментов инерции можно складывать, если они вычислены относительно одной и той же оси. Для сложных фигур чаще всего центры тяжести отдельных простых фигур и всей фигуры не совпадают. Не совпадают, соответственно, и центральные оси для отдельных простых фигур и всей фигуры. В связи с этим существуют приемы приведения моментов инерции к одной оси, например, центральной оси всей фигуры. Это может быть связано с параллельным переносом осей инерции и дополнительными вычислениями.

studfiles.net

3. Условия и уравнения равновесия для различных систем сил.

Условия равновесия произвольной плоской системы сил. Случай параллельных сил.

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M₀ = 0.

Здесь О — любая точка плоскости.

Найдем вытекающие из равенств аналитические условия равновесия.

Величины R и М_о определяются равенствами:

где НоR может равняться нулю только тогда, когда одновременно R_x = 0 и R_y = 0. Следовательно, условия будут выполнены, если будет:

Равенства выражают, следующие аналитические условия равновесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.

; ;

Равновесие плоской системы параллельных сил.

В случае, когда все действующие на тело силы параллельны друг другу, мы можем направить ось Ох перпендикулярно к силам, а ось Оу параллельно им (рис. 29). Тогда проекция каждой из сил на Ox будет равна нулю и первое из 3-х равенств обратится в тождество вида 0 = 0. В результате для параллельных сил останется два условия равновесия:

Где ось Оу параллельна силам.

Рис.29

Кинематика

1. Кинематика точки.

Кинематика точки. Введение в кинематику.

Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

Под движением мы понимаем в механике изменение, с течением времени положения данного тела в пространстве по отношению к другим телам.

Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета.

Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны).

Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство.

Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т, е. как функции времени.

Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).

Кинематически задать движение или закон движения тела (точки) — значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.

Основная задача кинематики точки и твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих данное движение.

Способы задания движения точки

Для задания движения точки можно применять один из следующих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор , проведенный из начала координатО в точку М (рис. 1).

Рис.1

При движении точки М вектор будет с течением времени изменяться и по модулю, и по направлению. Следовательно,является переменным вектором (вектором-функцией), зависящим от аргумента:

Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.

Геометрическое место концов вектора , т.е.годограф этого вектора, определяет траекторию движущейся точки.

2. Координатный способ задания движения точки.

Положение точки можно непосредственно определять ее декартовыми координатами х, у, z (рис.1), которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости

, ,.

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

Чтобы получить уравнение траектории надо из уравнений движения исключить параметр .

Нетрудно установить зависимость между векторным и координатным способами задания движения.

Разложим вектор на составляющие по осям координат:

где — проекции вектора на оси;– единичные векторы направленные по осям, орты осей.

Так как начало вектора находится в начале координат, то проекции вектора будут равны координатам точкиM. Поэтому

studfiles.net

Условия равновесия произвольной системы сил

Геометрические условия равновесия, как это видно из предыдущего пункта, соответствуют двум векторным уравнениям

Проектируя эти уравнения на оси декартовой системы координат, получим шесть независимых уравнений равновесия

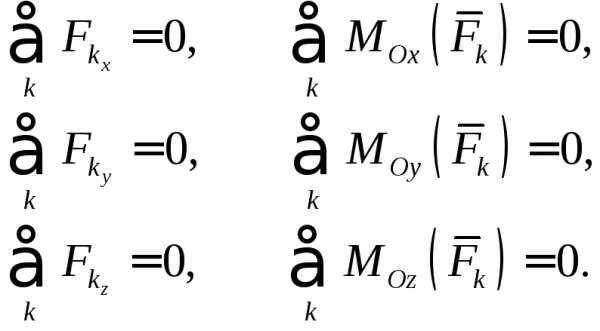
Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на выбранные координатные оси и суммы моментов всех сил относительно этих осей.

Различные типы систем сил и условия их равновесия:

пространственная система сходящихся сил. Выбираем начало координат совпадающее с точкой пересечения линий действия сил, входящих в рассматриваемую систему. Момент каждой из этих сил относительно любой оси, проходящей через начало отсчёта (пересекаемой линией действия силы), равен нулю. Поэтому три из шести уравнений равновесия выполнятся тождественно и условиями равновесия в этом случае будут:

пространственная система параллельных сил. Выбираем систему координат так, чтобы одна из осей (например,) была направлена параллельно силам. Проекции сил на ос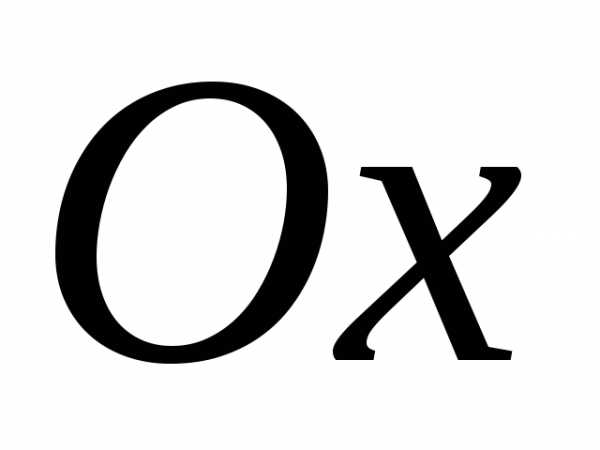ииравны нулю, момент любой из сил, параллельной оси, относительно этой оси равен нулю. Поэтому из шести уравнений равновесия получаем три условия:

произвольная плоская система сил. Совместим одну из координатных плоскостей (например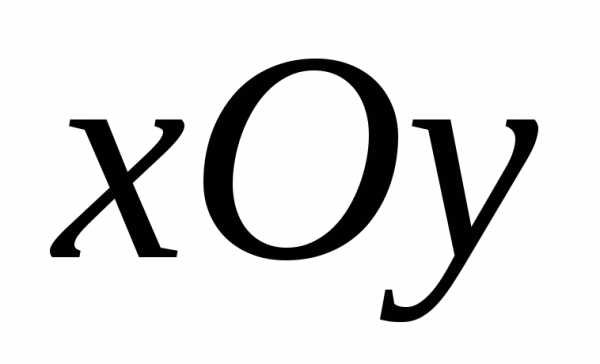) с плоскостью действия сил, тогда, очевидно, будут тождественно равными нулю следующие параметры произвольной силы:

Поэтому условия равновесия запишутся в виде трёх уравнений:

Теорема о моменте равнодействующей (теорема Вариньона)

Векторный момент равнодействующей рассматриваемой системы сил относительно любой точки равен сумме векторных моментов всех сил этой системы относительно той же точки.

Иными словами, если, то

Для плоской системы сил данная теорема запишется в виде алгебраических моментов относительно произвольной точки на плоскости

Эта теорема широко применяется в вычислениях моментов сил при решении практических задач.

Применение условий равновесия Различные формы условий равновесия

Условия равновесия произвольной плоской системы сил в виде

называют основной формой условий.

Эта система уравнений равновесия не является единственной. Условия равновесия можно сформулировать в других, эквивалентных основной, формах.

Для равновесия плоской системы сил необходимо и достаточно, чтобы равнялись нулю суммы алгебраических моментов всех сил системы относительно трёх любых точек в плоскости действия сил, не лежащих на одной прямой.

Для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов относительно двух точек, лежащих в плоскости действия сил, и сумма проекций всех сил на ось, не перпендикулярную линии АВ, соединяющей выбранные точки, равнялись нулю.

Статически определимые и статически неопределимые задачи

Число независимых условий равновесия определяется тем, к какому классу относится рассматриваемая система сил. Например, для произвольной плоской системы сил таких уравнений три, а для произвольной пространственной уже шесть.

Число неизвестных параметров определяется спецификой каждой задачи. В частности, оно зависит от количества и типов опор и неизвестных активных сил.

В том случае, когда число уравнений равновесия равно числу неизвестных задачи, она разрешима и называется статически определённой, в случае превышения числа неизвестных над количеством уравнений — статически неопределенной задачей. Если число неизвестных меньше числа уравнений, то либо часть уравнений тождественно удовлетворяется, либо задача переопределена (это, обычно, случаи, полученные при неправильно проведённом анализе сил) или система не находится в равновесии.

В статике абсолютно твёрдого тела рассматриваются только статически определённые задачи, т. к. для решения статически неопределённых задач нужно учитывать деформируемость тела.

studfiles.net

Условия и уравнения равновесия твердого тела

Привет! Меня зовут Константин Вавилов и в этой статье я рассказу об условиях, при которых любая система сил, твердое тело, элемент конструкции или конструкция в целом находится в равновесии. А также напишу про уравнения равновесия, которые вытекают из этих условий. Рассмотрим три основные формы этих уравнений.

Условия равновесия произвольной системы сил

Еще Ньютон говорил, что если геометрическая сумма сил, действующая на тело, равна нулю, то тело:

либо находится в состоянии покоя;
либо движется равномерно прямолинейно.

Из теоретической механики известно, что действие нескольких сил, просуммировав, можно заменить равнодействующей силой:

\[ \bar { { R }_{ 1 } } +\bar { { R }_{ 2 } } +\bar { { R }_{ 3 } } +\bar { { R }_{ n } } =\bar { R } \]

Тогда обязательное условие равновесия можно записать так:

\[ \bar { R } =0 \]

Однако для полного равновесия, часто, этого условия недостаточно, если тело имеет возможность вращаться относительно какой-то точки или оси, то для равновесия такой системы, необходимо, чтобы выполнялось условие:

\[ \bar { M } =0 \]

где M — главные момент системы, который эквивалентен сумме моментов системы относительно некоторого центра.

Условия равновесия плоской системы сил

Выше описанные условия означают, что система будет находится в равновесии, когда все силы, действующие на систему, будут взаимно уравновешиваться и момент относительно любой произвольной точки будет равен нулю, отсюда вытекает первая и основная форма условий равновесия для плоской системы сил:

\[ \begin{cases} { ΣM }_{ A }=0 \\ { ΣF }_{ kx }=0 \\ { ΣF }_{ ky }=0 \end{cases} \]

Вторая форма условий равновесия записывается следующим образом:

\[ \begin{cases} { ΣM }_{ A }=0 \\ { ΣM }_{ B }=0 \\ { ΣF }_{ ky }=0 \end{cases} \]

Из данного условия следует, что для равновесия системы достаточно равенство нулю суммы моментов относительно двух точек (A и B), а также суммы проекций всех сил относительно некоторой оси.

Важно! Ось не должна быть перпендикулярна прямой AB.

И, наконец, третья форма условий равновесия выглядит так:

\[ \begin{cases} { ΣM }_{ A }=0 \\ { ΣM }_{ B }=0 \\ { ΣM }_{ С }=0 \end{cases} \]

Из данной системы уравнений следует, что для равновесия системы достаточно равенства нулю суммы моментов относительно трех точек.

Важно! Точки, относительно которых записываются уравнения не должны лежать на одной прямой.

Уравнения равновесия для плоской системы сил

Рассмотрим на примере плоской балки, как записываются уравнения равновесия. Использовать будет классическую (первую) форму условия равновесия:

\[ \begin{cases} { ΣM }_{ A }=0 \\ { ΣF }_{ kx }=0 \\ { ΣF }_{ ky }=0 \end{cases} \]

Сумма моментов относительно точки A:

\[ { ΣM }_{ A }=-q\cdot 4\cdot 4-M+{ R }_{ B }\cdot 8=0 \]

Сумма проекций всех сил на вертикальную ось (y):

\[ { ΣF }_{ ky }=-q\cdot 4+{ R }_{ A }+{ R }_{ B }-F=0 \]

Сумма проекций всех сил на горизонтальную ось(x):

\[ { ΣF }_{ kx }={ H }_{ A }=0 \]

Условие равновесия пространственной системы сил

Для пространственной системы сил условие равновесие выглядит вот так:

\[ \begin{cases} \begin{matrix} { ΣF }_{ kx }=0 \\ { ΣF }_{ ky }=0 \\ { ΣF }_{ kz }=0 \end{matrix} \\ \begin{matrix} { ΣM }_{ x }=0 \\ { ΣM }_{ y }=0 \\ { ΣM }_{ z }=0 \end{matrix} \end{cases} \]

Таким образом, пространственная система будет находиться в равновесии, если суммы проекций сил на координатные оси, а также суммы моментов относительно осей будут равны нулю.

Уравнения равновесия для пространственной системы сил

В качестве примера рассмотрим пространственную раму, закруженную сосредоточенными силами. Составим для нее шесть уравнений равновесия:

\[ { ΣF }_{ kx }=F=0 \]

\[ { ΣF }_{ ky }=P=0 \]

\[ { ΣF }_{ kz }=T-G=0 \]

\[ { ΣM }_{ x }=-T\cdot b+G\cdot b=0 \]

\[ { ΣM }_{ y }=-T\cdot a+G\cdot (a+c)=0 \]

\[ { ΣM }_{ z }=P\cdot a=0 \]

sopromats.ru

Условия равновесия произвольной системы сил в векторной форме

Векторные условия равновесия произвольной системы сил: для равновесия системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен нулю и главный момент системы сил относительно любого центра приведения также был равен нулю. Иначе: для того чтобы ~0, необходимы и достаточны условия:

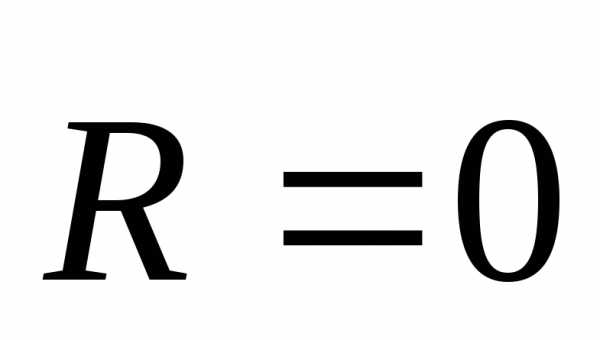, или,. (19)

Условия равновесия пространственной системы сил в аналитической форме

Для равновесия пространственной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю.

. (20)

Условия равновесия пространственной системы сходящихся сил

Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны нулю:

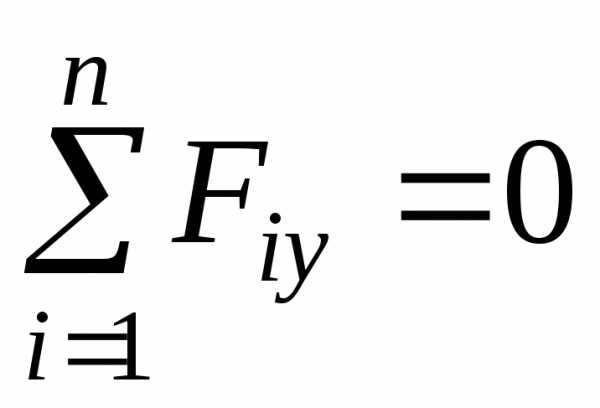; ;, (21)

В случае плоской системы сходящихся сил одну из осей координат, обычно , выбирают перпендикулярной силам, а две другие оси – соответственно в плоскости сил. Для равновесия плоской системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координатных осей, лежащих в плоскости сил, были равны нулю:

; , (22)

Условия равновесия пространственной системы параллельных сил

Направим ось параллельно силам:для равновесия пространственной системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма этих сил была равна нулю и суммы моментов сил относительно двух координатных осей, перпендикулярных силам, также были равны нулю:

(23)

Условия равновесия плоской системы сил

Расположим оси 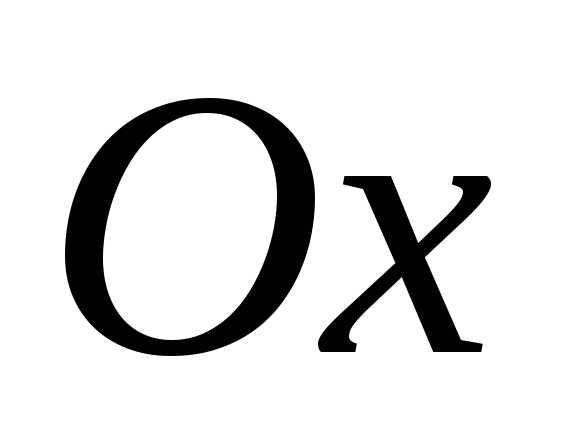ив плоскости действия сил.

Условия равновесия плоской системы сил в первой форме: для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости действия сил, также была равна нулю:

(24)

Для равновесия плоской системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма сил была равна нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости сил, также была равна нулю:

(25)

Теорема о трех моментах (вторая форма условий равновесия): для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю:

. (26)

Третья форма условий равновесия: для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил относительно двух любых точек, лежащих в плоскости действия сил, были равны нулю и алгебраическая сумма проекций этих сил на какую-либо ось плоскости, не перпендикулярную прямой, проходящей через две моментные точки, также была равна нулю, т.е.

. (27)

studfiles.net

Уравнения равновесия | Лекции и примеры решения задач механики

Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.

При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат

что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы

из условия отсутствия ее вращения относительно указанных осей.

Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.

Пример составления уравнений равновесия

В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F₁-F₆, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.

Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.

Суммы проекций сил

Сумма проекций всех сил на ось x (с учетом правила знаков для сил):

— на ось z:

Суммы моментов

Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):

в плоскости xOy:
в плоскости xOz:
в плоскости yOz:

Определение момента от распределенной нагрузки рассмотрено здесь.

Из полученных шести уравнений можно определить не более шести неизвестных усилий.

Примеры решения задач >
Краткая теория >

isopromat.ru