Расчетно-графическая работа. Определение опорных реакций балки.
ОПРЕДЕЛЕНИЕ ОПОРНЫХ РЕАКЦИЙ БАЛКИ
Последовательность решения задачи
1. Балку освободить от связей (связи) и их (его) действие заменить силами реакций.
2. Выбрать координатные оси.
3. Составить и решить уравнения равновесия.
Реакции опор можно определить, исходя из трех форм уравнений равновесия:
а)
å Fi х = 0;
å Fi у = 0;
åМА = 0;
б)
å Fi х = 0;
åМА = 0;
åМВ = 0;
в)
åМА = 0;
åМВ = 0;
åМС = 0.
4. Проверить правильность решения задачи. Проверку необходимо производить по тому уравнению равновесия, которое не было использовано при решении данной задачи (задача решена правильно лишь в том случае, если после постановки значений активных и реактивных сил в уравнение равновесия выполняется условие равновесия).
5. Сделать анализ решенной задачи (если при решении задачи реакции опор или реактивный момент получается отрицательным, то их действительное направление противоположно принятому).
Пример 1. Определить реакции опор балки, если известно
F = 20 кН, М =10 кН м, q = 1 кН/м (рис. 1).
Рис. 1 — Схема задачи
Решение:
1. Изображаем балку вместе с нагрузками.
2. Выбираем расположение координатных осей, совместив ось Х с балкой, а ось У направив перпендикулярно оси Х.
3 . Производим необходимые преобразования заданных активных сил: силу, накопленную к оси балки под углом α, заменяем двумя взаимно перпендикулярными составляющими
Fх = F сos 30 = 20 0,866 = 17, 32 кН
Fу = F сos 60 = 20 0,5 = 10 кН,
а равномерно распределенную нагрузку — её равнодействующей
Q = q CD = 1 2 = 2 кН,
Равнодействующая Q приложена в середине участка CD, в точке К (рис. 2).
Рис. 2 — Схема преобразования заданных активных сил
4.Освобождаем балку от опор, заменив их опорными реакциями, направленными вдоль выбранных осей координат (рис 3).
Рис. 3 — Схема реакций балки
5.Составляем уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор и определяем неизвестные реакции опор.
å МА = 0; Fу АВ + M + Q AK — RDy AD = 0 (1)
å МD = 0; RAy AD — Fу ВD + M — Q KD = 0 (2)
å Fiх = 0; RAх — Fх = 0 (3)
6. Определяем реакции опор балок RAy, RDy и RAх решая уравнения.
Из уравнения ( 1 ) получаем
RDy = Fу АВ + M + Q AK / AD = 10 1 + 10 + 2 3 / 4 = 6,5 кНИз уравнения ( 2 ) получаем
RAy = Fу ВD — M + Q KD / AD =10 3 — 10 + 2 / 4 = 5,5 кН
Из уравнения ( 3 ) получаем
RAх = Fх = F сos 30 = 20 0,866 = 17, 32 кН
7. Проверяем правильность найденных результатов:
å Fi y = 0; RAy — Fу — Q + RDy = 5,5 — 10 — 2 + 6,5 = 0
Условие равновесия å Fi y = 0 выполняется, следовательно, реакции опор найдены верно.
Пример 2. Определить реакции заделки, если известно
F = 20 кН, М =10 кН м, q
Рис. 4 — Схема задачи
Решение:
1. Изображаем балку вместе с нагрузками.
2. Выбираем расположение координатных осей, совместив ось Х с балкой, а ось У направив перпендикулярно оси Х.
3. Производим необходимые преобразования заданных активных сил: силу, накопленную к оси балки под углом α, заменяем двумя взаимно перпендикулярными составляющими
Fх = F сos 30 = 20 0,866 = 17, 32 кН
Fу = F сos 60 = 20 0,5 = 10 кН,
а равномерно распределенную нагрузку — её равнодействующей
Q = q CD = 1 2 = 2 кН,
Равнодействующая Q приложена в середине участка CD, в точке К (рис. 5). 
Рис. 5 — Схема преобразования заданных активных сил
4.Освобождаем балку от заделки, заменив её опорными реакциями, направленными вдоль выбранных осей координат и реактивным моментом (моментом заделки, М3)(рис 6).
Рис. 6 — Схема реакций балки
5.Составляем уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор и определяем неизвестные реакции опор.
å МА = 0; M3 + Fу АВ + M + Q AK = 0 (1)
å МВ = 0; M
å Fiх = 0; RAх — Fх = 0 (3)
6. Определяем реакции опор балки RAх , RAy и момента заделки М3решая уравнения.
Из уравнения ( 1 ) получаем
M3 = — Fу АВ — M — Q AK = — 10 1 — 10 — 2 3 = — 26 кН м
Из уравнения ( 2 ) получаем
RAy = — Q ВK — M — M3 / AВ = — 2 2 — 10 -(-26) / 1 = 12 кН
Из уравнения ( 3 ) получаем
RAх = Fх = F сos 30 = 20 0,866 = 17, 32 кН
7. Проверяем правильность найденных результатов:
å Fi y = 0; RAy — F у — Q = 12 — 10 — 2 = 0
Условие равновесия å Fi y = 0 выполняется, следовательно, реакции опоры найдены верно.
Задача 1. Определить реакции опор двухопорной балки (рисунок 7). Данные своего варианта взять из таблицы 1
Таблица 1 — Исходные данные
Номер схемы на рисунке 7
F
q
M
1
2
3
4
5
6
7
8
9
10
Варианты
кH
кH/м
кHм
1
3
4
5
6
7
8
9
10
20
2
28
11
12
13
14
15
16
17
18
19
20
30
4
8
21
22
23
24
25
26
27
28
29
30
40
2
24Рис. 7 — Схема задачи
Задача 2. Определить реакции заделки (рисунок 8). Данные своего варианта взять из таблицы 1
Таблица 1 — Исходные данные
Номер схемы на рисунке 8
F
q
M
1
2
3
4
5
6
7
8
9
10
Варианты
кH
кH/м
кHм
1
2
3
4
5
6
7
8
9
10
16
2
38
11
12
13
14
15
16
17
18
19
20
22
2
12
21
22
23
24
25
26
27
28
29
30
34
2
14










Рис. 8 — Схема задачи
Задача 3. Определить реакции опор балки (рисунок 9).
Рис. 9 — Схема задачи
infourok.ru
Определить опорные реакции балки на двух опорах решение задач
В треугольнике ABC проведены медиана BM и высота BH. Известно, что AC = 59 и BC = BM. Найдите AH., Геометрия, 5 — 9 классы.
Определение реакций опор балки – решение задачи
Порядок решения задач на определение реакций опор балок
- Выбираем систему координат. Можно ось x направить вдоль балки, ось y – вертикально вверх. Ось z будет направлена перпендикулярно плоскости рисунка, на нас. Центр системы координат можно выбрать в одной из точек опор балки. Отбрасываем опоры и заменяем их силами реакций. Если есть распределенная нагрузка, то заменяем ее равнодействующей силой. Величина этой силы равна площади эпюры. Точка приложения силы находится в центре тяжести эпюры. Так если нагрузка q равномерно распределена на отрезке AB, то ее равнодействующая имеет величину Q = q· | AB | и приложена посередине отрезка AB. Составляем уравнения равновесия для действующих сил. В общем случае они имеют вид:
Спроектируем это векторное уравнение на оси координат. Тогда сумма проекций сил на каждую из осей координат равна нулю:
Находим проекции сил на оси координат и составляем уравнения (1). Для плоской системы сил, последнее уравнение, с проекциями на ось z, не используется. Составляем уравнения равновесия для моментов сил. Сумма моментов сил относительно произвольной оси A′A′′ равна нулю:
Чтобы составить это уравнение, мы должны выбрать ось, относительно которой вычисляются моменты. Ось лучше выбрать так, чтобы сделать вычисления более простыми. Чаще всего оси выбирают так, чтобы они проходили через точки опор балки, перпендикулярно плоскости рисунка. Решаем уравнения и получаем значения реакций опор. Делаем проверку результата. В качестве проверки можно выбрать какую-нибудь ось, перпендикулярную плоскости рисунка, и относительно нее подсчитать сумму моментов сил, действующих на балку, включая найденные реакции опор. Сумма моментов должна равняться нулю.
Пример решения задачи на определение реакций опор балки
Условие задачи
Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и В, вызываемые указанными нагрузками.
P = 20,2 Н ; G = 22,6 Н ; q = 2 Н/м ; M = 42,8 Н·м ; a = 1,3 м ; b = 3,9 м ; α = 45° ;
Решение задачи
Проводим оси x и y системы координат. Начало системы координат поместим в точку A. Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас. На рисунке она не указана.
Отбрасываем опоры и заменяем их силами реакций.
В шарнире A, разложим силу реакции на составляющие и вдоль осей координат.
Реакция, в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.
Заменим равномерно распределенную нагрузку q равнодействующей. Абсолютное значение равнодействующей равно площади эпюры:
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD :
AC = CD = b/2 = 1,95 м.
Уравнения равновесия для сил
Определяем проекции сил на оси координат.
Разложим силу на составляющие вдоль координатных осей:
Абсолютные значения составляющих:
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
Сумма проекций всех сил на ось y равна нулю:
Уравнения равновесия для моментов
Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и. Чтобы их определить, нам нужно составить еще одно уравнение.
Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A, перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.
Находим моменты сил относительно выбранной оси.
Силы, и пересекают ось. Поэтому их моменты равны нулю:
Сила перпендикулярна плечу AB. Ее момент:
Поскольку, относительно оси A, сила направлена против часовой стрелки, то ее момент положительный.
Сила перпендикулярна плечу AK. Поскольку, относительно оси A, эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
Аналогичным способом находим моменты остальных сил:
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
Решение уравнений равновесия
Итак, для трех неизвестных величин, мы получили три уравнения:
Решаем эти уравнения. Вычисляем расстояния.
Из уравнения (П1) находим:
Из уравнения (П3) находим:
Из уравнения (П2) имеем:
Абсолютное значение реакции опоры в точке A :
Проверка правильности решения
Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.
Возьмем ось, проходящую через точку E. Вычисляем сумму моментов сил относительно этой оси:
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н. Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм. Мы получили значение -0,03 Нм. Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.
Второй способ решения
Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.
Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
Вычисляем моменты сил относительно оси B.
Сумма моментов сил относительно оси B равна нулю:
Итак, вторым способом, мы также имеем три уравнения:
Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее. Находим силу из уравнения (П4):
Значение реакции совпало со значением, полученным первым способом из уравнения (П2).
Автор: Олег Одинцов. Опубликовано: 14-10-2017
Определить опорные реакции балки на двух опорах решение задач
Определение реакций опор балки – решение задачи
Порядок решения задач на определение реакций опор балок
- Выбираем систему координат. Можно ось x направить вдоль балки, ось y – вертикально вверх. Ось z будет направлена перпендикулярно плоскости рисунка, на нас. Центр системы координат можно выбрать в одной из точек опор балки. Отбрасываем опоры и заменяем их силами реакций. Если есть распределенная нагрузка, то заменяем ее равнодействующей силой. Величина этой силы равна площади эпюры. Точка приложения силы находится в центре тяжести эпюры. Так если нагрузка q равномерно распределена на отрезке AB, то ее равнодействующая имеет величину Q = q· | AB | и приложена посередине отрезка AB. Составляем уравнения равновесия для действующих сил. В общем случае они имеют вид:
Спроектируем это векторное уравнение на оси координат. Тогда сумма проекций сил на каждую из осей координат равна нулю:
Находим проекции сил на оси координат и составляем уравнения (1). Для плоской системы сил, последнее уравнение, с проекциями на ось z, не используется. Составляем уравнения равновесия для моментов сил. Сумма моментов сил относительно произвольной оси A′A′′ равна нулю:
Чтобы составить это уравнение, мы должны выбрать ось, относительно которой вычисляются моменты. Ось лучше выбрать так, чтобы сделать вычисления более простыми. Чаще всего оси выбирают так, чтобы они проходили через точки опор балки, перпендикулярно плоскости рисунка. Решаем уравнения и получаем значения реакций опор. Делаем проверку результата. В качестве проверки можно выбрать какую-нибудь ось, перпендикулярную плоскости рисунка, и относительно нее подсчитать сумму моментов сил, действующих на балку, включая найденные реакции опор. Сумма моментов должна равняться нулю.
Пример решения задачи на определение реакций опор балки
Условие задачи
Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и В, вызываемые указанными нагрузками.
P = 20,2 Н ; G = 22,6 Н ; q = 2 Н/м ; M = 42,8 Н·м ; a = 1,3 м ; b = 3,9 м ; α = 45° ;
Решение задачи
Проводим оси x и y системы координат. Начало системы координат поместим в точку A. Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас. На рисунке она не указана.
Отбрасываем опоры и заменяем их силами реакций.
В шарнире A, разложим силу реакции на составляющие и вдоль осей координат.
Реакция, в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.
Заменим равномерно распределенную нагрузку q равнодействующей. Абсолютное значение равнодействующей равно площади эпюры:
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD :
AC = CD = b/2 = 1,95 м.
Уравнения равновесия для сил
Определяем проекции сил на оси координат.
Разложим силу на составляющие вдоль координатных осей:
Абсолютные значения составляющих:
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
Сумма проекций всех сил на ось y равна нулю:
Уравнения равновесия для моментов
Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и. Чтобы их определить, нам нужно составить еще одно уравнение.
Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A, перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.
Находим моменты сил относительно выбранной оси.
Силы, и пересекают ось. Поэтому их моменты равны нулю:
Сила перпендикулярна плечу AB. Ее момент:
Поскольку, относительно оси A, сила направлена против часовой стрелки, то ее момент положительный.
Сила перпендикулярна плечу AK. Поскольку, относительно оси A, эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
Аналогичным способом находим моменты остальных сил:
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
Решение уравнений равновесия
Итак, для трех неизвестных величин, мы получили три уравнения:
Решаем эти уравнения. Вычисляем расстояния.
Из уравнения (П1) находим:
Из уравнения (П3) находим:
Из уравнения (П2) имеем:
Абсолютное значение реакции опоры в точке A :
Проверка правильности решения
Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.
Возьмем ось, проходящую через точку E. Вычисляем сумму моментов сил относительно этой оси:
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н. Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм. Мы получили значение -0,03 Нм. Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.
Второй способ решения
Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.
Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
Вычисляем моменты сил относительно оси B.
Сумма моментов сил относительно оси B равна нулю:
Итак, вторым способом, мы также имеем три уравнения:
Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее. Находим силу из уравнения (П4):
Значение реакции совпало со значением, полученным первым способом из уравнения (П2).
Автор: Олег Одинцов. Опубликовано: 14-10-2017
Определить опорные реакции балки на двух опорах решение задач
Пример определения опорных реакций двухопорной балки
Условие задачи
Для заданной двухопорной балки с консольной частью, нагруженной комплексом нагрузок: силой F, моментом m и распределенной нагрузкой q, определить величину и направление опорных реакций.
Длина пролета балки 3м. Длина консольной части – 1,5м.
Пример решения
Рекомендуем посмотреть наш видеоурок по расчету опорных реакций балки:
Для решения задачи, обозначим характерные точки (сечения) балки (точки A, B, C и D) и определим положение системы координат y-z, выбрав ее начало например в т. A (рис.2)
Обе опоры балки являются шарнирными, поэтому в каждой из них будет возникать только сила, обозначим их соответственно RA и RC
Так как все заданные нагрузки раположены исключительно в вертикальной плоскости (плоский поперечный изгиб) и не дают проекций на ось z, то опорные реакции будут тоже только вертикальными.
Вообще говоря, реакции в опорах являются такими силами, которые необходимы для удержания балки с приложенными к ней нагрузками, в статичном (неподвижном) состоянии. В данном случае эти силы не позволяют ей вращаться и перемещаться в вертикальной плоскости.
Данная балка является статически определимой, т. к. уравнений равновесия достаточно для определения неизвестных усилий в опорах балки.
Для составления уравнений статики, опорные реакции RA и RC предварительно направляются произвольно, например, вверх (рис.3).
Для определения двух неизвестных реакций потребуется два уравнения.
Балка не перемещается по вертикали, т. е. сумма проекций всех сил на ось y равна нулю:
Как записывается момент распределенной нагрузки показано здесь.
Сила приложенная в точке относительно которой рассматривается сумма моментов в уравнении не участвует, так как плечо момента для нее равно нулю.
Здесь сумму моментов лучше записывать относительно точки расположенной на опоре (например, A), т. к. в этом случае соответствующая реакция RA в уравнении не участвует.
Из выражения (2) определяем RC:
И подставив его в выражение (1) находим RA:
Направление и величина реакций, как правило, необходимы для дальнейших расчетов балки на прочность и жесткость, поэтому во избежание возможных ошибок рекомендуется выполнять проверку найденных значений.

poiskvstavropole.ru
2.3. Балки и опоры. Реакции и их вычисление
Балками будем называть прямолинейные стержни, работающие на изгиб. В сопротивлении материалов термин «балка» значительно шире, чем в обычном употреблении этого слова: с точки зрения расчета на прочность, жесткость и устойчивость балкой является не только строительная балка, но также и вал, болт, ось железнодорожного вагона, зуб шестерни и т. д.
Вначале ограничимся построением эпюр для простейшего случая изгиба балок, при котором все заданные нагрузки лежат в одной плоскости, называемой силовой (на рис. 4, а — плоскость П), причем эта плоскость совпадает с одной из главных плоскостей балки. Такой случай будем называть плоским изгибом.
На расчетной схеме балку принято заменять ее осью (рис. 4, б). При этом все нагрузки, естественно, должны
Рис 4 быть приведены к оси балки и силовая плоскость будет совпадать с плоскостью чертежа.
Как правило, балки имеют опорные устройства — опоры. Для расчета же их схематизируют в виде трех основных типов опор:
а) шарнирно-подвижная
опора (рис.
5, а), в которой может возникать только
одна составляющая реакции — 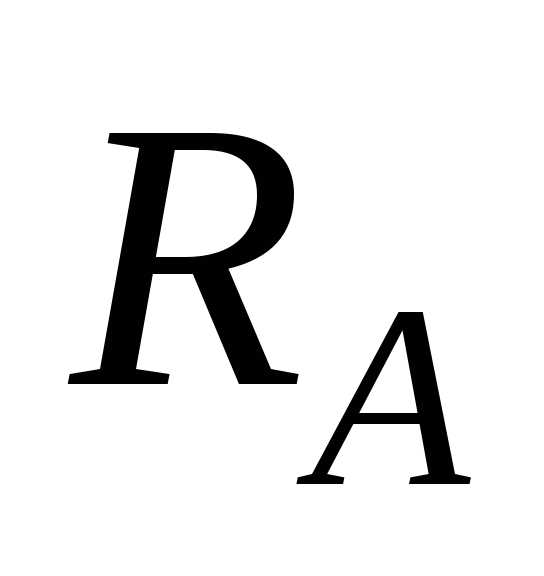 , направленная
вдоль опорного стерженька;
, направленная
вдоль опорного стерженька;
б) шарнирно-неподвижная
опора (рис.
5, б), в которой могут возникать две
составляющие — вертикальная реакция 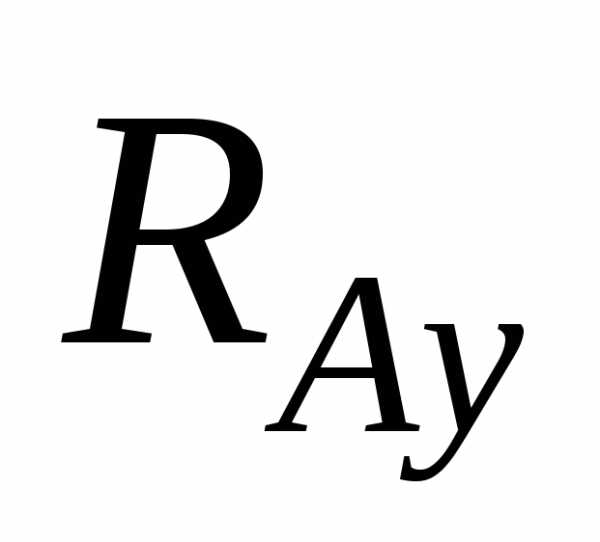 и горизонтальная
реакция
и горизонтальная
реакция 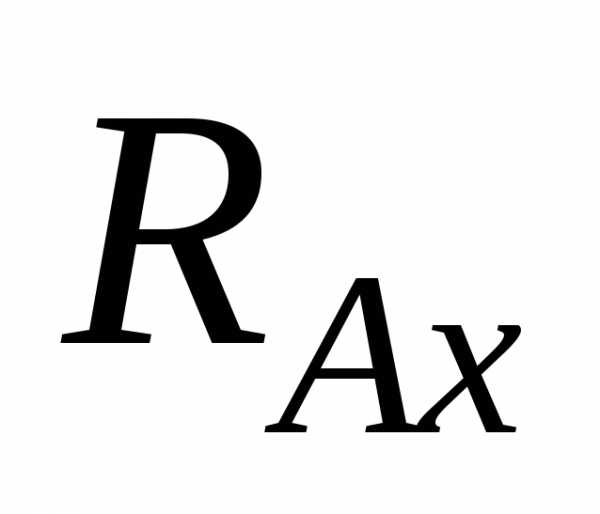
в) защемление (иначе жесткое
защемление или заделка), где
могут быть три составляющие — вертикальная 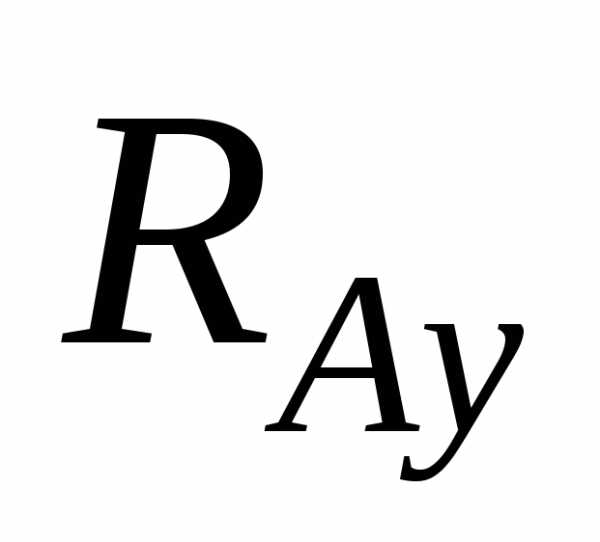 и
горизонтальная
и
горизонтальная 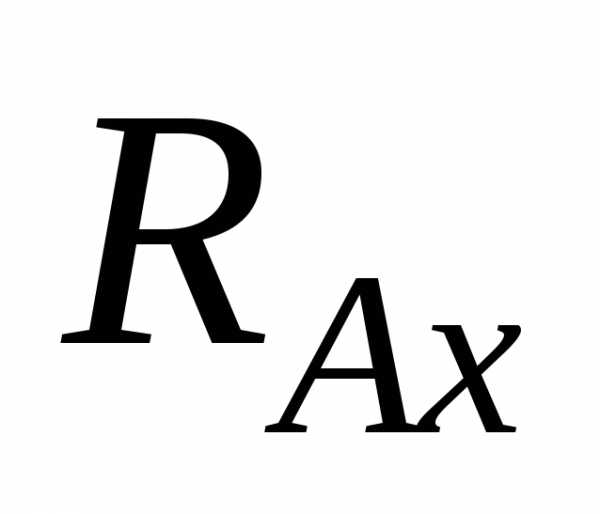 реакции
и опорный момент Ма (рис.
5, в).
реакции
и опорный момент Ма (рис.
5, в).
Рис 5
Все реакции и моменты считаются приложенными в точке А — центре тяжести опорного сечения.
Балка, показанная на рис. 6, с, называется простой, или однопролетной , или двухопорной, а расстояние l между опорами — пролетом.
Рис 6
Консолью называется балка, защемленная одним концом и не имеющая других опор (рис. 4, б), или часть балки, свешивающаяся за опоры (часть ВС на рис. 6, б; части АС и BD на рис. 6, е). Банки, имеющие свешивающиеся части, называют консольными (рис. 6, б, в).
Для плоской системы сил можно составить три уравнения статики для определения неизвестных реакций.
Поэтому балка будет статически определимой, если число неизвестных опорных реакций не превышает трех; в противном случае балка статически неопределима. Очевидно, что балки, изображенные на рис. 4 и 6, статически определимы.
Рис 7
Балка, изображенная на рис. 7, а, называется неразрезной и является статически неопределимой, поскольку имеет пять неизвестных опорных реакций: три в опоре А и по одной в опорах В и С.
Поставив в сечениях балки шарниры, например в точках D и Е (рис. 7, б), получим статически определимую шарнирную балку, ибо каждый такой промежуточный шарнир к трем основным уравнениям статики прибавляет одно дополнительное уравнение: сумма моментов относительно центра шарнира от всех сил, расположенных по одну сторону от него, равна нулю.
Построение эпюр для статически неопределимых балок требует умения вычислять деформации, а поэтому ограничимся пока исключительно статически определимыми балками.
Способы определения опорных реакций изучают в курсе теоретической механики. Поэтому здесь остановимся только на некоторых практических вопросах. Для этого рассмотрим простую балку (рис. 6, а).
1. Опоры обычно обозначают буквами А и В. Три неизвестные реакции находят из следующих уравнений равновесия:
а)
сумма проекций всех сил на ось балки
равна нулю: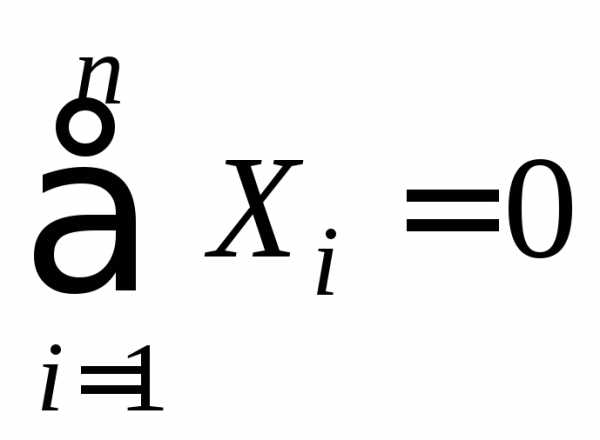 откуда находят
откуда находят 
б)
сумма моментов всех сил относительно
опорного шарнира А равна
нулю: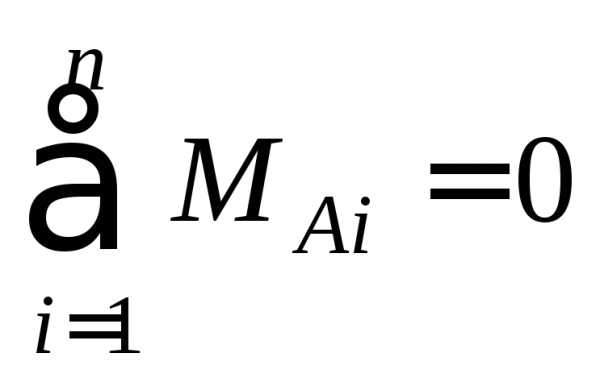 откуда находят
откуда находят 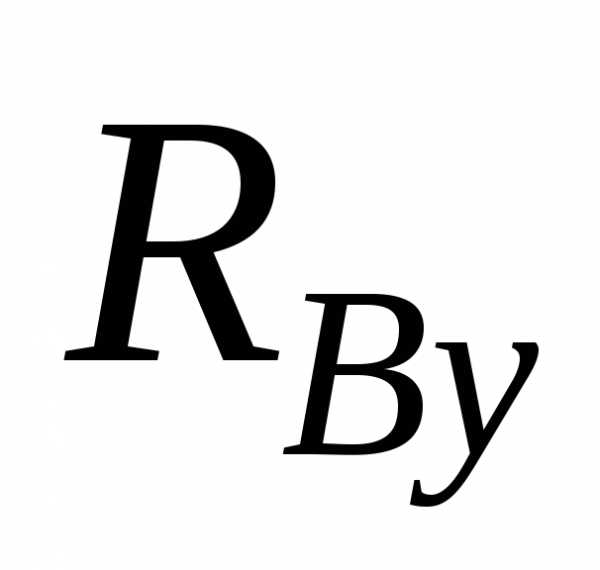 .
.
в)
сумма моментов всех сил относительно
опорного шарнира В равна
нулю: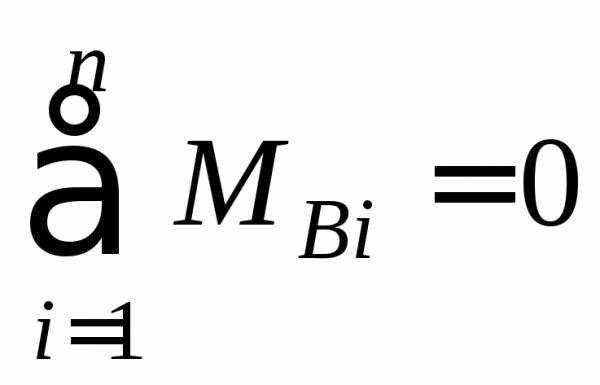
откуда
находят  .
.
2. Для контроля можно использовать или условие равенства нулю суммы проекций на вертикаль:
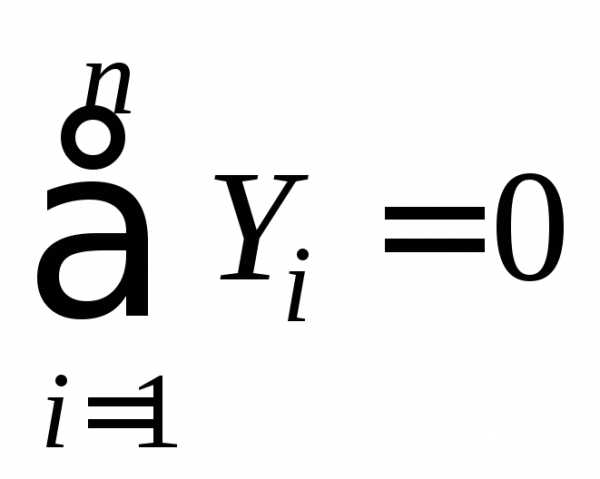
или условие равенства нулю суммы моментов относительно какой-либо точки С, отличной от А и В, т. е.
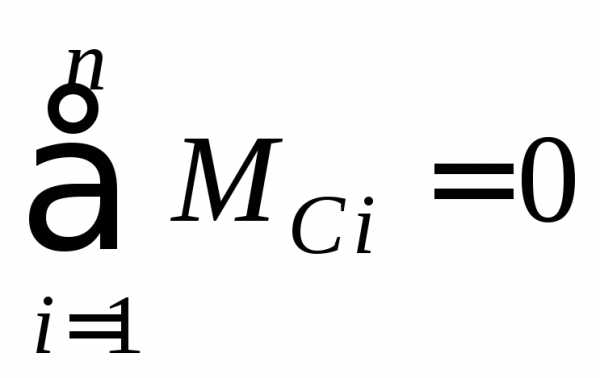 У
У
Условием 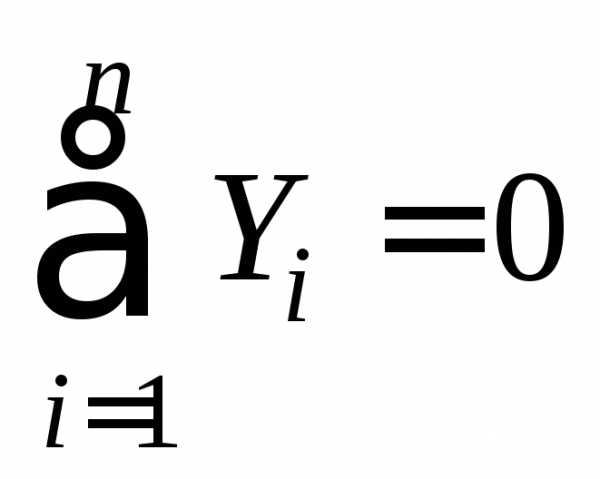 пользоваться
проще, но оно дает надежную проверку
только в тех случаях, когда к балке не
приложены сосредоточенные моменты.
пользоваться
проще, но оно дает надежную проверку
только в тех случаях, когда к балке не
приложены сосредоточенные моменты.
3. Перед составлением уравнений равновесия нужно выбрать (вообще говоря, произвольно) направления реакций и изобразить их на рисунке. Если в результате вычислений какая-либо реакция получается отрицательной, нужно изменить на рисунке ее направление на обратное и в дальнейшем считать эту реакцию положительной,
5. Если на балку действует распределенная нагрузка, то для определения реакций ее заменяют равнодействующей, которая равна площади эпюры нагрузки и приложена в центре тяжести этой эпюры.
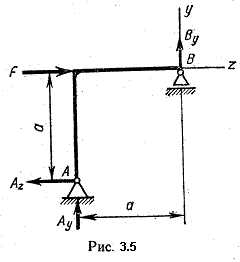
Пример 5. Вычислить опорные реакции для балки, показанной на рис. 8.
Прежде всего находим равнодействующие Р1 и Р2 нагрузок, распределенных на участках АС н СВ:
; .
Сила Р1 приложена в центре тяжести прямоугольника, а Р2 — в центре тяжести треугольника. Находим реакции:
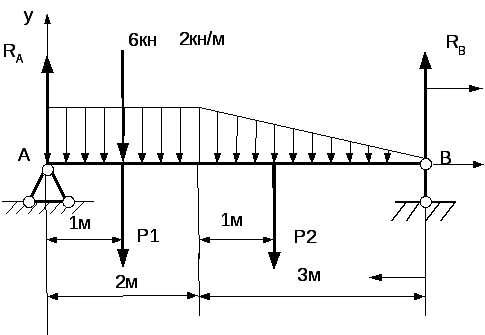
Рис 8
Проверка:
studfiles.net
Расчётные схемы балок и определение реакции их опор
Задание
Задана горизонтальная двух опорная балка. Балка нагружена активными силами: сосредоточенной F, распределенной силой интенсивностью q и парой сил с моментом М (табл.2.1 и рис 2.6).
Цель работы – построить расчётную схему балки, составить уравнения равновесия балки, определить реакции ее опор и выявить наиболее нагруженную опору.
Теоретическое обоснование
Во многих машинах и сооружениях встречаются конструктивные элементы, предназначенные преимущественно для восприятия нагрузок, направленных перпендикулярно их оси. Расчетные схемы таких элементов (валы, части металлоконструкции и др.) могут быть представлены балкой. Балки имеют опорные устройства для передачи усилий и сопряжения с другими элементами.
Основными типами опор балок являются шарнирно – подвижная, шарнирно – неподвижная опоры и жесткая заделка.
Шарнирно – подвижная опора (рис.2.1,а) допускает поворот балки вокруг оси шарнира и линейное перемещение на незначительное расстояние параллельно опорной плоскости. Точкой приложения опорной реакции является центр шарнира. Направление реакции R – перпендикуляр к опорной поверхности.
Шарнирно – неподвижная опора (рис.2.1,6) допускает только поворот балки вокруг оси шарнира. Точкой приложения являются также центр шарнира. Направления реакции здесь неизвестно, оно зависит от нагрузки, приложенной к балке. Поэтому для такой опоры определяются две неизвестные – взаимно перпендикулярные составляющие Rx и Ry опорной реакции.
Жесткая заделка (защемление) (рис.2.1,в) не допускает ни линейных перемещений, ни поворота. Неизвестными в данном случае являются не только величина, но и её точка приложения. Таким образом, для определения опорной реакции необходимо найти три неизвестные: составляющие Rx и Ry по осям координат и реактивный момент MR относительно центра тяжести опорного сечения балки.
А б в
Рис.2.1
Равновесие балки под действием любой системы заданных сил, расположенных в одной плоскости, может быть обеспечено одной жёсткой заделкой или двумя опорами – подвижной и неподвижной. Балки называются соответственно консольными (рис.2.2,а) или двух опорными (рис.2.2,б)
А б
Рис.2.2
На балку действуют заданные силы и пары сил. Силы по способу приложения делятся на распределенные и сосредоточенные. Распределенные нагрузки задаются интенсивно q, Н/м и длиной 1, м. равномерно распределенные нагрузки условно изображаются в виде прямоугольника, в котором параллельные стрелки указывают, в какую сторону действует нагрузка (рис.2.3). В задачах статики равномерно – распределенную нагрузку можно заменять равнодействующей сосредоточенной силой Q, численно равной произведению q*1, приложенной посредине длины и направленной в сторону действия q.
Рис.2.3 Рис. 2.4
Сосредоточенные нагрузки приложены на сравнительно небольшой длине, поэтому считается, что они приложены в точке. Если сосредоточенная сила приложена под углом к балке, то для определения реакции опор удобно разложить её на две составляющие – Fx = Fcos α и Fy =F sin α (рис.2.4).
Реакции опор балки определяются из условий равновесия плоской системы произвольно расположенных сил. Для плоской системы можно составить три независимых условия равновесия:
∑Fix = 0; ∑Fiy = 0; ∑Mio = 0 или
∑Мia = 0; ∑MiB = 0; ∑MiC = 0 или } (2.1)
∑MiA = 0; ∑MiB = 0; ∑Fix = 0.
Где О, А ,В, С – центры моментов.
Рационально выбрать такие уравнения равновесия, в каждое из которых входила бы по одной неизвестной реакции.
Порядок выполнения работы
1. В соответствии с заданием изобразить балку и действующие заданные силы.
Выбрать расположение координатных осей: совместить ось х с балкой, а ось у направить перпендикулярно оси х.
1. Произвести необходимые преобразования: силу, наклоненную к оси балки под углом а, заменить двумя взаимно перпендикулярными составляющими, а равномерно распределенную нагрузку – её равнодействующей.
2. Освободить балку от опор, заменив их действие реакциями опор, направленными вдоль осей координат.
3. Составить уравнения равновесия балки, чтобы решением каждого из трёх уравнений было определение одной из неизвестных реакций опор.
4. Проверить правильность определения реакций опор по уравнению, которое не было использовано для решения задач.
5. Сделать вывод о наиболее нагруженной опоре.
6. Ответить на контрольные вопросы.
Контрольные вопросы
1.Сколько независимых уравнений равновесия можно составить для плоской системы параллельных сил?
2.Какие составляющие реакции опор балок возникают в шарнирно – подвижной, шарнирно – неподвижной опорах и жёсткой заделке?
3.Какую точку целесообразно выбрать в качестве центра момента при определении реакций опор?
4.Какая система является статически неопределимой?
Пример выполнения
1.Задание:
q = 5 H/м, F = 25 H, M = 2 H*м, α = 60°
2.Преобразование заданных сил:
Fx = F cos α = 25cos 60° = 12.500H, Fy = F sinα = 25 sin60° = 21.625H
Q = q*1 = 5*6 =30 H.
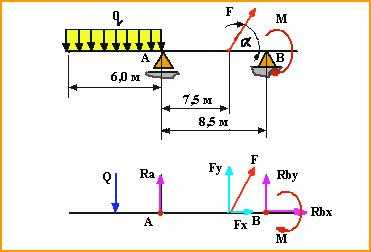 Рис.2.5
Рис.2.5
3.Составим расчётную схему (рис.2.5)
4.Уравнения равновесия и определение реакций опор:
а) ∑Mia = 0; -Q *3 – Fy*7.5+ RB* 8.5 – M = 0;
RB =
б) ∑MiB =0: — RAy*8.5 + Q *5.5 + Fy *1 – M = 0:
RAy =
в) ∑Fix=0: RAx + Fx =0: RAx= — Fx = — 12.500H.
5.Проверка:
∑Fiy = 0; RAy = Q – Fy + RB = 0; 21.724 – 30 – 21.651 + 29.927 = 0; 0 = 0
Вывод:
Наиболее нагруженной является опора В – RB =29.927 Н. Нагрузка на опору А – RA =
Литература:
Таблица 2.1
| № варианта | № схемы на рис. 2.6 | q , Н/м | F, Н | М, Н м | , град |
| 4,5 | |||||
| 2,5 | |||||
| 4,5 | |||||
| 3,5 | |||||
| 6,5 | |||||
| 1,5 | |||||
| 0,5 | |||||
Рис.2.6
Практическая работа № 3
Рекомендуемые страницы:
lektsia.com
Меню сайтаРасчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты |
Базовый курс лекций по сопромату, теория, практика, задачи.::Оглавление:: 3. Изгиб. Определение напряжений. 3.3. Определение опорных реакций. Рассмотрим несколько примеров. Пример 3.1. Определить опорные реакции консольной балки (рис. 3.3). Решение. Реакцию заделки представляем в виде двух сил Az и Ay, направленных, как указано на чертеже, и реактивного момента MA. Составляем уравнение равновесия балки. 1. Приравняем нулю сумму проекций на ось z всех сил, действующих на балку. Получаем Az = 0. При отсутствии горизонтальной нагрузки горизонтальная составляющая реакции равна нулю. 2. То же, на ось y: сумма сил равна нулю. Равномерно распределенную нагрузку q заменяем равнодействующей qaз, приложенной посредине участка aз: Ay — F1 — qaз = 0, откуда Ay = F1 + qaз. Вертикальная составляющая реакции в консольной балке равна сумме сил, приложенных к балке. 3. Составляем третье уравнение равновесия. Приравняем нулю сумму моментов всех сил относительно какой-нибудь точки, например относительно точки А: откуда Знак минус показывает, что принятое вначале направление реактивного момента следует изменить на обратное. Итак, реактивный момент в заделке равен сумме моментов внешних сил относительно заделки. Пример 3.2. Определить опорные реакции двухопорной балки (рис. 3.4). Такие балки обычно называют простыми. Решение. Так как горизонтальная нагрузка отсутствует, то Az = 0 Вместо второго уравнения можно было использовать условие того, что сумма сил по оси Y равна нулю, которое ы данном случае следует применить для проверки решения: Пример 3.3. Определить реакции опор балки ломаного очертания (рис. 3.5). Решение. ::Оглавление:: Полезные ресурсы по теме «Определение опорных реакций»1. Он-лайн программа (версия 2004 года), которая выдаст расписанное решение любой балки. Пример результата. 2. Он-лайн программа (версия 2008 года), которая строит 4 вида эпюр и рассчитывает реакции для любых балок (даже для статически неопределимых). |
СообществоВходРешение задачРасчет редукторовДля Android (рекомендую)NEW Mobile Beam 2.0 Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME |
www.sopromat.org
Определение опорных реакций. Решение задач. |
Балки предназначены для восприятия поперечных нагрузок. По способу приложения нагрузки делятся на сосредоточенные (действуют на точку) и распределенные (действуют на значительную площадь или длину).
q — интенсивность нагрузки, кн/м
G = q L – равнодействующая распределенной нагрузки
Балки имеют опорные устройства для сопряжения их с другими элементами и передачи на них усилий. Применяются следующие виды опор:
· Шарнирно-подвижная
Эта опора допускает поворот вокруг оси и линейное перемещение параллельно опорной плоскости. Реакция направлена перпендикулярно опорной поверхности.
· Шарнирно-неподвижная
Эта опора допускает поворот вокруг оси, но не допускает никаких линейных перемещений. Направление и значение опорной реакции неизвестно, поэтому заменяется двумя составляющими RAу и RAх вдоль осей координат.
· Жесткая заделка (защемление)
Опора не допускает перемещений и поворотов. Неизвестны не только направление и значение опорной реакции, но и точка её приложения. Поэтому заделку заменяют двумя составляющими RAу , RAх и моментом МА. Для определения этих неизвестных удобно использовать систему уравнений.
∑ Fkx = 0
∑ Fkу = 0
∑ mА(Fк)= 0
Для контроля правильности решения используется дополнительное уравнение моментов относительно любой точки на консольной балке, например точка В ∑ mВ(Fк)= 0
Пример. Определить опорные реакции жесткой заделки консольной балки длиной 8 метров, на конце которой подвешен груз Р = 1 кн. Сила тяжести балки G = 0,4 кн приложена посередине балки.
Освобождаем балку от связей, т.е отбрасываем заделку и заменяем её действие реакциями . Выбираем координатные оси и составляем уравнения равновесия.
∑ Fkx = 0 RAх = 0
∑ Fkу = 0 RAу – G – P = 0
∑ mА(Fк)= 0 — MA + G L / 2 + P L = 0
Решая уравнения, получим RAу = G + P = 0,4 + 1 = 1,4 кн
MA = G L / 2 + P L = 0,4 . 4 + 1. 8 = 9,6 кн . м
Проверяем полученные значения реакций:
∑ mв(Fк)= 0 — MA + RAуL — G L / 2 = 0
— 9,6 + 1,4. 8 – 0,4. 4 = 0
— 11,2 + 11,2 = 0 реакции найдены верно.
Для балок расположенных на двух шарнирных опорах удобнее определять опорные реакции по 2 системе уравнений, поскольку момент силы на опоре равен нулю и в уравнении остается одна неизвестная сила.
∑ Fkх = 0
∑ mА(Fк)= 0
∑ mВ(Fk)= 0
Для контроля правильности решения используется дополнительное уравнение ∑ Fkу = 0
Задача.
1) Освобождаем балку от опор, а их действие заменяем опорными реакциями;
2) Заменяем распределенную нагрузку на равнодействующую G = q . L;
3) Выбираем координатные оси;
4) Составляем уравнения равновесия.
∑ Fkx = 0 RВх = 0
∑ mА(Fк)= 0 G .L/2 + m — RВу (L + B)= 0
RВу = [G .L/2 + m]/(L + B) = [5. 6/2 + 10](6+6) = 2,08 кн
∑ mВ(Fk)= 0 RAу.(L + B) — Q .(L/2 + B) + m = 0
RAу = [Q .(L/2 + B) — m] / (L + B) =[5 .(6/2 + 6) — 10] / (6 + 6) = 2,92 кн
Если испытываете трудности в написании контрольной работы по теоретической механике, оформите заявку и Вы узнаете сроки и стоимость работы.
Заказать работу
Тип работы
Дипломная работаКурсовая работаКонтрольная работаРефератОтчет по практикеЭссеАспирантский рефератАннотацияАвторефератАттестационная работаБакалаврская работаБизнес-планБилеты к экзаменамВКР (выпускная квалификационная работа)Вычитка и рецензирование работДипломная работа (для колледжа)Дипломная работа МВАДиссертацияДиссертация докторскаяДиссертация кандидатскаяДиссертация магистерскаяДистанционный экзамен, online тестДневник по практикеДокладДомашняя работаИсправление и доработка готовой работыКейсКонспектКопирайтингЛабораторная работаЛитературный обзорМаркетинговое исследованиеМонографияНабор текста (компьютерный)Научная статьяНаучный трудНИР (научно-исследовательская работа)Online помощьОтветы на вопросыОтзыв на дипломПереводПлан к дипломной работеПовышение уникальностиПрактическая работаПрактическая работа МВА (задания, кейсы)Презентации (PPT, PPS, Prezi)Проверка выполненной работыПроверочная работаРаздаточный материал (речь, аннотация, презентация)РГР (расчетно-графическая работа)Статья, рецензия, аннотацияРечьРешение задачРешение контрольных работСамостоятельная работаСеместровая работаСочинениеСтатьяСтатья ВАКТворческая работаТезисный планТехнико-экономическое обоснованиеХарактеристика по практикеЧаст
moscowstud.com
Как найти опорные реакции. Опоры и опорные реакции. Определение опорных реакций балок
Рассмотренный в § 2.7 свободный брус был нагружен заданными нагрузками (силами и моментами), находящимися в равновесии (см. рис. 3.7). Обычно заданные нагрузки не бывают взаимно уравновешенными; неподвижность конструкции под действием этих нагрузок обеспечивается благодаря наличию опор, соединяющих ее с основанием. В опорах возникают реакции, которые вместе с заданными нагрузками представляют уравновешенную систему внешних сил, действующих на конструкцию.
Одной из областей, где твердая механика, как обсуждалось в этой книге, является наиболее эффективной, является загрузка пучка. Нагрузки на балке могут представлять собой точечные нагрузки, распределенные нагрузки или различные нагрузки. Могут также быть точечные моменты на балке. Сам луч поддерживается в одной или нескольких точках. Условия поддержки зависят от типа используемой поддержки. Если носитель представляет собой ролик, он может иметь только реакцию, перпендикулярную движению ролика. Если поддержка является штырем, она не может нести момент.
Как известно из курса теоретической механики, любое тело обладает в плоскости тремя степенями свободы. Поэтому для обеспечения геометрической неизменяемости системы (бруса) необходимо наложить на нее (в плоскости) три связи.
Рассмотрим различные типы опор плоских систем.
1. Защемление, или заделка (рис. 4.7, а). Защемленный (или заделанный) конец бруса не может ни смещаться поступательно, ни поворачиваться. Следовательно, число степеней свободы бруса с защемленным концом равно нулю. В опоре могут возникать: вертикальная реакция (сила R — рис. 4.7, а), препятствующая вертикальному смещению конца бруса; горизонтальная реакция (сила Н), исключающая возможность его горизонтального смещения и реактивный момент препятствующий повороту. Таким образом, закрепление бруса с помощью заделки накладывает на него три связи и обеспечивает его неподвижность.
Определение опорных реакций балок
Если поддержка фиксирована, то она может иметь реакцию в любом направлении и поддерживать момент. Он имеет закрепленный контакт на одном конце и контакт качения на другом конце. На приведенном выше рисунке показан идеальный момент, действующий в центре луча. Идеальный момент — это тот, который не связан с силой.
Общий метод анализа проблем пучка заключается в том, чтобы найти нагрузки, реакции и моменты, и придумать значения для нагрузок и моментов в каждом разделе. Это, вообще говоря, будет кусочной функцией расстояния вдоль луча. Для нагрузок мы устанавливаем оси, и это решает знак силы. Для моментов мы устанавливаем, что момент по часовой стрелке положителен.
2. Шарнирно неподвижная опора (рис. 4.7, б). Поперечное сечение бруса, проходящее через шарнирно неподвижную опору, не может смещаться поступательно. В опоре возникает реактивная сила, проходящая через центр шарнира. Ее составляющими являются вертикальная сила R, препятствующая вертикальному смещению, и горизонтальная сила Н, исключающая горизонтальное смещение закрепленного сечения бруса. Опора не препятствует повороту бруса относительно центра шарнира, и, следовательно, брус, закрепленный при помощи одной такой опоры, имеет одну степень свободы. Закрепление бруса с помощью шарнирно неподвижной опоры, накладывает на него две связи.
Рассмотрим случай описанного выше пучка. На приведенном выше рисунке показана сдвиговая диаграмма для этой проблемы. Обратите внимание, что положительные и отрицательные направления являются условностями, но важно выбрать одно направление для положительного сдвига и придерживаться его. Как видно, значение сдвига изменяется в точке приложения нагрузки.
На приведенном выше рисунке показана диаграмма момента для луча. В последующих главах мы увидим, что напряжения и деформации из-за моментов являются наиболее важными для лучей. Кроме того, найдите момент в этот момент. Вышеуказанный пучок показывает загрузку двумя отдельными точечными нагрузками.
3. Шарнирно подвижная опора (рис. 4.7, в). Поперечное сечение бруса, проходящее через шарнирно подвижную опору, может смещаться параллельно опорной плоскости и поворачиваться, но оно не может смещаться перпендикулярно к опорной плоскости. В опоре возникает только одна реакция в виде силы R, перпендикулярной к опорной плоскости. Закрепление бруса с помощью такой опоры накладывает на него одну связь.
Исчисление для решения проблем с лучами
Найдите сдвиг и момент в каждой точке вдоль луча с точечной нагрузкой и моментом, действующим в двух разных точках. Как может произойти точечный момент на практике? Методы исчисления могут использоваться для работы с функциями непрерывной нагрузки. Однако эти методы могут быть расширены до точечных нагрузок и моментов с помощью дельта-функции Дирака.
Такие нагрузки используются для моделирования собственного веса пучка, где он действует равномерно по всей его длине. Это также можно использовать для загрузки, скажем, моста из-за всех транспортных средств на нем. Отдельные точечные нагрузки, действующие через шины, могут быть смоделированы как непрерывная нагрузка, если количество транспортных средств велико. Применяя равновесие сил для этого сегмента, имеем. Применяя моментное равновесие к одному и тому же отрезку.
Рассмотренные типы опор принято также изображать с помощью стерженьков.
Шарнирно подвижную опору изображают в виде стерженька, имеющего по концам шарниры (рис. 5.7, а). Нижний шарнир неподвижен, а верхний может смещаться лишь по прямой линии, перпендикулярной к оси стерженька.
Вышеупомянутые дифференциальные уравнения могут быть интегрированы с соответствующими граничными условиями для получения сдвига и момента в каждой точке. Мы имеем общее соотношение для сдвига. Сдвиг при происхождении — это просто реакция в этот момент.
Легко видеть, что момент в нуле равен нулю. Вышеуказанное хорошо работает для непрерывных функций с плавной нагрузкой. Но в реальных ситуациях нам приходится иметь дело с точечными нагрузками и моментом. Теперь ранее сформулированные уравнения могут быть использованы по правилам для функции Дирака. Сама функция определяется как.
Это соответствует тем условиям закрепления, которые обеспечивает шарнирно подвижная опора (см. рис. 4.7, в). Опорная реакция действует только вдоль оси стерженька. Собственные деформации его при расчетах не учитываются, т. е. стерженек считается бесконечно жестким.
Шарнирно неподвижную опору изображают с помощью двух стерженьков с шарнирами по концам (рис. 5.7, б). Верхний шарнир является общим для обоих стерженьков. Направления стерженьков могут быть произвольными. Они, однако, не должны быть расположены на одной прямой.
Из определения Дирака мы имеем. Сдвиг в любой точке задается формулой. Момент на одном конце равен нулю. Момент в любой момент дается. Применяя определение функции Дирака, имеем: сдвиг. Обратите внимание, что приведенное выше является частным случаем общего метода, называемого преобразования Лапласа.
Найдите сдвиг и момент в указанном пучке с использованием методов Дирака. Луч, показанный выше, имеет две нагрузки, которые могут быть смоделированы, как показано. Найдите сдвиг и момент в любой точке луча. Рассмотрим луч, показанный выше, с выступом. Найдите сдвиг и момент в точках вдоль оси.
Заделку (защемление) можно изображать с помощью трех стерженьков с шарнирами по концам, как показано на рис. 5.7, в.
Число стерженьков в схематическом изображении опоры равно числу составляющих опорной реакции и числу связей, накладываемых этой опорой на конструкцию.
Для того чтобы брус не перемещался под нагрузкой, он должен быть геометрически неизменяемо (неподвижно) соединен с основанием, что в случае плоского действия сил, как уже отмечалось, достигается путем наложения на него трех внешних связей.
Учитывая нагрузки и моменты в каждом поперечном сечении, мы можем рассчитать напряжение и деформацию в каждом месте. Рассмотрим изгиб тонкого луча. Момент, действующий на пучок, вызывает деформацию, называемую изгибом. Пусть радиус соприкасающейся окружности луча равен ρ. Этот элемент подставляет угол θ в центр кривизны, так что. Это дает нам осевую деформацию в любой точке х как. Кроме того, используя закон Гука, мы имеем.
Вышеприведенное уравнение дает нам расположение нейтральной плоскости. Далее, применяя часть сохранения момента равновесных соотношений, имеем. Таким образом, мы имеем выражение для напряжения, обусловленного чистым моментом, как. Теперь легко видеть, что комбинация моментов фактически эквивалентна моменту, действующему на пучок произвольного сечения. Ранее мы видели методы расчета поперечных сил на пучке. Тепе
starer.ru