Балки эпюра – Построение эпюр при изгибе для балки

Содержание

Построение эпюр при изгибе для балки

Привет! Вы находитесь на сайте – sopromats.ru, проекте о сопромате и не только! Это новая статья из серии – «сопромат для чайников», в которой я расскажу о построении эпюр при изгибе для балки. Как обычно, буду писать просто и по делу. Здесь я не буду спамить специфическими фразами из сопромата и рассматривать сложные примеры. Будем учиться на простейшей балке. Ну что же давайте начнем учиться!

Сколько можно нарисовать эпюр при изгибе для балок?

Для простого изгиба, который будем рассматривать в этой статье, можно нарисовать всего две эпюры. Одна именуется как эпюра поперечных сил, другая зовется эпюрой изгибающих моментов. Одна показывает распределение внутренних сил внутри элемента, работающего на изгиб, другая моментов. Если хотите, можете изучить больше информации по этим силовым факторам в следующих материалах:

Как построить эпюру поперечных сил? Здесь вы можете найти полное досье на поперечную силу: кто такая, зачем нужна и как обозначается. Тут же можно почитать подробную инструкцию по построению эпюры этой величины. В статье рассказано про 3 методики расчета и построения.

Как построить эпюру изгибающих моментов? В этом материале можно узнать много всего об изгибающем моменте. Например, зачем он нужен и как определяется, как обозначается и в чем измеряется. А также подробнейшим образом изучить методики построения эпюры этой величины, 3-мя способами.

Если Вам лень читать эти статьи, то ничего. Это нормально 🙂 Просто хотел пропиарить немного эти материалы, не зря же я их писал…В этой статье, для чайников, мы, итак, научимся строить эти эпюры, но только одним методом.

Подготовительные работы

Для того, чтобы построить эпюры, первым делом вычертите расчетную схему, с указанием всех нагрузок и размеров:

После этого нужно определить реакции опор. Без них дальше никуда. Если Вы не умеет этого делать, обязательно прочтите этот урок про расчет реакций опор для чайников. Здесь же сразу приведу результат вычислений:

Расчет и построение эпюр

Для расчета эпюр сначала нужно наметить участки, на которых эпюра будет либо постоянна, либо меняться по одному закону. Опознать эти участки достаточно просто. Границами участков служат те места, где прикладываются нагрузки (сосредоточенные силы и моменты, в том числе реакции опор). Если на балку действует распределенная нагрузка, то границы – это ее начало и конец. В нашем случае, как видите, 2 участка, каждый по 2 метра:

Рассматриваем произвольное сечение первого участка, которое обзовем буквой – С. Оно будет находится на расстоянии z1 от левого торца балки. И относительного него будем записывать законы, по которым меняются поперечные силы и изгибающие моменты на этом участке:

Записываем уравнение для поперечной силы

Поперечная сила будет равняться сумме всех сосредоточенных сил, находящихся слева от сечения (или справа). Мы будем подсчитывать все, что находится слева, т.к. там меньше нагрузки. В уравнении поперечной силы, все внешние нагрузки нужно учитывать с учетом правила знаков: если сила, относительно рассматриваемого сечения, поворачивает ПО часовой стрелке, то в уравнение она пойдет с ПЛЮСОМ (и наоборот).

В рассматриваемом примере, реакция RA поворачивает ПО часовой стрелке, и уравнение получится такое:

Причем, как видно, эта зависимость справедлива для любого сечения на первом участке, тем самым поперечная сила в пределах этого участка постоянна и равна – 5 кН. Откладываем это значение на графике:

Эпюры заштриховываются перпендикулярно нулевой линии и на каждом участке проставляются знаки поперечной силы.

Записываем уравнение для изгибающего момента

Что касается изгибающего момента, то тут в уравнении нужно учесть сумму моментов, находящихся по одну сторону от сечения. Реакция RA, относительно сечения С создает момент RA·z1. Напомню, что момент – это сила, умноженная на плечо. Где плечо – это расстояние от силы до центра момента (в этом случае, центр – это рассматриваемое сечение). В уравнении моментов, все моменты нужно учитывать с учетом правила знаков: если момент силы, стремится растянуть нижние волокна, то в уравнении будем записывать его со знаком «+». И наоборот.

Придерживаясь этого правила, будем откладывать эпюры изгибающих моментов со стороны РАСТЯНУТЫХ волокон. Что практикуется у инженеров-строителей. У механиков, другие правила, они рисуют эти эпюры со стороны сжатых волокон. Кстати, что такое растянутое и сжатое волокно? Покажу на нашем же примере:

Как видно, сила RA, при повороте, стремится растянуть нижние волокна, поэтому в уравнение будем записывать момент этой силы со знаком плюс:

Анализируя это уравнение, видим, что изгибающий момент будет меняться по линейному закону и зависеть от координаты z1. И чтобы рассчитать и построить эпюру на этом участке достаточно подставить в уравнение координаты начала участка z1=0 и конца z1=2 м. После чего отложить эти точки на графике и соединить прямой линией:

Эпюры для второго участка балки

С учетом всех вышеописанных рекомендаций, я думаю Вы сами теперь сможете построить эпюры для второго участка. Подробно комментировать уже не буду, приведу сразу решение и окончательные эпюры для этой балки:

Сегодня мы рассмотрели урок по построению эпюр для простой балки. Однако, много нюансов по расчету и построению я не рассказал, т.к. все это уместить в одном уроке, довольно сложно и не всем это нужно, статья ведь для чайников! Если Вы хотите прокачать свой знания, в этих вопросах, обязательно прочитайте эти материалы о эпюрах. Здесь можно найти подробные статьи о поперечной силе, о изгибающем моменте. Где я рассказывал о 3-х методиках расчета, причем один из них, даже проще, чем мы рассматривали в данной статье. С помощью которого можно устно рисовать эти эпюры. Также там можно посмотреть, как учитывать моменты и распределенные нагрузки при расчете эпюр и какие особенности есть по построению при действии данных видов нагрузок.

Спасибо за внимание! Если Вам понравилась статья, да и сайт в целом, добавляйте его в свои закладки, чтобы иметь быстрый доступ к нему, а также подписывайтесь на наши соц. сети, делитесь этой статьей с друзьями и т.д. Буду благодарен 🙂

sopromats.ru

Построение эпюр балки | buildingbook.ru

Эпюра — это вид графика, показывающий распределение нагрузки по стержню. Эпюра необходима, чтобы вычислить максимальные напряжения в стержне и на основе этих данных подобрать сечение для конструкции. Как построить эпюру подробно расписано в курсе сопротивления материалов, мы же остановимся на самых необходимых эпюрах для проектирования балок.

Из эпюры балки нам необходимо будет вычислить максимальный изгибающий момент, поперечную силу, опорные реакции стержня. Эти данные нам понадобятся для подбора сечения и проверочного расчета элемента конструкции.

Рассмотрим самые распространенные эпюры балки:

1) Балка имеет шарнирное закрепление по двум сторонам и равномерно-распределенную нагрузку.

Здесь и далее Q — Это поперечная сила, M — изгибающий момент.

Как видим максимальная поперечная нагрузка на балку находится в опорах балки, а максимальный момент в центре балки.

К полезной нагрузке можно прибавить и вес балки т.к. он, как правило, также равномерно распределен по длине балки.

2) Балка имеет шарнирное закрепление по двум сторонам и сосредоточенную нагрузку.

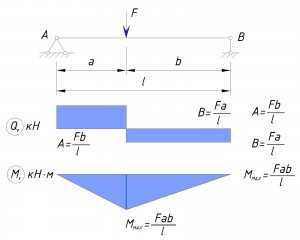
Этот вариант загрузки можно применить к подкрановой балке, хотя чаще всего подкрановая балка имеет несколько пролетов.

Максимальная поперечная сила возникает по всей длине участка от точки приложения силы до ближайшей опоры, причем чем ближе к опоре, тем больше поперечная сила. В расчетах этот показатель необходим чтобы рассчитать стенку балки на устойчивость и подобрать ребра жесткости в случае необходимости.

Максимальный момент возникает в точке приложения силы. Чем ближе точка приложения силы к центру балки, тем выше момент, поэтому если точка приложения нагрузки движется по балке, то подбор сечения необходимо сделать для приложения нагрузки по центру балки.

Эта эпюра не учитывает вес балки, но ее вес также необходимо считать. Для этого можно отдельно построить эпюру моментов для веса балки и сложить показатели в одинаковых точках.

3) Балка защемлена в опорах и равномерно-нагружена по всей длине

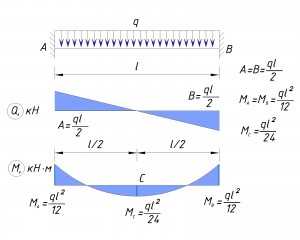
При защемлении в узлах максимальный момент в балке в 2-а раза ниже, чем в балке с равномерно-распределённой, однако необходимо сделать жесткий узел с колонной, что создает некоторые сложности. Кроме того момент от балки будет передаваться на колонны, как и момент с колонн будет передаваться на балку.

В расчетных программах необходимо быть внимательным и контролировать закрепление балок т.к. если расчет балки и подбор сечения будет произведен для жестко закрепленной балки, а в реальности узлы будут шарнирными, то балка будет посчитана не правильно и запас прочности может быть не достаточен.

4) Двухпролетная балка с шарнирными опорами и равномерно-распределенной нагрузкой

В данной схеме мы видим, что максимальный момент находиться на средней опоре, причем больше растянута верхняя часть балки.

Максимальная поперечная сила также находится в точке «В».

При расчете многопролетных балок необходимо учитывать то, что все пролеты могут быть не загружены равномерно, в этом случае эпюра 2-х пролетной балки выглядит следующим образом:

Как видим момент в пролете увеличился, все остальные параметры уменьшились, поэтому момент в пролете для расчета надо брать по этому варианту загружения.

_____________________________________________________________________

Как подобрать сечение стальной балки читайте в статье Расчет балки

Как правильно закрепить балку на колонне читайте в статье Опорные узлы балки

buildingbook.ru

Построение эпюр Q и M для двухопорной балки

Задача

Для заданной двухопорной балки, нагруженной силой F, моментом M и равномерно распределенной нагрузкой q построить эпюры внутренних поперечных сил Q_y и изгибающих моментов M_x.

Решение задачи

Опорные реакции для данной расчетной схемы были определены здесь.

Балка имеет 3 силовых участка. Обозначим их римскими цифрами, например, справа налево.

Для расчета внутренних силовых факторов по участкам балки воспользуемся методом сечений.

Расчет значений

Начнем с первого силового участка (CD).

Проведем поперечное сечение в пределах участка, в любом месте между точками C и D.

Данное сечение делит балку на две части (левую и правую). Для определения внутренних факторов можно выбрать любую из них, но лучше выбирать менее нагруженную часть балки. Очевидно это будет ее правая часть.

Расстояние от правой границы участка до рассматриваемого сечения обозначим переменной z₁, которая может принимать значения от 0 до 1,5 метров (т.е. 0 ≤ z₁≤ 1,5м).

Мысленно отбросим на время всю левую часть балки.

Поперечная сила Q в данном сечении первого участка будет равна сумме всех внешних сил приложенных к рассматриваемой части балки с учетом их знака, т.е.

Здесь сила F записана положительной, т.к. стремится повернуть правую часть балки по ходу часовой стрелки относительно рассматриваемого сечения.

В данном выражении отсутствует переменная z₁, что говорит о том, что внутренняя поперечная сила будет одинакова для всех сечений этого участка.

Изгибающий момент M в рассматриваемом сечении определяется как сумма изгибающих моментов от всех внешних нагрузок выбранной части балки.

С учетом правила знаков при изгибе получаем

Здесь сила F по правилу знаков записана отрицательной, т.к. стремиться сжать нижний слой балки.

В полученном выражении переменная z₁ является плечом момента силы F для данного сечения балки.

Как видно из полученного выражения изгибающий момент по длине участка меняется линейно (т.к. z₁ в первой степени), поэтому для построения эпюры на данном участке нам достаточно двух точек.

Этими точками будут значения изгибающего момента на границах I участка, т.е. при z₁=0 и при z₁=1,5м

На первом участке внутренние усилия определены.

Переходим на второй силовой участок (BC).

Так же начинаем с того, что проводим сечение в любом месте участка и выбираем рассматриваемую часть балки. Здесь также удобнее рассмотреть правую часть балки.

Расстояние до рассматриваемого сечения от правой границы участка обозначим переменной z₂. При этом 0 ≤ z₂≤ 1м.

Запишем выражения и рассчитаем граничные значения внутренней поперечной силы Q

И изгибающего момента M

Здесь опорная реакция R_C положительна, потому что сжимает верхний слой, а сила F и распределенная нагрузка q отрицательны, т.к. сжимают нижний слой балки.
Как записывается момент распределенной нагрузки показано здесь.

В выражении для M_xII переменная во второй степени, поэтому эпюра моментов на втором участке будет иметь вид параболы.

Как известно, для построения параболы необходимо знать положение минимум трех ее точек. Но как будет показано дальше, в некоторых случаях при построении эпюр, параболы можно вычерчивать всего лишь по двум точкам. Рассчитаем их значения:

Осталось найти внутренние усилия на III силовом участке (AB).

Рассекаем балку между точками A и B. Выбираем менее нагруженную левую часть. 0 ≤ z₃ ≤ 2м – интервал возможных положений сечения относительно левой границы участка.

Записываем выражения для Q и M и вычисляем значения в крайних точках

Здесь видно что выражение для Q_yIII — линейное, а на эпюре M_x на данном участке будет парабола.

По полученным данным строим эпюры.

Построение эпюр

Для построения эпюр рассчитанные значения откладываем от базовой линии на соответствующих участках.

Начинаем с эпюры поперечных сил Q.

На первом участке выражение для Q не зависело от z₁ поэтому его значение будет постоянным (Q_yI=const) по длине участка, т.е. линия эпюры будет параллельна базовой.

На втором участке были получены два значения Q: -58,3 кН при z₂=0 и -18,3кН при z₂=1м. Переменная z₂ откладывалась от правой границы участка, поэтому z₂=0 в точке C, соответственно в т. B переменная z₂=1м.

Аналогично откладываются значения Q на третьем участке и значения M на эпюре изгибающих моментов.

Точки на II и III участках эпюры Q и на I участке эпюры M соединяются отрезками, так как распределение внутренних сил и моментов там линейное (переменная z в первой степени).

А при соединении точек эпюры M параболами, надо смотреть на эпюру Q.

Дело в том, что эпюра поперечных сил это первая производная эпюры изгибающих моментов. Поэтому в сечениях балки, где Q=0 на эпюре M будет экстремум.

Как видно эпюра Q пересекает нулевую линию только на третьем силовом участке балки. Поэтому, ввиду того что нас интересуют только пиковые значения изгибающих моментов, на втором участке две крайние точки достаточно соединить параболой, не имеющей экстремума, выпуклость которой направлена навстречу распределенной нагрузке.

Для более точного построения линии параболы на данном участке можно найти значения момента для промежуточных положений сечения, например при z₂=0,5м.

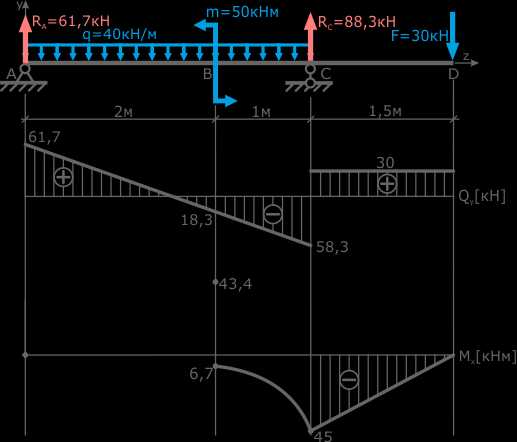
На третьем участке, в сечении, где Q пересекает базовую линию необходимо рассчитать точку экстремума.

Для этого выражение для Q_yIII приравнивается к нулю и рассчитывается значение z₃, при котором изгибающий момент на участке принимает экстремальное значение. Его подставляют в выражение для M_xIII

Это значение откладывается на эпюре M под точкой пересечения эпюры Q с базовой линией

после чего три точки соединяются плавной линией.

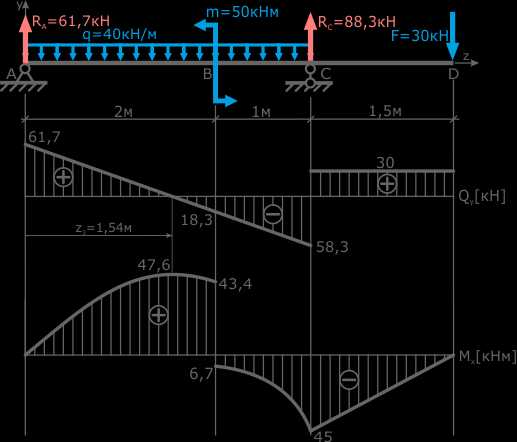
Эпюры внутренних поперечных сил и изгибающих моментов построены.

Проверка эпюр поперечных сил >
и изгибающих моментов >
Расчеты для подбора сечений балки >
Другие примеры решения задач >

isopromat.ru

Построение эпюр для балки — Доктор Лом. Первая помощь при ремонте

При этом школьнику, особенно мечтающему стать писателем или водителем, труднее всего объяснить, зачем эти самые функции, графики и прочие абстракции ему нужны, если после экзаменов он больше никогда в жизни о них не вспомнит? Во всяком случае до тех пор, пока у него самого не появятся дети, которым снова нужно будет выучить эти понятия и термины.

Между тем с инженерами, физиками и представителями прочих точных наук дело обстоит иначе. Так например студенты строительных специальностей на втором году обучения с удивлением узнают, что у абстрактных функций и их графиков, а также производных и дифференциалов есть вполне конкретный смысл. А в чем этот смысл заключается, мы ниже и рассмотрим на примере балок.

Примечание: перед продолжением чтения данной статьи настоятельно рекомендую ознакомиться с основами теории сопротивления материалов.

Эпюры распределенной нагрузки

Это может показаться странным, но когда мы изображаем равномерно распределенную нагрузку, действующую по всей длине балки, например такую:

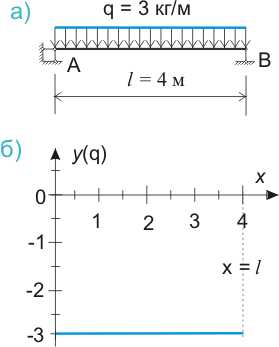
Рисунок 545.1. Равномерно распределенная нагрузка, а) общепринятое изображение, б) график функции — равномерно распределенной нагрузки

То это с одной стороны вроде бы просто нагрузка q = 3 кг/м, равномерно распределенная по всей длине балки (рис.545.1.а)), а с другой стороны — это график функции у, показывающий изменение значения функции в зависимости от изменения значения аргумента х (рис.545.1.б)). Соответственно функциональное уравнение в данном случае будет иметь вид:

у = — 3 = const (545.1)

или

q = — 3 = const (545.1.2)

А смысл этих достаточно простых уравнений в том, что значение нагрузки является постоянной величиной и не зависит от значения аргумента функции, в данном случае от положения рассматриваемого поперечного сечения.

Примечание: В данном случае знак «-» используется потому, что нагрузка направлена вниз.

Вроде бы ничего сложного, но это и есть основные принципы построения эпюр для распределенной нагрузки.

Конечно же распределенная нагрузка может быть не только равномерно распределенной, действующей по всей длине балки, но и линейно или нелинейно изменяющейся, или действующей не по всей длине балки, а также может быть направлена не вниз, а вверх. Некоторые возможные варианты распределенных нагрузок показаны на рисунке 545.2:

Рисунок 545.2. Распределенные нагрузки: а) линейно изменяющаяся, б) линейно изменяющаяся, действующая не по всей длине балки, в) линейно изменяющаяся, описываемая двумя уравнениями, г) нелинейно изменяющаяся.

Но общего принципа построения эпюр нагрузок и составления соответствующего уравнения или уравнений это ни как не меняет.

Так функциональное уравнение для нагрузки, показанной на рисунке 545.2.а):

y = — x/2 (545.2)

По той простой причине, что максимальное значение нагрузки q = 2 кг/м будет в конце балки длиной l = 4 м. Другими словами значение функции у = 2 при аргументе функции х = 4.

Для нагрузки, показанной на рисунке 545.2.в) на участке от начала балки до середины:

y = x (545.3.1)

на участке от середины до конца балки:

у = 2 — х (545.3.2)

Одним словом почти для любой распределенной нагрузки можно составить уравнение, описывающее характер изменения этой нагрузки. А если нагрузка уж слишком мудреная или на балку действуют несколько распределенных нагрузок, то можно воспользоваться принципом суперпозиции, но об этом чуть позже.

Все это хорошо, скажете вы, но зачем нам строить эпюры нагрузки, ведь они у нас и так как бы есть? Действительно от студентов строительных вузов не требуют строить эпюры нагрузок. Считается, что это и так понятно. Не спорю, для тех, кому и так понятно, могут эту часть статьи пропустить (хотя уже поздно), а всем остальным это новое знание должно пригодиться, так как дальше мы будем работать именно с уравнениями функций.

Построение эпюр поперечных сил

Расчет строительных конструкций, в частности балок, основан на общих принципах статического равновесия системы. Исходя из этих принципов, мы можем заменить любые опоры балки сосредоточенными силами — опорными реакциями, при этом балка все равно останется в состоянии статического равновесия.

Но и это еще не все, теоретически мы можем отсечь любую часть балки, а вместо отсеченной части приложить в месте полученного сечения еще некоторые силы или даже моменты сил так, чтобы балка опять оставалась в состоянии статического равновесия. На этой теоретической предпосылке основан метод сечений, упоминавшийся выше.

Конечно же поперечные силы (действие продольных сил мы пока не рассматриваем) и изгибающие моменты, которые необходимо приложить в различных сечениях балки для сохранения статического равновесия системы, могут иметь разные значения. При этом эпюры поперечных сил и изгибающих моментов как раз и показывают нам, как изменяются значения поперечных сил и изгибающих моментов в поперечных сечениях по длине балки.

Собственно именно для этого эпюры и нужны, так как позволяют даже визуально определить сечение в котором действуют максимальные нормальные и(или) касательные напряжения. Весь остальной расчет на прочность — дело техники. Но вернемся к эпюрам, в частности рассмотрим равномерно распределенную нагрузку показанную на рисунке 545.1, как наиболее простую.

Когда мы рассекаем балку, и рассматриваем оставшуюся часть, то часть нагрузки, действующей на балку, также отсекается:

Рисунок 545.3. Отсечние части балки вместе с нагрузкой, метод сечений

Так, если мы рассматриваем сечение на расстоянии 1 м от начала балки, то общая нагрузка, действующая на рассматриваемую часть балки, составит 3 кг, на расстоянии 2 м — 6 кг и так далее.

Получается, что чем больше расстояние от точки А до рассматриваемого сечения (или от начала координат до точки х), тем большую силу нужно приложить в рассматриваемом сечении, чтобы отсеченная часть балки оставалась в равновесии. Более того, мы видим здесь явную закономерность, которую можно выразить следующим уравнением:

Q = — 3x (545.4.1)

А если присмотреться к формулам (545.1.2) и (545.4.1) повнимательнее, то мы увидим, что поперечная сила есть ничто иное, как дифференциал функции нагрузки. Другими словами, чтобы определить значение поперечных сил в том или ином поперечном сечении, нам нужно проинтегрировать уравнение (545.1.2):

Q = ∫qdx = — ∫3dx + A = — 3x + A (545.4.2)

где А — некая постоянная величина, как это следует из общих правил интегрирования. В данном случае А — это значение опорной реакции. Как именно определяются опорные реакции в зависимости от нагрузки на балку — это отдельная большая тема. Здесь просто отметим, что при равномерно распределенной нагрузке на балку А = В = ql/2. В данном случае при значении нагрузки q = 3 кг/м опорные реакции составят A = B = 3·4/2 = 6 кг.

Теперь у нас есть все необходимые данные для построения эпюры поперечных сил при действии на балку равномерно распределенной нагрузки:

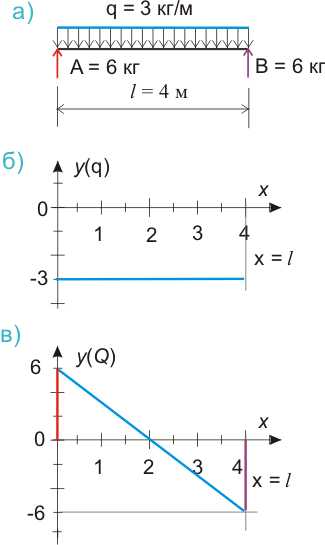
Рисунок 545.4. Равномерно распределенная нагрузка: а) общепринятое обозначение, опорные реакции, б) график функции — равномерно распределенной нагрузки, в) график функции — поперечных сил, действующих в сечениях балки.

Сразу отметим важную особенность эпюр поперечных сил, из которой вытекает одно из общих правил построения эпюр:

1. В местах приложения сосредоточенных сил, будь то опорные реакции или любые другие сосредоточенные силы, направленные вертикально, на эпюре «Q» всегда будет резкое изменение. При этом разница значений, определяемая по эпюре, будет равна значению приложенной сосредоточенной силы, а направление изменения будет такое же, как и у приложенной силы.

Подтверждение этой особенности мы видим и на рисунке 545.4.в), где в начале и в конце балки наблюдается скачкообразное изменение значений поперечных сил, равное значению опорных реакций.

Это правило действует для всех балок вне зависимости от степени статической неопределимости, количества и вида опор. Более того, это правило действует и при построении эпюр поперечных сил для рам.

Построение эпюр изгибающих моментов

Как тонко подметил Архимед, любая сила, приложенная с некоторым плечом относительно рассматриваемой точки, создает вращающий момент. И чем больше плечо, тем больше значение вращающего момента при одном и том же значении приложенной силы.

Это правило рычага действительно и при построении эпюр изгибающих моментов. Вот только моменты называются не вращающими, а изгибающими, но суть от этого не меняется. Так предполагается, что в любом поперечном сечении балки, находящемся на расстоянии х от начала балки (начала координат) могут действовать изгибающие моменты.

Например в нашем случае в начале балки приложена сосредоточенная сила — опорная реакция А = 6 кг, соответственно эта сила будет создавать изгибающий момент Ах, где х — плечо действия силы. При этом равномерно распределенная нагрузка также будет создавать изгибающий момент. А чтобы определить значение этого момента, сначала определяется общее значение нагрузки -qx, что мы и делали при построении эпюры поперечных сил. Общее значение распределенной нагрузки в рассматриваемом сечении можно рассматривать как равнодействующую сосредоточенную силу, а прикладывается эта сила в центре тяжести эпюры нагрузки. Т.е. в этом случае мы рассматриваем эпюру нагрузки, как некое физическое тело, имеющее плотность и соответственно центр тяжести. Впрочем с точки зрения теории сопротивления материалов в этом нет ничего удивительного.

Определить положение центра прямоугольной эпюры нагрузки несложно. Подобными упражнениями мы занимались в школе, когда определяли центр тяжести линейки. И находится этот центр тяжести посредине длины линейки, а в данном случае посредине рассматриваемой части эпюры нагрузки и составляет х/2.Таким образом плечо действия равнодействующей сосредоточенной силы при равномерно распределенной нагрузке составляет х/2. При этом функциональное уравнение изгибающих моментов, необходимое для построения эпюры моментов, будет иметь следующий вид:

M = Ax — qx·x/2 = Ax — qx²/2 (545.5.1)

Примерно такой же результат мы получим, если проинтегрируем уравнение поперечных сил:

M = ∫(A — qx)dx = M₀ + Ax — qx²/2 (545.5.2)

Где М₀ = 0 — это опять же постоянная интегрирования. В данном случае — значение момента на опоре А. Так как мы рассматриваем однопролетную безконсольную балку на шарнирных опорах, то в этом частном случае значение момента на опоре А равно нулю. Кроме того значение момента на опоре В для шарнирной безконсольной балки также равно нулю, так как шарнирные опоры повороту сечений ни как не препятствуют. Эта особенность в частности используется при определении опорных реакций однопролетной безконсольной балки на шарнирных опорах. Другими словами, зная, что момент на опоре В равен нулю, мы можем определить значение опорной реакции А из уравнения (45.5.2):

М_В = 0 = Аl — ql²/2 (545.5.3)

A = (ql²/2)/l = ql/2 (545.5.4)

В общем случае значение момента в начале координат может быть не равно 0.

А теперь рассмотрим еще одну особенность изгибающих моментов: для рассматриваемого сечения не имеет принципиального значения, какой будет знак у момента, положительный или отрицательный, так как при любом знаке в сечении будет как растягиваемая, так и сжимаемая зона сечения. А вот какая именно зона сечения будет растягиваемой, верхняя или нижняя — имеет большое значение, потому что не все материалы имеют равное сопротивление растяжению и сжатию, а кроме того форма сечения далеко не всегда бывает прямоугольной.

В связи с этим при построении эпюр изгибающих моментов принято следующее правило:

2. Эпюра моментов строится с той стороны, где будет растянутая зона сечения. При этом момент, пытающийся вращать рассматриваемое сечение по часовой стрелке, считается положительным, а против часовой стрелки — отрицательным.

Примечание: это правило не является общепринятым. В некоторых справочниках и учебниках по теории сопротивления материалов положительный момент строится сверху от оси х, что в общем то логично, но при этом получается, что положительный момент там, где сжатая зона сечения. В других он строится с той стороны, где растянутая зона сечения, но при этом может показываться со знаком «-«, если строится снизу от оси х. Но как я уже говорил выше, принципиального значения это не имеет, главное понимать общий смысл изгибающих моментов.

Если мы посмотрим на направление действия опорной реакции А и распределенной нагрузки q (рисунок 545.4), то увидим, что относительно любого из рассматриваемых сечений опорная реакция А пытается вращать это сечение по часовой стрелке, а распределенная нагрузка q — против. Это означает, что функциональное уравнение, описывающее изменение изгибающих моментов по длине балки, составлено у нас правильно.

При этом растянутой будет нижняя зона сечения балки по той причине, что балка прогнется вниз при таком действии нагрузки. Следовательно эпюру моментов в данном случае следует строить снизу от оси координат х.

Теперь у нас есть все данные для построения эпюры изгибающих моментов. Судя по уравнению (545.5.2) это будет квадратная парабола, а максимальное значение изгибающего момента будет посредине балки, так как нагрузка у нас симметричная, и составит М = 6·2 -3·2²/2 = 6 кгм.

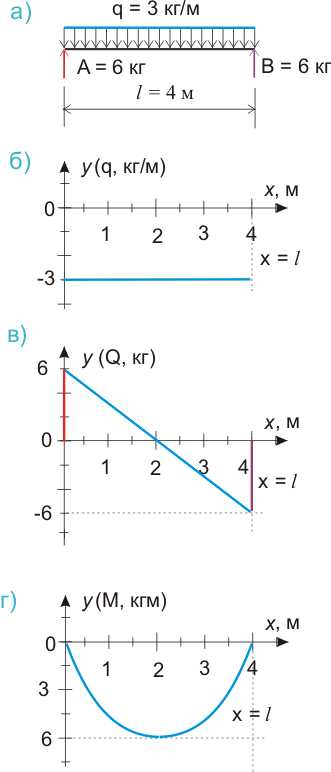
Рисунок 545.5.г) эпюра изгибающих моментов, как график функции у = 6х — 3х²/2

В общем случае, когда нагрузка несимметричная, как показано на рисунках 545.2.а) и б) или на балку действуют несколько распределенных нагрузок, то определить сечение в пролете балки, в котором действует максимальный изгибающий момент. можно, воспользовавшись следующим общим правилом:

3.1. При действии распределенных нагрузок максимальный момент в пролете балки будет в том сечении, в котором значение поперечных сил равно нулю.

Если мы посмотрим на рисунки 545.5.в) и г), то увидим, что это так и есть. Если на балку действуют только сосредоточенные силы, то следует использовать другое правило:

3.2. При действии на балку сосредоточенных сил максимальный момент будет в точке приложения как минимум одной из таких сил.

А вообще в ряде случаев при действии нескольких сосредоточенных сил на балку их, для упрощения расчетов, можно привести к эквивалентной равномерно распределенной нагрузке.

У многопролетных статически неопределимых балок на шарнирных опорах, у балок с жестким защемлением на опорах и у балок с относительно большой длиной консоли максимальный момент может быть не в пролете, а на одной из опор. Тем не менее правило определения момента в пролете по поперечным силам действует и для таких балок.

При построении эпюр изгибающих моментов можно выделить еще несколько общих правил.

4. В точке приложения сосредоточенных сил к балке всегда резко изменяется угол наклона касательной к эпюре моментов «М».

В нашем случае сосредоточенные силы — опорные реакции приложены в начале и в конце балки и если мысленно рассматривать ось х до начала и после конца балки как все ту же балку, то действительно в начале и конце балки мы видим резкое изменение угла наклона касательных, которые можно провести к кривой эпюры моментов в этих точках.

Это правило действует даже в тех случаях, когда эпюра моментов — не кривая, а ломаная линия. Например, при действии на балку только сосредоточенных сил.

5. В местах приложения к балке внешних изгибающих моментов на эпюре «М» всегда будет резкое изменение. При этом разница значений, определяемая по эпюре, будет равна значению приложенного изгибающего момента.

Как видим данное правило подобно правилу 1, используемому при построении эпюр поперечных сил и в этом нет ничего удивительного, так как закономерности построения графиков функций общие.

Примечание: Касательные и нормальные напряжения, действующие в рассмариваемых поперечных сечениях балки, распределяются не равномерно по высоте сечения балки. Формально для определения максимальных касательных и нормальных напряжений в рассматриваемом сечении требуется дополнительное построение эпюр касательных и нормальных напряжений, но как правило большой необходимости в этом нет, особенно если балка имеет прямоугольное сечение. Какой эти эпюры могут иметь вид, можно посмотреть здесь. Тут лишь упомянем, что на вид эпюры нормальных напряжений геометрическая форма поперечного сечения ни как не влияет, а на вид эпюры касательных напряжений геометическая форма сечения влияет значительно.

Построение эпюр углов поворота и прогибов

Для дальнейшего расчета балки по второй группе предельных состояний — расчета по деформациям часто требуется построить эпюры углов поворота и прогибов. Начнем с эпюры углов поворота.

Вообще-то более правильно данную эпюру называть «эпюрой тангенсов углов поворота поперечных сечений балки», тем не менее в специализированной литературе принято упрощенное название для этой эпюры, мы тоже не будем нарушать традицию.

В целом значение и углов поворота и прогибов зависит от жесткости балки. Чем больше жесткость ЕI, тем меньше будут углы поворота и прогибы. Более подробно эта тема рассматривается отдельно, здесь лишь отметим, что угол поворота — это дифференциал функции изгибающих моментов:

θ = ∫Мdx (545.6.1)

В нашем случае при действии равномерно распределенной нагрузки на однопролетную балку на шарнирных опорах:

θ = — θ₀ + Ах²/2EI — qx³/6EI (545.6.2)

где θ₀ — постоянная интегрирования, в данном случае θ₀ — угол поворота на опоре А (начальный угол поворота) не равен нулю, так как шарнирные опоры не препятствуют повороту поперечных сечений балки на опорах.

Примечание: Тут может возникнуть вопрос, а почему в данном случае перед начальным углом поворота стоит знак «-«. Объяснение этому можно найти в статье, ссылка на которую дана выше. Здесь лишь сформулируем еще одно правило, используемое при построении эпюр углов поворотов

6. Знак «-» перед начальным углом поворота означает, что угол между касательной к эпюре «θ» и осью х откладывается вниз от оси х (по часовой стрелке).

Соответственно в начале и в конце безконсольной балки с шарнирными опорами мы можем наблюдать резкое изменение значений углов поворота, но это уже даже не правило, а так, общая закономерность. Пойдем дальше.

Прогиб балки — это дифференциал функции углов поворота:

f = ∫θdx (545.7.1)

В данном случае

f = — θх + Ах³/6EI — qx⁴/24EI (545.7.2)

Хотя шарнирные опоры не препятствуют повороту поперечных сечений на опорах, но они препятствуют перемещениям этих сечений вдоль оси у, поэтому в данном случае f₀ = 0 и эта постоянная интегрирования в формуле (545.7.2) не приводится. Более того, если нагрузка на балку несимметричная, т.е. углы поворота поперечных сечений на опорах разные, то начальный угол поворота определяется, исходя из того, что прогиб и на опоре А и на опоре В равен нулю, тогда в нашем случае точке В:

f_B = 0 = -θ₀l + Al³/6EI — ql⁴/24EI (545.7.3)

θ₀ = (ql·l³/(2·6EI) — ql4/24EI)/l = ql³/24EI (545.7.4)

Примечательно, что при определении опорных реакций однопролетной шарнирной балки мы использовали похожую особенность — значения моментов на опорах А и В равны нулю.

На основании этих данных мы можем построить эпюры углов поворота и прогиба балки. При этом значения углов поворота и прогибов будут зависеть, как уже говорилось, от жесткости балки, но в данном случае нас интересует только общий вид эпюр:

Рисунок 545.6. а) эпюра углов поворота, б) эпюра прогибов — как графики функции.

Как видим, между эпюрами углов поворота и прогибов существует такая же связь, как и между эпюрами поперечных сил и изгибающих моментов. Опять же в этом нет ничего удивительного — это общая закономерность. Тем не не менее одну из этих закономерностей выделим особо:

7. Максимальный прогиб балки на шарнирных опорах будет в том сечении, в котором значение угла поворота равно нулю.

Вот собственно и все, что мне хотелось сказать по поводу построения эпюр для балки.

doctorlom.com

Построение эпюр однопролетной шарнирно-опертой балки

Мы уже рассматривали типовые эпюры и построение эпюры консольной балки.

В этой статье мы рассмотрим как построить эпюру однопролетной шарнирно-опертой балки.

Эпюра однопролетной балки строится также ка эпюра консоли с той лишь разницей, что для определения опорных реакций необходимо решить систему уравнений. После нахождения опорных реакций метод построения эпюры аналогичен описанной в статье «Построение эпюр консольной балки».

Давайте рассмотрим построение эпюры балки на данном примере:

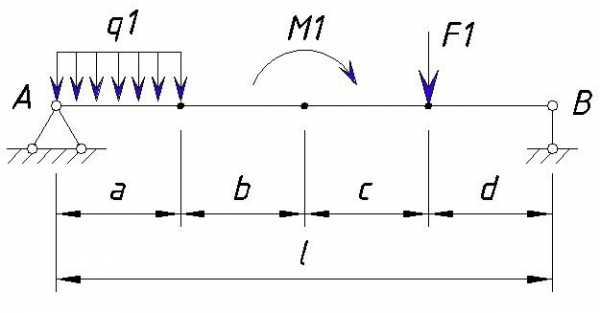
Значения нагрузок:

q1=20 кН/м

M1=10 кН·м

F1=30 кН

Расстояния между точками равны т,е. a=b=c=d=1м

Опорные реакции

Чтобы вычислить опорные реакции необходимо решить систему уравнений

Т.к. система неподвижна, а узлы вокруг точки A и B шарнирные, то сумма изгибающих моментов вокруг точек A и B равны нулю (если одна или обе опоры жестко закреплены, то это условие не работает и этот способ нахождения опорных реакций не работает).

Давайте обозначим опорные реакции в узлах крепления балки

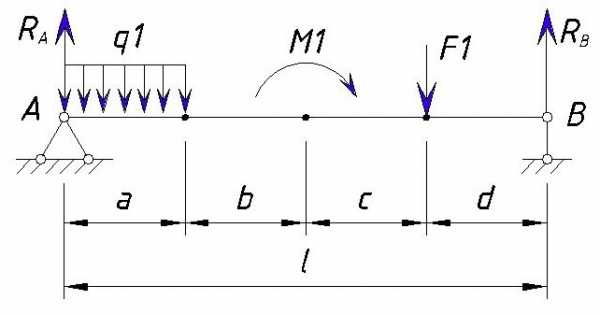
Опорных изгибающих моментов в точках A и B нет, да и на эпюрах изгибающий момент в данных точках должен быть равен нулю (может быть не равен нулю только если в этом узле прикладывается изгибающий момент или балка многопролетная/с жестким соединением в узле).

Давайте напишем условие равенства изгибающих моментов относительно точки A

Реакции опоры Ra нет в уравнении т.к. плечо приложения нагрузки равно нулю, поэтому он не создает изгибающий момент в этой точке.

Из уравнения, приведенного выше, мы можем вычислить реакцию Rb:

Теперь напишем уравнение равенства изгибающих моментов вокруг точки B

Из уравнения находим значение опорной реакции Ra:

Вычисленные значения опорных реакций необходимо проверить по формуле:

Равенство верно, поэтому значение опорных реакция мы нашли правильно.

Назначение контрольных точек

Чтобы построить эпюру изгибающих моментов балки важно правильно определить все контрольные точки, для которых мы будем вычислять значения напряжения. Прежде всего это будут все точки, в которых приложена нагрузка, а также начинается или заканчивается равномерно-распределенная нагрузка. Также надо рассмотреть точки, в которых эпюра Q принимает значение равное нулю — в этой точке изгибающий момент может принимать максимальное значение (вы можете увидеть это на примере 2-х пролетной балки, рассмотренной в статье «Построение эпюр балки»).

Для начала мы назначим точки только в точках приложения нагрузки, в начале и конце приложения равномерно-распределенной нагрузки, но после построения эпюры Q может добавится еще точки для построения эпюры M.

Построение эпюры Q (поперечной силы)

Я уже рассматривал построение эпюры Q для консольной балки в статье «Построение эпюр консольной балки», для построения эпюры поперечной силы одно-пролетной балки мы пользуемся тем же методом.

Эпюру Q мы строим перемещаясь от точки A в сторону точки B вычисляя значение поперечной силы в каждой точке и строя график в зависимости от вида нагрузки, приложенной к данному участку.

Для точки, в которой приложена сосредоточенная сила F нужно вычислить значение слева от точки (без учета этой силы) и справа (с учетом этой силы). В этой точке будет скачок поперечной силы. В остальных случаях поперечная сила изменяется прямолинейно (для равномерно-распределенной) или по кривой (для переменной нагрузки).

Не забываем про правило знаков:

Если внешняя нагрузка, приложенная к рассматриваемой части, стремится повернуть сечение на заданном участке по часовой стрелке, то значение будет положительным и откладывается вверх.

Если внешняя нагрузка стремится повернуть сечение на заданном участке против часовой стрелки, то значение будет отрицательным и откладывается вниз.

Определяем напряжения Q на участке AC

Значение поперечной силы в точке А равно значению опорной реакции Ra, которое мы вычислили ранее. Не забываем про правило знаков — если сила стремится повернуть рассматриваемый участок по часовой стрелке, то значение принимается со знаком плюс, если против часовой, то со знаком минус. Мы как-бы откидываем закрепление балки в точке А, заменив ее силой Ra, и закрепляем в точке C. Сила Ra стремится повернуть участок вокруг точки C по часовой стрелке, поэтому Ra принимается со знаком плюс.

На участке AC действует равномерно-распределенная нагрузка q1. Нагрузка q1 стремится повернуть рассматриваемый участок против часовой стрелки, поэтому данная нагрузка принимается со знаком минус. Рассчитываем значение поперечной силы в точке C

На участке AC нагрузка изменяется прямолинейно, поэтому эпюра Q на участке AC выглядит следующим образом:

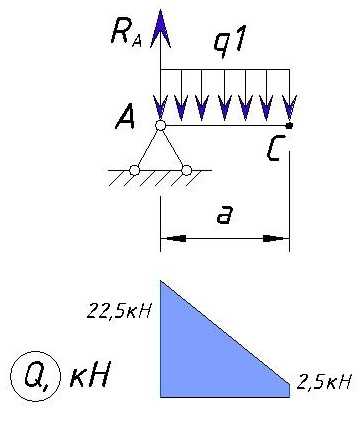
Определяем напряжения Q на участке CD

На участке CD нет нагрузки, поэтому значение поперечной силы на данном участке не изменяется. В точке D приложен изгибающий момент, но он не влияет на поперечную силу (влияние момента на поперечную силу отражено в реакции опоры). Поэтому значение Q в точке D равно:

На участке CD значение не Q не изменилось, поэтому эпюра Q выглядит следующим образом:

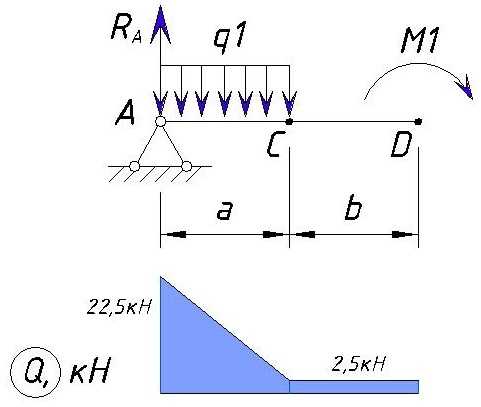
Определяем напряжения Q на участке DE

На участке DE нет нагрузок, поэтому значение Q не изменяется. В самой точке E приложена сосредоточенная сила F1, т.е. справа от точки E будет скачок поперечной силы на величину F, сила F будет со знаком минус т.к. она стремится повернуть сечение против часовой стрелки (относительно точки E справа).

Эпюра на участке DE будет выглядеть следующим образом:

Определяем напряжения Q на участке EB

На участке нет нагрузок, поэтому напряжение на участке не изменяется. В самой точке B эпюра Q должна быть равна -Rb, что мы и видим

Итоговая эпюра Q

Построим эпюру Q на основе всех этих данных

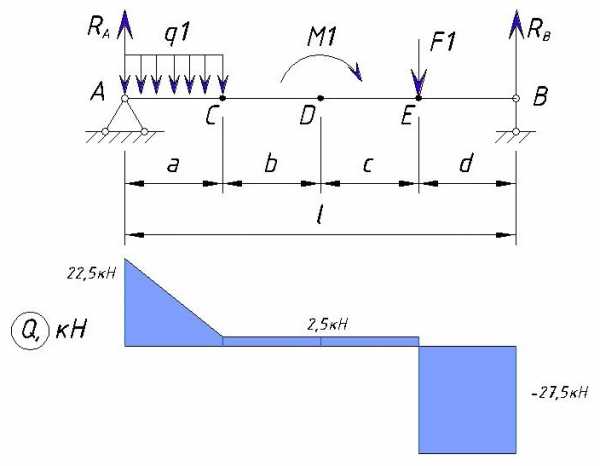
Эпюра в конце балки должна быть равна -Rb, что мы и имеем. То, что значение эпюры Q имеет знак минус в точке B не значит, что тут сечение растянуто, здесь сечение также сжато, но по правилу знаков значение отрицательное т.к. сил которые стремятся повернуть сечение против часовой стрелки больше чем сил стремящихся повернуть по часовой.

Можно отметить следующие закономерности при построении эпюры Q:

1) На участке приложения равномерно-распределенной нагрузки значение поперечной силы изменяется прямолинейно

2) На участке приложения переменной нагрузки изменение поперечной силы криволинейно

3) В точках приложения сосредоточенной силы эпюра Q имеет скачок напряжения

4) Изгибающий момент сам по себе не влияет на поперечную силу, но он воздействует на опорную реакцию, что конечно создает поперечное напряжение в балке

Построение эпюры M (изгибающих моментов)

Эпюра изгибающих моментов строится по тому же принципу, что описан в статье «Построение эпюр консольной балки».

Для построения эпюры М мы используем те же контрольные точки и те же участки, что мы использовали при построении эпюры Q.

Последовательно передвигаясь от точки А к точке B мы вычисляем значения моментов в контрольных точках и соединяем их в график который и будет указывать изгибающий момент в любой точке балки.

Изгибающий момент вычисляется произведением силы или центра приложения силы на плечо.

Для сосредоточенной силы мы умножаем значение нагрузки на расстояние до рассматриваемой точки. На графике эпюра M от действия сосредоточенной силы имеет прямую линию.

Чтобы определить изгибающий момент от действия равномерно-распределенной нагрузки определяем расстояние до середины рассматриваемого участка равномерно-распределенной нагрузки, умножаем на длину рассматриваемого участка и на величину нагрузки. На графике эпюра М от действия равномерно-распределенной нагрузки напоминает изогнутую линию, гиперболу.

Для переменной нагрузки изгибающий момент определяем следующим образом: определяется центр приложения нагрузки (длина приложения нагрузки делится в соотношении 1/3-2/3, центр приложения нагрузки находится ближе к максимальной нагрузке), определяем длину от этой точки до рассматриваемой, умножаем на длину приложения нагрузки, и умножаем на половину от приложенной нагрузки (q).На графике эпюра М от действия переменной нагрузки также как и для равномерно-распределенной напоминает изогнутую линию, но с большим изгибом.

Приложенный момент в точке просто суммируется с вычисляемым изгибающим моментом от других нагрузок. В точке где приложен момент эпюра совершает скачок. Значение момента не умножается на расстояние, а остается неизменным по всей длине.

Правило знаков для построения эпюры M

Тут есть 2-а метода: метод которым пользуются строители и метод, которым пользуются машиностроители.

У строителей изгибающий момент считается положительным, если внешняя нагрузка приводит к растяжению верхних волокон и график откладываем вверх. Если внешняя нагрузка приводит к растяжению нижних волокон, то изгибающий момент считается отрицательным и график откладывается вверх. Т.е. график всегда откладывается в сторону растянутых волокон.

У машиностроителей все наоборот — положительное значение откладывается в сторону сжатых волокон.

Ни в том, ни в другом случае ошибки нет, просто разные методы и итоговые значения будут одинаковыми, только знаки противоположными.

Не могу с уверенностью сказать почему у строителей изгибающий момент направлен в сторону растянутых волокон. Возможно из-за того, что при данном рассмотрении эпюра моментов во многих случаях повторяет изгиб балки.

Мы будем рассматривать метод, которым пользуются строители.

Определяем напряжения M на участке AC

Рассмотрим участок от точки A до точки C.

Значение изгибающего момента в точке A равно нулю, в точке B тоже равно нулю т.к. мы имеем однопролетную шарнирно-опертую балку.

На значение изгибающего момента в точке C влияют следующие силы:

1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки C), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до C в данном случае)

2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2)

Вычислим значения изгибающего момента в точке C:

Т.к. на данном участке действует равномерно-распределенная нагрузка, то форма эпюры M на данном участке имеет изгиб в сторону действия нагрузки. Эпюра M на данном участке будет выглядеть следующим образом:

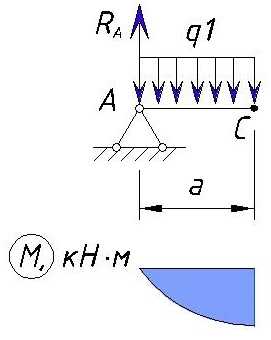
Определяем напряжения M на участке CD

На участке между точками C и D нет никаких нагрузок, а в точке D приложен изгибающий момент M1, поэтому необходимо считать вначале значение изгибающего момента без учета M1 (точка D слева), затем считать с учетом изгибающего момента M1 (точка D справа). На эпюре в точке D будет скачок напряжения изгибающих моментов.

На значение изгибающего момента в точке D влияют следующие силы:

1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки D), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до D в данном случае)

3) Изгибающий момент M1. Значение изгибающего момента не зависит от расстояния до нагрузки. Для расчета необходимо вначале рассчитать значение слева от точки где приложен данный момент, не учитывая его, и справа с учетом действия этого момента. Т.к. изгибающий момент растягивает нижние волокна, то учитываем его со знаком минус.

Вычислим значение изгибающего момента в точке D слева:

Вычислим значение изгибающего момента в точке D справа:

Эпюра M между точками C и D изменяется прямолинейно т.к. между этими нет сил. Эпюра на этом участке выглядит следующим образом:

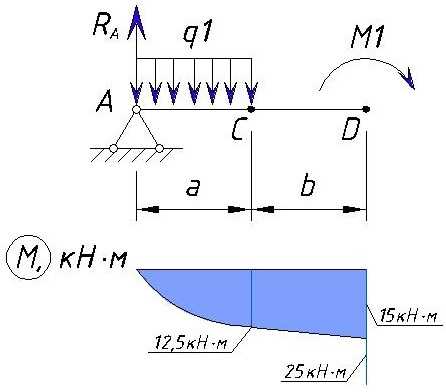
Определяем напряжения M на участке DE

На участке между точками D и E нет никаких нагрузок, а в точке E приложена сосредоточенная нагрузка F1, но т.к. плечо в данной точке равно нулю, то и изгибающий момент сила F не создает в точке E.

На значение изгибающего момента в точке E влияют следующие силы:

1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки E), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до E в данном случае)

Вычислим значение изгибающего момента в точке E:

Эпюра M между точками D и E изменяется линейно т.к. между этими нет сил. Эпюра на этом участке выглядит следующим образом:

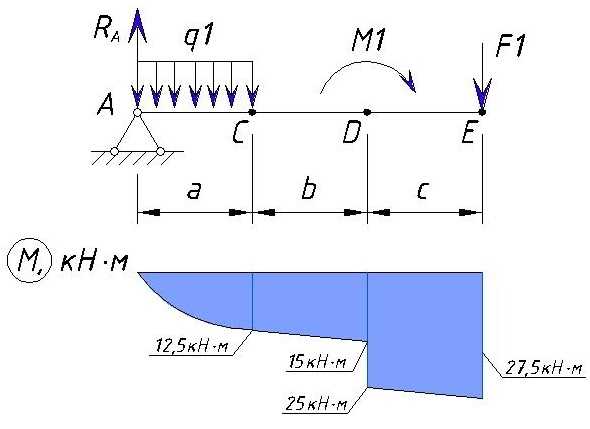
Определяем напряжения M на участке EB

На участке между точками E и B нет никаких нагрузок, а в точке B приложена опорная нагрузка Rb, но т.к. плечо в данной точке равно нулю, то и изгибающий момент опорная сила Rb не создает.

Изгибающий момент в точке B должен быть равен нулю, мы это сейчас проверим.

На значение изгибающего момента в точке B влияют следующие силы:

4) Сила F1. Действие силы растягивает верхние волокна, поэтому учитывается со знаком плюс. Плечо действия силы равно d.

Вычислим значение изгибающего момента в точке B:

В принципе это тоже самое уравнение, которое мы решали при определении опорных реакций.

Т.к. на участке EB нет никаких нагрузок, то изменение изгибающего момента происходит прямолинейно.

Итоговая эпюра M

Теперь нарисуем всю эпюру M для данного примера

Можно отметить следующие правила при построении эпюры изгибающих моментов:

1) на участке приложения равномерно-распределенной или переменной нагрузки эпюра имеет изгиб

2) на участках где не приложены силы эпюра изменяется прямолинейно

3) в точке где приложен изгибающий момент происходит скачок напряжения

Итоговая эпюра Q и M

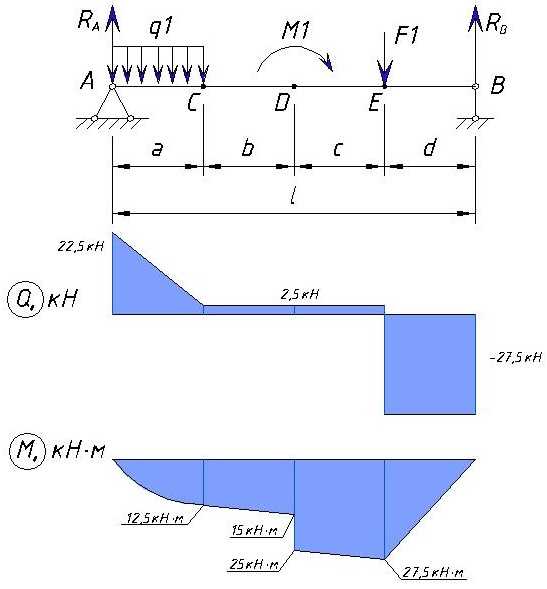
Удачи в учебе.

buildingbook.ru

Эпюры поперечных сил и изгибающих моментов

Эпюрами поперечных сил и изгибающих моментов называют графические изображения функций Q и M по длине балки при изгибе.

Посмотреть подробные примеры построения эпюр >>

Эпюры строятся для визуального представления распределения внутренних силовых факторов и определения опасных (т.е. наиболее нагруженных) с точки зрения прочности участков бруса.

Рассмотрим некоторые примеры на построение эпюр в балках:

Эпюры при чистом изгибе

Для консольной балки:

Рис. 1

имеем два силовых участка (AB и BC) и на каждом из них, применяя метод сечений, будем рассматривать, например правую от сечения часть, используя формулы и правило знаков для расчета внутренних силовых факторов.

Отсчет координаты z можно вести от единого начала координат или для каждого силового участка в отдельности.
I силовой участок (BC): 0 ≥ z₁ ≥ 2a (рис. 2 а,г)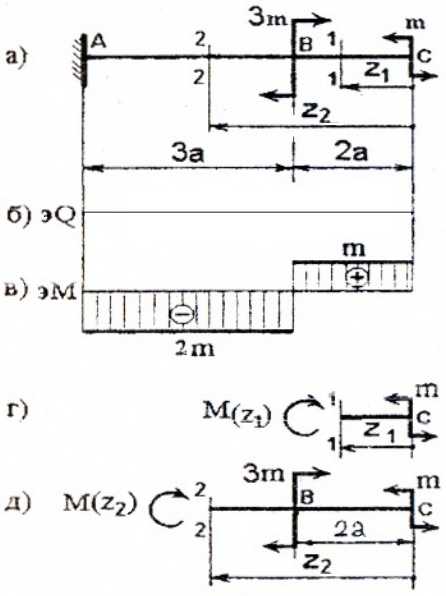

Рис. 2

т.е. Q(z₁)=0 на всем участке, а M(z₁)=m=const.
Ординаты эпюр Q и M со знаком плюс (+) будем откладывать вверх от нулевой (базовой) линии, при этом эпюру M будем строить на сжатых волокнах.

II силовой участок (AB): 2a ≥ z₂ ≥ 5a (рис. 2 а,д)

Откладывая на границах участков в сечениях C, B и A значения полученных ординат Q и M, строим эпюры (рис. 2 б, в).

Более нагруженным оказался участок AB, он и является опасным: M_max=|2m|.
Так как поперечные силы Q по всей длине балки равны нулю, балка испытывает чистый изгиб.

Эпюры при поперечном изгибе

Построение эпюр Q и M для балки, изображенной на рис. 3

Рис. 3

проводим аналогично, но рассматривать будем левые от сечений части, т.к. в правые войдут реакции в заделке, что несколько усложняет вычисления.

I силовой участок (AB): 0 ≥ z₁ ≥ l₁ (рис. 4, а, г)
Q(z₁)= F=const, на всем участке постоянная величина,
M(z₁)=F×z₁, уравнение прямой, график строим по двум граничным точкам:
M(z₁=0)=F×0=0 – в сечении A;
M(z₁=l₁)=F× l₁ — в сечении B.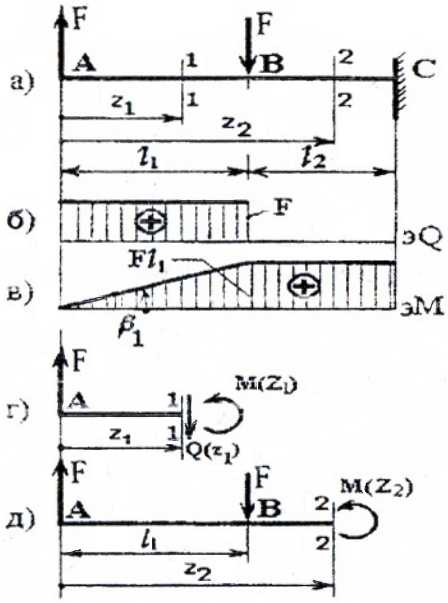

Рис. 4

II силовой участок (BC): l₁ ≥ z₂ ≥ (l₁+ l₂) (рис. 4, а, д)
Q(z₂)= F-F=0;
M(z₂)=F×z₂— F×(z₂— l₁)=F ×l₁=const.
Построив эпюры Q и M по всей длине балки (рис. 4 а, б, в), видим, что на первом участке — деформация прямого поперечного изгиба, т.к. Q≠0, M≠0; а на втором – прямого чистого изгиба.

Опасным является сечение B, в котором действуют Q_max=F, M_max=Fl₁.

Геометрическая проверка эпюр

Геометрическая проверка правильности построения эпюр Q и M по дифференциальным зависимостям заключается в следующем:
Для всех силовых участков находим:

где α, β – углы наклона касательных к эпюрам Q и M относительно оси абсцисс (базовой линии).
На участке “AB” α₁=0 (линия эпюры Q горизонтальна), следовательно,

распределенная нагрузка отсутствует;

функция M (z₁) – возрастающая.

На участке “BC”:

Так как все дифференциальные проверки выполняются, эпюры построены верно.

Эпюры для двухопорных балок

Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),

Рис. 5

необходимо вначале найти опорные реакции и только потом строить эпюры.

Определим реакции в обеих опорах, для этого используем два независимых уравнения статики, т.к. у нас плоская система параллельных сил.

Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑M_A=0 и ∑M_B=0.

Записываем уравнения и находим значения реакций:

Чтобы убедиться в правильности полученных значений необходимо провести «арифметическую проверку» тождества по оставшемуся из зависимых уравнений: ∑F_Y=0 или ∑M_С=0.

Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).

Для построения эпюр рассмотрим два силовых участка: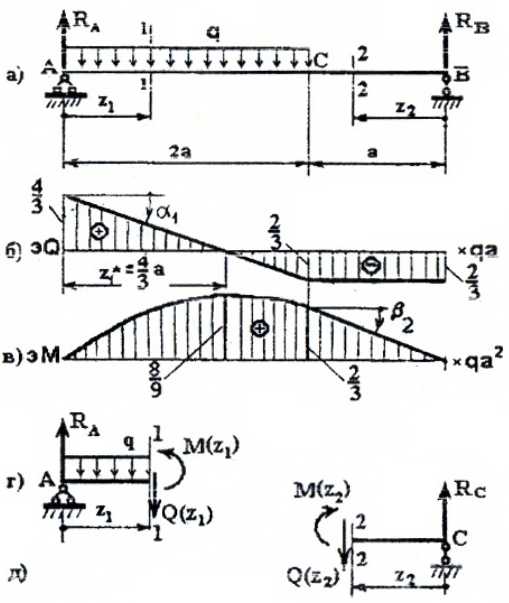

Рис. 6

I участок (AC): 0 ≥ z₁ ≥2a (рис. 6, а, г)
Q(z₁)=R_A-qz₁ — прямая, которую строим по двум граничным точкам:

M(z₁)=R_Az₁-qz₁(z₁/2)= R_Az₁-qz₁²/2 – парабола.

Строим эту кривую по трем точкам: по двум граничным (0 и 2a) и z*, которая соответствует M_max(z*), и дифференциальной зависимости: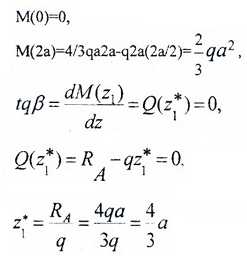

Определяем экстремум эпюры M на участке:

II участок (BC): 0 ≥ z₂ ≥ a (рис. 6, а, д)
Q(z₂)= -R_B= -2/3qa;
M(z₂)=R_Bz₂,
M(z₂=0)=0,
M(z₂=a)=2/3qa².
Выполним проверку дифференциальных зависимостей.
I силовой участок: 0 ≥ z₁ ≥ 2a

— направлена вниз, функция Q(z₁) – убывающая.

— проверка визуально: чем больше угол наклона β₁, тем больше значение Q(z₁).

II силовой участок: 0 ≥ z₂ ≥ a.

следовательно, q=0.

функция M(z) – убывающая.
Все проверки выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасных сечений два (рис. 6):
По моменту при z₁*=4/3a

По силе в сечении «A»

После построения и проверки эпюр можно приступать к расчетам балки на прочность и жесткость.

Подробные примеры построения эпюр >
Лекции по сопромату >
Примеры решения задач >

isopromat.ru

Построение эпюр изгибающих моментов и поперечных сил для балок

Очень важно уметь строить эпюры для балок, работающих на изгиб! Так как построение эпюр, является неотъемлемой частью любого прочностного расчёта и большинство элементов, из которых состоят современные инженерные сооружения, работают на изгиб. Поэтому в сопромате, очень много внимания уделяется как раз данным эпюрам: поперечных сил и изгибающих моментов. Для краткости, их ещё называют эпюрой моментов и эпюрой сил. В этой статье, рассмотрим, как рассчитать эпюры традиционным методом, а также быстрым, с помощью которого эпюры рисуются за считаные минуты. В статье, построение показано на примере консольной и опирающейся на две опоры балки. Показано, как учитывать сосредоточенные силы и моменты, а также распределённые нагрузки.

Построение эпюр для консольной балки

В качестве первого примера, возьмём балку, защемлённую с левого торца жёсткой заделкой и загруженной силой равной 5 кН и моментом равным 10 кНм. Длины участков даны на расчётной схеме. Нам предстоит рассмотреть два участка. Границами участков будут являться места приложения сил, моментов, начало и конец приложения распределённых нагрузок.

Первым делом, вводим систему координат, ось x пускаем вдоль оси балки, ось y перпендикулярно ей, а ось z будет перпендикулярна плоскости, в которой размещены две первые оси и будет направлена «к нам».

В поперечных сечениях балки под действием приложенной нагрузки будут возникать два внутренних силовых фактора: поперечная сила и изгибающий момент. Наша задача выяснить, какой величины эти факторы во всех сечениях балки. Для наглядности, результат решения фиксируют в виде так называемых эпюр.

Эпюра строится по всей длине балки, ордината эпюры, под исследуемым сечением, показывает величину внутреннего усилия в этом сечении.

Эпюра поперечных сил

Начнём знакомство с поперечными силами с правила знаков для эпюр. После чего последовательно рассчитаем и построим эпюры для первого и второго участка балки.

Правило знаков для поперечной силы

При построении эпюр поперечных сил нужно придерживаться следующих правил знаков:

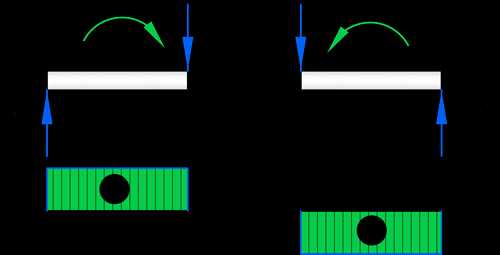
Если внешняя сила стремится повернуть балку по часовой стрелке, то поперечную силу считаем положительной. Эпюру откладываем выше нулевой линии со знаком плюс.
Если сила поворачивает балку против часовой стрелки, то поперечная сила будет отрицательной, и на эпюре будет откладывать ниже нулевой линии.

Возможно, сейчас будет немного непонятны данные правила, но прочитав следующие 2 блока статьи, вы поймёте, как применять эти правила в действии.

Поперечные силы на первом участке

Рассмотрим первым участок равный двум метрам. Сделаем мысленно сечение на расстоянии x₁ от свободного торца и запишем законы изменения эпюр на этом участке. Законы эти выражаются из уравнений равновесия статики. Статика говорит нам, что тело находится в равновесии, если выполняются следующие условия:

Если суммы проекций всех сил на обе оси равны нулю и сумма моментов относительно точки равна нулю.

Для поперечной силы возьмём сумму проекций на ось y:

Из этого уравнения выражаем поперечную силу Q = F. Так как внешняя сила стремиться повернуть балку по часовой стрелке, то поперечную силу считаем положительной. Причем видно, из полученного закона поперечной силы, что Q постоянна по всей длине участка. Откладываем на эпюре Q = F = 5 кН. Эпюру подписываем как Q_y, где y значит, что направление поперечные силы совпадет с направлением этой оси.

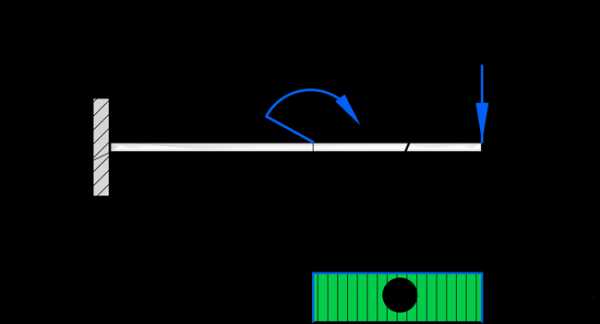
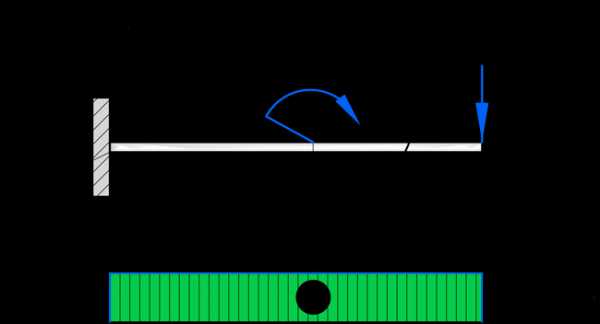
Поперечные силы на втором участке

На втором участке, поперечная сила будет равна: Q_y2= Q_y₁;

Так как на этом участке, действует все та же сила F. Момент в уравнениях поперечных сил не учитывается, что является следствием уравнений статики.

Эпюра изгибающих моментов

В этом блоке статьи будем учиться строить эпюру моментов, здесь нюансов несколько больше, чем для эпюры поперечных сил. Начнём, пожалуй, с правил знаков, которые приняты для этой эпюры.

Правила знаков для изгибающих моментов

Если внешняя сила или момент растягивают «верхние волокна» то эпюра откладывается сверху.
Если сила или момент силы растягивают «нижние волокна», то эпюра откладывается ниже нулевой линии.

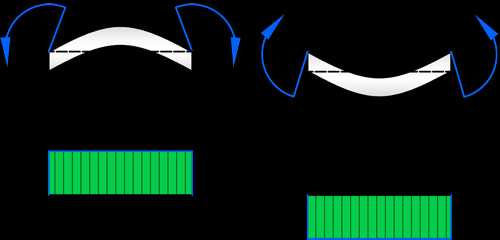
То есть, обычно, при построении эпюр изгибающий моментов знаки не указываются. Эти эпюры откладываются со стороны «растянутых волокон». Так, и удобнее читать эпюры и откладывать их.

Не всегда их откладывают так! Студентов некоторых специальностей, чаще всего машиностроительных, учат откладывать эпюры со стороны «сжатых волокон». Строители откладывают со стороны «растянутых волокон», в своих статьях я буду придерживаться этого правила, так как привык к нему.

Изгибающий момент на первом участке

Для изгибающих моментов на первом участке, запишем сумму моментов, относительно точки С, в которой ранее сделали сечение:

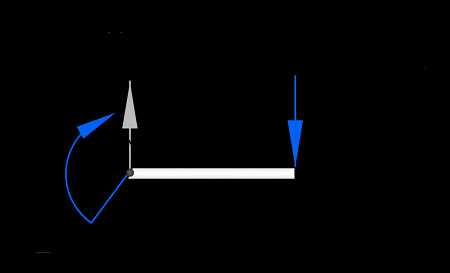
Отсюда получаем:

Это закон изменения изгибающих моментов по длине участка. В отличие от поперечных сил, изгибающие моменты будут меняться в пределах этого участка.

Если подставить вместо x₁ —ноль, который соответствует началу участка, то получим, что М = 0.
Если подставим вместо x₁ — 2 (конец участка), то получим:

С учётом вышеописанных правил знаков, мысленно представляем себе, что сила стремится растянуть верхние волокна, поэтому откладываем рассчитанные значения на эпюре сверху, получив эпюру в виде прямоугольного треугольника. Обязательно, подписываем эпюру как M_z, где z означает, что все изгибающие моменты поворачивают относительно этой оси.

Будет продолжение…

ssopromat.ru