Условия равновесия плоской произвольной системы сил
Выведенные нами ранее условия равновесия для плоской и пространственной систем сходящихся сил, произвольной плоской системы сил и плоской системы параллельных сил также можно было бы получить, пользуясь условиями равновесия (2) произвольной пространственной системы сил. [c.187]Аналитические условия равновесия плоской системы произвольно расположенных сил [c.42]
Если заменить одно уравнение проекций, то условия равновесия плоской системы произвольно расположенных сил будут выглядеть так [c.43]
Поясним смысл этих условий, для чего применим три условия равновесия плоской системы произвольно расположенных сил [c.63]
Условия равновесия плоской системы сил. Для равновесия плоской системы сил необходимо и достаточно, чтобы главный вектор / и главный момент Мо этой системы относительно любого произвольного выбранного центра О равнялись нулю, т.
Устраняется проблема согласования лекций и практических занятий, обусловленная тем, что при традиционном изложении статики условия равновесия плоской (или произвольной) системы сил устанавливаются после изложения теории пар сил и приведения системы сил к простейшему виду. [c.4]
Эти три условия равновесия плоской системы сил можно выразить в другой форме, приравнивая нулю сумму моментов всех сил системы относительно каждой из трёх произвольно выбранных точек, не лежащих на одной прямой. [c.361]
Аналитический метод. Им можно пользоваться при любом числе приложенных сил. Для составления условий равновесия, которых в случае плоской системы сходящихся сил будет два [формулы (12)1, а в случае пространственной системы три [формулы(11)1, надо сначала выбрать координатные оси. Этот выбор можно производить произвольно, но полученные уравнения будут решаться проще, если одну из осей направить перпендикулярно какой-либо неизвестной силе.
Вторая форма условий равновесия для равновесия произвольной плоской системы сил,необходимо и достаточно, чтобы суммы моментов всех этих, сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось Ох, не перпендикулярную прямой АВ, были равны нулю [c.46]
Другой способ решения подобных задач состоит в том, что конструкцию сразу расчленяют на отдельные тела и составляют условия равновесия каждого из тел в отдельности (см. задачу 24). При этом реакции внутренних связей будут попарно равны по модулю и противоположны по направлению. Для конструкции из п тел, на каждое из которых действует произвольная плоская система сил, полу-
Для произвольной плоской системы сил из этих двух условий непосредственно получаем три уравнения равновесия [c.97]
Следовательно, необходимое и достаточное условие равновесия, произвольной плоской системы сил состоит в том, чтобы главный вектор этой системы и ее главный момент были равны нулю
[c. 43]
43]
При решении задач статики обычно исходят из того, что рассматриваемое в задаче тело находится в покое и, значит, согласно первой аксиоме на него действует уравновешенная система внешних сил. Приступая к решению такой задачи, где на тело действует произвольная плоская система сил, мы заранее знаем, что условие равновесия, выраженное равенствами (1.33), выполняется, т. е. если произвольная плоская система сил уравновешена, то ее главный вектор равен нулю и алгебраическая сумма моментов всех сил относительно любой точки также равна нулю. [c.43]
Из предыдущего параграфа известно, что условие равновесия произвольной плоской системы сил выражается тремя уравнениями, значит с их помощью можно определить реакции опор только в том случае, если число реакций связи не превышает трех. Таким образом, балка статически определима, если она, например, опирается на три непараллельных шарнирно-прикрепленных стержня (рис.

Значения реакций и R зависят от силы тяжести шара и и длины нити АВ. Если заданы О и длина АВ, то значения / д и R можно определить из геометрического (см. 1.5) либо аналитического (1.18) условия равновесия системы сходящихся сил, либо уравнения равновесия для произвольной плоской системы сил (см. [c.55]
Равновесие рычага. Рычагом называется твердое тело которое может вращаться вокруг неподвижной оси под действием сил, расположенных в плоскости, перпендикулярной к этой оси. Пусть на рычаг действуют активные силы Яр Pj.
Пусть дана плоская система сил. Возьмем в плоскости произвольную точку А и определим сумму моментов всех сил относительно этой точки. Если бы сумма моментов не равнялась нулю, то система, конечно, не была бы в равновесии. Если же М ==0, то система может либо находиться в равновесии, либо быть приведенной к равнодействующей, проходящей через точку А (см. таблицу на стр. 79). Следовательно, написанное условие хотя и необходимо, но не достаточно для равновесия системы. Возьмем в той же плоскости другую произвольную точку В и определим сумму моментов всех сил системы относительно точки В. Если
Основной особенностью. метода Риттера является требование автономного определения всех неизвестных усилий из уравнений равновесия. Следовательно, уравнения равновесия надо составлять так, чтобы в каждо.м было лишь одно неизвестное. Чаще всего для этого пользуются условием о том, что для уравновешенной плоской системы сил алгебраическая сумма их моментов относительно произвольной точки равна нулю. Будем выбирать центры моментов а тех точках, в которых пересекаются направления двух перерезанных стержней. Эти точки будем называть точками Риттера.
[c.283]
Следовательно, уравнения равновесия надо составлять так, чтобы в каждо.м было лишь одно неизвестное. Чаще всего для этого пользуются условием о том, что для уравновешенной плоской системы сил алгебраическая сумма их моментов относительно произвольной точки равна нулю. Будем выбирать центры моментов а тех точках, в которых пересекаются направления двух перерезанных стержней. Эти точки будем называть точками Риттера.
[c.283]
Итак, условия равновесия произвольной плоской системы сил могут быть выражены тремя алгебраическими уравнениями [c.58]
УСЛОВИЯ РАВНОВЕСИЯ ПРОИЗВОЛЬНОЙ ПЛОСКОЙ СИСТЕМЫ СИЛ [c.93]
Условия (1) являются необходимыми и достаточными условиями равновесия произвольной плоской системы сил. В самом деле, условия (1) являются необходимыми, так как если какое-нибудь из них не выполняется, то рассматриваемая система действующих на тело сил приводится или к равнодействующей (когда или к паре (когда
[c. 93]
93]
Найдем теперь вытекающие из равенств (1) аналитические условия равновесия произвольной плоской системы сил. [c.94]
Эти равенства выражают следующие аналитические условия равновесия произвольной плоской системы сил для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из двух любым образом выбранных в плоскости действия этой системы сил координатных осей и алгебраическая сумма моментов всех сил относительно любой точки той же плоскости были равны нулю.
Одновременно равенства (2) выражают необходимые и достаточные условия равновесия свободного твердого тела, находящегося под действием произвольной плоской системы сил. [c.94]
Равенства (2) являются основной формой условий равновесия произвольной плоской системы сил. Они могут быть выражены и в другом виде. [c.94]
Необходимость этих условий очевидна, так как при равновесии произвольной плоской системы сил алгебраическая сумма моментов всех сил системы относительно любой точки, взятой в плоскости действия этой системы сил, должна равняться нулю. Докажем, что эти условия и достаточны.
[c.94]
Докажем, что эти условия и достаточны.
[c.94]
Докажем теперь, что условия равновесия произвольной плоской системы сил можно сформулировать так для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно каждой из двух любых точек А и В, взятых в плоскости действия этой системы, и алгебраическая сумма проекций всех этих сил на любую ось Ох, не перпендикулярную к прямой, проходяш,ей через точки А и В, были равны нулю [c.95]
Необходимость этих условий вытекает из того, что при равновесии произвольной плоской системы сил равны нулю как алгебраическая сумма моментов всех сил относительно любой точки, взятой в плоскости действия этой системы, так и алгебраическая сумма проекции всех сил на любую ось. [c.96]
Если линии действия всех сил данной системы расположены в одной плоскости и параллельны между собой, то такая система называется плоской системой параллельных сил.
Таким образом, графические условия равновесия произвольной плоской системы сил можно сформулировать так для равновесия произвольной плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы силовой и веревочный многоугольники, построенные для этих сил, были замкнутыми. [c.139]
Так же как и аналитический метод, графический метод определения опорных реакций фермы (или балки). Имеющей одну подвижную и одну неподвижную шарнирные опоры, основан на предположении, что под действием приложенных к ферме активных сил и опорных реакций ферма находится в равновесии. При этом графический метод определения опорных реакций состоит в применении графических условий равновесия произвольной плоской системы сил. [c.139]
[c.139]
Пусть по условию задачи требуется определить реакцию перерезанного стержня 8, зная F vi Y vi не определяя неизвестных реакций Sg и S, двух других перерезанных стержней 6 и 7. Для этого нужно составить такое уравнение равновесия произвольной плоской системы сил F ,, У2, 5g, S,, Sg, в которое неизвестные Sg и iS, не входили бы. Мы [c.154]
Как формулируются условия равновесия произвольной плоской системы сил в графостатике [c.218]
Условия равновесия произвольной плоской системы сил. Различные формы уравнений равновесия [c.55]
Равенства (41) называют условиями равновесия произвольной системы сил в геометрической форме. Сравнивая их с полученными ранее условиями (31) равновесия плоской системы сил, мы видим, что различие заключается в том, что в (41) главный момент системы написан как вектор, а в (31) — как скалярная величина. По сути дела равгнства. (31) являются частным случаем равенств (41), как и плоская система сил является частным случаем системы сил, расположенных, произвольно в пространстве. [c.101]
[c.101]
Формулы (29) выражают следующие аналитические условия равновесия для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лезкащеео в плоскости действия сил, были равны нулю. Одновременно равенства (29) выражают условия равновесия твердого тела, находящегося под действием плоской системы сил. [c.46]
Третья форма условий равновесия уравнения трех моментов) для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А, В и С, не леокащих на одной прямой, были равны нулю [c.47]
Равновесие произвольной плоской системы сил. Метод последовательного сложения. Если твердое тело находится в равновесии под действием произвольной плоской системы сил, то путем последовательного графического сложения таких сил можно определить з 1ачение неизвестных из условий равновесия. При этом число неизвестных не должно превышать трех для системы сил, приложенных к одному твердому телу, иначе задача будет статически неопределенной. Этот графический метод решения задач целесообразно применять, если общее число сил, действующих на твердое тело, невелико. По сравнению с аналитическим методом решения задач на равновесие плоской системы сил указанный графический способ более нагляден, но его применение при большом числе сил очень громоздко.
[c.123]
При этом число неизвестных не должно превышать трех для системы сил, приложенных к одному твердому телу, иначе задача будет статически неопределенной. Этот графический метод решения задач целесообразно применять, если общее число сил, действующих на твердое тело, невелико. По сравнению с аналитическим методом решения задач на равновесие плоской системы сил указанный графический способ более нагляден, но его применение при большом числе сил очень громоздко.
[c.123]
Если же крайние стороны Аа и сВ сливаются, то веревочный многоугольник замыкается (рис.. 271, в), плечо пары обращается в нуль и система находится в равновесии. Таким образом, необходимые и достаточные условия равновесия произвольной плоской системы сил (в геометрической или графической форме) состоят в том, что построенные для этой системы силовой и веревочный многоугольники до.г1Жны быть замкнутыми. [c.261]
При этом силовой многоугольник, построенный для пр оизвольной плоской системы сил, окажется замкнутым.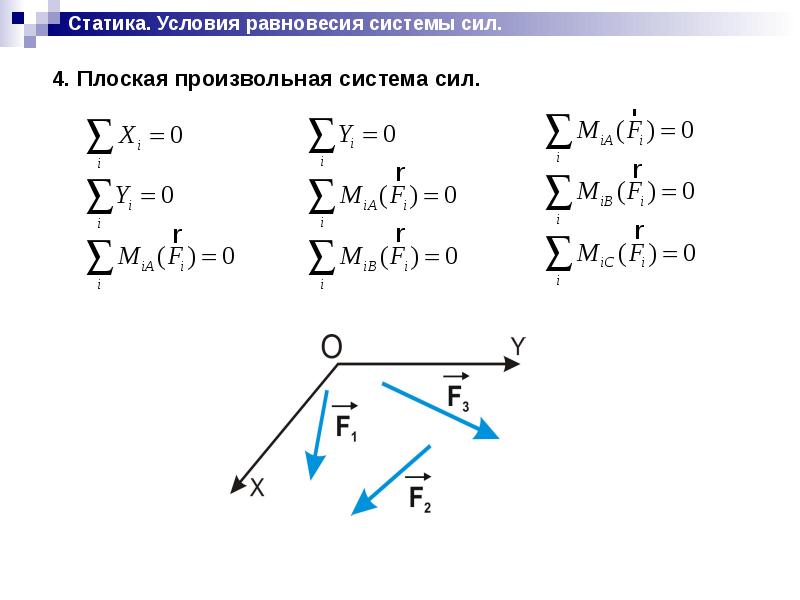 Этого условия было бы достаточно для равновесия системы сходящихся сил. Однако при выполнении только этого условия произвольная плоская система сил не будет находиться в равновесии (см. 22).
[c.92]
Этого условия было бы достаточно для равновесия системы сходящихся сил. Однако при выполнении только этого условия произвольная плоская система сил не будет находиться в равновесии (см. 22).
[c.92]
Мо ФО), и, следовательно, эта система сил не будет находиться в равновесии. Одновременно условия (1) являются достаточными, потому что при / =0 произвольная плоская система сил может приводиться только к паре с моментом Мо, а так какМо = 0, то эта система сил будет находиться в равновесии. [c.93]
Каковы векторные и аналитическа. е условия равновесия произвольной плоской системы сил [c.108]
3. Равновесие плоской системы тел
3.1.Общие сведения о системе тел
Строительные конструкции состоят, как правило, из нескольких тел, соединенных между собой связями. Связи, соединяющие части данной конструкции, называются внутренними связями, а связи, соединяющие данную конструкцию с телами, не входящими в эту систему – внешними связями. Реакции внутренних связей попарно равны, направлены по одной прямой в противоположные стороны, поэтому алгебраическая сумма проекций внутренних сил на любую ось равна нулю так же, как равна нулю сумма моментов этих сил относительно любого центра.
Реакции внутренних связей попарно равны, направлены по одной прямой в противоположные стороны, поэтому алгебраическая сумма проекций внутренних сил на любую ось равна нулю так же, как равна нулю сумма моментов этих сил относительно любого центра.
Важной задачей статики системы твердых тел является определение реакций связей.
Если после отбрасывания внешних связей конструкция остается жесткой (неизменяемой), то для нее задачи статики решаются также как и для абсолютно твердого тела. К таким конструкциям в частности относится ферма (рис. 3.1а), двухшарнирная арка (3.1б) и др.
Рис. 3.1
Вместе с тем в инженерной практике встречаются такие конструкции, которые после отбрасывания связей не остаются жесткими. Примером таких конструкций являются трехшарнирные арки (рис.3.2а), шарнирные рамные системы (рис.3.2б), составные балки (рис.3.2в) и др.
Если у трехшарнирной арки отбросить опоры А и В, то арка станет нежесткой, так как ее части смогут поворачиваться вокруг шарнира С.
Рис.3.2
Согласно аксиоме отвердевания, равновесие изменяемого (деформируемого) тела, находящегося под действием приложенных к нему сил не нарушится, если тело считать отвердевшим, т.е. абсолютно твердым, и к нему можно применять уравнения равновесия абсолютно твердого тела.
Однако эти уравнения при определении внешних реакций изменяемой системы тел, будучи необходимыми, не являются достаточными. Как известно, для абсолютно твердого тела можно составить только три независимых уравнения равновесия, а для изменяемой системы тел необходимо дополнительно составить столько уравнений, сколько в системе содержится тел. Например, для трехшарнирной рамы (рис. 3.2б) можно составить три уравнения равновесия, а число неизвестных связей – четыре. Для нахождения внешних опорных реакций связи необходимо составить три уравнения для всей рамы, а, затем, расчленить раму в шарнире С и составить еще три уравнения равновесия для правой (или левой) части рамы. Эти уравнения будут содержать неизвестные внутренние реакции связи xС, yС. Решая полученную систему из шести уравнений с шестью неизвестными, получим все шесть неизвестных реакций.
Решая полученную систему из шести уравнений с шестью неизвестными, получим все шесть неизвестных реакций.
3.2. Методические указания к решению задач по исследованию условий равновесия системы тел, находящихся под действием произвольной плоской системы сил
При решении таких задач чаще всего сразу расчленяют систему и рассматривают равновесие каждого из тел в отдельности. При этом надо учитывать аксиому о равенстве действия и противодействия, согласно которой силы взаимодействия двух тел равны между собой по абсолютной величине, лежат на одной прямой и направлены в противоположные стороны.
При расчленении систем следует руководствоваться правилом, чтобы в месте расчленения появлялось не более двух неизвестных реакций связей.
Расчленяют систему в следующих соединениях (рис. 3.3):
Рис. 3.3
Порядок решения задач
1. Выделить одно тело системы, равновесие которого следует рассмотреть.
2. Приложить к выделенному телу все активные (заданные) силы. Если к телу приложена распределенная нагрузка, то ее необходимо заменить равнодействующей.
Если к телу приложена распределенная нагрузка, то ее необходимо заменить равнодействующей.
3. Освободить тело от связей, приложив соответствующие реакции. При этом необходимо убедиться, что данная задача является статически определимой.
4. Направить оси координат и выбрать моментные точки. Для каждого тела системы могут быть выбраны различные системы координат.
5. Составить уравнения равновесия произвольной плоской системы сил для выделенного тела.
Составляем уравнения равновесия по вышеизложенной схеме для каждого тела рассматриваемой системы. Все полученные уравнения равновесия решаем совместно, определяя неизвестные реакции связей.
Если в результате решения искомая реакция получается положительной, то это значит, что ее направление выбрано верно, если отрицательной, то истинное направление реакции противоположно выбранному (модуль же реакции определен верно).
После того, как задача решена, необходимо произвести проверку правильности решения. Для этого следует составить не применявшуюся при решении сумму моментов, при этом необходимо учитывать истинные направления реакций. Равенство нулю алгебраической суммы моментов подтвердит правильность решения задачи.
Равенство нулю алгебраической суммы моментов подтвердит правильность решения задачи.
При решении подобных задач можно применять и другой прием. Можно рассмотреть условия равновесия для всей конструкции в целом (как для одного абсолютно твердого тела), а затем к этим трем уравнениям присоединить три уравнения равновесия, составленные только для одного из двух тел данной системы. Этот прием нередко предпочтительнее, так как в уравнения равновесия, составленные для всей системы в целом, входят только внешние силы и поэтому эти уравнения оказываются, обычно, проще.
Пример. Определить внешние (опорные) и внутренние связи рамы, изображенной на рис. 3.4, при следующих исходных данных: q=2кН/м, P=4кН.
Рис. 3.4
Решение.
Составим уравнение равновесия для всей конструкции:
Уравнения равновесия для правой части рамы:
Решая совместно уравнения (3) и (6), получим:
Подставляя найденные значения XВ и YB в уравнения (1) и (2) определим реакции опоры А:
Из уравнений (4) и (5) определим реакции внутренних связей:
Сделаем проверку, составив уравнение моментов для всей конструкции относительно точки В:
Подставляя численные значения, получаем:
Ответ:
Поскольку силы XC и YC – внутренние, то знак силы определяется в зависимости от того, для какой части конструкции рассматривается равновесие.
В том случае, когда части конструкции опираются друг на друга, или когда одна из опор является гладкой поверхностью, целесообразно сразу расчленять систему на отдельные тела и составлять уравнения равновесия для каждого тела в отдельности (см. рис.3.5). При этом реакции внутренних связей будут попарно равны по модулю и противоположны по направлению.
Для расчета составной конструкции (рис. 3.5) следует сразу расчленить конструкцию и рассмотреть равновесие балки DЕ. Уравнение равновесия балки DЕ будет содержать только три неизвестные реакции ХD, YD, NE. Определив внутреннюю реакцию связи NE, нетрудно найти внешние реакции связи балки АВ: XА, YА, NВ.
Пример. Однородная балка АВ весом Р2= 2 кН и длиной 6 м удерживается в горизонтальной плоскости с помощью неподвижной шарнирной опоры и гладкой опоры.
На балку АВ свободно опирается однородная балка DЕ весом Р1=1,5 кН и длиной 6 м. К балке DE приложена сила F=1 кН.
К балке DE приложена сила F=1 кН.
Определить опорные реакции и силу взаимодействия балок AB и DE (рис. 3.5).
Рис. 3.5
Решение. Заданную конструкцию расчленим на систему тел (рис.3.6) и рассмотрим равновесие сначала балки DЕ, а затем балки АВ.
Рис. 3.6
Уравнения равновесия балки DЕ:
Уравнения равновесия балки АВ:
Из уравнения (1):
Из уравнения (3):
Из уравнения (6):
Ответ: XD = 0,5кН, YD = 0,85кН, XA = 1,35кН, YA = 1,21кН, NB=2,67 кН.
Проверка: Составим уравнение моментов относительно точки D для всей конструкции:
Проверка сошлась.
Кирсанов М.Н. — Решебник по теоретической механике — DJVU, страница 2
Автор будет благодарен всем приславшим свои замечания о комплексе РЕШЕБНИК «Теоретическая механика» и предложения по адресу: 111250 Москва, ул. Красноказарменная, д. 17, Московский энергетический институт (ТУ), кафедра теоретической механики. Е-ша11: Кпвапогмфсегшес1ьшре1.ас.гп.
Красноказарменная, д. 17, Московский энергетический институт (ТУ), кафедра теоретической механики. Е-ша11: Кпвапогмфсегшес1ьшре1.ас.гп.
хХаСть | СТАТИКА В статике изучается равновесие тел под действием свл и свойства систем сил,необязательно находящихся в равновесии. Задачи статики можно условно разделить на три типа: задачи на равновесие системы сходящихся сил,т.е, сил, линии действия которых пересекаются в одной точке (глава 1), задачи произвольной плоской системы снл (главы 2,3) и задачи пространственной системы сил (глава 4). Нахождение координат центра тяжести (глава 5) тоже считается задачей статики.
Хотя силы в этой задаче явно не присутствуют, основные формулы задачи следуют из уравнений равновесия системы параллельных сил. Искомыми величинами в задачах статики могут быть реакции опор, усилия в элементах конструкций, геометрические (размеры, углы) и материальные (вес, коэффициент трения) характеристики систем. В статически определимых задачах число уравнений равновесия совпадает с числом неизвестных. Именно такие задачи и будут рассмотрены в этой части. Для решения задач статики потребуются понятия проекции силы на ось и момента силы относительно точки и оси.
Именно такие задачи и будут рассмотрены в этой части. Для решения задач статики потребуются понятия проекции силы на ось и момента силы относительно точки и оси.
Напомним, что проекция вектора силы Р на ось х определяется по формуле Г, = усово, где а — угол между положительным направлением оси и вектором силы, отсчитываемый против часовой стрелки. Если угол острый, то проекция положительная, если тупой — отрицательная. Общее определение момента ЛХо силы Е относительно точки О дается векторным произведением ЛХ (Е) = гв х Е, где ге — радиус-вектор точки приложения вектора силы относительно точки О. Модуль момента вычисляем по формуле ЛХ, (Р) = г Рвш у, 12 где 3 — угол между векторами го и Ф. Направление вектора момента вычисляется по правилу векторного произведения. Плечо 6 силы относительно точки О — это кратчайшее расстояние от точки до линии действия силы; 6 = г в1п у. Вектор момента перпендикулярен плоскости, в которой располагаются силы.
Поэтому в задачах статики плоской системы сил момент можно рассматривать как скалярную величину — величину проекции вектора момента на нормаль к плоскости (ось г). Индекс х для сокращения записи часто опускают и отождествляют момент силы ЛХо относительно точки на плоскости со скалярной величиной — Мо,. Отсюда вытекает практическое правило определения момента силы относительно точки в плоских задачах статики.
Индекс х для сокращения записи часто опускают и отождествляют момент силы ЛХо относительно точки на плоскости со скалярной величиной — Мо,. Отсюда вытекает практическое правило определения момента силы относительно точки в плоских задачах статики.
Для вычисления момента силы относительно точки О (рис. 1) сначала находим проекции силы на оси, а затем момент вычисляем по формуле Мо (Е»‘) = — Р до + Е„. то. Другой способ вычисления момента; М,,(Е) = +г’6, где 6 — плечо силы относительно точки О. о х Рис. 2 Рис. 1 Рис. 3 Знак определяется по правилу векторного произведения. Если сила поворачивает тело относительно центра по часовой стрелке — момент отрицательный, против часовой стрелки положительный.
На рис. 2 момент силы Е относительно точки О отрицательный. Если сила или линия ее действия пересекает точку, то момент силы относительно этой точки равен нулю. Прн решении задач пространственной статики Я 4.3 — з 4.6) требуется вычислять момент силы относительно оси, или, что то же, проекцию момента силы относительно точки (1) на ось, проходятцую через нее. Иногда зту величину удобнее искать как момент проекции Е„ силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью (рис.
Иногда зту величину удобнее искать как момент проекции Е„ силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью (рис.
3). Знак определяем по направлению вращения вокруг оси с точки зрения наблюдателя,находящегося на конце оси. Если вращение происходит по часовой стрелке, то момент отрицательный, против часовой стрелки — положительный. Момент силы относительно осн равен нулю, если сила параллельна оси или пересекает ее, т.е., если сила и ось лежат в одной плоскости. Кроме сил в статике рассматриваются и пары сил. Пара — это совокупность двух равных параллельных противоположно направленных сил. Пара характеризуется моментом — суммой моментов ее сил относительно некоторой точки.
Легко показать, что положение точки не существенно и на величину момента не влияет, поэтому момент пары является свободным вектором. Напомним, что вектор силы является вектором скользящим. В зависимости от знака момента пары на плоскости изображать пару будем изогнутой стрелкой 1 ~ или 1. Не путать эту стрелку с вектором пары! Вектор пары перпендикулярен ее плоскости.
Не путать эту стрелку с вектором пары! Вектор пары перпендикулярен ее плоскости.
Решение двух задач статики в системе Мар1е У приведено в з 15.1, 15.2. Большинство задач статики сводится к решению систем линейных уравнений. Рутинную часть работы по составлению и решению уравнений можно поручить Мар1е Ч. Простейшая программа может выглядеть, например,так: Записывая уравнение на компьютере, а не на бумаге, вы достигаете сразу же нескольких целей.
Во-первых, компьютер выполняет математические действия, часто весьма громоздкие. Во-вторых, уравнение легко поправить и сразу же пересчитать, если вы ошиблись при составлении уравнения и ответ не сходится. В-третьих, решение удобно оформить, распечатав его на принтере. Можно вывести график, таблицу результатов и т.д. Все эти действия можно выполнить и в других системах, в частности, в пакете Асае1еппаХХ1, представленном на сайте яснчя.асас1еппаххйгп. Глава 1 ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ При изучении темы ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ вы научитесь составлять уравнения проекций и решать задачи равновесия плоских стержневых систем методом вырезания узлов.
Этот метод лежит в основе компьютерной программы расчета ферм 1З15.1). 1.1. Простая стержневая система ПОСТАНОВКА ЗАДАЧИ. Плоская шарнирно-стерлснсвал конструкция закреплена на неподвижном основании и нагружена в шарнирах силами. Найти уси ия в сгпержнлх. ПЛАН РЕШЕНИЯ Рассматриваем равновесие внутренних шарниров системы, не соединенных с неподвижным основанием. Такие шарниры будем называть узлами. Действие каждого стержня заменяем его реакцией —. силой, направленной из узла к стержню.
Усилие — — это проекция реакции стержня на внешнюю нормаль к сечению. Если в результате решения задачи реакция стержня, приложенная таким образом к узлу, оказывается отрицательной, то стержень сжат, в противном случае стержень растянут. 1. Вырезаем узел, соединенный только с двумя стержнями. Действие стержней заменяем их реакциями. 2. Для полученной системы сходящихся сил составляем уравнения равновесия в проекциях на выбранные для этого узла оси. 3. Решаем систему двух линейных уравнений и находим искомые усилия. 4.
4.
Вырезаем очередной узел системы, тот, к которому подходят не более двух стержней с неизвестными усилиями. Составляем и решаем уравнения равновесия в проекциях на оси, выбранные для этого 1.1. Простая етержнееая система 15 узла. Этот пункт плана выполняем несколько раз для всех узлов до нахождения всех усилий. 5. Для проверки решения мысленно отделяем конструкцию от основания, заменяя действие рассеченных стержней найденными реакциями. Проверяем выполнение условий равновесия полученной системы сил.
Зямнчянин 1. Существуют фермы *), у которых к каждому узлу присоединены более двух стержней. Например, на рис. 4 изображена конструкция (сетчатая ферма В.Г.Шухова), к каждому узлу которой подходит по три стержня. Диагональные стержни расположены в разных плоскостях и не пересекаются. Здесь нельзя определять усилия по предложенной схеме, переходя от одного узла к другому, так как нет узла, с которого можно начать расчет.
В этом случае сначала составляются уравнения равновесия отдельных узлов, а потом совместно решается система полученных уравнений. Систему можно решать любым известным способом (Решебнин ВМ, 32.1). Рис. 4 Рис. 5 Зямнчяпин 2. Для упрощения уравнений равновесия одну из осей координат можно направить вдоль стержня с неизвестным усилием. Для каждого узла можно выбрать свою систему координат. Злмнчапин 3. Углы между осями и векторами усилий легче определять, если проводить через узлы вспомогательные вертикальные или горизонтальные прямые. Зямнчяпиг.
Систему можно решать любым известным способом (Решебнин ВМ, 32.1). Рис. 4 Рис. 5 Зямнчяпин 2. Для упрощения уравнений равновесия одну из осей координат можно направить вдоль стержня с неизвестным усилием. Для каждого узла можно выбрать свою систему координат. Злмнчапин 3. Углы между осями и векторами усилий легче определять, если проводить через узлы вспомогательные вертикальные или горизонтальные прямые. Зямнчяпиг.
4. Усилия в стержнях можно найти с помощью системы Мар1е Ъ’ (Программа 1, с. 350). О 1Парнирно-стержневая конструкция, нагруженная в шарнирах силами, называется фермой, Весом стержней фермы и трением в шарнирах пренебрегают. Гл. 1. Плоская система сходли~ хся сил 16 Пеиыее. Плоская шарнирно-стержневая конструкция закреплена на неподвижном основании шарнирами Е, Р, С и нагружена в шарнире А горизонтальной силой Р = 100 кН (рис. 5). Даны углы: ЕВРА = 135′, САВВ = 60′, ~ВСВ = 60′, ОВВС = 30′, ~ВЕЕ = 30′. Найти усилия в стержнях. РЕШЕНИЕ Конструкция состоит из шести стержней, соединенных тремя шарнирами (узлами). Узлы фермы находятся в равновесии.
Узлы фермы находятся в равновесии.
Для каждого узла А, В, Е составляем по два уравнения равновесия в проекциях на выбранные оси. Из шести уравнений находим шесть искомых усилий. 1. Решение задачи начинаем с рассмотрения узла А, так как этот узел соединен только с двумя стержнями АВ и АЕ. При вырезании узла действие каждого стержня заменяем силой, направленной из шарнира к стержню (рис.
6). 2. Составляем уравнения равновесия. Для упрощения уравнений ось у направляем по стержню АВ. Получаем ~ Х, = Ял,сов15′ — Рв1п30′ = О, 2,’У = — Ялесцп15’+ Ялв + Р сов 30′ = О. где Х, — проекции силы г на ось т, а У, — проекции силы 1 на ось р 3. Решаем уравнения. Из первого уравнения сис гемы находим усилие Зле — — 51.76 кН, из второго — усилие Ялн — — — 73.21 кН. 4. Рассматриваем узел Е. К нему подходят три стержня (рис. 7). Рис. 7 Рис. 6 Усилие в одном из них уже известно Ял — — 51.76 кН. Усилия в двух других находим из уравнений для проекций: 1.1, ??растая стержневая система 17 2„Х, = — $,,яп30’+ $ сое45′ = О, 1; = — $рк сое 30′ — $рр + $др а1п 45′ = О.
Находим $рн — — 73.21 кН, $ = — 26.79 кН. Составляем уравнения равновесия узла В в проекциях на оси, направленные по стержням ВС и ВВ (рис. 8): д Х = $ов+ $дввш30′ = О, ~ 1; = $вп — $дв сов 30′ = О. Решая уравнения, получаем: $пв — — — $дн яп30′ = 73.21 0.5 = 36.6 кН, $вн — — $дн сов 30′ = — 73.21 . 0.866 = — 63.4 кН.
5. Проверка. Рассматриваем равновесие конструкции в целом. $дв С и 30′ $ев Рис. 8 1’ис. 9 Горизонтальным сечением отсекаем ферму от основания. Действия стержней заменяем силами, которые направляем, как и раньше, по внешним нормалям к сечениям стержней, т.е. вниз (рис. 9). Система сил, действующих на ферму, не является сходящейся. Для такой системы справедливы три уравнения равновесия, одно из которых . уравнение моментов.
Страница 5 из 8 ЗАДАЧА 2. РАВНОВЕСИЕ ПЛОСКОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩЕЙ НА РАМУ Рассчитать величины реакций связей изображенной на рисунке рамы с использованием приведенных на схемах и таблице 2 исходных данных. Таблица 2. Исходные данные к задаче 2.
Методические указания к решению задачи 2 Решение задач на равновесие твердого тела, независимо от взаимного расположения приложенных к телу сил, рекомендуется проводить в следующем порядке:
Точку, относительно которой должно быть составлено уравнение моментов, следует выбрать в точке пересечения линий действия двух неизвестных сил. Это дает возможность непосредственно определить из соответствующего уравнения моментов величину третьей неизвестной силы. Однако, если эта точка расположена так, что вычисление плеч при определении моментов сил представляет значительные трудности, то лучше уравнение моментов составить относительно другой точки, в которое войдут величины двух неизвестных сил, и затем совместно решить полученную систему уравнений; 7. составить уравнение равновесия твердого тела.
|
1.1.4. Система произвольно расположенных сил
Теорема о параллельном переносе силы. Действие силы на АТТ не из-менится, если перенести ее параллельно самой себе в некоторую точку (центр приведения) присоединив при этом пару сил. Момент присоединенной пары равен моменту приведенной силы, относительно центра приведения. В точке А (рис. 1.31) приложена сила , предстоит перенести ее в точку В. Как это сделать? В точке В прикладываем силы равные по модулю силе ; . Получили эквивалентнуюсистему трех сил, которую можно рассматривать как совокупность силы и пары сил с моментом (рис. 1.32).
1.32).Пару называют п р и с о е д и н е н н о й; ее момент равен моменту переносимой силы относительно центра приведения и, следовательно, зависит от положения этого центра.
Приведение произвольной пространственной системы сил к данному центру. Главный вектор и главный момент. Систему сил, приложенных к телу, можно упростить, используя теорему о параллельном переносе силы. В результате приведения произвольной пространственной системы сил к данному центру в общем случае получаем главный вектор, равный геометрической сум-ме всех сил системы, и главный момент, равный геометрической сумме момен-тов всех приводимых сил относительно центра приведения (рис. 1.33).
Сложим и т.д., получим силовой многоугольник, где
(1.15)
Затем векторно сложим векторы моментов
(1.16) ; (1.17)
Главный вектор инвариантен по отношению к центру приведения.
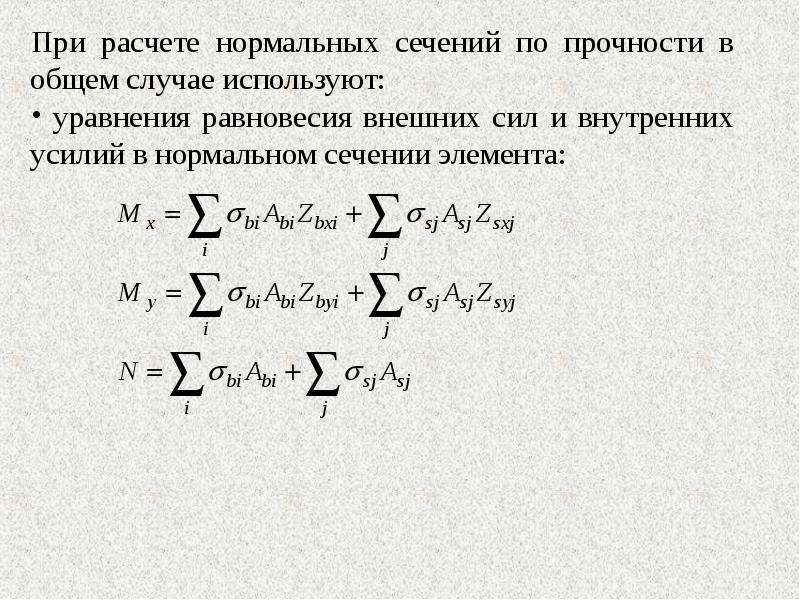 Главный момент зависит от вы-бора центра приведения. По
модулю главный вектор вычисляется
Главный момент зависит от вы-бора центра приведения. По
модулю главный вектор вычисляетсяR*= (1.18)
Рис. 1.33
где
проекции главного вектора на координатные оси *(Rx, Ry, Rz), а проекции каждой из сил (X1, Y1 , Z1), (X2, Y2, Z2) и т.д.Направление находим по направляющим косинусам
Главный момент
Для равновесия произвольной пространственной системы сил необходимо и дос-таточно, чтобы алгебраическая сумма проекций всех этих сил на каждую из коор-динатных осей равнялась нулю, и чтобы алгебраическая сумма моментов всех сил системы относительно каждой из трех координатных осей равнялась нулю.
Система параллельных сил. Если ось OZ параллельна силам, то три уравнения (1.23) обращаются в тождества, так как проекции сил на оси OX и OY и их моменты относительно оси OZ равны нулю. Оставшиеся три уравнения явля-ются уравнениями равновесия параллельных сил в пространстве (рис.
 1.34).
1.34). Для параллельных сил расположенных в плоскости XOY (рис. 1.35), имеем два уравнения равновесия:
(1.25)
Плоская система произвольно расположенных сил. Если силы дейст-вуют в плоскости XOY (рис. 1.36), то суммы проекций их на ось OZ и моментов относительно осей OX и OY равны нулю. При равновесии тела под действием плоской системы сил суммы их про-екций на оси координат и сумма моментов относительно произвольного центра, лежащего в плоскости сил, равны нулю
Рис. 1.34 Рис. 1.35 Рис. 1.36 Примеры упрощения системы сил, действующих на самолет. Силы взаимодействия самолета с поверхностью взлетно-посадочной полосы (ВПП) и воздухом при движении по земле и в полете подчиняются сложным закономер-ностям. Во всех случаях систему сил, действующих на самолет, упрощают. На-пример, воздушное давление, неравномерно распределенное по нижней и верх-ней поверхностям крыла (или стабилизатора, киля), часто суммируют и относят к одной поверхности.
 Силы,
действующие на самолет в горизонтальном полете с постоянной скоростью без
бокового ветра, могут быть приведены к плоской системе сил (рис. 1.37).
Силы,
действующие на самолет в горизонтальном полете с постоянной скоростью без
бокового ветра, могут быть приведены к плоской системе сил (рис. 1.37).Рис. 1.37
Вес самолета , подъемная сила крыла и горизонтального оперения , тяга двигателей и сила лобового сопротивления удовлетворяют трем уравнениям равновесия:
1) условие сохранения постоянной скорости
(1.27)2) условие сохранения постоянной высоты
(1.28)
3) условие сохранения горизонтального положения самолета (1.29)
Теорема о моменте равнодействующей (теорема Вариньона). Момент равнодействующей произвольной системы сил относительно любой точки (оси) равен сумме моментов составляющих сил относительно той же точки (оси) (рис. 1.38).
Пусть действующая на тело
произвольная система сил приводится к равнодействующей . Уравновесим тело, приложив
к нему
силу * = — . Новая система сил находится
в
равновесии и для нее справедливо уравнение равновесия.
Новая система сил находится
в
равновесии и для нее справедливо уравнение равновесия.
но
,то ,
или
(1.30)
Рис. 1.38 Рис. 1.39
Понятие о моменте устойчивости и моменте опрокидывания. При опробовании двигателя главные колеса шасси уперты в подкладки D, а хвостовое колесо не отрывается от земли. Будем считать, что на самолет действует только две силы: — тяга винта и — вес самолета, лежащие в вертикальной плоскости (рис. 1.39).
Выясним условия, при которых хвост прижат к земле. Для этого найдем равнодействующую сил и . Возможны два случая:
1) равнодействующая проходит слева от точки D;
2) равнодействующая проходит справа от точки D.
В первом случае самолет находится в равновесии, опрокидывание невозможно. Равнодействующая стремится повернуть самолет вокруг точки D против часовой стрелки , то
, тогда
(1.
 31)
31)или — момент устойчивости больше момента опрокидывания.
Второй случай, если лежит справа от точки D, то , а т.к
, (1.32)
то или , равновесие самолета нарушится, его хвост поднимется, возможно к а п о т и р о в а н и е самолета. Отношение момента устойчивости к опрокидывающему моменту называется коэффициентом устойчивости. T>
СТАТИКА 5 Произвольная плоская система сил 5
СТАТИКА 5. Произвольная плоская система сил
5. 1. Приведение произвольной плоской системы сил к простейшему виду Опр. Произвольной плоской системой сил называется такая система, линии действия которых лежат в одной плоскости. Примечание. Частным случаем произвольной плоской системы сил является плоская система сходящихся сил. Теорема о приведении произвольной плоской системы сил к простейшему виду. Любая плоская система сил, действующих на абсолютно твердое тело, приведении к произвольно выбранному равной главному вектору, центру О заменяется одной силой и приложенной в центре приведения О, и одной парой с равным алгебраической сумме моментов всех моментом сил относительно центра О, то есть:
Примечание. Главный момент для плоской системы сил заменен на алгебраическую сумму моментов всех сил относительно центра приведения, так как все векторные моменты сил будут параллельны. 5. 2. Равновесие произвольной плоской системы сил Необходимые и достаточные условия равновесия любой системы сил ранее были получены в виде формул (*): Из этих выражений вытекают аналитические условия равновесия плоской системы сил. Их можно получить в трех различных формах. 1. Основная форма условий равновесия ∑ Fkх = 0, ∑ Fkу = 0, (1)
Главный момент для плоской системы сил заменен на алгебраическую сумму моментов всех сил относительно центра приведения, так как все векторные моменты сил будут параллельны. 5. 2. Равновесие произвольной плоской системы сил Необходимые и достаточные условия равновесия любой системы сил ранее были получены в виде формул (*): Из этих выражений вытекают аналитические условия равновесия плоской системы сил. Их можно получить в трех различных формах. 1. Основная форма условий равновесия ∑ Fkх = 0, ∑ Fkу = 0, (1)
Вывод Формулы (1) выражают следующие аналитические условия равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций всех сил на две координатные оси и сумма моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю. 2. Вторая форма условий равновесия. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось Ох, не перпендикулярную прямой АВ, были равны нулю: ∑ Fkх = 0, А О В F х (2)
3. Третья форма условий равновесия (уравнения 3 -х моментов) Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю: (3) Равновесие плоской системы параллельных сил В случае, когда все действующие на тело силы параллельны другу, можно направить ось Ох перпендикулярно силам, а ось Оу параллельно им. Тогда первое уравнение в выражении (1) обратиться в тождество вида 0 ≡ 0. В результате для параллельных сил останется только два условия равновесия ∑ Fkу = 0, у F 1 О F 2 х Fn
Третья форма условий равновесия (уравнения 3 -х моментов) Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю: (3) Равновесие плоской системы параллельных сил В случае, когда все действующие на тело силы параллельны другу, можно направить ось Ох перпендикулярно силам, а ось Оу параллельно им. Тогда первое уравнение в выражении (1) обратиться в тождество вида 0 ≡ 0. В результате для параллельных сил останется только два условия равновесия ∑ Fkу = 0, у F 1 О F 2 х Fn
Другая форма условий равновесия для параллельных сил, получающаяся из равенств (2) или (3), имеет вид 5. 3. Решение задач на равновесие произвольной плоской системы сил. Реакции неподвижной шарнирной опоры и жесткой заделки. В технике часто встречаются задачи с тремя типами опорных закреплений: подвижная шарнирная опора, неподвижная шарнирная опора и жесткая заделка. Реакции этих опор были рассмотрены ранее. Рассмотрим опорные реакции неподвижной шарнирной опоры и жесткой заделки подробнее.
Реакции этих опор были рассмотрены ранее. Рассмотрим опорные реакции неподвижной шарнирной опоры и жесткой заделки подробнее.
1. Неподвижная шарнирная опора. Реакция такой опоры проходит через ось шарнира и может иметь любое направление в плоскости чертежа. RА / Р у УА Q RА Неизвестную по направлению реакцию можно разложить на две составляющие по координатным осям. ХА неподвижной шарнирной опоры представляют в виде двух составляющих направленных по координатным осям. q В А Освободимся от связей. Вывод. Реакцию RВ RА Р R В/ RВ х
2. Жесткая заделка. Ранее был сделан вывод о том, что действие жесткой заделки заменяется наперед неизвестной реакцией , которая может иметь любое направление в плоскости действия сил, и парой сил, с наперед неизвестным моментом МА. Освободимся от связи. F RА МА / МА А RА / В у УА F RА ХА Неизвестную по направлению реакцию А можно разложить на две составляющие МА по координатным осям. В Вывод. Жесткую заделку заменяют двумя составляющими направленными по координатным осям, и парой сил, с наперед неизвестным моментом МА. х
х
Решение задач. Применяют алгоритм действий, рассмотренный ранее. Пример 1. Однородный брус АВ весом Р опирается концом А на гладкую горизонтальную плоскость и выступ D, а концом В – на наклонную плоскость, образующую с горизонтальной плоскостью угол α. Сам брус наклонен под углом β. Определить силы давления бруса на обе плоскости и выступ D. R D N 1 β А В α N 2 Р 1. Выберем объект равновесия. Брус АВ. 2. Приложим к объекту равновесия заданные силы. Сила P. 3. Освободимся от связей.
3. Освободимся от связей. В точке В свободное опирание. Реакция связи R направлена по общей нормали в точке соприкосновения В. R D N 1 β А N 2 Р В других точках также свободное опирание. Реакции связей N 1 , N 2 будут направлены перпендикулярно соответствующим плоскостям. 4. Выберем систему координат. В α
К у 5. Выберем моментную точку. R h Удобно взять точку А, так как в ней сходится большее число неизвестных сил (реакций связей). N 1 D g α β А N 2 Р 6. Составим таблицу проекций и моментов. Fk N 1 N 2 P R Fkx 0 N 2 0 — R sin (α) Fkу N 1 0 -P R cos (α) m. А (Fk ) 0 0 — P a cos (β) R 2 a cos ( γ ) Обозначим АВ = 2 а. Найдем плечо силы R относительно точки А: h = АК. Введем угол γ = α – β. Тогда h = 2 a cos ( γ ). В х
N 1 D g α β А N 2 Р 6. Составим таблицу проекций и моментов. Fk N 1 N 2 P R Fkx 0 N 2 0 — R sin (α) Fkу N 1 0 -P R cos (α) m. А (Fk ) 0 0 — P a cos (β) R 2 a cos ( γ ) Обозначим АВ = 2 а. Найдем плечо силы R относительно точки А: h = АК. Введем угол γ = α – β. Тогда h = 2 a cos ( γ ). В х
7. Составим условия (уравнения) равновесия. х: N 2 — R sin (α) = 0, у: N 1 – P + R cos (α) = 0, МА: — P a cos (β) + R 2 a cos ( γ ) = 0. Из последнего уравнения находим R = (P cos (β))/ 2 cos ( γ ) или R = (P cos (β))/ 2 cos (α – β ). Подставляя значение R во второе уравнение, получим N 1 = Р [1 – ]. Решая первое уравнение, найдем N 2 = Р .
Пример 2. d Симметричная арка загружена системой сил, приводящейся к силе Q = 40 к. Н, приложенной в точке D, и паре сил с моментом m. D = 120 к. Н м. Вес арки Р=80 к. Н. Дано: АВ = а = 10 м, d = 2 м, h = 3 м, α = 600. D α m. D P А Q В а Решение. 1. Выберем объект равновесия. Арка. 2. Приложим к объекту равновесия заданные силы. Силы P, Q и пара сил с моментом m. D. h
Силы P, Q и пара сил с моментом m. D. h
3. Освободимся от связей. В точке А подвижный шарнир, который заменяется одной реакцией УА , перпендикулярной плоскости, по которой шарнир может перемещаться. у d D m. D P УА А h УВ Q В а В точке В неподвижный шарнир, который заменяется двумя реакциями 4. Выберем систему координат. 5. Выберем две моментные точки для того, что бы составить вторую форму условий равновесия. Удобно взять точки А и В, так как в них сходится большее число неизвестных сил (реакций связей). х ХВ
Удобно взять точки А и В, так как в них сходится большее число неизвестных сил (реакций связей). 6. Составим таблицу проекций и моментов. Предварительно разложим силу Q на две составляющие Q 1, Q 2. Модули составляющих: Q 1 = Q cos α , Q 2 =Q sin α. Fk УА ХВ Fkx 0 m. А ( F k ) 0 m. В (Fk) — УАа УВ P ХВ 0 0 0 УВ а 0 0 Q 1 Q cos α у d D Q 1 Q 2 УА А m. D P h УВ Q В х ХВ а Q 2 0 — — Q cos(α)h — Q sin(α)d Рa/2/2 Q sin(α)(а-d) -Q Рa/2 cos(α)hh m. D 0 m. D При вычислении момента силы Q была использована теорема Вариньона о моменте равнодействующей:
D 0 m. D При вычислении момента силы Q была использована теорема Вариньона о моменте равнодействующей:
7. Составим уравнения равновесия. ∑ Fkx = ХВ + Q cos α = 0, ∑ m. А ( Fk) = УВ а — Рa/2 — h Q cos α — d Q sin α + m. D= 0, ∑ m. В ( Fk ) = — УАа + Рa/2 — h Q cos α + (а-d) Q sin α + m. D= 0. 8. Решим уравнения Из первого уравнения получим ХВ = — Q cos α = — 20 к. Н. Из второго уравнения найдем УВ = Р/2 + Q (d sinα + h cosα)/а — m. D /а ≈ 40, 9 к. Н. Из третьего уравнения вычислим УА = Р/2 + Q [(а — d) sin α — h cos α] /а + m. D /а = 73, 7 к. Н.
Модуль полной реакции в опоре В найдется по формуле: 9. Сделаем проверку Составим уравнение проекций на ось Ау ∑ Fkу = УА + УВ — Q sin α – Р = 114, 6 – 114, 6 ≡ 0.
Уравнение равновесия — обзор
Уравнения равновесия могут быть записаны для каждого сочленения по очереди в терминах коэффициентов натяжения и координат сочленения, относящихся к некоторой удобной системе осей. Решение этих уравнений дает t AB и т. Д., Откуда T AB = t AB L AB , в котором можно вычислить L AB , если не указано иное. используя теорему Пифагора, т.е. LAB = (xB − xA) 2+ (yB − yA) 2.Опять же, первоначальное предположение о растяжении в элементе приводит к отрицательным значениям, соответствующим сжатию. Обратите внимание на порядок суффиксов в уравнениях (4.3) и (4.4).
Решение этих уравнений дает t AB и т. Д., Откуда T AB = t AB L AB , в котором можно вычислить L AB , если не указано иное. используя теорему Пифагора, т.е. LAB = (xB − xA) 2+ (yB − yA) 2.Опять же, первоначальное предположение о растяжении в элементе приводит к отрицательным значениям, соответствующим сжатию. Обратите внимание на порядок суффиксов в уравнениях (4.3) и (4.4).
Определите силы в элементах фермы с шарнирным соединением, показанной на рис. 4.21.
Рисунок 4.21. Расчет фермы с использованием коэффициентов натяжения (Пример 4.6).
Сначала рассчитываются опорные реакции, которые показаны на рис. 4.21.
Следующим шагом является выбор системы осей xy , а затем вставка координат соединения в диаграмму.На рис. 4.21 мы выберем точку опоры A в качестве начала осей, хотя на самом деле достаточно любого соединения; тогда совместные координаты будут такими, как показано.
Опять же, как и в методе соединений, решение может начинаться только с соединения, в котором существует не более двух неизвестных сил стержня, в данном случае соединения A и E. Теоретически неважно, в каком из этих соединений начинается анализ. но поскольку A является началом осей, мы начнем с A. Обратите внимание, что нет необходимости вставлять стрелки, чтобы указать направления сил стержня, поскольку предполагается, что элементы находятся в напряжении, а направления компонентов сил стержня равны автоматически указывается при записи в терминах коэффициентов натяжения и координат соединения (уравнения (4.3) и (4.4)).
Уравнения равновесия в сочленении A:
(i) xdirection: tAB (xB − xA) + tAC (xC − xA) −RA, H = 0
(ii) ydirection: tAB (yB − yA) + tAC (yC − yA) −RA, V = 0
Подставляя значения R A, H , R A, V и совместные координаты в уравнения (i) и (ii), получаем , из уравнения. (i),
tAB (0−0) + tAC (1. 5−0) –3 = 0
5−0) –3 = 0
tAC = + 2.0
и из уравнения. (ii)tAB (1.5−0) + tAC (0−0) + 1 = 0
, так чтоtAB = −0.67
Из вывода уравнений (4.3) и (4.4) видно, что единицей измерения коэффициента натяжения является сила на единицу длины, в данном случае кН / м. Однако, как правило, мы опускаем единицы измерения.
Теперь мы можем перейти к стыку B, в котором, поскольку было вычислено t BA (= t AB ), есть два неизвестных
(iii) xdirection: tBA (xA − xB) + tBC (xC − xB) + tBD (xD – xB) + 3 = 0
(iv) направление y: tBA (yA − yB) + tBC (yC − yB) + tBD (yD − yB) = 0
Подстановка значений совместных координат и t BA в уравнениях (iii) и (iv) мы имеем, из уравнения.(iii)-0,67 (0-0) + tBC (1,5-0) + tBD (1,5-0) + 3 = 0
, что упрощается до(v) 1,5tBC + 1,5tBD + 3 = 0
и из уравнения . (iv)−0,67 (0−1,5) + tBC (0−1,5) + tBD (1,5−1,5) = 0
, откудаtBC = + 0,67
Следовательно, из уравнения. (v)
(v)
tBD = −2,67
Теперь есть только две неизвестные стержневые силы в соединении D. Следовательно, в D
(vi) xdirection: tDB (xB − xD) + tDF (xF − xD) + tDC ( xC − xD) = 0
(vii) y направление: tDB (yB − yD) + tDF (yF − yD) + tDC (yC − yD) –5 = 0
. t DB (= t BD ) в уравнениях (vi) и (vii) мы получаем из уравнения.(vi)
−2,67 (0−1,5) + tDF (3,0−1,5) + tDC (1,5−1,5) −5 = 0
, так чтоtDF = −2,67
и из уравнения. (vii)−2,67 (1,5−1,5) + tDF (1,5−1,5) + tDC (0−1,5) = 0
, откудаtDC = −3,33
Затем решение переходит к соединению C, чтобы получить t CF и t CE или соединить F для определения t FC и t FE ; соединение F было бы предпочтительнее, поскольку в F встречается меньше элементов, чем в C. Наконец, оставшийся неизвестный коэффициент натяжения ( т EC или т EF ) находится с учетом равновесия соединения E. Тогда
Тогда
tFC = + 2.67, tFE = −2.67, tEC = 0
, что читатель должен проверить.Силы в элементах фермы теперь рассчитываются путем умножения коэффициентов растяжения на длины элементов, т. Е.
TAB = tABLAB = −0,67 × 1,5 = −1,0 кН (сжатие) TAC = tACLAC = + 2,0 × 1,5 = + 3,0 кН (натяжение) TBC = tBCLBC
, в которомLBC = (xB − xC) 2+ (yB − yC) 2 = (0-1,5) 2+ (1,5-0) 2 = 2,12 м
Тогда
TBC = + 0,67 × 2,12 = + 1,42 кН (растяжение)
Обратите внимание, что при расчете длин элементов не имеет значения, в каком порядке координаты соединения появляются в скобках, поскольку скобки имеют квадратную форму.Также
TBD = tBDLBD = −2,67 × 1,5 = −4,0 кН (сжатие)
Аналогично
TDF = −4,0 кН (сжатие) TDC = −5,0 кН (сжатие) TFC = + 5,67 кН (растяжение) TFE = — 4,0 кН (сжатие) TEC = 0
Срок действия
| Определение
| ||
Термин
| Определение | ||
flashcardmachine.com/images/preview_card_back.gif»>
Термин
| Определение
| ||
Срок
| flashcardmachine.com/images/preview_card_back.gif»>
Определение | ||
Условие
| Определение | ||
Условие
| Определение
| ||
Срок
| Определение
| ||
flashcardmachine.com/images/preview_card_back.gif»>
Условие
| Определение | ||
Условие
| gif»>
Определение | ||
Условие
| Определение | ||
Условие
| Определение
| ||
Срок
| Определение | ||
Условие
| Определение | ||
Условие
| Определение | ||
Условие
| Определение | ||
Срок действия
| Определение
| ||
com/images/preview_card_back.gif»>
Условие
| Определение | ||
Член
| flashcardmachine.com/images/preview_card_back.gif»>
Определение | ||
Срок действия
| Определение | ||
Член
| Определение | ||
Член
| Определение
| ||
gif»>
Условие
| Определение | ||
Срок
| Определение
| ||
Срок
| Определение
| ||
flashcardmachine.com/images/preview_card_back.gif»>
Член
| Определение | ||
Член
| Определение | ||
flashcardmachine.com/images/preview_card_back.gif»>
Условие
| Определение | ||
Условие
| gif»>
Определение
| ||
Член
| Определение | ||
Срок
| Определение | ||
Срок
| Определение | ||
flashcardmachine.com/images/preview_card_back.gif»>
Срок
| Определение
| ||
Член
| Определение | ||
Условие
| Определение | ||
Условие
| Определение
| ||
Термин
| flashcardmachine.com/images/preview_card_back.gif»>
Определение
| ||
| Член ,
| Определение | ||
| flashcardmachine.com/images/preview_card_back.gif»>
Термин ,
| Определение | ||
Термин
| Определение | ||
flashcardmachine.com/images/preview_card_back.gif»>
Термин
| Определение | ||
Ключ
| gif»>
Определение | ||
Условие
| Определение | ||
Условие
| Определение | ||
Член
| Определение
| ||
flashcardmachine.com/images/preview_card_back.gif»>
Условие
| Определение | ||
Член
| gif»>
Определение | ||
Условие
| Определение | ||
Условие
| flashcardmachine.com/images/preview_card_back.gif»>
Определение
| ||
Термин
| Определение | ||
flashcardmachine.com/images/preview_card_back.gif»>
Условие
| Определение | ||
Член
| flashcardmachine.com/images/preview_card_back.gif»>
Определение | ||
Термин
| Определение | ||
Срок
| Определение
| ||
Термин
| Определение
| ||
Обозначение
| Определение
| ||
flashcardmachine.com/images/preview_card_back.gif»>
Срок
| Определение
| ||
Условие
| Определение
| ||
Условие
| Определение
| ||
flashcardmachine.com/images/preview_card_back.gif»>
Термин
| Определение | ||
Термин
| com/images/preview_card_back.gif»>
Определение
| ||
Термин
| Определение
| ||
flashcardmachine.com/images/preview_card_back.gif»>
Член
| Определение | ||
Срок действия
| Определение | ||
flashcardmachine.com/images/preview_card_back.gif»>
Условие
| Определение | ||
Условие
| flashcardmachine.com/images/preview_card_back.gif»>
Определение | ||
Срок действия
| Определение | ||
Срок
| Определение | ||
Срок
| Определение | ||
Член
| Определение | ||
Условие
| Определение
| ||
Термин
| Определение | ||
Термин
| Определение | ||
Термин
| Определение | ||
Условие
| Определение | ||
Член
| Определение
| ||
Условие
| Определение | ||
Срок
| Определение | ||
Условие
| Определение | ||
Условие
| Определение | ||
% PDF-1.3 % 1782 0 объектов> эндобдж xref 1782 95 0000000016 00000 н. 0000004366 00000 н. 0000002244 00000 н. 0000004506 00000 н. 0000004534 00000 п. 0000004582 00000 н. 0000004982 00000 н. 0000005067 00000 н. 0000005152 00000 н. 0000005235 00000 п. 0000005318 00000 н. 0000005401 00000 п. 0000005484 00000 н. 0000005567 00000 н. 0000005650 00000 н. 0000005733 00000 н. 0000005816 00000 н. 0000005899 00000 н. 0000005982 00000 п. 0000006065 00000 н. 0000006148 00000 п. 0000006231 00000 п. 0000006314 00000 н. 0000006397 00000 н. 0000006480 00000 н. 0000006563 00000 н. 0000006646 00000 п. 0000006729 00000 н. 0000006812 00000 н. 0000006895 00000 н. 0000006978 00000 н. 0000007061 00000 п. 0000007144 00000 н. 0000007227 00000 н. 0000007310 00000 н. 0000007393 00000 н. 0000007476 00000 н. 0000007559 00000 н. 0000007642 00000 н. 0000007725 00000 н. 0000007808 00000 н. 0000007891 00000 н. 0000007974 00000 н. 0000008057 00000 н. 0000008140 00000 п. 0000008223 00000 п. 0000008306 00000 н. 0000008388 00000 п. 0000008470 00000 н. 0000008552 00000 п. 0000008634 00000 н. 0000008716 00000 н. 0000009345 00000 п. 0000010518 00000 п. 0000010605 00000 п. 0000010635 00000 п. 0000010704 00000 п. 0000011116 00000 п. 0000016065 00000 п. 0000016727 00000 п. 0000016964 00000 п. 0000017452 00000 п. 0000023744 00000 п. 0000024483 00000 п. 0000024795 00000 п. 0000025325 00000 п. 0000031705 00000 п. 0000032116 00000 п. 0000033286 00000 п. 0000033395 00000 п. 0000033855 00000 п. 0000034345 00000 п. 0000034709 00000 п. 0000035515 00000 п. 0000036238 00000 п. 0000036587 00000 п. 0000040484 00000 п. 0000041003 00000 п. 0000041339 00000 п. 0000041505 00000 п. 0000042164 00000 п. 0000042794 00000 н. 0000043313 00000 п. 0000043945 00000 п. 0000045113 00000 п. 0000045200 00000 п. 0000045240 00000 п. 0000046410 00000 п. 0000047036 00000 п. 0000048198 00000 п. 0000049369 00000 п. 0000049456 00000 п. 0000049506 00000 п. 0000050041 00000 п. 0000004153 00000 п. трейлер ] >> startxref 0 %% EOF 1784 0 obj> поток x ڴ ViPSW ~ YQX @ P`k1 EPE1HD @ * ULUZABDA * AEPRB3 $ ss} N # p’A, + V`! «Ӱ0
инженерная механика 1 — Engenharia Mecânica
рычаг силы F с
относительно 0.Направление вращения момента задается
направление вращения силы F около 0.
= =
ж
f ′ f
0ч0 ч
f ′ f ′
ж
0
F
M (0) = hF
FF
F F
Рис. 3.7
Следует отметить, что момент пары не зависит от
точка отсчета, тогда как величина и направление вращения
момента силы зависят от этой точки.
Часто бывает полезно заменить силу F ее декартовой
компоненты F x = Fx ex и F y = Fy ey (рис. 3.8). Принятие
обычно используемое знаковое соглашение о том, что момент положителен, если
он имеет тенденцию вращать тело против часовой стрелки, если смотреть со стороны
выше (�) момент силы F относительно точки 0 на рис.3.8 это
задается формулой M (0) = hF. Используя отношения
h = x sinα− y cosα
и
sinα = Fy / F, cosα = Fx / F
момент также можно представить как
М (0) = hF =
(
Икс
Fy
F
- y Fx
F
)
F = xFy - y Fx. (3.8)
3.1 Общие системы сил на плоскости 59
0
αx
x sinα
у
у
Икс
час
y cosα
α
α
F y
F x
F
Рис. 3.8
0
у
Икс
F 1
у
Икс
F 2y
F 1y
F 2xF 1x
F 2
р
Рис. 3.9
Следовательно, момент равен сумме моментов силы
компонентов около 0. Обратите внимание на направление вращения соответствующих
компоненты: они определяют алгебраические знаки при суммировании.Рассмотрим теперь две силы F1 и F2 и их равнодействующую R
(Рис. 3.9). Моменты двух сил относительно точки 0
являются
M
(0)
1 = xF1y - y F1x, М
(0)
2 = xF2y - y F2x,
а их сумма равна
M
(0)
1 + М
(0)
2 = х (F1y + F2y) −y (F1x + F2x) = xRy − y Rx = M
(0)
Р .
Следовательно, неважно, добавляются ли сначала силы и
то определяется момент или, если сумма индивидуальных моментов
ments. Это свойство выполняется для произвольного числа
сил:
Сумма моментов единичных сил равна мо-
мент их результирующего.3.1.3 Результат систем копланарных сил
Рассмотрим твердое тело, на которое действует общая система
копланарные силы (рис. 3.10). Чтобы исследовать, как эта система может быть
сводится к более простой системе, выбирается точка отсчета A и
линии действия сил перемещаются без изменения их
60 3 Общие системы сил, равновесие твердого тела
==
знак равно
знак равно
Икс
у
M
(А)
1
M
(А)
2
M
(А)
R A
А
А
M
(А)
я
F1 Fi
F2
F1 Fi
F2
р
р
α
час
Рис. 3.10
направлениях, пока они не пройдут через A. Чтобы избежать изменения эффекта
сил на теле, соответствующие моменты сил
об А. должно быть представлено.Следовательно, данная общая система
сил заменяется системой конкурирующих сил и системой
моменты. Эти две системы можно свести к равнодействующей силе
R с компонентами Rx и Ry и результирующим моментом M
(А)
Р .
Согласно (2.7) и (3.6) они имеют вид
Rx =
∑
Fix, Ry =
∑
Фий, М
(А)
R =
∑
M
(А)
я. (3.9)
Величину и направление результирующей силы можно вычислить.
от
R =
√
R2x + R
2
y, tanα =
Ry
Rx
. (3.10)
Система результирующего R (линия действия через A) и
момент M
(А)
R можно дополнительно упростить.Это эквивалентно
одиночная сила только R, если линия действия перемещена соответствующим образом. В
расстояние по перпендикуляру h (рис. 3.10) необходимо выбирать таким образом, чтобы
что момент M
(А)
R равно hR, т. Е. HR = M
(А)
R, что дает
h =
M
(А)
р
р
. (3.11)
3.1 Общие системы сил на плоскости 61
Если М
(А)
R = 0 и R = 0, уравнение (3.11) дает h = 0. В этом случае
случай линия действия равнодействующей общей системы сил
проходит через A. С другой стороны, если R = 0 и M
(А)
R = 0, а
дальнейшее сокращение невозможно: система сил сводится к
только момент (т.е., пара), которая не зависит от выбора
ориентира.
Уравнения (3.9) - (3.11) можно использовать для вычисления величины
и направление результирующего, а также место его действия
линия.
E3.1 Пример 3.1 На диск действуют четыре силы, как показано на рис.
3.11a. Силы имеют данные величины F или 2F соответственно.
Определите величину и направление результирующих и
расположение его линии действия.
а б
а
р
2F
F
F
2F
Икс
у
2F
2F
F
F
060◦
αa
час
Рис. 3.11
Решение Выберем систему координат x, y (рис.3.11b), и
его начало отсчета 0 принимается за точку отсчета. Согласно
знакового соглашения, положительные моменты имеют тенденцию вращать диск
по часовой стрелке (�). Таким образом, из (3.9) получаем
Rx =
∑
Fix = 2F cos 60
◦ + F cos 60◦
+ F cos 60◦ - 2F cos 60◦ = F,
Ry =
∑
Fiy = - 2F sin 60◦ + F sin 60◦.
+ F sin 60◦ + 2F sin 60◦ =
√
3F,
M
(0)
R =
∑
M
(0)
i = 2 aF + aF + 2 aF - aF = 4 aF,
62 3 Общие системы сил, равновесие твердого тела
которые дают (см. (3.10))
R =
√
R2x + R
2
y = 2F, tanα =
Ry
Rx
знак равно
√
3 → α = 60◦.Перпендикулярное расстояние равнодействующей от точки 0 следует
из (3.11):
h =
M
(0)
р
р
знак равно
4 аФ
2F
= 2 а.
3.1.4 Условия равновесия
Как показано в разделе 3.1.3, общая система копланарных сил может
сводится к системе совпадающих сил и системе движущих сил.
относительно произвольной реперной точки A. Система
моментов состоит из моментов сил и возможных
пара моментов. Системы будут подчиняться условиям
равновесия (2.11) и (3.7) соответственно.Следовательно, твердое тело
под действием общей системы копланарных сил равноценно
librium, если выполняются следующие условия равновесия:
∑
Fix = 0,
∑
Fiy = 0,
∑
M
(А)
я = 0. (3.12)
Количество условий равновесия (три) равно количеству
возможных движений (трех) тела в компланарной задаче:
переводы в направлениях x и y, соответственно, и вращение
относительно оси, перпендикулярной плоскости x, y. Тело
Говорят, что он имеет три степени свободы.Теперь показано, что точка отсчета в момент равен
Значение (3.12) можно выбрать произвольно. Для этого мы
сформулируем уравнение моментов относительно точки A (см. рис.
3.12):
∑
M
(А)
я =
∑
{(xi - xA) Fiy - (yi - yA) Fix}
знак равно
∑
(xiFiy - yiFix) - xA
∑
Fiy + yA
∑
Исправить (3.13)
знак равно
∑
M
(В)
я - xA
∑
Fiy + yA
∑
Исправить .
3.1 Общие системы сил на плоскости 63
Рис. 3.12
у
xB
F2
C
А
xC xA xi
F1
Fi
Исправить
Fiy
yC yiyA
Если выполняются условия равновесия (3.12), уравнение (3.13)
немедленно уступает
∑
M
(В)
я = 0.С другой стороны, если
∑
Fix = 0, ∑
Fiy = 0 и
∑
M
(В)
i = 0, тогда
∑
M
(А)
i = 0 также должно быть
довольный. Поэтому неважно, какая точка выбрана в качестве
точка отсчета.
Вместо использования двух условий силы и одного момента
может быть определено одно силовое условие и два моментных условия.
применяемый. Представляем условия
∑
Fix = 0,
∑
M
(А)
я = 0,
∑
M
(В)
я = 0 (3,14)
в (3.13),
∑
Fiy = 0 также выполняется, если xA = 0. Следовательно, равенство
Условия либриума (3.14) эквивалентны условиям (3.12) if (если)
две точки A и B не лежат на прямой (здесь
ось y), которая перпендикулярна направлению силы равновесия -
rium (здесь x-направление). Аналогично условия
∑
Fiy = 0,
∑
M
(А)
я = 0,
∑
M
(В)
я = 0 (3,15)
также привести к
∑
Fix = 0, если yA = 0.
Также можно выбрать три точки A, B и C, и только момент
используются следующие уравнения равновесия:
∑
M
(А)
я = 0,
∑
M
(В)
я = 0,
∑
M
(С)
я = 0. (3,16)
64 3 Общие системы сил, равновесие твердого тела
Эти уравнения эквивалентны (3.12) если точки A, B и C
не лежат на прямой. Чтобы доказать это утверждение
воспользуемся (3.13) и соответствующим соотношением для произвольного
точка C:
∑
M
(А)
я =
∑
M
(В)
я - xA
∑
Fiy + yA
∑
Исправить ,
∑
M
(С)
я =
∑
M
(В)
я - xC
∑
Fiy + yC
∑
Исправить .
(3,17)
Вводя (3.16), получаем
−xA
∑
Fiy + yA
∑
Fix = 0, −xC
∑
Fiy + yC
∑
Fix = 0,
и устранение
∑
Фий и
∑
Fix соответственно приводит к
(
−xC
да
xA
+ yC
) ∑
Fix = 0,
(
−xC +
xA
да
yC
) ∑
Fiy = 0.
Следовательно,
∑
Fix = 0 и
∑
Fiy = 0 обеспечивается, если слагаемые в
круглые скобки отличны от нуля, т.е., если yA / xA = yC / xC Приведение плоской произвольной системы сил к центру. Доведение плоской системы сил к центру
Лекция 5
Резюме: Приведение силы к заданному центру. Приведение системы сил к заданному центру. Условия равновесия пространственной системы параллельных сил. Условия равновесия плоской системы сил. Теорема о трех точках. Статически определяемые и статически неопределимые задачи.Равновесие системы тел.
Приведение системы сил к заданному центру. УСЛОВИЯ Равновесия
Приведение силы к данному центру.
Равнодействующая системы сходящихся сил находится непосредственно путем сложения сил согласно правилу параллелограмма. Очевидно, что аналогичная задача может быть решена для произвольной системы сил, если мы найдем для них метод, позволяющий передать все силы в одну точку.
Теорема о параллельной передаче силы . Сила, приложенная к абсолютно твердому телу, может передаваться из данной точки в любую другую точку тела без изменения оказываемого ею действия, добавляя пару с моментом, равным моменту переданной силы относительно точки, в которой сила передается.
Пусть сила приложена в точке A. Действие этой силы не изменится, если две уравновешенные силы приложены в точке B.Результирующая система трех сил — это сила, равная, но приложенная к точке B и паре с моментом. Процесс замены силы силой и парой сил называется приведением силы к данному центру B.
Приведением системы сил к данному центру.
Основная теорема статики (Пуансо).
Любую произвольную систему сил, действующих на твердое тело, можно в общем случае свести к силе и паре сил. Этот процесс замены системы сил одной силой и одной парой сил называется , приводя систему сил к заданному центру .
Основным вектором системы сил называется вектор, равный векторной сумме этих сил.
Основная точка системы сил, относительно точки O тела, называется вектором, равным векторной сумме моментов всех сил системы относительно этой точки.
Формулы для вычисления главного вектора и главного момента
Формулы для вычисления модуля и направляющих косинусов
главный вектор и главный момент
Условия равновесия системы сил.
Векторная форма.
Для равновесия произвольной системы сил, приложенной к твердому телу, необходимо и достаточно, чтобы главная векторная система сил была равна нулю, а главный момент системы сил относительно любого центра отсчета также был равен нулю. равняется нулю.
Алгебраическая форма.
Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на декартову координатную ось равнялись нулю, а три суммы моментов всех сил относительно трех осей координат также равны нулю.
Условия равновесия для пространственной системы
параллельные силы.
На тело действует система параллельных сил. Расположим ось Oz параллельно силам.
Уравнения
Для равновесия пространственной системы параллельных сил, действующих на твердое тело, необходимо и достаточно, чтобы сумма проекций этих сил была равна нулю, а сумма моментов этих сил Относительно двух координатных осей, перпендикулярных перпендикулярам, силы также равны нулю.
— проекция силы на ось Oz.
СИСТЕМА ПЛОСКОЙ СИЛЫ
Условия равновесия для плоской системы сил.
На тело действует плоская система сил. Размещаем оси Ox и Oy в плоскости действия сил.
Уравнения
Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил равны нулю и сумма моментов этих сил относительно любой точки, расположенной в плоскости действия сил, также равна нулю.
Теорема о трех точках.
Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно любых трех точек, расположенных в плоскости действия сил и не лежащие на одной прямой равны нулю.
Статически определяемые и статически неопределимые задачи.
Для любой плоской системы сил, действующих на твердое тело, существует три независимых условия равновесия. Следовательно, для любой плоской системы сил из условий равновесия можно найти не более трех неизвестных.
В случае пространственной системы сил, действующих на твердое тело, существует шесть независимых условий равновесия. Следовательно, для любой пространственной системы сил из условий равновесия можно найти не более шести неизвестных.
Задачи, в которых число неизвестных не превышает числа независимых условий равновесия для данной системы сил, приложенных к твердому телу, называются статически определяемыми .
В противном случае задачи статически не определены.
Равновесие системы тел.
Рассмотрим баланс сил, приложенных к системе взаимодействующих тел. Корпуса могут быть соединены друг с другом на шарнирах или иным способом.
Силы, действующие на рассматриваемую систему тел, можно разделить на внешние и внутренние.
Внешними называются силы, с которыми тела рассматриваемой системы действуют на тела, не входящие в эту систему сил.
Внутренними называются силы взаимодействия между телами рассматриваемой системы.
Рассматривая баланс сил, приложенных к системе тел, можно мысленно разделить систему тел на отдельные твердые тела и применить условия равновесия, полученные для одного тела, к силам, действующим на эти тела. Эти условия равновесия будут включать как внешние, так и внутренние силы системы тел. Внутренние силы на основе аксиомы о равенстве сил действия и противодействия в каждой точке сочленения двух тел образуют равновесную систему сил.
Покажем это на примере системы двух тел и плоской системы сил.
Если составить условия равновесия для каждого твердого тела системы тел, то для тела I
.
для тела II
Кроме того, из аксиомы о равенстве сил действия и противодействия для двух взаимодействующих тел имеем .
Представленные равенства являются условиями равновесия внешних сил, действующих на систему.
Реакция встраивания.
Рассмотрим балку, один конец которой AB встроен в стену. Такое присоединение конца балки AB называется окончанием в точке B. Пусть на балку действует плоская система сил. Определим силы, которые необходимо приложить к точке B балки, если часть балки AB отбрасывается. К секции балки (B) прилагаются распределенные силы реакции. Если заменить эти силы элементарными сосредоточенными силами и затем привести их в точку B, то в точке B мы получим силу (главный вектор сил реакции) и пару сил с моментом M (главный вектор сил реакции относительно точки Б).Моментом M называют момент закрытия или реактивный момент. Силу реакции можно заменить двумя составляющими и .
Уплотнение, в отличие от шарнира, создает не только реакцию, неизвестную по величине и направлению, но и пару сил с неизвестным моментом M в уплотнении.
Предположим, что произвольная плоская система сил сводится к одной силе, равной главному вектору и приложенной к центру редукции, и к одной паре с моментом, равным главному моменту
(рис. 57, a ).Докажем, что рассматриваемая произвольная плоская система сил сводится в этом общем случае к равнодействующей силе
, линия действия которой проходит через точку A на расстоянии от выбранного центра отсчета O на расстоянии
. .. Для этого преобразуем пару с моментом
так, чтобы сила и
, составляющие эту пару, оказались равными по модулю главному вектору R «. В этом случае плечо пары должно быть выбран так, чтобы его момент m
оставался равным M 0.Для этого плечо пары
необходимо, очевидно, найти из равенства
. (1)
Воспользовавшись тем фактом, что пару всегда можно перемещать в своей плоскости действия по желанию, мы переместим пару
так, чтобы ее сила
оказалась прикрепленной к центру призрака O и напротив основного вектора
(Рисунок 57, b ).
Следовательно, рассматриваемая произвольная плоская система сил эквивалентна силе
и паре
…. Отбрасывая силы
и
как сбалансированные, мы получаем, что вся рассматриваемая система сил заменяется одной силой
, которая, следовательно, является равнодействующей. В этом случае линия действия результирующей будет проходить через точку A , положение которой относительно выбранного центра отсчета определяется по формуле (1).
Если в результате редукции произвольной плоской системы сил окажется, что
, а
, то в данном частном случае эта система сил сразу заменяется одной силой, т.е.е., результирующий
, линия действия которого проходит через выбранный опорный центр.
Задача 7 … К точкам V и С тела, соответственно, приложены равные по величине и взаимно перпендикулярные силы и
удаленных от точки O тел на равных расстояниях
… Принесите это систему сил к точке О (рисунок 58).
Решение. Перенесем силы и параллельно себе на точку О … В результате этого переноса получаем (Рис. 58) силы
и
, приложенные в точке O , и присоединенные пары
и
, лежащие в одной плоскости с моментами
и
(силы, образующие эти пары отмечены пунктиром на рисунке 58). Из геометрического сложения сил и приложенных в точке O , мы получаем главный вектор этой системы сил
, модуль которого, очевидно, равен
. Из сложения присоединенных пар мы получаем результирующую пару, момент из которых равен главному моменту
этой системы сил относительно точки O :
Следовательно, эта система двух сил и имеет равнодействующие
,
, приложенные в точке A , которая находится далеко от точки O на расстоянии
.
;
,
, то есть результирующие формы с заданными силами и равными углами по 45 0 каждый.
Задача 8. Вертикальные силы действуют на балку моста (Рисунок 59)
т и
т соответственно на расстоянии 10 м и 40 м от левого конца фермы и горизонтальная сила
t на уровне верхнего пояса фермы высота фермы 6 м … Ведущая система сил, причем простейшего вида.
Решение.Рисуем оси координат, как показано на рисунке 59, беря начало координат в точке A. Найдем проекции главного вектора данной системы сил на ось выбранной системы координат:
откуда находим модуль главного вектора
:
T
.
Найдем теперь главный момент данной системы сил относительно начала координат A:
t m
.
Следовательно, эта система сил имеет равнодействующее
, модуль которого равен
Т.
Теперь найдем, как действует результат. Момент результирующего относительно исходной точки A будет определяться по формуле
,
, где X и y — координаты точки, лежащей на линии действия равнодействующей. Поскольку
т и
т, то
.
С С другой стороны, по теореме Вариньона о моменте результирующего (5, § 11) имеем
Отсюда
.
Это уравнение линии действия результирующей.
Устанавливая в этом уравнении
, мы находим, что точка пересечения линии действия равнодействующей с верхним поясом фермы находится на расстоянии
м от левого конца фермы. Но, принимая
м , мы находим, что точка пересечения линии действия равнодействующей с нижним поясом фермы находится на расстоянии
м от левого конца фермы.Определенные таким образом соединения являются точками пересечения линий действия равнодействующей с верхними и нижними поясами фермы по прямой линии, мы находим линию действия равнодействующей.
Метод приложения одной силы к заданной точке может применяться к любому количеству сил. Предположим, что в некоторых точках тела (рис. 1.24) приложены силы F 1 F 2, F 3 и F 4. Требуется привести эти силы к точке O плоскости.Сначала представим силу, приложенную в точке A. Применим (см. § 16) в точке O две силы, по отдельности равные данной силе, параллельные ей и направленные в противоположных направлениях. В результате приведения силы получаем силу , приложено в точке O, и пара сил с плечом . То же самое с силой , прикладываем в точке В, получаем мощность , , приложенный в точке O, и пара сил с плечом и т. Д.Плоская система сил, приложенная в точках A, B, C и D, мы заменили сходящимися силами , , приложенный в точке O, и пары сил с моментами, равными моментам данных сил относительно точки O:
Рисунок 1.24
Силы, сходящиеся в точке, могут быть заменены одной силой, равной геометрической сумме компонентов,
Эта сила, равная геометрической сумме данных сил, называется главным вектором системы сил и обозначается.
По величине проекций главного вектора на координатную ось находим модуль главного вектора:
Исходя из правила сложения пар сил, их можно заменить на получившуюся пару, момент которой равен алгебраической сумме моментов заданных сил относительно точки O и называется основной. точка относительно исходной точки
Таким образом, произвольная плоская система сил сводится к одной силе (главный вектор системы сил) и к одному моменту (основной момент системы сил).
Необходимо усвоить, что главный вектор ста не является равнодействующим данной системы сил, поскольку эта система не эквивалентна одной силе. Поскольку главный вектор равен геометрической сумме сил в данной системе, ни модуль, ни его направление не зависят от выбора опорного центра. Величина и знак главного момента зависят от положения опорного центра, поскольку плечи составляющих пар зависят от взаимного положения сил и точки (центра), относительно которой снимаются моменты.
Частные случаи приведения системы сил:
ед.); система находится в равновесии, т.е. для равновесия плоской системы сил необходимо и достаточно, чтобы ее главный вектор и главный момент одновременно были равны нулю.
Плоская система сил также сводится к силе, равной и приложенной в произвольно выбранном центре O, и к паре с моментом
в этом случае вектор может быть определен либо геометрически, построив силовой многоугольник (см. П. 4), либо аналитически.Таким образом, для плоской системы сил
R x = F kx, R y = F ky,
, где все моменты в последнем равенстве алгебраические, а сумма также алгебраическая.
Давайте найдем простейшую форму данной плоской системы сил, которая не находится в равновесии. Результат зависит от значений R и M О.
- 1. Если для данной системы сил R = 0, a M O? 0, то он сводится к одной паре с моментом MO, значение которой не зависит от выбора центра O.
- 2. Если для данной системы сил R? 0, то сводится к одной силе, то есть к равнодействующей. В этом случае возможны два случая:
- а) R? 0, М O = 0. В этом случае видимая сразу система сводится к результирующему R, проходящему через центр O;
- б) R? 0, Пн? 0. В этом случае пара с моментом MO может быть представлена двумя силами R «и R», при этом R «= R, a R» = — R. Более того, если d = OC — плечо пары, тогда должно быть Rd = | МО | …
Отбрасывая теперь силы R и R «как сбалансированные, мы обнаруживаем, что вся система сил заменяется результирующей R» = R, проходящей через точку C. Положение точки C определяется двумя условиями: 1) расстоянием OC = d () должно удовлетворять равенству Rd = | МО |; 2) знак момента относительно центра O силы R «, приложенной в точке C, то есть знак m O (R») должен совпадать со знаком MO.
Лекция 3
Краткое описание: Выдвижение произвольной и плоской системы сил в центр.Теорема о параллельной передаче силы, основная теорема статики Приведение системы сил к заданному центру Главный вектор и главный момент системы сил. Зависимость главного момента от выбора центра. Аналитическое определение главного вектора и главного момента системы сил. Инварианты системы сил. Приведение системы сил к простейшему виду. Частные случаи редукции произвольной системы сил, динамический винт. Теорема Вариньона о моменте равнодействующей.
Приведение силы к заданному центру (лемма Пуансо)
Равнодействующая системы сходящихся сил находится непосредственно путем сложения сил в соответствии с правилом параллелограмма. Очевидно, что аналогичная задача может быть решена для произвольной системы сил, если мы найдем для них метод, позволяющий передать все силы в одну точку.
Лемма Пуансо о параллельной передаче силы . . Не изменяя действие силы на твердое тело, ее можно передать параллельно себе в любую точку тела, добавив пару, момент которой равен моменту данной силы относительно новой точки приложения.
Пусть сила приложена в точке A. Действие этой силы не изменится, если две уравновешенные силы приложены в точке B. Результирующая система из трех сил является силой, равной, но приложенной в точке B и паре с моментом. Процесс замены силы силой и парой сил называется приведением силы к заданному центру B. ■
Приведение системы сил к заданному центру.
Основным вектором системы сил называется вектор, равный векторной сумме этих сил.
Основной точкой системы сил относительно точки O тела называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки.
Теорема Пуансо (Основная теорема статики)
Произвольную систему сил, действующих на твердое тело, можно заменить эквивалентной системой, состоящей из силы и пары сил. Сила равна главному вектору системы сил и приложена в произвольно выбранной точке (опорном центре), момент пары равен основному
момент системы сил относительно этой точки.
ДОКАЗАТЕЛЬСТВО.
Точка O — центр приведения. По лемме Пуансо передадим силу F1 ровно O. В этом случае вместо F1 мы имеем в точке O ту же силу F1 ‘и дополнительно пару сил с моментом m1.
Таким же образом перенесем все остальные силы. В результате мы получаем систему сходящихся сил и систему пар сил. По теореме о существовании результирующей системы сходящихся
силы их можно заменить одной силой R, равной главному вектору.Согласно теореме парного сложения систему пар можно заменить одной парой, момент которой равен главному моменту Мо. ■
Статические инварианты
Статические инварианты — это характеристики системы сил, не зависящие от выбора центра отсчета.
Первый инвариант статики — главный вектор системы сил (по определению).
Второй инвариант статики — скалярное произведение главного вектора и главного момента.
Действительно, главное, очевидно, зависит от выбора центра отсчета. Рассмотрим произвольную систему сил … Приведем ее сначала к центру O, а затем к центру O 1.
Это показано на рисунке. Следовательно, формула для принимает вид
Или.
Умножим обе части этого равенства на соответственно, учитывая, что главным вектором системы сил является первый инвариант статика :.К
смешанное произведение векторов, отсюда:
.
Если использовать определение скалярного произведения, то для второго инварианта можно получить еще одну форму:
Так как предыдущее выражение примет вид:
Таким образом, проекция главного момента на направление главного вектора является постоянной величиной для данной системы сил и не зависит от выбора центра отсчета.
Частные случаи приведения произвольной системы сил к простейшему виду
1) Если при приведении системы сил к центру О, то, исходя из (6.4) можно написать
.
результирующий , нанесенный в центре отсчета и совпадающий по величине и направлению с главным вектором.
2) Если при приведении системы сил к центру O
затем представим как пару сил с плечом,
получаем :.
В этом случае система сил сводится к равнодействующей , совпадающей по величине и направлению с главным вектором, а линия действия равнодействующей удалена от линии действия главного вектора на некоторое расстояние.
3) Если, доводя систему сил до центра О, то можно написать
, то есть система сил сводится к паре сил с моментом, равным основному моменту системы сил.
4) Если, доводя систему сил до центра О, то можно написать
Тех. система сил находится в равновесии .
Определение: Система, состоящая из силы и пары сил, момент которой коллинеарен силе (плоскость пары перпендикулярна линии действия силы), называется динамо или динамический винт .
Если при приведении системы сил к центру O второй инвариант не равен нулю, то эта система сил сводится к динамо .
Разложив на две составляющие — по основному вектору и — перпендикулярно основному вектору, ибо и у нас будет случай 2), причем вектор, как свободный, можно перенести параллельно себе в точку O 1:
Векторы представляют собой динамо-машину, где,.
В рассматриваемом случае приведения системы сил главный момент имеет минимальное значение.Это значение момента сохраняется, когда данная система сил приводится в любую точку, лежащую на линии действия главного вектора и главного момента. Уравнение этой линии (центральной винтовой оси системы сил) определяется из условия коллинеарности векторов и :.
Урок 3: Равновесие — BS Гражданское строительство — BSCE 2
Урок 3
РАВНОВЕСИЕ
Временные рамки: 9 часов
Цели:
Ознакомить с концепцией диаграммы свободного тела для частицы.
Показать, как решать задачи равновесия частиц с помощью уравнений равновесия.
Когда равнодействующая всех сил, действующих на частицу, равна нулю, частица находится в равновесии.
Также, когда чистый эффект данных сил равен нулю и частица считается находящейся в равновесии.
3.1 Диаграммы свободного тела
При решении задачи, касающейся твердого тела в равновесии, важно учитывать все силы
, действующие на тело.Не менее важно исключить любую силу, которая не приложена напрямую к корпусу
. Отсутствие силы или добавление посторонней силы нарушило бы условия равновесия.
Следовательно, первым шагом в решении проблемы является построение диаграммы свободного тела твердого тела с учетом
.
Шаги, которые вы должны выполнить, чтобы построить правильную диаграмму свободного тела:
1. Начните с четкого решения относительно выбора свободного тела для анализа.Мысленно вам необходимо отделить это тело от земли и отделить его от всех остальных тел. Затем вы можете нарисовать контур этого изолированного тела
.
2. Обозначьте все внешние силы на диаграмме свободного тела. Эти силы представляют собой воздействия
на свободное тело со стороны земли и оторвавшихся тел. На схеме приложите эти силы
к различным точкам, где свободное тело поддерживалось землей или было соединено с
другими телами.Как правило, вы должны включать вес свободного тела в число внешних сил,
, потому что он представляет собой притяжение, оказываемое землей на различные частицы, образующие свободное тело.
Нарисуйте гирю, она действует в центре тяжести тела. Если свободное тело состоит из нескольких частей, не учитывайте усилия, которые разные части оказывают друг на друга.
3. Четко отметьте величины и направления известных внешних сил на диаграмме свободного тела
.Напомним, что при указании направлений этих сил это силы, действующие на свободное тело, а не на
. Известные внешние силы обычно включают в себя вес свободного тела и силы
, приложенные для данной цели.
4. Неизвестные внешние силы обычно состоят из реакций, посредством которых земля и другие тела
противодействуют возможному движению свободного тела. Реакции вынуждают свободное тело оставаться в том же положении
; по этой причине их иногда называют сдерживающими силами.Реакции проявляются в
точках, где свободное тело поддерживается другими телами или соединяется с ними; Вы должны четко указать
этих точек.
5. Схема свободного тела также должна включать размеры, поскольку они могут потребоваться для
вычисления моментов сил. Однако любые другие детали следует опустить.
Трактор, поддерживающий ковшовый груз. Как показано, его диаграмма свободного тела
должна включать все внешние силы, действующие на трактор.
Нормальное напряжение и напряжение сдвига | |
Тяга на плоскостях, которые пересекаются в исходной точке рисунка. 12 можно разделить на перпендикулярные и параллельные составляющие для каждого самолет. Компонент, перпендикулярный каждой плоскости, называется нормальным напряжением. ( с n ) и компонент параллельно каждой плоскости называется напряжением сдвига ( т ).На рисунке 14 показано соотношение тяги ( с ) и нормальный ( с n ) и напряжение сдвига ( т ) компоненты действующие на одной плоскости, след которой в двух измерениях соответствует отрезку AB. | |
Рисунок 14.Двумерный след прямоугольной призмы с нормальным ( с н ) и на сдвиг ( т ) напряжения, действующие на заданную плоскость по отрезку AB . Нормальные и касательные напряжения — составляющие тяги, с . | |
Нормальные и касательные напряжения могут быть рассчитаны на плоскости любой ориентации. если величина и направление двух из трех главных напряжений ( с 1 , с 2 , и s 3 ) известны.На рисунке 15 нормальное напряжение, с n , и напряжения сдвига, т, действуют на след плоскости, определяемой отрезком линии, обозначенным как AB на Рисунок 14. На рисунке 15 основные напряжения, с 1 и с 3 ориентированы перпендикулярно к ножкам AC и BC соответственно прямоугольного треугольника ABC . | |
Рисунок 15. Графическая взаимосвязь между нормальным, с n , и напряжение сдвига, т , и два основных напряжения, с 1 и с 3 . | |
Уравнения для нормального напряжения и напряжения сдвига обычно называют как фундаментальные уравнения напряжений.Предполагая статическое равновесие и используя отношения, показанные на рисунке 15, вывод фундаментальное уравнение для нормального напряжения начинается с уравновешивания сил где: | |
| (39) | |
Отмена аналогичных условий и упрощение: | |
| (40) | |
Подстановка тригонометрических тождеств и в Уравнение (40) дает: | |
| (41) | |
Дальнейшее упрощение показывает стандартную форму уравнения для нормальный стресс: | |
| (42) | |
Опять же, предполагая статическое равновесие и используя проиллюстрированные соотношения на рисунке 17 вывод основного уравнения для касательного напряжения начинается с уравновешивания сил где: | |
| (43) | |
Отмена аналогичных условий и упрощение: | |
| (44) | |
| (45) | |
замена тригонометрического тождества в уравнение (45) дает уравнение фундаментального напряжения для касательного напряжения: | |
| (46) | |
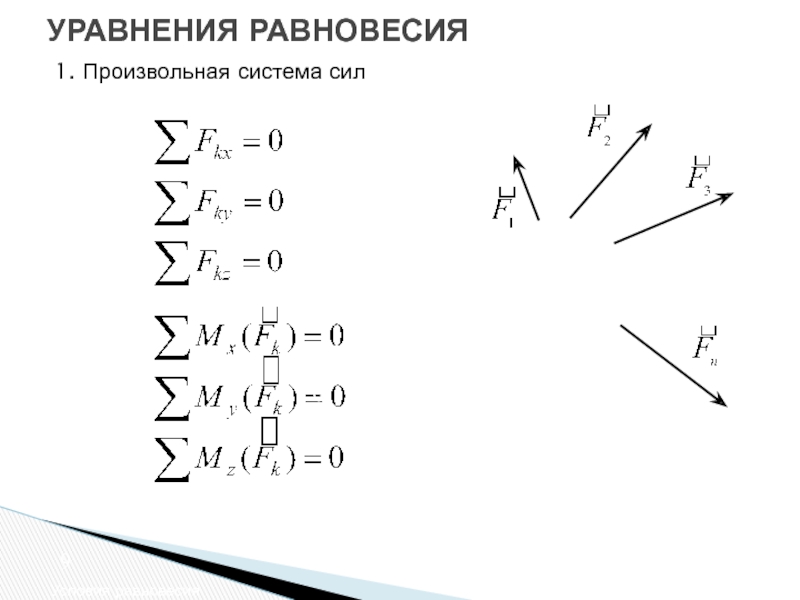
 5
5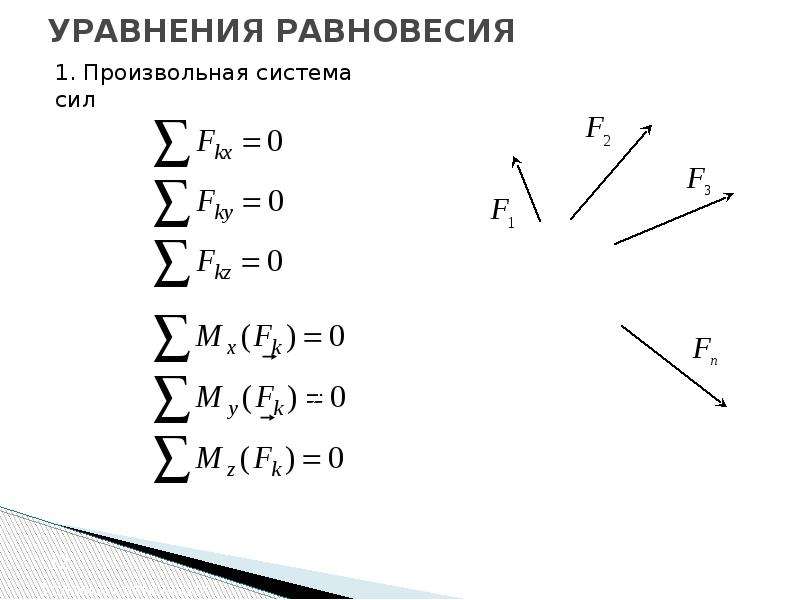 5
5 е. число неизвестных величин не более трех;
е. число неизвестных величин не более трех; При решении задачи используется любое из трех видов уравнений равновесия:
При решении задачи используется любое из трех видов уравнений равновесия: Если в результате решения знак величины какой-либо силы или момента окажется отрицательным, то это означает, что направление силы или момента противоположно тому, которое было предварительно выбрано;
Если в результате решения знак величины какой-либо силы или момента окажется отрицательным, то это означает, что направление силы или момента противоположно тому, которое было предварительно выбрано;
 .. системы или отдельной паре, называемой ….
.. системы или отдельной паре, называемой ….  …
… 

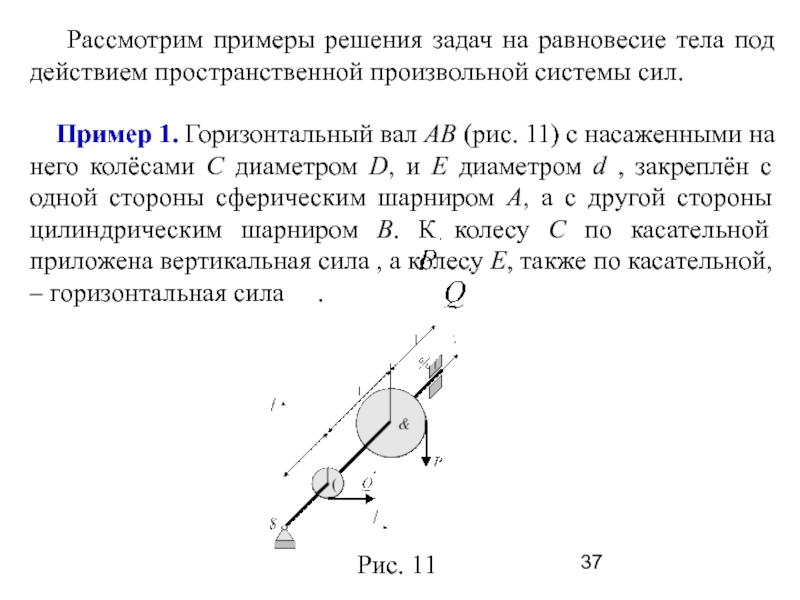


 ..
.. 




