§15. Решение задач

Решение многих задач статики сводится к определению реакций опор, с помощью которых закрепляются балки и мостовые фермы.

В технике обычно встречаются три типа опорных закреплений (кроме рассмотренных в § 2):

1. Подвижная шарнирная опора (рис. 28, опора А). Реакция такой опоры направлена по нормали к поверхности на которую опираются катки подвижной опоры.

2. Неподвижная шарнирная опора (рис. 28, опора В). Реакция такой опоры проходит через ось шарнира и может иметь любое направление в плоскости чертежа. При решении задач будем реакциюизображать ее составляющимиипо направлениям координатных осей. Модульопределим по формуле .

3. Жесткая заделка (рис. 29, а). Рассматривая заделанный конец балки и стену как одно целое, жесткую заделку изображают так, как показано на рис. 29, б. В этом случае на балку в ее поперечном сечении действует со стороны заделанного конца система распределенных сил (реакций).

Считая эти силы приведенными к центру А сечения, можно их заменить одной силой и парой с неизвестным моментомm_A (рис. 29, а). Силу можно изобразить ее составляющими,(рис. 29, б).

Таким образом, для нахождения реакции жесткой заделки надо определить три неизвестные величины X_A, Y_A, m_A.

Рис. 28 Рис. 29

Отметим также, что в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль поверхности по тому или иному закону. Рассмотрим некоторые примеры распределенных сил.

Плоская система распределенных сил характеризуется ее интенсивностью q, т.е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в ньютонах, деленных на метры (Н/м).

а) Силы, равномерно распределенные вдоль отрезка прямой (рис.  30, а). Для такой системы интенсивность q имеет постоянное значение. При расчетах эту систему сил можно заменить равнодействующей . По модулю

Q = aq . (33)

Приложена сила Q в середине отрезка АВ.

б) Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 30, б). Для этих сил интенсивность q является величиной переменной, растущей от нуля до максимального значения q_m. Модуль равнодействующей в этом случае определяется по формуле

Q = 0,5aq_m . (34)

Приложена сила на расстоянииа/3 от стороны ВС треугольника АВС.

Рис. 30

Задача 3. Определить реакции неподвижной шарнирной опоры А и подвижной опоры В балки (рис.  31), на которую действуют активные силы: одна известная сосредоточенная сила F = 5 кН, приложенная в точке С под углом 60⁰, и одна пара сил с моментом m = 8 кНм.

Рис. 31

Решение. 1) Выбираем объект исследования, т.е. рассматриваем равновесие балки АВС. 2) Изобразим внешние силы, действующие на балку: силу , пару сил с моментомm и реакции связей , , (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими). В результате имеем произвольную плоскую систему сил. 3) Проведем координатные оси x, y и составляем условия равновесия (28). Для вычисления момента силы , иногда, удобно разложить ее на составляющие и , модули которых равняются F

1 = F cos60⁰ = 2,5 кН, F₂ = F cos30⁰ = 4,33 кН. Тогда получим:

, ,

.

Решая эту систему уравнений, найдем:

X_A = F₁ = 2,5 кН, Y_B = (m + F₂∙5)/3 = 9,88 кН, Y_A = F₂ – Y_B = – 5,55 кН.

Знак минус реакции Y_A показывает, что эта реакция направлена вертикально вниз.

Для проверки составим уравнение моментов относительно нового центра, например, относительно точки В:

, 5,55∙3 – 8 – 4,33∙2 = – 0,01 ≈ 0.

Задача 4. Определить реакции заделки консольной балки (рис. 32), на которую действуют активные силы: сосредоточенная сила F = 6 кН, приложенная в точке С под углом 45⁰, равномерно распределенная нагрузка интенсивностью q = 2 кН/м и пара сил с моментом m = 3 кНм.

Рис. 32

Решение. 1) Выбираем объект исследования, т.е. рассматриваем равновесие балки АВС. 2) Изобразим внешние силы, действующие на балку: силу , равномерно распределенную нагрузку интенсивностьюq, пару сил с моментом m и реакции заделки, т.е. три неизвестные величины X_A, Y_A, m_A (реакцию жесткой заделки изображаем двумя ее составляющими X_A, Y_A, а пару – неизвестным моментом m_A, как на рис.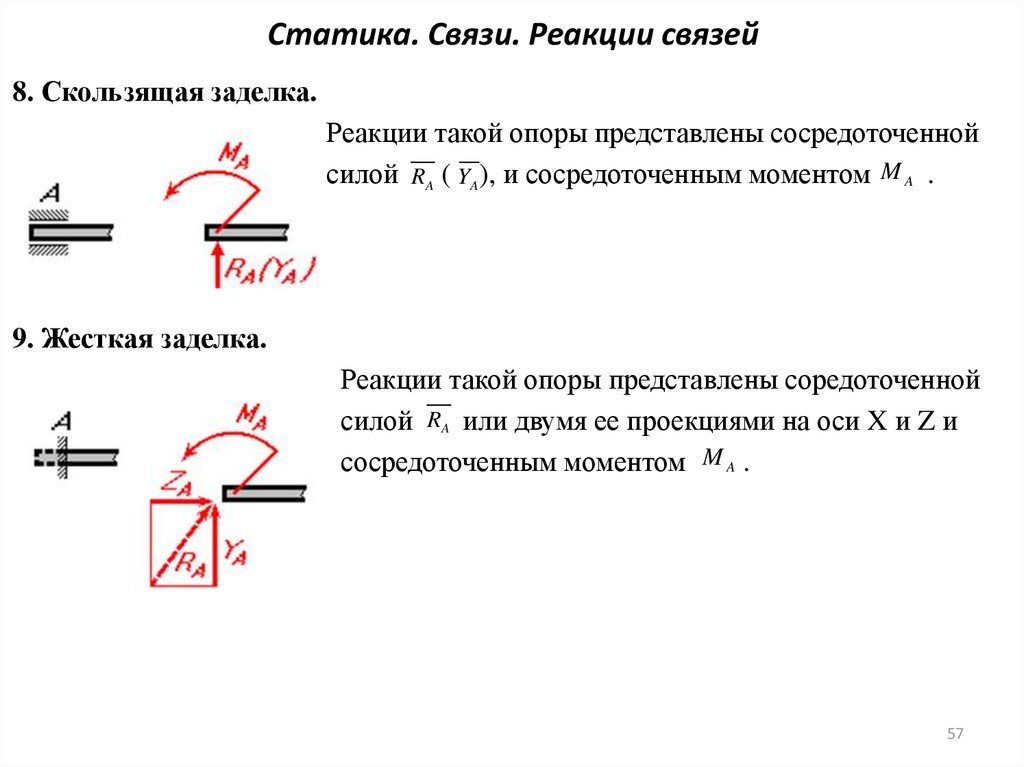

 29). Силу разложим на две составляющие и , модули которых равняются F₁ = F₂ = F cos45⁰ = 4,24 кН, а распределенную нагрузку интенсивностью q заменим сосредоточенной силой с модулем равным

Q = 3∙q = 6 кН.

Сила приложена в середине отрезка АВ. В результате имеем произвольную плоскую систему сил. 3) Проведем координатные оси x, y и составляем уравнения равновесия (2):

, ,

.

Решая эти уравнения, найдем:

X_A = F₁ = 4,24 кН, Y_A = Q – F₂ = 1,76 кН, m_A = Q∙1,5 + m – F₂∙5 = – 9,2 кНм.

Для проверки составим уравнение моментов относительно точки С:

, – 9,2 + 21 – 3 – 8,8 = 0.

Задача 5. Определить реакции опор А, В, С и усилие в промежуточном шарнире D составной конструкции (рис.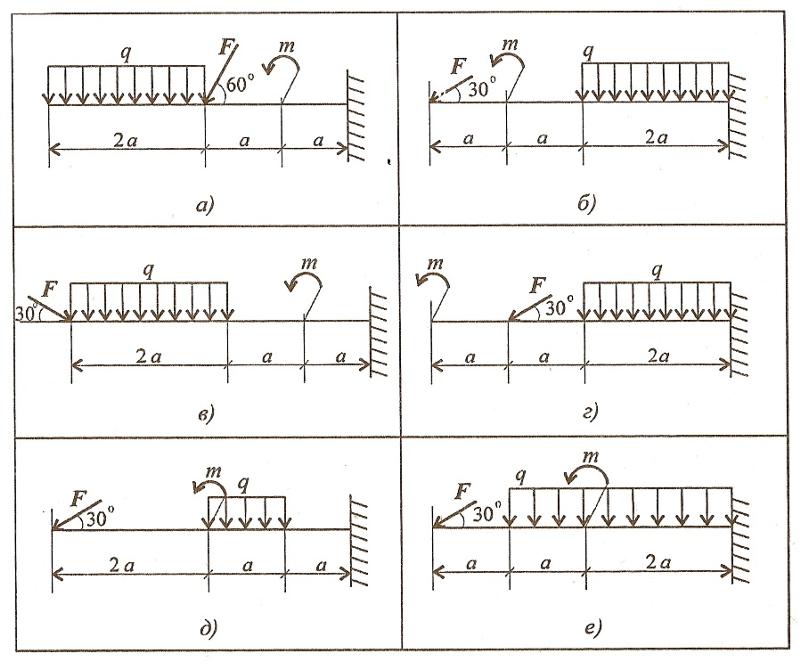

 33), на которую действуют активные силы: сосредоточенная сила F = 4 кН, приложенная в точке Е под углом 45⁰, равномерно распределенная нагрузка интенсивностью q = 2 кН/м и пара сил с моментом m = 10 кНм.

Рис. 33

Решение. Один из способов решения задач об определении реакции опор составной конструкции состоит в том, что конструкцию расчленяют на отдельные тела и составляют условия равновесия каждого из тел в отдельности. Воспользуемся этим способом и разобьем конструкцию на две части: левую AD и правую DC. В результате приходим к задаче о равновесии двух тел. Силовые схемы задачи показаны на рис. 7,8. Для упрощения вычислений разложим силу на составляющие и , модули которых равны F

1 = F₂ = F cos45⁰ = 2,83 кН, а распределенную нагрузку интенсивностью q заменим сосредоточенной силой с модулем равнымQ = 10 кН. Сила приложена в середине отрезкаBD.

Рис. 34 Рис. 35

Анализ приведенных силовых схем показывает, что они включают шесть неизвестных величин: X_A, Y_A, Y_B, X_D, Y_D, Y_C.

Так как на рис. 34,35 имеются плоские системы уравновешенных сил, то для них можно записать условия равновесия (28) в виде шести линейных алгебраических уравнений:

Левая часть Правая часть

, ,

, ,

, .

Поскольку составленная система шести уравнений зависит от шести неизвестных X_A, Y_A, Y_B, X_D, Y_D, Y_C, то она является замкнутой.

Решая систему, найдем:

X_A = – 2,83 кН, Y_A = – 0,93 кН, Y_B = 11,76 кН, Y_C = 2 кН, X_D = 0, Y_D = 2 кН.

Для проверки составим уравнение моментов относительно точки D:

= 2,83∙7 – (– 0,93)∙15 – 11,76∙5 + 10∙2,5 – 10 + 2∙5 = – 0,04 ≈ 0.

Сопротивление материалов

Сопротивление материалов

Дарков А.В., Шапиро Г.С. Сопротивление материалов. — М.: Высшая школа, 1975. — 654 с. Настоящий курс предназначен для студентов высших технических учебных заведений. В каждой его главе приведены подробно решенные примеры, задачи для самостоятельного решения и даны вопросы для самопроверки пройденного материала. Оглавление ПРЕДИСЛОВИЕ Глава 1. ОСНОВНЫЕ ПОНЯТИЯ § 2.1. РАСЧЕТНАЯ СХЕМА. НАГРУЗКИ § 3.1. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ § 4.1. НАПРЯЖЕНИЯ § 5.1. ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ § 6.1. ОСНОВНЫЕ ПРЕДПОСЫЛКИ НАУКИ О СОПРОТИВЛЕНИИ МАТЕРИАЛОВ Вопросы для самопроверки Глава 2. РАСТЯЖЕНИЕ И СЖАТИЕ § 1.2. ПРОДОЛЬНАЯ СИЛА § 2.2. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ И НАКЛОННЫХ СЕЧЕНИЯХ БРУСА § 3.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ § 4.2. ДИАГРАММЫ РАСТЯЖЕНИЯ И СЖАТИЯ § 5.2. ПЕРЕМЕЩЕНИЯ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСЬЕВ § 6.2. РАБОТА СИЛЫ ПРИ ЕЕ СТАТИЧЕСКОМ ДЕЙСТВИИ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ § 7.2. СОБСТВЕННЫЙ ВЕС БРУСА § 8.2. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. РАСЧЕТЫ НА ПРОЧНОСТЬ § 9.2. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ § 10.2. МЕСТНЫЕ НАПРЯЖЕНИЯ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 3. ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ § 1. 3. ВИДЫ НАПРЯЖЕННОГО СОСТОЯНИЯ § 2.3. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ § 3.3. ГЛАВНЫЕ НАПРЯЖЕНИЯ. ГЛАВНЫЕ ПЛОЩАДКИ § 4.3. ЭКСТРЕМАЛЬНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ § 5.3. ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ С ПОМОЩЬЮ КРУГА МОРА § 6.3. ПОНЯТИЕ О ПРОСТРАНСТВЕННОМ НАПРЯЖЕННОМ СОСТОЯНИИ § 7.3. ОБОБЩЕННЫЙ ЗАКОН ГУКА § 8.3. ОБЪЕМНАЯ ДЕФОРМАЦИЯ § 9.3. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 4. СДВИГ § 1.4. ЧИСТЫЙ СДВИГ § 2.4. ДЕФОРМАЦИЯ ПРИ СДВИГЕ. ЗАКОН ГУКА ПРИ СДВИГЕ § 3.4. ОБЪЕМНАЯ ДЕФОРМАЦИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРИ ЧИСТОМ СДВИГЕ. ЗАВИСИМОСТЬ МЕЖДУ E, G и «мю» § 4.4. ПРАКТИЧЕСКИЕ РАСЧЕТЫ НЕКОТОРЫХ ПРОСТЕЙШИХ КОНСТРУКЦИЙ, РАБОТАЮЩИХ НА СДВИГ Расчет заклепочных соединений Расчет сварных соединений Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ § 2. 5. СТАТИЧЕСКИЕ МОМЕНТЫ СЕЧЕНИЙ § 3.5. МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЙ § 4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЕЧЕНИЙ ПРОСТОЙ ФОРМЫ § 5.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ § 6.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ § 7.5. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ. ГЛАВНЫЕ ОСИ ИНЕРЦИИ § 8.5. ИССЛЕДОВАНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ СЕЧЕНИЙ С ПОМОЩЬЮ КРУГА МОРА § 9.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ СЕЧЕНИЙ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 6. КРУЧЕНИЕ § 1.6. ОСНОВНЫЕ ПОНЯТИЯ. КРУТЯЩИЙ МОМЕНТ § 2.6. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 3.6. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.6. РАСЧЕТ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ § 5.6. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ВИНТОВЫХ ПРУЖИН § 6.6. КРУЧЕНИЕ ПРЯМОГО БРУСА НЕКРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 7.6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 7. ПРЯМОЙ ИЗГИБ § 1.7. ВНУТРЕННИЕ УСИЛИЯ § 3.7. ОПОРЫ И ОПОРНЫЕ РЕАКЦИИ § 4.7. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 5.7. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗГИБАЮЩИМ МОМЕНТОМ, ПОПЕРЕЧНОЙ СИЛОЙ И ИНТЕНСИВНОСТЬЮ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ § 6.7. ПРИМЕРЫ ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ УСИЛИЙ § 7.7. ПРЯМОЙ ЧИСТЫЙ ИЗГИБ § 8.7. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ § 9.7. ГЛАВНЫЕ НАПРЯЖЕНИЯ ПРИ ПРЯМОМ ПОПЕРЕЧНОМ ИЗГИБЕ § 10.7. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ § 11.7. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ § 12.7. ПОНЯТИЕ О ЦЕНТРЕ ИЗГИБА § 13.7. ПОНЯТИЕ О РАСЧЕТЕ СОСТАВНЫХ БАЛОК § 14.7. ПОНЯТИЕ О БАЛКАХ РАЗНОРОДНОЙ УПРУГОСТИ § 15.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НЕПОСРЕДСТВЕННОГО ИНТЕГРИРОВАНИЯ § 16.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НАЧАЛЬНЫХ ПАРАМЕТРОВ § 17.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В БАЛКАХ ГРАФО-АНАЛИТИЧЕСКИМ МЕТОДОМ § 18.7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 8. ТЕОРИИ ПРОЧНОСТИ § 1.8. КЛАССИЧЕСКИЕ И ЭНЕРГЕТИЧЕСКАЯ ТЕОРИИ ПРОЧНОСТИ § 2.8. ТЕОРИЯ ПРОЧНОСТИ МОРА § 3.8. ЕДИНАЯ ТЕОРИЯ ПРОЧНОСТИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 9. СЛОЖНОЕ СОПРОТИВЛЕНИЕ § 1.9. КОСОЙ ИЗГИБ § 2.9. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ БРУСЬЕВ БОЛЬШОЙ ЖЕСТКОСТИ § 3.9. ЯДРО СЕЧЕНИЯ § 4.9. ИЗГИБ С КРУЧЕНИЕМ БРУСЬЕВ КРУГЛОГО СЕЧЕНИЯ § 5.9. ОБЩИЙ СЛУЧАЙ ДЕЙСТВИЯ СИЛ НА БРУС КРУГЛОГО СЕЧЕНИЯ § 6.9. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ ПРОСТРАНСТВЕННЫХ БРУСЬЕВ С ЛОМАНОЙ ОСЬЮ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 10. РАСЧЕТ КРИВЫХ БРУСЬЕВ § 2.10. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 3.10. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ БРУСА БОЛЬШОЙ КРИВИЗНЫ § 4.10. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ ПРИ ЧИСТОМ ИЗГИБЕ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 11. 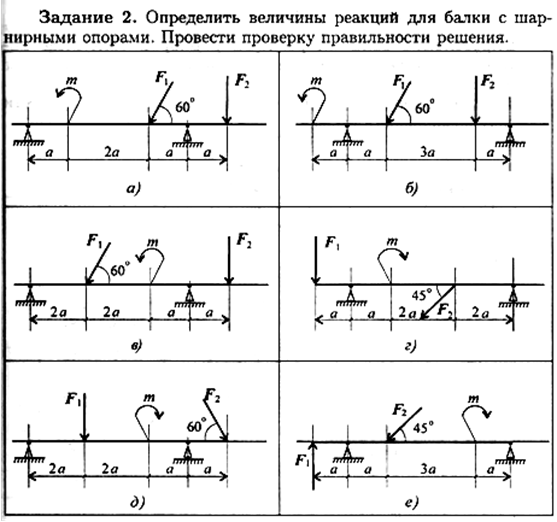ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В УПРУГИХ СИСТЕМАХ § 1.11. РАБОТА ВНЕШНИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ § 2.11. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ § 3.11. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЯ 4.11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ. ИНТЕГРАЛ МОРА § 5.11. ПРАВИЛО ВЕРЕЩАГИНА Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 12. РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ § 1.12. СТАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ § 2.12. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 3.12. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 4.12. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 5.12. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ § 6.12. ПРОВЕРКА ПРАВИЛЬНОСТИ ЭПЮР М, Q И N § 7.12. НЕРАЗРЕЗНЫЕ БАЛКИ ПРИМЕРЫ РАСЧЕТА Вопросы для самопроверки Глава 13. ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОГО СТЕРЖНЯ § 1.13. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ УПРУГИХ ТЕЛ § 2.13. ПРОДОЛЬНЫЙ ИЗГИБ § 3.13. ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАПРЯЖЕНИЯХ, ПРЕВЫШАЮЩИХ ПРЕДЕЛ ПРОПОРЦИОНАЛЬНОСТИ § 4. 13. ПРАКТИЧЕСКИЕ РАСЧЕТЫ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ § 5.13. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 14. ДИНАМИЧЕСКАЯ НАГРУЗКА § 2.14. ДИНАМИЧЕСКИЕ ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ СТАТИЧЕСКОГО РАСЧЕТА СИСТЕМ § 3.14. УДАР § 4.14. ЧАСТНЫЕ СЛУЧАИ УДАРНОГО ДЕЙСТВИЯ НАГРУЗКИ § 5.14. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 15. НАПРЯЖЕНИЯ, ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ § 1.15. ПЕРЕМЕННЫЕ НАПРЯЖЕНИЯ. УСТАЛОСТЬ § 2.15. ПРЕДЕЛ ВЫНОСЛИВОСТИ § 3.15. ДИАГРАММЫ ПРЕДЕЛЬНЫХ АМПЛИТУД И ПРЕДЕЛЬНЫХ НАПРЯЖЕНИИ § 4.1. ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЕЛИЧИНУ ПРЕДЕЛА ВЫНОСЛИВОСТИ § 5.15. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ Примеры расчета Вопросы для самопроверки Глава 16. ТОНКОСТЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ОБОЛОЧКИ И ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ § 1.16. РАСЧЕТ ТОНКОСТЕННЫХ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕК § 2. 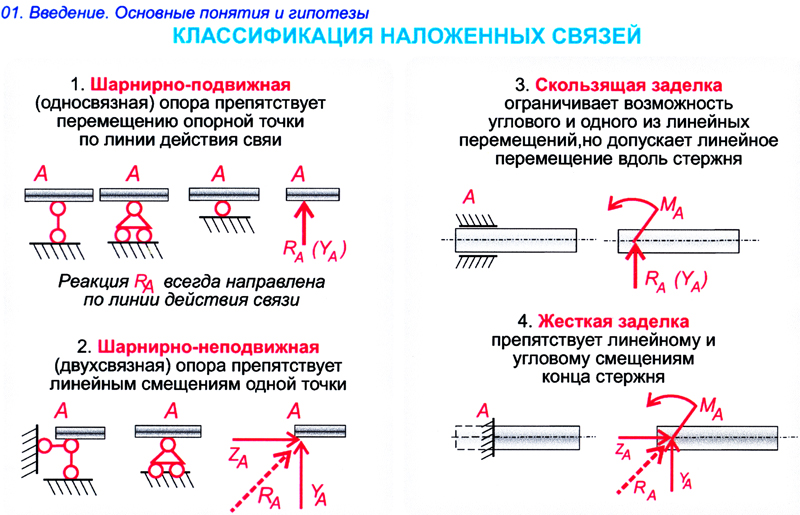16. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 17. РАСЧЕТ КОНСТРУКЦИЙ ПО НЕСУЩЕЙ СПОСОБНОСТИ § 2.17. РАСТЯЖЕНИЕ И СЖАТИЕ § 3.17. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.17. ИЗГИБ БАЛОК § 5.17. МЕТОД РАСЧЕТА КОНСТРУКЦИЙ ПО РАСЧЕТНЫМ ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки ПРИЛОЖЕНИЯ

РЕАКЦИЯ ЗАКРЫТИЯ ВЕК | JAMA Ophthalmology

РЕАКЦИЯ ЗАКРЫТИЯ ВЕК | JAMA Офтальмология | Сеть ДЖАМА [Перейти к навигации]

Эта проблема

• Скачать PDF
• Полный текст

• Поделиться

  Твиттер Фейсбук Электронная почта LinkedIn

• Процитировать это
• Разрешения

Артикул

Март 1943 г.

М. Б. БЕНДЕР, MD

Принадлежности автора

НЬЮ-ЙОРК

Из неврологической службы доктора И. С. Векслера и лабораторий больницы Маунт-Синай.

Арка Офтальмол. 1943; 29(3):435-440. дои: 10.1001/архофт.1943.00880150109004

Полный текст

Абстрактный

Одной из редко тестируемых нормальных реакций является реакция закрытия век. Эта реакция, также известная как круговой рефлекс, на самом деле представляет собой ассоциированное движение. Он состоит из сужения зрачка в сочетании с активным сокращением круговой мышцы глаза и закатыванием глазного яблока вверх. Его вызывают следующим образом: пациента просят плотно закрыть глаза, и когда веки насильно раздвигают, исследователь замечает легкое сужение зрачка. ¹

Хотя реакцию закрытия век можно вызвать у здорового человека, ее не всегда можно наблюдать, если не провести тщательное пупиллографическое исследование. ² Piltz ³ обнаружил реакцию только у 1 из 23 человек. Сужение зрачков в связи с закрытием век впервые было отмечено у пациента, у которого отсутствовал световой рефлекс. Von Graefe, ⁴ Westphal ⁵ и Piltz ³ описали это явление в большом количестве

Полный текст

Добавить или изменить учреждение

• Академическая медицина
• Кислотно-основное, электролиты, жидкости
• Аллергия и клиническая иммунология
• Анестезиология
• Антикоагулянты
• Искусство и изображения в психиатрии
• Кровотечение и переливание
• Кардиология
• Уход за тяжелобольным пациентом
• Проблемы клинической электрокардиографии
• Клиническая задача
• Поддержка принятия клинических решений
• Клинические последствия базовой нейронауки
• Клиническая фармация и фармакология
• Дополнительная и альтернативная медицина
• Заявления о консенсусе
• Коронавирус (COVID-19)
• Медицина интенсивной терапии
• Культурная компетентность
• Стоматология
• Дерматология
• Диабет и эндокринология
• Интерпретация диагностических тестов
• Разработка лекарств
• Электронные медицинские карты
• Скорая помощь
• Конец жизни
• Гигиена окружающей среды
• Справедливость, разнообразие и инклюзивность
• Этика
• Пластическая хирургия лица
• Гастроэнтерология и гепатология
• Генетика и геномика
• Геномика и точное здоровье
• Гериатрия
• Глобальное здравоохранение
• Руководство по статистике и методам
• Рекомендации
• Заболевания волос
• Модели медицинского обслуживания
• Экономика здравоохранения, страхование, оплата
• Качество медицинской помощи
• Реформа здравоохранения
• Медицинская безопасность
• Медицинские работники
• Различия в состоянии здоровья
• Несправедливость в отношении здоровья
• Информатика здравоохранения
• Политика здравоохранения
• Гематология
• История медицины
• Гуманитарные науки
• Гипертония
• Изображения в неврологии
• Наука внедрения
• Инфекционные болезни
• Инновации в оказании медицинской помощи
• Инфографика JAMA
• Право и медицина
• Ведущее изменение
• Меньше значит больше
• ЛГБТК-медицина
• Образ жизни
• Медицинский код
• Медицинские приборы и оборудование
• Медицинское образование
• Медицинское образование и обучение
• Медицинские журналы и публикации
• Меланома
• Мобильное здравоохранение и телемедицина
• Нарративная медицина
• Нефрология
• Неврология
• Неврология и психиатрия
• Примечательные примечания
• Сестринское дело
• Питание
• Питание, Ожирение, Упражнения
• Ожирение
• Акушерство и гинекология
• Гигиена труда
• Онкология
• Офтальмологические изображения
• Офтальмология
• Ортопедия
• Отоларингология
• Лекарство от боли
• Патология и лабораторная медицина
• Уход за пациентами
• Информация для пациентов
• Педиатрия
• Повышение производительности
• Показатели эффективности
• Периоперационный уход и консультации
• Фармакоэкономика
• Фармакоэпидемиология
• Фармакогенетика
• Фармация и клиническая фармакология
• Физическая медицина и реабилитация
• Физиотерапия
• Руководство врача
• Поэзия
• Здоровье населения
• Профилактическая медицина
• Профессиональное благополучие
• Профессионализм
• Психиатрия и поведенческое здоровье
• Общественное здравоохранение
• Легочная медицина
• Радиология
• Регулирующие органы
• Исследования, методы, статистика
• Реанимация
• Ревматология
• Управление рисками
• Научные открытия и будущее медицины
• Совместное принятие решений и общение
• Медицина сна
• Спортивная медицина
• Трансплантация стволовых клеток
• Наркомания и наркология
• Хирургия
• Хирургические инновации
• Хирургический жемчуг
• Обучаемый момент
• Технологии и финансы
• Искусство JAMA
• Искусство и медицина
• Рациональное клиническое обследование
• Табак и электронные сигареты
• Токсикология
• Травмы и травмы
• Приверженность лечению
• УЗИ
• Урология
• Руководство пользователя по медицинской литературе
• Вакцинация
• Венозная тромбоэмболия
• Здоровье ветеранов
• Насилие
• Женское здоровье
• Рабочий процесс и процесс
• Уход за ранами, инфекция, лечение

Сохранить настройки

Политика конфиденциальности | Условия использования

Закрытие «Обсуждения динамических силовых реакций в двухходовых регулирующих клапанах» (1951, Trans.

ASME, 73, стр. 1106) | J. Fluids Eng.

Пропустить пункт назначения навигации

Закрытия

К. Ф. Кинг,

Г. Ф. Брокетт

Информация об авторе и статье

Транс. АСМЭ . ноябрь 1951 г., 73(8): 1106-1107 (2 страницы)

https://doi.org/10.1115/1.4016555

Опубликовано в Интернете: 29 июля 2022 г.

История статьи

Опубликовано:

1 ноября 1951 г.

Онлайн:

29 июля 2022 г.

Статья

Статья обсуждалась| Посмотреть статью

Обсуждения

Обсуждение этой статьи| Посмотреть обсуждение

Подключенный контент

Был опубликован комментарий: Обсуждение: «Динамические силовые реакции в двухходовых регулирующих клапанах» (Кинг, К. Ф., и Брокетт, Г.Ф., 1951, Trans. ASME, 73, стр. 1101–1106)

Это комментарий к: Динамические силовые реакции в двухходовых регулирующих клапанах

• Разделенный экран
• Взгляды
  • Содержание артикула
  • Рисунки и таблицы
  • Видео
  • Аудио
  • Дополнительные данные
  • Экспертная оценка
• PDF
• Делиться
  • Facebook
  • Твиттер
  • LinkedIn
  • MailTo

• Иконка Цитировать Цитировать

• Разрешения

• Поиск по сайту

Citation

Кинг, К.