Расчет вала на кручение

Расчет позполяет вычислить внутренние моменты на участках вала, построить эпюру крутящих моментов, вычислить касательные напряжения и углы закручивания участков а также построить эпюру углов закручивания.

При необходимости предварительно раскрывается статическая неопределимость для вала, закрепленного с обоих концов.

---

---

Для более удобной и быстрой оплаты Вы можете зарегистрироваться, пополнить счет на сайте и оплачивать со своего счета

---

Почему не бесплатно? — Сайт создан исключительно на энтузиазме автора и дабы этот энтузиазм не угас, хотелось бы его подкрепить хоть каким-нибудь материальным поощрением. Кроме того, возросшее количество пользователей вынудило перейти на платный хостинг.

Условия оплаты? — Взнос денег считаем спонсорским взносом, поэтому ни о каком возврате речь идти не может, тем более суммы мизерные — практически не о чем спорить.
Но! Если Вы оплатили взнос, но недовольны результатом, Вы всегда можете обратиться за помощью к автору — Telegram: sopromat_xyz WhatsApp

А Ваш сайт не сворует мой номер карты, пароли и т.д.??? — Это невозможно! После того, как Вы нажмете «Перевести», Вы будете направлены на страницу Яндекса (можете проверить в адресной строке), и все дальнейшие операции будете производить на сервисе Яндекса, так что со стороны сайта Вам ничего не грозит.

название схемы заделка в начале
заделка в конце
Модуль сдвига G=МПа

Участки вала:

Момент в конце вала M = Нм

Моменты «от себя» указывайте с минусом

---

Расчетная схема №1847254

---

---

Обозначаем участки вала, начиная с незакрепленного правого конца

Моменты инерции сечений вала

J_k1 = π×d⁴×(1-α⁴)/32 = π×6⁴×(1-0.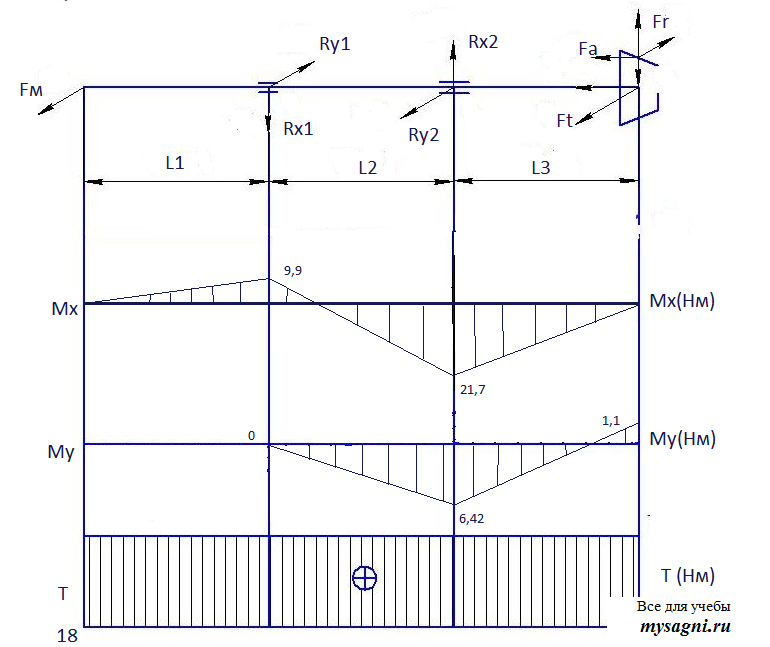 6⁴)/32 = 111 см⁴

J_k2 = β×b⁴ = 0.229×2⁴

= 3.66 см⁴

J_k3 = π×d⁴/32 = π×4⁴/32 = 25.1 см⁴

Моменты сопротивления сечений вала

W_k1 = π×d³×(1-α⁴)/16 = π×6³×(1-0.6⁴)/16 = 36.9 см³

W_k2 = α×b³ = 0.246×2³ = 1.97 см³

W_k3 = π×d³/16 = π×4³/16 = 12.6 см³

Моменты на участках вала определяем, используя метод сечений

— первый участок

M₁ = -30 = -30Нм

— второй участок

M₂ = -30 +20 = -10Нм

— третий участок

M₃ = -30 +20 +50 = 40Нм

Угол закручивания на одном участке определяется по формуле

$$ \phi = \frac{M*l}{G*J_k} $$

— первый участок

φ₁ = -30×0.8 / 78000×10⁶×111×10^-8 = -0.

0002772 рад

— второй участок

φ₂ = -10×2 / 78000×10⁶×3.66×10^-8 = -0.007006 рад

— третий участок

φ₃ = 40×1.2 / 78000×10⁶×25.1×10^-8 = 0.002452 рад

По полученным данным строим эпюры. Эпюру углов закручивания строим, начиная с левого закрепленного конца вала.

---

Посмотреть примеры

---

Не получается решить задачу? Есть вопросы? Нужна помощь? Обратитесь к авторам сайта через ВКонтакте Telegram: sopromat_xyz WhatsApp: +380936422175

---

Онлайн калькулятор: Построение эпюр внутренних усилий

Данный онлайн калькулятор предназначен для построения эпюр внутренних усилий. Эпюра внутренних усилий — график, показывающий характер изменения внутренних усилий по длине стержня. Построение эпюр необходимо для определения положения наиболее нагруженного (опасного) сечения стержня. Калькулятор наглядно изображает эпюру изгибающего момента M и поперечной силы Q.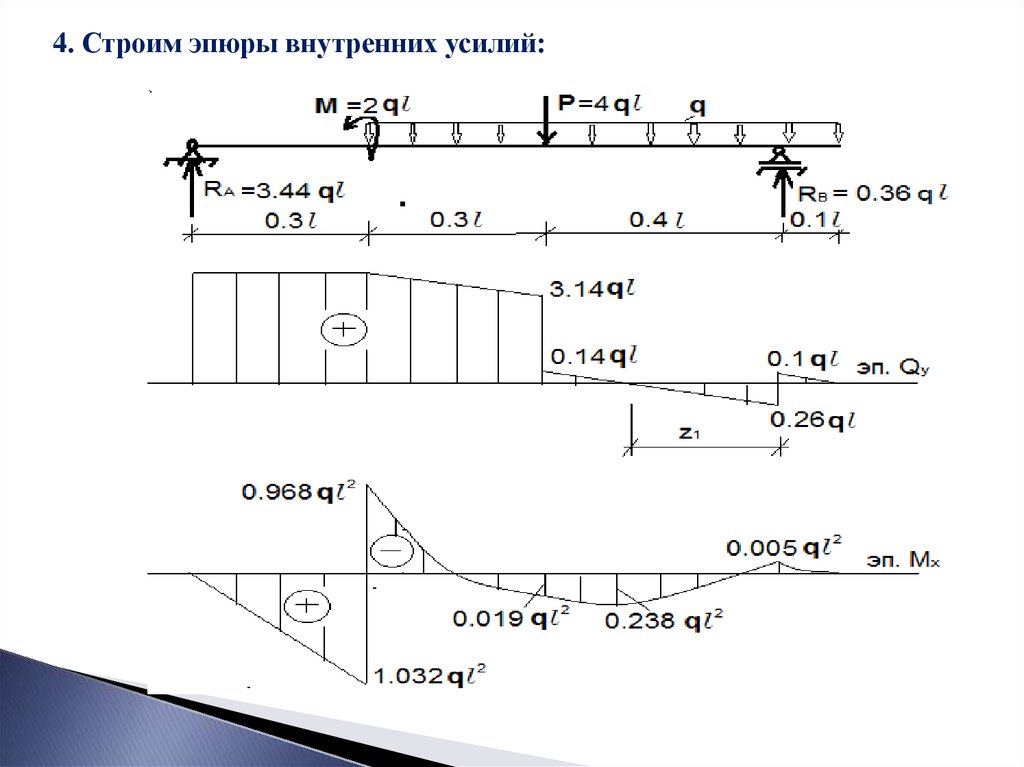 Теорию и формулы расчета можно найти ниже под калькулятором.

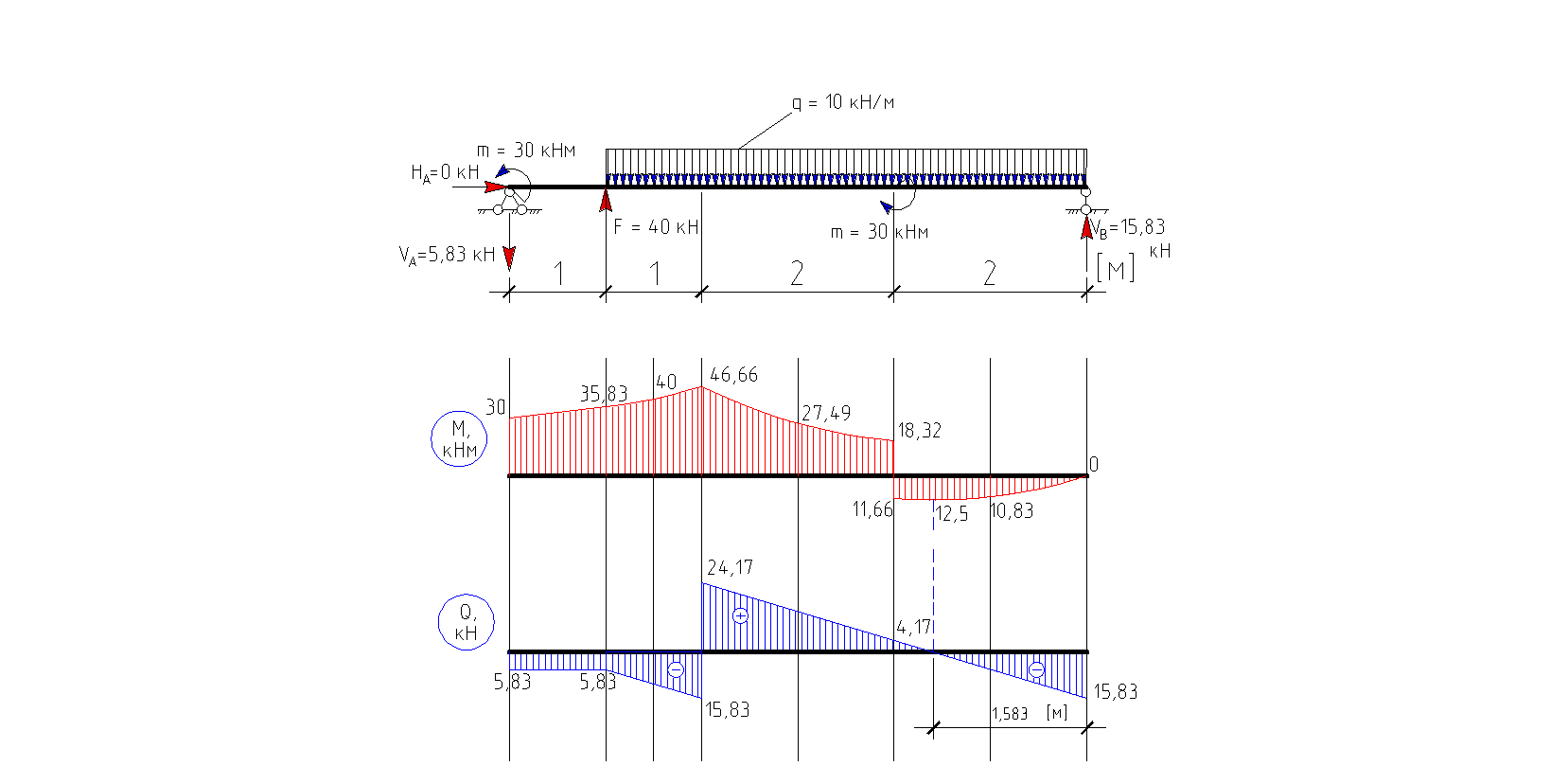
Эпюры поперечных сил и моментов в простой балке

Расстояние между опорами, м

Нагрузка

	Расстояние от опоры A	Нагрузка	Значение	Направление	Направление момента	Протяженность	Изменение

Записей:

51020501001000

Нагрузка

Расстояние от опоры A

Отрицательное, если нагрузка приложена к точке, лежащей левее опоры.

НагрузкаСосредоточенная нагрузка, кНРавномерно распределенная, кН/мЛинейно распределенная, кН/мМомент, кН*М

Значение

Направление↓ вниз↑ вверх

Направление момента↻ По часовой стрелке↺ Против часовой стрелки

Протяженность

Изменение\ Убывание/ Возрастание

Импортировать данныеОшибка импорта

Данные

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;L;50.5;up;anticlockwise;50.5;increase

Загрузить данные из csv файла

Детали

Точность вычисления

Знаков после запятой: 2

Эпюры внутренних сил и моментов в балке

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.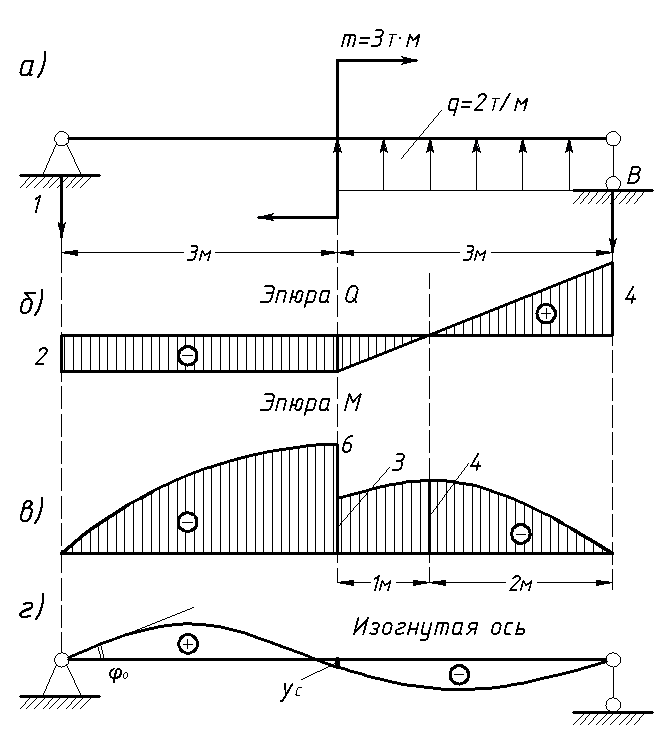

Внутренние силы

Для иллюстрации внутренних сил, действующих в балке под нагрузкой, рассмотрим следующий рисунок.

Балка под нагрузкой, определение внутренних сил в сечении

Мысленно рассечем балку на два сегмента в точке B, где мы будем определять внутренние силы, действующие в балке.

Диаграмма свободного тела для сечения балки

Внутренние силы, действующие в сечении балки можно показать как внешние, на диаграмме свободного тела рассеченной балки. Компонента N_B, действующая вдоль балки, называется нормальной силой. В калькуляторе мы не рассматриваем нормальную силу, так как можно ввести только поперечные нагрузки.
Компонента внутренних сил Q_B, действующая параллельно сечению называется поперечной силой. На рисунке отражена только y-составляющая поперечных сил, в действительности возможна еще и z-составляющая. Калькулятор не допускает поворота нагрузки вокруг оси x, поэтому в наших вычислениях эта составляющая отсутствует.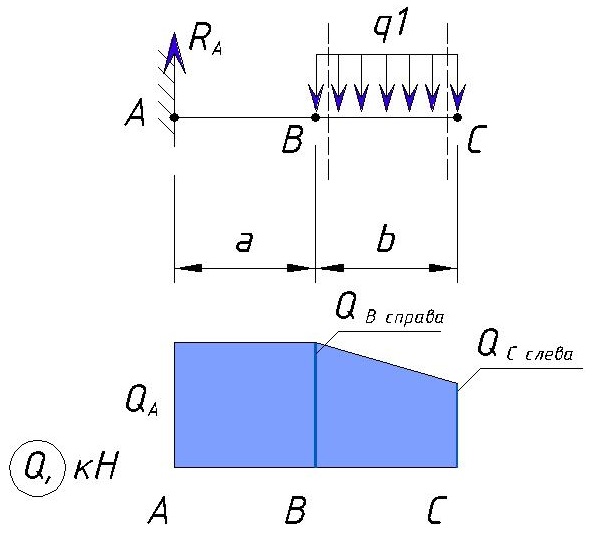
Моменты M_B называются изгибающими моментами. Изгибающий момент равен сумме моментов всех внешних сил, приложенных к рассматриваемой части балки, относительно центра тяжести проведенного сечения.
Компоненты сил препятствуют относительному смещению двух сегментов, моменты препятствуют относительному вращению.¹

Построение эпюр методом интегрирования.

Мы будем искать формулы для вычисления значений поперечной силы Q(x) и изгибающего момента M(x) отдельно для разных участков балки.
Границами участков являются характерные точки: концевые сечения балки, точки опор, точки приложения сосредоточенных сил и моментов, точки начала и конца действия распределенных нагрузок.
Для каждого участка, вычисляется интеграл от функции распределенной нагрузки q(x) для определения поперечной силы Q(x), следующим шагом вычисляется интеграл от Q(x) для определения функции изгибающего момента M(x) в соответствии с формулами:

²

Распределенная нагрузка q(x) в нашем калькуляторе может быть линейной, равномерно убывающей или возрастающей. В первом случае q(x) — константа , во втором — линейная функция: kx+b, в случае отсутствия распределенных нагрузок на участке q(x)=0, поперечная сила будет равна константе.
Таким образом для отыскания функций Q(x) и M(x) потребуется вычисление неопределенного интеграла от многочлена и вычисление константы интегрирования. Константу интегрирования можно найти, зная какую либо точку, через которую проходит искомая функция. См.: Интеграл многочлена.

В качестве такой точки будем брать значения Q(x) и M(x) по левой границе участка.
Q(x_l) будет равно значению функции поперечной силы Q(x) для предыдущего участка в точке l, смещенное на величину сосредоточенной силы (или опорной реакции) в этой точке. Если сила действует вверх, то смещение положительно, если вниз — отрицательно.
M(x_l) будет равно значению функции изгибающего момента M(x) для предыдущего участка в точке l, смещенное на величину сосредоточенного момента, приложенного к этой точке. Если сосредоточенный момент направлен по часовой стрелке, то смещение положительно, в противном случае — отрицательно.

Значение Q(x) на левом краю балки будет соответствовать сумме сосредоточенных сил и опорной реакции в этой точке, или будет равно нулю при отсутствии таковых. Значение M(x) по краям балки равно сумме значений сосредоточенных моментов приложенных к концам балки. Если сосредоточенных моментов в этих точках нет, то M(x) будет равен нулю.
Знаки для М(x) и Q(x) можно связать с характером деформации балки при действии внешних сил. Если изгибающий момент в сечении положителен, то балка в этом сечении гнется выпуклостью вниз, если же он отрицателен, то балка гнется выпуклостью вверх.

Пример

Рассмотрим получение функций Q(x) и M(x) на примере:

Приложенные нагрузки и опорные реакции

Открыть этот пример

1. Первым делом вычисляются реакции опор. Посмотреть как они находятся можно в этом калькуляторе.
   Получаем реакции опор:
   
   
2. Балка делится на участки по ключевым точкам с координатами: 0, 2, 4, 5, 6.
   Участок А — характерные точки 0,2
   Участок B — характерные точки 2,4
   Участок C — характерные точки 4,5
   Участок D — характерные точки 5,6
3. Для каждого участка находим формулу распределенной нагрузки, интегрируем ее дважды получая формулу для поперечных сил Q(x) и изгибающих моментов M(x). 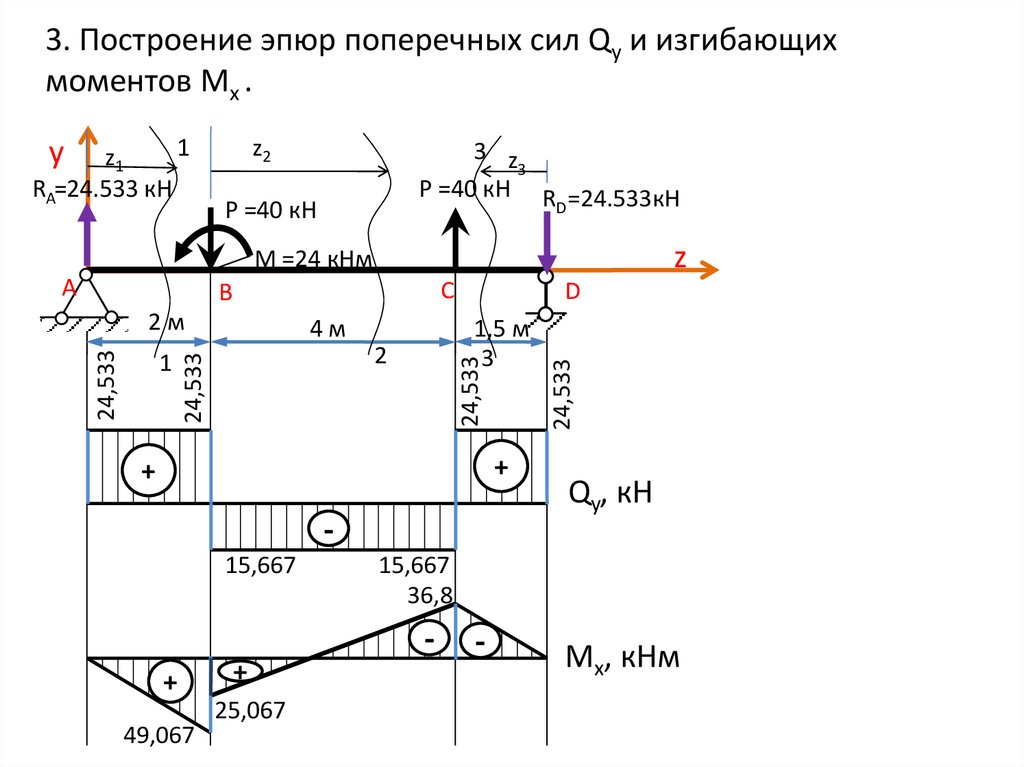Константы интегрирования вычисляются по левой границе участка по формулам для предыдущих участков.
   
   Участок А, значения в характерных точках
   Участок А

   Распределенная нагрузка на участке равна: q(x) = 5. Найдем функцию поперечной силы на участке, путем интегрирования функции распределенной нагрузки:
   
   Выразим константу C = Q(x)+5x, и подставим в формулу x=0 и значение поперечной силы в этой точке. Поперечная сила на концах балки равна нулю, но в точке 0 она изменена реакцией опоры V_A=11.56кН, которая направленна вверх. Соответственно поперечная сила в точке 0 будет равна Q(0) = 0 + 11.56 = 11.56.
   Поэтому C = 11.56 — 5 ⋅ 0 = 11.56
   Формула для поперечной силы на участке А:
   
   Интегрируя функцию поперечной силы, получаем функцию изгибающего момента:
   
   Аналогичным образом, значение момента на концах балок = 0, сосредоточенных моментов в начальной точке нет, поэтому M(0) = 0.
   Подставляя x=0 и M(0) = 0 в выражение для C = M(x) + 2.

   5x² — 11.56x = 0 + 2.5 · 0² — 11.56 · 0 получаем значение C = 0
   Формула для изгибающего момента на участке А:
   

Участок В, значения в характерных точках

Участок B

Чтобы найти распределенную нагрузку q(x) воспользуемся уравнением прямой линии по двум точкам.
По точкам (2;0) и (4;8) получаем уравнение для распределенной нагрузки: q(x) = 4x-8.
Найдем функцию поперечной силы на участке, интегрируя полученную функцию распределенной нагрузки.

По формуле Q(x) для предыдущего участка вычисляем значение Q на левой границе участка: Q(2)=-5∙2+11.56 = 1.56. Аналогично, как и на предыдущем участке вычисляем интеграл и константу интегрирования по точке (2;1.56).
Получим формулу для поперечной силы на участке B:
^{см. расчет}
По формуле из предыдущего участка вычислим значение момента на левой границе участка: M(2) = -2.5 ∙ 2² + 11.56 ∙ 2 + 0= 13.12 .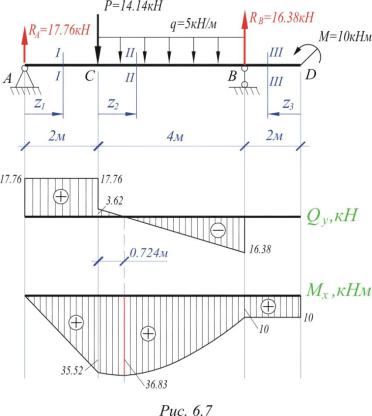
Интегрируя формулу Q(x) и вычисляя константу интегрирования по граничной точке получим формулу для изгибающего момента на участке B:
^{см. расчет}

Участок С, значения в характерных точках

Участок C

По формуле Q(x) для предыдущего участка вычисляем значение Q на левой границе участка: Q(4) = -2 ∙ 4² + 8 ∙ 4 – 6.44 = -6.44.
Сосредоточенная сила скачком изменяет Q_x в данной точке, она направлена вниз и потому отрицательна: Q(4) = -6.44 — 4 = -10.44
На третьем участке нет распределенной нагрузки, поперечная сила равна константе по последней точке.
Получим формулу для поперечной силы на участке С:

По формуле из предыдущего участка вычислим значение момента на левой границе участка: M(4) = -0.67 ∙ 4³ + 4 ∙ 4² – 6.44 ∙ 4 + 15.33 = 10.91
Интегрируя формулу Q(x) и вычисляя константу интегрирования по граничной точке получим формулу для изгибающего момента на участке С:
^{см. расчет}

Участок D, значения в характерных точках

Участок D

К данному участку также не приложена распределенная нагрузка, поперечная сила равна константе.
Формула для поперечной силы на участке D:

По формуле из предыдущего участка вычислим значение момента на левой границе участка: M(5) = -10.44 ∙ 5 + 52.67 = 0.47
Сосредоточенный момент скачком изменяет M_x в данной точке, он направлен по ходу часовой стрелки и поэтому положителен: M(5) = 0.47 + 10 = 10.47
Интегрируя формулу Q(x) и вычисляя константу интегрирования по граничной точке получим формулу для изгибающего момента на участке D:
^{см. расчет}

Чтобы проверить правильность формул найдем значения поперечной силы и изгибающего момента в крайней точке балки.

Сосредоточенная сила в данной точке по величине равна опорной реакции с противоположным знаком. Изгибающий момент на концах балки равен нулю.

---

1. R. C.Hibbeler Engineering mechanics. Statics 12th edition, стр. 330 ↩

2. Н. М. Беляев. Сопротивление материалов, М.: Издательство «Наука», 1965г, изд. 14, 231 стр.  ↩

 балка внутренний момент Инженерные поперечные силы теоретическая механика эпюра

Wolfram|Alpha Примеры: чертежи и графика

Ого! Wolfram|Alpha не работает без JavaScript.

Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.

Примеры для

Построение графиков — это методы визуализации поведения математических функций. Используйте Wolfram|Alpha для построения графиков функций, уравнений и неравенств в одном, двух и трех измерениях. Получите дополнительную перспективу, изучая полярные графики, параметрические графики, контурные графики, графики областей и многие другие типы визуализации интересующих вас функций и уравнений. 93 t)

Укажите диапазон для параметра:

параметрический график (sin 10t, sin 8t), t=0..2pi

Нарисуйте параметрическую кривую в трех измерениях:

3D параметрический график (cost, sin 2t, sin 3t )

Рисование параметрической поверхности в трех измерениях:

3D-параметрический график (cos u, sin u + cos v, sin v), u=0–2pi, v=0–2pi

3D-графики

График функции двух переменных как поверхность в трехмерном пространстве.

График функции двух переменных:

график sin x cos y 92>5, 0<=x<3Больше примеров

СВЯЗАННЫЕ ПРИМЕРЫ

Алгебра

Приложения исчисления

Область и диапазон

Геометрия

Числа

Полярная кривая или график 5 точек 9001 система.

Нарисуйте полярную диаграмму:

полярную диаграмму r=1+cos theta

Укажите диапазон для переменной тета:

полярную диаграмму r=theta, theta=0 to 8 pi

Создайте график онлайн и найдите кратчайший путь или используйте другой алгоритм

Построить граф и найти кратчайший путь. На странице помощи вы найдете обучающее видео.

График

Алгоритм создания

Вставьте свой алгоритм ниже и нажмите «Выполнить».

Вес края

не имеет веса 1

заменить текущий

добавить (мультиграф)

Текст над краем  

Введите название

Настройка матрицы смежности. Используйте запятую «,» в качестве разделителя

Матрица мультиграфа содержит вес минимальных ребер между вершинами.

Матрица неверна. Используйте запятую «,» в качестве разделителя. Матрица должна быть квадратной

Настроить матрицу заболеваемости. Используйте запятую «,» в качестве разделителя.

Матрица неверна. Используйте запятую «,» в качестве разделителя.

Ваш алгоритм отправлен на проверку и в случае успеха он будет добавлен на сайт.

Невозможно создать график. Матрица смежности имеет неправильный формат. Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «помощь», чтобы открыть справку о формате матрицы смежности

Невозможно создать график. Матрица заболеваемости имеет неправильный формат. Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «Справка», чтобы открыть справку о формате матрицы заболеваемости

.

Невозможно создать график. Список краев имеет неправильный формат. Нажмите кнопку «исправить», чтобы исправить список краев, или кнопку «Справка», чтобы открыть справку о формате

.

Какие функции мы должны добавить в первую очередь?

Напишите, пожалуйста, какой алгоритм вы бы хотели видеть на этом сайте?

Наш сервис уже поддерживает следующие функции: Поиск кратчайшего пути с помощью алгоритма Дейкстры, Матрица смежности, Матрица инцидентности.

Непрозрачность

Выбор и перемещение объектов мышью или перемещение рабочей области.

Перетащите курсор для перемещения объектов

Выбор и перемещение объектов мышью или перемещение рабочей области.

Перетащите курсор для перемещения объектов

Щелкните рабочую область, чтобы добавить новую вершину. Перечисление вершин

Выберите первую вершину ребра

Выберите вторую вершину ребра

Выберите начальную вершину кратчайшего пути

Выберите конечную вершину кратчайшего пути

Длина кратчайшего пути составляет %d

Путь не существует

Нажмите на объект, чтобы удалить

Добавить ребро

Режиссер

Ненаправленный

Матрица смежности

Сохранить

Отменить

наименьшее расстояние

Матрица заболеваемости

Сохранение графика

закрыть

Количество подключаемых компонентов

Количество слабо связанных компонентов

Что вы думаете о сайте?

Имя (электронная почта для обратной связи)

Обратная связь

Отправить

Чтобы задать нам вопрос или отправить нам комментарий, напишите нам по телефону

исправить матрицу

помощь

Матрица имеет неправильный формат

Сохранить изображение графика

Полный отчет

Краткий отчет

Граф не имеет эйлерова цикла

Граф имеет эйлеров цикл

Обработка. ..

Добавить вершину

Переименовать вершину

Переименовать

и

Редактировать вес

не имеет веса

Переименование группы

Проголосовать

Рекомендовать алгоритмы

Граф не имеет эйлерова пути

Граф имеет эйлеров путь

График минимальных расстояний

Проверить, чтобы сохранить

Показать матрицу расстояний

Матрица расстояний

Выберите источник максимального расхода

Выберите сток максимального расхода

Максимальный расход от %2 до %3 равен %1

Поток из %1 в %2 не существует

Источник

Раковина

Граф не имеет гамильтонова цикла

Граф имеет гамильтонов цикл

Граф не имеет гамильтоновой траектории

Граф имеет гамильтонов путь

Выбор начальной вершины обхода

Порядок обхода:

Изгиб кромки

Отменить

Сохранить график

По умолчанию

Вершинный стиль

Стиль кромки

Цвет фона

Мультиграф поддерживает не все алгоритмы

не имеет веса

Используйте Cmd⌘ для выбора нескольких объектов.

Используйте Ctrl для выбора нескольких объектов.

Перетаскивающая группа.

Группа копирования

Удалить группу

Поиск в ширину

Раскраска графика

Найти подключенные компоненты

Поиск в глубину

Найти цикл Эйлера

Найти эйлеров путь

Алгоритм Флойда-Уоршалла

Упорядочить график

Найти цикл Гамильтона

Найти гамильтонов путь

Найти максимальный расход

Поиск минимального остовного дерева

Визуализация на основе веса

Радиус и диаметр графа поиска

Найти кратчайший путь с помощью алгоритма Дейкстры

Вычислить степень вершин

Вес минимального остовного дерева

При расчете мы не учитывали направление ребер.

График отключен

Выберите первый график для проверки изоморфности.