Построение эпюр для рам — Энциклопедия по машиностроению XXL
Моменты поперечных сил не учитываем, так как их плечи относительно точки С бесконечно малы. Из рассмотренного вытекает следующее правило, весьма удобное при построении эпюр для рам алгебраическая сумма изгибающих моментов в сечениях стержней рамы, взятых бесконечно близко к данному узлу, равна нулю. В частном случае, когда в узле сходятся два стержня, это означает, что моменты в сечениях, бесконечно близких к узлу, одинаковы. Следовательно, вблизи узла эпюра М . для того и другого стержня расположена по одну сторону контура рамы. Конечно, последнее верно, если к рассматриваемому узлу не приложено внешних моментов, в противном случае этот внешний момент должен войти в ураЕ нение равновесия узла. [c.112]Вполне посильны для учащихся следующие темы докладов кручение брусьев тонкостенного замкнутого профиля расчет на растяжение (сжатие) статически неопределимых систем по методу предельного равновесия расчет на кручение брусьев круглого поперечного сечения по методу предельного равновесия расчет на изгиб статически определимых балок по методу предельного равновесия изгиб балок, составленных из материалов с разными модулями упругости изгиб биметаллических элементов при изменении температуры построение эпюр для статически определимых плоских рам.

Ось рамы представляет собой ломаную линию. Каждый прямолинейный участок рамы можно рассматривать как балку. Поэтому при построении какой-либо эпюры для рамы нужно построить ее для каждой отдельной балки, входящей в состав рамы. Однако в отличие от обыкновенных балок в сечениях стержней рамы.кроме [c.158]
УУ(ф) + Я, г/(ф) + Я и М (ф) + R соответственно в полярной системе координат. При построении эпюр для определенности радиус рамы R принят равным 5. Это сделано для наглядности в соответствии с правилом построения эпюр в криволинейных рамах (ординаты соответствующих функций отложены по нормали к оси стержня). [c.502]
Для проверки правильности построения эпюр вырезают узлы рамы и в местах разреза прикладывают внутренние силовые факторы Q, М и Л , принимая их значения, взятые с построенных эпюр. Для каждого из узлов должны выполняться условия равновесия. На рис. 3.24, ж, з представлены схемы для проверки равновесия узлов С и К .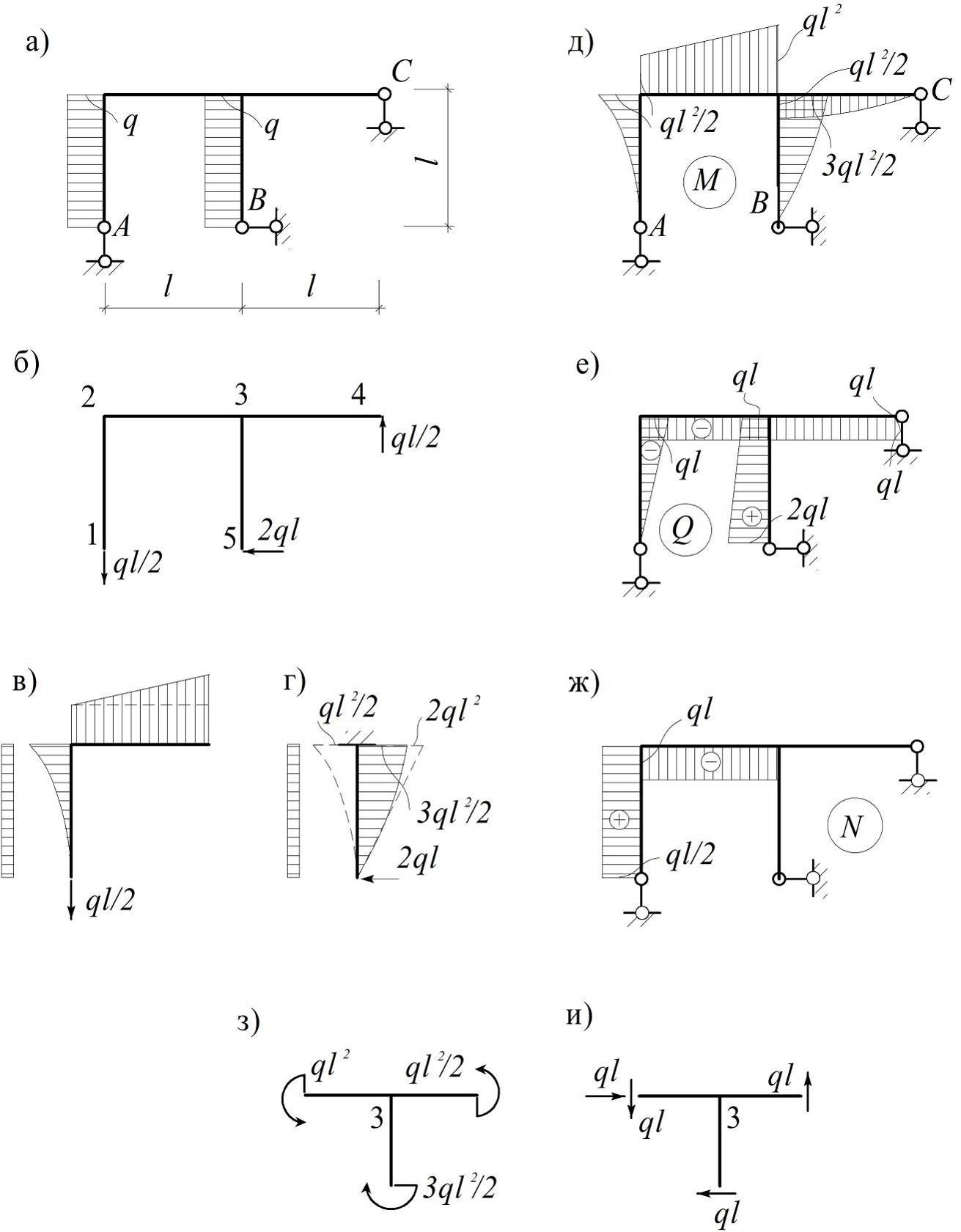 [c.266]
[c.266]
Построение эпюр для пространственной рамы с ломаной осью [c.179]
Придерживаясь изложенного метода, рассмотрим пример построения эпюр для пространственной рамы. [c.183]
При раскрытии статической неопределимости рам студенты часто затрудняются построить эпюры для рамы статически определимой, что является составной частью всего решения. Рассмотрим построение эпюр для статически определимой рамы.
Ниже приводятся примеры построения эпюр для статически определимых рам. [c.143]
На рис. 8.11 изображены эпюры М п N в раме, по очертанию совпадающей с контуром пластины и загруженной той же нагрузкой, что и пластина распределенной нагрузкой q и реакциями R. В нижнем горизонтальном стержне для упрощения построения эпюр введен разрез на оси симметрии, что, как разъяснено в -4.4, допускается при формулировке граничных условий с помощью рампой аналогии.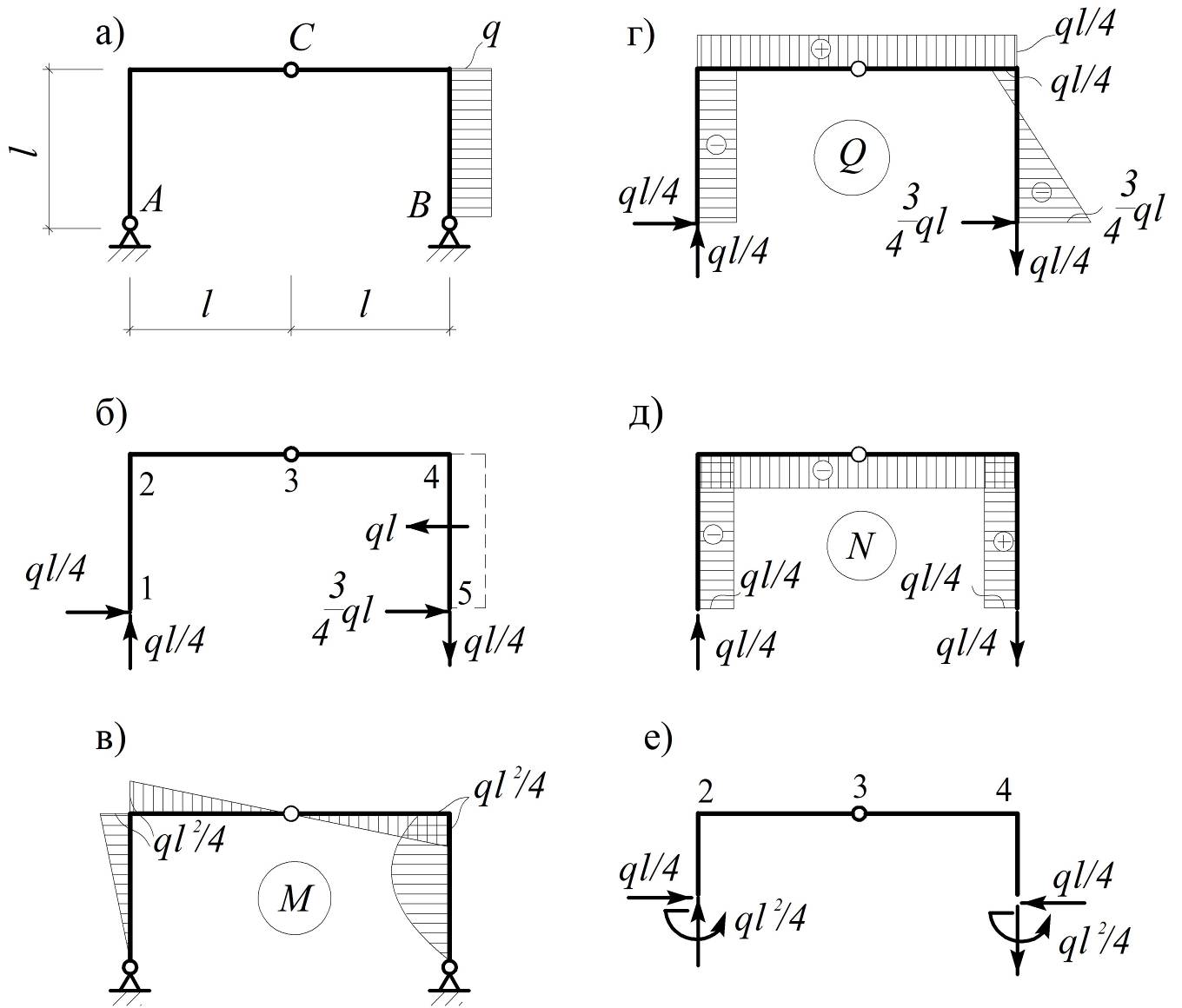 [c.237]
[c.237]
ПОСТРОЕНИЕ ЭПЮР ПРОДОЛЬНЫХ СИЛ, ПОПЕРЕЧНЫХ СИЛ и ИЗГИБАЮЩИХ МОМЕНТОВ ДЛЯ РАМ [c.50]
ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ ДЛЯ БАЛОК И ПЛОСКИХ РАМ [c.91]
Прежде чем перейти к построению эпюр внутренних силовых факторов для балок и рам, напомним некоторые положения из статики твердого тела. Различают три основных вида опорных закреплений [c.91]
Для балок будем считать, что внешняя сила, стремящаяся повернуть оставленную часть балки по часовой стрелке, дает положительную поперечную силу. Соответствующая ордината откладывается вверх от оси балки. При построении эпюр поперечных сил для рам условимся откладывать ординаты Q , по направлению левых внешних сил, не ставя при этом знака. [c.93]
ПОСТРОЕНИЕ ЭПЮР О, N и М ДЛЯ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ РАМ [c.158]
Для построения эпюр Н, Q, М разобьем раму на три участка и найдем внутренние силовые факторы, действующие по их длине. Продольные силы по участкам будут соответственно равны N1 = 3 кН N2 = 0 N3 = —34 кН.
Продольные силы по участкам будут соответственно равны N1 = 3 кН N2 = 0 N3 = —34 кН.
Для деформационной проверки можно использовать единичные эпюры изгибающих моментов в основной системе, построенные при расчете рамы. Проверка в этом случае сводится к перемножению каждой такой единичной эпюры с окончательной эпюрой изгибающих моментов. Результат каждого перемножения должен быть равен нулю. [c.473]
Перед построением эпюра следует на схеме нагружения рамы изобразить произвольное для каждого участка направление его оси X (рис. V.15, а). Ордината откладывается в направлении проекций внешней силы, от которой она возникает, если построение идет в направлении оси х на участке, и в направлении, противоположном проекции внешней силы, если построение идет в направлении, противоположном оси х. [c.142]
Ординаты эпюры изгибающих моментов, откладываются со стороны растянутого волокна. Начинать построение эпюры М.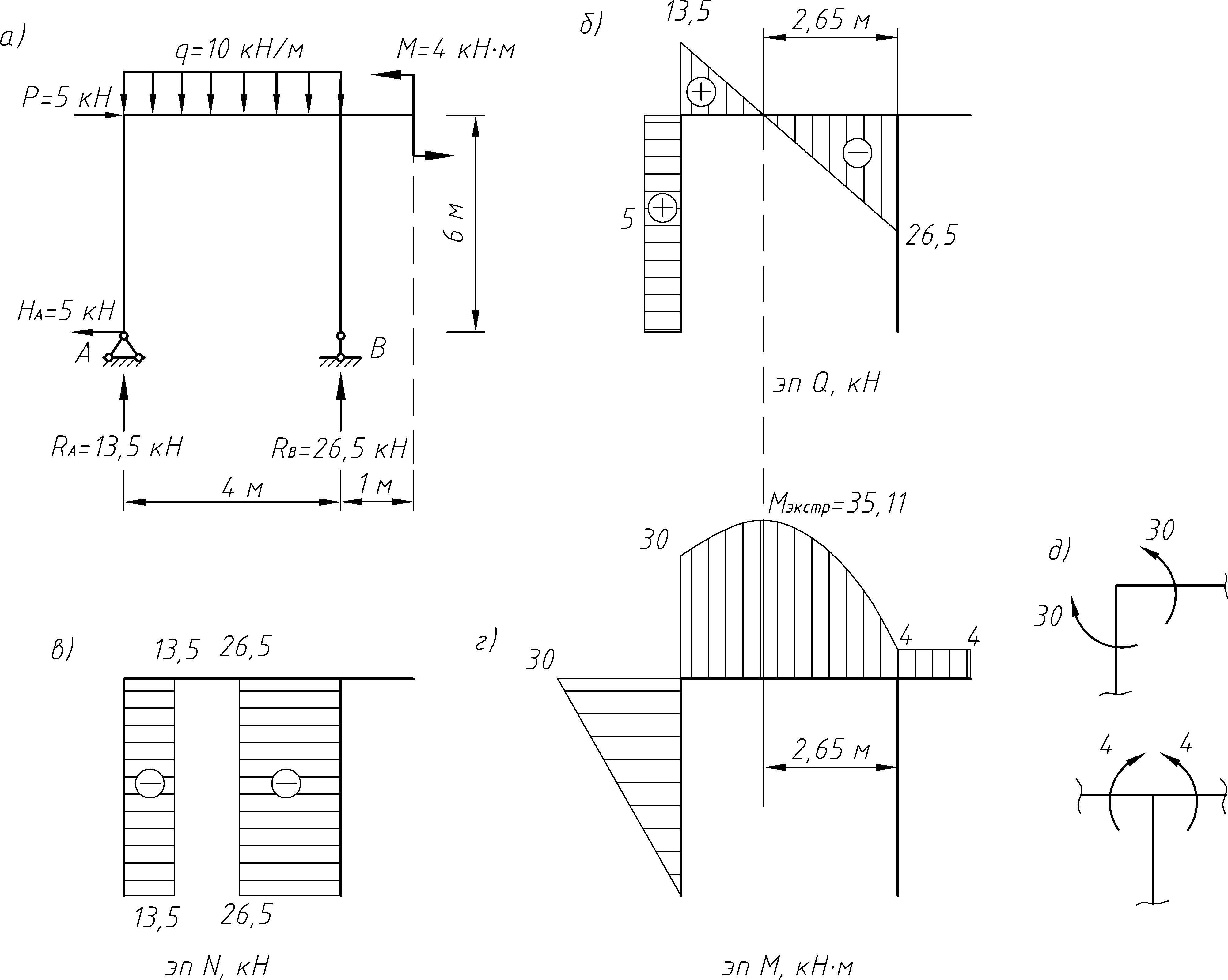
Для построения эпюры крутящих моментов вычисляем крутящие моменты на каждом участке рамы. [c.538]
Для построения эпюры поперечных сил определим опорные реакции рамы, [c.538]
ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИИ для ПРОСТЕЙШЕЙ ОДНОКОНТУРНОЙ РАМЫ [c.46]
Нагрузка перпендикулярна плоскости рамы. Расчет начинается с построения эпюры изгибающих моментов /Ио и крутящих /М для основной системы. [c.165]
Согласно рисунку 5.21 рама разбивается на 4 стержня, нумеруются узлы, стрелками указываются начало и конец каждого стержня. Исходные данные решения краевой задачи рамы и построения эпюр напряженно-деформированного состояния формируем для каждого стержня в отдельности. [c.324]
Фундаментальные функции поперечных колебаний представлены в главе 3. Ориентированный граф расчета принимаем такой же, как у задачи статики рамы.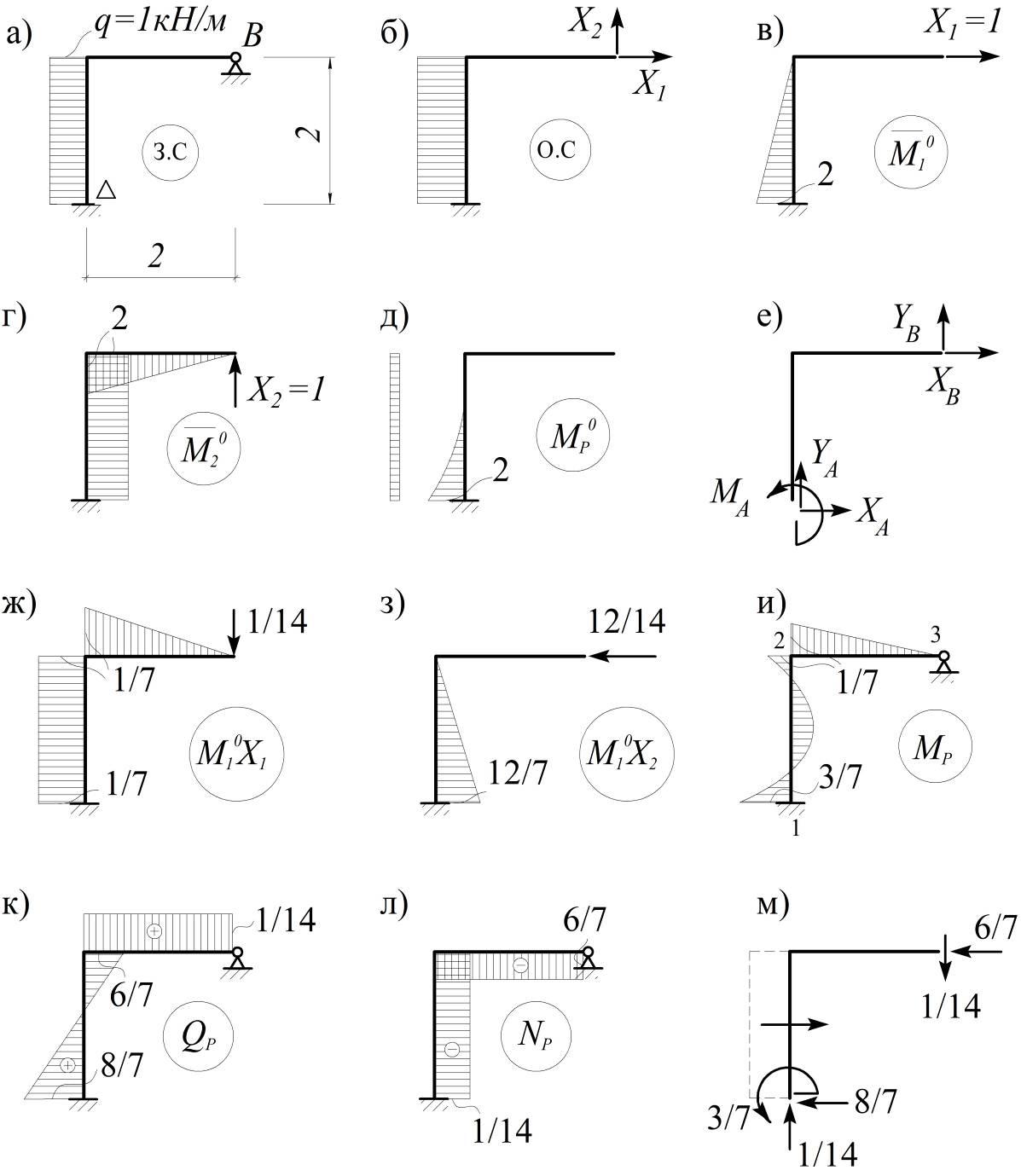 Расчет рамы на вынужденные колебания сводится к решению уравнения краевой задачи А X = -В и построению эпюр напряженно-деформированного состояния стержней. Для ухода от резонанса частоту
[c.337]
Расчет рамы на вынужденные колебания сводится к решению уравнения краевой задачи А X = -В и построению эпюр напряженно-деформированного состояния стержней. Для ухода от резонанса частоту
[c.337]
Для построения эпюры продольных сил (рис. 26) последовательно вырезаются узлы рамы (рис. 24, 25) и составляются уравнения проекций всех сил на соответствующие оси координат. [c.17]
Эпюры в рамах строятся непосредственно на контурах рамы. Все правила построения эпюр в балках применимы и для рам, если каждый прямолинейный элемент ее рассматривать как балку. [c.37]
Все правила контроля правильности построения эпюр в балках применимы и для рам. Кроме того в рамах для контроля правильности построения эпюр всегда проверяют равновесие узлов. [c.38]
В поперечных сечениях элементов пространственных стержневых систем могут действовать все шесть внутренних усилий N, Qy, Q , =М , М , М . Все правила построения эпюр в балках и плоских рамах применимы и для пространственных стержневых систем, только для каждого прямолинейного элемента необходимо изображать на расчетной схеме систему координат.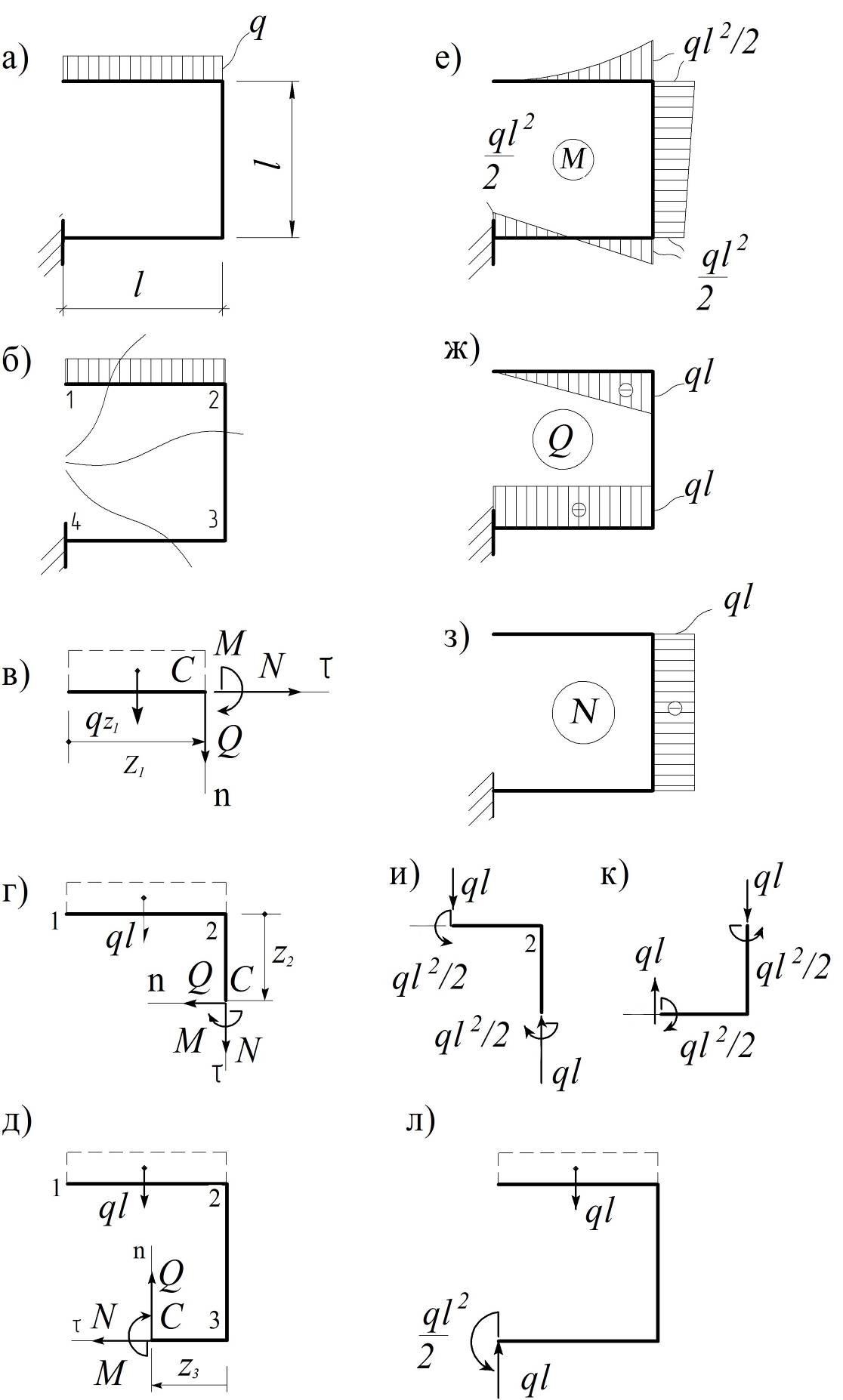 Ось j всегда совмещается с осью стержня, а оси у и z направляются так, чтобы вращение от оси к оси z совершалось против часовой стрелки по отношению к наблюдателю, расположенному со стороны положительной оси j ( рис.3.8 ).
[c.39]
Ось j всегда совмещается с осью стержня, а оси у и z направляются так, чтобы вращение от оси к оси z совершалось против часовой стрелки по отношению к наблюдателю, расположенному со стороны положительной оси j ( рис.3.8 ).
[c.39]
Обозначение узлов рамы приведено на рис. 7.7 а. Здесь же на каждом участке указаны местные системы координат. Отметим, что все они правые. Ось Ож, как обычно, является продольной. Положение осей Оу и Oz для построения эпюр, в общем, может быть произвольным, однако для дальнейших расчетов (определение напряжений и перемещений) они должны быть главными центральными осями текущих поперечных сечений.
Б. Основная система с приложенной к ней внешней нагрузкой изображена на рис. 7.19 г. Для построения эпюры моментов разрезаем раму по шарниру С. Неизвестные внутренние усилия N и Q в этом сечении находим из условий равенства нулю моментов относительно шарниров А и В для частей рамы А-С и В-С [c.
 257]
257]Все это позволяет распространить на рамы те приемы построения эпюр внутренних силовых факторов, которые использовались для бруса (см. гл. 4) и балки (см. гл. 8). Напомним, что в основе этих приемов лежит метод сечений. [c.271]
Однако при такой проверке, если ошибка сделана при построении эпюр Ml или М2, она войдет как в решение, так и в проверку и не будет замечена. Чтобы избежать этого, можно воспользоваться тем, что результат решения, т.е. внутренние силовые факторы в эквивалентной системе, не зависят от выбора эквивалентной системы, так как все они эквивалентны одной и той же исходной системе. Поэтому проверку можно производить с более обш их позиций соответствуют ли деформации эквивалентной системы связям, наложенным на исходную систему. Для этого достаточно построить новую эквивалентную систему и проверить равенство нулю перемеш ений, соответствующих новым отброшенным лишним связям, при уже определенных ранее внутренних силовых факторах. Для рассмотренной в примере 10. 3 рамы новая эквивалентная система показана на рис. 10.17 а. На рис. 10.17 б построена единичная эпюра для горизонтальной от-
3 рамы новая эквивалентная система показана на рис. 10.17 а. На рис. 10.17 б построена единичная эпюра для горизонтальной от-
Построение эпюр моментов, продольных и поперечных сил. Для изгибающих моментов вместо правила знаков устанавливается следующее правило ординаты эпюры откладываются со стороны растянутого волокна изогнутого стержня. В случае необходимости ввести знак момента стержни рамы уподобляются балкам и отмечается нижнее и верхнее волокно. Положительным считается момент, вызывающий растяжение в нижнем волокне. Продольная сила считается положительной, если она вызывает растяжение, отрицательной, — если вызывает сжатие. Поперечная сила считается положительной или отрицательной в зависимости от схемы (фиг.24,в или соответственно 24, б). Если рама имеет свободный конец, то построение эпюр начинается от этого конца. [c.150]
Для Р и N сохраняются ранее принятые правила знаков Р считается положительной, если перемещает левый конец балки вверх или правый вниз, и наоборот N берется со знаком плюс, если она растягивает участок балки, и берется со знаком минус, если участок сжимается. Для М специального правила нет. Эпюра строится на растянутых или сжатых волокнах. Если рама имеет одну жесткозащемленную опору, то построение эпюр нужно начинать со свободного конца. Это позволяет избежать определения опорных реакций при решении такой рамы. При построении эпюр для рамы, имеющей более одной опоры, решение нужно начинать С определения опорных реакций, используя обычные приемы статики.
[c.159]
Для М специального правила нет. Эпюра строится на растянутых или сжатых волокнах. Если рама имеет одну жесткозащемленную опору, то построение эпюр нужно начинать со свободного конца. Это позволяет избежать определения опорных реакций при решении такой рамы. При построении эпюр для рамы, имеющей более одной опоры, решение нужно начинать С определения опорных реакций, используя обычные приемы статики.
[c.159]
Наиболее надежной проверкой правильности определения лишних неизвестных и построения эпюр внутренних силовых факторов для заданной системы является ее повторное решение при другом выборе основной системы. Совпадение окончательных эпюр, полученных в результате двух указанных решений, является гарантией их правильности. Большая трудоемкость такой проверки заставляет в большинстве случаев от нее отказываться, ограничиваясь так называемыми статической и деформационной проверками. Первая из них заключается в проверке равновесия некоторой отсеченной части рамы под действием приложенных к ней внешних сил и внутренних силовых факторов, заменяющих действие отброшенных частей рамы на оставленную.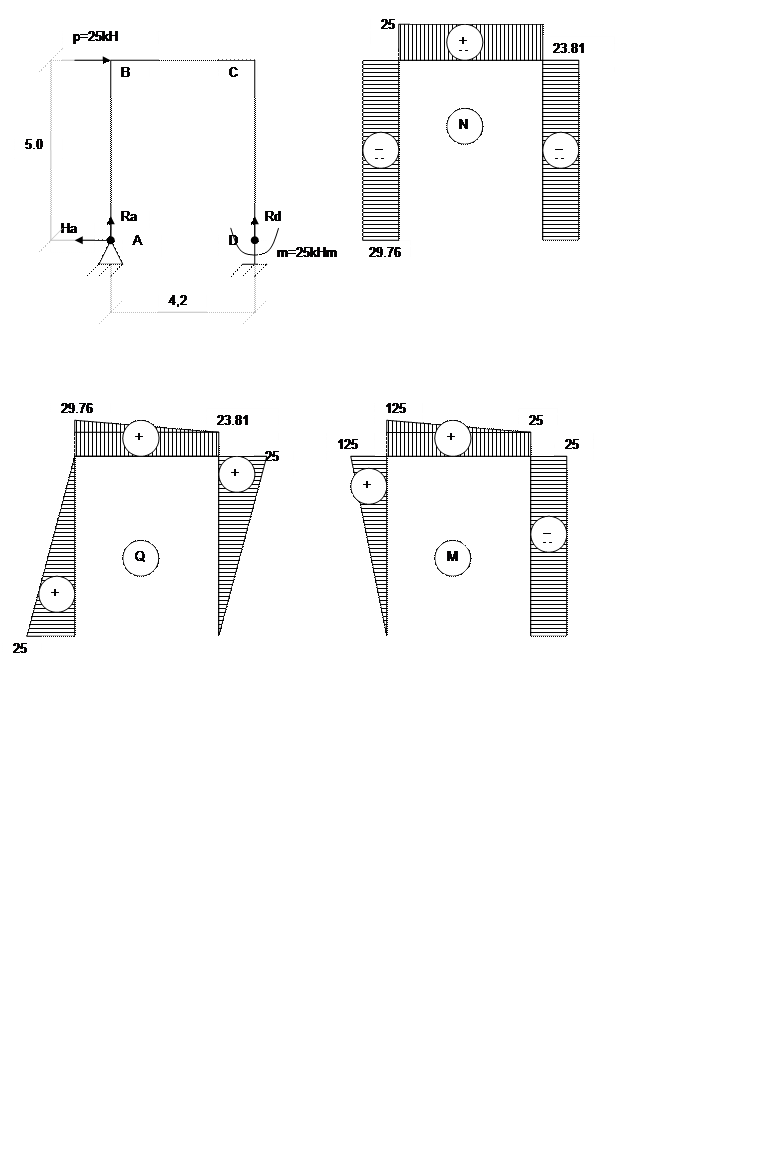 уПри деформационной проверке производится перемно-
[c.163]
уПри деформационной проверке производится перемно-
[c.163]
Для определения пяти реакций (рис. У.19, й) к трем уравнениям (У. 11) следует добавить два уравнения, составленные иэ условий равенства нулю моментов сил, действующих на раму по одну сторону от шарниров 4 и б относите.тьио этих шарниров. Построение эпюр можно выполнить после того, как будут найдены и (рама станет консольной), и определение В , и Мв не является необходимым. Поэтому уравнения (У.П) использовать не следует. Составляем систему уравнений [c.145]
На рис. 16.20, 6 показана рама и эпюра изгибающих моментов от узловых моментов. В пределах незагруженных стержней эта эпюра представляет собой полную эпюру изгибающ х моментов. Загруженным является стержень 3—4. Для получения эпюры изгибающих моментов в пределах загруженного стержня строим балочную эпюру изгибающих моментов, как это показано на рис. 16.20, в и складываем ее с ранее построенной эпюрой. Ордината эпюры М под силой Р. 777
[c.564]
777
[c.564]
Задачи, связанные с использованием элементов векторной и линейной алгебры построение эпюр внутренних силовых факторов в криволинейных рамах (см. 7.1), исследование напряженного состояния в точке (см. гл. 8). Для их решения применяются встроенные в систему Math AD операции скалярного и векторного произведения векторов, а также функции решения задачи на собственные значения и векторы матриц. [c.483]
Расчет статически неопределимой рамы методом сил
Задача №5.
Расчет статически неопределимой рамы методом сил
Для статически неопределимой Е-образной рамы с одной скользящей и двумя неподвижными опорами используя метод сил, формулу Мора и правило Верещагина необходимо определить реакции опор и построить эпюры моментов, поперечных и продольных сил
Построить эпюры M, Q и N.
Решение
Данная система дважды статически неопределима, так как рама прикреплена пятью связями, а уравнений статики для их определения – три. Выбираем основную систему путем отбрасывания лишних связей и заменой их неизвестными усилиями Х1 и Х2. Фактически Х1 будет являться реакцией опоры С, а Х2– вертикальной составляющей реакции опоры В.
Выбираем основную систему путем отбрасывания лишних связей и заменой их неизвестными усилиями Х1 и Х2. Фактически Х1 будет являться реакцией опоры С, а Х2– вертикальной составляющей реакции опоры В.
Составляем систему канонических уравнений метода сил:
d11×Х1 + d12×Х2 + D1Р = 0;d21×Х1 + d22×Х2 + D2Р = 0.
Для определения коэффициентов при неизвестных и свободных членах необходимо построить эпюры изгибающих моментов поочередно для каждой силы.
Эпюра единичных изгибающих моментов от единичной силы Х1
Эпюра единичных изгибающих моментов от единичной силы Х2
Грузовая эпюра от заданной нагрузки – силы Р.
Подсчитываем коэффициенты по формуле Мора используя правило Верещагина:
где
– величина изгибающего момента единичной эпюры Хj в точке, где расположен центр тяжести фигуры, образованной единичной эпюрой Хi; – площадь фигуры, образованной единичной эпюрой Хi.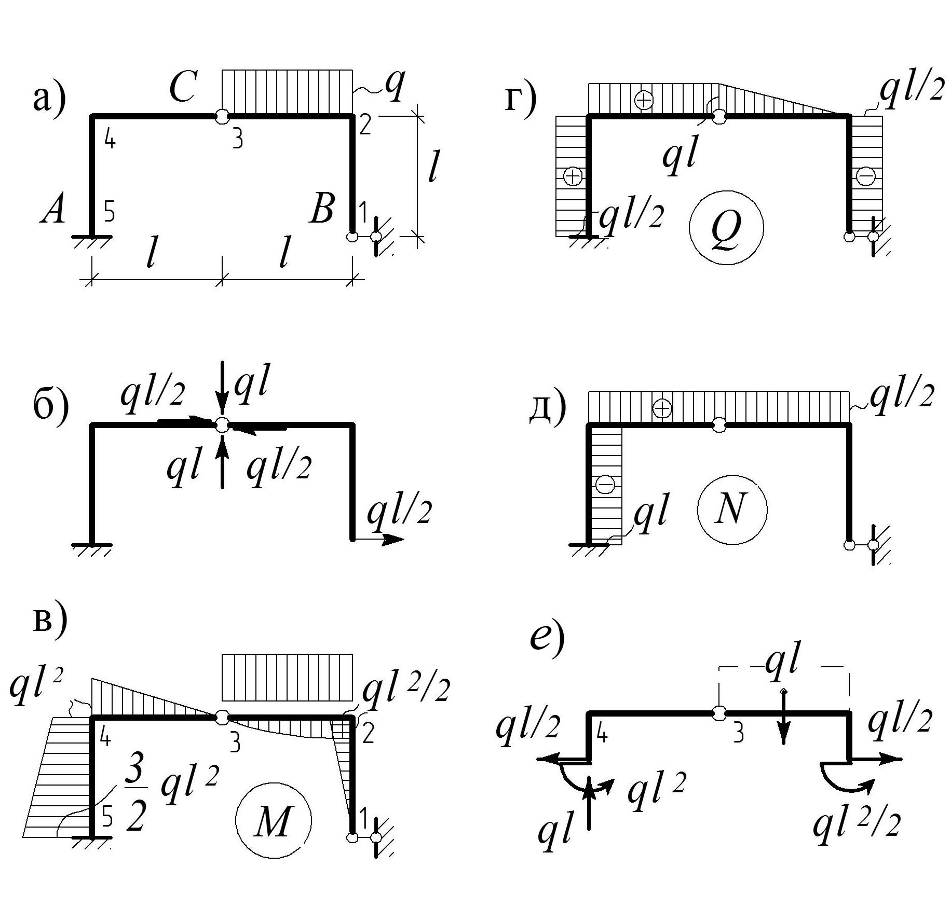
Например, для трапециевидного участка длиной L и размерами сторон м и М единичной эпюры Х1 находим координату центра тяжести для трапеции:
;Далее находим значение Мц.т. в этой точке для всех эпюр.
– для эпюры Х1 это будет:
,– для эпюры Х2 в любой точке данного участка М равно а, следовательно:
– для эпюры Р это будет:
Соответственно площади эпюр на данном участке будут равны:
Аналогичным образом находим составляющие уравнения Мора для других, более простых участков и вычисляем требуемые коэффициенты:
Подставив найденные коэффициенты в систему канонических уравнений и сократив на
и а3 получим систему двух уравнений с двумя неизвестными: ×Х1 + ×Х2 + Р = 0; 56×Х1 + 11×Х2 + 6Р = 0; ×Х1 + ×Х2 + ×Р = 0.11×Х1 + 10×Х2 + 7Р = 0;Вычитая из первого уравнения второе, получим более простое выражение, из которого выразим Х2 и подставим затем во второе уравнение;
45Х1 + Х2 – Р = 0;®Х2 = Р – 45Х1;
11 Х1 + 10Р – 450 Х1 + 5Р = 0;
Х1 =
Р = 0,034Р;Х2 = Р –
Р = – Р = –0,538Р;Найдя значения неизвестных усилий Х1 и Х2, обратимся к основной системе и найдем ХА, УА и ХВ.
SУ = 0;
УА – Х1 – Х2 – Р = 0;
УА = Х1 + Х2 + Р = 0,034Р – 0,538Р + Р = 0,496Р;
SМА = 0;
Х1×а + ХВ×а – Р×а = 0;
ХВ = Р – Х1 = 0,966Р;
SХ = 0;
ХА – ХВ = 0;
ХА = ХВ = 0,966Р;
Зная значения всех усилий, действующих на раму, строим эпюры М, Q и N:
решение задач. Пример решения задачи. Расчет статически неопределимой рамы методом перемещений.
Меню сайта
Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!
Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.
Лекции — теория, практика, задачи…
Примеры решения задач
Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое.
Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).
Форум сопромата и механики
Книги — разная литература по теме.
Заказать задачу
Друзья сайта (ссылки)
WIKIbetta
Разработчикам (сотрудничество)
Веб-мастерам (партнёрка)
О проекте, контакты
Подпроекты
Пример №2.
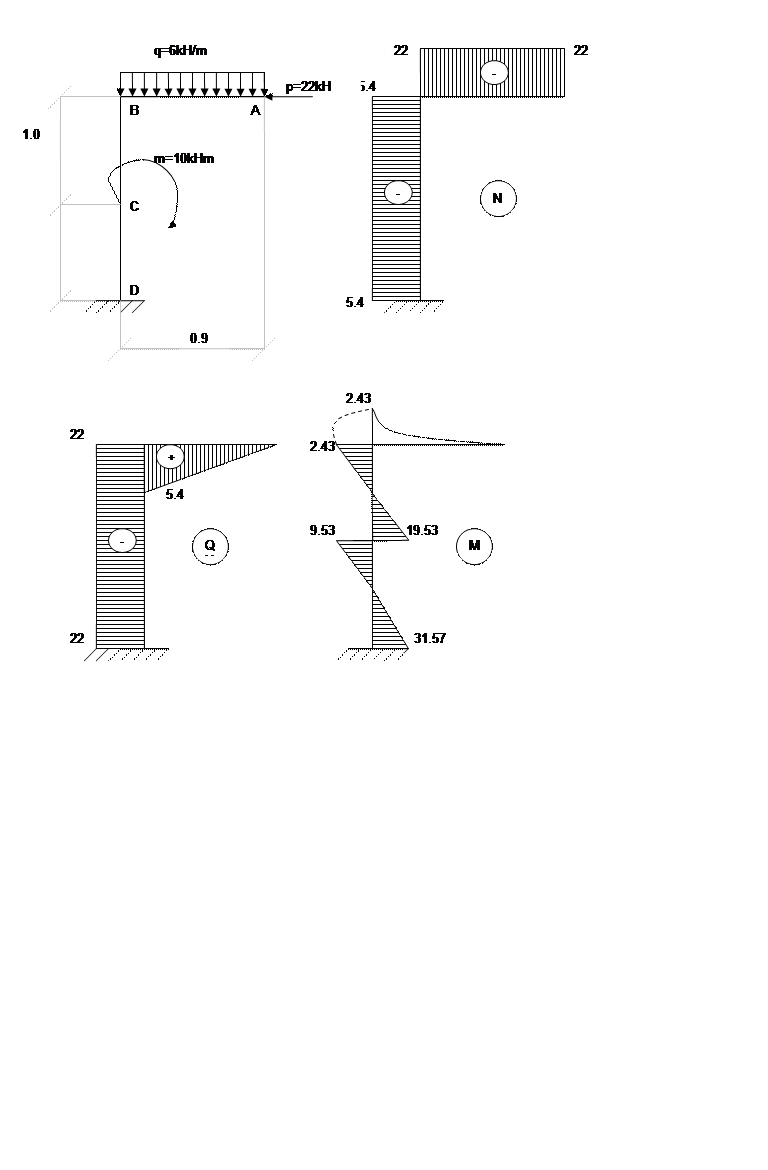 Расчет статически неопределимой рамы методом перемещений.
Расчет статически неопределимой рамы методом перемещений.Необходимо построить эпюры внутренних силовых факторов, а так же найти реакции.
Решение.
1.Определяем число неизвестных метода перемещений.
n=1+1=2
V=2·6-5-6=1
2.Выбираем основную систему метода перемещений.
3.Записываем канонические уравнения метода перемещений.
r11 + z1 + r12 + z2 + R1P = 0
r21 + z1 + r22 + z2 + R2P = 0
4.Строим эпюры изгибающих моментов в основной системе от z1=1, z2=1 и от нагрузки.
5.Определяем реакции во вновь введённых связях.
6.Подставляем найденные значения реакций в уравнения.
15·z1 + 2,25·z2 — 81 = 0
2,25·z1 + 0,75·z2 + 0 = 0
z1 = 9,8185 кН·м, z1 = -29,4569 кН.
7.Определяем концевые моменты и поперечные силы в стержнях заданной системы.
8.Строим эпюры изгибающих моментов и поперечных сил в заданной системе от нагрузки.
9.Определяем продольные силы в стержнях рамы, используя способ вырезания узлов.
10.Строим эпюру продольных сил в заданной системе от нагрузки.
11.Выполняем статическую проверку.
Все.
Автор решения: cтудент гр.193 Шубочкин.А.В. (Нижегородский государственный архитектурно-строительный университет).
Копирование материалов допускается при наличии ссылки на первоисточник (на эту страницу).
Полезные ссылки
Программа для расчета любых рам, ферм он-лайн.
Расчет простых однопролетных рам на действие вертикальной нагрузки
Пример расчета простой рамы с шарнирными опорами
Если рама, состоящая из 3 элементов имеет простую прямоугольную или квадратную форму, как показано на рисунке 487.1.а), то такую раму достаточно легко рассчитать, если рассматривать ее как неразрезную трехпролетную балку (рис.487.1.б)):
Рисунок 487.1. а) простая рама б) расчетная схема, принимаемая при рассмотрении простой рамы как трехпролетной неразрезной балки
В принципе, в этом нет ничего удивительного, по сути простейшая рама — это и есть ломаная неразрезная балка, степень статической неопределимости такой рамы равна 2, как и для трехпролетной неразрезной балки. Вот только форма рамы значительно отличается от прямолинейной балки.
В связи с этим моменты, действующие в различных сечениях такой рамы, будут такими же как и для неразрезной трехпролетной балки. А в местах перехода из горизонтального элемента рамы в вертикальные элементы касательные напряжения, действующие в крайних поперечных сечениях горизонтального элемента, будут превращаться в нормальные напряжения, действующие в вертикальном элементе, а нормальные напряжения, действующие в горизонтальном элементе — в касательные напряжения в вертикальных элементах. Ну и наоборот касательные напряжения в вертикальных элементах будут превращаться в нормальные напряжения в горизонтальном элементе.
Таким образом, если рассматривать данную раму как балку, то для дальнейших расчетов можно воспользоваться уравнениями трех моментов. При l = l1 и при постоянной жесткости элементов EI расчеты значительно упрощаются. Тогда
2MB(2l) + MCl = — 6·Rф1;
MBl + 2MC(2l) = — 6·Rф2; (315.4.1)
где
Rф1 = Rф2 = Вф = Аф = ql3/24
Так как наша балка является симметричной и приложенная нагрузка является симметричной и соответственно МВ = МС, то мы сразу можем определить значение моментов:
MB = MС = — 6(ql3/24)/5l = — ql2/20
Чтобы определить момент в середине среднего пролета, нужно сначала вычислить значения опорных реакций, впрочем, при выбранной схеме загружения трехпролетной балки это будет сделать опять-таки не сложно:
Для первого пролета:
Аl = MB; A = ( — ql2/20)/l = — ql/20
Для 2 пролета:
A(2l) + Bl — ql2/2 = MC; B = (-ql2/20 + ql2/10 + ql2/2)/l = 11ql/20
тогда максимальное значение момента в среднем пролете (в середине горизонтального элемента рамы) составит
Mmax = A(1.5l) + B(0.5l) — ql2/8 = — 3l2/40 +11l2/40 — 5ql2/40 = 3ql2/40
Для проверки расчетов следует убедиться, то прогиб равен нулю на опорах. Для этого нужно сначала определить угол поворота на опоре А:
fB = tgΘAl + Al3/6EI = 0;
тогда
tgΘA = — Аl2/6EI = — (- ql3/(20·6EI)) = ql3/120EI;
при таком тангенсе угла наклона на опоре А прогиб на опоре С составит:
fС = 2ltgΘA + A(2l)3/6EI + Bl3/6EI — ql4/24EI = 2ql4/120EI — 8ql4/120EI + 11ql4/120EI — 5ql4/120EI = 0;
Вроде бы мы нигде не ошиблись и на основании полученных данных можно построить все необходимые эпюры как для балки, так и для рамы.
Рисунок 487.2. Эпюры для трехпролетной балки и для рамы.
Примечание: Вообще-то для стоек рамы принято считать, что если действие момента приводит к растяжению правой части сечения вертикальной стойки, то такой момент считается положительным, а если к растяжению левой части сечения, то отрицательным. В связи с этим знак на эпюре «М» для правой стойки должен быть положительным, однако для наглядности я оставил такие знаки, которые соответсвуют эпюрам неразрезной трехпролетной балки.
А вот если размеры рамы будут другие или у вертикальных элементов и горизонтального будет разная жесткость, то конечные эпюры будут иметь другой вид.
Чем меньше будет длина вертикальных элементов, тем больше в итоге будет момент на краях горизонтального элемента и тем меньше посредине. При l1 → 0 Моп → — ql2/12, Мпр → ql2/24 (для горизонтального элемента), т.е. такая рама, точнее ее горизонтальный элемент, будет все больше напоминать обычную однопролетную балку с жестким защемлением на опорах. Подобная же ситуация будет и в том случае, если жесткость вертикальных элементов будет значительно больше, чем жесткость горизонтального.
Но как правило в простых рамах, используемых в малоэтажном строительстве, жесткость горизонтального элемента значительно больше жесткости вертикальных элементов и в этом случае Моп → 0, Мпр → ql2/8 (для горизонтального элемента), т.е. такая рама, точнее ее горизонтальный элемент, будет все больше напоминать обычную балку на шарнирных опорах.
Все это позволяет не то, чтобы рассчитать, но предварительно оценить нагрузки на элементы простых рам, не погружаясь в точные расчеты.
А еще примечательно то, что если у рамы будет как бы один горизонтальный элемент и сколь угодно много вертикальных, то при равномерно распределенной нагрузке на горизонтальный элемент принципы расчета, изложенные в данной статье, тоже годятся, если рассматривать все промежуточные вертикальные элементы просто как шарнирные опоры многопролетной балки для упрощения расчетов.
Тем не менее, для более точных расчетов неободимо учитывать появление углов поворота на промежуточных опорах неразрезной балки. Эти углы поворота будут приводить к появлению изгибающего момента в промежуточных вертикальных элементах, впрочем довольно незначительному.
Пример расчета простой рамы с жестким защемлением на опорах
Если у рассматриваемой рамы будет не шарнирное опирание, а жесткое защемление на концах, то такая рама будет 4 раза статически неопределимой для расчета такой рамы потребуется составить 4 уравнения, правда решить их будет сложнее. Жесткие защемления на концах при этом заменяются на шарнирные опоры и добавляются условные дополнительные пролеты нулевой длины. Соответственно возникают моменты на опорах А и D.
Такой расчет займет гораздо больше времени, однако на конечный результат сильно не повлияет при нагрузке, действующей только на горизонтальный элемент.
Тем не менее и тут расчеты можно значительно упростить, так как мы знаем, что в балке с жестким защемлением на одной опоре и с шарнирным опиранием на другой при действии момента на шарнирной опоре в жестком защемлении возникает опорный момент, имеющий в 2 раза меньшее значение и противоположного знака. Тогда
MAl + 2MB(2l) + MCl = — ql3/4;
MBl + 2MC(2l) +MDl = — ql3/4;
При МА = МD = — МВ/2, и МВ = МС, мы получаем следующие уравнения:
— MВl/2 + 5MBl = — ql3/4;
MВ = — ql2/(4·4.5) = — ql2/18
Соответственно
МА = — (- ql2/18)/2 = ql2/36
Примечание: тот же результат мы бы получили, составив полную систему из 4 уравнений. Первое уравнение при этом имело бы вид (с учетом нулевой длины дополнительного пролета):
2МА(l + 0) + MBl = 0
преобразовав которое мы получим:
2MA = — MB
MA = — MB/2
Как видим, наличие жесткости на опорах рамы немного увеличивает значение момента на краях горизонтального элемента и немного уменьшает значение момента в пролете горизонтального элемента (вычисление момента в пролете здесь не приводится, добавлю только, что выполнить его можно по приведенному выше алгоритму).
черчение — Как сделать обрамленные участки одинакового размера?
Как сказал Ягра, обычное решение — вручную указать значения ImagePadding . Проблема в том, что если метки графика или рамки слишком велики, фиксированный ImagePadding может их обрезать.
Но можем ли мы это автоматизировать?
В идеале мы бы сделали:
Создайте два графика фиксированного размера по вертикали и извлеките их по вертикали
ImagePaddingИзмените
ImagePaddingобоих, чтобы использовать большее значение.Это гарантирует, что они будут одинакового размера, при этом этикетки не будут обрезаны.
Итак, как нам измерить ImagePadding существующего графика? К сожалению, это сложно, поскольку значение зависит от размера участка . Поскольку графики будут располагаться горизонтально, нам нужно исправить размер изображения по вертикали, прежде чем пытаться получить отступы. Но вот довольно полезное решение (которое я использую регулярно):
Во-первых, обратите внимание, что я фиксирую вертикальный размер вместо горизонтального.2, {x, -10, 10}, PlotRange -> {-10, 1000}, Рамка -> Правда, FrameLabel -> {«\! \ (\ * SuperscriptBox [SubscriptBox [\» x \ «, \» a \ «], \ \ «2 \»] \) (\! \ (\ * SuperscriptBox [\ «nm \», \ «2 \»] \)) », «\! \ (\ * SuperscriptBox [SubscriptBox [\» y \ «, \» b \ «], \» 2 \ «] \) \ (\! \ (\ * SuperscriptBox [\ «nm \», \ «2 \»] \)) «}, BaseStyle -> {FontFamily -> «Arial», 20}, Размер изображения -> {Автоматический, вертикальный размер}];
Эта функция измеряет заполнение (на основе кода @ Heike):
getPadding [g_]: = Модуль [{im},
im = Изображение [Показать [g, LabelStyle -> Белый, Фон -> Белый]];
BorderDimensions [im]
]
Теперь давайте выберем большее из верхнего и нижнего отступов двух фигур.Это даст нам минимальное заполнение изображения, которое по-прежнему не обрезает метки.
{p1h, p1v} = getPadding [plot1];
{p2h, p2v} = getPadding [plot2];
verticalPadding = Макс / @ Транспонирование [{p1v, p2v}]
Строка[{
Показать [plot1, ImagePadding -> {p1h, verticalPadding}],
Показать [plot2, ImagePadding -> {p2h, verticalPadding}]
}]
Проблема с этим подходом состоит в том, что часто требуется исправить горизонтальный размер всего изображения (чтобы соответствовать ширине текста документа).Я признаю, что когда у меня была такая же проблема, я сделал это, итеративно уточняя размеры, что не очень элегантно, но автоматически дает хорошие результаты.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.АВТОР}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Связывание кадров в Tecplot 360 EX
«Назад к видеоурокам
Продолжительность 2:24Описание
В этом видео показано, как связать несколько кадров вместе, чтобы облегчить сравнение графиков при анализе нескольких наборов данных.
В этом видео рассматривается связывание кадров и другие инструменты для уточнения сравнительных графиков нескольких наборов 2D переходных данных для ветряной турбины с вертикальной осью.
Хотя в серии переходных данных использовались данные от ветряной турбины с одной вертикальной осью, этот набор данных является частью случая оптимизации формы, в котором рассматривались различные формы аэродинамического профиля. В этом видео мы будем сравнивать только два из этих наборов данных.
Начните с первого набора данных, уже загруженного в Tecplot 360, график уже настроен так, как мы хотим.
- Сохраните стиль рамки как таблицу стилей, выбрав Рамка> Сохранить стиль рамки…
- Создайте новый фрейм и загрузите набор данных с другой геометрией.Примените тот же стиль кадра, выбрав Frame> Load Frame Style… Чтобы лучше выровнять эти два графика, мозаично разместите кадры, используя Frames> Tile Frames…
- На данный момент у нас есть два похожих участка рядом. Однако, если мы взаимодействуем с одним из графиков путем панорамирования или масштабирования, это будет применяться только к одному, а не к другому. Чтобы это изменить, элементы каркаса должны быть соединены вместе.
- Выберите Frame> Frame Linking… и включите Время решения (что позволяет одновременную анимацию), Диапазон оси X , Диапазон оси Y и положение оси XY (которые связывают масштабирование и положение панорамирования) .Затем, наконец, переключитесь на Contour levels , которые свяжут уровни вместе, если мы хотим настроить окраску графика. Обратите внимание, что мы не используем размер и положение кадра, которые будут размещать кадры непосредственно друг над другом. Выберите Применить настройки ко всем кадрам этой группы (группа 1 по умолчанию).
- Отрегулируйте положение графика или анимируйте график, и оба кадра обновятся соответствующим образом.
Связывание фреймов позволяет сравнивать различные геометрические формы и похожие наборы данных, указывая на тонкие различия между ними, сохраняя при этом согласованность определенных аспектов графиков.
Спасибо за просмотр!
Бесплатная пробная версия программного обеспечения
Похожие видео
Фреймы, метки, заголовки и метки — PyGMT
Примечание
Нажмите здесь чтобы загрузить полный пример кода
Установка стиля фреймов карты, отметок и т. Д. Обрабатывается параметром frame что все методы построения графика pygmt.Рисунок .
Рамка участка
По умолчанию PyGMT не добавляет рамку к вашему графику. Например, мы можем построить график береговые линии мира с проекцией Меркатора:
Ушел:
<объект IPython.core.display.Image>
Чтобы добавить рамку GMT по умолчанию к графику, используйте frame = "f" в pygmt.Figure.basemap или любой другой модуль построения:
Ушел:
<объект IPython.core.display.Image>
Тики и линии сетки
Автоматический фрейм ( фрейм = True или фрейм = "a" ) устанавливает фрейм в стиле GMT по умолчанию.
и автоматически определяет метки галочки из области графика.
Ушел:
<объект IPython.core.display.Image>
Добавьте автоматические линии сетки на график, добавив рамку g к :
Ушел:
<объект IPython.core.display.Image>
Название
Заголовок рисунка можно задать, передав + t title в параметр кадра pygmt.Figure.basemap . Передача нескольких аргументов в кадр может быть выполнена с помощью
используя список, как показано в примере ниже.
Ушел:
<объект IPython.core.display.Image>
Чтобы использовать заголовок, состоящий из нескольких слов, заголовок должен быть помещен в другой набор
кавычки. Чтобы кавычки не появлялись в заголовке рисунка,
параметр frame можно передавать в одинарных кавычках, а заголовок может быть
заключены в двойные кавычки.
Ушел:
<объект IPython.core.display.Image>
Этикетки Axis
Ярлыки Axis можно установить, пропустив x + l ярлык (или начиная с y , если
маркировка оси Y) к параметру frame из pygmt.Рисунок. Базовая карта .
По умолчанию все 4 границы карты (или оси графика) нанесены как с делениями, так и с
метки осей. Оси обозначены как W (запад / лево), S (юг / низ), N (север / верх) и E (восток / правая) стороны фигуры. Если ось верхнего регистра
имя передается, ось отображается с делениями и метками осей. Нижний регистр
Имя оси отображает только ось и деления.
В приведенном ниже примере используется декартова проекция, так как GMT не позволяет меткам осей быть установленным для географических карт.
fig = pygmt.Figure ()
fig.basemap (
регион = [0, 10, 0, 20],
projection = "X10c / 8c",
# Нанести ось, отметки и метки осей на западную / левую и южную / нижнюю оси
# Постройте ось и отметки на северной / верхней и восточной / правой осях
frame = ["WSne", "xaf + lx-axis", "yaf + ly-axis"],
)
fig.show ()
Ушел:
<объект IPython.core.display.Image>
Общее время работы скрипта: (0 минут 10,405 секунды)
Галерея создана Sphinx-Gallery
© Авторские права 2017-2021, Разработчики PyGMT.Ревизия 3644860 .
Последнее обновление 14 мая 2021 г.
Построен со сфинксом используя тему предоставлено Read the Docs
Этот веб-сайт использует Google Analytics для сбора статистики использования. Однако он не использует файлы cookie и не отслеживает вас на разных веб-сайтах. Данные о просмотрах страниц используются, чтобы помочь нам улучшить сайт и дать оценку использование программного обеспечения.
Организация участков в matplotlib — Ваш универсальный путеводитель | автор: Матиас Кальдерини
Записную книжку Jupyter для этого руководства можно найти на моей странице Github.
Если вы читаете это, вероятно, потому, что вы согласны со мной, что в большинстве учебных пособий по matplotlib отсутствует важный аспект построения графиков и визуализации данных.
Хотя могут быть тысячи руководств о том, как изменить толщину линии или размер ваших заголовков, все они, кажется, забывают, что организация подзаголовков играет огромную роль в передаче истории, которую рассказывают ваши данные. Иногда вы можете захотеть подчеркнуть важность сюжета, увеличив его, или дополнить сюжет, добавив еще один в качестве вставки поверх него.
Чтобы сделать эти правки, я видел (тоже), что многие люди сохраняли отдельные графики, сделанные с помощью Python, а затем переупорядочивали все вместе в каком-то другом программном обеспечении для редактирования изображений. Это не только неэффективно, но и не масштабируется для построения графиков большого объема или графиков, которые необходимо настраивать и / или повторять несколько раз.
Для всех тех друзей и для всех вас, кто все еще борется с такими проблемами, вот ваше универсальное руководство по организации ваших графиков и подзаголовков, используя только matplotlib на Python.
Картинка стоит тысячи слов, поэтому для тех, кто хочет быстро просмотреть, перечитывает это или страдает синдромом TLDR, вот пример кода того, что мы сделаем в этом руководстве:
import matplotlib.pyplot как pltОбзор элементов организации подзаговора
из matplotlib.gridspec import GridSpec
import numpy as nptime = np.linspace (0, 10, 1000)
height = np.sin (time)
weight = time * 0.3 + 2
score = time * * 2 + высота
распределение = np.random.normal (0, 1, len (время)) fig = plt.figure (figsize = (10, 5))
gs = GridSpec (nrows = 2, ncols = 2) ax0 = fig.add_subplot (gs [0, 0])
ax0.plot (время, высота) ax1 = fig.add_subplot (gs [1, 0])
ax1.plot (время, вес) ax2 = fig.add_subplot (gs [:, 1])
ax2.plot (время, оценка) ax3 = fig.add_axes ([0.6, 0.6, 0.2, 0.2])
ax3.hist (distribution) plt.show ()
А вот схема того, как мы подойдем к вопросу организации подзаговора:
Схема элементов организации подзаговораЕсли это интересно ваш интерес или если вы вернулись, чтобы просмотреть то, что вы читали ранее, добро пожаловать в подробное руководство для начинающих по организации ваших графиков в Python с использованием matplotlib !
Мы подойдем к вопросу организации, прояснив различие между фигурами, частями и осями, и как мы можем оптимизировать их с помощью gridSpec matplotlib .Без лишних слов, давайте начнем с первого и самого простого.
Самым основным элементом графика matplotlib является фигура . Объект-фигура следует рассматривать как ваш frame . Представьте себе любую визуализацию как потенциальный коллаж из графиков, а фигуру — как место, куда вставляются и перемещаются все эти графики.
Однако, как и рамка изображения, фигура сама по себе является пустой структурой, ожидающей содержимого. Это первый элемент нашей исходной схемы: Схема
— Рис. В matplotlib мы создаем объект-фигуру, используя строку fig = plt.рисунок () . Также можно не указывать fig = . Это просто для того, чтобы мы сохраняли объект фигуры в некоторой переменной на случай, если нам понадобится его использовать позже. Например, если вы хотите сохранить фигуру как изображение с помощью fig.save () . Если вы сохранили только что созданную фигуру, вы увидите красивое, недавно созданное пустое изображение.
Если бы все, что вы хотели, — это построить один график, вам не нужно было бы думать об осях или подзаголовках. Вы можете просто сделать это так:
# Synthetic Data
time = np.linspace (0, 10, 1000)
height = np.sin (time) # Построение на фигуре
fig = plt.figure ()
plt.plot (time, height)
fig.savefig ('sizes / basicFigure.png ')
plt.show ()
Мы можем деконструировать предыдущий блок кода:
-
plt.figure ()создает объект-фигуру -
plt.plot (время, высота)займет доступное пространство и нарисуйте взаимосвязь между временем (ось x) и высотой (ось y) -
plt.show ()просто отобразит график.В записных книжках в этом нет необходимости, но это хорошая практика, если вы пишете код в текстовом редакторе или менее интерактивном редакторе, чем тот, который мы используем здесь.
Если бы у вас было больше данных, вы могли бы добавить больше линий к этому простому графику. Но что, если мы захотим построить вторую переменную на другом графике? Вот где пригодятся оси и подсюжеты.
В то время как объект-фигура был вашей рамкой построения, холст , на котором вы будете рисовать, является объектом осей .Сами по себе оси свободно плавают, что означает, что их можно разместить в любом положении на фигуре. Мы можем добавить их в нашу исходную схему: Схема
— ОсиВ коде это просто делается так:
# Исходный график
fig = plt.figure ()
plt.plot (time, height) # Добавление нового пустого оси
fig.add_axes ([0.43, 0.6, 0.15, 0.15]) # [lowerCorner_x, lowerCorner_y, width, height]
fig.add_axes ([0.2, 0.4, 0.1, 0.1]) # [lowerCorner_x, lowerCorner_y, width, height ]Рисунок.savefig ('figure / figureAxes')
plt.show ()
Здесь мы видим, что функция add_axes ([left, bottom, width, height]) добавила две новые области построения к исходному графику. Конкретное положение и размер новых осей указываются в соответствующих входных массивах функций.
Однако добавление пустых осей не имеет особого смысла, поэтому давайте посмотрим, как их использовать для построения:
# Исходный график
fig = plt.figure ()
plt.plot (time, height) # Первые новые оси
ax1 = рис.add_axes ([0.43, 0.6, 0.15, 0.15])
ax1.hist (height) # Вторая новая ось
ax2 = fig.add_axes ([0.2, 0.3, 0.1, 0.1])
ax2.plot (time, time ** 2) fig.savefig ('characters / figureAxes2.png')
plt.show ()
В этом примере мы видим, что add_axes () фактически дает или возвращает фактический объект оси, на котором мы можем построить, которые мы сохранили в переменных ax1 и ax2. Затем мы можем использовать эти переменные для построения различных значимых данных, которые добавляют ценность нашему графику так же, как мы это делали раньше.
В этом случае мы добавили гистограмму значений высоты и построили квадрат времени (это не очень значимая информация, кроме как показать, как строить по осям).
Различие между подзаголовками и осями не особенно ясно, когда кто-то впервые учится строить с помощью matplotlib . Это потому, что обычно подзаголовки вводятся до введения осей. Как вы теперь увидите, эта крошечная деталь может изменить все ваше восприятие того, как вы организуете свою визуализацию.
В двух словах, подзаголовки — это просто способ организовать ваши свободно плавающие оси в жесткую сетку. Вы можете представить, что подзаголовков создает таблицу, и каждая отдельная ячейка таблицы представляет собой новую ось, которую вы должны заполнить данными. Точно так же, как в этом новом варианте исходной схемы:
Schematic — SubplotsВот как можно использовать subplots :
# Synthetic Data
time = np.linspace (0, 10, 1000)
height = np.sin (время)
вес = нп.cos (time) # Построение всех подзаголовков
fig, axes = plt.subplots (2, 3) axes [0, 0] .plot (time, height)
axes [0, 1] .plot (time, time ** 2)
осей [0, 2] .hist (высота) осей [1, 0] .plot (время, вес, цвет = 'зеленый')
осей [1, 1] .plot (время, 1 / (время + 1), color = 'green')
axes [1, 2] .hist (weight, color = 'green') plt.tight_layout ()
fig.savefig ('characters / figureAxesSubplots.png')
plt.show ( )
Опять же, давайте возьмем по одной строке за раз:
-
plt.subplots (), создал сетку (2 строки и 3 столбца).Функция вернула объект фигуры (сохраненный врис.), который будет содержать все подзаголовки, а также все отдельные оси (сохраненные восях). - Оси содержатся в двумерном массиве numpy (матрица или таблица, если хотите), и к ним можно получить доступ индивидуально по их положению. Например, верхняя левая ось с
осями [0, 0]. Если бы у нас было много графиков, здесь мы могли бы перебирать эти позиции, чтобы построить их индивидуально. -
шт.tight_layout ()обычно используется при использованииplt.subplots (), чтобы гарантировать, что отметки и метки оси не перекрываются на подзаголовках. Не стесняйтесь удалить его, чтобы увидеть, что это значит.
Я настоятельно рекомендую посмотреть официальную документацию для дальнейшей настройки сетки подзаголовков, например, расстояние между строками / столбцами или совместимость осей.
Итак, мы знаем, как построить несколько графиков в определенных, свободно плавающих местах или в хорошо структурированной сетке.Что же тогда делать с организацией? А что, если бы мы хотели сделать акцент на одном сюжете, сделав его вдвое больше другого? Что, если бы мы хотели создать какую-то мозаичную галерею сюжетов? Вот где GridSpec становится полезным.
Принцип работы GridSpec заключается в том, что, как и в случае с подзаголовками, определяется сетка. Однако вместо автоматического связывания осей с каждой ячейкой сетки можно выбрать, сколько ячеек будет занимать каждая отдельная область построения. Поэтому, если мы хотим, чтобы участок занимал в два раза больше площади другого графика, мы могли бы связать его с удвоенным количеством ячеек в сетке.
Давайте посмотрим на это в коде:
# Новый набор данных
time = np.linspace (0, 10, 1000)
height = np.sin (time)
weight = time * 0.3 + 2
distribution = np .random.normal (0, 1, len (time)) # Настройка поверхности графика
fig = plt.figure (figsize = (10, 5))
gs = GridSpec (nrows = 2, ncols = 2) # Сначала оси
ax0 = fig.add_subplot (gs [0])
ax0.plot (time, height) # Вторые оси
ax1 = fig.add_subplot (gs [1, 0])
ax1.plot (time, weight) # Третья ось
ax2 = рис.add_subplot (gs [:, 1])
ax2.hist (distribution) fig.savefig ('figure / gridspec.png')
plt.show ()
- Сначала мы создаем сетку (2 на 2) с
gs. = gridspec.GridSpec (nrows = 2, ncols = 2). -
fig.add_subplot (gs [0, 0])в этом случае возьмет поднабор этих ячеек, обращаясь к ним по индексу[0, 0]. - Это подмножество может включать несколько ячеек нашей сетки gridSpec, просто обращаясь к более чем одной ячейке, как с
ax2 = рис.add_subplot (gs [:, 1]), который выбирает все строки и второй столбец.
Мы можем дополнительно настроить наши графики, установив размер каждой строки или столбца. Это означает, что некоторые строки могут быть уже или шире других. Например:
# Настройка поверхности графика
fig = plt.figure (figsize = (10, 5))
gs = gridspec.GridSpec (nrows = 2, ncols = 2, width_ratios = [3, 1], height_ratios = [3, 1]) # Первые оси
ax0 = fig.add_subplot (gs [0, 0])
ax0.plot (time, height) # Вторые оси
ax1 = рис.add_subplot (gs [1, 0])
ax1.plot (time, weight) # Третьи оси
ax2 = fig.add_subplot (gs [:, 1])
ax2.hist (distribution) plt.show ()
И с этим мы, наконец, можем добраться до нашей исходной схемы:
Схема элементов организации подзаголовкаИз всего, что мы узнали до этого момента, мы можем полностью деконструировать схему: мы видим здесь то, что мы применили спецификацию сетки к сетке, которая ( 5, 5), но одни ряды меньше других. Затем мы добавили подзаговор, покрывающий всю первую строку, подзаголовок, покрывающий примерно половину третьей строки, два подзаголовка для последней строки и 1 подзаголовок, покрывающий последний столбец и последние три строки.Поверх этого последнего участка мы добавили две свободно плавающие оси.
Как и раньше, я настоятельно рекомендую обратиться к официальной документации для дальнейшей настройки gridSpec, такой как интервалы между строками / столбцами или как создавать вложенные gridSpec.
И с этим, надеюсь, теперь вы знаете, как вы можете структурировать свои графики, используя фигур , оси , подзаголовки и GridSpec . Если у вас есть вопросы или комментарии, оставьте комментарий ниже.
СЮЖЕТ в R ⭕ [тип, цвет, ось, pch, заголовок, шрифт, линии, добавить текст, точки метки]
Самая простая графическая функция в R — это функция plot . Эта функция имеет несколько аргументов для настройки окончательного графика : среди прочего, добавить заголовок, изменить метки осей, настроить цвета или изменить типы линий. В этом уроке вы узнаете, как построить график в R и как полностью настроить получившийся график .
Функция графика в R
Функция R plot позволяет создать график , передающий два вектора (одинаковой длины), фрейм данных, матрицу или даже другие объекты, в зависимости от его класса или типа ввода.Мы собираемся смоделировать две случайные нормальные переменные, называемые x и y , и использовать их почти во всех примерах графиков.
набор. Семян (1)
# Создать образец данных
х <- rnorm (500)
y <- x + rnorm (500) Вы можете построить график предыдущего набора данных:
# Постройте данные
сюжет (x, y)
# Эквивалент
M <- cbind (х, у)
участок (М) С помощью функции plot вы можете создать широкий диапазон графиков, в зависимости от входных данных .В следующей таблице мы суммируем все доступные возможности для базовой функции построения графиков R.
| Функция и аргументы | График выходных данных | ||
|---|---|---|---|
| график (x, y) | График рассеяния числовых векторов x и y | ||
| график (фактор) | Гистограмма фактора | plot (factor, y) | Boxplot of the numeric vector and the levels of the factor |
| plot (time_series) | time series plot | ||
| plot (data_frame) | Correlation plot of all dataframe columns (более двух столбцов) | ||
| график (дата, y) | Строит вектор на основе даты | ||
| график (функция, нижний, верхний) | График функции между нижним и максимальным значением указано |
Если вы выполните следующий код, вы получите различные примеры графиков.2 # Диаграмма рассеяния
plot (x, y, main = "Scatterplot") # Barplot
сюжет (my_factor, main = "Barplot") # Boxplot
plot (my_factor, rnorm (32), main = "Boxplot") # Сюжет временного ряда
plot (my_ts, main = "Временной ряд") # Сюжет, основанный на времени
plot (my_dates, rnorm (50), main = "График на основе времени") # Построить функцию R
plot (fun, 0, 10, main = "Постройте функцию") # График корреляции
plot (деревья [, 1: 3], main = "Корреляционный график") номинал (mfrow = c (1, 1)) Когда вы создаете несколько графиков в базе R (не в RStudio), следующий график переопределит предыдущий .Однако вы можете создать новые окна графика с функциями windows , X11 и quartz в зависимости от вашей операционной системы, чтобы решить эту проблему.
R окно
При создании графиков в базе R они будут открываться в новом окне. Однако вам может потребоваться настроить высоту и ширину окна, которые по умолчанию составляют 7 дюймов (17,78 см). Для этой цели вы можете использовать аргументы высота и ширина следующих функций, в зависимости от вашей системы.
Следует отметить, что в RStudio график будет отображаться в макете панели, но если вы используете соответствующую функцию, график откроется в новом окне, как и в базе R.
windows () # Windows
X11 () # Unix
кварц () # Mac В дополнение к возможности открывать и устанавливать размер окна, эти функции используются, чтобы избежать переопределения графиков, которые вы создаете, поскольку при создании нового графика вы потеряете предыдущий. Обратите внимание, что в RStudio вы можете перемещаться по всем графикам, которые вы создали в своем сеансе, на панели графиков.
# Откроется первый участок
# новое окно
сюжет (x, y)
# Новое окно
окна ()
# Другой сюжет в новом окне
участок (x, x) Вы также можете очистить окно графика в R программно с помощью функции dev.off , чтобы очистить текущее окно, и с помощью graphics.off , чтобы очистить все графики и восстановить графические параметры по умолчанию.
# Очистить текущий график
dev.off ()
# Очистить все графики
graphics.off ()
в то время как (dev.cur ()> 1) dev.off () # Эквивалент Обратите внимание, что функция dev.cur подсчитывает количество текущих доступных графических устройств.
R тип участка
Вы также можете настроить тип графика с помощью аргумента type . Выбор типа будет зависеть от данных, которые вы рисуете. . В следующем блоке кода мы показываем наиболее популярные типы сюжетов в R.
j <- 1:20
к <- j
номинал (mfrow = c (1, 3))
plot (j, k, type = "l", main = "type = 'l'")
plot (j, k, type = "s", main = "type = 's'")
plot (j, k, type = "p", main = "type = 'p'")
номинал (mfrow = c (1, 1))
номинал (mfrow = c (1, 3))
plot (j, k, type = "l", main = "type = 'o'")
plot (j, k, type = "s", main = "type = 'b'")
plot (j, k, type = "p", main = "type = 'h'")
номинал (mfrow = c (1, 1)) | Тип участка | Описание |
|---|---|
| p | Точечный график (по умолчанию) |
| l | Линейный график |
| b | 41 905Оба (с перекрытием) |
| s | Лестничный график |
| h | График в виде гистограммы |
| n | Без построения |
R участок пч
Аргумент pch позволяет изменять символ точек на графике .Основные символы можно выбрать, передав в качестве параметров чисел от 1 до 25 . Вы также можете изменить размер символов с помощью аргумента cex и ширину строки символов (кроме 15–18) с помощью аргумента lwd .
r <- c (sapply (seq (5, 25, 5), function (i) rep (i, 5)))
t <- rep (seq (25, 5, -5), 5)
plot (r, t, pch = 1:25, cex = 3, yaxt = "n", xaxt = "n",
ann = FALSE, xlim = c (3, 27), lwd = 1: 3)
текст (р - 1.5, т, 1:25) Обратите внимание, что символов с 21 по 25 позволяют вам установить ширину границы, а также цвет фона с аргументами lwd и bg соответственно.
сюжет (r, t, pch = 21:25, cex = 3, yaxt = "n", xaxt = "n", lwd = 3,
ann = FALSE, xlim = c (3, 27), bg = 1:25, col = rainbow (25)) В следующем блоке кода мы показываем простой пример того, как настроить один из этих символов.
# Пример
сюжет (x, y, pch = 21,
bg = "red", # Цвет заливки
col = "blue", # Цвет границы
cex = 3, # Размер символа
lwd = 3) # Ширина границы Стоит отметить, что вы можете использовать любой символ в качестве символа .Фактически, некоторые символьные символы могут быть выбраны с помощью чисел от 33 до 240 в качестве параметра аргумента pch .
# Пользовательские символы
сюжет (1: 5, 1: 5, pch = c («☺», «❤», «✌», «❄», «✈»),
col = c ("оранжевый"; 2: 5), cex = 3,
xlim = c (0, 6), ylim = c (0, 6)) R Название участка
Заголовок может быть добавлен к графику с помощью основного аргумента или функции title .
сюжет (x, y, main = "Мое название")
# Эквивалент
сюжет (x, y)
title («Мой титул») Основное различие между использованием функции title или аргумента состоит в том, что аргументы, которые вы передаете функции, влияют только на заголовок .
Чтобы изменить положение заголовка графика, вы можете установить аргумент adj со значением от 0 (слева) до 1 (справа) и аргумент line , где значения больше 1,7 (по умолчанию) перемещают заголовок вверх и значения ниже 1,7, чтобы переместить его вниз. Отрицательные значения строки заставят заголовок войти внутрь графика. Следует отметить, что если вы установите эти аргументы для функции plot , изменения будут применены ко всем текстам.
участок (x, y)
title ("Мое название",
adj = 0.2 + ГРП (бета, 3))) Тем не менее, синтаксис функции сильно отличается от синтаксиса LaTeX. При желании вы можете использовать функцию TeX из пакета latex2exp . Однако обратите внимание, что эта функция переводит нотацию TeX в нотацию , выражение , нотацию функции, поэтому символы и нотация, доступные в обеих функциях , одинаковы.
# install. 3, \\ beta \\ in 1 \ ldots 10 $')) Выражения LaTeX могут использоваться также в субтитрах, метках осей или в любом другом месте в качестве текста, добавляемого к графику.Подзаголовок на R графике
Кроме того, вы можете добавить подзаголовок к графику в R с аргументом sub , который будет отображаться под графиком. Можно добавить подзаголовок, даже если вы не укажете заголовок.
сюжет (x, y, main = "My title", sub = "My subtitle")
# Эквивалент
сюжет (x, y)
title (main = "My title", sub = "My subtitle") Ось в R
На графиках R вы можете изменять метки осей Y и X, добавлять и изменять метки отметок осей, размер оси и даже устанавливать пределы оси.
R график x и y метки
По умолчанию R будет использовать имена векторов вашего графика в качестве меток осей X и Y. Однако вы можете изменить их с помощью аргументов xlab и ylab .
участок (x, y, xlab = "Моя метка X", ylab = "Моя метка Y") Если вы хотите, чтобы удалили метки осей , вы можете установить для них пустую строку или установить для аргумента ann значение FALSE .
# Удалить метки
сюжет (x, y, xlab = "", ylab = "")
# Эквивалент
plot (x, y, xlab = "My X label", ylab = "My Y label", ann = FALSE) Функция оси R
Аргумент осей функции plot может быть установлен на FALSE , чтобы не отображало оси , поэтому, если вы хотите, вы можете добавить только одну из них с помощью функции axis и настроить Это.При передаче 1 в качестве аргумента будет построена ось X, при передаче 2 будет построена ось Y, 3 - для верхней оси и 4 - для правой оси.
график (x, y, оси = FALSE)
# Добавить ось X
ось (1)
# Добавить ось Y
ось (2) Изменить отметки оси
Также можно изменить отметки осей. С одной стороны, аргумент at функции axis позволяет указать точки, в которых будут рисоваться метки.
график (x, y, оси = FALSE)
ось (1, при = -2: 2) С другой стороны, функция minor.tick пакета Hmisc позволяет создавать меньшие отметки между основными отметками.
# install.packages ("Hmisc")
библиотека (Hmisc)
сюжет (x, y)
minor.tick (nx = 3, ny = 3, tick.ratio = 0,5) Наконец, вы можете создать внутренние отметки, указав положительное число в аргументе tck следующим образом:
# Внутренние клещи
сюжет (x, y, tck = 0.02) Удалить метки осей
Установка аргументов xaxt или yaxt - "n" функции plot позволит избежать нанесения меток осей X и Y соответственно.
номинал (mfrow = c (1, 3))
# Удалить метки отметки оси X
plot (x, y, xaxt = "n", main = "xaxt = 'n'")
# Удалить метки отметки оси Y
plot (x, y, yaxt = "n", main = "yaxt = 'n'")
# Удаляем метки меток обеих осей
plot (x, y, yaxt = "n", xaxt = "n", main = "xaxt = 'n', yaxt = 'n'")
номинал (mfrow = c (1, 1)) Изменить метки деления оси
Метки меток осей будут пронумерованы в соответствии с нумерацией ваших данных.Тем не менее, вы можете изменить метки меток , если необходимо, с помощью аргумента меток функции оси . Вам также необходимо указать, где будут отображаться метки галочки, с аргументом at .
номинал (mfrow = c (1, 2))
# Изменить метки отметок оси X
сюжет (x, y, xaxt = "n")
ось (1, at = seq (round (min (x)), round (max (x)), by = 1), labels = 1: 8)
# Изменить метки отметок оси Y
сюжет (x, y, yaxt = "n")
ось (2, at = seq (round (min (y)), round (max (y)), by = 1), labels = 1: 9) Метки оси вращения
Аргумент las функции plot в R позволяет вам на вращать метки осей ваших графиков на .В следующем блоке кода вы найдете объяснение различных альтернатив.
номинал (mfrow = c (2, 2))
plot (x, y, las = 0, main = "Parallel") # Параллельно оси (по умолчанию)
plot (x, y, las = 1, main = "Horizontal") # Horizontal
plot (x, y, las = 2, main = "Perpendicular") # Перпендикулярно оси
plot (x, y, las = 3, main = "Vertical") # Вертикально
номинал (mfrow = c (1, 1)) Установить пределы оси
Вы можете увеличивать или уменьшать масштаб графика. изменяя пределы осей графика R. Эти аргументы очень полезны, чтобы избежать обрезки линий при добавлении их на график.
участок (x, y,
ylim = c (-8, 8), # пределы оси Y от -8 до 8
xlim = c (-5, 5)) # Пределы оси X от -5 до 5 Изменить масштаб оси в R
Аргумент log позволяет изменять масштаб осей графика. Вы можете преобразовать ось X, ось Y или обе оси следующим образом:
# Новые данные, чтобы избежать отрицательных чисел
с <- 1:25
u <- 1:25
номинал (mfrow = c (2, 2))
# По умолчанию
сюжет (s, u, pch = 19,
main = "Без преобразования")
# Шкала журнала.Ось X
plot (s, u, pch = 19, log = "x",
main = "ось X преобразована")
# Шкала журнала. Ось Y
plot (s, u, pch = 19, log = "y",
main = "ось Y преобразована")
# Шкала журнала. Оси X и Y
plot (s, u, pch = 19, log = "xy",
main = "Оба преобразованы") | Лог | Преобразование |
|---|---|
| «x» | Преобразование оси X |
| «y» | Преобразование оси Y | Оба
Однако вы можете подумать, что использование функции log эквивалентно, но это не так.Как вы можете видеть на предыдущем графике, использование аргумента log не изменяет данные, но функция log преобразует их. Посмотрите на разницу между осями следующего графика и предыдущего.
номинал (mfrow = c (1, 3))
# Журнал-журнал
график (log (s), log (u), pch = 19,
main = "журнал-журнал")
# журнал (x)
сюжет (log (s), u, pch = 19,
main = "журнал (x)")
# журнал (y)
plot (s, log (u), pch = 19,
main = "журнал (y)")
номинал (mfrow = c (1, 1)) R шрифт графика
Размер шрифта
. Вы также можете изменить размер шрифта на графике R с помощью cex.основные аргументы , cex.sub , cex.lab и cex.axis для изменения заголовка, подзаголовка, меток осей X и Y и меток отметок осей соответственно. Обратите внимание, что при больших значениях будут отображаться более крупные тексты.
plot (x, y, main = "My title", sub = "Subtitle",
cex.main = 2, # Размер заголовка
cex.sub = 1.5, # Размер субтитров
cex.lab = 3, # Размер меток по осям X и Y
cex.axis = 0.5) # Размер меток осей | Аргумент | Описание |
|---|---|
| cex.main | Устанавливает размер заголовка |
| cex.sub | Устанавливает размер субтитра |
| cex.lab | Устанавливает размер меток осей X и Y |
| cex.axis | Устанавливает размер меток оси деления
Стиль шрифта
Кроме того, вы можете изменить стиль шрифта графиков R с помощью аргумента font . Вы можете установить для этого аргумента значение 1 для обычного текста, 2 для полужирного шрифта (по умолчанию), 3 для курсива и 4 для полужирного курсива.Этот аргумент не изменит стиль заголовка.
номинал (mfrow = c (1, 3))
plot (x, y, font = 2, main = "Bold") # Полужирный
plot (x, y, font = 3, main = "Italics") # Курсив
plot (x, y, font = 4, main = "Bold italics") # Полужирный курсив
номинал (mfrow = c (1, 1)) Вы также можете указать стиль каждого из текстов графика с помощью аргументов font.main , font.sub , font.axis и font.lab .
участок (x, y,
main = "Мое название",
sub = "Субтитры",
шрифт.main = 1, # Стиль шрифта заголовка
font.sub = 2, # Стиль шрифта субтитров
font.axis = 3, # Стиль шрифта меток осей
font.lab = 4) # Стиль шрифта меток осей X и Y Обратите внимание, что по умолчанию заголовок графика выделяется жирным шрифтом.
| Стиль шрифта | Описание | ||
|---|---|---|---|
| 1 | Обычный текст | ||
| 2 | Полужирный | ||
| 3 |
| Тип | Описание | ||
|---|---|---|---|
| 0 | Пустой | ||
| 1 | Сплошная линия (по умолчанию) | ||
| 2 | с штриховкой с штрихами | ||
| 4 | Точечная линия | ||
| 5 | Длинная линия | ||
| 6 | Двойная линия |
Добавить текст на график в рублях
С одной стороны, функция mtext в R позволяет добавлять текст ко всем сторонам графического поля.Всего имеется 12 комбинаций (по 3 с каждой стороны коробки, выровнены по левому, центру и правому краю). Вам просто нужно изменить сторону и прил , чтобы получить нужную вам комбинацию.
С другой стороны, функция text позволяет добавлять текст или формулы внутри графика в некоторой позиции, задавая координаты. В следующем блоке кода показаны некоторые примеры для обеих функций.
сюжет (x, y, main = "Main title", cex = 2, col = "blue")
# ---------------
# функция mtext
# ---------------
# Внизу по центру
mtext ("Нижний текст", сторона = 1)
# Слева по центру
mtext ("Левый текст", сторона = 2)
# Топ-центр
mtext ("Верхний текст", сторона = 3)
# Право-центр
mtext ("Правый текст", сторона = 4)
# Левая нижняя
mtext ("Нижний левый текст", side = 1, adj = 0)
# В правом верхнем углу
mtext ("Правый верхний текст", side = 3, adj = 1)
# Топ с разделением
mtext ("Верхний верхний текст", side = 3, line = 2.5)
# --------------
# Текстовая функция
# --------------
# Добавить текст с координатами (-2, 2)
текст (-2, 2, «Еще текст»)
# Добавить формулу в координатах (3, -3)
текст (3, -3, выражение (frac (alpha [1], 4))) точек маркировки в рандах
В этом разделе вы узнаете, как маркировать точки данных в R . Для этой цели вы можете использовать функцию text , указать координаты и метку точек данных в аргументе labels . С помощью аргумента pos вы можете установить положение метки относительно точки: 1 снизу, 2 слева, 3 сверху и 4 справа.
прикрепить (USJudgeRatings)
# Создаем сюжет
сюжет (FAMI, INTG,
main = "Знакомство с законом vs честность судей",
xlab = "Знакомство", ylab = "Целостность",
pch = 18, col = "синий")
# Нанесите метки
текст (FAMI, INTG,
label = row.names (USJudgeRatings),
cex = 0,6, pos = 4, col = "красный")
отсоединить (USJudgeRatings) Вы также можете пометить отдельные точки данных , если проиндексируете элементы функции text следующим образом:
прикрепить (USJudgeRatings)
сюжет (FAMI, INTG,
main = "Знакомство с законом vs честность судей",
xlab = "Знакомство", ylab = "Целостность",
pch = 18, col = "синий")
# Выберите индекс элементов, которые нужно пометить
selected <- c (10, 15, 20)
# Индексируйте элементы вектором
текст (FAMI [выбрано], INTG [выбрано],
метки = строка.имена (USJudgeRatings) [выбрано],
cex = 0,6, pos = 4, col = "красный")
отсоединить (USJudgeRatings) Изменить тип поля с аргументом bty
Аргумент bty позволяет изменить тип прямоугольника R-графиков. Есть несколько вариантов, которые представлены в следующей таблице:
| Тип коробки | Описание |
|---|---|
| «o» | Вся коробка (по умолчанию) |
| «7» | Сверху и справа |
| «L» Слева и снизу | |
| «U» | Слева, снизу и справа |
| «C» | Сверху, слева и снизу |
| «n» | Без коробки |
номинал (mfrow = c (2, 3))
plot (x, y, bty = "o", main = "Default")
plot (x, y, bty = "7", main = "bty = '7'")
plot (x, y, bty = "L", main = "bty = 'L'")
plot (x, y, bty = "U", main = "bty = 'U'")
plot (x, y, bty = "C", main = "bty = 'C'")
plot (x, y, bty = "n", main = "bty = 'n'")
номинал (mfrow = c (1, 1)) Обратите внимание, что на других графиках, таких как коробчатые, вам нужно будет указать аргумент bty внутри функции par .
R Легенда сюжета
Наконец, мы рассмотрим, как добавить легенду к графику R с помощью функции legend .Вы можете установить координаты, в которых вы хотите добавить легенду, или указать «сверху» , «снизу» , «сверху вниз», , «вверху справа» , «снизу слева» или «снизу справа» . Вы также можете указать множество аргументов, как в функции plot . Например, вы можете изменить bty в легенде R, цвет фона с помощью аргумента bg , среди прочего.
участок (x, y, pch = 19)
строки (-4: 4, -4: 4, lwd = 3, col = "красный")
строки (-4: 1, 0: 5, lwd = 3, col = "зеленый")
# Добавление легенды
легенда ("снизу справа", легенда = c ("красный", "зеленый"),
lwd = 3, col = c ("красный", "зеленый")) Прочтите статью R legends, чтобы узнать больше о том, как добавлять легенды к графикам.
Анимации · Сюжеты
Анимации
Анимации создаются в 3 этапа:
- Инициализировать объект
Animation. - Сохраните каждый кадр анимации с
кадром (аним). - Преобразуйте кадры в анимированный gif с
gif (anim, filename, fps = 15)
Вспомогательные макросы @gif и @animate значительно упрощают этот код. См. Домашнюю страницу для примеров короткой версии или пример gr для длинной версии.
Макросы удобства
Есть два макроса для разного уровня удобства при создании анимации: @animate и @gif . Основное отличие состоит в том, что @animate вернет объект Animation для последующей обработки, а @gif создаст анимированный файл gif (и отобразит его при возврате в ячейку IJulia).
Используйте @gif для простых одноразовых анимаций, которые вы хотите сразу просмотреть.Используйте @animate для чего-нибудь более сложного. Создание Animation объектов может быть выполнено, когда вам нужен полный контроль над жизненным циклом анимации (хотя обычно это и не нужно).
Примеры:
с использованием графиков @userplot CirclePlot
@recipe функция f (cp :: CirclePlot)
x, y, i = cp.args
n = длина (x)
inds = circshift (1: n, 1 - я)
ширина линии -> диапазон (0, 10, длина = n)
seriesalpha -> диапазон (0, 1, длина = n)
аспект_ratio -> 1
метка -> ложь
x [индексы], y [индексы]
конец n = 150
t = диапазон (0, 2π, длина = n)
х = грех.(т)
у = cos. (t) anim = @animate для i ∈ 1: n
круговой график (x, y, i)
конец
gif (anim, "anim_fps15.