Презентация на тему: Лекция 2

ПРИКЛАДНАЯ МЕХАНИКА

Тема

Сопротивление материалов

Деформация растяжения

Деформация, при которой в поперечном сечении бруса возникает один силовой фактор—продольная сила N, называется растяжением (сжатием).

Продольной силой N называется равнодействующая внутренних сил, распределенных по площади поперечного сечения (нормальных напряжений):

N	dS
	S	N	S
При равномерном распределении нормальных напряжений :

Правило знаков: растягивающая продольная сила считается положительной, а сжимающая– отрицательной.

Сущность метода сечений заключается в том, что величина продольной

силы в сечении стержня равна сумме всех внешних продольных сил приложенных по одну из сторон от выбранного сечения.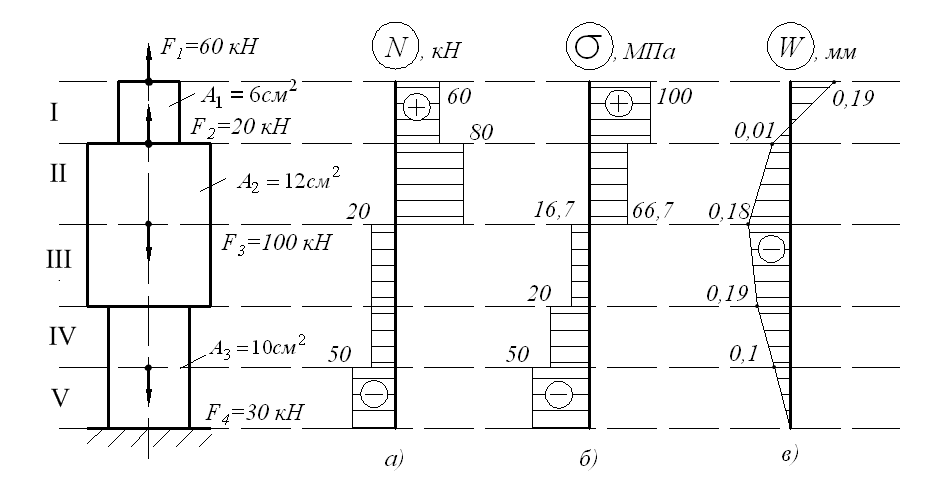

y			I		II
						F1=10 кН, F2=15 кН, F3=55 кН, F4=30 кН;
						F5
1		F		3			Определим продольные силы в
F		2		F		K z
x	A	B		C D			сечениях I-I и II-II.
			I		II

N	1-1	= -F -F = -10-15= -25 кН,	N11-11= -F1-F2+F3= -10-15+55=30 кН.
		1 2

Построение эпюры продольных сил

Характерными называются сечения стержня где: 1) приложены внешние продольные силы; 2) происходит ступенчатое, или начинается участок постепенного изменения площади поперечного сечения бруса.

Эпюрой продольных сил называется график изменения продольной силы по длине стержня (бруса).

y

1	F	3
F	2	F
x	A	B C D

Эпюра N , кН

30

10

25

		Дано: F1=10 кН, F2=15 кН, F3=55 кН,
		F4=30 кН.
F4	F5
	K	z Построить эпюру продольных сил
		Участок АВ NАВ=-F1=-10 кН.
		Участок ВС NВС= -F1-F2= -10-15= -25 кН.
		Участок CD NCD= -F1-F2= -10-15= -25 кН.
		Участок DE NDE= -F1-F2+F3=-10-15+55=30 кН
	15	Участок ЕК NEK= -F1-F2+F3-F4=
		= -10-15+55-15=15 кН.

Построение эпюры продольных сил

Правила контроля эпюры продольных сил

Основные правила контроля правильности построения эпюры продольных сил можно сформулировать так:

1.

В сечении, где приложена сосредоточенная сила F, эпюра продольных сил делает скачок на величину этой силы и с ее знаком.

2.Изменение площади поперечного сечения стержня влияния на эпюру продольных сил не оказывает, независимо от характера этого изменения (ступенчатое или постепенное).

3.На участке, где приложена равномерно распределенная нагрузка эпюра продольных сил имеет вид прямой наклонной линии.

Деформация растяжения

Правила контроля эпюры нормальных напряжений

Основные правила контроля правильности построения эпюры нормальных напряжений можно сформулировать так:

1.На участке или в сечении стержня, где происходит изменение площади поперечного сечения, нормальные напряжения изменяются обратно пропорционально изменению площади, если площадь изменяется ступенчато, то на эпюре наблюдается скачок, если площадь изменяется постепенно, то эпюра имеет вид прямой наклонной линии

2.В сечении, где приложена сосредоточенная сила эпюра нормальных напряжений, делает скачок на величину пропорциональную силе и с ее знаком.

3.На участке, где приложена равномерно распределенная нагрузка эпюра нормальных напряжений имеет вид прямой наклонной линии

Напряжения в наклонных сечениях

Знак нормального напряжения определяется знаком продольной силы, то есть растягивающее напряжение положительно, сжимающее – отрицательно.

Касательное напряжение считается положительным, если изображающий его вектор стремится вращать тело относительно любой точки, лежащей на внутренней нормали к сечению по часовой стрелке.

N

N cos

N

2

2

cos

0 cos

,

S

S0 / cos

S0

Q

N sin

N

cos sin 0,5 0 sin 2

S

S0 / cos

S0

Наибольшие нормальные напряжения (по абсолютной величине) действуют в поперечном сечении стержня.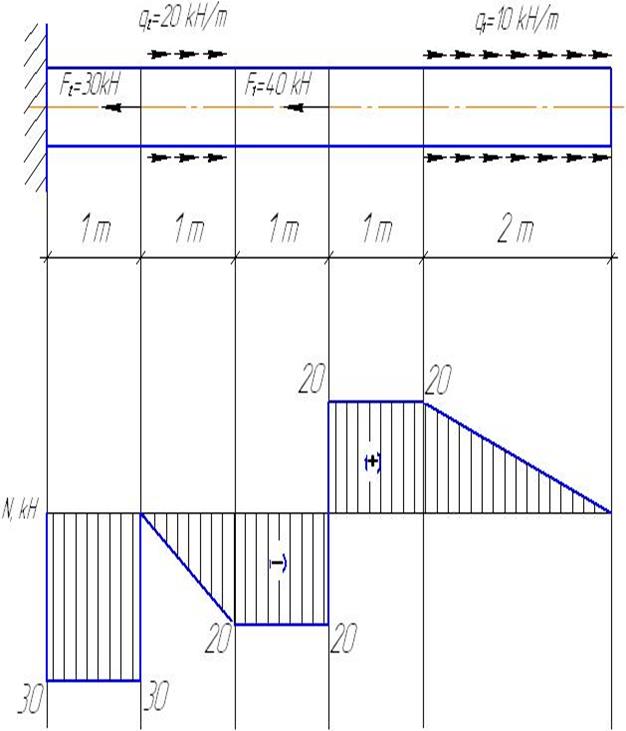

Наибольшие касательные напряжения действуют в сечениях наклоненных под углом в 45о к оси стержня.

Касательные напряжения в поперечном сечении стержня равны нулю.

Закон Гука

Закон Гука имеет два аналитических выражения— через относительные, и через абсолютные величины

В относительных величинах В абсолютных величинах

				l	Nl
			E		ES

Жесткостью поперечного сечения стержня называют произведение площади поперечного сечения S на модуль продольной упругости материала Е:

Сп.с. SЕ

Способность стержня сопротивляться деформированию оценивают величиной относительной жесткости стержня, которая равна отношению жесткости

поперечного сечения ЕS к длине стержня l:

С SЕl

	Податливость стержня:		l
			ES

Деформации и перемещения

l0

lк

	F	l
0
b b
b/2	a	a/2
	a0

Величина, на которую изменится длина бруса

(или одного из его участков) под действием продольных сил, называется продольной

деформации

l lк l0 ,

Относительной продольной деформацией

называется отношение абсолютной продольной деформации l к первоначальной длине стержня l0:

ll0

Величина а ( b), на которую изменится размер поперечного сечения бруса а0 (b0) под действием

продольной силы, называется поперечной деформацией.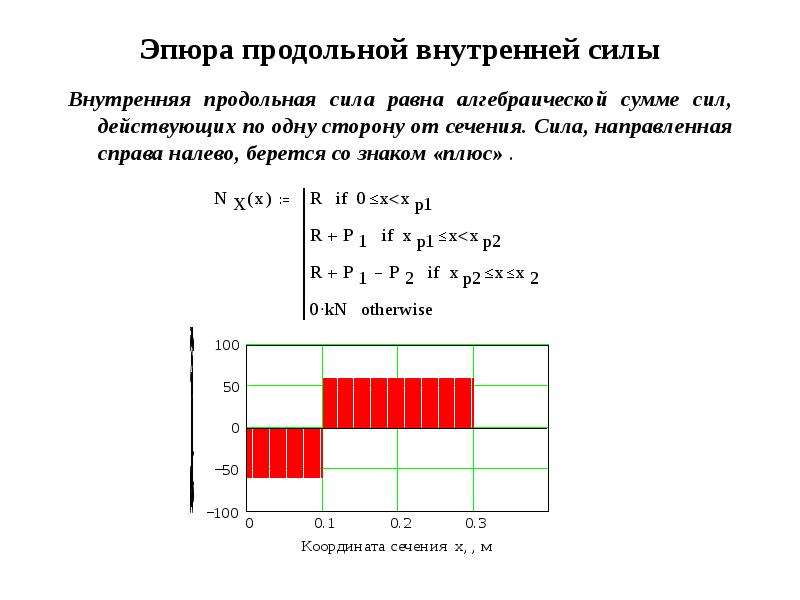

Отношение абсолютной поперечной деформации, а ( b) к первоначальному размеру сечения бруса а0 (b0), называется относительной поперечной

деформаций:	a ,		b
а /		b /
	a0		b0

Растяжение. Эпюры продольных сил — Энциклопедия по машиностроению XXL

Растяжение. Эпюры продольных сил  [c.268]

Растяжение или сжатие стержня вызывается силами, действующими вдоль его оси. В этом случае в поперечных сечениях стержня из шести внутренних силовых факторов возникает только один — продольная (осевая) сила N. Простейший случай растяжения стержня и эпюра продольных сил показаны на рис. 95, а, б. Осевая сила в сечении является равнодействующей возникающих в каждой из точек сечения нормальных напряжений. Отсутствие поперечных сил дает основание предположить, что касательные напряжения в каждой точке поперечного сечения равны нулю.  [c.85]

Для наглядного представления о характере распределения и значении крутящих моментов по длине стержня строят эпюры (графики) этих моментов. Построение их вполне аналогично построению эпюр продольных сил при растяжении или сжатии. Для построения эпюр необходимо условиться о правиле знаков. Общепринятого правила знаков для крутящих моментов не существует. Может быть принято любое правило знаков. Важно лишь принятое правило выдержать на всем протяжении эпюры.  [c.110]

В общем случае продольные силы, возникающие в различных поперечных сечениях бруса, не одинаковы по величине и направлению. Для расчета бруса на прочность приходится исследовать закон изменения продольных сил по длине бруса. Рез льтат такого исследования обычно представляют в виде графика (диаграммы), называемого эпюрой продольных сил (см. пример 2.1). При построении этой эпюры продольные силы, соответствующие растяжению, т. е. направленные от соответствующих поперечных сечений бруса, считают положительными. При сжатии продольные силы считают отрицательными.  [c.210]

После определения параметров винта для него строят эпюры продольных сил и крутящих моментов, по этим эпюрам устанавливают опасное поперечное сечение винта и производят проверочный расчет на сложное сопротивление — совместное действие сжатия (или растяжения) и кручения. Так, для винта домкрата, изображенного на рис. 426, опасными будут сечения нарезанной части, расположенные выше гайки. В этих сечениях возникает продольная сила, равная осевой нагрузке Q винта (грузоподъемности домкрата), и крутящий момент, равный моменту в резьбе (см. стр. 402). Применяя теорию прочности наибольших касательных напряжений (см. стр. 309), получают следующее условие прочности винта  [c.416]

Закон изменения крутящих моментов по длине бруса принято представлять в виде эпюры. Построение этой эпюры аналогично построению эпюры продольных сил при растяжении (сжатии) бруса. Пусть, наиример, брус (рис. 2.62, а) находится в равновесии под действие.м нескольких скручивающих моментов (естественно,  [c.224]

Эпюры продольных сил при растяжении и сжатии  [c.185]

При растяжении и сжатии в поперечных сечениях бруса возникает единственный внутренний силовой фактор — продольная сила Nz- Эпюрой продольных сил является график, показывающий, как изменяется продольная сила по длине бруса. Рассмотрим пример построения эпюры для бруса, изображенного на рис. 2.12,а.  [c.185]

При растяжении и сжатии напряжения равномерно распределены по площади сечения, поэтому напряжение в любой точке данного сечения равноопасно. Опасное сечение и напряжение в его любой точке найдем, построив эпюры продольных сил и нор.мальных напряжений, как это было объяснено в 2. 1 и 3.1, Эпюры и о изображены соответственно на рис. 2.104, б и 2.104, в. Опасными оказались все сечения верхнего участка нагружения, где =  [c.287]

Решение. 1-й способ. Разобьем брус на участки и, применяя метод сечений, определим значения продольных сил на каждом из них N1 = N2 = = -40 кН (сжатие), Л() = 20 кН (растяжение). Строим эпюру продольных сил.  [c.191]

Необходимо рассмотреть расчет конструкции из материала, различно сопротивляющегося растяжению и сжатию. Надо, чтобы была задача на определение опасного поперечного сечения с построением эпюр продольных сил и нормальных напряжений. При подборе сечений должны быть использованы стандартные профили.  [c.84]

В случае растяжения продольную силу М будем считать положительной, при сжатии — отрицательной. Изменение продольной силы по длине стержня удобно представить в виде диаграммы, называемой эпюрой продольных сил.  [c.71]

Решение. Сила Р вызывает растяжение балки, а равномерно распределенная нагрузка интенсивностью q—поперечный изгиб. На рис. 340, б показаны эпюры продольных сил и изгибающих моментов. Продольная сила во всех сечениях одинакова, а изгибающий момент имеет наибольшее значение в сечении заделки, следовательно, сечение заделки и является опасным. Наибольшее растягивающее напряжение от растяжения и изгиба в опасном сечении  [c.244]

Для расчета на прочность, так же как и при растяжении (сжатии) бруса, надо найти его опасное сечение. В случае, если размеры поперечного сечения по длине бруса постоянны, опасными будут сечения, в которых крутящий момент максимален. График, показывающий закон изменения крутящих моментов по длине бруса, называется эпюрой крутящих моментов. Построение этих эпюр принципиально ничем не отличается от построения эпюр продольных сил и производится  [c.151]

Для построения эпюры продольных сил N под рисунком бруса проводим ось или базу эпюры, параллельную оси бруса,, и штриховыми линиями ограничиваем его участки. Величины продольных сил в произвольном масштабе откладываем перпендикулярно к оси эпюры, причем положительные значения N (растяжение) откладываются вверх, а отрицательные (сжатие) — вниз от оси. Эпюра штрихуется тонкими линиями, перпендикулярными к оси. Линия штриховки в выбранном масштабе (ордината графика) дает значение продольной силы в соответствующем поперечном сечении бруса.  [c.201]

Для заданных брусьев построить эпюры продольных сил. Ответ. Наибольшие продольные силы а) 2Р (растяжение) 6) 2Р  [c.142]

Эпюры продольных сил и изгибающих моментов показаны на рис. б. На первом участке балка работает на совместное действие изгиба и сжатия, на втором — изгиба и растяжения.  [c.271]

Продольные силы при растяжении и сжатии. Построение эпюр продольных сил  [c.140]

При растяжении продольную силу N будем считать положительной, при сжатии — отрицательной. Изменение продольной силы по длине стержня удобно представить в виде диаграммы, называемой эпюрой продольных сил. Для построения эпюры выбирают параллельную оси стержня линию, перпендикулярно которой откладывают в масштабе величины продольных сил.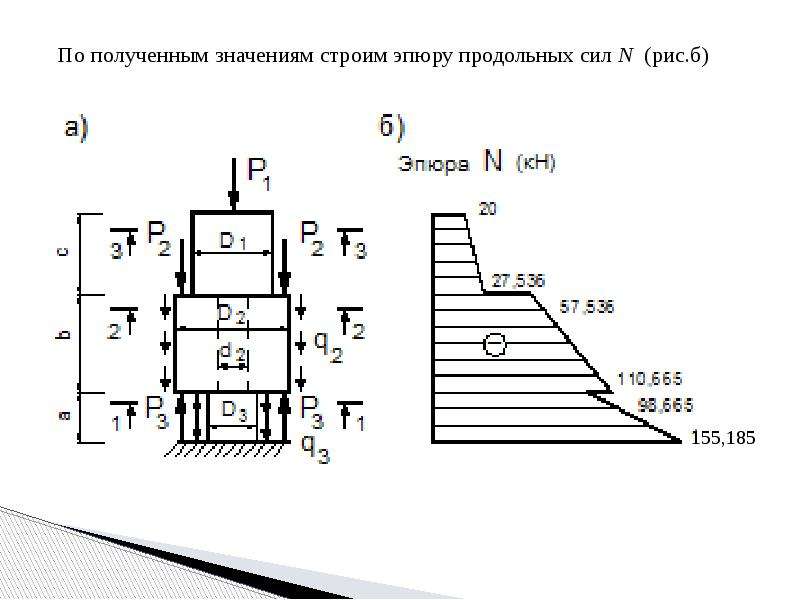 Положительные значения продольной силы (при растяжении) откладывают по одну сторону от выбранной линии или оси (базы) эпюры, а отрицательные (при сжатии) — по другую.  [c.141]

Для заданных брусьев построить эпюры продольных сил. Ответ. Наибольшие продольные силы а) 2Р (растяжение) б) 2Р (сжатие) в) ЗР (сжатие) г) 30 кн (сжатие)  [c.162]

Рис. 1.2. Эпюры продольной силы, напряжений и перемещений в задаче о растяжении стержня под действием собственного веса.

В табл. 1.6 даны основные схемы нагружения образцов при их усталостных испытаниях в условиях растяжения — сжатия, изгиба и кручения, приведены эпюры продольной силы при растяжении и сжатии (рис, 1,15, а),  [c.54]

Разделим раму на четыре участка АБ, БВ, ВД и ВГ. На каждом участке в произвольном месте проведем сечение и составим уравнения равновесия для рассматриваемой (отсеченной) части рамы для определения продольной силы — сумму проекций сил на ось стержня для нахождения поперечной силы — сумму проекций сил на ось, перпендикулярную оси стержня для определения изгибающего момента — сумму моментов сил относительно оси, перпендикулярной плоскости рамы.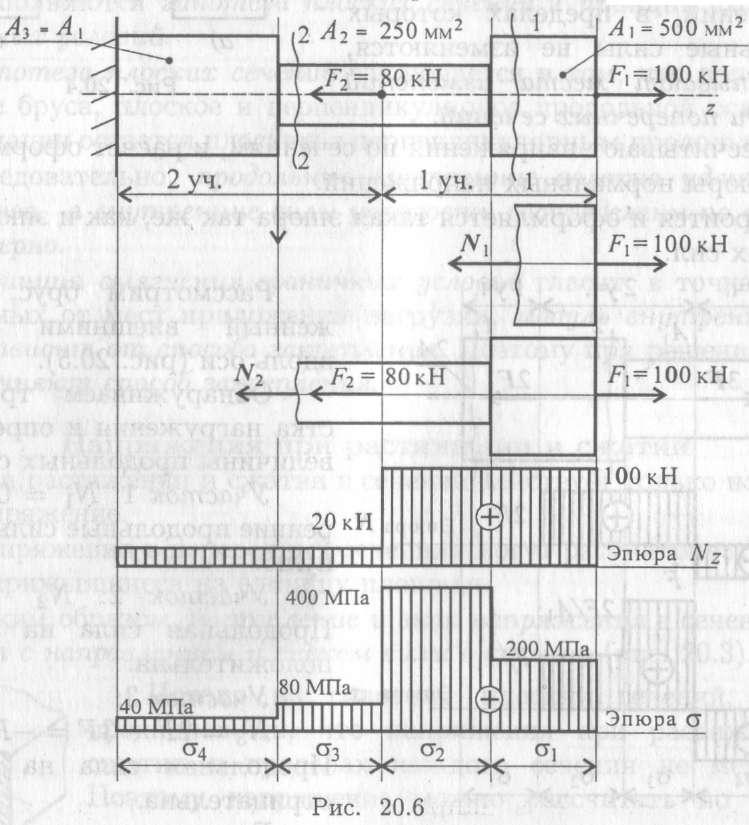 Продольную силу считаем положительной, если она вызывает деформацию растяжения поперечную силу принимаем положительной, если внешние силы поворачивают рассматриваемую часть относительно оси, перпендикулярной плоскости рамы, по ходу часовой стрелки. Знаки на эпюре изгибающих моментов указывать не будем. Ординаты эпюры М откладываем в сторону растянутых волокон.  [c.110]

Условимся о правилах знаков для внутренних силовых факторов. Продольную силу, соответствующую растяжению, будем считать положительной (см. гл. II). Знаки будем указывать непосредственно на эпюре.  [c.93]

Вертикальный стержень сжат, следовательно, продольная сила считается отрицательной. Мы изобразили М , направленной от сечения, т. е. соответствующей деформации растяжения, и из уравнения равновесия получили результат со знаком минус. Изгибающий момент на II участке постоянен, эпюра отложена влево, т. е. в сторону сжатых волокон.  [c.104]

В качестве примера рассмотрим задачу о совместном действии изгиба и растяжения или сжатия на стержень прямоугольного сечения. Обозначим продольную силу через Qi, изгибающий момент через Q2, высота сечения пусть будет h, ширина Ь, смещение нейтральной оси Тогда qt представляет собою удлинение средней линии, дг — кривизну. Очевидно, что gi = 592-Эпюра распределения напряжений показана на рис. 5.8.3. Подсчитывая продольную силу и изгибающий момент, найдем  [c.169]

Эпюру (Т строят после построения эпюры продольных сил, так как величину напряжения а в любой точке некоторого сечения при растяжении и сжатии можно найти, лишь зная величину продольной силы, возыикаюгцей в данном сечении и зная площадь самого поперечного сечения.  [c.208]

Для построения эпюры продольных сил N под рисунком бруса проводим ось эпюры, параллельную оси бруса. Величины продольных сил в произвольном масштабе откладьгааем перпендикулярно оси эпюры, причем положительные значения N (растяжение) откладываются вверх, а отрицательные (сжатие) — вниз от оси. Эпюру отштриховывают, как показано на рисунке.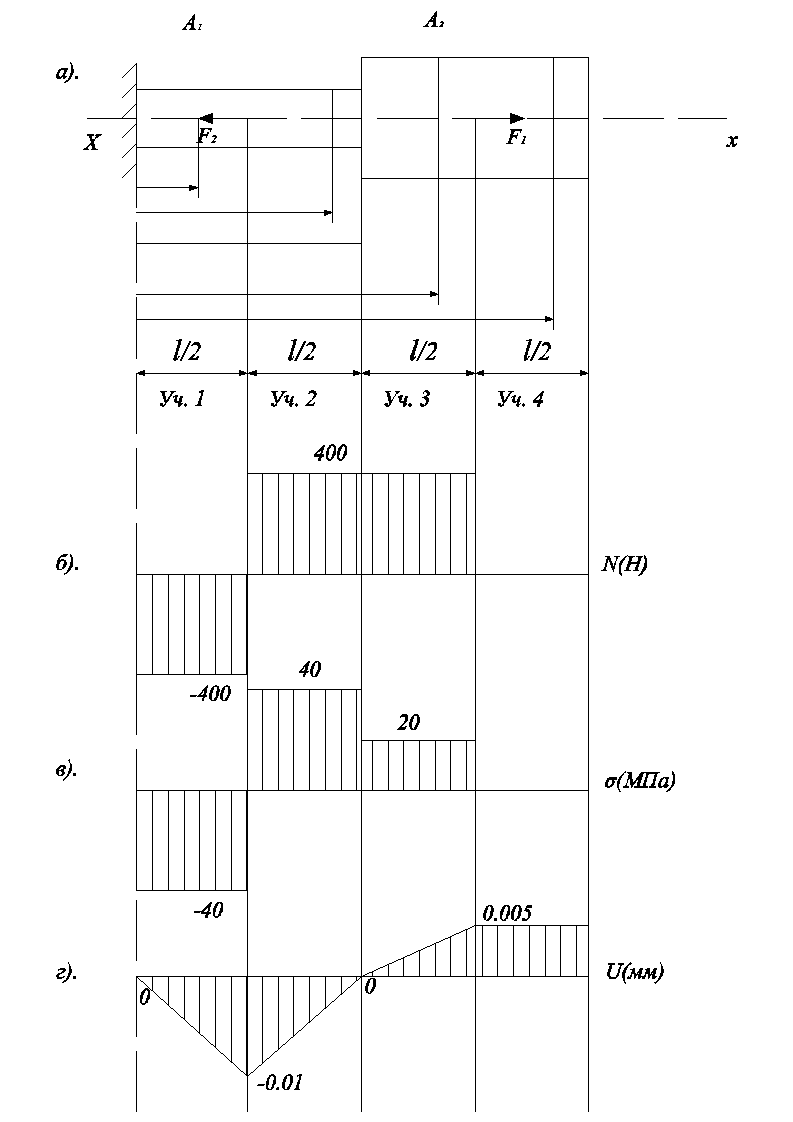 В точках приложения сил на эпюре N получаются  [c.188]

Для ступенчатых стальных брусьев, изображенных на чертеже, определить реакции в заделках, построить эпюры продольных сил N, нормальных напряжений а, продольных перемещений X. Определить опасное сечение и подобрать необходимую площадь F из условия прочности на растяжение или сжатие. Дано Я= 20 Т, й=50 см, [c.23]

Построить эпюры продольных сил, нормальных напряжении и удлинений для конического стержня, растягиваемого собственным весом. Вычислить предельную длину, допускаемую по условию fip04H0 TH, если у=7,85 Г/см , а допускаемое напряжение на растяжение 1а -1600 кГ/смК  [c.32]

Решение. 1. Проверяем полосу на растяжение. На рис. 4.13 покагага эпюра продольных сил для полосы, построенная иа основе допущения, что  [c.145]

Теперь построим эпюру крутящих моментов. На каждом из участков отложим в выбранном масштабе Ai p так же, как строили эпюру продольных сил N при растяжении. Общее правило построения эпюры крутящих моментов Л-lnp аналогично правилу построения эпюры продольных сил N в местах приложения крутящих моментов в эпюре крутящих моментов наблюдаются скачки, равные величине действующих крутящих моментов. Так, в нашем случае, рассматривая вал слева направо, мы наблюдаем первый скачок, равный Ai pi, второй скачок. Л1кр.2 и третий /Икр д. Причем направление скачка связано с направлением и знаком крутящего момента. Если  [c.87]

Построить эпюру продольных сил с учетом действия собственного веса бруса. Удельный вес материала бруса у-Ответ. Наибольшие (по абсолютной величине) продольные силы а) 8уР1 (сжатие) б) 5,5уР1 (растяжение) б)  [c.9]

Для наглядного представления эпюр продольных сил пр растяжении или сжатии. Для построе ния эпюр необходимо условиться о правиле знаков. Общепринято го правила знаков для крутящих моментов не существует. Може быть принято любое правило знаков. Важно лишь принятое прави ло выдержать на всем протяжении эпюры.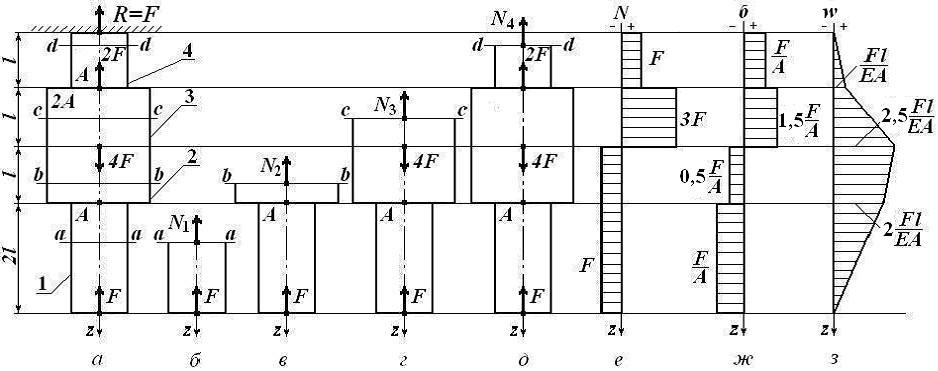  [c.96]

Для расчета на прочность, так же как и при растяжении (сжатии) бруса, надо найти его опасное сечение. В случае если размеры поперечного сечения по длине бруса постоянны, опасными будут сечения, в которых крутящий момент максимален. График, показывающий закон изменения крутящих моментов по длине бруса, называется эпкфой крутацах мюмвтов. Построение этих эпюр принципиально ничем не отличается от построения эпюр продольных сил и производится на основе сформулированного выше правила вычисления крутящих моментов. Для бруса, изображенного на рис. 5.2, а, б, эпюра М Рис. S.3 представлена на рис. 5.2, д.  [c.116]

Решение. Сила Р вызывает растяжение и по всей длине бруса продольная сила, вызванная ею, постоянна. Сила / з вызывает прямой изгиб в вертикальной плоскости. На рнс. 2.123, б схемртично изображен брус и эпюры /V, н Л1д-.  [c.312]

На рис.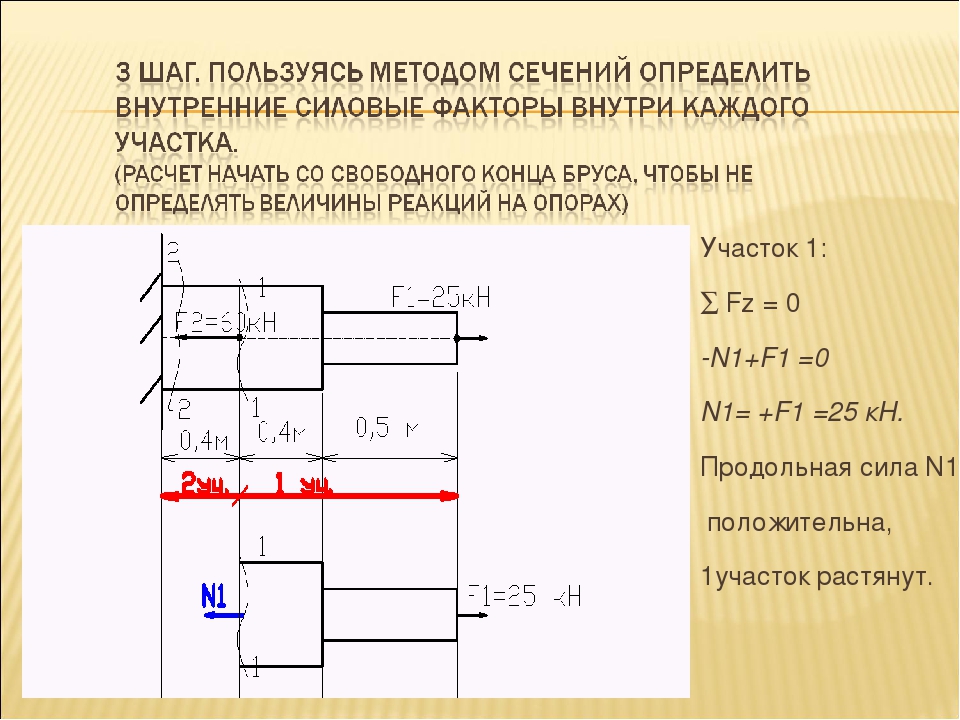 8.8 изображена расчетная схема червяка, к которому в среднем сечении приложены окружная сила F,, осевая сила радиальная сила а также приложен вращающий момент Т . Очевидно, что силы F,. и изгибают червяк в вертйкальной плоскости, а сила F, создает крутящий момент и изгибает вал в горизонтальной плоскости. Эпюры изгибающих и крутящих моментов показаны на рис. 8.8. Кроме указанных внутренних силовых факторов в сечениях червяка будет действовать продольная сила, равная осевой силе напряжения растяжения и сжатия, соответствующие продольной силе, сравнительно невелики и ими можно пренебрегать.  [c.176]

При решении первых примеров на построение эпюр необходимо отдельно изобразить оставленную (отсеченную) часть бруса и составить уравнение равновесия для действующих на нее сил. Здесь иногда возникают споры, как следует направлять продольную силу. Есть две возмо кпости. Первая — всегда направлять силу от сечения, тогда положительный результат ре-щения уравнения равновесия укажет, что сила действительно соответствует растяжению, в этом случае мы условились считать ее положительной. Вторая — направлять продольную силу так, как представляется правдоподобным (по смыслу). При этом знак плюс в решении укажет ( угадали или не угадали ), каково истинное направление силы. Может получиться, что сила соответствует сжатию, а получилась она со знаком плюс при построении эпюры придется менять знак на противоположный.  [c.61]

Используются брусья постоянной и переменной кривизны. Рассмотрим вопрос построения эпюр для криволинейных стержней постоянной кривизны, т. е. очерченных по дуге окружности. На кривом стержне любое сечение можно задать полярным углом ф, и тогда поперечная и продольная силы, а также изгибающий момент в сечении будут функциями Р = 1(ф) Н = 1(ф) М = 1(ф). Для Q и N принимаются обычные правила знаков. Изгибающий момент считаем положительным, если он увеличивает кривизну, т. е. если вызывает растяжение наружных волокон стержня. На рис. 10.9.1, а представлен криволинейный стержень с R = onst, на который под углом а к оси х действует сила Р. Рассмотрим построение эпюр Q, N и М для этого стержня. Силу Р разложим на две составляющие Рх = Р os а и Ру = Р sin а. Стержень рассечем плоскостью OF. Левую часть отбросим. Правую рассмотрим. Для ее равновесия в полученном сечении необходимо приложить Q, N и М, вызываемые внешними нагрузками, т. е. силой Р.  [c.163]

---

–аст¤жение и сжатие. Ёпюры продольных сил и нормальных напр¤жений

–аст¤жение и сжатие. Ёпюры продольных сил и нормальных напр¤жений

Растяжением или сжатием называется такой вид нагружения, при котором в поперечных сечениях бруса возникает только продольная сила N, действующая перпендикулярно плоскости поперечного сечения.

Многие детали и узлы авиатехники в процессе эксплуатации испытывают деформацию растяжения или сжатия. Болты и шпильки при затяжке растягиваются. Тяги управления самолетом и двигателем, в зависимости от характера и режима полета, растягиваются или сжимаются. Растяжение и сжатие воспринимают полки лонжеронов, шатуны кривошипных механизмов, рама крепления двигателя к самолету, стойки шасси и т. д.

Рассмотрим невесомый, защемленный левым концом прямой брус, вдоль оси которого действуют силы 2F и 3F (рис. 2.4).

1. Разбиваем брус на участки, границами которого являются точки приложения сосредоточенных сил или изменение поперечного сечения.

                                                                2. Методом сечений на каждом участке определяем продольные силы N₁ и N₂, начиная со свободного конца. Во всех точках поперечного сечения бруса будут действовать внутренние распределенные силы, равнодействующая которых определится из условия равновесия одной из частей бруса.

                                                                   Σ Z = — N₁ + 3F = 0,    N₁  = 3F.

      

 

 

 

 

Рис. 2.4

Аналогично находим продольную силу N₂:   Σ Z =- N₂  -2F + 3F = 0,  N₂  = F.

В пределах одного участка продольная сила будет иметь постоянное значение. Растягивающие продольные силы будем считать положительными, а сжимающие — отрицательными.

3. Нормальные напряжения равномерно распределенные по сечению определяются по формуле:

                                                      σ  =                                                       (2.5)

Для наглядного изображения распределения вдоль оси бруса продольных сил и нормальных напряжений строят графики, называемые эпюрами, причем для нормальных напряжений применяется тоже правило знаков, что и для продольных сил (рис. 2.4).

Условие прочности при растяжении — сжатии:

                                               s_max = < [σ ]                                                (2.6)

Три задачи, решаемые из условия прочности:

1. Определение безопасной нагрузки, если известны размеры и материал                                                F =N < A [ σ ]

2. Проектный расчет — определение размеров поперечного сечения, если известна нагрузка и материал  A >

3. Проверка прочности σ_max < [ σ ].

Деформации при растяжении, сжатии. Закон Гука. Английский ученый Роберт Гук (1635-1703) установил зависимость между напряжением и деформацией, которое формулируется так: н о р м а л ь н о е  н а п р я ж е н и е 

п р я м о  п р о п о р ц и о н а л ь н о   о т н о с и т е л ь н о м у   у д л и н е н и ю  или  у к о р о ч е н и ю.

Математически закон можно записать в виде равенства:

                                                σ = E ε .                                                          (2.7)

Коэффициент пропорциональности E характеризует жесткость материала, т.е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости  первого рода.

Модуль упругости и напряжения выражаются в одинаковых единицах:

E = σ  / ε  (MПа).

Значения E, МПа, для некоторых материалов:

                    Чугун ……………(1,5…1,6) 10⁵

                    Сталь…………….(1,96…2,1) 10⁵

                    Сплавы алюминия……(0,69…0,71) 10⁵

                    Титановые сплавыЕ..1,1 10⁵

Если в формулу закона Гука подставить выражения относительной продольной деформации  и нормального напряжения , то абсолютная продольная деформация

                                               .                                                         (2.8)

Произведение EA, стоящее в знаменателе, называется жесткостью сечения при растяжении и сжатии. Эта формула читается так: а б с о л ю т н о е  у д л и н е н и е  или  у к о р о ч е н и е  п р я м о  п р о п о р ц и о н а л ь н о  п р о-

д о л ь н о й  с и л е,  д л и н е   и  о б р а т н о  п р о п о р ц и о н а л ь н о  ж е с т к о с т и   с е ч е н и я  б р у с а.

Dl = l₁ — l

Приведенные выше формулы закона Гука применимы только для брусьев или их участков постоянного поперечного сечения, изготовленных из однородного материала и при постоянной продольной силе.

Для бруса, имеющего несколько участков, отличающихся материалом, размерами поперечного сечения, величиной продольной силы, изменение длины всего бруса равно алгебраической сумме удлинений и укорочений отдельных участков:

Δ l = Σ (Δ l_i).

При растяжении и сжатии возникает и поперечная деформация стержня. Поперечный размер бруса первоначально равный b, уменьшился до b₁ . Абсолютное сужение Δb = b Ц b₁.

Отношение абсолютной поперечной деформации к первоначальному поперечному размеру называется относительной поперечной деформацией 

ε’ = Δb/ b

 

 

 

 

                      

                                             Рис. 2.5

 

Опытами французского ученого Пуассона (1781-1840) установлено, что отношение относительной поперечной деформации к относительной продольной деформации есть величина постоянная для данного материала и называется коэффициентом поперечной деформации или коэффициентом Пуассона  μ =.

Коэффициент Пуассона, как и модуль упругости первого рода, зависит только от материала и характеризует его упругие свойства. Коэффициент Пуассона величина безразмерная. Значения для некоторых материалов: Сталь Ц 0,24…0,30; Ал. сплавы Ц 0,3Е0,35

Продольные силы и их эпюры

Содержание:

Продольные силы и их эпюры

• Продольная сила и ее контур Растяжение и сжатие очень распространены в строительных конструкциях и механических элементах. Например, происходит натяжение троса — подъемный трос (рис. 16, а), буксирный трос — при буксировке автомобиля, вес заводской трубы (рис. 16, б), колонна, поддерживающая потолок, и т.

Д. В зависимости от того, как зафиксирован шток и от характера влияния нагрузки, могут возникать различные типы растяжения или сжатия. Если внутренняя сила поперечного сечения стержня уменьшается только до одного фактора силы —

продольной силы N (также называемой нормальной силой, потому что она Людмила Фирмаль

перпендикулярна поперечному сечению стержня), и О) б) Рисунок 16 А Поскольку оставшаяся внутренняя сила равна нулю, происходит чистое (центральное) расширение или сжатие. В этой главе рассматривается только центральное действие продольных сил. Другие более сложные случаи расширения или сжатия описаны в разделе. Xi. Внешние силы, которые вызывают растяжение или

сжатие, приложенные к концу или середине стержня, также должны быть направлены вдоль этой оси или уменьшены до результата, направленного вдоль этой оси. Чтобы определить продольную силу, стержень мысленно рассекают плоскостью, перпендикулярной оси стержня, и заменяют двумя продольными силами N, а две части из равновесия являются значениями этой силы Это зависит от Мы

• согласны думать, что сила N положительна, если она вызывает натяжение (ведущее от сечения), и отрицательна, если она вызывает сжатие (ведущее к сечению). Части. Часть взаимодействия между Рисунок 17 А Если направление силы N неизвестно, мы рекомендуем положительное значение. Если при решении уравнения равновесия сила N получена со знаком плюс, стержень в этом разделе будет растянут, а при наличии знака минус он будет сжат. Так, например, чтобы определить нормальную силу сечения стержня m-n, показанного на рисунке, рассмотрите баланс левой части зажима 17а (рис. 17, б). Создание уравнения £ X = 0, D ‘-P = 0; N = + P Знак плюс

означает, что вал выдвинут. Если сложно, рекомендуется построить прозрение внутренне и в х с и л. Диаграмма продольной силы N представляет собой график, где каждая ордината равна значению продольной силы для определенного сечения. Сюжет обычно строится на базовой линии, проведенной параллельно оси стержня. Чтобы построить кривую N, необходимо установить закон изменения продольной силы вдоль длины стержня и определить значение N нескольких поперечных сечений. Поэтому для стержня, показанного на рисунке 18a, нормальные силы в сечениях / b / 2 и / 3 различны

на рисунке 18a. Это установлено с учетом равновесия отсечки, показанного на рисунке 18. 18, b, c, d Применение статическог Людмила Фирмаль

о уравнения EL = O к этим частям дает Nt-30 T, N 2 = 40T и N 3–20 T. Поскольку нормальная сила не изменяется по длине каждого участка, условие равновесия отрезанной части, значение нормальной силы Ni, например, сечение I — I График нормальной силы показан на рисунке для примера, который рассмотрел 20 случаев / Р на графике. 18, д. График N является сложным, если внешняя нагрузка с силой р распределена вдоль оси стержня. Закон (рис. 19, а и б). Чтобы решить эту проблему, рассмотрим равновесие микроэлементов, разрезанных двумя сечениями на расстоянии dx друг от друга (рис. 19, в). Внутренняя сила N прикладывается к нижней части режущего элемента, а сила N + dN применяется к верхней части. Из состояния равновесия S X = О элемента выреза стержня, + dN-N-pdx = O о, о И- = р. (2.1) о X N x-J pdx, ок. Другими словами, величина нормальной силы в любом сечении равна сумме проекций всех внешних сил в отсечной части на ось стержня. Рисунок 19 А Применяется к (интеграция) 21

Легко видеть, что это верно даже в случае концентрации. Поэтому в будущем, когда вы будете наносить N, вы не увидите отрезанную часть стержня, а сразу запишите значение нормальной силы, основанное на указанных правилах. Точность графика N можно проверить с помощью дифференциальной зависимости (2.1). Например, в секции стержня без внешней нагрузки (p = 0) участок N должен быть прямой линией, параллельной оси. На участке стержня, где осевая нагрузка равномерно распределена, график изменяется

линейно. Когда внешняя осевая нагрузка изменяется Рисунок 20 А [-F H | «Я 1LG к-т (- * + * тг * ■ * 1 А • Вт / Согласно линейному закону диаграмма N представляет собой квадратную параболу. Создайте схему N стержня (рис. 20, а), встроенную в стену в П р и м е р с. / 2. В этом разделе предполагается, что сила трения равномерно распределена на стороне погружения. Сила силы трения равна /. CA EX = 0-3 P-P + [12 = 0; 2 Для секции / -1 внутренняя сила равна внешней силе на левой стороне секции со знаком плюс (сила направлена ​​от

секции I- /). 2 22 Сила второго сечения / V2 изменяется линейно. х = ОН 2-ЗР ´, х = l2 Н 2-3П-4Р = —Р. Используя две полученные ординаты, график IV был построен на графике / 2 (рис. 20, б). В разделах 111-111 выгодно рассмотреть отрезанную часть на правой стороне стержня, заданную условиями равновесия. N 3 = -P-

Смотрите также:

Построение эпюр продольных сил

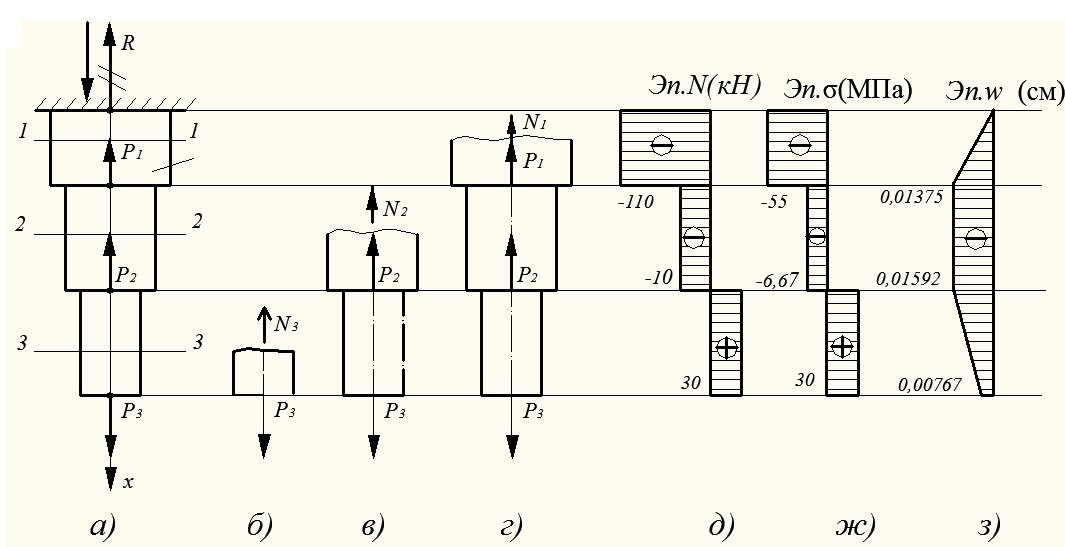
Рассмотрим порядок построения эпюр продольных сил в стержне, работающем на растяжение – сжатие (рис. 3.14).

1. В соответствии с общим алгоритмом построения эпюр прежде всего определяем все внешние силовые факторы, действующие на рассматриваемый стержень (рис. 3.14а). Активные силы заданы. Определим реакции связей. В рассматриваемом примере связью является заделка. В заделке при плоской системе сил в общем случае возникают три реакции – две силы и момент. Однако в данном примере активные силы приложены на оси стержня и действуют вдоль оси, представляющей прямую линию. Равнодействующая активных сил направлена вдоль этой прямой и может быть уравновешена силой, действующей также вдоль этой прямой. Таким образом, возникает только одна реакция, направленная вдоль оси стержня. Выбираем систему координат YOZ, изображаем реакцию связи , и так как направление ее неизвестно, предварительно направляем ее слева направо. Величину и истинное направление реакции определяем из уравнения статики (рис. 3.14а):

ΣF_Z = 0; – P₃ – P₂ + P₁ = – 7 – 3 + 5 = 0; = 5 кН.

Если при решении уравнения результат получают со знаком «минус», то направление реакции изменяют на обратное (влево от т. А).

2. Так как в рассматриваемом примере все силы приложены на оси и действуют вдоль нее, то уточнять расчетную схему не следует.

3. Разбиваем стержни на участки, проводя вертикальные линии через точки приложения сосредоточенных сил. Получаем три участка АВ, ВС и СD.

4. На каждом участке методом сечений определяем внутренние силовые факторы.

Рассмотрим участок АВ. Рассечем стержень на две части поперечным сечением на расстоянии z от начала координат (от т. А) и правую часть отбросим (рис. 3.14б). Абсцисса z в пределах участка АВ изменяется от 0 до 1 м, т.е. 0 ≤ z ≤ 1. На рассматриваемую часть стержня действует только внешняя сила , направленная вдоль оси стержня. Эта сила может быть уравновешена силой, также действующей вдоль оси стержня, т.е. продольной силой N. Прикладываем в рассматриваемом сечении продольную силу N. Так как направление силы N неизвестно (от сечения или на сечение), то направляем ее вдоль оси произвольно, например, от сечения. Записываем уравнение статики (составляем условие равновесия) для рассматриваемой части стержня:

ΣF_Z = 0; + N = 5 + N = 0; N = — 5 кН.

Знак «минус» означает, что сила N должна действовать на сечение. Так как сила N не зависит от абсциссы z, то продольная сила по длине участка АВ не изменяется.

5. Выбираем ось отсчета в виде линии, параллельной оси стержня. При построении эпюры продольных сил принимают следующее правило знаков:

Продольную силу N считают положительной, если имеет место растяжение (N направлена от сечения) и отрицательной, если сжатие (N направлена на сечение).

При горизонтальном расположении оси отсчета положительные значения продольной силы откладывают вверх, отрицательные – вниз. Так как на участке АВ сила N действует на сечение, т.е. имеет место сжатие, то график изменения N на участке АВ представляет собой прямую, параллельную оси отсчета в отрицательной области значений (рис. 1д).

Рассмотрим участок ВС (рис. 3.14в, сеч. II-II). Абсцисса z при начале координат в т. А будет изменяться от 1 м до 1,5 м. Рассуждая так же, как и в предыдущем случае, убеждаемся, что в сечении II-II действует только продольная сила N. Записываем уравнение статики для рассматриваемой части стержня:

ΣF_Z = 0; – P₃ + N = 5 – 7 + N = 0; N = 7 – 5 = 2 кН.

Эпюра продольной силы на участке ВС представляет собой прямую, параллельную оси отсчета в положительной области значений (рис. 3.14д).

Аналогично можно найти продольную силу и на участке СD.

=5 кН

=5 кН

=5 кН

Рис. 3.14. Построение эпюр нормальных сил

Из эпюры продольных сил следует (рис. 3.14д), что в точках А, В, С и D значения продольной силы изменились скачком на величину сосредоточенных сил в этих точках. Эта закономерность справедлива при действии любой сосредоточенной силы и значительно облегчает построение эпюр продольных сил для стержней, нагруженных сосредоточенными силами.

Так, для рассмотренного примера можно было бы поступить следующим образом.

Рассмотрим стержень, начиная с т. А (слева направо). В т. А в соответствии с отмеченной закономерностью должен быть скачок на величину . Сила в сечении I-I (рис. 3.14а) может быть уравновешена внутренней силой N, равной по модулю и направленной на сечение, т.е. имеет место сжатие и ординату откладываем вниз от оси отсчета (скачок направлен вниз). Если выбрать другое сечение в пределах участка АВ, то результат не изменится. Таким образом, на участке АВ имеем:

N_АВ = — = — 5 кН.

График представляет собой прямую, параллельную оси отсчета.

В т. В должен быть скачок на величину силы P₃. Так как сила P₃ направлена в сторону, противоположную силе , то скачок направлен вверх и продольная сила на участке ВС равна:

N_ВС = N_АВ + 7 = -5 + 7 = 2 кН.

Учитывая скачок в т. С, для участка CD получаем:

N_CD = N_ВС + 3 = 2 + 3 = 5 кН.

Если учесть скачок в точке D от силы P₁, то находим:

N_CD — P₁ = 5 – 5 = 0,

что и должно быть, т.к. ΣF_Z = 0.

В заключении отметим основные закономерности:

1. В поперечных сечениях прямого стержня, нагруженного силами, приложенными на оси стержня и направленными вдоль оси, возникает только один внутренний силовой фактор – продольная сила N, т.е. имеет место растяжение или сжатие.

2. В сечениях, где приложены сосредоточенные силы, действующие вдоль оси стержня, на эпюре продольных сил имеет место скачок на величину этих сил.

3. Форма и размеры поперечных сечений не влияют на величину продольных сил.

4. Продольная сила в рассматриваемом сечении равна алгебраической сумме проекций на продольную ось всех сил, действующих на рассматриваемую часть стержня. Проекцию любой силы берут со знаком «плюс», если соответствующая ей внутренняя продольная сила направлена от сечения, и «минус» — если на сечение.

Замечание: Это правило справедливо для любой системы внешних сил. В случае криволинейных стержней силы проектируют на ось, перпендикулярную рассматриваемому сечению.

Методика построения эпюр изгибающих моментов, поперечных и продольных сил. Изгиб Продольная сила в балке

Изгибающий момент, поперечная сила, продольная сила — внутренние усилия возникающие от действия внешних нагрузок (изгиб, поперечная внешняя нагрузка,растяжение-сжатие).

Эпюры -графики изменения внутренних усилий вдоль продольной оси стержня, построенные в определённом масштабе.

Ордината на эпюре показывает значение внутреннего усилия в данной точке оси сечения.

17.Изгибающий момент. Правила (порядок) построения эпюры изгибающих моментов.

Изгибающий момент — внутреннее усилие возникающее от действия внешней нагрузки(изгиба, внецентренного сжатия –растяжения).

Порядок построения эпюры изгибающих моментов :

1.Определение опорных реакций данной конструкции.

2.Определение участков данной конструкции,в пределах которых изгибающий момент будет изменяться по одному и тому же закону.

3.Произвести сечение данной конструкции в окрестности точки, которая разделяет участки.

4.Отбросить одну из частей конструкции, разделённой пополам.

5.Найти момент,который уравновесит действие на одну из оставшихся частей конструкции всех внешних нагрузок и реакций связи.

6.Нанести значение этого момента, с учётом знака и выбранного масштаба, на эпюру.

Вопрос № 18.Поперечная сила. Построение эпюры поперечных сил, используя эпюру изгибающих моментов.

Поперечная сила Q –внутреннее усилие возникающее в стержне под воздействием внешней нагрузки(изгиб, поперечная нагрузка). Поперечная сила направлена перпендикулярно оси стержня.

Эпюра поперечных сил Q строится исходя из следующей дифференциальной зависимости: ,т.е. Первая производная от изгибающего момента по продольной координате равна поперечной силе.

Знак поперечной силы определяется исходя из следующего положения:

Если нейтральная ось конструкции на эпюре моментов поворачивается к оси эпюры по часовой стрелке, то эпюра поперечных сил имеет знак плюс, если против- минус.

В зависимости от эпюры M эпюра Q может принимать тот или иной вид:

1.если эпюра моментов имеет вид прямоугольника, то эпюра поперечных сил равна нулю.

2.Если эпюра моментов представляет собой треугольник, то эпюра поперечных сил имеет вид прямоугольника.

3.Если эпюра моментов имеет вид квадратной параболы, то эпюра поперечных сил имеет треугольника и строится по следующему принципу

Вопрос №19 . Продольная сила. Метод построения эпюры продольных сил используя эпюру поперечных сил. Правило знаков.

Полольная сила N- внутреннее усилие возникающее вследствие центрального и внецентренного растяжения-сжатия. Продольная сила направлена вдоль оси стержня.

Для того что бы построить эпюру продольных усилий нужно:

1.Вырезать узел данной конструкции. Если мы имеем дело с одномерной конструкцией, то сделать сечение на интересующем нас участке этой конструкции.

2.Снять с эпюры Q значения усилий действующих в непосредственной близости от вырезанного узла.

3.Дать направление векторам поперечных сил, исходя из того какой знак имеет данное поперечное усилие на эпюре Q по следующим правилам: если поперечная сила имеет на эпюре Q знак плюс, то её нужно направить так, что бы она вращала данный узел по часовой стрелке, если поперечная сила имеет знак минус –против часовой стрелки. Если внешняя сила проложена к узлу, то её нужно оставить и рассматривать узел вместе с ней.

4.Уравновесить узел продольными усилиями N.

5.Правило знаков для N:если продольная сила направлена к сечению, то она имеет знак минус (работает на сжатие).если продольная сила направлена от сечения, она имеет знак плюс (работает на растяжение).

Вопрос № 20.Правилаприменяемые для проверки правильности построения эпюр внутренних усилий M , Q , N .

1. В сечении, где приложена сосредоточенная сила F, на эпюре Q будет скачок, равный значению этой силы и направленный в ту же сторону (при построении эпюры слева направо), а эпюра М будет иметь перелом, направ- ленный в сторону действия силы F.

2. В сечении, где приложен сосредоточенный изгибающий момент на эпюре М, будет скачок, равный значению момента М; на эпюре Q изменений не будет. При этом направление скачка будет вниз (при построении эпюры слева направо), если сосредоточенный момент действует по ходу часовой стрелки, и вверх, если против хода часовой стрелки.

3.Если на участке, где имеется равномерно распределенная нагрузка, поперечная сила в одном из сечений равна нулю (Q=M»=0), то изгибающий момент в этом сечении принимает экстремальное значение М экстр — максимум или минимум (здесь касательная к эпюре М горизонтальна).

4.Для проверки правильности построения эпюры М можно использовать метод вырезания узлов. При этом момент приложенный в узле нужно при вырезании узла оставлять.

Правильность построения эпюр Q и M можно проверить, дублируя метод вырезания узлов методом сечений и наоборот.

Рассчитывать балку на изгиб можно несколькими вариантами:
1. Расчет максимальной нагрузки, которую она выдержит
2. Подбор сечения этой балки
3. Расчет по максимальным допустимым напряжениям (для проверки)
Давайте рассмотрим общий принцип подбора сечения балки на двух опорах загруженной равномерно распределенной нагрузкой или сосредоточенной силой.
Для начала, вам необходимо будет найти точку (сечение), в которой будет максимальный момент. Это зависит от опирания балки или же ее заделки. Снизу приведены эпюры изгибающих моментов для схем, которые встречаются чаще всего.

После нахождения изгибающего момента мы должны найти момент сопротивления Wx этого сечения по формуле приведенной в таблице:

Далее, при делении максимального изгибающего момента на момент сопротивления в данном сечении, мы получаем максимальное напряжение в балке и это напряжение мы должны сравнить с напряжением, которое вообще сможет выдержать наша балка из заданного материала.

Для пластичных материалов (сталь, алюминий и т.п.) максимальное напряжение будет равно пределу текучести материала , а для хрупких (чугун) – пределу прочности . Предел текучести и предел прочности мы можем найти по таблицам ниже.

Давайте рассмотрим пару примеров:
1. [i]Вы хотите проверить, выдержит ли вас двутавр №10 (сталь Ст3сп5) длиной 2 метра жестко заделанного в стену, если вы на нем повисните. Ваша масса пусть будет 90 кг.
Для начала нам необходимо выбрать расчетную схему.

На данной схеме видно, что максимальный момент будет в заделке, а поскольку наш двутавр имеет одинаковое сечение по всей длине , то и максимальное напряжение будет в заделке. Давайте найдем его:

P = m * g = 90 * 10 = 900 Н = 0.9 кН

М = P * l = 0.9 кН * 2 м = 1.8 кН*м

По таблице сортамента двутавров находим момент сопротивления двутавра №10.

Он будет равен 39.7 см3. Переведем в кубические метры и получим 0.0000397 м3.
Далее по формуле находим максимальные напряжения, которые у нас возникают в балке.

б = М / W = 1.8 кН/м / 0.0000397 м3 = 45340 кН/м2 = 45.34 МПа

После того, как мы нашли максимальное напряжение, которое возникает в балке, то мы его может сравнить с максимально допустимым напряжением равным пределу текучести стали Ст3сп5 – 245 МПа.

45.34 МПа – верно, значит данный двутавр выдержит массу 90 кг.

2. [i]Поскольку у нас получился доволи-таки большой запас, то решим вторую задачу, в которой найдем максимально возможную массу, которую выдержит все тот же двутавр №10 длиной 2 метра.
Если мы хотим найти максимальную массу, то значения предела текучести и напряжения, которое будет возникать в балке, мы должны приравнять (б=245 Мпа = 245 000 кН*м2).

Размещенно 13/11/2007 12:34

Итак, beam

1. балка; прогон; ригель

2. луч

3. брус; поперечина, траверса

4. коромысло (весов)

5. стрела или рукоять стрелы (крана)

beam and column — балочно-стоечная конструкция; концевая [торцовая] рама металлического каркаса

beam carrying transverse loads — балка, нагруженная поперечными силами [поперечной нагрузкой]

beam fixed at both ends — балка с защемлёнными концами

beam loaded unsymmetrically — балка, нагруженная несимметричной нагрузкой (действующей вне плоскости симметрии сечения и вызывающей косой изгиб)

beam made of precast hollow blocks — балка, собираемая из пустотелых [коробчатых] секций (с натяжением продольной арматуры)

beam on elastic foundation — балка на упругом основании

beams placed monolithically with slabs — балки, бетонируемые совместно с плитами перекрытий

beam precast on site — сборная железобетонная балка, изготовленная на стройплощадке [построечного изготовления]

beam subjected to (both) transverse and axial loads — балка, нагруженная поперечными и продольными силами; балка, подверженная воздействию поперечной и осевой нагрузок

beam supported on a girder — балка, опирающаяся на прогон; балка, поддерживаемая прогоном

beam with overhangs — консольная балка

beam with rectangular section — балка прямоугольного сечения

beam with symmetrical (cross) section — балка симметричного (поперечного) сечения

beam with unsymmetrical (cross) section — балка несимметричного (поперечного) сечения

beam of constant depth — балка постоянной высоты

beam of one span — однопролётная балка

beam of uniform strength — равнопрочная балка

anchor beam — анкерная балка

angle beam — металлический уголок; уголковая сталь

annular beam — кольцевая балка

arch(ed) beam

2. выпуклая балка с поясами различной кривизны

baffle beam — забральная балка

balance beam — балансирная балка; коромысло весов

bamboo-reinforced concrete beam — бетонная балка, армированная бамбуком

basement beam — балка надподвального перекрытия

bedplate beam — балка [ребро] опорной плиты

bending test beam — балочка(-образец){балочка-образец¦балочка} для испытания на изгиб

Benkelman beam — балка Бенкельмана, прогибомер

bind beam — свайная насадка

bisymmetrical beam — балка с сечением, симметричным относительно двух осей

block beam — преднапряжённая железобетонная балка из отдельных блоков [секций] (соединяемых натяжением арматуры)

bond beam — связывающая [усиливающая] балка (железобетонная балка, усиливающая каменную стену и предупреждающая образование в ней трещин)

boundary beam — подстропильная балка; краевая балка

box beam — балка коробчатого сечения; коробчатая балка

braced beam — шпренгельная балка

bracing beam — раскрепляющая балка; распорка

brake beam — тормозная балка

breast beam — перемычка [балка] над широким проёмом в стене

brick beam — рядовая кирпичная перемычка (с усилением стальными прутками)

bridge beam — мостовая балка, мостовой прогон

bridging beam — поперечная балка (между балками перекрытия)

broad-flange(d) beam — широкополочная двутавровая балка, широкополочный двутавр

buffer beam — буферный брус, бампер

built-in beam — встроенная (в каменную кладку) балка; балка с защемлёнными концами

built-up beam — составная балка

camber beam

1. балка с выпуклым верхним поясом

2. балка, слегка выгнутая вверх (для создания строительного подъёма)

candle beam — балка, поддерживающая свечи или светильники

cantilever beam

1. консольная балка, консоль

2. балка с одной или двумя консолями

capping beam

1. оголовок; насадка (опоры моста)

2. ростверк ленточного свайного фундамента

cased beam

1. стальная балка, замоноличенная в бетон

2. стальная балка с наружной оболочкой (как правило, декоративной)

castellated beam — перфорированная балка

castella Z beam — перфорированный зетовый профиль

ceiling beam — потолочная балка; балка, выступающая из потолка; балка ложного потолка

channel beam — швеллерная балка

chief beam — главная балка, прогон

circular beam — кольцевая балка

collar beam — повышенная затяжка висячих стропил

composite beam — составная балка

compound beam — составная балка

conjugate beam — сопряжённая балка

constant-section beam — балка постоянного сечения

continuous beam — неразрезная балка

crane lifting beam — монтажная траверса

crane runway beam — подкрановая балка

cross beam

1. поперечная балка

2. гидр. шапочный брус

curved beam

1. балка с криволинейной осью (в плоскости нагружения)

2. криволинейная (в плане) балка

deck beam — балка, поддерживающая настил; ребро настила

deep beam — балка-стенка

double-T beam

1. сборная железобетонная балка в форме двойного «Т»

2. сборная железобетонная панель с двумя рёбрами

doubly symmetrical beam — балка симметричного сечения с двумя осями симметрии

dragging beam — отрезок бруса, поддерживающий внизу накосную стропильную ногу; подбалка

drop-in beam — висячая балка; балка, поддерживаемая (на обоих концах) консолями

eaves beam — под стропильная балка (наружного ряда колонн)

edge beam

1. краевая балка

2. бортовой камень

elastically restrained beam — упруго-защемлённая балка, балка с упруго защемлёнными концами

encastre beam — балка с защемлёнными концами

externally reinforced concrete beam — железобетонная балка, усиленная наружными арматурными элементами (обычно наклейкой стальных полос на верхней и нижней гранях балки)

false beam — ложная балка

fish(ed) beam

1. деревянная составная балка с боковыми металлическими стыковыми накладками

2. балка с выпуклыми криволинейными поясами

fixed(-end) beam — балка с защемлёнными концами

flitch(ed) beam — составная деревометаллическая балка (состоящая из средней стальной полосы и двух боковых досок, скреплённых болтами)

floor beam

1. балка перекрытия; балка пола, лага

2. поперечная балка проезжей части моста

3. балка лестничной площадки

footing beam — затяжка стропильной фермы (на уровне концов стропильных ног)

foundation beam — фундаментная балка, рандбалка

framework beam — ригель рамы (рамной конструкции)

free beam — свободноопёртая балка на двух опорах

gantry beam — подкрановая балка

Gerber beam — шарнирная балка, балка Гербера

glue(d) laminated (timber) beam — многослойная дощатоклеёная балка

grade beam — фундаментная балка, рандбалка

grillage beams — балки ростверка

ground beam

1. фундаментная балка, ростверк; рандбалка

2. нижняя обвязка каркасной стены; лежень

H beam — широкополочная балка, широкополочный двутавр

hammer beam — опорный консольный брус [подбабок] стропильной ноги

haunched beam — балка с вутами

high strength concrete beam — балка из высокопрочного железобетона

hinged beam — шарнирная балка

hollow beam — пустотелая балка; коробчатая [трубчатая] балка

hollow prestressed concrete beam — пустотелая преднапряжённая железобетонная балка

horizontally curved beam — криволинейная в плане балка

hung-span beam — многопролётная консольно-подвесная балка, балка Гербера

hybrid beam — стальная составная балка (изготовленная из сталей разных марок)

I beam — двутавровая балка, двутавр

inverted T beam — тавровая (железобетонная) балка со стенкой, обращённой вверх

jack beam — подстропильная балка

jesting beam — декоративная [орнаментная] балка

joggle beam — составная балка из деревянных брусьев, соединённых по высоте ответными выступами и пазами

jointed beam

1. монолитная железобетонная балка, бетонируемая с устройством стыковых швов

2. сборная железобетонная балка, собираемая из отдельных секций

keyed beam — балка из брусьев с соединениями на призматических шпонках

L beam — балка Г-образного сечения

laminated beam — дощатоклеёная балка

laterally-unsupported beam — балка без боковых связей

lattice beam — решётчатая [сквозная] балка

leveling beam — рейка для проверки ровности дорожного покрытия

lifting beam — грузоподъёмная траверса

link beam — перемычка (над проёмом в стене)

longitudinal beam — продольная балка

main beam — главная балка

modified I beam — сборная железобетонная балка с выпусками хомутов из верхней полки (для соединения с верхней монолитной железобетонной плитой)

multispan beam — многопролётная балка

nailed beam — составная деревянная балка с соединениями на гвоздях; гвоздевая балка

needle beam

1. балка для временного опирания стены (при усилении фундамента)

2. верхний упорный прогон спицевого затвора

outrigger beam — балка выносной [дополнительной] опоры (крана, экскаватора)

overhead runway beam — кран-балка

parallel flanges beam — балка с параллельны ми полками

partition beam — балка, несущая перегородку

precast beam — сборная железобетонная балка

precast toe beam — сборная опорная балка (напр. поддерживающая кирпичную облицовку)

prestressed concrete beam — предварительно напряжённая железобетонная балка

prestressed precast concrete beam — сборная предварительно напряжённая железобетонная балка

prismatic beam — призматическая балка

propped cantilever beam — балка с одним защемлённым и другим шарнирно опёртым концами

rectangular beam — балка прямоугольного сечения

reinforced concrete beam — железобетонная балка

reinforced floor beam — балка железобетонного ребристого перекрытия

restrained beam — балка с защемлёнными концами

ridge beam — коньковый брус, коньковая балка

ring beam — кольцевая балка

rolled beam with cover plates — прокатная (двутавровая) балка с поясными листами

rolled I beam — прокатная [горячекатаная] двутавровая балка

rolled steel beam — прокатная стальная балка

roof beam — балка покрытия

runway beam — кран-балка

sandwich beam — составная балка

secondary beam — второстепенная [вспомогательная] балка

simple beam — простая [однопролётная свободно опёртая] балка

simple-span beam — однопролётная балка

simply supported beam — свободно опёртая балка

single web beam — (составная) балка с одной стенкой, одностенчатая (составная) балка

slender beam — гибкая балка (балка, требующая проверочного расчёта на потерю устойчивости из плоскости изгиба)

soldier beam — стальная стойка крепления стенок траншей или больверка

spandrel beam

1. фундаментная балка, рандбалка

2. ригель каркаса, поддерживающий [несущий] наружную стену

spreader beam — распределительная балка

statically determinate beam — статически определимая балка

statically indeterminate beam — статически неопределимая балка

steel beam — стальная балка

steel binding beam — стальная распорка, стальная соединительная балка

stiff beam — жёсткая балка

stiffening beam — балка жёсткости

straight beam — прямая [прямолинейная] балка

strengthened beam — усиленная балка

strut-framed beam — шпренгельная балка

supporting beam — опорная [поддерживающая] балка

suspended-span beam — подвесная [висячая] балка консольно-балочного пролёта (моста)

T beam — тавровая балка

tail beam — укороченная деревянная балка перекрытия (у проёма)

tee beam — тавровая балка

tertiary beam — балка, поддерживаемая вспомогательными балками

test beam — испытательная балочка, балочка-образец

through beam — неразрезная многопролётная балка

tie beam

1. затяжка (стропил, арки) на уровне опор

2. распределительная фундаментная балка (распределяет внецентренную нагрузку)

top beam — повышенная затяжка стропил

top-running crane beam — опорная кран-балка (перемещающаяся по верхнему поясу подкрановых балок)

transverse beam — поперечная балка

trolley I beam — катучая (двутавровая) балка

trussed beam

1. ферма с параллельными поясами, балочная ферма

2. шпренгельная балка

uniformly loaded beam — балка, нагруженная равномерно распределённой нагрузкой; равномерно нагруженная балка

unjointed beam

1. монолитная железобетонная балка без рабочего шва

2. стальная балка без стыка в стенке

upstand beam — балка ребристого перекрытия, выступающая над плитой

valley beam — подстропильная балка среднего ряда колонн; балка, поддерживающая ендову

vibrating beam — виброрейка, вибробрус

vibrating leveling beam — выравнивающий вибробрус

vibratory beam — виброрейка, вибробрус

wall beam — стальной анкер для крепления деревянных балок или перекрытий к стене

welded I beam — сварной двутавр

wide-flanged beam — широкополочная балка, широкополочный двутавр

wind beam — повышенная затяжка висячих стропил

wood I beam — деревянная двутавровая балка

AZM

Использовано фото из материалов пресс-службы ASTRON Buildings

Все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых

наиболее часто встречаются: шарнирно-подвижная опора (возможные обозначения для нее представлены на рис.1,а), шарнирно-неподвижная опора (рис.1,б) и жесткое защемление , или заделка (рис.1,в).

В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения.
В шарнирно-неподвижной опоре возникают вертикальная и горизонтальная реакции. Здесь невозможны перемещения по направлениям опорных стержней, но допускается поворот опорного сечения.
В жесткой заделке возникают вертикальная и горизонтальная реакции и опорный (реактивный) момент. При этом опорное сечение не может смещаться и поворачиваться.При расчете систем, содержащих жесткую заделку, возникающие опорные реакции можно не определять, выбирая при этом отсеченную часть так, чтобы заделка с неизвестными реакциями в нее не попадала. При расчете систем на шарнирных опорах реакции опор должны быть определены обязательно. Уравнения статики, используемые для этого, зависят от вида системы (балка, рама и др.) и будут приведены в соответствующих разделах настоящего пособия.

2. Построение эпюр продольных сил Nz

Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.

Правило знаков для Nz: условимся считать продольную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части стержня, вызывает растяжение и отрицательной — в противном случае.

Пример 1. Построить эпюру продольных сил для жестко защемленной балки (рис.2).

Порядок расчета:

1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
2. Определяем продольную силу Nz в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.

По найденным значениям строим эпюру Nz. Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные — под осью.

3. Построение эпюр крутящих моментов Мкр .

Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.

Правило знаков для Мкр : условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным — в противном случае.

Пример 2. Построить эпюру крутящих моментов для жестко защемленного стержня (рис.3,а).

Порядок расчета.

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил .

1.Намечаем характерные сечения.
2.Определяем крутящий момент в каждом характерном сечении.

По найденным значениям строимэпюру Мкр (рис.3,б).

4. Правила контроля эпюр Nz и Мкр .

Для эпюр продольных сил и крутящих моментов характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.

1. Эпюры Nz и Мкр всегда прямолинейные.

2. На участке, где нет распределенной нагрузки, эпюра Nz(Мкр) — прямая, параллельная оси, а на участке под распределенной нагрузкой — наклонная прямая.

3. Под точкой приложения сосредоточенной силы на эпюре Nz обязательно должен быть скачок на величину этой силы, аналогично под точкой приложения сосредоточенного момента на эпюре Мкр будет скачок на величину этого момента.

5. Построение эпюр поперечных сил Qy и изгибающих моментов Mx в балках

Стержень, работающий на изгиб, называется балкой . В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора — Qy и изгибающий момент Mx .

Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.

Правило знаков для Qy: условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной — в противном случае.

Схематически это правило знаков можно представить в виде

Изгибающий момент Mx в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение.

Правило знаков для Mx: условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной — в противном случае.

Схематически это правило знаков можно представить в виде:

Следует отметить, что при использовании правила знаков для Mx в указанном виде, эпюра Mx всегда оказывается построенной со стороны сжатых волокон балки.

6. Консольные балки

При построении эпюр Qy и Mx в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.

Пример 3. Построить эпюры Qy и Mx (рис.4).

Порядок расчета .

1. Намечаем характерные сечения.

В точках поперечных сечений бруса при продольнопоперечном изгибе возникают нормальные напряжения от сжатия продольными силами и от изгиба поперечными и продольными нагрузками (рис. 18.10).

В наружных волокнах балки в опасном сечении суммарные нормальные напряжения имеют наибольшие значения:

В рассмотренном выше примере сжатой балки с одной поперечной силой согласно (18.7) получаем такие напряжения в наружных волокнах:

Если опасное сечение симметрично относительно его нейтральной оси, то наибольшим по абсолютной величине будет напряжение в наружных сжатых волокнах:

В сечении, не симметричном относительно нейтральной оси, наибольшим по абсолютной величине может быть как сжимающее, так и растягивающее напряжение в наружных волокнах.

При установлении опасной точки следует учитывать различие в сопротивлении материала растяжению и сжатию.

Учитывая выражение (18.2), формулу (18.12) можно записать так:

Применяя приближенное выражение для получаем

Опасным в балках постоянного сечения будет то сечение, для которого числитель второго слагаемого имеет наибольшее значение.

Размеры поперечного сечения бруса должны быть подобраны так, чтобы не превышало допускаемого напряжения

Однако полученная зависимость между напряжениями и геометрическими характеристиками сечения сложна для проектировочного расчета; размеры сечения можно подобрать только методом повторных попыток. При продольно-поперечном изгибе проводится, как правило, поверочный расчет, назначение которого установить запас прочности детали.

При продольно-поперечном изгибе между напряжениями и продольными силами нет пропорциональности; напряжения при переменной осевой силе растут быстрее, чем сама сила, что видно, например, из формулы (18.13). Поэтому запас прочности в случае продольно-поперечного изгиба надо определять не по напряжениям, т. е. не из отношения а по нагрузкам, понимая под запасом прочности число, показывающее, во сколько раз надо увеличить действующие нагрузки, чтобы максимальное напряжение в рассчитываемой детали достигло предела текучести.

Определение запаса прочности связано с решением трансцендентных уравнений, так как сила содержится в формулах (18.12) и (18.14) под знаком тригонометрической функции. Например, для балки, сжатой силой и нагруженной одной поперечной силой Р, запас прочности согласно (18.13) находится из уравнения

Для упрощения задачи можно воспользоваться формулой (18.15). Тогда для определения запаса прочности получаем квадратное уравнение:

Заметим, что в случае, когда продольная сила остается постоянной, а изменяются по величине только поперечные нагрузки, задача определения запаса прочности упрощается, и возможно определение не по нагрузке, а по напряжениям. Из формулы (18.15) для этого случая находим

Пример. Двухопорная дюралюминиевая балка двутаврового тонкостенного сечения сжата силой Р и подвергнута действию равномерно распределенной поперечной нагрузки интенсивностью и моментов приложенных на концах

балки, как показано на рис. 18.11. Определить напряжение в опасной точке и максимальный прогиб с учетом и без учета изгибающего действия продольной силы Р, а также найти запас прочности балки по пределу текучести .

В расчетах принять Характеристики двутавра:

Решение. Наиболее нагруженным является среднее сечение балки. Максимальный прогиб и изгибающий момент от одной только поперечной нагрузки:

Максимальный прогиб от совместного действия поперечной нагрузки и продольной силы Р определим по формуле (18.10). Получим

Продольная сила

— обзор

2.7.1 Модель щетки

В этом разделе мы обсуждаем теорию установившегося комбинированного скольжения шины с помощью простой модели шины щеточного типа. Теория этого раздела не будет рассматривать изгиб и поворот (проскальзывание) колеса (см. [32], где подробно рассматривается модель щетки). Мы обращаемся к рис. 2.36 для схематического представления модели. Шина оснащена небольшими линейными балками (щеточными элементами), некоторые из которых касаются земли (зоны контакта) и в результате деформируются в виде линейной балки.Предполагается, что в зоне контакта действуют как поперечная, так и продольная сила. Следовательно, предполагается, что шина движется вбок с углом скольжения α в сочетании с продольным скольжением κ , т.е. мы предполагаем общий случай комбинированного скольжения. Каждый щеточный элемент в зоне контакта соединяет землю («кончик» щеточного элемента) с шиной («основание» щеточного элемента). Элемент щетки пытается следовать направлению скорости, что означает, что в случае ненулевого угла скольжения и до тех пор, пока наконечник прикреплен к дороге (сцепление), кончики последующих элементов щетки следуют линейному шаблону.Этот рисунок, очевидно, определяется этим углом скольжения. В условиях чистого бокового скольжения наконечник движется только вбок по отношению к шине. Продольное скольжение заставит наконечник двигаться назад в зоне контакта при торможении и вперед при движении. Когда предел трения на кончике щетки превышен, кончик начинает скользить. Эти явления обсуждались в предыдущих разделах, и мы пришли к выводу, что идентифицированы две области: ведущая область сцепления, где линия контакта (соединяющая концы элементов щетки) прямая, и область скольжения, где напряжение сдвига подчиняется закону Кулона

.

τ = τx2 + τy2 = μ · σz

для касательных напряжений τ _x , τ _y в зоне контакта, трение дороги μ и нормальное контактное напряжение σ _z .Шина движется со скоростью V , складывающейся из скорости качения (см. Уравнение (2.35)) и скорости скольжения V _s как с поперечной, так и с продольной составляющими.

Вид сверху шины при прогибе элементов протектора (щеток) показан на рисунке 2.38. На передней кромке контактной площадки общей длиной 2 a деформация все еще равна нулю. Основание и вершина элемента протектора совпадают. Когда шина движется со скоростью V и катится со скоростью качения V _r , основание протектора прикрепляется к плоскости колеса и будет перемещаться внутри зоны контакта со скоростью качения, скажем, до точки B.При этом кончик элемента протектора переместится в точку А, противоположную скорости V . Рисунок 2.38 предполагает наличие положительного продольного (ведущего) скольжения, но это не ограничение, а сделано только для рисунка. Приведенные ниже обсуждения не зависят от знака слипа κ .

Рисунок 2.38. Модель кисти, вид сверху.

Если принять интервал времени Δ t , это означает, что смещение w _A в зоне фактического контакта вдоль деформированных ступеней может быть записано как

wA = V · Δt

Новые позиции ξ _A (наконечник) и ξ _B (основание) находятся из

ξA = V · cos (α) · Δt, ξB = Vr · Δt

из которых выражения для прогибы u и v (ср.Рисунок 2.38) можно вывести

u = (Vr − V · cosα) · Δt

v = V · sinα · Δt

Это означает, что смещения могут быть выражены в терминах любого положения в деформированной ситуации протектора ξ _A или в координатах недеформированного протектора ξ _B следующим образом:

(2,74) (uv) = (Vr − VxVxtanα) · ξA = (Vr − VxVrVxVr · tanα) · ξ

Вектор коэффициентов соответствует либо практическому, либо теоретическому скольжению, как определено ранее.Выражение (2.74) имеет общий вид

Смещение = скольжение × положение

, где скольжение определяется либо на основе положения ξ _A относительно деформированной шины, либо положения ξ _B в отношении недеформированной шины. Следовательно, практические величины скольжения связаны с количествами деформированной шины, тогда как теоретические величины скольжения выводятся на основе количества недеформированной шины.

Площадь контакта принимается как квадрат длиной 2 a и шириной 2 b . Обычно принимают параболическое распределение давления σ _z ( x ), которое принимается однородным по ширине контакта 2 b

(2,75) σz (x) = σz0 · [1− (xa) 2]

с σ _{z 0} , следующим из условия, что

Fz = contactareaσz (x) · dxdy

и, таким образом,

σz0 = 3 · Fz8ab

. распределение параболического контактного давления (2.75) не является настоящим ограничением, и можно легко использовать другие дистрибутивы.

Теперь мы выведем выражения для полного смещения в области контакта, где проводится различие между адгезией и скольжением. В области сцепления следует, что

(2,76) e = u2 + v2 = ρ · ξB = ξB1 + κ · κ2 + tan2α

с общим теоретическим скольжением ρ . В области скольжения , предполагая кулоновское трение с коэффициентом трения μ , напряжение сдвига τ ( x , y ) ограничено μ · σ ( x ).Таким образом, смещение e также ограничено, и это следует из жесткости протектора, обозначенной как k :

e = emax = τ (x, y) k = μ · σz (x) k = 3 · Μ · Fz8 · a3 · b · k · (a2 − x2)

Обратите внимание, что k не будет одинаковым в направлениях x и y . Рассматривая этот анализ для чистого скольжения в случае поперечного или продольного направления, можно различить разные жесткости k _x и k _y .Для комбинированного скольжения мы ограничиваем наш анализ равной жесткостью протектора k = k _x = k _y (изотропная модель).

Введем параметр шины θ на

(2,77) θ = 43 · a2 · b · kμ · Fz

, в результате получим

emax = ξB · (2 ​​· a − ξB) 2 · a · θ

.

Точка отрыва ξ _s (указана на рисунке 2.38), в которой адгезия становится скользящей, находится, принимая e _max равным выражению (2.76), что дает:

ξs = 2 · a · (1 − θ · ρ)

Следовательно, для ρ = 0 точка отрыва определяется как ξ _s = 2 a и полное контактная площадка находится в состоянии сцепления. При увеличении ρ точка отрыва ξ _с перемещается к значению ξ _с = 0, достигаемому при ρ = 1/ θ . Другими словами, параметр θ > 1 — это обратное полное скольжение, при котором скользит вся площадь контакта.Когда общее теоретическое скольжение превышает величину 1/ θ , шина остается в состоянии полного скольжения. В случае чистого скольжения эта ситуация достигается либо для

αm = | α | = arctan (1 / θ)

, либо для

κm = 1θ − 1, в случае движения (κ> 0)

κm = −1θ + 1, в случае торможения (κ <0)

В области сцепления напряжения сдвига следуют из прогибов (2.76):

τ¯adh = k · e¯ = k · ξB · ρ¯≡k · ξB · (ρxρy)

В области скольжения касательные напряжения подчиняются правилу Кулона, предполагая, что вектор напряжения сдвига имеет ту же ориентацию, что и теоретический вектор скольжения,

τ¯sliding = μ · σz (x) · ρ¯ ρ = k · emaxρ · (ρxρy) = kρ · ξB · (2 ​​· a − ξB) 2 · a · θ · (ρxρy)

Ясно, что для чистого скольжения вектор касательного напряжения и вектор скольжения будут иметь одинаковые ориентация.В случае комбинированного скольжения эти ориентации не будут идентичными, но разница небольшая.

С помощью этих выражений мы теперь можем получить выражения для контактных сил F _x и F _y , а также центровочного момента M _z по интегрируя (момент) касательные напряжения по площади контакта. Для вектора поперечной силы получаем

F¯shear [∫0ξsq¯adh (ξB) dξB + ∫ξs2 · aq¯sliding (ξB) dξB]

, а компоненты силы (поперечная и продольная сила) получаются из

(2.78) F¯shear = ρ¯ρ · F≡ρ¯ρ · Fx2 + Fy2

с F , как оказалось, определяется как

(2.79a) F = μ · Fz · [3 · θ · ρ − 3 · (Θ · ρ) 2+ (θ · ρ) 3] ρ <1 / θ

(2.79b) = μ · Fz; ρ≥1 / θ

где q¯adh и q¯sliding обозначают интегрированный сдвиг напряжение по ширине шины

(2,80) q¯ = (qxqy) = tirewidthτ¯.dy

Обратите внимание, что жесткость скольжения C _ρ (где ρ относится к поперечному или продольному скольжению ) находится путем линеаризации уравнений.(2.79a) и (2.79b) около ρ = 0:

Cρ = 4 · a2 · b · k

Выбор различной жесткости протектора в поперечном и продольном направлениях (без изотропной модели) позволяет получить разные значения для жесткость на поворотах и ​​продольном скольжении, как и ожидалось.

Продольная и поперечная силы показаны на рис. 2.39 для изменения скольжения тормоза и выбранных значений угла скольжения, где мы выбрали:

Рис. 2.39. F _x и F _y в зависимости от продольного скольжения, для переменного угла скольжения и нагрузки на колесо 4000 [Н], на основе модели физической щетки см.Уравнения. (2.79a) и (2.79b).

k = 2 × 10 ⁷ [Н / м ³ ]

b = 0,1 [м]

μ = 1.0

We select

Радиус шины без нагрузки R = 0,32 [м], и предположим, что радиус шины под нагрузкой R _l соответствует рисунку 2.5. Длина полуконтакта может быть приблизительно равна:

a = R2 − Rl2

или, исходя из радиального прогиба шины d

(2.81) a = 2 · R · d − d2≈2 · R · d = 2 · R · Fz / CFz

для жесткости шины C _Fz . Это выражение переоценивает длину контакта. Шина на рисунке 2.5 имеет жесткость C _Fz = 2,10 ⁵ [Н / м]. Полагая F _z = 4000 [Н], получаем a = 0,11 [м].

Обратите внимание, что рисунки 2.31 и 2.39 очень похожи, где результаты на рисунке 2.31 основаны на эмпирической модели Magic Formula и результатах на рисунке 2.39 основаны на простой модели кисти. Однако можно заметить два отличия. Продольная сила в соответствии с моделью щетки насыщается, не показывая типичного локального пика в характеристике продольной силы, с последующим уменьшением для большего скольжения κ . Следовательно, уровень насыщения тормоза или движущей силы достигается намного раньше и не изменяется за пределами этого значения скольжения. Неровности шины не учитываются в поперечной силе при малом угле скольжения.

На рисунках 2.40 и 2.41, мы показываем вид сверху отклонений щеток в случае чистой боковой скорости (Рисунок 2.40) и комбинированного скольжения с фиксированным углом скольжения и увеличивающимся тормозным скольжением (Рисунок 2.41). Скольжение увеличивается от изображения вверху к изображению внизу этих фигур. На рисунке 2.40 ясно показано расширение области скольжения. Сначала большая часть отклонения щетки развивается линейно от передней кромки области контакта. При увеличении угла скольжения точка пересечения между областями скольжения и сцепления перемещается вперед, что означает, что область сцепления уменьшается, а область скольжения расширяется.

Рисунок 2.40. Отклонения щеток вдоль контактной поверхности для чистого бокового скольжения с увеличением угла скольжения.

Рисунок 2.41. Отклонения щеток по поверхности контакта для комбинированного скольжения с увеличивающимся тормозным скольжением и фиксированным углом скольжения.

На Рисунке 2.41 боковые отклонения щеток уменьшаются в размере, когда увеличивается проскальзывание тормозов. Из-за этого проскальзывания тормоза происходит значительное отклонение в плоскости, которое невозможно увидеть в проекции сверху вниз. В то же время наблюдается изменение ориентации щеточных элементов с чисто бокового на отклонение назад.Элементы протектора, входящие в зону контакта, растягиваются из-за силы контакта тормоза, как описано в разделе 2.4.1. Явление, показанное на рис. 2.41, согласуется с общими физическими соображениями в разделе 2.4.1. Наконец, при увеличении тормозного скольжения увеличивается общее скольжение и скольжение, как показано на Рисунке 2.41. Вид сбоку для чистого продольного скольжения (торможения) показан на рисунке 2.42. Вертикальные щетки остаются вертикальными на передней кромке, при этом основание движется назад вдоль области контакта, и это отклонение исчезает на задней кромке области контакта.

Рисунок 2.42. Удалите отклонения щеток вдоль контактной поверхности для чистого скольжения тормоза.

Так же, как и для поперечных сил, получаем выражение в замкнутой форме для центрирующего момента M _z :

Mz = −∫02 · aqy (ξB) · (a − ξB) dξB =

(2,82) = — ρyρ · μ · Fz · a · [θρ − 3 · (θρ) 2 + 3 · (θρ) 3− (θρ) 4]; ρ <1 / θ

В случае ρ ≥1 / θ , M _z исчезнет. Обратите внимание, что это может быть результатом увеличения угла скольжения α или увеличения скольжения тормоза или привода | κ |.Пневматический след следует из отношения F _y и — M _z :

(2.83a) tp = 13 · a · 1−3 · θ · ρ + 3 · ( θ · ρ) 2− (θ · ρ) 31 − θ · ρ + 13 · (θ · ρ) 2; ρ <1 / θ

(2.83b) = 0; ρ≥1 / θ

Выравнивающий момент и Пневматический след в зависимости от угла скольжения показан на рисунке 2.43 для тех же значений сцепления с дорогой и параметров модели, которые были выбраны ранее. Нагрузка на колесо варьировалась от 1000 до 5000 [Н].

Рисунок 2.43.Согласование крутящего момента и пневматического следа в зависимости от угла скольжения в случае чистого скольжения для различных колесных нагрузок на основе физической модели щетки, см. Уравнения. (2.82), (2.83a) и (2.83b).

Центрирующий момент достигает пика при α = arctan (1 / (4 · θ )), после чего он уменьшается в абсолютном размере до нуля при α = arctan (1/ θ ). Центрирующий момент не меняет знак с увеличением угла скольжения в отличие от результатов, основанных на описании Magic Formula (см. Рисунки 2.24 и 2.28). Пневматический след представляет собой монотонную функцию в α , начиная с ненулевого наклона при α = 0. Он стремится к нулю, что достигается при α = arctan (1/ θ ). Его значение при исчезающем угле скольжения

tp → a3; α ↓ 0

меньше, чем обычно (около a /2), см. Также Ref. [32].

Мы завершаем этот раздел некоторыми замечаниями, касающимися влияния тормозной / приводной силы на выравнивающий момент и приближениями для комбинированной контактной силы скольжения в соответствии с формулой.(2.71).

Примечания

1.

Полярный график F _x по сравнению с F _y , как показано на рисунке 2.30 для эмпирической магической формулы, также может быть получен для физическая модель кисти. Поскольку силовые характеристики, основанные на модели кисти, насыщаются без затухания при большом скольжении, этот график в полярных координатах будет аналогичен графику на рис. 2.29. Мы определили этот полярный график для модели кисти для F _z = 4000 [N] (см. Рисунок 2.44). Когда мы строим график выравнивающего момента относительно F _x , выражение (2.82) приводит к графику, который является симметричным для F _x , в отличие от рисунка 2.33. Это можно исправить, добавив модели кисти простую гибкость каркаса. Это означает, что весь каркас прикреплен к выступающему центру колеса посредством пружин, действующих в поперечном и продольном направлениях с разными значениями жесткости. Так же, как в обсуждении на рисунке 2.33, результирующие прогибы каркаса будут способствовать центрирующему крутящему моменту, что приведет к потере симметрии, как показано на рис. 2.33. Мы ссылаемся на Ref. [32] для получения дополнительных сведений.

Рисунок 2.44. Полярная диаграмма F _x по сравнению с F _y для постоянного угла скольжения для F _z = 4000 [Н] и μ = 1,0 в зависимости от модели кисти.

2.

Комбинированные уравнения (2.79a) и (2.79b) показывают, что явное выражение контактной поперечной силы в зависимости от скольжения не меняется, если мы переходим от чистого скольжения к комбинированному. Единственное отличие состоит в том, что ρ равно α или — κ / (1+ κ ) в случае чистого бокового или продольного скольжения, или полному теоретическому скольжению согласно уравнению. (2,76). Это означает, что выражение (2.78) можно интерпретировать как

(Fx (ρx, ρy) Fy (ρx, ρy)) = (ρxρy) · Fpure (ρ) ρ

До сих пор мы обсуждали модель изотропной щетки.Предыдущее выражение было вдохновением для приближения (2.71), которое дало точные результаты, которых было достаточно во многих случаях, особенно если целью является качественный анализ (тенденции, чувствительность).

Измерение продольной силы в непрерывном сварном рельсе с помощью двунаправленных тензодатчиков FBG

С конца 1920-х годов, когда в Германии началась прокладка длинномерных сварных рельсов, общая длина непрерывных сварных рельсов (CWR) уже превысила 500000 км .С ускорением глобальной модернизации железных дорог общий пробег CWR продолжает расти с огромной скоростью. Усиление путевой структуры снижает вероятность дефектов в CWR (таких как поломка рельсов, коробление рельсов и другие проблемы с прочностью и устойчивостью). Однако, если CWR находится в зонах с большим перепадом температур, малыми радиусами или большими пролетами мостов, продольная сила значительно возрастет из-за увеличенного диапазона изменения температуры рельсов и усиленного взаимодействия между путями и мостами.Кроме того, температура без напряжения CWR изменяется неравномерно и нелинейно, что дополнительно увеличивает продольную силу после длительного времени работы. Кроме того, повышенная сила может привести к деформации продольного изгиба, изгибу рельсов и поломке рельсов [1, 2]. Аварии со сходом с рельсов происходят каждый год из-за продольного изгиба или поломки рельсов, что наносит большой ущерб жизни и имуществу пассажиров [3–5]. Таким образом, мониторинг продольной силы в CWR необходим для научной оценки, управления и технического обслуживания CWR, а также для обеспечения безопасности движения железнодорожного транспорта.

Современные методы измерения продольной силы рельсов, широко известные, могут быть сгруппированы в энергетический метод [6–11], метод напряжения [12–14] и метод деформации по принципам измерения. Среди них метод деформации считается основным направлением исследований по мониторингу продольной силы рельсов из-за его простой конфигурации оборудования и возможности долгосрочного мониторинга. Самые популярные датчики делятся на две категории: тензодатчики сопротивления, основанные на принципе изменения сопротивления металла, и датчики FBG, основанные на оптическом принципе.Тензорезистор может вызвать дрейф нуля и увеличить погрешность измерения под долгосрочным воздействием температуры, влажности и солнечного света, поэтому его реже используют при долгосрочном мониторинге. Напротив, датчик FBG все чаще используется на железных дорогах за его способность противодействовать электромагнитным помехам, высокую точность, длительный срок службы и другие преимущества [15–21]. Предыдущие исследования в основном сосредоточены на применении датчика FBG для измерения динамического изменения соответствующих физических величин во время проезда транспортного средства, но применение датчика FBG для мониторинга продольной силы в CWR менее изучено.Ян и др. , Вэй и др. , Ли и др. подтвердили возможность установки системы счета осей с датчиком ВБР посредством теоретических, внутренних и полевых испытаний [22–24]. Там и др. , Юэн и др. , Лай и др. проводили мониторинг пути и транспортного средства в реальном времени на основе взаимосвязи между деформацией рельса и нагрузкой на рельс, когда транспортное средство движется по определенному участку рельса [25–27 ]. Эти два исследования зависят от мониторинга мгновенной деформации и сильно отличаются от долгосрочного мониторинга.Chung-Yue Wang и Weilai Li протестировали продольную силу рельса в зоне дыхания CWR с датчиком FBG на основе трехмерной модели пучка и метода калибровки деформации соответственно [28, 29]. Компания Xin DAI предоставила установку и конструкцию уплотнения для датчика FBG для контроля температурного усилия рельсов, относительного смещения многослойных конструкций и состояния закрытия стрелочного перевода, а также провела испытания на месте [30]. Вышеупомянутые анализы реализовали долгосрочный мониторинг, но принцип испытания не учитывал влияние разницы между коэффициентами теплового расширения датчика FBG и рельса и ограниченными условиями рельса на выходе датчика.Поэтому результаты испытаний и проверенные физические величины не были идентифицированы.

Таким образом, принцип измерения продольной силы CWR с датчиком FBG был выведен в статье путем учета влияния разницы между коэффициентами теплового расширения датчика FBG и рельса и ограниченных условий рельса на основе принципа двойного действия. метод направленной деформации. И этот принцип был проверен на месте, выбрав несколько контрольных точек на китайской высокоскоростной железнодорожной линии.Исследование обеспечивает теоретическую и тестовую поддержку для модернизации и продвижения методов испытаний на продольную силу CWR с датчиком FBG и может гарантировать эффективный контроль состояния для безопасности эксплуатации высокоскоростной железной дороги.

Продольная деформация рельса в фиксированной области CWR была ограничена, поэтому при изменении температуры рельса на Δ t (положительное значение для повышения температуры, отрицательное для падения температуры) может возникать определенная сила по отношению к температуре без напряжений.Это так называемая температурная сила CWR, которая может быть выражена как:

, где F _t , E, F и β обозначают температурную силу, модуль Юнга, площадь поперечного сечения. и коэффициент теплового расширения рельса соответственно. Модуль Юнга, площадь поперечного сечения и коэффициент теплового расширения рельса CHN60 приняты равными 2,1 × 10 ¹¹ Па, 77,45 × 10 ^–4 м ² и 1.18 × 10 ⁻⁵ / ° C соответственно. В уравнении (1) отрицательный знак указывает, что сила растяжения положительна, а сила сжатия отрицательна. Так как продольная деформация рельса ограничена, но рельс свободен в вертикальном направлении. Вертикальная деформация может возникать в рельсе из-за зависимости напряжения от деформации, выражаемой как ( μ + 1) β Δ t , коэффициент страсти рельса, принимаемый равным 0,3.

Для CWR на мосту продольная сила рельса может состоять из температурной силы и дополнительной силы, вызванной взаимодействием рельсов с мостом.Учитывая, что продольная деформация, вызванная дополнительной силой, составляет _f , дополнительная сила будет EF _f , а соответствующая вертикальная деформация рельса будет — μ _f . В фиксированной зоне CWR на мосту продольная деформация рельса _x = _f , вертикальная деформация _y = ( μ + 1) β Δ t — μ _f и продольная сила рельса является суммой температурной силы и дополнительной силы

Как видно из уравнения (2), продольную силу в CWR можно определить путем измерения напрягайте как минимум в двух направлениях.Таким образом, уравнение (2) отражает основной принцип измерения продольной силы в CWR методом двунаправленной деформации.

Следовательно, при испытании продольной силы в CWR с датчиками FBG, два датчика, установленные перпендикулярно друг другу, будут использоваться для измерения продольной и вертикальной деформации рельса. Расположение датчиков показано на рисунке 1, что также применимо к полевым испытаниям.

Увеличить Уменьшить Сбросить размер изображения

Рисунок 1. Схема расположения датчиков ВБР.

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Суть принципа датчика FBG заключается в том, что изменение физических величин (температуры, деформации и т. Д.) Приведет к изменению центральной длины волны датчиков, которую можно измерить демодулятором, а затем вывести изменение физических величин на основе определенно соответствует между ними.

3.1. Δλ / λ датчика ВБР в свободном состоянии

Когда датчик ВБР в свободном состоянии, учитывая изменение температуры Δ T , изменение осевой деформации Δ , вызванное внешней силой, относительное значение изменения центральной длины волны датчика будет:

, где λ представляет центральную длину волны датчика FBG, Δ λ обозначает изменение центральной длины волны, K и K _T относятся к коэффициенту чувствительности к деформации и температуре коэффициент чувствительности соответственно.Влияние термооптического коэффициента ВБР ζ (показатель преломления изменяется с температурой) и коэффициента теплового расширения волокна (коэффициент теплового расширения = α ) на период решетки учитывается для коэффициента температурной чувствительности, K _T = ζ + α [31].

Когда датчик прикреплен к объекту в свободном состоянии, температура испытуемого образца изменяется медленно (Δ T ), а коэффициент теплового расширения испытуемого образца составляет α _r .Поскольку температура испытуемого образца изменяется медленно, можно считать, что температуры сенсора и испытуемого образца все время совпадают. В этом случае относительное изменение центральной длины волны датчика будет:

Физический смысл уравнения (4) заключается в том, что, когда коэффициенты теплового расширения испытуемого образца и датчика ВБР различны, состояние свободного расширения датчик несколько ограничен, проявляется деформацией ( α _r — α ) Δ T. Этот принцип подробно проиллюстрирован на рисунке 2.

Увеличить Уменьшить Сбросить размер изображения

Рисунок 2. Принципиальная схема (образец для испытаний в свободном направлении).

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

На рис. 2 (а) показано исходное состояние датчика ВБР, прикрепленного к исследуемому образцу. Рисунок 2 (b) показывает, что образец подвержен медленному изменению температуры Δ T , и температура датчика FBG изменяется соответственно Δ T .Принимая во внимание свободное расширение датчика ВБР и испытательного образца, соответствующие деформации будут равны α Δ T и α _r Δ T соответственно. Несмотря на разницу в коэффициентах теплового расширения между ними, деформации должны оставаться постоянными, чтобы возникла деформация, представленная заштрихованной областью на рисунке 2 (c). И, следовательно, две деформации становятся одинаковыми в конечном состоянии, как показано на рисунке 2 (d). Вычитание температурной деформации α Δ T из общей деформации α _r Δ T и подстановка результата в уравнение (3) дает (4).

3.2. Δλ / λ датчика FBG в ограниченном состоянии

Принцип в уравнении (4) основан на предположении, что испытуемый образец находится в свободном состоянии, что может считаться таким же, как рельс в вертикальном направлении. Поскольку рельс в CWR ограничен в продольном направлении, при изменении температуры рельса не возникает продольной деформации, и тогда относительное изменение центральной длины волны датчика будет:

, где — α Δ T представляет деформацию датчика которая удерживается относительно образца в исследуемом направлении.Принцип показан на рисунке 3.

Увеличить Уменьшить Сбросить размер изображения

Рис. 3. Принципиальная схема (направление испытуемого образца полностью ограничено).

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

На рис. 3 (а) показано исходное состояние датчика ВБР, прикрепленного к исследуемому образцу. На рис. 3 (b) показано, когда температура испытуемого образца изменяется постепенно (Δ T ), когда испытуемый образец полностью удерживается в направлении испытания датчика ВБР, в этом направлении нет деформации.Если предположить, что датчик может свободно перемещаться, его деформация будет α Δ T . Рисунок 3 (c) показывает, что деформация датчика в присоединенном положении должна соответствовать деформации испытательного образца, поэтому деформация изменяется — α Δ T по сравнению с показателем на рисунке 3 (b). На рисунке 3 (d) показано конечное состояние, когда деформация испытуемого образца становится равной нулю, деформация сенсора ограничивается, что выражается влиянием на деформацию сенсора под действием внешней силы, т.е.е. K (- α ) Δ T в уравнении (4). Однако изменения температуры Δ T датчика FBG могут по-прежнему влиять на изменение показателя преломления, что приводит к изменению центральной длины волны. Таким образом, коэффициент ζ Δ T также в определенной степени включен в уравнение (4).

3.3. Принцип испытания продольной силы рельса

На основе вышеуказанного метода и принципа измерения, когда для датчика ВБР принята схема испытаний, показанная на рис. продольное и вертикальное направления могут быть выражены следующим образом:

Вычитание уравнения (7) из (6) дает:

Комбинация уравнений (2) и (8) дает продольную силу рельса:

где, F _z — точное измерение продольной силы рельса без учета погрешности измерения.Поскольку коэффициент теплового расширения датчика FBG составляет около 10 ^-7 / ° C, α Δ t в уравнении (9) можно игнорировать в фактических расчетах, и тогда фактический принцип испытания может быть изменен на:

Как видно из уравнения (10), ошибка измерения F _w неизбежна при измерении продольной силы рельса с помощью FBG, которая в основном вызвана сдерживаемой продольной деформацией рельса.

Уравнение (10) также показывает, что коэффициент деформационной чувствительности K датчика FBG больше всего влияет на результат теста.Уравнение (9) является выводом, сделанным в предположении, что параметры двух датчиков в одной контрольной точке согласованы. Датчик ВБР работает на основе теории распространения света, поэтому несколько датчиков, соединенных последовательно одним оптическим волокном, могут работать одновременно. Но эти датчики должны различаться по центральной длине волны, чтобы облегчить идентификацию демодулятором. Для датчиков, различающихся центральной длиной волны, их коэффициенты чувствительности к деформации также могут различаться, даже если они изготовлены из одного и того же материала.Поскольку на коэффициенты также могут легко повлиять ошибки при изготовлении, калибровке или другом аспекте. Следовательно, влияние разницы в коэффициенте чувствительности к деформации на результат испытания необходимо в принципе проанализировать. Предположим, что коэффициент чувствительности к деформации вертикального датчика ( K ₂ ) составляет n раз больше, чем у продольного датчика ( K ₁ ), то есть K ₂ = n K ₁ = n K , поэтому:

Подставляя уравнение (11) в (10), получаем:

Сравнивая уравнения (12) и (10), получаем:

Это видно из уравнения (13) что ошибка измерения, вызванная разницей в коэффициенте чувствительности к деформации между двумя датчиками, связана не только с действительной продольной силой, но и с отношением двух коэффициентов чувствительности к деформации.Учитывая, что погрешность измерения, не превышающая 5% действительной продольной силы рельса, допустима, получаем:

Для рельса CHN60 n находится в пределах 0,78 ~ 1,22, как получено из уравнения (14). То есть, когда отношение коэффициентов чувствительности к деформации двух датчиков (продольно и вертикально установленных) находится в пределах 0,78 ~ 1,22, продольная сила может быть получена с помощью уравнения (10). Когда два датчика изготовлены из одного материала, отношение коэффициентов чувствительности к деформации будет равно отношению центральных длин волн для двух датчиков [32].Таким образом, чтобы минимизировать ошибку измерения на месте, длины волн двух датчиков в одной контрольной точке должны быть как можно ближе друг к другу.

4.1. Расположение контрольных точек на площадке

Метод испытания продольной силы в CWR, основанный на вышеупомянутом принципе испытания с датчиком FBG, был подтвержден полевыми испытаниями на станции высокоскоростной железной дороги Чэнду-Мяньян-Лешань в Китае. В ходе испытаний были выбраны две контрольные точки на земляном полотне, а не на мосту. Что касается контрольных точек на земляном полотне, теоретическую продольную силу рельса можно легко получить, и это очень поможет при сравнении измеренного значения и теоретического значения.Однако для контрольных точек на мосту продольная сила также может зависеть от взаимодействия путевого моста и моста, и фактическое теоретическое значение получить невозможно.

Рисунок 4 представляет собой схему полевых испытательных точек, где испытательная точка 1 находится на расстоянии более 150 м от перекрестной пятки стрелочного перевода станции CWR, контрольная точка 2 находится на расстоянии более 70 м от опоры ближайшего моста (32 м. просто поддерживаемый балочный мост), поэтому можно считать, что две контрольные точки расположены в фиксированной зоне пути CWR, что соответствует основным требованиям принципа испытаний.

Увеличить Уменьшить Сбросить размер изображения

Рис. 4. Расположение контрольных точек на месте.

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Поскольку теоретическая температурная нагрузка рельса на земляное полотно должна быть получена из уравнения (1), изменение температуры рельса должно быть измерено в контрольной точке 1.

4.2. Датчик FBG и контрольно-измерительные приборы

Как указано в подразделе 2.3, разница в центральных длинах волн двух датчиков ВБР, установленных в одной контрольной точке, должна быть как можно меньше, чтобы обеспечить согласованность их коэффициентов чувствительности к деформации. Таким образом, центральные длины волн датчиков в контрольной точке 1 были приняты равными 1554 нм и 1555 нм с соотношением между ними 0,999; и те, что в контрольной точке 2, были взяты как 1550 нм и 1551 нм с соотношением 0,999. Датчик температуры рельса — это независимый прибор с неограниченной центральной длиной волны. Тем не менее, его центральная длина волны должна отличаться от четырех вышеупомянутых, взятых как 1548 нм.

Дрейф центральных длин волн датчиков ВБР измерялся одноканальным запросчиком ВБР (SM130 от MOI Inc, США, макс. Частота дискретизации 100 Гц, точность 1 пм). Поскольку диапазон изменения температуры рельса и продольной силы рельса изменяются медленно и постоянно, частота дискретизации при испытании была установлена ​​на 0,5 Гц.

4.3. Калибровка коэффициента чувствительности датчика

Точность коэффициента деформационной чувствительности напрямую связана с точностью результатов испытаний.Коэффициент чувствительности к деформации обычно калибруется путем определения деформации методом нагружения. Этот метод калибровки довольно сложен и требует высокоточных динамометров. Однако процесс калибровки коэффициента температурной чувствительности намного проще и не требует дополнительных усилий к устройству. Итак, в этой статье был предложен новый метод калибровки коэффициента чувствительности к деформации путем калибровки коэффициента температурной чувствительности датчика, основанный на уравнениях (3) и (4).Этот метод состоит из трех шагов. Во-первых, коэффициент температурной чувствительности K _T = ζ + α калибруется путем исследования зависимости между Δ T и Δλ / λ с использованием волокна в свободном состоянии. Во-вторых, прикрепите датчик к объекту (например, к медной трубке, использованной в тесте) в свободном состоянии из материала, отличного от материала датчика, и с заданным коэффициентом теплового расширения. В-третьих, номинальный коэффициент температурной чувствительности K = K ( α _r — α ) + K _T калибруется так же, как на первом этапе, а затем K получается с помощью K и K _T как:

В общих условиях, порядок величины коэффициента теплового расширения датчика FBG составляет 10 ^-7 / ° C, что для обычного металл 10 ⁻⁵ / ° C, поэтому α датчика можно не учитывать при фактических расчетах.Специальная проверка данных будет предоставлена ​​во время обработки данных.

Коэффициенты температурной чувствительности датчиков (центральные длины волн 1554 и 1551 нм) в свободном состоянии были откалиброваны с результатами, показанными на рисунках 5 и 6.

Как видно из рисунков 5 и 6, коэффициенты температурной чувствительности два датчика: 7,69 × 10 ⁻⁶ / ° C и 7,71 × 10 ⁻⁶ / ° C соответственно. Это в основном связано с тем, что коэффициент температурной чувствительности решетки без покрытия определяется коэффициентом теплового расширения и термооптическим коэффициентом.Поскольку два датчика в основном изготовлены из одного и того же материала, два коэффициента температурной чувствительности также будут аналогичными, что согласуется с фактическими условиями.

Увеличить Уменьшить Сбросить размер изображения

Рис. 5. Результаты тестирования и подгонки (1554 нм).

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Увеличить Уменьшить Сбросить размер изображения

Рисунок 6. Результаты тестирования и подгонки (1551 нм).

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

На рисунках 7 и 8 показаны результаты калибровки коэффициента температурной чувствительности при присоединении датчиков ВБР с разными центральными длинами волн к медной трубке (коэффициент теплового расширения 1,95 × 10 ⁻⁵ / ° C).

Увеличить Уменьшить Сбросить размер изображения

Рисунок 7. Результаты тестирования и подгонки (1554 нм).

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Увеличить Уменьшить Сбросить размер изображения

Рис. 8. Результаты тестирования и подгонки (1551 нм).

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Коэффициенты чувствительности к деформации в контрольных точках 1 и 2 составляют 0,144 и 0,122 соответственно, полученные из приведенных выше результатов калибровки и уравнения (15).Результаты могут быть применены непосредственно к обработке данных, взятых из контрольных точек 1 и 2.

4.4. Процесс и результаты испытаний

Чтобы гарантировать постоянство деформаций датчика и рельса, поверхность рельса перед установкой датчика необходимо отшлифовать для удаления ржавчины. Затем датчики были закреплены на стенке рельса с помощью авиационного клея и защищены уплотнительной установкой от воздействия внешней среды в процессе эксплуатации. Во время установки продольный датчик крепился вдоль нейтральной оси рельса, вертикальный датчик держался вертикально к нейтральной оси в центральном положении, чтобы избежать влияния других нагрузок на результаты испытаний.Процесс установки на месте показан на рисунке 9.

Увеличить Уменьшить Сбросить размер изображения

Рисунок 9. Установка датчиков на месте.

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Работа по измерению началась с 9:30 утра в первый день и закончилась в 8:30 утра во второй день, продолжаясь около 23 часов, чтобы гарантировать целостность данных.

На рисунке 10 показаны результаты проверки температуры рельса; на рисунках 11 и 12 показаны результаты испытаний в контрольных точках 1 и 2.Для лучшего понимания оси x на рисунках 10–12 представляют время (с), ось и на рисунке 10 представляет изменение температуры рельса по сравнению с начальным значением, оси и на рисунках 11 и 12 представляют разницу между относительным изменением длин волн продольных и вертикальных датчиков в контрольных точках 1 и 2, то есть Δλ ₁ / λ ₁ –Δλ ₂ / λ ₂ .

Увеличить Уменьшить Сбросить размер изображения

Рисунок 10. Изменение температуры рельса.

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Увеличить Уменьшить Сбросить размер изображения

Рисунок 11. Результаты в контрольной точке 1.

Загрузить рисунок:

Стандартное изображение Изображение высокого разрешения

Увеличить Уменьшить Сбросить размер изображения

Рисунок 12. Результаты в контрольной точке 2.

Загрузить рисунок:

Стандартное изображение Изображение высокого разрешения

Вариация исходных данных на рисунках 10–12 — это текстовый шум, связанный с разрешающей способностью одноканального запросчика ВБР. Поскольку тест представляет собой квазистатический процесс, для сглаживания сигнала используется фильтр S-G, который может сделать форму и ширину сигнала неизменными при уменьшении шума.

5.1. Без взвешивания Коэффициент теплового расширения датчика

Коэффициент теплового расширения датчика намного меньше, чем у рельса, принятого в анализе за 0.Тенденцию изменения продольной силы в CWR можно получить из рисунка 10 и уравнения (1), как показано на рисунке 13. На рисунке 13 также есть две другие линии, представляющие продольную силу, полученную из рисунков 10, 11 и уравнения (10). . Поскольку CWR заблокирован перед началом теста, все значения измерений являются результатами относительно начального состояния теста.

Увеличить Уменьшить Сбросить размер изображения

Рисунок 13. Сравнение результатов испытаний.

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Рисунок 13 показывает, что результаты испытаний в контрольных точках 1 и 2 хорошо согласуются с теоретическими результатами с незначительной разницей. Максимальные перепады в контрольных точках 1 и 2 составляют 8,6 кН и 13,8 кН соответственно. Это различие может быть связано с двумя аспектами: (i) объективным аспектом, включая ошибки измерения температуры рельса и изменением длины волны, неравномерным распределением температуры рельса и различной чувствительностью двух датчиков в одной контрольной точке, и (ii) предметным аспектом, включая недостаточный учет коэффициента теплового расширения датчика и погрешности обработки данных при анализе данных.Тем не менее, с учетом правила испытаний и размера измерения, датчик FBG может получить точную продольную силу CWR и обосновать принцип измерения продольной силы CWR с помощью FBG и калибровки коэффициента чувствительности к деформации посредством калибровки коэффициента чувствительности к деформации FBG, как предложено. в газете.

Для дальнейшего обоснования принципа испытания результаты испытаний будут скорректированы с учетом коэффициента теплового расширения датчика.

5.2. Взвешивание коэффициента теплового расширения датчика

Поскольку датчик FBG имеет меньший коэффициент теплового расширения, чем рельс, измерение коэффициента теплового расширения датчика напрямую может быть довольно сложной задачей для измерительных приборов.Из-за ограничений лабораторных условий получить точное значение коэффициента может быть сложно. Как упоминалось в разделе 4.1, теория испытаний и метод калибровки были обоснованы, поэтому мы рассматриваем коэффициент теплового расширения датчика как неизвестный фактор в этом разделе и пытаемся получить его с помощью метода математического программирования, основанного на сравнении значений измерения и теоретические значения. Цели программирования и ограничения следующие:

, где F _zgi — теоретическое значение продольной силы рельса, полученное по уравнению (1).

Результаты для целей программирования при различных значениях коэффициента теплового расширения датчика FBG показаны на рисунке 14. На рисунке есть значение в контрольных точках 1 и 2 соответственно, которое может привести к минимальной функции программирования, из которых соответствующие коэффициенты теплового расширения составляют 0,781 × 10 ^-7 / ° C и 0,848 × 10 ^-7 / ° C соответственно. Эти два значения отличаются от коэффициента теплового расширения в нормальных условиях, так как ошибка, вызванная коэффициентом теплового расширения, не может быть отделена от ошибки, вызванной другими факторами во время программного расчета.Таким образом, уравнение (16) отражает результат, полученный путем объединения ошибок, вызванных другими причинами, и коэффициента теплового расширения. Поскольку ошибки в двух контрольных точках происходят из одних и тех же источников, результаты программирования в этих двух точках немного отличаются. Проведенный выше анализ также был оправдан.

Увеличить Уменьшить Сбросить размер изображения

Рис. 14. Результаты при различных значениях α .

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Из рисунка 14 видно, что, независимо от величины коэффициента теплового расширения, результаты в контрольной точке 1 ближе к теоретическому значению продольной силы по сравнению с результатами в контрольной точке 2. Это связано с тем, что температура рельса распределяется неравномерно в продольном направлении, и контрольная точка для температуры рельса находится ближе к контрольной точке 1.

Коэффициент теплового расширения, полученный с помощью метода программирования, можно использовать для калибровки измеренного значения.На рисунке 15 показано сравнение скорректированного значения и теоретического значения.

Увеличить Уменьшить Сбросить размер изображения

Рисунок 15. Сравнение результатов.

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

После калибровки максимальная разница между значениями, измеренными в контрольных точках 1 и 2, и теоретическими значениями составляет 7,5 кН и 10,9 кН соответственно.Она уменьшилась на 1,1 кН и 2,9 кН по сравнению с разницей до коррекции. Сравнивая рисунки 15 и 13, можно обнаружить, что корректировка значений измерения с учетом коэффициента теплового расширения датчика FBG может до некоторой степени уменьшить разницу между измеренным значением и теоретическим значением. Однако эта величина смягчения мало влияет на практическое применение. Следовательно, на практике коэффициентом теплового расширения датчика FBG можно пренебречь, а продольную силу CWR можно получить с помощью данных, собранных в контрольных точках.

Принцип испытания продольной силы CWR с FBG был предложен и исследован на основе метода двунаправленной деформации, который также был проверен на месте со следующими выводами:

• (1)

  При применении датчика FBG для измерения продольной силы CWR необходимо учитывать влияние различных ограниченных условий рельса в вертикальном и продольном направлениях на результаты испытаний. Кроме того, отношение коэффициентов чувствительности к деформации двух датчиков ВБР в одной контрольной точке должно быть в пределах 0.78 ~ 1,2 для ограничения относительной погрешности результатов испытаний в пределах 5%.

• (2)

  Был проанализирован принцип испытания датчика ВБР в различных ограниченных условиях в направлении испытания исследуемого образца. Принцип испытания продольной силы CWR был выведен и обоснован на месте.

• (3)

  На основе принципа испытания датчика ВБР в свободном состоянии испытуемого образца был предложен и проверен на месте метод определения коэффициента чувствительности к деформации путем двукратной калибровки коэффициента температурной чувствительности.

• (4)

  Принимая во внимание коэффициент теплового расширения датчика FBG, можно скорректировать результат испытания продольной силы рельса, чтобы уменьшить разницу между измеренным значением и теоретическим значением. Однако исправление мало что изменит. Таким образом, рекомендуется рассчитывать продольную силу в CWR непосредственно с данными, собранными в контрольных точках, не принимая во внимание коэффициент теплового расширения датчика FBG.

Авторы благодарят за финансовую поддержку Национального фонда естественных наук Китая (No.51425804, № U1234201, № 1334203, № 61475128 и № 51378439), Программа международного сотрудничества в области науки и технологий Китая (2014DFA11170), Фонд фундаментальных исследований для центральных университетов (2682014RC22) и Фонд докторских инноваций Юго-Запада Университет Цзяотун.

Оценка коэффициента трения дороги в различных дорожных условиях на основе динамики торможения автомобиля | Китайский журнал машиностроения

Расчет тормозного момента

Коэффициент продольного скольжения передних и задних колес можно описать как.

$$ \ lambda _ {\ text {f}} = \ frac {{V — \ omega _ {\ text {f}} R _ {\ omega}}} {V}, $$

(6)

$$ \ lambda _ {\ text {r}} = \ frac {{V — \ omega _ {\ text {r}} R _ {\ omega}}} {V}, $$

(7)

где λ _f и λ _r обозначает коэффициент продольного скольжения переднего и заднего колес соответственно, и производная которого по времени, соответственно, определяется выражением.

$$ \ dot {\ lambda} _ {\ text {f}} = \ frac {{\ dot {V} (1 — \ lambda _ {\ text {f}}) — \ dot {\ omega} _ { \ text {f}} R _ {\ omega}}} {V}, $$

(8)

$$ \ dot {\ lambda} _ {\ text {r}} = \ frac {{\ dot {V} (1 — \ lambda _ {\ text {r}}) — \ dot {\ omega} _ {\ текст {r}} R _ {\ omega}}} {V}. $$

(9)

Подставляя уравнения. (8), (9) в уравнение динамики транспортного средства, тогда

$$ \ dot {V} = f_ {2} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}), $

долл. США (10)

$$ \ dot {\ lambda} _ {\ text {f}} = \ frac {{f_ {2} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) (1 — \ lambda _ {\ text {f}}) — R _ {\ omega} f_ {3} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) + u _ {\ text {f}} }} {V}, $$

(11)

$$ \ dot {\ lambda} _ {\ text {r}} = \ frac {{f_ {2} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) (1 — \ lambda _ {\ text {r}}) — R _ {\ omega} f_ {4} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) + u _ {\ text {r}} }} {V}, $$

(12)

, где

$$ f_ {2} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) = — g \ frac {{\ mu (\ lambda _ {\ text {f}) }) m_ {1} + \ mu (\ lambda _ {\ text {r}}) m_ {2}}} {{m — \ mu (\ lambda _ {\ text {f}}) m_ {3} + \ mu (\ lambda _ {\ text {r}}) m_ {3}}}, $$

$$ f_ {3} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) = \ frac {1} {{2J _ {\ text {f}}}} (\ mu ( \ lambda _ {\ text {f}}) m_ {1} R _ {\ omega} g — \ mu (\ lambda _ {\ text {f}}) m_ {3} R _ {\ omega} f_ {2}), $

долл. США

$$ f_ {4} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) = \ frac {1} {{2J _ {\ text {r}}}} (\ mu ( \ lambda_ {r}) m_ {2} R _ {\ omega} g + \ mu (\ lambda _ {\ text {r}}) m_ {3} R _ {\ omega} f_ {2}), $$

$$ u _ {\ text {f}} = \ frac {{T _ {\ text {bf}} R _ {\ omega}}} {{2J _ {\ text {f}}}}, \; \; \; \; u _ {\ text {r}} = \ frac {{T _ {\ text {br}} R _ {\ omega}}} {{2J _ {\ text {r}}}}.{+}, $$

(16)

$$ 0 \ le \ mu (\ lambda _ {\ text {f}}), \; \; \ mu (\ lambda _ {\ text {r}}) \ le 1, $$

(17)

где диапазон изменения f ₂ , ф ₃ и f ₄ может быть соответственно выражено как

$$ — g \ le f_ {2} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) \ le 0, $$

(18)

$$ 0 \ le f_ {3} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) \ le \ frac {{R _ {\ omega} g}} {{2J _ {\ text {f}}}} (m_ {1} ^ {+} + m_ {3} ^ {+}), $$

(19)

$$ \ hbox {min} \ left [{\ frac {{R _ {\ omega} g}} {{2J _ {\ text {r}}}}} (m_ {2} ^ {-} — m_ {3} ^ {+}), 0} \ right] \ le f_ {4} \ le \ frac {{R _ {\ omega} g}} {{2J _ {\ text {r}}}} m_ {2} ^ {+ }.{+}} \ right \}. $$

(26)

Определите разницу между фактическим и заданным коэффициентом скольжения передних и задних колес как поверхность переключения режима скольжения. Уравнения можно описать как

$$ S_ {1} = \ tilde {\ lambda} _ {\ text {f}} = \ lambda _ {\ text {f}} — \ lambda _ {\ text {fd}}, $

(27)

$$ S_ {2} = \ tilde {\ lambda} _ {\ text {r}} = \ lambda _ {\ text {r}} — \ lambda _ {\ text {rd}}, $$

(28)

где λ _f и λ _r обозначает фактический коэффициент скольжения передних и задних колес соответственно, λ _fd и λ _rd обозначает целевой коэффициент скольжения передних и задних колес соответственно.Чтобы достичь эквивалентного управляющего момента, производная формул. (27), (28) относительно времени соответственно даются как

$$ T _ {{{\ text {eq}}. {\ text {bf}}}} = \ frac {{2J _ {\ text {f}}}} {{R _ {{{\ omega}}}}}} \ left [{\ dot {\ lambda} _ {\ текст {fd}} V — \ hat {f} _ {2} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) (1 — \ lambda _ {\ text {f}}) + R _ {{{\ omega}}} \ hat {f} _ {3} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}})} \ right], $$

(29)

$$ T _ {{{\ text {eq}}.{\ text {br}}}} = \ frac {{2J _ {\ text {r}}}} {{R _ {{{\ omega}}}}}} \ left [{\ dot {\ lambda} _ {\ текст {rd}} V — \ hat {f} _ {2} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) (1 — \ lambda _ {\ text {r}}) + R _ {{{\ omega}}} \ hat {f} _ {4} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}})} \ right], $$

(30)

Тормозной момент передних и задних колес равен

$$ T _ {\ text {b}} = T _ {{{\ text {eq}}. {\ text {b}}}} — k \ text {sgn} (S). $$

(31)

По условиям доступности коммутационной поверхности должно выполняться неравенство:

Идеальный тормозной момент передних и задних колес определяется как

$$ T _ {\ text {bf}} = \ frac {{2J _ {\ text {f}}}} {{R _ {{{\ omega}} }}} \ left [\ begin {align} & \ dot {\ lambda} _ {\ text {fd}} V — \ hat {f} _ {2} (\ lambda _ {\ text {f}}, \ lambda_ {\ text {r}}) (1 — \ lambda _ {\ text {f}}) + R _ {{{\ omega}}} \ hat {f} _ {3} (\ lambda _ {\ text {f}} , \ lambda _ {\ text {r}}) \\ & — (F _ {\ text {f}} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) + \ eta_ {1 }) \ text {sgn} (S_ {1}) \\ \ end {align} \ right], $$

(33)

$$ T _ {\ text {br}} = \ frac {{2J _ {\ text {r}}}} {{R _ {{{\ omega}}}}} \ left [\ begin {align} & \ dot {\ lambda} _ {\ text {rd}} V — \ hat {f} _ {2} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) (1 — \ lambda_ { \ text {r}}) + R _ {{{\ omega}}} \ hat {f} _ {4} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) \\ & — (F _ {\ text {r}} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) + \ eta_ {2}) \ text {sgn} (S_ {2}) \ \ \ end {выровнено} \ right].$

(34)

соответственно

$$ F _ {\ text {f}} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) = F_ {2} (1 — \ lambda _ {\ text {f }}) + R _ {{\ omega}}} F_ {3}, $$

$$ F _ {\ text {r}} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) = F_ {2} (1 — \ lambda _ {\ text {r}}) + R _ {{{\ omega}}} F_ {4}, $$

, где η ₁ , η ₂ — положительные константы.

Устранение вибрации

Явление вибрации является одним из нежелательных эффектов управления скользящим режимом. Чтобы устранить явление дребезга при управлении в скользящем режиме, была введена насыщенная функция sat ( S / φ ), а контроллер скользящего режима был переработан с использованием интегральной переключающей поверхности, чтобы сделать закон управления плавным [24]. Определение интегральной поверхности переключения как

$$ S_ {1} = \ lambda _ {\ text {f}} — \ lambda _ {\ text {fd}} + \ xi_ {1} \ int {(\ lambda _ {\ text {f }} — \ lambda _ {\ text {fd}}}) {\ text {d}} t, $$

(35)

$$ S_ {2} = \ lambda _ {\ text {r}} — \ lambda _ {\ text {rd}} + \ xi_ {2} \ int {(\ lambda _ {\ text {r}} — \ lambda_ { \ text {rd}}}) {\ text {d}} t, $$

(36)

где ξ ₁ и ξ ₂ — постоянные.

Используя метод интегральной переключающей поверхности, идеальный тормозной момент передних и задних колес, соответственно, определяется как

$$ \ begin {align} T _ {\ text {bf}} = \ hfill \\ \; \ ; \; \; \ frac {{2J _ {\ text {f}}}} {{R _ {{{\ omega}}}}} \ left [\ begin {align} & (\ dot {\ lambda} _ { \ text {fd}} — \ xi_ {1} \ tilde {\ lambda} _ {\ text {f}}) V — \ hat {f} _ {2} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) (1 — \ lambda _ {\ text {f}}) + R _ {{{\ omega}}} \ hat {f} _ {3} (\ lambda _ {\ text {f} }, \ lambda _ {\ text {r}}) \ hfill \\ & — (F _ {\ text {f}} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) + \ eta_ {1}) \ text {sat} \ left ({\ frac {{\ tilde {\ lambda} _ {\ text {f}} + \ xi_ {1} \ int {\ tilde {\ lambda} _ {\ текст {f}} {\ text {d}} t}}} {{\ varphi_ {1}}}} \ right) \ hfill \\ \ end {выровнен} \ right], \ hfill \\ \ end {выровнен } $$

(37)

$$ \ begin {align} T _ {\ text {br}} = \ hfill \\ \; \; \; \ frac {{2J _ {\ text {r}}}} {{R _ {{{\ omega} }}}} \ left [\ begin {align} & (\ dot {\ lambda} _ {\ text {rd}} — \ xi_ {2} \ tilde {\ lambda} _ {\ text {r}}) V — \ hat {f} _ {2} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) (1 — \ lambda _ {\ text {r}}) + R _ {{{\ omega}}} \ hat {f} _ {4} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) \\ & — (F _ {\ text {r}} (\ lambda_ {\ text {f}}, \ lambda _ {\ text {r}}) + \ eta_ {2}) \ text {sat} \ left ({\ frac {{\ tilde {\ lambda} _ {\ text {r }} + \ xi_ {2} \ int {\ tilde {\ lambda} _ {\ text {r}} {\ text {d}} t}}} {{\ varphi_ {2}}}} \ right) \ \ \ конец {выровнено} \ право], \ hfill \\ \ end {выровнено} $$

(38)

где φ ₁ и φ ₂ — постоянная, φ ₁ и φ ₂ — толщина пограничного слоя, которая варьируется, чтобы использовать полосу пропускания системы.Как получить значения представлены в Ref. [23].

Мы не можем найти эту страницу

(* {{l10n_strings.REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}} *

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{добавить в коллекцию.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.АВТОР}}

{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}

Механика материалов: комбинированное нагружение »Механика тонких конструкций

---

Сосуды высокого давления с тонкими стенками

Существует множество промышленных применений, для которых требуются конструкции с тонкими оболочками для хранения сжатых газов и жидкостей.Эти сосуды под давлением помогают хранить пропан, транспортировать нефть на нефтеперерабатывающие заводы и поддерживать надутость наших баскетбольных мячей. Наиболее распространенные формы, с которыми вы столкнетесь, включают цилиндрические сосуды и сферические давления . Используя простой статический баланс равновесных сил, мы можем сразу определить напряжения в этих конструкциях. Начнем с нормальных напряжений на поверхности цилиндрической оболочки. Поскольку он тонкий, нам нужно учитывать только напряжение на поверхности конструкции. Это предположение значительно упрощает математику и приводит только к прогнозируемому напряжению, которое примерно на 4% ниже фактического напряжения.Мы поговорим об этом предположении о напряжении плоскости более подробно в следующем уроке. Для поверхности цилиндра не имеет особого смысла думать о направлениях x и y , проще думать о продольной оси и окружной оси цилиндра. Напряжение в окружном направлении часто называют обручем напряжением — это такое же напряжение, которое вы чувствуете вокруг талии, когда затягиваете ремень.Нарисуем две схемы свободного тела, разрезав цилиндр пополам по длинной оси и по окружной оси.

Обозначим сигму ₁ как кольцевое напряжение и сигму ₂ как продольное напряжение. Баланс сил в направлениях x и y , частично определяемый умножением напряжения на соответствующую площадь t dy , дает следующие уравнения:

Из этих балансов сил мы можем легко найти для два главных напряжения :

В обоих случаях напряжение увеличивается линейно с увеличением внутреннего (или внешнего) давления и радиуса цилиндра и обратно пропорционально толщине оболочки.Мы можем применить тот же процесс к сферической оболочке. На приведенной ниже иллюстрации мы разрезали эту скорлупу пополам:

Вы заметите, что баланс сил выглядит так же, как продольное напряжение в цилиндрической оболочке выше. Поскольку он имеет сферическую форму, два главных напряжения такие же, как и продольное напряжение, указанное выше:

Комбинированная загрузка

На этих уроках мы рассмотрели множество различных способов создания нормальных и касательных напряжений в конструкциях — вытягивание / толкание, изгиб, скручивание, создание давления.Различные уравнения, описывающие эти напряжения, являются линейными , и это имеет очень важное последствие: эти напряжения можно просто сложить вместе, чтобы определить общее напряжение на объекте из-за принципа суперпозиции. Это дает нам мощные средства для расчета общего нормального напряжения и напряжения сдвига для сложных комбинированных нагрузок .

Следует помнить лишь о нескольких правилах:

1. Нормальные напряжения добавляются только к другим нормальным напряжениям, а напряжения сдвига сочетаются с напряжениями сдвига.
2. Напряжения складываются, если они направлены в одном направлении (например, сигма _x + сигма _x или сигма _y + сигма _y )

Вот полезная таблица нормальных напряжений и напряжений сдвига, которые мы обсуждали:

Вы заметите, что я оставил нижние индексы для релевантных напряжений, моментов и моментов областей. Самая трудная часть задач комбинированного нагружения — это определение направления напряжений в проблеме.Я не могу достаточно подчеркнуть этот момент: хорошая схема (а иногда и пара хороших чертежей) — самое важное, что вы можете сделать при настройке этих задач. Изгиб в нескольких направлениях, потому что множественные нормальные и поперечные силы очень сложно визуализировать. Вы никогда не пожалеете, что потратили время на то, чтобы нарисовать нагруженную конструкцию под разными углами. Здесь действительно нет другого нового контента, но это не значит, что проблемы, с которыми вы столкнетесь, будут тривиальными.Лучше всего увидеть несколько примеров того, как рассчитать напряжения в конструкциях при комбинированной нагрузке.

Сводка

В этом уроке мы представили напряжения, возникающие в результате давления, оказываемого на тонкостенные сосуды высокого давления . Мы сосредоточились на двух конструкциях: цилиндрической и сферической оболочках. Баланс сил для этих примеров дает основные напряжения, которые действуют в продольных и окружных направлениях на оболочки.Кроме того, мы суммировали все соответствующие нормальные и касательные напряжения, описанные в этом курсе. Все эти напряжения линейны и поэтому могут складываться в случае комбинированной нагрузки (например, изгиб тонкостенного сосуда высокого давления). Важно помнить, что нормальные напряжения складываются, а напряжения сдвига складываются. И только напряжений , действующих на в том же направлении , могут быть сложены вместе.

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта No.1454153. Любые мнения, выводы, заключения или рекомендации, выраженные в этом материале, принадлежат автору (авторам) и не обязательно отражают точку зрения Национального научного фонда.

Круг трения говорит вам, с чем могут справиться ваши шины; Вот как это работает

Ты на улице и один. Пересекая горизонт, вы видите восходящее солнце и один великолепный уголок за другим. Некоторые из них медленные, другие быстрые, с несколькими хорошими прямыми между ними.Давление в шинах проверено и отрегулировано. Двигатель прогрелся. Бензобак полный. Пришло время испытать экстаз от вождения.

Но погоди. Вы понимаете, как быстро вы действительно можете спуститься по этой эпической улице? Да, ваш автомобиль может замедляться с силой до 1 g и и с почти такой же силой поворачивать. Но он не может делать и то, и другое одновременно. Современные шины — это потрясающая технология, но даже у них есть ограничения. Все сводится к силам трения и векторной математике. Ваш автомобиль и шина вместе создают одну общую силу трения, но когда она применяется в двух разных направлениях одновременно, эта сила разделяется.Круг трения показывает, как он разделен, и дает вам возможность лучше использовать шины.

Круг трения — это буквально участок на графике, представляющий максимальное сцепление шины с дорогой как в поперечном (поворот влево или вправо), так и в продольном (торможение и ускорение). Обычно, хотя и по-разному, поворот вправо — это положительный боковой захват, а поворот влево — отрицательный боковой захват. Ускорение — положительное продольное сцепление, а торможение — отрицательное продольное сцепление. Наконец, поперечное ускорение или широтное ускорение находится справа / слева или по оси x, а продольное ускорение или длинное ускорение — по оси вверх / вниз или по оси y.

На диаграмме, которую вы видите выше, есть два «круга». Тот, что отмечен черным, представляет собой реальный круг и представляет собой теоретическое сцепление шины с дорогой при каждом сценарии торможения, ускорения и поворота. Красный представляет собой более реалистичное представление типичного уличного автомобиля, не относящегося к суперкарам, поскольку двигатель может разгонять транспортное средство только так быстро. Другими словами, ваш двигатель ограничен, а не покрыты шинами.

Из таблицы видно, что когда вы начинаете добавлять автомобилю силу поворота или поперечную силу, он теряет способность тормозить или ускоряться.Вы должны уравновесить два. Вот почему, если шина уже визжит в повороте, а вы нажимаете на тормоз, она начинает проявлять недостаточную поворачиваемость и меньше поворачивает. Шина просто не может действовать одновременно с обеими силами.

Допустим, вы входите в крутой поворот и на повороте замедляетесь. Согласно диаграмме, если вы поворачиваете с усилием 0,7 g , вы также можете тормозить с усилием 0,7 g . По мере того, как вы поворачиваете сильнее и приближаетесь к 1 g , ослабьте тормоза. Затем, когда вы выходите из поворота, давите на педаль газа и трогайтесь с места.Сделайте это правильно, и вы получите максимальную отдачу от шины и сможете поворачивать так быстро, как только способна машина.

Конечно, это относится и к гоночной трассе. И настоящие эксперты в управлении кругом трения обычно находятся на подиуме в конце. Чтобы узнать больше о том, как работает круг трения и как улучшить вождение, посмотрите видео ниже. А теперь иди и испытай экстаз!

Этот контент импортирован с YouTube. Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.

Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти больше информации об этом и подобном контенте на сайте piano.io.

1.4: Внутренние силы в балках и рамах

Глава 4

Внутренние силы в балках и рамах

4.1 Введение

Когда балка или рама подвергаются поперечным нагрузкам, возникают три возможных внутренних силы: нормальная или осевая сила, сила сдвига и изгибающий момент, как показано в секции k консоли на Рисунке 4.1. Чтобы предсказать поведение конструкций, необходимо знать величины этих сил. В этой главе учащийся узнает, как определить величину силы сдвига и изгибающего момента в любой части балки или рамы и как представить вычисленные значения в графической форме, которая называется «силой сдвига». и «диаграммы изгибающего момента». Диаграммы изгибающего момента и усилия сдвига неизмеримо помогают при проектировании, поскольку они показывают максимальные изгибающие моменты и усилия сдвига, необходимые для определения размеров элементов конструкции.

Рис. 4.1. Внутренние силы в балке.

4.2 Основные определения

4.2.1 Нормальная сила

Нормальная сила в любом сечении конструкции определяется как алгебраическая сумма осевых сил, действующих по обе стороны от сечения.

4.2.2 Сила сдвига

Сила сдвига (SF) определяется как алгебраическая сумма всех поперечных сил, действующих по обе стороны от секции балки или рамы. Фраза «с обеих сторон» важна, поскольку подразумевает, что в любом конкретном случае усилие сдвига можно получить, суммируя поперечные силы на левой стороне или на правой стороне сечения.

4.2.3 Изгибающий момент

Изгибающий момент (BM) определяется как алгебраическая сумма моментов всех сил, действующих по обе стороны от секции балки или рамы.

4.2.4 Диаграмма усилия сдвига

Это графическое представление изменения усилия сдвига на части или по всей длине балки или рамы. Как правило, диаграмма силы сдвига может быть нарисована выше или ниже центральной оси конструкции x , но при этом необходимо указать положительную или отрицательную силу сдвига.

4.2.5 Диаграмма изгибающего момента

Это графическое представление изменения изгибающего момента на сегменте или по всей длине балки или рамы. Обычно положительные изгибающие моменты изображаются над центральной осью конструкции x , а отрицательные изгибающие моменты — под этой осью.

4.3 Соглашение о знаках

4.3.1 Осевое усилие

Осевая сила считается положительной, если она стремится к расслоению стержня в рассматриваемом сечении.Такая сила считается растягивающей, в то время как элемент, как говорят, подвергается осевому растяжению. С другой стороны, осевое усилие считается отрицательным, если оно стремится раздавить элемент в рассматриваемом сечении. Такая сила считается сжимающей, в то время как элемент находится в осевом сжатии (см. Рис. 4.2a и рис. 4.2b).

4.3.2 Сила сдвига

Сила сдвига, которая имеет тенденцию перемещать левую часть секции вверх или правую сторону секции вниз, будет считаться положительной.Точно так же поперечная сила, которая имеет тенденцию перемещать левую сторону секции вниз или правую сторону вверх, будет считаться отрицательной поперечной силой (см. Рисунок 4.2c и Рисунок 4.2d).

4.3.3 Изгибающий момент

Изгибающий момент считается положительным, если он вызывает вогнутость вверх (провисание). Если изгибающий момент имеет тенденцию вызывать вогнутость вниз (коробление), это будет считаться отрицательным изгибающим моментом (см. Рисунок 4.2e и Рисунок 4.2f).

Рис.4.2. Соглашения о знаках для осевой силы, силы сдвига и изгибающего момента.

4.4 Связь между распределенной нагрузкой, усилием сдвига и изгибающим моментом

Для вывода соотношений между w, V и M рассмотрим свободно опертую балку, подверженную равномерно распределенной нагрузке по всей ее длине, как показано на рисунке 4.3. Пусть поперечная сила и изгибающий момент на участке, расположенном на расстоянии x от левой опоры, равны V и M соответственно, а на участке x + dx — V + dV и M + dM соответственно.Полная нагрузка, действующая через центр бесконечно малой длины, составляет wdx .

Рис. 4.3. Балка с простой опорой.

Для вычисления изгибающего момента на участке x + dx используйте следующее:

Уравнение 4.1 подразумевает, что первая производная изгибающего момента по расстоянию равна поперечной силе. Уравнение также предполагает, что наклон диаграммы моментов в определенной точке равен поперечной силе в этой же точке.Уравнение 4.1 предлагает следующее выражение:

Уравнение 4.2 утверждает, что изменение момента равно площади под диаграммой сдвига. Точно так же усилие сдвига на участке x + dx составляет:

V _{x + dx} = V — wdx

В + dV = В — wdx

или

Уравнение 4.3 означает, что первая производная силы сдвига по расстоянию равна интенсивности распределенной нагрузки. Уравнение 4.3 предлагает следующее выражение:

Уравнение 4.4 утверждает, что изменение поперечной силы равно площади под диаграммой нагрузки. Уравнения 4.1 и 4.3 предполагают следующее:

Уравнение 4.5 подразумевает, что вторая производная изгибающего момента по расстоянию равна интенсивности распределенной нагрузки.

Порядок расчета внутренних сил

• Нарисуйте схему свободного тела конструкции.

• Проверьте устойчивость и определенность конструкции. Если структура устойчивая и детерминированная, переходите к следующему этапу анализа.

• Определите неизвестные реакции, применяя условия равновесия.

• Проведите воображаемое сечение перпендикулярно нейтральной оси конструкции в точке, где необходимо определить внутренние силы.Пройденный раздел делит структуру на две части. Рассмотрим любую часть конструкции для расчета требуемых внутренних сил.

• Для расчета осевой силы определите сумму осевых сил на детали, рассматриваемой для анализа.

• Для вычисления силы сдвига и изгибающего момента сначала запишите функциональное выражение для этих внутренних сил для сегмента, на котором находится сечение, относительно расстояния x от начала координат.

• Вычислите основные значения силы сдвига и изгибающего момента на участке, где находится секция.

• Нарисуйте диаграмму осевого усилия, усилия сдвига и изгибающего момента для конструкции, принимая во внимание условные обозначения, обсуждаемые в разделе 4.3.

• Для консольных конструкций третий шаг можно пропустить, если рассматривать свободный конец конструкции как начальную отправную точку анализа.

Пример 4.1

Нарисуйте диаграммы силы сдвига и изгибающего момента для консольной балки, поддерживающей сосредоточенную нагрузку на свободном конце, как показано на рисунке 4.4а.

Рис. 4.4. Консольная балка.

Решение

Поддерживающие реакции. Сначала вычислите реакцию опоры. Поскольку опора на B является фиксированной, на этой опоре будут три реакции, а именно B _y , B _x и M _B , как показано на диаграмме свободного тела. на рисунке 4.4b. Применение условий равновесия предполагает следующее:

Сила сдвига (SF).

Функция сдвигающего усилия. Пусть x — это расстояние произвольного сечения от свободного конца консольной балки (рис. 4.4b). Сила сдвига в этом сечении из-за поперечных сил, действующих на сегмент балки слева от сечения (см. Рисунок 4.4e), составляет В = –5 k.

Знак минус указывает на отрицательную силу сдвига. Это связано с тем, что в соответствии с соглашением о знаках силы сдвига, направленная вниз поперечная сила слева от рассматриваемой секции вызовет отрицательную силу сдвига в этой секции.

Диаграмма усилия сдвига. Обратите внимание: поскольку сила сдвига постоянна, она должна быть одинаковой величины в любой точке балки. Как правило, диаграмма поперечной силы наносится выше или ниже линии, соответствующей нейтральной оси балки, но должен быть указан знак плюс, если это положительная сила сдвига, и знак минус, если это отрицательная сила сдвига, как показано на рисунке 4.4c.

Изгибающий момент (BM).

Функция изгибающего момента.По определению изгибающий момент в секции представляет собой сумму моментов всех сил, действующих по обе стороны секции. Таким образом, выражение для изгибающего момента силы 5 k на участке на расстоянии x от свободного конца консольной балки выглядит следующим образом:

Полученное выражение справедливо для всего луча (область 0 < x <3 фута). Отрицательный знак указывает на отрицательный момент, который на данный момент установлен из условного обозначения.Как видно на рис. 4.4f, момент, обусловленный силой 5 k, имеет тенденцию вызывать в сегменте балки на левой стороне сечения вогнутость вверх, что соответствует отрицательному изгибающему моменту согласно условию знаков. на изгибающий момент.

Диаграмма изгибающего момента. Поскольку функция изгибающего момента является линейной, диаграмма изгибающего момента представляет собой прямую линию. Таким образом, для построения диаграммы изгибающего момента достаточно использовать два основных значения изгибающих моментов, определенных при x = 0 футов и x = 3 фута.Как правило, диаграммы отрицательного изгибающего момента строятся под нейтральной осью балки, а диаграммы положительного изгибающего момента строятся над осью балки, как показано на рисунке 4.4d.

Пример 4.2

Изобразите диаграммы силы сдвига и изгибающего момента консольной балки, подверженной равномерно распределенной нагрузке по всей ее длине, как показано на рисунке 4.5a.

Рис. 4.5. Консольная балка.

Решение

Поддерживающие реакции.Сначала вычислите реакцию опоры. Поскольку опора на B является фиксированной, на этой опоре, возможно, будут три реакции, а именно B _y , B _x и M _B , как показано в свободном теле. диаграмма на рисунке 4.4b. Применение условий равновесия предполагает следующее:

Сила сдвига (SF).

Функция сдвигающего усилия. Пусть x — это расстояние произвольного сечения от свободного конца консольной балки, как показано на рисунке 4.5б. Сила сдвига всех сил, действующих на сегмент балки слева от сечения, как показано на рисунке 4.5e, определяется следующим образом:

Полученное выражение справедливо для всей балки. Отрицательный знак указывает на отрицательную силу сдвига, которая была установлена ​​из соглашения о знаках для силы сдвига. Выражение также показывает, что сила сдвига линейно зависит от длины балки.

Диаграмма усилия сдвига. Обратите внимание, что поскольку выражение для силы сдвига является линейным, его диаграмма будет состоять из прямых линий.Сила сдвига при x = 0 м и x = 5 м были определены и использованы для построения диаграммы силы сдвига, как показано на рисунке 4.5c. Как показано на диаграмме, сила сдвига изменяется от нуля на свободном конце балки до 100 кН на неподвижном конце. Вычисленную вертикальную реакцию B _y на опоре можно рассматривать как проверку точности анализа и диаграммы.

Изгибающий момент (BM).

Выражение изгибающего момента.Выражение для изгибающего момента на участке на расстоянии x от свободного конца консольной балки выглядит следующим образом:

Знак минус указывает на отрицательный момент, который был установлен из условного обозначения момента. Как видно на рис. 4.5f, момент, обусловленный распределенной нагрузкой, имеет тенденцию приводить к тому, что сегмент балки на левой стороне сечения демонстрирует вогнутость вверх, что соответствует отрицательному изгибающему моменту, согласно соглашению о знаках для изгибающий момент.

Диаграмма изгибающего момента. Поскольку функция изгибающего момента является параболической, диаграмма изгибающего момента представляет собой кривую. В дополнение к двум основным значениям изгибающего момента при x = 0 м и x = 5 м необходимо определить моменты в других промежуточных точках, чтобы правильно построить диаграмму изгибающего момента. Диаграмма изгибающего момента балки показана на рисунке 4.5d.

Пример 4.3

Изобразите диаграммы силы сдвига и изгибающего момента консольной балки, подверженной нагрузкам, показанным на рисунке 4.6а.

Рис. 4.6. Консольная балка.

Решение

Поддерживающие реакции. Схема балки со свободным телом показана на рис. 4.6b. Сначала вычислите реакции на опоре B . Применение условий равновесия предполагает следующее:

Функции сдвигающего усилия и изгибающего момента. Из-за неоднородности распределенной нагрузки в точке B и наличия сосредоточенной нагрузки в точке C три области описывают функции сдвига и момента для консольной балки.Функции и значения поперечной силы ( V ) и изгибающего момента ( M ) в секциях в трех областях на расстоянии x от свободного конца балки следующие:

Сегмент AB 0 < x <2 футов

В = −3 x

Когда x = 0, V = 0

Когда x = 1, В = −3 тысячи фунтов

Когда x = 2 фута, В = −6 тысяч фунтов

Когда x = 0, M = 0

Когда x = 1 фут, M = -1.5 кип. фут

Когда x = 2 фута, M = −6 тысяч фунтов. фут

Сегмент BC 2 фута < x <3 фута

В = −3 (2) = −6 тысяч фунтов

Когда x = 2 фута, M = −6 тысяч фунтов. фут

Когда x = 3 фута, M = −12 тысяч фунтов. фут

Сегмент CD 3 фута < x <4 фута

V = — (3) (2) — 10 = −16 тысяч фунтов

M = — (3) (2) ( x — 1) — 10 ( x — 3)

Когда x = 3 фута, M = −12 тысяч фунтов.фут

Когда x = 4 фута, M = −28 тысяч фунтов. фут

Вычисленное усилие сдвига можно частично проверить с помощью опорных реакций, показанных на диаграмме свободного тела на рис. 4.6b.

Диаграммы усилия сдвига и изгибающего момента. Расчетные значения силы сдвига и изгибающего момента показаны на рисунках 4.6c и 4.6d. Важно помнить, что всегда будет резкое изменение диаграммы силы сдвига при наличии сосредоточенной нагрузки в балке.Числовое значение изменения должно быть равно значению сосредоточенной нагрузки. Например, в точке C , где сосредоточенная нагрузка в 10 тысяч фунтов находится в балке, изменение поперечной силы на диаграмме поперечных сил составляет 16 k — 6k = 10 тысяч фунтов. Диаграмма изгибающего момента представляет собой кривую на участке AB и прямые линии на участках BC и CD .

Пример 4.4

Изобразите диаграммы силы сдвига и изгибающего момента для балки с выступом, подверженной нагрузкам, показанным на рисунке 4.7а.

Рис. 4.7. Балка с вылетом.

Решение

Поддерживающие реакции. Реакции опор показаны на схеме балки со свободным телом на рис. 4.7b. Они вычисляются с применением следующих условий равновесия:

Функции сдвига и изгибающего момента. Из-за сосредоточенной нагрузки в точке B и выступающей части CD рассматриваются три области для описания функций поперечной силы и изгибающего момента для выступающей балки.Выражение для этих функций в секциях внутри каждой области и основные значения в конечных точках каждой области следующие:

0 < x <3

В = 25 — 8 x

Когда x = 0, В = 25 тысяч фунтов

Если x = 3, В = 1 тысячу

Когда x = 0, M = 0

Когда x = 3, M = 39 тысяч фунтов.фут

3 < x <6

В = 25 — 14 — 8 x

Когда x = 3, В = −13 тысяч фунтов

Когда x = 6, В = −37 тысяч фунтов

М =

Когда x = 3, M = 39 k. фут

Когда x = 6, M = −36 тысяч фунтов. фут

0 < x <2

В = 10 + 8 x

Когда x = 0, В = 10 тысяч фунтов

Когда x = 2, В = 26 тысяч фунтов

М =

Когда x = 0, M = 0

Когда x = 2, M = −36 тысяч фунтов.фут

Диаграмма усилия сдвига и изгибающего момента. Определенная диаграмма силы сдвига и момента в конечных точках каждой области представлена ​​на рисунках 4.7c и 4.7d. Для точного построения кривой изгибающего момента иногда необходимо определить некоторые значения изгибающего момента в промежуточных точках, вставив некоторые расстояния внутри области в полученную функцию для этой области. Обратите внимание, что в месте сосредоточенных нагрузок и на опорах числовые значения изменения силы сдвига равны сосредоточенной нагрузке или реакции.

Пример 4.5

Нарисуйте диаграммы силы сдвига и изгибающего момента для балки с выступом, подверженной нагрузкам, показанным на рисунке 4.8a. Определите положение и величину максимального изгибающего момента.

Рис. 4.8. Балка с вылетом.

Решение

Поддерживающие реакции. Реакции на опорах балки показаны на диаграмме свободного тела на рис. 4.8b. Реакции рассчитываются с использованием следующих уравнений равновесия:

Функции сдвига и изгибающего момента.Из-за неоднородности оттенков распределенных нагрузок на опоре B для описания и функций момента рассматриваются две области x , как показано ниже:

0 < x <4

В =

Когда x = 0, V = 6,10 кН

Когда x = 2, V = 1,1 кН

Когда x = 4, V = −13,9 кН

М =

Когда x = 0, M = 0

Когда x = 2, M = 8.87 кН. м

Когда x = 4, M = −2,3 кН. м

0 < x <1,5

В = 2 x

Когда x = 0, V = 0

Когда x = 1,5, V = 3 кН

M = — (2) ( x )

Когда x = 0, M = 0

Когда x = 1,5 м, M = −2,3 кН. м

Диаграммы усилия сдвига и изгибающего момента.Расчетные значения силы сдвига и изгибающего момента показаны на рисунках 4.8c и 4.8d. Обратите внимание, что значения поперечной силы на опорах равны значениям опорных реакций. Также обратите внимание на диаграмму, что сдвиг в области AB, является кривой, а сдвиг в области BC является прямым, что соответствует параболической и линейной функциям, соответственно полученным для областей. Диаграммы изгибающего момента для обеих областей криволинейны.Кривая для области AB более глубокая, чем кривая для области BC . Это связано с тем, что полученная функция для области AB является кубической, а для области BC — параболической.

Положение и величина максимального изгибающего момента. Максимальный изгибающий момент возникает там, где сила сдвига равна нулю. Как показано на диаграмме усилия сдвига, максимальный изгибающий момент возникает в части AB . Приравнивая выражение для поперечной силы для этой части к нулю, можно сделать следующее:

Величину максимального изгибающего момента можно определить, положив x = 2.21 м в выражение для изгибающего момента для участка AB . Таким образом,

Пример 4.6

Нарисуйте диаграммы силы сдвига и изгибающего момента для составной балки, подверженной нагрузкам, показанным на рисунке 4.9a.

Рис. 4.9. Составная балка.

Решение

Схема свободного тела. Схема балки со свободным телом показана на рис. 4.9b.

Классификация строения. Составная балка имеет r = 4, м = 2 и f _i = 2.Поскольку 4 + 2 = 3 (2), структура статически определима.

Идентификация первичной и дополнительной структуры. Принципиальная схема взаимодействия элементов балки показана на рисунке 4.9c. Часть AC является первичной структурой, а часть CD — дополнительной структурой.

Анализ комплементарной структуры.

Поддержка реакции.

C _y = D _y = 25 кН, из-за симметрии нагрузки.

Сила сдвига и изгибающий момент.

0 < x <0,5

V = 25 кН

M = 25 x

Когда x = 0, M = 0

Когда x = 0,5, M = 12,5 кН. м

Анализ первичной структуры.

Поддерживающие реакции.

Отрицательный подразумевает реакцию на A действует вниз.

Функции поперечной силы и изгибающего момента.

0 < x <1

В = 25 + 14 x

Когда x = 0, V = 25 кН

Когда x = 1, V = 39 кН

М =

Когда x = 0, M = 0

Когда x = 1, M = −32 кН. м

0 < x <2

В = −2 — 14 x

Когда x = 0, V = −2 кН

Когда x = 2, V = −30 кН

М =

Когда x = 0, M = 0

Когда x = 2, M = −32 кН.м

Диаграммы усилия сдвига и изгибающего момента. Расчетные значения силы сдвига и изгибающего момента для основной и вспомогательной частей составной балки показаны на рисунках 4.9d и 4.9e.

Пример 4.7

Нарисуйте диаграммы силы сдвига и изгибающего момента для рамы, подверженной нагрузкам, показанным на рисунке 4.10a.

Рис. 4.10. Рамка.

Решение

Схема свободного тела. Схема балки со свободным телом показана на рисунке 4.10а.

Поддерживающие реакции. Реакции на опоре балки можно рассчитать следующим образом, рассматривая диаграмму свободного тела и используя уравнения равновесия:

Функции сдвига и изгибающего момента балки BC.

0 < x ₁ <3

В = 0

М = 0

3 < x ₂ <6

V = 20 кН

M = −20 ( x — 3)

Когда x = 3, M = 0

Когда x = 6, M = −60 кН.м

Обратите внимание, что расстояние x до секции в выражениях находится от правого конца балки.

Функции сдвига и изгибающего момента колонны AB.

0 < x ₃ <10

В

Когда x = 0, V = 0

Когда x = 10, V = 50 кН

М =

Когда x = 0, M = −60 кН.м

Когда x = 10, M = −226,67 кН. м

Обратите внимание, что расстояние x до секции на колонне находится от верхней части колонны и что аналогичный треугольник использовался для определения интенсивности треугольной нагрузки в секции колонны, как показано ниже:

Диаграммы усилия сдвига и изгибающего момента. Расчетные значения силы сдвига и изгибающего момента для рамы нанесены на график, как показано на рисунке 4.10c и рис. 4.10d.

Пример 4.8

Нарисуйте диаграммы силы сдвига и изгибающего момента для рамы, подверженной нагрузкам, показанным на рисунке 4.11a.

Рис. 4.11. Рамка.

Решение

Схема свободного тела. Схема балки со свободным телом показана на рис. 4.11b.

Поддерживающие реакции. Реакцию на опоры рамы можно рассчитать, рассматривая диаграмму свободного тела всей рамы и части рамы.Вертикальные реакции опор в точках A и E вычисляются с учетом равновесия всей рамы следующим образом:

Знак минус указывает, что A _y действует вниз, а не вверх, как предполагалось изначально.

С учетом равновесия детали CDE рамы горизонтальная реакция опоры в точке E определяется следующим образом:

Опять же, учитывая равновесие всего кадра, горизонтальная реакция на A может быть вычислена следующим образом:

Моменты сдвига и изгиба колонн каркаса.

Сила сдвига и изгибающий момент в столбце AB.

0 < x ₁ <10 футов

В = 13-2 x

Когда x = 0, В = 13 тысяч фунтов

Когда x = 10 футов, В = −7 тысяч фунтов

М =

Когда x = 0, M = 0

Если x = 10 футов, M = 30 тысяч фунтов. фут

Если x = 5 футов, M = 30 тысяч фунтов.фут

Сила сдвига и изгибающий момент в столбце ЕД.

0 < x ₂ <10 футов

В = 7 тысяч фунтов

M = 7 x

Когда x = 0, M = 0

Если x = 10 футов, M = 70 тысяч фунтов. фут

Моменты сдвига и изгиба балки каркаса.

Сила сдвига и изгибающий момент в балке BC .

0 < x ₃ <4 футов

В = −7.5 тысяч фунтов

M = −7,5 x + 13 (10) — 2 (10)

Когда x = 0, M = 30 тысяч фунтов фут

Когда x = 4 фута, M = 0

Сила сдвига и изгибающий момент в балке CD .

0 < x ₄ <4 футов

В = −17,5 тысяч фунтов

M = 17,5 x — 7 (10)

Когда x = 0, M = −70 тысяч фунтов.фут

Когда x = 4 фута, M = 0

Расчетные значения силы сдвига и изгибающего момента для рамы показаны на Рисунках 4.11c и 4.11d.

Краткое содержание главы

Внутренние силы в балках и рамах: Когда балка или рама подвергаются воздействию внешних поперечных сил и моментов, в элементе развиваются три внутренних силы, а именно нормальная сила ( Н, ) и поперечная сила ( V ). ) и изгибающий момент ( М ).Они показаны на следующем рисунке.

Нормальная сила : Нормальная сила в любом сечении балки может быть определена путем сложения горизонтальных нормальных сил, действующих с обеих сторон сечения. Если равнодействующая нормальной силы стремится переместиться в сторону сечения, это рассматривается как сжатие и обозначается как отрицательное. Однако, если он имеет тенденцию отходить от секции, это рассматривается как напряжение и обозначается как положительное.

Сила сдвига : Сила сдвига в любом сечении балки определяется как сумма всех поперечных сил, действующих по обе стороны от сечения.Ниже приведены условные обозначения, принятые для поперечных сил. Диаграмма, показывающая изменение поперечной силы вдоль балки, называется диаграммой поперечной силы.

Изгибающий момент : изгибающий момент в секции балки может быть определен путем суммирования момента всех сил, действующих по обе стороны секции. Условные обозначения для изгибающих моментов показаны ниже. Графическое изображение изгибающего момента, действующего на балку, называется диаграммой изгибающего момента.

Взаимосвязь между распределенной нагрузкой, поперечной силой и изгибающим моментом: Между распределенными нагрузками, поперечными силами и изгибающими моментами существует следующая взаимосвязь.

Практические задачи

4.1. Нарисуйте диаграммы силы сдвига и изгибающего момента для балок, показанных на рисунках с P4.1 по P4.11.

Рис. P4.1. Луч.

Рис. P4.2. Луч.

Рис.P4.3. Луч.

Рис. P4.4. Луч.

Рис. P4.5. Луч.

Рис. P4.6. Луч.

Рис. P4.7. Луч.

Рис. P4.8. Луч.

Рис. P4.9. Луч.

Рис. P4.10. Луч.

Рис. P4.11. Луч.

4.2. Нарисуйте диаграммы силы сдвига и изгибающего момента для рам, показанных на рисунках с P4.12 по P4.19.

Рис. P4.12. Рамка.

Рис. P4.13. Рамка.

Рис. P4.14. Рамка.

Рис. P4.15. Рамка.

Рис. P4.16. Рамка.

Рис. P4.17. Рамка.

Рис. P4.18. Рамка.

Рис. P4.19. Рамка.

.