Эпюра моментов отображает: Построение эпюр поперечных сил и изгибающих моментов

Содержание

Построение эпюр поперечных сил и изгибающих моментов

8 (6год)

Построение эпюр поперечных сил и изгибающих моментов.

1. Цель работы.

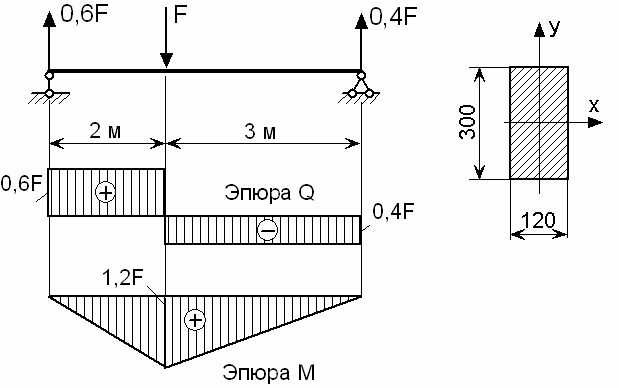
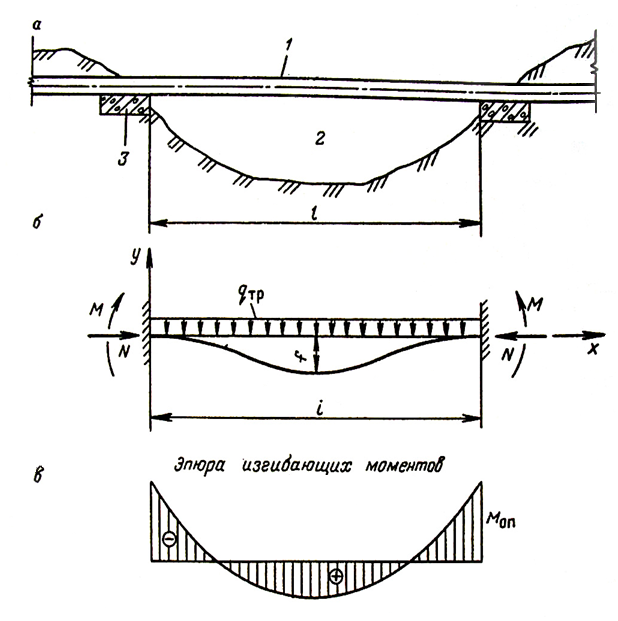
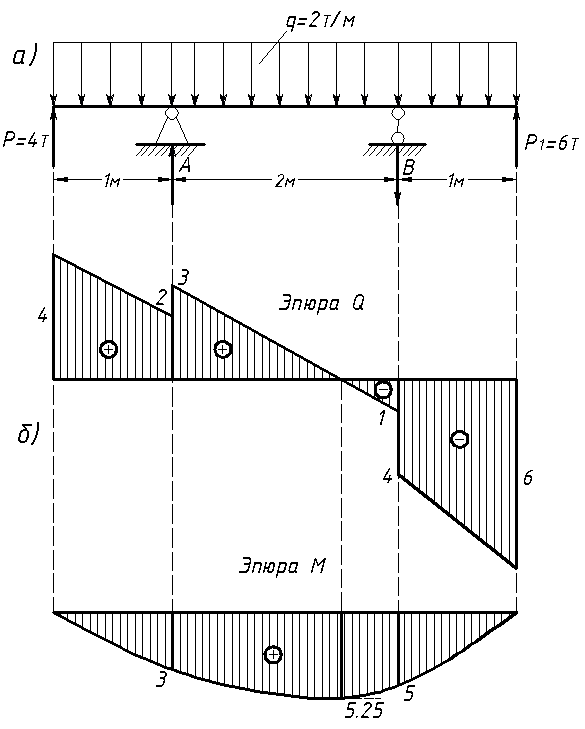
2. Типовые задачи: Задача. Для заданной консольной балки (рис. 1.) Построить эпюры поперечных сил и изгибающих моментов.

Решения.

1. Для построения эпюр делим балку на участки по характерным точкам О, В, С, Д (рис. 1а). Построение эпюр начинаем со свободного конца балки, что позволяет не определять опорные реакции.

2. Определяем величины поперечных сил в характерных сечениях. На свободном конце балки (в точке О) приложена сосредоточенная сила F. Поперечная сила в этой точке слева равна

Q0лив =-F =-20kH.

Это значение сохраняется по всей длине участка ОВ. Поперечная сила в точке В

Qв =-F =-20kH.

Наличие сосредоточенной пары сил в точке В на эпюре Qy не отображается. На участке ВС действует распределенная нагрузка и поперечная сила изменяется по линейному закону.

Для построения этой части эпюры надо знать два значения Qy. Одно из них известно Qb = 20 кН. Определяем Qy в сечении С как сумму сил, приложенных к балке справа от этого сечения

Qc =-F + q х CB = -20 + 5х 6 = 10 кН.

В сечении D Qy равна

Qd = — F + qхCB = -20 + 5х6 = 10кН.

По полученным результатам строим ЭпюруПоперечных сил (рис.1. б).

3. Строим эпюру изгибающих моментов.

На свободном конце балки МХО = 0, так сосредоточенной пары сил в сечении О нет. На участке ОB изгибающий момент Мх меняется по линейному закону (Qyl = const). Определяем момент в сечении, бесконечно близком (справа) до точки В

Микроволновая nр = FхОB = 20х2 = 40кН.

В сечении В на эпюре Мх прыжок вниз соответствует моменту приложенной в этом сечении пары

Микроволновая лев = FхOB-М = 20 х 2 — 10 = 30 кНм.

На участке ВС момент изменяется по квадратичному закону. Эпюра обратная выпуклостью вверх, т. е. навстречу нагрузке. Итак, в сечении С изгибающий момент равен алгебраической сумме моментов от распределенной нагрузки q, момента М пары сил и сосредоточенной Силы F

На участке CD Mx изменяется по линейному закону. В сечении D имеем:

MxD = FхOD — M-qхCB (0.5CB + DC) = 20х10-10-5х6 (3 +2) = 40 кНм

Рис. 1.

На участке ВС эпюра Qy проходит через нуль (точка К), следовательно, эпюра Мх (парабола) имеет экстремальное значение — Мх мах.

Определяем абсциссу z сечения К, в котором Qy = 0, использовав сходство треугольников DСС1К и DКВВ1.

Итак, изгибающий момента сечении К будет

Эпюру изгибающих моментов изображены на рис.1в. Исходя из эпюры Мх наибольшее значение изгибающего момента — в точке К.

Мх мах = 70 кНм.

3.Вопросы для самоконтроля.

1. Что такое чистый и поперечный изгибы?

2. Какие напряжения возникают при деформации изгиба балок?

3. Что такое момент изгиба и поперечная сила?

4. Как определяются знаки моментов изгиба и поперечных сил?

5. Что такое эпюра моментов изгиба и поперечных сил?

6. Как строятся эпюры моментов изгиба и поперечных сил?

7. Что называется статическим моментом плоского сечения?

8. Как определить координаты центра тяжести с помощью статических моментов
Плоского сечения?

9. Что называется осевым, полярным и центробежным моментом инерции
Плоского сечения?

10. Что называется центральным осевым моментом инерции плоского
сечения?

11. Как вычислить осевой момент инерции плоского сечения относительно

Параллельной оси?

12. Чему равна осевой момент инерции прямоугольника, квадрата и круга,

И полярный момент инерции круга?

13. Как определить осевые моменты сопротивления плоского сечения?

14. Что называется кручением?

15. Расскажите о таких понятиях: крутящий и крутящий моменты, вал.

16. Как строятся эпюры крутящего момента?

17. Какие расчетные формулы при изгибе и крученые?

18. Как определяется диаметр вала, если на него действуют моменты изгиба и

Крутящий момент?

Сопротивление материалов.

Эпюры крутящих моментов.
Сопротивление материалов

Деформация кручения



Построение эпюр крутящих моментов

Для наглядного изображения распределения крутящих моментов вдоль оси бруса строят эпюры крутящих моментов — графическое отображение величины крутящих моментов на каждом участке бруса.

Крутящий момент в сечениях бруса определяется с помощью метода сечения. Так как равномерно вращающийся или неподвижный вал находится в равновесии, очевидно, что внутренние силы, возникающие в поперечном сечении, должны уравновешивать внешние моменты, действующие на рассматриваемую часть бруса. Отсюда следует, что крутящий момент в любом поперечном сечении численно равен алгебраической сумме внешних моментов, приложенных к брусу справа или слева от сечения.

Эпюры крутящих моментов дают возможность определить опасное сечение. В частности, если брус имеет постоянное поперечное сечение по всей длине, то опасными будут сечения на участке, где возникает наибольший крутящий момент.

Следует очень внимательно отнестись к определению знаков крутящего момента. Крутящий момент считается положительным, если при взгляде со стороны сечения результирующий момент внешних пар сил, приложенных к рассматриваемой части бруса, будет направлен против часовой стрелки, и наоборот (это положение условно и принимается для облегчения проверки расчетов, выполненных несколькими исполнителями).

Рассматривая величины крутящих моментов, действующих в каждом конкретном сечении бруса, полагаем, что в сечении, где приложен вращающий (скручивающий) момент, значения крутящего момента изменяются скачкообразно (принцип смягченных граничных условий).

***



Пример построения эпюры крутящих моментов

Силовая передача (трансмиссия), изображенная на рис. 2 состоит из вала, на котором размещены три шестерни — одна ведущая (А) и две ведомые (В и С).
К шестерням приложены вращающие моменты: РА= 300 Нм, РВ = 120 Нм, РС= 180 Нм.
Построим эпюру крутящих моментов для этой силовой передачи.

Решение

Очевидно, что свободные концы вала, (вращающиеся в подшипниках) не подвержены действию вращающих моментов, т. е. крутящие моменты на участках 1 и 4 равны нулю.

К шестерне А приложен вращающий момент 300 Н м, следовательно в сечении, расположенном под этой шестерней скачкообразно возникает крутящий момент, равный 300 Нм, и величина этого момента сохраняется неизменной по всем сечениям участка 2 (до шестерни В).

К шестерне В приложен вращающий момент 120 Нм, который направлен в противоположную сторону от ведущего скручивающего момента, приложенного к шестерне А. Следовательно крутящий момент на участке 3 будет равен разности крутящих моментов, приложенных к шестерням А и В. На эпюре это отобразится в виде ступени величиной 120 Нм, расположенной напротив сечения, где размещена шестерня В.
На всем протяжении участка 3 величина этого крутящего момента будет сохраняться неизменной, до сечения, расположенного под шестерней С.

К шестерне С приложен вращающий момент 180 Нм, направление которого противоположно моменту, приложенному к ведущей шестерне А, поэтому, начиная с сечения под шестерней С, крутящий момент будет равен разнице между скручивающим моментом шестерни А и моментами, приложенными к шестерням В и С, т. е.
МКРс = ТА — ТВ — ТС= 300 — 120 — 180 = 0 Нм, и величина этого момента будет распространяться на весь участок 4, расположенный за шестерней С.

Построив эпюру крутящих моментов, действующих в сечениях вала данной силовой передачи как показано на рис. 2, отмечаем, что максимальной величины — 300 Нм крутящий момент достигает на участке 2, т. е. этот участок и является критическим (наименее надежным).

Теперь попробуем изменить расположение шестерен на валу, разместив ведущую шестерню А между ведомыми шестернями В и С, как показано на рис. 3. Приложенные к шестерням вращающие моменты оставим без изменения и построим эпюру крутящих моментов для измененной конструкции (рис.

3).

Из полученной эпюры видно, что на участке 2 (между шестернями В и А) крутящий момент равен —120 Нм, на участке 3 — +180 Нм, а на участках 1 и 4 крутящие моменты равны нулю, как и в предыдущей конструкции. И если в рассмотренной ранее конструкции максимальный крутящий момент достигал 300 Нм, то теперь его величина снизилась до 180 Нм.
Рациональным размещением шестерен на валу силовой передачи мы смогли значительно уменьшить максимальный крутящий момент, возникающий в сечениях этого вала, повысив надежность передачи. При этом передаточные отношения и функционал самой передачи не изменились.

***

Материалы раздела «Деформация кручения»:

Основные гипотезы и допущения Сопромата


Главная страница


Дистанционное образование

Специальности

Учебные дисциплины

Олимпиады и тесты

3.

1. Эпюра изгибающего момента

Тогда с целью сокращения выходных результатов для КЭ без нагрузки в их пределах

в разделе Назначения [2 − 5] на инструментальной панели необходимо нажать кнопку «Назначение промежуточных сечений для расчета усилий». Откроется диалоговое окно «Вычисление усилий…..» (см. в программе SCAD справку к этому окну). В диалоговом окне на поле «количество сечений» вносится цифра 2. Далее надо закрыть окно и отметить конечные элементы на схеме стержневой системы, на которых ожидаются линейные эпюры M . Как это делается, показано в пособиях [2 − 5].

На рис. 3.2, 3.3 концевые сечения стержня обозначены узлами « н » и « к » МСК. После назначения для расчета усилий в отмеченных элементах только двух сечений, в программе SCAD в соответствующей таблице усилий [2 − 5] будут выдаваться значения изгибающих моментов M н (M1) и M к (M 2 ) только в узлах «н» (1) и «к» (2) (со своими

знаками в МСК).

При оцифровке ординат эпюры моментов, которая выполняется при нажатии кнопки

фильтра отображения, в пределах каждого конечного элемента из указанных двух моментов ( M1, M 2 ) приводится момент с максимальным значением.

Построение эпюры М на элементе стержня при действии по его длине равномерно распределенной нагрузки

Если по всей длине КЭ расположена равномерно распределенная нагрузка, то эпюра изгибающих моментов на нем будет иметь вид параболы с выпуклостью направленной в сторону действия нагрузки.

Примечание. В программе SCAD с помощью процедуры, которая только что была рассмотрена по назначению для вычисления изгибающих моментов только в двух сечениях КЭ, можно назначить вычисление моментов в ряде сечений между узлами « н » и « к » элемента в МСК.

Для приближенного построения параболы достаточно вычислить ординаты эпюры M в трех сечениях КЭ: в начале «н», в середине «с» и в конце «к». В результирующей таблице усилий программы SCAD эти сечения обозначены соответственно 1, 2, 3. В программе SCAD вычисление моментов в указанных сечениях может быть обеспечено по умолчанию. Однако, если по какой-то причине у расчетчика оказались известными только две ординаты эпюры M по концам элемента ( M н и M к), то можно легко вычислить

ординату M c в среднем сечении, применив принцип независимости действия сил.

Пример. Вырежем (по узлам «н» (1) и «к» (3) МСК) из стержневой системы элемент, загруженный равномерно распределенной нагрузкой интенсивностью q (рис. 3.4,а).

Рассмотрим его, как балку на двух опорах, под действием внутренних усилий по концам элемента и распределенной нагрузки (рис. 3.4,б). Добавление указанных трех опорных связей не влияет на усилия в элементе, так как в вырезанном состоянии он находится в равновесии, поэтому в добавленных связях усилия (реакции) будут нулевыми.

Изгибающий момент M c в среднем сечении элемента (см. рис. 3.4, б) можно вычислить как сумму средней ординаты (рис. 3.4, в) линейной эпюры моментов (линии

Построение эпюр поперечных сил изгибающих моментов: пример (сопромат)

Порядок построения эпюр поперечных сил и изгибающих моментов на примере балки (см. рис. 7.4).

Разобьем балку на 3 отдельных участка (рис. 7.7, а), границами которых являются точки приложения сосредоточенных усилий и точки, соответствующие началу и окончанию действия распределенной нагрузки. По границам выделенных участков наметим шесть поперечных сечений, в которых будем вычислять значения поперечных сил и изгибающих моментов.

Построение эпюр поперечных сил и изгибающих моментов

Определение поперечных сил и изгибающих моментов — сечение 1

Отбросим правую часть балки и заменим ее действие на левую часть поперечной силой и изгибающим моментом . Для удобства вычисления закроем отбрасываемую правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением 1.

Поперечная сила в сечении 1 балки равна алгебраической сумме всех внешних сил, которые видим после закрытия

Видим только реакцию опоры, направленную вниз. Таким образом, поперечная сила равна:

кН.

Знак «минус» нами взят потому, что сила вращает видимую нами часть балки относительно первого сечения против хода часовой стрелки (или потому, что одинаково направлена с направлением поперечной силы по правилу знаков)

Изгибающий момент в сечении 1 балки, равен алгебраической сумме моментов всех усилий, которые мы видим после закрытия отброшенной части балки, относительно рассматриваемого сечения 1.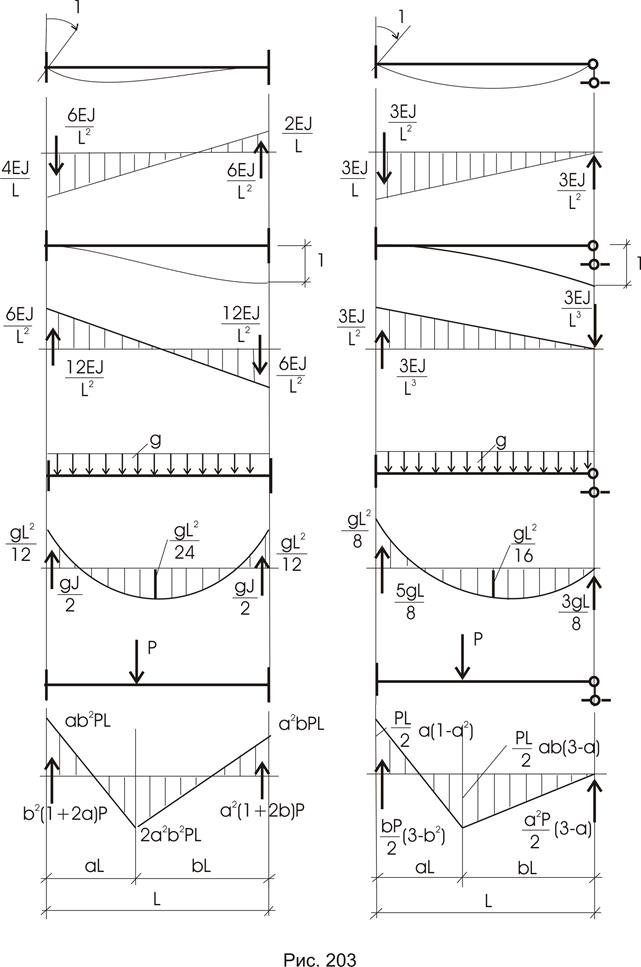

Видим два усилия: реакцию опоры и момент M. Однако у силы плечо практически равно нулю. Поэтому изгибающий момент равен:

кН·м.

Здесь знак «плюс» нами взят потому, что внешний момент M изгибает видимую нами часть балки выпуклостью вниз. (или потому, что противоположно направлен направлению изгибающего момента по правилу знаков)

Определение поперечных сил и изгибающих моментов — сечение 2

В отличие от первого сечения, у силы реакциипоявилось плечо, равное а.

поперечная сила:

кН;

изгибающий момент:

кН·м.

Определение поперечных сил и изгибающих моментов — сечение 3

поперечная сила:

кН;

изгибающий момент:

кН ·м.

Определение поперечных сил и изгибающих моментов — сечение 4

Теперь удобнее закрывать листком левую часть балки.

поперечная сила:

кН;

изгибающий момент:

кН ·м.

Определение поперечных сил и изгибающих моментов — сечение 5

поперечная сила:

кН;

изгибающий момент:

кН ·м.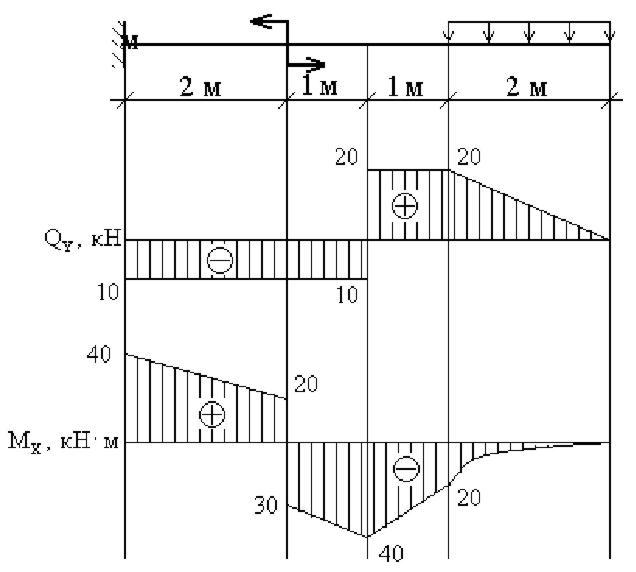

Определение поперечных сил и изгибающих моментов — сечение 1

поперечная сила и изгибающий момент:

.

По найденным значениям производим построение эпюры поперечных сил (рис. 7.7, б) и изгибающих моментов (рис. 7.7, в).

Контроль правильности построения эпюр

Убедимся в правильности построения эпюр по внешним признакам, пользуясь правилами построения эпюр.

Проверка эпюры поперечных сил

Убеждаемся: под незагруженными участками эпюра поперечных сил идет параллельно оси балки, а под распределенной нагрузкой q – по наклоненной вниз прямой. На эпюре продольной силы три скачка: под реакцией – вниз на 15 кН, под силой P – вниз на 20 кН и под реакцией – вверх на 75 кН.

Проверка эпюры изгибающих моментов

На эпюре изгибающих моментов видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой q эпюра изгибающих моментов изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре изгибающего момента – экстремум, поскольку эпюра поперечной силы в этом месте проходит через нулевое значение.

Solidworks simulation. Построение графиков балки — Cadregion.ru

Модель нагружена и ограничена, как показано:

lb — обозначение фунта (единица измерения массы)

В настоящем упражнении Вы изучите следующее:

· Создание исследования с сеткой балок

· Определение балок и соединений

· Приложение нагрузок и ограничений к балкам

· Создание сетки и запуск исследования сетки балок

· Просмотр графиков поперечных сил и момента

· Вывод списка усилий на балке

· Просмотр напряжения при изгибе

4.1. Открытие детали и создание исследования

1. Открыть файл примера Beam_Diagrams.SLDPRT (файл находится в папке C:\Program Files\SolidWorks Corp\SolidWorks\Simulation\Examples\Beams\).

2. Выберите новое исследование (Simulation CommandManager).

3. В PropertyManager:

a. Введите ShearMoment.

b. В окне Тип нажмите Статическое.

4. Нажмите кнопку .

5. В дереве исследования Simulation разверните папку Beam_Diagrams и:

a. Нажмите правой кнопкой мыши на SolidBody 1 и выберите Рассматривать как балку.

b. Нажмите правой кнопкой мыши на SolidBody 2 и выберите Рассматривать как балку.

6. Нажмите правой кнопкой мыши на параметр Группа соединений и выберите Редактировать.

7. В PropertyManager Редактировать соединения в разделе Выбранные балки нажмите Вычислить. Три соединения появятся в окне Результаты.

8. Нажмите кнопку .

Два значка балок отобразятся в папке Beam_Diagrams и папка Группа соединений появится в дереве исследования Simulation.

4.2. Применение материала

1. Нажмите правой кнопкой мыши папку Beam_Diagrams и выберите Применить материал ко всем телам .

2. Назначить Легированная сталь из библиотеки материалов SolidWorks.

 

4.
3. Определение соединений

Соединения определены на свободном конце балки и в каждом месте пересечения двух или более балок. Крепления применены только к соединениям.

Чтобы проверить соединения:

1. Нажмите правой кнопкой мыши папку Группа соединений и выберите Редактировать.

2. В PropertyManager (Менеджере свойств), три соединения появятся в окне Результаты.

3. Щелкните правой кнопкой мыши по одному из соединений в графической области для проверки вытянутых тел, образующих соединение. Элементы выделятся в графической области.

4. Нажмите кнопку .

 

4.4. Применение креплений

Добавить крепления к свободным концам балки на сочленениях. Один конец заделан шарнирно, а на другом конце ролик.

Чтобы смоделировать шарнир на конце A:

1. Нажмите правой кнопкой мыши папку Крепления и выберите Зафиксированная геометрия.

2. Измените ориентацию вида на * Изометрия, чтобы безошибочно выбрать правильные соединения.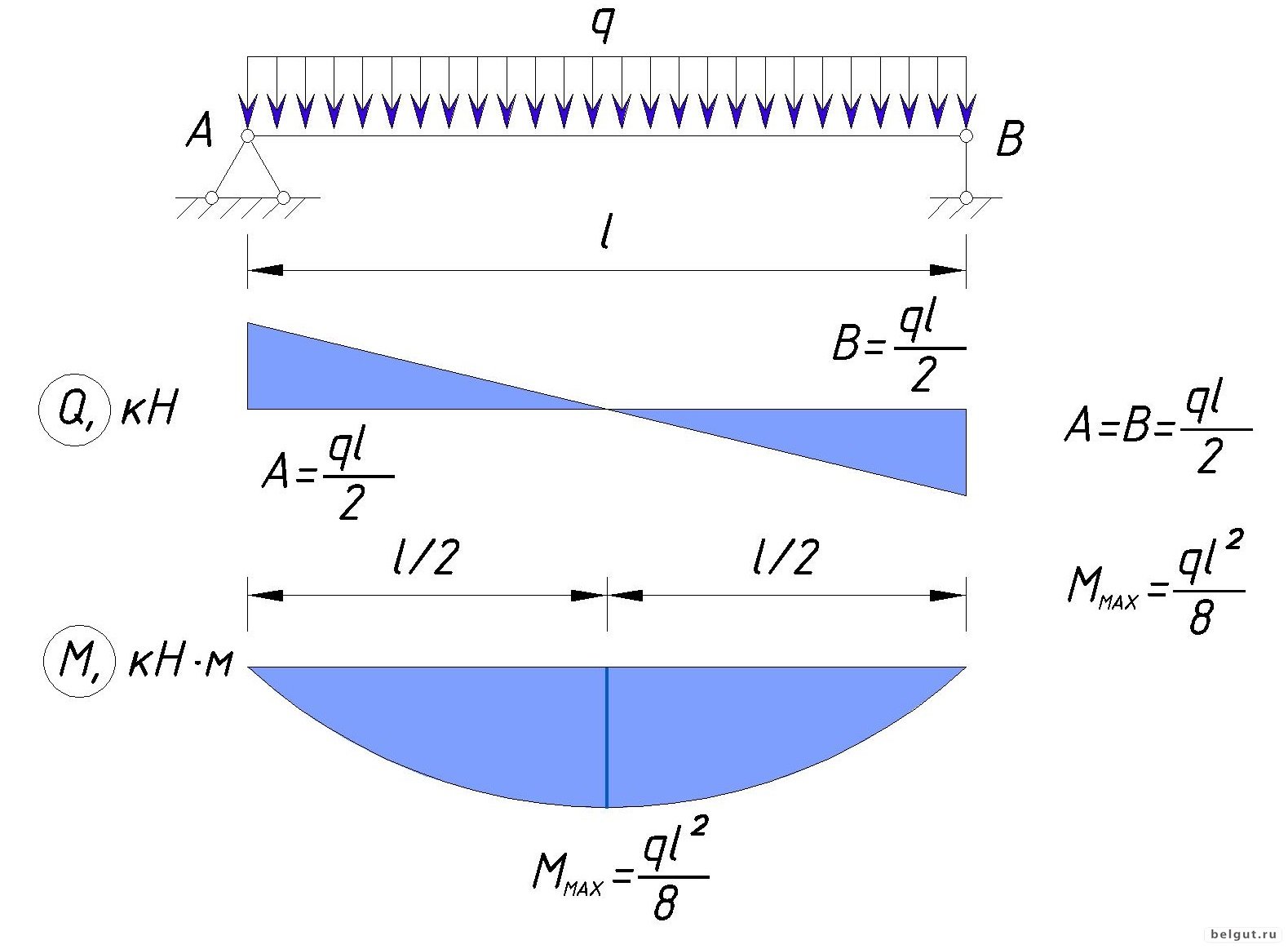

3. В PropertyManager (Менеджере свойств):

a. Выберите Неподвижная (нет перемещений) в списке Стандартный.

b. Выберите соединение показанное для Соединений .

4. Нажмите кнопку .

Чтобы смоделировать ролик на конце B:

1. Нажмите правой кнопкой мыши папку Крепления и выберите Зафиксированная геометрия.

2. В PropertyManager (Менеджере свойств):

a. Выберите Использовать справочную геометрию в списке Стандартный.

b. Выберите соединение показанное для Соединений .

c. Выберите Передняя в плавающем дереве конструирования для Грань, Кромка, Плоскость, Оси для направления .

3. В окне Перемещения, нажмите Вдоль плоскости — направление 1 и Вдоль плоскости — направление 2 для предотвращения перемещений в этих направлениях.

4. Нажмите кнопку .

 

4.5.  Приложение нагрузок в точках

Приложите силу в одной контрольной точке, а момент в другой.

Чтобы приложить силу:

1. Чтобы правильно выбрать контрольную точку, убедитесь, что ориентация вида является *Изометрия.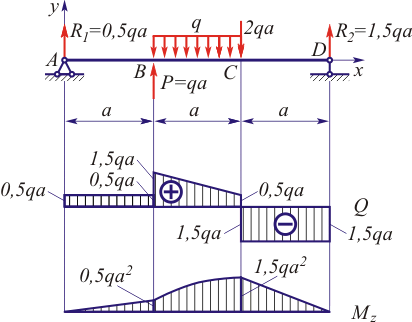

2. Нажмите правой кнопкой мыши папку Внешние нагрузки и выберите Сила .

3. В окне PropertyManager (Менеджер свойств), в разделе Выбор:

a. Нажмите Точки и выберите Точка 1 в плавающем дереве конструирования.

b. Выберите Передняя в плавающем дереве конструирования для Грань, Кромка, Плоскость, Оси для направления .

4. В меню Единицы измерения выберите Английская (ДФС).

5. В списке Сила:

a. Нажмите Вдоль плоскости — направление 2 .

b. Введите 500 фунтов.

c. Выберите Реверс направления.

6. Нажмите кнопку .

 

Приложение нагрузок в точках, продолжение

Чтобы приложить сосредоточенный момент:

1. Нажмите правой кнопкой мыши папку Внешние нагрузки и выберите Сила.

2. В окне PropertyManager (Менеджер свойств), в разделе Выбор:

a. Нажмите Точки и выберите Точка 2 в плавающем дереве конструирования.

b. Выберите Переднюю плоскость в плавающем дереве конструирования для Грань, Кромка, Плоскость, Оси для направления .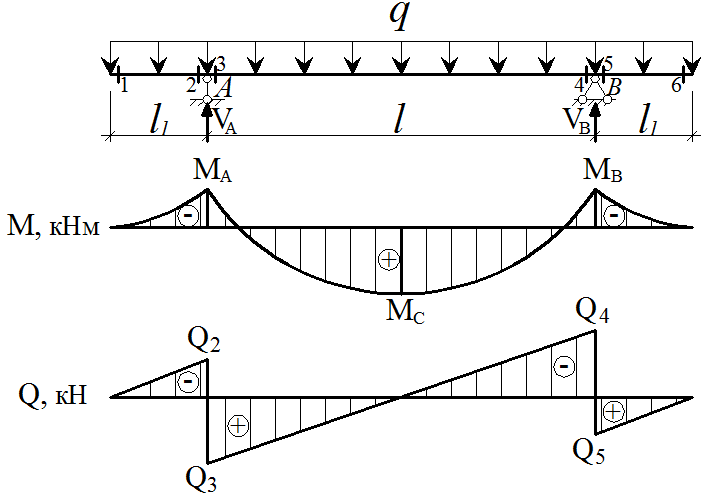

3. В меню Единицы измерения выберите Английская (ДФС).

4. В окне Момент (на объект):

a. Нажмите Вдоль плоскости — направление 1 .

b. Введите 1200 фунт·дюйм.

5. Нажмите кнопку .

 

4.6. Приложение нагрузок по длине балок

Чтобы приложить распределенную нагрузку по всей длине балки:

1. Нажмите правой кнопкой мыши папку Внешние нагрузки и выберите Сила.

2. В окне PropertyManager в разделе Выбор:

a. Щелкните Балки и выберите Вытяжка2 в графической области.

Можно приложить распределенные нагрузки только на всю длину балки. Вытянутые тела были созданы в качестве отдельных тел, чтобы сделать участок балки несущим свои распределенные нагрузки.

b. Выберите Переднюю плоскость в плавающем дереве конструирования для Грань, кромка, плоскость, оси для направления .

3. В меню Единицы измерения выберите Английская (ДФС) и выберите На единицу длины.

4. В списке Сила:

a. Нажмите Вдоль плоскости — направление 2 .

b. Введите 4,1667фунт/дюйм.

c. Выберите Реверс направления.

5. Нажмите кнопку .

 

4.7. Создание сетки модели и запуск исследования

Чтобы создать сетку модели и запустить исследование:

1. В дереве исследования Simulation нажмите правой кнопкой мыши значок Сетка и выберите Создать сетку .

Обратите внимание, что каждая из балок разделена на несколько элементов.

2. В дереве исследования Simulation нажмите правой кнопкой мыши исследование и выберите Выполнить .

 

4.8. Просмотр эпюры поперечных сил

1. Нажмите правой кнопкой мыши на папку Результаты и выберите Определить графики балки.

2. В окне PropertyManager в разделе Отобразить:

a. Выберите Поперечная сила в направлении 1 в Компонент .

Почему поперечная сила в направлении 1?

b. Выберите фунты в меню Единицы измерения .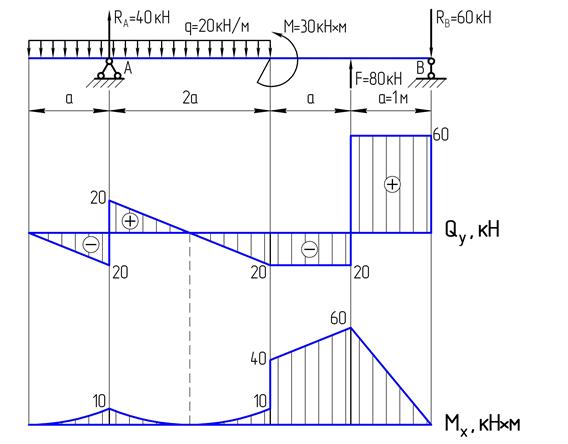

3. Нажмите кнопку .

4. Измените ориентацию вида, установив *Слева.

Сравните кривую с теоретическим решением (заметьте, что значения имеют единицы измерения фунты):

Нагрузки и ограничения балки показаны для удобства.

 

4.9. Просмотр эпюры изгибающих моментов

1. Нажмите правой кнопкой мыши на папку Результаты и выберите Определить графики балки.

2. В окне PropertyManager в разделе Отобразить:

a. Выберите Момент в направлении 2 в Компонент .

b. Выберите фунт·дюйм в меню Единицы измерения .

3. Нажмите кнопку .

4. Измените ориентацию вида на *Сверху и поверните график на 90° против часовой стрелки.

Сравните кривую с теоретическим решением:

Для удобства отображаются нагрузки и крепления балки.

 

4.10. Вывод списка усилий на балке

1. Нажмите правой кнопкой мыши на папку Результаты и выберите Список сил балки.

2. В окне PropertyManager (Менеджер свойств) в разделе Список:

· Выберите Силы.

· Выберите Английская (ДФС) в меню Единицы измерения .

3. Нажмите кнопку .

В диалоговом окне рассмотрите значения поперечных сил и момента в ключевых точках вдоль балки:

Точка A Точка D Точка B
Сдвигающее усилие 1 SolidWorks Simulation (фунт): -470,01 29,99 530,03
Поперечная сила 1, теория (фунты): -470 30 530
Момент 2 SolidWorks Simulation (фунт·дюйм): 1,75e-8 32401 4,83e-6
Момент 2, теория (фунт·дюйм): 0 32400 0

 

4.

3)

Настоящий расчет дает 22560,67 ф/кв.дюйм, что хорошо согласуется с максимальным напряжением при изгибе, показанным на вышеприведенной эпюре.

P.S. Туры в любую точку мира!

Феодосьев В.И (Сопротивление материалов — В.И. Феодосьев

6.1.Пример 6.3. Построить эпюру изгибающих моментов для ра­мы (рис. 6.19, а). Точки А и В рамы связаны между собой податливымстержнем с жесткостью на растяжение EqFq.276Система один раз статически неопределима. Разрезая стержень АВв верхней точке, получаем основную систему (рис. 6.19, б). Строим, да­лее, эпюры моментов от заданной силы Р и от единичной силы (рис. 6.19,вк а). Кроме того, на участке АВ, где необходимо учесть растяжение, стро­им эпюру нормальной силы 7V.

Вычисляем коэффициенты каноническогоуравнения6ц Xi + 61р = О,проводя перемножение не только эпюр изгибающих моментов, но и растя­гивающей силы:5/3/3EJ + E0F0’5Р/36£J‘Определяем Xi:_6ip _ Р_____ 1______6ц2 13EJSEqFqPКак видим, усилие в стержне зависит от отношения жесткости рамына изгиб к жесткости стержня АВ на растяжение.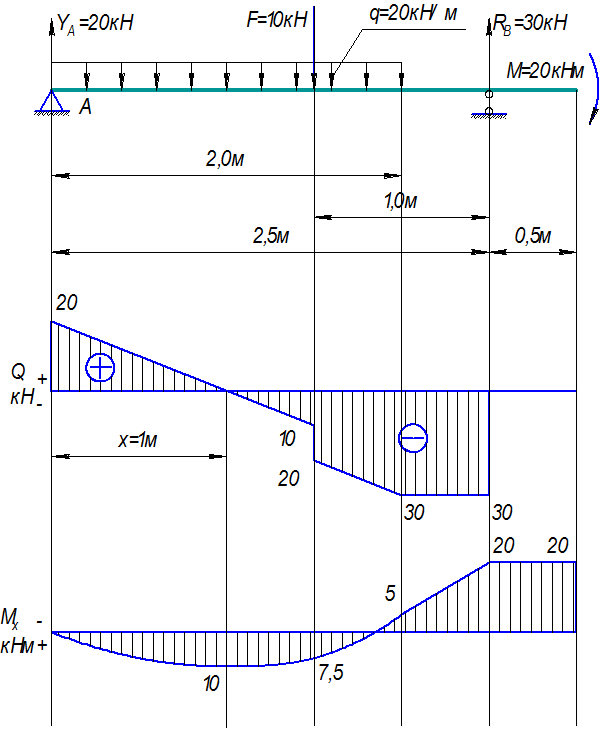 Если жесткость стерж­ня АВ очень велика, то= Р/2, и стержень воспринимает половинусилы Р.

Если стержень АВ очень податлив, то Xi —► 0, и вся сила Рвоспринимается рамой.Рис. 6.20На рис. 6.20 представлена эпюра изгибающих моментов в раме и фор­ма ее изогнутой оси.6.4. Использование свойств симметриипри раскрытии статической неопределимостиПоложим, имеется некоторая симметричная рама(рис. 6.21, а). Ее правую часть можно рассматривать какзеркальное отображение левой части относительно плоскости277симметрии. При расчете таких рам оказывается возможнымупростить решение задачи и снизить число искомых силовыхфакторов.Рис. 6.21Рассмотрим случаи нагружения рамы симметричной и ко­сосимметричной нагрузками.

Под симметричной нагрузкой бу­дем понимать такую, при которой все внешние силы, прило­женные к правой части рамы, являются зеркальным отобра­жением сил, приложенных к ее левой части (рис. 6.21, б). Подкососимметричной, или антисимметричной, нагрузкой будемпонимать такую, при которой силы, приложенные к правой по­ловине рамы, также являются зеркальным отображением сил,приложенных к ее левой половине, но противоположны им познаку (рис.

6.21, в).Аналогично классифицируем и внутренние силовые фак­торы. Рассмотрим для этого некоторое произвольное сечениерамы, в котором возникает шесть силовых факторов. В правойи левой плоскостях произведенного сечения (рис. 6.22) силы имоменты равны. Посмотрим, какие из шести силовых факто­ров образуют зеркальное отображение относительно плоскостиМхРис. 6.22278сечения. Такими оказываются три: два изгибающих моментаи нормальная сила. Будем их называть симметричными вну­тренними факторами. Крутящий момент и обе поперечныесилы в принятой терминологии должны быть названы косо­симметричными факторами.

Каждый из них противоположенпо знаку зеркальному отображению взаимного фактора. Не­трудно теперь доказать следующие положения.У симметричной рамы в плоскости симметрии при сим­метричной внешней нагрузке обращаются в нуль кососимме­тричные силовые факторы, а при кососимметричной внешнейнагрузке — симметричные силовые факторы.Рис.

В.23Обратимся к симметричной раме, например к показаннойна рис. 6.21, и выберем основную систему, разрезая раму поплоскости симметрии (рис. 6.23). Обозначим через Xi и Х2кососимметричные, а через Х3, Х4, Х5, Xq — симметричныесиловые факторы и выпишем систему канонических уравне­ний. В данном случае их будет шесть:6цХ1621X1631X1641X1651X1«61X1+ £12X2+ 622X2+ 632X2+ 642X2+ 652X2+ 652X2+ £13X3+ 623X3+ 633X3+ 643X3+ 653X3+ 653X3+ £14X4+ 624X4+ 634X4+ 644X4+ 654X4+ 654X4+ 615X5+ 625X5+ 635X5+ 645X5+ 655X5+ 655X5+ 616Хб+ 625X5+ 635X5+ 645X5+ 655X5+ 6ббХб======—6ц>;~б2р;—6зР;—647»;— бзр;-6бр.Заметим теперь, что в этих уравнениях многие из коэффици­ентов обращаются в нуль.

Это будут все коэффициенты, у ко­торых один индекс принадлежит симметричному, а другой 279кососимметричному фактору. Например, обращается в нулькоэффициент «и. Индекс 1 принадлежит кососимметричномуфактору (Xi и %2 » кососимметричные факторы), а индекс3 — симметричному фактору (Х3, Х4, Х5 и Xq — симметрич­ные факторы). Обращаются также в нуль «14, «15, «16, «23>«24 И Т.Д.Происходит это потому, что в симметричной раме не воз­никает взаимных кососимметричных перемещений под дей­ствием симметричных нагрузок.Р == 0. Тогда Хз = 0, Х4 — 0, Ag = 0, Хв = 0. В этом слу­чае в плоскости симметрии обращаются в нуль симметричныесиловые факторы.Все сказанное, понятно, сохраняет силу не только дляплоских, но и для пространственных рам при любой степенистатической неопределимости.Если нагрузка, приложенная к симметричной раме, необладает ни прямой, ни косой симметрией, всегда имеется воз­можность разложить ее на кососимметричную и симметрич­ную, как это показано, например, на рис. 6.25.

Задача, такимобразом, распадается на две. Рассматривают отдельно сим­метричную раму с кососимметричной нагрузкой и раму с сим­метричной нагрузкой. Внутренние силовые факторы в рамеопределяют в дальнейшем наложением полученных решений.Рис. в.25В случае, если рама геометрически кососимметрична(рис. 6.26), можно также путем сопоставления эпюр для двухполовин рамы получить упрощения в системе каноническихуравнений.

Нетрудно, например, таким способом установить,281что для рамы, показанной на рис. 6.26, при выбранной основ­ной системе 613 = 0, 623 = О, 6^Р — 0, &2р — 0- Тогда уравненияпринимают вид+ $12X2 = 0;621X1 + 622X2 = 0; 633X3 + бзр = 0.Следовательно, в сечении А возникает только изгибающий мо­мент, а нормальная и поперечная силы обращаются в нуль.Пример 6.4. Раскрыть статическую неопределимость и постро­ить эпюру изгибающих моментов для рамы, показанной на рис. 6.27, а.Рис.

6.27Рама симметричная и нагружена кососимметрично расположенны­ми силами. Разрезаем ее по оси симметрии и в произведенном сече­нии прикладываем силы Xi (рис. 6.27, б). Строим эпюры моментов(рис. 6.27, в, г). Симметричные силовые факторы, как мы уже знаем, рав­ны здесь нулю.Взамен трех уравнений получаем одно: 6цХ1 4- 61Р = 0, где7Z3PZ335п = 77TF7’= — • г j * откуда Xi = — Р. Эпюра изгибающих мо12z>j4£у7ментов и форма изогнутой оси рамы представлены на рис.

6.28.Пример 6.5.Определить наибольший изгибающий момент вкольцевой раме, нагруженной двумя силами Р (рис. 6.29).282Рис. 6.29Рис. 6.28Рама три раза статически неопределима, но условия симметрии по­зволяют сократить число неизвестных до одного. Разрежем раму по вер­тикальному диаметру АВ (рис.). Момент единичного силового фактора равен Mi == -1.Определяем коэффициенты канонического уравненияir/2f М2 R dtp __ irR ‘_6111г/2J0EJ~ 2ЁГ$[ MpMiRdtp ___1P~ JEJPR2 / x~~2EJ\1J’0Тогда283Изгибающий момент в произвольном сечении равен алгебраической сум­ме моментаот заданных сил и момента Mi, увеличенного в Xi раз.В итогеМ = Мр — Xi = PR ( — — 1 cos\ 1Г£’✓Л7Согласно этому выражению, нарассматриваемой четверти окружно­сти может быть построена эпюра из­гибающего момента, которую затемпо условиям симметрии можно рас­пространить и на другие участкиокружности (рис.

6.31). Наибольшийизгибающий момент возникает в точ­ках приложения сил Р и равен PRI.*Рис. 6.31Пример 6.6. Раскрыть статическую неопределимость и постро­ить эпюру моментов для рамы, показанной на рис. 6.32, а.!№!!!»»№!!№!аРяс. 6.32Рама геометрически кососимметрична. Разрезаем ее в центре сим­метрии и прикладываем в сечении три неизвестных силовых фактора(рис. 6.32, б). Строим все четыре эпюры моментов (одну — от заданныхсил и три — от единичных силовых факторов). Сопоставляя эти эпюры(рис. 6.33), убеждаемся, что 6qp = 6$р = 6ц = 6ц = 0.

Следовательно,система трех канонических уравнений принимает вид6цХ1 = —6ipj622X2 4- 623-Хз = 0;632X2 4- 633X3 «= 0,откуда Х2 = Хз = 0.Далее, перемножая эпюры, находимX _ 8i.611 «ЁГ284а _ 2<в1₽“зЁТх _я/2/12Рис. в.33Рис. в.34Суммарная эпюра изгибающих моментов показана на рис. 6.34.Рассмотрим еще один пример, не относящийся к свой­ствам симметрии, но наглядно иллюстрирующий значениеправильно выбранной основной системы при раскрытии ста­тической неопределимости.Пример 6.7. Раскрыть статическую неопределимость стержняпостоянного сечения, расположенного на десяти равноотстоящих одна отдругой опорах (рис. 6.35, а).В данном случае (и не только в данном, но и вообще для многопро,летного стержня) удобно образовать основную систему, врезая на опорах285X Л/X, %аX* XjXsXsX,Рис.

в.35шарниры и вводя в качестве неизвестных так называемые опорные момен­ты (рис. 6.35, d). Таких моментов будет восемь.Построим эпюры от заданного и от единичных моментов (рис. 6.35,e-J). Эпюры от единичных моментов представляют собой треугольники,расположенные лишь на смежных с опорой пролетах, а эпюра от внешнихсил изображается треугольником на первом пролете.Составим систему из восьми уравнений. В первом уравнении отлич­ными от нуля будут следующие коэффициенты:_2/1 “ ЗЕГI19 ” 6ЕГ£Ml1Р ~ 6EJ’Во втором уравнении также обратятся в нуль все коэффициенты, крометрех:*316Е J ’баз =21ЗЕГбаз ———6£Jи т.д. В итоге после сокращений система уравнений примет вид4X1 + Хз +0…Xi 4″ 4 Хз 4″ Хз 4″ 0 4″ ■ ■ ■О +Хз 4-4Хз 4- Х4 4- 0 + …О 4″ Хз 4″ 4Х< 4″ Ха 4″ 0 4″= -м,= О,= о,= о,О +Xi+4Xt= 0.288Мы получили систему уравнений трехдиагональной структуры.Термин не требует разъяснений, и говорит сам эа себя.

Вообще, диаго­нальные матрицы (таблицы) коэффициентов при раскрытии статическойнеопределимости получаются для систем, имеющих однотипные, повторя­ющиеся элементы. Такими элементами в данном случае являются проле­ты многоопорного стержня. В более сложных задачах системы уравнениймогут получиться не только трех-, но и пяти-, семи- или девятидиаго­нальными. Эти системы обладают относительной простотой и особенноудобны (при большом числе неизвестных) для машинного счета. Именнопоэтому в последние годы получили развитие приемы расчета, основанныена предварительном разбиении сложных конструкций (типа оболочек с ре­брами) на множество однотипных элементов, наделенных определеннымисвойствами. Условия совместной деформации элементов записывают с та­ким расчетом, чтобы матрица обладала диагональными свойствами.

Loads | IDEA StatiCa

Усилия на концах элемента стержневой расчётной схемы приводятся к усилиям, приложенным к элементам сечения элемента в IDEA StatiCa. При приведении усилий учитываются эксцентриситеты отдельных элементов, вызванные конструкцией узла. 

Расчётная КМКЭ-модель очень точно учитывает реальную форму узла, в то время как величины внутренних усилий берутся из идеализированной КЭ пространственной стержневой схемы, в которой балки и колонны моделируются просто осевыми линиями, а узлы – сопряжения этих элементов – просто узлами, не имеющими размеров.

Узел стыка балки с колонной. Реальная форма узла и его теоретическая КЭ модель

Внутренние усилия находятся в пространственных стержневых элементах. Ниже приводится пример – эпюры внутренних усилий в стержневом элементе.

Эпюры изгибающего момента и поперечной силы в балке. M и V – величины усилий в узле

При конструировании и расчёте узла (соединения) важно учесть его реальные размеры. Это в свою очередь влияет на процедуру задания нагрузок – см. поясняющие рисунки ниже:

Влияние реальных размеров узла на нагрузки в КМКЭ модели (выделена тёмно-синим цветом)

Изгибающий момент М и поперечная сила V действуют в теоретическом узле. Эта точка – теоретический узел, в КМКЭ модели фактически не существует. Следовательно, в ней не могут быть заданы нагрузки. Их можно приложить только к концам элементов, но значения этих нагрузок должны быть пересчитаны с учётом реальных размеров элементов узла – расстояний r (от конца элемента до т.н. теоретического узла)

Mc = M – V ∙ r

Vc = V

IКМКЭ модель узла оперирует именно усилиями, приложенными к торцам элементов – Mc и Vc, несмотря на то, что в загружениях задаются именно усилия из стержневой модели — M и V.

При расчёте и конструировании узла необходимо также учитывать его реальное положение в составе конструкции относительно теоретического узла. Обычно внутренние усилия, действующие в реальном узле, отличаются от усилий, действующих в теоретическом узле. Благодаря использованию точной КМКЭ модели расчёт соединений производится на заниженные значения усилий – см. рисунок с эпюрой Mr:

Эпюра изгибающего момента в КМКЭ модели. Стрелка указывает на фактическое расположение стыка элементов

При задании нагрузок необходимо понимать, что реальная конструкция узла должна соответствовать принятой ранее теоретической модели с точки зрения внутренних усилий. Для жёстких соединений всё кажется довольно очевидным – внутренние усилия идентичны, но в случае шарнирных узлов есть существенные различия.

Положение шарнира в теоретической КЭ модели 3D узла и его фактическое положение в реальной конструкции (КМКЭ модели)

Предыдущий рисунок как раз демонстрирует различия в положении шарнира в стержневой КЭ модели и в реальной конструкции узла. Следует помнить, что любая теоретическая модель в полной мере не соответствует реальности. При приложении к узлу вычисленных значений внутренних усилий (см. рисунок выше), в шарнире возникнет существенный изгибающий момент (шарнир смещен относительно теоретического узла). В этом случае узел будет перегружен или же вовсе не сможет быть рассчитан. Решение данной проблемы весьма простое – модели должны согласоваться друг с другом. Либо шарнир будет задаваться в нужном положении в КЭ стержневой модели, либо же эпюра внутренних усилий будет смещаться в сторону до тех пор, пока изгибающий момент в шарнире не станет нулевым.

Смещённая эпюра изгибающего момента в балке: момент в шарнире нулевойСмещение эпюр может быть задано в таблице задания внутренних усилий (в версии 9.0 и новее это задаётся в свойствах самого элемента).

Положение заданных внутренних усилий оказывает большое влияние на правильность результатов расчёта. Во избежание недоразумений пользователь сам может выбрать место приложения усилий – Узел/ Болты / Позиция. Второй вариант предназначен для тех случаев, когда болты перпендикулярны оси элемента и физически пересекают какой-либо из его элементов сечения.  

Варианты приложения усилий – в узле, в болтах, в заданной позиции

Обратите внимание на то, что при выборе опции «Узел» для задания положения нагрузок, усилия будут прикладываться в начале выбранного элемента, которое, как правило, находится в главной (теоретической) точке узла, если только вручную не было задано смещение этого элемента.

Импорт нагрузок из сторонних КЭ-программ

IDEA StatiCa при импорте из сторонних КЭ-программ считывает из них результаты расчётов (внутренние усилия, деформации, реакции). Также считывается информация по комбинациям. Список и содержание комбинаций отображаются в мастере (или же BIM приложении).

При расчётах в КЭ программах обычно работают с огибающими комбинациями. В IDEA StatiCa Connection узлы стальных конструкций рассчитываются в нелинейной постановке (модель материал конструкций – упругопластическая). Это значит, что использовать огибающие комбинации в данном случае нельзя, так как они являются совокупностью линейных расчётов. При расчёте в IDEA StatiCa определяется наихудшее сочетание внутренних усилий (N, Vy, Vz, Mx, My, Mz) из всех заданных комбинаций усилий, приложенных к концам элементов, сходящихся в узле. Для каждого экстремального значения также определяются соответствующие значения внутренних усилий, приложенных к остальным элементам. Это сочетание усилий и используется как загружение при моделировании узла в IDEA StatiCa Connection.

Пользователь может при желании вносить изменения в список загружений. Он может работать с загружениями в специальном мастере (или BIM-связке) или же может удалить некоторые из загружений непосредственно в IDEA StatiCa Connection.

Внимание!

При импорте обязательно нужно контролировать равновесие нагрузок, действующих в узле. В следующих случаях можно получить несбалансированные усилия:

  • В импортируемой схеме имеются нагрузки, приложенные к рассматриваемому узлу как сосредоточенные. Программа может не понять, какому из элементов следует воспринимать эту узловую нагрузку, и проигнорирует её в расчётной модели.
    Возможное решение: Не прикладывайте узловых нагрузок при расчёте всей конструкции. При необходимости усилие может быть вручную назначено выбранному элементу как продольная или поперечная сила.
  • К рассматриваемому узлу крепится неметаллический (обычно бетонный или деревянный) элемент, воспринимающий нагрузку. Такой элемент не участвует в расчёте и усилия в нём не будут учитываться.
    Возможное решение: замените рассматриваемый элемент бетонным блоком с анкерами. 
  • Узел является частью какой-нибудь стены или плиты (обычно из ЖБ). Плита или стена не рассматриваются как часть расчётной схемы, и усилия в них будут проигнорированы.
    Возможное решение: замените плиту или стену бетонным блоком с анкерами.
  • Некоторые элементы присоединяются к узлу при помощи жёстких вставок. Такие элементы не будут включены в модель, и усилия в них будут проигнорированы.
    Возможное решение: добавьте эти элементы в IDEA StatiCa вручную.
  • В программе, из которой осуществляется импорт, производился расчёт на сейсмические нагрузки. Большинство программ на основе МКЭ для решения задач, связанных с сейсмикой, используют процедуру модального расчёта. Результаты внутренних усилий при расчётах на сейсмические нагрузки обычно представляются в виде огибающих по сечениям. Ввиду импользуемого метода расчёта (извлечение квадратного корня из суммы квадратов) все внутренние усилия будут положительными, а найти усилия, соответствующие заданному экстремальному значению. В этом случае внутренние усилия не будут находиться в равновесии.
    Возможное решение: знаки внутренних усилий можно изменить вручную.

Bentley — Документация по продукту

MicroStation

Справка MicroStation

Ознакомительные сведения о MicroStation

Справка MicroStation PowerDraft

Ознакомительные сведения о MicroStation PowerDraft

Краткое руководство по началу работы с MicroStation

Справка по синхронизатору iTwin

ProjectWise

Справка службы автоматизации Bentley

Ознакомительные сведения об услуге Bentley Automation

Bentley i-model Composition Server для PDF

Подключаемый модуль службы разметки

PDF для ProjectWise Explorer

Справка администратора ProjectWise

Справка службы загрузки данных ProjectWise Analytics

Коннектор ProjectWise для ArcGIS — Справка по расширению администратора

Коннектор ProjectWise для ArcGIS — Справка по расширению Explorer

Коннектор ProjectWise для ArcGIS Справка

Коннектор ProjectWise для Oracle — Справка по расширению администратора

Коннектор ProjectWise для Oracle — Справка по расширению Explorer

Коннектор ProjectWise для справки Oracle

Коннектор управления результатами ProjectWise для ProjectWise

Справка портала управления результатами ProjectWise

Ознакомительные сведения по управлению поставками ProjectWise

Справка ProjectWise Explorer

Справка по управлению полевыми данными ProjectWise

Справка администратора геопространственного управления ProjectWise

Справка ProjectWise Geospatial Management Explorer

Ознакомительные сведения об управлении геопространственными данными ProjectWise

Модуль интеграции ProjectWise для Revit Readme

Руководство по настройке управляемой конфигурации ProjectWise

Справка по ProjectWise Project Insights

ProjectWise Plug-in для Bentley Web Services Gateway Readme

ProjectWise ReadMe

Матрица поддержки версий ProjectWise

Веб-справка ProjectWise

Справка по ProjectWise Web View

Справка портала цепочки поставок

Услуги цифрового двойника активов

PlantSight AVEVA Diagrams Bridge Help

PlantSight AVEVA PID Bridge Help

Справка по экстрактору мостов PlantSight E3D

Справка по PlantSight Enterprise

Справка по PlantSight Essentials

PlantSight Открыть 3D-модель Справка по мосту

Справка по PlantSight Smart 3D Bridge Extractor

Справка по PlantSight SPPID Bridge

Управление эффективностью активов

Справка по AssetWise 4D Analytics

AssetWise ALIM Web Help

Руководство по внедрению AssetWise ALIM в Интернете

AssetWise ALIM Web Краткое руководство, сравнительное руководство

Справка по AssetWise CONNECT Edition

Руководство по внедрению AssetWise CONNECT Edition

Справка по AssetWise Director

Руководство по внедрению AssetWise

Справка консоли управления системой AssetWise

Анализ мостов

Справка по OpenBridge Designer

Справка по OpenBridge Modeler

Строительное проектирование

Справка проектировщика зданий AECOsim

Ознакомительные сведения AECOsim Building Designer

AECOsim Building Designer SDK Readme

Генеративные компоненты для Building Designer Help

Ознакомительные сведения о компонентах генерации

Справка по OpenBuildings Designer

Ознакомительные сведения о конструкторе OpenBuildings

Руководство по настройке OpenBuildings Designer

OpenBuildings Designer SDK Readme

Справка по генеративным компонентам OpenBuildings

OpenBuildings GenerativeComponents Readme

Справка OpenBuildings Speedikon

Ознакомительные сведения OpenBuildings Speedikon

OpenBuildings StationDesigner Help

OpenBuildings StationDesigner Readme

Гражданское проектирование

Дренаж и коммунальные услуги

Справка по OpenRail ConceptStation

Ознакомительные сведения по OpenRail ConceptStation

Справка по OpenRail Designer

Ознакомительные сведения по OpenRail Designer

Справка по конструктору надземных линий OpenRail

Справка OpenRoads ConceptStation

Ознакомительные сведения по OpenRoads ConceptStation

Справка по OpenRoads Designer

Ознакомительные сведения по OpenRoads Designer

Справка по OpenSite Designer

OpenSite Designer ReadMe

Инфраструктура связи

Справка по Bentley Coax

Справка по PowerView по Bentley Communications

Ознакомительные сведения о Bentley Communications PowerView

Справка по Bentley Copper

Справка по Bentley Fiber

Bentley Inside Plant Help

Справка по OpenComms Designer

Ознакомительные сведения о конструкторе OpenComms

Справка OpenComms PowerView

Ознакомительные сведения OpenComms PowerView

Справка инженера OpenComms Workprint

OpenComms Workprint Engineer Readme

Строительство

ConstructSim Справка для руководителей

ConstructSim Исполнительный ReadMe

ConstructSim Справка издателя i-model

Справка по планировщику ConstructSim

ConstructSim Planner ReadMe

Справка стандартного шаблона ConstructSim

ConstructSim Work Package Server Client Руководство по установке

Справка по серверу рабочих пакетов ConstructSim

Руководство по установке сервера рабочих пакетов ConstructSim

Справка управления SYNCHRO

SYNCHRO Pro Readme

Энергетическая инфраструктура

Справка конструктора Bentley OpenUtilities

Ознакомительные сведения о Bentley OpenUtilities Designer

Справка по подстанции Bentley

Ознакомительные сведения о подстанции Bentley

Справка подстанции OpenUtilities

Ознакомительные сведения о подстанции OpenUtilities

Promis.e Справка

Promis.e Readme

Руководство по установке Promis.e — управляемая конфигурация ProjectWise

Руководство по настройке подстанции

— управляемая конфигурация ProjectWise

Геотехнический анализ

PLAXIS LE Readme

Ознакомительные сведения о PLAXIS 2D

Ознакомительные сведения о программе просмотра вывода 2D PLAXIS

Ознакомительные сведения о PLAXIS 3D

Ознакомительные сведения о программе просмотра 3D-вывода PLAXIS

PLAXIS Monopile Designer Readme

Управление геотехнической информацией

Справка администратора gINT

Справка gINT Civil Tools Pro

Справка gINT Civil Tools Pro Plus

Справка коллекционера gINT

Справка по OpenGround Cloud

Гидравлика и гидрология

Справка по Bentley CivilStorm

Справка Bentley HAMMER

Справка по Bentley SewerCAD

Справка Bentley SewerGEMS

Справка Bentley StormCAD

Справка Bentley WaterCAD

Справка Bentley WaterGEMS

Управление активами линейной инфраструктуры

AssetWise ALIM Linear Referencing Services Help

Руководство администратора мобильной связи TMA

Справка TMA Mobile

Картография и геодезия

Справка карты OpenCities

Ознакомительные сведения о карте OpenCities

OpenCities Map Ultimate для Финляндии Справка

OpenCities Map Ultimate для Финляндии Readme

Справка по карте Bentley

Справка по мобильной публикации Bentley Map

Ознакомительные сведения о карте Bentley

Проектирование шахты

Помощь по транспортировке материалов MineCycle

Ознакомительные сведения по транспортировке материалов MineCycle

Моделирование мобильности и аналитика

Справка по подготовке САПР LEGION

Справка по построителю моделей LEGION

Справка по API симулятора LEGION

Ознакомительные сведения об API симулятора LEGION

Справка по симулятору LEGION

Моделирование и визуализация

Bentley Посмотреть справку

Ознакомительные сведения о Bentley View

Анализ морских конструкций

SACS Close the Collaboration Gap (электронная книга)

Ознакомительные сведения о SACS

Анализ напряжений в трубах и сосудов

AutoPIPE Accelerated Pipe Design (электронная книга)

Советы новым пользователям AutoPIPE

Краткое руководство по AutoPIPE

AutoPIPE & STAAD.Pro

Завод Проектирование

Ознакомительные сведения об экспортере завода Bentley

Bentley Raceway and Cable Management Help

Bentley Raceway and Cable Management Readme

Bentley Raceway and Cable Management — Руководство по настройке управляемой конфигурации ProjectWise

Справка по OpenPlant Isometrics Manager

Ознакомительные сведения о диспетчере изометрических данных OpenPlant

Справка OpenPlant Modeler

Ознакомительные сведения для OpenPlant Modeler

Справка по OpenPlant Orthographics Manager

Ознакомительные сведения об OpenPlant Orthographics Manager

Справка OpenPlant PID

Ознакомительные сведения о PID OpenPlant

Справка администратора проекта OpenPlant

Ознакомительные сведения для администратора проекта OpenPlant

Техническая поддержка OpenPlant Support

Ознакомительные сведения о технической поддержке OpenPlant

Справка по PlantWise

Ознакомительные сведения о PlantWise

Выполнение проекта

Справка рабочего стола Bentley Navigator

Моделирование реальности

Справка консоли облачной обработки ContextCapture

Справка редактора ContextCapture

Файл ознакомительных сведений для редактора ContextCapture

Мобильная справка ContextCapture

Руководство пользователя ContextCapture

Справка Декарта

Ознакомительные сведения о Декарте

Структурный анализ

Справка по концепции RAM

Справка по структурной системе RAM

STAAD Закройте пробел в сотрудничестве (электронная книга)

STAAD.Pro Help

Ознакомительные сведения о STAAD.Pro

Программа физического моделирования STAAD.Pro

Расширенная справка по STAAD Foundation

Дополнительные сведения о STAAD Foundation

Детализация конструкций

Справка ProStructures

Ознакомительные сведения о ProStructures

ProStructures CONNECT Edition Руководство по внедрению конфигурации

ProStructures CONNECT Edition Руководство по установке — Управляемая конфигурация ProjectWise

Диаграммы пучка

Нагрузки / сочетания нагрузок

Выберите желаемый вариант нагрузки, комбинацию нагрузок или конверт.

Этап строительства, применимый для вывода анализа этапа строительства, определяется на панели «Выбор этапа строительства для отображения» или на панели инструментов этапа. Щелкните справа, чтобы ввести новые или изменить существующие сочетания нагрузок. (См. «Нагрузки / сочетания нагрузок»)

Примечание
Когда результаты выдаются в максимальном, минимальном и всех значениях в таких случаях, как движущиеся нагрузки, осадки опор, анализ временной истории и комбинации нагрузок огибающей, при выборе «все» создаются диаграммы балок, отображаемые в абсолютных значениях сил стержня независимо от знаков сил стержня.Чтобы получить диаграммы направленности, отражающие знаки, отметьте «Учитывать знаки в типе сочетания нагрузок огибающей» все в Инструменты> Предпочтения> Среда> Результаты.

Шаг
Укажите шаг, для которого должны быть получены результаты анализа. Шаг определяется в геометрическом нелинейном анализе как Шаг нагрузки, а дополнительные шаги определяются на этапах строительства мостов или анализа теплоты гидратации.

Примечание
Этап строительства, применимый для вывода анализа этапа строительства, определяется в разделе «Выбор этапа строительства для отображения» или на панели инструментов этапа.

Диаграмма макс. / Мин.
Абсолютные максимальные значения Envelope можно проверить в Beam Diagram.

Примечание
Если выбран вариант «Конверт / все», активируется «Диаграмма макс. / Мин.». Если опция не отмечена, создается диаграмма с абсолютными максимальными значениями Envelope.

Компоненты

Выберите требуемый компонент силы стержня из следующих:

Деталь: выберите конкретную деталь, для которой будут созданы силы стержня.Эта функция активируется, когда детали определены в составном разделе для этапа строительства.

Fx: Осевая сила в локальном x-направлении элемента

Примечание
Когда выбрано осевое усилие (Fx) и установлен флажок «Показать усилие фермы», одновременно создаются силы на стержнях фермы. Когда выбрано осевое усилие (Fx) и установлен флажок «Только сила фермы», генерируются только силы стержня фермы.

Mx: крутящий момент относительно локальной оси x элемента

Fy: поперечная сила в локальном y-направлении элемента

Fz: поперечная сила в локальном z-направлении элемента

Fyz: поперечные силы, Fy и Fz отображаются одновременно

My: изгибающий момент относительно локальной оси y элемента

Mz: изгибающий момент относительно локальной оси z элемента

Myz: изгибающий момент, My и Mz отображаются одновременно

Мб: Би-момент

Mt: крутящий момент

Mw: момент деформации

Показать усилие на ферме: опция вывода для одновременного создания сил на стержнях фермы

Только усилие на ферме: вариант вывода для создания только усилий на стержнях фермы

Параметры отображения

Точно: отображение сил стержня, рассчитанных в процессе детального анализа, по всей длине каждого элемента балки, включая оба конечных узла.

Примечание
Опция Exact применима только к линейному статическому анализу. Таким образом, опция неактивна, когда выбраны подвижные загружения, загружения нелинейного анализа или комбинации нагрузок огибающей.

5 точек: отображение сил стержня, рассчитанных в обоих конечных узлах и четвертях каждого элемента балки. Схема представлена ​​соединением 5 точек.

Без заливки: отображение только контура, представляющего величины сил стержня.

Line Fill: отображение диаграммы, заполненной цветными линиями.

Сплошная заливка: отображение диаграммы с цветными поверхностями.

Масштаб: чертёжный масштаб для стержневых сил.

Тип дисплея

Определите тип отображения следующим образом:

Контур

Отображение стержневых сил элементов балки по контуру.

Диапазоны: определение диапазонов контура.

: Назначьте диапазон цветового распределения контура. С помощью функции можно назначить определенные цвета для определенных диапазонов.

Примечание
Максимальные / минимальные значения диапазона контура могут быть больше максимальных / минимальных выходных значений. Если значения Contour Range превышают выходные значения, они вводятся в ранг 0 и ранг 11.

Количество цветов: укажите количество цветов, которые будут включены в контур (выберите из 6, 12, 18, 24 цветов)

Цвета: назначение или управление цветами контура.

Таблица цветов: назначьте тип цветов.

: управление цветами по зонам контура.

Обратный контур: установите этот флажок, чтобы изменить последовательность изменения цвета контура на обратную.

Contour Line: Назначьте цвет границы контура

Кромка элемента: назначение цвета краев элемента при отображении контура

Параметры контура: укажите параметры представления контура

Контурная заливка

Градиентная заливка: отображение цветового градиента (затенения) контура.

Нарисовать контурные линии: отображение цветных границ контура.

Нарисовать только контурную линию
Отображать только цветные границы контура.

Монохромная линия: отображение границ контура в монохромном цвете.

Контурная аннотация
Отображаются легенды или аннотации, обозначающие диапазоны контура.

Интервал: укажите интервал легенды или аннотации.

Coarse Contour (быстрее) (для больших пластин или твердотельных моделей)
Представьте упрощенный контур для большой модели с помощью пластин или твердых элементов, чтобы сократить время, необходимое для представления полного контура.

Экструзия
Если пластинчатые элементы или твердые элементы вдоль плоскости разреза представлены в контуре, создается трехмерный контур. Положительное направление результатов анализа ориентировано в направлении оси z локальной системы координат элемента.
Этот параметр не применяется одновременно с параметром «Деформированная форма». Точно так же этот параметр не может применяться одновременно к случаям, когда параметр «Скрытый» используется для отображения толщины пластинчатых элементов или параметр «Оба» используется для представления сил (напряжений) на верхних и нижних элементах.

Деформация

Отобразите деформированную форму модели.

Масштабный коэффициент деформации
Увеличьте или уменьшите размер смещения, графически отображаемого в окне модели.

Деформационный тип
Выберите тип отображения смещения

Узловая деформация: отображение деформированной формы, отражающей только узловые смещения.

Реальная деформация: отображение деформированной формы детали, рассчитанной по сечениям между обоими концами элементов балки, вместе с узловыми смещениями.

Real Displacement (Auto-Scale off): истинная деформация конструкции графически представлена ​​без увеличения или уменьшения. Эта опция обычно используется для геометрического нелинейного анализа, отражающего большое смещение.

Относительное смещение: деформация конструкции графически представлена ​​относительно минимального узлового смещения, которое установлено на «0»

Значения

Отображение стержневых сил элементов балки в числовых значениях.
Типом шрифта и цветом чисел можно управлять в параметрах отображения.

Десятичные точки: назначьте десятичные точки для отображаемых чисел

Exp .: Выразите в виде экспонент

Min & Max: отображение максимального и минимального значений

Abs Max: отображение абсолютного максимального значения

Max: отображение только максимального значения

Min: отображение только минимального значения

Limit Scale (%): установка экрана отображение предела сил стержня относительно выбранного максимального или минимального значения

Установить ориентацию: отображение ориентации числовых значений

Примечание
Десятичными точками по умолчанию можно управлять в «Настройках».
Установите Orientation = 0 по горизонтали: числовые значения отображаются справа от узлов или элементов.
Угол ориентации представляет собой направление против часовой стрелки, которое можно использовать для улучшения читаемости чисел.

Легенда

Отображение различных ссылок, связанных с результатами анализа, справа или слева от рабочего окна.

Положение легенды: положение легенды в окне дисплея

Тип значения ранга: укажите тип значений в легенде и количество десятичных знаков.

Анимация

Динамическое моделирование стержневых сил элементов балки.
Щелкните, затем щелкните Запись справа от панели управления анимацией в нижней части рабочего окна.

Режим анимации: определение типа анимации для результатов анализа.

Animate Contour: возможность изменения цвета контура, представляющего переход, в соответствии с величинами вариации

Repeat Half / Full Cycle: выбор цикла повторения для динамического представления перехода

Примечание
Выберите «Half Cycle» для переходных форм конструкции и «Full Cycle» для динамического моделирования режимов вибрации или режима продольного изгиба.

Параметры AVI: введите параметры, необходимые для создания окна анимации.

битов на пиксель: количество битов на пиксель для создания окна по умолчанию для анимации

: назначить метод сжатия данных изображения

кадров за полупериод (3 ~ 300): количество кадров для имитации «полупериода»

кадров в секунду (5 ~ 60): количество кадров в секунду для динамического моделирования

Параметр этапа строительства: выберите параметры анимации при выполнении анализа этапа строительства.

Stage Animation: Анимация по этапам строительства

Current Stage-Step: Анимация по шагам на текущем этапе строительства

From ~ To: Начальные и конечные этапы строительства или этапы для анимации

недеформированный

Перекрыть недеформированную и деформированную формы модели.

Зеркальный

«Зеркальное отражение» позволяет пользователю расширить результаты анализа, полученные от половинной или четвертой модели, до результатов для полной модели путем отражения плоскостей.

Зеркальное отражение половинной модели

Зеркальное отражение модели

Зеркальное отражение: Укажите плоскость (и) зеркала, указав плоскость и координату в направлении, перпендикулярном плоскости в GCS.

Быстрый просмотр

Отобразите подробную диаграмму силы луча для элемента в отдельном окне.

Элемент: введите номер элемента, для которого создаются силы стержня. Или щелкните поле ввода и соответствующий элемент в представлении модели.

Нагрузка: выберите желаемое нагружение или комбинацию нагрузок.

Выберите Load / Step / Comp.

Шаг: укажите шаг, для которого должны быть созданы результаты анализа.

Компонент: выберите требуемый компонент силы стержня.

Результат

Отображение усилий стержня на I-End и J-End, а также максимальных и минимальных значений выбранного элемента.

Значение: переместите курсор мыши на диаграмме, чтобы отобразить силы стержня в соответствующем положении.

Общая длина: отображение длины элемента.

Расположение выходной секции

Укажите места сечения, в которых стержневые силы элементов балки возникают в числовых значениях.

I: отображение силы стержня в начальном узле (N1) элемента балки.

Центр: отображение силы стержня в центре элемента балки.

J: отображение силы стержня в конечном узле (N2) элемента балки.

Abs Max: Максимальные абсолютные значения сил стержня среди 5 точек (4-секционных) элементов балки отображаются в центрах элементов балки.

Мин. / Макс. Минимальные и максимальные силы стержня численно отображаются в соответствующих местах среди 5 точек (4-х секционных) элементов балки.

Все: силы стержня на конце i, центре и конце j отображаются в числовом виде.

Генерация пакетного вывода (,)
Учитывая типы результатов анализа для графических выходных данных, последовательно сгенерируйте графические выходные данные для выбранных загружений и комбинаций. Создается общее количество файлов, равное произведению количества отмеченных элементов в трех столбцах диалогового окна ниже.

Назначьте базовое имя файла, под которым сохраняются типы результатов (данные выбора в диалоговом окне «Генерация пакетного вывода» для графических выводов).

Укажите базовые файлы для генерации пакетного вывода, этапов строительства, загружений (комбинаций), этапов и т. Д. В следующем диалоговом окне.

Сохраненная информация о строке меню: Здесь перечислены основные файлы. Выберите базовые имена файлов для пакетного вывода.

: Удалите все базовые файлы, выбранные с помощью мыши.

При проведении анализа стадии строительства перечисляются все стадии строительства.Мы просто выбираем этапы интересов, которые будут включены в пакетный вывод. Если анализ этапа строительства не выполняется, столбец в диалоговом окне становится неактивным и перечисляет условия нагрузки (комбинации).

Этапы
Приведены результаты всех этапов строительства. Этапы строительства перечислены ниже.

Нагрузки на финальном этапе
Вывод результатов только для Финального этапа. Этапы строительства перечислены ниже.Если анализ этапа строительства не проводится, отображаются условия нагрузки (комбинации).

Использование сохранено
Примените только (сохраненный) шаг или условие загрузки (комбинацию), выбранные во время создания каждого базового файла.

Этап LCase / LComb
Когда выполняется анализ этапа строительства, отображаются автоматически сгенерированные условия нагрузки этапа строительства и дополнительно введенные комбинации нагрузок этапа строительства. Проверяйте только условия нагрузки (комбинации), которые будут использоваться для создания пакетных выходов.Этот столбец становится неактивным, если выбран параметр «Нагрузки на финальном этапе» или если анализ этапа строительства не выполняется.

Step Option
Укажите шаги, для которых будут производиться выходные данные при выполнении анализа этапа строительства или геометрического нелинейного анализа большого смещения.

Сохраненный шаг: используйте только шаги, использованные для создания базовых файлов

Все шаги: используйте все шаги

Опции вывода

Тип выходного файла
Выберите тип графического файла: BMP или EMF.

Автоматическое описание: в верхнем левом углу графических выходов, созданных в пакетном режиме, автоматически создается и включает примечания, такие как типы и компоненты результатов анализа, этапы и этапы строительства, условия нагрузки (комбинации) и т. Д. Размер шрифта , цвет, тип и т. д. могут быть изменены нажатием кнопки.

Выходной тракт
Укажите путь для сохранения графических файлов, которые будут создаваться в пакетном режиме.

Префикс файла: укажите префикс создаваемых графических файлов.Имена файлов будут состоять из «Prefix» _ «Base File Name» _ «Load Comb.». Bmp (emf) или «Prefix» _ «Base File Name» _ «Stage» _ «Stage LCase» _ «Step». BMP (ЭДС).

: создать указанные пакетные графические файлы, отражающие содержимое диалогового окна.

/

Создает содержимое входных данных в диалоговом окне «Базовые файлы и создание пакетного вывода» в файле двоичного типа (fn.bog). Нажмите кнопку и выберите файл fn.bog, чтобы использовать тот же формат вывода.

Примечание
Импорт / экспорт имеет значение только для разных проектов.В данной структурной модели базовые файлы автоматически сохраняются и перечисляются.

Мы не можем найти эту страницу

(* {{l10n_strings.REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}} *

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{добавить в коллекцию.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.АВТОР}}

{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}

Мы не можем найти эту страницу

(* {{l10n_strings.REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}} *

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.АВТОР}}

{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}} Диаграмма силы сдвига

— обзор

3.5 Взаимосвязь нагрузки, силы сдвига и изгибающего момента

Из Exs 3.6–3.11 ясно, что нагрузка, сила сдвига и изгибающий момент взаимосвязаны. Так, например, равномерно распределенные нагрузки создают линейно изменяющиеся поперечные силы, а максимальные значения изгибающего момента совпадают с нулевой поперечной силой.Теперь мы рассмотрим эти отношения математически.

Длина балки, показанная на рис. 3.21 (a), несет общую систему нагрузки, состоящую из сосредоточенных нагрузок и распределенной нагрузки w ( x ). Элементная длина балки δ x подвергается действию системы сил и момента, показанной на рис. 3.21 (b); поскольку δ x очень мало, распределенную нагрузку можно рассматривать как постоянную по длине δ x. Для вертикального равновесия элемента

Рисунок 3.21. Взаимосвязь нагрузки, поперечной силы и изгибающего момента.

S + w (x) δx− (S + δS) = 0

, так что

+ w (x) δx – δS = 0

Таким образом, в пределе δ x → 0

( 3.1) dSdx = + w (x)

Из уравнения. Из уравнения (3.1) видно, что скорость изменения поперечной силы на участке балки, другими словами, градиент диаграммы поперечных сил равен значению интенсивности нагрузки на этом участке. На рис. 3.14 (c), например, поперечная сила изменяется линейно от — wL в точке A до нуля в точке B, так что градиент диаграммы поперечной силы на любом участке балки составляет + wL / L. = + w , где w — интенсивность нагрузки.Уравнение (3.1) также применимо к участкам балки, подвергающимся сосредоточенным нагрузкам. На рис. 3.15 (а) интенсивность нагрузки в точке B теоретически бесконечна, как и градиент диаграммы поперечных сил в точке B (рис. 3.15 (d)). На практике диаграмма поперечных сил будет иметь конечный градиент в этом сечении, как показано на рис. 3.16.

Теперь интегрируя уравнение. (3.1) относительно x получаем

(3.2) S = + ∫w (x) dx + C1

, где C 1 — постоянная интегрирования, которая может быть определена в конкретном случае. из граничных условий нагружения.

Если, например, w ( x ) представляет собой равномерно распределенную нагрузку с интенсивностью w , то есть это не функция x , уравнение. (3.2) принимает вид

S = + wx + C1

, что является уравнением прямой линии градиента + w , как показано для консольной балки на рис. 3.14 в предыдущем абзаце. Кроме того, для этого конкретного примера S = 0 при x = L , так что C 1 = — wL и S = — w ( L — x ) как прежде.

В случае балки, несущей только сосредоточенные нагрузки, тогда в отсеках между нагрузками w ( x ) = 0 и уравнение. (3.2) уменьшается до

S = C1

, так что поперечная сила остается постоянной по всей длине балки без нагрузки (см. Рис. 3.13 и 3.15).

Предположим теперь, что уравнение. (3.1) интегрируется по длине балки между секциями X 1 и X 2 . Тогда

∫x1x2dSdxdx = + ∫x1x2w (x) dx

, что дает

(3.3) S2 − S1 = ∫x1x2w (x) dx

, где S 1 и S 2 — поперечные силы на сечениях X 1 и X 2 соответственно. Уравнение (3.3) показывает, что изменение на поперечной силы между двумя секциями балки равно площади под кривой распределения нагрузки по этой длине балки.

Аргумент может быть применен к случаю сосредоточенной нагрузки W , которую можно рассматривать как равномерно распределенную нагрузку, действующую на чрезвычайно малую элементарную длину балки, скажем δ x .Площадь под кривой распределения нагрузки тогда будет w δ x (= W ), а изменение поперечной силы от сечения x к сечению x + δ x будет + W. . Другими словами, изменение поперечной силы от участка, расположенного непосредственно слева от сосредоточенной нагрузки, до участка, расположенного непосредственно справа, равно значению нагрузки, как отмечено в Прим. 3.8.

Теперь рассмотрим вращательное равновесие элемента δ x на рис.3.21 (b) о B. Таким образом,

M − Sδx − w (x) δxδx2− (M + δM) = 0

Член, включающий квадрат δ x , является членом второго порядка и им можно пренебречь. Следовательно,

−Sδx – δM = 0

или, в пределе δ x → 0

(3.4) dMdx = −S

Уравнение (3.4) устанавливает для общего случая, что может наблюдаться, в частности, в диаграммы силы сдвига и изгибающего момента Exs 3.6–3.11, т. е. градиент диаграммы изгибающего момента в сечении балки равен минус значению силы сдвига в этом сечении.Например, на рис. 3.18 (e) изгибающий момент в AB является математическим максимумом на участке, где поперечная сила равна нулю.

Интегрирующее уравнение. (3.4) относительно x имеем

(3.5) M = −∫Sdx + C2

, в котором C 2 — постоянная интегрирования. Подставляя S в уравнение. (3.5) из уравнения. (3.2) дает

M = −∫ [+ ∫w (x) dx + C1] dx + C2

или

(3.6) M = −∫∫w (x) dx + C1x + C2

Если w (x) — это равномерно распределенная нагрузка с интенсивностью w , уравнение.(3.6) принимает вид

M = −wx22 − C1x + C2

, что показывает, что уравнение диаграммы изгибающего момента на длине балки, несущей равномерно распределенную нагрузку, является параболическим.

В случае балки, несущей только сосредоточенные нагрузки, тогда между нагрузками w ( x ) = 0 и уравнение. (3.6) уменьшается до

M = −C1x + C2

, что показывает, что изгибающий момент изменяется линейно между нагрузками и имеет градиент — C 1 .

Константы C 1 и C 2 в уравнении. (3.6) для данной балки можно найти из граничных условий нагружения. Таким образом, для консольной балки на рис. 3.14 мы уже показали, что C 1 = — wL , так что M = — wx 2 /2 + wLx + C 2 . Кроме того, когда x = L, M = 0, что дает C 2 = — wL 2 /2 и, следовательно, M = — wx 2 /2 + wLx — wL 2 /2 как и раньше.

Теперь интегрируя уравнение. (3.4) по длине балки между секциями X 1 и X 2 (рис. 3.21 (a))

∫x1x2dMdxdx = −∫x1x2Sdx

, что дает

(3,7) M2 − M1 = — ∫x1x2Sdx

, где M 1 и M 2 — изгибающие моменты на сечениях X 1 и X 2 соответственно. Уравнение (3.7) показывает, что изменение на изгибающего момента между двумя секциями балки равно минус площади диаграммы поперечных сил между этими секциями.Опять же, используя консольную балку на рис. 3.14 в качестве примера, мы видим, что изменение изгибающего момента от A до B составляет wL 2 /2, а площадь диаграммы поперечных сил между A и B равна — WL 2 /2.

Наконец, из уравнений (3.1) и (3.4)

(3.8) d2Mdx2 = −dSdx = −w (x)

Установленные выше соотношения могут быть использованы для более простого построения диаграмм поперечной силы и изгибающего момента для некоторых балок. чем при использовании методов, показанных в Exs 3.6–3.11 используются. Кроме того, они могут использоваться для более простых решений некоторых проблем с пучком.

Пример 3.13

Постройте диаграммы поперечной силы и изгибающего момента для балки, показанной на рис. 3.22 (a).

Рисунок 3.22. Диаграммы поперечной силы и изгибающего момента балки Ex. 3.13.

Первоначально реакции опоры рассчитываются с использованием методов, описанных в разделе 2.5. Тогда для момента равновесия балки около E

RA × 4−2 × 3−5 × 2−4 × 1 × 0,5 = 0

, из которых

RA = 4.5kN

Теперь, учитывая вертикальное равновесие балки

RE + RA − 2−5−4 × 1 = 0

, так что

RE = 6.5kN

При построении диаграммы поперечных сил мы можем использовать Факты о том, что, как установлено выше, поперечная сила постоянна в ненагруженных секциях балки, изменяется линейно, когда нагрузка равномерно распределена, и изменяется в положительную сторону, когда направленная вертикально вниз сосредоточенная нагрузка пересекает в положительном направлении x величиной нагрузка.Таким образом, на рис. 3.22 (b) поперечная сила увеличивается отрицательно на 4,5 кН при движении слева от A вправо от A, постоянна между A и B, изменяется положительно на 2 кН при перемещении слева от B. справа от B и т. д. Обратите внимание, что между D и E поперечная сила изменяется линейно от +2,5 кН в точке D до +6,5 кН в участке, расположенном непосредственно слева от точки E, другими словами, она изменяется на +4 кН, общее значение действующей вниз равномерно. распределенная нагрузка.

Диаграмма изгибающего момента также может быть построена с использованием вышеуказанных соотношений, а именно, изгибающий момент изменяется линейно по длине балки без нагрузки и параболически по длине балки, несущей равномерно распределенную нагрузку.Кроме того, изменение изгибающего момента между двумя секциями балки равно минус площади диаграммы поперечных сил между этими секциями. Таким образом, на рис. 3.22 (a) мы знаем, что изгибающий момент на шарнирной опоре в точке A равен нулю и что он изменяется линейно в отсеке AB. Изгибающий момент в точке B тогда равен минус площади диаграммы поперечных сил между A и B, то есть — (- 4,5 × 1) = 4,5 кНм. Фактически это представляет собой изменение изгибающего момента от нулевого значения в точке A до значения в точке B. В точке C площадь диаграммы поперечных сил справа или слева от C составляет 7 кНм (обратите внимание, что изгибающий момент в точке E тоже равен нулю) и т. д.В отсеке DE форму параболической кривой, представляющей распределение изгибающего момента по длине равномерно распределенной нагрузки, можно найти с помощью части уравнения. (3.8), т.е.

d2Mdx2 = −w (x)

Для равномерно распределенной нагрузки, направленной вертикально вниз, это выражение принимает вид

d2Mdx2 = −w

, что из математической теории показывает, что кривая, представляющая изменение изгибающего момента, является выпуклой в положительное направление изгибающего момента. Это можно наблюдать на диаграммах изгибающих моментов на рис.3.14 (d), 3.17 (d) и 3.18 (e). В этом примере диаграмма изгибающего момента для всей балки показана на Рис. 3.22 (c) и снова нарисована на стороне растяжения балки. Пример 3.14

Сборная бетонная балка длиной L должна быть поднята с станину и транспортируют так, чтобы максимальный изгибающий момент был как можно меньше. Если балка поднимается двумя симметрично расположенными стропами, покажите, что каждая стропа должна находиться на расстоянии 0,21 L от соседнего конца.

Внешняя нагрузка на балку складывается исключительно из ее собственного веса, который равномерно распределяется по ее длине.Таким образом, проблема сводится к проблеме балки с простой опорой, несущей равномерно распределенную нагрузку, в которой опоры расположены на некотором расстоянии — от каждого конца (рис. 3.23 (a)).

Рисунок 3.23. Определение оптимального положения опор в сборной бетонной балке Ex. 3.14.

Диаграммы поперечной силы и изгибающего момента могут быть построены в терминах и с использованием методов, описанных выше, и будут иметь формы, показанные на рис.3.23 (б) и (в). Изучение диаграммы изгибающего момента показывает, что существует два возможных положения для максимального изгибающего момента. Сначала в точках B и C, где изгибающий момент слишком большой и имеет равные значения по симметрии; второй — в средней точке пролета, где изгибающий момент имеет значение поворота и прогибается, если опоры в точках B и C расположены на достаточном расстоянии друг от друга. Предположим, что B и C расположены таким образом, что значение изгибающего момента изгиба в точках B и C численно равно изгибающему моменту провисания в средней точке пролета.Если теперь B и C сдвинуть дальше друг от друга, момент в середине пролета увеличится, а момент в B и C уменьшится. И наоборот, если B и C приблизить друг к другу, момент захвата в B и C увеличивается, а момент в середине пролета уменьшается. Отсюда следует, что максимальный изгибающий момент будет как можно меньше, если момент провисания в точках B и C численно равен провисающему моменту в середине пролета.

Решение будет упрощено, если использовать соотношение в уравнении. (3.7). Таким образом, когда опоры находятся в оптимальном положении, изменение изгибающего момента от A до B (отрицательное) равно минус половине изменения изгибающего момента от B до точки середины пролета (положительное).Отсюда следует, что площадь диаграммы поперечных сил между A и B равна минус половине площади между B и средней точкой пролета. Тогда

+ 12awa = −12 [−12 (L2 − a) w (L2 − a)]

, что сводится к

a2 + La − L24 = 0

, решение которого дает

a = 0,21 L (отрицательное решение не имеет практического значения)

2015 Справка по SOLIDWORKS — PropertyManager Диаграммы балок

Создает диаграммы сдвига, момента, крутящего момента или осевых сил для балок или диаграммы осевых сил для ферм.Диаграммы лучей генерируются в локальных направлениях для каждого луча.

Чтобы отобразить это PropertyManager, запустите исследование Simulation. Щелкните правой кнопкой мыши «Результаты» и выберите «Определить диаграммы балок».

Дисплей

Компонент Выберите одно из следующего:
  • Осевая сила
  • Сила сдвига в реж. 1
  • Сила сдвига в Dir 2
  • Момент в реж. 1
  • Момент в реж. 2
  • Момент

Для ферм доступно только осевое усилие.
шт. Выберите единицы на диаграмме.
Визуализация профиля пучка (медленнее) Отображает диаграммы балок с фактической геометрией балки в отличие от цилиндров.

выбранных лучей

Все Выбирает все лучи.
Выбрать Выберите балки в графической области.Программа учитывает только лучи в выбранных лучах.
Ширина диаграммы направленности Управляет шириной участков луча для лучшей видимости.

Недвижимость

Включить текст заголовка Введите собственное название для сюжета.
Свяжите график с ориентацией вида имени Позволяет связать предварительно определенную ориентацию вида с активным графиком.
Связать с текущим представлением Связывает текущий вид с активным графиком.

Чтобы показать направления лучей для активной диаграммы, щелкните правой кнопкой мыши значок диаграммы направленности и выберите «Настройки». В PropertyManager в разделе «Параметры деформированного графика» выберите «Показать направления балки».

Направление лучей показано в центре каждого луча

Диаграммы сдвига и момента, созданные для неподвижно-неподвижной балки, подверженной равномерно распределенной нагрузке:

2018 Справка по SOLIDWORKS — PropertyManager Диаграммы балок

Создает диаграммы сдвига, момента, крутящего момента или осевых сил для балок или диаграммы осевых сил для ферм.Диаграммы лучей генерируются в локальных направлениях для каждого луча.

Чтобы отобразить это PropertyManager, запустите исследование Simulation. Щелкните правой кнопкой мыши «Результаты» и выберите «Определить диаграммы балок».

Дисплей

Компонент Выберите одно из следующего:
  • Осевая сила
  • Сила сдвига в реж. 1
  • Сила сдвига в Dir 2
  • Момент в реж. 1
  • Момент в реж. 2
  • Момент

Для ферм доступно только осевое усилие.
шт. Выберите единицы измерения на диаграмме.
Визуализация профиля луча (медленнее) Отображает диаграммы балок с фактической геометрией балки в отличие от цилиндров.

выбранных лучей

Все Выбирает все лучи.
Выбрать Выберите балки в графической области.Программа учитывает только лучи в выбранных лучах.
Ширина диаграммы направленности Управляет шириной участков луча для лучшей видимости.

Недвижимость

Включить текст заголовка Введите собственное название для сюжета.
Свяжите график с ориентацией вида имени Позволяет связать предварительно определенную ориентацию вида с активным графиком.
Связать с текущим представлением Связывает текущий вид с активным графиком.

Чтобы показать направления лучей для активной диаграммы, щелкните правой кнопкой мыши значок диаграммы направленности и выберите «Настройки». В PropertyManager в разделе «Параметры деформированного графика» выберите «Показать направления балки».

Направление лучей показано в центре каждого луча

Пример неподвижно-неподвижной балки, подверженной равномерно распределенной нагрузке по Dir 1.Показаны диаграмма сдвига в Dir1 и диаграмма моментов в Dir 2. Для балки, подверженной распределенной нагрузке по Dir 2, поперечные силы будут показаны в Dir 2, а силы момента — в Dir 1.
Неподвижная неподвижная балка подвергается равномерной нагрузке в направлении 1.

Добавить комментарий

Ваш адрес email не будет опубликован.

2019 © Все права защищены.
[an error occurred while processing the directive]