1.Основные задачи сопротивления материалов.
Основные задачи сопротивления материалов.
Допущения принятые в сопротивлении материалов.
Геометрическая схематизация элементов строительных конструкций.
Классификация сил, действующих на элемент конструкции.
Внутренние силы.
Деформация и перемещения.
Расчетная схема.
Продольная сила и её определение. Построение эпюры продольной силы.
Напряжения при растяжении-сжатии (нормально напряжение). Построение эпюры нормальных напряжений.
Закон Гука при растяжении-сжатии. Модуль упругости (модуль Юнга).
Определение перемещений при растяжении-сжатии. Закон Гука для участка бруса.
Определение механических характеристик материалов. Испытание на растяжение. Испытание на сжатие.
Методы расчёта элементов конструкций на прочность и жесткость.
Статические неопределимые задачи при растяжении-сжатии и методы их решения.
Особенности стержневых статически неопределимых конструкций.
Сдвиг. Поперечная сила.
Напряжение при сдвиге (касательное напряжение). Закон парности касательных напряжений.
Закон Гука при сдвиге. Модуль упругости при сдвиге. Связь модуля при сдвиге с модулем при растяжении.
Практические расчёты на сдвиг. Расчет сварных соединений. Расчёт болтовых и заклёпочных соединений.
Геометрические характеристики плоских сечений. Общие сведения. Статический момент сечения. Определение центра тяжести сечения.
Моменты инерции площади сечения.
Зависимость между моментами инерции относительно параллельных осей. Вычисление моментов инерции сложных сечений.
Зависимость между моментами инерции при повороте осей. Главные оси и главные моменты инерции.
Вычисление главных центральных осевых моментов инерции простых сечений.
Вычисление главных центральных осевых моментов инерции сложных сечений.
Крутящийся момент и его определение. Построение эпюры крутящего момента.
Напряжения при кручении (вывод формулы).
Практические расчёты на кручение.
Изгиб. Внутренние усилия при изгибе. Разновидности изгиба. Виды балок.
Определение внутренних усилий при изгибе. Дифференциальные зависимости при изгибе. Правила построения эпюр.
Нормальные напряжения при изгибе (вывод формулы).
Касательные напряжения при изгибе (вывод формулы).
Расчёт на прочность при изгибе.
Расчёт балок на жёсткость. Методы определения перемещений при изгибе (перечислить методы).
Определение перемещений при помощи дифференциального уравнения изогнутой оси балки.
Определение перемещений при изгибе при помощи универсального уравнения изогнутой оси бруса (метода начальных параметров).
Определение перемещений при изгибе при помощи интеграла Мора. Правило Верещагина.
Напряжённое состояние в точке элемента конструкции. Виды напряжённого состояния.
Линейное напряжённое состояние. Плоское напряжённое состояние.
Изгиб с растяжением.
Изгиб с кручением.
Изгиб, кручение и сжатие.
Сопротивление материалов наука о прочности, жесткости и устойчивости элементов инженерных конструкций. Методами сопротивления материалов выполняются расчеты, на основании которых определяются необходимые размеры деталей машин и конструкций инженерных сооружений.
В отличие от теоретической механики сопротивление материалов рассматривает задачи, в которых наиболее существенными являются свойства твердых деформируемых тел, а законами движения тела как жесткого целого здесь пренебрегают. В то же время, вследствие общности основных положений, сопротивление материалов рассматривается как раздел механики твердых деформируемых тел.
В состав механики деформируемых тел входят также такие дисциплины, как: теория упругости, теория пластичности, теория ползучести, теория разрушения и др., рассматривающие, по существу, те же вопросы, что и сопротивление материалов. Различие между сопротивлением материалов и другими теориями механики твердого деформируемого тела заключается в подходах к решению задач.
Строгие теории механики деформируемого тела базируются на более точной постановке проблем, в связи с чем, для решения задач приходится применять более сложный математический аппарат и проводить громоздкие вычислительные операции. Вследствие этого возможности применения таких методов в практических задачах ограничены.
В свою очередь, методы сопротивления материалов базируются на упрощенных гипотезах, которые, с одной стороны, позволяют решать широкий круг инженерных задач, а с другой, получать приемлемые по точности результаты расчетов.
При этом главной задачей курса является формирование знаний для применения математического аппарата при решении прикладных задач, осмысления полученных численных результатов и поиска выбора наиболее оптимальных конструктивных решений. То есть данный предмет является базовым для формирования инженерного мышления и подготовки кадров высшей квалификации по техническим специализациям.
2.Допущения принятые в сопротивлении материалов.
1. Материал считается однородным (независимо от его микроструктуры физико-механические свойства считаются одинаковыми во всех точках).
2. Материал полностью заполняет весь объем тела, без каких-либо пустот (тело рассматривается как сплошная среда).
3. Обычно сплошная среда принимается изотропной, т.е. предполагается, что свойства тела, выделенного из нее, не зависят от его ориентации в пределах этой среды. Материалы, имеющие различные свойства в разных направлениях, называют анизотропными (например, дерево).
4. Материал является идеально упругим (после снятия нагрузки все деформации полностью исчезают, т.е. геометрические размеры тела полностью или частично восстанавливаются). Свойство тела восстанавливать свои первоначальные размеры после разгрузки называется упругостью.
5. Деформации тела считаются малыми по сравнению с его размерами. Это допущение называется принципом начальных размеров. Допущение позволяет при составлении уравнений равновесия пренебречь изменениями формы и размеров конструкции.
6. Перемещения точек тела пропорциональны нагрузкам, вызывающим эти перемещения (до определенной величины деформации материалов подчиняются закону Гука). Для линейно деформируемых конструкций справедлив принцип независимости действия сил (или принцип суперпозиции): результат действия группы сил не зависит от последовательности нагружения ими конструкции и равен сумме результатов действия каждой из этих сил в отдельности.
7. Предполагается, что в сечениях, достаточно удаленных от мест приложения нагрузки, характер распределения напряжений не зависит от конкретного способа нагружения. Основанием для такого утверждения служит принцип Сен-Венана.
8. Принимается гипотеза плоских сечений (гипотеза Бернулли): плоские поперечные сечения стержня до деформации остаются плоскими и после деформации.
studfiles.net
Задачи | ПроСопромат.ру
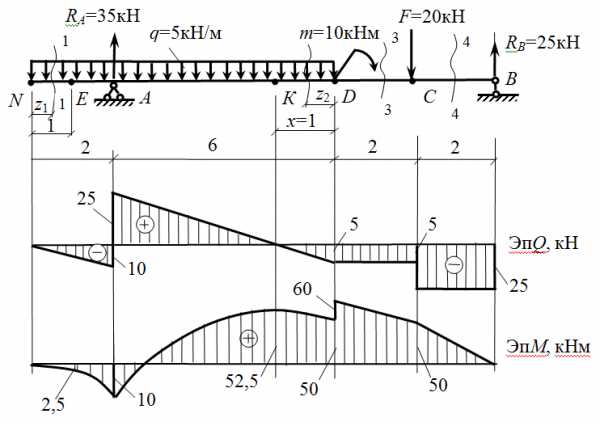
Для балки определить опорные реакции и построить эпюры изгибающих моментов (М) и поперечных сил (Q).
- Обозначаем опоры буквами А и
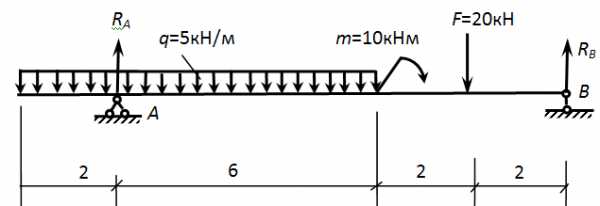
Составляем уравнения равновесия.

Проверка
Записываем значения RА и RВ на расчетную схему.
2. Построение эпюры поперечных сил методом сечений. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 4 участка, 4 сечения.
сеч. 1-1 ход слева.
Сечение проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z1 влево от сечения до начала участка. Длина участка 2 м. Правило знаков для Q — см. здесь.
Строим по найденным значением эпюру Q.
сеч. 2-2 ход справа.
Сечение вновь проходит по участку равномерно распределенной нагрузкой, отмечаем размер z2 вправо от сечения до начала участка. Длина участка 6 м.
Строим эпюру Q.
сеч. 3-3 ход справа.
сеч. 4-4 ход справа.
Строим эпюру Q.

3. Построение эпюры М методом характерных точек.
Характерная точка – точка, сколь-либо заметная на балке. Это точки А, В, С
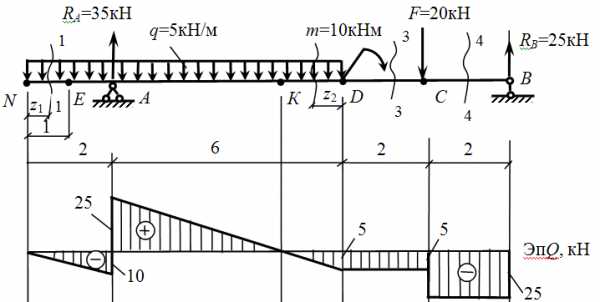
Итак, точки расставлены, приступаем к определению в них значений изгибающих моментов. Правило знаков — см. здесь.
Участки NA, AD – параболическая кривая (правило «зонтика» у механических специальностей или «правило паруса» у строительных ), участки DС, СВ – прямые наклонные линии.
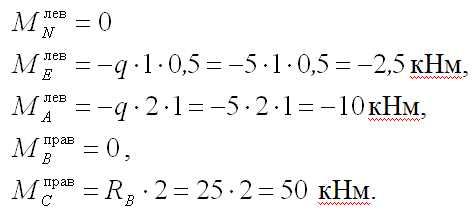
Момент в точке D следует определять как слева, так и справа от точки D. Сам момент в эти выражения не входит. В точке D получим два значения с разницей на величину m – скачок на его величину.
Теперь следует определить момент в точке К (Q=0). Однако сначала определим положение точки К, обозначив расстояние от нее до начала участка неизвестным х.
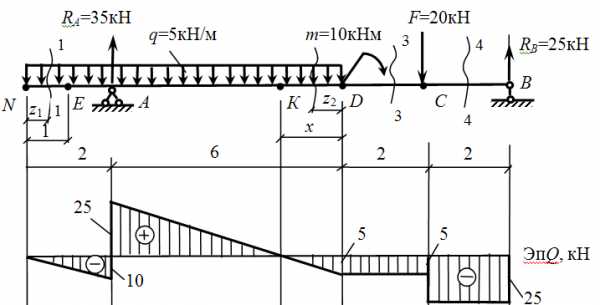
Т. К принадлежит второму характерному участку, его уравнение для поперечной силы (см. выше)
Но поперечная сила в т. К равна 0, а z2 равняется неизвестному х.
Получаем уравнение:
Теперь, зная х, определим момент в точке К с правой стороны.
Строим эпюру М. Построение выполним для механических специальностей, откладывая положительные значения вверх от нулевой линии и используя правило «зонтика».
prosopromat.ru
Задачи Сопромата | ПроСопромат.ру
Сопромат – это предмет, который изучается во всех технических вузах, и вот почему. Дело в том, что этот предмет является основой для изучения всех без исключения конструкций – машиностроительных, строительных и др. Что же изучает сопромат? В старых учебниках ответ на этот вопрос таков – сопромат является наукой о прочности, которая занимается расчетом инженерных конструкций и определяет их надежные размеры. Это, безусловно, правильное определение, но не совсем полное. В учебниках нового поколения сопромат определяется как наука, занимающаяся расчетами конструкций на прочность, жесткость и устойчивость. Разберемся, что же это такое.
Прочность – это свойство конструкций не разрушаться под действием нагрузки. Жесткость – свойство конструкций получать предельно малые деформации под нагрузкой (крайне незначительно менять свою форму и размеры, в определенных пределах). Устойчивость – это свойство конструкций сохранять проектную, заданную форму равновесия. Таким образом, можно обобщить, что сопромат – это наука о расчетах элементов конструкций на механическую надежность (прочность, жесткость и устойчивость).
Требования к сооружениям – надежность, долговечность, экономичность, эстетичность. Надежность обеспечивается грамотными расчетами на перечисленные выше свойства. Долговечность вполне понятна, она гарантирует длительный период эксплуатации конструкции без разрушений. Экономичность заставляет подбирать такие варианты размеров элементов сооружений, при которых были бы обеспечены их прочность, жесткость и устойчивость, и не было лишнего расхода материалов. Кроме того, сооружение должно радовать взгляд, но это уже задача архитекторов и дизайнеров.
Для достижения этих требований определяются задачи сопромата – изучение методов расчета на прочность, жесткость и устойчивость элементов конструкций.
Сопромат дает теоретические основы для расчета инженерных конструкций, это азбука для технических специалистов.
prosopromat.ru
Задачи на кручение стержня круглого сечения (задачи по сопромату)
Пример решения задачи на кручение стержня круглого сечения
Кручение стержня круглого сечения – условие задачи
К стальному валу постоянного поперечного сечения (рис. 3.8) приложены четыре внешних скручивающих момента: кН·м; кН·м; кН·м; кН·м. Длины участков стержня: м; м, м, м. Требуется: построить эпюру крутящих моментов, определить диаметр вала при кН/см2 и построить эпюру углов закручивания поперечных сечений стержня.
Кручение стержня круглого сечения – расчетная схема
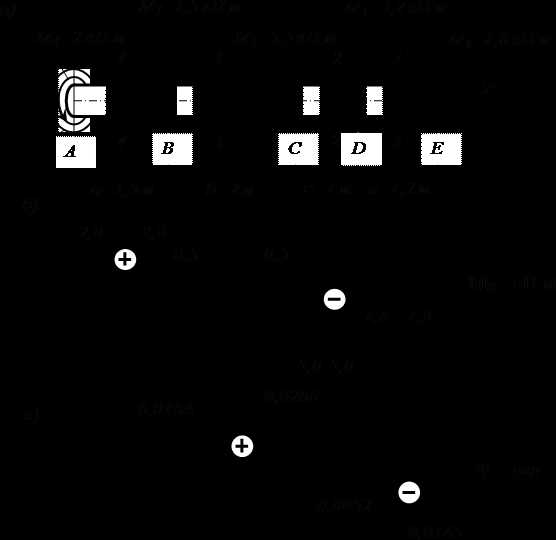 Рис. 3.8
Рис. 3.8
Решение задачи кручение стержня круглого сечения
Определяем реактивный момент, возникающий в жесткой заделке
Обозначим момент в заделке и направим его, например, против хода часовой стрелки (при взгляде навстречу оси z).
Запишем уравнение равновесия вала. При этом будем пользоваться следующим правилом знаков: внешние скручивающие моменты (активные моменты, а также реактивный момент в заделке), вращающие вал против хода часовой стрелки (при взгляде на него навстречу оси z), считаем положительными.
Тогда
кН·м.
Знак «плюс» в полученном нами выражении говорит о том, что мы угадали направление реактивного момента , возникающего в заделке.
Строим эпюру крутящих моментов
Напомним, что внутренний крутящий момент , возникающий в некотором поперечном сечении стержня, равен алгебраической сумме внешних скручивающих моментов, приложенных к любой из рассматриваемых частей стержня (то есть действующих левее или правее сделанного сечения). При этом внешний скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки (при взгляде на поперечное сечение), входит в эту алгебраическую сумму со знаком «плюс», а по ходу – со знаком «минус».
Соответственно, положительный внутренний крутящий момент, противодействующий внешним скручивающим моментам, направлен по ходу часовой стрелки (при взгляде на поперечное сечение), а отрицательный – против ее хода.
Разбиваем длину стержня на четыре участка (рис. 3.8, а). Границами участков являются те сечения, в которых приложены внешние моменты.
Делаем по одному сечению в произвольном месте каждого из четырех участков стержня.
Cечение 1 – 1. Мысленно отбросим (или закроем листком бумаги) левую часть стержня. Чтобы уравновесить скручивающий момент кН·м, в поперечном сечении стержня должен возникнуть равный ему и противоположно направленный крутящий момент . С учетом упомянутого выше правила знаков
кН·м.
Сечения 2 – 2 и 3 – 3:
кН·м;
кН·м.
Сечение 4 – 4. Чтобы определить крутящий момент, в сечении 4 – 4 отбросим правую часть стержня. Тогда
кН·м.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим теперь не правую, а левую часть стержня. Получим
кН·м.
Для построения эпюры крутящих моментов проводим тонкой линией ось, параллельную оси стержня z (рис. 3.8, б). Вычисленные значения крутящих моментов в выбранном масштабе и с учетом их знака откладываем от этой оси. В пределах каждого из участков стержня крутящий момент постоянен, поэтому мы как бы «заштриховываем» вертикальными линиями соответствующий участок. Напомним, что каждый отрезок «штриховки» (ордината эпюры) дает в принятом масштабе значение крутящего момента в соответствующем поперечном сечении стержня. Полученную эпюру обводим жирной линией.
Отметим, что в местах приложения внешних скручивающих моментов на эпюре мы получили скачкообразное изменение внутреннего крутящего момента на величину соответствующего внешнего момента.
Определяем диаметр вала из условия прочности
Условие прочности при кручении имеет вид
,
где – полярный момент сопротивления (момент сопротивления при кручении).
Наибольший по абсолютному значению крутящий момент возникает на втором участке вала: кН·см.
Тогда требуемый диаметр вала определяется по формуле
см.
Округляя полученное значение до стандартного, принимаем диаметр вала равным мм.
Определяем углы закручивания поперечных сечений A, B, C, D и E и строим эпюру углов закручивания
Сначала вычисляем крутильную жесткость стержня , где G – модуль сдвига, а – полярный момент инерции. Получим
кН·см2.
Углы закручивания на отдельных участках стержня равны:
рад;
рад;
рад;
рад.
Угол закручивания в заделки равен нулю, то есть . Тогда
рад;
рад;
рад;
рад.
Эпюра углов закручивания показана на рис. 3.8, в. Отметим, что в пределах длины каждого из участков вала угол закручивания изменяется по линейному закону.
Пример задачи на кручение «круглого» стержня для самостоятельного решения
Условие задачи на кручение «круглого» стержня
Жестко защемленный одним концом стальной стержень (модуль сдвига кН/см2) круглого поперечного сечения скручивается четырьмя моментами (рис. 3.7).
Требуется:
· построить эпюру крутящих моментов;
· при заданном допускаемом касательном напряжении кН/см2 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм;
· построить эпюру углов закручивания поперечных сечений стержня.
Варианты расчетных схем к задаче на кручение стержня круглого сечения для самостоятельного решения
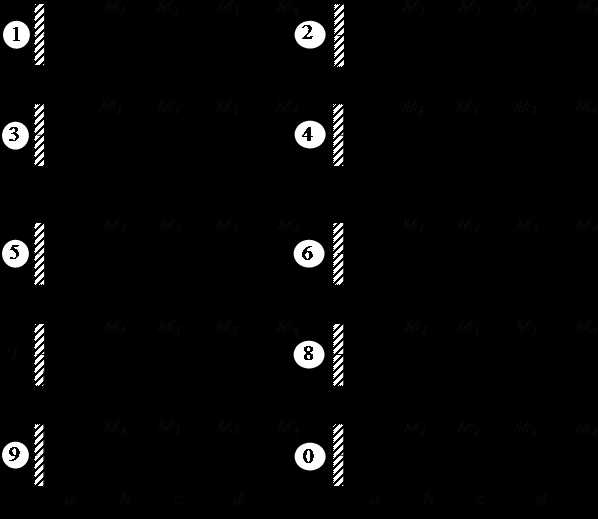
Рис. 3.7
Пример задачи на кручение круглого стержня – исходные условия для самостоятельного решения
Номер схемы | М1, кН·м | М2, кН·м | М3, кН·м | М4, кН·м | a, м | b, м | c, м | d, м |
1 | 1,0 | 2,0 | 1,0 | 1,0 | 1,0 | 1,2 | 1,4 | 1,6 |
2 | 1,0 | 2,0 | 1,0 | 0,8 | 1,2 | 1,4 | 1,6 | 1,9 |
3 | 2,0 | 4,0 | 1,0 | 1,0 | 1,4 | 1,6 | 1,0 | 1,2 |
4 | 3,0 | 5,0 | 1,6 | 1,4 | 1,6 | 1,0 | 1,2 | 1,4 |
5 | 4,0 | 6,0 | 1,8 | 1,4 | 1,1 | 1,1 | 1,8 | 1,5 |
6 | 2,0 | 4,0 | 1,2 | 1,2 | 1,3 | 1,3 | 1,5 | 1,1 |
7 | 2,0 | 3,0 | 1,2 | 1,0 | 1,5 | 1,5 | 1,3 | 1,3 |
8 | 3,0 | 4,0 | 1,0 | 1,0 | 1,7 | 1,7 | 1,5 | 1,4 |
9 | 4,0 | 5,0 | 1,8 | 1,6 | 1,9 | 1,9 | 1,7 | 1,3 |
0 | 5,0 | 6,0 | 2,0 | 1,6 | 1,2 | 1,4 | 1,4 | 1,2 |
sopromato.ru
Задачи сопротивления материалов
Глава 1
ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Задачи сопротивления материалов
Сопротивление материалов представляет собой одно из направлений механики деформируемого твердого тела, которое под действием приложенных к нему сил изменяет свою форму и размеры — деформируется.
На основе методов сопротивления материалов и смежных областей механики деформируем ого тела (математической и прикладной теории упругости, математической и прикладной теории пластичности, статики и динамики сооружений) выполняют расчеты машин, аппаратов, приборов, конструкций промышленных и гражданских сооружений. Эти расчеты служат для обеспечения надежности и долговечности проектируемых конструкций при минимальной затрате материалов для их изготовления.
Для балки, показанной на рис. 1.1, методами статики абсолютно твердого тела может быть решена задача об определении реакции шарнирно-неподвижной опоры А и реакции тяги ВС, возникающих под действием приложенной к балке нагрузки (в нашем случае силы F). Эти реакции показаны на чертеже, реакция тяги ВС условно несколько смещена от оси тяги. Напомним, что тело называют абсолютно твердым (или абсолютно жестким), если независимо от приложенных к нему сил расстояние между любыми двумя точками тела остается неизменным. Реальные твердые тела под действием приложенных к ним сил деформируются; в рассматриваемом случае тяга удлинится, а балка изогнется примерно так, как показано штриховыми линиями на рис. 1.1.
Допустим теперь, что балка разгружена: сила F удалена. При этом в зависимости от силы F (силу тяжести конструкции не учитываем), материалов, размеров балки и тяги могут возникнуть два случая (конечно, полагаем, что при действии силы F ни один из элементов конструкции не разрушается).
1. Балка и тяга полностью восстанавливают те формы и размеры, которые они имели до нагружения; в этом случае говорят, что в системе (конструкции) при заданной нагрузке возникают лишь упругие деформации.
2. Деформации балки и тяги уменьшаются, но система все же остается в деформированном состоянии; такое положение означает, что в системе при заданной нагрузке возникают
наряду с упругими также и пластические (остаточные) деформации.
Как правило, возникновение пластических деформаций связано с нарушением нормальной работы конструкции и потому считается недопустимым.
Пусть, например, тяга, изготовленная из стального прутка, имеет круглое поперечное сечение, а балка (также стальная)— двутавровый профиль. При заданной силе F следует выбрать диаметр сечения тяги и номер двутаврового профиля балки, чтобы ни один из элементов конструкции не разрушился и в нем не возникли пластические деформации. При соблюдении указанных условий балка и тяга имеют достаточную прочность. Легко понять, что возможна и обратная постановка задачи: размеры и материалы балки и тяги известны и требуется определить то наибольшее значение силы F, при котором прочность конструкции обеспечена.
Из рассмотренного примера вытекает, что первая задача сопротивления материалов — расчет элементов конструкций на прочность. При этом подчеркиваем еще раз, что в сопротивлении ‘материалов под нарушением прочности понимают не только разрушение в буквальном смысле слова — разрыв, излом, но и возникновение пластических (остаточных) деформаций.
Говоря о достаточной прочности конструкции, полагают, что прочность обеспечена не только при заданном значении нагрузок, но и при некотором их увеличении, т. е. конструкция имеет определенный запас прочности.
В конструкциях одноразового применения допустимо возникновение пластических деформаций. Для некоторых машин и аппаратов химических производств, а также в некоторых других случаях допускают возникновение небольших местных пластических деформаций, которые не являются признаком нарушения прочности. В кратком курсе сопротивления материалов расчеты, где учитывается развитие пластических деформаций, не рассматриваются.
Возникновение упругих деформаций в нагруженной конструкции неизбежно, также неизбежны и обусловленные этими деформациями перемещения отдельных точек конструкции, Так, в частности, в рассматриваемом примере конец балки по
лучает некоторое вертикальное перемещение f (рис. 1.1). Может оказаться, что значение /’ больше допустимого по условиям нормальной работы конструкции, хотя ее прочность вполне достаточна. В этом случае говорят, что конструкция имеет недостаточную жесткость.
Вообще жесткостью называют способность материала нлн элемента конструкции сопротивляться упругим деформациям. Можно также сказать, что жесткостью конструкции называют ее способность воспринимать нагрузку без существенного изменения геометрических размеров. На рис. 1.2 показан пример, иллюстрирующий последствия недостаточной жесткости конструкции: значительные прогибы валов зубчатой передачи приводят к неравномерному распределению нагрузки по длине зубьев, что связано с повышенным износом и даже опасностью поломки зубьев.
Вторая задача сопротивления материалов — расчет элементов конструкций на жесткость.
Соответствующий расчет при проектировании конструкции должен обеспечить выбор таких ее размеров, при которых упругие перемещения, вызванные рабочими нагрузками, будут лежать в допустимых пределах.
Обратимся еще к одному примеру (рис. 1.3,а), отличающемуся от первого лишь тем, что здесь стержень ВС, поддерживающий балку, испытывает не растяжение, а сжатие. Если стержень ВС сравнительно длинный и тонкий, то при некоторой силе F он может внезапно изогнуться (выпучиться), как показано штриховыми линиями на рис. 1.3,б, или, как говорят, потерять устойчивость. В этом случае стержень ВС помимо сжатия будет испытывать так называемый продольный изгиб. Иными словами, при достижении нагрузкой критического значения первоначальная прямолинейная форма равновесия стержня становится неустойчивой и возникает новая устойчивая форма равновесия — криволинейная. При этом качественном изменении характера деформации конструкция практически выходит из строя: она или разрушается, или в ней возникают недопустимо большие перемещения (прогибы). Поэтому расчет конструкции должен обеспечить такое соотношение нагрузок, размеров и свойств материалов, при котором гарантирована (с определенным запасом) устойчивость заданной (прямолинейной) формы равновесия.
Итак, третья задача сопротивления материалов — расчет элементов конструкций на устойчивость.
Подводя итог всему сказанному выше, заключаем, что сопротивление материалов дает основы расчета элементов конструкций на прочность, жесткость и устойчивость.
Сопротивление материалов — расчетно-теоретическая дисциплина, основные положения которой проверяются и дополняются экспериментальными исследованиями. Опытная проверка теоретических расчетов и формул необходима потому, что они основаны на ряде упрощающих предпосылок и допущений. Эти предпосылки и допущения связаны как со свойствами материалов, так и с характером деформаций элементов конструкций. В ряде случаев приходится специально изготовлять модель проектируемой конструкции (или отдельных ее элементов) и подвергать ее испытаниям, чтобы получить данные о характере и величине деформаций, так как чисто теоретическим путем создание методов расчета оказывается вообще невозможным. Наконец, необходимо учесть, что все расчеты, выполняемые методом сопротивления материалов, базируются на знании физико-химических свойств конструкционных материалов. Эти свойства определяют путем лабораторных испытаний специально изготовленных образцов.
При решении задач сопротивления материалов широко применяют уравнения равновесия различных систем сил, полученные в статике абсолютно твердого тела. Вместе с тем не все приемы и методы статики могут быть использованы в сопротивлении материалов. Замена одной системы сил другой, статически эквивалентной, в частности перенос силы по линии ее действия и замена ряда сил их равнодействующей, резко изменяет характер деформации детали и поэтому недопустима. Поясним это положение некоторыми примерами.
На рис. 1.4, а, б показан брус, нагруженный растягивающей силой F; в первом случае сила приложена к концу бруса, во втором она перенесена по линии действия в некоторую точку В. В результате этого переноса деформироваться будет не весь брус, а только часть АВ.
Перенос сил по линиям их действия может привести к еще более резкому изменению характера деформации, чем в рассмотренном случае. Например, в результате переноса сил, приложенных к торцам бруса (рис. 1.5,и), можно получить нагружение, показанное на рис. 1.5, б, т. е. брус будет испытывать не растяжение, а сжатие.
На рис. 1.6,а изображена балка, нагруженная парой сил на левой опоре. Штриховой линией показан характер ее деформации. При переносе этой пары сил в положение, показанное на рис. 1.6,б, характер деформации резко изменяется. При втором положении нагрузки допускаемое по условию прочности значение момента пары вдвое больше, чем в первом. Реакции опор балки в том и другом случаях, конечно, одинаковы.
На рис. 1.7,а,б показаны две одинаковые балки, первая нагружена равномерно распределенной нагрузкой интенсивностью q, а вторая — силой F ф (т. е. силой, равной равнодействующей этой нагрузки). Опорные реакции рассматриваемых балок одинаковы, но наибольший прогиб второй балки в 1,6 раза больше, чем первой, а допускаемая по условию ее прочности нагрузка вдвое меньше.
Из рассмотренных примеров следует, что при определении опорных реакций в статически определимых системах статически эквивалентные преобразования нагрузки допустимы, но при вычислении перемещений и расчетах на прочность замена некоторой системы сил другой, статически эквивалентной заданной, приводит к весьма серьезным ошибкам.
studfiles.net
Сопротивление материалов
(Для студентов механического и строительного направлений)
Скачать учебник А.В. Александров Сопротивление материалов (для строит. спец. ВУЗов, 2003г, 7.5Мб )
Скачать учебник В.И. Феодосьев «Сопротивление материалов». изд. МГТУ им Баумана, для ВТУЗов 1999г, 8Мб)
Скачать учебник А.В. Дарков Г.С.Шпиро «Сопротивление материалов» ( для ВТУЗов, Москва, 1975г, 15Мб)
Скачать учебник М.Д. Подскребко «Сопротивление материалов» ( для ВТУЗов, Минск, 2007г, 14Мб)
Скачать пособие Б.А. Ободовский Сопротивление материалов в примерах и задачах
( для ВТУЗов, 1982г, 5Мб)
Скачать задачник Н.М.Беляев Сборник задач по сопромату
( для ВТУЗов, 1968г, 4,3Мб)
Скачать пособие к решению задач. И.Н.Миролюбов, 1967г. ( для механ. спец, 5Мб)
Скачать руководство к решению задач. В.А.Бобрин, 2006г. ( для стр. трансп. спец , 1Мб)
Скачать решение задач по сопротивлению материалов. Э.А.Буланов,
1994г. ( для немашиностр. спец , 17Мб)
Ознакомиться, (скачать — если нужно) мою программу МКЕ для расчёта плоских рам (и балок)
Скачать или открыть документ MS Excel «Геометрические характеристики плоских сечений» (нужно ввести данные и просмотреть результаты). Есть примеры, формулы, инструкция. 250 кб
Скачать или открыть документ MS Excel «Построение эпюр нормальных, касательных и главных напряжений в поперечном (двутавровом) сечении» (нужно ввести данные и просмотреть результаты) 31кб
Скачать или открыть документ MS Excel «Вычисление напряжений в опасных точках при внецентренном сжатии» (нужно ввести данные и просмотреть результаты) 38кб
Рассчитать в on-line (платно) балку, ферму, раму ( перейти на сайт sopromat.org)
Скачать учебники, методички (в виде RAR-архивов или смотреть в формате PDF)
подготовленные кафедрой СМиСМ
КубГТУ
Содержание
- Основные термины, гипотезы.
- Определение реакций опор.
- Деформации, внутренние силы, внутренние силовые факторы.
- Пример построения эпюр ВСФ для балки.
- Правила контроля эпюр
- Простой способ построения эпюр для балок. New: 21.03.2012
Разделы, предназначенные только для механических специальностей помечены знаком (М), разделы для строителей — знаком (С).
Примеры построения эпюр В.С.Ф. (для строителей)
Примечания к этим примерам:- Размерности не проставлены. Имеется в виду: силы — в кН, моменты — в кНм, распределённые нагрузки — в кН/м.
- Масштаб не соблюдается
- Картинки задач перекрываются, т е на страничке могут быть лишние эпюры (от предыдущей или следующей задачи)
Примеры решения заданий РГР (для механиков)
www.win-ni.narod.ru