1.4. Внутренние усилия. Метод сечений

1.4. ВНУТРЕННИЕ УСИЛИЯ. МЕТОД СЕЧЕНИЙ Величиной внутренних усилий определяется степень деформации элемента конструкции и возможность разрушения в том или ином опасном сечении элемента конструкции. Внутренние усилия – силы взаимодействия между частицами тела (кристаллами, молекулами, атомами), возникающие внутри элемента конструкции, как противодействие внешним нагрузкам. Для выявления внутренних усилий пользуются методом сечений. 1. Рассечь нагруженное тело плоскостью Р на две части (рис. 1.10, а). 2. Отбросить одну из частей (рис. 1.10, б). Реальное тело представляет собой конгломерат различно ориентированных зерен, от граней которых в разных направлениях действуют элементарные внутренние усилия. 3. Заменить действие отброшенной части внутренними усилия- ми. При этом используется аппарат теоретической механики: определение равнодействующей системы сходящихся сил, параллельных сил, перенос сил в заданную точку – центр тяжести сечения 0 (рис. 1.10, в). По- лученные в результате приведения главный вектор R и главный момент M спроецировать на главные оси инерции z, y и геометрическую ось x. 4. Уравнения равновесия позволяют определить внутренние усилия. Всего их шесть: три силы – проекции главного вектора R (рис. 1.10, г): Σx = 0; N = … Продольное усилие от англ. normal Σy = 0; Qy =… Поперечное усилие Σz = 0; Qz =… Поперечное усилие от нем. querlaufend и три момента – проекции главного момента М: ΣMx = 0; T = … Крутящий момент от англ. torsional, torque ΣMy = 0; My =… Изгибающий момент ΣMz = 0; Mz =… Изгибающий момент от англ. moment Таким образом, можно сформулировать правило определения внутренних силовых факторов: внутренние силы N, Qy, Qz численно равны алгебраической сумме проекций всех внешних сил (в том числе и реакций), приложенных к брусу по одну сторону от рассматриваемого сечения. Аналогично: внутренние моменты T, My, Mz численно равны алгебраической сумме моментов от внешних сил, действующих по одну сторону от рассматриваемого сечения. Какую именно сторону, правую или левую, верхнюю или нижнюю следует рассматривать, зависит от схемы нагружения. Предпочтение следует отдавать более простому варианту. Принимая во внимание важность описанных выше процедур, запишем кратко последовательность основных этапов метода сечения: Р – рассечь тело на две части плоскостью; О – отбросить одну из частей тела; З – заменить действие отброшенной части внутренними усилиями; У – уравнения равновесия составить. Единица измерения усилий – ньютон (обозначение: Н). Это производная единица. Исходя из второго закона Ньютона (F = m•a) она определяется как сила, изменяющая за 1 с скорость тела массой 1 кг на 1 м/с в направлении действия силы. Таким образом, 1 Н = 1 кг•м/с2. Измерять силу в ньютонах стали спустя два века после смерти великого ученого, когда была принята система СИ. 1 Н = 0,10197162 кгс; 1 кгс = 9,80665 Н. Каждая компонента внутренних усилий характеризует сопротивление тела какому-либо одному виду деформации – простому сопротивлению. Например, при N ≠ 0, будет растяжение или сжатие. При Q ≠ 0 имеет место сдвиг, при Т ≠ 0 – кручение, а при М ≠ 0 – изгиб. При наличии двух и более компонентов будет сложное сопротивление тела.

dx-dy.ru

Внешние и внутренние силы в сопромате.

В сопромате силы, приложенные к телу в результате взаимодействия тел, называются внешними. Внешние силы бывают объемными (например, собственный вес) и поверхностными. Поверхностные силы делятся на сосредоточенные (теоретически действующие в точке), и на распределенные (приложенные по длине или на площади). Величина распределенной нагрузки, приходящейся на единицу длины или площади, называется интенсивностью нагрузки. Сопротивление материалов изучает не только статические , но и динамические нагрузки.  По времени действия нагрузки делятся на постоянные и временные. По характеру действия нагрузки подразделяются на статические и динамические. Статические нагрузки прилагаются постепенно, они не меняются, или меняются незначительно. Динамические нагрузки меняют величину в течение короткого промежутка времени. Под действием внешних сил в материале возникают внутренние силы, сопровождающие деформацию.

Метод сечений, напряжения.

Для определения внутренних сил, возникающих в брусе от действия внешних сил, в сопромате применяется метод сечений.

 

  Изучаемый брус мысленно рассекаем плоскостью на две части. Предполагаем, что каждая из частей находится в равновесии под действием внешних сил, приложенных к этой части, и внутренних сил, возникающих в сечении и представляющих собой силы взаимодействия между оставшейся и отброшенной частями. Равнодействующая внутренних сил в сечении называется внутренним усилием. Рассмотрим пространственный брус, находящийся в равновесии под действием внешних сил (рис. 1).

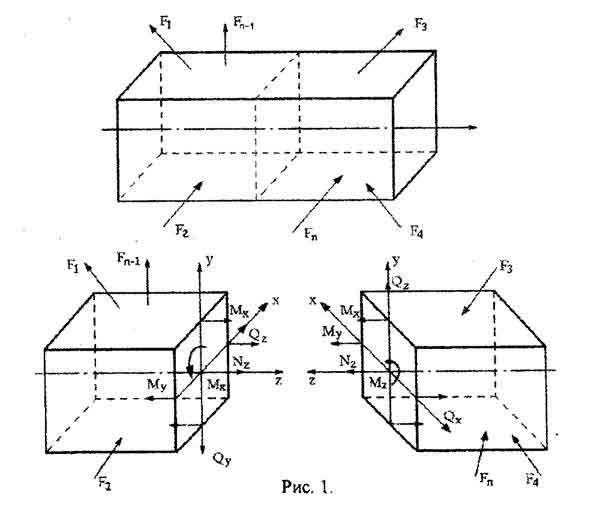
  Если брус рассечь плоскостью (использование метода сечений), перпендикулярной оси, т.е. поперечным сечением (рис. 1) и разложить главный вектор и главный момент внутренних сил по осям x,y,z, то на каждой стороне сечения получим шесть внутренних силовых факторов: три силы (N, Qx, Qy) и три момента (Mx, My, Mz).

 

 Эти шесть усилий, совместно с внешними силами, действующими на отсеченную часть бруса, должны обеспечить равновесия этой части. Таким образом, для каждой части бруса должны быть выполнены шесть условий равновесия: сумма моментов сил относительно осей координат, сумма проекций сил на оси координат равна нулю. В этом и есть суть метода сечений 

сопромата.

 Усилия, возникающие в сечении бруса, имеют в сопромате следующие наименования: 

 

N — продольная сила; Qу, Qх — поперечные силы;

Мz — крутящий момент; Мх, Му — изгибающие моменты.

 

  Внутренняя сила (Nz, Qу , Qх) численно равна алгебраической сумме проекций на соответствующую ось бруса всех внешних сил, расположенных по одну сторону от сечения.

 

  Момент (Мz Мx Мy) в любом сечении численно равен алгебраической сумме моментов относительно соответствующей оси бруса от всех внешних сил, расположенных по одну сторону от сечения.

 

  Графики, показывающие как изменяются внутренние усилия при переходе от сечения к сечению, в сопромате называются эпюрами.

  Интенсивность внутренних сил, приходящихся на единицу площади, в сопротивление материалов называется напряжением.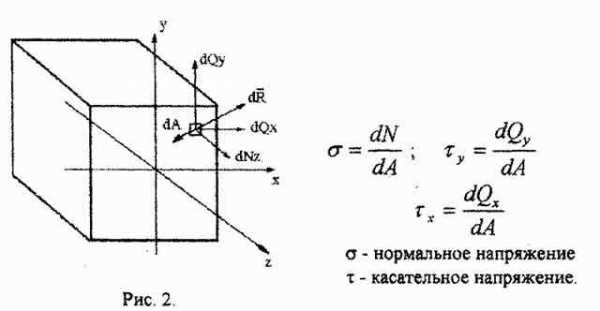

  Допустим, что около некоторой точки поперечного сечения бруса, выделена элементарная площадка dА (рис.2). Равнодействующая внутренней силы, действующая на данной площадке, равна dR.. Проекциями dR на оси будут dN, dQy и dQx.

Разделив величины dN, dQy и dQx на площадь dA, получим величины продольных и попе-

речных сил, приходящихся на единицу площади: 

 

 

 

 

 Их измеряют в единицах напряжения — паскалях (Па) и кратных ему — (кПа и мПа)

Полное напряжение в данной точке рассматриваемого сечения:

Сила — величина векторная, следовательно, и напряжение – вектор того же направления.

Между напряжениями и деформациями существует зависимость. В случае упругой деформации эта зависимость выражается законом Гука.

 

 Закон Гука при линейной деформации (растяжение или сжатие) выражает прямолинейную зависимость между нормальными напряжениями и относительными деформациями.

 

 

При угловой деформации (сдвиг) существует прямолинейная зависимость между касательными напряжениями и углами сдвига:   т = уе.

В этих выражениях Е и G — коэффициенты пропорциональности,

характеризующие упругие свойства материалов:

Е — модуль нормальной упругости или модуль Юнга;

G — модуль упругости при сдвиге или модуль сдвига;

е — относительная продольная деформация;

у — относительная угловая деформация.

 

studfiles.net

Внутренние силы. Метод сечений | ПроСопромат.ру

Силы, как известно, бывают внешние и внутренние. Если взять в руки обычную ученическую линейку и изогнуть ее, то делаем мы это, прикладывая внешние силы – руки. Если усилие рук убрать, то линейка вернется в исходное положение самостоятельно, под воздействием своих внутренних сил (это силы взаимодействия между частицами элемента от воздействия внешних сил). Чем больше внешние силы, тем больше и внутренние, но внутренние не могут постоянно увеличиваться, они растут лишь до определенного предела, и когда внешние силы превысят внутренние, произойдет

разрушение. Поэтому крайне важно знать о внутренних силах в материале с точки зрения его прочности. Внутренние силы определяются с помощью метода сечений. Рассмотрим его подробно. Допустим, стержень нагружен  некоторыми силами (верхний левый рис.). Разрезаем стержень сечением 1–1 на две части, и будем рассматривать любую из них – ту, которая покажется нам проще. К примеру, отбрасываем правую часть и рассмотрим равновесие левой части (верхний правый рис.).

Действие отброшенной правой части на оставшуюся левую заменяем внутренними силами, их бесконечно много, так как это силы взаимодействия между частицами тела. Из теоретической механики известно, что любую систему сил можно заменить эквивалентной ей системой, состоящей из главного вектора и главного момента. Поэтому все внутренние силы приведем к главному вектору R и главному моменту М (рис.1.1,б). Поскольку наше пространство трехмерно, то главный вектор R можно разложить по осям координат и получить три силы — Q

x, Q_y, N_z(рис.1.1,в). По отношению к продольной оси стержня силы Q_x, Q_yназываются поперечными или перерезывающими силами (расположены поперек оси),  N_zполучил название продольной силы (расположена вдоль оси).

Главный момент М при разложении по осям координат также даст три момента(рис.1.1,г) в соответствии с той же продольной осью  — два изгибающих момента M_x и M_y и крутящий момент Т (может обозначаться как М_к   или М_z).

Таким образом, в общем случае нагружения существует  шесть компонентов внутренних сил, которые называются внутренними силовыми факторами или внутренними силами. Для их определения в случае пространственной системы сил составляются шесть

уравнений равновесия,  а в случае плоской – три.

Чтобы запомнить последовательность метода сечений, следует использовать мнемотехнический прием – запомнить слово РОЗУ из первых букв действий: Разрезаем (сечением), Отбрасываем (одну из частей), Заменяем (действие отброшенной части внутренними силами), Уравновешиваем (т.е. с помощью уравнений равновесия определяем значение внутренних сил).

В практике возникают следующие виды деформаций. Если при случае нагружения в элементе под действием сил возникает один внутренний силовой фактор, то такая деформация называется простой или основной. Простые деформации —  это растяжение-сжатие (возникает продольная сила), сдвиг (поперечная сила), изгиб (изгибающий момент), кручение (крутящий момент). Если одновременно элемент испытывает несколько деформаций (кручение с изгибом, изгиб с растяжением и др.), то такая  деформация называется сложной.

 

prosopromat.ru

7.1. Внутренние усилия при изгибе

7.1. ВНУТРЕННИЕ УСИЛИЯ ПРИ ИЗГИБЕ

Из шести внутренних усилий, действующих в сечении в общем случае, при плоском поперечном изгибе только два не равны нулю: Qy и Mz (индексы часто опускают). Правила знаков устанавливают не по направлению действию сил, как в теоретической механике, а по виду деформации. Поперечная сила Q в сечении положительна, если ее векторы стремятся вращать части рассеченной балки по ходу часовой стрелки (положительная поперечная сила вызывает положительное касательное напряжение). Изгибающий момент М в сечении положителен, если он вызывает сжатие в верхней части бруса, а растянутая область изгибаемого элемента – в нижней. Часто эпюры изгибающего момента строят со стороны сжатой зоны элемента, но удобнее – со стороны растянутой. Пример 7.1. Определить внутренние усилия в поперечном сечении консольной балки, нагруженной сосредоточенной силой. Решение. Опора (защемление) накладывает три связи, обусловливающие возникновение трех реакций: вертикальную и горизонтальную составляющие реакции Rx и Ry, а также опорный момент М. В целях упрощения расчета внутренние усилия определяем со свободного конца. Используем метод сечений: Рассекаем балку на две части; Отбрасываем одну из частей; Заменяем действие отброшенной части внутренними усилиями ( с установленными правилами знаков), составляем Уравнения равновесия, из которых находим внутренние усилия. Система координат помещена в центр тяжести С рассматриваемого сечения. I участок: 0 ≤ х ≤ ℓ. Поперечная сила Q(x) – функция от абсциссы х – величина постоянная. Изгибающий момент M(x) – линейная функция от абсциссы х – описывается уравнением прямой; для ее построения находим значение функции в двух точках – в начале и конце участка: Строим эпюры Q и M. Пример 7.2. Определить внутренние усилия в поперечном сечении консольной балки, на- груженной сосредоточенным моментом. Решение. Внутренние усилия в произвольном сечении I участка: 0 ≤ х ≤ ℓ. Поперечная сила Q(x) отсутствует, изгибающий момент M(x) – величина постоянная; имеет место чистый изгиб Строим эпюры Q и M. Общий подход к определению внутренних усилий при изгибе В балке бесконечной протяженности выберем начало координат на левом конце. Внутренние усилия находим методом сечений Здесь Сq – множитель, имеющий смысл координаты центра тяжести распределенной нагрузки. Рис. 7.2. Схема к определению внутренних усилий Поперечная сила в произвольном сечении равна алгебраической сумме всех внешних сил, действующих по одну сторону от сечения х. Изгибающий момент в произвольном сечении равен алгебраической сумме моментов от всех внешних сил, действующих по одну сторону от сечения х, взятых относительно центра тяжести рассматриваемого сечения.

dx-dy.ru

Метод сечений (сопромат)

Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.

Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).

Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.

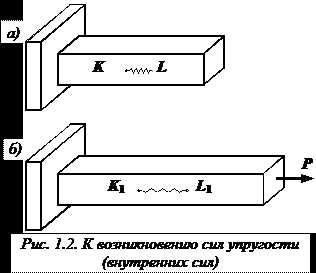Приложим теперь к стержню растягивающую силу (рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение , а частица L – в положение . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.

Этапы метода сечений

Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.

Разрежем стержень, находящийся в равновесии под действием некоторой системы сил (рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.

Отбросим одну из частей стержня и рассмотрим оставленную часть.

Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами (рис. 1.3, б).

Внутренние силы в методе сечений

Полученную бесконечную систему сил по правилам теоретической механики можно привести к центру тяжести поперечного сечения. В результате получим главный вектор R и главный момент M (рис. 1.3, в).

Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.

Получим 6 внутренних силовых факторов, возникающих в поперечном сечении стержня при его деформировании: три силы (рис. 1.3, г) и три момента (рис. 1.3, д).

Сила N — продольная сила

– поперечные силамы,

момент относительно оси z () – крутящий момент

моменты относительно осей x, y () – изгибающие моменты.

Запишем для оставленной части тела уравнения равновесия (уравновесим):

.

Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.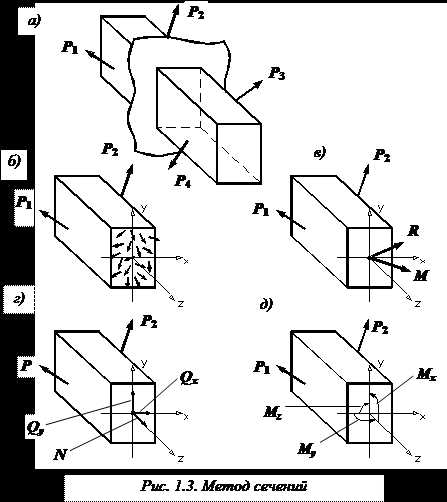

Вычисление продольной и поперечных сил, крутящего и изгибающих моментов

продольная сила N равна сумме проекций всех сил (активных и реактивных), действующих на любую из частей рассеченного стержня, на ось z;

поперечные силы равны сумме проекций всех сил, действующих на любую из частей стержня, на оси x и y, соответственно;

крутящий момент равен сумме моментов всех сил, действующих на любую из частей стержня, относительно продольной оси z;

изгибающие моменты равны сумме моментов всех сил, действующих на любую из частей стержня, относительно осей x и y, соответственно.

sopromato.ru

Внутренняя сила | Лекции и примеры решения задач механики

Внутренняя сила (ВС)– один из двух (наряду с внутренним моментом) силовых факторов возникающих в поперечном сечении бруса под действием внешних нагрузок.

Рассмотрим некоторый брус, находящийся под воздействием произвольной системы внешних сил.

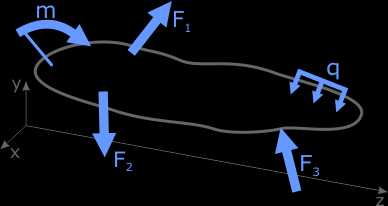
Оговоримся, что эти нагрузки удерживают брус в состоянии равновесия.

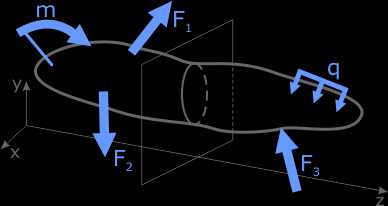
Для расчета внутренних сил применяется метод сечений.

Если данный брус мысленно рассечь в любом месте и рассмотреть одну из частей, то для обеспечения ее неподвижности отброшенная часть заменяется действием внутренней силы R и внутреннего момента M.

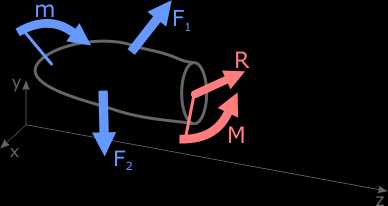
Другими словами, внутренняя сила это некоторое усилие, с которым обе части бруса «удерживают» друг друга.

В общем случае нагружения внутренняя сила может располагаться под любым углом к поперечному сечению рассматриваемого бруса. Поэтому для некоторого упрощения расчетов её раскладывают на составляющие, проецируя на соответствующие оси координат.

Всего может быть три составляющие полной внутренней силы: продольная сила N и две поперечные силы Q_x и Q_y.

Величина и направление внутренних сил определяется из условия статичности отсеченных частей бруса. Для этого записываются необходимые уравнения статики: суммы проекций всех внешних и внутренних сил приложенных к рассматриваемой части приравниваются к нулю

откуда

При растяжении-сжатии внутренняя сила в поперечном сечении направлена вдоль оси стержня (продольная сила N).

При кручении ВС равна нулю (имеет место только внутренний скручивающий момент).

При поперечном изгибе ВС направлена поперек продольной оси балки (поперечная сила Q).

Знак внутренних сил зависит от направления и расположения по отношению к рассматриваемой части бруса и принимается согласно соответствующих правил.

Практически все прочностные расчеты в механике начинаются с определения внутренних усилий в элементах конструкций.

В случаях, когда внутренние усилия меняют величину и знак по длине бруса для наглядности строят их эпюры.

Пример эпюры внутренних продольных сил при растяжении-сжатии

Расчет внутренних сил >>
Другие примеры решения задач >>

isopromat.ru

Метод сечений в сопротивлении материалов. Внутренние и внешние силовые факторы. Напряжение.

Сопротивление материалов

Метод сечений. Напряжения



Сущность метода сечений

Для расчетов элементов конструкции на прочность необходимо знать внутренние силы упругости, возникающие в результате приложения внешних сил в разных точках и частях конструкции.
Но как заглянуть внутрь материального тела, чтобы выяснить, какие же силы возникают между его частицами или отдельными частями, при приложении нагрузок? Представление о внутренних усилиях, возникающих в теле или элементе конструкции можно получить лишь с помощью воображения и аксиом статики, поясняющих условия равновесного состояния материальных тел.
Способы определения этих внутренних сил с помощью науки сопротивление материалов включают такой прием, как метод сечений.

Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза со стороны отброшенной части. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием приложенных к сечению внешних и внутренних сил (третий закон Ньютона – действие равно противодействию).
При применении этого метода выгоднее отбрасывать ту часть элемента конструкции (тела), для которой проще составить уравнение равновесия. Таким образом, появляется возможность определить внутренние силовые факторы в сечении, благодаря которым оставшаяся часть тела находится в равновесии (прием, часто применяемый в Статике).

Применяя к оставленной части тела условия равновесия, невозможно найти закон распределения внутренних сил по сечению, но можно определить статические эквиваленты этих сил (равнодействующие силовые факторы).
Так как основным расчетным объектом в сопротивлении материалов является брус, рассмотрим, какие статические эквиваленты внутренних сил проявляются в поперечном сечении бруса.

Рассечем брус (рис. 1) поперечным сечением а-а и рассмотрим равновесие его левой части.
Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а-а, будут главный вектор F_гл, приложенный в центре тяжести сечения, и главный момент М_гл = М_и, уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.

Разложим главный вектор на составляющую N, направленную вдоль оси бруса, и составляющую Q, перпендикулярную этой оси и лежащую в плоскости сечения. Эти составляющие главного вектора и главный момент называют внутренними силовыми факторами, действующими в сечении бруса. Составляющую N называют продольной силой, составляющую Q – поперечной силой, пару сил с моментом М_и – изгибающим моментом.

Для определения указанных трех внутренних силовых факторов применим известные из Статики уравнения равновесия оставленной части бруса:

Σ Z = 0;     Σ Y = 0;     Σ M = 0;    (ось z всегда направляем по оси бруса).

Если внешние силы, действующие на брус, не лежат в одной плоскости, т. е. представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 2), для определения которых применяют известные из Статики шесть уравнений равновесия оставленной части бруса:

Σ X = 0;     Σ Y = 0;     Σ Z = 0;
Σ M_x = 0;     Σ M_y = 0;     Σ M_z = 0.

Эти силовые факторы в общем случае носят следующие названия: N – продольная сила, Q_x, Q_y – поперечные силы, М_кр – крутящий момент, М_ихи М_иу – изгибающие моменты.

При разных деформациях в поперечном сечении бруса возникают различные силовые факторы.
Рассмотрим частные случаи:

1. В сечении возникает только продольная сила N. Это деформация растяжения (если N направлена от сечения) или сжатия (если N направлена к сечению).

2. В сечении возникает только поперечная сила Q. Это деформация сдвига.

3. В сечении возникает только крутящий момент М_кр. Это деформация кручения.

4. В сечении возникает только изгибающий момент М_и. Это деформация чистого изгиба. Если в сечении одновременно возникает изгибающий момент М_и и поперечная сила Q, то изгиб называют поперечным.

5. Если в сечении одновременно возникает несколько внутренних силовых факторов (например, изгибающий момент и продольная сила), то имеет место сочетание основных деформаций (сложное сопротивление).

***



Напряжение

Наряду с понятием деформации одним из основных понятий сопротивления материалов является напряжение (обозначается р).
Напряжение характеризует интенсивность внутренних сил, действующих в сечении, и определяется, как отношение величины внутренней силы к площади сечения.
Напряжение является величиной векторной.

Вектор напряжения можно разложить на две составляющие (рис. 3) – одну вдоль оси сечения, вторую – в плоскости сечения (перпендикулярно оси). Эти составляющие носят название нормальное напряжение (обозначается σ) и касательное напряжение (обозначается τ).
Поскольку нормальные и касательные напряжения расположены под прямым углом друг к другу, модуль полного напряжения p можно определить по теореме Пифагора:

р² = σ² + τ²

Единица измерения напряжения – паскаль (Па).
1 Па = Н / м². Поскольку эта единица очень мала, в расчетах часто применяют более крупную кратную единицу – мегапаскаль (МПа), который равен миллиону паскалей (10⁶ Па).

Объяснить сущность напряжения можно на таком простом примере.
В соответствии с гипотезой об отсутствии первоначальных внутренних усилий, считается, что когда к телу не приложены внешние нагрузки его частицы не взаимодействуют друг с другом, т. е. абсолютно равнодушны к «соседкам» справа, слева и т. п. Но стоит приложить к телу внешнюю нагрузку, его частицы начинают лихорадочно цепляться друг за друга, пытаясь удержаться в «кучке». Если нагрузка растягивает тело, его частицы держатся друг за дружку, не давая разорвать тело, если нагрузка сжимающая — частицы тела стараются удержать «соседок» на прежнем расстоянии.
Совокупность всех этих усилий внутренних частиц, противостоящих внешним раздражителям-нагрузкам, и является напряжением.
Задачи сопромата чаще всего сводятся к тому, чтобы определить предельные величины нагрузок, способных разорвать связи между частицами, из которых состоит тело или, по известным предельным напряжениям определить, какие нагрузки способно выдержать тело не разрушаясь, не деформируясь и т. д.

Нетрудно заметить, что напряжение измеряется в тех же единицах, что и давление, поэтому можно провести некоторую аналогию между этими физическими понятиями. Принципиальная разница заключается в том, что давление — внешний силовой фактор (т. е. воздействующий на тело или его части извне), а напряжение — внутренний силовой фактор, характеризующий степень взаимодействия (взаимосвязи) частиц тела между собой.

***

Правила построения эпюр



№ вопроса	1	2	3	4	5	6	7	8	9	10
Правильный вариант ответа	3	2	3	2	2	3	1	2	1	2

k-a-t.ru