Лекция №3-механика
Лекция №3
Тема: «Внутренние усилия в поперечных сечениях стержня»
Вопросы:
1. Опоры и опорные реакции, и их определение
2. Поперечная сила и изгибающий момент
3. Взаимосвязь между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки
1. Опоры и опорные реакции, и их определение
При расчете конструкций в основном встречаются элементы, испытывающие изгиб. Стержни, работающие преимущественно на изгиб, называют балками. Для того чтобы балка могла испытывать нагрузку и передавать ее на основание, она должна быть соединена с ним опорными связями. На практике применяют несколько типов опорных связей, или, как говорят, несколько типов опор.
Различают три основных типа опор:
а) шарнирно-подвижная опора:
б) шарнирно-неподвижная опора:
в) жесткая заделка.
Рис. 1
На рис. 1 показана шарнирно-подвижная опора, такая опора позволяет балке свободно поворачиваться и перемещаться в горизонтальном направлении. Поэтому реакция в опоре будет одна вертикальная сила. Условное обозначение такой опоры показано справа.
Рис. 2
На рис. 2 показана шарнирно-неподвижная опора. Такая опора позволяет балке свободно поворачиваться, но перемещаться она не может. Поэтому могут возникать две реакции — вертикальная и горизонтальная силы. Их можно сложить и получить одну результатирующую силу, но нужно знать угол, под которым oна будет направлена. Более удобно будет пользоваться вертикальной и горизонтальной составляющими реакции.
На рис. 3 показана жесткая заделка. Она не позволяет балке ни поворачиваться, ни перемещаться. Поэтому могут возникать три опорные реакции: момент, вертикальная и горизонтальная силы. Если балка не имеет на конце опоры, то эта часть ее называется консолью.
Рис. 3
Определим реакции опор для балки (см. рис. 4).
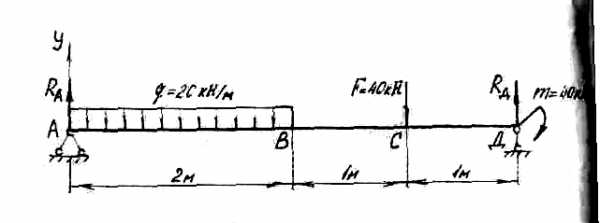
Рис.4
В опоре
А горизонтальная реакция равна нулю,
так как распределенная
нагрузка q
и сосредоточенная сила F
имеют
вертикальное
направление. Реакции опор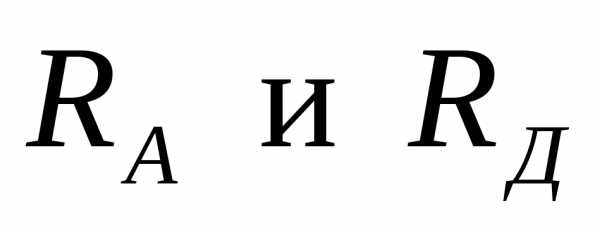 
направим
вверх.
Составим два уравнения статического
равновесия сил. Сумма моментов относительно
каждой из опор равна нулю. Уравнения
моментов нужно составлять относительно
опор, так как в этом случае получаются
уравнения с одним неизвестным. Если
составить уравнения
относительно точек В и С, то получим
уравнения с двумя неизвестными,
а их решать сложнее. Моменты против
часовой стрелки будем считать
положительными, по часовой
отрицательными.
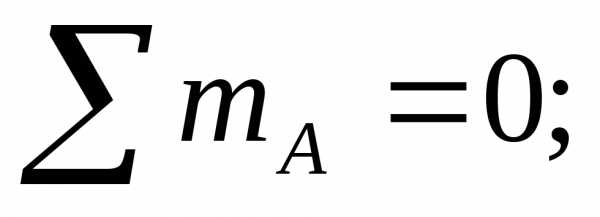
где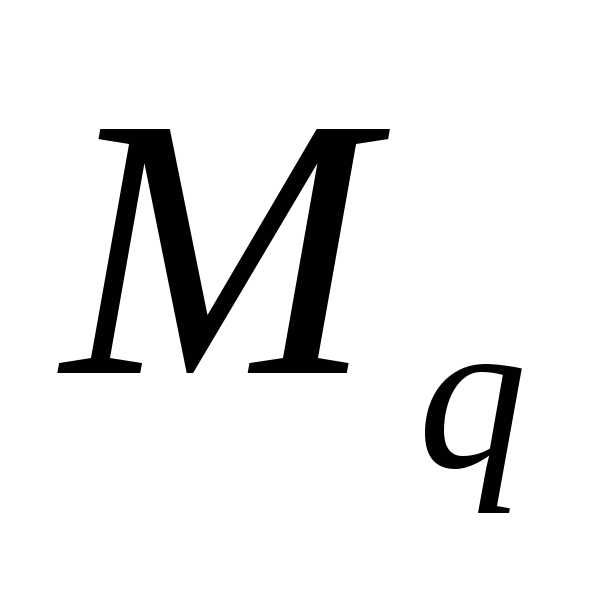 
момент от равномерно распределенной
нагрузки.
Произведение q на расстояние, на котором она приложена,
из условия
равновесия системы равно сосредоточенной
силе, приложенной
посредине отрезка. Поэтому момент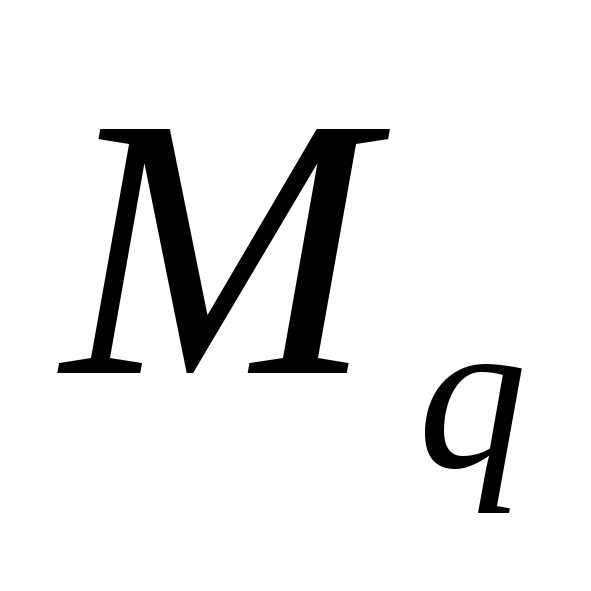 
равен:
–момент силы F
Внешний момент m на плечо не умножается, так как это пара сил, т.е. две равные по величине, противоположно направленные силы, имеющие постоянное плечо.
или
.
Проверка: Сумма всех сил на вертикальную ось Y должна быть равна нулю:
.
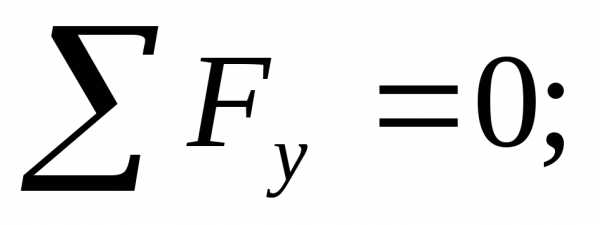
Момент m в условие статического равновесия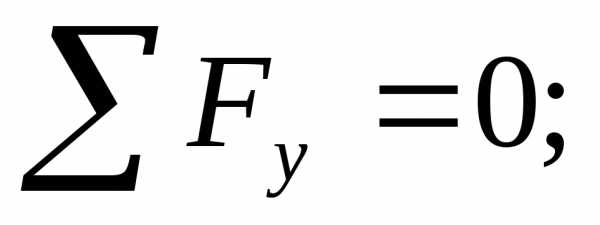 
не записывают,
так как момент
это две равные по величине, противоположно
направленные силы и в проекции на любую
ось они дадут
ноль.
30-20-2-40+50=0:
80-80=0.
Реакции определены правильно.
Пусть
на балку действуют силы 
,
реакции опор
.
Определим внутренние усилия в сечении,
расположенном на расстоянии от нулевого
конца (см. рис.5).
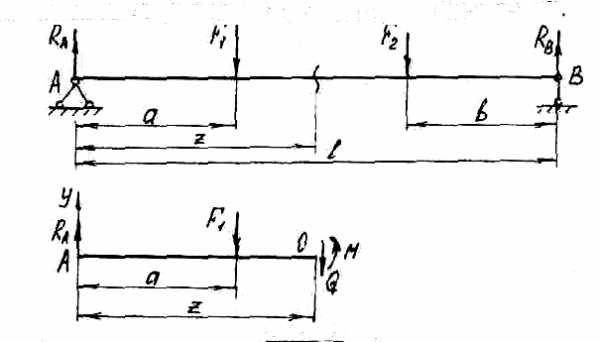
Рис. 5
Поскольку
все внешние силы действуют вертикально,
то горизонтальной составляющей у реакции
опоры А не будет. Балка не будет сжиматься или
растягиваться, т.е. продольная сила в
поперечных сечениях равна нулю. Можно
было взять пример, когда
силы 
были бы не вертикальными по направлению.
Тогда бы в опоре А была бы и вторая реакция
горизонтальная сила, а в сечениях балки
продольная сила N.
В этом случае балка испытывала бы изгиб
с растяжением (сжатием), т.e.
был бы случай сложного сопротивления.
Его мы будем изучать позднее. Вначале
рассматривают более простые задачи и
идут к более сложным, а не наоборот.
Поскольку
внешние силы 
лежат в одной плоскости,
проходящей через ось бруса, то возможно
возникновение
тpex
внутренних усилий: изгибающею момента М,
поперечной силы Q и
продольной силы N,
которая, как мы отмечали, равна нулю.
Значения М и Q определим
из уравнения статического равновесия
левой
части балки:
.
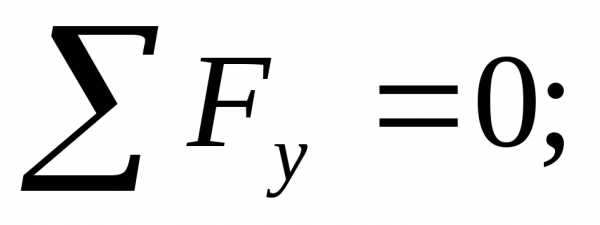
Вывод: поперечная сила в сечении численно равна алгебраической сумме всех внешних сил, а изгибающий момент
Для поперечных сил и изгибающих моментов приняты обязательные правила знаков (см. рис. 6).
Если
сила пытается повернуть рассматриваемую
часть балки по часовой
стрелке, то она вызывает положительную
поперечную силу, и, наоборот, если
действует против часовой стрелки
то поперечная
сила
отрицательная. На рис. 5
сила 
вызывает положительное Q, а 
отрицательное. Следует отметить, что
направление силы положительное для
левой части будет отрицательным для
правой части.
Это вызвано тем, что внутренние силы,
действующие на правую
и левую часть балки обязательно должны
быть равны и противоположно
направлены.
Если внешняя сила или внешний момент изгибают балку выпуклостью вниз, то возникающий изгибающий момент положительный и, наоборот, выпуклостью вверх отрицательный.
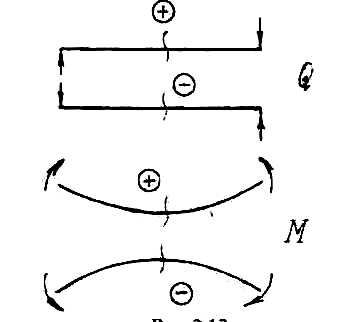
Рис. 6
3. Взаимосвязь между изгибающим моментом,
поперечной силой и интенсивностью распределенной нагрузки
Пусть на консольную балку (см. рис. 7) действует распределенная нагрузка, изменяющаяся по длине балки. На расстоянии z от левого конца возьмем бесконечно малый отрезок dz.
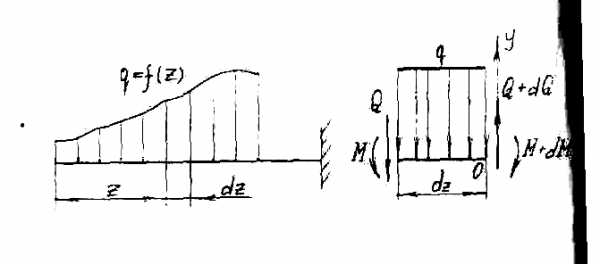
Рис. 7
Тогда распределенную нагрузку на нем можно рассматривать как постоянную. В левой части рассматриваемого отрезка будут внутренние усилия Q и М, в правой с учетом приращения внутренних усилий Q+dQ и M+dM.
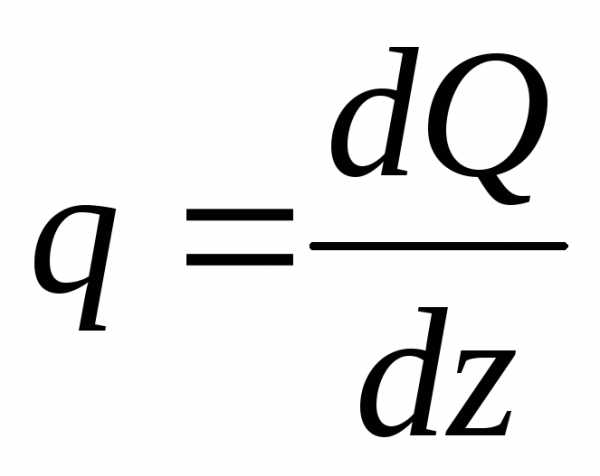(1)
Третьим членом можно пренебречь, как бесконечно малой величиной более высокого порядка, т.е.:
После преобразований получим:
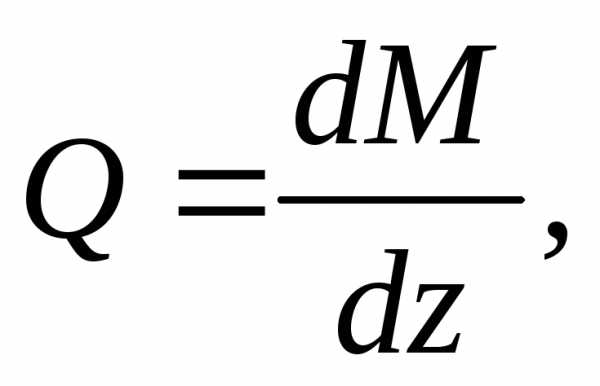(2)
т.е. первая производная от изгибающего момента по абсциссе (длине балки) есть поперечная сила.
Если в формулу (1) подставить значение Q из формулы (2), то получим:
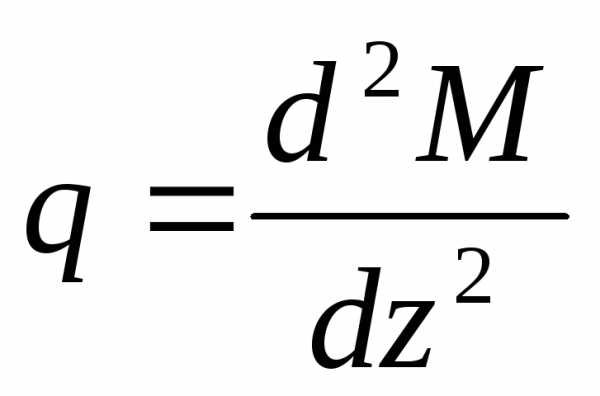, (3)
т.е. вторая производная от изгибающего момента есть интенсивность распределенной нагрузки.
studfiles.netБиомеханика ходьбы и бега. Величина силы реакции опоры
Биомеханика ходьбы и бега. Величина силы реакции опоры
Динамометрические платформы позволяют зарегистрировать в обычной ходьбе три составляющие силы реакции опоры: вертикальную и горизонтальные (переднезаднюю и боковую). Повышенной скорости спортивной ходьбы сопутствуют более высокие, чем при обычной ходьбе, составляющие силы реакции опоры. Например, первый пик вертикальной составляющей может быть почти в два раза больше, чем при обычной ходьбе, но второй, относящийся к отталкиванию, больше только на 10 – 20 %. Переднезадняя составляющая обычно больше на 50 – 60 % в обеих своих частях, т. е. тормозящей и ускоряющей. Если движения бёдер и туловища, а также компенсирующие движения верхних конечностей выполняются технически правильно, то они уменьшают размах колебательного движения более высоко расположенных точек тела: таза, середины туловища и головы.
Скорость бега и способ постановки стопы на опору связаны с характером и величиной силы реакции опоры в беге. Нагрузка на нижние конечности, как правило, больше во время амортизации, чем отталкивания. При спринтерских скоростях в начале фазы опоры появляется высокий пик силы реакции опоры, который в пять раз превышает вес тела. Этот амортизационный пик снижается в соответствии со скоростью бега и способом постановки стопы на опору.
Различают четыре способа постановки стопы на опору. Основной заключается в том, что сначала в контакт с опорой вступает пятка и внешняя часть стопы: таким способом бегают спортсмены на всех дистанциях, но наиболее типичен он для стайеров. Плоскую постановку стопы применяют чаще на средних дистанциях. Более раннее вхождение в контакт с опорой внешней частью плюсны и последующая плоская опора на всю стопу типична для большинства спринтеров.
Отталкивание от опоры осуществляется посредством: 1) собственно отталкивания ногами от опоры; 2) маховыми движениями свободных конечностей тела. Эти движения должны быть тесно взаимосвязаны в едином действии – отталкивании. От их согласованности в значительной мере зависит совершенство отталкивания.
Во время отталкивания бегуна от опоры стопа зафиксирована неподвижно (трение покоя). На стопу как на опорное звено со стороны голени действует давление ускоряемых звеньев тела, направленное вниз и назад (F отт). Через стопу оно передаётся на опору. Противодействием этому давлению служит реакция опоры (R оп). Она приложена к стопе и направлена вперёд – вверх (рис. 1).
Рисунок 1. Отталкивание от опоры
Реакция опоры и давление голени приложены к стопе в противоположных направлениях; они взаимно уравновешиваются и фиксируют стопу на опоре. Реакция опоры и является той внешней силой, сообщающей ускорение ОЦТ тела во время отталкивания.
Маховые движения при отталкивании – это быстрые движения свободных звеньев тела, одинаковые в основном по направлению с отталкиванием ногой от опоры. При маховых движениях перемещаются ЦМ соответствующих звеньев тела.
Когда ускорения маховых звеньев направлены от опоры вверх вперёд, возникают силы инерции этих звеньев, направленные к опоре вниз назад. Совместно с весом тела бегуна, силой отталкивания опорной ноги – они увеличивают силу отталкивания, что дает прирост количества движения, т. е. увеличивают скорость ОЦМ тела.
Таким образом, маховые движения свободных звеньев тела, одинаковые по направлению с отталкиванием ногой от опоры, можно считать составной частью отталкивания. Маховые движения увеличивают силу отталкивания и создают условия для быстрого завершения отталкивания.
opace.ru
Определение реакций опор твердого тела
Для определения реакций опор твердого тела, мы заменяем связи в опорах силами реакций и составляем уравнения равновесия, которые можно разбить на две группы.
1) Сумма проекций всех сил, действующих на тело (включая реакции опор), на произвольную ось рана нулю.
2) Сумма моментов всех сил относительно произвольной оси равна нулю.
Далее, для каждой из групп, мы, на свое усмотрение, выбираем оси и составляем уравнения равновесия.
Если полученные уравнения имеют единственное решение, то задача является статически определимой. Она решается методами статики. Если же, при любом выборе осей, мы получаем систему уравнений, в которой число переменных больше числа независимых уравнений, то такая система имеет бесконечно много решений. Выбрать единственное решение, используя только методы статики, нельзя. Задача является статически неопределимой. Такие задачи решаются методами сопротивления материалов.
Далее мы рассмотрим вопросы, связанные с определением реакций опор твердого тела более подробно и разберем пример решения задачи.
Методы определения реакций опор твердого тела
Рассмотрим некоторое твердое тело, на которое действуют заданные внешние силы. Пусть это тело поддерживается, в состоянии равновесия, некоторой системой опор. То есть тело определенным образом закреплено в некоторых точках – опорах. Эти точки закрепления также называются связями.
Далее мы мысленно отбрасываем опоры и прикладываем вместо них силы. Эти силы называются силами реакций опор. Их направления определяются устройствами соответствующих опор. Нам нужно найти такие значения сил реакций, чтобы при их действии на тело, оно находилось в состоянии равновесия, как это происходит в закрепленном состоянии.
Составляем уравнения равновесия. Их можно записать в виде двух векторных уравнений.
1) Векторная сумма всех действующих на тело сил (включая и силы реакций опор) равна нулю:
(1) .
2) Векторная сумма моментов этих сил относительно, произвольным способом, выбранной точки O равна нулю:
(2) .
Второе уравнение можно записать в эквивалентном виде – сумма моментов сил относительно произвольной оси A′A′′ равна нулю:
(2′) .
Самый простой способ составления уравнений равновесия
Разберем самый простой способ составления уравнений равновесия. С его помощью можно гарантированно получить значения сил реакций опор или определить, что схема закрепления тела в опорах является статически неопределимой.
Выберем прямоугольную систему координат с началом в любой точке. Часто за начало системы координат удобно выбрать точку крепления одной из опор, но это не обязательно. Итак, пусть мы выбрали систему координат Oxyz с началом в точке O.
Спроектируем уравнение (1) на оси этой системы. В результате мы получим три уравнения, связывающие проекции сил на оси xyz:
(1.x) ;
(1.y) ;
(1.z) .
Здесь – n сил, действующих на тело. В их состав также включены и силы реакций опор.
Составим уравнения равновесия (2′) для моментов, относительно осей Ox, Oy, Oz системы координат:
(2.x) ;
(2.y) ;
(2.z) .
Заметим, что эти уравнения являются проекциями векторного уравнения (2) на оси Ox, Oy и Oz.
Уравнения (1.x,y,z) и (2.x,y,z) представляют собой полную систему уравнения равновесия для твердого тела. Если мы попытаемся добавить сюда еще одно уравнение, то оно будет являться линейной комбинацией этих уравнений. Например, мы можем выбрать еще одну ось и, относительно нее, составить уравнение для моментов (2′). Или мы можем спроектировать уравнение (1) для сил на другую ось, не совпадающей ни с одной из осей координат. В результате мы получим еще одно уравнение, но оно нам ничего не даст, поскольку оно будет являться линейной комбинацией уже составленных уравнений.
Таким образом, для одного тела, методами статики, мы можем составить максимум шесть независимых уравнений равновесия. В некоторых случаях их число может быть еще меньше. Так, в случае плоской системы сил, у нас будет всего три независимых уравнения.
Неизвестными в этих уравнениях являются проекции реакций опор на оси координат. Если число неизвестных совпадает с числом независимых уравнений, то задача статически определима, и мы можем получить значения неизвестных, решая линейную систему уравнений. Если число неизвестных меньше числа независимых уравнений и система не имеет решений, то, при такой схеме закрепления тела, равновесие не возможно. Если число неизвестных превышает число независимых уравнений, то система уравнений имеет бесконечное множество решений. Выбрать единственное решение, используя только методы статики, нельзя. Задача является статически неопределимой. Такие задачи решаются методами сопротивления материалов. Например, если у стола три ножки, то мы можем определить силы давления ножек на пол методами статики. Если же у стола четыре ножки, то определить эти силы из уравнений статики нельзя.
Эффективные способы составления уравнений равновесия
В некоторых случаях, вычисления реакций опор твердых тел можно упростить. Это можно сделать соответствующим выбором осей координат, относительно которых вычисляются проекции сил в уравнении (1), а также выбором осей, относительно которых вычисляются суммы моментов (2′). Оси в уравнениях (2′) не обязательно должны быть взаимно перпендикулярными. На странице «Определение реакций опор балки» приводится пример, в котором выбраны две параллельные оси, проходящие через разные точки опор балки. Из уравнений (2′), составленных для этих осей, сразу определяются два значения сил реакций.
Ниже приводится пример, в котором требуемая реакция определяется из одного уравнения за счет соответствующего выбора оси.
Пример решения задачи на определение реакций опор твердого тела
Условие задачи
Три способа закрепления твердого тела.
Твердое тело представляет собой ломаный брус. Показаны три способа его закрепления. Внешние силы и размеры одинаковы для всех способов закрепления. Определить реакции опор для того способа закрепления, при котором момент MA в опоре A имеет наименьшее абсолютное значение.
Дано:
P = 5 kН; M = 8 kН·м; q = 1,2 kН/м.
Решение задачи
Схема 1
Рассмотрим схему 1. Проводим систему координат Axyz с началом в точке A. Ось Az перпендикулярна плоскости рисунка и направлена на нас.
Реакции опор для схемы №1.
Опора A представляет собой жесткую заделку. Отбросим ее и заменим силами реакций. Силы реакций удобно разложить на три составляющие: на две силы и , параллельные осям координат; и на момент (пару сил) MA.
Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
kН.
Точка приложения равнодействующей находится в центре тяжести эпюры – в точке C, посередине отрезка EB:
EC = CB = 1 м.
Итак, мы имеем три неизвестные величины: силы XA, YA и момент MA. Нам нужно определить только одну из них – это момент MA. Заметим, что если мы будем определять моменты относительно оси Az, то моменты от сил XA и YA обратятся в нуль, поскольку они пересекают эту ось. Тогда мы получим уравнение, содержащее только одну неизвестную: MA.
Разложим силу на составляющие вдоль осей координат:
.
Абсолютные значения составляющих:
; .
Находим моменты сил относительно оси Az. По правилу правого винта, положительным направлением является направление против часовой стрелки.
Силы , и пересекают ось A. Поэтому их моменты равны нулю:
; ; .
Сила перпендикулярна плечу AD. Ее момент:
.
Проводим прямую через вектор . Из точки A опускаем перпендикуляр AH на эту прямую. Отрезок AH является плечом силы . Он лежит на оси Ax. Момент силы :
.
Составляем уравнение равновесия. Сумма моментов сил, действующих на тело относительно оси Az равна нулю:
;
;
.
Отсюда
кН·м.
Итак, в первом варианте закрепления тела, момент в заделке A равен
кН·м.
Схема 2
Рассмотрим схему 2.
Реакции опор для схемы №2.
Опора A представляет собой скользящую заделку. Отбросим ее и заменим силами реакций. Силы реакций имеют две составляющие: силу , направленную вдоль оси Ay; и момент MA.
Опора B представляет собой подвижный цилиндрический шарнир. Его реакцией является сила , направленная горизонтально.
Итак, мы имеем три неизвестные величины: силы RA, RB и момент MA. Нам нужно определить только момент MA. Проведем прямые через векторы и . Пусть O – точка пересечения этих прямых. Через эту точку проведем ось Oz′, перпендикулярно плоскости рисунка. Мы будем определять моменты относительно оси Oz′. Поскольку силы и пересекают эту ось, то их моменты равны нулю. Поэтому уравнение для моментов будет содержать только одну неизвестную: MA.
Заметим, что из построения, угол . Тогда вектор пересекает ось Oz′. Поэтому момент от этой силы равен нулю.
Плечом силы является отрезок OC. Тогда момент равен
.
Составляем уравнение равновесия. Сумма моментов сил, действующих на тело относительно оси Oz′ равна нулю:
;
;
.
Отсюда
кН·м.
Итак, во втором варианте закрепления, момент в заделке A равен
кН·м.
Схема 3
Рассмотрим третий вариант закрепления тела.
Реакции опор для схемы №3.
Опора A представляет собой бискользящую заделку. Реакцией здесь является момент (пара сил) MA.
В шарнире B разложим силу реакции на составляющие и вдоль осей координат.
Будем определять моменты относительно оси Bz′′, проходящую через точку B перпендикулярно плоскости рисунка. Тогда моменты от сил XB и YB обратятся в нуль, поскольку они пересекают эту ось. И мы получим уравнение, содержащее только одну неизвестную MA.
Также, как и в первом случае, разложим силу на составляющие вдоль осей координат:
;
; .
Находим моменты сил относительно оси Bz′′.
Плечом силы является отрезок CB = 1 м. Поэтому
.
Проведем прямую через вектор . Она совпадает с осью Ax. Из точки B опустим на нее перпендикуляр BH1. Тогда BH1 будет плечом силы . Ее момент:
.
Точно также проводим прямую через вектор и из точки B опускаем на нее перпендикуляр BH2. Тогда BH2 является плечом силы .
.
Составляем уравнение равновесия. Сумма моментов сил, действующих на тело относительно оси Bz′′ равна нулю:
;
;
.
Отсюда
кН·м.
Для третьего варианта,
кН·м.
Определение остальных реакций
Сравнивая найденные значения момента MA для трех способов закрепления тела, находим, что момент имеет наименьшее значение для второй схемы. Для этой схемы определяем значения остальных реакций.
Составляем уравнения равновесия. Сумма проекций сил на ось x равна нулю:
;
;
.
Отсюда
кН.
Знак “минус” указывает на то, что реакция RB направлена в сторону, противоположную той, что указана на рисунке.
Сумма проекций сил на ось y равна нулю:
;
;
.
Отсюда
кН.
Ответ
Момент MA имеет наименьшее значение для второго способа закрепления тела. Реакции опор, для этого способа закрепления, имеют следующие величины:
кН; кН; кН·м.
Использованная литература:
Сборник заданий для курсовых работ по теоретической механике, под редакцией проф. А.А. Яблонского, Москва «Интеграл-пресс», 2006.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru