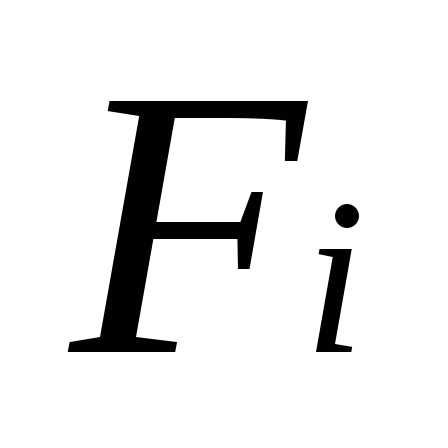3 Расчет балки на двух опорах

И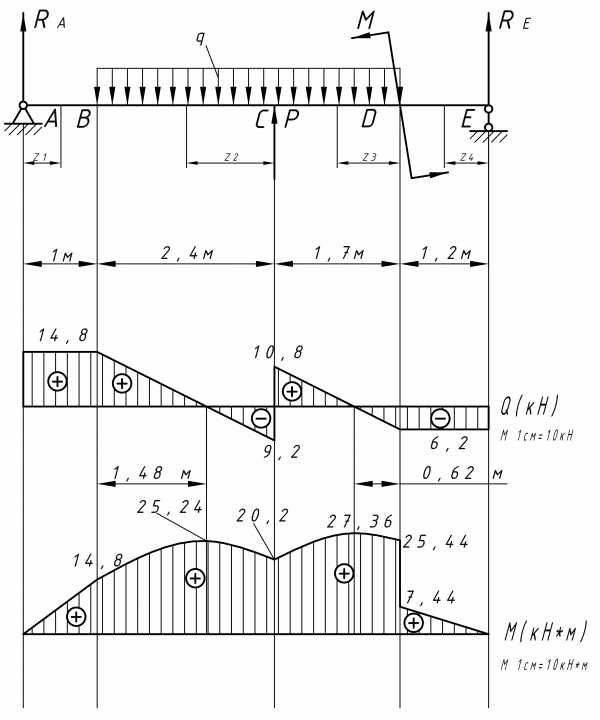сходные данные: М=18 кН*м;P=20 кН; q=10 кН/м; [σ]=110 МПа; k=h/b=1,8.

Рис.3 Расчетная схема

3.1 Определяем реакции опор

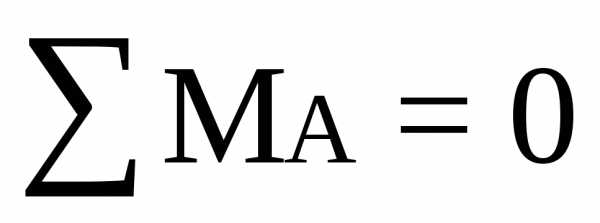
q∙4.1(1+4.1/2)-P∙3.4-M-RE∙6.3=0

10∙4.1∙3.05-20∙3.4-18-RE∙6.3=0

125.05-68-18-RE∙6.3=0

RE=6.2 кН

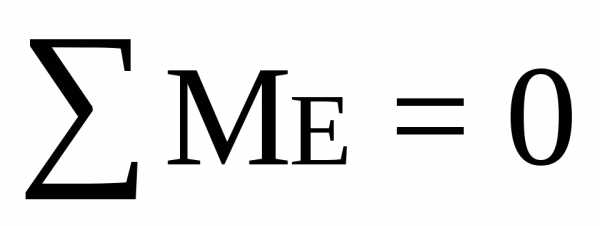
RA∙6.3-q∙4.1(4.1/2+1.2)+P∙2.9-M=0

RA∙6.3-10∙4.1∙3.25+20∙2.9-18=0

RA∙6.3-133.25+58-18=0

RA=14.8 кН

Проверка

∑y=0

RA-q∙4.1+P+RF=0

14.8-10∙4.1+20+6.20=0

41-41=0

0=0

3.2 Определяем значения изгибающих моментов и перерезывающих сил по участкам и строим их эпюры.

Участок АВ: 0≤ Z1≤ 1 м

Q=RA=14.8 кН.

M(Z1)=RA∙Z1;

M(0)=0;

M(1)=14.8 кН∙м.

Участок ВС: 0≤ Z2≤ 2,4 м

Q(Z2)=RA-q∙Z2;

Q(0)=14.8 кН;

Q(2.4)= -9.2 кН.

M(Z2)=RA(1+Z2)-q∙Z2∙Z2/2;

M(0)=14.8 кН∙м;

M(2.4)=20.2 кН∙м,

Определим экстремальное значение на участке:

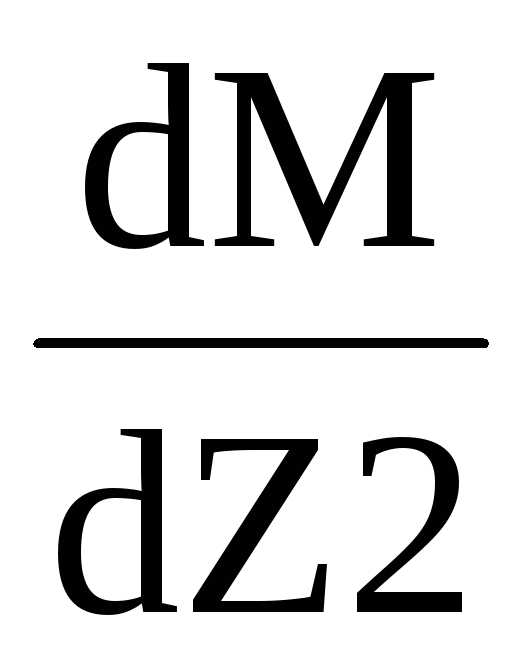
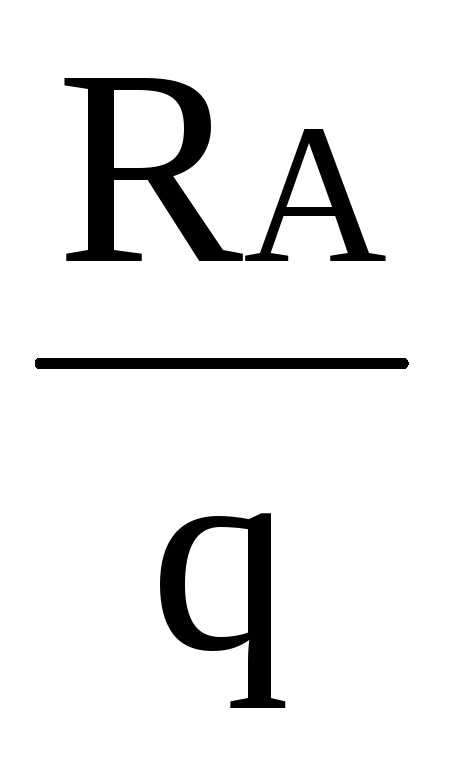=Q=0, RA-q∙Z2=0, Z2==1.48 м

M(1.48)= 25.24 кН∙м

Участок СD: 0≤ Z3≤ 1,7 м

Q(Z3)=-RE+q∙Z3;

Q(0)= -6.2 кН;

Q(1.7)= 10.8 кН.

M(Z3)=RE(1.2+Z3)-q∙Z3∙Z3/2+M;

M(0)=25.44 кН∙м;

M(1.7)=20.2 кН∙м.

Определим экстремальное значение на участке:

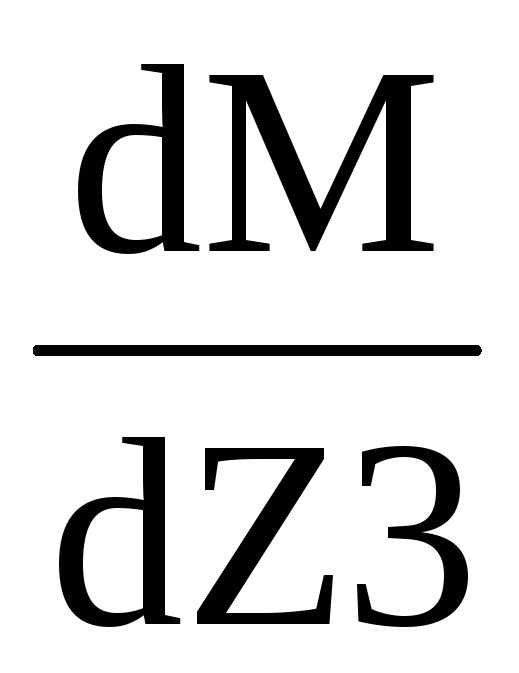=-Q=0, RA-q∙Z3=0, Z3=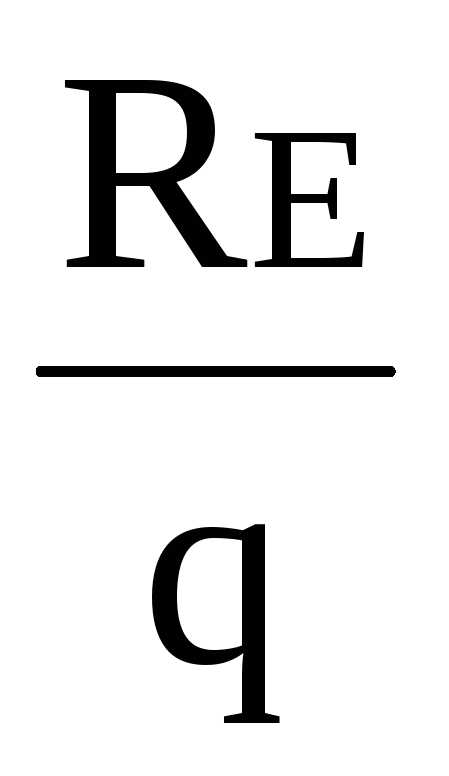=0.62 м

M(0.62)= 27.36 кН∙м

Участок DE: 0≤ Z3≤ 1,2 м

Q=-RE=-6.2 кН

М(Z4)=RE∙Z4

M(0)=0

M(1.2)=7.44 кН∙м

3.3 Из условия прочности подбираем сечения

=

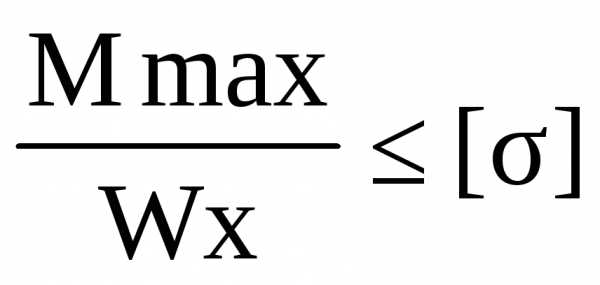
Wx=;

3.3.1 Круглое сечение

Wx=; .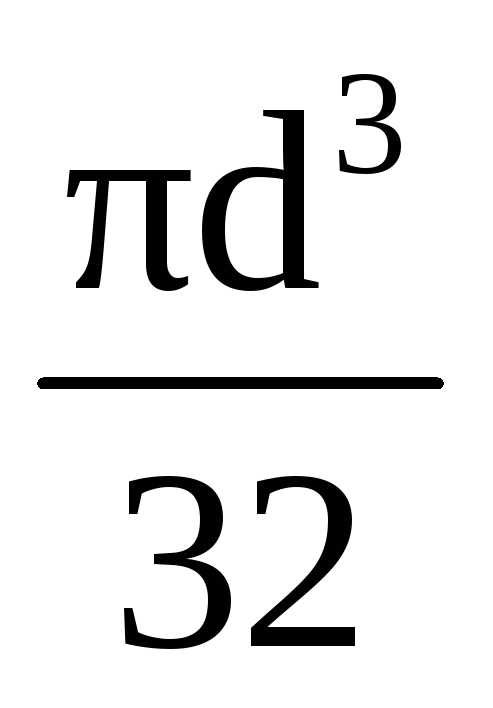

F=

3.3.2 Квадратное сечение

Wx=; .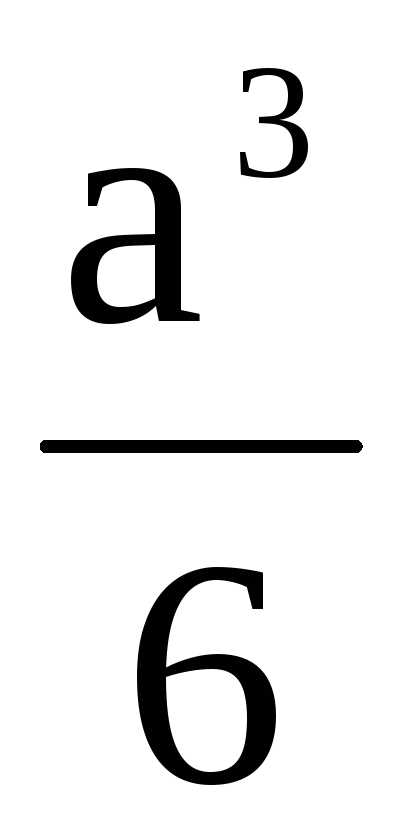

F=

3.3.3 Прямоугольное сечение

;

.

F=b∙h=7.8∙14=109.2

3.3.4 Сечение из двух швеллеров

По /1/ табл. 2 стр. 301 выбираем швеллер №18а, для которого Wx=132

, F=22.2. Для двух швеллеров Wx=264, F=44.4.

3.3.5 Двутавровое сечение

По /1/ табл. 2 стр. 300 выбираем двутавр №22а, для которого Wx=254, F=32.8.

Сравниваем площади сечений. Наименьшая площадь у двутаврового сечения является экономически выгодным.

3.4 Построение эпюр нормальных, касательных и эквивалентных напряжений

Исходные данные: сечение ;M=25.44 кН∙м; Q=-6.2 кН; [σ]=110 МПа; h=220 мм; b=120 мм; d=5.4 мм; t=8.9 мм; Ix=2790

; Sx=143

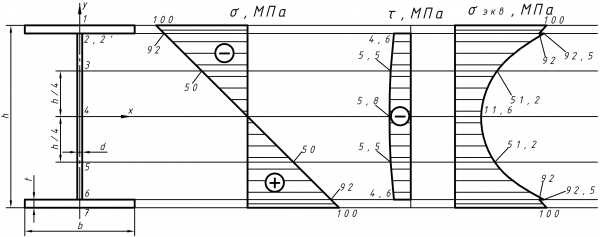
Рис.4 Расчетная схема

3.4.1 Нормальные напряжения в точках сечения вычислим по формуле:

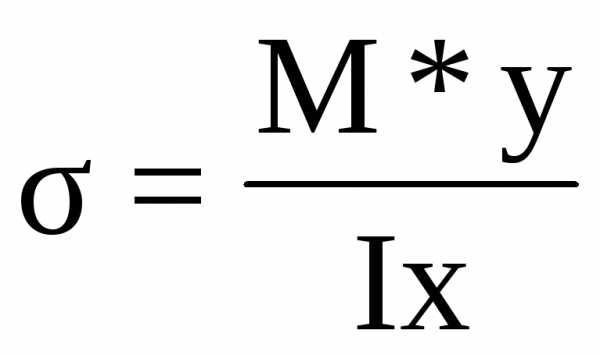;(1)

где: y-расстояние от нейтральной оси до точки, в которой определяются напряжения.

Так как M>0, то в точках 1,2,3 будут возникать сжимающие напряжения, а в точках 5,6,7 растягивающие.

В точке 1: y=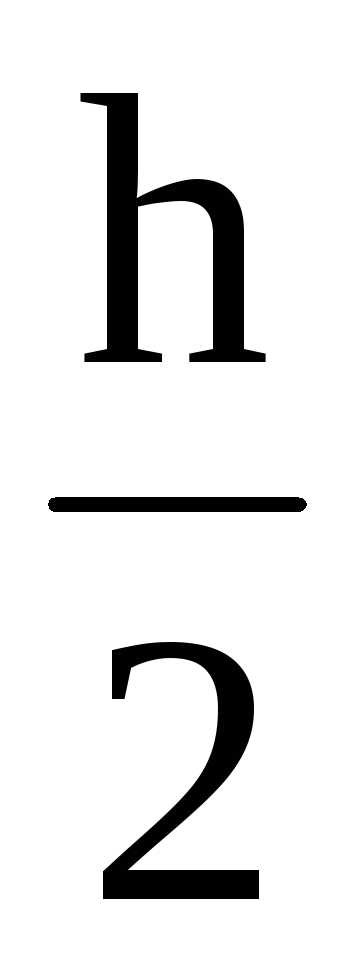=11 см;;

В точке 2: y=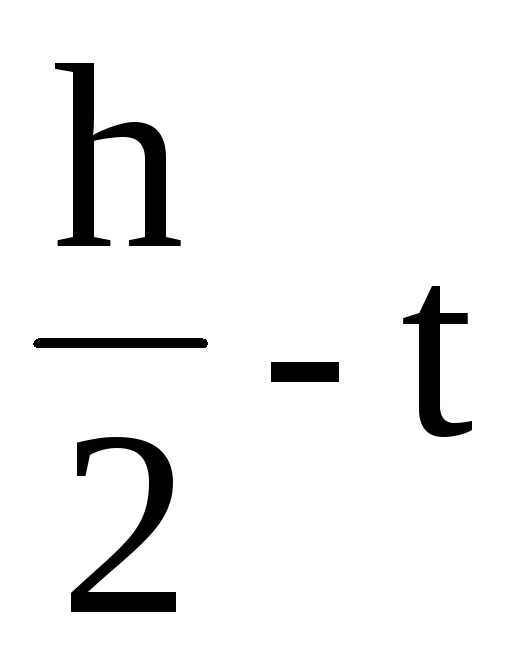=10.11 см;;

В точке 3: y=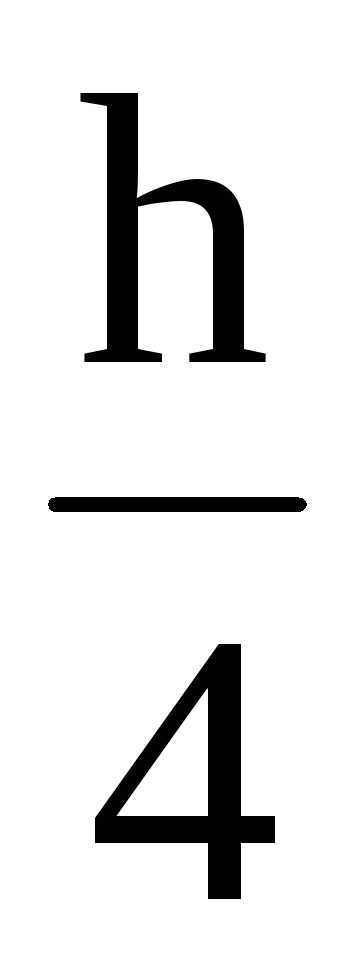=5,5 см;;

В точке 4: y=0;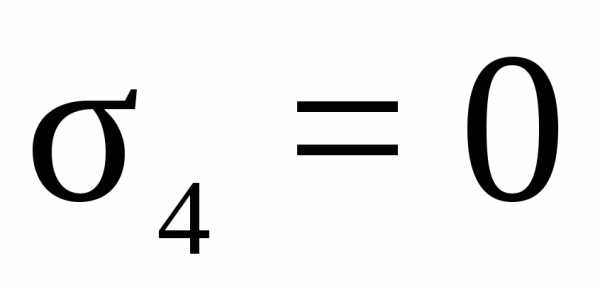

3.4.2 Касательные напряжения в точках сечения вычислим по формуле:

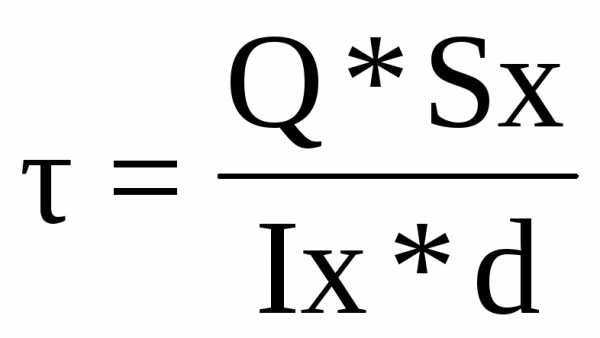;(2)

где: Sx-статический момент части сечения;

В точке 1: ;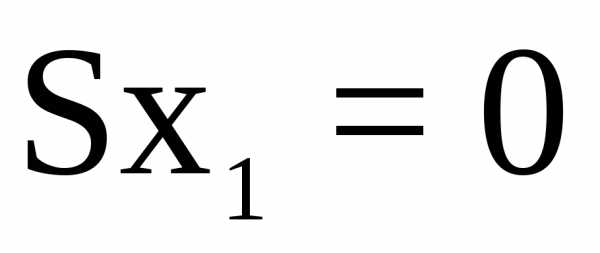

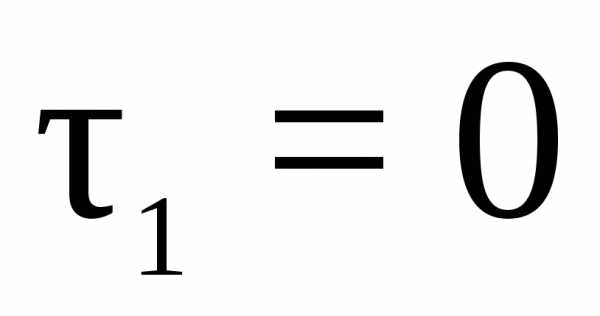
В точке 2: Статический момент найдем, принимая полку двутавра за прямоугольник с размерами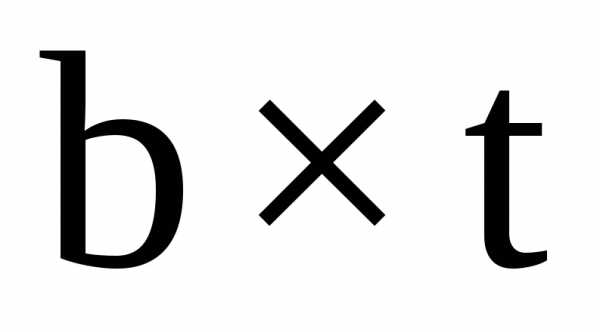

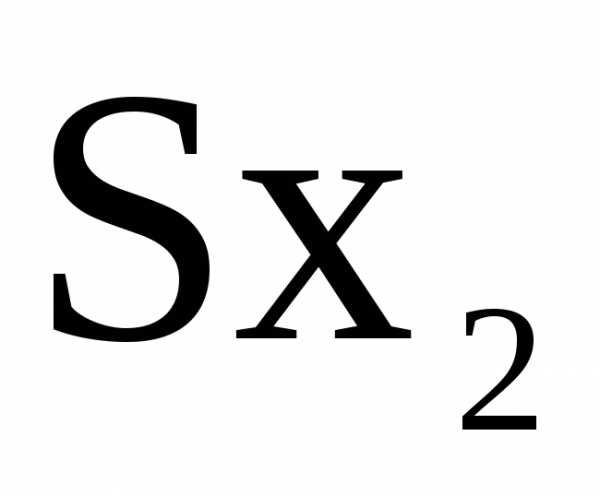=b∙t(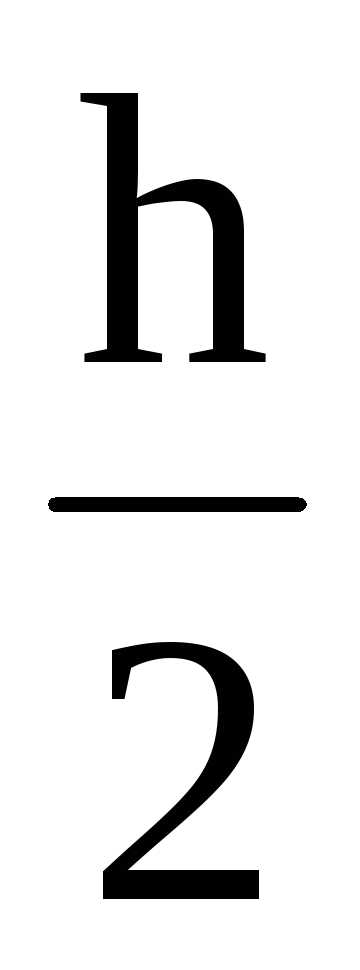—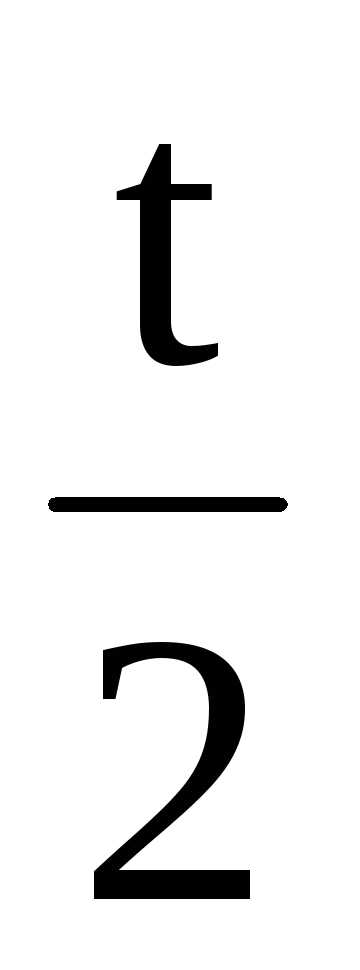)=12∙0.89∙10.55=112.7

;

.

В точке 3: Статический момент отсеченной части (расположенной выше точки 3) найдем как разность статического момента Sx полусечения двутавра и статического момента прямоугольника с размерами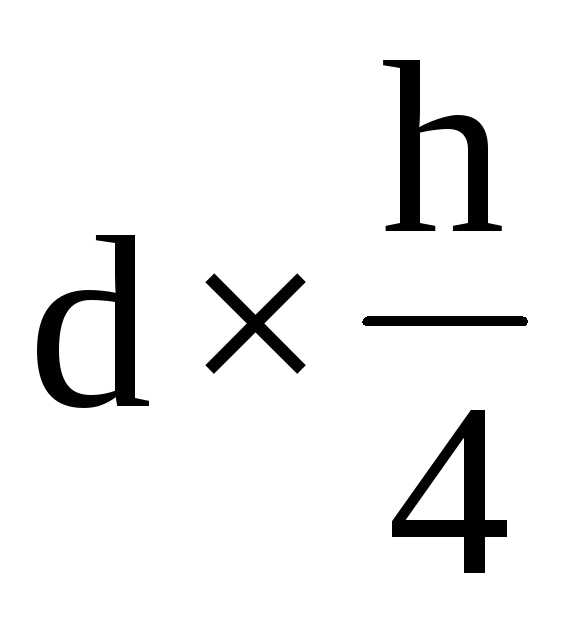

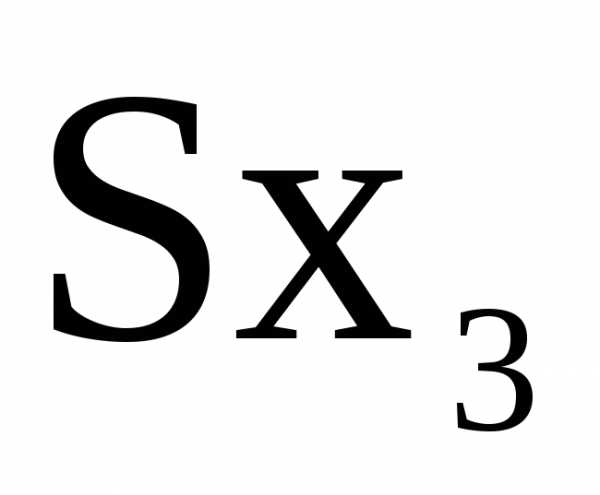=Sx-d∙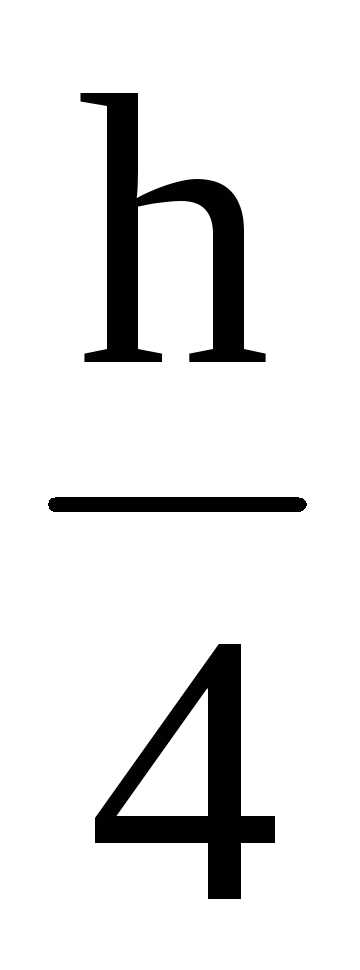∙=143-0.54∙5.5∙2.75=134.8 ;

.

В точке 4: .

3.4.3 Эквивалентные напряжения в точках сечения вычислим по формуле:

;(3)

В точке 1: ;

В точке 2: ;

В точке 2’ принадлежащей стенке двутавра ;

В точке 3: ;

В точке 4: .

Напряжения в точках не превышают допускаемых условие прочности выполнено.

studfiles.net

Балки на двух шарнирных опорах

Добавить комментарий Отменить ответ

Ваш e-mail не будет опубликован. Обязательные поля помечены *

Комментарий

Имя *

E-mail *

Сайт

Лимит времени истёк. Пожалуйста, перезагрузите CAPTCHA.  ×   =  63

saitinpro.ru

6. Расчет кузова как балки на 2-х опорах.

6.1.Формирование поперечного сечения кузова

Проектируемая сборочная единица должна быть совершеннее, чем такая же сборочная единица вагона-аналога. Улучшение достигается за счет следующего:

— применения более прочных и коррозионностойких материалов, что позволяет уменьшить площади поперечных сечений несущих элементов и снизить тару;

— применения для несущих элементов оптимальных профилей, позволяющих снизить тару и уменьшить стоимость сборочной единицы;

— применения более прогрессивных конструкторских решений, позволяющих облегчить процесс сборки и повысить надежность узлов соединения несущих элементов.

Для этого сформируем эскиз сборочной единицы поперечного сечения. В качестве верхней обвязки используем гнутый замкнутый прямоугольный профиль (для облегчения конструкции), вместо предыдущего. Также заменим омегообразный профиль стойки на швеллер №12. Для несущих элементов кузова используем вместо сталей 09Г2Д 10ХНДП сталь 10ХСНД,- это позволит уменьшить толщину листового материала балок рамы. В результате добьемся снижения тары проектируемого вагона.

Поперечное сечение кузова имеет следующий вид:

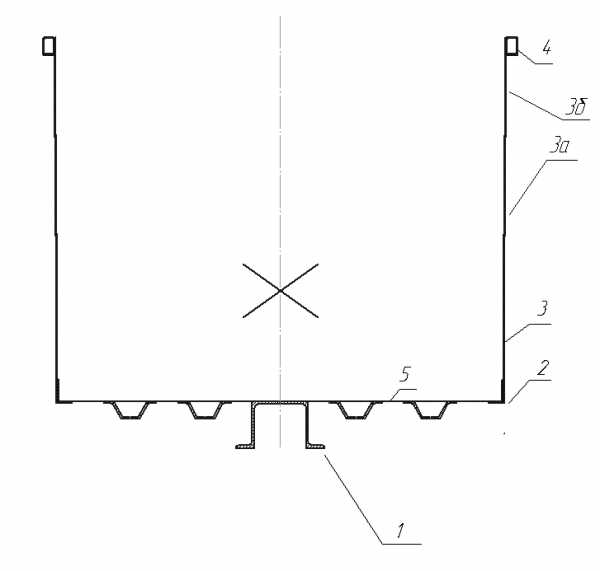
Рис.4 Поперечное сечение кузова

Геометрические характеристики рассчитаем в табличной форме (см. таблицу 2).

Таблица 2

Геометрические характеристики элементов кузова

Элемент и его №
1.Хр.балка	178,8	16,5	2950,2	48678,3	27862,5
2.Уголок №160˟100˟10	50,56	35,23	1781,23	62752,7	1333,2
3.Обшивка	255,14	151,95	38760,86	5889712,67	1441752,08
4.Обвязка верх.	45,12	268,9	12132,77	3262501,3	873,44
5.Продольная балка с полом	211,3	25,5	5388,15	137397,8	3274
∑	740,92	—	61013,21	9401042,77	1475095,22

В таблице использованы следующие обозначения:

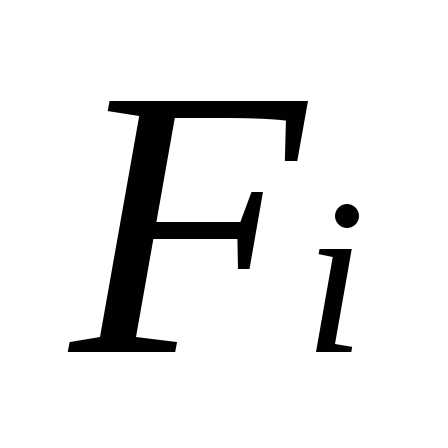— площадь поперечного сечения i-того элемента;

— координата центра тяжести сечения i-того элемента в принятой системе координат;

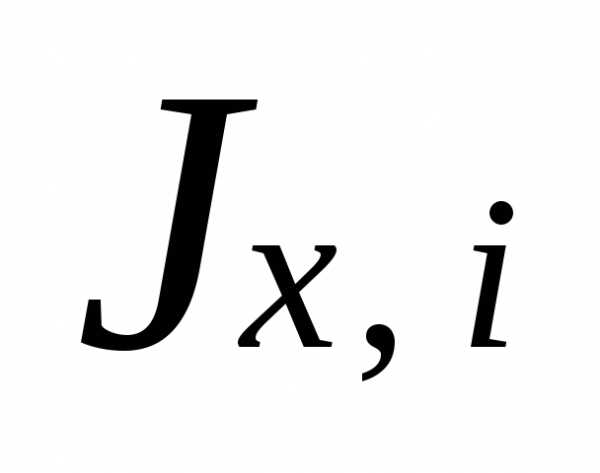— осевой момент инерции i-того элемента относительно горизонтальной оси, проходящей через центр тяжести сечения i-того. Ось ОХ проводим через центр тяжести сечения хребтовой балки.

Рассчитаем координату yo центра тяжести всего сечения

Вычислим осевой момент инерции всего сечения относительно оси ОХ, проходящей через центр тяжести сечения

где — высота всех элементов поперечного сечения кузова.

6.2.Проверка размеров поперечного сечения кузова проектируемого вагона по условию прочности

Для проверки правильности принятых размеров поперечного сечения будем использовать приближенный расчет как балки, а также расчет по II основной системе, предложенный проф. Никольским Е.Н.

6.2.1. Прикидочный расчет как балки на 2-х опорах

На стадии эскизного проектирования для проверки прочности можно воспользоваться приближенной расчетной схемой кузова как балки на двух опорах-пятниках. Расчет необходимо выполнить на нагрузки, предусмотрены I и III расчетными режимами «Норм проектирования вагонов». Целесообразно вначале рассчитать кузов на вертикальную статическую нагрузку.

Рис.5 Схема нагружения кузова как балки на 2-х опорах

Напряжения, возникающие в сечениях кузова, можно рассчитать по следующей формуле:

,

где q – вертикальная распределенная нагрузка,

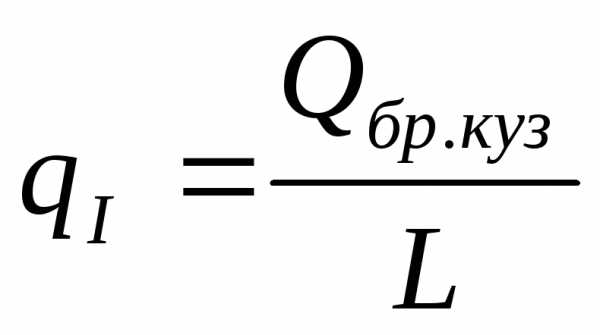
где Q_бр.куз – вес брутто кузова вагона,

e – эксцентриситет приложения продольной нагрузки относительно центра тяжести кузова.

При расчете напряжений в среднем сечении кузова по I расчетному режиму учитывается вертикальная статическая нагрузка, равная весу кузова вагона с грузом, и продольная по осям сцепления автосцепок: сжимающая N = 3,0 МН и растягивающая N = 2,5 МН.

Для определения напряжений в среднем сечении кузова по III расчетному режиму (режим движения вагона с конструкционной скоростью) следует учесть влияние на вагон динамической и боковой нагрузок.

Вертикальная динамическая нагрузка зависит от величины коэффициента вертикальной динамикиК_дв, который определим по следующей зависимости:

,

где β – параметр распределения, для грузовых вагонов;

р(Кдв) — доверительная вероятность, по Нормам;

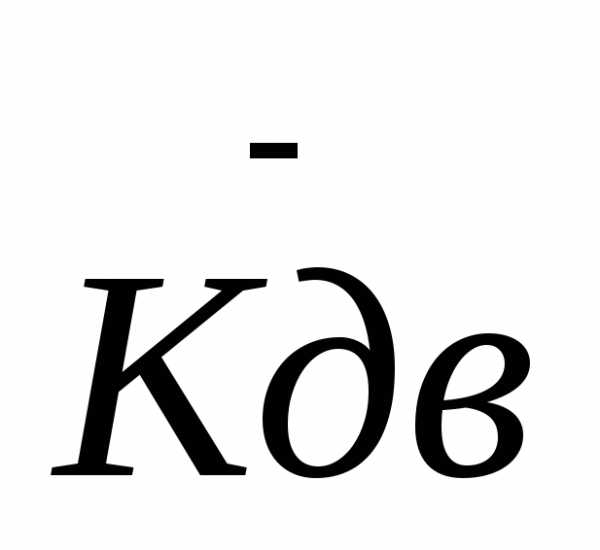–среднее значение коэффициента вертикальной динамики:

,

где а = 0,05 – коэффициент, принимаемый для элементов кузова;

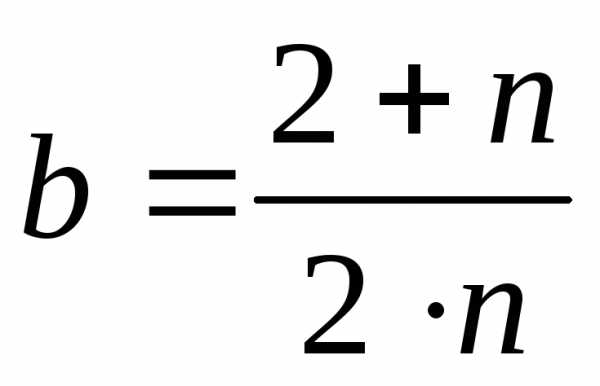–коэффициент, учитывающий влияние числа осей под одним концом вагона;

n – количество осей под одним концом вагона;

V– конструкционная скорость;

f_ст.- статический прогиб рессорного комплекта.

Влияние боковых сил учтем с помощью коэффициента боковых сил .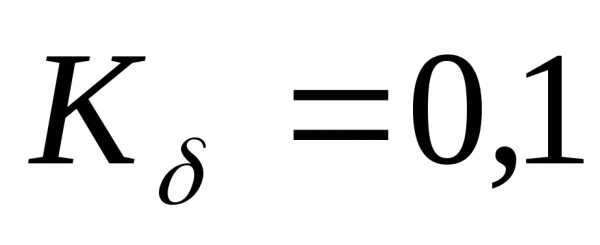

Вертикальная распределенная нагрузка составит:

Машинограммы представлены далее.

Результаты прикидочного расчета кузова как балки на двух опорах

studfiles.net

Общий случай расчета балки на шарнирных опорах при действии нескольких сосредоточенных нагрузок

Рассмотрим следующий пример: имеется балка перекрытия на двух шарнирных опорах с расчетной длиной l = 230.5 см. На балку опираются 4 лаги, первая на расстоянии l₁ = 18 см от шарнирной опоры, расстояние между 1 и 2, между 2 и 3 и между 3 и 4 лагами l₂ = l₃ = l₄ = 60 см, расстояние от 4 лаги до второй шарнирной опоры l₅ = 32.5 см.

Как видим, сосредоточенные нагрузки к балке приложены несимметрично, да и значения сосредоточенных нагрузок вряд ли могут быть равными. Как минимум потому, что на лаги передается нагрузка от перекрытия, а значит нагрузка на первую лагу будет меньше, чем на все остальные даже при равномерно распределенной нагрузке на напольное покрытие. А во-вторых, равномерно распределенная нагрузка на напольное покрытие принимается исключительно в целях упрощения расчета, в действительности возле стен обычно стоит всякая разная мебель и потому нагрузка на крайние лаги как правило больше, чем на лаги, расположенные ближе к середине пролета.

Итак у нас есть два варианта проведения расчетов: упрощенный и полный. Сначала рассмотрим

Упрощенный вариант первого этапа расчета балки

Если мы для дальнейшего упрощения расчетов примем значения сосредоточенных нагрузок от лаг равными между собой Q₁ = Q₂ = Q₃ = Q₄ = Q = 200 кг, а приложение этих нагрузок будем рассматривать как симметричное, т.е. l₁ = l₅ = l₂/2, то сможем относительно легко перевести эти сосредоточенные нагрузки в эквивалентную равномерно распределенную.

q_экв = γmQ/l = 1·4Q/l = 4·200/230.5 = 3.47 кг/см (305.1.4)

где m — количество сосредоточенных нагрузок, γ = 1 — коэффициент перехода от сосредоточенных нагрузок к эквивалентной равномерно распределенной.

Таким образом максимальный момент составит

M = q_эквl²/8 = 3.47·230.5²/8 = 23050 кгс·см

и теперь подобрать необходимое сечение будь то деревянной, металлической или железобетонной балки — не проблема (варианты подбора необходимого сечения рассматриваются в соответствующих статьях). Да и определить значения поперечных сил на опорах не сложно. А после того, как будет подобрано необходимое сечение и станут известны его параметры, можно будет проверить допустимость максимального прогиба для такой балки по формуле

f = 5q_эквl⁴/384EI

Вот в сущности и весь упрощенный расчет, в результате которого мы получили несколько завышенные значения момента. Насколько завышенные, нам поможет узнать

Полный вариант первого этапа расчета балки

 

1. Определение опорных реакций

Так как первая лага опирается максимально близко к первой шарнирной опоре рассматриваемой балки, то сосредоточенная нагрузка от этой лаги скорее всего будет меньше, чем от остальных лаг. Предположим, что от остальных лаг сосредоточенная нагрузка как и прежде составляет Q₂ = Q₃ = Q₄ = 200 кг, а от первой лаги

Q₁ = Q₂(l₁ + l₂/2)/l₂ = 200(18 + 60/2)/60 = 0.8Q₂ = 160 кг

Тогда опорные реакции составят

А = (Q₁(l — l₁) + Q₂(l — l₁ — l₂) + Q₃(l₄ + l₅) + Q₄l₅)/l = (160(230.5 — 18) + 200((230.5 — 18 — 60) + (60 + 32.5) + 32.5)/230.5 = 388.286 кг

В = (Q₁ l₁ + Q₂( l₁ + l₂) + Q₃(l — l₄ — l₅) + Q₄(l — l₅)/l = (160·18 + 200((18 + 60) + (230.5 — 60 — 32.5) + (230.5 — 32.5))/230.5 = 371.713 кг

Проверим наш расчет, сумма опорных реакций должна быть равна сумме сосредоточенных нагрузок

388.286 + 371.71 = 759.999 ≈ 760 кг = 160 + 3·200 

Это значит, что одно из условий равновесия системы выполняется, так как опорные реакции направлены в сторону, противоположную нагрузкам, а значит и сумма всех сил, действующих относительно оси у, будет = 0. Кроме того опорные реакции соответствуют значениям поперечных сил, действующих на опорах балки.

Теперь мы можем продолжать расчет, но сразу отметим, что разница опорных реакций для нашего случая загружения балки не так уж и велика, около

100%(388.286 — 371.713)/371.713 = 4.4%

2. Определение максимального изгибающего момента

Для того, чтобы определить максимальный изгибающий момент при несимметричной нагрузке, мы сначала должны построить эпюру моментов. Впрочем, схема загружения нашей балки не такая уж и сложная и очевидно, что максимальный момент будет в сечении под второй или третьей лагой, поэтому ограничимся тем, что определим значения моментов в сечениях под 2 и 3 сосредоточенной нагрузкой.

М₂ = А(l₁ + l₂) — Q₁l₂ = 388.286(18 + 60) — 160·60 = 20686.308 кгс·см

М₃ = А(l₁ + l₂ + l₃) — Q₁(l₂ + l₃) — Q₂l₃= 388.286(18 + 60 + 60) — 160(60 + 60) — 200·60 = 22383.468 кгс·см

Как видим, максимальный момент будет в сечении под 3 лагой, при этом разница с максимальным моментом, полученным при упрощенном расчете, составит около

100%(23050 — 22383.468)/22383.468 = 3%

что можно рассматривать, как дополнительный запас прочности. С учетом того, что при расчетах частно принимаются коэффициенты надежности по нагрузке от 1.1 до 1.4, дополнительный коэффициент 1.03 на мой взгляд не кардинально влияет на расчеты. К тому же доступные сечения деревянного бруса и металлопроката, точнее разница размеров поперечных сечений, иногда требуют принять больший запас по прочности или пересматривать расчетную схему.

Тем не менее продолжим расчет. Для определения максимального прогиба нам сначала нужно определить значение угла поворота поперечного сечения хотя бы на одной из опор, например, на опоре А.

3. Определение угла поворота на опоре А и максимального прогиба поперечного сечения

Так как нагрузки, приложенные к балке, несимметричны и не равны, то максимальный прогиб будет не посредине пролета балки, а в точке, где угол поворота поперечного сечения = 0, где-то между 2 и 3 лагами (на расстоянии х от первой опоры и судя по всему достаточно близко к середине пролета балки). На основании этого мы можем составить следующее уравнение:

θ_(х) = — θ_A + Ax²/2EI — Q₁(x — l₁)²/2EI — Q₂(x — l₁ — l₂)²/2EI = 0

В этом уравнении 2 неизвестных: угол поворота на опоре А и собственно расстояние х. Для того, чтобы определить угол поворота на опоре А, необходимо решить дополнительное уравнение, исходя из условия, что прогиб на опорах А и В равен нулю.

f_В = — θ_Al + Al³/6EI — Q₁(l — l₁)³/6EI — Q₂(l — l₁ — l₂)³/6EI — Q₃(l₄ + l₅)³/6EI — Q₄l₅³/6EI = 0

После определения этих неизвестных мы, наконец можем определить максимальный прогиб по формуле

f_(x) = — θ_Ax + Ax³/6EI — Q₁(х — l₁)³/6EI — Q2(x — l₁ — l₂)³/6EI

Лично у меня нет большого желания решать все эти уравнения, тем более, что итоговые результаты будут отличаться от полученных при упрощенном расчете на несколько процентов. А есть ли у вас необходимость в столь точном расчете — решать вам.

doctorlom.com

Балка на шарнирных опорах с консолями. Линии влияния усилий в шарнирно-консольных балках. Расчет однопролетной балки на двух шарнирных опорах

29-10-2012: Андрей

Допущена опечатка в формуле изгибающего момента для балки с жестким защемлением на опорах(3-я снизу): длина должна быть в квадрате. Допущена опечатка в формуле максимального прогиба для балки с жестким защемлением на опорах (3-я снизу): должно быть без «5».

29-10-2012: Доктор Лом

Да, действительно, были допущены ошибки при редактировании после копирования. На данный момент ошибки исправлены, спасибо за внимательность.

01-11-2012: Вик

опечатка в формуле в пятом сверху примере (перепутаны степени рядом с иксом и эль)

01-11-2012: Доктор Лом

И это правда. Исправил. Спасибо за внимательность.

10-04-2013: flicker

В формуле Т.1 2.2 Mmax, похоже, не хватает квадрата после a.

11-04-2013: Доктор Лом

Верно. Эту формулу я скопировал из «Справочника по сопротивлению материалов» (под ред. С.П. Фесика, 1982г, стр. 80) и даже не обратил внимания, что при такой записи даже размерность не соблюдается. Сейчас пересчитал все лично, действительно расстояние «а» будет в квадрате. Таким образом получается, что наборщик пропустил маленькую двоечку, а я повелся на эту пшенку. Исправил. Спасибо за внимательность.

02-05-2013: Timko

Добрый день хотел бы спросить у вас в таблице 2, схема 2.4, интересует формула «момент в пролете» где не ясен индекс Х -? не могли бы вы ответить)

02-05-2013: Доктор Лом

Для консольных балок таблицы 2 уравнение статического равновесия составлялось слева направо, т.е. началом координат считалась точка на жесткой опоре. Однако если рассматривать зеркальную консольную балку, у которой жесткая опора будет справа, то для такой балки уравнение момента в пролете будет намного проще, например, для 2.4 Мх = qx2/6, точнее -qx2/6, так как сейчас считается, что если эпюра моментов расположена сверху, то момент при этом отрицательный.
С точки зрения сопромата знак момента — достаточно условное понятие, так как в поперечном сечении, для которого определяется изгибающий момент все равно действуют как сжимающие, так и растягивающие напряжения. Главное понимать, что если эпюра расположена сверху, то и растягивающие напряжения будут действовать в верхней части сечения и наоборот.
В таблице минус для моментов на жесткой опоре не проставлен, однако направление действия момента учитывалось при составлении формул.

25-05-2013: Дмитрий

Скажите пожалуйста, при каком соотношении длины балки к ее диаметру справедливы сии формулы?
Я хочу узнать или это подкодит только для длинных балок, которые в строительстве зданий, или можна применять также для расчета прогибов валов, длиной до 2 м. Пожалуйста ответте так l/D>…

25-05-2013: Доктор Лом

Дмитрий, я вам уже говорил, для вращающихся валов расчетные схемы будут другие. Тем не менее, если вал в неподвижном состоянии, то его можно рассматривать как балку, причем не важно, какое у нее сечение: круглое, квадратное, прямоугольное или какое-то еще. Данные расчетные схемы наиболее точно отражают состояние балки при l/D>10, при соотношении 5

25-05-2013: Дмитрий

Спасибо за ответ. Можете еще назвать литературу, на которую я могу сослаться, в своей работе?
Вы имеете в виду, что для вращающихся валов схемы будут другие из-за вращательного момента? Не знаю на сколько это важно, так как в книге по техмашу написано, что в случае токарной обработки, прогиб, вносимый вращательным моментом на валу, очень мал по сравнению с прогибом от радиальной составляющей силы резания. Что думаете?

25-05-2013: Доктор Лом

Не знаю, какую именно задачу вы решаете, и потому вести предметный разговор трудно. Попробую объяснить свою мысль по другому.
Расчет строительных конструкций, деталей машин и т.п., как правило состоит из двух этапов: 1. расчет по предельным состояниям первой группы — так называемый расчет на прочность, 2. расчет по предельным состояниям второй группы. Одним из видов расчета по предельным состояниям второй группы является расчет на прогиб.
В вашем случае на мой взгляд более важным будет расчет на прочность. Более того на сегодняшний день существуют 4 теории прочности и расчет по каждой из этих теорий — разный, но во всех теориях при расчете учитывается влияние как изгибающего так и крутящего момента.
Прогиб при действии крутящего момента происходит в другой плоскости, но все равно при расчетах учитывается. А уж малый этот прогиб или большой — расчет покажет.
Я не специализируюсь на расчетах деталей машин и механизмов и потому авторитетную литературу по этому вопросу указать не смогу. Впрочем, в любом справочнике инженера-конструктора узлов и деталей машин эта тема должна быть должным образом раскрыта.

25-05-2013: Дмитрий

Можно тогда с вами пообщаться через mail или Skype? Я вам расскажу что за работу я делаю и для чего были предыдущие вопросы.
mail: [email protected]
Skype: dmytrocx75

25-05-2013: Доктор Лом

Можете написать мне, адреса электронной почты на сайте найти не трудно. Но сразу предупрежу, никакими расчетами я не занимаюсь и партнерские контракты не подписываю.

08-06-2013: Виталий

Вопрос по таблице 2, вариант 1.1, формула прогиба. Просьба уточнить размерность.
Q — в килограммах.
l — в сантиметрах.
E — в кгс/см2.
I — см4.
Все верно? Что-то странные результаты получаются.

09-06-2013: Доктор Лом

Все верно, на выходе получаются сантиметры.

20-06-2013: Евгений Борисович

Здравствуйте. Помогите прикинуть. У нас возле ДК стоит сцена летняя деревянная, размер 12,5 х 5.5 метров, по углам стойки — металлические трубы диаметром 100 мм. Заставляют делать крышу типа фермы (жаль что нельзя рисунок прикрепить) покрытие поликарбонад, фермы изготавливать из профильной трубы (квадрат или прямоугольник) стоит вопрос о моей работе. Не будешь делать уволим. Я говорю что не пойдет, а администрация вместе с моим начальником говорят все пойдет. Как быть?

20-06-2013: Доктор Лом

22-08-2013: Дмитрий

Если балка (подушка под колонной) лежит на плотном грунте (точнее закопана ниже глубины промерзания), то какой схемой следует воспользоваться для расчета такой балки? Интуиция подсказывает, что вариант «на двух опорах» не подходит и что изгибающий момент должен быть существенно меньше.

22-08-2013: Доктор Лом

Расчет фундаментов — отдельная большая тема. К тому же не совсем понятно о какой балке идет речь. Если имеется в виду подушка под колонну столбчатого фундамента, то основой расчета такой подушки является прочность грунта. Задача подушки — перераспределить нагрузку от колонны на основание. Чем меньше прочность, тем больше площадь подушки. Или чем больше нагрузка, тем больше площадь подушки при той же прочности грунта.
Если речь идет о ростверке, то в зависимости от способа его устойства, он может рассчитываться как балка на двух опорах, или как балка на упругом основании.
Вообще при расчете столбчатых фундаментов следует руководствоваться требованиями СНиП 2.03.01-84.

23-08-2013: Дмитрий

Имеется в виду подушка под колонну столбчатого фундамента. Длина и ширина подушки уже определены исходя из нагрузки и прочности грунта. Но вот высота подушки и количество арматуры в ней под вопросом. Хотел посчитать по аналогии со статьей «Расчет железобетонной балки», но полагаю, что считать изгибающий момент в подушке, лежащей на грунте, как в балке на двух шарнирных опорах будет не совсем верно. Вопрос — по какой расчетной схеме считать изгибающий момент в подушке.

24-08-2013: Доктор Лом

Высота и сечение арматуры в вашем случае определяются как для консольных балок (по ширине и по длине подушки). Схема 2.1. Только в вашем случае опорная реакция — это нагрузка на колонну, точнее часть нагрузки на колонну, а равномерно распределенная нагрузка — это отпор грунта. Другими словами, указанную расчетную схему нужно перевернуть.
Кроме того, если нагрузка на фундамент передается от внецентренно нагруженной колонны или не только от колонны, то на подушку будет действовать дополнительный момент. При расчетах это следует учитывать.
Но еще раз повторю, не занимайтесь самолечением, руководствуйтесь требованиями указанного СНиПа.

10-10-2013: Ярослав

Добрый вечер.Помогите пожалуста,подобрать метал. балку для прольота 4.2 метра.Жилой дом в два етажа,цоколь перекрыт пустотелыми плитами длиной 4.8 метра,сверху несущая стена в 1.5 кирпича длиной в 3.35 м высотой 2.8м.дальше дверной пройом.Сверху на етой стене плиты перекрытия с одной стороны длиной 4.8м. с другой 2.8 метра на плитах опять несущая стена как етажом ниже и сверху деревяные бал

starer.ru

1.10 БАЛКИ НА ДВУХ ОПОРАХ : Сурьянинов Н.Г.

В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.

Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия (IFiX = 0) обращается в тождество. Таким образом, для

определения реакций в опорах шарнирной балки используются два уравнения статики:

I Ma = 0;

I Mb = 0.

Условие I Fiy = 0 используется для проверки вычисленных значений опорных реакций.

Пример 5. Построить эпюры Qy,MX для балки с шарнирным опиранием

(рис.8).

Порядок расчета.

Вычисляем реакции опор.

IMA = 0: RB • 5- M — F • 3 — q • 2 • 1 = 0; RB = 30 кН; IMB = 0: RA • 5 + M — F • 2 — q • 2 • 4 = 0; RA = 40 кН.

Проверка:

IFiy = 0: RA — q • 2 — F + RB = 40- 20• 2 — 30 + 30 = 0

Намечаем характерные сечения.

В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть.

3. Определяем поперечные силы в характерных сечениях.

Qy,1 = Ra = 40 кН;

Qy,2 = Qy,3 = Ra — q • 2 = 40 — 40 = 0; Qy,4 = Qy,5 = Qy,6 = Qy,7 = — Rb = -30 кН.

Строим эпюру Qy .

4. Определяем изгибающие моменты в характерных сечениях.

Mx,1 = 0;

MX 2 = RA • 2 — q • 2 • 1 = 80 — 40 = 40 кН • м; MX>3 = MX 4 = RA • 3 — q • 2 • 2 = 120 — 80 = 40 кН • м; MX5 = RB • 1 — M = 30- 20 = 10 кН • м; MX 6 = RB • 1 = 30 кН • м;

Строим эпюру MX

Mx,7 = 0.

Пример 6. Построить эпюры Qy и Mx для балки на двух опорах с

консолью (рис.9,а) Порядок расчета. 1. Вычисляем опорные реакции.

IMAi = 0: M + F• 1 + q• 3^3,5-RB • 4 = 0; RB = 40 кН IMBi = 0: M-F• 3-q• 3• 0,5 + RA • 4 = 0; RA = 30 кН

Во втором уравнении равновесия (впрочем, как и в первом) момент от распределенной нагрузки q вычислен без разбиения ее на две части — слева и

справа от опоры В, то есть определена равнодействующая нагрузки q — q ^3, ее положение (в середине участка с распределенной нагрузкой), что позволяет определить плечо равнодействующей относительно опоры В и направление создаваемого ею момента. В то же время можно было в уравнении равновесия учитывать отдельно части нагрузки q , приложенные слева и справа от опоры В; при этом второе уравнение равновесия имеет вид:

I MBi = 0: M-F • 3-q • 2 • 1 + q • 1 • 0,5+ RA • 4 = 0

Вычисленное из этого уравнения значение реакции RA, разумеется, совпадает с полученным ранее. Проверка:

IFyi = 0: RA — F — q • 3 + RB = 30- 40 — 30 + 40 = 0

Намечаем характерные сечения.

Вычисляем поперечную силу и изгибающий момент в характерных сечениях.

Из рассмотрения левой отсеченной части:

Qy,1 = Qy,2 = Ra = 30кН;

Qy,3 = Qy,4 = Ra — F = 30- 40 = -10кН;

Mx1 = M = 15 кН • м;

Mx 2 = Mx 3 = M + RA • 1 = 15 + 30 = 45 кН • м; Mx4 = M + RA • 2 -F• 1 = 15 + 60-40 = 35 кН• м.

Для сечений 5-7 удобнее рассматривать правую отсеченную часть:

Qy5 = q • 1 — RB = 10 — 40 = -30кН; Qy,6 = q 4 = 10кН; Qy,7 = 0;

Mx,5 = Mx,6 =-q • Ь 0,5 = -5 кН • м;

Mx,7 = 0.

По вычисленным значениям строим эпюры Qy и Mx (рис.9,б,в).

www.ahmerov.com