Реакции опоры | Лекции и примеры решения задач механики

Опорными называют реакции связей возникающие под действием внешних нагрузок в опорах и удерживающие рассматриваемый элемент или конструкцию в равновесии.

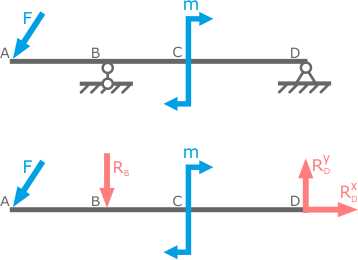
Замена опор их реакциями

При расчете элементов конструкций реакции опор также выступают в качестве внешних усилий приложенных к рассматриваемому телу.

Вопрос определения опорных реакций подробно рассматривается в курсе теоретической механики, но на практике часто применяется и при решении задач сопротивления материалов.

При этом некоторые задачи в сопромате можно решить без их определения. Это возможно в случаях, когда за расчетную схему принимается брус, закрепленный в жесткой опоре (заделке) без дополнительных опор, например, статически определимые консольные балки, стержни либо стержневые системы.

Определение реакций

Количество и направление реакций зависит как от вида опор, так и от способа нагружения бруса и для статически определимых систем определяются из уравнений равновесия конструкции или ее элементов.

Для общего случая нагружения (пространственных систем), при котором может возникать до 6 реакций опор, требуется соответствующее количество уравнений.

Например, из условия, что заданная система относительно опор не перемещается в пространстве (вправо-влево, вверх-вниз, и вперед-назад) можем приравнять к нулю сумму проекций всех сил на оси x, y и z.

∑F(x)=0;
∑F(y)=0;
∑F(z)=0.

Из условия, что система не вращается, приравниваем к нулю суммы моментов всех нагрузок относительно соответствующих осей.

∑m(x)=0;
∑m(y)=0;
∑m(z)=0.

Совместное решение системы полученных уравнений позволяет определить величину и направление реакций в опорах.

Для плоской системы нагружения можно составить максимум три уравнения равновесия для определения до трех искомых усилий в опорах.

Линейно нагруженные элементы позволяют записать лишь одно уравнение равновесия.

Для расчета реакций опор статически неопределимых систем помимо уравнений статики требуются дополнительные зависимости, связывающие усилия с соответствующими им деформациями.

В некоторых случаях опорные реакции могут быть равны нулю. Это говорит лишь о том, что внешние нагрузки и остальные реакции взаимно уравновешены таким образом, что система может оставаться статичной и без соответствующего усилия в данной точке.

Примеры определения опорных реакций >
Внутренние силовые факторы >

isopromat.ru

Как определить реакцию опоры сопромат. Определение опорных реакций. Решение задач

Балки предназначены для восприятия поперечных нагрузок. По способу приложения нагрузки делятся на сосредоточенные (действуют на точку) и распределенные (действуют на значительную площадь или длину).

q — интенсивность нагрузки, кн/м

G = q L – равнодействующая распределенной нагрузки

Балки имеют опорные устройства для сопряжения их с другими элементами и передачи на них усилий. Применяются следующие виды опор:

· Шарнирно-подвижная

Эта опора допускает поворот вокруг оси и линейное перемещение параллельно опорной плоскости. Реакция направлена перпендикулярно опорной поверхности.

· Шарнирно-неподвижная

Эта опора допускает поворот вокруг оси, но не допускает никаких линейных перемещений. Направление и значение опорной реакции неизвестно, поэтому заменяется двумя составляющими R A у и R A х вдоль осей координат.

· Жесткая заделка (защемление)

Опора не допускает перемещений и поворотов. Неизвестны не только направление и значение опорной реакции, но и точка её приложения. Поэтому заделку заменяют двумя составляющими R A у, R A х и моментом М А. Для определения этих неизвестных удобно использовать систему уравнений.

∑ m А (F к)= 0

Для контроля правильности решения используется дополнительное уравнение моментов относительно любой точки на консольной балке, например точка В ∑ m В (F к)= 0

Пример. Определить опорные реакции жесткой заделки консольной балки длиной 8 метров, на конце которой подвешен груз Р = 1 кн. Сила тяжести балки G = 0,4 кн приложена посередине балки.

Освобождаем балку от связей, т.е отбрасываем заделку и заменяем её действие реакциями. Выбираем координатные оси и составляем уравнения равновесия.

∑ F kx = 0 R A х = 0

∑ F k у = 0 R A у – G – P = 0

∑ m А (F к)= 0 — M A + G L / 2 + P L = 0

Решая уравнения, получим R A у = G + P = 0,4 + 1 = 1,4 кн

M A = G L / 2 + P L = 0,4 . 4 + 1 . 8 = 9,6 кн. м

Проверяем полученные значения реакций:

∑ m в (F к)= 0 — M A + R A у L — G L / 2 = 0

— 9,6 + 1,4 . 8 – 0,4 . 4 = 0

— 11,2 + 11,2 = 0 реакции найдены верно.

Для балок расположенных на двух шарнирных опорах удобнее определять опорные реакции по 2 системе уравнений, поскольку момент силы на опоре равен нулю и в уравнении остается одна неизвестная сила.

∑ m А (F к)= 0

∑ m В (F k)= 0

Для контроля правильности решения используется дополнительное уравнение ∑ F k у = 0

1) Освобождаем балку от опор, а их действие заменяем опорными реакциями;

2) Заменяем распределенную нагрузку на равнодействующую G = q . L;

3) Выбираем координатные оси;

4) Составляем уравнения равновесия.

∑ F kx = 0 R Вх = 0

∑ m А (F к)= 0 G . L/2 + m — R Ву (L + B)= 0

R Ву = /(L + B) = (6+6) = 2,08 кн

∑ m В (F k)= 0 R A у. (L + B) — Q . (L/2 + B) + m = 0

R A у = / (L + B) = / (6 + 6) = 2,92 кн

Если испытываете трудности в написании , оформите заявку и Вы узнаете сроки и стоимость работы.


3. Изгиб. Определение напряжений.

3.3. Определение опорных реакций.

Рассмотрим несколько примеров.

Пример 3.1. Определить опорные реакции консольной балки (рис. 3.3).

Решение. Реакцию заделки представляем в виде двух сил Az и Ay , направленных, как указано на чертеже, и реактивного момента MA .

Составляем уравнение равновесия балки.

1. Приравняем нулю сумму проекций на ось z всех сил, действующих на балку. Получаем Az = 0. При отсутствии горизонтальной нагрузки горизонтальная составляющая реакции равна нулю.

2. То же, на ось y: сумма сил равна нулю. Равномерно распределенную нагрузку q заменяем равнодействующей qaз , приложенной посредине участка aз :

Ay — F1 — qaз = 0,

Откуда

Ay = F1 + qaз .

Вертикальная составляющая реакции в консольной балке равна сумме сил, приложенных к балке.

3. Составляем третье уравнение равновесия. Приравняем нулю сумму моментов всех сил относительно какой-нибудь точки, например относительно точки А:

Откуда

Знак минус показывает, что принятое вначале направление реактивного момента следует изменить на обратное. Итак, реактивный момент в заделке равен сумме моментов внешних сил относительно заделки.

Пример 3.2. Определить опорные реакции двухопорной балки (рис. 3.4). Такие балки обычно называют простыми.

Решение. Так как горизонтальная нагрузка отсутствует, то Az = 0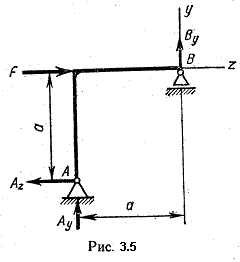

Вместо второго уравнения можно было использовать условие того, что сумма сил по оси Y равна нулю, которое ы данном случае следует применить для

mirhat.ru

Определение реакций опор

Работающий на изгиб стержень обычно называют балкой. Балка при изгибе опирается на опоры, расстояние между которыми называют пролетом. Опорные закрепления в балках могут быть различными. В инженерных расчетах обычно применяют два основных вида закреплений. Балка опирается на шарнирное закрепление(шарнирно-неподвижное и шарнирно-подвижное) и защемление (жесткая заделка).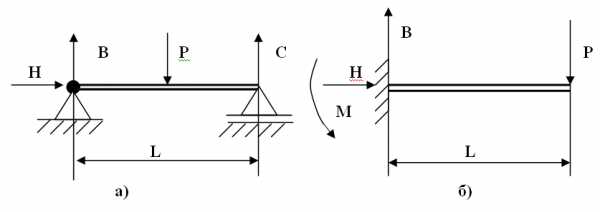 

Схема опор для балок: а) шарнирное закрепление; б) защемление

В шарнирно-неподвижной опоре возникают две реакции: вертикальная В и горизонтальная Н. В шарнирно-подвижной – одна вертикальная реакция С. Взащемлении (жесткой заделке) возникают три реакции: вертикальная реакция В, горизонтальная реакция Н и изгибающий момент М.

Подвижные опоры ставятся для того, чтобы в балке при изменении температуры не возникали дополнительные температурные напряжения. Для определения опорных реакций необходимо пользоваться приемами, известными из курса теоретической механики.

Последовательность решения задач на определние реакций

1. Балку освободить от связей и их действие заменить силами реакций.

2. Выбрать координатные оси.

3. Составить и решить уравнения равновесия.

4. Проверить правильность решения задачи. Проверку необходимо производить по тому уравнению равновесия, которое не было использовано при решении данной задачи (задача решена правильно лишь в том случае, если после постановки значений активных и реактивных сил в уравнение равновесия выполняется условие равновесия).

5. Сделать анализ решенной задачи (если при решении задачи реакции опор или реактивный момент получается отрицательным, то их действительное направление противоположно принятому).

 

Пример 1. Определить реакции опор балки, если известно

F = 20 кН, М =10 кНм, q = 1 кН/м (рис. 1).

Рис. 1 — Схема задачи

 

Решение:

1. Изображаем балку вместе с нагрузками.

2. Выбираем расположение координатных осей, совместив ось Х с балкой, а ось У направив перпендикулярно оси Х.

3. Производим необходимые преобразования заданных активных сил: силу, накопленную к оси балки под углом α, заменяем двумя взаимно перпендикулярными составляющими

Fх = F × сos 30 = 20 × 0,866 = 17, 32 кН

Fу = F× сos 60 = 20× 0,5 = 10 кН,

а равномерно распределенную нагрузку — её равнодействующей

Q = q × CD = 1 × 2 = 2 кН,

Равнодействующая Q приложена в середине участка CD, в точке К (рис. 2).

 

 

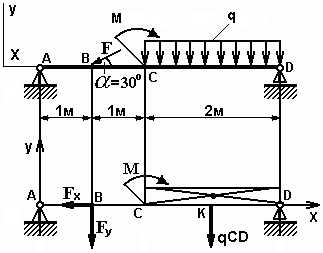
Рис. 2 — Схема преобразования заданных активных сил

 

4.Освобождаем балку от опор, заменив их опорными реакциями, направленными вдоль выбранных осей координат (рис 3).

Рис. 3 — Схема реакций балки

5.Составляем уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор и определяем неизвестные реакции опор.

å МА = 0; Fу  АВ + M + Q AK — RDy AD = 0 (1)

å МD = 0; RAy AD — Fу  ВD + M — Q KD = 0 (2)

å Fiх = 0; RAх — Fх = 0 (3)

6. Определяем реакции опор балок RAy, RDy и RAх решая уравнения.

Из уравнения ( 1 ) получаем

RDy = Fу  АВ + M + Q AK / AD = 10  1 + 10 + 2  3 / 4 = 6,5 кН

Из уравнения ( 2 ) получаем

RAy = Fу  ВD — M + Q KD / AD =10  3 — 10 + 2 / 4 = 5,5 кН

Из уравнения ( 3 ) получаем

RAх = Fх = F сos 30 = 20 0,866 = 17, 32 кН

7. Проверяем правильность найденных результатов:

å Fi y = 0; RAy — Fу — Q + RDy = 5,5 — 10 — 2 + 6,5 = 0

Условие равновесия выполняется, следовательно, реакции опор найдены верно.

sopromat.xyz

Определение опорных реакций — экспресс курс для чайников

Привет! Меня зовут Константин Вавилов и сегодня я решил начать свой экспресс курс: «сопромат для чайников». Начнем продвигаться через дебри «сопротивления материалов» именно с нее. Решение практически любой задачи по сопромату начинается с определения всех действующих, на элемент конструкции, внешних нагрузок. Помимо заданных условием задачи внешних сил, на объект расчета действуют силы, возникающие в связях, которые определяют условия закрепления элемента. Эти силы именуются как опорные реакции, также их называют еще реакциями опор или реакциями связей. Так вот, наша задача в рамках этого урока научиться определять эти реакции, чтобы далее перейти к построению эпюр, подбору сечений и т.д., к тому, чем знаменит сопромат. Ведь реакции опор изучаются еще в теоретической механике, но так как курс рассчитан на чайников, и реакции в сопромате встречаются сплошь и рядом, этот урок более чем уместен. Перейдем непосредственно к обучению!

Как определяются опорные реакции?

Опорные реакции определяются из уравнений равновесия статики, которые подразумевают, что рассчитываемая конструкция находится в состоянии равновесия. Существуют всего три формы уравнений равновесия, о чем можно, более подробно, почитать в этой статье.

Мы будем использовать классическую форму записи уравнений, вот эту:

Что значат эти три строчки? Эта система говорит нам, что так как система находится в состоянии равновесия, то для нее должны выполняться следующие условия:

• суммы проекций всех сил на вертикальную и горизонтальную оси равны нулю;
• сумма моментов относительно произвольного центра также равна нулю.

Записав правильно эти уравнения для конкретной системы, можно выразить из них искомые опорные реакции. Собственно, давайте рассмотрим пример и научимся записывать эти уравнения.

Пример определения опорных реакций

Возьмем двух опорную балку, загруженную сосредоточенной силой в середине пролета и равной 5 кН:

Эту же балку будем использовать в других статьях для чайников, для наглядности, рассчитаем для нее эпюры, подберем сечение, определим прогибы и т.д. Сегодня же ограничимся опорными реакциями. Продолжение следует.

sopromats.ru

Определение опорных реакций | ПроСопромат.ру

Определить опорные реакции в балке с шарниром

Обозначим буквами опоры — жесткую заделку А, шарнирно-подвижную опору В — и  шарнир С.

Нанесем опорные реакции — в заделке вертикальная реакция R_А и опорный момент М_{А ,}(горизонтальная реакция равна 0, ее не показываем), в шарнирно-подвижной опоре реакция R_В.

Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.

Если рассмотреть левую часть, то в уравнении       будут присутствовать две неизвестные R_А и М_А. Значит, следует рассмотреть правую часть (из него найдем R_В).

Теперь   из него найдем М_А

Следующее уравнение  из него найдем R_А

Выполним проверку. Спроецируем все силы на ось y.

Σy=0        R_А+R_B — q·4 = 0    2,5 +5,5 — 8 = 0

Проверка верна. Опорные реакции определены верно.

 

prosopromat.ru

заделка, шарнирно-подвижная или неподвижная опора

Привет! Меня зовут Константин Вавилов, я являюсь автором статей данного сайта – SoproMats.ru. В этой статье расскажу какие бывают виды опор или связей. Подробно разберем жесткую заделку, шарнирно-подвижную опору и шарнирно-неподвижную опору.

Существует несколько видов связей, которые ограничивают разное количество степеней свобод и соответственно в них может появляться разное количество реакции. Начнем знакомство с видами связей, с их условным обозначением, принятым в сопромате, а также в теоретической механике. Для простоты все связи будем рассматривать применительно к плоским системам.

Жесткая заделка

Жесткая заделка ограничивает сразу все возможные степени свободы, дает запрет на перемещение в вертикальном и горизонтальном направлении, а также исключает все возможные повороты. Таким образом, в заделке может возникать как реактивная сила, так и момент. Сила, как правило, раскладывается на вертикальную и горизонтальную составляющие.

Шарнирно-неподвижная опора

Шарнирно-неподвижная опора ограничивает линейные перемещения, но допускает поворот относительно точки B. Таким образом, в отличие от жесткой заделки, в неподвижной опоре не возникает реактивного момента, а только сила. Последнюю, обычно, также раскладывают на две составляющие.

Шарнирно-подвижная опора

В шарнирно-подвижной опоре может возникать только одна реакция. В такой опоре допустим поворот сечения, линейное перемещение в одном из направлений. Например, для подвижной опоры, показанной на рисунке, допустимо горизонтальное перемещение, но невозможно перемещение по вертикали. Тем самым в опоре возникает одна вертикальная реакция.

Это основные виды связей, которые можно встретить при решении задач. Конечно, есть и другие виды, но встречаются они редко, узнать о них вы сможете из интересного видеоролика представленного ниже.

Полезный видеоролик про виды связей

В этой статье поговорили о видах связей, как они обозначаются и какие реакции в них возникают. Самое время перейти к определению реакций опор. 

sopromats.ru

Виды опор балок (сопромат)

Существуют виды опор балок (рис. 7.2):

шарнирно неподвижная опора;

шарнирно подвижная опора;

жесткая заделка.

Шарнирно неподвижная опора

Шарнирно неподвижная опора (рис. 7.2, а, опора А) — это закрепление конца балки, при котором балка может поворачиваться, но не может перемещаться ни в горизонтальном (влево или вправо), ни в вертикальном (вверх или вниз) направлениях, то есть не может перемещаться ни в каком направлении. В шарнирно неподвижной опоре может возникнуть реакция, которую удобно представить в виде двух составляющих: вертикальной () и горизонтальной ().

Шарнирно неподвижная опора на расчетной схеме условно изображается посредством двух стерженьков. Нижние их концы шарнирно прикреплены к «земле», а верхние концы соединены между собой и с балкой шарниром.

Шарнирно подвижная опора

Шарнирно подвижная опора (рис. 7.2, б, опора B) — это устройство, в котором конец балки может свободно перемещаться в горизонтальном направлении, может поворачиваться при изгибе, но не может перемещаться в вертикальном направлении. Со стороны шарнирно подвижной опоры может возникнуть только вертикальная реакция (). Шарнирно подвижная опора изображается посредством одного стерженька, шарнирно соединенного и с землей, и с балкой.

Жесткая заделка

Жесткая заделка — это закрепление (рис. 7.2, в), при котором конец балки не может ни поворачиваться, ни перемещаться. В заделке могут возникнуть реактивный момент (момент жесткой заделки) и реакции и . Балка при жестком закреплении показывается заделанной в часть стены, которая штрихуется.

sopromato.ru