Расчет деформации стержня при растяжении-сжатии
Задача
Рассчитать деформации участков и общее изменение длины прямого стержня постоянного сечения.
Модуль продольной упругости стали E=200ГПа.
Пример решения
Предыдущие пункты решения задачи
- Определение опорных реакций,
- Построение эпюр внутренних продольных сил,
- Подбор размеров поперечного сечения стержня,
- Построение эпюр нормальных напряжений.
Стержень имеет три силовых участка, на которых площадь сечения одинакова, но внутренние силы и нормальные напряжения отличаются, поэтому определим абсолютные деформации всех участков в отдельности, после чего сложив их, получим изменение длины всего стержня в целом.
Изменение длины участков стержня при растяжении-сжатии рассчитывается по формуле:
где N – величина внутренней продольной силы,
l – длина рассматриваемого участка,
A – площадь его поперечного сечения,
E – модуль Юнга (продольной упругости) для материала стержня,
Значения внутренних сил и напряжений принимаются с построенных эпюр N (σ).

По эпюрам видно, что первый участок сжимается, а участки II и III растягиваются, следовательно, деформации Δl второго и третьего участков будут положительны (их длина увеличивается), а первого отрицательны (продольный размер уменьшается).
Рассчитаем их:
Деформация I участка (KM)
II участок (CK)
Удлинение третьего участка BC
Сложив (с учетом их знака) деформации всех участков получим величину изменения длины всего стержня в целом:
В результате деформации общая длина стержня увеличится на 0,51мм.
Расчет и построение эпюры перемещения сечений >
Другие примеры решения задач >
isopromat.ru
Задача № 1 Проверка прочности ступенчатого стержня при деформации растяжение и сжатие.
Содержание
| Задача № 1 Проверка прочности ступенчатого стержня при деформации растяжение и сжатие.……………………………………………………………………3 |
| Задача № 2 Расчет оптимального сечения ступенчатого стержня при деформации растяжение и сжатие……………………………………………..8 |
| Задача № 3 Расчет статически определимой стержневой системы, работающей на растяжение и сжатие………………………………………….12 |
| Задача № 4 Расчет вала на прочность и жесткость……………………………15 |
| Задача № 5 Расчет балки на прочность при плоском изгибе…………………20 |
| Задача №6 Расчет балки на прочность при плоском изгибе…………………23 |
| Задача № 7 Сравнение прочности балок различных сечений……………….27 |
| Задача № 8 Расчет сжатого стержня на устойчивость……………………….29 |
| Список литературы………………………………………………………………33 |
Задача № 2 Расчет оптимального сечения ступенчатого стержня при деформации растяжение и сжатие.
Задание:Определить оптимальный диаметр сечения круглого стержня на каждом участке по условию прочности. Определить продольные деформации, возникающие на каждом участке стержня. Стержень изготовлен из стали:
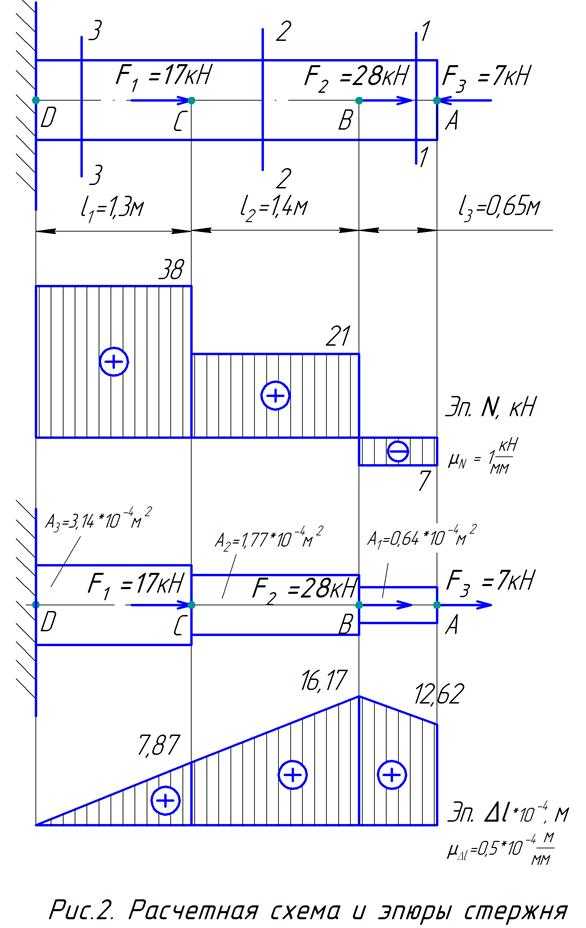
Е = 2*105 МПа; σТ = 240 МПа. Допускаемый коэффициент запаса статической прочности [n] выбрать самостоятельно ([n]= 1,2…1,8). Весом стержня пренебречь. Схема стержня приведена на рис. 2.
Исходные данные:F1=17 кН; F2=28 кН; F3=7кН; l1=130 см=1,3 м;
l2=140 см=1,4 м; l3=65 см=0,65 м.
Решение:Для определения продольной силы используем метод сечений.
Эпюру продольных сил необходимо строим, руководствуясь правилом: продольная сила в любом сечении стержня равна алгебраической сумме проекций всех внешних сил, расположенных по одну сторону от сечения на ось стержня. Продольная сила считается положительной, если она соответствует деформации растяжения (направлена от сечения) и отрицательной, если она вызывает сжатие (направлена к сечению).
1.Разобьем стержень на отдельные участки, начиная от свободного конца. Границы участков определяются точками приложения внешних сил. Всего по длине стержня в данной задаче будет три участка. Проведя сечения и отбрасывая левые части стержня, можно определить продольные силы в его поперечных сечениях без вычисления опорных реакций в заделке.
1 участок (сечение 1-1) : NI = -F3 = -7 кН.
на первом участке осуществляется деформация сжатия.
2 участок (сечение 2-2): N2 = -F3 +F2 = -7+28=21 кН.
на втором участке осуществляется деформация растяжения.
3 участок (сечение 3-3) N3 =-F3 +F2+F1 = -7+28+17=38 кН.
на третьем участке осуществляется деформация растяжения.
Таким образом, в заделке действует реакция равная N3 =38кН.
Эпюра продольных сил показана на рис.1. Эпюру продольных сил строим в масштабе = .
2. Допускаемое напряжение вычисляем по формуле: .
Допускаемые напряжения при сжатии и растяжении для пластичного материала, при условии, что коэффициент запаса n=1,8.
=240/1,8=133,3Мпа
3. Требуемая площадь сечения определяется из формулы условия прочности на растяжения.
Þ
Площадь круглого сечения А=
1 участок:
Принимаем d1=0,09м, А1=2 участок:
Принимаем d2=0,015 м, А2=
3 участок:
Принимаем d1=0,02м, А3=
Удлинения (укорочения) части стержня определяем по формуле ,где – соответственно длина участка, внутреннее усилие, площадь поперечного сечения, Е–модуль упругости материала.
Укорочение 1 участка .
Удлинение 2 участка
Удлинение 3 участка .
В правом конце стержня заделка, перемещение в этом конце отсутствует. Поэтому построение эпюры смещения стержня необходимо строить, начиная с левого конца.
На третьем участке смещение изменяется от нуля до =7,87*10-4 м;
на втором участке: от =7,87*10-4м до
=16,17*10-4 м;
на первом участке: от 16,17*10
до 7,87*10-4 +8,3*10-4 -3,55*10-4=12,62*10-4 м.
Эпюры смещения строим в масштабе:
= .
Ответ: Полное удлинение стержня составило 12,62*10-4м.
Задача № 3 Расчет статически определимой стержневой системы,
Задача № 4 Расчет вала на прочность и жесткость.
Задание:Определить диаметры ступенчатого вала из условия прочности и жесткости на кручение. Определить угол закручивания вала.
Вал изготовлен из стали: [Θ] = 1,75 *10-2 рад/м, G = 8 *1010 Па
Схема вала приведена на рис. 4.
Исходные данные:
а=1,4м; b=0,6м, c=0,6м, М1 =360Н*м; М2 = 400Н*м;М3 = 400Н*м; М4 = 500Н*м; [t] = 55 Мпа.
Решение.
1. Определение внутренних крутящих моментов по участкам.
Для определения знака крутящего момента примем следующее правило: если смотреть на отсеченную часть бруса со стороны внешней нормали к сечению, то момент сечении будет положителен в том случае, когда сумма внешних скручивавших моментов поворачивает отсеченную часть бруса по часовой стрелке, и отрицателен при повороте части бруса в противоположном направлении.
Неизвестный момент М5 в заделке найдем из уравнения равновесия для всего вала. Условно примем направление момента М5 за отрицательное. Тогда уравнение равновесия принимает вид
-М1 +М2 +М3 -М4-М5
Из решения этого уравнения получим
М5 =-М1 +М2 +М3 -М4=-360+400+400-500= -60Н*м.
Для построения эпюры крутящих моментов применяем метод сечений к каждому участку вала в отдельности (следует заметить, что построение эпюры крутящих моментов совершенно аналогично построению эпюры продольных сил). Крутящие моменты в сечениях определяются как алгебраические суммы внешних моментов, приложенных по одну сторону от сечения.
Определим крутящие моменты на каждом участке, проведя последовательно
сечения на четырехучастках вала и рассмотрим равновесие соответствующих
оставшихся правых частей.
В сечении 1-1: .
В сечении 2-2: .
В сечении 3-3:
В сечении 4-4:
По полученным данным строим эпюру крутящих моментов, откладывая по вертикальной оси значения моментов. Отрицательные моменты откладываем вниз по осевой линии (рис. 4). Эпюру моментов строим в масштабе = .
2. По найденным значениям крутящих моментов из расчетов на прочность и жесткость в каждом сечении определим диаметры валов.
Расчет на прочность ведется по допускаемому напряжению при кручении
где –крутящий момент, действующий в сечении бруса;
–полярный момент сопротивления для круглого сечения, –диаметр вала. Из формулы выразим диаметр
По формуле определим диаметры для всех сечений.
Сечение 1-1: 0,0359м, принимаем d1=0,036м.
Сечение 2-2: 0,021м, принимаем d2=0,022м.
Сечение 3-3: 0,0303м, принимаем d1=0,032м.
Сечение 4-4: 0,0177м, принимаем d4=0,018м.
3. Расчет на жесткость ведется по допускаемому относительному углу закручиванию , где –полярный момент сопротивления круглого сечения.
В соответствии с формулой определим диаметр вала из условия жесткости
По формуле определим диаметры для всех участков.
Сечение 1-1: 0,0437м, принимаем d1=0,045м.
Сечение 2-2: 0,0292м, принимаем d2=0,03м.
Сечение 3-3: 0,0384м, принимаем d1=0,04м.
Сечение 4-4: 0,0257м, принимаем d4=0,026м.
4. В соответствии с расчетами на прочность и жесткость выбираем наибольшее значение диаметров для каждого участка. В результате получим следующие значения:
5. Абсолютные углы закручивания для каждого участка можно определить по формуле , где – длина участка.
Полярные моменты инерции для каждого сечения
Сечение 1-1: м4;
Сечение 2-2: м4.
Сечение 3-3: м4;
Сечение 4-4: м4.
Далее определим углы закручивания.
= -0,0218 рад – угол поворота сечения В относительно сечения А (или угол закручивания участка АВ).
= -0,0095 рад – угол поворота сечения С относительно сечения В (или угол закручивания участка ВС).
= 0,009 рад – угол поворота сечения D относительно сечения C (или угол закручивания участка CD).
=- 0,0233 рад – угол поворота сечения Е относительно сечения D (или угол закручивания участка DЕ).
Строим эпюру углов закручивания для всего вала (рис. 4). За начало координат выбран крайний левый конец бруса (сечение D). В пределах каждого из участков бруса эпюра линейна, поэтому достаточно знать углы поворота только для граничных сечений участков.
В сечении от Е до D полный угол закручивания вала равен
-0,0233 рад;
В сечении от Е до С полный угол закручивания вала равен
-0,0233+0,009=-0,0143 рад;
В сечении от Е до В полный угол закручивания вала равен
— 0,0233+0,009-0,0095=-0,0238 рад;
В сечении от Е до А полный угол закручивания вала равен
— 0,0233+0,009-0,0095-0,0218=-0,0456рад.
Ординаты этой эпюры дают значения углов поворота соответствующих поперечных сечений вала.
Эпюру углов поворота строим в масштабе
= .
Ответ: и полный угол закручивания -0,0456 рад.

Список литературы
1. Сопротивление материалов: учебное пособие для вузов/ Н.Н.Вассерман и др. — Пермь: Изд-ва ПНИПУ, 2011 – 364 с.
2. Прикладная механика: Учеб. Для вузов/ В.В.Джамай, Ю.Н.Дроздов, Е.А.Самойлов и др. – М. Дрофа, 2004. – 414 с.
3. Феодосьев В.И. Сопротивление материалов. М.: МГТУ им. Н.Э. Баумана, 1999 – 592 с.
Содержание
| Задача № 1 Проверка прочности ступенчатого стержня при деформации растяжение и сжатие.……………………………………………………………………3 |
| Задача № 2 Расчет оптимального сечения ступенчатого стержня при деформации растяжение и сжатие……………………………………………..8 |
| Задача № 3 Расчет статически определимой стержневой системы, работающей на растяжение и сжатие………………………………………….12 |
| Задача № 4 Расчет вала на прочность и жесткость……………………………15 |
| Задача № 5 Расчет балки на прочность при плоском изгибе…………………20 |
| Задача №6 Расчет балки на прочность при плоском изгибе…………………23 |
| Задача № 7 Сравнение прочности балок различных сечений……………….27 |
| Задача № 8 Расчет сжатого стержня на устойчивость……………………….29 |
| Список литературы………………………………………………………………33 |
Задача № 1 Проверка прочности ступенчатого стержня при деформации растяжение и сжатие.
Задание:Оценить прочность ступенчатого стержня из хрупкого материала. Определить его деформацию. Стержень изготовлен из чугуна: Е = 1,2*105 МПа; σвр= 113 МПа; σвсж= 490 МПа. Допускаемый коэффициент запаса статической прочности [n] выбрать самостоятельно (в данной задаче принимаем [n]= 1,2…1,8). Весом стержня пренебречь.
Схема стержня приведена на рис. 1.
Исходные данные: l1=0,5м; l2=0,2м; l3=0,4м; А=4*10-4м2; А1=А=
=4*10-4м2; А2=3А=12*10-4м2; А3=1,5А=6*10-4м2; F1=30кН; F2=60кН; F3=20кН.
Решение. Разобьем стержень на отдельные участки, начиная от свободного конца. Границы участков определяются точками приложения внешних сил или местами изменения размеров поперечного сечения. Всего по длине стержня в данной задаче будет три участка. Проведя сечения и отбрасывая левые части стержня, можно определить продольные силы в его поперечных сечениях без вычисления опорных реакций в заделке.
Для того, чтобы определить усилие NI, проводим сечения в пределах первого участка. Рассмотрим равновесие оставшейся правой части стержня.
Из уравнения равновесия оставшейся правой части выразим внутреннюю продольную силу NIчерез внешние силы, приложенные к оставленной части
NI =- F1 = -30 кН
Так как положительное направление совпадает с деформацией растяжения, то знак минус означает, что на первом участке осуществляется деформация сжатия.
Аналогично находим внутреннее усилие NII, действующее на втором
участке. Для этого проводим произвольное сечение на втором участке и рассматриваем равновесие оставшейся правой части стержня .
Уравнение равновесия в проекции на ось стержня для второго участка
-F1 + F2 -NII = 0
Решая это уравнение, получим
NII = -F1 -F2 = -30+60 = 30 кН.
на втором участке осуществляется деформация растяжения.
Для того, чтобы определить внутреннее усилие NIII, действующее на третьем участке рассмотрим равновесие оставшейся части стержня.
-F1 +F2 + F3 – NIII = 0.
Решая это уравнение, получим
NIII =-F1 + F2 +F3 = -30+60 +20=50 кН.
Таким образом, в заделке действует реакция равная NIII =50 кН.
на третьем участке осуществляется деформация растяжения.
Эпюра продольных сил показана на рис.1. Эпюру продольных сил строим в масштабе =
Чтобы определить напряжение в поперечных сечениях бруса, нужно разделить числовые значения продольных сил на площади этих сечений.
Для первого участка
.
Допускаемые напряжения при сжатии, при условии, что коэффициент запаса n=1,2
=490/1,2=408 Мпа.
Условие прочности для первого участка выполняется .
Недогруз конструкции на первом участке составил
*100%= = 81,7%, что выше допустимого (10%).
Для сечения 2-2: .
На втором участке деформация растяжения. Допускаемые напряжения при растяжении, при условии, что коэффициент запаса n=1,2
=113/1,2=94,2 Мпа.
Условие прочности для первого участка выполняется .
Недогруз конструкции на втором участке составил
*100%= = 73,4%, что выше допустимого (10%).
Для сечения 3-3: .
На третьем участке деформация растяжения. Допускаемые напряжения при растяжении =94,2 Мпа.
Условие прочности для третьего участка выполняется .
Недогруз конструкции на третьем участке составил
*100%= =11,6 %, что выше допустимого (10%).
Эпюра нормальных напряжений по длине бруса показана на рис. 1.
Эпюры нормальных напряжений строим в масштабе:
= .
укорочение участков бруса определяются по формуле
,
где – соответственно длина участка, внутреннее усилие, площадь поперечного сечения, напряжение в сечении. Е–модуль упругости материала.
укорочение первого участка
.
удлинение второго участка
удлинение третьего участка
.
В левом конце стержня заделка, перемещение в этом конце отсутствует. Поэтому построение эпюры деформации стержня необходимо строить, начиная с левого конца.
На третьем участке деформация изменяется от нуля до =27,78*10-5м;
на втором от =27,78*10-5м
до =31,95*10-5м;
на первом от 31,95*10-5м
до 27,78*10-5 +4,17*10-5-31,25*10-5=0,7*10-5м.
Эпюры смещения строим в масштабе:
= .
Ответ: Полное удлинение бруса составило 0,7*10-5м и прочность стержня по допускаемым напряжениям выполняется.

infopedia.su
Растяжение_сжатие студентам
Растяжение-сжатие.
Растяжением (сжатием) стержня называется такое напряженное состояние, при котором в любом его поперечном сечении все внутренние силы, распределенные равномерно по всему сечению, приводятся к равнодействующей осевой силе N, называемой продольной силой.
Применяя метод сечений, т. е. рассматривая равновесие любой отсеченной части стержня под действием внешних нагрузок и внутренней осевой силы N, получим, что продольная сила N равна алгебраической сумме проекций всех внешних нагрузок, находящихся по одну сторону сечения, на ось стержня.
При растяжении-сжатии, в поперечных сечениях стержня возникают нормальные напряжения, которые определяются по формуле:
 (2.1)
(2.1)
Условия прочности имеет вид:
 (2.2)
(2.2)
здесь N – продольная сила,
F – площадь поперечного сечения,
 — допускаемое
напряжение материала стержня,
— допускаемое
напряжение материала стержня,
о – опасные напряжения материала (равные пределу текучести для пластичного материала и пределу прочности – для хрупкого),
nо – основной коэффициент запаса прочности.
Из условия прочности (2.2) можно вычислить необходимую площадь поперечного сечения стержня:

или определить допускаемую нагрузку:
или проверить надежность конструкции.
Абсолютная величина деформации участка стержня при постоянной продольной силе, действующей на этом участке, и известной площади поперечного сечения определяется по закону Гука:

 ; (2.3)
; (2.3)
где Е – модуль продольной упругости или модуль Юнга.
При действии на некотором участке стержня продольной равномерно распределенной нагрузки интенсивностью q продольная сила определяется следующим образом:
, (2.4)
где Nо – продольная сила в начале участка.
В этом случае напряжения можно вычислить по формуле:
 . (2.5)
. (2.5)
Деформации только от распределенной нагрузки равны:
 . (2.6)
. (2.6)
С учетом всех нагрузок деформацию участка стержня длиной L проще всего определять по формуле:
 , (2.7)
, (2.7)
где Nср – средняя величина продольной силы на участке с распределенной нагрузкой.
Если у системы (конструкции) число связей (следовательно, реакций связей) больше чем число уравнений статики, то такие системы называются статически неопределимыми. По числу «лишних» связей определяют степень статической неопределимости системы. Для составления недостающих уравнений, исходя из условий совместимости деформаций, рассматривают геометрическую сторону задачи и находят связь между деформациями элементов конструкции. Выражая деформации в соответствии с законом Гука через усилия, получим недостающие уравнения.
Пример №1. Представленный на рис. 2.1 ступенчатый стержень нагружен системой внешних нагрузок. Требуется построить эпюры продольных сил, нормальных напряжений и перемещений.
Рисунок 2.1
Решение.
Определяем на участках стержня значения продольных сил:
N1-2 = Р1 = 20 кН;
N2-3 = Р1 – Р2 = 20 – 10 = 10 кН;
N3-4 = Р1 – Р2 = 10 кН;
N4-5 = Р1 – Р2 – qх,
при х = 0 N4 = Р1 – Р2 = 10 кН.
при х = 2м кН.
.
Эпюра продольных сил приведена на рис. 2.2. Находим на каждом участке величины напряжений:

Эпюра нормальных напряжений показана на рис. 2.2.

Рисунок 2.2.
Эпюра перемещений строится со стороны закрепленного конца, т. к. защемленное сечение неподвижно т. е. 6 = 0. Далее определяем перемещения соответствующих точек стержня:
т. к. N5-6 = 0, получим
,
м.
На участке 4-5 эпюра перемещений имеет экстремум в сечении Хо, где продольная сила равна нулю. Найдем значение Хо из условия:
N(хо)
= — 30 + qхо = 0, 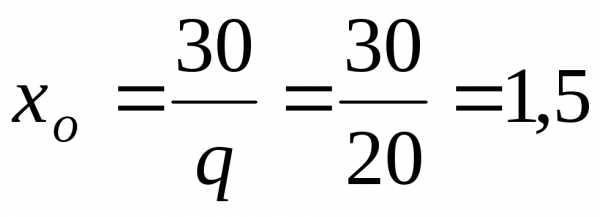 м
м
и тогда экстремальное значение перемещения на этом участке будет:
м.
Определяем перемещение сечения «3», которое равно деформации участка 6-3, при известных деформациях участков 5-6 и 4-5:
м.
Аналогично определяем:
м.
м.
Эпюра перемещений представлена на рис. 2.2.
Анализ эпюр показывает, что сосредоточенные силы вызывают скачки в эпюрах «N» и «», а в эпюре «» — излом. На участках с распределенной нагрузкой эпюры «N» и «» переменны, а эпюра «» изменяется по параболическому закону. Резкое изменение поперечного сечения вызывает скачок на эпюре «» (сечение «3»).
Пример №2. Ступенчатый брус защемлен обоими концами и нагружен системой внешних нагрузок, как показано на рис. 2.3. Материал бруса сталь Ст.3 с пределом текучести т = 240 МПа и основным коэффициентом запаса прочности пт = 1,5.
Модуль упругости Е = 2* 105 Мпа. Площадь сечения принять F = 4 см2.
Требуется:
Построить эпюру «N» в долях «Р»;
Построить эпюру «» в долях «Р/ F»;
Определить из условия прочности допускаемую нагрузку [Р];
При данной нагрузке [Р] построить эпюру перемещений «».
Рисунок 2.3.
Решение.
Из уравнений равновесия определим реакции опор (рис. 2.4а).
Имеем систему сходящихся сил, для которой уравнение равновесия имеет вид:

Т. е. одно уравнение статики с двумя неизвестными R1 и R2. Система один раз статически неопределима.

а) б) в) г) д)
Рисунок 2.4.
Рассмотрим геометрическую сторону задачи. Поскольку опорные сечения неподвижны, их взаимное перемещение равно нулю, т. е.
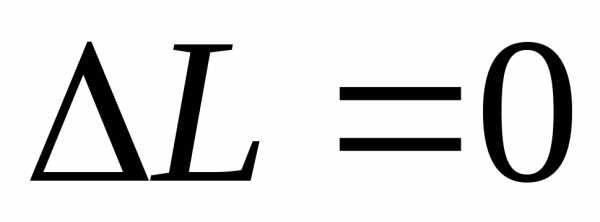 ;
;
Освободим один конец стержня (верхний) как показано на рис. 2.4б. В соответствии с принципом независимости действия сил, взаимное перемещение определяется как сумма деформаций от действующих на стержень нагрузок:
;
Запишем последнее выражение, заменив каждую составляющую с помощью закона Гука:
.
Умножив обе части
этого уравнения на  и подставив значения усилий Р1 = Р и Р2 = 3Р, получим:
и подставив значения усилий Р1 = Р и Р2 = 3Р, получим:
,
откуда  .
.
Знак «минус»
указывает на то, что R1 направлена в противоположную сторону.
На рис. 2.4 старое направление R1 зачеркнуто, а действительно направленная
вниз реакция  .
.
Построим эпюру «N» в долях «Р» (рис. 2.4в), для чего запишем выражения продольной силы на каждом участке стержня:
N1-2 = -R1 =-2/11P;
N2-3 = -R1 – Р1 = – 13/11P;
N3-4 = -R1 – Р1 = -13/11P;
N4-5 = -R1 — Р1 + Р2 = -13/11P + 3P = 20/11P.
Учитывая площади поперечных сечений каждого участка находим напряжения и строим эпюру нормальных напряжений в долях Р/ F (рис. 2.4г):
.
Очевидно, что
наибольшее напряжение 
Запишем условие прочности:
,
где .
Тогда
Построим эпюру перемещений, определив смещения в характерных точках стержня.
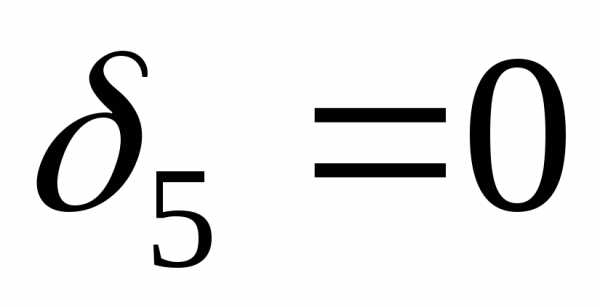 ,
,
м;
м;
м;
м.
Как видно из результатов расчета, перемещения в защемленных сечениях 1 и 5 равны нулю, что подтверждает правильность решения. Эпюра перемещений показана на рис. 2.4д.
Пример №3. Абсолютно жесткий брус ОВ закреплен шарнирно в точке О, подпоркой АС и тягой ВД. Брус нагружен силой Р = 100 кН. Материал подпорки и тяги – сталь Ст. 4 с пределом текучести т =300 Мпа. Определить площади поперечного сечения подпорки и тяги – F1 и F2, если F1/ F2 = ½. В расчетах принять коэффициент запаса прочности nт = 1,5.

Рисунок 2.5.
Решение.
Составим план предполагаемых усилий (рис. 2.6).
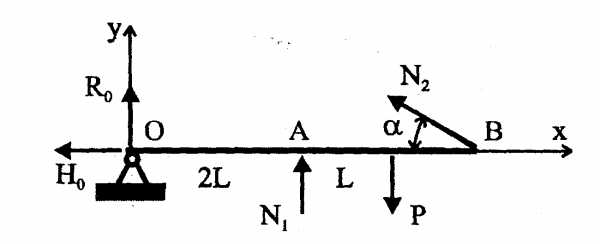
Рисунок 2.6.
Запишем уравнение равновесия системы:


.
В результате получим три уравнения статики с четырьмя неизвестными Rо, Hо, N1 и N2. Т. е. система один раз статически неопределима.
Для раскрытия статической неопределимости построим план предполагаемых перемещений (рис. 2.7).

Рисунок 2.7.
Под действием силы Р жесткий брус ОАВ повернется вокруг точки О, при этом точки А и В соответственно займут положение А1 и В1. Из подобия треугольников ОАА1 и ОВВ1 имеем:
 ,
где
.
,
где
.
В треугольнике ВВ1В угол  =α,
т. к.ВВ1 ОВ,
а В1В ДВ,
поэтому
=α,
т. к.ВВ1 ОВ,
а В1В ДВ,
поэтому  .
ПодставивиВВ1 в пропорцию, получим условие совместимости
деформаций в виде:
.
ПодставивиВВ1 в пропорцию, получим условие совместимости
деформаций в виде:
.
Выражаем  и
и в соответствии с
законом Гука через усилия, действующие
в стержнях:
в соответствии с
законом Гука через усилия, действующие
в стержнях:
здесь:
 ; ,
; ,
Учитывая, что  ,
получим после подстановки:
,
получим после подстановки:
После упрощения этого выражения получим недостающее уравнение в виде:
Решаем совместно с этим уравнением третье уравнение равновесия и учитывая, что
получим величины усилий:
кН; кН.
Определим площади поперечных сечений стержней. Для этого сначала найдем допускаемое напряжение:
Мпа.
Записываем условие прочности для подпорки АС и определяем площадь поперечного сечения:
 ;
;
.
Из соотношения площадей находим:
см2.
Далее из условия
прочности для тяги АС проверяется правильность определения
площади  .
В случае, если условие прочности не
удовлетворяется, необходимо сначала
определить
.
В случае, если условие прочности не
удовлетворяется, необходимо сначала
определить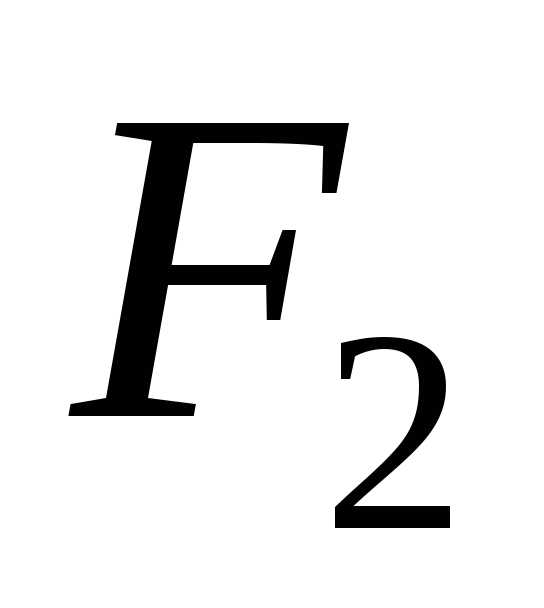 ,
а затем из соотношения площадей найти
новое значение площади
,
а затем из соотношения площадей найти
новое значение площади .
.
Проверим прочность стержня ВД:
.
Таким образом, прочность конструкции обеспечена.
studfiles.net
Расчет на растяжение стержня — Доктор Лом. Первая помощь при ремонте
где N — продольная растягивающая сила, действующая на стержень;
F — площадь поперечного сечения стержня;
σ — нормальные напряжения, возникающие в рассматриваемом поперечном сечении стержня в ответ на действие растягивающей продольной силы;
Rр — расчетное сопротивление материала стержня растяжению (для некоторых материалов расчетные сопротивления растяжению, сжатию, изгибу и т.п. могут различаться).
Визуально это может выглядеть так:

Рисунок 525.1. Нормальные напряжения при растяжении прямолинейного стержня.
На рисунке 525.1.а) мы видим прямолинейный стержень длиной l, показанный серым цветом, к которому приложена растягивающая сила N. При этом точка приложения силы находится на нейтральной оси стержня, совпадающей с осью х, показанной пунктирной линией.
Для упрощения расчетов заменяем опору А соответствующей опорной реакцией А (рис.525.1.б). Исходя из условий статического равновесия:
∑х = А + N = 0 (149.5.2)
А = — N (525.2)
Это означает, что опорная реакция A равна по значению растягивающей силе N, но направлена в противоположную сторону.
Если взглянуть на эту ситуацию под некоторым углом, то она будет выглядеть так, как показано на рисунке 525.1.в). На этом рисунке мы видим, что нормальные напряжения — это реакция материала на действие растягивающей силы и направлены эти напряжения в сторону, противоположную действию сил. Другими словами нормальные напряжения препятствуют деформации растяжения, и направлены на то, чтобы вернуть материалу исходную форму. Иногда для упрощения восприятия нормальные напряжения, возникающие при растяжении, принято изображать направленными от сечения, как показано на рисунке 525.1.г), а сжимающие напряжения — направленными к сечению. С точки зрения физики такая замена вполне допустима, так как нормальные напряжения (внутренние силы) можно рассматривать как плоскую нагрузку, распределенную по всей площади сечения (внешнюю силу). Как правило растягивающие нормальные напряжения рассматриваются как положительные, а сжимающие — как отрицательные.
Сечение стержня, показанное на рисунке 525.1.в) розовым цветом, является перпендикулярным нейтральной оси стержня и называется поперечным сечением.
Как следует из формулы (525.1) и из приведенного рисунка, длина стержня l на значение нормальных напряжений никак не влияет. А вот параметры поперечного сечения стержня: ширина сечения b и высота сечения h, если сечение прямоугольное, очень даже влияют, так как от этих параметров зависит площадь F поперечного сечения.
Примечание: конечно же поперечное сечение стержня далеко не всегда имеет прямоугольную форму, как показано на рисунке 525.1.в). Поперечное сечение может быть и круглым, и овальным, и ромбическим, и вообще иметь любую сколь угодно сложную форму, тем не менее форма поперечного сечения никак на значение нормальных напряжений не влияет (во всяком случае такое допущение принимается в теории сопротивления материалов), а влияет только площадь сечения, определить которую тем сложнее, чем более сложной является форма поперечного сечения.
Проверить данные постулаты теории сопротивления материалов очень легко и просто. Достаточно взять нитку и попробовать ее разорвать (вариант а)). Затем разорвать нитки с с той же катушки, но б) более короткую и в) более длинную, чем в первом случае. Во всех трех случаях усилие, которое необходимо приложить для разрыва нитки, будет примерно одинаковым.
Но если одну из ниток сложить вдвое и попробовать разорвать, то усилие, необходимое для разрыва нитки, увеличится в 2 раза. Все потому, что условная площадь сечения стержня, работающего на растяжение, увеличится при складывании нитки в 2 раза.
Таким образом известная пословица: «где тонко, там и рвется» в переводе на язык теории сопротивления материалов будет звучать примерно так: «при действии растягивающих нормальных напряжений разрушение материала, обладающего постоянным сопротивлением растяжению по всей длине, будет происходить в сечении с минимальной площадью». Это особенно актуально для стержней с изменяющейся по длине площадью сечения.
С учетом различных факторов формула (525.1) может иметь другой вид:
Nγn/Fn = σ ≤ Rрγs (512.1.2)
где γn — коэффициент надежности по нагрузке (как правило больше единицы), Fn — минимальная площадь сечения (с учетом возможных ослаблений отверстиями, пазами и т.п.), γs — коэффициент условий работы (как правило меньше единицы).
Т.е. теория сопротивления материалов допускает, что нормальные напряжения в стержне могут быть равны расчетному сопротивлению материала на растяжение, умноженному на коэффициент условий работы.
Пример расчета стержня на растяжение
Дано: На стальной стержень (см. рис.525.1.а)) с расчетным сопротивлением Rp = 2250 кг/см2 действует продольная растягивающая сила N = 30 тонн. Коэффициент надежности по нагрузке γn = 1.05, коэффициент условий работы γs = 0.9. Собственным весом стержня в виду его незначительности по сравнению с действующей нагрузкой для упрощения расчетов можно пренебречь. Предполагается, что нагрузка прикладывается по всей площади поперечного сечения стержня, т.е. возникающие нормальные напряжения будут равномерно распределенными по всей площади сечения.
Требуется: Подобрать диаметр стержня.
Решение:
1. Определяем требуемую площадь сечения стержня, преобразовав формулу (525.1.2)
F = Nγn/Rpγs = 30000·1.05/(2250·0.9) = 15.56 см2.
2. Определяем диаметр стержня
d = √4F/п = √4·15.56/3.14 = 4.45 см
Как видим сам расчет занимает гораздо меньше времени, чем описание физических характеристик используемых данных и даже формулировка условия задачи.
doctorlom.com
Задача № 2 Расчет оптимального сечения ступенчатого стержня при деформации растяжение и сжатие. Прикладная механика
Похожие главы из других работ:
Пластинчатый конвейер
3.2. Расчет винта на сжатие
Усилие, действующее на винт P = 162254 Н (3.10) где[?] — допускаемое натяжение ([?] = 500МПа) (3.11) Принимаем диаметр винта d = 20 мм…
Прикладная механика
Задача № 1 Проверка прочности ступенчатого стержня при деформации растяжение и сжатие
Задание: Оценить прочность ступенчатого стержня из хрупкого материала. Определить его деформацию. Стержень изготовлен из чугуна: Е = 1,2*105 МПа; увр = 113 МПа; увсж = 490 МПа…
Прикладная механика
Задача № 8 Расчет сжатого стержня на устойчивость
Задание: Определить влияние длины стойки на величину допускаемой нагрузки. Материал стойки — сталь Ст.3: Е = 2,1 * 105 МПа; уТ = 240 МПа; лпред. = 100; л0 = 40; a = 310 МПа; b = 1,14 МПа. Требуемый коэффициент запаса устойчивости [nу] = 2. Схема стойки приведена на рис. 1…
Проектирование трехфазного асинхронного электродвигателя
4.5 Ток и площадь поперечного сечения стержня ротора
где ki = 0,899 — коэффициент, учитывающий влияние намагничивающего тока и сопротивление обмоток, определяемый по рис.4.1. — коэффициент приведения тока ротора к обмотке статора…
Проектирование трехфазного асинхронного электродвигателя
4.9 Окончательные значения сечения стержня и плотности тока
мм2…
Проектирование трехфазного асинхронного электродвигателя
9.3 Площадь сечения части стержня, ограниченной высотой hr
мм2 мм 9.4 Отношение площади всего сечения стержня qC к площади qr 9.5 Коэффициент увеличения сопротивления фазы ротора под влиянием эффекта вытеснения тока где и из п.6.4. 9…
Проектирование трехфазного асинхронного электродвигателя
9.3а. Площадь сечения части стержня, ограниченной высотой hr
мм2 мм 9.4а. Отношение площади всего сечения стержня qC к площади qr 9.5а. Коэффициент увеличения сопротивления фазы ротора под влиянием эффекта вытеснения тока где и из п.6.4. 9.6а…
Проектирование трехфазного асинхронного электродвигателя
9.4 Отношение площади всего сечения стержня qC к площади qr
9.5 Коэффициент увеличения сопротивления фазы ротора под влиянием эффекта вытеснения тока где и из п.6.4. 9.6 Приведенное активное сопротивление обмотки ротора с учетом действия эффекта вытеснения тока Ом где см. п.6.4. 9…
Проектирование трехфазного асинхронного электродвигателя
9.4а. Отношение площади всего сечения стержня qC к площади qr
9.5а. Коэффициент увеличения сопротивления фазы ротора под влиянием эффекта вытеснения тока где и из п.6.4. 9.6а. Приведенное активное сопротивление обмотки ротора с учетом действия эффекта вытеснения тока Ом где см. п.6.4. 9.7а…
Разработка комплекта инструментальной оснастки для обработки детали «Ротор»
2.5 Расчет прочности рёбер на растяжение
В процессе резания рёбра жёсткости на оправке, образованные группой отверстий, принимают на себя нагрузку, вызванную силой резания. Одна из составляющих силы резания — Py, нагружает рёбра на растяжение и сжатие. Ребро имеет сложное сечение…
Расчет балочной клетки и колонн рабочей площадки
3.1 Расчет стержня колонны
· Отметка верха колонны 7,1м; · Колонна центрально сжатая; · Шарнирно оперта вверху и внизу; · Сталь С235>Ry=23кН/см2; · Реакция главной балки VГБ=934,75кН; · Ориентированный вес колонны QС.В…
Расчет металлорежущих инструментов (протяжка шлицевая, сверло комбинированное и фреза червячная для обработки шлицевого вала)
2. Расчет ступенчатого сверла
Исходные данные для проектирования: диаметр первой ступени сверла мм; диаметр второй ступени сверла мм; длина сверления первой ступенью мм; длина сверления второй ступенью…
Расчет растяжения и сжатия стержня
1. Растяжение, сжатие
сечение эпюра кручение Для стержня, загруженного по данным табл. 1: а) построить эпюру продольных сил; б) подобрать из условия прочности размеры стержня круглого и квадратного сечений; в) определить перемещение свободного конца стержня…
Расчет стержня круглого поперечного сечения, находящегося под действием изгиба с кручения
1.4 Расчет на прочность при изгибе с кручением стержня круглого поперечного сечения
При расчете на прочность в опасных точках опасного сечения анализируется неравенство: уэкв ? [у], где уэкв — эквивалентные нормальные напряжения, учитывающие главные напряжения у1, у2…
Составление расчетной схемы вала
3.1 Эпюра растяжение-сжатие
Зубчатые колеса посажены на вал с гарантированным натягом и закрепляются гайкой от осевого смещения под действием осевой силы Fx. Растягивающие усилия на валу принимаем равными Fx= 5Fx. Нормальная сила на участках вала будет: NI=Fx2=6…
prod.bobrodobro.ru
Растяжение – сжатие прямолинейного ступенчатого стержня
Прямолинейный упругий ступенчатый стержень нагружен вдоль оси нормативными сосредоточенными силами F1н, F2н и равномерно распределённой нагрузкой qн. Модуль упругости материала Е = 210 ГПа, предел текучести материала sт.
Вычислить продольную силу N, напряжения в поперечных сечениях s, относительную линейную деформацию e и перемещения u для характерных сечений; построить эпюры N, s, e, u; проверить прочность конструкции по первой группе предельных состояний.
Исходные данные
| Шифр | qн … кН/м | F1н кН | F2н кН | R МПа | l м | A cм2 | ||
| 31–6 | 0,95 | 1,1 | 1,0 | 2,0 |
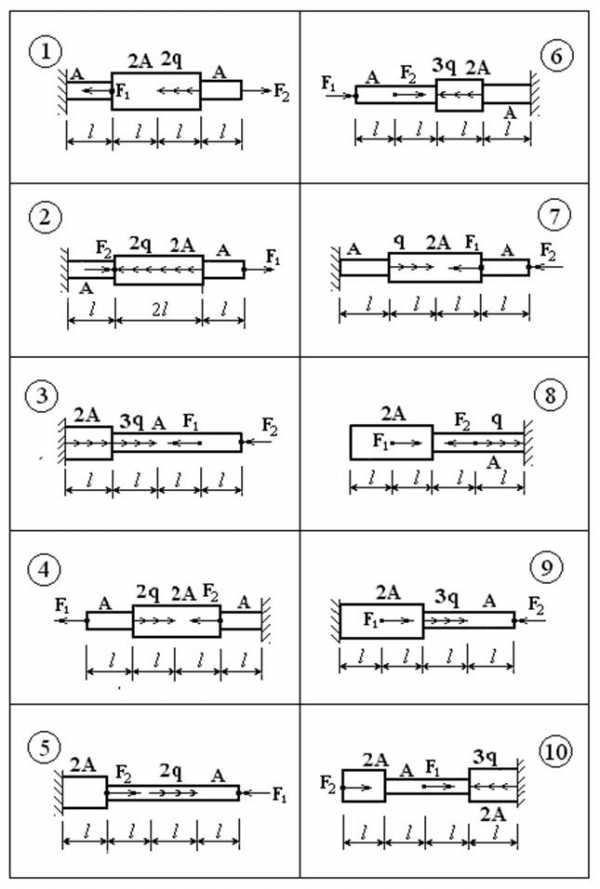
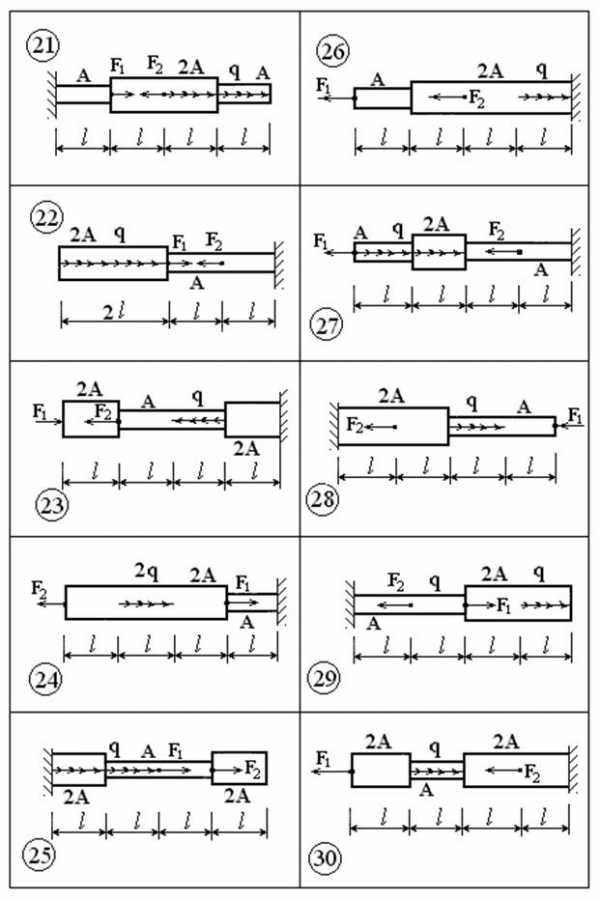
Расчётная схема и эпюры

Решение
На рисунке показываем координатную ось z-ов с началом на левом конце стержня, направленную вправо. В заделке правого конца возникает опорная реакция R0. Она единственная, поскольку все силы, приложенные к стержню, направлены вдоль одной прямой, в данном случае вдоль продольной осевой линии стержня. Она войдет в уравнения равновесия, поэтому вычислим её. Направление вправо, показанное на чертеже, выбрано произвольно. Истинное направление будет найдено в ходе вычислений.
Расчёты на первом этапе будем проводить по второй группе предельных состояний, т.е. по нормативным нагрузкам. В целом стержень находится в равновесии. Поэтому система сил, приложенных к нему, включая и опорную реакцию, должна удовлетворять уравнению равновесия
.
Отсюда находим
Знак минус, полученный в ответе, означает, что истинное направление реакции противоположно направлению, выбранному на схеме.
Стержень вдоль длины имеет четыре участка. Обозначим их на расчётной схеме. Для определения продольных сил далее применим метод сечений. С этой целью внутри каждого участка, в произвольном месте, проводим поперечные сечения 1–1, 2–2, 3–3, 4–4. В результате стержень каждый раз разделяется на левую и правую части. Уравнение равновесия любой из них даёт значение продольной силы и её направление. Рассмотрим каждый участок отдельно.
1 участок z [0; l]
Возьмём для рассмотрения левую отсечённую часть, так как к ней приложено меньшее количество сил. Укажем ось z-ов с началом на левом конце и продольную силу N. Её лучше направлять в положительную сторону, что в данном случае означает направление на растяжение, т.е. направо. Удобство такого приёма состоит в том, что при его применении автоматически получается ответ, учитывающий правило знаков для продольной силы.
Составим уравнение равновесия для отсечённой части:
F1н + N = 0.
Отсюда имеем
N = –F1н = –16 кН.
Полученный в ответе знак минус означает, что направление продольной силы, показанное на рисунке, не соответствует истинному, т. е. она направлена влево, на сжатие.
Для построения эпюры N проводим её нулевую линию параллельно продольной оси стержня. Полученный результат является постоянной отрицательной величиной. Поэтому на эпюре ей соответствует горизонтальная линия, проведенная ниже нулевой линии на расстоянии, отложенном в выбранном масштабе. Знак минус на таком рисунке указывается в кружочке, сама эпюра штрихуется перпендикулярно нулевой линии, т.е. вертикально. В избранном масштабе штриховые линии изображают значения продольных сил в сечениях. Поэтому штриховать эпюры следует строго вертикально (не горизонтально, не наклонно!).
Теперь найдём нормальные напряжения в сечениях
Здесь при подстановке чисел в формулу следует перейти к единицам измерения в системе СИ:
1 кН = 103 Н, 1 см2 = 10-4 м2.
Перейдём к определению относительных деформаций. По закону Гука
В таком же порядке рассматриваются и другие участки.
2 участок z [0; l]
Такие же действия, как для первого участка, приведут к следующим результатам:
.
.
Получена линейная функция. Поэтому эпюра будет прямолинейной. Достаточно найти две её точки.
N(0) = –16 кH.
Знак минус означает, что избранное направление стрелки не соответствует действительному, т.е. здесь сила направлена влево, к сечению, на сжатие.
N(l)= –16 + 24·1 = 8 кH.
По полученным двум числам строим эпюру продольной силы для данного участка в виде прямой наклонной линии.
Найдём нормальные напряжения. В общем виде имеем линейную функцию
Определим её значения в двух точках. На левом конце участка
На правом конце
Соответствующие относительные деформации
3 участок z [0; l]
Здесь целесообразно рассматривать правую отсечённую часть. Ось z-ов направляем произвольно, вправо. Продольную силу N изображаем в виде стрелки, направленной влево, в положительную сторону, т.е. на растяжение.
Знак плюс, полученный здесь, означает, что продольная сила по направлению совпадает с показанным на рисунке, т.е. направлена от сечения, налево, на растяжение.
Получен результат в виде постоянной величины. Поэтому на эпюре будет горизонтальная линия, отложенная от нулевой в том же масштабе, как для предыдущих участков.
Нормальные напряжения в поперечном сечении:
Относительные деформации:
4 участок
Составляем уравнение равновесия и находим продольную силу:
Нормальные напряжения:
Соответствующие относительные деформации:
Перейдём к определению перемещений. С этой целью по длине стержня намечаем характерные точки a, b, c, e, f, для которых будем вычислять перемещения.
Они совпадают с границами участков. На втором участке действует распределённая нагрузка. Здесь эпюра перемещений будет криволинейной. Поэтому для её построения нужна ещё одна дополнительная точка. В качестве таковой изберём точку d, где N, , равны нулю. Перемещение в этой точке экстремальное (max или min) для этого участка. Найдём её положение, приравнивая продольную силу к нулю
Отсюда имеем
Теперь можно приступить к непосредственному определению перемещений точек. Точка а закреплена, неподвижна. Поэтому
Перемещение точки b равно удлинению четвёртого участка стержня, т.е.
Перемещение точки c равно сумме деформаций третьего и четвёртого участков
Перемещение ub уже найдено, поэтому
Перемещение точки d равно сумме
где – удлинение участка cd. На этом участке относительная деформация – переменная величина, поэтому его удлинение равно площади треугольника на эпюре т.е.
Таким образом,
Аналогично определяются перемещения точек e и f:
Прочность конструкции проверяем по первой группе предельных состояний. Условие прочности имеет вид
Максимальное по модулю значение нормального напряжения в сечениях стержня, равное 80 МПа, вычислено по нормативным нагрузкам. Его расчётное значение должно быть определено с учётом коэффициента надёжности по нагрузкам, т.е.
.
Следовательно, условие прочности выполняется. Вывод: прочность конструкции обеспечена.
ВАРИАНТЫ ЗАДАНИЙ
| Второе число шифра | q кН/м | F1 кН | F2 кН | R МПа | l м | A cм2 | ||
| 0,85 | 1,2 | 1,0 | 2,0 | |||||
| 0,90 | 1,3 | 1,5 | 1,8 | |||||
| 0,95 | 1,1 | 1,2 | 1,6 | |||||
| 0,90 | 1,2 | 1,8 | 1,4 | |||||
| 0,85 | 1,4 | 1,4 | 1,9 |

refac.ru
I. Расчеты стержня на прочность и жесткость при растяжении (сжатии)
Центральным растяжением (сжатием) называется такой вид нагружения бруса, при котором внешние нагрузки или их равнодействующие приложены вдоль оси бруса. Брус с прямолинейной осью, работающий в условиях центрального растяжения (сжатия), называется стержнем. В поперечных сечениях стержня возникает один внутренний силовой фактор (ВСФ) — нормальная сила Nz . Для определения нормальной силы используется метод сечения. Нормальная сила Nz в поперечном сечении равна сумме проекций всех сил, расположенных по одну сторону от этого сечения, на ось стержня. Нормальная сила Nz принимается положительной и направляется от сечения, если она вызывает растяжение. Величина нормальной силы в произвольном поперечном сечении стержня определяется по формуле:
(1)
где  — сосредоточенные силы,
— сосредоточенные силы,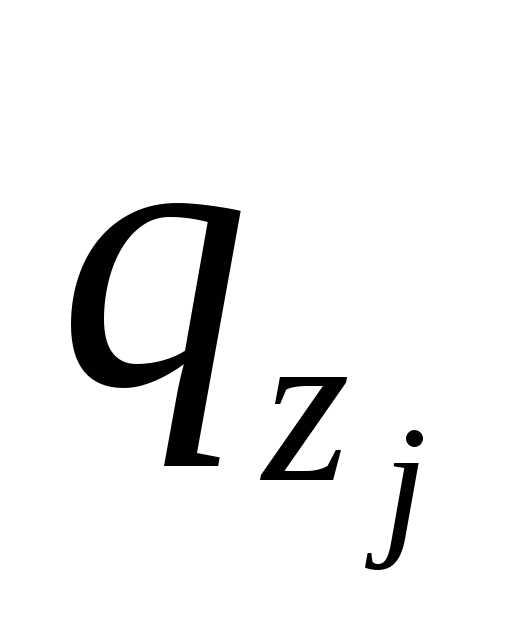 — распределенные нагрузки.
— распределенные нагрузки.
Нормальное напряжение в произвольном поперечном сечении стержня вычисляется по соотношению:
 (2)
(2)
где  — площадь поперечного сечения i —
участка стержня.
— площадь поперечного сечения i —
участка стержня.
При
расчетах стержней на прочность находится
опасное сечение, в котором напряжение
достигает наибольших значений по
абсолютной величине  ,
и для этого сечения записывается условие
прочности:
,
и для этого сечения записывается условие
прочности:
 (3)
(3)
где 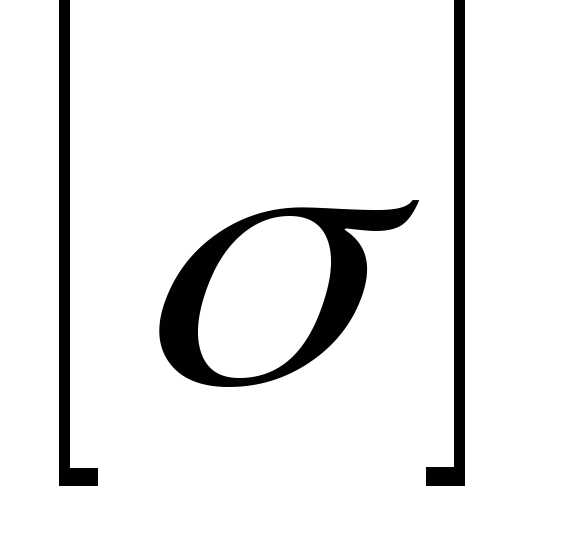 — допускаемое нормальное напряжение
для материала стержня. Для пластичных
материалов -,
для хрупких материалов -,
где
— допускаемое нормальное напряжение
для материала стержня. Для пластичных
материалов -,
для хрупких материалов -,
где — предел текучести и предел прочности
материала стержня,
— предел текучести и предел прочности
материала стержня, — коэффициенты запаса прочности по
пределу текучести и пределу прочности.
Назначение величины коэффициента запаса
прочности зависит от условий эксплуатации
и области применения рассчитываемой
конструкции, от методов расчета
напряжений, свойств материала. Для
пластичных материаловnт принимается меньшим, чем nв в случае расчета детали из хрупкого
материала. Это обусловлено тем, что
хрупкий материал более чувствителен к
наличию различных дефектов структуры
материала и возможным перегрузкам в
процессе эксплуатации.
— коэффициенты запаса прочности по
пределу текучести и пределу прочности.
Назначение величины коэффициента запаса
прочности зависит от условий эксплуатации
и области применения рассчитываемой
конструкции, от методов расчета
напряжений, свойств материала. Для
пластичных материаловnт принимается меньшим, чем nв в случае расчета детали из хрупкого
материала. Это обусловлено тем, что
хрупкий материал более чувствителен к
наличию различных дефектов структуры
материала и возможным перегрузкам в
процессе эксплуатации.
Перемещение рассматриваемого сечения стержня A§i, в соответствии с законом Р. Гука, вычисляется по формуле:
 .
(4)
.
(4)
Произведение EAi — в формуле (4) называется жесткостью сечения стержня при растяжении (сжатии).
По результатам вычислений нормальной силы Nz , нормального напряжения а и перемещений 5 строятся эпюры. Эпюра — это график, который показывает изменение силового фактора, напряжения, перемещения и других величин по длине бруса (стержня).
В ряде случаев для обеспечения надежной работы стержня необходимо выполнение условия жесткости:
(5)
где  — наибольшее абсолютное удлинение
стержня, к — коэффициент, определяемый
из эпюры перемещений,
— наибольшее абсолютное удлинение
стержня, к — коэффициент, определяемый
из эпюры перемещений,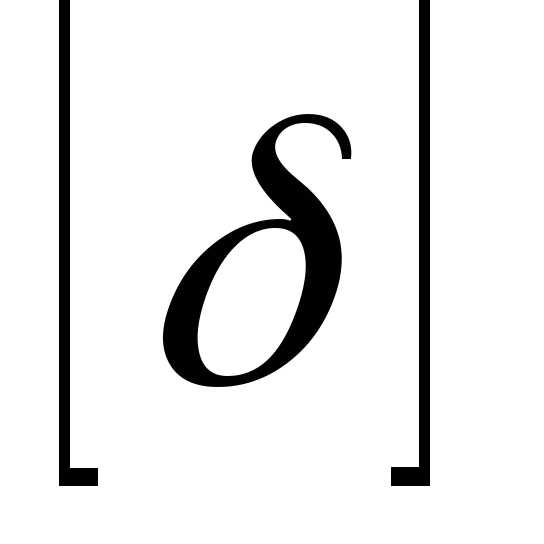 — допускаемое удлинение стержня,
зависящее от назначения и области
применения конструкции.
— допускаемое удлинение стержня,
зависящее от назначения и области
применения конструкции.
studfiles.net