Балки Изгибающий момент — Энциклопедия по машиностроению XXL
| Рис. 5. Балка на двух опорах весом 500 даН со сосредоточенной нагрузкой Р 2500 и F 1500 даН и нагрузкой Q — 2000 даН, равномерно распределенной на длине 2 м. Диаграмма общих изгибающих моментов получается в результате сложения соответствующих координат диаграмм от сосредоточенных и распределенной нагрузок, а также от силы веса балки. Изгибающий момент, например в сечении D, равен тт 6. |  |
Решение. Начало координат поместим на левом конце балки. Изгибающий момент в сечении с абсциссой г определяем как момент внешних сил, расположенных меж.цу данными сечением и началом координат [c.167]
При составлении дифференциального уравнения упругой линии балки изгибающий момент может рассматриваться как сумма момента [c.455]
Эпюра Qy по всей длине балки Изгибающий момент па участке
В сечении на свободном или шарнирно опертом конце балки изгибающий момент равен нулю, если в этом месте не приложена сосредоточенная пара сил. Поперечная сила в этом сечении равна внешней сосредоточенной силе. [c.209]
Доказать, что при любой нагрузке на консольной части балки изгибающий момент в опорном сечении М = -0,5Мд. [c.182]
Решение. Такая схема нагружения балки была рассмотрена на стр. 281 при этом было установлено, что для сечения, отстоящего на расстоянии г от свободного конца балки, изгибающий момент [c.290]
На конце балки изгибающий момент равен нулю, если там не приложена пара сил. [c.240]
Далее установим закон изменения зоны пластических деформаций в сред- ей трети балки. Изгибающий момент на этом участке, выраженный через нормальные напряжения (рис. б), равен УИ =0тЬ/1 1——yV(3h )]. Приравнивая что [c.143]
Строим изогнутую ось балки. Так как на всей длине балки изгибающий момент положителен, то изогнутая ось направлена выпуклостью вниз. [c.106]
Полезно иметь в виду, что в поперечном сечении, совпадающем с осью прямой симметрии балки, поперечная сила (обратно симметричная сила) равна нулю, а в сечении, совпадающем с осью обратной симметрии балки, изгибающий момент (прямо симметричный момент) равен нулю. Если по оси прямой симметрии на балку действует внешняя сосредоточенная сила, то поперечные силы в сечении левее и правее оси симметрии численно равны половине этой силы. [c.96]
На левом свободном конце балки изгибающей момент М = Q. В сечении над опорой [c.100]
Если в каком-нибудь поперечном сечении балки изгибающий момент равен нулю или имеет малую величину, а поперечная сила соответственно отлична от нуля или имеет большую величину, то форма балки равного сопротивления, установленная по уравнению (123), корректируется условием прочности (104) по касательным напряжениям.
Если изгиб происходит с искривлением оси балки в одной из главных це1[тральных плоскостей инерции, например балка изгибается лишь в плоскости Оуг, то этот изгиб называют прямым. В этом случае изгибающий момент М,., как вектор, составляет прямой угол с плоскостью Оуг. Если прямой изгиб происходит при наличии лишь постоянного по длине балки изгибающего момента Мх, то изгиб на этом участке называют чистым. Если прямой изгиб происходит при наличии поперечной силы Qy, то это прямой поперечный изгиб. Если изгиб происходи г с выходом изогнутой оси балки в обе главные центральные плоскости, то такой изгиб называется косым. Он может быть чистым косым изгибом, если отсутствует поперечная нагрузка, и пространственным поперечным изгибом, если происходит при действии поперечной нагрузки. Обычно косой изгиб представляют как наложение двух прямых изгибов. Для того чтобы на каком-либо участке длины балки имел место изгиб, в поперечном сечении должен быть отличен от нуля по крайней мере один из внутренних изгибающих моментов [c.227]
В сечении двутавровой балки изгибающий момент М = =3000 кГм и поперечная сила Q=10 000 кГ. Определить главные напряжения в двух точках а— в верхней точке полки на линии т—т, совпадающей с гранью стенки Ь — в верхнем волокне стенки на уровне нижней грани полки п — п, [c.120]
Ответ. Задачу опреде.чения прогибов балки постоянного сечения, находящейся в упруго-пластическом состоянии, можно заменить [8] задачей определения прогибов балки некоторого переменного сечения, находящейся якобы в упругом состоянии в условиях чистого изгиба (т. е. по всей балке изгибающий момент постоянен и равен Л/упр). [c.214]
Плоскости двух смежных поперечных сечений деформированной балки, отстоящих друг от друга на расстоянии бх, пересекаются в центре кривизны участка бх оси балки. Расстояние р от центра кривизны до оси балки называется радиусом кривизны оси (рис. 7.54). В 7.7 получена формула (7.16), выражающая связь между радиусом кривизны оси балки, изгибающим моментом в поперечном сечении балки и жесткостью поперечного сечения при изгибе
Решение. Начало координат выберем на левом конце балки. Изгибающий момент в сечении / — I на расстоянии 2 от начала координат [c.238]
В рассмотренном примере симметричного сечения балки изгибающий момент относительно оси у равен нулю, и мы можем написать [c.16]
Реакции опор Z определяются, как указано выше, в расчёте продольной балки. Изгибающие моменты [c.681]
Антисимметричная нагруз-к а (фнг. 98. а). Продолжив балку в обе стороны до бесконечности (фиг, 98. б), приложим в точках А и В антисимметричные силы Pq и моменты которые сохранят антисимметричную форму изгиба балки. Изгибающие моменты в точках Л и В будут отличаться знаком, а поперечные силы будут одинаковы. Для точки S на основании формул (136) и (137) будем иметь [c.69]
Последнее условие требует, чтобы сумма моментов относительно точки С сил, приложенных слева или справа от этого шарнира, равнялась нулю. Другими словами, для соблюдения равновесия балки изгибающий момент в шарнире должен равняться нулю. Это добавочное требование делает балку AD статически определимой. [c.211]
Для первого участка возьмем произвольное сечение на расстоянии х от конца В балки. Изгибающий момент в этом сечении равен [c.322]
Критические нагрузки бокового выпучивания тонких высоких балок определены также и в случае действия переменных по длине балки изгибающих моментов. Обобщенная формула для критической нагрузки может быть записана в виде 1, стр. 626] [c.565]
Начало координат поместим на левом конце балки. Изгибающий момент в произвольном сечении, расположенном на расстоянии X от начала координат
При загружении балки изгибающими моментами, приложенными к торцам, согласно (36.4), имеем [c.131]
Определим значения изгибающих моментов для каждого участка балки. Для этого воспользуемся теми же участками балки и сечениями, которые были выбраны ранее. На первом участке балки изгибающий момент [c.153]
Прежде всего заметим, что при вычислении прогибов и углов поворота сечений балки изгибающий момент от единичного усилия М (1) представляет собой функцию, линейную но участкам балки. А Mz P) в зависимости от характера нагрузки может быть нелинейной функцией с угловыми точками и разрывами. Поэтому для балок постоянной жесткости вычисление интегралов Мора сводится к вычислению по участкам балки интегралов вида [c.239]
В соотношениях (6.34) для энергии деформации учитываются только эффекты, обусловленные действием на балку изгибающего момента. Кроме того, в каждом элементе будет накоплено некоторое количество энергии деформации сдвига. Этот вид энергии будет обсуждаться ниже (разд. 6.11). Однако для тонких балок энергией деформации сдвига можно пренебречь по сравнению с гораздо большей энергией деформации, связанной с изгибающим моментом. [c.239]
Таким образом, в сечении С внутренние факторы сводятся к перерезывающей силе внутренних факторов Q и Ж зг в разных частях балки получились противоположными, а их числовые значения — одинаковыми. Следовательно, для определения Q и тИ зг достаточно рассмотреть равновесие лишь одной части балки. Изгибающий момент в сечении равен сумме моментов всех сил, расположенных по одну сторону сечения, а перерезывающая сила равна сумме всех сил, расположенных по эту сторону сечения. Изгибающие моменты будем считать положительными, если они изгибают балку так, что сжатые слои будут находиться сверху (выпуклостью вниз), и отрицательными, если сжатые слои снизу
Строим приближенно изогнутую ось балки. Так как на всем протяжении балки изгибающий момент отрицательный, то изогнутая ось будет представлять кривую вьшуклостью вверх по всей длине балки. Через четыре точки — у л, Уо У в Ус — проводим приближенно изогнутую ось вьшукхюстью вверх. [c.101]
Приложим эти правила к балке, изображенной на рис. 3.4.3. Распределенная нагрузка направлена вниз в направлении положительной оси у, следовательно, оиа положительна. Каждая из реакций опор равна да и направлепа вверх. По определению, на участке I перерезывающая сила постоянна и равна —qa, на участке III Qy = +да. Так как сосредоточенных сил нет, то согласно правилу (а) эпюра должна быть непрерывна. Поэтому крайние точки эпюр на участках 1 и III нужно соединить прямой. Согласно правилу (з) на левом и правом концах балки изгибающий момент равен нулю, на участках 1 и III по правилу (д) эпюра прямолинейна. Поэтому достаточно вычислить изгибающш момент на границе между первым и вторым, а также вторым и третьим участками. И тут и там этот момент равен — qa(l — а). Отложим соответствующие отрезки по вертикали вверх и соединим концы их прямыми с концами отрезка, изображающего балку. В соответствии с правилом (и) на участке II [c.86]
После того как опорные реакции для задаН Ной балки будут найдены, можно переходить к определению внутренних силовых факторов, вО Зникающих в поперечных сечениях балки, — изгибающего момента и поперечной силы. [c.187]
Попереший изгиб балки вызывается внешними моментами, действующими в плоскости оси балки, или внешними силами, перпендикулярными к оси. Простой (прямой) изгиб получается, если изгибающий момент действует в плоскости, заключающей в себе главную ось поперечного сечения балки главная плоскость балки). Косой изгиб получается, если изгибающий момент действует в плоскости, не содержащей главной оси сечения, и может рассматриваться как сочетание изгибов в двух главных плоскостях. Чистым изгибом на участке балки называется изгиб, при котором во всех сечениях участка балки изгибающий момент имеет постоянное значение (поперечная сила отсутствует).
Таким образом, второй участок эпюры моментов изображается прямой DiBi. На всем протяжении балки изгибающий момент положителен и достигает максимума в сечении С — в месте приложения силы Р, где он равен РаЬ [c.203]
Изгибающий момент в сечении равен алгебраической сульме моментов (относительно рассматриваемого сечения) всех сил, приложенных к отсеченной части С7пержня (балки). Перерезывающая сила в сечении равна алгебраической сумме всех сил, приложенных к отсеченной части стержня (балки). Изгибающий момент и перерезывающая сила выражают действие отсеченной части стержня на оставшуюся. [c.396]
Над шарнирными опорами двухшарнирной балки изгибающий момент может быть только в тех случаях, когда в опорных сечениях приложены сосредоточенные моменты или когда на консолях, расположенных за опорами, приложены нагрузки. Во всех других случаях изгибающйе моменты в шарнирах равны нулю. [c.80]
Следуя допущению Мариотта относительно положения нейтральной оси на вогнутой стороне балки и дополнив его гипотезой плоских сечений, Я. Бернулли приравнял момент растягиваюпщх усилий в волокнах поперечного сечения балки изгибающему моменту в данном сечении. Используя закон Гука, он получил уравнение, из которого следует, что кривизна HR кривой изгиба в каждой ее точке пропорциональна изгибающему моменту в этой точке [c.165]
Имитация нагружения материала. Смоделированный материал представлялся в виде балки, работающей на изгиб при циклической нагрузке. Предполагается, что во всех поперечных сечениях балки изгибающие моменты равны (рис. 127). Это предположение соохветствует испытанию материала в условиях чистого изгиба или в условиях поперечного изгиба [c.241]
mash-xxl.info
Изгибающий момент и поперечная сила в поперечных сечениях балки
Мы можем допустить, с гарантией в достаточной точности, что напряжения в любом поперечном сечении балки, на значительном расстоянии от грузов, зависят только от величины изгибающего момента и перерезывающей силы в этом сечении и могут быть определены наложением друг на друга полученных выше для консоли решений. [c.337]Чтобы определить величину изгибающего момента и поперечной силы в любом сечении балки, возьмем сечение I — I на расстоянии z от опоры А. Тогда [c.231]
Нормальные и касательные напряжения, возникающие в поперечных сечениях балки, зависят соответственно от величин изгибающих моментов М и поперечных сил Q. Поэтому для определения наиболее опасных сечений, т. е. таких, в которых появляются наибольшие напряжения, необходимо знать изменения моментов и поперечных сил по длине всей балки. Обычно для большей наглядности эти изменения величин УИ и Q по длине балки представляют графически. Такие графики изменения М и Q называются эпюрами изгибающих моментов и поперечных сил. Эпюры эти строятся совершенно таким же образом, как мы строили эпюры крутящих моментов валов откладывая от оси, параллельной оси балки, в некотором масштабе величины изгибающих моментов, действующих в различных сечениях, и соединяя концы отложенных отрезков, получим эпюру изгибающих моментов. Для построения эпюры поперечных сил откладывают отрезки, представляющие в определенном масштабе величины поперечных сил в различных сечениях балки. При построении эпюр изгибающих моментов и поперечных сил принято положительные А1 п Q откладывать вверх от оси, а отрицательные — вниз. [c.199]
Эпюры Q п М. Для полного исследования напряженного состояния балки необходимо знать усилия не в одном каком-либо сечении, а во всех. Это сводится к необходимости определить величины изгибающих моментов и поперечных сил во всех сечениях балки. Чтобы иметь наглядное представление об изменении М и Q по длине балки, прибегают к построению эпюр (графиков), ординаты которых представляют величины изгибающих моментов и поперечных сил в соответствующих сечениях балки. Процесс построения эпюр О я М принципиально несложен и сводится к составлению уравнений этих эпюр на различи. ных участках длины балки. Поясним это примерами. [c.156]
Графический способ построения изогнутой оси балки основан на полном совпадении процесса вычисления изгибающего момента М и поперечной силы С с процессом вычисления прогиба у и угла наклона ф. Для определения прогиба у и угла наклона ф в каком-либо сечении балки необходимо построить действительную эпюру изгибающих моментов и, загрузив ею фиктивную балку, найти величины /И и С в этом сечении. Поделив эти величины на жесткость EJ, получим прогиб у и угол наклона ф в рассматриваемом сечении балки. Эпюры М п Q можно построить также графически с помощью веревочного и силового многоугольников. Совершенно аналогично можно построить и эпюры М и С, которые представляют собой EJ—кратные законы распределения прогибов и углов наклона по длине балки. Величины фиктивного изгибающего момента и фиктивной поперечной силы в любом сечении балки определим по формулам [c.323]
В общем случае изгиба (при поперечном изгибе) в поперечных сечениях балки возникают изгибающие моменты и поперечные силы. Наличие изгибающего момента связано с возникновением в поперечных сечениях балки нормальных напряжений, для определения которых можно пользоваться формулой (У1.8) (см. 52). [c.153]
Как вычисляются изгибающий момент и поперечная сила в поперечном сечении балки [c.58]
Как вычисляются изгибающие моменты и поперечные силы в произвольном сечении неразрезной балки (а также опорные реакции балки) после определения неизвестных опорных моментов [c.339]
Плоский изгиб называется поперечным, если в данном поперечном сечении балки действуют два внутренних силовых фактора изгибающий момент М(х) и поперечная сила Q(x). Если поперечная сила в рассматриваемом сечении равна нулю, то плоский изгиб называется чистым. [c.172]
Таким образом, поперечная сила Q(j ) и изгибающий момент М х) являются функциями от X. Для краткости в дальнейшем будем их обозначать QnM, сохраняя значок х) лишь в тех случаях, когда необходимо подчеркнуть, что Qn М — величины переменные, зависящие от х. При построении эпюр откладывают под каждым сечением от оси абсцисс, проведенной параллельно оси балки, ординаты, которые в выбранном масштабе изображают величину изгибающего момента или поперечной силы в этом сечении. Положительные ординаты эпюр Q i М будем откладывать вверх, а отрицательные — вниз. Заметим, что в некоторых руководствах рекомендуется строить эпюры моментов на выпуклой стороне изгибаемой балки, откладывая для этого положительные ординаты М вниз, а отрицательные — вверх. Впрочем, это дело вкуса, не имеющее существенного значения. [c.197]
При таком выборе знаков изгибающих моментов и поперечных сил в данном сечении знак последних не зависит от того, какую часть балки мы рассматривали при их вычислении. [c.156]
Итак, при поперечном изгибе в любом сечении балки возникают нормальные и касательные напряжения, которые приводятся соответственно к изгибающему моменту М и поперечной силе Q. [c.147]
Покажем, как, зная опорные моменты, найденные из системы уравнений трех моментов, найти изгибающий момент Nix и поперечную силу в произвольном сечении я-го пролета неразрезной балки (рис. 158, а). [c.240]
Таким образом, поперечная сила Q (х) и изгибающий момент Л1(х) являются функциями от X. Для краткости в дальнейшем будем их обозначать Q и М, сохраняя значок (Jf) лишь в тех случаях, когда необходимо подчеркнуть, что Q и М — величины переменные, зависящие от х. При построении эпюр откладывают под каждым сечением от оси абсцисс, проведённой параллельно оси балки ординаты, которые в выбранном масштабе изображают величину изгибающего момента или поперечной силы в этом сечении. Ниже ( 72) мы покажем построение этих эпюр на примерах. [c.230]
Согласно закону равенства действия и противодействия, внутренние силы по сечению тп для левой и правой частей одинаковы, но направлены в противоположные стороны. Внутренние силы в любом сечении балки могут быть заменены силой О и парой сил с моментом М. Сила называется поперечной силой, а момент М — изгибающим моментом в поперечном сечении балки. [c.91]
Таким образом, полная эпюра изгибающих моментов при заданном нагружении представляется на каждом участке наклонной линией и имеет для балки вид треугольника (рис. 137, в). Изгибающий момент во всех сечениях положителен. Из сопоставления эпюр С и М следует, что изгибающий момент имеет наибольшую величину в том сечении, в котором поперечная сила меняет знак. Значение этого наибольшего момента [c.219]
В качестве простейшего примера рассмотрим балку прямоугольного сечения (см. фиг. 146). Выделим из нее двумя смежными поперечными сечениями элемент длиной dx (фиг. 170, а). Пусть в левом сечении элемента действуют изгибающий момент М и поперечная сила Q. В правом сечении изгибающий момент получит бесконечно малое приращение dM и будет равен М -f dM. Так как на участке dx не приложено никаких нагрузок, то поперечная сила в правом сечении останется прежней. [c.171]
Если в поперечном сечении балки имеют место одновременно большие значения изгибающего момента и перерезывающей силы (консольные и неразрезные балки, двухопорные балки с сосредоточенными грузами), надлежит проверить приведенные напряжения в поясных швах [c.252]
Расчет общей продольной прочности. Корпус плавающего судна с точки зрения С. м. к. представляет собой клепаную балку переменного сечения, подвергающуюся действию вертикальных сил веса и давления воды т. к. силы эти распределяются по длине корпуса по различным законам, то в каждом поперечном сечении корпуса появляются изгибающие моменты и срезывающие силы, вызывающие в нем соответствующие напряжения напряжения эти называются напряжениями от общей продольной прочное т и или напряжениями эквивалентного бруса определение этих напряжений и проверка условий прочности продольных связей судна, принимая во внимание напряжения от местных нагрузок, и составляют задачу расчета общей продольной прочности. Расчет общей продольной прочности носит поверочный характер, так как, чтобы произвести его точно и в полном объеме, необходимо уже иметь все размеры рассчитываемого корпуса. Расчет общей продольной прочности разбивается на следующие три части 1) вычисление изгибающих моментов и срезывающих сил 2) определение напряжений (расчет эквивалентного бруса) 3) проверка условий прочности. [c.102]
Однако, хотя и редко, но встречаются случаи, когда опасная точка принадлежит нейтральному слою. В ней материал испытывает чистый сдвиг (рис. 249, б и 250, б), и для расчета следует пользоваться условием прочности (10.29). Такое положение может быть тогда, когда при больших поперечных силах в сечениях балки действуют незначительные изгибающие моменты, например, при коротких пролетах и значительной поперечной нагрузке. [c.262]
Сложный изгиб с растяжением (сжатием) прямого бруса. Если па балку действуют и продольные и поперечные нагрузки, пересекающие ось бруса, то в общем случае (рис. 325, а) в поперечных сечениях возникают изгибающие моменты и в двух плоскостях, поперечные силы и Qy, а также продольная сила М (рис. 325, б). Таким образом, в этом случае будет сложный изгиб с [c.338]
Перемещения Д/р и б,, входящие в канонические уравнения, чаще всего определяют по методу Мора или по способу Верещагина. При этом для балок и рам влиянием поперечных и продольных сил обычно пренебрегают и учитывают лишь изгибающие моменты. Однако, определяя перемещения в балках прямоугольного поперечного сечения, для которых отношение высоты сечения к длине [c.401]
Как уже было сказано, при плоском поперечном изгибе в поперечных сечениях балки возникают два внутренних усилия (внутренних силовых фактора) — изгибающий момент М и поперечная сила Q. Для их определения применим метод сечений. В интересующем нас месте сделаем мысленный разрез балки, например на расстоянии г от левой опоры (рис. VI.6, а). Отбросим одну нз частей балки, например правую, и рассмотрим равновесие левой части. [c.135]
Определив построением силового и веревочного многоугольников реакции 5 п 6 (рис. 278), мы можем найти поперечную силу и изгибающий момент в любом сечении балки, что необходимо для ее расчета. [c.264]
Общий случай прямого изгиба, при котором в поперечных сечениях балки возникают и изгибающие моменты и поперечные силы, называют прямым поперечным изгибом. [c.276]
Найдя реакции опор, перейдем к определению внутренних усилий, возникающих в поперечных сечениях балки, т. е. изгибающих моментов и поперечных сил. Для этого применим метод сечения. [c.277]
Определение изгибающих моментов и поперечных сил необходимо для расчета балок на прочность, так как только зная внутренние усилия, можно найти нормальные и касательные напряжения, возникающие в поперечных сечениях балки. [c.278]
Чему равны поперечная сила и изгибающий момент в произвольном сечении балки [c.206]
Изгиб, при котором в поперечном сечении балки действуют изгибающий момент и поперечная сила, называется поперечным. [c.236]
Определить изгибающий момент и поперечную силу в сечении т—п балки (Z = 15 м, / = 6,25 МН-м ), которая нагружена силами Рх = 200 кН, Рг = 180 кН, Рз = 160 кН (см. рисунок). Расстояние между силами 1,8 м. Коэффициент жесткости основания fe = 25 МПа. [c.184]
Руководствуясь третьей теорией прочности, произвести полную проверку прочности балки трубчатого прямоугольного сечения с наружными размерами 24 X 20 см и внутренними — 20 X 18 см (см. рисунок к задаче 4.92), если изгибающий момент в опасном сечении балки равен М ,Ътм, а поперечная сила Q = 20m. [c.146]
Уяк было показано вышеЗ При изгибе величина нормальных напряжений зависит от величины изгибающего момента, а величина касательных напряжений — от величины поперечной силы. Изгибающий момент или поперечная сила в любом сечении балки могут быть определены рассмотренными вывде методами, с помощью эпюр, rit и расчетах на прочность большое значение имеет распределение нот1аЛ1 ных и касательных напряжений по сечению. [c.171]
Иэ рис. 128 показано построение эпюр изгибающих моментов и поперечных сил на примере балки, защемленной одним конном. Такого рода балки называются обычно консолями. В денном случае с правой стороны на балку не [ аложено связей и определение изгибающих моментов и поперечных сил в любом сечении может быть произведено без предварительного определения реакций. [c.123]
Изгибающий момент в текущем сечении -го участка балки (рис. XIII. 1) равен сумме изгибающих моментов от поперечных и продольных сил в этом сечении [c.380]
Задача, которая решается при анализе нарряженного состояния, уже сформулирована нами (см, начало 31). Для решения этой задачи вспомним, что при изгибе в поперечном сечении балки возникают нормальные напряжения, вызванные изгибающим моментом, и касательные напряжения, вызванные поперечной силой. Появление в сечении напряжений обоих видов показывает, что поперечное сечение не совпадает с главной площадкой, и, следовательно, нормальное напряжение в поперечном сечении, определяемое формулой (109), не есть максимальное напряжение в данной точке в главной площадке, проведенной через ту же точку, оно имеет большую величину. [c.171]
Пример модели балки, рассмотренной К. К. Керопян [42] приведен на фиг. IV. 1. Модель балки составлена в виде линии АВ из сопротивлений АК, соответствующих участкам Д/ балки. Подводимые токи и /г соответствуют приложенным сосредоточенным нагрузкам и Рг. Эпюра изменения напряжения на участке соответствует эпюре изгибающих моментов. Токи 1 , протекающие по отдельным участкам линии АВ, дают в некотором масштабе поперечные силы в соответствующих сечениях. Развитие этой аналогии на определении углов поворота сечений и прогибов в балке [42] основано на графоаналитическом методе определения перемещений. [c.259]
Аналогия заключается в том, что статическим величинам Мп (а) и 5 (а) в теории изгиба балок соответствуют изгибающий момент и перерезывающая сила, а компонентам перемещения (а), 7 (а) — прогиб упругой оси балки и угол поворота элемента этой оси. Аналогия идет еще дальше, а именно при и = О и га = 1 дифференциальное уравнение (686) полубезмоментной теории переходит в дифференциальное уравнение изгиба балки, т. е. описывает деформированное состояние, соответствующее закону плоских сечений, а члены га 2 описывают деформированное состояние, возникающее под действием самоуравновешенных нагрузок, когда имеется депланация поперечных сечений оболочки. [c.206]
Изгибающие моменты и поперечные силы, возникающие в различных поперечных сечениях балки, как правило, не одинаковы по величине и направлению (знаку). Законы изменения этих внутренних усилий по длине балки принято представлять в виде графиков (диаграмм), называемых эпюрами изгибающих моментов и поперечных сил. По построенным эпюрам устанавливают, в каких сечениях возникают наибольшие изгибающие моменты и поперечные силы и их величины, что необходимо для расчета балки на прочность. Действительно, если балка имеет постоянное по всей длине поперечное сечение (а только такие балки здесь будем рассматривать), то наибольщие нормальные напряжения возникают в том поперечном сечении, где изгибающий момент максимален — [c.278]
mash-xxl.info
Статически неопределимые балки. Уравнения трех моментов
1. Двухпролетная балка
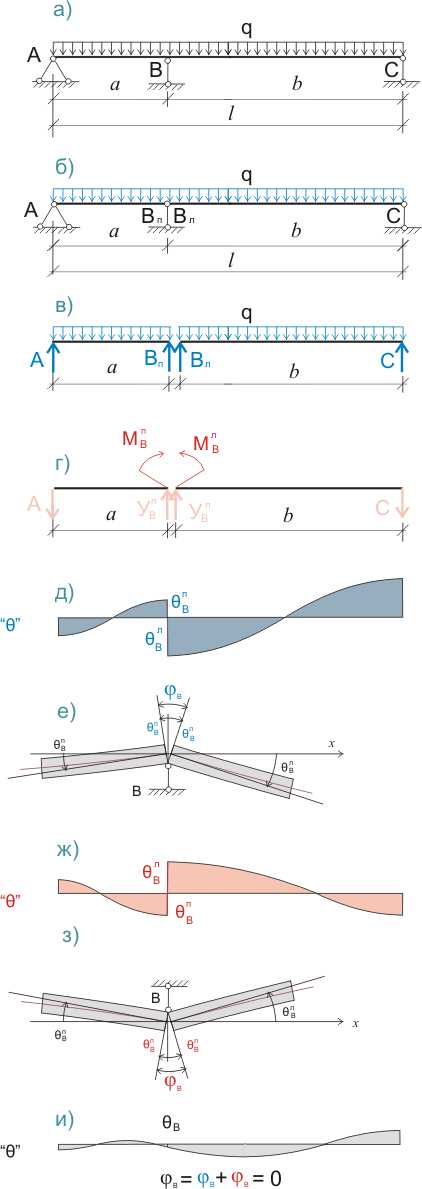
Рисунок 315.1. Приведение двухпролетной балки к основной и вспомогательной системам при методе моментов.
1. Когда мы рассекаем балку на промежуточной статически неопределимой опоре (рис. 315.1.б)), мы получаем две статически определимых балки с общей опорой В (рис.315.1.в)). Рассчитать такие балки — не проблема, а для удобства расчетов даже созданы соответствующие таблицы, пример такой таблицы можно посмотреть здесь. Балки, показанные на рисунке 315.1.в), являются элементами основной системы. Балки, показанные на рисунке 315.1.г), являются элементами вспомогательной системы.
2. Под действием приложенной нагрузки поперечные сечения балок не будут находиться в плоскости, перпендикулярной к основной оси (оси х), а будут иметь некоторый наклон. Другими словами, между плоскостью, перпендикулярной к основной оси, и поперечным сечением будет некоторый угол, называемый углом поворота поперечного сечения Θ. На рисунке 315.1.е) показаны углы поворота для крайнего правого сечения левой балки и крайнего левого сечения правой балки. Таким образом между указанными поперечными сечениями образуется угол наклона φ. Общая эпюра углов поворотов поперечных сечений для статически определимых балок основной системы будет выглядеть приблизительно так, как показано на рисунке 315.1.д).
3. Между тем балка-то у нас неразрезная, а это означает, что угол между двумя очень близкими относительно оси х сечениями будет стремиться к нулю, а так как мы рассекаем балку мысленно, то крайнее правое сечение левой балки и крайнее левое сечение правой балки — это одно и то же поперечное сечение неразрезной балки и для такого сечения угол наклона φ = 0.
4. Если к рассматриваемым поперечным сечениям балок приложить изгибающие моменты (рис. 315.1.г), то при определенном значении моментов суммарный угол наклона поперечных сечений будет равен углу наклона между поперечными сечениями балок основной системы, только значение это будет иметь обратный знак (рис.315.1.ж).
5. Таким образом, если сложить угол наклона смежных поперечных сечений балок основной системы и угол наклона смежных поперечных сечений балок вспомогательной системы, то угол наклона φ на общей эпюре углов поворотов будет равен нулю (рис.315.1.и)), при этом угол поворота поперечного сечения Θ неразрезной балки может быть не равен нулю.
6. Так как в действительности никакие внешние моменты на статически неопределимых опорах не прикладываются, а мы всего лишь заменяем внутренние напряжения внешними моментами, то на суммарной эпюре моментов (на рисунке 315 не показана) на статически неопределимых опорах не может быть скачков (могут быть только точки экстремума). Из этого следует, что значение момента, приложенного к крайнему правому сечению, должно быть равно значению момента, приложенного к крайнему левому сечению:
Мл = Мп = М (315.1.1)
Примечание: Самое трудное при работе с моментами и углами поворота — уследить за знаками. Сейчас считается, что если сила или момент приводят к растяжению нижней части сечения, то эпюра моментов рисуется снизу, но такой момент считается положительным, соответственно, если сила или момент приводят к растяжению верхней области сечения, то эпюра моментов рисуется сверху, но такой момент считается отрицательным. Дело в том, что вне зависимости от того, сверху или снизу рисуется эпюра моментов в поперечных сечениях рассматриваемых конструкций возникают нормальные напряжения и если рассматривать только нижнюю часть сечения, то положительный момент означает растяжение в нижней части и таким образом знак «+» символизирует увеличение длины в нижней части рассматриваемой конструкции, а отрицательный момент означает сжатие в нижней части сечения и знак»-» символизирует уменьшение длины конструкции в нижней части. Из этого следует, что если момент для рассматриваемого сечения (точки на оси х) направлен по часовой стрелке, то такой момент положительный, а если против часовой стрелки, то момент отрицательный. Таким образом знак момента зависит от точки (поперечного сечения), относительно которой данный момент рассматривается. Так для смежных статически определимых балок моменты, показанные на рисунке 315.1.г), будут отрицательными, а для поперечного сечения на опоре В неразрезной балки моменты будут иметь различный знак и в сумме дадут ноль. Приблизительно то же самое можно сказать и о углах поворота поперечных сечений. Если сечение наклонено вправо от оси у, то такой угол поворота можно считать отрицательным, если влево от оси у, то такой угол поворота будет считаться положительным, что и отражено на соответствующих эпюрах углов поворотов на рисунке 315.1. Между тем при определении прогиба знак угла поворота крайних сечений будет зависеть от направления интегрирования и от того, прогиб вверх или вниз будет считаться положительным. Так, если начальный угол поворота (угол поворота на одной из опор) будет приводить к растяжению в нижней области, то такой угол поворота может считаться положительным, например, для рассматриваемых нами статически определимых балок основной системы значения углов поворота на обеих опорах могут рассматриваться, как положительные. При действии положительного изгибающего момента углы поворота на опорах также будут положительными.
7. Если к одной из опор статически определимой балки, например опоре В, приложить положительный изгибающий момент, то в это приведет к изменению угла поворота поперечного сечения на опоре В на угол θB= Мl/3EI и к изменению угла поворота на опоре А на угол θА = Ml/6EI. На рисунке 315.1 для наглядности суммарного взаимодействия показаны отрицательные изгибающие моменты, которые приводят к отрицательным значениям углов поворота, но чтобы не путаться со знаками, изначально значения углов поворота для основной и для вспомогательной систем принимаются положительными.
Например, для двухпролетной балки, показанной на рисунке 315.1, угол наклона между поперечными сечениями балок основной системы будет составлять:
φВ = qa3/24EI +qb3/24EI = q(a3 + b3)/24EI (315.1.2)
значение угла наклона на смежной опоре при приложении моментов к балкам вспомогательной системы
φВ = МВпa/3EI + MВлb/3EI = M(a + b)/3EI = Ml/3EI (315.1.3)
φВ = φВ + φВ = q(a3 + b3)/24EI + Ml/3EI = 0 (315.1.4)
M = — q(a3 + b3)/8l (315.1.5)
после этого с учетом опорного момента определяются опорные реакции
A = A + A = qa/2 + M/a = qa/2 — q(a3 + b3)/8la (315.1.6)
C = C + C = qb/2 + M/b = qb/2 — q(a3 + b3)/8lb (315.1.7)
B = Bп + Вл + Вп + Вл = qa/2 + q(a3 + b3)/8la + qb/2 + q(a3 + b3)/8lb (315.1.8)
После того, как расчетные реакции определены, дальнейший расчет выполняется, как для обычной статически определимой балки, вот только необходимо выполнить дополнительные проверки, так прогиб на всех опорах при действующих нагрузках должен быть равен нулю.
При равных пролетах, т.е. при а = b = l/2
φВ = ql3/192EI + ql3/192EI = ql3/96EI = qa3/12 (315.1.9)
φВ = ql3/96EI + Ml/3EI = qa3/12EI + 2Mа/3EI = 0 (315.1.10)
M = — ql2/32 = — qa2/8 (315.1.11)
Опорные реакции составят
A = C = qa/2 — qa/8 = 3qа/8 (315.1.12)
B = 2(qa/2 + qa/8) = 10qa/8 (315.1.13)
Если однопролетная балка имеет одну жестко защемленную опору и шарнирную опору, то такую балку можно рассматривать как двухпролетную неразрезную шарнирно опертую балку, у которой один из пролетов равен нулю и соответственно момент на жестко защемленной опоре будет М = — ql2/8, согласно формулы (315.1.5). Это позволяет рассчитывать данным методом не только шарнирно опертые многопролетные балки, но и балки, имеющие жесткое защемление на концах.
2. Трехпролетная балка
При рассмотрении трехпролетной балки у нас появится еще одна неизвестная величина — момент на опоре С:
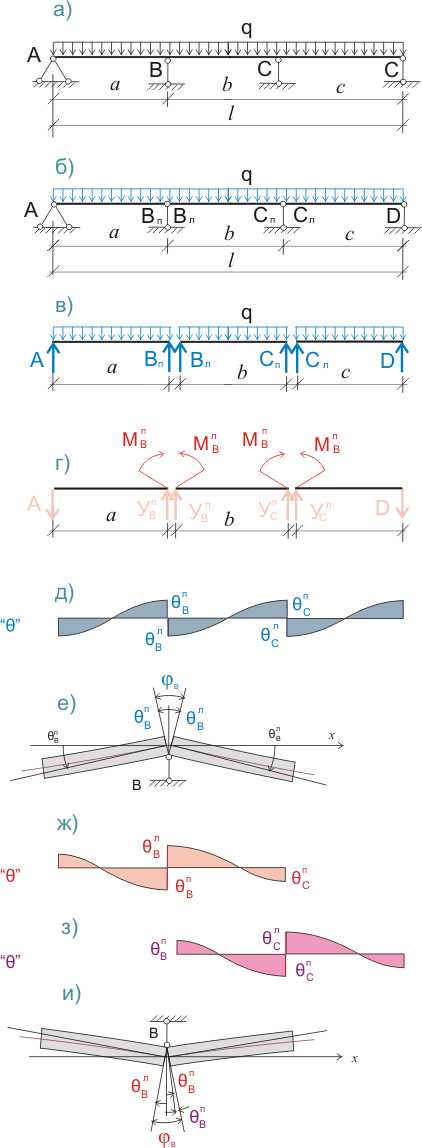
Рисунок 315.2. Приведение трехпролетной балки к основной и вспомогательным системам
То есть угол наклона между смежными сечениями на опоре В балок вспомогательной системы будет зависеть не только от значения моментов, приложенных на рассматриваемой опоре, но также и от значения момента, приложенного на опоре С. И тогда формула для определения угла наклона на опоре В будет выглядеть так:
φВ = МВпa/3EI + MВлb/3EI — МСпb/6EI = MB(a + b)/3EI + MCb/6EI (315.2.2)
φВ = q(a3 + b3)/24EI + MB(a + b)/3EI + MCb/6EI = 0 (315.2.3)
Соответственно для опоры С:
φС = MС(b + c)/3EI — MВb/6EI (315.2.4)
φС = q(b3 + c3)/24EI + MC(b + c)/3EI + MBb/6EI = 0 (315.2.5)
Решая систему из двух уравнений (315.4.3) и (315.4.4), можно найти значения моментов на опорах. Например при равных пролетах a = b = c решение задачи значительно упрощается, так как и моменты МВ и МС, действующие на опорах, при этом будут равными из-за симметричности балки и равномерно распределенной нагрузки:
φВ = φС= qa3/12EI + 2Ma/3EI + Ma/6EI = 0 (315.2.6)
5Ma/6EI = — qa3/12EI (315.2.7)
M = — qa2/10 (315.2.8)
Когда мы решали подобную задачу методом сил, то получили следующие уравнения:
Δ10 + Δ1У1 + Δ1У2 = 0 (314.4.2)
Δ20 + Δ2У1 + Δ2У2 = 0
Если мы угол наклона заменим греческой буквой Δ, а статически неопределимые опоры пронумеруем, то уравнения (315.2.3) и (315.2.5) примут вид:
Δ10 + Δ11 + Δ12 = 0 (314.4.2)
Δ20 + Δ21 + Δ22 = 0
т.е. мало чем будут отличаться от канонических уравнений метода сил.
Если у балки будет 4 пролета, то в итоге мы получим систему из 3 уравнений, в одном из которых будет 3 неизвестных члена, а в первом и последнем — по 2 неизвестных члена. Соответственно для расчетов 5 пролетной балки придется составить систему из 4 уравнений, в двух из которых будет по 3 неизвестных члена, а в первом и последнем также по 2 неизвестных члена, для 6 пролетной — из 5 уравнений и так далее, но при этом количество неизвестных членов в первом и последнем уравнении всегда будет равно двум, а в остальных уравнениях — трем, так как количество моментов, действующих на опорах смежных балок вспомогательных систем, не может быть больше 4. А так как моменты, действующие на рассматриваемой опоре, равны согласно (315.1.1), то количество неизвестных в уравнениях сокращается до 3 и потому уравнения вида (315.2.3) и (315.2.5) называются уравнениями трех моментов.
Для любой многопролетной балки уравнение трех моментов для n-ной опоры можно записать так:
Mn-1ln/6EI + Mn(ln + ln+1)/3EI + Mn+1ln+1/6EI = — φn (315.3.1)
А если обе части уравнения умножить на 6EI, то уравнение трех моментов будет выглядеть так:
Mn-1ln + 2Mn(ln + ln+1) + Mn+1ln+1 = — 6φnEI (315.3.2)
где φn — рассмотренный нами суммарный угол наклона между смежными сечениями на n-ной опоре.
Произведение φnEI иногда для упрощения записи рассматривается, как суммарная фиктивная опора Rnф:
φnEI = Rnф = Вnф + An+1ф = ωnan/ln + ωn+1bn+1/ln+1 (315.3.3)
Физический смысл этой формулы следующий: с точки зрения строительной физики сила, момент, угол поворота и прогиб — это не какие-то случайные понятия, а четко связанные между собой. Например, когда мы определяем опорную реакцию В при действии равномерно изменяющейся нагрузки (от 0 на опоре А до q на опоре В), мы умножаем площадь нагрузки (ql/2) на расстояние от опоры А до центра тяжести этой площади (2/3l) и затем делим это все на длину пролета (l), в итоге В = ql/3, соответственно А = ql/6. А если в качестве грузовой эпюры рассматривать эпюру моментов, также имеющую вид треугольника (например, при моменте, приложенном на опоре В), то значение фиктивных реакций составит Вф = Мl/3, Аф = Ml/6. В общем случае эту закономерность можно отобразить так:

Рисунок 315.3. Определение суммарной фиктивной реакции по эпюрам моментов для балок основной системы.
Однако в большинстве случаев чертить эпюры моментов для балок основной системы, затем определять центры тяжести этих эпюр и расстояния до центров тяжести нет большой необходимости, так как для наиболее распространенных вариантов приложения нагрузки фиктивные опорные реакции давно известны и определить их можно по соответствующим таблицам. Пример такой таблицы представлен ниже.
Таблица 315.1. Фиктивные опорные реакции для различных вариантов загружения балки основной системы
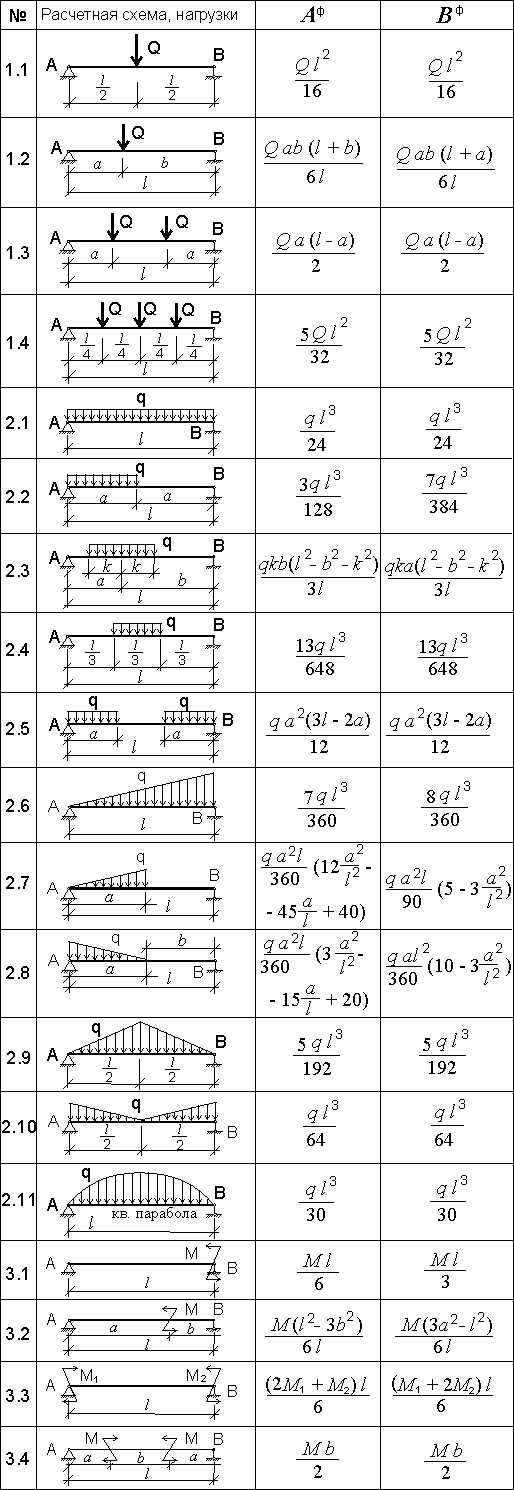
4. Решение системы уравнений
После того, как углы поворота на опорах (фиктивные опорные реакции) для всех балок основной системы определены, можно приступать к решению системы уравнений. Вот только, если пролетов у балки много, то запись окончательного уравнения, позволяющего определить один из неизвестных моментов, может занять не одну минуту и не одну страницу. В таких случаях можно воспользоваться следующей методикой:
Для балки, имеющей k пролетов, потребуется составить k — 1 уравнений. Если значения выражений — 6Rnф заменить параметром ci, то уравнения будут иметь следующий вид:
(315.4.1)
Если умножить все уравнения на пока произвольные параметры αi, а затем сложить все левые и правые части уравнений системы (315.4.1), то итоговое уравнение после соответствующих преобразований, позволяющих сократить запись, будет иметь вид:
(315.4.2)
Теоретически множители α могут иметь такие значения, при которых все выражения в квадратных скобках (множители для Мn в формуле (315.4.2)), кроме последнего, будут равны нулю. На основании этого предположения из уравнения (315.4.2) можно составить еще одну дополнительную систему уравнений:
(315.4.3)
Количество уравнений в такой системе будет k — 2, с k — 1 неизвестными параметрами α. Так как число параметров α на единицу больше количества уравнений, то для решения системы значение одного из этих параметров задается произвольно. Наиболее удобным для дальнейших расчетов будет принять значение α1 = 1. Тогда значения остальных коэффициентов α можно определить, решая систему уравнений (315.4.3):
(315.4.4.1)
В общем виде:
(315.4.5)
Примечание: Если придать абстрактным математическим коэффициентам α конкретный физический смысл, то коэффициенты αn есть не что иное, как такое соотношение моментов на соседних опорах , при котором суммарный угол наклона на рассматриваемой опоре будет равен нулю и тогда эти коэффициенты можно выразить так αn = Mn/Mn-1. Например, если первое уравнение системы (315.4.1) разделить на М1, то это уравнение c учетом вышесказанного можно записать так:
(315.4.6)
тогда
(315.4.4.2)
После подставления определенных вышеуказанным способом параметров α уравнение (315.4.2) примет вид
(315.4.7)
Соответственно значение Мk-1 будет составлять
(315.4.8)
После этого полученное значение Мk-1 подставляется в последнее уравнение системы (315.4.1) и определяется значение Мk-2. Из предпоследнего уравнения после подставления значений Мk-1 и Мk-2 определяется значение Мk-3 и т.д. Таким образом количество неизвестных в уравнениях системы (315.4.1) сводится к одному.
Если на одном или обоих концах балки есть нагруженные консоли, то определить изгибающие моменты на крайних опорах — не проблема. Значения этих моментов подставляются в уравнение трех моментов, как известные величины, тогда в первом и последнем уравнениях также будет по 3 члена. Если один или оба конца рассчитываемой балки защемлены, то жесткое защемление рассматривается как дополнительный пролет с длиной l = 0, таким образом придется составить еще одно или два уравнения.
5. Уравнение трех моментов для балки с переменной жесткостью:
Когда мы умножали обе части уравнения (315.3.1) на 6EI, то тем самым задавали момент инерции I, как некую постоянную величину. Между тем момент инерции также может быть переменной величиной (например, когда многопролетная железобетонная плита имеет различное армирование в пролетах) и для таких случаев уравнение моментов можно записать так:
(315.5.1)
где
(315.5.2)
Io — момент инерции одного из участков балки, принятый за основу.
Вот, в принципе и все теоретические предпосылки для расчета статически неопределимых конструкций методом моментов. А как эту теорию можно применить на практике, рассказывается отдельно.
doctorlom.com