При расчете сборных или монолитных железобетонных балок (ригелей) всегда нужно внимательно относиться к крутящему моменту. Очень часто расчет на кручение требует увеличить сечение или армирование балки. Сечение балки при кручении эффективней увеличивать в ширину (увеличение балки по высоте дает малый эффект), оптимально при кручении уходить от прямоугольного сечения к квадратному.

В каких ситуациях в балке возникает крутящий момент?

1) Если на балку опирается перекрытие только с одной стороны – оно своим весом пытается крутить балку в сторону пролета перекрытия.

2) Если на балку опирается перекрытие с двух сторон, но пролет этих перекрытий разный – тогда нагрузка от перекрытия с большим пролетом перевешивает в свою сторону и крутит балку.

3) Если на балку опирается перекрытие равных пролетов, но нагрузки на этих перекрытиях отличаются (разное назначение помещений, наличие оборудования на перекрытии и т.п.) – тогда балка также прокручивается в сторону большей нагрузки.

4) Если вдоль балки действует вертикальная нагрузка (например, от веса перегородки), сбитая в сторону от оси балки.

Рассмотрим определение крутящего момента на примерах.

Пример 1. Монолитное балочное перекрытие. Необходимо определить крутящий момент в крайней балке. Суммарная нагрузка от веса монолитного перекрытия и всех нагрузок на нем равна: qн = 675 кг/м² (нормативная) и qр =775 кг/м² (расчетная).

Расчет ведется на 1 погонный метр балки.

В монолитном перекрытии связь перекрытия с балками жесткая. При такой схеме расчетный пролет перекрытия равен пролету плиты в свету между балками L₀ = 2,8 м, а нагрузка от плиты на балку передается в месте примыкания балки к перекрытию.

Найдем нагрузку на 1 п.м балки от половины пролета плиты 2,8/2 = 1,4 м:

Рн = 675∙1,4 = 945 кг/м;

Рр = 775∙1,4 = 1085 кг/м.

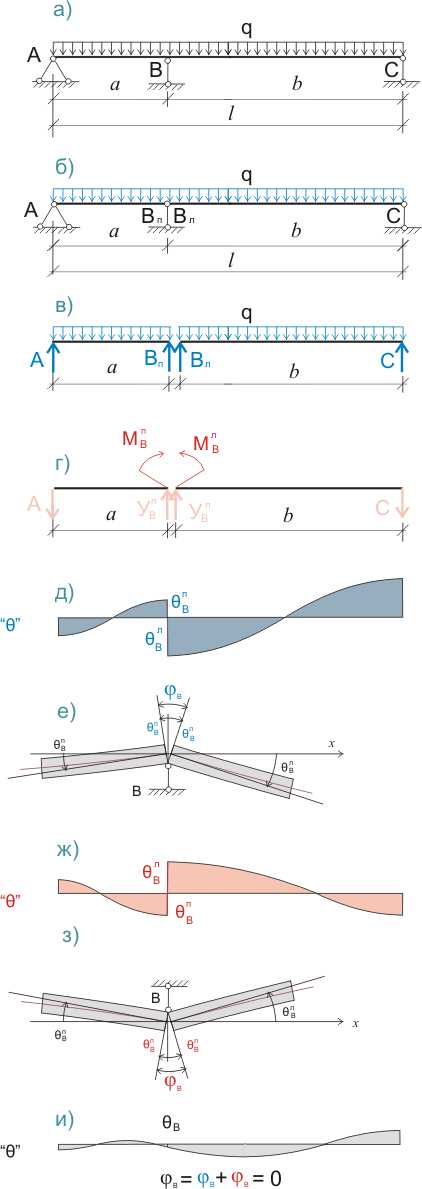
Крутящий момент в балке рассчитывается умножением вертикальной нагрузки на эксцентриситет – расстояние от оси приложения этой нагрузки до оси, проходящей через центр тяжести балки. В нашем случае эксцентриситет равен половине ширины балки, т.е. 100 мм = 0,1 м.

Итак, определяем крутящий момент в балке (на 1 п.м балки):

Мн = 945∙0,1 = 94,5 кг∙м/м;

Мр = 1085∙0,1 = 108,5 кг∙м/м.

Пример 2. Сборное перекрытие опирается на балку с двух сторон. С одной стороны пролет перекрытия 6 м и есть пригруз в виде перегородки, опирающейся параллельно балке; с другой стороны пролет перекрытия 3,6 м. Нагрузка от перегородки  0,65 т/м, расстояние от оси балки до перегородки 1,5 м. Нагрузка от собственного веса перекрытия 0,3 т/м². Нагрузка на перекрытии: постоянная 0,1 т/м²; временная 0,3 т/м². Ширина балки 0,3 м. Глубина опирания плит перекрытия на балку 0,14 м.

Расчет ведется на 1 п.м балки.

Определим расчетный пролет каждого перекрытия и найдем точку приложения нагрузки от перекрытия на балку.

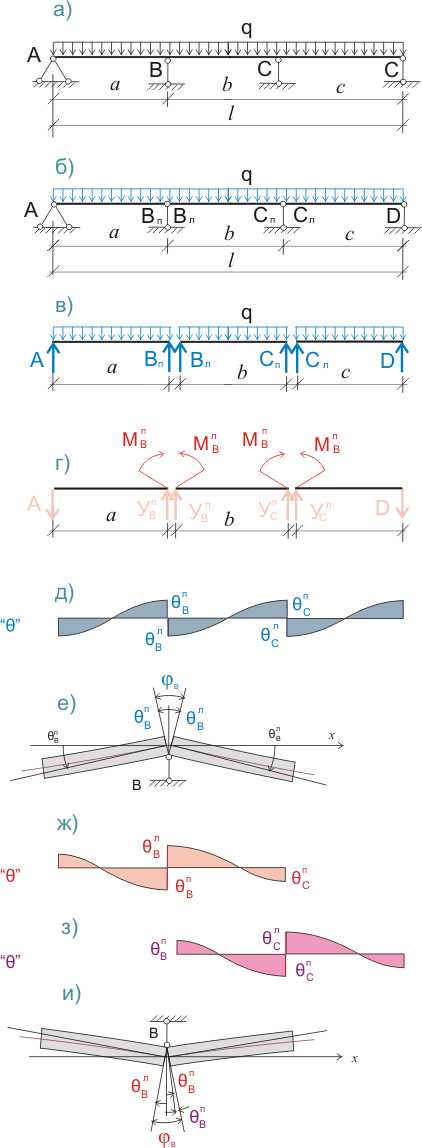
Плита опирается на балку на 140 мм. Нагрузка от плиты на этой площади распределена не равномерно, а по треугольнику. Максимально плита давит со стороны пролета (с края балки), а к краю плиты нагрузка сходит к нулю. Чтобы привести эту распределенную нагрузку к сосредоточенной, нужно принять ось приложения этой сосредоточенной нагрузки – в центре тяжести треугольника, на расстоянии 1/3 от края балки. У нас получается, что расстояние от края балки до сосредоточенной нагрузки 140/3 = 47 мм, а расстояние от этой нагрузки до оси, проходящей через центр тяжести балки 150 – 47 = 103 мм. Расстояние между сосредоточенными нагрузками равно расчетному пролету плиты L₀, который для наших плит будет равен:

— для плиты 6 м: L₀ = 6000 – 2∙103 = 5794 мм;

— для плиты 3,6 м: L₀ = 3600 – 2∙103 = 3394 мм.

Построим эпюры поперечных сил для наших плит.

Равномерно-распределенная нагрузка на 1 погонный метр плиты равна:

— нормативная qн = 1∙(0,3 + 0,1 + 0,3) = 0,7 т/м;

— расчетная qр = 1∙(1,1∙0,3 + 1,1∙0,1 + 1,2∙0,3) = 0,8 т/м.

Сосредоточенная нагрузка от перегородки на плите Nн = 0,65 т/м (нормативная) и Nр = 1,1∙0,65 = 0,72 т/м (расчетная) находится на расстоянии 1500 мм от оси балки и на расстоянии 1500 – 103 = 1397 мм от принятой нами точки опоры плиты, через которую проходит ось передачи вертикальной нагрузки на балку.

Схема для нормативных нагрузок будет следующая (так как плиты опираются шарнирно, то каждую из них нужно посчитать по отдельной схеме):

Левая плита разбита на два участка: 1-2 и 2-3, правая плита представляет собой один участок 4-5.

В правой плите мы сразу можем найти значения поперечной силы:

Q = 0,5∙qL₀ = 0,5∙0,65∙3,394 = 1,1 т.

Построим эпюру для правой плиты:

Значение поперечной силы на опоре (в точке 4) равно искомой нагрузке, которую плита передает на балку: Р₄= 1,1 т (направлена вниз).

Теперь разберемся с эпюрой для левой плиты. Так как помимо распределенной нагрузки у нас есть сосредоточенная сила, у нас будет несколько больше операций.

Для удобства расчета левой плиты заменим равномерно распределенную нагрузку q равнодействующей силой N:

N_1-2 = 0.65∙4,397 = 2,86 т;

N_2-3 = 0,65∙1,397 = 0,91 т.

Зная, что в шарнирно-опирающейся плите моменты на опоре равны нулю, составим уравнение равновесия, чтобы найти реакции на опоре.

ΣМ₁ = 0:

2,86∙2,199 + 0,65∙4,397 + 0,91∙5,096 – R₃∙5,794 = 0, откуда найдем реакцию:

R₃ = -13.78/5,794 = 2,38 т.

ΣМ₃ = 0:

0,91∙0,698 + 0,65∙1,397 + 2,86∙3,595 – R₁∙5,794 = 0, откуда найдем реакцию:

R₁ = 11,82/5,794 = 2,04 т.

Строить эпюру поперечных сил в плите для определения крутящего момента в балке нам не нужно, т.к. найденная нами реакция на опоре R₃ равна максимальной поперечной силе и равна нагрузке, передаваемой плитой на балку: Р₃= 2,38 т (направлена вниз).

Теперь у нас есть все исходные данные для определения крутящего момента.

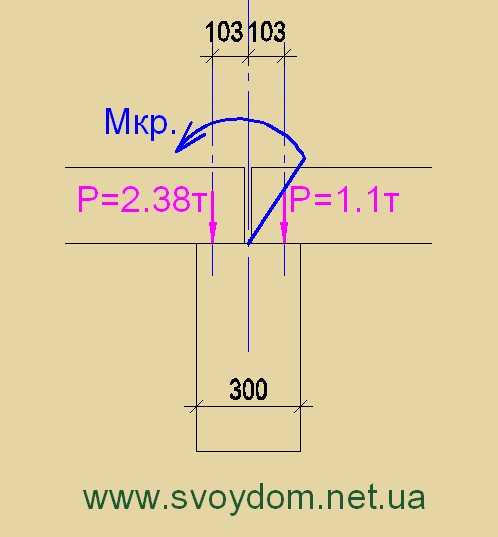
Определим нормативный крутящий момент путем умножения сил на плечо. Принимаем силу, вращающую балку против часовой стрелки со знаком «+», а по часовой – со знаком «-«:

Мн = 2,38∙0,103 – 1,1∙0,103 = 0,13 т∙м/м – нормативный крутящий момент, приходящийся на 1 п.м балки.

Расчетный крутящий момент находится точно так же.

Пример 3. Вдоль балки расположена перегородка, которая сбита относительно оси балки на 150 мм. Перекрытие опирается на балку с двух сторон, пролеты перекрытия и нагрузки – одинаковые. Толщина перегородки 0,12 м, материал кирпич (1,8 т/м³), высота 3 м.

Расчет ведем на 1 погонный метр балки.

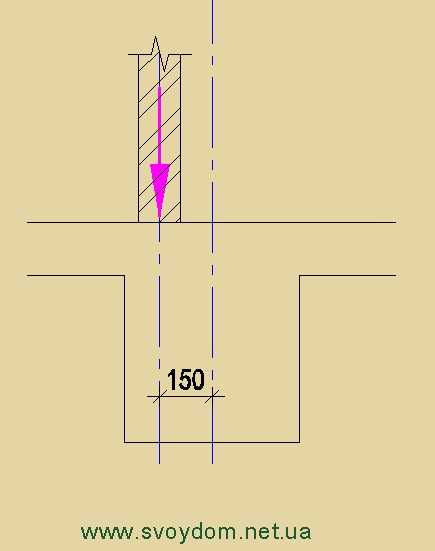
Определим вертикальную нагрузку от перегородки:

0,12∙3∙1,8 = 0,65 т/м – нормативная нагрузка;

1,1∙0,65 = 0,72 т/м – расчетная нагрузка.

Определим крутящий момент в балке путем умножения силы на плечо:

Мн = 0,65∙0,15 = 0,1 т∙м/м;

Мр = 0,72∙0,15 = 0,11 т∙м/м.

Добавить комментарий

Реакции, эпюры и перемещения в балках

Опорные реакции, эпюры поперечных сил и изгибающих моментов а также линейные и угловые перемещения для простых балок при изгибе.

Консольные балки

Сосредоточенный изгибающий момент на конце консольной балки

Опорные реакции

Линейные и угловые перемещения

Сосредоточенная сила на конце консольной балки

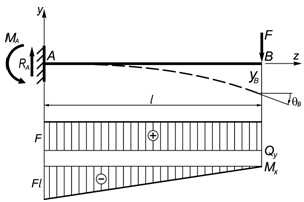
Опорные реакции

Линейные и угловые перемещения

Равномерно распределенная нагрузка по всей длине консоли

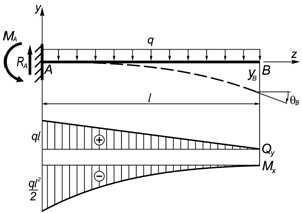
Опорные реакции

Линейные и угловые перемещения

Двухопорные балки

Сосредоточенный изгибающий момент на левой опоре двухопорной балки

Опорные реакции

Линейные и угловые перемещения

Сосредоточенный изгибающий момент в пролете балки

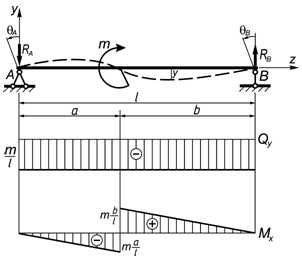
Опорные реакции

Линейные и угловые перемещения

Сосредоточенная поперечная сила в пролете балки

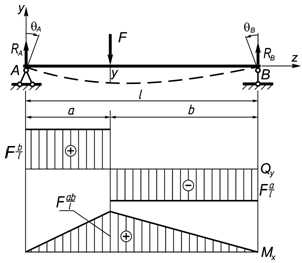
Опорные реакции

Линейные и угловые перемещения

Сосредоточенная поперечная сила в середине пролета балки

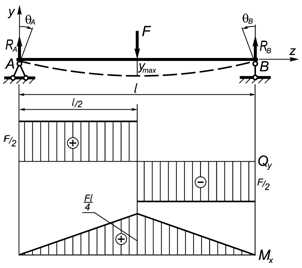
Опорные реакции

Линейные и угловые перемещения

Равномерно-распределенная поперечная нагрузка по длине пролета балки

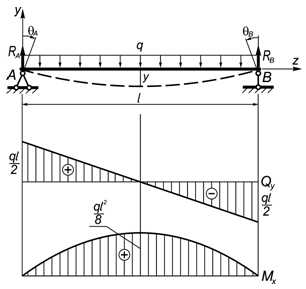
Опорные реакции

Линейные и угловые перемещения

Обозначения в сопромате >
Примеры решения задач >
Краткая теория >

Новости проектировщикам и техническим специалистам России

Запуск ФГИС ЦС перенесут на 2022 год

Провал реформы ценообразования в строительстве закрепят документально. Минстрой разработал проект постановления правительства о переносе запуска ФГИС ЦС на 2022 год. Документ размещен для общественного обсуждения, процедура продлится до 8 февраля.

Утверждены первые национальные «зелёные стандарты»

Нормативный вакуум, существовавший до этого момента в «зеленом» строительстве, кажется, начинает заполняться. МГСУ разработал, а Росстандарт утвердил первые национальные «Зеленые стандарты», которыми, наконец, могут воспользоваться в своей работе российские девелоперы. Раньше в качестве ориентиров использовались неофициальные переводы международных аналогов.

Проектируй себя!

Международная выставка MosBuild вместе с порталом arch:speech, экспертами Московской школы коммуникаций MACS и Архитектурной школы МАРШ и при участии компании Pilkington объявляет кастинг в проект. Чтобы попасть в финал нужно пройти три этапа: кастинг, успешно выполнить задание и принять активное участие в реалити-воркшопе.

Старт дают аграрии

Девять межрегиональных специализированных выставок по самой различной тематике – от агротехнической и нефтегазовой до продовольственной и медицинской, которые в общей сложности посетили более 32 000 человек.

Здания обезопасят от зелёных крыш

Российская система стандартизации, наконец, добралась до зеленых крыш. Соответствующий ГОСТ должен появиться уже через полгода. В документе будут прописаны требования безопасности зданий с озелененной крышей. Сейчас озеленение кровли ведется без каких-либо правил.

Итоги 100+ Forum Russia, прошедшего с 5 по 7 декабря в Екатеринбурге

В Екатеринбурге подвели итоги V Международного форума и выставки высотного и уникального строительства 100+ Forum Russia. Главной темой форума стали технологии информационного моделирования и цифровое строительство. За три дня в мероприятиях 100+ Forum Russia приняли участие больше 8878 делегатов из 137 городов мира.

Проект-победитель экологического конкурса привнёс в МАРХИ новогоднее настроение и уют

У главного входа Московского архитектурного института установлен арт объект, созданный по проекту, победившему в открытом молодежном конкурсе на разработку концепции общественной зоны учебного заведения «Зона отдыха в университете: пространство для учебы, релакса и общения». Организатор конкурса — Департамент природопользования и охраны окружающей среды города Москвы.

Форум АРХ ЕВРАЗИЯ завершается. Подводим итоги

Завершился трехдневный форум международный архитектуры, дизайна и градостроительства АРХ ЕВРАЗИЯ 2018. За три дня форума посетило несколько тысяч человек, были проведены: Архитектурный конгресс, Саммит дизайна и технологий, панельная дискуссия «Город 4.0: От дизайн-кода до умного города», организована выставка-инсталляция «Дом будущего».

Минстрой дал определение ветхого жилья

Минстрой впервые дал определение ветхого жилья. Оно внесено в проект изменений в Постановление Правительства РФ №47 от 26 января 2006 года о признании помещения непригодным для проживания и дома аварийным. Документ опубликован на портале проектов нормативно-правовых актов в рамках процедуры общественного обсуждения, которая продлится до 20 декабря.

Екатеринбург принял архитекторов мира. Итоги первого дня форума АРХ ЕВРАЗИЯ

5 декабря прошел первый день форума АРХ ЕВРАЗИЯ 2018. Как отметил бывший главный архитектор Екатеринбурга и заслуженный архитектор Российской Федерации Михаил Вяткин, тема форума АРХ ЕВРАЗИЯ будет каждый год меняться. Но темой этого года был выбран круг вопросов, связанный с жильем, начиная с градостроительства, архитектуры и дизайна.

Город 4.0: от дизайн-кода до умного города

Современный город – это сложная экосистема с десятками факторов, тысячами транспортных и пешеходных сетей, миллионами жителей и бесконечным потоком информации. Усложняясь, он теряет свою гуманность и сопричастность к личности человека. Город становится безликим цифровым отражением в наших гаджетах, оттесняя нашу зону комфорта все дальше за свои границы.

Екатеринбург – лучшая площадка для встречи архитекторов и дизайнеров Европы и Азии!

5-7 декабря 2018 г. в МВЦ «ЭКСПО-Екатеринбург» пройдет уникальное событие, которое будет интересно не только профессионалам, но и обычным людям. Это международный форум архитектуры, дизайна и градостроительства «АРХ ЕВРАЗИЯ-2018». Он объединит на одной площадке мировые имена в архитектуре и дизайне. Вот, что думают видные архитекторы о приближающемся мероприятии.

Что такое агломерация, и зачем она нужна? Ответы даст форум АРХ ЕВРАЗИЯ 2018

Слово «агломерация» прочно вошло в политический лексикон. С недавних пор из Москвы стали поступать сигналы о необходимости объединения малых и крупных городов в единые экономическо-административные территории. У такого способа развития страны есть свои плюсы и минусы. У концепции агломерации есть как сторонники, так и ярые противники.

Архитектурные решения на службе экологии города

В Экологическом форуме студентов приняли участие более 300 молодых профессионалов! 15 ноября 2018 года в Московском Архитектурном институте состоялся второй Экологический форум студентов. Его участниками стали студенты московских и российских ВУЗов, а также молодые профессионалы из ряда регионов России. На форуме были представлены проектные решения и технологии, способствующие улучшению экологической ситуации в городах.

Building Skin Russia 2019: открыт сезон высокой моды в архитектуре

В условиях усиливающейся конкуренции среди девелоперских проектов за привлечение содержимого кошельков инвесторов и частных покупателей все большее значение приобретают архитектурная выразительность и внешний облик зданий. Особенно этот тренд проявляется в сегментах бизнес и премиум класса. Но даже для строительства жилья эконом класса сегодня девелоперы привлекают именитых дизайнеров и архитекторов, чтобы выделить проект среди конкурентов и создать вокруг него ауру позитивной социальной среды.

www.proektant.ru

Расчет многопролетной балки методом моментов

Пример расчета железобетонной плиты перекрытия по балкам

Планируется перекрытие по балкам в помещении размерами 5х8 метров. Если использовать 4 балки — дополнительные опоры, то плита будет представлять собой 5 пролетную балку. При этом шаг между балками можно выбирать, руководствуясь эстетическими соображениями, т.е. принять одинаковый шаг для всех балок. А если потолки в последствии будут зашиваться, то шаг балок лучше выбирать из конструктивных соображений. Дальнейший расчет будет произведен для балок, расположенных с одинаковым шагом. Расчет параметров таких балок приводится отдельно.

Рассмотрим следующую расчетную схему:

Рисунок 313.1

Монолитная плита по балкам, показанная на рис. 313.1 а), представляет собой 5 пролетную неразрезную балку, на которую будет действовать как минимум два вида нагрузок: постоянная и временные. Как правило к постоянной нагрузке относится собственный вес конструкции, а вес стяжки и напольного покрытия относятся к временной нагрузке. При расчете однопролетных балок это принципиального значения не имеет, так как учитываются все действующие нагрузки. При расчете же многопролетных балок следует учитывать возможные максимально неблагоприятные сочетания нагрузок. Варианты приложения таких нагрузок показаны на рис. 313.1. г) и д). Потому для упрощения расчетов с использованием указанных расчетных схем, вес стяжки и напольного покрытия можно отнести к постоянной нагрузке.

Таким образом расчетное значение постоянной нагрузки составит:

q_п = (0.08·1 + 0.11·0.17/1.62)2500·1.1 + 200 = 251.7 +200 = 451.7 кг/м

где γ_н = 1.1 — коэффициент надежности по нагрузке.

Значение нормативной временной нагрузки на перекрытие определяется по СНиП 2.01.07-85 «Нагрузки и воздействия», и составляет 150 кг/м². Тогда с учетом коэффициента надежности по нагрузке, при таком значении нормативной нагрузки составляющем γ_н = 1.3 (1.4 по старым нормам), расчетное значение временной нагрузки составит

q_в = 150·1·1.3 = 195 ≈ 200 кг/м

Примечание: Устройство перегородок, установка тяжелого инженерного оборудования и другие дополнительные значительные нагрузки данным расчетом не предусматриваются.

Теперь, когда действующие нагрузки определены, осталось только рассчитать плиту:

1. Расчет на действие постоянной нагрузки

Расчетная схема для данного расчета представлена на рис. 313.1 б). Так как нагрузка во всех пролетах одинаковая, длина пролетов одинаковая и жесткость балки во всех пролетах одинаковая, то система уравнений трех моментов значительно упростится и будет иметь следующий вид:

2M_B(2l) + M_Cl = — 6·86.0542l;

M_Bl + 2M_C(2l) + M_Dl = — 6·86.0542l;

            M_Cl + 2M_D(2l) + M_El = — 6·86.0542l; (316.1)

M_Dl + 2M_E(2l) = — 6·86.0542l;

где

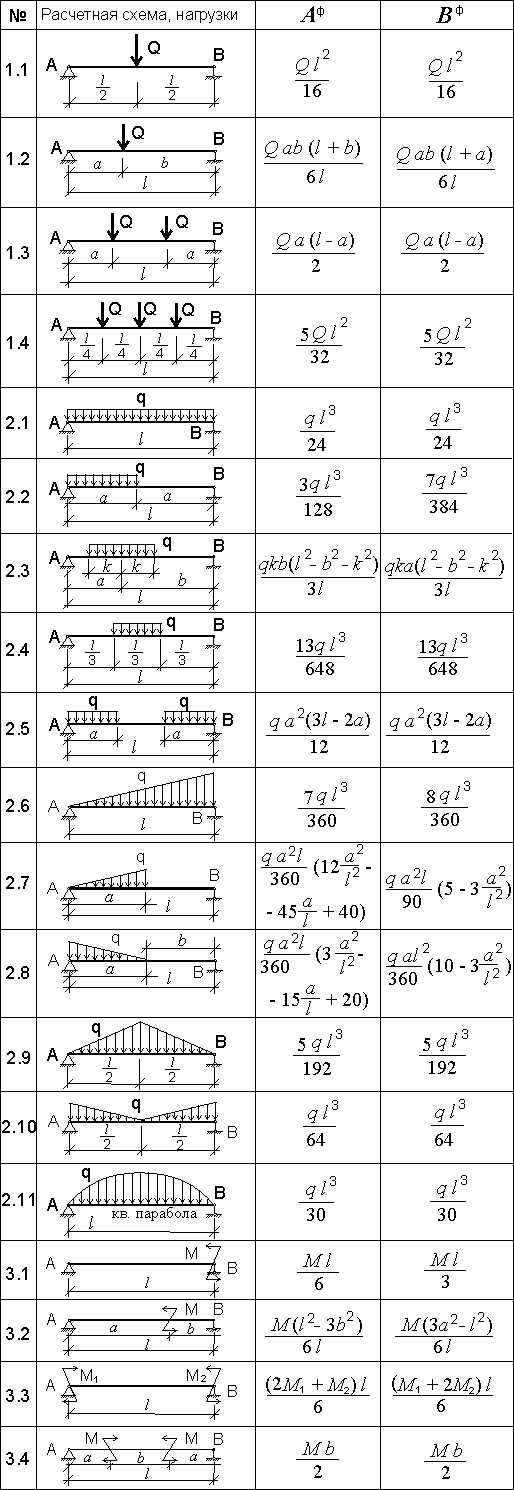
R^ф₁ = R^ф₂ = R^ф₃ = R^ф₄ = A^ф + В^ф = 2ql³/24 = 451.7·1.512²·l/12 = 86.0542l

тогда

4M_B + M_C = — 516.3256;

M_B + 4M_C + M_D = — 516.3256;

M_C + 4M_D + M_E = — 516.3256;

M_D + 4M_E = — 516.3256;

Принимаем а_B = 1, тогда согласно формул (315.4):

а_C = — 2(1 + 1) = -4;

a_D = — 2(1 + 1)a₂ — a₁ = 15

a_E = — 2(1 + 1)a₃ — a₂ = -56

тогда

М_Е = — 516.3256l(a_B + a_C +a_D +a_E)/(l(a_D + 4a_E) = — 516.3256(1 — 4 + 15 — 56)/(15 — 4·56) = — 22718.327/209 = — 108.7 кгс·м (ql²/9.5)

Подставляя полученное значение в последнее уравнение системы (316.1) получим следующее значение момента:

M_D = 4·108.7 — 516.3256 = — 81.5256 кгс·м (ql²/12.67)

Так как наша балка является симметричной и приложенная нагрузка является симметричной, то значение момента на опоре С должно быть равно значению момента на опоре D, а значение момента на опоре В должно быть равно значению момента на опоре Е. Проверяем:

M_С = 4·81.5256 + 108.7 — 516.32 = — 81.5232 кгс·м

M_В = (81.5232 — 516.32)/4 = — 108.7 кгс·м 

Так как значения сошлись (небольшие расхождения не учитываем), то дальнейшую проверку в принципе можно не выполнять. Для определения моментов в пролетах определим значения опорных реакций, исходя из следующих условий:

Для первого и последнего (1 и 5) пролетов:

Аl — ql²/2 = Fl — ql²/2 = M_B = M_E A = F = (M_B + ql²/2)l = (-108.7 + 451.7·1.512²/2)1.512 = 269.5936 кгс

Так как максимальный момент в пролетах будет действовать в сечении, где поперечные силы будут равны 0, то расстояние от начала балки до рассматриваемого сечения составит:

A — qx = 0; x = A/q = 269.5936/451.7 = 0.5968 м (0.3947l)

Максимальный момент в этом сечении будет равен:

M_1,5 = Ax — qx²/2 = 269.59·0.5968 — 451.7·0.5968²/2 = 80.45 кгс·м (ql²/12.835)

Момент посредине 1 и 5 пролета будет равен:

M_1,5(l/2) = Al/2 — q(l/2)²/2 = 269.59·1.512/2 — 451.7·(1.515/2)²/2 = 74.73 кгс·м (ql²/13.82)

Для 2 и 4 пролетов:

2Al + Bl — q(2l)²/2 = M_C; B = Е = (M_C — 2Al + q(2l)²/2)l = ( — 81.52 — 2·269.59·1.512 + 451.7· 4.5723)/1.512 = 772.845 кгс

А + В — qx = 0; x = (A + B)/q = (269.59 + 772.845)/451.7 = 2.3078 м (или 2.3078 — 1.512 = 0.7958 м (0.526l) от опоры В)

M_2,4 = Ax + B(x — l) — qx²/2 = 269.59·2.3078 + 772.845·0,7958 — 451.7·2.3078²/2 = 34.326 кгс·м (ql²/30.1)

Для 3 пролета:

3Al + 2Bl +Сl — q(3l)²/2 = M_D; C = (M_D — 3Al — 2Bl + q(3l)²/2)l = ( — 81.52 — 3·269.59·1.512 — 2·772.845·1.512 + 451.7· 10.2876)/1.512 = 665 кгс

А + В +C — qx = 0; x = (A + B + C)/q = (269.59 + 772.845 + 665)/451.7 = 3.78 м (или 3.78 — 2·1.512 = 0.756 м (l/2) от опоры С)

M₃ = Ax + B(x — l) + C(x — 2l) — qx²/2 = 269.59·3.78 + 772.845·2,268 + 665·0.756 — 451.7·3.78²/2 = 47.57 кгс·м (ql²/21.71)

На основании этих данных мы можем построить эпюру моментов для плиты:

Рисунок 316.1

2. Проверка по деформациям

Если мы правильно определили значения моментов и опорных реакций, то прогибы на промежуточных опорах должны быть равны 0. Проверим прогиб на опоре В. Для основной балки с опорами А и В угол поворота на опоре А равен фиктивной опорной реакции, деленной на жесткость, для вспомогательной балки с опорами А и В, угол поворота на опоре А зависит от значения момента на опоре В, тогда:

EIΘ_А = — ql³/24 + ql³/(6·9.5) = — 33ql³/1368 = — ql³/41.45

тогда прогиб на опоре В составит:

EIf_B = Θ_Al + Al³/6 — ql⁴/24 = — 451.7·33·1.512⁴/1368 + 269.5936·1.512³/6 — 451.7·1.512⁴/24 = — 56.948868 + 155.31514 — 98.36622 = 0.00005 ≈ 0

В данном случае, как и в предыдущем, небольшая погрешность набежала из-за того, что при расчетах мы использовали округленные данные.

Примечание: если есть сомнения в правильности расчетов, то следует проверить прогибы на всех опорах.

3. Расчет на действие временной нагрузки, действующей по всей длине плиты

Так как временная нагрузка при варианте загружения, показанном на рис. 313.1. в) будет действовать по всей длине плиты, то для определения моментов в пролетах и на опорах достаточно умножить значения, полученные при расчетах на действие постоянной нагрузки на отношение временной нагрузки к постоянной:

k = q_в/q_п = 200/451.7 = 0.44277 ≈ 0.443

Таким образом суммарные моменты на опорах и в пролетах при действии постоянной и временной равномерно распределенных нагрузок, действующих по всей длине балки, будут составлять:

М^б+в = М^б(1 + k) = 1.443М^б

Тогда

М^б+в_В = М^б+в_Е = — 108.7·1.443 = — 156.85 кгс·м

М^б+в_С = М^б+в_D = — 81.53·1.443 = — 117.65 кгс·м

М^б+в₁ = М^б+в₅ = 80.45·1.443 = 116.1 кгс·м

М^б+в_1(l/2) = М^б+в_5(l/2) = 74.73·1.443 = 107.83 кгс·м

М^б+в₂ = М^б+в₄ = 34.33·1.443 = 45.54 кгс·м

М^б+в₃ = 47.57·1.443 = 68.64 кгс·м

Эпюра моментов при действии временной нагрузки по схеме в) ничем не будет отличаться от эпюры, показанной на рис. 316.1. Суммарная эпюра от действия постоянной нагрузки и временной по схеме в) будет иметь такой же вид, изменятся только значения моментов. А если временная нагрузка будет приложена так, как показано на схеме г) или д), то суммарная эпюра изменит свой вид, но сначала следует определить значения моментов.

4. Расчет на действие временной нагрузки, действующей по схеме г)

При выбранной схеме загружения изменится сумма фиктивных опорных реакций. Так как нагрузка будет действовать через пролет, то сумма фиктивных опорных реакций уменьшится в 2 раза и составит:

R^ф₁ = R^ф₂ = R^ф₃ = R^ф₄ = A^ф + 0 или 0 + В^ф = ql³/24 = 200·1.512²·l/24 = 19.0512l

Если мы разделим это значение, на значение фиктивной опорной реакции при действии постоянной нагрузки, то получим:

19.0512l/86.0542l = 0.22138 = k/2

Это позволяет не решать еще раз систему уравнений, а сразу определить значения моментов на опорах при временной нагрузке по схеме г)

М^г_В = М^г_Е = — 108.7·0.22138 = — 24.064 кгс·м

М^г_С = М^г_D = — 81.53·0.22138 = — 18.049 кгс·м

М^г₁ = М^г₅ = 80.45·0.22138 = 17.81 кгс·м

Так как во 2 и 4 пролетах временная нагрузка отсутствует, то момент в этих пролетах будет отрицательным и значение момента посредине пролета будет равно:

М^г_2(l/2) = М^г_4(l/2) = (М_В + М_С)/2 = — (24.064 + 18.049)/2 = — 21.06 кгс·м

М^г₃ = 47.57·0.22138 = 10.53 кгс·м

5. Расчет на действие временной нагрузки, действующей по схеме д)

Как ни странно, но при схеме загружения д) сумма фиктивных реакций не изменится, а значит и не изменятся значения моментов на опорах, а изменятся только значения моментов в пролетах:

М^д_1(l/2) = М^д_5(l/2) = М_В/2 = — 24.064/2 = — 12.032 кгс·м

М^д₂ = М^д₄ = 34.33·0.22138 = 7.6 кгс·м

М^д₃ = М_С = М_D = — 18.049 кгс·м

6. Построение огибающей эпюры моментов

На основании полученных данных мы можем построить так называемую «огибающую» эпюру моментов, т.е. такую эпюру, на которой будут учтены значения моментов в пролетах при временной нагрузке по схемам г) и д). Другими словами мы на основную эпюру «М^б+в» наложим эпюры «М^б+г» и «М^б+д«. Огибающая эпюра нужна нам для того, чтобы определить пределы, в которых изгибающий момент будет вызывать растяжение верхней зоны сечения плиты.

Дополнительных данных будет не так уж и много

М^б+д_1(l/2) = 74.73 — 12.032 = 62.7 кгс·м

М^б+г₂ = 34.326 — 21.06 = 13.266 кгс·м

М^б+д₃ = 47.47 — 18.049 = 29.52 кгс·м

М^б+г_В = М^б+д_В = — 108.7 — 24.064 = — 132.76 кгс·м

М^б+г_С = М^б+д_С = — 81.53 — 18.049 = — 99.58 кгс·м

Огибающая эпюра для выбранных расчетных схем будет выглядеть так:

Рисунок 316.2

Теперь, когда максимальные значения моментов на опорах и в пролетах определены, подобрать требуемую арматуру для всех пролетов не сложно.

Например, для первого пролета на приопорном участке потребуется армирование при h₀ = 6 см и при R_b = 117·0.9 = 105.3 кг/см²:

a_m = 156.9/(1·0.06²·1053000) = 0.0414

A_s = 105.3·100·6(1 — √‾(1 — 2·0.0414)) / 3600 = 0.742 см².

Получается, что даже для самого нагруженного участка плиты шириной 1 м достаточно 4 стерженей d = 5 мм с площадью 0.79 см². При этом коэффициент армирования получается:

μ% = 100·0.79/100·6 = 0.13 %

что в 2-4 раза меньше рекомендуемого. С учетом того, что в остальных пролетах и на остальных опорах момент меньше, мы можем уменьшить высоту плиты. Согласно СНиП 2.01.03-84 п.5.3 толщина плит междуэтажных перекрытий в жилых зданиях должна быть не менее 5 см. Согласно п.5.5 высота защитного слоя при высоте конструкции до 100 мм — не менее 10 мм и не менее диаметра арматуры. Исходя из этих требований мы можем принять высоту плиты 6 см, а расстояние а = 1.5 см, что обеспечит высоту защитного слоя 10 мм даже при диаметре арматуры 10 мм. Тогда при h_o = 4.5 см

a_m = 156.9/(1·0.045²·1053000) = 0.0736

A_s = 105.3·100·4.5(1 — √‾(1 — 2·0.0736)) / 3600 = 1.007 см².

Тогда для армирования приопорных участка (опоры В и Е) достаточно 4 стерженей d = 6 мм с площадью 1.13 см², для надежности можно принять 5 стержней диаметром 6 мм и высоту h_o = 4.7 см.

Такое уменьшение высоты плиты приведет к ощутимому изменению значения постоянной нагрузки, но также и к изменению параметров тавровой балки. Поэтому и плита и балки при таком изменении параметров нуждаются в перерасчете.

Уточненное расчетное значение постоянной нагрузки составит:

q_п = (0.06·1 + 0.11·0.24/1.62)2500·1.1 + 200 = 210+200 = 410 кг/м

Значение временной нагрузки оставляем без изменения. Тогда при соотношении нагрузок 410/451.7 = 0.91 значение расчетных моментов при максимальной нагрузке составит:

М^б+в_В = М^б+в_Е = — 156.85·0.91 = — 142.34 кгс·м

М^б+в_С = М^б+в_D = — 117.65·0.91 = — 106.8 кгс·м

М^б+в₁ = М^б+в₅ = 116.1·0.91 = 105.4 кгс·м

М^б+в_1(l/2) = М^б+в_5(l/2) = 107.83·0.91 = 97.9 кгс·м

М^б+в₂ = М^б+в₄ = 45.54·0.91 = 41.3 кгс·м

М^б+в₃ = 68.64·0.91 = 62.3 кгс·м

Уточненная огибающая эпюра моментов будет выглядеть так:

Рисунок 316.3

Примечание: Следует учитывать, что в чистом виде эти данные можно применить только для первого и последнего метров плиты. Так как железобетонные балки, на которые опирается плита, в отличие от стен — опор А и F, будут прогибаться и чем ближе к середине, тем больше прогиб будет стремиться к максимальному. Такой прогиб будет приводить к перераспределению моментов. Для приближенных расчетов можно уменьшить значение моментов на опорах В и Е на 10% и на столько же увеличить значение моментов в 1 и 5 пролете. Более точный учет влияния проседающих опор — отдельная история.

Согласно Пособия по проектированию «Армирование элементов монолитных железобетонных зданий» 2007 года издания толщину балочных плит в перекрытиях жилых и общественных зданий с отношением сторон l₂/l₁ >2 следует принимать не менее 70 мм, а защитный слой бетона — не менее 20 мм. В целом это очень правильное требование, однако оно не предусматривает возможную разницу в длине пролетов, а шаг ребер —  балок 1.6 м является довольно частным. Тем не менее при использовании для бетонной смеси щебня с крупностью зерен более 30 мм это требование следует выполнять.

doctorlom.com

Изгибающие моменты в балках однопролетных

В эту эпюру вписывают эпюру предельных изгибающих моментов для простой (однопролетной) балки от нагрузки в данном пролете (рис. 21.17). В тех местах, где вписываемая эпюра имеет общие точки с эпюрой предельных моментов, возникают пластические шарниры.  [c.566]

С момента возникновения в сечении г = 8 м пластического шарнира расчетная схема балки приобретает вид, показанный на рис. 12.105, в. Дальнейшее увеличение параметра Р приводит к возрастанию опорного изгибающего момента, в сечении же 2 = 8 щ изгибающий момент возрастать не может. При том значении параметра нагрузки (обозначим его символом Р ), при котором и в опорном сечении изгибающий момент достигает величины Мд, в опорном сечении также возникает пластический шарнир, и балка теряет геометрическую неизменяемость. Эпюра изгибающих моментов приобретает вид, показанный на рис. 12.23, г. Вместе с тем, при действии на однопролетную балку пролетом 1,5/ сил Р и 1,5Р, как это показано на рис. 12.. 105, д, в сечении  [c.272]

ПОПЕРЕЧНЫЕ СИЛЫ И ИЗГИБАЮЩИЕ МОМЕНТЫ В ОДНОПРОЛЕТНЫХ БАЛКАХ 45  [c.45]

Т а б л и ц а 66. Опорные реакции н изгибающие моменты в консольных и однопролетны-х балках  [c.148]

Сначала возьмем левый пролет. Эпюру от внешней нагрузки построим как в обычной однопролетной балке длиной В частном случае при наиболее распространенных типах нагрузок она может быть треугольником (от сосредоточенной силы), параболой (от равномерно распределенной нагрузки) и т. д. Обозначим через (о площадь эпюры изгибающих моментов в пролете / , а через а — расстояние от центра тяжести этой эпюры до левой опоры, т. е до опоры п—I.  [c.355]

Допустим, что нагрузки приложены не в узлах ферм, а по длине панели (рис. 18-1,в) тогда их следует разложить по узлам и обычным путем от этих нагрузок определять продольные силы в стержнях фермы. В нагруженных панелях, помимо продольных сил, действуют поперечные силы Q и изгибающие моменты М, которые определяются при рассмотрении нагруженного пояса фермы в качестве балки. В первом приближении вычисляют Q и М в нагруженной панели, как в однопролетной балке, у которой пролет равен длине панели. Допустим, что панель (стержень пояса) нагружена сосредоточенной силой Р. приложенной на ее середине. В этом случае изгибающий момент в двухопорной балке с шарнирным опорами определится по формуле  [c.442]

Т ч Д 1 с ве основной системы заданной рамы. Для облегчения построения эпюр бимоментов и изгибающих моментов в этой основной системе от заданных нагрузок следует иметь таблицы готовых формул реакции в однопролетных балках от различных загружений их и от различных перемещений опор. Для опорных реакций и опорных изгибающих моментов такие таблицы имеются почти во всех курсах строительной механики и в справочниках. Готовые же формулы опорных бимомеитов и общих крутящих моментов представлены нами в форме таблицы приложения 9. Общие же формулу положенные в основу при составлении этой таблицы, даны в следующем параграфе.  [c.362]

Если эпюры изгибающих моментов, возникающих от заданной внешней нагрузки в однопролетных балках основной системы, представляют собой сложные фигуры, то их следует расчленить на ряд простых фигур (площадь и положения центров тяжести которых известны). В этих случаях в правые части уравнения (7.76) вместо выражений лвв[c.311]

Для вычисления правых частей уравнений трех моментов строим эпюру изгибающих моментов, рассматривая каждый пролет как простую однопролетную балку (рис. 7.83, в). Эпюру моментов для консоли строим начиная с правого конца, т. е. так же, как для консоли статически определимой балки.  [c.328]

Учитывая это обстоятельство, некоторые инженеры рекомендовали ) назначать размеры поперечных сечений для элементов сооружений, исходя из предельного сопротивления. Они указывали, что если распределение напряжений в сечении при достижении предельдого сопротивления представляется эпюрой (рис. 200, б), то легко может быть найдена и соответствующая этому состоянию материала предельная нагрузка. Например, для однопролетной балки с защемленными концами, нагруженной в середине пролета (рис. 201, а), мы можем заключить, что окончательная утрата ею несущей способности наступит, когда предельное значение М изгибающего момента будет достигнуто в трех сечениях а, Ъ, с. Всякое дальнейшее загружение приведет ее в состояние, тождественное с состоянием двух шарнирно соединенных между собой двухшарнирных брусьев (рис. 201, б). Величина предельной разрушающей нагрузки определится тогда из соответствующей эпюры изгибающих моментов (рис. 201, а), которая дает нам  [c.509]

Для подвижной системы грузов максимальный изгибающий момент гюлучается в точке приложения веса одного из грузов, называемого критическим. Для однопролетной балкп (см. рис. 83, а) наибольший изгибающий момент Жщах получается тогда, когда равнодействующая Я всех нагрузок, действующих в пролете балки, и критическая сила тяжести Р,ф располагаются симметрично относительно середины пролета  [c.105]

Свободно опертая по концам однопролетная балка (рис. 10.35). На левом и правом ее концах прогибы равны нулю, а углы наклона касательной в опорных сечениях отличны от нуля. Следовательно, на концах фиктивной балки должны обращаться в нуль фиктивные изгибающие моменты М. Фиктивные же поперечные силы С в этих сечениях не должны быть равны нулю.  [c.311]

Однопролетная балка с консолью (рис. 10.36). Построим для нее фиктивную балку. На правом свободном конце этой балки прогиб и угол наклона должны быть отличны от нуля. Следовательно, в этом сечении фиктивной балки должны быть отличны от нуля фиктивный изгибающий момент и фиктивная поперечная сила С. Этим условиям можно удовлетворить, если в этом сечении фиктивной балки ввести заделку.  [c.311]

В простейшей системе, состоящей из двух пересекающихся балок, сила Р, приложенная в узле пересечения, воспринимается одновременной работой обеих балок. При равенстве пролетов 1х=1у и равенстве жесткостей Е/х = Е1у сила поровну раскладывается на обе балки и каждая испытывает изгибающий момент Мх=Му=Р118, что в 2 раза меньше момента в однопролетной разрезной балке тех же пролета и жесткости, равного М = Р1/4 (рис. 205, а, б). При одинаковых пролетах, но при разных жесткостях балок Е1х>Е1у, балка с большей жесткостью воспринимает большую часть момента, так как балка с меньшей жесткостью следует за деформацией другой балки (рис. 205, в). Такой же эффект получается в случае, если жесткости балок одинаковы, но одна балка короче другой.  [c.241]

Касательные напряжения в сварных балках, как правило, весьма небольшие и значительно ниже допускаемых. Нередко в балках наибольшие изгибающие моменты и поперечные силы имеют место в одних и тех же поперечных сечениях, например, в балках консольных, неразрезных, а также в однопролетных или сосредоточенных грузах. При этом на крайних кромках вертикального листа следует определить эквивалентные напряжения  [c.283]

Чтобы выяснить, в каком случае в гибкой ленте не будет возникать изгибающих моментов, рассмотрим ее как однопролетную балку длиной I (рис. 12.16, б). За лишнее неизвестное в этой балке примем рас-пор Яд. Переменные 6 и А соответственно от Я = 1 по направлению его действия и от нагрузки дс по направлению распора составляют  [c.343]

Для определения трех опорных реакций Ra, Rb, R имеем систему двух уравнений. Привлекаем дополнительное условие (4.7.1). ОгНоси одну лишнюю опсфную реакцию Rb = Ху В результате получим однопролетную балку, показанную на рис. 4.7.4, б. Для полученной однопролетной балки строим эпюру изгибающих моментов Мр от внешней сипы F. Предварительно находим =2/Лс-0,5/F = О, откуда R = 0,25F. Далее  [c.149]

Задача 4.7.10. На рнс. 4.2.2 изображена однопролетная балка и соответствующие эпюры изгибающих моментов М и поперечных сил Q. Как изменятся эпюры М и Q, если поставить дополнительно в точке D пгар-нирно подвижную onq)y.  [c.150]

mash-xxl.info

Изгибающие моменты в балках многопролетных

ПОПЕРЕЧНЫЕ СИЛЫ И ИЗГИБАЮЩИЕ МОМЕНТЫ В МНОГОПРОЛЕТНЫХ БАЛКАХ И БАЛКАХ НА УПРУГОМ ОСНОВАНИИ ПРИ НЕПОДВИЖНОЙ НАГРУЗКЕ  [c.66]

ПОПЕРЕЧНЫЕ СИЛЫ И ИЗГИБАЮЩИЕ МОМЕНТЫ В МНОГОПРОЛЕТНЫХ БАЛКАХ  [c.62]

В основу этих методов заложено следующее общее представление. При свободных поперечных колебаниях многопролетной балки каждый ее пролет может рассматриваться как двухопорная балка с упруго защемленными концами, так что изгибающие моменты в опорных сечениях пропорциональны углам поворота этих сечений. Коэффициент пропорциональности, часто называемый динамической жесткостью, зависит от жесткостных и инерционных характеристик остальных пролетов, а также от частоты колебаний. Из рассмотрения условий сопряжения на опорах следует, что при свободных поперечных колебаниях системы динамические жесткости, определяемые для соседних пролетов на общей опоре, равны по величине и противоположны по знаку, так как изгибающие моменты в крайних сечениях соседних пролетов равны по величине и противоположны по направлению.  [c.229]

Неправильный выбор расчетной схемы влечет за собой ошибку в определении расчетного изгибающего момента, в связи с чем неправильно назначается расстояние между поддерживающими опорами. Для примера сравним величины изгибающих моментов при расчете дренажной ветви длиной 4,5 м, состоящей из трех труб, соединенных на фланцах. Возьмем два случая каждая из трех труб работает самостоятельно как балка на двух опорах и все три трубы работают как неразрезная многопролетная балка. Расчетный изгибающий момент в первом случае будет в 1,5 раза больше, чем во втором, причем с увеличением числа труб эта разница будет возрастать.  [c.146]

Рассчитывая многопролетный рельс, подвешенный на тягах по схеме разрезной балки, при наличии на трассе нескольких самостоятельно работающих тележек, необходимо проверить напряжения от изгибающего момента в сечении на опоре В при одновременном нахождении тележек в рядом расположенных пролетах. При этом значение относительного опорного момента Мв от подвижной нагрузки при равных значениях пролетов I и грузоподъемностей тележек определяют по табл. 3.9, где Р — подвижная нагрузка брутто в каждом пролете. Хотя значения опорных моментов от подвижной нагрузки, как правило, меньше максимальных значений пролетных моментов для разрезного рельса, проверка его сечения по прочности на опоре может оказаться решающей, так как моменты сопротивления верх и для верхнего и ниж-  [c.53]

Ниже приведены формулы для вычисления прогибов и изгибающих моментов в одно- и многопролетных балках, загруженных равномерно распределенной статической д и динамической р нагрузками. Коэффициенты динамичности принимают по приведенным выше формулам и графикам в зависимости от закона изменения динамической нагрузки во времени. Максимальные изгибающий момент и прогиб  [c.16]

Применение методов строительной механики к расчету многопролетной неразрезной балки позволяют получить максимально приближенную к реальности картину изменения эпюры изгибающего момента в пролете, загруженном поперечной силой, которая свидетельствует о возможности расчета направляющей как статически определимой двухопорной балки с расчетным пролетом меньшим расстояния между её опорами (рис. 10.8).  [c.254]

Растягивающие и сжимающие усилия в угловых зонах по сечению, расположенному под углом 45° к Контуру, у средней диафрагмы на 20—40% больше, чем у крайних (см. рис. 2.43). Следовательно, сдвигающие силы у диафрагм неразрезных оболочек также больше, чем у отдельно стоящих оболочек. Следует отметить также, что суммарный изгибающий момент, действующий в пределах всего сечения оболочек, находящихся в системе многоволнового покрытия, аналогичен отрицательному моменту в многопролетных неразрезных балках.  [c.110]

Разделим многопролетную балку на две части. Отбрасывая одну из частей, именно ту, к которой приложено возбуждение (в данном случае левую), заменим ее действие системой усилий, которая в общем случае складывается из перерезывающей силы и изгибающего момента, изменяющихся во времени по гармониче-  [c.250]

Неразрезными многопролетными балками называют статически неопределимые балки, опирающиеся более чем на две опоры. В таких балках более рационально распределяются изгибающие моменты по сравнению с разрезными балками. Все опоры таких балок должны воспринимать как положительные, так и отрицательные опорные реакции. Одна из опор в неразрезной балке должна быть обязательно шарнирно неподвижной для обеспечения неподвижности балки в горизонтальном направлении и для восприятия горизонтальной реакции. Все остальные опоры должны быть шарнирно подвижными. К категории неразрезных балок относятся также и балки с заделками на одном или двух концах. Степень статической неопределимости неразрезной балки, у которой все опоры шарнирные, равна чй[c.124]

Прн расчете неразрезных многопролетных балок можно принять в качестве расчетной трехпролетную балку с загрузкой только крайнего пролета, например, при пропуске грузов (см. рис. 84, а). Исследования показывают, что при числе пролетов более трех максимальное значение изгибающего момента изменяется незначительно, например, при пяти пролетах всего лишь на 5%.  [c.107]

Расчет многоопорных (многопролетных) валов иногда ведут отдельно по пролетам, т. е. рассматривают вал как бы разрезанным на отдельные двухопорные балки. Такой расчет дает довольно существенную ошибку — максимальный расчетный изгибающий момент получается значительно больше, чем фактически действующий. Следовательно, ошибка идет, как принято говорить, в запас прочности. Если необходимо выполнить расчет более точно, то вал рассматривают как статически неопределимую балку и раскрывают статическую неопределимость методами, изложенными в предмете сопротивления материалов.  [c.223]

Теория расчета таких балок была разработана инженером Г. П. Семиколеновым в 1871 г., поэтому такие балки иногда называют балками Семиколенова. Многопролетная статически определимая балка с промежуточными шарнирами обычно выгоднее неразрезной балки, перекрывающей эти же пролеты при той же несущей нагрузке. Это объясняется тем, что в промежуточных шарнирах момент всегда равен нулю и величина изгибающих моментов, действующих по длине балки, снижается.  [c.155]

Уравнения перемещений в форме уравнений трех моментов рекомендуется применять для раскрытия статической неопределимости многопролетных неразрезных балок (фиг. 28, а) за основную систему принимают балку с врезанными над опорами шарнирами (фиг. 28, б), т. е. за лищние неизвестные принимают изгибающие моменты М1, Л1 ц.1… в над-опорных сечениях.  [c.239]

mash-xxl.info

Типовые эпюры. Однопролетная шарнирно-опертая балка

Мы уже рассматривали типовые эпюры для консольной балки с статье Типовые эпюры. Консольная балка. Теперь рассмотрим типовые эпюры для однопролетной, шарнирно-опретой балки.

Также как и в прошлой статье рассматривать будем только эпюры Q (поперечная сила), M (изгибающий момент).

Типовые эпюры однопролетной шарнирно-опертой балки

В однопролетной балке оба конца имеют шарнирное закрепление.

Сосредоточенная нагрузка приложена в пролете балки

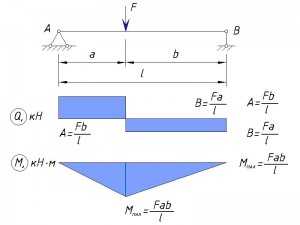
2-е сосредоточенные нагрузки приложены в пролете балки на равном удалении от опор

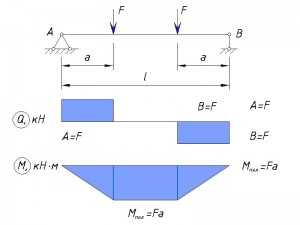
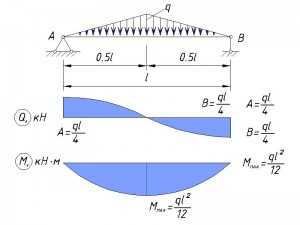
Равномерно-распределенная нагрузка по всей длине балки

Равномерно-распределенная нагрузка на участке балки, начинающаяся у одного узла и прерывающаяся в пролете

Равномерно-распределенная нагрузка на участке балки, расположена по центру балки

Переменная нагрузка по всей длине балки

Переменная нагрузка на участке балки, начинающаяся у одного узла и прерывающаяся в пролете

Переменная нагрузка, имеющая максимальную нагрузку в центре балки

Крутящий момент, приложенный в опорном узле балки

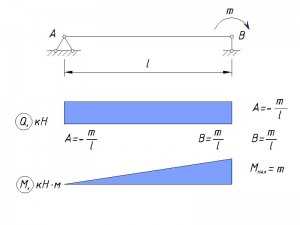
Крутящий момент, приложенный в пролете балки

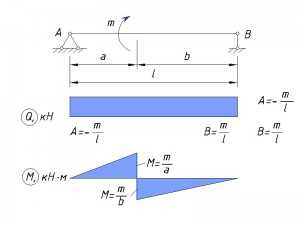
buildingbook.ru