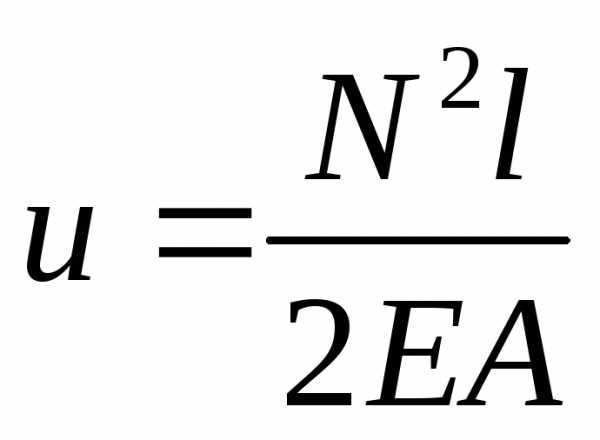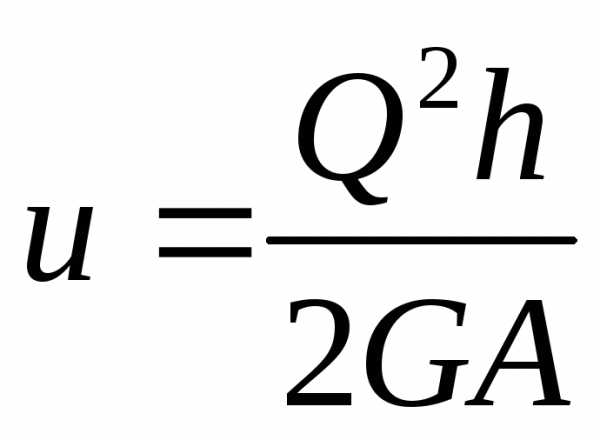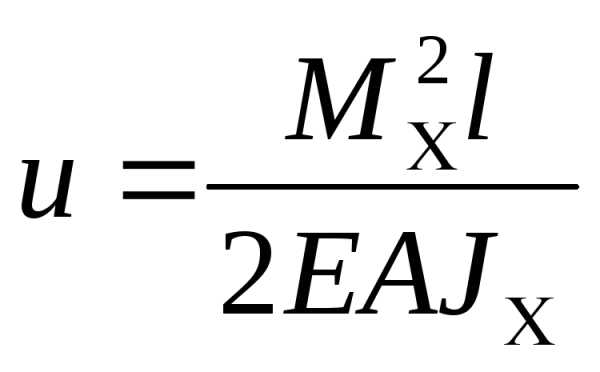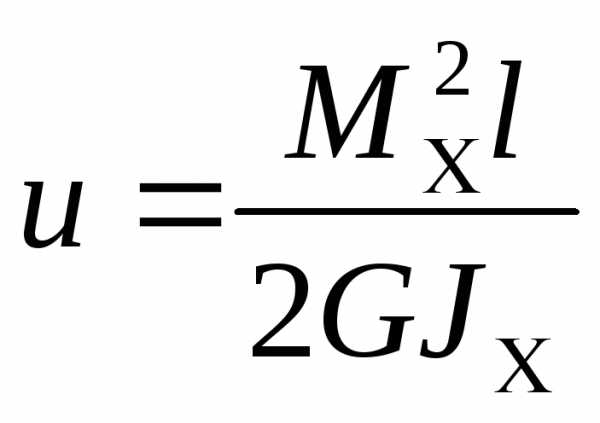Формулы по сопромату
Приветствую, Вас на проекте — «СопроМат». Эта страничка будет навигатором по самым ходовым формулам сопромата, которые используются при расчетах на прочность, жесткость или устойчивость. Все формулы по сопромату классифицированы по виду деформации: растяжение или сжатие, кручение и изгиб.
Навигация по формулам:
- Поперечный изгиб : напряжения,
Формулы по теме поперечный изгиб
В рамках этого раздела опубликованы основные формулы по теме «Поперечный изгиб». Также его часто называют простым или прямым изгибом.
Формулы для определения напряжений при поперечном изгибе
Формула для определения нормальных напряжений в точках поперечного сечения:
где Mx — изгибающий момент в поперечном сечении, Ix — момент инерции относительно центральной оси, y — расстояние от центральной оси до точки в которой вычисляется напряжение.

Формула для определения максимального (минимального) нормального напряжения в наиболее опасных точках поперечного сечения:
где Mx — изгибающий момент в поперечном сечении, Wx — момент сопротивления относительно центральной оси.
Формула для определения момента сопротивления поперечного сечения:
где Ix — момент инерции относительно центральной оси, ymax — расстояние до наиболее удаленных точек поперечного сечения.

Формула для определения касательных напряжений в точках поперечного сечения:
где Qy — поперечная сила в рассматриваемом сечении, Sотс — статический момент относительно центральной оси отсеченной части поперечного сечения, Ix — момент инерции относительно центральной оси, b
— ширина поперечного сечения на высоте h, где рассчитываются касательные напряжения.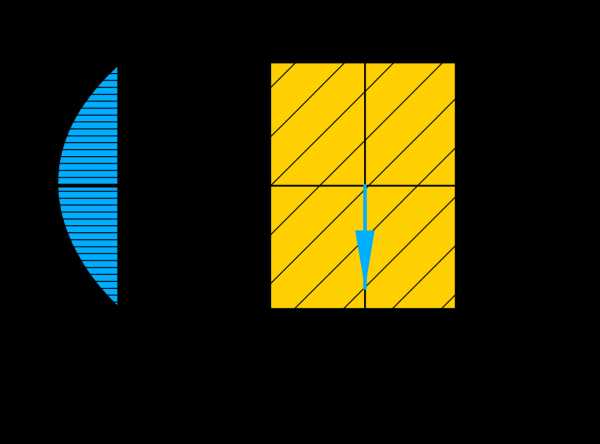
Формула для определения главных напряжений (максимальное и минимальное) при поперечном изгибе:
ssopromat.ru
Формулы по сопромату
Список формул по дисциплине «Сопротивление материалов.»
РАСТЯЖЕНИЕ СЖАТИЕ | СДВИГ | ИЗГИБ | КРУЧЕНИЕ | |
З-Н. Гука | | | | |
ОТНОСИТЕЛЬН. ДЕФОРМАЦИЯ | | | | |
НАПРЯЖЕНИЕ |
| | | |
УСЛОВИЕ ПРОЧНОСТИ | | | | |
ПЕРЕМЕЩЕНИЕ | | | | |
| | — разнос. мах. нагрузок | — предельная нагрузка |
напряжение |
ПОТЕНЦ. ЭНЕР. | | |
|
|
E-модуль Юнга.N-продольная сила
G- модуль сдвига. -относительный
угол сдвига
-относительный
угол сдвига
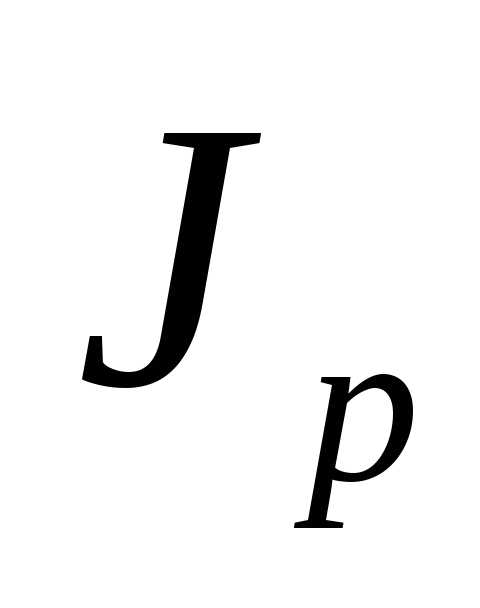 -полярный
момент инерции
-полярный
момент инерции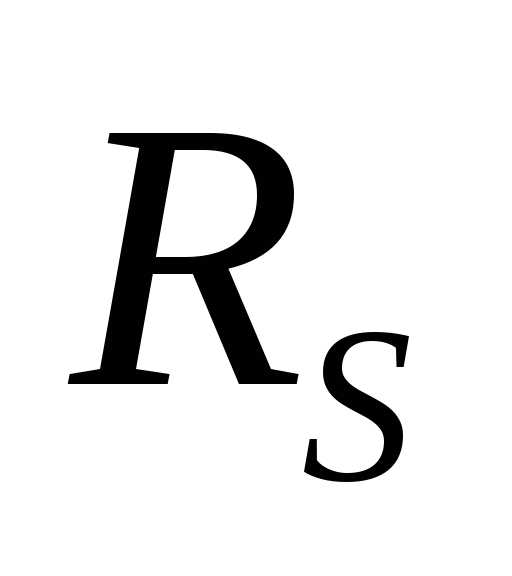 -расчет.
сопротивлений
-расчет.
сопротивлений
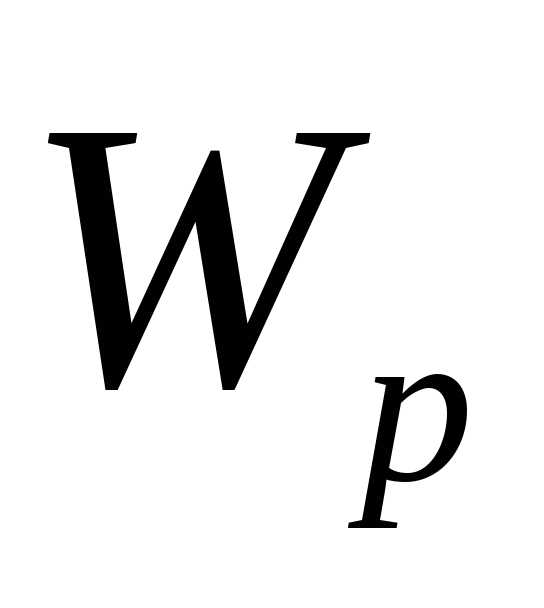 -полярный
момент сопрот. сечения
-полярный
момент сопрот. сечения -радиус
кривизны изогн. нейтр. оси
-радиус
кривизны изогн. нейтр. оси
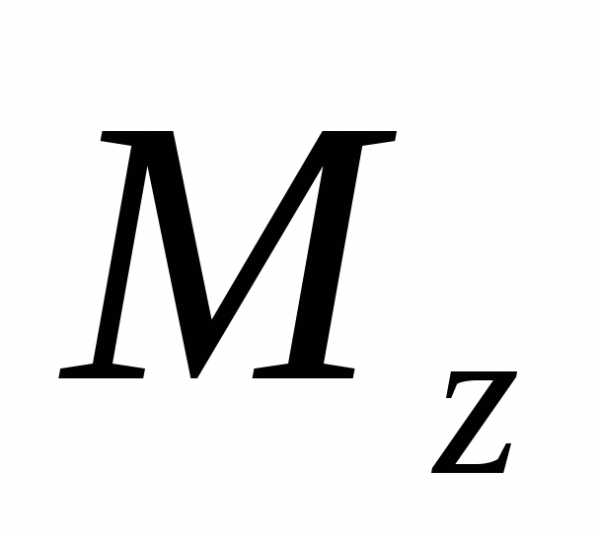 -крутящийся
момент
-крутящийся
момент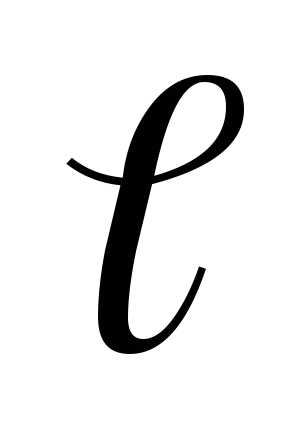 -раст
между сечен кот опред
-раст
между сечен кот опред -угол
пов
-угол
пов
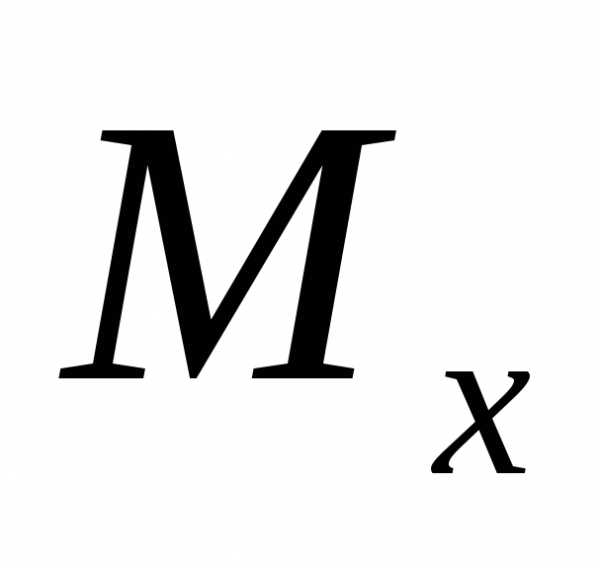
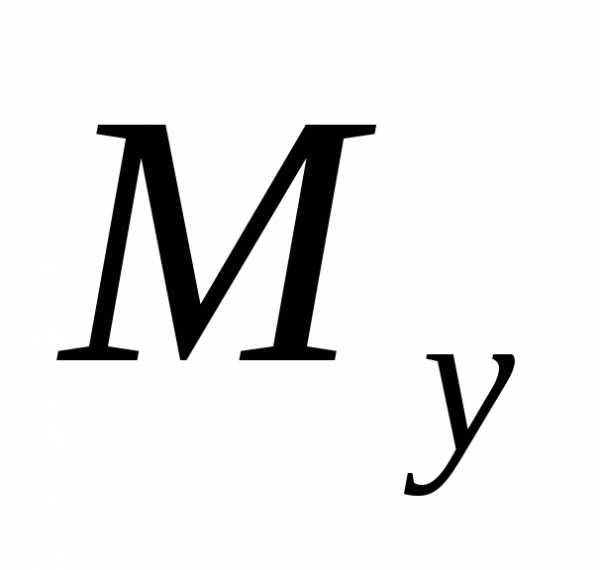 -изгиб.
момент.
-изгиб.
момент.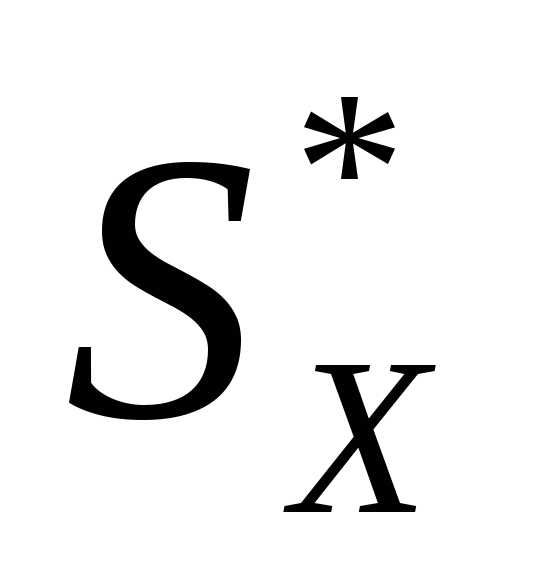 -статичес.
момент отсеч. части
-статичес.
момент отсеч. части
 -момент
инерцииh-расстояние
между внешн. силами
-момент
инерцииh-расстояние
между внешн. силами
y-расстоян. от расм. вол.
до нейт слоя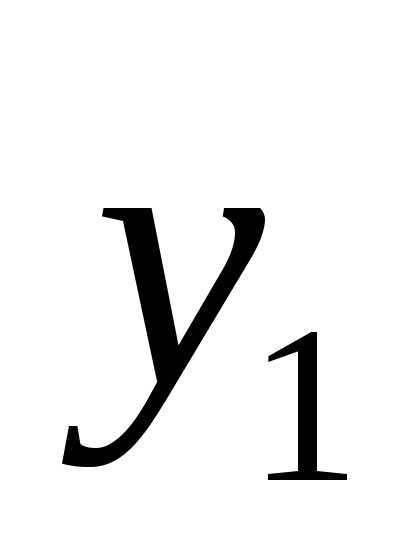 -координата
рассматрив. точки в попер.
-координата
рассматрив. точки в попер.
 -полный
угол закручивания сечении
-полный
угол закручивания сечении
 -относит.
угол закручивания
-относит.
угол закручивания
 -касательное
напряжение
-касательное
напряжение
studfiles.net
Шпаргалки, Сопромат (труд)
Вход на портал Вход на портал Регистрация Начало Поиск по сайту ТОПы Учебные заведения Предметы Проверочные работы Обновления Подписка Я+ Новости Переменка Отправить отзыв- Архив
- Сопромат (труд)
-
Основные понятия
-
Основные гипотезы сопротивления материалов
-
Расчетная схема
-
Внутренние силы
-
Классификация внешних сил
-
Метод сечений (розу)
-
Построение эпюр внутренних силовых факторов
-
Эпюры внутренних усилий
-
Понятие о напряжениях
-
Понятия о деформациях
-
Виды нагружения (или виды деформации стержня)
-
Основные условия прочности. допускаемые напряжения. условие жесткости
-
-
Растяжение — сжатие
-
Напряжения и расчет на прочность
-
Деформации и перемещения при растяжении — сжатии
-
Статистически неопределимые задачи
-
-
Кручение
-
Построение эпюр крутящих моментов
-
Напряжение и расчет на прочность
-
-
Геометрические характеристики плоских сечений
-
Статистические моменты сечения
-
Моменты инерции сечения
-
Моменты сопротивления сечения
-
Рациональные формы поперечных сечений
-
-
Изгиб
-
Напряжение при изгибе и расчет брусьев на прочность
-
Построение эпюр изгибающих моментов
-
-
Определение перемещений в статистически определимых системах. расчеты на жесткость
-
Определение перемещения методом мора
-
Правило верещагина
-
Примеры определения перемещений при изгибе
-
-
Сложное нагружение
-
Косой изгиб
-
Внецентренное растяжение — сжатие
-
Изгиб с кручением круглых валов
-
Расчет на прочность пространственнс рамы с ломаной осью
-
-
Устойчивость сжатых стержней
-
Определение критической силы по формуле эйлера
-
Определение критической силы с помощью эмпирической формулы
-
Практический метод расчета на устойчивость
-
Определение критической силы с помощью дифференциального уравнения (точечный метод определения ркр)
-
Энергетический метод определения критической силы
-
-
Основные обозначения, принятые в сопромате
www.yaklass.ru
Формулы для расчетов на кручение
τ — касательные напряжения,
T – внутренний крутящий момент,
Ip – полярный момент инерции сечения вала,
Wp – полярный момент сопротивления сечения,
[τ] – допустимое напряжение,
G – модуль упругости II рода (модуль сдвига),
ρ — расстояние от центра сечения до рассматриваемой точки,
D – внешний диаметр вала,
d – внутренний диаметр вала кольцевого сечения.
Закон Гука при кручении (чистом сдвиге)
Расчет касательных напряжений в произвольной точке сечения вала
Условие прочности при кручении (проверочный расчет)
Формулы полярных моментов инерции и сопротивления
- для вала сплошного (круглого) сечения
- для вала кольцевого сечения
Формулы для подбора диаметра вала по условию прочности
- сплошное круглое сечение
- кольцевое сечение
Абсолютные деформации (угол закручивания участков вала)
Перемещение (угол поворота) сечений.
Здесь: φi — угол поворота рассматриваемого сечения,
φi-1 — перемещение предыдущего сечения,
Другие формулы >
Примеры решения задач >
Краткая теория >
isopromat.ru
Шпаргалка по сопромату
1. Основные понятия и допущения. Жесткость – способность конструкции в определенных пределах воспринимать воздействие внешних сил без разрушения и существенного изменения геометрических размеров. Прочность – способность конструкции и ее материалов сопротивляться нагрузкам. Устойчивость – способность конструкции сохранять форму первоначального равновесия. Выносливость – прочность материалов в условиях нагрузок. Гипотеза сплошности и однородности: материал, состоящий из атомов и молекул, заменяют сплошным однородным телом. Сплошность обозначает, что сколь угодно малый объем содержит в-во. Однородность обозначает, что во всех точках св-ва материала одинаковы. Использование гипотезы позволяет применять сист. координат и для исследования интересующих нас функций использовать матем анализ и описывать действия различными моделями. Гипотеза изотропности: предполагает, что во всех направлениях св-ва материала одинаковы. Анизотропным явл дерево, у к-ого св-ва вдоль и поперек волокон значительно отличаются.
2. Механические хар-ки материала. Под пределом текучести σТ понимается то напряжение, при к-ом происходит рост деформации без заметного увеличения нагрузки. Под пределом упругости σУ понимается такое наибольшее напряжение, до к-ого материал не получает остаточных деформаций. Предел прочности(σВ)– отношение максимальной силы, к-ую способен выдержать образец, к его начальной площади поперечного сечения. Предел пропорциональности (σПР) – наибольшее напряжение, до к-ого материал следует закону Гука. Величина Е представляет собой коэф пропорциональности, называемый модулем упругости первого рода. Величина G назыв модулем сдвига или модулем упругости 2 рода. (G=0.5E/(1+µ)). µ — безразмерный коэф пропорциональности, называемый коэф Пуассона, хар-ет св-ва материала, определяется экспериментальным путем, для всех металлов числовые значения лежат в пределах 0,25…0,35.
3. Силы. Взаимодействие между частями рассматриваемого объекта хар-ют внутренние силы. Они возникают не только между отдельными взаимодействующими узлами конструкции, но также и между всеми смежными частицами объекта при нагружении. Внутренние силы определяются методом сечений. Различают поверхностные и объемные внешние силы. Поверхностные силы могут быть приложены к малым участкам поверхности (это сосредоточенные силы, например Р) или к конечным участкам поверхности (это распределенные силы, например q). Они хар-ют взаимодействие конструкции с другими конструкциями или с внешней средой. Объемные силы распределены по объему тела. Это силы тяжести, магнитного напряжения, силы инерции при ускоренном движении конструкции.
4. Понятие напряжения, допустимое напряжение. Напряжение – мера интенсивности внутренних сил.lim∆R/∆F=p – полное напряжение. Полное напряжение может быть разложено на три составляющие: по нормали к плоскости сечения и по двум осям в плоскости сечения. Составляющую вектора полного напряжения по нормали обозначают через σ и назыв нормальным напряжением. Составляющие в плоскости сечения назыв касательными напряжениями и обознач через τ. Допускаемое напряжение – [σ]=σПРЕД/[n] – зависит от марки материала и коэф запаса прочности.
5. Деформация растяжения-сжатия. Растяжение (сжатие) – вид нагружения, при к-ом из шести внутренних силовых факторов (Qx, Qy, Mx, My, Mz, N) пять равны нулю, а N≠0. σmax=Nmax/F≤[σ]+ — условие прочности при растяжении; σmax=Nmax/F≤[σ]— — условие прочности при сжатии. Математическое выражение з-на Гука: σ=εЕ, где ε=∆L/L0. ∆L=NL/EF – развернутый з-он Гука, где EF – жесткость стержня поперечного сечения. ε – относительная (продольная) деформация, ε’=∆а/а0=∆в/в0 – поперечная деформация, где при нагружении а0, в0 уменьшились на величину ∆а=а0-а, ∆в=в0-в.
6. Геометрические хар-ки плоских сечений. Статический момент площади: Sx=∫ydF, Sy=∫xdF, Sx=ycF, Sy=xcF. Для сложной фигуры Sy=∑Syi , Sx=∑Sxi .Осевые моменты инерции: Jx=∫y2dF, Jy=∫x2dF. Для прямоугольника Jx=bh3/12, Jy=hb3/12, для квадрата Jx=Jу=а4/12. Центробежный момент инерции: Jxy=∫xydF, если сечение симметрично хотя одной оси, Jxу=0. Центробежный момент инерции несимметричных тел будет положительным, если большая часть площади будет находиться в 1 и 3 квадранте. Полярный момент инерции: Jρ=∫ρ2dF, ρ2=х2+у2, где ρ – расстояние от центра координат до dF. Jρ=Jx+Jy. Для круга Jρ=πd4/32, Jx=πd4/64. Для кольца Jρ=2Jх=π(D4-d4)/32=πD4(1-α4)/32. Моменты сопротивления: для прямоугольника Wx=Jx/уmax, где уmax – расстояние от центра тяжести сечения до границ по у. Wx=bh2/6, Wx=hb2/6, для круга Wρ=Jρ/ρmax, Wρ=πd3/16, для кольца Wρ=πD3(1-α3)/16. Координаты центра тяжести: xc=(x1F1+x2F2+x3F3)/(F1+F2+F3). Главные радиусы инерции: iU=√JU/F, iV=√JV/F. Моменты инерции при параллельном переносе осей координат: Jx1=Jхc+b2F, Jy1=Juc+a2F, Jx1y1=Jхcyc+abF.
7. Деформация сдвига и кручения. Чистым сдвигом называется такое напряженное состояние, когда на гранях выделенного эоемента возникают только касательные напряжения τ. Под кручением понимают вид движения, при к-ом в поперечном сечении стержня возникает силовой фактор Mz≠0, остальные Мх=Му=0, N=0, Qx=Qy=0. Изменение внутренних силовых факторов по длине изображаются в виде эпюры с использованием метода сечений и правила знака. При деформации при сдвиге касательное напряжение τ связано с угловой деформацией γ соотношением τ =Gγ. dφ/dz=θ – относительный угол закручивания – это угол взаимного поворота двух сечений, отнесенный к расстоянию между ними. θ=МК/GJρ , где GJρ – жесткость поперечного сечения при кручении. τmax=MKmax/Wρ≤[τ] – условие прочности при кручении круглых стержней. θmax=МК/GJρ≤[θ] – условие жесткости при кручении круглых стержней. [θ] – зависит от типа опор.
8. Изгиб. Под изгибом понимают такой вид нагружения, при к-ом ось стержня искривляется (изгибается) от действия нагрузок, расположенных перпендикулярно оси. Изгибу подвергаютя валы всех машин от действия сил, пары сил – момента в местах посадки зубчатых колес, шестерен, полумуфт. 1) Изгиб назыв чистым, если в поперечном сечении стержня возникает единственный силовой фактор – момент изгибающий, остальные внутренние силовые факторы равны нулю. Образование деформаций при чистом изгибе можно рассматривать как результат поворота плоских поперечных сечений одно относительно другого. σ=Му/Jx – формула Навье для определения напряжений. ε=у/ρ – продольная относительная деформация. Диф зависимости: q=dQz/dz, Qz=dMz/dz. Условие прочности: σmax=Мmax/Wx≤[σ] 2) Изгиб назыв плоским, если силовая плоскость, т.е. плоскость действия нагрузок, совпадает с одной из центральных осей. 3) Изгиб назыв косым, если плоскость действия нагрузок не совпадает ни с одной из центральных осей. Геометрическое место точек в сечении, удовлетворяющее условию σ=0, назыв нейтральной линией сечения, она перпендикулярна к плоскости кривизны изогнутого стержня. 4) Изгиб назыв поперечным, если в поперечном сечении возникает момент изгибающий и поперечная сила. τ=QSxотс/bJx – формула Журавского, τmax=QmaxSxmax/bJx≤[τ] – условие прочности. Полная проверка прочности балок при поперечном изгибе заключается в определении размеров поперечного сечения по формуле Навье и дальнейшей проверки по касательным напряжениям. Т.к. наличие τ и σ в сечении относится к сложному нагружению, то оценку напряженного состояния при совместном их действии можно вычислить, используя 4 теорию прочности σэкв4=√σ2+3τ2≤[σ].
9. Напряженное состояние. Исследуем напряженное состояние (НС) в окрестностях точки А, для этого выделим бесконечно малый параллелепипед, к-ый в увеличенном масштабе поместим в сист координат. Действия отброшенной части заменяем внутренними силовыми факторами, интенсивность к-ых можно выразить через главный вектор нормальных и касательных напряжений, к-ые разложим по трем осям – это компоненты НС точки А. Как бы сложно не было нагружено тело, всегда можно выделить взаимно перпендикулярные площадки, у к-ых касательные напряжения равны нулю. Такие площадки назыв главными. Линейное НС – когда σ2=σ3=0, плоское НС – когда σ3=0, объемное НС – когда σ1≠0, σ2≠0, σ3≠0. σ1, σ2,σ3 – главные напряжения. Напряжения на наклонных площадках при ПНС: τβ=-τα=0,5(σ2-σ1)sinα, σα=0.5(σ1+σ2)+0.5(σ1-σ2)cos2α, σβ=σ1sin2α+σ2cos2α.
10. Теории прочности. В случае ЛНС оценка прочности выполняется по условию σmax=σ1≤[σ]=σпред/[n]. При наличии σ1>σ2>σ3 в случае НС опред экспериментальным путем опасное сост трудоемко из-за большого кол-ва экспериментов при различных сочетаниях напряжений. Поэтому используют критерий, позволяющий выделить преимущественное влияние одного из факторов, к-ый будет назван критерием и будет положен в основу теории. 1) первая теория прочности (наибольших нормальных напряжений): напряженное сост равнопрочны по хрупкому разрушению, если у них равны растягивающие напряжения (не учит σ2 и σ3) – σэкв=σ1≤[σ]. 2) вторая теория прочности (наибольших растягивающих деформаций-т Мариотта): н6апряжен сост равнопрочны по хрупкому разрушению, если у них равны наибольшие растягивающие деформации. εmax=ε1≤[ε], ε1=(σ1-μ(σ2+σ3))/E, σэкв=σ1-μ(σ2+σ3)≤[σ]. 3) третья теория прочности (наиб касат напряжений – Кулон): напряж сост равнопрочны по появлению недопустимых пластич деформаций, если у них равны наиб касат напряжения τmax=0.5(σ1-σ3)≤[τ]=[σ]/2, σэкв=σ1-σ3≤[σ] σэкв=√σ2+4τ2≤[σ]. 4) четвертая теория удельной потенциальной энергии формоизменения (энергетическая): при деформировании потенц энергия расход на изменение формы и объема U=Uф+UV напряжен сост равнопрочны по появлению недопустимых пластич деформаций, если у них равны удельные потенц энергии изменения формы. Uэкв=Uф. С учетом обобщенного з-на Гука и матем преобразований σэкв=√(σ12+σ22+σ32-σ1σ2-σ2σ3-σ3σ1)≤[σ], σэкв=√(0,5[(σ1-σ2)2+(σ1-σ3)2+(σ3-σ2)2] )≤[τ]. В случае ПНС σэкв=√σ2+3τ2. 5) пятая теория прочности Мора (обобщ теория предельных сост): опасное предельное сост опред двумя главными напряженияи, наиб и наим σэкв=σ1-кσ3≤[σ], где к-коэф неравнопрочности, к-ый учитывает способность материала неодинаково сопротивляться растяжению и сжатию к=[σр]/[σсж].
11. Энергетические теоремы. Перемещение при изгибе – в инженерных расчетах встречаются случаи, когда балки, удовлетворяя условию прочности, не обладают достаточной жесткостью. Жесткость или деформативность балки опред перемещениями: θ – угол поворота, Δ – прогиб. Под нагрузкой балка деформируется и представляет собой упругую линию, к-ая деформируется по радиусу ρА. Прогиб и угол поворота в т А образован касательной упругой линией балки и осью z. Рассчитать на жесткость значит опред максимальный прогиб и сравнить его с допустимым. Метод Мора – универсальный метод опред перемещений для плоских и пространственных систем с постоянной и переменной жесткостью, удобен тем, что может быть запрограммирован. Для опред прогиба рисуем фиктивную балку и прикладываем единичн безразмерную силу. Δ=1/EJx*∑∫MM1dz. Для определения угла поворота рисуем фиктивную балку и прикладываем единичн безразм момент θ=1/EJx*∑∫MM’1dz. Правило Верещагина – удобно тем, что при постоянной жесткости интегрирование можно заменить алгебраическим перемножением эпюр изгибающих моментов грузового и единичного сост балки. Явл осн методом, к-ый применяется при раскрытии СНС. Δ=1/EJx*∑ωpM1c – правило Верещагина, в к-ом перемещение обратно пропорционально жесткости балки и прямо пропорционально произведению площади грузового сост балки на ординату центра тяжести. Особенности применения: эпюру изгиб моментов делят на элементарные фигуры, ωp и M1c берутся с учетом знаков, если на участке одновременно действуют q и Р или R, то эпюры необходимо расслаивать, т.е. строить отдельно от каждой нагрузки или применять различные приемы расслоения.
12. Статически неопределимые системы. СНС назыв те сист, у к-ых уравнений статики недостаточно для определения реакций опор, т.е. связей, реакций в ней больше, чем необходимо для их равновесия. Разность между общ числом опор и кол-вом независимых уравнений статики, к-ые можно сост для данной сист назыв степенью статической неопределимости S. Связи, наложенные на сист сверхнеобходимых назыв лишними или дополнительными. Введение дополнительных опорных закреплений приводит к уменьшению изгибающих моментов и максимального прогиба, т.е. повышается прочность и жесткость конструкции. Для раскрытия статич неопределимости дополнительно условие совместимости деформации, к-ое позволяет опред дополнительные реакции опор, а затем решение по опред эпюр Q и М выполняется как обычно. Основная система получается из заданной- путем отбрасывания лишних связей и нагрузок. Эквивалентная система – получается путем нагружения основной системы нагрузками и лишними неизвестными реакциями, заменяющими действия отброшенной связи. Используя принцип независимости действия сил, находим прогиб от нагрузки Р и реакции х1. σ11х1+Δ1р=0 – каноническое уравнение совместности деформации, где Δ1р – перемещение в точке приложения х1 от силы Р. Δ1р – Мр*М1, σ11-М1*М1 – это удобно выполнить методом Верещагина. Деформационная проверка решения – для этого выбираем другую основную систему и опред угол поворота в опоре, должна быть равна нулю, θ=0 — М∑*М’.
13. Циклическая прочность. В инженерной практике до 80% деталей машин разрушаются по причине статической прочности при напряжениях гораздо меньших, чем σв в тех случаях, когда напряжения являются знакопеременными и циклически изменяющимися. Процесс накопления повреждений при циклически измен. напряжениях называется усталость материала. Процесс сопротивления усталостному напряжению наз циклической прочностью или выносливостью. Т-период цикла. σmax τmax это нормальные напряжения. σm, τm – среднее напряжение; r-коэффициент ассиметрии цикла; факторы, влияющие на придел выносливости: а) Концентраторы напряжения: проточки, галтели, шпонки, резьба и шлицы; это учитывается эффективным коэффиц конц напряжений, которые обозначаются Кσ=σ-1/σ-1к Кτ=τ-1/τ-1к ; б)Шероховатость поверхности: чем грубее выполнена механическая обработка металла, тем больше пороков металла имеется при литье, тем придел выносливости детали будет ниже. Любая микро трещина или углубление после резца может явиться источником усталостной трещины. Это учитывается коэф влияния качества поверхности. КFσ КFτ — ; в) Масштабный фактор влияет на придел выносливости, с увеличением размеров детали вероятность наличия пороков увеличивается, следовательно чем больше размеры детали, тем хуже при оценке ее выносливости это учит коэф влияния абсолютных размеров поперечного сечения. Кdσ Кdτ. Дефектный коэф: KσD=[Kσ/Kdσ-1/KFσ-1]/Kv ; Kv – коэф упрочнения зависит от вида термообработки.
14. Устойчивость. Переход системы из устойчивого состояния в неустойчивое называется потерей устойчивости, а соответствующая ей сила называется критической силой Ркр В 1774 г Э. Эйлер провел исследование и определил математически Ркр. По Эйлеру Ркр – сила необходимая для самого малого наклонения колонны. Ркр=П2*Е*Imin/L2; Гибкость стержня λ=ν*L/imin; Критическое напряжение σкр=П2Е/λ2. Предельная гибкость λ зависит только от физико-механических свойств материала стержня и она постоянна для данного материала.
studfiles.net
Формулы для расчетов на сложное сопротивление и устойчивость
Основные формулы для решения задач сложного сопротивления и расчетов сжатых стержней на устойчивость.
σ — нормальные напряжения,
Mx, My – внутренние изгибающие моменты относительно осей x и y,
T – внутренний крутящий момент,
Ix, Iy – осевые моменты инерции сечения,
Wx, Wy – осевые моменты сопротивления сечения,
[σ] – допустимые напряжения,
E – модуль упругости I рода (модуль Юнга),
x, y — координаты рассматриваемой точки сечения,
A – площадь поперечного сечения.
Формула расчета напряжений в произвольной точке поперечного сечения балки
Условия прочности при косом изгибе
Расчет полного прогиба сечения
здесь x и y — горизонтальное и вертикальное перемещения сечения.
Условие прочности
Эквивалентный (приведенный) момент по III и IV гипотезам прочности
Формула Эйлера
Коэффициент приведения длины
где n — количество полуволн, образуемых изогнутой осью стержня.
Гибкость стержня
Радиус инерции стержня
Другие формулы >
Примеры решения задач >
Краткая теория >
isopromat.ru
Сопромат | ПроСопромат.ру
Потенциальную энергию можно определять через работу внешних сил (см. — здесь).
В общем случае: , где Р0 – любой силовой фактор (растягивающая сила, крутящий момент и тому подобное) называется обобщённой силой;
δ0 – соответствующая этой силе деформация (удлинение, угол закручивания, угол поворота и тому подобное) называется обобщённым перемещением.
Под обобщённой силой Р0 следует понимать не одну силу, а уравновешенную систему сил (включая сюда и реактивные усилия), которая производит деформацию.
Рассмотрим общий случай нагружения при изгибе.
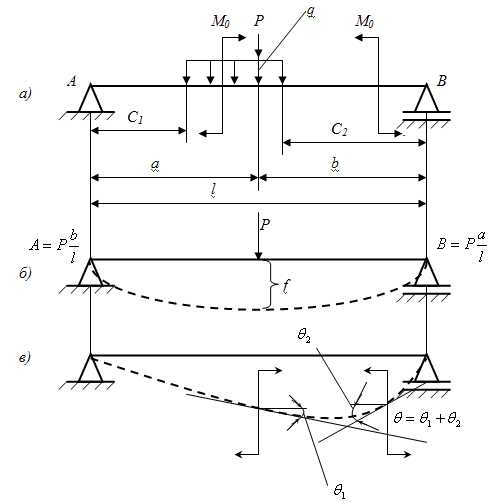
За отдельные обобщенные силы здесь можно принимать:
1) Сосредоточенную силу Р с реакциями и
2) Два момента М0 с соответствующими реакциями.
3) Равномерно распределённую нагрузку q с реакциями А и В.
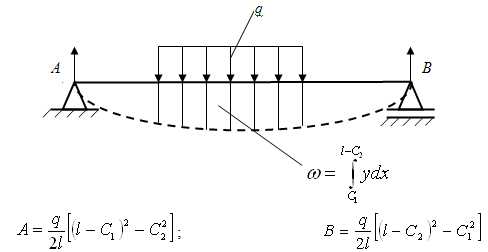
Обобщённым перемещением δ0 будем называть величину, характеризующую деформацию, на которую нужно умножить обобщённую силу, чтобы подсчитать произведённую ею работу.
Обобщённым перемещением будут:
1) Прогиб f под силой P,
.
2) Взаимный угол поворота сечений, где приложены моменты М0 :
θ=θ1+θ2, или углы поворота в отдельности θ1 и θ2.
3) Площадь, заключённая между первоначальной и изогнутой осью балки в районе расположения распределённой нагрузки:
Следует отметить, что если действующая на конструкцию нагрузка представлена несколькими обобщёнными силами (Р01, P02, P03,… и т. д.),то каждое из обобщённых перемещений (δ01, δ02, δ03 и т. д.) является, вообще говоря, функцией всех обобщённых сил:
,
и так далее.
Так, прогиб под силой Р (см. рисунок) является результатом действия не только силы Р , но и моментов М0 и распределённой нагрузки q.
Обобщённое перемещение будем считать положительным, если соответствующая обобщённая сила на этом перемещении совершает положительную работу.
Обобщённое перемещение, соответствующее определённой обобщённой силе, не изменится при изменении способа закрепления элемента конструкции.
Зависимости могут быть записаны так:
Здесь а11, а21 и т. д. – некоторые коэффициенты пропорциональности.
Первый индекс указывает порядковый номер перемещения, второй – порядковый номер обобщённой силы.
Потенциальная энергия деформации, создающаяся в упругой системе в результате действия нескольких обобщённых сил, равна половине суммы произведений обобщённых сил на соответствующие обобщённые перемещения, получающиеся от совместного действия всех обобщённых сил:
prosopromat.ru
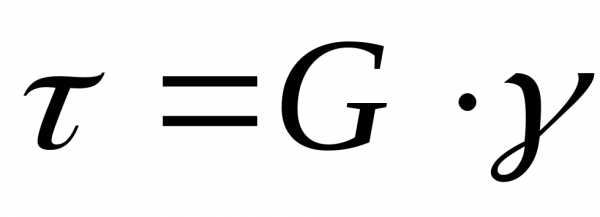
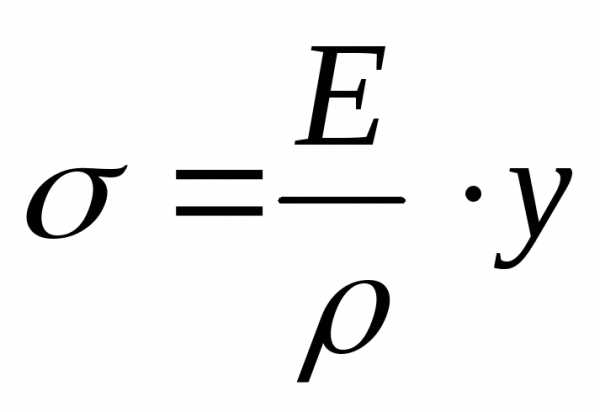
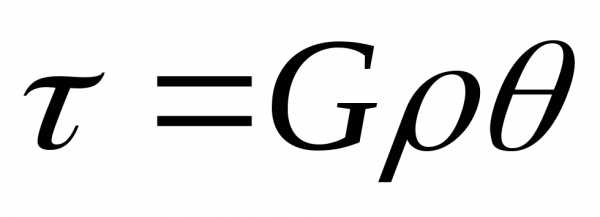
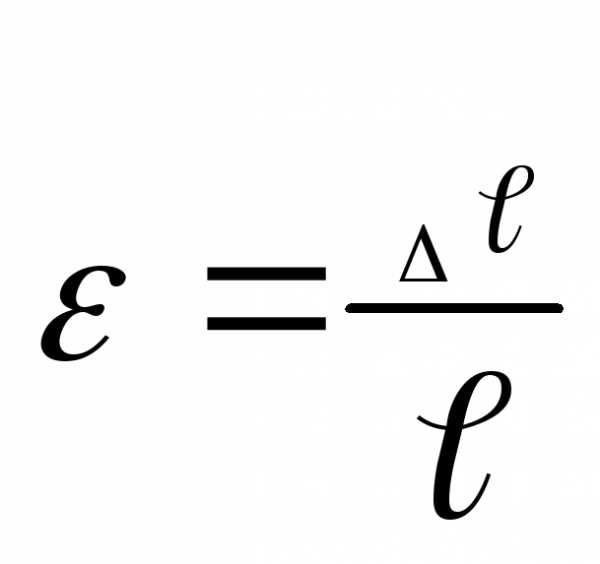
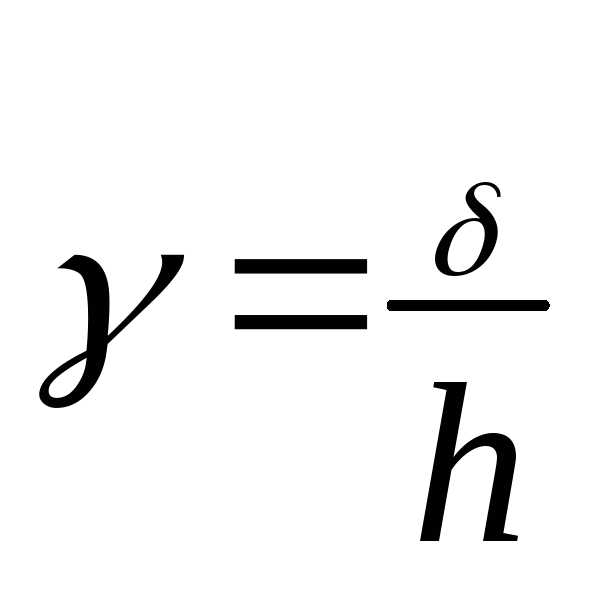
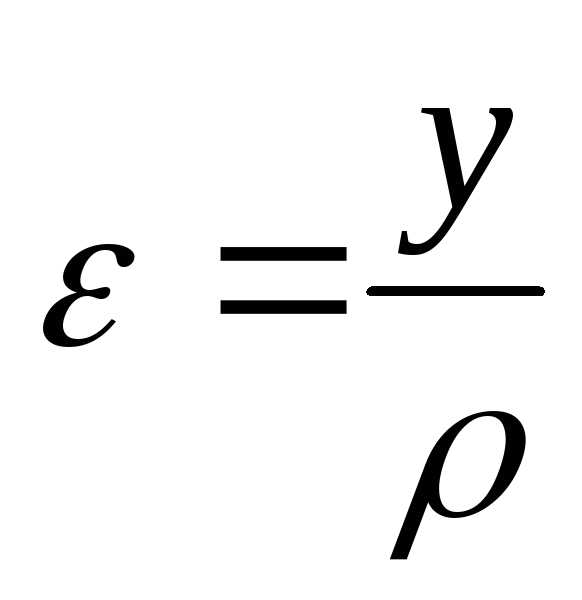
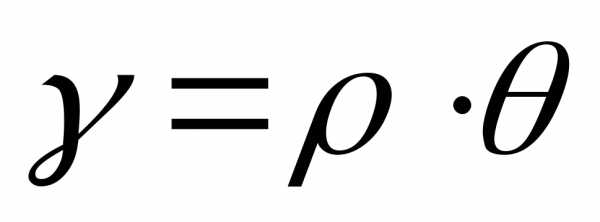

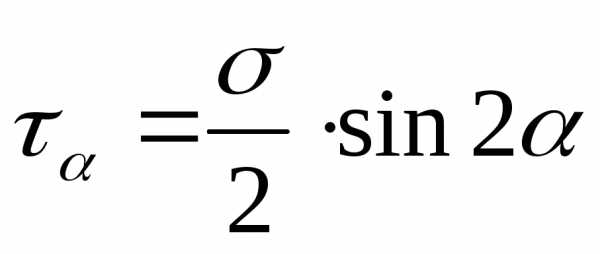
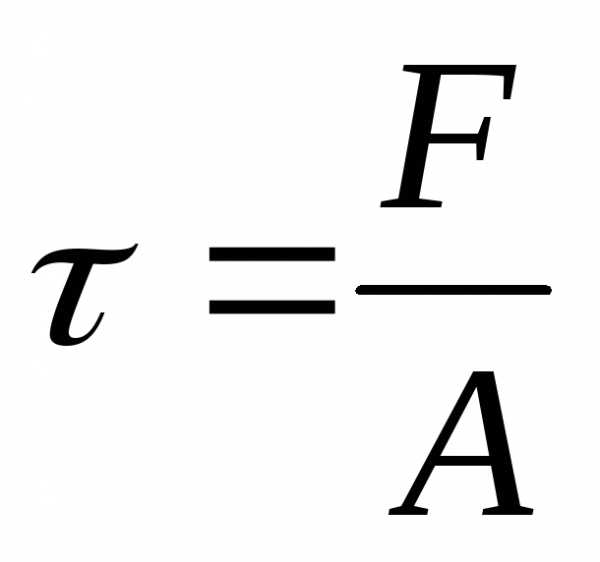
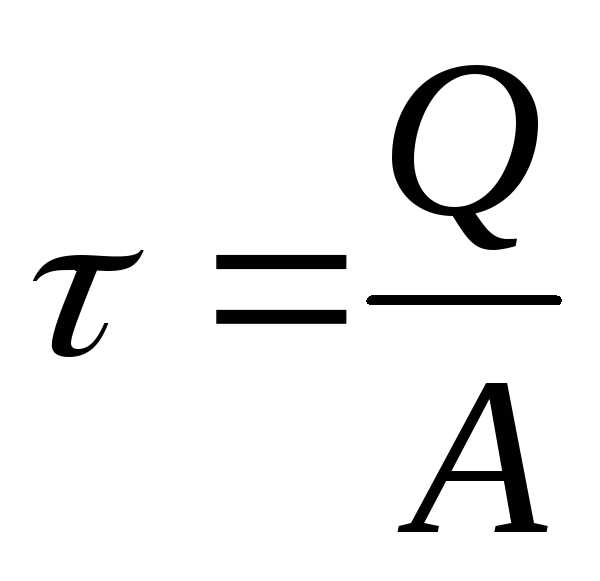
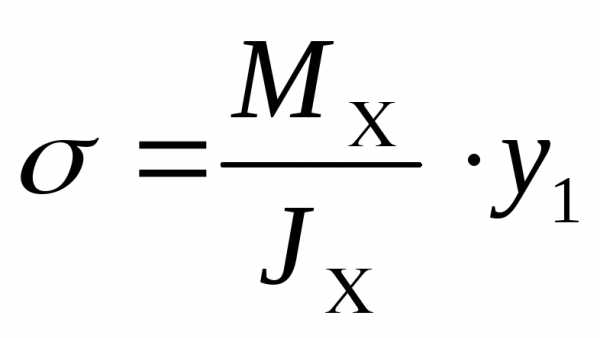
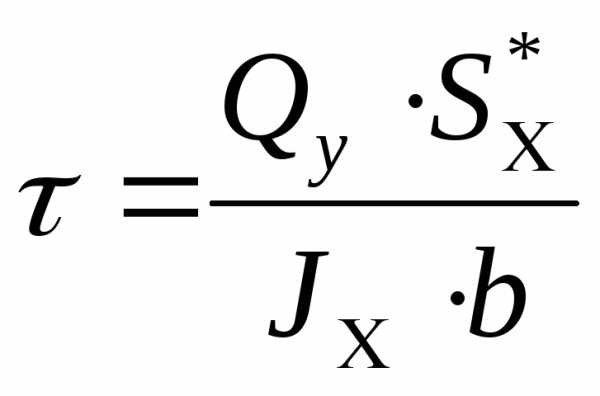
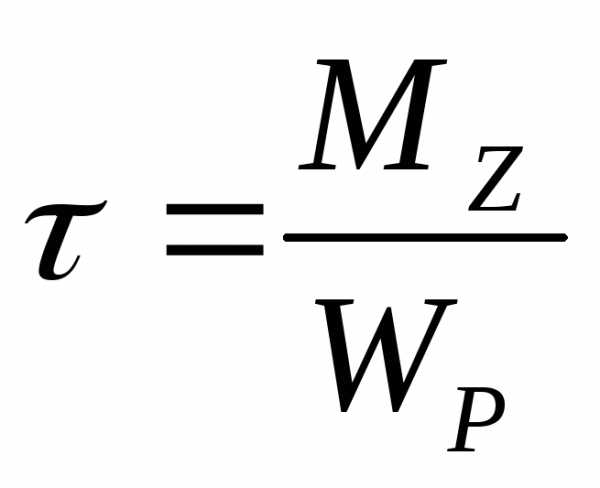
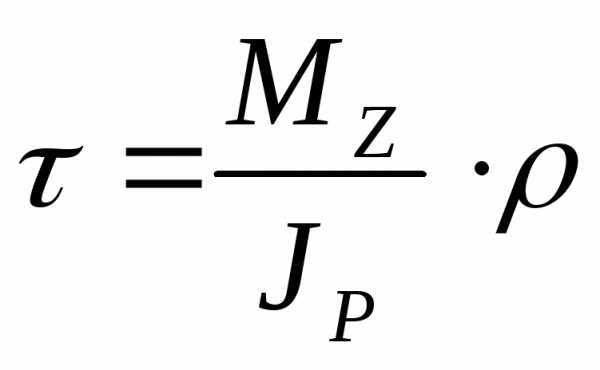
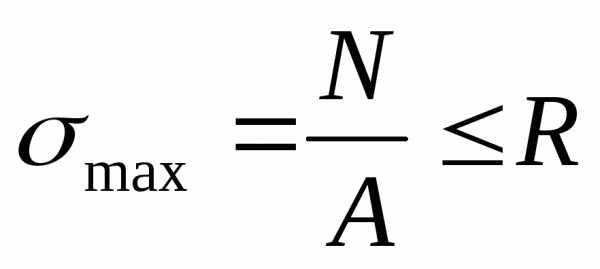
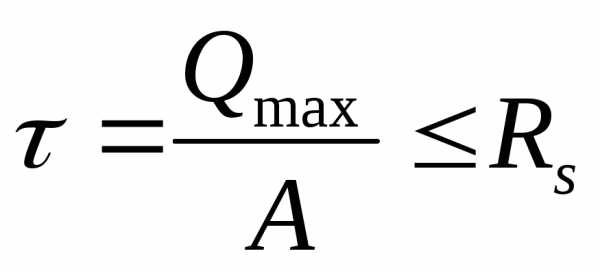
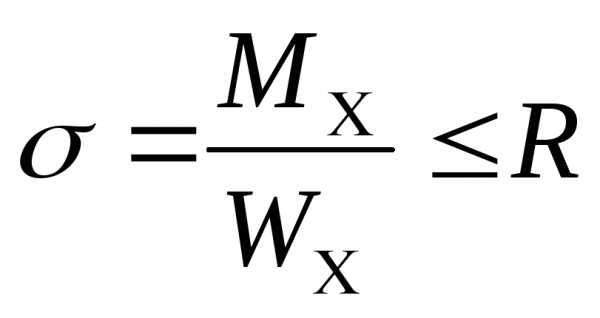
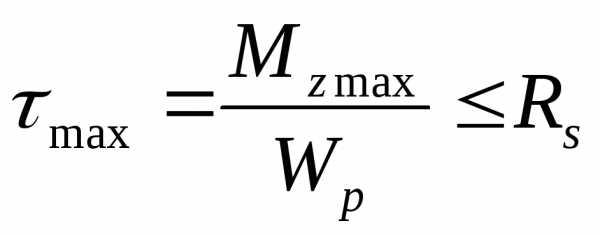
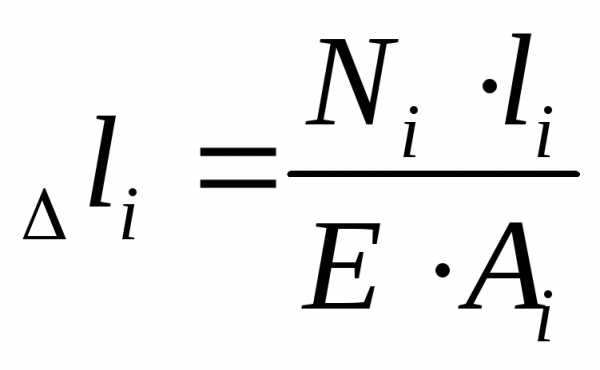

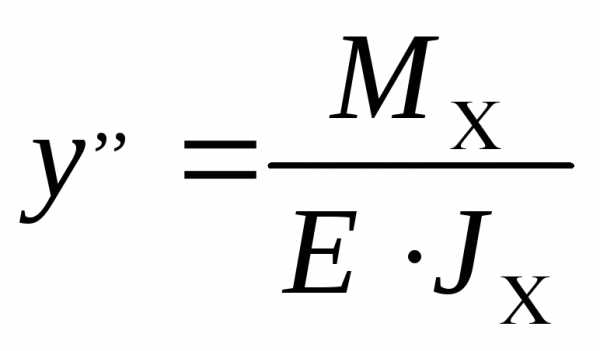

 —
коэфиц. запаса
—
коэфиц. запаса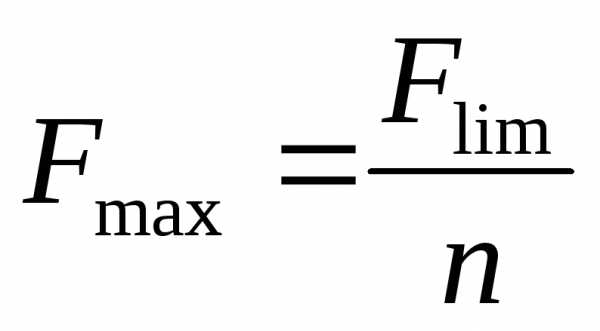 -допуск.
нагруз.
-допуск.
нагруз. —
допуск.
—
допуск.