Эпюра продольных сил (сопромат)
Если продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика N(z), называемого эпюрой продольных сил. Эпюра продольных сил необходима для оценки прочности стержня и строится для того, чтобы найти опасное сечение (поперечное сечение, в котором продольная сила принимает наибольшее значение ).
Как строить эпюру продольных сил?
Для построении эпюры N используется метод сечений. Продемонстрируем его применение на примере (рис. 2.1).
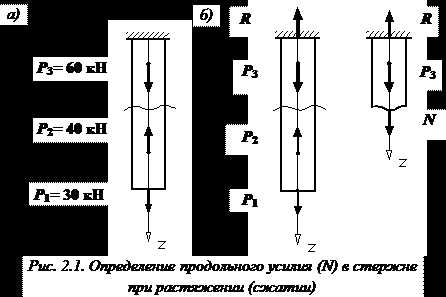Определим продольную силу N, возникающую в намеченном нами поперечном сечении стержня.
Разрежем стержень в этом месте и мысленно отбросим нижнюю его часть (рис. 2.1, а). Далее мы должны заменить действие отброшенной части на верхнюю часть стержня внутренней продольной силой N.
Для удобства вычисления ее значения закроем рассматриваемую нами верхнюю часть стержня листком бумаги. Напомним, что продольное усилие N, возникающее в поперечном сечении, можно определить как алгебраическую сумму всех продольных сил, действующих на отброшенную часть стержня, то есть на ту часть стержня, которую мы видим.
При этом применяем следующее правило знаков: силы, вызывающие растяжение оставленной части стержня (закрытой нами листком бумаги) входят в упомянутую алгебраическую сумму со знаком «плюс», а силы, вызывающие сжатие – со знаком «минус».
Итак, для определения продольной силы N в намеченном нами поперечном сечении необходимо просто сложить все внешние силы, которые мы видим. Так как сила кН растягивает верхнюю часть, а сила кН ее сжимает, то кН.
Знак «минус» означает, что в этом сечении стержень испытывает сжатие.
Можно найти опорную реакцию R (рис. 2.1, б) и составить уравнение равновесия для всего стержня, чтобы проверить результат:
или
кН.
Теперь заменим действие отброшенной нижней части неизвестным внутренним усилием N, направив его, например, от сечения, что соответствует растяжению.
Уравновешиваем оставленную нами верхнюю часть стержня:
кН.
Знак «минус» сигнализирует, что мы не угадали направление продольного усилия N. Оно будет не растягивающим, как мы предполагали, а сжимающим.
Таким образом, мы получили тот же самый результат.
sopromato.ruПостроение расчетной эпюры продольных сил
Эпюра строится по расчетной эпюре поперечных сил методом вырезания узлов. Взамен отброшенных стержней к узлу прикладывают известные поперечные силы из эпюры и неизвестные нормальные силы. При этом N изначально считают растягивающими, т.е. направленными от узла. Направление Q считается положительным, если поперечная сила вращает узел по часовой стрелке и отрицательным – при вращении против часовой стрелке. Затем составляются уравнения равновесия Σx =0 и Σy = 0 , из которых определяются продольные усилия. Если окажется, что сила N направлена к узлу, то такая сила сжимает стержень и считается отрицательной.
Статическая проверка расчетных эпюр
Для проверки правильности построенных эпюр Мрас, , составляются условия статического равновесия всей рамы. В заданной раме отбрасываются все опорные стержни, а вместо них прикладываются внутренние усилия, взятые с расчетных эпюр (моменты с М
(16)
Построение расчетных эпюр другим способом
Эпюры Мрас, , могут быть построены по иному. Для этого к основной системе прикладываются найденные в п. 10 неизвестные усилия и заданная нагрузка. В полученной статически определимой раме
определяются опорные реакции, затем внутренние усилия методом сечений и строятся расчетные эпюры изгибающих моментов, поперечных и продольных сил. Этот способ удобно применять для контроля правильности построения эпюр, если не выполняются деформационная и статическая проверки.
ПРИМЕР РАСЧЕТА РАМЫ
Для статически неопределимой рамы, показанной на рис. 9, требуется построить эпюры внутренних усилий от заданной нагрузки.
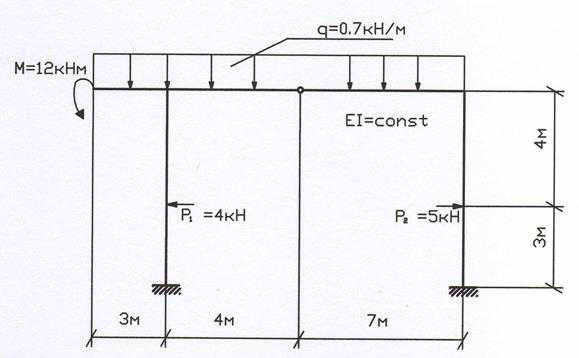
Рис. 9
1. Определяем степень статистической неопределимости рамы по формуле (8):
n = – 3 – Ш =6 – 3– 1=2,
Данная рама дважды неопределима.
2. Выбираем основную систему (рис. 10).
Вариант 1 Вариант 2 Рис. 10
К расчету выберем вариант 1 основной системы, т.к. он не требует определения опорных реакций (рис. 11)..
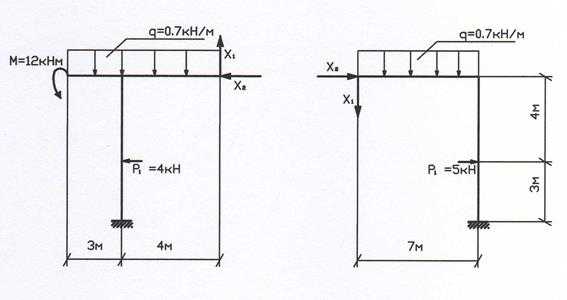
3. Для определения неизвестных составляем каноническое уравнение метода сил
4. Строим единичные эпюры последовательного приложения сил и (рис. 12).
Рис. 12
5. Определяем главные и побочные коэффициенты канонических уравнений по интегралу Мора (2), с помощью способа Верещагина:
;
;
.
6. Делаем проверку правильности вычисления коэффициентов. Для этого построим суммарную единичную эпюру моментов (рис. 13) и вычислим по формуле (4) с помощью способа Верещагина и трапеций:
Рис. 13
;
.
Проверка выполнилась.
7. Строим грузовую эпюру изгибающих моментов в основной системе от действия только внешней нагрузки (рис. 14), отдельно прикладывая q и P, M.
Рис. 14
8. Определяем грузовые коэффициенты канонических уравнений по формуле (3) способом Верещагина, используя формулы Симпсона и трапеций:
9. Проверяем правильность вычисления грузовых коэффициентов по формуле (5):
.
Проверка выполнилась.
10. Составляем и решаем систему канонических уравнений.
=>
Проверка:
Погрешность допустима за счет сокращений.
11. Для построения окончательной эпюры моментов строим исправленные эпюры и (рис. 15).
Рис. 15
Расчетную эпюру моментов (рис. 16) строим по формуле
.
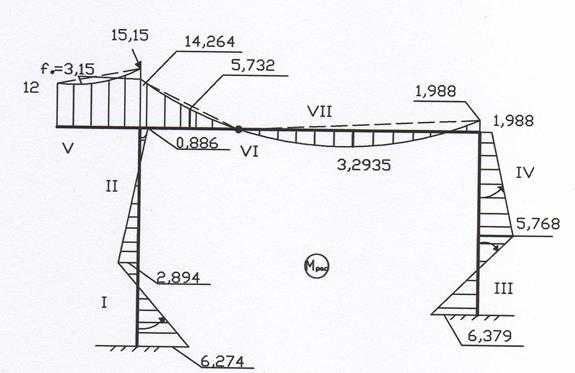
Рис. 16
Делаем узловую проверку построенной эпюры
.
Проверка выполнилась, узлы находятся в равновесии.
12. Делаем деформационную проверку , для чего строим суммарную единичную эпюру моментов (рис. 17) в другом варианте основной системы.
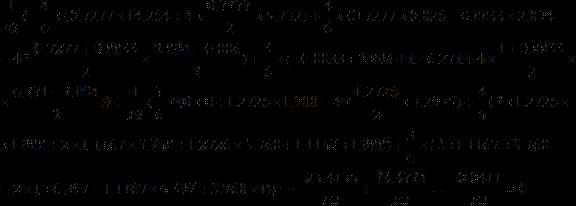
Погрешность 0.18%. Проверка выполнилась. Расчетная эпюра моментов построена верно.
13. По эпюре строим расчетную эпюру поперечных сил по участкам.
I участок:
.
II участок:
.
III участок:
.
IV участок:
На остальных участках действует распределенная нагрузка, поэтому поперечную силу вычисляем в соответствии с рис. 18.
Рис. 18
Строим эпюру (рис. 19) по полученным данным и правилам знаков для внутренних усилий в балках.
Рис. 19
14. Строим расчетную эпюру продольных усилий (рис. 20) по эпюре методом вырезания узлов.
: , : ,
: . : .
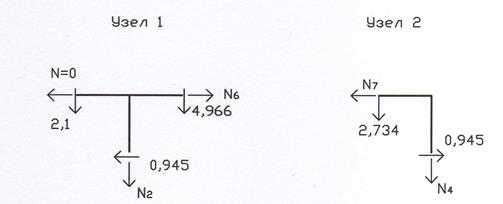
Рис. 20
15. Делаем статическую проверку правильности построения расчетных эпюр. Покажем заданную нагрузку и освободим раму от связей, заметив их реактивными усилиями, взятыми с эпюр , , (рис. 21).
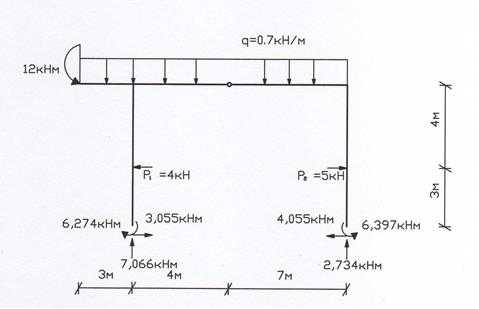
Рис. 21
: -4+5+3.055-4.055=0, 0=0;
: -0.7*14+7.066+2.734=0, 0=0;
: 0.7*14*7+12+4*3-5*3-6.274+6.397-7.066*11=0, 0=0.
Проверка выполнилась. Эпюры построены верно.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. В чем состоит суть метода сил?
2. Как определить степень статической неопределимости системы?
3. Что представляет собой система канонических уравнений метода сил?
4. Как выбирается основная система метода сил, какие требования к ней предъявляются?
5. Какой физический смысл заключается в главных и побочных коэффициентах СКУ?
6. Как вычисляются грузовые коэффициенты СКУ?
7. Система проверок правильности вычислений коэффициентов СКУ?
8. Как можно определить усилия в заданной системе после определения лишних неизвестных?
9. Как проверить правильность расчета статически неопределимой системы методом сил?
ЛИТЕРАТУРА
1. Киселев В.А. Строительная механика / В.А. Киселев – М.: Стройиздат, 1986. – 520 с.
2. Дарков А.В. Строительная механика / А.В. Дарков,
Н.Н. Шапошников. – М.:Высшая школа, 1986. –607 с.
3. Снитко Н.К. Строительная механика / Н.К. Снитко. – М.: Стройиздат, 1980. – 431 с.
4. Строительная механика / Ю.И. Бутенко, Н.А. Засядько, С.Н. Кан и др. – К.: Выща школа, 1989. – 479 с.
5. Селюков В.Н. Расчетно-проектировочные работы по строительной механике / В.Н. Селюков. – Минск: Вышэйшая школа, 1989. – 205 с.
Приложение
ДАННЫЕ ДЛЯ ВЫПОЛНЕНИЯ РАБОТЫ
| № строки | М | м | м | м | кН | кН | кН/м | кНм |
| 0,3 0,5 0,7 0,9 1,1 0,9 0,7 0,5 0,3 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,3 1,1 0,5 0,9 0,7 0,3 0,3 1,1 |
ПРИМЕНЕНИЕ МЕТОДА СИЛ К РАСЧЕТУ
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ РАМ
Методические указания
к выполнению расчетно-графической работы
Составили: ПЕТРУНИНА Елена Анатольевна
КРИВОШЕИН Игорь Васильевич
Рецензент П.К. Семенов
Редактор Н.Н. Крылова
Подписано в печать Формат 60×84 1/16
Бум.офсет. Усл.печ.л Уч.-изд.л.
Тираж 100 экз. Заказ Бесплатно
Саратовский государственный технический университет
410054, Саратов, Политехническая ул., 77
Отпечатано в РИЦ СГТУ, 410054, Саратов, Политехническая ул., 77
infopedia.su
Построение эпюр при растяжении-сжатии | Лекции и примеры решения задач механики
Задача
Для ступенчатого бруса, нагруженного силами F1 и F2, приложенными к середине участков длиной l1 и l2, требуется построить эпюры продольной силы, напряжений, перемещений и дать оценку прочности.
Исходные данные:
F1=200кН; F2=150кН;
A1=15см2; A2=10см2;
l1=80см; l2=40см;
Модуль Юнга: E=2×105МПа;
[σ]=160МПа.
Решение задачи
Расчет опорной реакции
При заданных нагрузках в опорном сечении возникает только осевая составляющая реакции – R.
Из уравнения равновесия:
откуда
Знак “-“ указывает на обратное по сравнению с принятым направление опорной реакции R.
Для решения поставленной задачи R можно было не определять, так как продольную силу в любом сечении можно вычислить, рассматривая только правую отсеченную часть бруса.
Построение эпюры продольных сил N
На рассматриваемом стержне три силовых участка – BC, CK и KM.
Для определения величины N по участкам воспользуемся методом сечений.
Вычисляем значения продольной силы на участках:
— участок BC
Или
— участок CK
или
— участок KM
или
По полученным данным строим эпюру N
Штриховка эпюр обычно производится перпендикулярно к базовой линии, ордината эпюры указывает значение продольной силы в соответствующем сечении бруса.
В поле эпюры, в кружочке проставляется её знак, а рядом с эпюрой — её обозначение и, в квадратных скобках, размерность.
Как видно из построенной эпюры N, в местах приложения сосредоточенных сил F1 и F2 (сечения C и K) имеют место скачки по модулю на величину этих сил.
Построение эпюры напряжений σ
Напряжения в поперечных сечениях вычисляются по формуле σ=N/A.
Характер изменения нормальных напряжений по длине бруса будет таким же, как для продольной силы. Только в месте резкого изменения формы бруса (сечение D) на эпюре σ, в отличие от эпюры N, возникает скачок значений из-за изменения площади сечения A.
Вычислим напряжения на участках: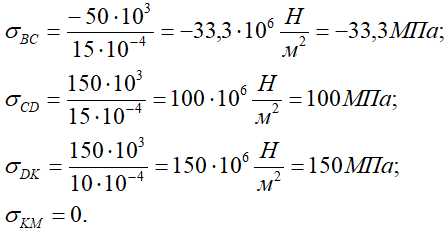
По рассчитанным значениям строим эпюру σ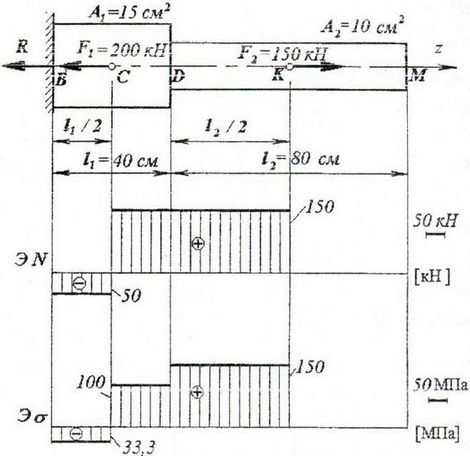
Построение эпюры перемещений δ
Перемещения характерных сечений определяются по зависимости
где
δ0 — перемещение начала участка;
Δ li — абсолютная деформация рассматриваемого участка.
Определяем абсолютные деформации отдельных участков стержня по формуле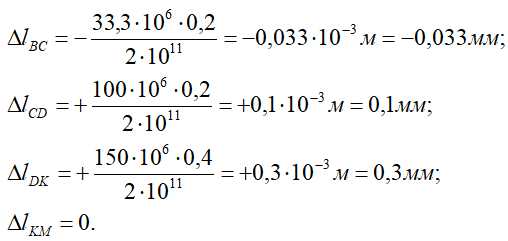
Вычисляем перемещения характерных сечений
По результатам этих расчетов строим эпюру продольных перемещений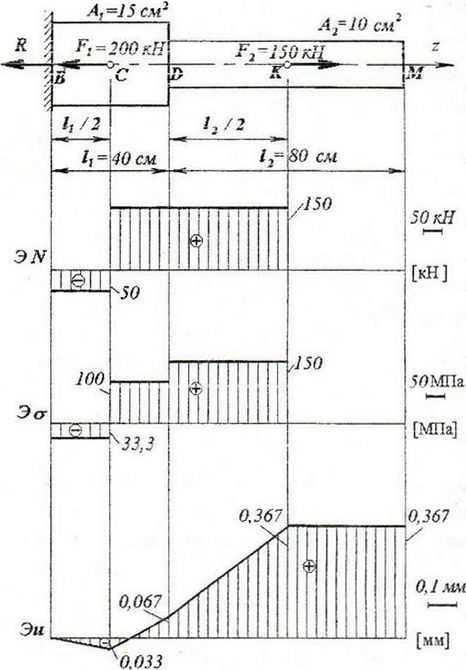
При этом необходимо учесть, что на участках без распределенной нагрузки эпюра δ меняется по линейному закону.
Проверка прочности стержня
Для оценки прочности бруса сравниваем максимальное по абсолютной величине значение напряжений с допускаемым
Условие прочности выполняется, недогрузка составляет
Другие примеры решения задач >
Краткая теория по сопромату >
isopromat.ru
Построение эпюры внутренних продольных сил при растяжении-сжатии
Задача
Для прямого стержня нагруженного системой внешних сил требуется построить эпюру внутренних продольных сил N.
Решение
В предыдущем пункте решения задачи была определена опорная реакция R в заделке стержня.
Для расчета величины внутренних сил обозначим характерные сечения стержня (B, C, D, K и M).
Заданный стержень имеет 3 силовых участка: BC, CK и KM. Обозначим эти участки римскими цифрами, например, справа налево.
Сечение D, где меняется поперечный размер стержня, границей силового участка не является.
На каждом из этих участков определим величину и знак внутренней продольной силы.
Для этого воспользуемся методом сечений.
Начнем с I силового участка (KM):
Проведем мысленно сечение в пределах рассматриваемого участка.
Это сечение делит стержень на две части: левую и правую.
Для упрощения расчетов рекомендуется выбирать ту часть стержня, к которой приложено меньше сил. Очевидно, это будет правая часть стержня (т.к. слева от сечения 4 силы, а справа всего одна).
Внутренняя сила в данном сечении будет равна сумме внешних сил рассматриваемой правой части стержня. С учетом правила знаков при растяжении-сжатии эта сумма будет иметь следующий вид:
Здесь сила F3 записана отрицательной, так как сжимает рассматриваемую часть стержня (направлена в сторону проведенного сечения).
Переходим на второй силовой участок (CK).
Рассекаем стержень в произвольном месте участка и рассматриваем, например левую его часть.
Здесь силы R и F1 положительны, т.к. стремятся растянуть II участок стержня (направлены от сечения).
Аналогично для третьего силового участка (BC)
По полученным данным строим эпюру продольных сил N.
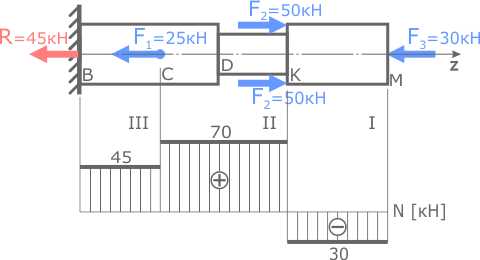
Правильность построения эпюры можно проверить по «скачкам».
Расчет размеров стержня постоянного сечения >
Подбор размеров стержня заданной формы >
Другие примеры решения задач >
isopromat.ru
Продольная сила, построение эпюр продольных сил.
Осевым растяжением (сжатием) прямого стержня называют такой вид его деформации, при котором в произвольном поперечном сечении возникает только одна составляющая внутренних усилий – продольная сила растяжения или сжатия.
Это возможно при условии, что внешняя нагрузка приводится к равнодействующим силам, действующим вдоль оси бруса.
Продольная сила растяжения принимается положительной величиной, а продольная сила сжатия – отрицательной.
Продольные силы определяются по методу сечений. Для этого необходимо разделить стержень на участки, которые ограничены точками оси бруса, где действуют внешние сосредоточенные силы. В пределах каждого участка нужно выбрать произвольное сечение на переменном расстоянии xот начала координат (от какого-нибудь торца стержня) и рассмотреть равновесие одной из частей стержня. При этом часть стержня, равновесие которой рассматривается, нагружается внешними силами и неизвестным продольным усилием N, которое направляется от сечения, то есть в соответствии с растяжением стержня. Используя условие равновесия ΣXi=0, составляем уравнение равновесия, из которого определяем продольную силу N на каждом участке.
Изменение продольной силы по длине стержня можно отобразить графиком, который имеет название эпюраэтого усилия.
Рассмотрим прямой стержень, расположенный горизонтально, жестко закрепленный на правом торце и нагруженный вдоль своей оси внешними силами F1, F2=2F1и F3=3F1 (рис.9.1,а). Эти силы приложены соответственно в точках а, b, c. Закрепленную точку оси стержня обозначим буквой d.
Для определения продольных сил разделим стержень на три участка ab, bc и cd. В пределах каждого участка проведем произвольные поперечные сечения 1-1, 2-2 и 3-3, взятые на расстояниях x1, x2и x3от левого свободного конца стержня.
Отбросим, мысленно, правую часть от сечения 1-1, а ее действие на левую часть заменим неизвестной продольной силой N1, которая направлена от сечения (рис.9.1,б) и составим уравнение равновесия:
ΣXi =0, N1 – F1 =0,откуда находим N1 = F1. Таким образом, продольная сила на участке ab не зависит от x1и имеет постоянное значение
N1= F1
Рис.9.1
Отбросим, мысленно, правую от сечения 2-2 часть бруса и заменим её действие на оставшуюся часть бруса неизвестной продольной силой N2, которая также направлена от сечения (рис.9.1,в). Составим уравнение равновесия:
ΣXi =0, N2 – F1 + 2F1 =0,откуда находим N1 = — F1. Таким образом, продольная сила на участке bc не зависит от x2и имеет отрицательное постоянное значение, то есть на этом участке стержень сжатучастку ильни переризиантажений вдоль оси середжени силы. В пределах каждого участка выбрать произвольный.
Аналогично определяем продольную силу N3на участке cd. Рассматриваем равновесие левой части стержня относительно сечения 3-3 (рис.9.1,г) и составляем уравнение равновесия:
ΣXi =0, N3 – F1 + 2F1 – 3F1 =0,откуда находим N3 = 2F1. На этом участке стержень растягивается силой N3 = 2F1, котораяне зависит от x3.
Построим А1= 20,2 см2; см4; см4;
эпюру N. Для этого:
— проведем нулевую прямую параллельно оси стержня;
— отложим вверх от нее положительные значения продольной силы, а вниз от нее отрицательные значения, приняв произвольный масштаб;
— соединим прямыми линиями вершины соседних ординат. Эти линии ограничивают эпюру продольных сил на отдельных участках.
На рис.9.1,д начерчена эпюра N. Для возможности ее использования, то есть для определения продольной силы в любом сечении, нужно заштриховать эпюру равномерно расположенными прямыми линиями перпендикулярно оси стержня.
Анализируя эту эпюру легко заметить, что она имеет скачки в точках, где действуют внешние силы. При этом величины скачков равняются действующим силам. На участках между внешними силами продольная сила остается постоянной, т.е. эпюра ограничена прямыми линиями параллельными оси бруса.
Похожие статьи:
poznayka.org
16…..Построение эпюр продольных сил Nz
Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня. Правило знаков для Nz: условимся считать продольную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части стержня, вызывает растяжение и отрицательной — в противном случае.
Пример 1. Построить эпюру продольных сил для жестко защемленной балки (рис.2). Порядок расчета:
1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке. 2. Определяем продольную силу Nz в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.
По найденным значениям строим эпюру Nz. Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные — под осью.
рис. 2
3. Построение эпюр крутящих моментов Мкр.
Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z. Правило знаков для Мкр: условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным — в противном случае.
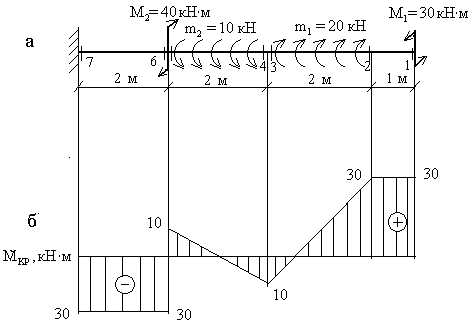
Пример 2. Построить эпюру крутящих моментов для жестко защемленного стержня (рис.3,а). Порядок расчета. Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил. 1.Намечаем характерные сечения. 2.Определяем крутящий момент в каждом характерном сечении.
По найденным значениям строим эпюру Мкр (рис.3,б).
17….. Метод расчета, при котором расчет рам на один вид нагрузки производится методом сил, а на другой — методом перемещений, называется комбинированным. Этот метод применяется главным образом для расчета симметричных многоэтажных статически неопределимых рам, хотя в отдельных случаях он может быть применим и для несимметричных рам.
При расчете рам комбинированным методом приложенная к раме произвольная нагрузка разлагается на симметричную и обратно симметричную. Расчет на эти виды нагрузки производится раздельно: на симметричную нагрузку — методом перемещений, а на обратно симметричную — методом сил.
Трудоемкость расчета данной рамы методом сил или методом перемещений приблизительно одинаковая, так как степени статической и кинематической неопределимости рамы равны и в обоих случаях для решения требуется составить и решить систему из девяти канонических уравнений с девятью неизвестными.
Расчета симметричных рам
Вырезав узел С в различных состояниях системы из уравнений равновесия 2Z = О, 2ЛХ = 0 и ЕМу = 0 определим коэффициенты и Rip; далее при составлении системы канонических уравнений следует учесть, что согласно выражению. Особенности расчета крыши деревянных домов, симметричных рам. Основная система любой симметричной системы должна быть симметричной. При этом так же, как и в методе сил, нагрузку следует разложить на симметричную и кососимметричную составляющие, а неизвестные — сгруппировать. Особенно удобен метод перемещений при расчете симметричных систем на действие симметричной нагрузки. В этом случае в силу симметрии будут заведомо равны нулю основные неизвестные, определяющие линейные перемещения частей рамы (ригелей), расположенных поперек оси симметрии, а также углы поворота узлов рамы, лежащих на ее оси симметрии. Естественно, будут также равны нулю все кососимметричные неизвестные. Изображенная на рис. 1.48, а рама 7 раз кинематически неопределима. Здесь пу = 5 и пп = 2 (см. рис. 1.48, б). Однако в силу сказанного выше Z3 = Z4 = Z5 = Z6 =**Z7 = 0 (рис. 1.48, в) и, таким образом, при расчете рамы надо решать только два уравнения с двумя неизвестными. На рис. 1.48, г — е построены единичные и грузовая эпюры моментов. Следует отметить особенность характера эпюры моментов на верхнем ригеле в первом единичном состоянии — она имеет прямоугольное очертание, так как построена от одновременного воздействия парных углов поворота
18… Метод перемещений является вторым основным методом расчета статически неопределимых систем. Использование его для расчета сложных статически неопределимых рам во многих случаях значительно снижает трудоемкость расчета по сравнению с методом сил.
Рассмотрим основные положения метода перемещений. По существу этот метод является обратным относительно метода сил.
В методе сил за основные неизвестные величины принимают внешние или внутренние силы, приложенные вместо отброшенных лишних связей, тогда как взаимные перемещения сечений, где приложены эти силы, известны. Для определения неизвестных составляются уравнения перемещений. В методе перемещений основными неизвестными являются перемещения (линейные и угловые) узлов статически неопределимой системы, для определения которых составляют уравнения- равновесия. Определив эти перемещения, находят внутренние силовые факторы в произвольных сечениях заданной системы.
Общее число неизвестных при расчете статически неопределимых систем определяется не статической, а кинематической неопределимостью. При этом род степенью кинематической неопределимости понимается число угловых и линейных перемещений системы, знание которых дает возможность определить характер деформации системы, а следовательно, и усилия в ее элементах. Деформированный вид системы будет полностью определен, если будут известны угловые и линейные перемещения узлов системы. Степень кинематической неопределимости системы будет равна числу углов поворота жестких узлов плюс число неизвестных линейных перемещений узлов. Для многих статически неопределимых систем степень кинематической неопределимости ниже их степени статической неопределимости.
В основу метода перемещений положен ряд допущений: не учитывается влияние поперечных и продольных сил на перемещения точек системы; не учитывается сближение узлов системы при деформации ее элементов; концы стержней, сходящихся в одном жестком узле, поворачиваются при деформации на один и тот же угол; углы поворота вследствие их небольшой величины принимаются равными тангенсам этих углов.
При определении степени кинематической неопределимости число неизвестных углов поворота узлов всегда равно числу жестких узлов системы, исключая опорные.
19… «Расчет статически неопределимых рам методом перемещений» 1.Определяем число неизвестных метода перемещений. n=1+1=2 V=2*6-5-6=2.Выбираем основную систему метода перемещений. 3.Записываем канонические уравнения метода перемещений. 4.Строим эпюры изгибающих моментов в основной системе от и от нагрузки. 5.Определяем реакции во вновь введённых связях. 6.Подставляем найденные значения реакций в уравнения.
7.Определяем концевые моменты и поперечные силы в стержнях заданной системы. 8.Строим эпюры изгибающих моментов и поперечных сил в заданной системе от нагрузки. 9.Определяем продольные силы в стержнях рамы, используя способ вырезания узлов. 10.Строим эпюру продольных сил в заданной системе от нагрузки. 11.Выполняем статическую проверку.
Расчет статически неопределимых рам методом перемещений
studfiles.net
Построение эпюр»эпюра моментов»эпюры сил»эпюры изгибающих моментов
Заказать решение Способ оплаты
1. Виды опорных закреплений
С технической точки зрения опорные закрепления конструкций весьма разнообразны. При решении задач сопромата, все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых
наиболее часто встречаются: шарнирно-подвижнаяопора (возможные обозначения для нее представлены на рис.1,а), шарнирно-неподвижная опора (рис.1,б) и жесткое защемление, или заделка (рис.1,в).
Рис. 1
В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения.
В шарнирно-неподвижной опоре возникают вертикальная и горизонтальная реакции. Здесь невозможны перемещения по направлениям опорных стержней, но допускается поворот опорного сечения.
В жесткой заделке возникают вертикальная и горизонтальная реакции и опорный (реактивный) момент. При этом опорное сечение не может смещаться и поворачиваться.При расчете систем, содержащих жесткую заделку, возникающие опорные реакции можно не определять, выбирая при этом отсеченную часть так, чтобы заделка с неизвестными реакциями в нее не попадала. При расчете систем на шарнирных опорах реакции опор должны быть определены обязательно. Уравнения статики, используемые для этого, зависят от вида системы (балка, рама и др.) и будут приведены в соответствующих разделах настоящего пособия.
Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.
Правило знаков для Nz: условимся считать продольную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части стержня, вызывает растяжение и отрицательной — в противном случае.
Пример 1.Построить эпюру продольных сил для жестко защемленной балки (рис.2).
Порядок расчета:
1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
2. Определяем продольную силу Nz в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.
По найденным значениям строим эпюру Nz. Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные — под осью.
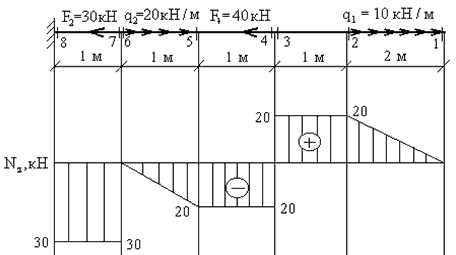
рис. 2
3. Построение эпюр крутящих моментов Мкр.
Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.
Правило знаков для Мкр: условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным — в противном случае.
Пример 2.Построить эпюру крутящих моментов для жестко защемленного стержня (рис.3,а).
Порядок расчета.
Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.
1.Намечаем характерные сечения.
2.Определяем крутящий момент в каждом характерном сечении.
По найденным значениям строимэпюру Мкр (рис.3,б).
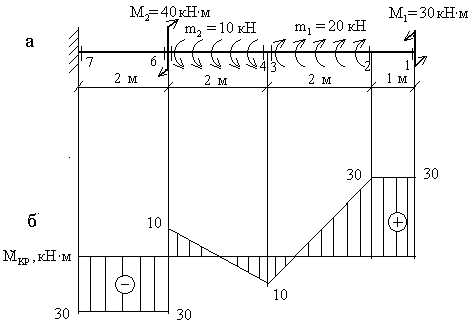
рис. 3
4. Правила контроля эпюр Nz и Мкр.
Для эпюр продольных сил и крутящих моментов характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.
1. Эпюры Nz и Мкр всегда прямолинейные.
2. На участке, где нет распределенной нагрузки, эпюра Nz(Мкр) — прямая, параллельная оси, а на участке под распределенной нагрузкой — наклонная прямая.
3. Под точкой приложения сосредоточенной силы на эпюре Nz обязательно должен быть скачок на величину этой силы, аналогично под точкой приложения сосредоточенного момента на эпюре Мкр будет скачок на величину этого момента.
5. Построение эпюр поперечных сил Qy и изгибающих моментов Mx в балках
Стержень, работающий на изгиб, называется балкой. В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора — поперечная сила Qy и изгибающий момент Mx .
Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.
Правило знаков для Qy: условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной — в противном случае.
Схематически это правило знаков можно представить в виде
Изгибающий момент Mx в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение.
Правило знаков для Mx: условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной — в противном случае.
Схематически это правило знаков можно представить в виде:
Следует отметить, что при использовании правила знаков для Mx в указанном виде, эпюра Mx всегда оказывается построенной со стороны сжатых волокон балки.
6. Консольные балки
При построении эпюр Qy и Mx в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.
Пример 3.Построить эпюры Qy и Mx (рис.4).
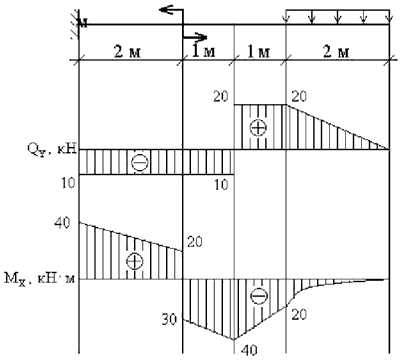
рис. 4
Порядок расчета.
1. Намечаем характерные сечения.
2. Определяем поперечную силу Qy в каждом характерном сечении.
По вычисленным значениям строим эпюру Qy.
3. Определяем изгибающий момент Mx в каждом характерном сечении.
По вычисленным значениям строим эпюру Mx, причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.
7. Балки на двух опорах
В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.
Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики:
Пример 4. Построить эпюры Qy, Mx для балки с шарнирным опиранием (рис.5).
Порядок расчета.
1. Вычисляем реакции опор.
Проверка:
</p>
2. Намечаем характерные сечения.
В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть.
3. Определяем поперечные силы в характерных сечениях.
Строим эпюру Qy.
4. Определяем изгибающие моменты в характерных сечениях.
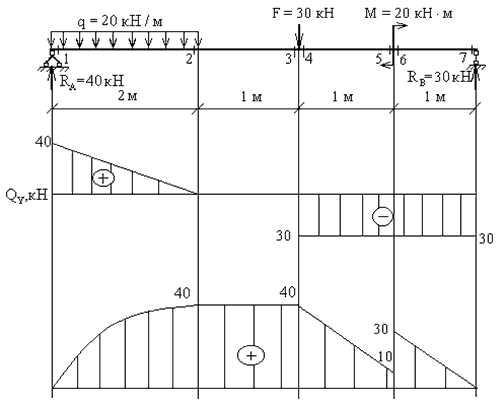
рис. 5
Строим эпюру Mx.
8. Правила контроля эпюр Qу и Mx
Дифференциальные зависимости между q, Qy, Mx определяют ряд закономерностей, которым подчиняются эпюры Qy и Mx.
Эпюра Qy является прямолинейной на всех участках; эпюра Mx — криволинейная (квадратная парабола) на участке под равномерно распределенной нагрузкой, причем, выпуклость кривой всегда обращена навстречу нагрузке q, и прямолинейная на всех остальных участках.
Под точкой приложения сосредоточенной силы (реакции) на эпюре Qy обязательно должен быть скачок на величину этой силы (реакции). Аналогично, под точкой приложения сосредоточенного момента на эпюре Mx обязателен скачок на величину момента.
Если на участке под распределенной нагрузкой эпюра Qy пересекает ось (Qy=0), то эпюра Mx в этом сечении имеет экстремум.
На участках с поперечной силой одного знака эпюра Mx имеет одинаковую монотонность. Так, при Qy>0 эпюра Mx возрастает слева направо; при Qy<0 — убывает.
Порядок линии на эпюре Qy всегда на единицу меньше, чем на эпюре Mx. Например, если эпюра Mx — квадратная парабола, то эпюра Qy на этом участке — наклонная прямая; если эпюра Mx — наклонная прямая, то эпюра Qy на этом участке — прямая, параллельная оси; если Mx=const (прямая, параллельная оси), то на этом участке Qy=0.
Заказать решение Способ оплаты
funnystudy.ru