Правила знаков в сопромате

В сопротивлении материалов, а также в технической и прикладной механике при решении задач принимаются следующие правила знаков:

При растяжении-сжатии

Внутренняя продольная сила N, которая стремится растянуть рассматриваемую часть бруса, считается положительной. Сжимающая продольная сила имеет отрицательный знак.

Положительное направление внутренней продольной силы N

Подборка видео по всем правилам знаков:

При кручении

Внутренний скручивающий момент T считается положительным, если он стремится повернуть рассматриваемую часть бруса против хода часовой стрелки, при взгляде на него со стороны внешней нормали.

Положительное направление внутреннего скручивающего момента T

При изгибе

Внутренняя поперечная сила Q считается положительной, в случае, когда она стремится повернуть рассматриваемую часть бруса по ходу часовой стрелки.

Положительное направление внутренней поперечной силы Q

Внутренний изгибающий момент M положителен, когда он стремится сжать верхние волокна бруса.

Положительное направление внутреннего изгибающего момента M

Примечание: Величина и знак внутренних сил и моментов зависит от вызывающих их внешних усилий, поэтому указанные правила знаков в том же виде справедливы и для внешних нагрузок.

Правило знаков при внецентренном нагружении

Положительными принимаются внешние усилия стремящиеся вызвать растяжение первой четверти сечения.

Положительное направление действия внешних нагрузок

Нормальные напряжения σ положительны, если они растягивают выделенный элемент бруса.

Положительные нормальные напряжения

Касательные напряжения τ будут положительными, если они стремятся повернуть рассматриваемый элемент бруса по ходу часовой стрелки.

Положительные касательные напряжения

Правило знаков для деформаций и перемещений

Деформация при растяжении-сжатии Δ

l считается положительной, если длина стержня при этом увеличивается.

Положительная деформация при продольном нагружении

При плоском поперечном изгибе

Вертикальное перемещение сечения бруса принимается положительным, если оно направлено вверх от начального положения.

Положительные перемещения сечений балки при изгибе

Для проекций сил на оси системы координат

Проекции внешних сил на оси системы координат принимаются положительными, если их направление совпадает с положительным направлением соответствующей оси.

Для моментов

Сосредоточенные моменты и моменты сил в уравнениях статики записываются с положительным знаком, если они стремятся повернуть рассматриваемую систему против хода часовой стрелки.

При составлении уравнений равновесия статичных (неподвижных) систем (например, при определении опорных реакций), последние два правила упрощаются до вида:

Проекции сил и моменты, имеющие одинаковое направление записываются с одинаковыми знаками, соответственно проекции сил и моменты обратного направления – с противоположными.

Метод сечений >
Примеры решения задач >

isopromat.ru

Сопромат.in.ua: Правило знаков

Правила знаков для продольного усилия

Растягивающие продольные усилия принято считать положительными, а сжимающие — отрицательными.
При построении эпюры продольных сил положительные значения N обычно откладывают вверх от горизонтальной линии или вправо от вертикальной линии; отрицательные значения N соответственно откладывают в противоположном направлении ( либо вниз, либо влево).

Правила знаков для изгибающего момента

Изгибающий момент принимается положительным, если он изгибает элемент балки так, что нижние волокна оказываются растянутыми, т.е. ось балки искривляется выпуклостью вниз.
При построении эпюры изгибающего момента в строительных и транспортных ВУЗах принято откладывать положительный момент

вниз ( со стороны растянутого волокна), а в машиностроительных ВУЗах — вверх (положительный момент откладывается со стороны сжатого волокна).

Правила знаков для поперечной силы

Поперечная сила считается положительной, если она стремится повернуть элемент балки по ходу часовой стрелки.
При построении эпюры поперечной силы положительные значения поперечной силы откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.

Правила знаков для крутящего момента

Крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он поворачивает сечение по ходу часовой стрелки.
При построении эпюры крутящих моментов, положительные значения откладываются вверх от горизонтальной базовой линии, а отрицательные –- вниз.

Правило знаков для прогиба

Прогиб считается положительным, если он направлен вниз

---

Связанные статьи

метки: внутренние усилия

sopromat.in.ua

Правила знаков для сил и моментов в уравнениях равновесия

При составлении уравнений статики для систем находящихся в равновесии (например при определении опорных реакций) правила знаков могут быть упрощены до следующего вида:
Нагрузки направленные в одну сторону принимаются положительными, а соответственно, нагрузки обратного направления записываются со знаком минус.

Знаки проекций сил

То есть, для уравнений сумм проекций сил на оси:
Проекции сил и нагрузок на координатную ось имеющие одинаковое направление принимаются положительными, а проекции усилий противоположного направления – отрицательными.

Например, для такой схемы нагружения:

уравнение суммы сил имеет вид

А так как суммы проекций разнонаправленных сил равны, то данное уравнение можно записать и так:

Здесь F(q) – равнодействующая от распределенной нагрузки, определяемая произведением интенсивности нагрузки на ее длину.

Знаки моментов

Сосредоточенные моменты и моменты сил стремящиеся повернуть систему относительно рассматриваемой точки по ходу часовой стрелки записываются в уравнения с одним знаком, и соответственно моменты, имеющие обратное направление с противоположным знаком.

Например, для суммы моментов относительно точки A

получаем

или, что одно и то же

Здесь m(F) – моменты сил F относительно точки A.
M(q) – моменты распределенных нагрузок q относительно рассматриваемой точки.

Примеры решения задач >

isopromat.ru

Правила знаков поперечных сил и изгибающих моментов (сопромат)

Правила знаков для поперечных сил

Внешняя сила, действующая на отбрасываемую часть балки и стремящаяся повернуть ее относительно сечения по ходу часовой стрелки, входит в алгебраическую сумму для определения поперечной силы () со знаком плюс (рис. 7.5, а). Заметим, что положительная поперечная сила () «стремится вращать» любую из частей балки также по ходу часовой стрелки.

Говоря простым языком: в сечении балки возникает поперечная сила, которую нужно определить и изобразить на эпюре поперечных сил. Чтобы правило знаков для поперечных сил выполнялось, нужно запомнить:

Если поперечная сила возникает справа от сечения, она направлена вниз, а если поперечная сила возникает слева от сечения – вверх (рис. 7.5, а).

Поперечная сила является внутренней силой, поэтому поперечная сила противоположна равнодействующей внешних сил, действующих на рассматриваемую часть балки. Поэтому если внешняя сила P (рис. 7.5, а) направлена вниз, то интересующая поперечная сила, возникающая от действия силы P, направлена вверх (и наоборот). Значит, внутренняя сила положительна, если внешняя сила, породившая ее, направлена противоположно направлению поперечной силы по правилу знаков.

Допустим, рассматривается правая часть балки (рис.7.5, а). Действует сила P, направленная вверх. По правилу, поперечная сила положительна, если направлена вниз (или внешняя сила P, породившая ее, направлена вверх).

Правила знаков для изгибающих моментов

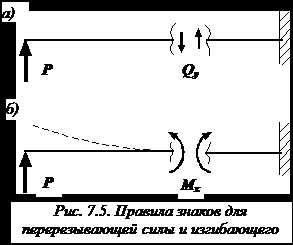Правила знаков для изгибающих моментов: внешняя нагрузка, приложенная к отбрасываемой части балки, создает момент относительно рассматриваемого сечения, стремящийся изогнуть отбрасываемую часть балки выпуклостью вниз, то этот момент входит в алгебраическую сумму для определения изгибающего момента () со знаком «плюс» (рис. 7.5, б).

По правилу знаков для изгибающих моментов, положительный изгибающий момент () «стремится изогнуть» любую из рассматриваемых частей балки тоже выпуклостью вниз. Кавычки использованы потому, что внутренние силовые факторы не являются активными силами и не могут вызывать деформацию балки.

Для удобства определения знака изгибающего момента рекомендуется поперечное сечение балки мысленно представлять в виде неподвижной жесткой заделки.

Иными словами: по правилу знаков изгибающий момент положителен, если «гнет балку» вверх, независимо от исследуемой части балки. Если в выбранном сечении результирующий момент всех внешних сил, порождающих изгибающий момент (является внутренней силой), направлен

противоположно направлению изгибающего момента по правилу знаков, то изгибающий момент будет положительным.

Допустим, рассматривается левая часть балки (рис. 7.5, б). Момент силы P относительно сечения направлен по часовой стрелке. По правилу знаков для изгибающих моментов для левой части балки изгибающий момент положителен, если направлен против часовой стрелки («гнет балку» вверх). Значит, изгибающий момент будет положительным (сумма моментов внешних сил и изгибающий момент по правилу знаков противоположно направлены).

sopromato.ru

решение задач. Лекции. Изгиб. Определение напряжений. Правило знаков для изгибающих моментов и поперечных сил.

Меню сайта Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления. Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. + Полное расписанное решение! Теперь и для статически неопределимых балок! Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты

Базовый курс лекций по сопромату, теория, практика, задачи. ::Оглавление:: 3. Изгиб. Определение напряжений. 3.4. Правило знаков для изгибающих моментов и поперечных сил. Поперечная сила в сечении балки mn (рис. 3.7, а) считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа — сверху вниз, и отрицательной — в противоположном случае (рис. 3.7, б). Изгибающий момент в сечении балки, например в сечении mn (рис. 3.8, а), считается положительным, если равнодействующий момент внешних сил слева от сечения направлен по часовой стрелке, а справа — против часовой стрелки, и отрицательным в противоположном случае (рис. 3.8, б). Моменты, изображенные на рис. 3.8, а, изгибают балку выпуклостью вниз, а моменты, изображенные на рис. 3.8, б, изгибают балку выпуклостью вверх. Это можно легко проверить, изгибая тонкую линейку. Отсюда следует другое, более удобное для запоминания правило знаков для изгибающего момента. Изгибающий момент считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз. Далее будет показано, что волокна балки, расположенные в вогнутой части, испытывают сжатие, а в выпуклой — растяжение. Таким образом, условливаясь откладывать положительные ординаты эпюры М вверх от оси, мы получаем, что эпюра оказывается построенной со стороны сжатых волокон балки. ::Оглавление::

Сообщество Вход Решение задач Расчет редукторов Для Android (рекомендую) NEW Mobile Beam 2.0 Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME

www.sopromat.org

Правило знаков для построения эпюр внутренних усилий 019

Рис.1

Внутренние усилия в стержне (рис. 1):
— продольное усилие,
— поперечное усилие (параллельное оси ),
— изгибающий момент относительно оси .

Внешняя нагрузка, действующая на стержень (рис. 1):
— сосредоточена продольная сила,
— сосредоточена поперечная сила,
— сосредоточен изгибающий момент,
— равномерно распределенная нагрузка.

Эпюра продольных сил

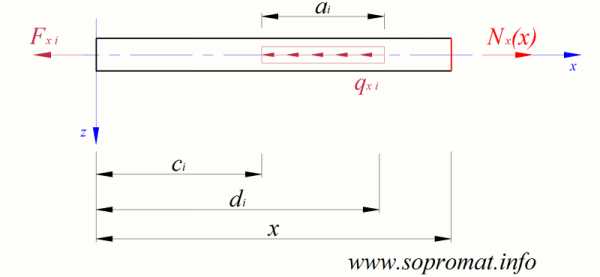
Рис. 2

Продольная сила в любом сечении стержня равна сумме проекций всех сил (которые находятся по одну сторону от рассматриваемого сечения, слева или справа) на продольную ось стержня (рис. 2):

, или

.

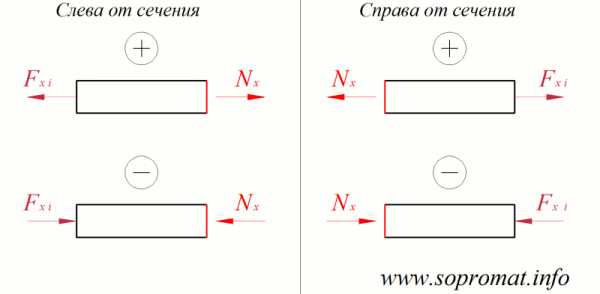
Рис. 3

Правило знаков (рис. 3): положительная продольная сила направлена ​​от сечения (растягивает отсеченную часть стержня), отрицательная — к сечению (сжимает отсеченную часть стержня). При этом рассматриваемое сечение считается неподвижным, а все вязи (опоры) заменяются реакциями в вязях.

Эпюра поперечных сил

Рис. 4

Поперечная сила в любом сечении стержня равна сумме проекций всех сил (которые находятся по одну сторону от рассматриваемого сечения, слева или справа) на поперечную ось стержня (рис. 4):

, или

.

Рис. 5

Правило знаков (рис. 5): положительная поперечная сила вращает отсеченную часть стержня вокруг рассматриваемого сечения по часовой стрелке, отрицательная — против. При этом рассматриваемое сечение считается неподвижным, а все вязи (опоры) заменяются реакциями в вязях.

Эпюра изгибающих моментов

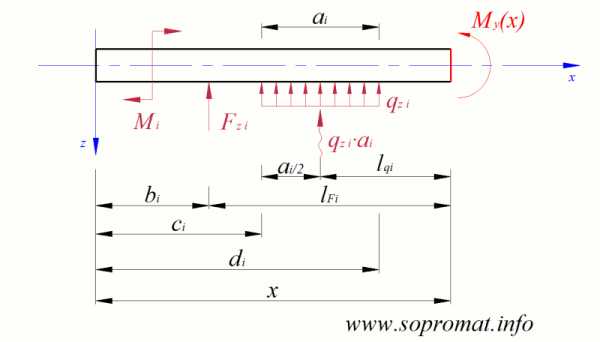
Рис. 6

Изгибающий момент в любом сечении стержня равен сумме моментов всех сил (которые находятся по одну сторону от рассматриваемого сечения, слева или справа) относительно рассматриваемого сечения (имеется в виду относительно одной из поперечных осей сечения) (рис. 6):

, или

.

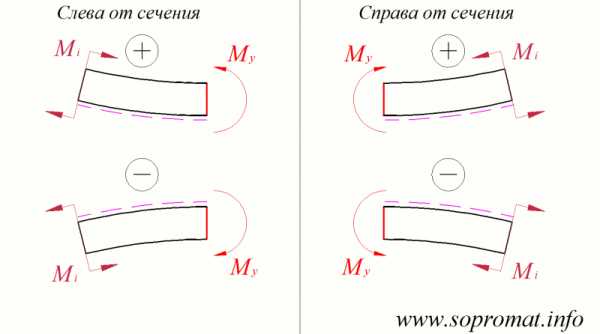
Рис. 7

Правило знаков (рис. 7): положительный изгибающий момент растягивает нижние волокна, отрицательный — верхние. При этом рассматриваемое сечение считается неподвижным, а все вязи (опоры) заменяются реакциями в вязях.

Момент — это произведение силы на плечо. Плечо — это кратчайшее расстояние (по перпендикуляру) от сечения до линии действия силы.

Эпюра крутящих моментов

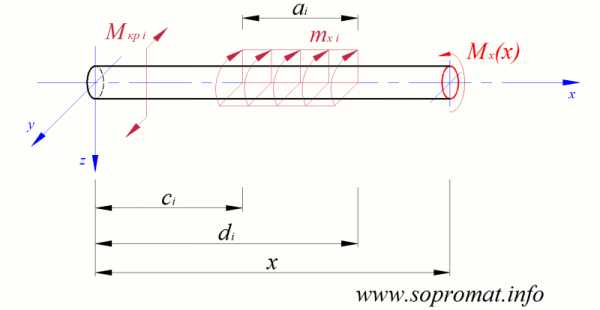
Рис. 8

Крутящий момент _кр в любом сечении стержня равен сумме моментов всех сил (которые находятся по одну сторону от рассматриваемого сечения, слева или справа) относительно продольной оси стержня (рис. 8):

, или

.

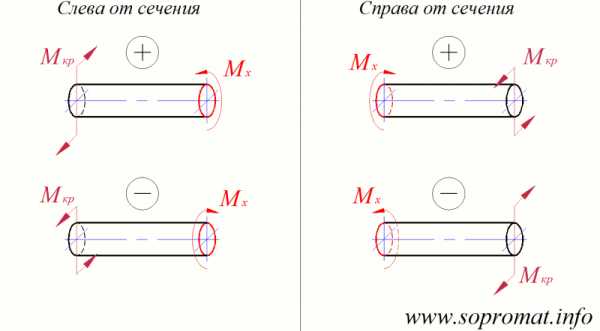
Рис. 9

Правило знаков (рис. 9): положительный крутящий момент вращает отсеченную часть стержня вокруг продольной оси по часовой стрелке, если смотреть со стороны сечения (т.е. видеть торец отсеченной части стержня), отрицательный — против часовой стрелки. При этом рассматриваемое сечение считается неподвижным, а все вязи (опоры) заменяются реакциями в вязях.

Понравилась статья! Поддержи проект! Ставь ЛАЙК!

www.sopromat.info

Правила знаков для изгибающих моментов — Мегаобучалка

2.1.Прямое правило:изгибающий момент считается положительным, если внешние силы, действующие на левый конец балки, поворачивают его по часовой стрелке, а действующие на правый — против часовой стрелки (рис.3).

Рис.3

 

2.2.Обратное правило:изгибающий момент считается отрицательным, если внешние силы, действующие на левый конец балки, поворачи­вают его против часовой стрелки, а действующие на правый — по часовой стрелке (рис. 4).

Рис.4

 

Последовательность построения эпюр поперечных сил и изгибающих моментов:

1.Под нагруженной балкой строим расчетно-графическую схему.

2.Используя три уравнения: ΣF_ix = 0, ΣF_iy= 0, ΣM(F_i) = 0, определяем реакции опор балки (обязательно выполнить проверку решения).

3.Используя метод сечений, определяем значения поперечных сил в ха­рактерных точках, т.е. точках, в которых приложены внешние нагрузки (при этом удобнее использовать прямое правило знаков, т.е. разбивать балку сле­ва направо).

4.По полученным значениям поперечных сил строим эпюру Q_y: под бал­кой проводим прямую, параллельную ее оси, и от этой прямой в характер­ных точках откладываем перпендикулярные поперечным силам отрезки, соответствующие выбранному масштабу.

5.Используя метод сечений, определяем величину М_Ив тех же характерных точках и по полученным значениям строим эпюру изгибающих моментов.

Характерные особенности построения эпюрQ_y,М_И:

1.На участке балки, где действуют сосредоточенные силы, эпюра Q_yочер­чивается прямой, параллельной оси балки, а эпюра М_И — наклонной прямой.

2.На участке балки, где действует распределенная нагрузка, эпюра Q_y очерчивается наклонной прямой, а эпюра М_И — параболой выпуклостью навстречу распределенной нагрузке.

3. В точке балки, где приложена сосредоточенная сила, на эпюре Q_y, наблюдается скачок на величину этой силы, а на эпюре М_И — излом.

4.В точке балки, где приложен внешний момент, на эпюре Q_yне наблю­дается никаких изменений, а на эпюре М_Инаблюдается скачок на величину внешнего момента.

Задача 6. Построить эпюры поперечных сил и изгибающих моментов для нагру­женной балки (рис. 5), если М= 10 кН • м, F= 8 кН, q = 5 кН/м.

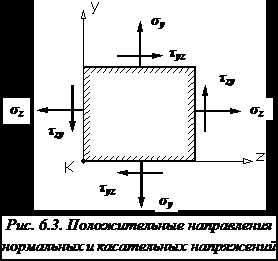Рис.5

 

Решение:

1.ΣΜ_D(F₁)=0

R_AAD – qABKD -FCD-Μ=0

R_A=(qABKD+FCD+Μ)/ AD=13,43кН;

 

2.ΣF_iy=0

R_A – qAB – F +R_D=0

R_D=-R_A + qAB + F =4,57кН

Проверка:

ΣΜ_А(F₁)=0

-М — R_DAD+FАС+ qABАК=0

3.Q_A=R_A=13,43 кН;

Q_В=R_A – qAB=3,43кН;

Q_Сслева=R_A – qAB=3,43кН;

Q_{С справа}=R_A – qAB — F = — 4,57кН;

Q_D=R_A – qAB — F = — 4,57кН;

4.Μ_A=0;

Μ_B=R_AAB — qABKB=16,86кН·м

Μ_С=R_AАС — qABKС=23,72кН·м

Μ_D=R_AD – qABKD — FСD =10,1кН·м

При деформации изгиба возникает нормальное напряжение. Напряжения одинаковы в сечении балки по ширине, но изменяются по высоте балки.

Условие прочности при изгибе:рабочее напряжение должно быть меньше или равно допускаемому напряжению, т.е.

где W_х —осевой момент сопротивления (величина, характеризующая способ ность элементов конструкции сопротивляться деформации изгиба.

Осевой момент сопротивления сечения определяется по формулам:

а) для круга (рис. 6а)

W_x= 0,1d³;

б) для кольца (рис. 6б)

W_x=0,1 d *(l –α⁴),

где α = d_вн/d_н;

в) для прямоугольника (рис.6в)

megaobuchalka.ru