Жесткая заделка.
В случае заделки одного тела в другое реакция связи состоит из силы и пары сил с моментом . Величина и направление реакции определяется из общих уравнений равновесия твердого тела.
Пример 2-1. На невесомую трехшарнирную арку действует горизонтальная сила . Определить линию действия реакции (реакции связи в точке А).
Решение: Рассмотрим правую часть арки отдельно. В точках В и С приложим силы реакции связей и . Тело под действием двух сил находится в равновесии. Согласно аксиоме о равновесии двух сил, силы и равны по величине и действуют вдоль одной прямой в противоположные стороны. Таким образом направление силы нам известно (вдоль линии ВС).
Рассмотрим
левую часть арки отдельно. В точках А
и С приложим силы реакции связей и
.
Сила
,
действие равно противодействию. На
тело действуют три силы, направления
двух сил (
и
.
Пример 2-2. Однородный стержень закреплен шарнирно в точке А и опирается на гладкий цилиндр. Определить линию действия реакции (реакции связи в точке А).
Решение: Так как стержень однородный, то равнодействующая сил тяжести (сила ), действующих на стержень, приложена в его геометрическом центре (точка С). Так как стержень опирается на гладкую поверхность, то реакция связи (сила ) в точке касания (точка D) направлена по нормали к этой поверхности. На тело действуют три силы, направления двух сил (и.) известно. Согласно теореме о трех силах линии действия всех трех сил пресекаются в одной точке. Следовательно, сила направлена вдоль линии AЕ.
Пример
2-3. Однородный
стержень АВ опирается на гладкую
вертикальную поверхность. В точке А
шарнирно закреплен.
Решение:
Система сходящихся сил
Системой сходящихся сил (или пучком сил) называется такая система сил, линии действия которой пересекаются в одной точке – центре пучка.
Равнодействующая системы сходящихся сил равна векторной сумме слагаемых сил и определяется замыкающей стороной силового многоугольника, построенного на слагаемых силах как на составляющих. Точка приложения равнодействующей силы совпадает с точкой пересечения линий действия сил.
Проекции равнодействующей силы на оси координат равны алгебраической сумме проекций составляющих сил на эти оси.
Рис. 3-3
Условия равновесия системы сходящихся сил в векторной форме
Условия равновесия системы сходящихся сил в алгебраической форме
Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех прямоугольных осей координат были равны нулю.
Момент силы относительно точки
Если под действием приложенной силы твердое тело может совершать вращение вокруг некоторой точки, то для того, чтобы охарактеризовать вращательный эффект силы, необходимо ввести новое понятие — момент силы относительно точки.
Рассмотрим силу , приложенную к телу в точке А. Из некоторой точки О опустим перпендикуляр на линию действия силы .
Плечом h силы относительно точки О называется кратчайшее расстояние между этой точкой и линией действия силы. Через
силу и точку О можно провести плоскость.
Сила пытается вращать тело вокруг оси, которая
проходит через точку О и которая
перпендикулярна плоскости в которой
лежит сила. Точка О называется моментной
точкой.
Моментом силы относительно точки О называется вектор , приложенный в этой точке и равный векторному произведению радиус-вектора , соединяющего эту точку с точкой приложения силы, на вектор силы .
Модуль вектора равен произведению модуля силы на ее плечо .
Момент силы относительно точки О направлен перпендикулярно плоскости, в которой лежат сила и моментная точка (радиус-вектор), в том направлении откуда видно стремление силы вращать тело против движения часовой стрелки.
Рис. 3-4
Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия.
Момент силы равен нулю, если линия действия силы проходит через моментную точку.
Если сила задана своими проекциями на оси координат и даны координаты точки приложения этой силы, то момент силы относительно начала координат вычисляется следующим образом:
Проекции момента на оси координат равны:
1 Связи и их реакции
Тела
в природе бывают свободными и несвободными.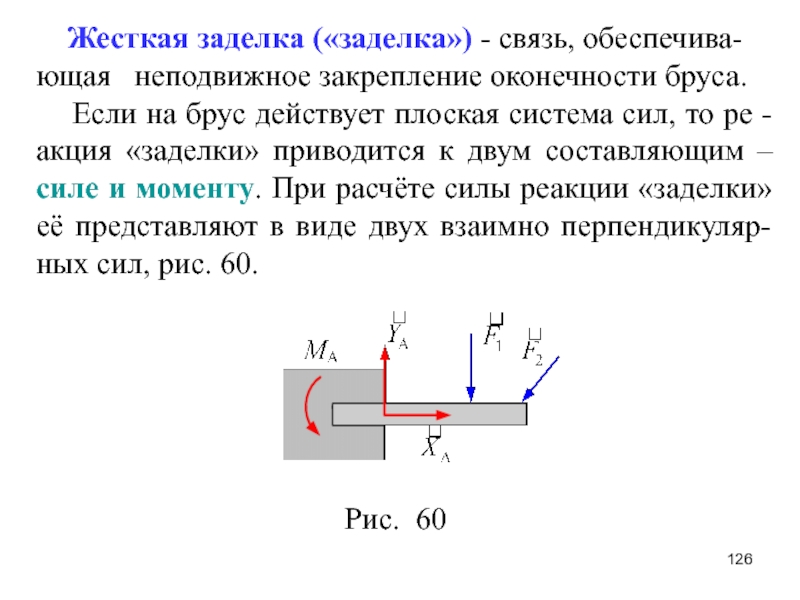
Тела, свобода перемещения которых ничем
не ограничена, называются свободными.
Тела, ограничивающие свободу перемещения
других тел, называются по отношению к
ним связями.
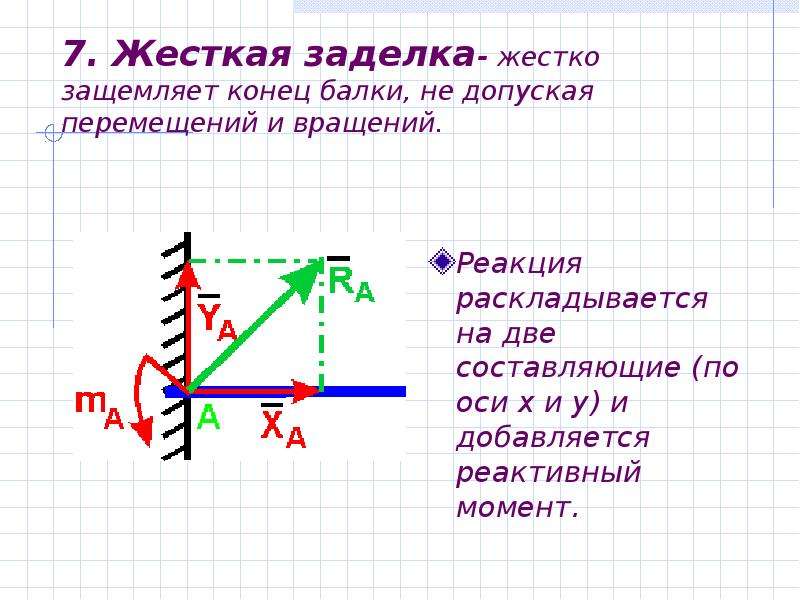
Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.
Шарнирно-неподвижная опора
Шарнирно-подвижная опора Реакция направлена по нормали к опорной поверхности
Соединение стержня и втулки в плоскости– скользящая заделка. Бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет момент MC Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила RA с углом α (или XA и YA ) и момент ΜA сферический шарнир
Рассмотрим плоскую систему сил (
.., Fn),действующих
на твердое тело в координатной плоскости
Oxy.Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:
R = F1 + F2 + … + Fn = Fi.
Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.
Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:
LO = MO(F1) + MO(F2) + … + MO(Fn) = MO(Fi).
Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться.
Для плоской системы
сил вместо векторного главного момента
используют понятие алгебраического
главного момента.
Алгебраическим
главным моментом LO плоской
системы сил относительно центра О,
лежащего в плоскости действия сил,
называют сумму алгебраических
моментовэтих сил относительно
центра О.
Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.
Правило знаков алгебраических моментов сил (в правой системе координат, принятой в механике): момент считается положительным, если сила стремится повернуть тело относительно точки О против хода часовой стрелки, и отрицательной — по ходу часовой стрелки.
Для сил
3-4.Систем тел. Равновесие системы тел. Пример.
Статический
расчет системы тел сводится к
рассмотрению условий равновесия
конструкций, состоящих из тел, соединенных
какими-нибудь связями.
Связи,
соединяющие части
конструкции называются внутренними,
скрепляющие конструкцию с другими
телами, в нее не входящими — внешними.
При решении задач статики реакции связей входят в число неизвестных, которые необходимо определить из уравнений равновесия. Система тел, для которых число неизвестныхреакций связей равно числу уравнений равновесия, называются статически определимыми. Система тел, для которых число неизвестных реакций связей больше числа уравненийравновесия, называются статически неопределимыми.
Если при отбрасывании внешних связей (опор) конструкция остается жесткой, то для нее задача о равновесии решается как для абсолютно твердого тела (при действии плоской системы сил число неизвестных реакций связей не должно быть больше трех).
Если
после отбрасывания внешних связей
конструкция не считается жесткой, то
наиболее рациональным способом решения
подобных задач является расчленение
на отдельные тела и составление уравнений
равновесия для каждого из тел в
отдельности.
Для конструкции из n тел, на каждое из которых действует произвольная плоская система сил, получится таким путем 3n уравнений равновесия, позволяющих найти 3nнеизвестных.
Например, если отбросить опоры А и В
При действии на трехшарнирную арку произвольной плоской системы сил для каждой части можно записать три уравнений равновесия:
Присоединить к
этой системе шести уравнений на основании
закона о действии и противодействии
уравнения для узла С (ХС = ХСў, YС = YСў),
получим систему уравнений из которой
можно найти реакции внешних связей ХА,
YА, ХВ, YВ и реакции внутренних связей
ХС, YС.
Жесткие клеммы | Физическая обработка аудиосигнала
Жесткое окончание является простейшим случаем струны (или трубки). прекращение. Это накладывает ограничение, что струна (или воздух) не может двигаться. при прекращении. (Мы рассмотрим более практичный случай с выходом завершение в §9.2.1.) Если мы завершаем идеальную строку длины в точке и тогда имеем «граничные условия»
| (7.9) |
где «»» означает «тождественно равный» , т.е. , равный для всех . Пусть обозначает время в выборках для распространения от одного конца струны к другому и обратно, или общее «строковая петля» задержка. Задержка цикла также равна удвоенной количество пространственных отсчетов вдоль строки.
Применяя разложение бегущей волны из уравнения (6.2), имеем
Следовательно, решение для отраженных волн дает
(7. 10) | |||
| (7.11) |
Схема цифрового моделирования для Идеальная струна с жестким окончанием показана на рис.6.3. В произвольном месте отображается «виртуальный пикап».
Волны скорости на жестком прекращении
Поскольку смещение всегда равно нулю на жестком конце, скорость там тоже равна нулю:
Следовательно, волны скорости отражаются от жесткого окончания с переворотом знака, как волны смещения: (7. 12) |
Такие инвертирующие отражения для волн скорости на жестком конце идентичны для моделей вибрирующих струн и акустических трубок.
Волны силы или давления на жестком конце
Чтобы выяснить, как волны силы или давления отскакивают от твердого прекращения, мы можем преобразовать волны скорости в силу или волны скорости с помощью соотношения закона Ома уравнения (6.6) для струн (или уравнение (6.7) для акустических труб), а затем использовать Уравнение (6.12), а затем снова уравнение (6.6):
Таким образом, волны силы (и давления) отражают от жесткого окончания с без инверсии знака : 7.3
Отражения от жесткой заделки в цифровом волноводе имитация акустической трубки в точности аналогична:
Заделки волноводов в акустических струнных и духовых инструментах
никогда не бывает абсолютно жестким. Однако обычно они пассивные ,
что означает, что волны на каждой частоте видят коэффициент отражения
не превышает 1 по величине.
Аспекты пассивной «уступчивости»
завершения обсуждаются в §C.11.
Следующий раздел:
Подвижная жесткая заделка
Предыдущий раздел:
Акустическая трубка Ideal
Подвижная жесткая заделка | Физическая обработка аудиосигнала
Полезно изучить «волноводную эквивалентную схему» простой случай жестко обрыва идеальной струны с левой конечная точка перемещается внешней силой, как показано на Рис.6.4. Этот случай относится к смычковым струнам. (§9.6) так как в промежутки времени, в которые смычок и тетива застревают вместе смычок обеспечивает окончание, которое делит струну на два в значительной степени изолированных сегмента. Таким образом, лук можно рассматривать как подвижное завершение во время «залипания».
Ссылаясь на рис.6.
4, левое окончание
Идеальная струна с жестким окончанием приходит в движение в момент времени с
постоянная скорость . Из уравнения (6.5) волновое сопротивление
идеальная строка
, где напряжение и
это массовая плотность. Следовательно, направленная вверх сила, приложенная движущимся
прекращение. изначально . В свое время,
бегущее возмущение достигает расстояния от вдоль
нить. Обратите внимание, что наклон струны на подвижном конце задается
к
, что выводит
тот факт, что волны силы представляют собой минус напряжение, умноженное на волны наклона.
(См. §C.7.2 для более полного обсуждения.)
Эквивалентные схемы цифровых волноводов
Две «эквивалентные схемы» цифровых волноводов показаны на рис.
Рис.6.5. В случае волны скорости на рис.6.5а,
завершающее движение появляется как аддитивная инъекция постоянной
скорость в крайнем левом углу цифрового волновода. В момент 0,
это инициирует шаг скорости от 0 до движения к
верно. Когда бегущая ступенчатая волна достигает правого конца, она
отражает с инверсией знака, посылая обратно «отменяющую волну»
Слева. За гасящей волной скорость равна нулю, а
струна не движется. Когда отменяющая ступенчатая волна достигает левой
завершение, он снова инвертируется и добавляется к внешнему вводу
сигнал постоянного тока, тем самым отправляя ступенчатую волну с положительной амплитудой на
справа, перезаписывая амплитудный сигнал в верхней рейке.
Это может быть добавлено к амплитудному сигналу в нижней рейке для
произвести шаг чистой скорости движения амплитуды, движущейся к
право. Этот процесс повторяется вечно, в результате чего возникает бегущая волна.
компоненты, которые неограниченно растут, но сумма которых всегда либо
0 или . Таким образом, в любой момент времени строку можно разделить на две части.
сегментов, где сегмент слева движется вверх со скоростью
, а правый сегмент неподвижен.
На этом этапе хорошим упражнением будет попытка мысленно представить форма струны во время этого процесса: изначально, так как оба левых конца опора и правый шаг скорости движутся с постоянной скорость , ясно, что форма струны кусочно-линейная, с сегмент с отрицательным наклоном слева примыкает к сегменту с нулевым наклоном справа. Когда шаг скорости достигает правильного окончания и отражает, чтобы создать гасящую волну, все слева от эта волна остается прямой линией, которая продолжает двигаться вверх на speed , а все точки справа от отменяющей волны передний край не двигается. Какова форма этой части нить? (Ответ дан в следующем абзаце, но попробуйте «посмотрите» сначала.)
Анимация подвижного конца струны и моделей цифровых волноводов
В моделировании силовой волны на рис. 6.5b, 7,4 окончание
движение появляется как аддитивная инъекция постоянной силы в крайнем левом углу.
В момент времени 0 это инициирует шаг силы от
0 к путешествию вправо. Поскольку силовые волны отрицаются
наклонных волн умножить на натяжение, т.е. ,
, наклон
струна за шагом движущей силы равна . Когда
бегущая ступенчатая волна достигает правого окончания, она отражается с нет инверсии знака , таким образом, волна удвоения возвращается влево
что увеличивает силу струны от до . За этим
волна, тогда наклон
. Это отвечает на вопрос о
предыдущий абзац: на самом деле строка является кусочно-линейной во время
первое обратное отражение, состоящее из двух отрезков прямой с наклоном
слева и вдвое больше справа. Когда возвращение
ступенчатая волна достигает левого окончания, снова отражается и
добавляется к внешнему сигналу силы постоянного тока, посылая амплитуду
положительная ступенчатая волна вправо (переписывая амплитуду
сигнал в верхнем рельсе). Это можно добавить к амплитуде
образцы в нижнем рельсе для создания шага чистой движущей силы
в струне амплитуды, бегущей вправо.
Склон
струны за этой волной
, а наклон в
фронт этой волны по-прежнему. Сила, приложенная к
строка по завершению поднялась до, чтобы сохранить
скорость стабильная при . (Мы можем интерпретировать ввод как дополнительных сил, необходимых каждый период, чтобы поддерживать завершение в движении
на скорости — см. следующий абзац ниже.)
Этот процесс повторяется бесконечно, в результате
компоненты бегущей волны, которые неограниченно растут и сумма которых
(что пропорционально минус физическому наклону струны) также растет
без ограничений. 7,5 Строка всегда кусочно-линейная, состоящая из
не более двух линейных отрезков с отрицательным наклоном, отличающихся на
. Последовательность снимков смещения строки показана на
Рис.6.6.
)Прекращено Импеданс струны
Обратите внимание, что импеданс цепочки с окончанием , если смотреть с одного его концов, не то же самое, что волновое сопротивление самой строки. Если строка бесконечно длинные, они одинаковые. Однако, когда есть отражения , они должны быть включены в расчет импеданса, что дает мнимая часть. Можно сказать, что импеданс имеет «реактивную» компонент. Импеданс ведущей точки струны с жестким окончанием является «чисто реактивным», и его можно назвать реактивное сопротивление (§7.1). Если обозначает силу в движущей точке струны и обозначает ее скорость, то движущая точка импеданс определяется выражением (§7.1)
где и обозначают преобразования Лапласа и . В случае жестко оканчивающейся строки выше, а также в любой системе, в которой вся энергия, поступающая в систему, в конечном итоге отражается обратно на вход, импеданс является чисто мнимое на каждой частоте («чистое реактивное сопротивление»), как легко показать: где обозначает длину строки.