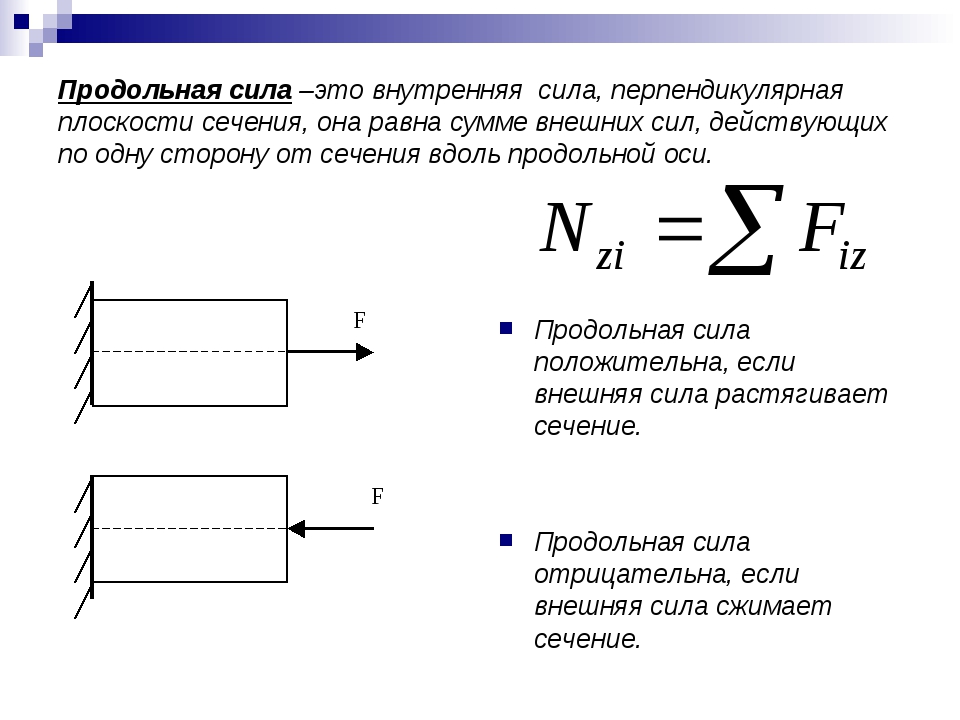
Задачи на растяжение сжатие по сопромату: Задачи на растяжение-сжатие

Содержание

Сопромат. Статически неопределимые задачи растяжения-сжатия 2.0

Сегодня мы разберем второй тип статически неопределимых задач на растяжение-сжатие. Это система «стержень в трубке». В отличие от стержня, зажатого между двумя заделками, здесь заделка только одна, но уравнений равновесия все равно недостаточно для решения задачи. Ситуация усугубляется тем, что часто трубка и стержень выполнены из разного материала. Давайте разбираться.

Вот типовая задача на эту тему. Стальной стержень находится в медной трубке. Для простоты сделаем и стержень, и трубку неизменными по площади сечения, но, чтобы не было совсем скучно, нагрузим двумя силами, одна сила сверху, другая — посередине. Вот исходная схема к задаче.

Площадь поперечного сечения трубки 2А, площадь стержня А. Длина трубки 2l, стержень, соответственно, тоже 2l, силы F приложены сверху и к середине стержня. Начинаем решать.

Первым делом (и это уже должно войти в привычку при начале решения задач сопротивления материалов) отбрасываем связи и вводим реакции опоры.

В нашем случае реакций будет две — одна в стержне, другая в трубке. Направление можно выбрать произвольно, но мы уже опытные ребята, так что замечаем, что и стержень, и трубка находятся в состоянии сжатия, так что реакции будут смотреть вверх. Рисуем.

Второе привычное для нас действие — записать уравнение равновесия. В данной задаче — это сумма проекций всех сил на вертикальную ось.

Как видим, в одном уравнении две неизвестных. Чтобы определить реакции в опоре, а следовательно, и внутренние сжимающие усилия в участках, нужно записать уравнение совместности деформаций. Для системы «стержень в трубке» уравнение совместности деформаций выглядит следующим образом: деформация стержня равна деформации трубки. Сечениями, в которых изменяется площадь сечения, или где приложена сосредоточенная сила, или на границах распределенной нагрузки, стержень или трубка разбивается на участки. В нашем случае трубка состоит из одного участка, стержень из двух. Их нужно пронумеровать и нанести на расчетную схему.

Далее вспоминаем метод РОЗУ и записываем внутренние усилия в трубке и стержне так, как будто реакции R1 и R2 нам известны. Это несложно.

Уравнение совместности деформаций в формульной записи:

Деформацию каждого участка мы записывать уже умеем

Аккуратно, не забывая следить за площадями, длинами и материалами,

Модули Юнга Eм и Eст обычно заданы соотношение Eст=2Eм. Подставляем деформации в уравнение совместности

Сокращаем, приводим подобные слагаемые и получаем второе уравнение с двумя неизвестными

Итак, получили систему из двух уравнений с двумя неизвестными, которую несложно решить.

Решаем

Собственно, сложная часть задачи готова. Статическая неопределимость раскрыта. Реакции в опорах найдены. Теперь легко посчитать внутренние усилия на участках (формулы мы уже выписали)

Как видим, внутренние усилия получились отрицательными, значит, интуиция нас не подвела, и стержни действительно сжимаются. Поделив внутренние усилия на площади участков, определяем напряжения.

Если в формулировке задачи стоит расчет коэффициента запаса по текучести или определение силы, при которой система потечет, то будьте внимательны — для участков из разных материалов пределы текучести отличаются, так что не факт, что участок с наибольшим напряжением потечет первым.

Перемещения также можно посчитать по известным нам формулам

Надо отметить, что нумерация участков выбрана не очень удачно: перемещение стержня имеет смысл считать от заделки, так что получается, что сначала пишем перемещение второго участка, а уже потом первого. Не очень красиво, но не критично.

Также важный момент: конечное перемещение верхнего сечения трубки должно быть равно конечному перемещению верхнего сечения стержня (собственно, это и было наше условие совместности деформаций). У нас это условие выполнилось. Если при решении задачи перемещения не сходятся, значит, ищите ошибку в расчетах.

Ну и не составляет труда по сделанным расчетам построить эпюры.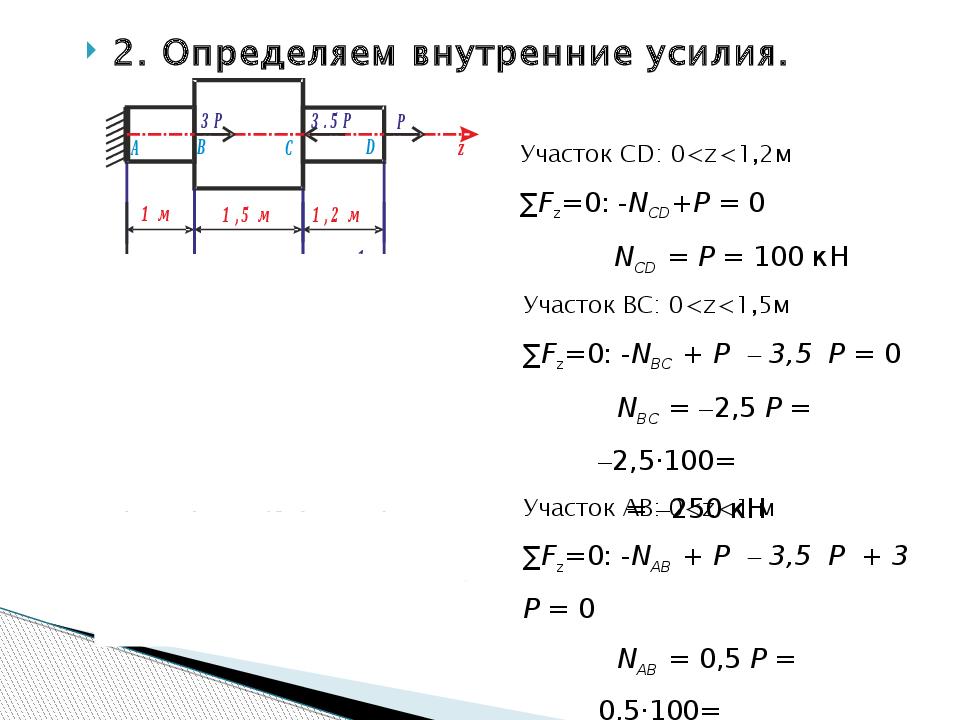 Для стержня и трубки нужно строить отдельно, так что получится 6 эпюр. Ну и расположение их будет непривычным — вертикальным.

Задача решена.

Всегда ваша, Botva-Project

Основные типы задач при расчете на прочность растянутых (сжатых) стержней

Определив напряжение в опасном сечении растянутого (сжатого) стержня по формуле 4.3 и установив допускаемое напряжение в соответствии с соображениями, изложенными выше, можно произвести оценку прочности стержня.

Для этого необходимо фактические напряжения в опасном сечении стержня сопоставить с допускаемыми:

(4.11)

Здесь имеется в виду допускаемое напряжение или на растяжение, или на сжатие в зависимости от того, с каким случаем мы имеем дело — с растяжением или сжатием.

Неравенство (4.11) называется условием прочности при растяжении (сжатии).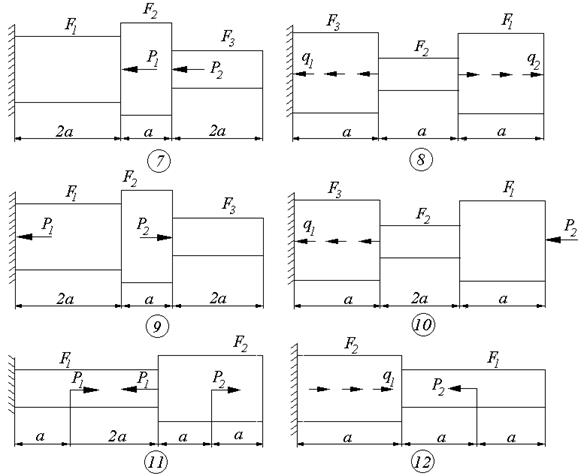 Пользуясь этим условием, можно решать следующие задачи:

1. Проверять прочность стержня, т. е. определять по заданным нагрузке и размерам поперечного сечения стержня фактические напряжения и сравнивать их с допускаемыми. Фактические напряжения не должны отклоняться от допускаемых более чем на ±5%. Перенапряжение больше этого значения недопустимо с точки зрения прочности, а недонапряжение свидетельствует о перерасходе материала.

2. Определять размеры поперечного сечения стержня (по известным нагрузке и допускаемому напряжению), требуемые по условию его прочности:

(4.12)

3. Определять допускаемую продольную силу по заданным размерам поперечного сечения стержня и известному допускаемому напряжению:

(4. 13)

Определив допускаемую продольную силу и установив связь между продольной силой и нагрузкой (методом сечений), можно определить и допускаемую нагрузку.

Следует иметь в виду, что сжатые стержни кроме расчета на прочность в наиболее ослабленном сечении должны также рассчитываться на

устойчивость, так как при определенном значении сжимающей силы может произойти выпучивание (продольный изгиб) сжатого стержня.

Решение задач по сопромату на растяжение сжатие.

Решение задач по сопротивлению материалов на растяжение и сжатие – самые первые, которые студент получает для индивидуального выполнения. Эти же задачи являются самыми простыми за весь курс изучения сопромата. Далее рассмотрим ход выполнения самых распространенных задач по сопромату на растяжение – сжатие.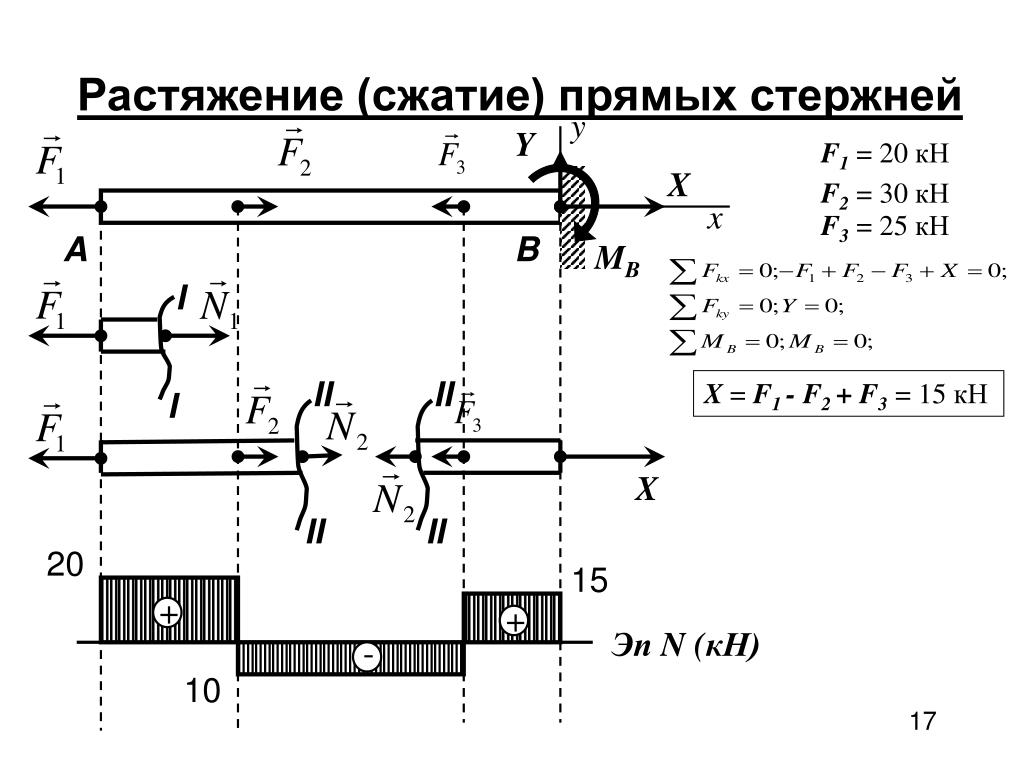

«Если вам требуется помощь в решении задач по сопромату на растяжение сжатие – заходите на мой сайт univer2.ru присылайте свое задание мне на почту [email protected] »

Самые простые задачи такого рода – на определение площади сечения стержня имеющего однородное или переменное сечение. Иногда просят найти перемещение какого либо сечения стержня или построение эпюры перемещений (относительных или абсолютных). Задача решается следующими образом: определяются реакции опор. Для статически определимой системы достаточно составления одного уравнения статики, если же система статически неопределима – дополнительно составляется уравнение деформаций . после определения реакций опор определяют величины внутренних усилий на участках стержня, строиться эпюра Nz , далее в общем виде определяется значения нормальных напряжений. Приравнивая эти выражения к допустимым параметрам материала, определяют размер сечения. Зная нормальные напряжения на участках стержня легко определить перемещение того или иного сечения.

Еще один типа задач по сопромату на растяжение и сжатие – определение сечений стержней и перемещение характерных точек принадлежащих стержневой системе. Порядок решения подобных задач: определяются усилия в стержнях. Для этого составляются уравнения статики. В случае, если система является статически неопределимой необходимо составить выражение совместных деформаций – кинематические соотношения между деформациями стержней системы. Дале, исходя из условия прочности или какого то другого условия, определяются размеры сечений стержней.

Тэги: News

Задача 1. Растяжение и сжатие. Задача 2. Кручение валов. — Контрольная работа #1501036 — Сопротивление материалов

Задача 1. Растяжение и сжатие. 3
Задача 2. Кручение валов. 9
Список использованной литературы 17

В работе решены 2 задачи:
Задача 1
Один конец стального вертикального бруса жестко защемлен, другой свободен. Общая длина бруса L (рис. 1). Одна часть бруса, длина которой l. имеет постоянную по длине площадь поперечного сечения F1 другая часть — постоянную площадь F2. На свободном торце действует сила Р1 в сечении, отстоящем от свободного конца бруса на расстоянии С действует сила Р2. На участке от точки на расстоянии l до точки на расстоянии  от свободного конца действует равномерно распределенная продольная нагрузка t. Модуль упругости Е = 2105 МПа. F = 12104 м2, Р = 10 кН.

Требуется:
1. Определить интенсивность равномерно распределенной нагрузки

2. Сделать схематический чертеж бруса по заданным размерам, соблюдая масштаб длин по вертикальной оси;
3. Составить для каждого участка бруса в сечении с текущей координатой z (0 4. Построить эпюры продольных усилий N и напряжений 2Р
5. Вычислить перемещение сечения, отстоящего от свободного конца бруса на расстоянии l.
Исходные данные:
№ схемы: 1.
L = 1,0 м;
Задача 2. Кручение валов.

Стальной вал ступенчатого поперечного сечения равномерно вращается вокруг своей оси.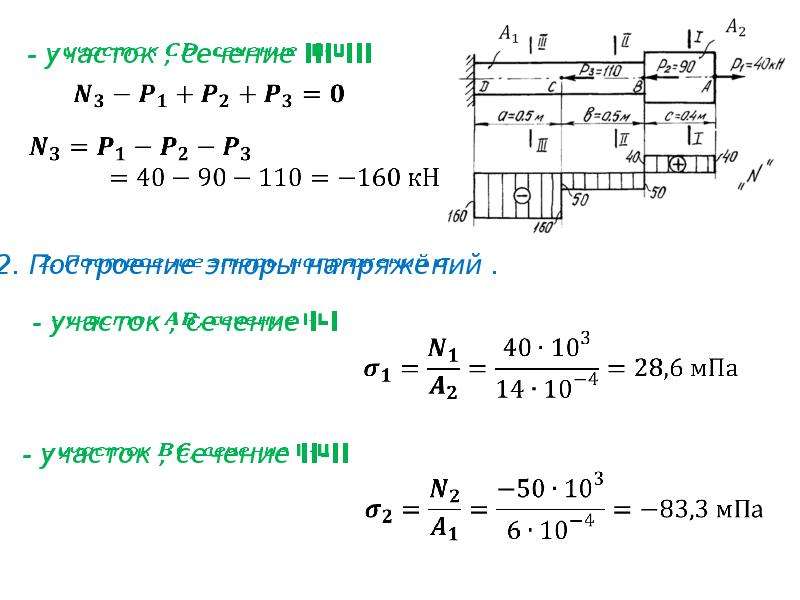 На вал действуют сосредоточенные моменты М1, М2, М3, МА, МЕ. Известно, что сечения Е и А вращаются синхронно, т.е. их взаимный поворот относительно друг друга равен 0. Остальные сечения повернуты друг относительно друга вследствие деформации кручения.

Требуется:
1. Установить при каком значении X = МА при равномерном вращении вала угол поворота правого сечения А = Е;
2. Построить эпюру крутящих моментов;
3. Определить размеры поперечного сечения вала из условий прочности и жесткости;
4. Показать распределение касательных напряжений в поперечных сечениях каждого участка вала.
5. Построить эпюру углов закручивания.
Принять G = 8104 МПа; []=1,8 °/м; М = 2 кНм.

1. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов. М.: Высшая школа, 1995. – 560 с.
2. Дарков А.В. Шапиро Г.С. Сопротивление материалов. М.: Высшая школа. 1995. — 763 с.
3. Сидоров В.Н. Лекции по сопротивлению материалов и теории упругости. М.: Изд-во Центр Генштаба Вооруженных сил РФ, 2002. – 352 с.
4. Смирнов А.Ф. Сопротивление материалов. М.: Высшая школа, 1975. – 390 с.
5. Ривош О.А. Сопротивление материалов, ч. 1 М.: Высшая школа, 1991. — 295 с.

Сопромат online | 1.1. Расчет ступенчатого стержня без учета собственного веса

Определить реакцию в защемлении стального ступенчатого стержня, нагруженного силами F₁=100 кН, F₂ = 8О кН, F₃ = 60 кН, и построить эпюру нормальных сил (рис. 1.9). Собственным весом стержня пренебречь.

Решение. Обозначим реакцию в защемлении через В_х. На стержень действует уравновешенная система сил, направленных по одной прямой — геометрической оси стержня, т.е. стержень находится под действием осевых сил. Расчет ступенчатого стержня начнем с определения опорной реакции стержня. Для определения неизвестной силы В_х составим условие равновесия в виде (1.10):

Опорная реакция Вх получилась отрицательной. Это означает, что в действительности она направлена вниз и на схеме ее направление необходимо заменить на обратное. Вх = 120 кН.

Рисунок 1.9.

Стержень имеет четыре участка, границами которых являются сечения, где приложены внешние силы и изменяются размеры поперечных сечений.

Мысленно рассечем стержень произвольным поперечным сечением I—I в пределах первого участка. Отбрасывая верхнюю часть бруса и заменяя ее действие на нижнюю неизвестной нормальной силой N_x₁, из уравнения равновесия ∑F_x=0 получаем

Нормальная сила N_x₁ направлена от сечения. Данный участок испытывает растяжение.

Аналогично поступаем по отношению ко второму участку:

Второй участок также испытывает растяжение. В дальнейшем, чтобы не рассматривать отдельно равновесие отсеченной части стержня, будем считать, что в сечении действует положительная нормальная сила. Действительный знак нормальной силы найдем, решив уравнение равновесия.

Предполагая на третьем участке в сечении III—III нормальную силу N_x положительной, находим ее величину и действительное направление, проектируя на ось х (на нормаль к сечению) с учетом знаков все внешние силы, приложенные к нижней части стержня:

Нормальная сила получилась отрицательной, т.е. на третьем участке стержень испытывает сжатие.

Нормальную силу в сечении IV—IV четвертого участка получаем, проектируя на ось х внешние силы, действующие на верхнюю часть стержня, и нормальную силу Nx , считая ее положительной:

Так как в уравнения не входят длины участков (координата х), то нормальные силы на участках будут постоянными, а их эпюры представляют прямые линии, параллельные оси стержня.

По полученным величинам сил строим для стержня эпюру нормальных сил N, соблюдая принятое правило знаков. Из эпюры нормальных сил следует, что нормальная сила на участках, без учета собственного веса стержня, определяется только приложенными к стержню внешними силами и не зависит от размеров его поперечного сечения.

Расчет ступенчатого стержня и построение эпюр продольных сил

Открытый урок на тему «Растяжение — сжатие» | Методическая разработка по теме:

План занятия

Тема: «Расчеты на прочность при растяжении – сжатии».

Цели урока

Дидактическая: дать основы практического расчета тел на прочность при растяжении – сжатии.
Воспитательная: прививать студентам аккуратность и четкость при выполнении схем и эпюр, внимательность при выполнении расчетов, добиваться активности и высокой работоспособности студентов на уроке.
Развивающая: формировать навыки и умения при решении задач, логическое и инженерное мышление.

Тип урока: урок совершенствования знаний, умений, навыков —

комплексное применение знаний.

Вид урока: урок самостоятельных работ, устных и письменных упражнений.

Методы проведения урока: метод «тихого обсуждения», «громкого обсуждения», «мозговой штурм», иллюстрация примеров, коллективная работа в микрогруппах.

Ход урока.

Организационная часть – 2 минуты

Проверка подготовленности аудитории к уроку.
Проверка наличия студентов.

Опрос по пройденному материалу – 30 минут.

2.1. Разгадывание кроссворда.

2.2. Индивидуальный программированный безмашинный опрос по

карточкам.

3. Обобщение материала и оценка его усвоения – 3 минуты.

Закрепление теоретической части темы – 12 минут.

Иллюстрация способов решения задач – 15 минут.

Закрепление материала в форме решения задач – 25 минут.

Заключительная часть: подведение итогов. -5минут.

Задание на дом.

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА И ПРОДОВОЛЬСТВИЯ

МОСКОВСКОЙ ОБЛАСТИ

ГОУ СПО МО «ЯХРОМСКИЙ АГРАРНЫЙ КОЛЛЕДЖ»

МЕТОДИКА

ПРОВЕДЕНИЯ УРОКА ПО ТЕМЕ:

«Расчеты на прочность при растяжении – сжатии»

Преподаватель Мифтяхетдинова Л. В.

Рассмотрена на заседании предметной цикловой комиссии. Протокол №

Председатель цикловой комиссии _______________(М.В. Горлова)

Методист ________________( В.А. Воронкова)

Новосиньково

2009 г.

Введение

«Техническая механика» является важным предметом цикла освоения общепрофессиональных дисциплин, состоящим из трех разделов: теоретической механики, сопротивления материалов и деталей машин. Знания, изучаемые в технической механике, необходимы студентам, так как они обеспечивают приобретение навыков для постановки и решения многих инженерных задач, которые будут встречаться в их практической деятельности. Для успешного усвоения знаний по данной дисциплине студентам необходима хорошая подготовка по физике и математике. В то же время, без знаний технической механики, студенты не смогут освоить специальные дисциплины.

При проектировании сооружений и машин приходится выбирать материал и поперечные размеры для каждого элемента конструкции так, чтобы он надежно, без риска разрушиться или исказить свою форму, сопротивлялся действию внешних сил, передаваемых другими деталями механизма, т. е. чтобы была обеспечена нормальная работа этого элемента. Основания для правильного решения этой задачи дает наука «Сопротивление материалов». Эта дисциплина изучает поведение различных материалов под действием нагрузки и указывает, как подобрать для каждой детали механизма необходимый материал и поперечные размеры при условии надежности работы и дешевизны механизма.

Требование прочности конструкции иногда связано с увеличением размеров поперечного сечения детали. Требование экономичности, наоборот, вызывает необходимость их уменьшения, так как увеличение размеров ведет не только к увеличению прочности, но и к утяжелению конструкции, перерасходу материала, к повышению стоимости механизма.

Основная задача науки «Сопротивление материалов» — разработка методов, позволяющих подбирать надежные и наиболее экономичные размеры поперечных сечений элементов конструкций, а также, наиболее целесообразную их форму. Кроме того, в сопротивлении материалов часто приходится решать и обратную задачу, т. е. проверять элементы конструкции на прочность, жесткость, устойчивость, а также находить допускаемые нагрузки, при которых конструкция может надежно работать.

Понять и усвоить содержание дисциплины можно лишь при достаточной подготовке студентов по математике, физике, инженерной графике, теоретической механике, материаловедению. Основной базой является теоретическая механика, которая изучает равновесие и движение твердых тел. Наука «Сопротивление материалов» широко применяется в инженерной практике. Эта наука изучается во всех высших и средних учебных заведениях, связанных с машиностроительными, строительными и сельскохозяйственными специальностями. Важнейшей основой подготовки высококвалифицированных специалистов является изучение одной из наиболее трудных дисциплин «Сопротивление материалов», знания которой необходимы для изучения таких наук, как «Теория механизмов и машин», «Детали машин», «Подъемно – транспортные машины», «Сельскохозяйственные машины», «Ремонт машин».

Условия работы тракторов и с/х машин имеют существенные особенности в виде специфических физико – механические свойства растений и почвы, не применяемых в других машинах, работа в условиях неустановившихся режимов и т. д. Эти особенности и вызывают необходимость изучения курса «Сопротивление материалов», базирующимся на опыте сельскохозяйственного машиностроения и эксплуатации машинно – тракторного парка. Значительные успехи достигнуты в развитии теоретических и экспериментальных исследований по сопротивлению материалов, а также в разработке теории и методов расчета в применении к сельскохозяйственному производству.

Академиком В.П. Горячкиным создана впервые в мире классическая теория с/х машин и основы их расчета. Расчеты, которыми пользовались 50 лет назад, характеризовались неполнотой анализа напряженного состояния; примитивными схемами, сведением циклических, вибрационных и ударных нагрузок к статическим, путем нередко необоснованного запаса прочности; применением в ряде случаев устаревших гипотез; недостаточным учетом условий работы механизмов и другими упрощениями.

Все это приводило к неточным расчетам и увеличению металлоемкости машин. Современный уровень развития требует создания новых машин, наиболее рациональных, экономически выгодных при изготовлении и эксплуатации, долговечных, надежных, высокопроизводительных, удобных в обслуживании.

При решении задач сопротивления материалов используются как опыт, так и теория, которые в этой науке неразрывно связаны между собой. Опытные исследования дают возможность изучить механические свойства и поведение материала как в самых простых так и в более сложных условиях его работы. Теория позволяет применить и обобщить результаты опытных исследований для построения метода расчета конструкции, находящейся в любых условиях работы. Соответствие теории с опытом устанавливается широкой практикой, на которой проверяются как теоретические выводы, так и опытные исследования. Выводы, полученные в сопротивлении материалов, широко используются во многих специальных, технических дисциплинах.

Чем сложнее техника, тем труднее уложить ее в рамки инструкций, и тем чаще специалисты будут сталкиваться с нестандартными ситуациями. Поэтому у студентов необходимо развивать самостоятельное творческое мышление, которое характеризуется тем, что человек не получает знания в готовом виде, а самостоятельно применяет их к решению познавательных и практических задач.

Большое значение при этом приобретают навыки самостоятельной работы. При этом важно научить студентов определять главное, отделяя его от второстепенного, научить делать обобщения, выводы, творчески применять основы теории к решению практических задач. Самостоятельная работа развивает способности, память, внимание, воображение, мышление.

В преподавании дисциплины практически применимы все известные в педагогике принципы обучения: научность, систематичность и последовательность, наглядность, сознательность усвоения знаний студентами, доступность обучения, связь обучения с практикой, наряду с объяснительно – иллюстративной методикой, которая была, есть и остается главной на уроках по сопротивлению материалов. Применяются вовлеченные методы обучения: тихое и громкое обсуждение, мозговой штурм, анализ конкретного примера, вопрос – ответ.

Тема «Расчеты на прочность при растяжении – сжатии» одна из важнейших в курсе «Сопротивление материалов». Она имеет большое значение с точки зрения практического применения. Многие детали конструкций испытывают деформацию растяжения – сжатия. Очень важно знать, какие факторы приводят к их разрушению, к невозможности дальнейшей эксплуатации.

Расчетные задания представляют схемы различной конструкции. Студенты выполняют проектный расчет, в котором нужно определить размеры детали, проверочный расчет, где определяются напряжения и сравниваются с допускаемыми значениями, расчет на допускаемую нагрузку, в котором определяются допускаемые в конструкции силы.

Работа над поставленными задачами проявляет активность и ответственность студентов, самостоятельность решения проблем, возникающих в ходе выполнения задания, дает навыки и умения решать эти проблемы. Преподаватель, задавая проблемные вопросы, заставляет студентов мыслить практически, с точки зрения инженерных расчетов, выполняемых при разработке конструкций. В результате проделанных расчетов, студенты делают выводы о прочности деталей конструкции.

Результаты работы желательно продемонстрировать, используя ТСО: графопроектор, кодоскоп.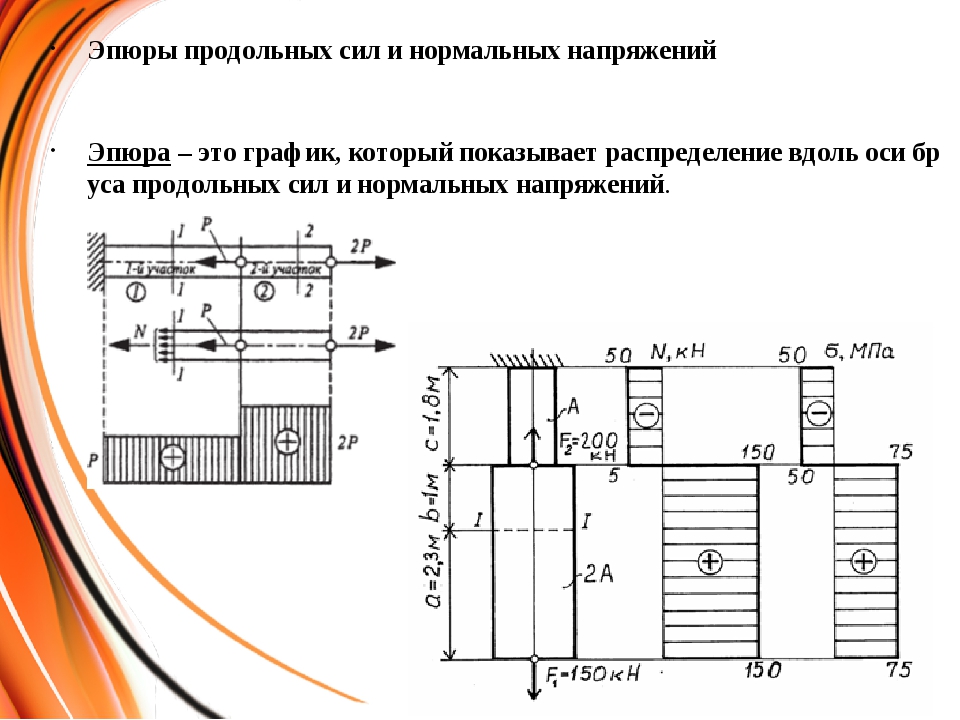

Организация и методика проведения занятия.

Организационная часть: включает проверку отсутствующих, готовность студентов к занятию, готовность аудитории, наглядных пособий.
Опрос студентов: разгадывание кроссворда, индивидуальный программированный безмашинный опрос по карточкам

Кроссворд

По горизонтали:

1. Способ решения задачи (ответ: расчет).

2. Метод сечения (ответ: РОЗУ).

3. Изменение формы и размеров тел под действием нагрузки (ответ: деформация).

4. Единица измерения напряжения (ответ: Паскаль).

5. Ученый, именем которого назван модуль упругости (ответ: Юнг).

6. Свойство материала сопротивляться проникновению одного тела в поверхность другого (ответ: твердость).

7. Внутренний силовой фактор, деленный на геометрическую характеристику сечения (ответ: напряжение).

8. Как называется напряжение, действующее перпендикулярно площади поперечного сечения (ответ: нормальное).

9. Величина, определяемая проектным расчетом (ответ: размер).

10. Способность материала сопротивляться действию нагрузок не разрушаясь (ответ: прочность).

11. Как называется напряжение, действующее по площади поперечного сечения (ответ: касательное).

12. Как называется момент, являющийся внутренним силовым фактором (ответ: крутящий).

13. Деформация, при которой внутренним силовым фактором является поперечная сила (ответ: сдвиг)

14. Ученый, именем которого назван закон сопромата (ответ: Гук).

По вертикали:

Характер деформации (ответ: срез).
Знак внешней силы, если она сжимает участок бруса (ответ: минус).
Величина, определяемая проектным расчетом вала (ответ: диаметр).
Знак внешней силы, если она растягивает участок бруса (ответ: плюс).
Диаграмма или график изменения внутреннего силового фактора по длине бруса (ответ: эпюра).
Способность материала давать большие остаточные деформации (ответ: пластичность).
Способность материала восстанавливать свою форму и размеры после снятия нагрузки (ответ: упругость).
Деформация, внутренним силовым фактором которой является момент (ответ: кручение).
Способность тела не давать больших деформаций (ответ: жесткость).

10. Деформация, внутренним силовым фактором которой является

продольная сила (ответ: растяжение).

11. Величина, равная произведению силы на плечо (ответ: момент).

12. Ученый, показавший зависимость между продольной и поперечной

деформациями (ответ: Пуассон).

13. Что вызывает деформацию (ответ: нагрузка).

Деформация, внутренними соловыми факторами которой являются

Мх , Мy (ответ: изгиб).

После разгадывания кроссворда, каждому студенту выдается индивидуальная карточка программированного опроса, содержащая 5 вопросов по теме «Деформация растяжения – сжатия». В течение 10 минут студенты отвечают на поставленные вопросы, выбирая правильный ответ из 5-ти предлагаемых на каждый вопрос. Затем результаты ответов сдаются преподавателю.

Обобщение материала и оценка его усвоения.

По разгадыванию кроссворда отмечаются лучшие студенты, давшие наибольшее количество ответов. Если ответы не были найдены, комментарии дает преподаватель. Объявляются оценки по индивидуальному опросу по карточкам. Преподаватель акцентирует внимание на лучших ответах.

Закрепление теоретической части темы.

Преподаватель предлагает студентам записать на доске формулу напряжений при растяжении – сжатии:  = Nz / A. После ее записи одним из студентов, преподаватель задает всем вопросы: «Какие параметры определяются в проектном расчете, проверочном расчете и расчете на допускаемую нагрузку?» Далее студентам предлагается вывести формулы каждого из расчетов на доске, воспользовавшись основной формулой. Три студента выводят формулы, остальным предлагается проверить правильность записи и исправить ошибки, если они допущены.

После этого преподаватель задает практический проблемный вопрос: «Что можно сказать о прочности троса подъемного крана, если допускаемое напряжение для материала троса составляет 40 МПа, а расчетное напряжение составило 42МПа?» Студенты должны рассчитать процент перегрузки, и, если он не превысит 5%, то прочность троса будет достаточной для дальнейшей эксплуатации.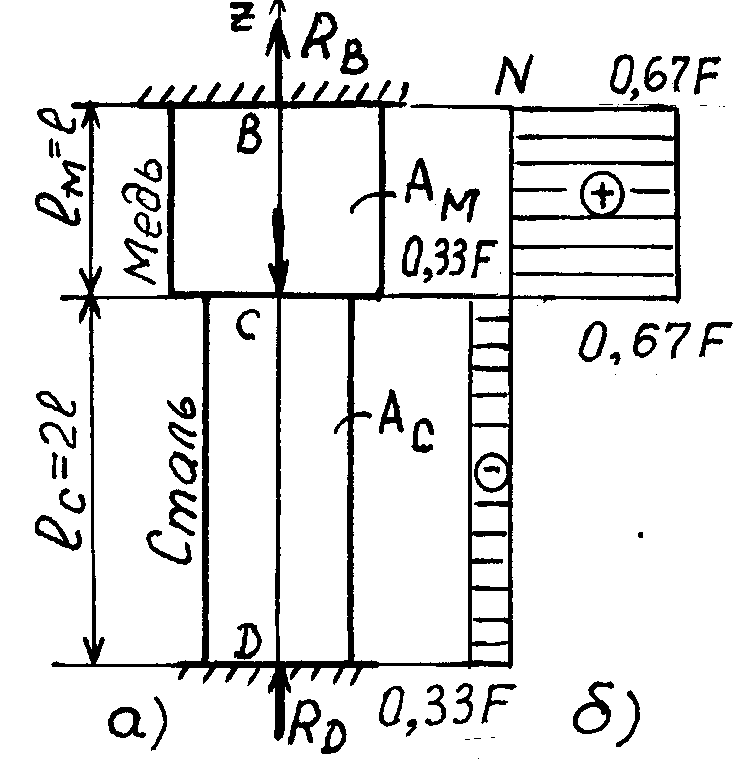

Иллюстрация способов решения задач.

Преподаватель разбирает три задачи: 1 задача на проектный расчет, 2 задача на проверочный расчет и 3 задача — расчет на допускаемую нагрузку.

Задача 1. Определить диаметры стальных стержней зажимного устройства,

если  =100 н/мм2

F=17,5 кН

Решение

В треугольнике отношение сил подобно отношению сторон:

0,5F / Nz =ℓ sin15/ℓ

Nz = 0,5Fℓ/ ℓ sin15, Nz = 0,5F/sin15

Nz =  A, тогда получим 0,5F/sin15 =  A, А = 0,5∙17500 / 100, А = 87,5 мм2

А = d2 /4 отсюда d1 =  4A / , d1 =  4∙87,5 / 3,14 = 21 мм

Так как на стержень с диаметром d2 действует та же Nz , то d2 = d1

Задача 2. Проверить на прочность деталь заклепочного соединения, если  =140 н/мм2

F=120 кН

d=24

130

Решение:

Площадь ослабленного сечения определяется: А = 130∙10 — 24∙10 = 820 мм2

 = Nz /А,  = 120000 / 820 = 146 МПа   =140 МПа

Определяем перегрузку детали: ( max —  ) ∙ 100% / 

(146 – 140) ∙ 100% /140 = 4,3  5%

Прочность детали соблюдается.

Задача 3. Оттяжка АВ подъемного крана представляет собой трос с площадью поперечного сечения 500 мм2. Допускаемое напряжение для материала троса

400 кГ / см2. Какой груз F может быть поднят краном из условия прочности оттяжки?

10 v

Решение:

Определяем длину оттяжки: АВ =  102 + 152 =18 м

cos = 15 / 18 = 0,83, sin = 10 / 18 = 0,55

Составляем уравнение равновесия:

 mc = 0; F∙5 – Nz cos∙10 = 0

Nz = F∙5 / cos∙10 Nz = F∙5 / 0,83∙10 = 0,6F

Из условия прочности Nz = ∙А = 400∙5 = 2000 кГ = 2 т

Получаем 0,6F = 2 F = 2 / 0,6 = 3,32 т

Закрепление материала в форме решения задач.

Студенты разбиты на микрогруппы по 2 человека. Каждой микрогруппе дается задание в виде задачи. В зависимости от задания студенты выполняют проектный расчет, проверочный расчет и расчет на допускаемую нагрузку.

Задача 1. Определить диаметры стержней, если  = 140 МПа

F=20 кН

Nz1

Nz2

Решение:

Fx=0; Nz1 — Nz2∙ cos = 0

 Fy=0; Nz2∙ sin — F =0; Nz2 = F / sin; Nz2 =20 / 0,5 Nz2 =40 кН

Nz1 = Nz2∙ cos Nz1 = 40 ∙ 0,866 Nz1 = 34,64 кН

Nz1 =  A A1 = Nz1 /  A1 = 34640 / 140 = 247мм2

А = d2 /4 отсюда d1 =  4A1 / , d1 =  4∙247 / 3,14  18 мм

A2 = Nz2 /  A2 = 40000 / 140 = 286мм2

d2 =  4∙286 / 3,14  19 мм

Задача 2.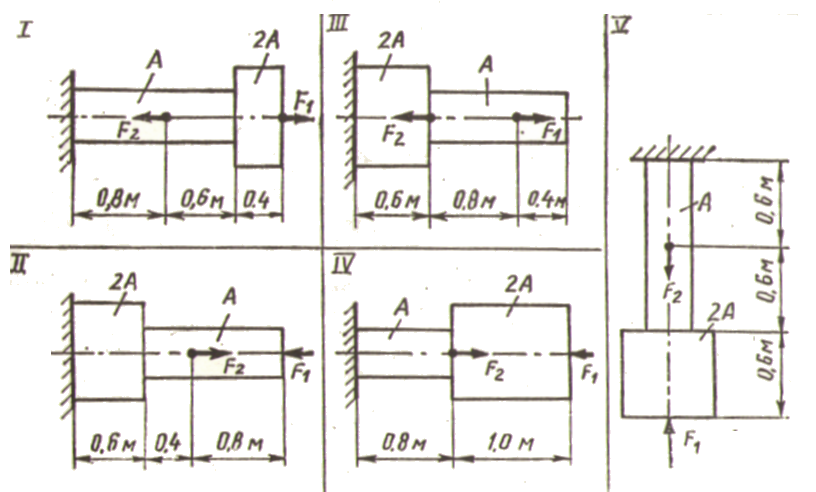 Определить диаметры стержней, если  = 160 МПа

Nz2

F=30кН

Nz1

Решение:

Fx=0; Nz1∙ cos45 — Nz2∙ cos45 = 0

 Fy=0; Nz1∙ sin45 — F + Nz2∙ sin45 =0; Nz1 = Nz2; 2Nz1 =F / sin45

Nz1 =30 / 2 ∙ 0,7 Nz1 = Nz2 =21,4 кН

A1,2 = Nz1,2 /  A1,2 = 21400 / 160 134 мм2

d1,2 =  4A1,2 / , d1,2 =  4∙ 134 / 3,14  13 мм

Задача 3. Определить диаметры стержней, если  = 160 МПа

F=100kH

q=20kH/м

Nz2

Nz1

Сс

Решение:

Q = q ∙ 5 = 20 ∙ 5 =100 кН

 Fy=0; Nz1 — F — Q+ Nz2 =0

 mc = 0; F∙3 – Nz2 ∙ 5 + Q∙ 2,5= 0 Nz2 = (F∙ 3 + Q∙ 2,5) / 5

Nz2 = (100∙3 +100∙2,5) / 5 = 110 кН

Nz1 = F + Q- Nz2 Nz1 = 100 +100 – 110 = 90 кН

A1 = Nz1 /  A1 = 90000 / 160 = 562,5 мм2 d1 =  4∙ 562,5 / 3,14  27 мм

A2 = Nz2 /  A2 = 110000 / 160 = 687,5 мм2 d2 =  4∙ 687,5 / 3,14  30 мм

Задача 4. Определить диаметры стержней, если  = 120 МПа

Nz2

F=40кН

Nz1

Решение:

Fx=0; -Nz1 + Nz2∙ cos30 = 0

 Fy=0; Nz2∙ sin30 — F =0; Nz2 = F / sin30; Nz2 =40 / 0,5 Nz2 =80 кН

Nz1 = Nz2∙ cos30 Nz1 = 80 ∙ 0,866 Nz1 = 69,28 кН

Nz1 =  A A1 = Nz1 /  A1 = 69280 / 120  577мм2

А = d2 /4 отсюда d1 =  4A1 / , d1 =  4∙577 / 3,14  27 мм

A2 = Nz2 /  A2 = 80000 / 120  667мм2

d2 =  4∙667 / 3,14  29 мм

Задача 5. Определить значение нагрузки F, если диаметр стержня 20 мм,

 = 160 МПа

100

150

Решение:

 mв = 0; F∙250 – Nz соs60∙ 100 = 0 Nz = F∙ 250 / соs60∙ 100

Nz = 5F Nz =  A А = d2 /4 A= 3,14∙ 202 /4 = 314 мм2

Nz = 160∙314 = 50240 5F = 50240 F = 10048 H  10,5 кН

Задача 6. Определить допускаемое значение силы F для стержней, если

 = 140 МПа, А1 = 226 мм2, А2 = 490 мм2

Nz1

Nz2

Решение:

Fx=0; Nz1 ∙ cos45- Nz2∙ cos30 + F = 0

 Fy=0; Nz1 ∙ cos45+ Nz2∙ sin30 — F =0;

-Nz2 ∙ cos30 — Nz2 ∙ sin30 +2F = 0 Nz2 =2F / (0,866 + 0,5) Nz2 =1,46F

Nz1 = (F — Nz2∙ cos30) / cos45 Nz1 = (F – 1,46F ∙ 0,866) / 0,7

Nz1  0,38F Nz1 =  A1 Nz1 = 140 ∙ 226 =31640 H 0,38F = 31640Н

F  83 кН Nz2 =  A2 Nz2 = 140 ∙ 490 = 68600 Н 1,46F = 68600H

F  47 кН

Задача 7. Определить допускаемое значение силы F для стержней, если

 = 140 МПа, диаметры d1 = 19 мм, d2 = 18 мм

Nz1

Nz2

Решение:

Fx=0; Nz1 — Nz2∙ cos30 = 0

 Fy=0; Nz2∙ sin30 — F =0; Nz2 = F / sin30; Nz2 = 2F

Nz1 = 2F∙ cos30=1,73F Nz1 =  A1 А1 = d2 /4 А1 = 3,14∙ 192 /4 = 283 мм2

Nz1 = 140 ∙ 283 = 39674H 1,73F = 39674 F = 22932 H  23 кH

Nz2 =  A2 А2 = d2 /4 А2 = 3,14∙ 182 /4 = 254 мм2

Nz2 = 140 ∙ 254 = 35608 Н 2F = 35608 F = 17804 H  18 кН

Задача 8. Определить допускаемое значение силы F для стержней, если

 = 160 МПа, диаметры d = 30 мм,

Nz2

Nz1

Решение:Fx=0; Nz1∙ cos60 — Nz2∙ cos60 = 0

 Fy=0; Nz1∙ sin60 — F + Nz2∙ sin60 =0; Nz1 = Nz2; 2Nz1 =F / sin60

Nz1 = 0,58F Nz1 =  A1 А1 = d2 /4 А1 = 3,14∙ 302 /4 = 706,5 мм2

Nz1 = 160 ∙ 706,5 = 113040 H 0,58F = 113040 F = 194897 H  195 кН

Задача 9. Проверить прочность стержней, если  = 160 МПа.

F=120k

F=120кН

Nz2

Nz1

Сс

d1=18мм

d2=25мм

1,5

Решение:

 Fy=0; Nz1 — F + Nz2 =0

 mc = 0; F∙1,5 – Nz2 ∙ 4,5 = 0 Nz2 = F∙ 1,5/ 4,5 = 120 ∙ 1,5 /4,5 = 40 кН

Nz1 = 120 – 40 = 80 кН

А1 = d2 /4 А1 = 3,14∙ 252 /4 = 491 мм2 1 = Nz1 / А1  

А2 = d2 /4 А2 = 3,14∙ 182 /4 = 254 мм2 2 = Nz2 / А2  

1 = 80000 / 491 = 163 МПа  160 МПа

2 = 40000 / 254 = 157 МПа  160 МПа

Перегрузка 1 стержня: (163 – 160) ∙ 100% /160 = 1,9%  5%

Задача 10. Проверить прочность стержня, если  = 140 МПа, площадь сечения А = 29 см2, F1 = 112 кН, F2 = 60 кН.

1,5

Решение:

 mв = 0; -F1∙4,5 + Nz соs60∙ 3 – F2∙1,5 = 0 Nz = (F1∙ 4,5+ F2∙1,5)/ соs60∙ 3

Nz = 396 кН  = Nz / А    = 396000 / 2900  137 МПа  140 МПа

Задача 11. Проверить прочность стержней, если  = 120 МПа.

F=90kH

q=20kH/м

Nz2

Nz1

Сс

d2=40мм

d1=30мм

Решение:

Q = q ∙ 6 = 20 ∙ 6 =120 кН

 Fy=0; Nz1 — F — Q+ Nz2 =0

 mc = 0; F∙2 – Nz1 ∙ 6 + Q∙ 3= 0 Nz1 = (F∙ 2 + Q∙ 3) / 6

Nz1 = (90∙2 +120∙3) / 6 = 90 кН

Nz2 = F + Q- Nz1 Nz2 = 90 +120 – 90 = 120 кН

А1 = d2 /4 А1 = 3,14∙ 302 /4 = 706,5 мм2 1 = Nz1 / А1  

А2 = d2 /4 А2 = 3,14∙ 402 /4 = 1256 мм2 2 = Nz2 / А2  

1 = 90000 / 706,5  127 МПа  160 МПа

2 = 120000 / 1256  96 МПа  160 МПа

Перегрузка 1 стержня: (127 – 120) ∙ 100% /120 = 5,8%  5%

Задача 12. Проверить прочность стержней, если  = 160 МПа, стержни имеют одинаковую площадь поперечного сечения А = 12 см2.

F=310kH

Nz3

Nz1

Сс

Nz2

Решение:

Fx=0; Nz2∙ cos60 = 0 Nz2 = 0

 Fy=0; Nz1 — F + Nz2 ∙ cos30 + Nz3=0

 mc = 0; F∙2,5 – Nz3 ∙ 4 = 0 Nz3 = F∙ 2,5/ 4 = 310 ∙ 2,5 /4 194 кН

Nz1 = F — Nz2 ∙ cos30 — Nz3=0 Nz1 = 310 – 194 = 116 кН

1 = Nz1 / А   1 = 116000 / 1200  97   2 = 0

3 = Nz3 / А   3 = 194000 / 1200  162  

Перегрузка: (162 – 160) 100%/160 = 1,25%  5%

Заключительная часть.

После расчетов представителю каждой микро группы предлагается показать с помощью графопроектора ход решения задачи и ее ответ. Правильные ответы оцениваются на «5». Если ход решения был верным, но студенты допустили ошибку в вычислениях, оценка снижается. Преподаватель проверяет ответы по своим данным и дает заключение о правильности решения задач, объявляет оценки за урок.

Задание на дом.

§ 3.1-3.4 Л[1]

§ 2.1 – 2.12 Л[2]

З. 1.67 Л[3]

Заключение.

Методика – форма общения педагога с аудиторией студентов. Каждый преподаватель постоянно ищет и испытывает новые способы раскрытия темы, возбуждению такого интереса к ней, который способствует развитию и углублению интереса студентов. Предлагаемая форма проведения занятия позволяет повысить познавательную деятельность, так как студенты на протяжении всего урока самостоятельно получают информацию и закрепляют ее в процессе решения задач. Это заставляет их активно работать на уроке.

«Тихое» и «громкое» обсуждение при работе в микро группах дает положительные результаты при оценке знаний студентов. Элементы «мозгового штурма» активизируют работу студентов на занятии. Совместное решение задачи позволяет менее подготовленным студентам разобраться в изучаемом материале с помощью более «сильных» товарищей. То, что они не смогли понять со слов педагога, может быть объяснено им еще раз более подготовленными студентами.

Некоторые проблемные вопросы, задаваемые преподавателем, приближают обучение на уроке к практическим ситуациям. Это позволяет развивать логическое, инженерное мышление студентов.

Оценка работы каждого студента на уроке также стимулирует его деятельность.

Все выше сказанное говорит о том, что данная форма урока позволяет студентам получить глубокие и прочные знания по изучаемой теме, активно участвовать в поиске решения задач.

Литература

А.Н. Митинский, М.С. Мовнин, А.Б. Израелит

« Техническая механика ч. II» Учебник для студентов немашиностроительных техникумов – Л.: Судпром ГИЗ, 1963 г.

М.С. Мовнин , А.Б. Израелит, А.Г.Рубашкин

«Основы технической механики». Учебник для немашиностроительных специальных техникумов – Л.: Машиностроение, 1978 г.

Г.И.Ицкович, А.И. Винокуров, Н.В. Барановский

«Сборник задач по сопротивлению материалов» — Л.: Судостроение, 1970 г.

Д.В. Чернилевский, Е.В. Лаврова, В.А. Романов

«Техническая механика» — М.: Наука, 1989 г.

Типы мостов: растягивающие и сжимающие силы — мероприятие

Быстрый просмотр

Уровень оценки: 8 (6-8)

Требуемое время: 45 минут

Расходные материалы на группу: 2,00 доллара США

Размер группы: 2

Зависимость действий: Нет

Тематические области: Физические науки

Ожидаемые характеристики NGSS:

Резюме

Студенты изучают, как силы растяжения и сжатия действуют на три разных типа мостовидных протезов.Используя губки, картон и веревку, они создают модели балочных, арочных и подвесных мостов и применяют силы, чтобы понять, как они распределяют или передают эти нагрузки. Эта инженерная программа соответствует научным стандартам нового поколения (NGSS).

Инженерное соединение

Используя бесчисленные возможности проектирования балочных, ферменных, арочных и подвесных мостов, инженеры-строители и строители создают мосты, которые необходимы для инфраструктуры нашего мира.Чтобы спроектировать мосты любого типа, инженеры должны понимать силы, которые действуют на каждый мост: сжатие и растяжение, а затем проектировать мосты, которые выдерживают эти силы без разрушения или разрушения. Команды инженеров выбирают тип моста, конструкцию и материалы, чтобы наилучшим образом распределять нагрузку на препятствие, и составляют подробные планы проектирования с указанием материалов, размеров, форм и углов для строительства моста.

Цели обучения

После этого занятия студенты должны уметь:

Определите три основных типа мостов, включая мост с балками или фермами, арочный мост и подвесной мост.
Опишите и определите сжимающие и растягивающие силы, действующие на различные типы мостов.
Объясните ситуации, для которых лучше всего подходят разные типы мостов.

Образовательные стандарты

Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными дисциплинами K-12, образовательные стандарты в области технологий, инженерии или математики (STEM).
Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты иерархически структурированы: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика; внутри типа по подтипу, затем по классу, и т. д. .
NGSS: научные стандарты нового поколения — наука
Ожидаемые характеристики NGSS
MS-ETS1-2.Оцените конкурирующие проектные решения, используя систематический процесс, чтобы определить, насколько хорошо они соответствуют критериям и ограничениям проблемы. (6-8 классы)
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Нажмите, чтобы просмотреть другие учебные программы, соответствующие этим ожиданиям от результатов.
В этом упражнении основное внимание уделяется следующим аспектам трехмерного обучения NGSS:
Наука и инженерная практика Основные дисциплинарные идеи Общие концепции
Оцените конкурирующие проектные решения на основе совместно разработанных и согласованных критериев проектирования.
Соглашение о выравнивании: Спасибо за ваш отзыв!
Существуют систематические процессы для оценки решений в отношении того, насколько хорошо они соответствуют критериям и ограничениям проблемы.
Соглашение о выравнивании: Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии — Технология
Выбор конструкций для конструкций основан на таких факторах, как строительные законы и нормы, стиль, удобство, стоимость, климат и функция.(Оценки 6 — 8) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Конструкции опираются на фундамент.(Оценки 6 — 8) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
ГОСТ Предложите выравнивание, не указанное выше
Какое альтернативное выравнивание вы предлагаете для этого контента?
Список материалов
Каждой группе необходимо:
Рабочий лист «Примечания к мосту», по одному на учащегося
1 маленькая губка (или плоский ластик)
1 ручка или маркер с темными чернилами
1 полоса картона или картона для плакатов (1 дюйм в ширину и 11 дюймов в длину; 2.5 см в ширину x 28 см в длину)
1 10-футовый (3-метровый) отрезок струны или каната малого диаметра
1 кусок каната длиной 11 футов (3 или 4 м)
несколько учебников (минимум четыре)
Рабочий лист типов мостов и сил, по одному на учащегося
Рабочие листы и приложения
Посетите [www.teachengineering.org/activities/view/cub_brid_lesson01_activity1] для печати или загрузки.
Больше подобной программы
Восполняя пробелы
Студентам предоставляется краткая история мостов, поскольку они узнают о трех основных типах мостов: балочных, арочных и подвесных. На них действуют две естественные силы — растяжение и сжатие, общие для всех мостов и конструкций.
Соломенные мосты
Работая в составе инженерных групп, студенты проектируют и создают модели мостов с балками, используя пластиковые соломинки для питья и ленту в качестве строительных материалов. Их цель — построить самый прочный мост с фермой собственной конструкции, соблюдая при этом проектные критерии и ограничения.
Проектирование мостов
Студенты узнают о типах возможных нагрузок, о том, как рассчитать предельные сочетания нагрузок, и исследуют различные размеры балок (балок) и колонн (опор) простой конструкции моста. Кроме того, они изучают шаги, которые инженеры используют для проектирования мостов.
Выполнение математических расчетов: анализ сил в ферменном мосту
Изучите основы анализа сил, которые инженеры применяют в соединениях фермы для расчета прочности моста фермы, известного как «метод соединений». Найдите напряжения и сжатия для решения системы линейных уравнений, размер которой зависит от количества элементов и узлов в ферме…
Введение / Мотивация
(Необязательно: предоставьте каждому учащемуся копию рабочего листа «Примечания по мостам», чтобы заполнить все, что они знают о мостах перед упражнением, и сделать записи во время вводной части упражнения.)
Как мосты влияют на наши сообщества и города? Мосты обеспечивают важные связи между местами, предоставляя нам доступ к ресурсам, другим местам и другим людям.Мосты позволяют проезжей части проезжать через различный рельеф, водные пути и горы с минимальным отклонением, экономя время на транспорте или поездках на работу или даже соединяя районы, которые иначе были бы недоступны. Кто проектирует эти мосты? Инженеры-строители делают. Думайте о мостах как о способе, с помощью которого инженеры помогают нам объединять миры. (Покажите карту Ванкувера, Британская Колумбия, Канада или другого города с множеством мостов.) Например, к выступающим частям Ванкувера было бы трудно добраться, если бы не мосты, связывающие этот регион вместе.
Три основных типа мостов, используемых на транспорте: балочные и ферменные, арочные и подвесные. Чтобы понять, как работают мосты, мы должны понимать силы, которые действуют на каждый мост. На мост в любой момент времени действуют две основные силы: сжатие и растяжение. Сжатие или сжимающая сила — это сила, которая сжимает или укорачивает предмет, на который она действует. Натяжение или растягивающая сила — это сила, которая расширяет или удлиняет предмет, на который она действует. В качестве простого примера представьте себе пружину.Если мы подтолкнем оба конца пружины друг к другу, мы сжимаем пружину. Таким образом, на него действует сила сжатия, укорачивающая пружину. Если мы оттягиваем оба конца пружины друг от друга, мы растягиваем пружину. Таким образом, на него действует сила натяжения, чтобы удлинить пружину. Цель конструкции моста — справляться с этими силами без разрушения или разрушения каким-либо образом.
Балочные и ферменные мосты
Broadway Bridge, Boulder, CO. Авторское право
Copyright © 2007 Denise W.Карлсон. Используется с разрешения
Балочные мосты — это самый простой и дешевый тип мостов для строительства. Самые простые балочные мосты состоят из горизонтальной балки, поддерживаемой с каждого конца колоннами или опорами. Вес балки и любая дополнительная нагрузка на мост передается непосредственно на опоры. Однако сама балка должна выдерживать собственный вес и нагрузки между опорами. Когда нагрузка давит на балку, верхняя часть балки сдвигается вместе под действием сжимающей силы, в то время как сила растяжения растягивает нижнюю часть.Чем дальше друг от друга опоры или опоры, тем слабее становится балочный мост. Для мостов с более крупными балками, предназначенных для интенсивного автомобильного и железнодорожного движения, балки заменяются простыми фермами или треугольными элементами, которые более экономичны, чем сплошные балки. Инженеры использовали в мостах много разных конструкций ферм. Таким образом, большинство балочных мостов редко превышают длину более 200 футов (61 м), однако старые мосты с фермой, пересекающие крупные реки, часто имеют длину 500–600 футов (152–183 м), не считая концевых опор, таких как опоры.
Арочные мосты
Арочные мосты — самый простой для распознавания тип мостов. Это один из старейших типов мостов, обладающий необычайной природной прочностью. Вместо того, чтобы толкать прямо вниз, как это делают балочные мосты, вес арочного моста и любая дополнительная нагрузка на мост переносятся наружу по изгибу арки к опорам на каждом конце. Эти опоры называются опорами. Абатменты распределяют нагрузку на мостовидный протез и не позволяют его концам расползаться.Римляне были хозяевами арочного моста. Многие из их арочных мостов использовали мало или совсем не использовали раствор или «клей», чтобы скрепить камни вместе. Цель арочного моста — выдерживать все нагрузки при сжатии без каких-либо растягивающих нагрузок. Камни в конструкциях держатся вместе за счет силы собственного веса и сжатия, передаваемого между ними. Размер арки или степень кривизны имеет большое влияние на эффективность этого типа мостовидного протеза. Иногда в очень больших арочных мостах арка часто уменьшается в размерах или уплощается, что приводит к значительным растягивающим усилиям, которые необходимо учитывать при проектировании.Большинство современных арочных мостов имеют длину от 30 до 457 метров.
Мосты подвесные
Висячие мосты двух категорий: современные висячие мосты и вантовые мосты. Современные подвесные мосты характеризуются М-образным рисунком троса. Кабели натягиваются на две башни, а затем закрепляются на обоих концах. Дорожное полотно подвешивается к тросам на более тонких тросах или стержнях. Вес проезжей части и любая дополнительная нагрузка передаются тросам, создавая в тросах силу натяжения.Затем тросы передают свою силу на башни и якоря. Типичные современные подвесные мосты простираются на расстояние от 2 000 до 7 000 футов (610–21 34 м). Для вантовых мостов характерна А-образная разводка кабеля. Кабели крепятся непосредственно к опорам и исключают необходимость в системе крепления. В вантовом мосту наблюдаются те же силы растяжения и сжатия, что и в современном подвесном мосту. Типичные вантовые мосты охватывают расстояния от 500 до 3000 футов (152–914 м), быстро становясь предпочтительным выбором для пролетов средней длины.Вантовые мосты тоже выглядят круто!
Сегодня мы собираемся создать простые модели каждого типа мостовидного протеза, которые мы только что обсудили, чтобы помочь нам больше узнать о том, как силы растяжения и сжатия действуют на каждый из них. Мы также будем думать о ситуациях, когда инженер может решить использовать каждый тип мостов при проектировании проезжей части.
Процедура
Перед мероприятием
Подготовьте следующие материалы для каждой группы:
Для модели балочного моста используйте ручку или маркер, чтобы нарисовать равноудаленные параллельные линии по ширине (а не по длине) губки (или ластика) (см. Рисунок 1).Если вы используете губку, немного смочите ее, чтобы она могла сгибаться.
Для модели арочного моста разрезать картон на полоски.
Для модели подвесного моста разрежьте струну (или веревку малого диаметра) на три отрезка длиной 2 фута (0,6 м) и один отрезок длиной 4 фута (1,2 м).
Для модели вантового моста разрежьте веревку большего диаметра на один кусок длиной 5 футов и другой кусок длиной 6 футов.
Сделайте копии рабочего листа «Типы мостов и сил», по одному на каждого учащегося.
Разделите класс на группы по два ученика в каждой.
Со студентами
Представьте студентам основные концепции каждого моста: балки, арки и обоих подвесных мостов, как описано во вводном разделе. Обсудите силы, присутствующие в каждом мосту — сжатие и растяжение — и различия в каждом из них. Раздайте учащимся рабочие листы, чтобы они могли заполнить их самостоятельно. После того, как студенты закончат, просмотрите свои ответы, чтобы убедиться в их понимании поведения сил сжатия и растяжения в различных типах мостов.
Пусть каждая команда построит простой балочный мост (см. Рис. 1). Разместите две стопки учебников примерно одинаковой высоты (3-4 дюйма или 8-10 см) так, чтобы плоская губка (или ластик) могла «охватить» их (расстояние между стопками должно составлять 1-2 дюйма или 2-5 см). ). Положите губку на две стопки учебников на расстоянии между ними. Используя ручку или карандаш, приложите направленную вниз силу к верхней части губки — ровно настолько, чтобы губка согнулась, но не разрушилась полностью.
Что происходит с параллельными линиями сверху и снизу? (Ответ: Линии наверху сближаются.Линии внизу расходятся дальше.)
Где находятся сжимающие силы? (Ответ: силы сжатия расположены сверху.)
Где находятся растягивающие силы? (Ответ: Силы растяжения расположены снизу.)
Рис. 1. Модель балочного моста. Авторское право
Copyright © ITL Program, Колледж инженерии, Университет Колорадо в Боулдере.
Пусть каждая группа построит простой арочный мост. Предложите им аккуратно согнуть картонные полоски так, чтобы они имели изогнутую форму.Затем положите картонную полоску на ровную ровную поверхность (настольный или кафельный пол, но не ковер) так, чтобы она напоминала арку. Используя ручку или карандаш, приложите силу, направленную вниз, к верхней части центра арки. Что происходит с аркой? (Ответ: Ожидайте, что арка обрушится, потому что ее концы выдвинутся наружу.) Затем поместите две стопки учебников на расстоянии примерно 5-6 дюймов (13-15 см) друг от друга. Поместите картонную полоску между двумя стопками изогнутой формой, напоминающей арочный мост. Нажмите на центр арки (см. Рисунок 2).
Что теперь происходит? (Ответ: арка не должна рушиться так легко.)
Какое усилие абатменты (в соответствии с учебниками) оказывают на арку: толкающее (сжатие) или тянущее (растяжение)? (Ответ: абатменты отталкиваются от арки, так как арка прижимается к абатментам.)
Укажите, как стопки книг действуют как опоры, не позволяющие развести концы арки.
Рисунок 2. Модель арочного моста.авторское право
Copyright © Программа ITL, Инженерный колледж, Университет Колорадо в Боулдере.
Пусть каждая группа построит простой подвесной мост. Сначала обвяжите один из отрезков бечевки (или веревки малого диаметра) длиной 2 фута (0,6 м) вокруг середины учебника толщиной около 2,5 см, пока он лежит на столе. . Повторите этот шаг со второй деталью длиной 2 фута вокруг другого учебника. Поставьте эти два учебника вертикально так, чтобы шнурок был вверху. Возьмите третий кусок двухметровой веревки и привяжите каждый конец к веревке на верхушках учебников.Разместите учебники на расстоянии 18 дюймов (0,5 м) друг от друга. Теперь нажмите на веревку, которая соединяет два учебника вместе (см. Рисунок 3). Что происходит? (Ответ: обратите внимание, как книги относительно легко падают внутрь.)
Рисунок 3. Модель подвесного моста. Нажатие на веревку между двумя соединенными книгами показывает, насколько они нестабильны; они легко падают внутрь. Copyright
Copyright © 2017 Дуа Чакер, Программа ITL, Колледж инженерии, Университет Колорадо в Боулдере
Затем удалите завязки из двух учебников.Возьмите кусок длиной 4 фута (1,2 м) и положите стопку учебников на один конец. На другой конец положите еще одну стопку учебников. Используя те же учебники толщиной 1 дюйм (2,5 см), что и раньше, поместите их под веревку, стоящую дыбом. Попробуйте установить расстояние между двумя учебниками, как и раньше, 18 дюймов (0,5 м). Теперь надавите на веревку между двумя учебниками (см. Рисунок 4).
Что происходит? (Ответ: Ожидайте, что книги не упадут так легко, даже при увеличивающейся нагрузке.)
Струна (трос) натянута или сжимается? (Ответ: струна натянута; она может выдерживать только растягивающее усилие.)
Книги (башни) в растяжении или сжатии? (Ответ: Книги в сжатом виде.)
Толкают или тянут стопки книг (якоря) за веревку (трос)? (Ответ: стопки книг тянут за веревку, потому что веревка тянет за них.)
Укажите, как крепления (стопки учебников) помогают стабилизировать мост.
Рисунок 4. Модель подвесного моста. С добавлением креплений с каждой стороны нажатие на веревку между двумя соединенными книгами показывает, что они более устойчивы. Авторское право
Copyright © 2017 Дуа Чакер, Программа ITL, Колледж инженерии, Университет Колорадо в Боулдере
Пусть каждая группа построит простой вантовый мост. Попросите учащихся встать и вытянуть руки горизонтально в каждую сторону. Попросите их представить, что их руки образуют мост, а их голова — башню посередине.В этом положении их мускулы держат руки вверх. Теперь, используя веревку, попросите учащихся стать вантовыми мостами (см. Рис. 5). Обвяжите каждый конец 5-футовой (1,5 м) веревки вокруг каждого локтя. Расположите середины веревок на макушках. Трос действует как опора и поддерживает локти. Используя 6-футовую (1,8-метровую) деталь, повторите этот процесс, завязав концы вокруг их запястий.
Где вы чувствуете толкающую или сжимающую силу? (Ответ: веревки натянуты из-за веса руки (мостика), а их головы сжаты.)
Обратите внимание, как нагрузка (вес стрелы) передается на башню (головы).
Сделайте шаг назад и обратите внимание на узор, образованный струнами, проходящими над их головами.
Рис. 5. Модель вантового моста. Авторское право
Авторское право © Джо Фридрихсен, программа ITL, Инженерный колледж, Университет Колорадо в Боулдере.
Завершите упражнение одним из действий по оценке после выполнения, описанных в разделе «Оценка». Например, пусть каждая команда выберет для проектирования мост одного типа.Используя свои заметки и рабочие листы, попросите их нарисовать мост в подходящем месте. Например, современный подвесной мост может пересекать водоем длиной 3 000 футов (914 м).
Словарь / Определения
опора: масса, как и каменная кладка, принимающая арку, балку, ферму и т. д. на каждом конце моста.
якорь: любое устройство для крепления подвесного моста с любого конца.
Арочный мост: мост, имеющий форму арки.
балка: длинный жесткий горизонтальный опорный элемент конструкции.
балочный мост: мост, состоящий из балок, поддерживаемых колоннами (опорами, башнями).
трос: очень прочный трос, сделанный из прядей металлической проволоки, используемый для поддержки канатных дорог или подвесных мостов.
вантовый мост: мост, состоящий из одной или нескольких башен (или колонн) с тросами, поддерживающими настил моста.Характеризуется А-образным рисунком кабеля.
Сжатие: толкающая сила, которая сокращает предметы.
палуба: «верх» моста, по которому мы едем или ходим.
инженер: человек, который применяет свое понимание науки и математики для создания вещей на благо человечества и нашего мира.
подвесной мост: мост, в котором платформа подвешена на тросах.
Натяжение: тянущая или растягивающая сила, которая имеет тенденцию удлинять предметы.
Оценка
Оценка перед началом деятельности
Рабочий лист : Попросите учащихся индивидуально заполнить рабочий лист «Примечания по мосту» перед упражнением и добавить его во время вводной / мотивационной части упражнения. Просмотрите их ответы, чтобы оценить их владение концепциями.
Встроенная оценка деятельности
Вопрос / ответ : Задайте студентам вопросы, приведенные в разделе «Процедура», и обсудите их в классе.
Рабочий лист : Попросите учащихся индивидуально заполнить Рабочий лист «Типы мостов и силы». Просмотрите их ответы, чтобы оценить их владение концепциями.
Оценка после деятельности
Создайте свой собственный : После упражнения опишите для студентов, как, когда сообществу нужен новый мост, команды инженеров выбирают тип моста, конструкцию и материалы, чтобы наилучшим образом распределить нагрузку на препятствие, а затем нарисуйте подробные планы проектирования. которые используются для строительства моста.Поручите студенческим командам выбрать тип моста и составить свой собственный подробный проект моста, указав материалы, размеры, формы и углы, как инженеры.
Инженерные сценарии : Инженеры используют свои знания о типах мостов, чтобы выбрать наиболее подходящую конструкцию для новой области. Предложите учащимся обсудить в парах и рассказать классу, какие типы мостов они бы выбрали для транспортировки по следующим сценариям:
Река шириной 300 футов (91 м).(Ответ: Ферма или арочный мост.)
Овраг шириной 305 м (1000 футов). (Ответ: Вантовый или арочный мост.)
Водоем размером 10 000 футов (3048 м) в поперечнике. (Ответ: Подвесной мост.)
Небольшой клочок болотистой земли. (Ответ: Ферма или арочный мост.)
Водный путь, по которому должны проходить высокие суда. (Ответ: Подвесной мост.)
Вопросы безопасности
Когда учащиеся создают свои вантовые мосты из людей, посоветуйте им не завязывать веревки настолько туго, что это может нарушить их кровообращение.
Расширения деятельности
Попросите учащихся вырезать из журналов картинки трех разных типов мостов и нарисовать стрелки, показывающие, где действуют силы растяжения и сжатия.
Масштабирование активности
Для младших классов заполните рабочие листы вместе, как класс.
Для старших классов, помимо индивидуального заполнения рабочих листов, каждый ученик должен выполнить следующее: 1) найти мост возле своего дома, 2) создать его изображение, используя цифровую камеру или сделав подробный рисунок, и 3) подготовить презентацию для класса, указав следующие особенности: тип моста, расположение моста, основные области применения и очевидные части моста, подверженные силам растяжения и сжатия.
Рекомендации
Dictionary.com. ООО «Издательская группа« Лексико ». По состоянию на 21 марта 2007 г. (Источник некоторых словарных определений с некоторой адаптацией) http://www.dictionary.com
Супер мост: Постройте мост. Обновлено в октябре 2000 г. NOVA Online. По состоянию на 14 марта 2007 г. (деятельность адаптирована из этого ресурса) http://www.pbs.org/wgbh/nova/bridge/build.html
Авторские права
© 2006 Регенты Университета Колорадо.
Авторы
Джонатан С. Гуд; Джо Фридрихсен; Натали Мах; Крис Валенти; Денали Лендер; Дениз В. Карлсон; Малинда Шефер Зарске
Программа поддержки
Комплексная программа преподавания и обучения, Инженерный колледж, Университет Колорадо в Боулдере
Последнее изменение: 30 апреля 2021 г.
Сильное как самое слабое звено — Урок
Быстрый просмотр
Уровень оценки: 8 (7-9)
Требуемое время: 45 минут
Зависимость уроков: Нет
Тематические области: Физические науки, физика
Ожидаемые характеристики NGSS:
Резюме
Чтобы представить два типа напряжений, которым подвергаются материалы — сжатие и растяжение, — учащиеся изучают сжимающие и растягивающие силы и узнают о мостах и небоскребах.Они строят свою собственную строительную конструкцию из зефира и спагетти, чтобы увидеть, какая конструкция выдержит наибольший вес. В соответствующем упражнении по обучению грамоте учащиеся изучают психологические концепции стресса и управления стрессом и выполняют письменное задание. Эта инженерная программа соответствует научным стандартам нового поколения (NGSS).
Инженерное соединение
Инженеры учитывают силы растяжения и сжатия при проектировании здания или конструкции для обеспечения нашей повседневной безопасности, комфорта и удобства.Искусственные сооружения включают дома, небоскребы, метро, мосты, туннели и плотины, а также такие товары, как ручки, банджи-джампинг, стиральные машины, инвалидные коляски, луноходы, протезы ног или книжные полки, и многие другие. Инженеры используют сложные математические модели для прогнозирования ожидаемых нагрузок на эти конструкции и изделия. Они определяют подходящие компоненты материала для поддержки ожидаемых сил.
Цели обучения
После этого урока учащиеся должны уметь:
Признайте, что силы сжатия и растяжения являются важными факторами в строительных конструкциях.
Сообщите, что конструкция здания будет определять вес, который оно может выдержать.
Объясните, насколько одни материалы хорошо сопротивляются силам растяжения, а другие — силам сжатия.
Поймите, что здания рушатся, когда инженеры не используют конструкции и материалы, достаточно прочные, чтобы противостоять силам сжатия и растяжения.
Образовательные стандарты
Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными дисциплинами K-12, образовательные стандарты в области технологий, инженерии или математики (STEM).
Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты иерархически структурированы: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика; внутри типа по подтипу, затем по классу, и т. д. .
NGSS: научные стандарты нового поколения — наука
Ожидаемые характеристики NGSS
MS-ETS1-1. Определите критерии и ограничения проблемы проектирования с достаточной точностью, чтобы обеспечить успешное решение, принимая во внимание соответствующие научные принципы и потенциальные воздействия на людей и окружающую среду, которые могут ограничить возможные решения.(6-8 классы)
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Нажмите, чтобы просмотреть другие учебные программы, соответствующие этим ожиданиям от результатов.
Этот урок посвящен следующим аспектам трехмерного обучения NGSS:
Наука и инженерная практика Основные дисциплинарные идеи Общие концепции
Определите проблему проектирования, которая может быть решена путем разработки объекта, инструмента, процесса или системы, и включает несколько критериев и ограничений, включая научные знания, которые могут ограничивать возможные решения.
Соглашение о выравнивании: Спасибо за ваш отзыв!
Чем точнее могут быть определены критерии и ограничения проектной задачи, тем больше вероятность того, что разработанное решение будет успешным. Спецификация ограничений включает рассмотрение научных принципов и других соответствующих знаний, которые могут ограничить возможные решения.
Соглашение о выравнивании: Спасибо за ваш отзыв!
Вся человеческая деятельность опирается на природные ресурсы и имеет как краткосрочные, так и долгосрочные последствия, как положительные, так и отрицательные, для здоровья людей и окружающей среды.
Соглашение о выравнивании: Спасибо за ваш отзыв!
Использование технологий и любые ограничения на их использование обусловлены индивидуальными или общественными потребностями, желаниями и ценностями; по результатам научных исследований; а также различиями в таких факторах, как климат, природные ресурсы и экономические условия.
Соглашение о выравнивании: Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии — Технология
ГОСТ Предложите выравнивание, не указанное выше
Какое альтернативное выравнивание вы предлагаете для этого контента?
Больше подобной программы
Достаточно фундаментальные факты о силах и структурах
Студенты знакомятся с пятью основными нагрузками: сжатие, растяжение, сдвиг, изгиб и кручение.Они узнают о различных видах напряжения, которое каждая сила оказывает на предметы.
Напряженные и деформированные
Студенты знакомятся с понятиями стресса и напряжения с примерами, которые иллюстрируют характеристики и важность этих сил в нашей повседневной жизни.Они исследуют факторы, влияющие на стресс, почему инженерам нужно знать о нем и как инженеры описывают силу материи …
Проектирование мостов
Студенты узнают о типах возможных нагрузок, о том, как рассчитать предельные сочетания нагрузок, и исследуют различные размеры балок (балок) и колонн (опор) простой конструкции моста.Кроме того, они изучают шаги, которые инженеры используют для проектирования мостов.
Восполняя пробелы
Студентам предоставляется краткая история мостов, поскольку они узнают о трех основных типах мостов: балочных, арочных и подвесных. На них действуют две естественные силы — растяжение и сжатие, общие для всех мостов и конструкций.
Введение / Мотивация
Посмотрите вокруг … что вы видите? Сооружения, сооружения везде! От ручки в руке до здания, в котором вы находитесь, вы окружены структурами всех форм и размеров. Каким был бы мир без структур? Структуры включают здания, дома, мосты, туннели и плотины — даже растения и животные имеют структуру! Инженеры, архитекторы и другие профессионалы проектируют конструкции, которые созданы для нашей повседневной безопасности, комфорта и удобства.
За прошедшие годы люди построили удивительные города и изобретательные транспортные пути, чтобы путешествовать между городами и континентами. Например, изобретение туннелей означает, что нам больше не нужно объезжать огромные горы — мы можем идти прямо через них! Мы строим мосты, чтобы перебраться с одного берега огромной реки на другой. Изобретение дамб позволило хранить огромное количество воды, чтобы обеспечить постоянное снабжение наших домов и уменьшить вероятность наводнения.
Команды архитекторов, инженеров-строителей и инженеров-механиков сделали возможным создание этих современных сооружений.Наша повседневная жизнь зависит от качества конструкций, которые они проектируют. Мы воспринимаем нашу безопасность как должное, но что, если мост рухнет, когда мы будем переходить по нему? Или, что, если бы мы были на 30-м этаже небоскреба, и он пошатнулся и рухнул на землю? Что, если обрушился второй этаж нашего дома? Представьте, что вы путешествуете по туннелю в горе, когда рухнула крыша? Без тщательно спроектированных и построенных сооружений жизнь была бы более рискованной.
Предпосылки и концепции урока для учителей
Силы растяжения и сжатия
Два основных типа сил, участвующих в строительстве любой конструкции: растяжение и сжатие .Каждый материал способен выдерживать определенное напряжение и определенное сжатие. Сила натяжения — это сила, которая разрывает материалы. Сила сжатия — это сила, при которой материал сжимается. Некоторые материалы лучше выдерживают сжатие, некоторые лучше сопротивляются растяжению, а другие хорошо использовать, когда присутствует как сжатие, так и растяжение. Например, если вы потянете за прочную веревку, она сможет выдержать большое натяжение. Если натянуть веревку, она не очень хорошо сопротивляется сжатию и просто гнется.Зефир — это пример материала, который легко сжимается, но разрывается под действием большого напряжения. Из этих примеров ясно, что материалы могут изгибаться или растягиваться под действием сжимающей или растягивающей силы. Обратитесь к соответствующему заданию «Падающая башня из макарон» для учащихся, чтобы проиллюстрировать эти силы, построив свои собственные конструкции из спагетти и зефира.
Напряжение изгиба
Когда два человека сидят на качелях, испытывает ли металлический стержень между двумя сиденьями напряжение сжатия или растяжения? Это вопрос с подвохом! «Изгибающийся стержень» испытывает как сжимающие, так и растягивающие напряжения! Чтобы визуализировать это, возьмите книгу в мягкой обложке и согните ее (см. Рис. 1).Когда вы это делаете, материалы книги «хотят» вернуться в свое нормальное состояние покоя, поэтому кажется, что верхние страницы пытаются свести пальцы вместе, потому что они находятся в напряжении, а нижние страницы раздвигают ваши пальцы, потому что они находятся в напряжении. сжатие. Гибочная гильза испытывает сжимающее и растягивающее напряжение, как гнущаяся штанга-качели!
Рис. 1. Демонстрация с использованием телефонной книги демонстрирует растягивающие и сжимающие напряжения из-за изгиба; верхние страницы растягиваются (растягиваются), а нижние страницы сдвигаются (сжатие).авторское право
Copyright © Крис Якацки, Программа и лаборатория ITL, Университет Колорадо в Боулдере, 2003.
При использовании гибочной гильзы наибольшие растягивающие и сжимающие напряжения возникают на наружных крышках; направление этих сил можно увидеть с помощью красных стрелок на рисунке 1. Нейтральная ось или слой проходит по середине книги между красными стрелками, как если бы это была средняя страница книги. Удивительно, но эта ось не испытывает нагрузок при изгибе! Это имеет практическое применение.Например, если вам когда-либо понадобится просверлить отверстие в опорной балке, например, в потолке в подвале, просверлите отверстие в центре балки, где нет напряжений (см. Рисунок 2).
Рис. 2. Диаграмма, показывающая влияние тяжелого груза на балку. Балка испытывает растяжение и сжатие. Если вес будет слишком большим, луч сломается! Copyright
Copyright © Крис Якацки, Программа и лаборатория ITL, Университет Колорадо в Боулдере, 2004.
Диаграмма на рисунке 2 показывает влияние на балку, когда на нее помещается тяжелый груз, вызывающий в балке как растяжение, так и сжатие.Вес вызывает сжатие в верхней части балки, когда она сжимается вместе, и вызывает растягивающее напряжение на нижней стороне балки, где она разрывается. Балка укорачивается сверху из-за сжатия и удлиняется снизу из-за растяжения. Имея это в виду, что бы произошло, если бы на балку поместили еще больший вес? В этом случае силы будут оказывать большее растяжение и сжатие на балку, и если бы силы были слишком большими, материал не смог бы выдержать напряжение и сломался бы пополам.
Силы растяжения и сжатия важно учитывать при проектировании здания или конструкции. Если мы построим мост из материалов, которые недостаточно прочны, чтобы выдержать такое сжатие и растяжение, которые вызывают транспортные средства, когда они проезжают по нему, мост может обрушиться! Все конструкции должны выдерживать действующие на них силы, иначе они не выдержали бы. Большая часть науки, дизайна и инженерии направлена на прогнозирование видов нагрузок, с которыми может столкнуться конструкция (например, ветер, снег, вес ванны, полной воды и т. Д.). Например, дома и мосты, построенные в Калифорнии, должны быть спроектированы так, чтобы выдерживать землетрясения.
Материалы и размер
Некоторые материалы трескаются при нагрузке на них. Эти материалы — например, лед — хрупкие. Сможете ли вы безопасно перейти реку, когда она только что замерзла? Наверное, нет, потому что слой льда тонкий и, скорее всего, потрескается. Поскольку лед хрупкий, тонкий слой не сможет противостоять сжатию и растяжению, вызванным вашим весом и движением.Но что, если вы перейдете реку, когда лед станет толщиной в полметра? В этот момент лед способен противостоять растяжению и сжатию, даже если он все еще хрупкий. Прочность конструкции зависит как от ее материалов, так и от ее размера. Эти концепции свойств материалов и размеров учитываются при строительстве мостов для транспортных средств. Например, в подвесных мостах, таких как мост Золотые Ворота в Сан-Франциско, используется стальная проволока, скрученная вместе, чтобы сделать ее настолько прочной, что диаметр всего 1 см достаточно, чтобы выдержать 8000 кг веса (два взрослых слона)!
Небоскребы и деревья
Как вы думаете, почему люди проектируют и строят огромные высокие здания? Небоскребы позволяют разместить множество предприятий на очень небольшой площади земли.Небоскребы способствуют экономическому росту и расширению, потому что в каждом городе может поместиться значительно больше отраслей и предприятий. Но опасны ли здания высотой 700–1100 футов? Неужели ветер дует против них опасно? Они много весят? Почему небоскребы не падают на землю со всей приложенной к ним силой? Небоскребы созданы для работы как деревья. Представьте себе гигантское дерево, подобное секвойю, которое может вырасти до более 350 футов в высоту. Что заставляет это огромное дерево стоять сотни лет? У него есть корни! Корни деревьев закреплены глубоко в земле, распространяются веером вокруг ствола, обеспечивая опору и прочное основание.Когда ветер дует дерево, оно изгибается, как балка, на которой лежит груз. Как и балка, ствол дерева должен выдерживать сильное сжатие и растяжение.
Небоскребы могут стоять, потому что они состоят из таких частей, как корни и ствол дерева. В небоскребах эти части называют фундаментом и каркасом. Перед тем, как построить небоскреб, глубоко в землю проводят огромные раскопки, где закладывается фундамент. Например, башни Петронас высотой 452 метра (1483 фута, 88 этажей) в Куала-Лумпуре, Малайзия, имеют фундамент, уходящий на 400 футов вглубь Земли! Стальные каркасы небоскреба — важный компонент, потому что сталь может выдерживать большие нагрузки как на растяжение, так и на сжатие (больше, чем бетон, который прочен на сжатие, но слаб на растяжение).Чем выше здание, тем важнее думать о силах, таких как ветер, которые могут на него давить. Высокие здания можно толкать ветром гораздо сильнее, чем более короткие! Ветер может оказывать на здание большую силу, поэтому здания должны быть достаточно прочными, чтобы противостоять большим силам. Самые ранние высокие здания были построены с очень толстыми внешними стенами и небольшим количеством окон. В новых разработках инженеров для увеличения прочности посредине высоких зданий помещается прочная сердцевина.Например, внутри дома часто встречаются туалеты, лифты и другие тяжелые конструкции, которые добавляют прочности высоким зданиям. Благодаря такой конструкции инженеры могут использовать более легкие внешние стены и предоставить пассажирам гораздо больше окон.
Инженеры
используют сложные математические модели для прогнозирования нагрузок на все виды конструкций. Понимание растяжения и сжатия является фундаментальным для предсказания того, как конструкции могут встать или упасть из-за сил! Студенты могут узнать больше о том, как инженеры справляются с такими сложными задачами, с помощью соответствующего мероприятия Stress, Inc.где они узнают, как восприятие служит питательной средой для многомиллиардной индустрии, направленной на минимизацию рисков и снятие стресса.
Сопутствующие мероприятия
Закрытие урока
Попросите учащихся обсудить различные строительные материалы и сделать предположения о том, подходят ли они для растяжения, сжатия или того и другого. Попросите учащихся привести примеры условий, которые могут вызвать нагрузку на конструкцию? (Примеры: вес, люди, ветер, вода, землетрясения, снег, автомобили и т. Д.) Нужно ли проектировать разные конструкции, чтобы выдерживать разные виды нагрузок? (Ответ: Да.) Каковы некоторые примеры структур, специально предназначенных для противодействия определенным силам? (Ответ: мосты для веса, перемещающегося по конструкции, небоскребы для сил, приложенных к сторонам конструкции, например, ветра.) Почему инженеры важны при создании конструкций? Какие роли они играют? (Ответ: инженеры используют сложные математические модели для прогнозирования нагрузок на всевозможные конструкции.Они проектируют конструкции, учитывая нашу повседневную безопасность, комфорт и удобство. Инженеры могут участвовать во всех этапах проектирования, строительства и обслуживания конструкции.)
Словарь / Определения
изгиб: комбинация сил, которая заставляет одну часть материала сжиматься, а другую — растягивать.
сжатие: сила, которая сжимает материал.
нейтральная ось: воображаемая плоскость, которая проходит через середину изгибаемого материала, на которой не возникает напряжения.
натяжение: сила, которая разрывает материал.
Оценка
Оценка перед уроком
Вопрос для обсуждения: Запрашивайте, объединяйте и обобщайте ответы студентов.
Что происходит с материалом, из которого сделан стол, когда вы кладете на него книгу? (Ответ: Немного гнется.) Что произойдет, если вы положите на стол действительно тяжелый груз? (Ответ: Стол сломается.) Что происходит с материалом, из которого сделана дорога, когда автомобиль проезжает по мосту? (Ответ: Тоже немного гнется). Как вы думаете, что инженеры должны учитывать, когда предлагают, какие материалы лучше всего подходят для той или иной конструкции? (Ответы: прочность материалов, виды сил, действующих на конструкцию и т. Д.)
Оценка после введения
Голосование: Задайте вопрос «правда / ложь» и попросите учащихся проголосовать, подняв палец вверх за истину и вниз за ложь.Подсчитайте голоса и запишите итоги на доске. Дайте правильный ответ.
Верно или неверно: туннели являются примером структуры. (Ответ: Верно. Сооружения можно строить как под землей, так и над землей.)
Верно или неверно: растения и животные имеют структуру! (Ответ: Верно. К строениям относятся все здания, дома, мосты, туннели, плотины, растения и животных.)
Верно или неверно: плотины значительно увеличивают вероятность затопления. (Ответ: Неверно. Плотины — это сооружения, предназначенные для уменьшения вероятности затопления.)
Верно или неверно: жизнь была бы более рискованной без тщательно спроектированных и построенных сооружений. (Ответ: Верно. Конструкции, построенные без учета приложенных к ним нагрузок и сил, могут сломаться и, возможно, нанести вред людям, животным или окружающей среде.)
Итоги урока Оценка
Командный дизайн / презентация: Работая в группах, попросите учащихся выбрать сооружение, которое они видели раньше, например, конкретное здание, туннель, плотину или мост, и записать его на листе бумаги.Затем попросите их описать свою структуру с помощью наброска с указанием используемых материалов. Попросите их объяснить, где силы растяжения и сжатия воздействуют на конструкцию; рисование стрелок может помочь. Попросите их поделиться некоторыми идеями о том, как можно улучшить их структуру, например, в отношении ее формы или материалов, из которых она построена. Наконец, предложите студенческим командам представить свои идеи классу.
Мероприятия по продлению урока
Если класс не выполнил упражнение «Разрушающие балки» на уроке 7 «Механика», проведите его как отличное упражнение на разгибание для этого урока сжатия и растяжения.Если класс построил и протестировал глиняные балки Скульпи на основе этого упражнения, попросите их обсудить, как напряжение и деформация от этого упражнения связаны с напряжением сжатия и растяжения, обсуждаемым в этом уроке.
Классный проект мышления Задача: Попросите своих учеников подумать о вещах, которые они используют в своей повседневной жизни, которые сломались из-за сжимающих и / или растягивающих напряжений. Вы можете получить некоторые из них, которые не подходят, поэтому по усмотрению учителя выберите три или четыре лучших и перечислите их на доске или где-нибудь в классе.Затем предложите учащимся (попарно) подумать, почему эти объекты не выдерживают нагрузки, и заново спроектировать объект (или спроектировать новый объект, выполняющий ту же функцию), который, скорее всего, не сломается. Студенты могут использовать Интернет для изучения альтернативных материалов и конструкций.
Попросите учащихся конкретно указать в письменном отчете следующее:
Что должен делать этот объект?
Что такого особенного в оригинальном объекте, что сделало его недостаточно прочным? Возможно, им потребуется опросить человека, который привел пример.
Дайте подробное описание вашего нового дизайна.
Как ваша новая конструкция соответствует научным концепциям напряжения сжатия и растяжения?
Представьте, что вы построили несколько прототипов этой новой идеи. Объясните, как вы будете проходить научный тест, чтобы определить, какой прототип работает лучше всего.
Проведите обсуждение результатов и попросите учащихся сдать отчет во время следующего урока.
Рекомендации
Building Big, Wonders of the World, мост Золотые Ворота, февраль 2004 г .: http: // www.pbs.org/wgbh/buildingbig/wonder/structure/golden_gate.html
Маколей, Дэвид. Здание Большое. Бостон, Массачусетс: Компания Houghton Mifflin, 2000.
Маллой, Бетси. Факты о мосте Золотые Ворота, Калифорния для посетителей. About, Inc., The New York Times Company. По состоянию на 12 сентября 2006 г. http://gocalifornia.about.com/cs/sanfrancisco/a/ggbridge_3.htm
Structures and Bridges, информационное сообщение, февраль 2004 г., по адресу: http://www.infoplease.com/ipa/A0001326.html.
Авторские права
© 2004 Регенты Университета Колорадо.
Авторы
Крис Якацки; Бен Хевнер; Малинда Шефер Зарске; Дениз Карлсон
Программа поддержки
Комплексная программа преподавания и обучения, Инженерный колледж, Университет Колорадо в Боулдере
Благодарности
Содержание этой учебной программы по цифровой библиотеке было разработано за счет гранта Фонда улучшения послесреднего образования (FIPSE), U.S. Министерство образования и Национальный научный фонд ГК-12, грант No. 0338326. Однако это содержание не обязательно отражает политику Министерства образования или Национального научного фонда, и вам не следует предполагать, что оно одобрено федеральным правительством.
Последнее изменение: 30 апреля 2021 г.
Модуль растяжения / сжатия
доступен как подэтап (модуль) или как полный «этап растяжения» до 10 кН! Также доступна версия, совместимая с EBSD.

Испытание на растяжение или испытание на растяжение / сжатие до 10 кН
Описание
Этот модуль растяжения (сжатие в качестве опции) для SEM (и ограниченный набор «атомных силовых микроскопов») подходит для предметного столика так же, как крупногабаритный образец. Испытуемые объекты должны быть длиной от 20 до 60 мм, толщиной не более 5 мм.
Ходовые винты силовой рамы имеют правую и левую резьбу на противоположных концах. Таким образом, область посередине, откуда образец удлиняется в обоих направлениях, будет стоять почти неподвижно.
Управляемая компьютером микропроцессорная электроника (DDS-3) с большим программным обеспечением (MDS) входит в стандартную поставку. Большое количество параметров испытаний и процедур экспериментов управляются с помощью меню и просты в использовании. Программа особенно подходит для циклических тестов. Многие подпрограммы, такие как компенсация индивидуального изгиба устройства и онлайн-запись модуля упругости, интегрированы. Кроме того, включены распознавание трещин, изменение скорости и многие другие функции.Например. Захват видео доступен как опция, а также многие другие функции.
В качестве альтернативы доступна система запуска с ручным управлением.
Ручной контроллер имеет ручной блок с дисплеем для перемещения и нагрузки, а также клавиатуру с потенциометром для плавной настройки скорости. Клавиши вверх и вниз со стрелками отмечены для направления нагрузки / расслабления. На задней панели контроллеров находится USB-порт, поддерживающий данные измерений.
Рекомендации по применению Bruker EBSD и модуль натяжения 5 кН
Обзор системы: см. Видео

Приложения
Статические или динамические наблюдения за изменениями поверхности при контролируемой механической нагрузке, ростом трещин, явлениями расслоения, образованием плоскостей скольжения и т. Д.
Металлы, керамика, стекло, керамические насыпные материалы или слои, гальванические покрытия, паяные или сварные соединения, минералы, древесина, органические материалы.
Это устройство для испытания материалов подходит для большинства современных этапов получения образцов с помощью SEM. Четыре небольших стойки позволяют разместить его под световым микроскопом, АСМ, лазерным или рамановским микроскопом.
Производительность
Диапазон нагрузки: от 10 мкН до 5000 Н (опция 10 кН)
Размеры образца в мм (макс. Размеры): 60 x 10 x 5
Диапазон скоростей деформаций: 0.От 1 до 20 мкм / сек. Другие диапазоны скорости по запросу.
Смещение: Модуль оборудован датчиком перемещения с линейным энкодером. Этот датчик покрывает полный диапазон перемещений до 45 мм с разрешением 100 нм.
Электрическое подключение: 230/110 В переменного тока.
Размеры модуля в мм (Ш x В x Д): 150 x 55 x 220.
Опции
Весоизмерительные ячейки: 10Н, 20Н, 50Н, 100Н, 200Н, 500Н, 1кН, 2кН, 5кН, 10кН
Экстензометр: диапазон: +/- 1 мм, разрешение: <100 нм; другое по запросу
Отопление / Охлаждение: от комнатной температуры до 1000 ° C или
+/- 100 ° C, вкл.ПИД-регулятор.
Зажим образца: для нагрузок> 500 Н, <500 Н, образец круглой формы, выбор из более чем 30 различных зажимов, изготовленных по индивидуальному заказу
Адаптация для: EBSP, дифрактометра, AFM или Synchotron.
Видеоэкстензометр: ВЭДДАК-штамм
Image-Capture: просмотр изображения по линии данных
Программный интерфейс для дистанционного управления, например LabView
…
Контроллеры
Выбор между ручным контроллером (система стартера) и микропроцессорным контроллером (DDS-3) с интерфейсом и программным обеспечением (MDS) для работы на ПК.
Модульность / гибкость
Наши системы могут быть адаптированы к вашим сегодняшним потребностям. Давайте поговорим об этом и выберем элемент из ряда уже доступных надстроек. Если он еще не разработан, давайте сделаем это, чтобы ваша задача была решена.
Эта система представляет собой группу тестовых подэтапов, которые могут работать с одного и того же контроллера.
Запросите более подробное описание сцены и компьютерного управления.
Уравнения растягивающего и сжимающего напряжения и деформации — класс физики [видео 2021]
Растяжение и сжатие
В зависимости от того, как сила приложена к объекту, он может подвергаться различным видам напряжения и деформации.Двумя наиболее распространенными типами являются растягивающие и сжимающие напряжения и деформации. Когда объект находится под напряжением ниже , он увеличивается в длине. Растягиваемая резинка — типичный пример объекта, испытывающего растягивающее напряжение и деформацию. Противоположность растяжению — сжатие , где объект претерпевает уменьшение длины. Если вы когда-либо сжимали в руках резиновый мяч или пищалку для домашнего животного, вы создавали сжимающее напряжение и деформацию в объекте.
В случае деформации растяжения и сжатия математическое определение — это изменение длины, деленное на исходную длину объекта. Разница между ними в том, как изменяется длина. Для растяжения это увеличение длины, а для сжатия — уменьшение длины. Если мы хотим разделить их на два разных уравнения, мы можем записать их следующим образом.
Модуль упругости и закон Гука
Любой объект способен испытывать растягивающие и сжимающие напряжения и деформации, но не все реагируют на это напряжение в одинаковой степени.Представим, что у вас в руках два небольших кубика. Один из стали, другой — из резины. Если к ним обоим приложить одинаковую нагрузку, кто из них будет испытывать большее напряжение? Какой будет растягиваться или сжиматься дальше? Вы знаете, что это будет резиновый блок. Стальной блок намного жестче, чем резиновый, и не растягивается и не сжимается так сильно.
В физике мы можем использовать так называемый модуль упругости для измерения жесткости материала.Оказывается, все, что нам нужно для определения модуля упругости, — это напряжение, приложенное к объекту, и деформации, которые он испытывает. Мы можем записать модуль упругости как отношение двух. Итак, модуль упругости равен напряжению, деленному на деформацию.
Модуль упругости на самом деле постоянный. Это означает, что любой материал всегда будет иметь один и тот же модуль упругости. Если мы изменим уравнение, чтобы получить стресс сам по себе, мы увидим кое-что интересное.Уравнение можно получить в виде
Это не сразу очевидно, но вы, возможно, уже видели подобное уравнение раньше. У вас есть напряжение, сила на единицу площади, равная постоянной, умноженной на деформацию, смещение. Это очень похоже на закон Гука, который вы, возможно, видели для пружин, где сила равна постоянной пружины, умноженной на смещение.
Оказывается, наше преобразованное уравнение модуля упругости также является законом Гука.Наше преобразованное уравнение модуля упругости является более общей формой закона Гука, применимого ко всем материалам, а не только к пружинам. Закон Гука показывает нам, что напряжение, необходимое для растяжения или сжатия материала, прямо пропорционально расстоянию, на которое он растягивается или сжимается.
Кривая напряжения-деформации
Еще один интересный способ сравнить напряжение и деформацию — это посмотреть на график этих двух величин.
Для создания этого графика к материалу прикладывается напряжение до тех пор, пока он не сломается.Мы можем немного узнать о материале, глядя на кривую графика. В начале нашего графика есть крутая диагональная линия, направленная вверх. После крутой диагональной линии вы увидите, что кривая начинает изгибаться. В начале этого изгиба находится предел пропорциональности . После этого закон Гука больше не применяется к нашему материалу. После предела пропорциональности на пике изгиба нашей кривой находится предел упругости . Диапазон от начала кривой до предела упругости известен как область упругости .В этой области, если вы перестанете подвергать наш материал нагрузке, он вернется к своей первоначальной форме.
По истечении предела упругости материал теряет эластичность. Мы называем диапазон от этой точки до конца нашего графика пластмассовой областью , потому что материал становится пластичным, как пластик. После приложения напряжения материал не полностью вернется к своей первоначальной длине. В конце нашего изгиба, где кривая снова начинает выпрямляться, находится предел текучести .С этого момента достаточно небольшого напряжения, чтобы значительно изменить длину нашего материала. Мы можем видеть это, потому что кривая намного менее крутая, чем раньше. Наконец, в конце нашей кривой, где она внезапно останавливается, находится точка перелома . Здесь материал порвался. Например, если материал испытывал напряжение растяжения, в этот момент он мог расколоться на две части.
Итоги урока
Когда на объект действует сила, она может создавать в нем напряжение и деформацию. Напряжение — это внутренняя сила на единицу площади, а деформация, которой подвергается объект из-за напряжения, — это деформация . Двумя наиболее распространенными типами напряжения и деформации являются растягивающее и сжимающее напряжение и деформация. Растяжение означает увеличение длины объекта, а сжатие означает уменьшение длины.
Из напряжения и деформации мы можем определить модуль упругости материала , который является мерой жесткости материала.Затем мы можем использовать модуль упругости, чтобы найти формулу закона Гука, которая работает для всех материалов, а не только для пружин. Эта общая форма закона Гука показывает нам, что напряжение, необходимое для растяжения или сжатия материала, прямо пропорционально расстоянию, на которое он растягивается или сжимается.
Наконец, мы можем многому научиться, глядя на график зависимости напряжения от деформации для материала. Мы можем видеть диапазон напряжений и деформаций, для которых материал обладает упругими свойствами и для которых он податлив, как пластик.Мы называем эти два диапазона упругой областью и пластической областью . При переходе между этими двумя областями мы также можем увидеть точку, в которой закон Гука перестает применяться к материалу, и точку, в которой начинает действовать лишь небольшое напряжение, чтобы вызвать большую деформацию. Наконец, кривая резко обрывается в точке разрыва материала из-за напряжения.
Результаты обучения
Достигните следующих целей после изучения тем в этом уроке:
Различайте стресс и напряжение и перечислите два общих типа
Контрастное растяжение и сжатие
Напишите модуль упругости и вычислите формулу закона Гука
Проиллюстрируйте график кривой зависимости напряжения от деформации и поймите, что он показывает
Свойства при растяжении, сжатии и разрушении толстостенных компонентов из высокопрочного чугуна
Свойства при растяжении
На протяжении всех выполненных анализов результаты испытаний на растяжение IE и GF показали одинаковые тенденции.Более того, не наблюдалось значительного эффекта от тестирования образцов разных размеров. Следовательно, все полученные данные о растяжении рассматриваются вместе в следующих обсуждениях.
Для каждого эксперимента на растяжение, проведенного в IE, была записана полная инженерная кривая напряжения-деформации. Исходя из измерений осевой деформации, можно было вывести кривые истинное напряжение — истинная деформация, по крайней мере, во время равномерного удлинения, то есть до образования шейки. Эти данные истинное напряжение — истинная деформация были необходимы для вероятностного анализа разрушения контейнеров, чтобы рассчитать пластические нагрузки на обрушение с помощью расчетов методом конечных элементов.Для вставки I25 кривые растяжения для разных образцов показали небольшие отклонения до тех пор, пока разрушение не произошло при различных уровнях напряжения и деформации. То же самое относится и к вставке I26, которая четко проиллюстрирована техническими кривыми растяжения, приведенными на рис. 5. Это наблюдение предполагает, что разрушение было вызвано дефектами, присутствующими в ковком чугуне. Кривые растяжения I24 показали большее разнообразие, особенно в верхней области вставки, что указывает на микроструктурные различия в дополнение к дефектам.Ковкий чугун I26 в ходе экспериментов достиг значительно более высоких уровней напряжения, чем материалы I24 и I25, как показано на рис. 6. Это наблюдение должно быть связано с более высоким уровнем Mn, связанным со вставкой I26, что приводит к более высокому содержанию перлита.
Рис. 5
Инженерные кривые растяжения, полученные из экспериментов I26, демонстрирующие идентичные тенденции до тех пор, пока не произойдет разрушение при разных уровнях напряжения-деформации
Рис. 6
Типичные тренды кривых истинного напряжения — истинной деформации, относящиеся к пластинам I24, I25 и I26
Предел текучести и напряжение текучести являются важными конструктивными характеристиками материала, которые связаны с определенной допустимой остаточной деформацией.В зависимости от используемой методологии вероятностный анализ отказов может потребовать предела текучести или напряжения течения в качестве стохастической входной переменной. Стандартно для металлических материалов, которые не имеют четко определенного предела текучести, было измерено 0,2% условного предела текучести, т.е. инженерное напряжение, соответствующее 0,2% инженерной пластической деформации. В таблице 3 приведены средние значения и стандартные отклонения данных R _p0.2, измеренные для трех условий отбора проб в каждой вставке: продольный верхний, поперечный верхний и поперечный нижний.Рисунок 7 представляет ту же информацию в графическом формате; каждая показанная полоса погрешности соответствует среднему значению плюс и минус одно стандартное отклонение (ссылка 8). Средние значения, наблюдаемые для вставки I26, явно выше, чем измеренные для I24 и I25, из-за более высокого содержания перлита. Для канистры I24 нижнее расположение работало значительно лучше, чем верхняя часть вставки, что также давало более высокие полосы рассеяния. Следует отметить, что различные индивидуальные наборы данных (т.е. для каждого условия выборки) обычно имеют нормальное распределение.Это было проверено с помощью теста нормальности Шапиро-Уилка, который подходит для относительно небольших популяций. После проведения дисперсионного анализа (ANOVA) стало даже очевидно, что все данные I26 0,2% по условному напряжению можно рассматривать вместе как одну нормальную популяцию (ссылка 8). Это проиллюстрировано на рис. 8. Использование напряжения течения, т. Е. Среднего значения 0,2% условного напряжения и предела прочности при растяжении, в анализе структурной целостности позволяет добиться более высокой пластической деформации. Эти данные о напряжении течения (σ _расход) представлены таким же образом, как и для R . _п0.2 результатов: см. Таблицу 4 и Рис. 9. Почти все наборы данных показали нормальное распределение. Также здесь нижняя часть вставки I24 работает значительно лучше, чем верхняя область, которая фактически была единственной областью, приводящей к низким средним значениям и более высоким полосам разброса.
Таблица 2 Химический анализ (массовая доля) высокопрочного чугуна, используемого для изготовления вставок канистр I24, I25 и I26 Таблица 3 0,2% Испытательное напряжение ( R _p0.2) средние значения и соответствующие стандартные отклонения Фиг.7
Средние значения условного сопротивления текучести 0,2% и планки погрешностей (= ± стандартное отклонение) в зависимости от 1 / вставки контейнера (I24, I25, I26), 2 / области отбора проб (вверху, внизу) и 3 / ориентации образца (продольной, поперечный)
Рис. 8
Вставка канистры I26, общие данные по условному пределу текучести 0,2%, показывающие нормальное распределение
Рис.9
Средние значения напряжения течения и планки погрешностей (= ± стандартное отклонение) в зависимости от 1 / вставки канистры (I24, I25, I26), 2 / области отбора проб (вверху, внизу) и 3 / ориентации образца ( продольный, поперечный)
Таблица 4 Средние значения напряжения потока (σ _расход) и соответствующие стандартные отклонения
Помимо свойств, связанных с определенной (ограниченной) величиной допустимой пластической деформации, также внимательно рассматривалось относительное удлинение после разрушения, связанное с разрушением, иногда в сочетании с пределом прочности при растяжении.Относительное удлинение после разрушения не используется в качестве прямого ввода для анализа структурной целостности, но оно является хорошим показателем локальной пластичности материала и, как будет показано ниже, также является отличным косвенным показателем размера дефектов литья, присутствующих в образце. . На рисунке 10 представлена модель R . _м — Соотношение для вставок канистр I24 и I26. Наблюдалась четкая тенденция: увеличение значений A шло вместе с увеличением R _м цифр до более-менее постоянной р _{м Достигнута отметка}.Свыше этого максимума R _{м Уровень}, еще виден был разброс А . Подобно наблюдениям, сделанным для предела текучести 0,2%, самый высокий предел прочности был обнаружен для I26 из-за более высокого содержания в нем перлита. В то же время более высокое содержание перлита привело к снижению максимальной пластичности. Также для данных об удлинении после разрушения показаны вариации в зависимости от местоположения и ориентации отбора проб: см. Таблицу 5 и Рис. 11 (Ссылка 8). Как правило, наблюдался значительный разброс как между вставками канистр, так и внутри них.Для различных мест были обнаружены как низкие средние значения, так и большие стандартные отклонения. Что касается I24, существует большая разница между результатами для верхней и нижней части канистры, и еще раз с лучшими результатами для нижней части. Из таблицы 1 очевидно, что многие образцы не соответствовали требованиям стандарта EN 1563.
Рис. 10
Предел прочности при растяжении как функция удлинения после разрушения для всех испытаний на растяжение I24 и I26
Рис. 11
Удлинение после разрушения средние значения и планки погрешностей (= ± стандартное отклонение) как функция 1 / вставка контейнера (I24, I25, I26), 2 / область отбора проб (верхняя, нижняя) и 3 / ориентация образца (продольный, поперечный)
Таблица 5 Относительное удлинение после разрушения ( A ), средние значения и соответствующие стандартные отклонения
Характеристики сжатия
Как уже было сказано, вставки канистр в основном предназначены для условий сжимающей нагрузки.По этой причине также была проведена ограниченная серия испытаний на сжатие. На рис. 12 кривые истинное напряжение сжатия — истинная деформация, полученные для трех вставок контейнера, сравниваются с тремя выбранными графиками истинного напряжения при растяжении — истинной деформации, соответствующих той же ориентации выборки (верхняя продольная). Для испытаний на сжатие кривые всегда можно было развить до высоких значений деформации, так как не происходило разрушения, и поскольку во время экспериментов можно было предполагать равномерное сжатие в пределах измерительной длины экстензометра.Как было обнаружено при испытании на растяжение, материал вставки I26 контейнера привел к более высоким уровням сжимающего напряжения, чем полученный для вставок I24 и I25, которые имели сравнимые характеристики сжатия. Очевидно, что ковкий чугун показал более выраженное деформационное упрочнение при сжатии, чем при растяжении, определенно до истинных значений деформации примерно 5% (см. 9). Показатели деформационного упрочнения оценивались с использованием следующего степенного закона типа Рамберга-Осгуда (ссылка 10):
$$ \ varepsilon _ {\ rm true} = \ frac {\ sigma _ {\ rm true}} {E} \ left [ {1+ \ alpha \ left ({\ frac {\ left | \ sigma _ {\ rm true} \ right |} {\ sigma_ {0}}} \ right) ^ {n-1}} \верно] $$
с: E (МПа): модуль Юнга (170 000 МПа для всех посадок) n : показатель деформационного упрочнения α: смещение «текучести» в том смысле, что при σ _{истинно} = σ ₀, ɛ _{истинно} = [1 + α] σ ₀/ E
Фиг.12
Все кривые истинного напряжения при сжатии и истинной деформации измерены вместе с тремя выбранными графиками истинного напряжения при растяжении и истинной деформации (одинаковая ориентация выборки)
Полученные средние показатели деформационного упрочнения при сжатии, а также эквивалентные значения растяжения приведены в таблице 6. Также включены значения σ ₀, которые тесно связаны с пределами пропорциональности. Однако следует отметить, что посадки Рамберга-Осгуда в целом были довольно плохими в области урожайности.
Таблица 6 Средние параметры сжатия при сжатии Рамберга-Осгуда n (показатель деформационного упрочнения) и σ ₀, вместе с соответствующими значениями растяжения из трех выбранных экспериментов на растяжение (та же ориентация образца: верхний продольный)
В Таблице 7 приведены средние значения условного предела текучести при сжатии 0,2% вместе с эквивалентными значениями растяжения, найденными для той же ориентации выборки (верхняя плита, продольное направление). Ясно, что значения сжатия лишь немного выше, чем полученные при растягивающей нагрузке (см. 9).
Таблица 7 0,2% Данные о испытательном напряжении, полученные в результате экспериментов по сжатию, вместе со значениями растяжения, относящимися к той же ориентации образца (т. Е. Продольной верхней части)
Данные о начале разрушения
Все образцы, которые были испытаны в IE, показали стабильное распространение вязких трещин. Случаев хрупкого разрушения не наблюдалось. Следует сказать, что вероятность наличия дефекта отливки в критическом объеме материала вокруг распространяющейся трещины довольно мала и что следует ожидать меньшего изменения вязкости разрушения, чем наблюдаемое при удлинении после разрушения.Значительное количество образцов показало крайне неравномерный фронт окончательной трещины — пример представлен на рис. 13 — и, следовательно, действительный J _Ic данные не могут быть получены для этих тестовых столбцов. Тем не менее было решено использовать результаты этих экспериментов и сообщить о «неквалифицированном» J _Q значений для всех выполненных тестов. В таблице 8 приведены эти J _Q данные, измеренные для трех вставок канистр в различных точках отбора проб (ссылка 11).Пластина I26 показывает значительно более низкую вязкость разрушения, чем другие пластины. Это опять же должно быть связано с более высоким содержанием перлита. Фактические изменения в пластинах в дальнейшем не исследовались в отношении возможных фрактографических или металлографических особенностей. Для вероятностного анализа конкретной канистры, интеграл J вблизи начала расширения трещины был введен как одна единственная стохастическая переменная, характеризующая всю вставку. По этой причине общие средние значения и стандартные отклонения были включены в Таблицу 8.Согласно тесту нормальности Шапиро-Уилка, глобальные наборы данных I24 и I25 показывают нормальное распределение. Для вставки I26 это не тот случай, но это просто из-за одной единственной низкой точки данных.
Рис. 13
Поверхность излома из вставки I24 испытательного образца, демонстрирующая неровный фронт окончательной трещины
Таблица 8 J — интегральные значения около начала устойчивого распространения трещины (средние значения и стандартные отклонения)
Максимальная сила бедра человека — Физика тела: движение к метаболизму
В отличие от сил растяжения, силы сжатия создаются материалом в ответ на сжатие, а не на растяжение.Сопротивление материалов деформации — это то, что вызывает нормальную силу (опорную силу), которую мы ввели в устройство в балансе. Например, бедро сжимается, поддерживая вес верхней части тела человека.
Бедренная кость человека. Изображение предоставлено: анатомография через Wikimedia Commons
«В анатомии человека бедренная кость (бедренная кость) — самая длинная и самая большая кость. Наряду с височной костью черепа это одна из двух самых крепких костей в организме. Средняя длина бедренной кости взрослого мужчины составляет 48 см (18.9 дюймов ) в длину и 2,34 см (0,92 дюймов ) в диаметре и может выдерживать вес, в 30 раз превышающий вес взрослого человека ». Средний вес взрослых мужчин в США составляет 196 фунтов ( 872 N ). Согласно заявлению, что бедренная кость может выдержать 30-кратную массу тела, бедренная кость взрослого мужчины может выдержать примерно 6000 фунтов сжимающей силы! Такие высокие силы редко создаются организмом самостоятельно, поэтому столкновения автомобилей являются причиной номер один переломов бедренной кости.
Размер объекта влияет на то, как он деформируется в ответ на приложенные силы сжатия и растяжения. Например, максимальная сила сжатия или растяжения, которую может выдержать кость, зависит от ее размера. В частности, чем больше площади доступно для распределения силы, тем большее усилие может выдержать кость. Это означает, что максимальное усилие, которое могут выдержать кости (и другие объекты), пропорционально площади поперечного сечения кости, перпендикулярной (90, °, ) направлению силы.Например, сила, которую бедренная кость может поддерживать в вертикальном направлении по своей длине, зависит от площади ее горизонтального поперечного сечения, которая является примерно круглой и несколько полой (костный мозг заполняет центральное пространство).
Эти поперечные сечения показывают середину диафиза бедренной кости 84-летней женщины с запущенным остеопорозом (справа) по сравнению со здоровой бедренной костью 17-летней женщины (слева). Кредит изображения: Смитсоновский национальный музей естественной истории
Более крупные кости и сухожилия могут выдерживать большее усилие, поэтому для анализа поведения самого костного материала нам нужно разделить прилагаемую силу на площадь поперечного сечения ().Результирующая величина известна как напряжение (σ) на материале. Напряжение имеет единицы силы на площадь, поэтому в системе СИ используются ( Н / м ² ), которые также известны как Паскали. Фунты на квадратный дюйм ( фунтов на квадратный дюйм, , фунтов / дюйм ² ) распространены в США
.
(1)
Максимальное напряжение, которое кость или любой другой материал может испытать до того, как материал начнет разрушаться или разорвется, называется предельной прочностью. Обратите внимание, что прочность материала определяется в терминах напряжения, а не силы, поэтому мы анализируем сам материал, не включая влияние на то, сколько материала присутствует.Для некоторых материалов предел прочности отличается, когда напряжение действует на раздавливание материала (сжатие), и когда действуют силы, растягивающие материал при растяжении, поэтому мы часто ссылаемся на предел прочности на растяжение или предел прочности на сжатие. Например, предел прочности на сжатие бедренной кости человека составляет 205 МПа (205 миллионов Паскалей) при сжатии по ее длине. Предел прочности бедренной кости при растяжении по длине составляет 135 МПа .Наряду с костью, бетон и мел являются другими примерами материалов с различным пределом прочности на сжатие и растяжение.
Повседневный пример: максимальная прочность бедренной кости
Давайте проверим, согласуются ли измеренные значения предела прочности на сжатие с утверждением о том, что бедренная кость человека может выдерживать 30-кратную массу тела взрослого человека, или примерно 6000 фунтов
Сначала преобразуем заявленные 6000 фунтов силы в Ньютоны и будем работать в единицах СИ.
Примерная минимальная площадь поперечного сечения бедренной кости составляет. ( * См. Нижнюю часть этого примера, если вам интересно узнать, как мы аппроксимировали это значение ). Мы делим сжимающую силу на площадь поперечного сечения, чтобы найти сжимающее напряжение на кости.
Наше приблизительное значение предельной прочности кости, которая потребуется для поддержки 30-кратного веса тела, составляло 80 МПа , что на самом деле меньше измеренного значения 205 МПа , поэтому утверждение, что бедренная кость может выдерживать 30-кратный вес тела кажется разумным.
* Вот как мы приблизительно рассчитали площадь поперечного сечения бедренной кости, пропустите, если вас не интересует:
Сначала мы делим диаметр бедренной кости 2,34 см , указанный ранее, на два, чтобы найти радиус бедренной кости, а затем переводим в стандартные единицы измерения.
Используя уравнение для площади круга, мы вычисляем общую площадь бедренной кости:
Наконец, мы должны вычесть площадь полой средней части, чтобы получить чистую площадь кости.Мы использовали линейку на приведенном выше изображении поперечных сечений бедренной кости, чтобы увидеть, что внутренний радиус составляет примерно половину внешнего радиуса, или, таким образом, мы вычислили недостающую внутреннюю площадь:
И вычтите из общей суммы внутреннюю площадь:
До сих пор мы обсуждали предел прочности вдоль длинной оси бедренной кости, известной как продольное направление. Некоторые материалы, такие как кость и дерево, имеют разную предельную прочность по разным осям.Предел прочности на сжатие для кости по короткой оси (в поперечном направлении) составляет 131 МПа , или примерно на 36 % меньше продольного значения 205 МПа . Материалы, которые имеют разные свойства по разным осям, известны как анизотропные. Материалы, которые ведут себя одинаково во всех направлениях, называются изотропными.
Интересный факт, чтобы завершить эту главу: когда человек стоит, бедренная кость действительно испытывает сжимающие и растягивающие напряжения с разных сторон кости.Это происходит потому, что структура тазобедренного сустава переносит нагрузку веса тела в сторону, а не прямо вдоль длинной оси кости.
В положении стоя к бедренной кости прикладываются как растягивающие, так и сжимающие нагрузки. Изображение предоставлено: Blausen Medical через Wikimedia Commons
(PDF) Усталость при растяжении, сжатии и сдвиге пенопласта с закрытыми порами
18
[3] Берман М. и Зенкерт Д., «Усталость многослойных балок с пенопластом, часть II: влияние
первоначальных повреждений» , Int.J. of Fatigue, 1997; 19 (7): 563-578.
[4] Шеной Р.А., Кларк С.Д. и Аллен Х.Г., «Усталостное поведение полимерных композитных балок
сэндвич-панелей», J. Comp. Мат, 1995; 29 (18): 2423-2445.
[5] Buene L., Echtermeyer A.T. и Сунд О.Е. «Усталостные свойства материалов с сердечником из пенопласта
», Отчет Det Norske Veritas 91-2049, 1991.
[6] Канни К. и Махфуз Х. «Характеристики усталости при изгибе многослойных конструкций при
различных скорость загрузки », Комп.Struct., 2005; 67 (4): 403-410.
[7] Канни К., Махфуз Х., Карлссон Л.А., Томас Т. и Джилани С., «Динамический
механический анализ и усталость при изгибе пен ПВХ», Comp. Struct., 2002; 58 (2). Комп. Struct., 2003;
59 (4): 499-505.
[9] Маккалоу К.Ю.Г., Флек Н.А. и Эшби М.Ф., «Усталостное поведение
пен из алюминиевого сплава», Fat. & Фракт. Engng. Мат. & Struct., 2000; 23 (3): 199-208.
[10] Харт А.-М., Флек Н.А. и Эшби М.Ф., «Усталостное разрушение открытого и закрытого пенопласта из алюминиевого сплава
», Acta Mater .

Ожидаемые характеристики NGSS
MS-ETS1-2.Оцените конкурирующие проектные решения, используя систематический процесс, чтобы определить, насколько хорошо они соответствуют критериям и ограничениям проблемы. (6-8 классы) Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Нажмите, чтобы просмотреть другие учебные программы, соответствующие этим ожиданиям от результатов.

В этом упражнении основное внимание уделяется следующим аспектам трехмерного обучения NGSS:
Наука и инженерная практика	Основные дисциплинарные идеи	Общие концепции
Оцените конкурирующие проектные решения на основе совместно разработанных и согласованных критериев проектирования. Соглашение о выравнивании: Спасибо за ваш отзыв!	Существуют систематические процессы для оценки решений в отношении того, насколько хорошо они соответствуют критериям и ограничениям проблемы. Соглашение о выравнивании: Спасибо за ваш отзыв!

Ожидаемые характеристики NGSS
MS-ETS1-1. Определите критерии и ограничения проблемы проектирования с достаточной точностью, чтобы обеспечить успешное решение, принимая во внимание соответствующие научные принципы и потенциальные воздействия на людей и окружающую среду, которые могут ограничить возможные решения.(6-8 классы) Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Нажмите, чтобы просмотреть другие учебные программы, соответствующие этим ожиданиям от результатов.

Этот урок посвящен следующим аспектам трехмерного обучения NGSS:
Наука и инженерная практика	Основные дисциплинарные идеи	Общие концепции
Определите проблему проектирования, которая может быть решена путем разработки объекта, инструмента, процесса или системы, и включает несколько критериев и ограничений, включая научные знания, которые могут ограничивать возможные решения. Соглашение о выравнивании: Спасибо за ваш отзыв!	Чем точнее могут быть определены критерии и ограничения проектной задачи, тем больше вероятность того, что разработанное решение будет успешным. Спецификация ограничений включает рассмотрение научных принципов и других соответствующих знаний, которые могут ограничить возможные решения. Соглашение о выравнивании: Спасибо за ваш отзыв!	Вся человеческая деятельность опирается на природные ресурсы и имеет как краткосрочные, так и долгосрочные последствия, как положительные, так и отрицательные, для здоровья людей и окружающей среды. Соглашение о выравнивании: Спасибо за ваш отзыв! Использование технологий и любые ограничения на их использование обусловлены индивидуальными или общественными потребностями, желаниями и ценностями; по результатам научных исследований; а также различиями в таких факторах, как климат, природные ресурсы и экономические условия. Соглашение о выравнивании: Спасибо за ваш отзыв!

Сопромат. Статически неопределимые задачи растяжения-сжатия 2.0

Основные типы задач при расчете на прочность растянутых (сжатых) стержней

Решение задач по сопромату на растяжение сжатие.

Решение задач по сопромату на растяжение сжатие.

Задача 1. Растяжение и сжатие. Задача 2. Кручение валов. — Контрольная работа #1501036 — Сопротивление материалов

Сопромат online | 1.1. Расчет ступенчатого стержня без учета собственного веса

Открытый урок на тему «Растяжение — сжатие» | Методическая разработка по теме:

Типы мостов: растягивающие и сжимающие силы — мероприятие

Быстрый просмотр

Резюме

Инженерное соединение

Цели обучения

Образовательные стандарты

Список материалов

Рабочие листы и приложения

Больше подобной программы

Введение / Мотивация

Процедура

Словарь / Определения

Оценка

Вопросы безопасности

Расширения деятельности

Масштабирование активности

Рекомендации

Авторские права

Авторы

Программа поддержки

Сильное как самое слабое звено — Урок

Быстрый просмотр

Резюме

Инженерное соединение

Цели обучения

Образовательные стандарты

Больше подобной программы

Введение / Мотивация

Предпосылки и концепции урока для учителей

Сопутствующие мероприятия

Закрытие урока

Словарь / Определения

Оценка

Мероприятия по продлению урока

Рекомендации

Авторские права

Авторы

Программа поддержки

Благодарности

Модуль растяжения / сжатия

Описание

Приложения

Производительность

Опции

Контроллеры

Модульность / гибкость

Уравнения растягивающего и сжимающего напряжения и деформации — класс физики [видео 2021]

Растяжение и сжатие

Модуль упругости и закон Гука

Кривая напряжения-деформации

Итоги урока

Результаты обучения

Свойства при растяжении, сжатии и разрушении толстостенных компонентов из высокопрочного чугуна

Свойства при растяжении

Характеристики сжатия

Данные о начале разрушения

Максимальная сила бедра человека — Физика тела: движение к метаболизму

Повседневный пример: максимальная прочность бедренной кости

(PDF) Усталость при растяжении, сжатии и сдвиге пенопласта с закрытыми порами

Добавить комментарий Отменить ответ