Устойчивость сжатых стержней | ПроСопромат.ру

Продольный изгиб 

При расчетах на прочность подразумевалось, что равновесие конструкции под действием внешних сил является устойчивым. Однако выход конструкции из строя может произойти  из-за того, что равновесие конструкций в силу тех или иных причин окажется неустойчивым. Во многих случаях, кроме проверки прочности, необходимо производить еще проверку устойчивости элементов конструкций.

Состояние равновесия считается устойчивым, если при любом возможном отклонении системы от положения равновесия возникают силы, стремящиеся вернуть её в первоначальное положение. 

Рассмотрим известные виды равновесия.

Неустойчивое равновесное состояние будет в том случае, когда хотя бы при одном из возможных отклонений системы от положения равновесия возникнут силы,

стремящиеся удалить её от начального положения.

Состояние равновесия будет безразличным, если при разных отклонениях системы от положения равновесия возникают силы, стремящиеся вернуть её в начальное положение, но хотя бы при одном из возможных отклонений система продолжает оставаться в равновесии при отсутствии сил, стремящихся вернуть её в начальное положение или удалить от этого положения.

При потере устойчивости характер работы конструкции меняется, так как этот вид деформации переходит в другой, более опасный, способный привести её к разрушению при нагрузке значительно меньшей, чем это следовало из расчета на прочность. Очень существенно, что потеря устойчивости сопровождается нарастанием больших деформаций, поэтому явление это носит характер катастрофичности.

При переходе от устойчивого равновесного состояния к неустойчивому конструкция проходит через состояние безразличного равновесия. Если находящейся в этом состоянии конструкции сообщить некоторое небольшое отклонение от начального положения, то по прекращении действия причины, вызвавшей это отклонение, конструкция в исходное положение уже не вернется, но будет способна сохранить приданное ей, благодаря отклонению, новое положение.

Состояние безразличного равновесия, представляющее как бы границу между двумя основными состояниями – устойчивым и неустойчивым, называется критическим состоянием. Нагрузка, при которой конструкция сохраняет состояние безразличного равновесия, называется критической нагрузкой.

Эксперименты показывают, что обычно достаточно немного увеличить нагрузку по сравнению с её критическим значением, чтобы конструкция из-за больших деформаций потеряла свою несущую способность, вышла из строя. В строительной технике потеря устойчивости даже одним элементом конструкции вызывает перераспределение усилий во всей конструкции и нередко влечет к аварии.

Изгиб стержня,связанный с потерей устойчивости, называется продольным изгибом.

Критическая сила. Критическое напряжение

Наименьшая величина сжимающей силы, при которой первоначальная форма равновесия стержня – прямолинейная становится неустойчивой – искривленной, называется критической.

При исследовании устойчивости форм равновесия упругих  систем первые шаги были сделаны Эйлером.

В упругой стадии деформирования стержня при напряжениях, не превышающих предел пропорциональности, критическая сила вычисляется по формуле Эйлера:

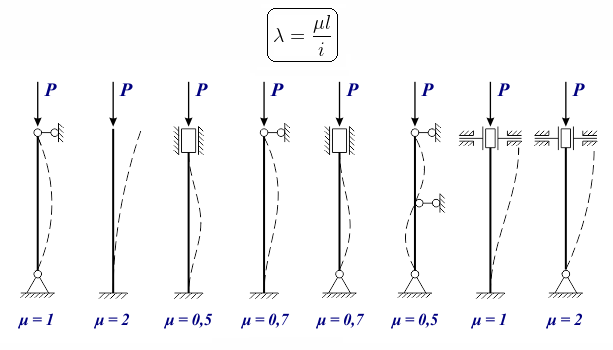
где I_min –

минимальный момент инерции сечения стержня (обусловлено тем, что изгиб стержня происходит в плоскости с наименьшей жесткостью), однако исключения могут быть только в случаях, когда условия закрепления концов стержня различны в разных плоскостях, ℓ — геометрическая длина стержня, μ – коэффициент приведенной длины или коэффициент приведения (зависит от способов закрепления концов стержня), Значения μ приведены под соответствующей схемой  закрепления стержней 

Критическое напряжение вычисляется следующим образом

, где  гибкость стержня  ,

а  радиус инерции сечения.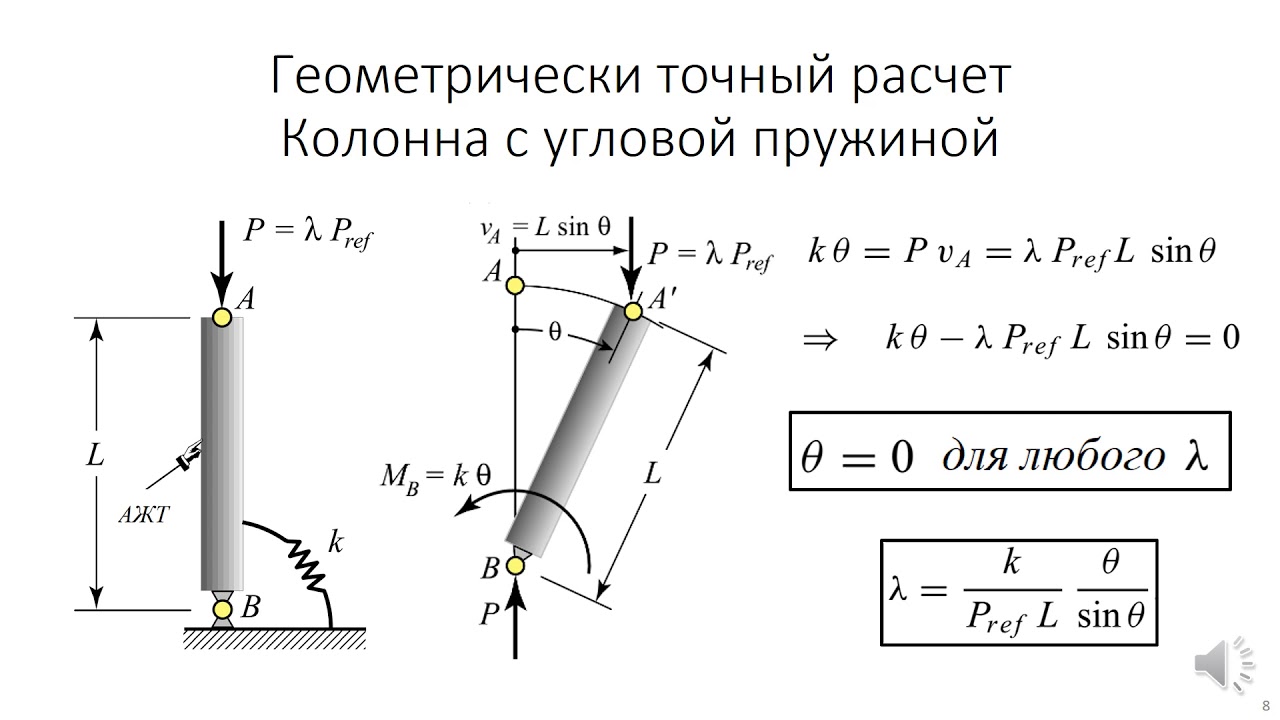

Введем понятие предельной гибкости.

Величина λ_пред зависит только от вида материала: 

Если у стали 3  Е=2∙10¹¹Па, а σ_пц=200МПа, то предельная гибкость

Для дерева (сосна, ель) предельная гибкость λпред=70, для чугуна λпред=80

Таким образом, для стержней большой гибкости λ≥λ_пред критическая сила определяется по формуле Эйлера.

В упругопластической стадии деформирования стержня, когда значение гибкости находится в диапазоне λ₀≤λ≤λ_пр, (стержни средней гибкости) расчет  проводится по эмпирическим формулам, например, можно использовать формулу Ясинского Ф.С. Значения введенных в нее параметров определены эмпирически для каждого материала.

σ_к=а-bλ,               или               F_кр= A(a— bλ)   

где a и  b – постоянные, определяемые экспериментальным путем (эмпирические коэффициенты).Так, для стали3  а=310МПа, b=1,14МПа.

При значениях гибкости стержня 0≤λ≤λ₀ (стержни малой гибкости) потеря устойчивости не наблюдается.

Таким образом, пределы применимости формулы Эйлера — применяется только в зоне упругих деформаций.

Условие устойчивости. Типы задач при расчете на устойчивость. Коэффициент продольного изгиба

Условием устойчивости сжатого стержня является неравенство:

Здесь допускаемое напряжение по устойчивости [σуст] — не постоянная величина, как это было в условиях прочности, а зависящая от следующих 

факторов:

1)    от длины стержня, от размеров и даже от формы поперечных сечений,

2)    от способа закрепления концов стержня,

3)    от материала стержня.

Как и всякая допускаемая величина, [σуст] определяется отношением опасного для сжатого стержня напряжения к коэффициенту запаса. Для сжатого стержня опасным является так называемое критическое напряжение σкр, при котором стержень теряет устойчивость первоначальной формы равновесия.

Поэтому 

Величину коэффициента запаса в задачах устойчивости принимают несколько большей, чем значение коэффициента запаса прочности, то есть если k=1÷2, то kуст=2÷5.

Допускаемое напряжение по устойчивости можно связать с допускаемым напряжением по прочности:

В этом случае ,

где σт – опасное с точки зрения прочности напряжение (для пластичных материалов это предел текучести, а для хрупких – предел прочности на сжатие σвс).

Коэффициент φ<1 и потому называется коэффициентом снижения основного допускаемого напряжения, то есть [σ] по прочности,  или иначе коэффициентом продольного изгиба.

С учетом сказанного условие устойчивости сжатого стержня принимает вид:

Численные значения коэффициента φ выбираются из таблиц в зависимости от материала и величины гибкости стержня , где:

μ – коэффициент приведенной длины (зависит от способов закрепления концов стержня), ℓ

 — геометрическая длина стержня,

i – радиус инерции поперечного сечения  относительно той из главных центральных осей сечения, вокруг которой будет происходить поворот поперечных сечений после достижения нагрузкой критического значения.

Коэффициент φ изменяется в диапазоне 0≤φ≤1, зависит ,как уже говорилось,  как от физико-механических свойств материала, так и от гибкости λ. Зависимости между φ и λ для различных материалов представляются обычно в табличной форме с шагом ∆λ=10.

При вычислении значений φ для стержней, имеющих значения гибкости не кратные числу 10, применяется правило линейной интерполяции.

Значения коэффициента φ в зависимости от гибкости λ для материалов

На основании условия устойчивости решаются три вида задач:

1. Проверка устойчивости.
2. Подбор сечения.
3. Определение допускаемой нагрузки (или безопасной нагрузки, или грузоподъемности стержня: [F]=φ[σ]А.

Наиболее сложным оказывается решение задачи о подборе сечения, поскольку необходимая величина площади сечения входит и в левую, и в правую часть условия устойчивости:

Только в правой части этого неравенства площадь сечения находится в неявном виде: она входит в формулу радиуса инерции , который в свою очередь включен в формулу гибкости , от которой зависит значение коэффициента продольного изгиба φ.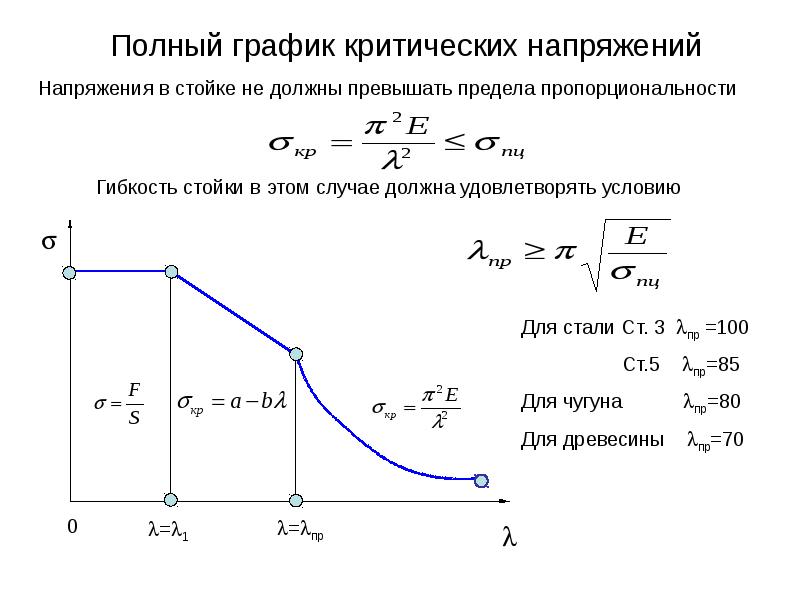 Поэтому здесь приходится использовать метод проб и ошибок, облеченный в форму 

способа последовательных приближений:

1 попытка: задаемся φ1 из средней зоны таблицы, находим  , определяем размеры сечения, вычисляем  , затем гибкость  , по таблице определяем  и сравниваем со значением φ1 . Если  , то:

2 попытка: принимаем  , находим  , определяем размеры сечения, вычисляем  , затем гибкость  , по таблице определяем , и если  , то:

3 попытка: принимаем  , находим  , определяем размеры сечения, вычисляем , затем гибкость  , по таблице определяем , и т.д.

Процесс приближений продолжается до тех пор, пока разница  не окажется менее 5%.

Устойчивость сжатых стержней. Формула Эйлера (Лекция №42)

   Во всем предыдущем изложении мы определяли поперечные размеры стержней из условий прочности. Однако разрушение стержня может произойти не только потому, что будет нарушена прочность, но и оттого, что стержень не сохранит той формы, которая ему придана конструктором; при этом изменится и характер напряженного состояния в стержне.

   Наиболее типичным примером является работа стержня, сжатого силами Р. До сих пор для проверки прочности мы имели условие

   Это условие предполагает, что стержень все время, вплоть до разрушения работает на осевое сжатие. Уже простейший опыт показывает, что далеко не всегда возможно разрушить стержень путем доведения напряжений сжатия до предела текучести или до предела прочности материала.

   Если мы подвергнем продольному сжатию тонкую деревянную линейку, то она может сломаться, изогнувшись; перед изломом сжимающие силы, при которых произойдет разрушение линейки, будут значительно меньше тех, которые вызвали бы при простом сжатии напряжение, равное пределу прочности материала. Разрушение линейки произойдет потому, что она не сможет сохранить приданную ей форму прямолинейного, сжатого стержня, а искривится, что вызовет появление изгибающих моментов от сжимающих сил Р и, стало быть, добавочные напряжения от изгиба; линейка потеряет устойчивость.

   Поэтому для надежной работы конструкции мало, чтобы она была прочна; надо, чтобы все ее элементы были устойчивы: они должны при действии нагрузок деформироваться в таких пределах, чтобы характер их работы оставался неизменным. Поэтому в целом ряде случаев, в частности, для сжатых стержней, помимо проверки на прочность, необходима и проверка на устойчивость. Для осуществления этой проверки надо ближе ознакомиться с условиями, при которых устойчивость прямолинейной формы сжатого стержня нарушается.

Рис.1. Расчетная схема

 

   Возьмем достаточно длинный по сравнению с его поперечными размерами стержень, шарнирно-прикрепленный к опорам (Рис. 1), и нагрузим его сверху центрально силой Р, постепенно возрастающей. Мы увидим, что пока сила Р сравнительно мала, стержень будет сохранять прямолинейную форму. При попытках отклонить его в сторону, например путем приложения кратковременно действующей горизонтальной силы, он будет после ряда колебаний возвращаться к первоначальной прямолинейной форме, как только будет удалена добавочная сила, вызвавшая отклонение.

   При постепенном увеличении силы Р стержень будет все медленнее возвращаться к первоначальному положению при проверках его устойчивости; наконец, можно довести силу Р до такой величины, при которой стержень, после небольшого отклонения его в сторону, уже не выпрямится, а останется искривленным. Если мы, не удаляя силы Р, выпрямим стержень, он уже, как правило, не сможет сохранить прямолинейную форму. Другими словами, при этом значении силы Р, называемом критическим , мы будем иметь такое состояние равновесия, когда исключается вероятность сохранения стержнем заданной ему прямолинейной формы).

   Переход к критическому значению силы Р происходит внезапно; стоит нам очень немного уменьшить сжимающую силу по сравнению с ее критической величиной, как прямолинейная форма равновесия вновь делается устойчивой.

   С другой стороны, при очень небольшом превышении сжимающей силой Р ее критического значения прямолинейная форма стержня делается крайне неустойчивой; достаточно при этом небольшого эксцентриситета приложенной силы, неоднородности материала по сечению, чтобы стержень искривился, и не только не вернулся к прежней форме, а продолжал искривляться под действием все возрастающих при искривлении изгибающих моментов; процесс искривления заканчивается либо достижением совершенно новой (устойчивой) формы равновесия, либо разрушением.

   Исходя из этого, мы должны практически считать критическую величину сжимающей силы эквивалентной нагрузке, «разрушающей» сжатый стержень, выводящей его (и связанную с ним конструкцию) из условий нормальной работы.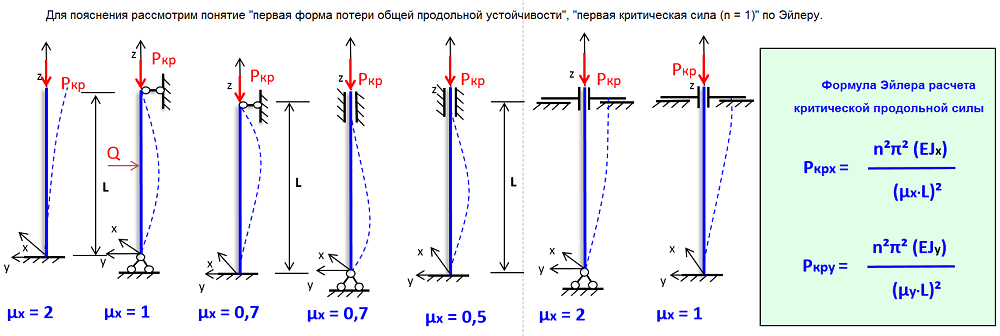 Конечно, при этом надо помнить, что «разрушение» стержня нагрузкой, превышающей критическую, может происходить при непременном условии беспрепятственного возрастания искривления стержня; поэтому если при боковом выпучивании стержень встретит боковую опору, ограничивающую его дальнейшее искривление, то разрушение может и не наступить.

   Обычно подобная возможность является исключением; поэтому практически следует считать критическую сжимающую силу низшим пределом «разрушающей» стержень силы.

Рис.2. Аналогия понятия устойчивости из механики твердого тела

 

   Явление потери устойчивости при сжатии можно по аналогии иллюстрировать следующим примером из механики твердого тела (рис.2). Будем вкатывать цилиндр на наклонную плоскость ab, которая потом переходит в короткую горизонтальную площадку bс и наклонную плоскость обратного направления cd. Пока мы поднимаем цилиндр по плоскости ab, поддерживая его при помощи упора, перпендикулярного к наклонной плоскости, он будет в. состоянии устойчивого равновесия; на площадке bс его равновесие делается безразличным; стоит же нам поместить цилиндр в точку с, как его равновесие сделается неустойчивым— при малейшем толчке вправо цилиндр начнет двигаться вниз.

   Описанную выше физическую картину потери устойчивости сжатым стержнем легко осуществить в действительности в любой механической лаборатории на очень элементарной установке. Это описание не является какой-то теоретической, идеализированной схемой, а отражает поведение реального стержня под действием сжимающих сил.

   Потерю устойчивости прямолинейной формы сжатого стержня иногда называют «продольным изгибом», так как она влечет за собой значительное искривление стержня под действием продольных сил. Для проверки на устойчивость сохранился и до сих пор термин «проверка на продольный изгиб», являющийся условным, так как здесь речь должна идти не о проверке на изгиб, а о проверке на устойчивость прямолинейной формы стержня.

   Установив понятие о критической силе, как о «разрушающей» нагрузке, выводящей стержень из условий его нормальной работы, мы легко можем составить условие для проверки на устойчивость, аналогичное условию прочности.

   Критическая сила вызывает в сжатом стержне напряжение, называемое «критическим напряжением» и обозначаемое буквой . Критические напряжения являются опасными напряжениями для сжатого стержня. Поэтому, чтобы обеспечить устойчивость прямолинейной формы стержня, сжатого силами Р, необходимо к условию прочности добавить еще условие устойчивости:

где — допускаемое напряжение на устойчивость, равное критическому, деленному на коэффициент запаса на устойчивость, т. е. .

   Для возможности осуществить проверку на устойчивость мы должны показать, как определять и как выбрать коэффициент запаса .

 

Формула Эйлера для определения критической силы.

   Для нахождения критических напряжений надо вычислить критическую силу , т. е. наименьшую осевую сжимающую силу, способную удержать в равновесии слегка искривленный сжатый стержень.

Эту задачу впервые решил академик Петербургской Академии наук Л. Эйлер в 1744 году.

   Заметим, что самая постановка задачи иная, чем во всех ранее рассмотренных отделах курса. Если раньше мы определяли деформацию стержня при заданных внешних нагрузках, то здесь ставится обратная задача: задавшись искривлением оси сжатого стержня, следует определить, при каком значении осевой сжимающей силы Р такое искривление возможно.

   Рассмотрим прямой стержень постоянного сечения, шарнирно опертый по концам; одна из опор допускает возможность продольного перемещения соответствующего конца стержня (рис.3). Собственным весом стержня пренебрегаем.

Рис.3. Расчетная схема в «задаче Эйлера»

 

   Нагрузим стержень центрально приложенными продольными сжимающими силами и дадим ему весьма небольшое искривление в плоскости наименьшей жесткости; стержень удерживается в искривленном состоянии, что возможно, так как .

   Деформация изгиба стержня предположена весьма малой, поэтому для решения поставленной задачи можно воспользоваться приближенным дифференциальным уравнением изогнутой оси стержня. Выбрав начало координат в точке А и направление координатных осей, как показано на рис.3, имеем:

(1)

   Возьмем сечение на расстоянии х от начала координат; ордината изогнутой оси в этом сечении будет у, а изгибающий момент равен

   По исходной схеме изгибающий момент получается отрицательным, ординаты же при выбранном направлении оси у оказываются положительными. (Если бы стержень искривился выпуклостью книзу, то момент был бы положительным, а у — отрицательным и .)

Приведенное только что дифференциальное уравнение принимает вид:

деля обе части уравнения на EJ и обозначая дробь через приводим его к виду:

Общий интеграл этого уравнения имеет вид:

Это решение заключает в себе три неизвестных: постоянные интегрирования а и b и значение , так как величина критической силы нам неизвестна.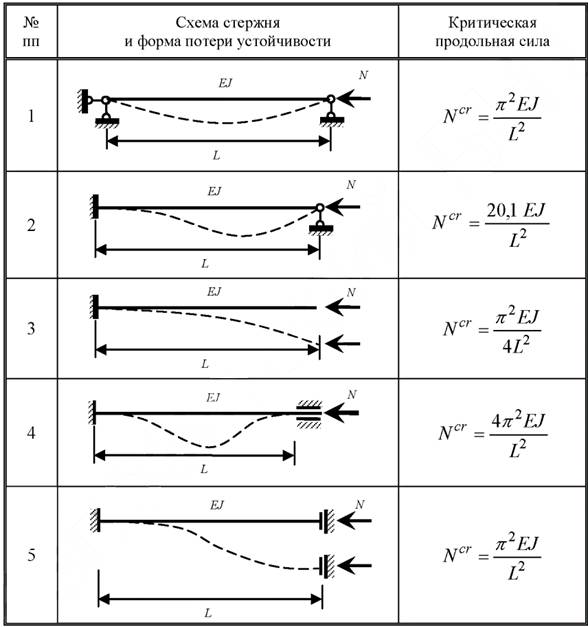

Краевые условия на концах стержня дают два уравнения:

в точке А при х = 0 прогиб у = 0,

В х = 1 у = 0.

Из первого условия следует (так как и cos kx =1)

0 = b.

Таким образом, изогнутая ось является синусоидой с уравнением

(2)

Применяя второе условие, подставляем в это уравнение

у = 0 и х = l

получаем:

Отсюда следует, что или а или kl равны нулю.

   Если а равно нулю, то из уравнения (2) следует, что прогиб в любом сечении стержня равен нулю, т. е. стержень остался прямым. Это противоречит исходным предпосылкам нашего вывода. Следовательно, sin kl = 0, и величина может иметь следующий бесконечный ряд значений:

где — любое целое число.

Отсюда , а так как то

и

   Иначе говоря, нагрузка, способная удержать слегка искривленный стержень в равновесии, теоретически может иметь целый ряд значений. Но так как отыскивается, и интересно с практической точки зрения, наименьшее значение осевой сжимающей силы, при которой становится возможным продольный изгиб, то следует принять .

   Первый корень =0 требует, чтобы было равно нулю, что не отвечает исходным данным задачи; поэтому этот корень должен быть отброшен и наименьшим корнем принимается значение . Тогда получаем выражение для критической силы:

(3)

(Здесь J—минимальный момент инерции поперечного сечения стержня.) Это — так называемая формула Эйлера для сжатого стержня с шарнирно-опертыми концами. Значению критической силы (3) соответствует изгиб стержня по синусоиде с одной полуволной [формула (2)]

Дальше…

Прочность материалов | Основы механики

Что такое прочность материалов?

Сопротивление материалов или просто SOM является одним из важных предметов, и почти это сердце поля Машиностроение , его также называют Механика прочности . В основном это касается поведения материалов при приложении к ним некоторой внешней нагрузки.

сом объясню напряжения , деформации , разрывы , разрушения и их различные типы, которые будут развиваться в материале. Поведение материала помогает Research , Design и решить , подходит он для конкретного применения или нет.

Например, Мы используем посуду из нержавеющей стали на наших кухнях для приготовления пищи, это означает, что посуда, которую мы использовали для приготовления пищи, должна поглощать тепло и передаваться на другой конец, выдерживая нагрев до определенной точки; тогда как такая оценка, выбор материала для посуды и проектирование могут быть сделаны только тогда, когда мы знаем о поведении материала.

Итак, Прочность материала или СОМ — это предмет, который помогает нам узнать о них.

Что мы можем узнать на этой странице?

1. Учебный план по сопротивлению материалов.
2. Основы сопротивления материалов и формулы сопротивления материалов.
3. Типы балок и нагрузки.
4. Книги по сопротивлению материалов. (для справки)

Сопротивление материалов Программа:

Учебный план — это сведения, которые мы читаем или изучаем в течение семестра или академических занятий . Поскольку учебная программа будет варьироваться в зависимости от их университета, поэтому я перечислил важную учебную программу, которой будут следовать все, и эта учебная программа равна GATE (тест на пригодность для выпускников в области инженерии).

• Осевая и крутильная нагрузка.
• Касательные и изгибающие напряжения и их наклоны, прогибы.
• Комбинированные нагрузки, их законы и константы упругости.
• Колонки и энергетические методы.

Сопротивление материалов Учебный план или SOM Учебный план будет часто обновляться в соответствии с новым шаблоном.

Сопротивление материалов Основы и формулы прочности материалов:

Напряжение:

Напряжение определяется как внутренних сил , которые сопротивляются внешним силам при приложении к конкретному телу. Математическое выражение для напряжения равно

F=сила, действующая на тело в ньютонах.

A= Площадь, на которую действует сила, в метрах или квадратных метрах

Выражается также в паскалях Па или Н/мм2.

Деформация:

Когда к телу приложена сила, из-за его свойства упругости оно деформируется. Итак, деформация определяется как отношение деформаций на единиц длины или площади. Математическое выражение для деформации:

Здесь дл — изменение длины при приложении нагрузки, а l — первоначальная длина тела.

Растягивающее напряжение:

Когда к телу прикладывают два равных и противоположных осевых растяжений, тогда тело будет сопротивляться этим силам , такое напряжение называется 900 03 Напряжение растяжения .

 Деформация растяжения:

Когда на тело воздействуют два равных и противоположных осевых растяжения, тело получает деформирует и приводит к изменению длины . Такая деформация называется деформацией растяжения .

Напряжение сжатия:

Когда на тело воздействуют два равных и противоположных осевых усилия, тело будет сопротивляться силам в осевом направлении . Такое осевое напряжение называется сжимающим напряжением .

Деформация сжатия:

При двух равных и противоположных осевых нагрузках подвергают кузову, то тело получит деформацию . Такая деформация называется деформацией сжатия .

Напряжение сдвига :

Напряжение сдвига определяется как воздействие на тело по касательной двух равных и противоположных сил, после чего тело подвергается сдвигу в этом сечении. Такой стресс, вызванный в организме, называется Напряжение сдвига .

Деформация сдвига:

Деформация сдвига определяется как то, что тело подвергается тангенциально две равные и противоположные силы , тогда в нем будет развиваться сдвиг тела и деформация, которая называется Деформация сдвига .

Модуль Юнга:

Модуль Юнга также называют модулем упругости . Это определяется тем, что когда материал нагружается в пределах предела упругости, в теле возникают напряжения и деформации, такие напряжения прямо пропорциональны деформации.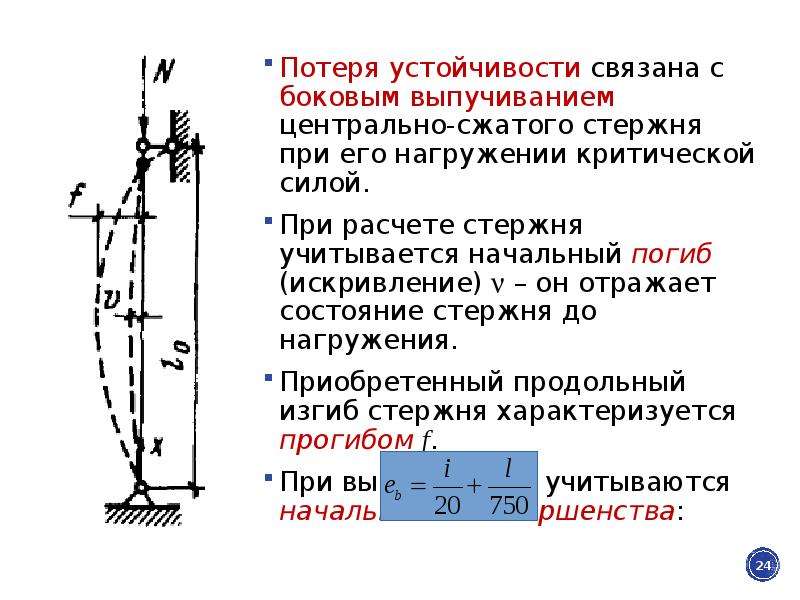 Такой процесс или закон также называют законом Гука. Обозначается как «Э» . Математическая формула задается как

Модуль жесткости:

Модуль жесткости также называется Модуль сдвига ; напряжение сдвига прямо пропорционально деформации сдвига в пределах его предела упругости называется модулем жесткости . Обозначается как N или G .

Линейная деформация:

Линейная деформация — это деформация объекта на единицу длины , развиваемая в направлении приложенной силы. Его также называют первичным штаммом .

Боковая деформация:

Боковая деформация — это деформация, развивающаяся в своем собственном направлении и противоположном во всех направлениях, а также под прямым углом, называется Боковая деформация . Его также называют вторичным штаммом.

Коэффициент Пуассона:

Это коэффициент Боковая деформация по Линейная деформация в объекте.

Объемная деформация:

Когда к телу приложена сила, объем изменится, тогда отношение изменения объема к исходному объему называется объемной деформацией .

Объемный модуль:

Объемный модуль представляет собой отношение прямого напряжения к соответствующему объемному напряжению . Его принимают при воздействии на тело трех взаимно перпендикулярных напряжений одинаковой интенсивности. В таких случаях Учитывается объемный модуль .

Упругость :

Упругость это энергия запасенная в теле из-за нагрузки внешних источников в пределах его упругости .

Хрупкость:

Хрупкость является свойством материала; всякий раз, когда применяется внешняя нагрузка, материал будет деформироваться и выходить из строя или разрушаться без каких-либо значительных симптомов. Он имеет высокую прочность на сжатие и низкую прочность на растяжение, что делает его более слабым при ударных нагрузках.

Пластичность:

Пластичность также является свойством материала; что материал будет постоянно деформироваться без какого-либо разрушения или разрушения. Это также свойство, которое позволяет материалам вытягиваться в тонкие листы. Эти типы материалов мягкие по своей природе.

Черные материалы:

Черные материалы — это тип материалов, в состав которых входит железо. Примерами черных металлов являются чугун, сталь, их сплавы и т. д.

Цветные металлы:

Цветные металлы — это тип материалов, в состав которых не входит железо. Примерами цветных металлов являются резина, пластик и т. д.

До сих пор мы изучали основы этого предмета. Теперь мы собираемся узнать о типах балок и нагрузок.

Типы балок и нагрузок:

Мы можем найти пять типов балок.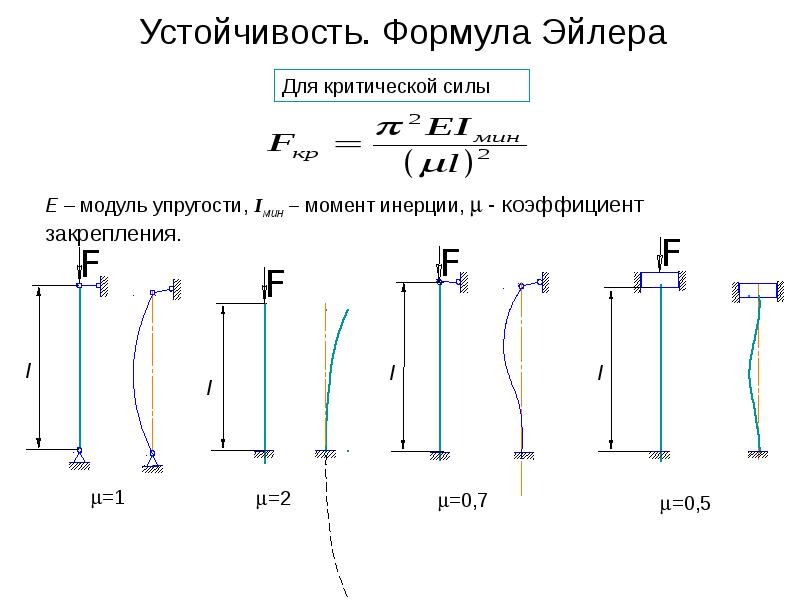 Это

• Консольная балка.

Это тип балки, где один конец фиксированный и другой конец оставлен свободно .

• Балка с простой опорой.

Просто поддерживаемая балка — это тип балки, которая опирается на оба конца.

• Непрерывный луч.

Если балка опирается более чем на две, то такая балка называется Неразрезной балкой .

• Неподвижный луч.

Если балка закреплена на обоих концах, такая балка называется фиксированной балкой .

• Нависающая балка.

Балка, концевая часть которой выходит за пределы опоры, называется нависающей балкой .

Типы нагрузок:

Существует три типа нагрузок.

• Точечная нагрузка

Если нагрузка действует в одной точке на балку, то ее называют точечной нагрузкой. Его также называют сосредоточенной нагрузкой .

• Равномерно распределенная нагрузка.

Если к балке приложена нагрузка и каждая единица длины должна быть загружена с одинаковой степенью, то такая нагрузка называется Равномерно распределенной нагрузкой .

• Равномерно изменяющаяся нагрузка.

Если нагрузка приложена ко всей балке и каждая единица длины должна изменяться равномерно, такая нагрузка называется Равномерно изменяющаяся нагрузка .

Книги по сопротивлению материалов:

Ученик должен обратиться к учебникам, чтобы получить знания, которые даже не были найдены в классе. Когда ученик начнет обращаться к учебникам, тогда зерно знаний начнет прорастать в нем самом. Поэтому не ограничивайтесь конспектами в классе, а также старайтесь обращаться к учебникам, расширяющим знания.

Здесь я упоминаю несколько ссылок, пожалуйста, просмотрите их.

• Сопротивление материалов по R K Bansal .
• Сопротивление материалов по РК Раджпут .
• Сопротивление материалов по Тимошенко .
• Сопротивление материалов by R S Khurmi .

Примечание : Пожалуйста, ознакомьтесь с программой каждого учебника, прежде чем обратиться к нему или купить его.

27 Полная сводка кратких фактов —

Существует два типа тел: твердое тело и деформируемое тело. Расстояние между любыми двумя точками остается постоянным с силой, приложенной к телу, известно как твердое тело и тело, в котором это изменение расстояния известно как деформируемое тело . Сопротивление материала изучает деформируемые тела. В этом мы изучаем различные свойства материалов, применяя к ним силу. Изучение прочности материалов помогает выбирать материалы для различных применений в зависимости от их свойств. Прочность материала также упоминается как Механика материала . Прочность материала включает напряжение, деформацию, кривую напряжения-деформации и т. д.

Инженерное напряжение

• Мгновенная нагрузка или сила, приложенная к единице исходной площади поперечного сечения (до любой деформации), называется инженерным напряжением.
•  Обозначается σ (сигма). Единицей инженерного напряжения в СИ является Н/м ² или Паскаль (Па).

Инженерное напряжение = (приложенная сила)/ (исходная площадь) Сопротивление материалов: инженерное напряжение

Нажмите здесь! подробнее

Классификация напряжений

Обычно следующие инженерные напряжения классифицируются в исследованиях прочности материалов. Сопротивление материалов: классификация напряжений

Нормальное напряжение

• Когда приложенная сила перпендикулярна заданному поперечному сечению образца (осевая нагрузка), тогда соответствующее напряжение, возникающее в материале, называется нормальным. стресс.
•  Много раз сила, прикладываемая к поверхности, неравномерна; в этом случае мы берем среднее значение приложенной силы.

Нормальное напряжение = (Перпендикулярная составляющая приложенной силы)/площадь

Напряжение растяжения

Когда приложенная сила направлена ​​от материала, возникающее напряжение называется напряжением растяжения.

Сопротивление материалов: напряжение растяжения

Напряжение сжатия

Когда сила приложена к объекту, возникающее напряжение называется напряжением сжатия.

Сопротивление материалов: напряжение сжатия

Напряжение изгиба

• Когда сила приложена к балочному материалу, верхняя поверхность материала подвергается напряжению сжатия, а нижняя поверхность испытывает напряжение растяжения, а середина балки остается нейтральной. Такое напряжение известно как напряжение изгиба.
•  Также известно как напряжение при изгибе.

Сопротивление материалов: напряжение изгиба

Напряжение сдвига

Когда приложенная сила параллельна площади, к которой она приложена, напряжение называется напряжением сдвига. Прочность материалов: напряжение сдвига

Формула напряжения сдвига

Напряжение сдвига = (сила, приложенная параллельно верхней и нижней сторонам) / площадь.

Напряжение растяжения в зависимости от напряжения сдвига

Напряжение растяжения	Напряжение сдвига
Приложенная сила перпендикулярна поверхности.	Приложенная сила параллельна на поверхность.
Обозначается σ.	Обозначается τ.

Уравнение комбинированного напряжения

При изучении прочности материалов на реальных примерах могут быть случаи, когда на материал действует более одного типа напряжения, в этом случае нам нужно иметь уравнение, которое может комбинировать различные типы напряжений

Ниже приводится уравнение, которое объединяет напряжения сдвига и напряжения растяжения.

Где,

f _x = растягивающее или сжимающее напряжение в направлении x

f _y = растягивающее или сжимающее напряжение в направлении y

f _s = касательное напряжение, действующее на грани в x и y-направление

f ₁ = принцип максимального напряжения

f ₂ = минимальное напряжение растяжения

q= максимальное напряжение сдвига

Коэффициент концентрации напряжения 9000 4

• В исследованиях сопротивления материалов, много раз материал, на который мы наносим напряжение, не является однородным. Он может иметь некоторые неровности в своей геометрии или в структуре, образованной из-за зазубрин, царапин, отверстий, галтелей, канавок и т. д., что приводит к тому, что концентрация напряжения в какой-то точке материала, известного как 9, становится очень высокой.0003 концентрация напряжения или концентратор/концентратор напряжения .
• Степень этой концентрации выражается как отношение максимального напряжения к эталонному напряжению, где эталонное напряжение представляет собой общее напряжение в элементе при тех же условиях нагрузки, без какой-либо концентрации или прерывистости.

Коэффициент концентрации напряжения Формула:

Концентрация напряжения = максимальное напряжение / эталонное напряжение

Щелкните здесь! подробнее

Коэффициент запаса прочности

• При изучении сопротивления материалов всегда имеются неточности в измеренных значениях напряжений; следовательно, напряжение, которое мы будем рассматривать для нашего использования, известное как рабочее напряжение (σ _w ), всегда меньше экспериментального значения напряжения. В большинстве приложений мы рассматриваем предел текучести (σ _y ).
• Рабочее напряжение определяется путем уменьшения предела текучести на коэффициент; этот фактор известен как фактор безопасности. Итак, запас прочности – это отношение предела текучести к рабочему напряжению. Его символ N. Это безразмерная величина.

            Коэффициент запаса прочности = предел текучести/ рабочее напряжение

Инженерная деформация

• Изменение длины материала в некоторый момент времени на единицу исходной длины (до приложения силы) называется инженерной деформацией.
•  Обозначается ε (Эпсилон) или γ (Гамма). Это безразмерная величина.

             Инженерная деформация = (изменение длины)/ (исходная длина) Сопротивление материалов: инженерная деформация

Коэффициент Пуассона

• Когда к материалу прилагается растягивающее напряжение, происходит удлинение вдоль оси приложенной нагрузки и укорочение вдоль направления, перпендикулярного приложенному напряжению. Таким образом, деформация, возникающая в направлении приложенного напряжения, известна как осевая деформация , а деформация, возникающая в направлении, перпендикулярном приложенному напряжению, известна как поперечная деформация или 9. 0003 поперечная деформация.
• Отношение поперечной деформации к осевой деформации известно как коэффициент Пуассона. Обозначается ʋ (nu). Это очень важная константа для данного материала.

            Коэффициент Пуассона = – (поперечная деформация/осевая деформация)

Пусть приложенная нагрузка направлена ​​в направлении оси Z, а деформация, возникающая в этом направлении, равна ε _x  и материал изотропен и однороден ( ), тогда коэффициент Пуассона равен Сила материалов: коэффициент Пуассона

Чтобы узнать больше о коэффициенте Пуассона, посетите здесь

Кривая напряжения-деформации

• Построение зависимости напряжения от деформации дает значительное количество свойств материала при изучении сопротивления материалов.
• Кривая напряжение-деформация представляет собой кривую зависимости напряжения от деформации, на которой деформация находится на независимой оси, т. е. по оси x, а напряжение — по зависимой, т. е. по оси y. Это важная характеристика материала.
• При приложении нагрузки в материале возникают два типа деформации в зависимости от величины деформации: первая — упругая деформация, а вторая — пластическая деформация.

Сопротивление материалов: кривая напряжения-деформации

Кривая истинного напряжения-деформации

Это кривая напряжения-деформации, на которой истинное напряжение отображается в зависимости от истинной деформации. И напряжение, и деформация основаны на мгновенном измерении. Следовательно, мгновенная площадь поперечного сечения рассматривается вместо первоначального поперечного сечения, а мгновенная длина рассматривается вместо исходной длины.

Упругая деформация

• Упругая деформация – это деформация, при которой материал восстанавливает свою первоначальную форму при снятии силы.
• Эта область имеет предел пропорциональности, предел упругости, верхний предел текучести и нижний предел текучести.

Модуль упругости | Закон Гука

• Когда происходит этот тип деформации, деформация металлической детали почти пропорциональна напряжению; следовательно, эта деформация проявляется в виде прямой линии на графике зависимости напряжения от деформации, за исключением некоторых материалов, таких как серый чугун, бетон и многие полимеры.
• Благодаря этому соотношению напряжение пропорционально деформации.

• Это известно как Закон Гука , где Y константа пропорциональности известна как Модуль Юнга или Модуль Эластичности . Его также обозначают буквой E. Это наклон кривой зависимости напряжения от деформации в пределе упругости. Это один из важнейших законов в исследованиях сопротивления материалов.

Модуль упругости Формула

Его значение несколько выше для керамики, чем для металлов, и значение для полимеров немного ниже, чем для металлов. Или от большинства конструкций требуется деформация только в пределе упругости; поэтому этот регион очень важен.

Пластическая деформация

• Если в этой области снять приложенную силу, то материал не восстанавливает свою первоначальную форму.
• Деформация материала необратима.
• В этом регионе закон Гука не действует.
• Эта область имеет предел прочности материалов при растяжении и предел прочности.

• На кривой есть несколько точек, вокруг которых изменяется тип деформации. Эти моменты очень важны, поскольку они говорят нам об ограничениях и диапазонах материала, которые в конечном итоге полезны при применении материала.

Пропорциональный предел

• Это точка на кривой, до которой напряжение пропорционально деформации.
• Когда материал растягивается сверх предела пропорциональности, напряжение не пропорционально деформации, но, тем не менее, проявляет эластичность.

Предел эластичности

• Это точка на кривой, до которой материал проявляет эластичность.
• После этого в материале начинается пластическая деформация.
• При превышении предела упругости напряжение вызывает текучесть или текучесть материала.

Точка текучести

Это точка, в которой происходит текучесть материала; следовательно, с этой точки начинается пластическая деформация материала.

Что такое предел текучести?

• Напряжение, соответствующее пределу текучести, известно как предел текучести — его сопротивление пластической деформации.
• Во многих случаях точное местонахождение невозможно. Упругопластический переход хорошо выражен и очень резок, обозначен как феномен предела текучести.

• Верхняя точка текучести: Это точка на графике, при которой требуется максимальная нагрузка или напряжение, чтобы инициировать пластическую деформацию материала.

• Нижний предел текучести : Это точка, при которой требуется минимальное напряжение или нагрузка для сохранения пластических свойств материала.

• Верхний предел текучести нестабилен, а нижний предел текучести стабилен, поэтому мы используем нижний предел текучести при проектировании компонентов.

Определение предельной прочности | Определение предельного напряжения

• После текучести по мере продолжения пластической деформации достигается максимальный предел, известный как предельное напряжение или предел прочности.
• Он также известен как предел прочности при растяжении (UTS) или предел прочности при растяжении. Это максимальное напряжение, которое может выдержать материал при растяжении.
• Все деформации до этого момента равномерны, но при этом максимальном напряжении начинает формироваться небольшое сужение материала, это явление называется «шейка».

Точка разрыва | Точка перелома | Точка разрушения

• Напряжение, необходимое для продолжения пластической деформации, начинает уменьшаться после предела прочности и, в конце концов, разрушает материал в точке, известной как точка разрыва или точка разрушения .
• Напряжение материала в точке разрыва известно как «прочность на разрыв».

Кривая напряжения-деформации для хрупкого материала Сопротивление материалов: Кривая напряжения-деформации для хрупкого материала

Кривая напряжения-деформации для пластичного материала Прочность материалов: Кривая напряжения-деформации ковкого материала

  9 0502 Арт. – Напряжение-деформация

Важные вопросы и ответы, относящиеся к сопротивлению материалов

Что такое инженерное напряжение?

Мгновенная нагрузка или сила, приложенная к единице исходной площади поперечного сечения (до приложения силы), называется инженерным напряжением.

Обозначается σ (сигма). Единицей инженерного напряжения в системе СИ является Н/м2 или Паскаль (Па).

Что такое инженерная деформация?

Изменение длины материала в некоторый момент времени на единицу исходной длины (до приложения силы) называется инженерной деформацией.

Обозначается ε (Эпсилон) или γ (Гамма). Это безразмерная величина.

Что такое растягивающее напряжение?

Когда приложенная сила находится вдали от материала, возникающее напряжение называется напряжением растяжения.

Сопротивление материалов: напряжение растяжения

Что такое напряжение сжатия?

Когда приложенная сила направлена ​​к объекту, возникающее напряжение называется напряжением сжатия. Сопротивление материалов: напряжение сжатия

Что такое напряжение сдвига?

Когда приложенная сила параллельна площади, к которой она приложена, напряжение называется напряжением сдвига.

Что такое фактор безопасности?

В измеренных значениях напряжений всегда есть некоторая неопределенность; поэтому напряжение, которое мы собираемся учитывать для нашего использования, известное как рабочее напряжение (σw), всегда меньше экспериментального значения напряжения. В большинстве приложений мы рассматриваем предел текучести (σy).

Рабочее напряжение определяется путем уменьшения предела текучести на коэффициент; этот фактор известен как фактор безопасности. Итак, запас прочности – это отношение предела текучести к рабочему напряжению. Его символ N. Это безразмерная величина.

Что такое кривая истинного напряжения-деформации?

Это кривая напряжение-деформация, на которой истинное напряжение отображается в зависимости от истинной деформации. И напряжение, и деформация основаны на мгновенном измерении, поэтому мгновенная площадь поперечного сечения рассматривается вместо исходного поперечного сечения, а мгновенная длина рассматривается вместо исходной длины.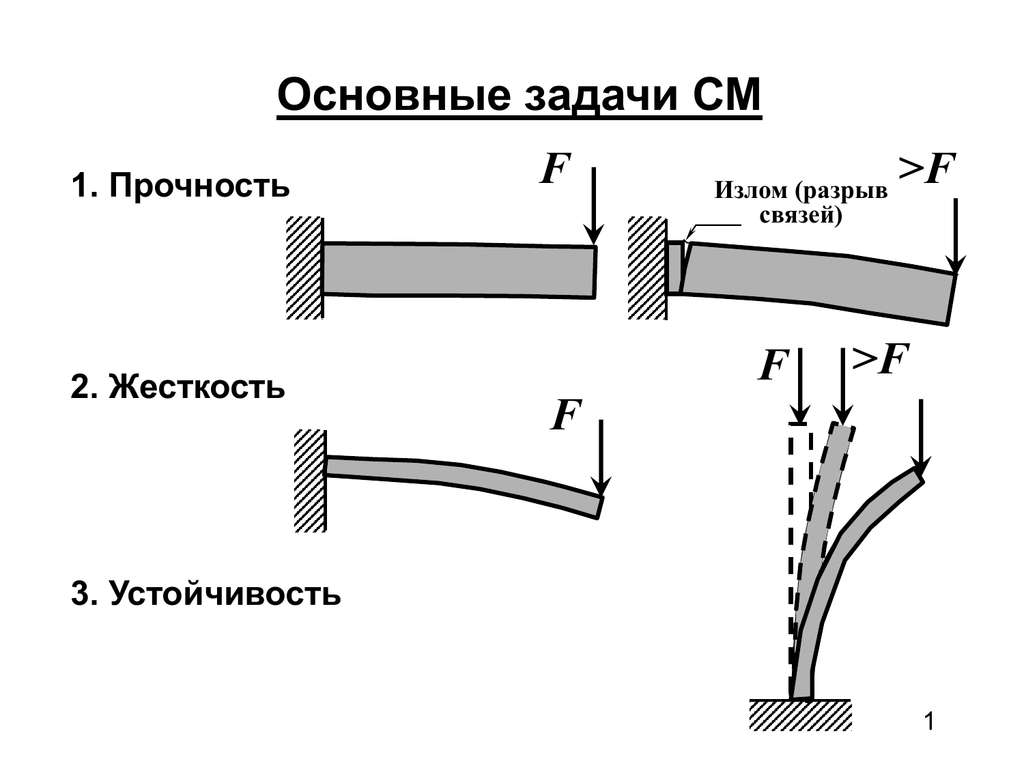

Что такое предел прочности?

Напряжение, необходимое для продолжения пластической деформации, начинает уменьшаться после предела прочности и, в конце концов, разрушает материал в точке, известной как предел прочности.

Что такое предел прочности при растяжении?

После текучести пластическая деформация достигает максимального предела, известного как предельное напряжение или предел прочности, также известный как предел прочности при растяжении (UTS)

Что такое закон Гука? | Объясните закон Гука

Когда происходит этот тип деформации, деформация металлической детали почти пропорциональна напряжению; следовательно, эта деформация проявляется в виде прямой линии на графике зависимости напряжения от деформации, за исключением некоторых материалов, таких как серый чугун, бетон и многие полимеры. Напряжение пропорционально деформации через эту связь.

Это известно как закон Гука, где константа пропорциональности Y известна как модуль Юнга.