1.3.2 Условия равновесия твердого тела в ИСО

Видеоурок: Равновесие тел 

Лекция: Равновесие тел

Под равновесием понимают такое состояние тела, при котором оно остается неподвижным относительно выбранной ИСО.

Раздел физики, который изучает равновесие, называется статикой.

Условия равновесия

Существует два основных условия равновесия тел:

1. Исходя из известного нам II закона Ньютона, чтобы тело оставалось неподвижным, суммарная (равнодействующая) сила должна быть равна нулю. То есть, чтобы определить условие, при котором тело будет находиться в равновесии, сумму проекций сил на любую ось, следует приравнять к нулю:

2. Второе условие касается моментов сил:

Чтобы тело находилось в равновесии, сумма моментов на все оси тоже должна равняться нулю.

Для определения знака момента следует помнить правило:

Если момент вращает тело против часовой стрелки, то он отрицательный, если по часовой стрелке — положительный.

Следует запомнить некоторое уточнение: Если тело находится в равновесии, это еще не значит, что оно покоится.

Общие рекомендации по решению задач на статику

В основе каждого алгоритма лежит два основных условия равновесия, которые следует записать в первую очередь в проекциях с учетом знаков.

Для тела, двигающегося поступательно без вращений, следует:

1. Сделать схематический рисунок условия задачи. На данном рисунке следует обозначить все силы, указывая направления и точки приложения. На рисунке следует указать ось и плечо.

2. На рисунке следует указать направления осей. Они выбираются произвольно с учетом удобства нахождения проекций.

3. Записать условия равновесия. Если количество сил не превышает трёх, то для удобства их следует объединить в один треугольник, в котором можно воспользоваться теоремой синусов, косинусов, Пифагора для определения неизвестных величин.

Решение задач для тел, имеющих ось вращения:

1. На рисунке указать все силы, плечи, направление моментов.

2. Составить уравнения равновесия относительно оси. Если ось не задана, то установить её в неподвижной точке тела. Относительно данной оси следует определить знаки моментов.

3. Составить систему уравнений равновесия и решить её относительно неизвестной величины.

2.2 Характерные химические свойства и получение простых веществ — металлов: щелочных, щелочноземельных, алюминия; переходных элементов (меди, цинка, хрома, железа)

1.2.4 Общая характеристика неметаллов IVA – VIIA групп в связи с их положением в Периодической системе химических элементов Д.И.Менделеева и особенностями строения их атомов

2.1.3 «Просвещенный абсолютизм». Законодательное оформление сословного строя

1. 4.6 Смута. Социальные движения в России в начале XVII в. Борьба с Речью Посполитой и со Швецией

1.2.1 Возникновение государственности у восточных славян. Князья и дружина. Вечевые порядки. Принятие христианства

• Вконтакте
• Сайт

Равновесие тела. Момент силы | Физика

Вы уже знаете, что если сумма всех действующих на точечное тело сил равна нулю, то это тело в инерциальной системе отсчета (ИСО) покоится или движется равномерно и прямолинейно. Следовательно, всегда можно выбрать такую инерциальную систему отсчета, в которой это тело покоится. В этом случае говорят, что

тело находится в равновесии. Таким образом, условием равновесия точечного тела в ОСО является равенство нулю суммы всех действующих на него сил.

А как быть, если интересующее нас тело не является точечным? В этом случае действующие силы могут быть приложены к разным точкам тела.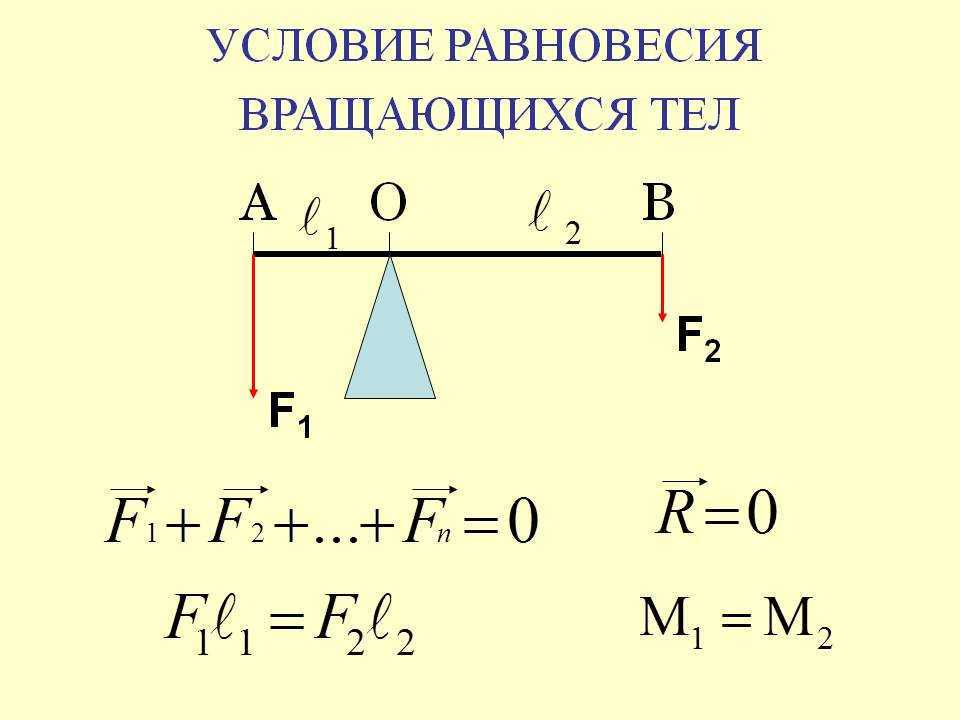 Тогда, даже если сумма сил равна нулю, реальное тело может деформироваться, т. е. различные его части могут двигаться относительно друг друга. Однако при изучении статики нас будут интересовать только такие тела, деформации которых пренебрежимо малы. Такие тела называют твердыми. Как правило, твердыми телами считают детали машин и механизмов, строительные конструкции из бетона, стали и т. п.

Если можно выбрать ИСО, в которой все точки твердого тела покоится, то о таком теле говорят, что оно находится в состоянии равновесия.

В отличие от точечного тела, не имеющего размеров, для твердого тела условия равенства нулю суммы всех действующих на него сил недостаточно для того, чтобы оно находилось в состоянии равновесия. Эксперименты показывают, что если сумма всех действующих на твердое тело сил равна нулю, то у тела можно найти точку, которая будет неподвижной в ИСО. При этом тело может оставаться неподвижным, а может начать раскручиваться вокруг этой точки. Понятно, что во втором случае не все точки тела будут покоиться и, следовательно, тело не будет находиться в равновесии.

Если сумма всех действующих на твердое тело сил равна нулю, то у тела можно найти точку, которая будет неподвижной в ИСО.

Поясним сказанное на примере. Лежащая на столе тетрадь покоится. Если же вы потяните эту тетрадь за противоположные углы с одинаковыми по модулю, но противоположными по направлению силами (рис. 135), то увидите, что тетрадь начнет раскручиваться. При этом центр – точка C пересечения диагоналей останется неподвижной.

Таким образом, одного условия (равенства нулю суммы всех действующих на твердое тело сил) недостаточно для того, чтобы все точки этого тела оставались в покое.

Найдем дополнительное условие равновесия, при котором изначально покоившееся твердое тело не начинает раскручиваться под действием прикладываемых к нему сил. Рассмотрим твердое тело, закрепленное на оси, вокруг которой оно может вращаться. Пусть это будет, например, велосипедное колесо, которое закреплено на оси, обозначенной точкой O (рис. 136). Исследуем, как будет изменяться вращение колеса под действием одной и той же силы F. Для этого приложим силу F к точке A обода колеса и будем изменять направление этой силы.

Вначале подействуем на колесо силой F в направлении, перпендикулярном радиусу OA (рис. 136, а). Эксперимент показывает, что в этом случае колесо начнет раскручиваться по ходу стрелки часов (по часовой стрелке). Если же направление силы F будет таким, как на рис. 136, б, то неподвижное колесо также начнет раскручиваться по часовой стрелке, но уже медленнее, чем в первом случае. Дальнейшие эксперименты показывают, что с увеличением угла α между направлением действия силы и радиусом OA раскручивающее действие силы будет уменьшаться. Наконец, если сила F будет направлена точно вдоль радиуса колеса (рис. 136, в), то колесо вообще не начнет раскручиваться.

Если продолжать увеличивать угол α между направлением силы F и радиусом OA (рис. 136, г), то неподвижное колесо начнет раскручиваться в противоположную сторону.

Понятно, что в случаях а, б и г увеличение модуля силы приведет к увеличению раскручивающего действия силы. Таким образом, раскручивающее действие силы на колесо зависит как от направления силы, так и от ее модуля. Как же описать это действие? Для того чтобы ответить на этот вопрос, введем новые понятия.

На каждом из рис. 136 пунктиром изображена линия, вдоль которой действует сила F. Эту линию называют линией действия силы F. Расстояние от оси вращения до линии действия силы F называют плечом силы. (На рис. 136 плечи силы F перпендикулярны линиям действия силы и обозначены буквой l.)

Линию, вдоль которой действует сила, называют линией действия этой силы. Расстояние от оси вращения до линии действия силы называют плечом этой силы.

Из рисунка видно, что чем больше плечо силы – длина отрезка l, тем большее раскручивающее действие оказывает сила. В случае, когда плечо силы равно нулю (см. рис. 136, в). раскручивающее действие силы также равно нулю.

Когда плечо силы F максимально (см. рис. 136, а), максимально и ее раскручивающее действие.

Раскручивающее действие силы описывают физической величиной – моментом силы. Его принято обозначать буквой M.

Моментом M силы F относительно данной оси называют физическую величину, равную произведению модуля силы на ее плечо.
M = F · l.

Если сила стремится раскручивать тело против часовой стрелки (см. рис. 136, г), то ее момент считают положительным (M > 0). Напротив, если сила стремится раскручивать тело по часовой стрелке (см. рис. 136, а и б), то ее момент считают отрицательным (M

Из определения понятно, почему единицу момента силы в СИ называют ньютон-метр (Н · м).

Эксперименты показывают, что если на твердое тело действуют несколько сил, то суммарное раскручивающее действие этих сил равно сумме моментов этих сил. Например, если на тело действуют две силы, моменты которых равны по модулю, но противоположны по знаку, то сумма моментов этих сил будет равна нулю и данное тело не будет раскручиваться.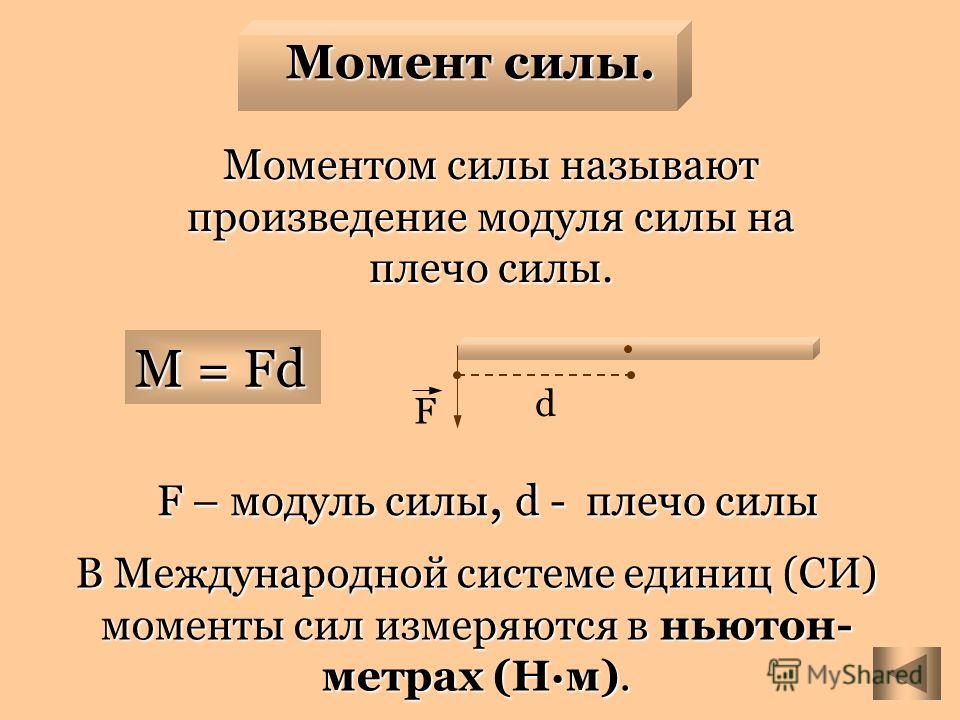

Таким образом,
твердое тело в ИСО остается в равновесии, если выполнены два условия:
1) сумма всех действующих на твердое тело сил равна нулю;
2) сумма моментов всех действующих на твердое тело сил равна нулю.

Итоги

Если можно выбрать ИСО, в котором точечное тело покоится, то говорят, что это тело находится в равновесии.

Условием равновесия точечного тела в ИСО является равенство нулю суммы всех действующих на него сил.

Если можно выбрать ИСО, в которой все точки твердого тела покоятся, то о таком теле говорят, что оно находится в положении равновесия.

Линию, вдоль которой действует сила, называют линией действия силы.

Расстояние от оси вращения до линии действия силы называют плечом силы.

Моментом M силы F относительно данной оси называют физическую величину, равную произведению модуля силы на ее плечо.
M = F · l

Если сила стремится раскручивать тело в направлении против часовой стрелки, то ее момент считают положительным (M > 0). Если сила стремится раскручивать тело в направлении по часовой стрелке, то ее момент считают отрицательным (M

Вопросы

1. В каком случае говорят, что точечное тело находится в равновесии?
2. Сформулируйте условие равновесия точечного тела в ИСО.
3. Какое тело называют твердым?
4. В каком случае говорят, что твердое тело находится в равновесии?
5. Что такое линия действия силы? Что называют плечом силы?
6. Какая физическая величина характеризует раскручивающее действие силы?
7. Сформулируйте определение момента силы относительно оси.
8. Как называют единицу момента силы в СИ?
9. Когда момент силы считают положительным (отрицательным)?
10. Сформулируйте условия равновесия твердого тела.
11. Почему дверную ручку прикрепляют на противоположной от петель стороне двери?

12.1 Условия статического равновесия — Университетская физика, том 1

Цели обучения

К концу этого раздела вы сможете:

• Определите физические условия статического равновесия.
• Нарисуйте диаграмму свободного тела для твердого тела, на которое действуют силы.
• Объясните, как условия равновесия позволяют решать задачи статики.

Мы говорим, что твердое тело находится в равновесии, когда его линейное и угловое ускорения равны нулю относительно инерциальной системы отсчета. Это означает, что тело, находящееся в равновесии, может двигаться, но в этом случае его линейная и угловая скорости должны быть постоянными. Мы говорим, что твердое тело находится в статическом равновесии, когда оно находится в состоянии покоя 9.0015 в выбранной нами системе отсчета . Обратите внимание, что различие между состоянием покоя и состоянием равномер- находится в равномерном движении с постоянной скоростью. Поскольку движение относительно , то, что для нас находится в статическом равновесии, находится в динамическом равновесии для движущегося наблюдателя, и наоборот. Поскольку законы физики одинаковы для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием.

Согласно второму закону движения Ньютона линейное ускорение твердого тела вызвано действующей на него результирующей силой, или

∑kF→k=ma→CM. ∑kF→k=ma→CM.

12,1

Здесь сумма всех внешних сил, действующих на тело, где м — его масса, а a→CMa→CM — линейное ускорение его центра масс (концепция, которую мы обсуждали в линейном импульсе и Столкновения по импульсу и столкновения). В состоянии равновесия линейное ускорение равно нулю. Если мы приравняем ускорение к нулю в уравнении 12.1, мы получим следующее уравнение:0005

Первое условие равновесия

Первое условие равновесия статического равновесия твердого тела выражает поступательное равновесие:

∑kF→k=0→.∑kF→k=0→.

12,2

Первое условие равновесия, уравнение 12.2, является условием равновесия сил, с которым мы столкнулись при изучении приложений законов Ньютона.

Это векторное уравнение эквивалентно следующим трем скалярным уравнениям для компонентов результирующей силы:

∑kFkx=0,∑kFky=0,∑kFkz=0.∑kFkx=0,∑kFky=0,∑kFkz=0.

12,3

Аналогично уравнению 12.1 можно утверждать, что вращательное ускорение α→α→ твердого тела вокруг неподвижной оси вращения вызывается чистым крутящим моментом, действующим на тело, или

∑kτ→k= Iα→.∑kτ→k=Iα→.

12,4

Здесь II — инерция вращения тела при вращении вокруг этой оси, а сумма по всех моментов τ→kτ→k внешних сил в уравнении 12.2. В состоянии равновесия ускорение вращения равно нулю. Приравняв к нулю правую часть уравнения 12.4, мы получим второе условие равновесия:

Второе условие равновесия

Второе условие равновесия статического равновесия твердого тела выражает вращательное равновесие:

∑kτ→k=0→. ∑kτ→k=0→.

12,5

Второе условие равновесия, уравнение 12.5, является условием равновесия крутящих моментов, с которым мы столкнулись при изучении динамики вращения. Стоит отметить, что это уравнение равновесия обычно справедливо для вращательного равновесия вокруг любой оси вращения (фиксированной или иной). Опять же, это векторное уравнение эквивалентно трем скалярным уравнениям для векторных составляющих чистого крутящего момента:

∑kτkx=0,∑kτky=0,∑kτkz=0.∑kτkx=0,∑kτky=0,∑kτkz=0.

12,6

Второе условие равновесия означает, что в равновесии нет чистого внешнего крутящего момента, вызывающего вращение вокруг какой-либо оси.

Первое и второе условия равновесия указаны в конкретной системе отсчета. Первое условие включает только силы и, следовательно, не зависит от начала системы отсчета. Однако второе условие включает крутящий момент, который определяется как векторное произведение τ→k=r→k×F→k,τ→k=r→k×F→k, где вектор положения r→kr→k с относительно оси вращения точки приложения силы входит в уравнение. Следовательно, крутящий момент зависит от положения оси в системе отсчета. Однако, когда условия вращательного и поступательного равновесия выполняются одновременно в одной системе отсчета, то они также выполняются в любой другой инерциальной системе отсчета, так что чистый крутящий момент относительно любой оси вращения по-прежнему равен нулю. Объяснение этому довольно простое.

Предположим, что вектор R→R→ является положением начала новой инерциальной системы отсчета S′S′ в старой инерциальной системе отсчета S . Из нашего исследования относительного движения мы знаем, что в новой системе отсчета S′,S′ вектор положения r→′kr→′k точки, к которой приложена сила F→kF→k, связан с r→ kr→k через уравнение

r→′k=r→k−R→.r→′k=r→k−R→.

Теперь мы можем просуммировать все моменты τ→′k=r→′k×F→kτ→′k=r→′k×F→k всех внешних сил в новой системе отсчета, S′:S′:

∑kτ→′k=∑kr→′k×F→k=∑k(r→k−R→)×F→k=∑kr→k×F→k−∑kR→×F→k= ∑kτ→k−R→×∑kF→k=0→.∑kτ→′k=∑kr→′k×F→k=∑k(r→k−R→)×F→k=∑kr→ k×F→k−∑kR→×F→k=∑kτ→k−R→×∑kF→k=0→.

На последнем этапе этой цепочки рассуждений мы использовали тот факт, что в равновесии в старой системе отсчета, S , первый член исчезает из-за уравнения 12.5, а второй член исчезает из-за уравнения 12.2. Отсюда мы видим, что чистый крутящий момент в любой инерциальной системе отсчета S′S′ равен нулю при условии, что оба условия равновесия выполняются в инерциальной системе отсчета С .

Практическим следствием этого является то, что при применении условий равновесия для твердого тела мы можем выбрать любую точку в качестве начала системы отсчета. Наш выбор системы отсчета продиктован физическими особенностями решаемой задачи. В одной системе отсчета математическая форма условий равновесия может быть довольно сложной, тогда как в другой системе те же самые условия могут иметь более простую математическую форму, которую легко решить. Начало выбранной системы отсчета называется точкой поворота.

В самом общем случае условия равновесия выражаются шестью скалярными уравнениями (уравнение 12. 3 и уравнение 12.6). Для плоских задач равновесия с вращением вокруг неподвижной оси, которые мы рассматриваем в этой главе, количество уравнений можно сократить до трех. Стандартная процедура заключается в принятии системы отсчета, где ось z является осью вращения. При таком выборе оси чистый крутящий момент имеет только z -компоненту, все силы, имеющие ненулевые крутящие моменты, лежат в xy -плоскость, поэтому вклад в чистый крутящий момент вносят только x — и y -составляющие внешних сил. Таким образом, для плоских задач с осью вращения, перпендикулярной плоскости xy , мы имеем следующие три условия равновесия сил и моментов: 12,7

F1y+F2y+⋯+FNy=0F1y+F2y+⋯+FNy=0

12,8

τ1+τ2+⋯+τN=0τ1+τ2+⋯+τN=0

12,9

где суммируется по всем N внешним силам, действующим на тело, и по их моментам.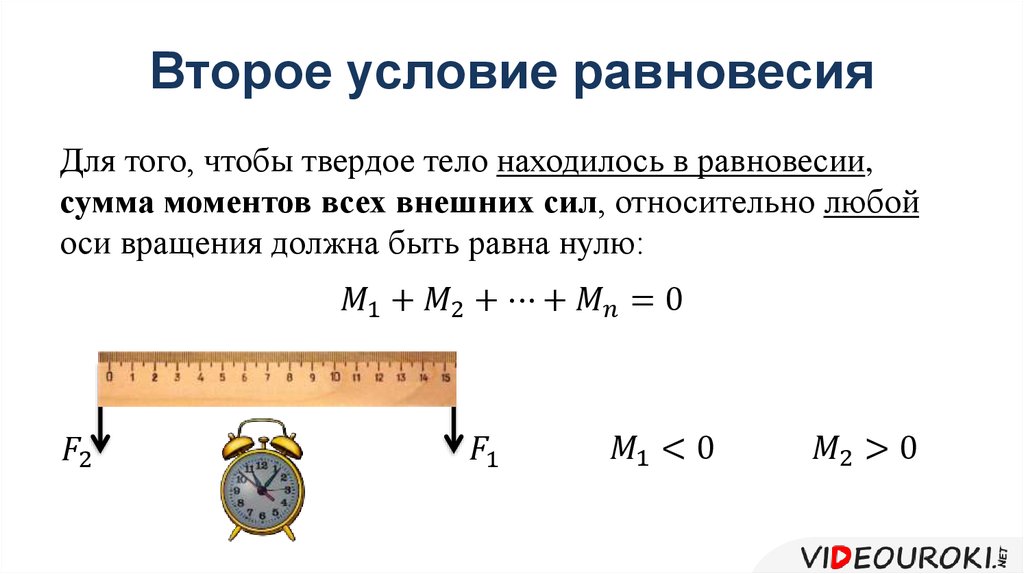 В уравнении 12.9 мы упростили запись, опустив нижний индекс z , но здесь мы понимаем, что суммирование производится по всем вкладам вдоль оси z , которая является осью вращения. В уравнении 12.9, Z -Component of крутящего момента τ → kτ → k из силы f → kf → k IS

τk = rkfksinθτk = rkfksinθ

12.10

, где rkrk -длина леверса. а FkFk — величина силы (как вы видели в разделе «Вращение с фиксированной осью»). Угол θθ — это угол между векторами r→kr→k и F→k,F→k, размером от вектора r→kr→k до вектора F→kF→k в направлении против часовой стрелки (рис. 12.2). Используя уравнение 12.10, мы часто вычисляем величину крутящего момента и присваиваем его значение как положительное (+)(+) или отрицательное (-),(-), в зависимости от направления вращения, вызванного только этим крутящим моментом.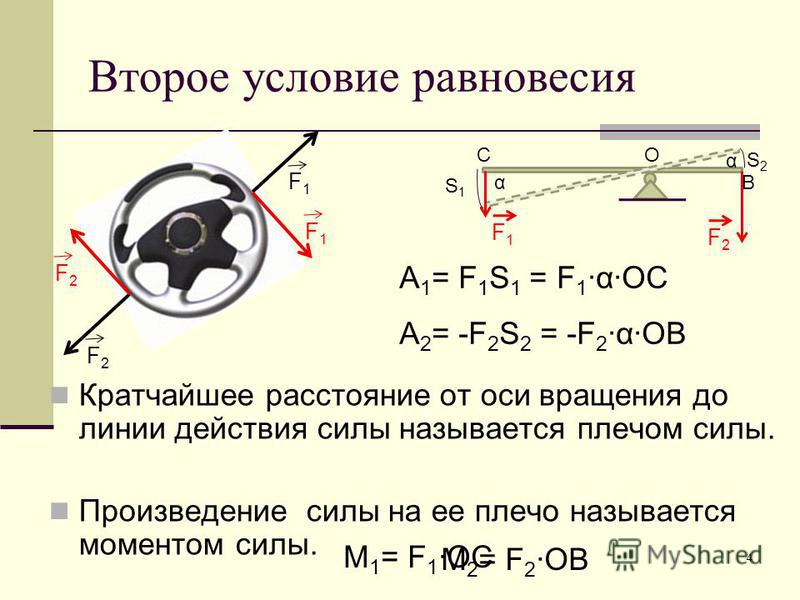 В уравнении 12.9 чистый крутящий момент представляет собой сумму членов, причем каждый член вычисляется из уравнения 12.10, и каждый член должен иметь правильный смысл . Точно так же в уравнении 12.7 мы присваиваем знак ++ компонентам силы в ++ 9.0015 x -направление и знак — для компонентов в — x -направлении. Этому же правилу следует последовательно следовать в уравнении 12.8 при вычислении компонентов силы вдоль оси y .

Рисунок 12.2 Момент силы: (а) Когда момент силы вызывает вращение вокруг оси вращения против часовой стрелки, мы говорим, что его смысл положительный, что означает, что вектор крутящего момента параллелен оси вращения. (b) Когда крутящий момент силы вызывает вращение по часовой стрелке вокруг оси, мы говорим, что его направление отрицательно, что означает, что вектор крутящего момента антипараллелен оси вращения.

Интерактивный

Посмотрите эту демонстрацию, чтобы увидеть, как две силы действуют на твердый квадрат в двух измерениях.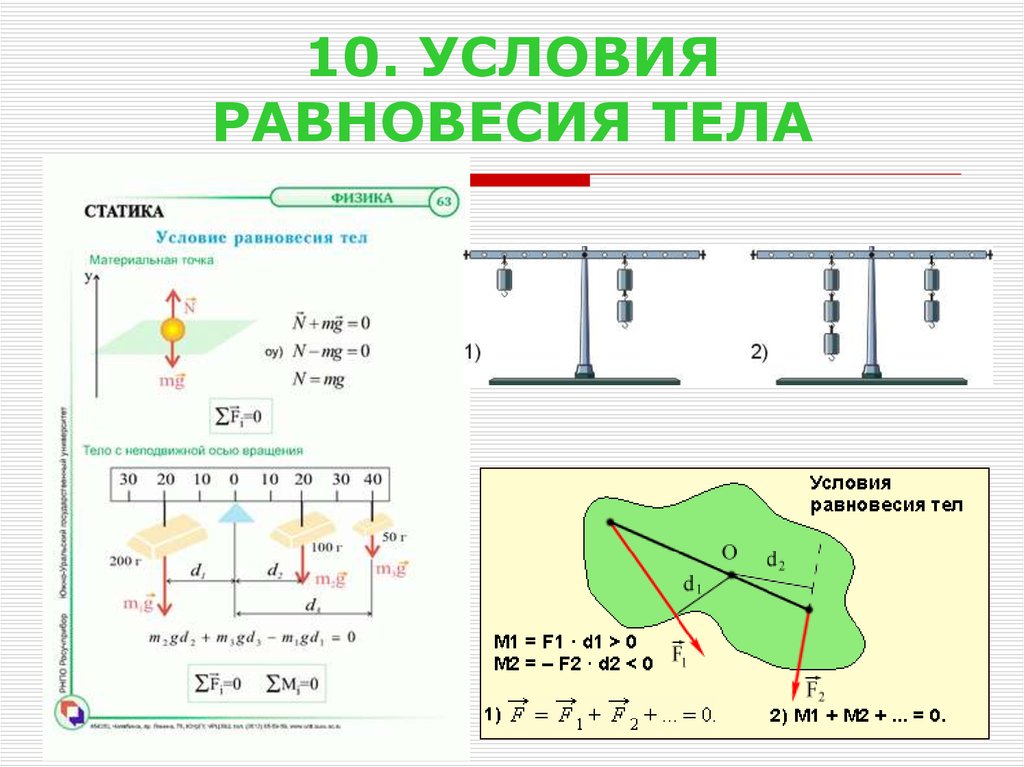 Все время выполняются условия статического равновесия, заданные уравнениями с 12.7 по 12.9. Вы можете варьировать величины сил и их плеч рычагов и наблюдать, как эти изменения влияют на квадрат.

Во многих ситуациях равновесия одной из сил, действующих на тело, является его вес. На диаграммах свободного тела вектор веса привязан к центру тяжести тела. Для всех практических целей центр тяжести идентичен центру масс, как вы узнали из линейного импульса и столкновений о линейном импульсе и столкновениях. Только в тех случаях, когда тело имеет большую пространственную протяженность, так что гравитационное поле неоднородно по всему его объему, центр тяжести и центр масс находятся в разных точках. Однако в практических ситуациях даже такие большие объекты, как здания или круизные лайнеры, находятся в однородном гравитационном поле на поверхности Земли, где ускорение свободного падения имеет постоянную величину g=9.0,8 м/с2.g=9,8 м/с2. В этих ситуациях центр тяжести идентичен центру масс. Поэтому на протяжении всей этой главы мы используем центр масс (ЦМ) как точку, к которой прикрепляется весовой вектор. Напомним, что ЦМ имеет особый физический смысл: при приложении внешней силы к телу точно в его ЦМ тело в целом совершает поступательное движение и такая сила не вызывает вращения.

Когда ЦМ находится вне оси вращения, на объект действует суммарный гравитационный момент. Гравитационный крутящий момент — это крутящий момент, вызванный весом. Этот гравитационный момент может вращать объект, если нет поддержки для его уравновешивания. Величина гравитационного момента зависит от того, насколько далеко от точки вращения находится ЦМ. Например, в случае самосвала (рис. 12.3) ось расположена на линии контакта шин с поверхностью дороги. Если ЦМ расположен высоко над поверхностью дороги, гравитационный момент может быть достаточно большим, чтобы перевернуть грузовик. Легковые автомобили с низко расположенным КМ, близко к тротуару, более устойчивы к опрокидыванию, чем грузовые.

Рисунок 12.3 Распределение массы влияет на положение центра масс (ЦМ), к которому присоединен весовой вектор w→w→. Если центр тяжести находится в пределах области опоры, грузовик возвращается в исходное положение после опрокидывания [см. левую панель в (b)]. Но если центр тяжести находится вне области опоры, грузовик переворачивается [см. правую панель в (b)]. Оба транспортных средства в (b) находятся вне равновесия. Обратите внимание, что автомобиль в (а) находится в равновесии: низкое расположение его центра тяжести затрудняет его опрокидывание.

Интерактивный

Если вы наклоните коробку так, что один край останется в контакте со столом под ним, то один край основания опоры станет стержнем. Пока центр тяжести ящика остается над основанием опоры, гравитационный момент поворачивает ящик обратно в исходное положение устойчивого равновесия. Когда центр тяжести перемещается за пределы основания опоры, гравитационный момент поворачивает ящик в противоположном направлении, и ящик переворачивается. Просмотрите эту демонстрацию, чтобы поэкспериментировать с устойчивыми и неустойчивыми положениями ящика.

Пример 12.1

Центр тяжести автомобиля

У легкового автомобиля с колесной базой 2,5 м 52 % веса приходится на передние колеса на ровной поверхности, как показано на рис. 12.4. Где находится ЦМ этого автомобиля относительно задней оси?

Рисунок 12,4 Распределение веса между осями автомобиля. Где находится центр тяжести? (кредит «автомобиль»: модификация работы Джейн Уитни)

Стратегия

Мы не знаем вес w автомобиля. Все, что мы знаем, это то, что когда автомобиль стоит на ровной поверхности, 0,52 w давит на поверхность в точках контакта передних колес и 0,48 w давит на поверхность в точках контакта задних колес. Также точки контакта отстоят друг от друга на расстояние d=2,5м. d=2,5м. В этих контактных точках автомобиль испытывает силы нормальной реакции с величинами FF=0,52wFF=0,52w и FR=0,48wFR=0,48w на передней и задней осях соответственно. Мы также знаем, что автомобиль является примером твердого тела, находящегося в равновесии, весь вес которого w действует на его КМ. ЦМ находится где-то между точками действия нормальных сил реакции, где-то на расстоянии х от точки действия FRFR. Наша задача найти х . Таким образом, мы определяем три силы, действующие на тело (автомобиль), и можем нарисовать диаграмму свободного тела для протяженного твердого тела, как показано на рис. 12.5.

Рисунок 12,5 На диаграмме свободного тела автомобиля четко указаны векторы сил, действующих на автомобиль, и расстояния до центра масс (ЦМ). Когда в качестве точки поворота выбрана CM, эти расстояния являются плечами нормальных сил реакции. Обратите внимание, что векторные величины и плечи рычагов не обязательно изображать в масштабе, но все релевантные величины должны быть четко обозначены.

Мы почти готовы записать условия равновесия (от уравнения 12.7 до уравнения 12.9) для автомобиля, но сначала мы должны определиться с системой отсчета. Предположим, мы выбрали ось x по длине автомобиля, ось y по вертикали и ось z , перпендикулярную этой плоскости xy . При таком выборе нам нужно написать только уравнения 12.7 и 12.9, потому что все и -компоненты тождественно равны нулю. Теперь нам нужно определиться с расположением опорной точки. Мы можем выбрать любую точку в качестве положения оси вращения ( z -ось). Предположим, мы поместили ось вращения в CM, как показано на диаграмме свободного тела для автомобиля. Теперь мы готовы записать условия равновесия автомобиля.

Раствор

Каждое условие равновесия содержит только три члена, так как на автомобиль действует N=3N=3 сил. Первое условие равновесия, уравнение 12.7, гласит:

+FF-w+FR=0.+FF-w+FR=0.

12,11

Это условие тривиально выполняется, потому что, когда мы подставляем данные, уравнение 12.11 становится +0,52w−w+0,48w=0,+0,52w−w+0,48w=0. Второе условие равновесия, уравнение 12.9., имеет вид

τF+τw+τR=0τF+τw+τR=0

12.12

где τFτF – момент силы FF,τwFF,τw – момент силы тяжести w , а τRτR – момент силы сила FR.FR. Когда точка вращения расположена в СМ, гравитационный момент тождественно равен нулю, потому что плечо рычага веса по отношению к оси, проходящей через СМ, равно нулю. Линии действия обеих нормальных сил реакции перпендикулярны плечам их рычагов, поэтому в уравнении 12.10 мы имеем |sinθ|=1|sinθ|=1 для обеих сил. Из диаграммы свободного тела мы читаем, что момент τFτF вызывает вращение по часовой стрелке вокруг оси в ЦМ, поэтому его смысл отрицательный; а момент τRτR вызывает вращение вокруг оси в ЦМ против часовой стрелки, поэтому его смысл положительный.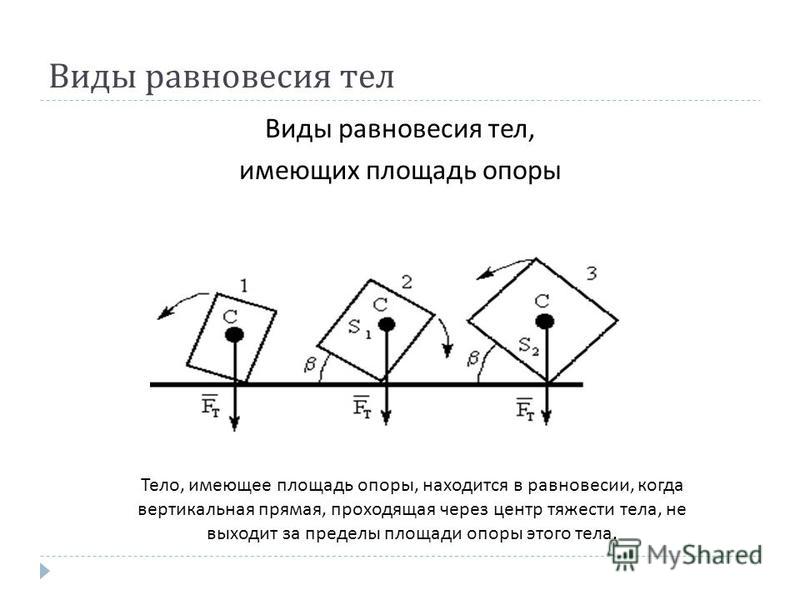 С этой информацией мы запишем второе условие равновесия как

−rFFF+rRFR=0.−rFFF+rRFR=0.

12,13

С помощью диаграммы свободного тела мы определяем величины силы FR=0,48wFR=0,48w и FF=0,52w, FF=0,52w и соответствующие им плечи рычагов rR=xrR=x и rF =d−x.rF=d−x. Теперь мы можем записать второе условие равновесия, уравнение 12.13, явно через неизвестное расстояние x :

−0,52(d−x)w+0,48xw=0,−0,52(d−x)w+0,48xw =0.

12.14

Здесь вес w сокращается, и мы можем решить уравнение для неизвестной позиции х см. Ответ: x=0,52d=0,52(2,5м)=1,3м.x=0,52d=0,52(2,5м)=1,3м.

Раствор

Выбор точки поворота в положении переднего моста не меняет результат. Диаграмма свободного тела для этого положения поворота представлена ​​на рис. 12.6. Для этого выбора точки разворота второе условие равновесия:

−rww+rRFR=0. −rww+rRFR=0.

12,15

Подставляя величины, указанные на диаграмме, получаем

−(d−x)w+0,48dw=0,−(d−x)w+0,48dw=0.

12,16

Ответ, полученный путем решения уравнения 12.13, снова равен x=0,52d=1,3m.x=0,52d=1,3m.

Рисунок 12,6 Эквивалентная диаграмма свободного тела для автомобиля; точка опоры четко обозначена.

Значение

Этот пример показывает, что при решении задач статического равновесия мы свободны в выборе точки опоры. Для разных вариантов точки разворота нам нужно решить разные наборы условий равновесия. Однако все варианты ведут к одному и тому же решению проблемы.

Проверьте свое понимание 12.1

Решите пример 12.1, выбрав точку опоры в месте расположения задней оси.

Проверьте свое понимание 12.2

Объясните, какая из следующих ситуаций удовлетворяет обоим условиям равновесия: (а) теннисный мячик, который не вращается при движении в воздухе; б) пеликан, парящий в воздухе с постоянной скоростью на одной высоте; или (c) коленчатый вал в двигателе припаркованного автомобиля.

Частный случай статического равновесия имеет место, когда все внешние силы на объект действуют на или вдоль оси вращения или когда пространственным расширением объекта можно пренебречь. В таком случае объект можно эффективно рассматривать как точечную массу. В этом особом случае нам не нужно беспокоиться о втором условии равновесия, уравнении 12.9., потому что все крутящие моменты тождественно равны нулю, и первое условие равновесия (для сил) является единственным условием, которое должно быть выполнено. Диаграмма свободного тела и стратегия решения проблем для этого особого случая были изложены в книге Ньютона «Законы движения и приложения законов Ньютона». В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.

Интерактивный

Просмотрите эту демонстрацию, чтобы увидеть три груза, соединенных веревками над шкивами и связанными узлом. Вы можете поэкспериментировать с весами, чтобы увидеть, как они влияют на положение равновесия узла, и в то же время увидеть векторное представление первого условия равновесия в действии.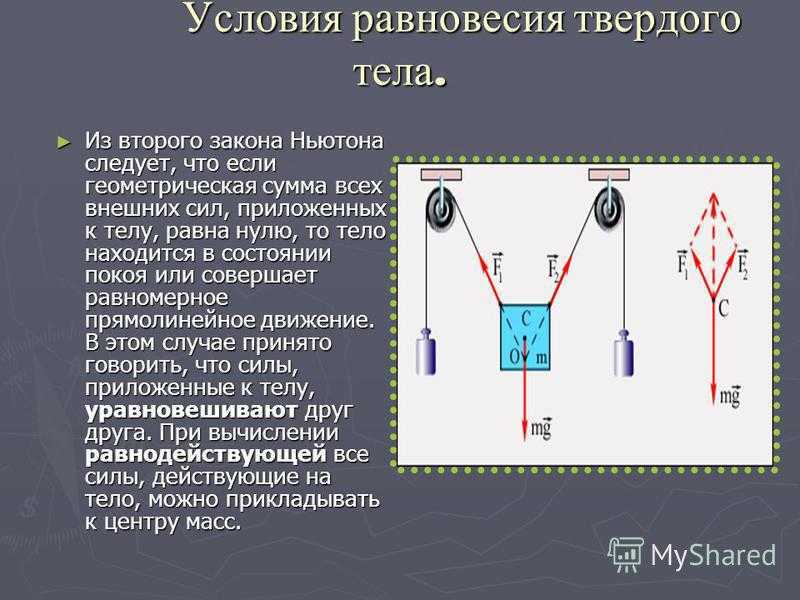

Пример 12.2

Разрывное напряжение

Небольшая кастрюля массой 42,0 г поддерживается двумя нитями, как показано на рис. 12.7. Максимальное натяжение, которое может выдержать струна, составляет 2,80 Н. Масса постепенно добавляется к чаше до тех пор, пока одна из струн не порвется. Какая это строка? Какое количество массы нужно добавить, чтобы это произошло?

Рисунок 12,7 Масса постепенно добавляется в кастрюлю, пока одна из нитей не порвется.

Стратегия

Эта механическая система, состоящая из струн, грузов и чаши, находится в статическом равновесии. В частности, узел, который связывает струны со сковородой, находится в статическом равновесии. Узел можно рассматривать как точку; поэтому нам нужно только первое условие равновесия. Три силы, тянущие узел, — это натяжение T→1T→1 нити длиной 5,0 см, натяжение T→2T→2 нити длиной 10,0 см и вес w→w→ чаши, удерживающей грузы. Мы принимаем прямоугольную систему координат с y — ось, направленная против направления силы тяжести, и нарисуйте диаграмму свободного тела для узла (см. рис. 12.8). Чтобы найти компоненты натяжения, мы должны отождествить направляющие углы α1α1 и α2α2, которые образуют струны с горизонтальным направлением, то есть с осью x . Как видно на рис. 12.7, нити составляют две стороны прямоугольного треугольника. Мы можем использовать теорему Пифагора, чтобы решить этот треугольник, показанный на рис. 12.8, и найти синус и косинус углов α1α1 и α2,α2. Затем мы можем разложить натяжения на их прямоугольные составляющие, подставить в первое условие равновесия (уравнения 12.7 и 12.8) и найти натяжение струн. Сначала порвется струна с большим натяжением.

Рисунок 12,8 Диаграмма свободного тела для узла в примере 12.2.

Раствор

Вес w , тянущий узел, обусловлен массой M чаши и массой m , добавленной к чаше, или w=(M+m)g.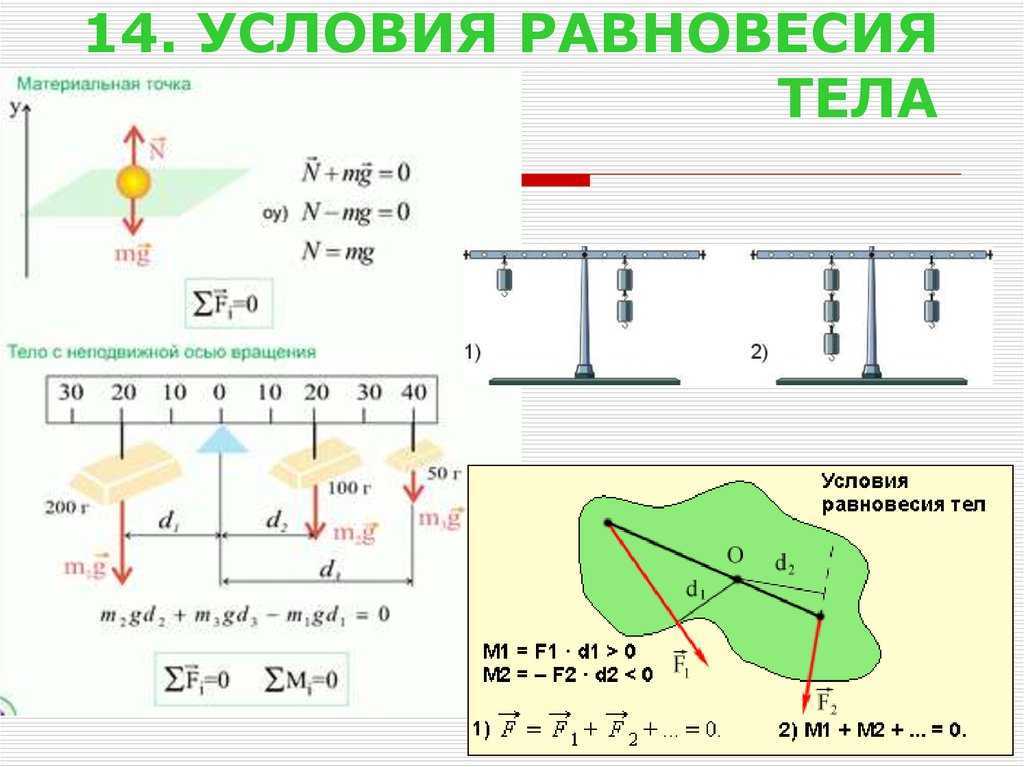 w=(M+m)g. С помощью диаграммы свободного тела на рис. 12.8 мы можем установить условия равновесия узла:

в x-направлении, -T1x+T2x=0 в они-направлении,+T1y+T2y-w=0.в x-направлении,-T1x+T2x=0 в они-направлении,+T1y+T2y-w=0.

Из диаграммы свободного тела величины компонентов в этих уравнениях составляют =T1cosα1=T1/5,T1y=T1sinα1=2T1/5T2x=T2cosα2=2T2/5,T2y=T2sinα2=T2/5.

Подставляем эти компоненты в условия равновесия и упрощаем. Затем мы получаем два уравнения равновесия для напряжений:

iny-направление, T1=2T2iny-направление, 2T15+T25=(M+m)g.iny-направление, T1=2T2iny-направление, 2T15+T25=(M+ м)г.

Уравнение равновесия для направления x говорит нам, что натяжение T1T1 нити длиной 5,0 см в два раза превышает натяжение T2T2 нити длиной 10,0 см. Следовательно, более короткая струна порвется. Когда мы используем первое уравнение для исключения T2T2 из второго уравнения, мы получаем соотношение между массой mm на чаше и натяжением T1T1 в более короткой струне:

2,5T1/5=(M+m)g. 2,5T1 /5=(М+т)г.

Струна рвется, когда натяжение достигает критического значения T1=2,80Н.T1=2,80Н. Предыдущее уравнение можно решить для критической массы м разрыва струны:

м=2,55T1g-M=2,552,80N9,8м/с2-0,042кг=0,277кг=277,0г.м=2,55T1g-M=2,552,80N9,8м/с2-0,042кг= 0,277 кг = 277,0 г.

Значение

Предположим, что механическая система, рассматриваемая в этом примере, прикреплена к потолку внутри поднимающегося лифта. Пока лифт движется вверх с постоянной скоростью, результат остается прежним, потому что вес ww не меняется. Если лифт движется вверх с ускорением, критическая масса меньше, потому что вес M+mM+m становится больше на кажущийся вес из-за ускорения лифта. Тем не менее, во всех случаях более короткая струна рвется первой.

3.6: Анализ равновесия для твердого тела

1. Последнее обновление

2. Сохранить как PDF

ID Page

51709

• Jacob Moore & Antormors
• Государственный университет Пенсильвании Монт Альто Виа. 0008

Для твердого тела , находящегося в статическом равновесии, то есть недеформируемого тела, на которое силы не действуют одновременно, сумма сил и моментов , действующих на тело, должна быть равна нулю. Добавление моментов (в отличие от частиц, где мы рассматривали только силы) добавляет еще один набор возможных уравнений равновесия, позволяя нам решать больше неизвестных по сравнению с проблемами частиц.

Моменты, как и силы, являются векторами. Это означает, что наше векторное уравнение необходимо разбить на скалярные компоненты, прежде чем мы сможем решить уравнения равновесия. В двумерной задаче тело может вращаться только по часовой стрелке или против часовой стрелки (что соответствует вращению вокруг оси \(z\)). Это означает, что твердое тело в двумерной задаче имеет три возможных уравнения равновесия; то есть сумма составляющих силы в направлениях \(x\) и \(y\) и моментов относительно оси \(z\). Сумма каждого из них будет равна нулю.

Для двумерной задачи мы разобьем наше уравнение одной векторной силы на два уравнения скалярных компонент. \[ \сумма \vec{F} \, = \, 0 \]

\[ \сумма F_x \, ​​= \, 0\, ; \,\, \sum F_y \, = \, 0 \] Одномоментное векторное уравнение становится одномоментным скалярным уравнением. \[ \сумма \vec{M} \, = \, 0 \]

\[ \сумма M_z \, = \, 0 \]

Если мы рассмотрим трехмерную задачу, мы увеличим количество возможных уравнений равновесия до шести. Имеются три уравнения равновесия для силы, где сумма компонентов в направлениях \(x\), \(y\) и \(z\) должна быть равна нулю. Тело также может иметь моменты относительно каждой из трех осей. Второй набор из трех уравнений равновесия утверждает, что сумма компонентов момента относительно осей \(x\), \(y\) и \(z\) также должна быть равна нулю.

Разобьем силы на три составляющие уравнения. \[ \сумма \vec{F} \, = \, 0 \]

\[ \сумма F_x \, ​​= \, 0 \, ; \,\, \сумма F_y \, = \, 0 \, ; \,\, \сумма F_z \, = \, 0 \]

Затем также разбиваем моменты на три составляющие уравнения. \[ \сумма \vec{M} \, = \, 0 \]

\[ \сумма M_x \, ​​= \, 0 \, ; \,\, \сумма M_y \, = \, 0 \, ; \,\, \сумма M_z \, = \, 0 \]

Как и в случае с частицами, первым шагом в поиске уравнений равновесия является построение диаграммы свободного тела анализируемого тела. На этой диаграмме должны быть показаны все векторы сил, действующих на тело. На диаграмме свободного тела задайте значения для любых известных величин, направлений и точек приложения векторов силы и задайте имена переменных для любых неизвестных (величин, направлений или расстояний).

Далее вам нужно выбрать оси \(x\), \(y\) и \(z\). Эти оси должны быть перпендикулярны друг другу, но они не обязательно должны быть горизонтальными или вертикальными. Если вы выберете координатные оси, которые совпадают с некоторыми из ваших векторов силы, вы упростите последующий анализ.

После того, как вы выбрали оси, вам необходимо разбить все векторы сил на составляющие по направлениям \(x\), \(y\) и \(z\) (см. страницу векторов на странице Приложения 1 для подробнее об этом процессе). Ваше первое уравнение будет суммой величин компонентов в направлении \(x\), равных нулю, второе уравнение будет суммой величин компонентов в направлении \(y\), равных ноль, а третья (если у вас трехмерная задача) будет равна сумме величин в направлении \(z\), равной нулю.

Далее вам нужно будет составить уравнения моментов. Для этого вам нужно будет выбрать точку, о которой будут сниматься моменты. Подойдет любая точка, но обычно выгоднее выбрать точку, которая уменьшит количество неизвестных в уравнении. Помните, что любой вектор силы, проходящий через данную точку, не будет иметь никакого момента относительно этой точки. Чтобы записать уравнения моментов, просто суммируйте моменты, создаваемые каждой силой (добавляя чистые моменты, показанные на диаграмме) относительно данной точки и данной оси, и приравняйте эту сумму к нулю. Все моменты будут относиться к оси \(z\) для двумерных задач, хотя моменты могут относиться к осям \(x\), \(y\) и \(z\) для трехмерных задач.

Если у вас есть уравнения равновесия, вы можете решить эти формулы для неизвестных. Количество неизвестных, которые вы сможете решить, снова будет количеством уравнений, которые у вас есть.

Видеолекция по этому разделу, прочитанная доктором Джейкобом Муром. Источник YouTube: https://youtu.be/OiJ2xbMIixY.

Пример \(\PageIndex{1}\)

Приведенный ниже автомобиль имеет вес 1500 фунтов с центром масс в 4 футах позади передних колес автомобиля. Каковы нормальные силы, действующие на переднее и заднее колеса автомобиля?

Рисунок \(\PageIndex{1}\): схема проблемы для примера \(\PageIndex{1}\). Адаптировано из общедоступного изображения Ebaychatter0.

Решение

Видео \(\PageIndex{2}\): рабочее решение примера проблемы \(\PageIndex{1}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/1LD5QW-70PA.

Пример \(\PageIndex{2}\)

Балка длиной 5 м имеет фиксированное соединение со стеной в точке A и силу, действующую, как показано, в точке B. Какие силы реакции действуют на балку в точке А?

Рисунок \(\PageIndex{2}\): схема проблемы для примера \(\PageIndex{2}\). На горизонтальную балку, прикрепленную одним концом к стене, действует сила, приложенная к ее свободному концу.

Решение

Видео \(\PageIndex{3}\): рабочее решение примера проблемы \(\PageIndex{2}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/JrVV7k1aQEk.

Пример \(\PageIndex{3}\)

Лестница незначительной массы поддерживает человека весом 120 фунтов, как показано ниже. Если точка контакта в точке А не имеет трения, а точка контакта в точке В представляет собой шероховатое соединение, определите силы, действующие в точках контакта А и В.

Рисунок \(\PageIndex{3}\): схема проблемы для примера \(\PageIndex{3}\). Лестница своим основанием на шершавом полу прислонена к стене без трения, а человек стоит на лестнице наполовину вверх.

Решение

Видео \(\PageIndex{4}\): рабочее решение примера проблемы \(\PageIndex{3}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/WzkAnPdhao4.

Пример \(\PageIndex{4}\)

Элемент ABC имеет длину 6 метров, точка B находится в его середине. Определить все силы, действующие на элемент ABC.

Рисунок \(\PageIndex{4}\): схема проблемы для примера \(\PageIndex{4}\). Диагональный элемент конструкции прикреплен к стене одним концом, соединен со стеной тросом в средней точке и выдерживает нагрузку 300 кг на своем свободном конце.

Решение

Видео \(\PageIndex{5}\): рабочее решение примера проблемы \(\PageIndex{4}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/sMQrjwUMpSQ.

Пример \(\PageIndex{5}\)

Сидя на стуле, человек прилагает силы, показанные на схеме ниже. Определите все силы, действующие на стул в точках A и B. (Предположим, что A не имеет трения, а B — шероховатая поверхность).

Рисунок \(\PageIndex{5}\): схема проблемы для примера \(\PageIndex{5}\). Стул стоит на плоской поверхности, при этом предполагается, что эта поверхность не имеет трения в месте контакта с передней ножкой стула (точка А) и создает трение в месте контакта с задней ножкой (точка В).

Решение

Видео \(\PageIndex{6}\): рабочее решение примера проблемы \(\PageIndex{5}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/nSOxK1ZMggA.

Пример \(\PageIndex{6}\)

Прицеп, показанный ниже, состоит из платформы весом 250 фунтов на оси с колесами весом 350 фунтов. Предположим, что силы веса действуют в центре каждого компонента. Если мы хотим, чтобы вес сцепки (\(F_T\)) незагруженного прицепа составлял 50 фунтов, на каком расстоянии \(d\) от передней части мы должны поместить ось?

Рисунок \(\PageIndex{6}\): схема проблемы для примера \(\PageIndex{6}\). Прицеп состоит из плоского прямоугольного настила поверх двух колес на оси.

Решение

Видео \(\PageIndex{7}\): рабочее решение примера проблемы \(\PageIndex{6}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/wpEBuitLD5s.

Пример \(\PageIndex{7}\)

Плоский стальной знак размером 12 на 24 дюйма поддерживается двумя тросами, каждый на расстоянии 6 дюймов от края знака.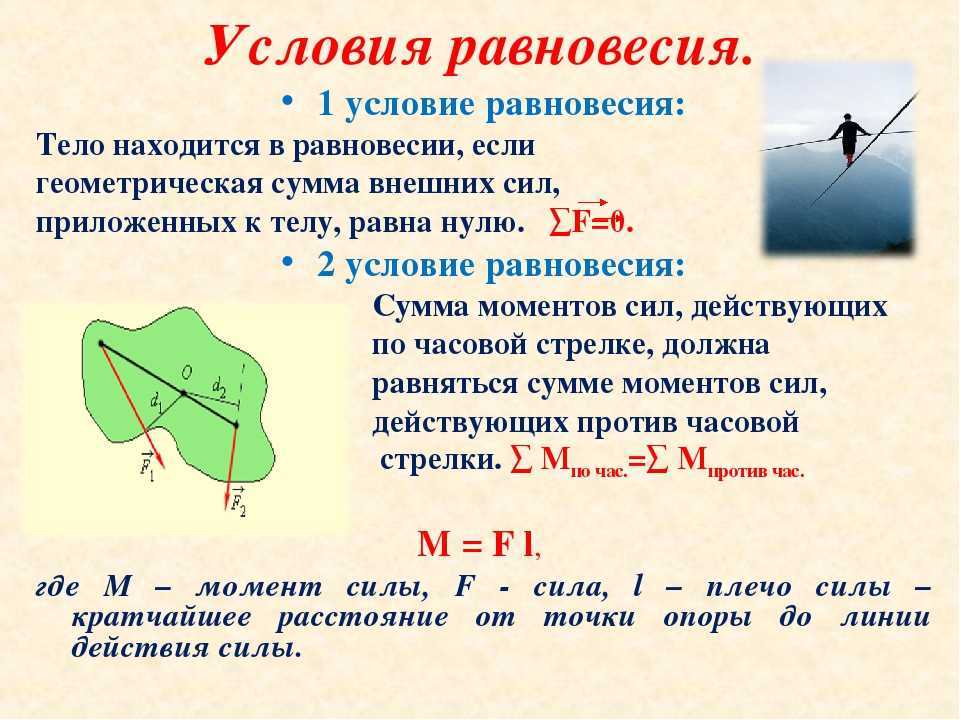 Знак имеет вес 10 фунтов, и ветер заставляет знак располагаться под углом 10 градусов к вертикали (ось \(y\)). Если мы рассматриваем ветер как точечную силу, действующую в отрицательном направлении \(z\) на центр знака, насколько сильной должна быть сила ветра, чтобы вызвать этот угол в десять градусов?

Рисунок \(\PageIndex{7}\): схема проблемы для примера \(\PageIndex{7}\). На висящий знак действует ветер, направление которого указывает на экран, в результате чего знак образует угол 10 ° с плоскостью экрана.

Решение

Видео \(\PageIndex{8}\): рабочее решение примера проблемы \(\PageIndex{7}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/pR-0xbj8wF0.

Пример \(\PageIndex{8}\)

Шестидесятикилограммовая акустическая панель подвешена на трех тросах, как показано ниже. Предполагая, что панель имеет равномерно распределенный вес, каково натяжение каждого из тросов?

Рисунок \(\PageIndex{8}\): схема проблемы для примера \(\PageIndex{8}\). Однородная прямоугольная панель подвешена сверху на 3 тросах, расположенных в разных точках по ее краям.

Решение

Видео \(\PageIndex{9}\): рабочее решение примера проблемы \(\PageIndex{8}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/Kbsc1m0f9pQ.

---

Эта страница под названием 3.6: Equilibrium Analysis for a Rigid Body распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Jacob Moore & Contributors (Mechanics Map) посредством исходного содержимого, которое было отредактировано для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.