Упругость и пластичность. Закон Гука (Лекция №8)
Действие внешних сил на твердое тело приводит к возникновению в точках его объема напряжений и деформаций. При этом напряженное состояние в точке, связь между напряжениями на различных площадках, проходящих через эту точку, определяются уравнениями статики и не зависят от физических свойств материала. Деформированное состояние, связь между перемещениями и деформациями устанавливаются с привлечением геометрических или кинематических соображений и также не зависят от свойств материала. Для того чтобы установить связь между напряжениями и деформациями, необходимо учитывать реальные свойства материала и условия нагружения. Математические модели, описывающие соотношения между напряжениями и деформациями, разрабатываются на основе экспериментальных данных. Эти модели должны с достаточной степенью точности отражать реальные свойства материалов и условия нагружения.
Наиболее распространенными для конструкционных материалов являются модели упругости и пластичности. Упругость это свойство тела изменять форму и размеры под действием внешних нагрузок и восстанавливать исходную конфигурацию при снятии нагрузок. Математически свойство упругости выражается в установлении взаимно однозначной функциональной зависимости между.компонентами тензора напряжений и тензора деформаций. Свойство упругости отражает не только свойства материалов, но и условия нагружения. Для большинства конструкционных материалов свойство упругости проявляется при умеренных значениях внешних сил, приводящих к малым деформациям, и при малых скоростях нагружения, когда потери энергии за счет температурных эффектов пренебрежимо малы. Материал называется линейно-упругим, если компоненты тензора напряжений и тензора деформаций связаны линейными соотношениями.
При высоких уровнях нагружения, когда в теле возникают значительные деформации, материал частично теряет упругие свойства: при разгрузке его первоначальные размеры и форма полностью не восстанавливаются, а при полном снятии внешних нагрузок фиксируются остаточные деформации. В этом случае зависимость между напряжениями и деформациями перестает быть однозначной. Это свойство материала называется пластичностью. Накапливаемые в процессе пластического деформирования остаточные деформации называются пластическими.
Высокий уровень нагружения может вызвать разрушение, т. е. разделение тела на части. Твердые тела, выполненные из различных материалов, разрушаются при разной величине деформации. Разрушение носит хрупкий характер при малых деформациях и происходит, как правило, без заметных пластических деформаций. Такое разрушение характерно для чугуна, легированных сталей, бетона, стекла, керамики и некоторых других конструкционных материалов. Для малоуглеродистых сталей, цветных металлов, пластмасс характерен пластический тип разрушения при наличии значительных остаточных деформаций. Однако подразделение материалов по характеру разрушения на хрупкие и пластичные весьма условно, оно обычно относится к некоторым стандартным условиям эксплуатации. Один и тот же материал может вести себя в зависимости от условий (температура, характер нагружены я, технология изготовления и др.) как хрупкий или как пластичный. Например, пластичные при нормальной температуре материалы разрушаются как хрупкие при низких температурах. Поэтому правильнее говорить не о хрупких и пластичных материалах, а о хрупком или пластическом состоянии материала.
Пусть материал является линейно-упругим и изотропным. Рассмотрим элементарный объем, находящийся в условиях одноосного напряженного состояния (рис. 1), так что тензор напряжений имеет вид
При таком нагружении происходит увеличение размеров в направлении оси Ох, характеризуемое линейной деформацией , которая пропорциональна величине напряжения
(1) |
Рис.1. Одноосное напряженное состояние
Это соотношение является математической записью закона Гука, устанавливающего пропорциональную зависимость между напряжением и соответствующей линейной деформацией при одноосном напряженном состоянии. Коэффициент пропорциональности E называется модулем продольной упругости или модулем Юнга. Он имеет размерность напряжений.
Наряду с увеличением размеров в направлении действия; же напряжения происходит уменьшение размеров в двух ортогональных направлениях (рис. 1). Соответствующие деформации обозначим через и , причем эти деформации отрицательны при положительных и пропорциональны :
(2) |
Коэффициент пропорциональности называется коэффициентом Пуассона,
Соотношения, аналогичные (1) и (2), в случае одноосного нагружения в направлении осей Оу, Ог напряжением , , соответственно имеют вид
(3) | |
(4) |
При одновременном действии напряжений по трем ортогональным осям, когда отсутствуют касательные напряжения, для линейно-упругого материала справедлив принцип суперпозиции (наложения решений):
С учетом формул (1 4) получим
(5) |
Касательные напряжения вызывают угловые деформации, причем при малых деформациях они не влияют на изменение линейных размеров, и следовательно, на линейные деформации. Поэтому они справедливы также в случае произвольного напряженного состояния и выражают так называемый обобщенный закон Гука.
Угловая деформация обусловлена касательным напряжением , а деформации и соответственно напряжениями и . Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости
(6) |
которые выражают закон Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига. Существенно, что нормальное напряжение не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними (рис. 1).
Линейная зависимость существует также между средним напряжением (2.18), пропорциональным первому инварианту тензора напряжений, и объемной деформацией (2.32), совпадающей с первым инвариантом тензора деформаций:
(7) |

Рис.2. Плоская деформация сдвига
Соответствующий коэффициент пропорциональности К называется объемным модулем упругости.
В формулы (1 7) входят упругие характеристики материала Е, , G и К, определяющие его упругие свойства. Однако эти характеристики не являются независимыми. Для изотропного материала независимыми упругими характеристиками являются две, в качестве которых обычно выбираются модуль упругости Е и коэффициент Пуассона . Чтобы выразить модуль сдвига G через Е и , рассмотрим плоскую деформацию сдвига под действием касательных напряжений (рис. 2). Для упрощения выкладок используем квадратный элемент со стороной а. Вычислим главные напряжения , . Эти напряжения действуют на площадках, расположенных под углом к исходным площадкам. Из рис. 2 найдем связь между линейной деформацией в направлении действия напряжения и угловой деформацией . Большая диагональ ромба, характеризующая деформацию , равна
Для малых деформаций
С учетом этих соотношений
До деформации эта диагональ имела размер . Тогда будем иметь
Из обобщенного закона Гука (5) получим
откуда
Сравнение полученной формулы с записью закона Гука при сдвиге (6) дает
(8) |
Сложим три соотношения упругости (5)
(9) |
В итоге получим
Сравнивая это выражение с объемным законом Гука (7), приходим к результату
Механические характеристики Е, , G и К находятся после обработки экспериментальных данных испытаний образцов на различные виды нагрузок. Из физического смысла все эти характеристики не могут быть отрицательными. Кроме того, из последнего выражения следует, что коэффициент Пуассона для изотропного материала не превышает значения 1/2. Таким образом, получаем следующие ограничения для упругих постоянных изотропного материала:
Предельное значение приводит к предельному значению , что соответствует несжимаемому материалу ( при ). В заключение выразим из соотношений упругости (5) напряжения через деформации. Запишем первое из соотношений (5) в виде
С использованием равенства (9) будем иметь
откуда
Аналогичные соотношения можно вывести для и . В результате получим
(10) |
Здесь использовано соотношение (8) для модуля сдвига. Кроме того, введено обозначение
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИ
Рассмотрим вначале элементарный объем dV=dxdydz в условиях одноосного напряженного состояния (рис. 1). Мысленно закрепим площадку х=0 (рис. 3). На противоположную площадку действует сила . Эта сила совершает работу на перемещении . При увеличении напряжения от нулевого уровня до значения соответствующая деформация в силу закона Гука также увеличивается от нуля до значения , а работа пропорциональна заштрихованной на рис. 4 площади: . Если пренебречь кинетической энергией и потерями, связанными с тепловыми, электромагнитными и другими явлениями, то в силу закона сохранения энергии совершаемая работа перейдет в потенциальную энергию,
Рис.3. Расчетная схема энергии деформации
Рис.4. Линейный закон сопротивления
При одновременном действии напряжений , и на главных площадках (т. е. при отсутствии касательных напряжений) потенциальная энергия равна сумме работ, совершаемых силами на соответствующих перемещениях . Удельная потенциальная энергия равна
.

Рис.5. Расчетная схема сдвигаемой энергии
В частном случае чистого сдвига в плоскости Оху, изображенном на рис. 5, сила совершает работу на перемещении . Соответствующая этому случаю удельная потенциальная энергия деформации равна
Подобные соотношения будут иметь место при сдвиге в других плоскостях.
В общем случае напряженно-деформированного состояния будем иметь
(11) |
Если деформации выразить через напряжения с помощью соотношений упругости (5) и (6), то получим эквивалентную (11) форму записи через компоненты тензора напряжений
(12) |
Выразив напряжения через деформации с использованием соотношений (6) и (10), получим еще одну форму записи для Ф через компоненты тензора деформаций
Еще одну форму записи для удельной потенциальной энергии деформации получим, разложив тензоры напряжений и деформаций на шаровые тензоры и девиаторы. В результате (11) можно привести к одной из форм
(13) |
Здесь введены обозначения для интенсивности касательных напряжений и интенсивности деформаций сдвига, которые выражаются через вторые инварианты и девиаторов тензора напряжений и тензора деформаций следующим образом:
Первые слагаемые в (13) соответствуют произведению шаровых составляющих тензоров напряжений и деформаций, а вторые произведению девиаторных составляющих. Так как шаровой тензор характеризует изменение объема, а девиатор изменение формы, то соотношения (13) можно интерпретировать как разложение удельной потенциальной энергии на две составляющие: Ф=Ф0+Фф, где Ф0 соответствует изменению объема без изменения формы, а Фф изменению формы без изменения объема. Первая составляющая будет вычисляться через компоненты тензора напряжений следующим образом:
(14) |
Удельную потенциальную энергию изменения формы проще найти не через интенсивность касательных напряжений, а как разность Ф Ф0. Вычитая (14) из (12), после преобразований получим
Дальше…toehelp.ru
УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА
УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА. Упругость – свойство тела деформироваться под действием нагрузки и восстанавливать первоначальную форму и размеры после ее снятия. Проявление упругости лучше всего проследить, проведя простой опыт с пружинными весами – динамометром, схема которого показана на рис.1.

При нагрузке в 1 кг стрелка-индикатор сместится на 1 деление, при 2 кг – на два деления, и так далее. Если нагрузки последовательно снимать, процесс идет в обратную сторону. Пружина динамометра – упругое тело, ее удлинение Dl, во-первых, пропорционально нагрузке P и, во-вторых полностью исчезает при полном снятии нагрузки. Если построить график, отложить по вертикали оси величины нагрузки, а по горизонтальной – удлинение пружины, то получаются точки, лежащие на прямой, проходящей через начало координат, рис.2. Это справедливо как для точек, изображающих процесс нагружения так и для точек, соответствующих нагрузке.
Угол наклона прямой характеризует способность пружины сопротивляться действию нагрузки: ясно, что «слабая» пружина (рис.3). Эти графики называются характеристиками пружины.
Тангенс угла наклона характеристики называется жесткостью пружины С. Теперь можно записать уравнение деформирования пружины Dl = P / C
Жесткость пружины С имеет размерность кг / см\up122 и зависит от материала пружины (например, сталь или бронза) и ее размеров – длины пружины, диаметра ее витка и толщины проволоки, из которой она сделана.
В той или иной мере все тела, которые можно считать твердыми, обладают свойством упругости, но заметить это обстоятельство можно далеко не всегда: упругие деформации обычно очень малы и наблюдать их без специальных приборов удается практически только при деформировании пластинок, струн, пружин, гибких стержней.
Прямым следствием упругих деформаций являются упругие колебания конструкций и природных объектов. Можно легко обнаружить дрожание стального моста, по которому идет поезд;иногда можно услышать, как звенит посуда, когда на улице проезжает тяжелый грузовик; все струнные музыкальные инструменты так или иначе преобразуют упругие колебания струн в колебания частичек воздуха;в ударных инструментах тоже упругие колебания (например, мембраны барабана) преобразуются в звук.
При землетрясении происходят упругие колебания поверхности земной коры; при сильном землетрясении кроме упругих деформаций возникают пластические (которые остаются после катаклизма как изменения микрорельефа), а иногда появляются трещины. Эти явления не относятся к упругости: можно сказать, что в процессе деформирования твердого тела сначала всегда появляются упругие деформации, потом пластические, и, наконец, образуются микротрещины. Упругие деформации очень малы – не больше 1%, а пластические могут достигнуть 5–10% и более, поэтому обычное представление о деформациях относится к пластическим деформациям – например, пластилин или медная проволока. Однако, несмотря на свою малость, упругие деформации играют важнейшую роль в технике: расчет на прочность авиалайнеров, подводных лодок, танкеров, мостов, туннелей, космических ракет – это, в первую очередь, научный анализ малых упругих деформаций, возникающих в перечисленных объектах под действием эксплуатационных нагрузок.
Еще в неолите наши предки изобрели первое дальнобойное оружие – лук и стрелы, используя упругость изогнутой ветки дерева; потом катапульты и баллисты, построенные для метания больших камней, использовали упругость канатов, свитых из растительных волокон или даже из женских длинных волос. Эти примеры доказывают, что проявление упругих свойств было давно известно и давно использовалось людьми. Но понимание того, что любое твердое тело под действием даже небольших нагрузок обязательно деформируется, хотя и на очень малую величину, впервые появилось в 1660 у Роберта Гука, современника и коллеги великого Ньютона. Гук был выдающимся ученым, инженером и архитектором. В 1676 он сформулировал свое открытие очень кратко, в виде латинского афоризма: «Ut tensio sic vis», смысл которого состоит в том, что «какова сила, таково и удлинение». Но опубликовал Гук не этот тезис, а только его анаграмму: «ceiiinosssttuu». (Таким образом тогда обеспечивали приоритет, не раскрывая сути открытия.)
Вероятно, в это время Гук уже понимал, что упругость – универсальное свойство твердых тел, но считал необходимым подтвердить свою уверенность экспериментально. В 1678 вышла книга Гука, посвященная упругости, где описывались опыты, из которых следует, что упругость есть свойство «металлов, дерева, каменных пород, кирпича, волос, рога, шелка, кости, мышцы, стекла и т.п.» Там же была расшифрована анаграмма. Исследования Роберта Гука привели не только к открытию фундаментального закона упругости, но и к изобретению пружинных хронометров (до того были только маятниковые). Изучая различные упругие тела (пружины, стержни, луки), Гук установил, что «коэффициент пропорциональности» (в частности, жесткость пружины) сильно зависит от формы и размеров упругого тела, хотя материал играет решающую роль.
Прошло более ста лет, в течение которых опыты с упругими материалами проводили Бойль, Кулон, Навье и некоторые другие, менее известные физики. Одним из основных опытов стало растяжение пробного стержня из изучаемого материала. Для сравнения результатов, полученных в разных лабораториях, нужно было либо использовать всегда одинаковые образцы, либо научиться исключать слияние размеров образца. И в 1807 появилась книга Томаса Юнга, в которой был введен модуль упругости – величина, описывающая свойство упругости материала независимо от формы и размеров образца, который использовался в опыте. Для этого нужно силу P, приложенную к образцу, разделить на площадь сечения F, а произошедшее при этом удлинение Dl разделить на первоначальную длину образца l. Соответствующие отношения – это напряжение s и деформация e.
Теперь закон Гука о пропорциональности можно записать в виде:
s = Еe
Коэффициент пропорциональности Е называется модулем Юнга, имеет размерность, как у напряжения (МПа), а обозначение его есть первая буква латинского слова elasticitat – упругость.
Модуль упругости Е – это характеристика материала того же типа, как его плотность или теплопроводность.
В обычных условиях, чтобы продеформировать твердое тело, требуется значительная сила. Это означает, что модуль Е должен быть большой величиной – по сравнению с предельными напряжениями, после которых упругие деформации сменяются пластическими и форма тела заметно искажается.
Если измерять величину модуля Е в мегапаскалях (МПа), получатся такие средние значения:
| Сталь | 20·104 |
| Медь | 10·104 |
| Алюминий | 7·104 |
| Стекло | 7·104 |
| Кость | 3·104 |
| Дерево | 1·104 |
| Резина* | 0,001·104 |
Физическая природа упругости связана с электромагнитным взаимодействием (в том числе с силами Ван-дер-Ваальса в решетке кристалла). Можно считать, что упругие деформации связаны с изменением расстояния между атомами.
Упругий стержень имеет еще одно фундаментальное свойство – утоньшаться при растяжении. То, что канаты при растяжении становятся тоньше, было известно давно, но специально поставленные опыты показали, что при растяжении упругого стержня всегда имеет место закономерность: если измерить поперечную деформацию e’, т.е. уменьшение ширины стержня db , деленное на первоначальную ширину b, т.е.
и разделить ее на продольную деформацию e, то это отношение остается постоянным при всех значениях растягивающей силы P, то есть
(Полагают, что e’< 0 ; поэтому используется абсолютная величина). Константа v называется коэффициентом Пуассона (по имени французского математика и механика Симона Дени Пуассона) и зависит только от материала стержня, но не зависит от его размеров и формы сечения. Величина коэффициента Пуассона для разных материалов изменяется от 0 (у пробки) до 0,5 (у резины). В последнем случае объем образца в процессе растяжения не изменяется (такие материалы называются несжимаемыми). Для металлов значения различны, но близки к 0,3.
Модуль упругости E и коэффициент Пуассона вместе образуют пару величин, которые полностью характеризуют упругие свойства любого конкретного материала (имеются в виду изотропные материалы, т.е. такие, у которых свойства не зависят от направления; пример древесины показывает, что это не всегда так – ее свойства вдоль волокон и поперек волокон сильно различаются. Это – анизотропный материал. Анизотропными материалами являются монокристаллы, многие композиционные материалы (композиты) типа стеклопластика. Такие материалы тоже в известных пределах обладают упругостью, но само явление оказывается значительно более сложным).
Если от рассмотрения растяжения стержня перейти к рассмотрению некоторого упругого тела, подверженного действию заданных сил, то следует выбрать некоторую точку M и перейти к рассмотрению ее малой окрестности в виде параллелепипеда с ребрами, параллельными координатным осям XYZ. Как известно (см. ДЕФОРМАЦИЯ), на гранях параллелепипеда действуют напряжения, которые задаются тензором s, что приводит к деформациям, которые задаются тензором e.
В общем случае закон Гука устанавливает связь между компонентами этих тензоров, которую можно записать в виде:
,
,
,
, ,
В последние три уравнения входит величина G, которая называется модулем сдвига и выражается через E и v по формуле:
Модуль сдвига можно непосредственно определить из опыта на кручение круглого образца.
В физике для идеального газа вводится уравнение состояния (уравнение Клапейрона – Менделеева). Можно сказать, что закон Гука – это уравнение состояния для идеально упругого тела.
Владимир Кузнецов
www.krugosvet.ru
Упругость — это… Что такое Упругость?
свойство макроскопических тел сопротивляться изменению их объёма или формы под воздействием механических напряжений. При снятии приложенного напряжения объём и форма упруго деформированного тела восстанавливаются.
У. тел обусловлена силами взаимодействия атомов, из которых они построены. В твёрдых телах при температуре абсолютного нуля в отсутствии внешних напряжений атомы занимают равновесные положения, в которых сумма всех сил, действующих на каждый атом со стороны остальных, равна нулю, а потенциальная энергия атома минимальна. Кроме сил притяжения и отталкивания, зависящих только от расстояния (рис. 1) между атомами (центральные силы), в многоатомных молекулах и макроскопических телах действуют также угловые силы, зависящие от т. н. валентных углов между прямыми, соединяющими данный атом с различными его соседями (рис. 2). При равновесных значениях валентных углов угловые силы также уравновешены. Энергия макроскопического тела зависит от межатомных расстояний и валентных углов, принимая минимальное значение при равновесных значениях этих параметров.
Под действием внешних напряжений атомы смещаются из своих равновесных положений, что сопровождается увеличением потенциальной энергии тела на величину, равную работе внешних напряжений по изменению объёма и формы тела. После снятия внешних напряжений конфигурация упруго деформированного тела с неравновесными межатомными расстояниями и валентными углами оказывается неустойчивой и самопроизвольно возвращается в равновесное состояние, точнее, атомы колеблются около равновесных положений. Запасённая в теле избыточная потенциальная энергия превращается в кинетическую энергию колеблющихся атомов, т. е. в тепло. Пока отклонения межатомных расстояний и валентных углов от их равновесных значений малы, они пропорциональны действующим между атомами силам, подобно тому как удлинение или сжатие пружины пропорционально приложенной силе. Поэтому тело можно представить как совокупность атомов-шариков, соединённых пружинами, ориентации которых фиксированы др. пружинами (рис. 2). Константы упругости этих пружин определяют Модули упругости материала, а упругая деформация тела пропорциональна приложенному напряжению, т. е. определяется Гука законом, который является основой упругости теории (См. Упругости теория) и сопротивления материалов.При конечных температурах (ниже температур плавления) даже без приложения и снятия внешних напряжений атомы совершают малые тепловые колебания около положений равновесия. Это приводит к тому, что модули упругости материала зависят от температуры, но не меняет существа рассмотренных явлений.
В жидкости тепловые колебания имеют амплитуду, сравнимую с равновесным расстоянием r0, вследствие чего атомы легко меняют своих соседей и не сопротивляются касательным напряжениям, если они прикладываются со скоростью, значительно меньшей скорости тепловых колебаний. Поэтому жидкости (как и газы) не обладают упругостью формы.
В газообразном состоянии средние расстояния между атомами или молекулами значительно больше, чем в конденсированном. Упругость газов (паров) определяется тепловым движением молекул, ударяющихся о стенки сосуда, ограничивающего объём газа.
Лит.: Фейнман Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике, [в.] 7, М., 1966, гл. 38, 39; Смирнов А. А., Молекулярно-кинетическая теория металлов, М., 1966, гл. 2; Френкель Я. И., Введение в теорию металлов, 4 изд., Л., 1972, гл. 2.
А. Н. Орлов.
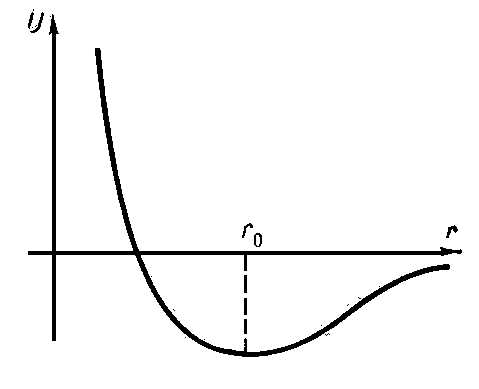
Рис. 1. Зависимость потенциальной энергии взаимодействия двух атомов от расстояния r между ними. Равновесное состояние r0 отвечает наименьшему значению потенциальной энергии. На этом расстоянии силы притяжения и отталкивания между атомами уравновешены.

Рис. 2. Шариковая модель элементарной ячейки кубического кристалла: а — в равновесии при отсутствии внешних сил; б — при действии внешнего касательного напряжения.
dic.academic.ru
УПРУГОСТЬ — это… Что такое УПРУГОСТЬ?
-свойство тел изменять форму и размеры под действием нагрузок и самопроизвольно восстанавливать исходную конфигурацию при прекращении внеш. воздействий.
Количественно У. выражается в том, что компоненты тензора напряжений (см. Напряжение механическое )в изо-термич. условиях являются ф-циями компонентов тензора деформации (см. Деформация), к-рые универсальны для данного материала и не зависят от того, в каком порядке происходит изменение разл. компонентов деформации до достижения ими рассматриваемых значений. В большинстве материалов (напр., в металлах, керамике, горных породах, древесине) при малых деформациях зависимости между напряжениями и деформациями можно считать линейными и описывать обобщённым Гука законом. Законам нелинейной У. можно придать форму, подобную обобщённому закону Гука, заменив модули упругости нек-рыми универсальными ф-циями (см. Упругости теория).
У. тел обусловлена силами взаимодействия атомов, из к-рых они построены. В твёрдых телах при темп-ре абс. нуля в отсутствие внеш. напряжений атомы занимают равновесные положения, в к-рых сумма всех сил, действующих на каждый атом со стороны остальных, равна нулю, а потенц. энергия атома минимальна. Кроме сил притяжения и отталкивания, зависящих только от расстояния между атомами (центральные силы), в многоатомных молекулах и макроскопич. телах действуют также нецентральные силы, зависящие от т. н. валентных углов между прямыми, соединяющими данный атом с его разл. соседями (рис.). При равновесных значениях валентных углов нецентральные силы также уравновешены. Энергия макроскопич. тела зависит от межатомных расстояний и валентных углов, принимая мин. значение при равновесных значениях этих параметров.
Под действием внеш. напряжений атомы смещаются из своих равновесных положений, что сопровождается увеличением потенц. энергии тела на величину, равную работе внеш. напряжений по изменению объёма и формы тела. После снятия внеш. напряжений конфигурация упруго де-формир. тела с неравновесными межатомными расстояниями и валентными углами оказывается неустойчивой и самопроизвольно возвращается в равновесное состояние. Запасённая в теле избыточная потенц. энергия превращается в энергию колеблющихся атомов, т.

Шариковая модель элементарной ячейки кубического кристалла: а- в равновесии в отсутствие внешних сил; б- под действием внешнего касательного напряжения.
В жидкости тепловые колебания имеют амплитуду, сравнимую с равновесным межатомным расстоянием, вследствие чего атомы легко меняют своих соседей и не сопротивляются касат. напряжениям, если они прикладываются со скоростью, значительно меньшей скорости тепловых колебаний. Поэтому жидкости (как и газы) не обладают упругостью формы, а только объёма: уменьшение объёма пропорц. приложенному давлению.
В газообразном состоянии ср. расстояния между атомами или молекулами значительно больше, чем в конденсированном. Упругость газов (паров) определяется тепловым движением молекул, ударяющихся о стенки сосуда, ограничивающего объём газа.
Лит.: Френкель Я. И., Введение в теорию металлов, 4 изд., Л., 1972, гл. 2; Фейнман Р., Лейтон Р., Сэндс М., Фейнманов-ские лекции по физике, 2 изд., [в.] 7, М., 1977, гл. 38-39; Смирнов А. А., Молекулярно-кинетическая теория металлов, М., 1966, гл. 2. А. Н. Орлов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
dic.academic.ru
Упругость материала
Детали конструкций работают на растяжение, сжатие, изгиб или кручение, при этом происходит деформация их материала.
Напряжение – мера внутренних сил, возникающих при деформации материала, численно представляющая собой отношение усилия P (растяжения или сжатия) к площади F поперечного сечения образца или детали:
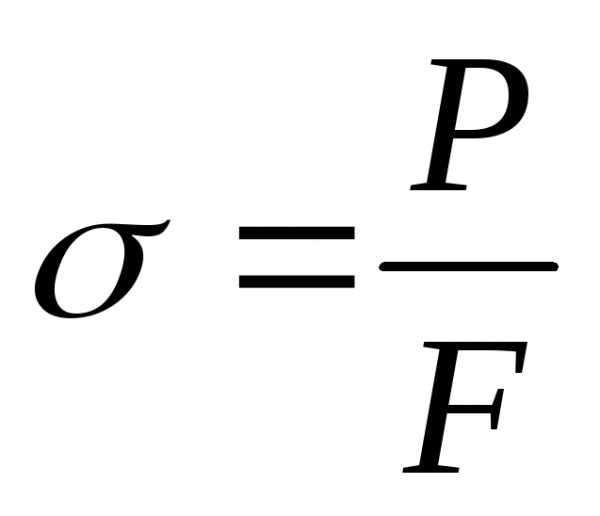 .
.
Упругость – свойство материала восстанавливать свою форму и объем при прекращении внешних воздействий. Упругость это очень важная характеристика материалов, т.к. от нее зависит жесткость конструкции. Она обусловлена взаимодействием между атомами и молекулами и их тепловым движением. Плотность материалов определяет во многом значения других показателей, в том числе и их упругость.
Количественных характеристик упругих свойств материалов несколько; важнейшими из них являются модули Е упругости Юнга (модуль продольной упругости) и коэффициент Пуассона (модуль поперечной упругости).
Модуль Юнга Е представляет собой меру жесткости материала и отражает сопротивляемость материала упругой деформации. Он практически не зависит от структуры материала и хорошо коррелируется с температурой его плавления. Жесткость конструкции повышается с увеличением модуля упругости.
Коэффициент Пуассона отражает соотношение между продольными и поперечными деформациями. Величина этого коэффициента для материалов находится в пределах 0,2…0,45, составляя для большинства металлов ~ 0,3.
Начальный участок диаграммы растяжения представляет собой прямую линию. Крутизна этого участка (отношение напряжения к деформации) является характеристикой металла — модулем упругости Юнга (модулем Е).
Модуль Юнга Е – отношение величины напряжения к вызванной им относительной деформации (рис.2.1):
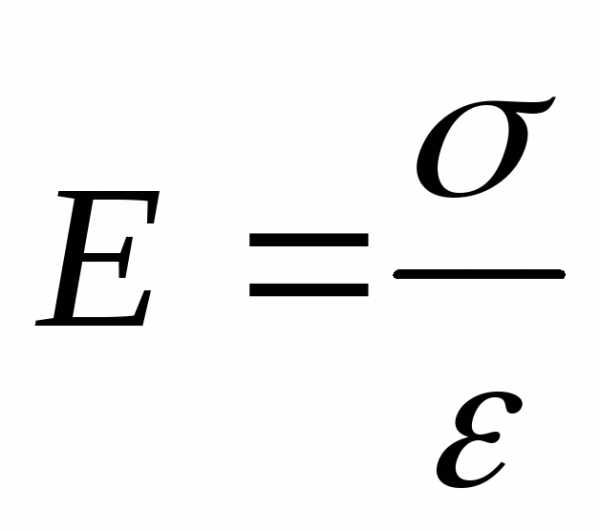 .
.
Рис. 2.1. Изменение напряжения в зависимости от относительного удлинения материала
Относительное удлинение (сжатие) испытываемого материала определяется по формуле:
 ,
,
г де l и l0– длины образца, соответственно, после растяжения и начальная.
 Коэффициент
Пуассона –
относительное изменение поперечного
размера тела d/dо,
деленное на относительное изменение
его длины l
/lо:
Коэффициент
Пуассона –
относительное изменение поперечного
размера тела d/dо,
деленное на относительное изменение
его длины l
/lо:
Жесткость – способность материала к наименьшему изменению размеров и формы при заданной нагрузке. Чем больше жесткость материала образца, или детали, тем происходят меньшие изменения его формы и размеров при нагружении.
2.4. Ультразвуковой метод определения модуля упругости Юнга
Модуль упругости определяют по диаграмме растяжения образца, но это возможно и ультразвуковым методом.
Ультразвуковой метод основан на зависимости скорости распространения Fр ультразвуковых колебаний (частота выше 20 кГц) в материалах от их упругости Е и плотности ρ:
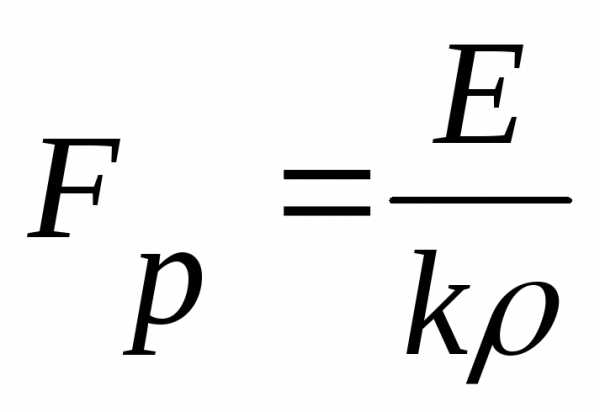 ,
м/с,
,
м/с,
где Е- модуль упругости Юнга, ГПа;
ρ — плотность материала, кг/м3;
к- коэффициент взаимосвязи.
Челябинское научно- производственное предприятие «Интерприбор» выпускает большую номенклатуру малогабаритных приборов для неразрушающего контроля строительных материалов. В лабораторных работах №2…№5 используются некоторые из них: прибор определения прочности бетонов Оникс-2.51, измерители влажности ВИМС -2.1 и теплопроводности материалов МИТ-1, ультразвуковой прибор Пульсар -1.1, двухканальный гигрометр ТЕМП-3.2.1.
Достоинства этих приборов:
Применяются в качестве методов неразрушающего контроля.
Дисплей и управление процессом измерения у этих приборов построены по одинаковым принципам.
Приборами выполняется первичная обработка информации (определяются среднее значение и ошибка измерений), проводится накопление ее и возможна связь с компьютером.
Для повышения точности измерений в программу вводится название исследуемого материала, т.е. закладываются некоторые основные его характеристики.
Приборы определяют какую то физическую величину (стабилизация температуры, скорость,…), которая далее пересчитывается в характеристику материала (теплопроводность, прочность материала,…).
При использовании этих приборов сначала устанавливаются параметры:
— в пункте «режим работы» — поверхностное или сквозное прозвучивание;
-в пункте «материал» — вид испытываемого материала;
— в меню «калибровка» — измеряемый параметр: скорость ультразвука, плотность, прочность и др.;
— в подменю «коэффициенты характеристик» — задать (ранее определенные опытным путем) коэффициенты для пересчета зависимости «скорость распространения УЗК – измеряемый параметр».
Кроме этих электронных приборов в работах используются такие простейшие измерительные средства как весы рычажные и электронные, линейки и штангенциркули.
Характеристика ультразвукового прибора Пульсар 1.1
Прибор Пульсар 1.1 предназначен для определения времени и скорости распространения ультразвуковых волн (УЗВ) в твердых материалах при поверхностном, угловом и сквозном прозвучиваниях (рис 2.3).
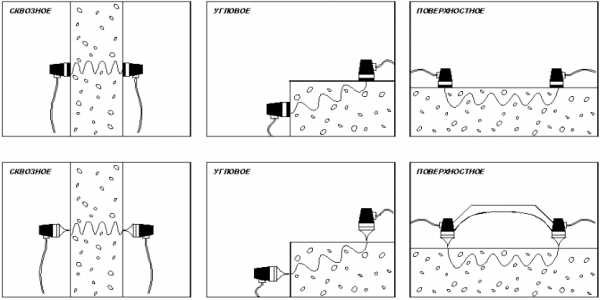
Рис. 2.3. Схемы прозвучивания материалов
Основные области применения прибора Пульсар 1.1:
Определение прочности бетона (ГОСТ 17624-87).
Определение прочности кирпича и камней силикатных (ГОСТ 24332).
Поиск дефектов в бетонных сооружениях.
Определение глубины трещин.
Оценка пористости, трещиноватости и анизотропии композитных материалов.
Определение модуля упругости и плотности.
Контроль качества дорожных покрытий.
В меню прибора заложены основные виды контролируемых материалов:
— бетоны;
— кирпичи;
— абразивы;
— другие материалы, задаваемые пользователем.
Основные функции прибора:
Способы прозвучивания: сквозное и поверхностное (см. рис.2.3).

Рис. 2.4. Вид электронного блока: 1 – вход приемного преобразователя, 2 – выход излучающего преобразователя
2. Виды акустического контроля:
— сухой контакт с коническим титановыми наконечниками или полиуретановыми протекторами;
— с контактной смазкой полиуретановыми протекторами.
Ультразвуковой прибор обеспечивает измерение времени сквозного прохождения ультразвуковых колебаний через образец.
Образцы изготовляются или принимаются готовые изделия в виде стержня квадратного или круглого сечения. Требования к размерам образцов:
L d; d > 0,34 ,
где L и d — длина и диаметр (ширина) образца, мм;
— длина волны ультразвуковых колебаний, м.
Клавиатура прибора состоит из 9 клавиш (рис.2.4). Клавиша « » используется для включения и выключения прибора. Если измерения не выполняются, происходит автоматическое отключение прибора через заданное оператором время.
Клавиша «М» служит для перевода прибора из режима меню в режим измерения (measuring), а также для фиксации очередного результата в памяти (memory).
Клавиша «F» является функциональной и предназначена для:
Клавишами «», «» управляется курсор (мигающий знак, цифра и т.п.) в режиме установки параметров работы и осуществляется просмотр памяти результатов по номерам из режима измерения.
Клавиши «», «» предназначены для:
выбора строки меню;
просмотра памяти результатов по датам из режима измерения;
установки числовых значений (кратковременное нажатие изменяет значение на единицу, а при удержании происходит непрерывное увеличение числа).
Клавишей «С» выполняется проверка на контрольных образцах, включение курсора при установке даты и времени, удаление результата непосредственно после его получения.
Клавиша « » (подсветка) включает/ выключает подсветку индикатора. Используется совместно с другими клавишами, т.е. при ее удерживании нажимается другая клавиша.
Модуль упругости материала определяется с использованием режима сквозного прозвучивания в следующей последовательности:
Включить прибор клавишей « ».
Измерить линейкой или штангенциркулем размер контролируемого образца материала (расстояние между излучателем и приемником) и ввести это значение через пункт главного меню База измерения.
В меню «Режим работы « указать «Сквозное прозвучивание».
В меню «Установки» указать число измерений в серии (например, 6). В этом случае после шести последовательных измерений прибор покажет среднее значение измеряемого параметра R, коэффициент вариации W и относительную ошибку измерений H.
В меню «Материал» указать клавишами «», «» материал (бетон, кирпич, абразив, разные), а клавишами «», «» состав или вид исследуемого материала.
В меню «Калибровка» указать «Коэффициенты характеристик» (см. пример для бетона тяжелого). При измерении модуля упругости необходимо задавать коэффициенты для пересчёта зависимости «скорость распространения – модуль упругости» в следующем виде:
 ,
,
где Е – модуль упругости;
V – скорость ультразвука, м/с;
— объемный вес материала, г/см3;
— коэффициент.
Установить датчики на контролируемый объект. В процессе измерений оператор прижимает усилием 5 …10 кг излучатель и приемник к контролируемому объекту до получения устойчивых показаний.
Убедиться в отсутствии грубых отклонений показаний от ожидаемого уровня и при стабильных показаниях нажать клавишу М, зафиксировав в памяти этим результат.
Снять датчик с объекта измерения, при этом показания на дисплее автоматически удерживаются до очередного прижатия.
Далее повторить измерения на других участках объекта, каждый раз фиксируя результат нажатием клавиши М, последний результат серии фиксируется клавишей М с выдачей среднего значения серии измерений R, ошибки измерения H и коэффициента вариации W. Выполняются 6 измерений, при этом датчики каждый раз переставляются.
Для получения более точного результата измерений рекомендуется удерживать датчик на объекте в течение 10… 30 секунд, наблюдая за сменой показаний и фиксируя результат по максимальной скорости ультразвука; разброс показаний вызван ненадежностью акустического контакта и неизбежными помехами, поэтому при измерениях датчик должен быть неподвижен.
studfiles.net
УПРУГОСТЬ — Физический энциклопедический словарь
Свойство тел изменять форму и размеры под действием нагрузок и самопроизвольно восстанавливать исходную конфигурацию при прекращении внеш. воздействий.
Количественно У. выражается в том, что компоненты тензора напряжений (см. НАПРЯЖЕНИЕ МЕХАНИЧЕСКОЕ) в изотермич. условиях явл. функциями компонентов тензора деформации (см. ДЕФОРМАЦИЯ механическая), к-рые универсальны для данного материала и не зависят от того, в каком порядке происходит изменение разл. компонентов деформации до достижения ими рассматриваемых значений. В большинстве материалов (напр., в металлах, керамике, горных породах, древесине) при малых деформациях зависимости между напряжениями и деформациями можно считать линейными и описывать обобщённым Гука законом. Законам нелинейной У. можно придать форму, подобную обобщённому закону Гука, заменив модули упругости нек-рыми универсальными функциями (см. УПРУГОСТИ ТЕОРИЯ).
У. тел обусловлена силами вз-ствия атомов, из к-рых они построены. В тв. телах при темп-ре абс. нуля в отсутствии внеш. напряжений атомы занимают равновесные положения, в к-рых сумма всех сил, действующих на каждый атом со стороны остальных, равна нулю, а потенц. энергия атома минимальна. Кроме сил притяжения и отталкивания, зависящих только от расстояния между атомами (центр. силы), в многоатомных молекулах и макроскопич. телах действуют также нецентральные силы, зависящие от т. н. валентных углов между прямыми, соединяющими данный атом с разл. его соседями (рис.). При равновесных значениях валентных углов нецентральные силы также уравновешены. Энергия макроскопич. тела зависит от межатомных расстояний и валентных углов, принимая миним. значение при равновесных значениях этих параметров.
Под действием внеш. напряжений атомы смещаются из своих равновесных положений, что сопровождается увеличением потенц. энергии тела на величину, равную работе внеш. напряжений по изменению объёма и формы тела. После снятия внеш. напряжений конфигурация упруго деформиров. тела с неравновесными межатомными расстояниями и валентными углами оказывается неустойчивой и самопроизвольно возвращается в равновесное состояние. Запасённая в теле избыточная потенц. энергия превращается в кинетич. энергию колеблющихся атомов, т. е. в теплоту.
Шариковая модель элем. ячейки кубич. кристалла: а — в равновесии при отсутствии внеш. сил; б — под действием внеш. касательного напряжения.
Пока отклонения межатомных расстояний и валентных углов от их равновесных значений малы, они пропорц. действующим между атомами силам, подобно тому, как удлинение или сжатие пружины пропорц. приложенной силе. Поэтому тело можно представить как совокупность атомов-шариков, соединённых пружинами, ориентации к-рых фиксированы др. пружинами (рис.). Константы упругости этих пружин определяют модули упругости материала.
В жидкости тепловые колебания имеют амплитуду, сравнимую с равновесным межатомным расстоянием, вследствие чего атомы легко меняют своих соседей и не сопротивляются касат. напряжениям, если они прикладываются со скоростью, значительно меньшей скорости тепловых колебаний. Поэтому жидкости (как и газы) не обладают упругостью формы, а только объёма: уменьшение объёма пропорционально приложенному давлению.
В газообразном состоянии средние расстояния между атомами или молекулами значительно больше, чем в конденсированном. Упругость газов (паров) определяется тепловым движением молекул, ударяющихся о стенки сосуда, ограничивающего объём газа.
Источник: Физический энциклопедический словарь на Gufo.megufo.me
Значение слова УПРУГОСТЬ. Что такое УПРУГОСТЬ?
В физике упругость — это свойство твёрдых материалов возвращаться в изначальную форму при упругой деформации. Твёрдые предметы будут деформироваться после приложенной на них силы. Если убрать силу, то упругий материал восстановит начальную форму и размер.Физические причины для упругого поведения могут быть совершенно различными для разных материалов. В металлах атомная решётка меняет размер и форму при приложении силы (добавлении энергии в систему). Когда сила убирается, решётка возвращается обратно в прежнее энергетическое состояние. Для резины и других полимеров упругость вызывается растяжением полимерной цепочки (см. «Высокоэластичное состояние»).
Абсолютная упругость — это идеализация реального мира, и даже при небольших деформациях мало материалов остаются совершенно упругими. В инженерном деле упругость материалов измеряется двумя типами параметров материала:
Модуль упругости показывает механическое напряжение (количество силы на единицу площади), которое необходимо приложить для достижения определённого уровня деформации. Модуль измеряется в паскалях (Па) или фунтах силы на кв. дюйм (psi или lbf/in2). Высокий модуль обычно показывает, что материал труднее деформировать.
Предел упругости — максимальное напряжение, после которого материал больше не ведёт себя как упругий, и будет иметь место пластическая (необратимая) деформация материала. После снятия напряжения материал сохранит некоторую остаточную деформацию.
Чтобы описать относительную упругость двух материалов, должны рассматриваться и модуль, и предел упругости. У резины, как правило, низкий модуль, и она обычно сильно растягивается (у неё высокий предел упругости), и поэтому проявляет большую эластичность, чем металлы в ежедневном применении. Если взять два резиновых материала с одним и тем же пределом упругости, то тот, у кого более низкий модуль, будет казаться более эластичным.
kartaslov.ru