Угол поворота, угол произвольной величины, поворот вокруг точки на заданный угол

Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.

Поворот точки вокруг точки

Определение 1

Центр поворота – точка, относительно которой осуществлен поворот.

Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О, в результате чего получается точка А1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А). При этом точка А1 лежит на окружности с центром в точке О радиуса ОА. Другими словами, когда точка А осуществляет поворот относительно точки О, она переходит в точку А1, лежащую на окружности с центром О радиуса ОА.

Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О, она переходит в саму себя.

Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса ОА.

Изобразим графически поворот точки А относительно точки О, перемещение точки А в точку А1 отметим стрелкой:

Полный оборот

Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А, пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О.

Проиллюстрируем:

Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:

В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.

Угол поворота

Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О. Любую точку окружности с центром О можно рассматривать как точку А1, полученную в результате поворота точки А. Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.

Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.

Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от -∞ до +∞, что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180°.

Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α, β, γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α1, α2, α3…..αn.

Разберем характеристики угла поворота подробнее.

Направление поворота

Отметим на окружности с центром О точки А и А1. В точку А1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

Величина угла поворота, угол произвольной величины

Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.

Как было сказано выше, величина угла поворота варьируется в пределах от -∞ до +∞;

Определение 2

Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.

Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.

Пусть угол поворота равен 0°. Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0° точка A остается на месте.

Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А1. В таком случае абсолютная величина угла АОА1, выраженная в градусах, не превосходит 180. Если поворот имел положительное направление, то величина угла поворота считается равной величине угла АОА1; если отрицательное – величина угла поворота равна величине угла АОА1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30°, 180° и -150°:

Углы поворота, превышающие 180 или меньшие –180 определяются, исходя из очевидного свойства последовательных поворотов:

Определение 3

Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.

Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45°, затем еще на 60° и еще раз — на -35°. Обозначим промежуточные точки поворотов А1, А2 и А3. В конечную точку А3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45°+ 60° + (-35°) = 70°. Проиллюстрируем:

Таким, образом, углы, превышающие 180°, будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298° соответствует последовательным поворотам на 180° и 118°, или 90°, 90°, 90° и 28°, или 180°, 180° и -62°, или 298 последовательных поворотов на 1°.

По такому же принципу определяются углы меньше -180°. Например, угол поворота -515° можно определить, как последовательные повороты на -180°,-180° и -155°.

Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от -∞ до +∞.

Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.

В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360° или 2π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в -360° или -2π радиан.

При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от -180° до 180°. К примеру, поворот осуществляется на 1478°. Представим эту величину как: 360 · 4 + 38, т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38°. Или еще один пример: угол поворота в -815° можно представить, как (-360) · 2 + (-95), т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на -95°.

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).

Определение 3

Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.

Как пример, иллюстрируем следующее действие: поворот отрезка АВ на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А1В1.

Формула угловой скорости в физике

Содержание:

• Определение и формула угловой скорости
• Равномерное вращение
• Формула, связывающая линейную и угловую скорости
• Единицы измерения угловой скорости
• Примеры решения задач

Определение и формула угловой скорости

Определение

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

Перемещение при вращении характеризуют при помощи угла поворота $(\varphi)$ . Часто используют вектор элементарного поворота $\bar{d\varphi}$ , который равен по величине элементарному углу поворота тела $(d \varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону, откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами. Углы вращения на конечные величины векторами не являются.

Определение

Угловой скоростью

называют скорость изменения угла поворота и обозначают ее обычно буквой $\omega$ . Математически определение угловой скорости записывают так:

$$\bar{\omega}=\frac{d \bar{\varphi}}{d t}=\dot{\bar{\varphi}}(1)$$

Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).

Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ($\bar{\omega}$ при этом изменяет направление).

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

$$\omega=\frac{\varphi}{t}(2)$$

где $(\varphi)$ – угол поворота, t – время, за которое этот поворот совершён.

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:

$$\omega=\frac{2 \pi}{T}(3)$$

С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:

$$\omega=2 \pi \nu(4)$$

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.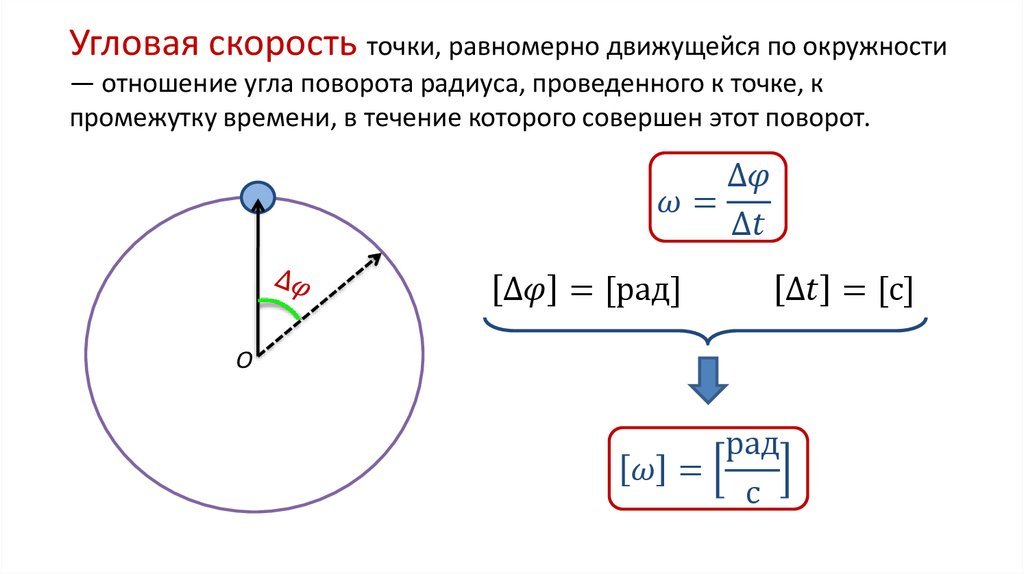

{3} \approx 20(\mathrm{rad})$$

Ответ. $\varphi = 20$ рад.

Читать дальше: Формула удельного веса.

6.1 Угол поворота и угловая скорость

Цели обученияУгол вращенияУгловая скорость

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Определение длины дуги, угла поворота, радиуса кривизны и угловой скорости
• Рассчитать угловую скорость вращения колеса автомобиля

В кинематике мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.

Угол поворота

Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (CD) на рис. 6.2 вращается вокруг своего центра — каждая точка объекта следует дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Определяем угол поворота Размер ΔθΔθ 12{Δθ} {} должен быть отношением длины дуги к радиусу кривизны.

6.1 Δθ=Δср.Δθ=Δср. размер 12{Δθ= {{Δs} над {r} } } {}

Рис. 6.2 Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол ΔθΔθ размер 12{Δθ} {} за время ΔtΔt размер 12{Δt} {}.

Рисунок 6.3 Радиус окружности поворачивается на угол ΔθΔθ величиной 12{Δθ} {}. Длина дуги ΔsΔs размером 12{Δs} {} описана на окружности.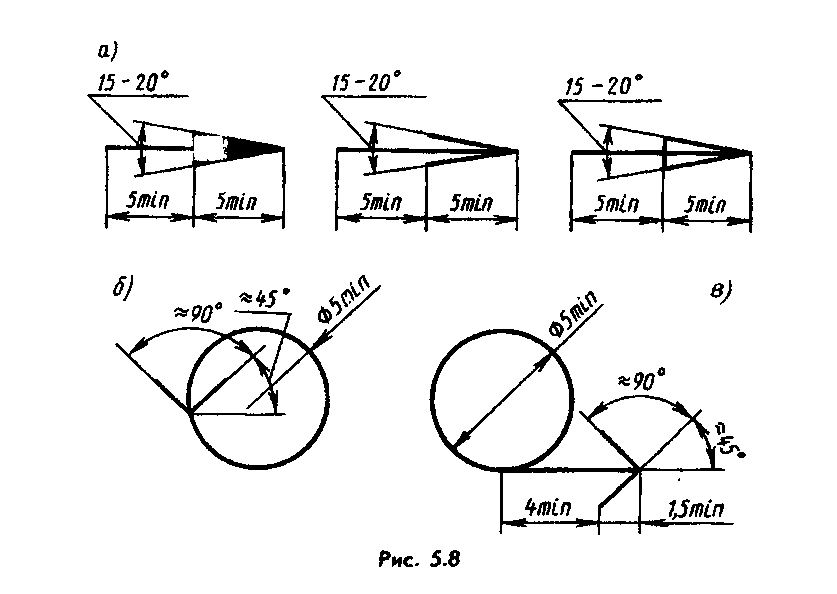

Длина дуги ΔsΔs размер 12{Δs} {} — это расстояние, пройденное по круговому пути, как показано на рис. 6.3. Обратите внимание, что rr размер 12{r} {} — это радиус кривизны кругового пути.

Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиуса rr размера 12{r} {}. Длина окружности равна 2πr2πr размера 12{2πr} {}. Таким образом, за один полный оборот угол поворота равен

.

6.2 Δθ=2πrr=2π.Δθ=2πrr=2π. size 12{Δθ= {{2πr} over {r} } =2π».»} {}

Этот результат является основой для определения единиц, используемых для измерения углов поворота, ΔθΔθ size 12{Δθ} {} в радианах (рад), определяемый таким образом, что

6,3 2πрад = 1 оборот. 2πрад = 1 оборот. размер 12{2π» рад «=» 1 оборот.»} {}

Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 6.1.

Градусы	Измерение в радианах
30º30º размер 12{«30″°} {}	π6π6 размер 12{ { {π} больше {6} } } {}
60º60º размер 12{«60″°} {}	π3π3 размер 12{ { {π} над {3} } } {}
90º90º размер 12{«90″°} {}	π2π2 размер 12{ { {π} более {2} } } {}
120º120º размер 12{«120″°} {}	2π32π3 размер 12{ { {2π} более {3} } } {}
135º135º размер 12{«135″°} {}	3π43π4 размер 12{ { {3π} больше {4} } } {}
180º180º размер 12{«180″°} {}	ππ размер 12{π} {}

Таблица 6. 1 Сравнение угловых единиц

Рисунок 6.4 Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ размер 12{Δθ} {}), но точка 2 перемещается по дуге большей длины ΔsΔs размер 12{ влево (Δs вправо )} {}, потому что она находится на большем расстояние от центра вращения (r)(r) размер 12{ \( r \) } {}.

Если Δθ=2πΔθ=2π размер 12{Δθ=2π} {} рад, то компакт-диск совершил один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку в круге или одном обороте есть 360º360º размера 12{«360″°} {}, соотношение между радианами и градусами, таким образом, равно

6,4 2πrad=360º2πrad=360º размер 12{2π» рад»=»360″ rSup { размер 8{ circ } } } {}

так что

6,5 1rad=360º2π≈57,3 º,1 рад=360º2π≈57,3º . размер 12{1″ рад»= {{«360″ rSup {размер 8{круг} } } более {2π} } =»57» «.» 3 rSup { size 8{ circ } } «.»} {}

Угловая скорость

Как быстро вращается объект? Определим угловую скорость ωω величиной 12{ω} {} как скорость изменения угла. В символах это

6,6 ω=ΔθΔt,ω=ΔθΔt, размер 12{ω= {{Δθ} над {Δt} } «,»} {}

где угловой поворот ΔθΔθ размер 12{Δθ} {} происходит за время ΔtΔt размер 12{Δt} {}. Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).

Угловая скорость ωω размера 12{ω} {} аналогична линейной скорости vv размера 12{v} {}. Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма перемещается по дуге длиной ΔsΔs размером 12{Δs} {} за время ΔtΔt размером 12{Δt} {}, поэтому она имеет линейную скорость

6,7 v=ΔsΔt.v=ΔsΔt. size 12{v= {{Δs} над {Δt} } «.»} {}

Из Δθ=ΔsrΔθ=Δsr size 12{Δθ= {{Δs} над {r} } } {} мы видим, что Δs= rΔθΔs=rΔθ размер 12{Δs=rΔθ} {}. Подстановка этого выражения в выражение для размера vv 12{v} {} дает

6,8 v=rΔθΔt=rω.v=rΔθΔt=rω. size 12{v= {{rΔθ} над {Δt} } =rω».»} {}

Мы запишем это отношение двумя разными способами и получим два разных понимания

6,9 v=rω или ω=vr. v=rω или ω=vr. размер 12{v=rω«»или «ω= { {v} над {r} } «.»} {}

Первое соотношение в v=rω или ω=vrv=rω или ω=vr size 12{v=rω«»или «ω= { {v} over {r} } } {} утверждает, что линейная скорость vv размер 12{v} {} пропорционален расстоянию от центра вращения, поэтому он является наибольшим для точки на ободе (наибольший размер rr 12{r} {}), как и следовало ожидать. Мы также можем назвать эту линейную скорость vv размером 12{v} {} точки на ободе тангенциальной скоростью . Второе соотношение в v=rω или ω=vrv=rω или ω=vr size 12{v=rω«» или «ω= {{v} over {r}}} {} можно проиллюстрировать, рассмотрев шину движущийся автомобиль. Обратите внимание, что скорость точки на ободе шины такая же, как скорость vv размера 12{v} {} автомобиля. (см. рис. 6.5). Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой размер vv 12{v} {} означает большой размер ωω 12{ω} {}, потому что v=rωv=rω размер 12{v=rω} {}. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ωω размер 12{ω} {}), будет производить большую линейную скорость (vv размер 12{v} {}) для автомобиля.

Рисунок 6.5 Автомобиль, движущийся со скоростью vv размера 12{v} {} вправо, имеет шину, вращающуюся с угловой скоростью ωω размера 12{ω} {}. Скорость протектора шины относительно оси равна vv размер 12{v}{}, такой же, как если бы автомобиль был на домкрате. Таким образом, автомобиль движется вперед с линейной скоростью v=rωv=rω размер 12{v=rω} {}, где rr размер 12{r} {} — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.

Пример 6.1 Как быстро вращается автомобильная шина?

Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с15,0 м/с Размер 12{«15» «.» 0`»м/с»} {} (около 54 км/ч54км/ч размер 12{«54″`»км/ч»} {}) (см. рис. 6.5.

Стратегия

Поскольку линейная скорость обод шины такой же, как и скорость автомобиля, мы имеем v=15,0 м/с. v=15,0 м/с. размер 12 {v} {} Радиус шины принимается равным r=0,300 м. r=0,300 м. размер 12{r} {} Зная vv size 12{v} {} и rr size 12{r} {}, мы можем использовать второе соотношение в v=rω, ω=vrv=rω, ω=vr size 12{v=rω,«ω= { {v} над {r} } } {} для вычисления угловой скорости.

Решение

Для расчета угловой скорости воспользуемся следующим соотношением

6.10 ω=vr.ω=vr. размер 12{ω= { {v} над {r} } «.»} {}

Подстановка известных,

6,11 ω=15,0м/с0,300м=50,0рад/с.ω=15,0м/с0. 300 м = 50,0 рад/с. размер 12{ω= {{«15» «.» 0″ м/с»} более {0 «.» «300»» м»} } =»50″ «.» 0″ рад/с.»} {}

Обсуждение

Когда мы исключаем единицы измерения в приведенном выше расчете, мы получаем 50,0/с. Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны, поскольку определяются как отношение расстояния, мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. Они будут иметь угловую скорость

6,12 ω=(15,0 м/с)/(1,20 м)=12,5 рад/с. ω=(15,0 м/с)/(1,20 м)=12,5 рад/с. размер 12{ω= \(«15» «.» 0`»м/с» \) / \( 1 «.» «20»`м \) =»12″ «.» 5`»рад/с.»} {}

Оба ωω размера 12{ω} {} и vv размера 12{v} {} имеют направления, следовательно, они являются угловой и линейной скоростями , соответственно. Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на рис. 6.6.

Эксперимент на вынос

Привяжите предмет к концу веревки и раскачивайте его по горизонтальному кругу над головой (покачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.

Рис. 6.6 Поскольку объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, ее мгновенная скорость всегда касается окружности.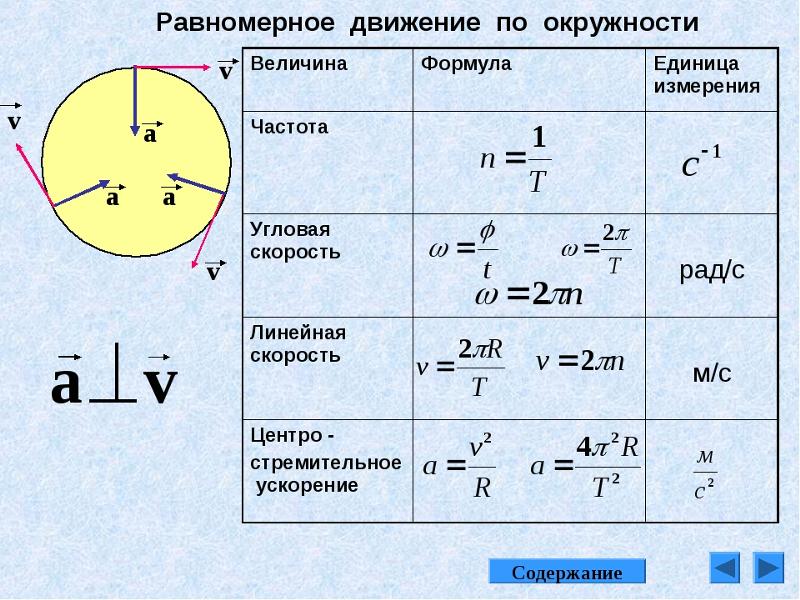 Направление угловой скорости в этом случае – по часовой стрелке.

Исследования PhET: революция божьей коровки

Рисунок 6.7. Революция божьей коровки

Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Узнайте, как круговое движение связано с ошибкой x,y — положение, скорость и ускорение с использованием векторов или графиков.

• Печать
• Поделиться

5.1 Угловое положение и смещение – биомеханика движения человека

Ранее мы изучали движение по прямой и вводили такие понятия, как перемещение, скорость и ускорение. Затем мы имели дело с движением одной точки в двух измерениях. Снарядное движение — это частный случай двумерной кинематики, при котором объект проецируется в воздух, при этом на него действует сила тяжести (постоянное ускорение). Его траектория предсказуема с помощью уравнений равноускоренного движения. В этой главе мы рассмотрим ситуации, когда объекты вращаются вокруг точки (оси вращения) при движении по круговой траектории. Обычно мы рассматриваем движение всего сегмента.

В биомеханике принято допущение, что сегменты тела являются твердыми телами. Твердые тела сохраняют постоянную длину. Вместо представления движения относительно точки (например, центра масс), как мы это делали в линейной кинематике, мы будем представлять движение твердого тела (например, бедра). Это повлияет на нашу систему отсчета, поскольку движение больше не происходит по осям x и y. Правильно, мы больше не описываем движение по отношению к осям x и y системы координат, а по отношению к оси вращения.

Угол
Угол образуется при пересечении двух прямых, двух плоскостей или прямой и плоскости. Углы используются для определения ориентации этих линий или плоскостей относительно друг друга.

Угловое движение происходит вокруг оси вращения. В человеческом теле эта ось вращения представляет собой сустав, а твердые тела — это кости, вращающиеся вокруг угла. Ось всегда перпендикулярна плоскости. Например. если нас интересует угол колена в сагиттальной плоскости, мы будем количественно оценивать движение вокруг медиолатеральной оси. Система отсчета больше не является декартовой системой отсчета с двумя ортогональными осями, а является комбинацией оси вращения и оси отсчета. При этом вращение вокруг оси вращения в направление по часовой стрелке всегда будет отрицательным, и вращение в направлении против часовой стрелки всегда будет положительным.

Вы помните разницу между абсолютным и относительным углами? В абсолютных углах сообщается угол сегмента тела относительно горизонтальной плоскости. Горизонтальная плоскость представляет собой фиксированную привязку. С помощью относительных углов мы измеряем угол между двумя сегментами тела или линиями. В этом случае обе линии способны двигаться.

 

 

Угловое положение (θ)

Угловое положение представляет собой ориентацию линии относительно другой линии или плоскости. Угловое положение определяется количественно путем измерения того, насколько далеко тело повернуто от исходного положения. Угловое положение обозначается символом тета (θ) и может быть измерено в градусах (°), радианах (rads) или оборотах. Хотя вам будет проще интерпретировать градусы, рады играют важную роль в биомеханике. Радиан — это угол, который вы получите, если сделаете длину дуги равной радиусу окружности. Радиан равен 180/pi или 57,3 градуса. Рис. 1. А радиан Δ θ i с определяется как угол, если Длина дуги Δ с имеет ту же длину, что и радиус 9 0130 (г) .

Этот результат является основой для определения единиц, используемых для измерения углов поворота, Δ θ равных радианам (рад), определенных таким образом, что

[латекс]\boldsymbol{2\pi\textbf{рад} = 1\textbf{революция}.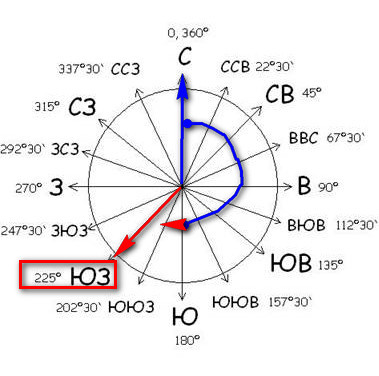 }[/латекс]

Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 1. 90}[/латекс] [латекс]\boldsymbol{\pi}[/латекс] Таблица 1. Сравнение угловых единиц. Угловое смещениеУгловое смещение определяется как изменение от конечного положения к начальному положению (Δθ = θ _f – θ _i ). Угловое смещение представляет собой угол, образованный между конечным положением и начальным положением вращающейся линии. Как и линейное смещение, угловое смещение имеет связанное с ним направление. Ротация в направление по часовой стрелке отрицательное, вращение в направлении против часовой стрелки положительное. В биомеханике угловое смещение полезно при попытке количественно определить диапазон движения в суставе. Если человек начинает с полного разгибания колена (положение 1) и приседает (положение 2), мы можем измерить диапазон движения в колене, измерив угол колена в обоих положениях и используя формулу:

диапазон движения = θ ₂ – θ ₁

Другое использование углового смещения в спорте — подсчет количества полных вращений тела.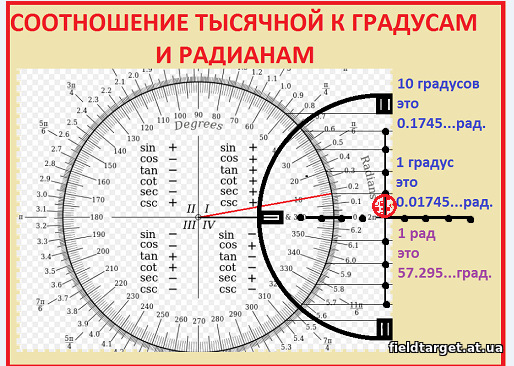 Количество поворотов или сальто, выполненных в таких видах спорта, как, например, дайвинг, гимнастика или сноубординг, определяют уровень сложности выступления. Этот аспект важен для судей, которые присваивают баллы выступлению.

Угловое смещение замаха (диапазон движения) в таких видах спорта, как гольф, теннис или хоккей, влияет на способ удара по мячу в этих видах спорта. См. взаимосвязь между угловым смещением сегмента (например, хоккейной клюшки) и результирующим линейным смещением точки (например, хоккейной шайбы) ниже:

В угловой кинематике мы описываем движение сегмента или твердого тела при его вращении вокруг точки. Этот сегмент можно описать как ряд точек, каждая из которых должна двигаться линейно, чтобы выполнить это изменение положения. Линейное перемещение каждой точки уникально для точки и зависит от того, насколько далеко она расположена от оси вращения. Расстояние от оси вращения до интересующей точки называется радиусом (r).

Рассмотрим две точки ( a и b ) по отрезку. Допустим, нас интересует движение руки во время прыжка. Мы наблюдаем за движением во фронтальной плоскости и измеряем изменение положения от 0 градусов до 180 градусов, когда участник поднимает руку над головой. Точка a расположена на локте, а точка b расположена на запястье. Обе точки a и b должны повернуться на 180 градусов. Фактически, каждая точка на руке должна поворачиваться на 180 градусов. Но каждая точка на руке перемещается на разное линейное расстояние, чтобы выполнить это угловое смещение в 180 градусов. Ближайшие к плечевому суставу точки (точка вращения) не должны линейно перемещаться до точек, ближайших к рукам, чтобы охватить 180 градусов. Точка а ( колено ) имеет меньшее линейное смещение, чем точка b ( запястье ). Точка a имеет меньший радиус, чем точка b , поэтому линейное смещение коррелирует с тем, насколько далеко точка находится от оси вращения ( r ).

Это соотношение выражается следующим уравнением:

d = rθ

Обратите внимание, что угловое положение/смещение ДОЛЖНО быть выражено в радах (а не в градусах или оборотах), чтобы это соотношение было точным.

• Равномерное круговое движение – это движение по окружности с постоянной скоростью. Угол поворота Δ θ определяется как отношение длины дуги к радиусу кривизны:

  [латекс] \boldsymbol{\Delta\theta\:=}\boldsymbol{\frac{\Delta{s}}{r}},[/latex]

  , где длина дуги Δ с — это расстояние, пройденное по круговому пути, а r — радиус кривизны кругового пути. Количество Δ 90=1\textbf{революция}}.[/latex]

• Преобразование между радианами и градусами: 1 рад = 57,3° .
• Угловое смещение определяет движение сегмента, представляющее изменение углового положения.
• Линейное смещение любой точки вдоль сегмента, являющегося вращением, можно рассчитать с помощью: d = rθ  , если угловое положение выражается в радах.