Полиграфический комплекс «Пушкинская площадь»

Углы поворота растра

Вот – новый поворот …

А.Макаревич

Терминология

Угол поворота – угол между осью растра и нулевой осью координатной системы, в принципе это угол наклона между опорным направлением и главной осью растра для выбранной сепарации.

Термины «угол поворота» и «угол наклона» одинаково правильны в применении, и в настоящий момент термин «угол наклона растра» более понятен не искушенному в исторических аспектах специалисту.

C точки зрения понимания структуры и принципов построения растровых изображений кроме термина «угол поворота» имеется ещё ряд важных понятий:

Ось растра – линия, вдоль которой растр имеет наибольшее число элементов – точек на единицу длины. Для линейного растра ось совпадает с направлением линий растровых элементов.

Главная или основная ось растра – в случае несимметричных растровых элементов — ось растра, совпадающая с направлением самого большого диаметра эллиптической или самой большой длины ромбической растровой точки. Симметричные растровые точки (круглые или квадратные) не имеют главной оси.

Опорное направления – горизонтальное направление при нормальном просмотре печатной формы со стороны клапана экспонирующего устройства, фактически направление параллельное клапану экспонирующего устройства.

элементы растровой структуры

Растровая розетка – минимальная интерференционная ячейка (объект) при наложении растровых сепараций.

Полиграфическая или растровая розетка образуется в результате наложения красочных сепараций. В классическом случае – при четырехцветном синтезе – наложением четырех растровых изображений.

Видимые низкочастотные периодические структуры заметно ухудшают визуальное восприятие изображений, и частота возникающего муара зависит от угла поворота образующих изображение сепараций.

Физическая сущность муара

Муар возникает при наложении периодических растровых структур, в результате которого получается другая периодическая структура. Образовавшаяся структура имеет период, отличающийся от периодов структур его образующих, и, к сожалению, не в меньшую сторону. В действительности муар присутствует на печатном изображении, полученном с применением автотипного синтеза, всегда с большей или меньшей степенью заметности. Он может быть как четко различимым, так и практически незаметным в зависимости от ряда параметров растрирования и характеристик воспроизводимого изображения.

Основным критерием выбора углов поворота растра

при периодическом растрировании является минимизация межсепарационного муара, неизбежно возникающего при цветовом автотипном синтезе.

Далее мы будем рассматривать исключительно межсепарационный муар, хотя в природе наблюдают и другие виды муара:

Для визуального восприятия большое значение имеет частота или период муаровой структуры. В случае, если величина ее частоты порядка 20-40 линии на сантиметр или более, то вероятность ее различения при печати мала. В случае если частота муара низкая и составляет менее 10 линии на сантиметр, то при печати муар будет хорошо заметен.

Почему возникает муар при совмещении периодических структур с равными пространственными частотами при повороте одной из сепараций на некоторый угол?

Дело в том, что поворот одной из сепараций приводит к относительному увеличению ее пространственной частоты в направлении основной оси другой сепарации. При этом величина приращения частоты проекции второй сепарации на ось основной сепарации и будет пространственной частотой образующегося муара.

При малых углах поворота растра, линиатура интерференционной структуры – муара так же имеет низкое значение и хорошо заметна.

Критерии выбора

Выбор или определение углов поворота производится по нескольким критериям

минимизация муарных явлений

уменьшение различимости растровой структуры

Для того чтобы правильно выбрать угол наклона растра в первую очередь необходимо определить систему координат и точку отчета для измерения угла.

И тут в полиграфии не все однозначно. Существуют две системы определения углов наклона растровой структуры применяемой в современных растровых процессорах

В первом случае начальная точка отчета находится на оси ординат и угол поворота растра для краски определяется углом между главной осью растра и осью ординат в направлении по часовой стрелки.

Во втором случае угол поворота определяется как угол между главной осью растра и осью абсцисс против часовой стрелки

Ось абсцисс в координатной системы располагается в соответствии с опорным направлением

В сущности, для выбора углов поворота система координат не имеет принципиального значения. Значение имеет только соотношение или разница между углами растровых структур получаемых в итоге.
Для различных видов растров различны и интервалы допустимых значений углов поворота.

• Для двухосевых растров имеющих главную ось (эллиптические растры) углы поворота располагаются в интервале от 0 до 180 градусов, причем регламентируется угол поворота, только для главной оси
• Для двухосевых растров не имеющих главной оси (растры с круглой и квадратной точкой) — от 0 до 90 градусов
• Для одноосевых растров (линейный растр) от 0 до 180 градусов

Чем больше угол поворота между двумя сепарациями тем выше частота образующегося муара. Естественно, оптимальным вариантом с точки зрения минимизации муара является поворот на 45 градусов, однако вариантов расстановки с дифферентом в 15 градусов всего два.

• 0º-90º
• 45º-135º

А куда девать еще две сепарации?

Поворот на 30 градусов

– тоже визуально малозаметен и технологически приемлем для печати, да и вариантов расстановки уже больше – три, например:

• 0º-90º
• 30º-120º
• 60º-150º

Но все равно для одной сепарации (краски) угла не хватает

Разница в углах поворота на 15 градусов при некоторых печатных условиях приводит к образованию хорошо различимого муара, поэтому применять углы, отличающиеся на 15 градусов крайне нежелательно.

• 0º-90º
• 15º-105º
• 30º-120º
• 45º-135º
• 60º-150º
• 75º-135º

Необходимых для триадной печати сепараций (красок) – четыре. Так что применение дефферента в 15 градусов неизбежно и одна из сепараций обязательно будет находиться под муарным углом к двум другим. Обычно это желтая краска, она «слепая» (не контрасная), поэтому образующаяся с этой краской муарная структура наименее заметна.

Теоретически муар должен полностью отсутствовать при нулевом угле поворота растров друг относительно друга. Однако это справедливо только для идеально совмещенных сепараций. На практике осуществить такой режим печати невозможно. Даже минимальное несовмещение красок при печати приведет к образованию низкочастотного (крупного) муара.

Стандартные углы

В стандарте офсетной печати ISO 12647-2 описан принцип, на основе которого рекомендуется устанавливать углы поворота растров. Угол поворота должен быть определен для каждой краски или цветовой сепарации. Непериодические растровые структуры углов наклона естественно не имеют.

В соответствии с ISO 12647-2, в случае двухосевых периодических растров, т.

е. с круглой или квадратной точкой, разница между углами поворота растра голубой, пурпурной и черной красками должна составлять 30°, а угол наклона желтой краски отличаться на 15° от двух остальльных. Угол поворота растра краски, доминирующей в изображении, должен быть равен 45°

В случае использования растров, имеющих главную ось (с овальной или ромбической точкой) , между углами поворота главных осей голубой, пурпурной и черной красок должно быть 60 градусов, а угол поворота желтой краски отличаться на 15°. Угол наклона доминирующей краски — 45° или 135°

Выбор доминирующей краски

Доминирующую краску необходимо ставить под углом 45 градусом. Здесь возможны три варианта

• Если доминирующим цветом в издании является цвет кожи или другие цвета содержащие пурпурную краску (основная масса глянцевых журналов), то под 45 градусов ставят именно пурпурную краску
• Если в издании иллюстрации отражают разгул зелени или воды, то под 45 градусов выводят голубую сепарацию
• Во всех остальных случаях можно под 45 градусов ставить черную краску

Кстати, а Вы знаете почему именно под 45 градусов? Все дело в интересном феномене пространственного зрения, который называется эффект наклона. Он заключается в том, что при восприятии растровых объектов, ориентированных под углом 0° и 90° (относительно линии, соединяющей глаза), острота зрения выше, чем при восприятии растровых решеток, ориентированных под углом 45°.

Поэтому растровые решетки доминирующего цвета выводят под углом 45°.

Итак в итоге для наиболее популярных двухосевых растров имеющих главную ось, т.е. для эллиптических растров получаем следующие практические рекомендации по установке углов поворота сепараций

• Под углом 90 градусов однозначно выводится желтая краска
• Доминирующую краску под 135 градусов – это либо пурпурная либо голубая сепарация
• Черную сепарацию под 75 градусов
• Под оставшийся угол в 15 или 105 градусов размещается соответственно оставшиеся не доминирующая пурпурная или голубая сепарация

Как оценить межсепарационный муар до печати?

Возможные варианты углов поворота растровых сепараций ограничены не только технологическими особенностями минимизации муара, но и имеющейся библиотекой скринсеттов (прописанных в программе растрирования вариантов параметров растрирования). Причем необходимо учитывать, что даже в стандартном наборе скринсетов могут быть и «паршивые овцы», поэтому предварительно необходимо проверить выбранный скринсет на наличие межсепарационного муара.

Существует несколько способов визуальной оценки

Пробная печать

Самый надежный, но и самый дорогостоящий способ

Аналоговая цветопроба

На настоящий момент фактически не актуальна

Фототехнический

Основан на посепарационном совмещении фотоформ. Естественно, если вы выводите фотоформы по технологии CtF, которая на настоящий момент фактически не актуальна.

Экранная растровая цветопроба

Экранная растровая цветопроба наиболее дешевый способ, и как показала практика, не менее надежный , чем пробная печать.

Многие растровые процессоры поддерживают вывод отрастрированных изображений на монитор для проверки. Именно этими «экранками» можно воспользоваться для оценки получаемых изображений на наличие муара.

Но для того чтобы оценить возможность образования муара на мониторе необходимо исключить аппаратный муар экрана монитора, возникающий при сложении растровой структуры изображения и периодической ячеистой структурой экрана монитора. Для этого изображение на мониторе необходимо выводить с таким увеличением, чтобы растровая точка воспроизводилась таким количеством пикселов, что и при выводе на фотовыводном устройстве. Однако это не всегда возможно, поэтому можно ограничиться половинным количеством точек. Если при просмотре растровая структура изображения видна, то необходимо увеличить расстояние просмотра. Таким образом, оценивается наиболее критические цвета на наличие межсепарационного муара.

Методы уменьшения различимости растровой структуры

Образование розеточной структуры или растровых «розеток» значительно ухудшает зрительное восприятие изображения. Очень часто именно образование розеточной структуры на информационно важных участках изображения приводит к необоснованным претензиям клиентов.

Увеличение линиатуры вывода

Наиболее интуитивно понятным методом уменьшения различимости является увеличение линиатуры при растрировании. Действительно при увеличении линиатуры приводит к уменьшению растровой розетки, но например, как показывают расчеты увеличение линиатуры с 150 до 175 линий на дюйм приводит к уменьшению розетки всего на 11 процентов, поэтому этот метод не очень продуктивен. А учитывая проблемы, возникающие при увеличении линиатуры при печати и возможные потери градаций, он вообще нежелателен.

применение растрирования с смещенными частотами растров

Более действенными методами являются методики, основанные на разрушении розеточной структуры. Например, изменение частоты отдельных сепараций. Но тут необходима осторожность и тщательная проверка перед промышленным использованием. Многие растровые процессоры предлагают готовые скринсеты с измененными частотами сепараций, подобранными именно с расчетом уменьшить розеточную структуру на изображении.

подбор метода цветового синтеза

Визуальная величина растровой розетки различна для разных цветов и зависит от CMYK-координат воспроизводимого цвета.

Давайте рассмотрим влияние CMYK-рецептуры на образование растровой розетки.
На рисунке показаны три вида растровых розеток образующихся в результате применения «классических» углов поворота растра для трех вариантов.

1 — растровая розетка образованна двумя красками

2 — растровая розетка образованна тремя красками

3 — растровая розетка состоящая из четырех красок

Как хорошо видно на приведённых иллюстрациях чем больше контурообразующих красок (СМК) участвует в образовании растровой розетки тем больше ее размер. Следовательно, необходимо выбирать для цветоделения такие методы, чтобы образующиеся при цветовом синтезе цвета, особенно в полутонах, имели оптимальную для растровой структуры рецептуру. Например, GCR c поздним стартом черной краски.

применение стохастического растрирования

Межсепарационный муар полностью устранить безусловно можно, но другими методами.
Одним из наиболее перспективных методов позволяющий полностью исключить образование интерференционных структур является применение стохастического растрирования. Нет периодической структуры – нет и муара. В настоящее время идет активная стандартизация печати с применением стохастических растров, поэтому в ближайшие 3-5 лет стохастика найдет широкое применение в промышленной печати как листовой так и ролевой.

применение комбинированного растрирования

Применение комбинированного растрирования (не путать с гибридным). Комбинированное растрирование это использование различных видов растров для растрирования различных красочных сепараций.

Для уменьшения растровой розетки черную краску можно вывести стохастикой, а голубую, пурпурную и желтую круглой или эллиптической точкой с углами поворота 15°, 45° и 75° соответственно.

В данном варианте величина растровой розетки практически равна линиатуре растра и соответственно визуально неразличима при нормальных условия просмотра.

Классический эллиптический растр

Комбинированное растрирование

Данный метод растрирования полностью по цвету подходит под стандарт печати и не требует специального профилирования процесса. Достаточно только скомпенсировать градационную кривую по черной краске.

В настоящий момент методика комбинированного растрирования на существующих растровых процессорах детально отработана в типографии «Пушкинская площадь» и с большим успехом применяется при печати ряда изданий.

Угол поворота, угол произвольной величины, поворот вокруг точки на заданный угол

Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.

Поворот точки вокруг точки

Определение 1

Центр поворота – точка, относительно которой осуществлен поворот.

Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О, в результате чего получается точка А1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А). При этом точка А1 лежит на окружности с центром в точке О радиуса ОА. Другими словами, когда точка А осуществляет поворот относительно точки О, она переходит в точку А1, лежащую на окружности с центром О радиуса ОА.

Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О, она переходит в саму себя.

Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса ОА.

Изобразим графически поворот точки А относительно точки О, перемещение точки А в точку А1 отметим стрелкой:

Полный оборот

Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А, пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О.

Проиллюстрируем:

Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:

В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.

Угол поворота

Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О.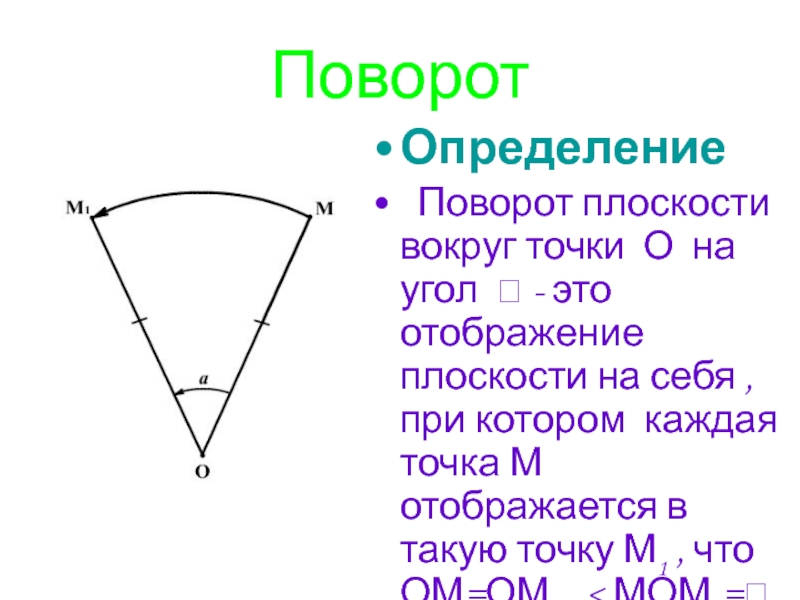 Любую точку окружности с центром О можно рассматривать как точку А1, полученную в результате поворота точки А. Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.

Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.

Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от -∞ до +∞, что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180°.

Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α, β, γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α1, α2, α3…. .αn.

Разберем характеристики угла поворота подробнее.

Направление поворота

Отметим на окружности с центром О точки А и А1. В точку А1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

Величина угла поворота, угол произвольной величины

Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.

Как было сказано выше, величина угла поворота варьируется в пределах от -∞ до +∞;

Определение 2

Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.

Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.

Пусть угол поворота равен 0°. Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0° точка A остается на месте.

Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А1. В таком случае абсолютная величина угла АОА1, выраженная в градусах, не превосходит 180. Если поворот имел положительное направление, то величина угла поворота считается равной величине угла АОА1; если отрицательное – величина угла поворота равна величине угла АОА1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30°, 180° и -150°:

Углы поворота, превышающие 180 или меньшие –180 определяются, исходя из очевидного свойства последовательных поворотов:

Определение 3

Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.

Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45°, затем еще на 60° и еще раз — на -35°. Обозначим промежуточные точки поворотов А1, А2 и А3. В конечную точку А3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45°+ 60° + (-35°) = 70°. Проиллюстрируем:

Таким, образом, углы, превышающие 180°, будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298° соответствует последовательным поворотам на 180° и 118°, или 90°, 90°, 90° и 28°, или 180°, 180° и -62°, или 298 последовательных поворотов на 1°.

По такому же принципу определяются углы меньше -180°. Например, угол поворота -515° можно определить, как последовательные повороты на -180°,-180° и -155°.

Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от -∞ до +∞. Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.

В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360° или 2π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в -360° или -2π радиан.

При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от -180° до 180°. К примеру, поворот осуществляется на 1478°. Представим эту величину как: 360 · 4 + 38, т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38°. Или еще один пример: угол поворота в -815° можно представить, как (-360) · 2 + (-95), т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на -95°.

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).

Определение 3

Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.

Как пример, иллюстрируем следующее действие: поворот отрезка АВ на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А1В1.

6.1 Угол поворота и угловая скорость

Цели обученияУгол вращенияУгловая скоростьРешение задач, связанных с углом вращения и угловой скоростьюПрактические задачиПроверьте свое понимание

Цели обучения

К концу этого раздела вы сможете делать следующее: своему линейному аналогу

Опишите угловую скорость и свяжите ее с ее линейным эквивалентом

Решение задач на угол поворота и угловую скорость

«>

Основные термины раздела

угол поворота	угловая скорость	длина дуги
круговое движение	радиус кривизны	вращательное движение
вращение	тангенциальная скорость

Угол поворота

Что именно мы подразумеваем под круговым движением или вращением ? Вращательное движение – это круговое движение объекта вокруг оси вращения. Мы обсудим конкретно круговое движение и вращение. Круговое движение — это когда объект движется по круговой траектории. Примеры кругового движения включают гоночный автомобиль, мчащийся по круговой кривой, игрушку, прикрепленную к веревке, которая качается по кругу вокруг вашей головы, или круговое движение. 0048 петля-петля на американских горках. Вращение — это вращение вокруг оси, проходящей через центр масс объекта, например, Земля, вращающаяся вокруг своей оси, колесо, вращающееся вокруг своей оси, вращение торнадо на пути разрушения или вращение фигуриста во время выступление на Олимпиаде. Иногда объекты будут вращаться во время кругового движения, например Земля, вращающаяся вокруг своей оси, вращаясь вокруг Солнца, но мы сосредоточимся на этих двух движениях отдельно.

При решении задач, связанных с вращательным движением, мы используем переменные, аналогичные линейным переменным (расстояние, скорость, ускорение и сила), но учитывающие кривизну или вращение движения. Здесь мы определяем угол поворота, который является угловым эквивалентом расстояния; и угловая скорость, которая является угловой эквивалентностью линейной скорости.

Когда объекты вращаются вокруг какой-либо оси — например, когда диск на рис. 6.2 вращается вокруг своего центра — каждая точка объекта движется по круговой траектории.

Рис. 6.2 Все точки на компакт-диске движутся по круговым траекториям. Ямки (точки) вдоль линии от центра к краю перемещаются на один и тот же угол ΔθΔθ за время ΔtΔt.

Длина дуги , , это расстояние, пройденное по круговой траектории. Радиус кривизны, r , является радиусом кругового пути. Оба показаны на рис. 6.3.

Рис. 6.3 Радиус ( r ) окружности повернут на угол ΔθΔθ. Длина дуги, ΔsΔs, представляет собой расстояние, пройденное по окружности.

Рассмотрим линию от центра компакт-диска до его края. В заданное время каждая яма (используемая для записи информации) на этой линии перемещается на один и тот же угол. Угол поворота представляет собой величину поворота и является угловым аналогом расстояния. Угол поворота ΔθΔθ — это длина дуги, деленная на радиус кривизны.

Δθ=ΔсрΔθ=Δср

Угол поворота часто измеряется в радианах. (Радианы на самом деле безразмерны, потому что радиан определяется как отношение двух расстояний, радиуса и длины дуги.) Оборот — это один полный оборот, когда каждая точка на окружности возвращается в исходное положение. Один оборот покрывает 2π2π радиан (или 360 градусов) и, следовательно, имеет угол поворота 2π2π радиан и длину дуги, которая равна длине окружности. Мы можем преобразовать радианы, обороты и градусы, используя соотношение

1 оборот = 2π2πрад = 360°. См. Таблицу 6.1 для преобразования градусов в радианы для некоторых распространенных углов.

6,12π рад=360°1 рад=360°2π≈57,3°2π рад=360°1 рад=360°2π≈57,3°

Градусы	Радианные меры
30∘30∘	π6π6
60∘60∘	π3π3
90∘90∘	π2π2
120∘120∘	2π32π3
135∘135∘	3π43π4
180∘180∘	ππ

Таблица 6. 1 Обычно используемые углы в градусах и радианах

Угловая скорость

Как быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Сначала рассмотрим угловую скорость (ω)(ω) — скорость изменения угла поворота. В форме уравнения угловая скорость равна

6.2ω=ΔθΔt,ω=ΔθΔt,

, что означает, что угловой поворот (Δθ)(Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота за заданное время, он имеет большую угловую скорость. Единицами угловой скорости являются радианы в секунду (рад/с).

Теперь давайте рассмотрим направление угловой скорости, а значит мы теперь должны называть ее угловой скоростью. Направление угловой скорости вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость направлена ​​от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.

Угловая скорость (ω) является угловой версией линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим ямку на вращающемся компакт-диске. Эта яма движется по дуге (Δs)(Δs) за короткое время (Δt)(Δt), поэтому ее тангенциальная скорость равна

6.3 v=ΔsΔt.v=ΔsΔt.

Из определения угла поворота Δθ=ΔsrΔθ=Δsr видно, что Δs=rΔθΔs=rΔθ. Подставляя это в выражение для v дает

v=rΔθΔt=rω.v=rΔθΔt=rω.

Уравнение v=rωv=rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем краю компакт-диска (с большими r ), чем для точки ближе к центру компакт-диска (с меньшими r ). Это имеет смысл, потому что точка, расположенная дальше от центра, должна пройти большую длину дуги за то же время, что и точка, расположенная ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. Рисунок 6.4.

Рисунок 6.4 Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ), но точка 2 перемещается по большей дуге (Δs2Δs2), поскольку она находится дальше от центра вращения.

Теперь рассмотрим другой пример: шина движущегося автомобиля (см. рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое против , потому что v=rωv=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет производить большую линейную (тангенциальную) скорость в, на машину. Это связано с тем, что больший радиус означает, что более длинная дуга должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.

Рис. 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят на домкрат и колеса крутились, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад относительно оси с тангенциальной скоростью v=rωv=rω, где r — радиус шины. Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Большая угловая скорость шины означает большую линейную скорость автомобиля.

Однако бывают случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда колеса автомобиля крутятся на льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля по льду длина дуги, по которой перемещаются протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль. Это похоже на бег на беговой дорожке или вращение педалей на велотренажере; вы буквально никуда не денетесь.

Советы по достижению успеха

Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны указать величину и направление. Направление угловой скорости находится вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как восходящая, нисходящая, левая, правая, северная, южная, восточная или западная, как показано на рис. 6.6.

Рис. 6.6 Когда муха на краю старой виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена ​​по касательной к кругу. В этом случае направление угловой скорости находится на странице.

Watch Physics

Взаимосвязь между угловой скоростью и скоростью

В этом видео рассматривается определение и единицы измерения угловой скорости, а также их связь с линейной скоростью. Он также показывает, как конвертировать между оборотами и радианами.

Проверка захвата

Для объекта, движущегося по круговой траектории с постоянной скоростью, изменится ли линейная скорость объекта при увеличении радиуса траектории?

1. Да, потому что тангенциальная скорость не зависит от радиуса.
2. Да, потому что тангенциальная скорость зависит от радиуса.
3. Нет, так как тангенциальная скорость не зависит от радиуса.
4. Нет, так как тангенциальная скорость зависит от радиуса.

Решение задач на угол поворота и угловую скорость

Snap Lab

Измерение угловой скорости

В этом упражнении вы создадите и измерите равномерное круговое движение, а затем сопоставите его с круговыми движениями с разными радиусами.

Материалы

• Одна струна (длиной 1 м)
• Один предмет (резиновая пробка с двумя отверстиями) для привязки к концу
• Один таймер

Процедура

1. Привяжите объект к концу нити.
2. Раскачивайте объект по горизонтальному кругу над головой (раскачивание с запястья). Важно, чтобы круг был горизонтальным!
3. Поддерживайте постоянную скорость объекта при его раскачивании.
4. Таким образом измерьте угловую скорость объекта. Измерьте время в секундах, за которое объект совершает 10 оборотов. Разделите это время на 10, чтобы получить угловую скорость в оборотах в секунду, которую вы можете преобразовать в радианы в секунду.
5. Какова приблизительная линейная скорость объекта?
6. Поднимите руку вверх по веревке так, чтобы длина веревки составила 90 см. Повторите шаги 2–5.
7. Переместите руку вверх по веревке так, чтобы ее длина составила 80 см. Повторите шаги 2–5.
8. Переместите руку вверх по веревке так, чтобы ее длина составила 70 см. Повторите шаги 2–5.
9. Переместите руку вверх по веревке так, чтобы ее длина составила 60 см. Повторите шаги 2–5
10. Переместите руку вверх по веревке так, чтобы ее длина составила 50 см. Повторите шаги 2–5
11. Постройте графики зависимости угловой скорости от радиуса (т.е. длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.

Проверка захвата

Если вы медленно качаете объект, он может вращаться со скоростью менее одного оборота в секунду. Каковы были бы обороты в секунду для объекта, который делает один оборот за пять секунд? Какова будет его угловая скорость в радианах в секунду?

1. Объект будет вращаться со скоростью 15 об/с. Угловая скорость объекта будет 2π5 рад/с.
2. Объект будет вращаться со скоростью 15 об/с. Угловая скорость объекта будет π5 рад/с.
3. Объект будет вращаться со скоростью 5 об/с. Угловая скорость объекта будет 10πрад/с.
4. Объект будет вращаться со скоростью 5 об/с. Угловая скорость объекта будет 5πрад/с.

Теперь, когда у нас есть понимание концепций угла поворота и угловой скорости, мы применим их к реальным ситуациям башни с часами и вращающейся шины.

Рабочий пример

Угол поворота на башне с часами

Часы на башне с часами имеют радиус 1,0 м. а) На какой угол поворачивается часовая стрелка часов, когда она движется с 12 часов дня до 12 часов дня. до 15:00? (b) Какова длина дуги по внешнему краю часов между часовой стрелкой в ​​эти два времени?

Стратегия

Мы можем вычислить угол поворота, умножив полный оборот (2π2π радиан) на долю 12 часов, покрываемых часовой стрелкой при переходе от 12 к 3. Получив угол поворота, мы можно определить длину дуги, переформулировав уравнение Δθ=ΔsrΔθ=Δsr, поскольку радиус задан.

Решение задачи (a)

При переходе от 12 к 3 часовая стрелка покрывает 1/4 из 12 часов, необходимых для совершения полного оборота. Следовательно, угол между часовой стрелкой в ​​положении 12 и 3 равен 14×2π рад=π214×2π рад=π2 (т. е. 90 градусов).

Решение (б)

Преобразовывая уравнение

6.4Δθ=Δsr,Δθ=Δsr,

получаем

6.5Δs=rΔθ.Δs=rΔθ.

Подстановка известных значений дает длину дуги

6,6Δs=(1,0 м)(π2 рад)=1,6 мΔs=(1,0 м)(π2 рад)=1,6 м

Обсуждение

Мы смогли убрать радианы из окончательного решения в части (b), поскольку радианы на самом деле безразмерны. Это связано с тем, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.

Рабочий пример

Как быстро вращается автомобильная шина?

Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с (около 54 км/ч). Смотрите этот рисунок.

Стратегия

В этом случае скорость протектора шины относительно оси шины равна скорости автомобиля относительно дороги, поэтому мы имеем v = 15,0 м/с. Радиус шины равен r = 0,300 м. Поскольку мы знаем v и r , мы можем изменить уравнение v=rωv=rω, чтобы получить ω=vrω=vr и найти угловую скорость.

Решение

Для нахождения угловой скорости используем соотношение: ω=vrω=vr.

Вставка известных количеств дает

6,7ω=15,0 м/с0,300 м=50,0 рад/с.ω=15,0 м/с0,300 м=50,0 рад/с.

Обсуждение

Когда мы отбрасываем единицы измерения в приведенном выше расчете, мы получаем 50,0/с (т. е. 50,0 в секунду, что обычно записывается как 50,0 с ⁻¹ ). Но угловая скорость должна иметь единицы рад/с. Поскольку радианы безразмерны, мы можем подставить их в ответ для угловой скорости, потому что мы знаем, что движение является круговым. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. У них будет угловая скорость

6,8ω=15,0 м/с1,20 м=12,5 рад/сω=15,0 м/с1,20 м=12,5 рад/с

Практические задачи

Чему равен угол в градусах между часовой и минутной стрелками часов, показывающих 9 часов утра?

1. 0°
2. 90°
3. 180°
4. 360°

Каково приблизительное значение длины дуги между часовой и минутной стрелками часов, показывающих 10:00, если радиус часов равен 0,2 м?

1. 0,1 м
2. 0,2 м
3. 0,3 м
4. 0,6 м

Проверьте свое понимание

Упражнение 1

Что такое круговое движение?

1. Круговое движение — это движение объекта по линейной траектории.
2. Круговое движение — это движение объекта по зигзагообразной траектории.
3. Круговое движение — это движение объекта по круговой траектории.
4. Круговое движение — это движение объекта по окружности окружности или вращение по круговой траектории.

Упражнение 2

Что понимается под радиусом кривизны при описании вращательного движения?

1. Радиус кривизны — это радиус кругового пути.
2. Радиус кривизны — это диаметр кругового пути.
3. Радиус кривизны – это длина окружности кругового пути.
4. Радиус кривизны – это площадь кругового пути.

Упражнение 3

Что такое угловая скорость?

1. Угловая скорость – это скорость изменения диаметра кругового пути.
2. Угловая скорость – это скорость изменения угла, образуемого круговой траекторией.
3. Угловая скорость — это скорость изменения площади кругового пути.
4. Угловая скорость — это скорость изменения радиуса кругового пути.

Упражнение 4

Какое уравнение определяет угловую скорость ω? Предположим, что r — радиус кривизны, θ — угол, t — время.

1. ω=ΔθΔt
2. ω=ΔtΔθ
3. ω=ΔrΔt
4. ω=ΔtΔr

Упражнение 5

Найдите три примера объекта, движущегося по кругу.

1. искусственный спутник Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и волчок, вращающийся вокруг своей оси
2. искусственный спутник, вращающийся вокруг Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и электрон, движущийся по круговой орбите вокруг ядра
3. Земля, вращающаяся вокруг своей оси, гоночный автомобиль, движущийся по круговой гоночной трассе, и электрон, движущийся по круговой орбите вокруг ядра.
4. Земля, вращающаяся вокруг своей оси, лопасти работающего потолочного вентилятора и волчок, вращающийся вокруг своей оси.

Упражнение 6

Какова относительная ориентация векторов радиуса и тангенциальной скорости объекта при равномерном круговом движении?

1. Вектор тангенциальной скорости всегда параллелен радиусу окружности, по которой движется объект.
2. Вектор тангенциальной скорости всегда перпендикулярен радиусу окружности, по которой движется объект.
3. Вектор тангенциальной скорости всегда находится под острым углом к ​​радиусу окружности, по которой движется объект.
4. Вектор тангенциальной скорости всегда находится под тупым углом к ​​радиусу окружности, по которой движется объект.

• Печать
• Поделиться

1.

5: Повороты и отражения углов

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

25002

• Майкл Коррал
• Колледж Скулкрафт

Теперь, когда мы знаем, как обращаться с углами любой величины, мы рассмотрим, как определенные геометрические операции могут помочь упростить использование тригонометрических функций любого угла и как можно установить некоторые основные отношения между этими функциями. Две операции, на которых мы сосредоточимся в этом разделе, — это вращение и отражение .

К повернуть на угол означает повернуть его конечную сторону вокруг начала координат, когда угол находится в стандартном положении. Например, предположим, что мы поворачиваем угол \(\theta \) вокруг начала координат на \(9\circ) ~ = ~ -\cot\;\theta \label{1.6} \]

Пример 1.26

Напомним, что любая невертикальная линия в координатной плоскости \(xy\) может быть записана как \(y=mx +b \), где \(m \) — это наклон линии (определяемой как \(m = \frac{\text{rise}}{\text{run}} \) ) и \(b \ ) — точка пересечения \(y\)- }, т. е. точка пересечения прямой с осью \(y\) (см. рис. 1.5.2(a)). Мы покажем, что наклоны перпендикулярных прямых являются отрицательными обратными величинами. То есть, если \(y=m_{1}x+b_1 \) и \(y=m_{2}x+b_2 \) являются невертикальными и негоризонтальными перпендикулярными прямыми, то \(m_2 = -\frac{1}{ m_1} \) (см. рис. 1.5.2(б)).

Рисунок 1.5.2

Во-первых, предположим, что линия \(y=mx+b \) имеет ненулевой наклон. Линия где-то пересекает ось \(x\), поэтому пусть \(\theta\) будет углом, который положительная ось \(x\) образует с частью линии над осью \(x\) , как на рис. 1.5.3. Для \(m > 0 \) мы видим, что \(\theta \) острое и \(\tan\;\theta = \frac{\text{rise}}{\text{run}} = m \).

Рисунок 1.5.3

Если \(m < 0 \), то мы видим, что \(\theta \) тупой и рост отрицательный. Поскольку пробег всегда положительный, наше определение \(\tan\;\theta \) из раздела 1.4 означает, что \(\tan\;\theta = \frac{-\text{rise}}{-\text{run }} = \frac{\text{rise}}{\text{run}} = m \) (просто представьте, что на рис. 1.5.3(b) вся линия сдвигается по горизонтали, чтобы пройти через начало координат, так что \( \theta \) не изменяется, а точка \((-\text{run},-\text{rise}) \) находится на конечной стороне \(\theta\)). Следовательно: 9\circ) ~ = ~ \tan\;\theta \]

отражение — это просто зеркальное отражение объекта. Например, на рис. 1.5.5 исходный объект находится в QI, его отражение вокруг оси \(y) — в QII, а его отражение вокруг оси \(x) — в QIV. Обратите внимание, что если мы сначала отразим объект в QI вокруг оси \(y\), а затем последуем отражению вокруг оси \(x\), мы получим изображение в QIII. \circ \) вокруг начала координат.

Рисунок 1.5.5

Применяя это к углам, мы видим, что отражение угла \(\theta\) вокруг оси \(x\) есть угол \(-\theta \), как на рис. 1.5. 6.

Рисунок 1.5.6 Отражение \(θ \text{ вокруг оси }x\text{-}\)

Итак, мы видим, что отражение точки \((x,y) \) вокруг \(x\)- ось просто заменяет \(y\) на \(-y\). Отсюда:

\[\label{1.13}\sin\;(-\theta) ~ = ~ -\sin\;\theta \]

\[\label{1.14} \cos\;(-\theta) ~ = ~ \cos\;\theta \]

\[\label{1.15} \tan\;(-\theta) ~ = ~ -\tan\;\theta \]

Обратите внимание, что функция косинуса не меняется в уравнении \ref{1.14}, потому что она зависит от \(x \), а не от \(y \), для точки \((x,y) \) на конечная сторона \(\тета\).

В общем, функция \(f(x)\) является четной функцией , если \(f(-x) = f(x)\) для всех \(x \), и она называется нечетная функция , если \(f(-x) = -f(x) \) для всех \(x \). Таким образом, функция косинуса четная, а функции синуса и тангенса нечетные.