Строительная механика

Строительная механика

Дарков А. В., Шапошников Н. Н. Строительная механика: Учеб. для строит. спец. вузов. —8-е изд., перераб. и доп. — М.: Высш. шк., 1986. — 607 с. В учебнике отражены вопросы курса строительной механики (статика и динамика сооружений). Изложение материала иллюстрируется конкретными примерами. В отличие от предыдущего издания (7-е— 1976 г.) рассматриваются методы расчета с использованием ЭВМ, указываются особенности этих методов. В учебнике отражено современное состояние строительной механики. Предназначается для студентов строительных специальностей вузов. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ Глава 1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ СООРУЖЕНИЙ § 1. 2. УСЛОВИЯ ГЕОМЕТРИЧЕСКОЙ НЕИЗМЕНЯЕМОСТИ СТЕРЖНЕВЫХ СИСТЕМ § 1.3. УСЛОВИЯ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ГЕОМЕТРИЧЕСКИ НЕИЗМЕНЯЕМЫХ СТЕРЖНЕВЫХ СИСТЕМ Глава 2. БАЛКИ § 2.2. ЛИНИИ ВЛИЯНИЯ ОПОРНЫХ РЕАКЦИЙ ДЛЯ ОДНОПРОЛЕТНЫХ И КОНСОЛЬНЫХ БАЛОК § 2.3. ЛИНИИ ВЛИЯНИЯ ИЗГИБАЮЩИХ МОМЕНТОВ И ПОПЕРЕЧНЫХ СИЛ ДЛЯ ОДНОПРОЛЕТНЫХ И КОНСОЛЬНЫХ БАЛОК § 2.4. ЛИНИИ ВЛИЯНИЯ ПРИ УЗЛОВОЙ ПЕРЕДАЧЕ НАГРУЗКИ § 2.5. ОПРЕДЕЛЕНИЕ УСИЛИЙ С ПОМОЩЬЮ ЛИНИЙ ВЛИЯНИЯ § 2.6. ОПРЕДЕЛЕНИЕ НЕВЫГОДНЕЙШЕГО ПОЛОЖЕНИЯ НАГРУЗКИ НА СООРУЖЕНИИ. ЭКВИВАЛЕНТНАЯ НАГРУЗКА § 2.7. МНОГОПРОЛЕТНЫЕ СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ БАЛКИ § 2.8. ОПРЕДЕЛЕНИЕ УСИЛИЙ В МНОГОПРОЛЕТНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ ОТ НЕПОДВИЖНОЙ НАГРУЗКИ § 2.9. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ ДЛЯ МНОГОПРОЛЕТНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК § 2.10. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ С ЛОМАНЫМИ ОСЯМИ ОТ НЕПОДВИЖНОЙ НАГРУЗКИ § 2.11. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ В БАЛКАХ КИНЕМАТИЧЕСКИМ МЕТОДОМ Глава 3. ТРЕХШАРНИРНЫЕ АРКИ И РАМЫ § 3. 1. ПОНЯТИЕ ОБ АРКЕ И СРАВНЕНИЕ ЕЕ С БАЛКОЙ § 3.2. АНАЛИТИЧЕСКИЙ РАСЧЕТ ТРЕХШАРНИРНОЙ АРКИ § 3.3. ГРАФИЧЕСКИЙ РАСЧЕТ ТРЕХШАРНИРНОЙ АРКИ. МНОГОУГОЛЬНИК ДАВЛЕНИЯ § 3.4. УРАВНЕНИЕ РАЦИОНАЛЬНОЙ ОСИ ТРЕХШАРНИРНОЙ АРКИ § 3.5. РАСЧЕТ ТРЕХШАРНИРНЫХ АРОК НА ПОДВИЖНУЮ НАГРУЗКУ § 3.6. ЯДРОВЫЕ МОМЕНТЫ И НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ Глава 4. ПЛОСКИЕ ФЕРМЫ § 4.1. ПОНЯТИЕ О ФЕРМЕ. КЛАССИФИКАЦИЯ ФЕРМ § 4.2. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ПРОСТЕЙШИХ ФЕРМ § 4.3. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ СЛОЖНЫХ ФЕРМ § 4.4. РАСПРЕДЕЛЕНИЕ УСИЛИЙ В ЭЛЕМЕНТАХ ФЕРМ РАЗЛИЧНОГО ОЧЕРТАНИЯ § 4.5. ИССЛЕДОВАНИЕ НЕИЗМЕНЯЕМОСТИ ФЕРМ § 4.6. ЛИНИИ ВЛИЯНИЯ УСИЛИИ В СТЕРЖНЯХ ПРОСТЕЙШИХ ФЕРМ § 4.7. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ В СТЕРЖНЯХ СЛОЖНЫХ ФЕРМ § 4.8. ШПРЕНГЕЛЬНЫЕ СИСТЕМЫ § 4,9. ТРЕХШАРНИРНЫЕ АРОЧНЫЕ ФЕРМЫ И КОМБИНИРОВАННЫЕ СИСТЕМЫ Глава 5. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В УПРУГИХ СИСТЕМАХ § 5.2. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ § 5.3. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЙ § 5.4. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ. ИНТЕГРАЛ МОРА § 5.5. ПРАВИЛО ВЕРЕЩАГИНА § 5.6. ПРИМЕРЫ РАСЧЕТА § 5.7. ТЕМПЕРАТУРНЫЕ ПЕРЕМЕЩЕНИЯ § 5.8. ЭНЕРГЕТИЧЕСКИЙ ПРИЕМ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ § 5.9. ПЕРЕМЕЩЕНИЯ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ, ВЫЗЫВАЕМЫЕ ПЕРЕМЕЩЕНИЯМИ ОПОР Глава 6. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ СИЛ § 6.2. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 6.3. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ НА ДЕЙСТВИЕ ЗАДАННОЙ НАГРУЗКИ § 6.4. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ § 6.5. СОСТАВЛЕНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ПРИ РАСЧЕТЕ СИСТЕМ НА ПЕРЕМЕЩЕНИЯ ОПОР § 6.6. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМАХ § 6.7. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ. ПРОВЕРКА ЭПЮР § 6.8. СПОСОБ УПРУГОГО ЦЕНТРА § 6.9. ЛИНИИ ВЛИЯНИЯ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 6.10. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 6.11. ГРУППИРОВКА НЕИЗВЕСТНЫХ § 6.12. СИММЕТРИЧНЫЕ И ОБРАТНОСИММЕТРИЧНЫЕ НАГРУЗКИ § 6.13. СПОСОБ ПРЕОБРАЗОВАНИЯ НАГРУЗКИ § 6. 14. ПРОВЕРКА КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ § 6.15. ПРИМЕРЫ РАСЧЕТА РАМ § 6.16. «МОДЕЛИ» ЛИНИЙ ВЛИЯНИЯ УСИЛИИ ДЛЯ НЕРАЗРЕЗНЫХ БАЛОК Глава 7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДАМИ ПЕРЕМЕЩЕНИЙ И СМЕШАННЫМ § 7.2. ОПРЕДЕЛЕНИЕ ЧИСЛА НЕИЗВЕСТНЫХ § 7.3. ОСНОВНАЯ СИСТЕМА § 7.4. КАНОНИЧЕСКИЕ УРАВНЕНИЯ § 7.5. СТАТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ § 7.6. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ ПЕРЕМНОЖЕНИЕМ ЭПЮР § 7.7. ПРОВЕРКА КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ СИСТЕМЫ КАНОНИЧЕСКИХ УРАВНЕНИЙ МЕТОДА ПЕРЕМЕЩЕНИЙ § 7.8. ПОСТРОЕНИЕ ЭПЮР M, Q И N В ЗАДАННОЙ СИСТЕМЕ § 7.9. РАСЧЕТ МЕТОДОМ ПЕРЕМЕЩЕНИЙ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ § 7.10. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ ПРИ РАСЧЕТЕ РАМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ § 7.11. ПРИМЕР РАСЧЕТА РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ § 7.12. СМЕШАННЫЙ МЕТОД РАСЧЕТА § 7.13. КОМБИНИРОВАННОЕ РЕШЕНИЕ ЗАДАЧ МЕТОДАМИ СИЛ И ПЕРЕМЕЩЕНИЙ § 7. 14. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ МЕТОДОМ ПЕРЕМЕЩЕНИЙ Глава 8. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ СТЕРЖНЕВЫХ СИСТЕМ И МЕТОДЫ ЕЕ РЕШЕНИЯ § 8.2. СОСТАВЛЕНИЕ УРАВНЕНИЙ РАВНОВЕСИЯ, СТАТИЧЕСКИЕ УРАВНЕНИЯ. ИССЛЕДОВАНИЕ ОБРАЗОВАНИЯ СИСТЕМ § 8.3. СОСТАВЛЕНИЕ УРАВНЕНИЙ СОВМЕСТНОСТИ, ГЕОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. ПРИНЦИП ДВОЙСТВЕННОСТИ § 8.4. ЗАКОН ГУКА. ФИЗИЧЕСКИЕ УРАВНЕНИЯ § 8.5. СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ. СМЕШАННЫЙ МЕТОД § 8.6. МЕТОД ПЕРЕМЕЩЕНИЙ § 8.7. МЕТОД СИЛ § 8.8. УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ И ИХ СВЯЗЬ С УРАВНЕНИЯМИ СТРОИТЕЛЬНОЙ МЕХАНИКИ Глава 9. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ЭВМ § 9.2. ПОЛУАВТОМАТИЗИРОВАННЫЙ РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ КАЛЬКУЛЯТОРОВ § 9.3. АВТОМАТИЗАЦИЯ РАСЧЕТА СТЕРЖНЕВЫХ СИСТЕМ. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ СТРОИТЕЛЬНОЙ МЕХАНИКИ ДЛЯ СТЕРЖНЯ § 9.4. МАТРИЦЫ РЕАКЦИЙ (ЖЕСТКОСТИ) ДЛЯ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ СТЕРЖНЕЙ И ИХ ИСПОЛЬЗОВАНИЕ § 9.5. ОПИСАНИЕ УЧЕБНОГО КОМПЛЕКСА ПО РАСЧЕТУ СТЕРЖНЕВЫХ СИСТЕМ. ВНУТРЕННЕЕ И ВНЕШНЕЕ ПРЕДСТАВЛЕНИЕ ИСХОДНЫХ ДАННЫХ. БЛОК-СХЕМА КОМПЛЕКСА ПО РАСЧЕТУ СТЕРЖНЕВЫХ СИСТЕМ Глава 10. УЧЕТ ГЕОМЕТРИЧЕСКОЙ И ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ ПРИ РАСЧЕТЕ СТЕРЖНЕВЫХ СИСТЕМ § 10.2. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С УЧЕТОМ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ § 10.3. УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ § 10.4. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ С УЧЕТОМ ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ Глава 11. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ (МКЭ) § 11.2. СВЯЗЬ МКЭ С УРАВНЕНИЯМИ СТРОИТЕЛЬНОЙ МЕХАНИКИ § 11.3. ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ РЕШЕНИЯ ПЛОСКОЙ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ § 11.4. ПРЕДЕЛЬНЫЙ ПЕРЕХОД ДЛЯ ПЛОСКОЙ ЗАДАЧИ § 11.5. ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ РЕШЕНИЯ ОБЪЕМНОЙ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ § 11.6. СЛОЖНЫЕ ЭЛЕМЕНТЫ, ПОСТРОЕНИЕ МАТРИЦ ЖЕСТКОСТИ ДЛЯ ЭЛЕМЕНТОВ С ИСКРИВЛЕННОЙ ГРАНИЦЕЙ § 11.7. ПОСТРОЕНИЕ МАТРИЦ РЕАКЦИЙ ДЛЯ РАСЧЕТА ПЛАСТИНОК И ОБОЛОЧЕК § 11.8. ОСОБЕННОСТИ КОМПЛЕКСОВ ДЛЯ РАСЧЕТА КОНСТРУКЦИЙ ПО МКЭ. СУПЕРЭЛЕМЕНТНЫЙ ПОДХОД Глава 12. ОСНОВЫ ДИНАМИКИ СООРУЖЕНИЙ § 12. 2. СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 12.3. РАСЧЕТ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ ДЕЙСТВИИ ПЕРИОДИЧЕСКОЙ НАГРУЗКИ § 12.4. РАСЧЕТ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ ДЕЙСТВИИ ПРОИЗВОЛЬНОЙ НАГРУЗКИ. ИНТЕГРАЛ ДЮАМЕЛЯ § 12.5. ДВИЖЕНИЕ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ. ПРИВЕДЕНИЕ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ К ДВУМ СИСТЕМАМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 12.6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ. УРАВНЕНИЕ ЛАГРАНЖА § 12.7. ПРИВЕДЕНИЕ КИНЕМАТИЧЕСКОГО ВОЗДЕЙСТВИЯ К СИЛОВОМУ § 12.8. СВЕДЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДИНАМИКИ К РАЗДЕЛЯЮЩИМСЯ УРАВНЕНИЯМ С ПОМОЩЬЮ РЕШЕНИЯ ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ § 12.9. МЕТОД ПОСТОЯННОГО УСКОРЕНИЯ И ЕГО ИСПОЛЬЗОВАНИЕ ДЛЯ РЕШЕНИЯ ДИНАМИЧЕСКИХ ЗАДАЧ Глава 13. СВЕДЕНИЯ ИЗ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ, ИСПОЛЬЗУЕМЫЕ В СТРОИТЕЛЬНОЙ МЕХАНИКЕ § 13.2. МАТРИЦЫ, ИХ ВИДЫ, ПРОСТЕЙШИЕ ОПЕРАЦИИ НАД МАТРИЦАМИ § 13.3. ПЕРЕМНОЖЕНИЕ МАТРИЦ. ОБРАТНАЯ МАТРИЦА § 13.4. МЕТОД ГАУССА ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ. РАЗЛОЖЕНИЕ МАТРИЦЫ В ПРОИЗВЕДЕНИЕ ТРЕХ МАТРИЦ § 13.5. ИССЛЕДОВАНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. ОДНОРОДНЫЕ УРАВНЕНИЯ. РЕШЕНИЕ n УРАВНЕНИЙ С m НЕИЗВЕСТНЫМИ С ИСПОЛЬЗОВАНИЕМ МЕТОДА ГАУССА § 13.6. КВАДРАТИЧНАЯ ФОРМА. МАТРИЦА КВАДРАТИЧНОЙ ФОРМЫ. ПРОИЗВОДНАЯ ОТ КВАДРАТИЧНОЙ ФОРМЫ § 13.7. СОБСТВЕННЫЕ ЧИСЛА И СОБСТВЕННЫЕ ВЕКТОРЫ ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННОЙ МАТРИЦЫ § 13.8. ОДНОРОДНЫЕ КООРДИНАТЫ И ИНТЕГРИРОВАНИЕ ПО ТРЕУГОЛЬНОЙ ОБЛАСТИ § 13.9. СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ, ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ И ЭКСПОНЕНЦИАЛЬНОЙ ФУНКЦИЕЙ ЗАКЛЮЧЕНИЕ ЛИТЕРАТУРА

§ 3. Уравнения равновесия произвольной системы сил.

Запишем полученные в предыдущем § е векторные условия равновесия произвольной системы сил:

Но

Замечаем, что условия равновесия произвольной системы сил в координатной форме запишутся:

Система уравнений (1 — 6) называется уравнениями равновесия произвольной системы сил в координатной форме.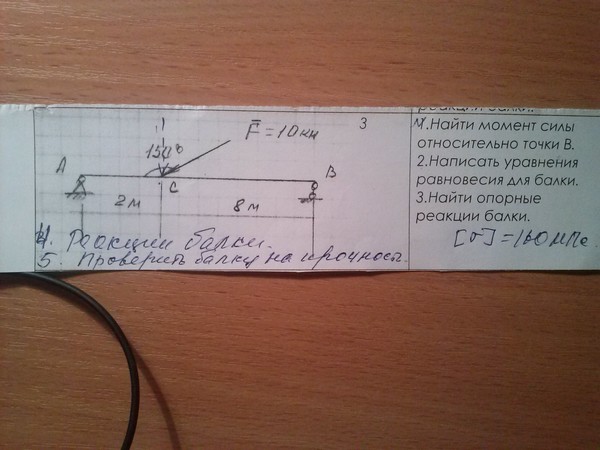

Эти уравнения содержат как задаваемые силы и моменты, так и силы и моменты от сил реакции связей. В задачах статики часть этих сил и моментов не задана и подлежит определению. Естественно, что число неизвестных сил и моментов не должно превышать числа уравнений равновесия. В противном случае говорят, что задача становится статически неопределимой.

§ 4. Теорема Вариньона.

При решении некоторых задач статики удобно пользоваться теоремой Вариньона.

Теорема: Если некоторая система сил в точке О приводится к равнодействующей (2-й случай приведения), то момент этой равнодействующей относительно другой точки О₁ равен сумме моментов сил системы относительно точки О₁.

Действительно:

Для силы системы F_i справедливы

соотношения:

_o1i=_oi_i

_i=_oi_i

Так как заданная система

сил в точке О сводится

к равнодействующей, то Представив,найдём сумму моментов сил системы относительно точки О₁:

Теорема Вариньона позволяет упростить задачу вычисления момента силы F относительно полюса О в тех случаях, когда определение плеча силы затруднительно. Например задан полюс О и вектор силы F с точкой приложения А, координаты которой X_A и Y_A (рис.20,а).

_y

Рис.20.

Представив силу F как равнодействующую двух взаимно перпендикулярных сил

вычислим момент силы F относительно полюса О:

M_O(F)=F*h=-F_x*Y_A+F_y*X_A=-F*cos*Y_A+F*sin*X_A.

§ 5.Уравнения равновесия системы сил в некоторых частных случаях.

а) Уравнения равновесия сходящейся системы сил.

Определение: Система сил называется сходящейся, если линии действия всех сил пересекаются (сходятся) в одной точке. Учитывая, что вектор силы есть скользящий вектор, все силы можно перенести в точку пересечения их линий действия и получить пучок сил.

Из рис.21 очевидно, что сходящаяся

система сил в точке О приводится к

равнодействующей

Рис. 21.

Сумма моментов этих сил относительно точки их пересечения О тождественно равна нулю.

Следовательно, векторным условием равновесия сходящейся системы сил является

В проекциях на прямоугольные оси координат это условие перепишется в виде трёх уравнений:

Уравнения (1-3) называются уравнениями равновесия сходящейся системы сил в координатной форме. Заметим, что если сходящаяся система сил лежит в плоскости XY, то уравнение (3) превращается в тождество.

Отметим также, что уравнение (1-3) легко получаются из общих уравнений равновесия (1-6) для произвольной системы сил (см. § 3), если учесть особенности сходящихся сил. Исходя из сказанного, легко наметить план решения задач на равновесие сходящейся системы сил:

1.Выбрать систему координат XYZ .

2.Освободиться от связей, заменив их силами реакции.

3.Найти проекции всех сил на координатные оси.

4.Составить и решить уравнения равновесия относительно неизвестных сил.

Примечание: В ряде случаев исследование равновесия сходящихся сил удобнее производить геометрическим способом, учитывая, что у равновесной системы сходящихся сил силовой многоугольник замкнут.

Рис.22.

Пример:

Определить усилия в шарнирных стержнях АС и ВС от действия вертикальной нагрузки P.

Обозначим усилия в стержнях S_A и S_B, приняв их растянутыми, составим уравнения равновесия

Решая систему уравнений в цифрах, получим:

S_B=-11,6 Н(сжат) S_A=5,8 Н(растянут).

Рис. 23.

б) Уравнения равновесия плоской системы сил. Система сил называется плоской, если линии действия всех сил располагаются в одной плоскости

Уравнения равновесия плоской системы

сил могут быть получены из уравнений

равновесия произвольной системы сил

(см.§ 3), если учесть аналитические

условия, определяющие особенности

плоской системы сил, например,

расположенной в плоскости XY:

(рис.24 )

Так для всех сил плоской системы, проекции их на ось Z равны нулю (F_{Z i}=0). Кроме того, нулю равны и Z-е координаты всех точек приложения сил. Таким образом, будем иметь:

Система уравнений(1-3)называется уравнениями равновесия плоской системы сил. Отметим, что при составлении этих уравнений равновесия выбор координатных осей произволен. Однако решение задачи значительно упростится, если назначенные оси координат окажутся перпендикулярными или параллельными большинству сил системы, а начало координат лежит на пересечении возможно большего числа линий действия неизвестных сил.

При решении задач на исследование равновесия тел, наряду с сосредоточенными силами, приложенными в одной точке, могут действовать и распределённые нагрузки. Примерами распределённых нагрузок могут служить массовые силы, аэродинамические силы и др.

Распределённые нагрузки на схемах задаются:

— эпюрой распределения нагрузки;

— интенсивностью распределённой нагрузки;

— протяжённостью распределённой нагрузки(рис.25)

а)Прямоугольная эпюра б)Треугольная эпюра

q, н/м-интенсивность q_max., н/м — максимальная интенсивность

а, м-протяжённость а, м — протяжённость

Q=q*a, Q — условная сосредо- Q=0.5*q_max*a, Q — условная сосредеточен-

точенная сила ная сила

Рис. 25.

Перед составлением уравнений равновесия следует распределённые нагрузки заменять условно сосредоточенными силами. Величина условно сосредоточенной силы пропорциональна площади эпюры, а линия её действия проходит через центр тяжести эпюры.

В этом § е уместно рассмотреть ещё один тип связей, не вошедший в таблицу 1 (см. § 3). Этот тип связей называется защемлённая или жёсткая заделка, схематически изображённая на рис. 26.

Жёсткая заделка А в плоской задаче

не позволяет задаваемым силам F

перемещать тело в направлении

координатных осей X и Y и не

позволяет поворачивать его

относительно точки А(оси Z).

Рис.26.

Следовательно, в жёсткой заделке возникают две составляющие силы реакции

A_X и A_Y, а также момент реакции M_A (M_Z).

Исходя из всего сказанного, можно наметить план решения задач на равновесие плоской системы сил:

1.Выбрать систему координат XY.

2.Освободиться от связей, заменив их силами и моментами реакций.

3.Заменить распределённые нагрузки условно сосредоточенными силами.

4.Составить и решить уравнения равновесия относительно неизвестных сил и моментов.

Пример: Однородная консольная балка длиной l=2 м и погонной массовой нагрузкой q=10кг/м нагружена сосредоточенной силой F=20Н и парой сил

M=10Н*м.Определить опорные реакции балки в точке защемления А.

Решение.

1.Вводим оси координат XY c

началом в точке А.

2.Освобождаемся от связи в виде

искомых реакций A_X;A_Y;M_A.

3.Заменяем массовую погонную

нагрузку балки q условно

сосредоточенной силой G

(силой тяжести), приложить её в

центре балки

Рис. 27.

G=q * g * l=10*9,8*2=19,6 Н.

4.Составляем уравнения равновесия:

или в цифрах: Решаем:

А_X+20*0,7=0; A_X=-14 H

А_Y-19,6-20*0,7=0; A_Y=33,6Н

M_A-10-19,6*1-20*0,7*2=0 М_А=57,6 Нм.

2.3 Уравнения равновесия для частиц. Инженерная механика: статика

Перейти к содержимому

Глава 2: Частицы

Для частицы, находящейся в статическом равновесии, второй закон Ньютона может быть адаптирован для [латекс]\vec a = 0[/латекс] и разделен на компоненты x y и z:

$$\sum\vec F=m*\vec a$$

$$\sum\vec F=0$$

$$\sum F_x=0\quad\quad\sum F_y=0\quad\quad\sum F_z=0$$

Обратите внимание, что слева в уравнении указано «сумма сил», что означает суммирование всех сил в этом направлении. В статике они все компенсируются. Если вы не уверены, что что-то находится в статическом движении, просуммируйте силы и посмотрите, равны ли они 0,9.0003

Статическое равновесие:

Объекты в статическом равновесии — это объекты, которые не ускоряются (либо линейное ускорение, либо угловое ускорение). Эти объекты могут быть стационарными или иметь постоянную скорость.

Второй закон Ньютона гласит, что сила, действующая на объект, равна произведению массы объекта на ускорение, которое он испытывает. Поэтому, если мы знаем, что ускорение объекта равно нулю, то можно считать, что сумма всех сил, действующих на объект, равна нулю. Отдельные силы, действующие на объект, представленные векторами сил, могут не иметь нулевой величины, но сумма всех векторов сил всегда будет равна нулю для объектов, находящихся в равновесии.

Уравнения, используемые при работе с частицами в равновесии:

$$\sum\vec F=0$$

Что приводит к:

$$\sum F_x=0\\\sum F_y=0\\ \sum F_z=0$$

Поскольку это частица, в ней нет моментов, как в твердых телах.

Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/2_равновесие_concurrent/2-1_static_равновесие/staticравновесие.html

Нахождение уравнений равновесия:

Первым шагом в поиске уравнений равновесия является построение диаграммы свободного тела анализируемого тела. На этой диаграмме должны быть показаны все известные и неизвестные векторы сил, действующих на тело. На диаграмме свободного тела укажите значения любых известных величин или направлений для векторов силы и укажите имена переменных для любых неизвестных (либо величин, либо направлений).

Первым шагом в анализе равновесия является построение диаграммы свободного тела. Это делается путем удаления всего, кроме тела, и привлечения всех сил, действующих на тело. Также полезно пометить все силы, основные размеры и углы.

Далее вам нужно будет выбрать оси x, y и z. Эти оси должны быть перпендикулярны друг другу, но они не обязательно должны быть горизонтальными или вертикальными. Если вы выберете координатные оси, которые совпадают с некоторыми из ваших векторов силы, вы упростите последующий анализ.

После того, как вы выбрали оси, вам нужно разбить все векторы сил на компоненты по направлениям x, y и z (см. страницу векторов в Приложении 1, если вам нужны дополнительные указания по этому вопросу). Ваше первое уравнение будет суммой величин компонентов в направлении x, равных нулю, второе уравнение будет суммой величин компонентов в направлении y, равных нулю, а третье (если вы имеют трехмерную задачу) будет равна сумме величин в направлении z, равной нулю. В совокупности они известны как уравнения равновесия .

Когда у вас есть уравнения равновесия, вы можете решить их для неизвестных, используя алгебру. Количество неизвестных, которые вы сможете решить, будет количеством имеющихся у вас уравнений равновесия. В случаях, когда у вас больше неизвестных, чем уравнений, проблема известна как статически неопределимая задача , и вам потребуется дополнительная информация для решения данных неизвестных.

Пример:

$$F_g=(9{\circ})=219,4N\\T_1=219,4N\\T_2=227,2N$$

Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/2_equations_concurrent/2-5_equations_particle/equationsparticle.html На этом сайте доступно множество других примеров.

См. дополнительные примеры: Пример 1, Пример 5, Пример 8

 

В основном: Уравнения равновесия позволяют разделить силы и движение по каждой оси.

Применение : Тяжелый объект поднимается с помощью веревки и шкива. Судя по силам, находится ли он в статическом равновесии? (Ответ: если сумма сил в каждом направлении равна нулю, то да!)

Забегая вперед : Далее мы применим уравнения равновесия к твердым телам, что позволит использовать их для решения более сложных задач.

Лицензия

Инженерная механика: Статика Либби (Элизабет) Осгуд; Гейла Кэмерон; Эмма Кристенсен; Аналия Бенни; и Мэтью Хатчисон находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4. 0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Твиттере

4.3 Уравнения равновесия твердого тела. Инженерная механика: статика

Глава 4. Твердые тела

Мы используем уравнения равновесия для расчета любых неизвестных сил и моментов, используя известные силы и значения, и следующие уравнения:

Уравнения равновесия частиц были рассмотрены в разделе 2.3. Это:

$$
\Сигма F_{x}=0, \Сигма F_{y}=0, \Сигма F_{z}=0 9{\prime}}=0
\end{собрано}
$$

Поскольку это статические тела, правая часть уравнений равна 0. В динамике они будут равны массе, умноженной на ускорение поступательного движения и вращения.

 

Для твердого тела , находящегося в статическом равновесии, т. е. недеформируемого тела, на которое силы не действуют одновременно, сумма сил и моментов , действующих на тело, должна быть равна нулю. Добавление моментов (в отличие от частиц, где мы рассматривали только силы) добавляет еще один набор возможных уравнений равновесия, позволяя нам решать больше неизвестных по сравнению с проблемами частиц.

Моменты, как и силы, являются векторами. Это означает, что наше векторное уравнение необходимо разбить на скалярные компоненты, прежде чем мы сможем решить уравнения равновесия. В двумерной задаче тело может вращаться только по часовой стрелке или против часовой стрелки (что соответствует вращению вокруг оси z). Это означает, что твердое тело в двумерной задаче имеет три возможных уравнения равновесия; то есть сумма компонентов силы в направлениях x и y и моментов относительно оси z. Сумма каждого из них будет равна нулю.

Для двумерной задачи мы разобьем одновекторное уравнение силы на два уравнения скалярных компонент.

$$\sum\vec F=0\\\sum F_x=0\:\sum F_y=0$$

Одномоментное векторное уравнение становится одномоментным скалярным уравнением.

$$\sum\vec M=0\\\sum M_z=0$$

Если мы рассмотрим трехмерную задачу, мы увеличим количество возможных уравнений равновесия до шести. Есть три уравнения равновесия для силы, где сумма компонентов в направлениях x, y и z должна быть равна нулю. Тело также может иметь моменты относительно каждой из трех осей. Второй набор из трех уравнений равновесия утверждает, что сумма компонентов момента относительно осей x, y и z также должна быть равна нулю.

Разобьем силы на три составляющие уравнения

$$\sum\vec F=0\\\sum F_x=0\:\sum F_y=0\:\sum F_z=0$$

Разобьем моменты в трехкомпонентные уравнения

$$\sum\vec M=0\\\sum M_x=0\:\sum M_y=0\:\sum M_z=0$$

Как и в случае с частицами, первый шаг в нахождении уравнения равновесия состоит в том, чтобы нарисовать диаграмму свободного тела анализируемого тела. На этой диаграмме должны быть показаны все векторы сил, действующих на тело. На диаграмме свободного тела задайте значения для любых известных величин, направлений и точек приложения векторов силы и задайте имена переменных для любых неизвестных (величин, направлений или расстояний).

Далее вам нужно будет выбрать оси x, y, z. Эти оси должны быть перпендикулярны друг другу, но они не обязательно должны быть горизонтальными или вертикальными. Если вы выберете координатные оси, которые совпадают с некоторыми из ваших векторов силы, вы упростите последующий анализ.

После того, как вы выбрали оси, вам нужно разбить все векторы сил на компоненты по направлениям x, y и z (см. страницу векторов в Приложении 1 для более подробной информации об этом процессе). Ваше первое уравнение будет суммой величин компонентов в направлении x, равных нулю, второе уравнение будет суммой величин компонентов в направлении y, равных нулю, а третье (если вы имеют трехмерную задачу) будет равна сумме величин в направлении z, равной нулю.

Далее вам нужно будет составить уравнения моментов. Для этого вам нужно будет выбрать точку, о которой будут сниматься моменты. Подойдет любая точка, но обычно выгоднее выбрать точку, которая уменьшит количество неизвестных в уравнении. Помните, что любой вектор силы, проходящий через данную точку, не будет иметь никакого момента относительно этой точки. Чтобы записать уравнения моментов, просто суммируйте моменты, создаваемые каждой силой (добавляя чистые моменты, показанные на диаграмме) относительно данной точки и данной оси (x, y или z), и установите эту сумму равной нулю. Все моменты будут относиться к оси z для двухмерных задач, хотя моменты могут быть связаны с осями x, y и z для трехмерных задач.

Когда у вас есть уравнения равновесия, вы можете решить эти формулы для неизвестных. Количество неизвестных, которые вы сможете решить, снова будет числом или уравнениями, которые у вас есть.

 

Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/3_equations_rigid_body/3-6_equations_rigid_body/equations_rigid_body.html

 

Вот наглядный пример использования уравнений равновесия:

Источник: Инженерная механика, Джейкоб Мур и др. http://mechanicsmap.psu.edu/websites/4_statically_equivalent_systems/4-1_statically_equivalent_systems/images/equivalentexample. png

Если рассматривать только направление Y (вертикальное), 200 фунтов, давящих на балку, должны быть уравновешены силами реакции толкая вверх. Две силы реакции эквивалентны, потому что силы сверху равномерно уравновешены между силами реакции. Если они находятся в разных местах, мы используем сумму уравнения моментов и расстояний людей, чтобы определить размер сил реакции.

Пример 1:

Автомобиль ниже имеет массу 1500 фунтов с центром масс в 4 футах позади передних колес автомобиля. Каковы нормальные силы, действующие на переднее и заднее колеса автомобиля?

 

Пример 2:

Сидя на стуле, человек прикладывает силы, показанные на схеме ниже. Определите все силы, действующие на стул в точках A и B. (Предположим, что A не имеет трения, а B — шероховатая поверхность).

Источник: Engineering Mechanics, Джейкоб Мур и др., http://mechanicsmap.psu.edu/websites/3_equations_rigid_body/3-6_equations_rigid_body/pdf/EquilibriumEquationsExtended_WorkedProblem5.