Правило Верещагина (способ перемножения эпюр)

Во многих случаях интегрирования по Мору можно избежать и применить способ«перемножения» эпюр. Одним из таких способов является способ Симпсона, но также можно определить перемещения по способу (правилу) Верещагина. Этот способ А.К. Верещагин предложил в 1924 году, будучи студентом.

Рассмотрим последовательность действий по правилу Верещагина. Начальный этап такой же, как по формуле Мора и способу Симпсона, т.е. вначале строится грузовая эпюра от действующих нагрузок (действительное состояние), затем рассматриваем балку во вспомогательном состоянии. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем 

линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила, равная единице , а если требуется найти угол поворота, то приложить следует сосредоточенную пару сил, момент, равный единице. Строится эпюра единичных моментов или эпюра от единичной нагрузки. Далее перемещение вычисляется по формуле:

, где в числителе — произведение площади грузовой эпюры на ординату  единичной (обязательно прямолинейной), взятой под центром тяжести грузовой эпюры, а в знаменателе — жесткость сечения.

Этот способ становится понятным,если доказать, что результат перемножения двух эпюр ,одна и которых произвольна ,а другая линейна, равен произведению площади грузовой эпюры на ординату  единичной,  взятой под центром тяжести грузовой эпюры.

Следует иметь в виду, что способы «перемножения» эпюр  применимы только при наличии двух условий:

1. Изгибная жесткость балки на рассматриваемом участке должна быть постоянной(EI=Const),
2. Одна из двух эпюр моментов на этом участке (грузовая или единичная)   должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома. 

Пусть грузовая эпюра произвольна, а единичная линейна (так как единичной нагрузкой бывает обычно либо сосредоточенная сила, либо пара сил, то единичная эпюра М⁰  оказывается ограниченной прямыми линиями). Пусть грузовая эпюра М(z) имеет криволинейное очертание, а эпюра М⁰ – прямолинейное

(см. рисунок). Произведение   можно рассматривать как элемент  площади эпюры М, заштрихованной на рисунке.

Так как ордината М⁰ равна то произведение  , а весь интеграл , где

 — статический момент площади эпюры М(z) относительно оси ординат

Но! Статический момент площади ,как известно, это произведение самой площади на координату центра тяжести. Тогда

, где  — это

ордината в единичной эпюре, расположенной под центром тяжести грузовой эпюры. Окончательно, перемещение равно:

Таким образом, результат перемножения двух эпюр равен произведению площади грузовой эпюры на ординату другой (обязательно прямолинейной), взятой под центром тяжести грузовой эпюры.

Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены по одну сторону от оси эпюры (то есть они одного знака), то перед их произведением мы должны поставить знак «плюс», а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».

Сопротивление материалов

Сопротивление материалов

Дарков А.В., Шапиро Г.С. Сопротивление материалов. — М.: Высшая школа, 1975. — 654 с. Настоящий курс предназначен для студентов высших технических учебных заведений. В каждой его главе приведены подробно решенные примеры, задачи для самостоятельного решения и даны вопросы для самопроверки пройденного материала. Оглавление ПРЕДИСЛОВИЕ Глава 1. ОСНОВНЫЕ ПОНЯТИЯ § 2.1. РАСЧЕТНАЯ СХЕМА. НАГРУЗКИ § 3.1. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ § 4.1. НАПРЯЖЕНИЯ § 5.1. ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ § 6.1. ОСНОВНЫЕ ПРЕДПОСЫЛКИ НАУКИ О СОПРОТИВЛЕНИИ МАТЕРИАЛОВ Вопросы для самопроверки Глава 2. РАСТЯЖЕНИЕ И СЖАТИЕ § 1. 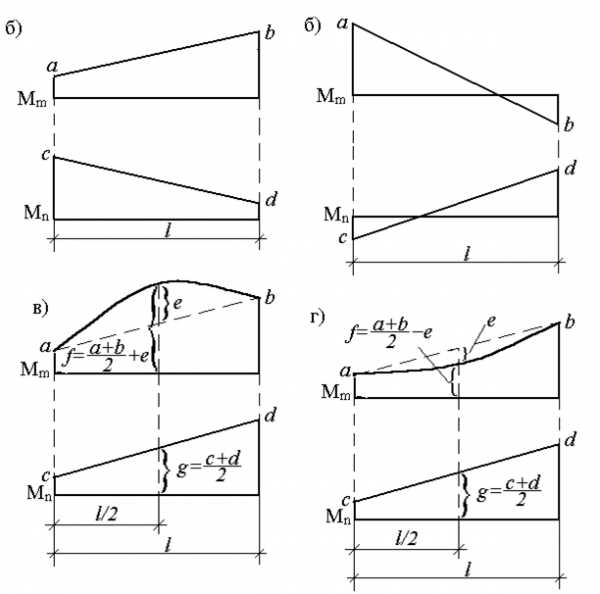2. ПРОДОЛЬНАЯ СИЛА § 2.2. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ И НАКЛОННЫХ СЕЧЕНИЯХ БРУСА § 3.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ § 4.2. ДИАГРАММЫ РАСТЯЖЕНИЯ И СЖАТИЯ § 5.2. ПЕРЕМЕЩЕНИЯ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСЬЕВ § 6.2. РАБОТА СИЛЫ ПРИ ЕЕ СТАТИЧЕСКОМ ДЕЙСТВИИ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ § 7.2. СОБСТВЕННЫЙ ВЕС БРУСА § 8.2. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. РАСЧЕТЫ НА ПРОЧНОСТЬ § 9.2. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ § 10.2. МЕСТНЫЕ НАПРЯЖЕНИЯ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 3. ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ § 1.3. ВИДЫ НАПРЯЖЕННОГО СОСТОЯНИЯ § 2.3. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ § 3.3. ГЛАВНЫЕ НАПРЯЖЕНИЯ. ГЛАВНЫЕ ПЛОЩАДКИ § 4.3. ЭКСТРЕМАЛЬНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ § 5.3. ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ С ПОМОЩЬЮ КРУГА МОРА § 6.3. ПОНЯТИЕ О ПРОСТРАНСТВЕННОМ НАПРЯЖЕННОМ СОСТОЯНИИ § 7.3. ОБОБЩЕННЫЙ ЗАКОН ГУКА § 8.3. ОБЪЕМНАЯ ДЕФОРМАЦИЯ § 9.3. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 4. СДВИГ § 1.4. ЧИСТЫЙ СДВИГ § 2.4. ДЕФОРМАЦИЯ ПРИ СДВИГЕ. ЗАКОН ГУКА ПРИ СДВИГЕ § 3.4. ОБЪЕМНАЯ ДЕФОРМАЦИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРИ ЧИСТОМ СДВИГЕ. ЗАВИСИМОСТЬ МЕЖДУ E, G и «мю» § 4.4. ПРАКТИЧЕСКИЕ РАСЧЕТЫ НЕКОТОРЫХ ПРОСТЕЙШИХ КОНСТРУКЦИЙ, РАБОТАЮЩИХ НА СДВИГ Расчет заклепочных соединений Расчет сварных соединений Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ § 2.5. СТАТИЧЕСКИЕ МОМЕНТЫ СЕЧЕНИЙ § 3.5. МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЙ § 4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЕЧЕНИЙ ПРОСТОЙ ФОРМЫ § 5.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ § 6.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ § 7.5. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ. ГЛАВНЫЕ ОСИ ИНЕРЦИИ § 8.5. ИССЛЕДОВАНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ СЕЧЕНИЙ С ПОМОЩЬЮ КРУГА МОРА § 9.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ СЕЧЕНИЙ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 6. 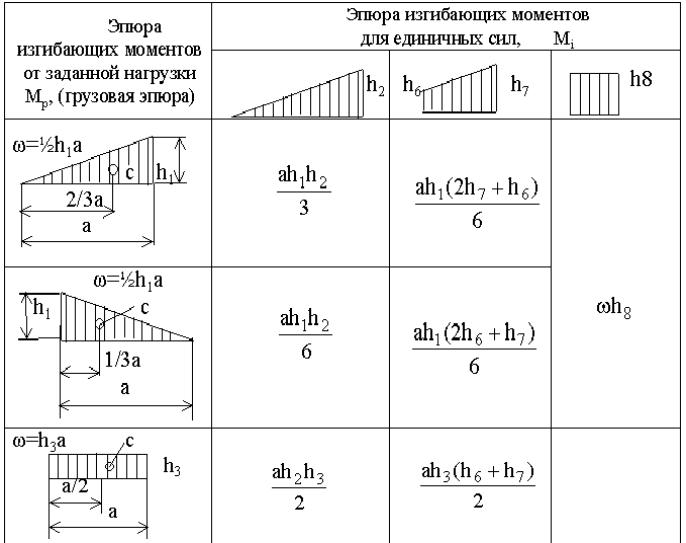КРУЧЕНИЕ § 1.6. ОСНОВНЫЕ ПОНЯТИЯ. КРУТЯЩИЙ МОМЕНТ § 2.6. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 3.6. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.6. РАСЧЕТ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ § 5.6. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ВИНТОВЫХ ПРУЖИН § 6.6. КРУЧЕНИЕ ПРЯМОГО БРУСА НЕКРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 7.6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 7. ПРЯМОЙ ИЗГИБ § 1.7. ВНУТРЕННИЕ УСИЛИЯ § 3.7. ОПОРЫ И ОПОРНЫЕ РЕАКЦИИ § 4.7. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 5.7. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗГИБАЮЩИМ МОМЕНТОМ, ПОПЕРЕЧНОЙ СИЛОЙ И ИНТЕНСИВНОСТЬЮ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ § 6.7. ПРИМЕРЫ ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ УСИЛИЙ § 7.7. ПРЯМОЙ ЧИСТЫЙ ИЗГИБ § 8.7. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ § 9.7. ГЛАВНЫЕ НАПРЯЖЕНИЯ ПРИ ПРЯМОМ ПОПЕРЕЧНОМ ИЗГИБЕ § 10. 7. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ § 11.7. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ § 12.7. ПОНЯТИЕ О ЦЕНТРЕ ИЗГИБА § 13.7. ПОНЯТИЕ О РАСЧЕТЕ СОСТАВНЫХ БАЛОК § 14.7. ПОНЯТИЕ О БАЛКАХ РАЗНОРОДНОЙ УПРУГОСТИ § 15.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НЕПОСРЕДСТВЕННОГО ИНТЕГРИРОВАНИЯ § 16.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НАЧАЛЬНЫХ ПАРАМЕТРОВ § 17.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В БАЛКАХ ГРАФО-АНАЛИТИЧЕСКИМ МЕТОДОМ § 18.7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 8. ТЕОРИИ ПРОЧНОСТИ § 1.8. КЛАССИЧЕСКИЕ И ЭНЕРГЕТИЧЕСКАЯ ТЕОРИИ ПРОЧНОСТИ § 2.8. ТЕОРИЯ ПРОЧНОСТИ МОРА § 3.8. ЕДИНАЯ ТЕОРИЯ ПРОЧНОСТИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 9. СЛОЖНОЕ СОПРОТИВЛЕНИЕ § 1.9. КОСОЙ ИЗГИБ § 2.9. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ БРУСЬЕВ БОЛЬШОЙ ЖЕСТКОСТИ § 3. 9. ЯДРО СЕЧЕНИЯ § 4.9. ИЗГИБ С КРУЧЕНИЕМ БРУСЬЕВ КРУГЛОГО СЕЧЕНИЯ § 5.9. ОБЩИЙ СЛУЧАЙ ДЕЙСТВИЯ СИЛ НА БРУС КРУГЛОГО СЕЧЕНИЯ § 6.9. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ ПРОСТРАНСТВЕННЫХ БРУСЬЕВ С ЛОМАНОЙ ОСЬЮ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 10. РАСЧЕТ КРИВЫХ БРУСЬЕВ § 2.10. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 3.10. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ БРУСА БОЛЬШОЙ КРИВИЗНЫ § 4.10. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ ПРИ ЧИСТОМ ИЗГИБЕ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В УПРУГИХ СИСТЕМАХ § 1.11. РАБОТА ВНЕШНИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ § 2.11. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ § 3.11. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЯ 4.11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ. ИНТЕГРАЛ МОРА § 5.11. ПРАВИЛО ВЕРЕЩАГИНА Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 12. РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ § 1. 12. СТАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ § 2.12. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 3.12. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 4.12. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 5.12. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ § 6.12. ПРОВЕРКА ПРАВИЛЬНОСТИ ЭПЮР М, Q И N § 7.12. НЕРАЗРЕЗНЫЕ БАЛКИ ПРИМЕРЫ РАСЧЕТА Вопросы для самопроверки Глава 13. ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОГО СТЕРЖНЯ § 1.13. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ УПРУГИХ ТЕЛ § 2.13. ПРОДОЛЬНЫЙ ИЗГИБ § 3.13. ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАПРЯЖЕНИЯХ, ПРЕВЫШАЮЩИХ ПРЕДЕЛ ПРОПОРЦИОНАЛЬНОСТИ § 4.13. ПРАКТИЧЕСКИЕ РАСЧЕТЫ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ § 5.13. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 14. ДИНАМИЧЕСКАЯ НАГРУЗКА § 2.14. ДИНАМИЧЕСКИЕ ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ СТАТИЧЕСКОГО РАСЧЕТА СИСТЕМ § 3.14. УДАР § 4.14. ЧАСТНЫЕ СЛУЧАИ УДАРНОГО ДЕЙСТВИЯ НАГРУЗКИ § 5.14. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 15. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт 2019 © Все права защищены.