Сопромат Лекции Часть 1 — Стр 15

ГЛАВА 8. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

140

Рис. 8.6. Стержень с защемл¼нным и шарнирным концами

Рассматривая этот случай аналогично предыдущему, получим

	кр =	2 · · наим	,
		(0, 7 · )2

òî åñòü кр в этом случае в два раза больше, чем при шарнирном закреп-

лении.

Анализируя полученные зависимости, русский инженер Ф.С. Ясинский предложил общую формулу для любого случая закрепления

кр = 2 · · наим

( · )2

формула Ясинского. Здесь коэффициент приведения длины, ука-

зывающий, на какой длине данного стержня реализуется схема Эйлера,· привед¼нная длина.

Тогда:

1) два шарнирно закрепл¼нных конца = 1;

2)	один защемл¼нный конец	= 2;
3)	два защемл¼нных конца	= 0,5;
4)	защемл¼нный и шарнирный концы = 0,7.

Формула Ясинского широко применяется для расч¼та критических сил. В справочниках приводятся значения для различных способов

закрепления, промежуточных опор, стержней переменного сечения и т.д.

ГЛАВА 8. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

141

8.3Пределы применимости формулы Эйлера. Полный график критических напряжений

Запишем формулу Эйлера для критических напряжений: кр = 2 ·

2 ,

·

ãäå = min.

Эту формулу широко применяли мостостроители, но бывали случаи, когда вс¼ — таки стержни выходили из строя и мосты разрушались. Тогда формулу Эйлера отбросили, заменив массой эмпирических формул. Затем формула Эйлера была реабилитирована. Оказалось, что у ней есть пределы применимости.

При выводе формулы Эйлера использовалось облегч¼нное дифференциальное уравнение изогнутой оси балки · · ′′ = ( ), которое спра-

ведливо только для линейно упругих систем, то есть когда справедлив закон Гука ( ≤ п).

Следовательно, условие применимости формулы Эйлера: кр ≤ п

	èëè	2 ·	≤	п. Разрешим относительно
		2
				≥ √
					2 ·		= пред,
					п

формулу Эйлера можно применять только для достаточно длинных стержней, у которых ≥ пред. Какие же это стержни?

Рассмотрим пример стержень из стали 20: п

= 200 ÌÏà, пред =

√

= √

·п

2

·200·

105

= 100. Итак для сжатого стержня из стали 20

2

2

формулу Эйлера можно применять, если ≥ 100.

Конкретизируем пусть шарнирно оп¼ртыé ñòåржень имеет круглое

поперечное сечение. В этом случае

= √

= √

64

·

· 2

= 4;

4

4

·

4 ·

≥

≥

·

·

·

=

=

100, отсюда

25

только в этом случае для

стержней из стали 20 можно применять формулу Эйлера (рис. 8.7).

Для деталей машин это условие выполняется редко, чаще оказывается < пред, тогда кр < 2 ·

2 , поэтому были случаи разрушения. Полный график критических напряжений

С точки зрения потери устойчивости все сжатые стержни делятся на три группы:

ГЛАВА 8. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

142

Рис. 8.7. Стержень круглого сечения с шарнирными опорами

1 группа. Стержни большой гибкости К ним относятся стержни, для которых ≥ пред. При сжатии они

выпучиваются, теряют устойчивость и критическое напряжение вычисляется по формуле Эйлера: кр = 2 ·

2 . Для стержней из стали 20 это

стержни у которых ≥ 100.

2 группа. Стержни средней гибкости.

К ним относятся стержни, для которых гр ≤ < пред, ãäå гр

нижняя граница стержней средней гибкости, зависящая от материала стержня. Для стержней из стали 20 гр = 40.

Стержни средней гибкости выпучиваются достаточно большими силами, но кр < 2 ·

2 , так как потеря устойчивости происходит при упруго-пластическом изгибе (в крайних волокнах происходят пластиче-

ские деформации).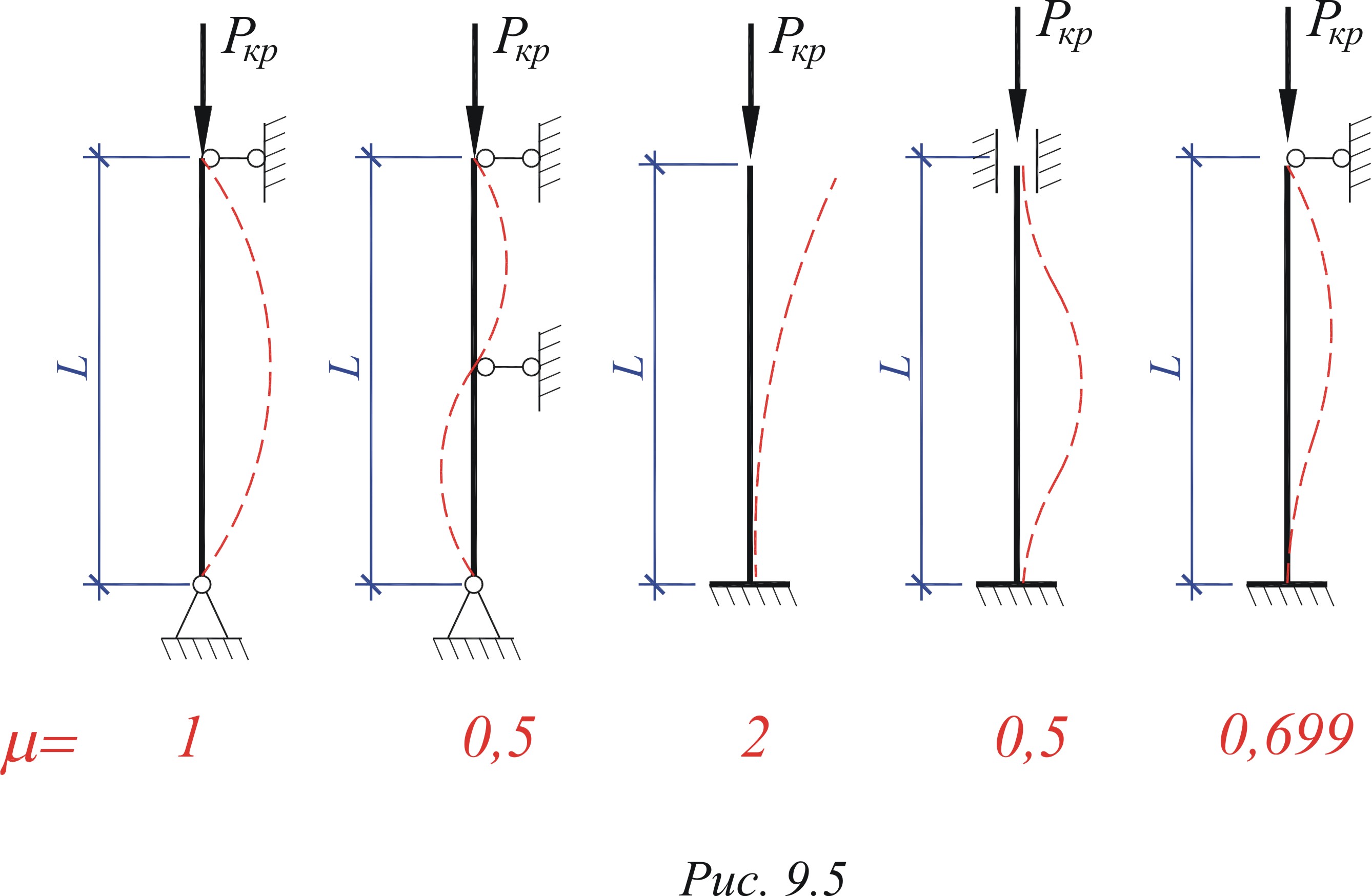 Чаще всего гр è кр определяются опытным пут¼м,

но в последнее время появились и аналитические методы. 3 группа. Стержни малой гибкости

К ним относятся стержни, для которых < гр. Для стержней из стали 20 это стержни, для которых < 40. При сжатии стержня выпучи-

вания не наблюдается, но при напряжениях, равных пределу текучести (пластичные материалы) или пределу прочности (хрупкие материалы) наблюдаются явления, формально похожие на потерю устойчивости внезапное нарастание деформаций. В этом случае кр = т èëè кр = в,

хотя никакого выпучивания и не происходит.

Полный график критических напряжений рассмотрим на примере стержней из стали 20, у которой п = 200 ÌÏà, т = 240 МПа, граница

стержней малой гибкости = 40, граница стержней средней гибкости= 100 (рис. 8.8).

Для стержней с гибкостью 100 кр = 200 МПа. С ростом гибкости

критическое напряжение уменьшается.

Для стержней малой гибкости кр = т = 240 ÌÏà.

Для стержней средней гибкости зависимость критического напряжения от гибкости определяются экспериментально или теоретически (В. И. Феодосьев). График зависимости почти прямая.

ГЛАВА 8. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

143

Рис. 8.8. Полный график критических напряжений для стержней из стали 20

Этот график для всего диапазона стержней называется полным графиком критических напряжений.

Если значение критического напряжения ( кр) взято с полного гра-

фика, то здесь учитывается не только потеря устойчивости как таковая,

но и опасные состояния для стержня любой длины. Поэтому, если при вычислении [ ]кр = кркр , кр взято с полного графика, то расч¼т нуж-

но провести только по устойчивости: ≤ [ ]кр, а простое сжатие уже учтено.

Необходимо сделать оговорку: сказанное справедливо для стержней без местных ослаблений.

8.4Расчёт сжатых стержней с помощью коэффициента снижения основного допускаемого напряжения

	Это практический метод расч¼та.
	Вспомним. Допускаемое напряжение на сжатие (основное): [ ] =				,
ãäå
	= т для пластичных материалов, = в для хрупких мате-
риалов.		кр
	Допускаемое напряжение на устойчивость: [ ]кр =		.
		кр

Обращаем внимание, что кр > т, т. к. потеря устойчивости являет-

ся более сложной деформацией, чем сжатие, и формулы сопротивления материалов здесь менее точны. Для стержней из пластичных материалов кр = 2 3 ( т = 1,5). Для стержней из хрупких материалов кр =

ГЛАВА 8. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

144

5, т. к. у хрупких материалов пластических деформаций практически не бывает и, если достигнуто предельное состояние, то стержень сразу разрушается, а у пластичных материалов разрушение происходит при значительных пластических деформациях.

Рассмотрим отношение допускаемых напряжений

[ ]кр	= ;	[ ]кр = · [ ] .
[ ]

В соответствии с этой формулой коэффициент называется коэффи-

циентом снижения основного допускаемого напряжения. Он показывает, как нужно снизить основное допускаемое напряжение, чтобы получить допускаемое напряжение на устойчивость. 0 ≤ ≤ 1. Для очень длин-

ных стержней → 0, а для весьма коротких → 1. Действительно,

если стержень короткий, то за предельное напряжение принимается предел текучести и поэтому = 1.

От чего зависит ? Подставим в формулу для значения допускаемых напряжений

=	кр	·			;	= (материал,	).
			кр

Напряжение кр зависит от гибкости стержня (по графику) и материала, предельное напряжение и коэффициенты запаса кр è т от материала, то есть зависит от гибкости и материала стержня. В справочниках приводятся таблицы и графики зависимости от гибкости и

материала.

Как решаются задачи расч¼та на прочность с уч¼том полученной формулы?

1. Проверка прочности.

Прежде чем решать задачу, покажем стержень с местным ослаблени-

åì (ðèñ. 8.9).

Теперь будем решать задачу бр ≤ · [ ] если нет ослабления.

Если есть ослабление, то нужно проверить ещ¼ на сжатие в ослабленном сечении нетто ≤ [ ] .

Необходимо подчеркнуть, что при проверке на устойчивость местное ослабление не учитывается, так как оно практически не влияет на устой-

чивость стержня. Это видно из дифференциального уравнения изогнутой оси балки: · · ′′ = , так как местное ослабление находится на

небольшой длине, поэтому при интегрировании изменений практически не будет. Но ослабленное сечение нужно проверить на сжатие.

чение коэффициента в первой попытке.

Затем проверяем, выполняется ли условие устойчивости

выполняется ли условие устойчивости при такой площади?

Находим (1)бр (1) (1) (1). Здесь (1) действительное зна-

ГЛАВА 8. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

145

Рис. 8.9. Стержень с местным ослаблением

2.Назначение поперечного сечения сжатого стержня.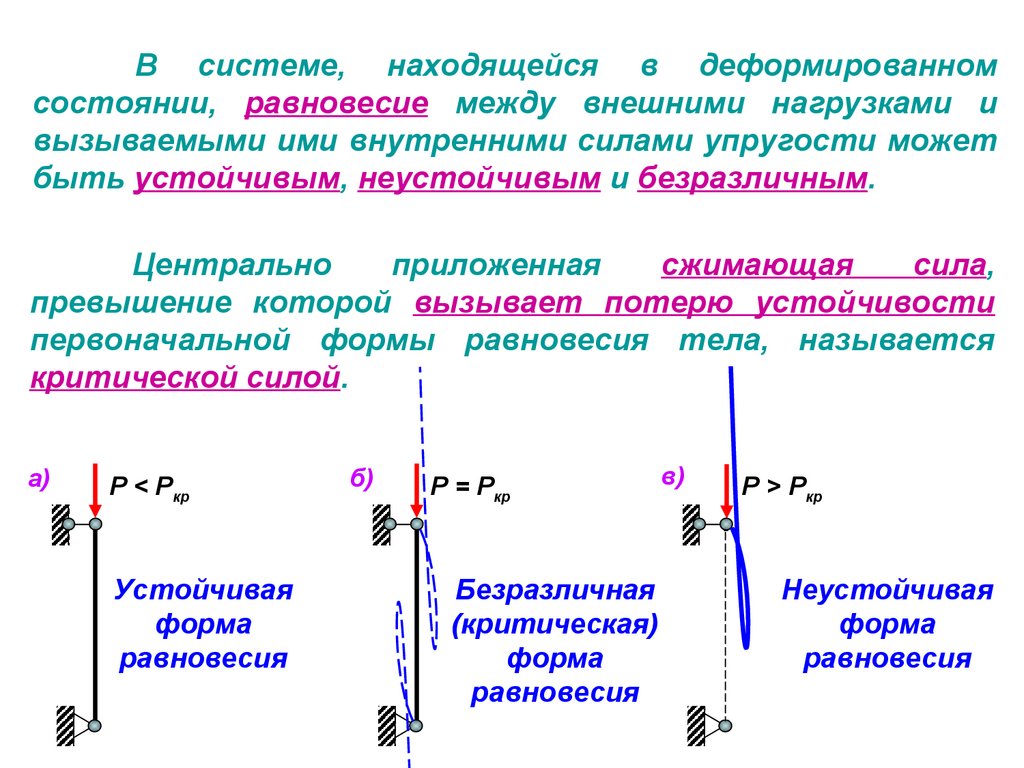 Разрешим условие устойчивости относительно бр

бр ≥ · [ ] .

На первый взгляд вс¼ просто, однако это не так. Коэффициент зависит

от , а от , в свою очередь зависит от площади сечения. Так что в явном виде относительно площади это неравенство не разрешено, так как в зависимости от площади в аналитическом виде не представля-

ется (только в графическом или табличном виде), поэтому при решении пользуются методом попыток.

Для первой попытки используем среднее значение = 0,5 и из усло-

вия устойчивости определим площадь бр(1) =				, затем выясним,
		·
0, 5			[ ]

(1)бр ≤ (1) · [ ] .

Как правило оно не выполняется, поэтому делается вторая попытка. (Нужно стремиться к тому, чтобы действительные напряжения сравнялись с допускаемыми).

Находим бр(2)		(2)		(2)	(2) и вновь обращаемся к условию
устойчивости:			≤ (2) · [ ]		и так далее до тех пор, пока условие
	(2)
		бр

устойчивости не выполнится, то есть пока разница между правой и левой

частями условия устойчивости не будет менее 1 3 %. Допустим, что в

последней попытке получено значение ( ), удовлетволяющее условию

бр

устойчивости. Обычно, попыток бывает не более тр¼х.

ГЛАВА 8. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ			146
Если стержень имеет местное ослабление, то нужно проверить на
обычное сжатие в ослабленном сечении:		≤ [ ] , если условие
	( )

нетто

выполняется, то расч¼т окончен. Если же не выполняется, то нужно

назначить площадь из этого условия. Здесь площадь нетто представлена

в явном виде.

3. Определение грузоподъ¼мности.

Разрешим условие устойчивости отностиельно

≤ · [ ] · бр,

≤ [ ] · нетто.

Вс¼, что в правой части , известно, поэтому необходимо вычислить зна- чения силы и взять меньшее значение, тогда будут выполнены условия

устойчивости и прочности.

8.5Выбор формы поперечного сечения и материала сжатого стержня на основании экономических соображений

Вначале о выборе формы.

Задачу поставим таким образом: площадь поперечного сечения постоянна. Требуется выяснить, при какой форме поперечного сечения крити- ческая сила будет наибольшей? Или иначе при какой форме попереч- ного сечения грузоподъ¼мность будет наибольшей? Чтобы решить эту задачу, вспомним полный график критических напряжений (рис. 8.10). Видим, что критическое напряжение возрастает при уменьшении гибко-

сти, т. е. нужно придать поперечному сечению такую форму, чтобы гиб-

·

кость была как можно меньше, но = , отсюда видно, что нужно

√

увеличивать минимальный радиус инерции = , откуда следу- ет, что нужно увеличивать наименьший из моментов инерции сечения.

Самый лучший случай тогда, когда = , то есть главные цен- тральные моменты инерции должны быть одинаковыми. Чтобы моменты инерции были больше, необходимо расположить площадь сечения как можно дальше от начала координат, что видно из формулы для момента

Ýòèì	∫	02	. второе =
инерции 0	=		.

условиям (первое условие увеличение

) удовлетворяет кольцевое сечение наиболее экономичное сечение.

ГЛАВА 8. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

147

Рис. 8.10. Полный график критических напряжений

Однако увлекаться разносом площади нельзя, т. к. у тонкостенной трубы может произойти местная потеря устойчивости задолго до выпучивания всего стержня.

Чтобы избежать такой потери устойчивости, применяют кольцевые диафрагмы (р¼бра ж¼сткости) (рис. 8.11).

Рис. 8.11. Рациональная форма поперечного сечения

О выборе материала.

Здесь необходимо рассмотреть раздельно стержни большой гибкости, стержни средней и малой гибкости.

1 Стержни большой гибкости.

Критическое напряжение определяется по формуле кр = 2 ·2 . Áó-

дем рассматривать не все материалы, а только сплавы на одной основе, например, стали. В соответствии с формулой материал влияет на устойчивость только через модуль продольной упругости , а в преде-

лах одного сплава практически не изменяется. Каким материалам, в

этом случае, отдать предпочтение? Наиболее деш¼вым, низкопрочным. Переход к высокопрочным материалам не обеспечивает увеличение критического напряжения, так как модуль упругости не изменяется.

2 Стержни средней и малой гибкости Здесь критическое напряжение зависит от предела текучести матери-

ала. Чем выше предел текучести, тем больше критическое напряжение, поэтому для стержней средней и малой гибкости оправдано применение высокопрочных материалов, так как они имеют более высокие значения

ГЛАВА 8. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

148

предела текучести.

Âзаключении. Устойчивость теряют не только сжатые стержни, но

èбалки при изгибе.

Âбалках с узким поперечным сечением потеря устойчивости происходит в изгибно-крутильной форме (рис. 8.12).

Рис. 8.12. Потеря устойчивости балки с узким поперечным сечением

Устойчивость теряют также сжатые тонкостенные оболочки. Например, обшивка крыла, фюзеляж самол¼та потеряли бы устойчивость, если бы они не подкреплялись стрингерами, нервюрами, шпангоутами.

8.6Вопросы для самопроверки

Âч¼м суть явления потери устойчивости сжатого стержня? Что такое критическая сила и по какой формуле она определяется? Укажите пределы применимости формулы Эйлера. Что такое гибкость стержня? Как определяется критическое напряжение для стержней большой, средней и малой гибкости? Какой вид имеет полный график критических напряжений? Как влияют условия закрепления стержня на значение критической силы? Как производится проверка стержня на устойчивость с помощью коэффициента снижения основного допускаемого напряжения?

Информационный центр по атомной энергии

Найди свой город

Что сделали физики Константин Петржак и Георгий Флёров в 1940 году на московской станции метро «Динамо»?

Экспериментально доказали спонтанное деление ядер урана

Правда ли, что мечехвосты живут на Земле уже 300 миллионов лет, у них 10 глаз и голубая кровь?

Да. Их кровью проверяют чистоту медицинских препаратов

Действительно ли с помощью радиационных технологий можно изменить цвет драгоценных камней?

Да, в НИИАРе так производят голубые топазы

Как вы считаете, в чём заключалась уникальная особенность духов «Шанель №5», на которой настаивала Коко Шанель?

Это искусственный аромат, созданный химиком

От названия какого животного произошло слово «вакцина»?

Коровы. В переводе с латинского «vaccinia» — «коровья»

Знаете ли вы, какие звёзды сопоставимы по размеру с земными городами?

Это нейтронные звёзды с диаметром 10-20 километров

Какую знаменитую фразу
Игорь Курчатов произнёс
во время пуска первой в мире
Обнинской АЭС?

«С лёгким
паром!»

Сколько топлива в сутки потребляют атомные ледоколы?

От 4,5 до нескольких десятков грамм

Как вы думаете, какой длины будет цепочка из ДНК всех клеток человеческого тела, если их раскрутить?

16 миллиардов км – это от Земли до Плутона и обратно

В каких частях мозга вырабатываются нейромедиаторы дофамин и серотонин, обеспечивающие нам позитивные эмоции?

В голубом пятне и чёрной субстанции

А знаете ли вы, какой из элементов считается самым дорогим в мире, а его мировой запас составляет 8 граммов?

Калифорний-252 стоит 10 млн. долларов за грамм

Какие животные смогли пройти «зефирный тест»: отказаться от угощения ради получения чего-то более вкусного позже?

Многие приматы, собаки, вороны и каракатицы

А вы знали, что все натуральные продукты содержат небольшое количество радиоактивных изотопов?

Например, средний банан содержит 0,42 грамма калия

Существует ли «одежда» для реактора и где у него можно найти «юбку» и «тюбетейку»?

Это неформальные названия верхней и средней части контейнмента

Как вы думаете, существуют ли животные, способные выжить в открытом космосе?

Это тихоходки, побывавшие на внешней стороне МКС

Какое явление возникает при взаимодействии солнечного ветра с верхними слоями атмосферы?

Полярное сияние

У какого наземного животного самый большой мозг?

У слона – из-за размеров тела

Новости

Все новости

Новости твоего города

Наши форматы

Все форматы

Команда ИЦАЭ

Информационные центры
по атомной энергии присутствуют в19 городах России

Найди свой город

Найди свой город

Эксперты ИЦАЭ

Все эксперты

ПОДПИШИСЬ НА РАССЫЛКУ
НАУЧНО-ПОПУЛЯРНЫХ
СОБЫТИЙ ТВОЕГО ГОРОДА

Некоторые соображения относительно образования дефектов в кристаллах на атомном уровне

Некоторые соображения относительно образования дефектов в кристаллах на атомном уровне

Засымчук В. И., Засымчук О.Е.

Институт физики металлов им. Г. В. Курдюмова НАН Украины, бульвар Академика Вернадского, 36, UA-03142, г. Киев, Украина

Поступила в редакцию: 19.12.2014; окончательная версия — 18.05.2018. Скачать: PDF

Исследуются колебания и взаимодействие двух положительных ионов, погруженных в электронный газ, в том числе и в области, далекой от линейного поведения. Как показано, для того, чтобы движение ионов было неустойчивым, необходимо, чтобы они хотя бы иногда во время своих колебаний удалялись друг от друга на расстояние больше 1,5$\alpha$. Оценены колебательная энергия иона, необходимая для того, чтобы произошло это разделение, и вероятность появления таких ионов для одновалентных металлов. Полученные результаты обобщены на объемный металл. Исследован случай большого количества «нестабильных ионов».

Ключевые слова: гидродинамический канал течения, дефекты, устойчивость, энергия собственных колебаний иона, предел текучести, активный ион, энтропия, критический размер.

---

ЛИТЕРАТУРА

1. Засимчук Э.Е., Маркашова Л.И. // Матер. науч. англ. А, 127: 33 (1990). Перекрёстная ссылка
2. М.Н. Белякова, Е.Е. Засимчук, Ю.В. Г. Гордиенко, Металлофиз. Новые технологии, 21, № 4: 59 (1999).
3. О. Э. Засимчук, В.И. Засимчук, Металлофиз. Новые технологии, 28, № 6: 803 (2006).
4. Лихачев В.А., Панин В.Е., Засимчук Е.Е. и др. Кооперативные деформационные процессы и локализация деформации. Киев: Наукова думка, 1989. С.
5. . 65 (на русском языке).
6. О. Э. Засымчук, В.И. Засымчук, Т.В. Турчак, Прог. физ. мет., 14, № 3: 275 (2013). Перекрёстная ссылка
7. Ю.В. Гордиенко и Е. Засимчук, Фил. Маг. А, 70, вып. 1: 99 (1994). Перекрёстная ссылка
8. Я. Френкель И. Введение в теорию металлов. Л.: Наука, 1972.
9. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1978.
10. Ансельм А.И. Введение в теорию полупроводников. М.: Наука, 1978.
11. Л. Д. Ландау, Е. М. Лифшиц, Теоретическая физика. Т. В. Статистическая физика. Ч. 1 [Теоретическая физика. Том. V. Статистическая физика. Пт. 1] (Москва: Наука, 1976).
12. Сена Л. А. Единицы физических величин и их размерностей (М.: Наука, 19).77) (на русском языке).
13. www.toehelp.ru/theory/sopromat/9.html
14. www.mehanika.ks.ua/index.php
15. Гаценко О.С., Засымчук О.Е., Теселько П.О., Стиренко С.Г., Сынов Ю.В. Г. Гордиенко, Металлофиз. Новые технологии, 36, № 9: 1207 (2014) (укр.). Перекрёстная ссылка
16. Ю.В. Полуэктов М., Физика низких температур, 34, № 4/5: 459 (2008) (на русском языке).
17. В.Х. Козловский, Изв. ВУЗов. Физика, 50, № 3: 16 (2007).

СОП по исследованиям стабильности готовых продуктов: Pharmaguideline

Стандартная операционная процедура анализа готовых продуктов для исследований стабильности в отделе фармацевтического контроля качества.

1.0 ЦЕЛЬ

Установить порядок сбора, хранения и анализа проб стабильности готовой продукции.

2.0 ОБЛАСТЬ ПРИМЕНЕНИЯ

Настоящая СОП должна применяться в отделе контроля качества

3.0 ОТВЕТСТВЕННОСТЬ

Супервайзер по контролю качества

4.0 ОТВЕТСТВЕННОСТЬ

Старший менеджер по обеспечению качества

5.0 ПРОЦЕДУРА

5.1 Ответственность за сбор, хранение и анализ образцов стабильности и рекомендации (если таковые имеются) должны выполняться в соответствии с блок-схемой.

5.2 Отбор проб

5.2.1 Отбор проб для каждого нового продукта должен проводиться для первых трех последовательных партий для исследования стабильности в условиях повышенной температуры и влажности.
5.2.2 Для всех продуктов, по крайней мере, одна партия в год должна проходить испытания на долгосрочную стабильность.
5.2.3 Инспектор по обеспечению качества должен собрать образец в соответствии с инструкциями менеджера по обеспечению качества в соответствии с графиком исследования стабильности

5.

3 Размер образца 5.3.1 Образцы должны быть собраны в виде неповрежденной товарной упаковки. Количество отобранных образцов должно быть достаточным в зависимости от продукта и результатов испытаний, указывающих на его стабильность.

5.4 Хранение пробы

5.4.1 Образцы должны храниться при контролируемой температуре (25 ± 2°C) и относительной влажности (60 ± 5%) для проведения испытаний на долговременную стабильность.
5.4.2 Образцы должны храниться при температуре (40 ± 2°C) и относительной влажности (75 ± 5%) для проведения ускоренных испытаний стабильности.
Связанный: Средняя кинетическая температура (MKT) в исследованиях стабильности

5.5 Параметры испытаний и периодичность анализа

5.5.1 Параметры испытаний для различных продуктов должны соответствовать программе стабильности.
5.5.2 Исходные данные анализа должны быть взяты из Сертификата анализа соответствующего продукта и серии, при условии, что Дата получения (До) образца для исследования стабильности находится в пределах периода одного месяца с даты выпуска серии. В случае, если период составляет более одного месяца, первоначальный анализ проводится еще раз в момент «Даты ввода».
5.5.3 Если метод анализа стабильности отличается от метода анализа высвобождения продукта, то первоначальный анализ должен быть выполнен в соответствии с методом анализа стабильности.
5.5.4 Дополнительные испытания, указывающие на стабильность (кроме спецификации выпуска продукта), если таковые имеются, в соответствии с программой стабильности, должны быть выполнены во время «даты ввода» (To).
5.5.5 Периодичность анализа образцов стабильности должна быть следующей:
a) Ускоренные условия испытаний на стабильность (45°C ±2°C/75%±5%) = 0,1,2,3 и 6 месяцев.
b) Условия испытаний на долговременную стабильность (25°C±2°C/60%±5%) = 0,3,6,9,12,18,24 36,48,60 месяцев.
c) Исследование долгосрочной стабильности должно проводиться до истечения срока годности продукта.
5.5.6 Анализ долгосрочной стабильности должен быть выполнен в течение ±7 рабочих дней от установленной даты. Образцы ускоренной стабильности должны быть проанализированы в течение ± 5 рабочих дней от установленной даты.
5.5.7 Образец для исследования стабильности должен быть взят в течение одного месяца с даты утверждения партии. Ежегодный график серий, подлежащих исследованию на стабильность, и дата анализа должны составляться каждый декабрь следующего года.
5.5.8 Запись в регистре остойчивости должна быть сделана соответствующим образом.
См. также: Руководство по исследованиям фармацевтической стабильности

5.6 Оценка данных о стабильности

5.6.1 Оценка данных о стабильности должна проводиться один раз в год. На основе оценки данных, рекомендации, если таковые имеются, должны быть сделаны старшим менеджером по обеспечению качества.
5.6.2 Во время тестирования стабильности любое неблагоприятное изменение физических параметров, pH, сбой в анализе, однородность содержимого, скорость растворения должны быть доведены до сведения старшего менеджера по обеспечению качества, GM-Technical Operation, GM-Technical Services и GM-R&D.