Статически неопределимые задачи кратко-Портал искусственного…
Брусья и шарнирно-стержневые системы, в которых внутренние усилия и реакции опор от заданной нагрузки можно определить с помощью лишь одних уравнений равновесия (уравнений статики), называются статически определимыми.
В отличие от них статически неопределимыми называются брусья и системы, внутренние усилия или реакции опор в которых нельзя определить с помощью одних лишь уравнений равновесия.Поэтому при их расчете необходимо составлять дополнительные уравнения –уравнения совместности деформаций или перемещений сечений, учитывающих характер деформации системы (геометрическая сторона задачи).Число дополнительных уравнений, необходимых для расчета системы, характеризует степень ее статической неопределимости.Всегда можно составить столько дополнительных уравнений, сколько не хватает уравнений статики для решения задачи.
Усилия в элементах статически определимых систем возникают только от действия внешней нагрузки (включая собственный вес конструкций).
Составление дополнительных (к уравнениям равновесия) уравнений перемещений (геометрическая сторона задачи) рассмотрим на примере.
Стержень защемлен по концам и нагружен силой F, действующей вдоль оси стержня (рис. 3.9). Собственный вес стержня не учитываем.
Под действием силы Fв этом случае в заделках могут возникать только показанные реакцииVAиVB, которые требуется определить. Направления неизвестных опорных реакций выбираем произвольно.
Для данного случая (когда все силы действуют вдоль одной прямой) можно составить только одно уравнение равновесия:
Для определения двух неизвестных VAиVBнеобходимо составить дополнительно одно уравнение, т.
Для составления дополнительного уравнения рассмотрим геометрическую сторону задачи – составим условие совместности деформаций отдельных участков: общая длина бруса не может изменяться, следовательно,
Удлинение можно выразить как сумму удлинений двух участков:
(3.18)
Рассмотрим физическую сторону задачии абсолютные удлинения участкови, используя закон Гука по формуле (3.13), выразим через продольные силы N1 иN2:
(3.19)
В этих формулах ипредставляют собой выражения продольных сил на участках 1 и 2, записываемые по методу сечений:
(3.20)
Подставим выражения (3.19) с учетом (3.20) в формулу (3.18) и получим:
(3.21)
Отсюда найдем
При условии получим:
(3.22)
Если то(3.23)
Если то(3.24)
Реакцию найдем из уравнения статики:
(3.25)
При равномерном изменении температуры окружающей среды вокруг бруса на tформулы (3. 19) запишутся в виде:
19) запишутся в виде:
где 1и2– коэффициенты линейного расширения материалов бруса.
Подставляя формулы (3.26) в формулу (3.18) и используя (3.20), найдем реакцию VBпри совместном воздействии на брус силыFи изменением температуры окружающей среды наtградусов.
ПРИМЕР 3.4
Требуетсяопределить реакции опор и построить эпюры продольных сил, нормальных напряжений и перемещений сечений для составного бруса ступенчатого сечения, изображенного на рис. 3.10а, при следующих исходных данных:
РЕШЕНИЕ
1. Найдем полное удлинение бруса при увеличении температуры наt = 30 Cи воздействии силыFпри отсутствии правой опоры
Имеющийся зазор между правой опорой и сечением В бруса меньше полученной величины полного удлинения т.е.
Таким образом, после закрытия зазора задача становится один раз статически неопределимой.
1. Статическая сторона задачи.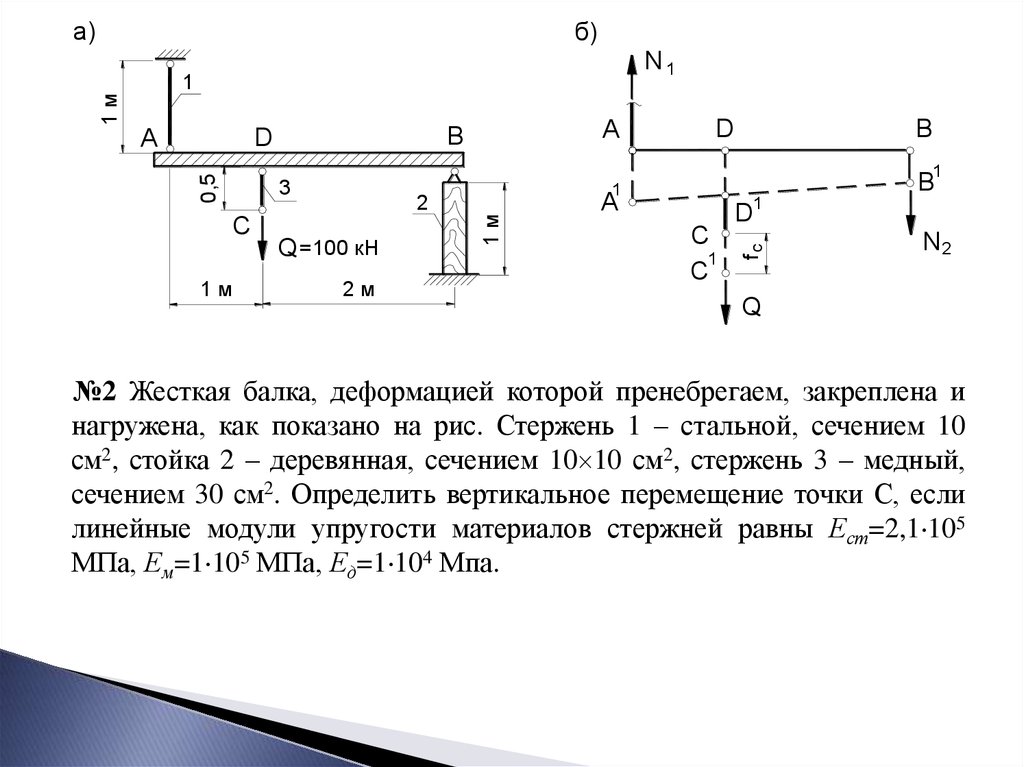
отсюда (3.27)
2. Геометрическая сторона задачи.
Полное удлинение всего бруса ограничено опорами и может равняться только монтажному зазору . Тогда перемещение сечения В будет равно:
(3.28)
3. Физическая сторона задачи.
Предварительно вычислим жесткости поперечных сечений на участках:
Удлинения участков от продольных сил и температуры запишутся:
(3.29)
Используя метод сечений, записываем:
(3.30)
После подстановки выражения (3.29) с учетом (3.30) в формулу (3.28), получим:
Отсюда
Из уравнения (3.27) найдем реакцию VA:
По формулам (3.30) определим значения продольных сил на участках:
По найденным значениям построим эпюру N (рис. 3.10в).
Определим нормальные напряжения на участках:
Определим перемещения сечений по формуле (3.16):
т.е. геометрическое условие (3.28) выполняется.
ПРИМЕР 3. 5
5
ДАНО: Абсолютно жесткий брус АВС, один конец которого опирается на шарнирно-неподвижную опору А, закреплен еще двумя стержнями 1 и 2 в точках В и С (рис. 3.11).
ТРЕБУЕТСЯ: 1. Определить усилия в стержнях 1 и 2 при заданной нагрузке и из условия прочности стержней определить площади их поперечных сечений А 1и А2при А1= 1,5А2иR= 200 МПа.
2. При полученных значениях площадей сечений определить величину допускаемой интенсивности равномерно распределенной нагрузки [q]прпо методу предельного равновесия и сравнить ее с заданной величиной q.
Предел текучести S= 240 МПа, коэффициент запаса прочностиn= 1,2.
РЕШЕНИЕ
Предварительно определим расстояние между точками А и С: =м.
Покажем на рисунке реакции опор: VA,HА,VDиHE. Продольные усилия в стержнях 1 и 2 – N1, N2– равны соответствующим реакциям опор, т.е. N1=VDиN2=HE.
1. Статическая сторона задачи.
Составим уравнение равновесия. Так как согласно условию задачи необходимо определить усилия в стержнях 1 и 2, напишем уравнение равновесия, в которое войдут только усилия N1и N2. Таким условием равновесия является
N16 +N24 –q63 = 0. (3.31)
2. Геометрическая сторона задачи.
Для получения недостающего уравнения дадим возможное перемещение системе и составим условие совместности деформациистержней 1 и 2. Брус АВС абсолютно жесткий (т.е. не деформируемый), поэтому при повороте бруса на некоторый уголточки прикрепления стержней В и С переместятся по дуге окружности на величинуuBиuCпропорционально радиусам поворота АВ и АС. В силу малости перемещений длины этих дуг можно считать равными перпендикулярам к радиусам АВ иАС.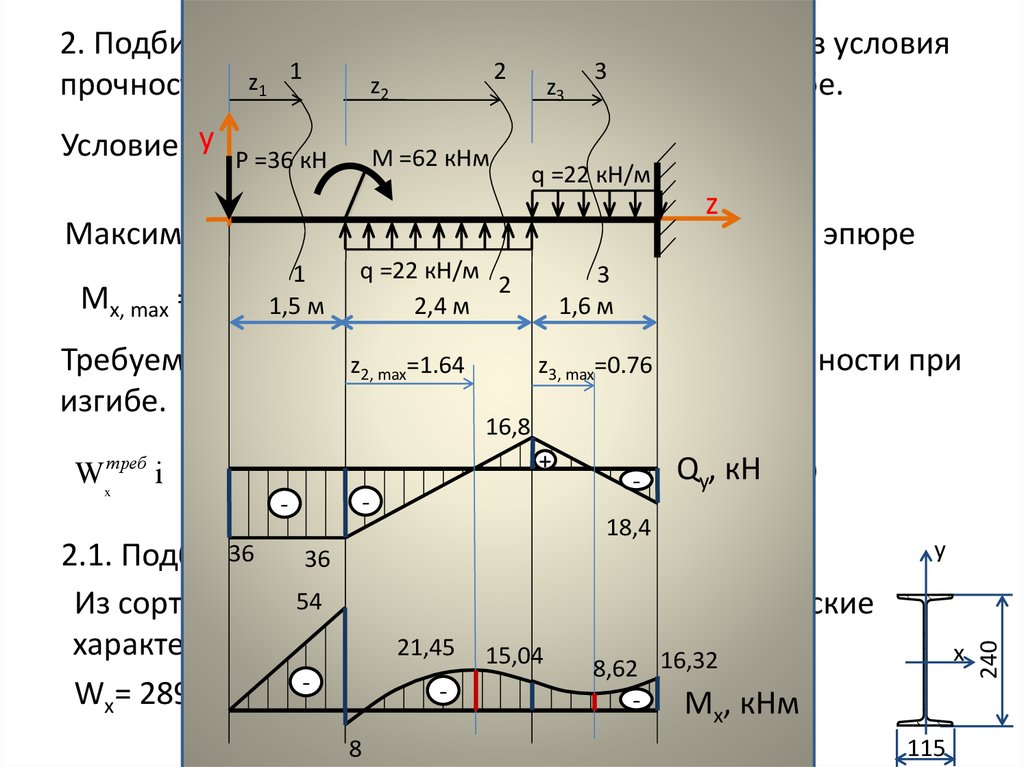
tg=или (3.32)
Равенство (3.32) представляет собой условие совместности перемещений точек крепления стержней 1 и 2 к абсолютно жесткому стержню.
Для получения абсолютных деформаций стержней ииз новых положений точек В1и С1опустим перпендикуляры на заданные первоначально направления стержней 1 и 2.
Из рис. 3.11а видно, что точки В1и В2совпали иа из рис. 3.11б следует, что удлинением стержня 2 является отрезок СС2, который представляет собой катет прямоугольного треугольника СС2С1. Из этого треугольника получаем:
. (3.33)
Равенства (3.33) подставим в уравнение (3.32) и получим уравнение совместности деформации стержней 1 и 2:
(3.34)
3. Физическая сторона задачи.
Удлинение стержней выражаем в соответствии с законом Гука через усилия в стержнях N1иN2:
(3. 35)
35)
Подставим выражения (3.35) в формулу (3.34) и получим:
4. Определение продольных усилий в стержнях 1 и 2.
Подставляя в эту формулу числовые значения и учитывая, что А1= 1,5А2, sin=получим
Отсюда N1= 1,799N2(3.36)
или N2= 0,556N1. (3.37)
Решая совместно уравнения (3.31) и (3.36), получаем:
при q = 20 кН/м,
N2 = 24,33 кН; N1 = 1,799 × 24,33 = 43,79 кН
5. Подбор сечений стержней 1 и 2:
Выразим напряжения в стержнях:
Так как из условия прочности в наиболее напряженном стержне определим требуемую площадь поперечного сечения:
Тогда А1= 1,5А2= 1,51,46 см2= 2,19 см2.
Определим напряжения в стержнях и проведем проверку прочности:
6. Определение допускаемой величины интенсивности нагрузки [q]пр по методу предельного равновесия.
Выше сечения стержней были подобраны из условия прочности по методу расчетных сопротивлений, т.е. когда
В расчете по методу предельного равновесия условие прочности ограничивает не напряжения, а допускаемую нагрузку, которая определяется как отношение предельной нагрузки к коэффициенту запаса:
В статически неопределимых системах при одинаковом коэффициенте запаса по напряжениям и нагрузкам, т.е. n=, этот метод может дать некоторую экономию материала стержней за счет более полного нагружения недонапряженных стержней.
При постепенном увеличении нагрузки напряжения в обоих стержнях будут возрастать до величины, равной пределу текучести сначала в более напряженном стержне 1, затем и в стержне 2, т.е. в предельном состоянии
Величина внешней нагрузки в этом случае и является предельной или разрушающей.
Тогда усилия в стержнях 1 и 2 будут равны:
Подставим эти усилия в уравнение равновесия (3.31) и найдем величину интенсивности разрушающей (предельной) нагрузки:
Коэффициент запаса n= 1,2.
Следовательно, величина допускаемой интенсивности распределенной нагрузки будет равна:
Сравним эту величину [q]предс величиной заданной нагрузки
Значит, при расчете по методу предельного равновесия нагрузка может быть увеличена на 5,5 %.
- В чем заключается суть метода сечений при определении внутренних усилий, в частности, при определении продольных сил?
- Приведите рабочее правило для определения продольных сил в поперечных сечениях стержней и правило знаков для них.
- Как определяется нормальное напряжение в поперечном сечении бруса при растяжении–сжатии?
- Что такое расчетное сопротивление материала?
- Как записываются условия прочности при растяжении-сжатии для пластичных и хрупких материалов?
- Как производится подбор требуемой площади поперечного сечения бруса из условия прочности?
- Как формулируется закон Гука? Как он записывается для случая растяжения–сжатия?
- Как определяется абсолютная деформация бруса при осевом растяжении–сжатии при наличии распределенной нагрузки на грузовом участке и при ее отсутствии?
- Какие системы называются статически неопределимыми? Каков порядок их решения?
- Назовите характеристики прочности материала.
 Как они определяются с помощью диаграммы растяжения для низкоуглеродистой стали?
Как они определяются с помощью диаграммы растяжения для низкоуглеродистой стали? - Назовите характеристики пластичности материала. Как они определяются?
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
3.12. Статически неопределимые задачи при осевом растяжении и сжатии
Статически неопределимыми называются задачи, которые нельзя решить с помощью только уравнений статики. Степень статической неопределимости таких задач определяется как разность между числом связей, наложенных на тело, и числом независимых уравнений равновесия, которые можно составить для рассматриваемого тела. Дополнительные уравнения можно составить, изучая деформации, которые испытывает тело. Оказывается, что всегда можно найти столько дополнительных уравнений, сколько нам нужно, чтобы полное число уравнений вместе с условиями равновесия равнялось числу неизвестных.
Эти
дополнительные уравнения составляют
на основе общего принципа, известного
как принцип
совместности деформаций. Всякая конструкция деформируется так,
что не происходит разрывов стержней,
отрывов стержней в узлах, не предусмотренных
схемой сооружения перемещений одной
части конструкции относительно другой.
В этом и заключается принцип совместности
деформаций элементов системы.
Всякая конструкция деформируется так,
что не происходит разрывов стержней,
отрывов стержней в узлах, не предусмотренных
схемой сооружения перемещений одной
части конструкции относительно другой.
В этом и заключается принцип совместности
деформаций элементов системы.
Общий метод расчета статически неопределимых систем состоит в следующем. Сначала следует выяснить, какие усилия необходимо определить; затем необходимо написать все возможные уравнения равновесия, затем определить степень статической неопределимости системы и составить столько дополнительных уравнений совместности деформаций, чтобы можно было найти все неизвестные усилия.
Рассмотрим несколько примеров расчета статически неопределимых систем.
Пример
3.7. Стержень, состоящий из верхней медной
части и нижней стальной (Рис.3.20,а),
нагружен силой
кН.
Оба конца стержня жестко защемлены.
Площадь его поперечного сечениясм2.
Определить напряжения на каждом участке
стержня. Модуль упругости стали
МПа.
Модуль упругости медиМПа.
Модуль упругости стали
МПа.
Модуль упругости медиМПа.
Рис.3.20
Решение:
1. Обрываем связи и заменяем действие связей реакциями (Рис.3.20,б). Составляем уравнение равновесия:
. (а)
2. Определяем степень статической неопределимости – вычитаем из числа связей (опорных реакций) число уравнений равновесия:
.
3.
Составляем одно дополнительное уравнение
совместности деформаций. Для этого
запишем уравнение для удлинения всего
стержня как сумму удлинений каждого из
участков. В качестве условия совместности
деформаций примем условие, что полное
удлинение стержня равно нулю, так как
оба конца стержня жестко защемлены.
. (б)
4. Подставляем в уравнение (б) численные значения длин участков и учитывая, что модуль упругости стали в два раза больше модуля упругости меди , получаем:
.
5. Подставляя реакции в уравнение (а), находим:
кН.
6. Вычисляем усилия на каждом участке стержня: кН;кН и строим диаграмму продольных усилий (Рис.3.20,в).
7. Определяем напряжения на каждом участке стержня:
МПа; МПа.
Пример 3.8. Жесткая балка поддерживается двумя стержнями (Рис.3.17,а). Площадь поперечного сечения первого стержня см2. Площадь поперечного сечения второго стержня см2. Материал стержней сталь с допускаемым напряжением МПа.Угол .Определить допускаемую величину силы , приложенной к балке.
Решение:
1.
Составляем расчетную схему. Для этого
обрываем связи и действие связей заменяем
реакциями. (Рис.3.17,б).
(Рис.3.17,б).
Рис.3.21
2. Составляем уравнения равновесия для балочно-стержневой системы:
; (а)
; (б)
. (в)
3. Определяем степень статической неопределимости задачи:
.
4.
Составляем уравнение совместности
деформаций. Для этого дадим балке
повернуться вокруг точки А. При этом
ось балки останется прямой, так как по
условию задачи балка является жесткой.
Узел В переместится в положение
,
при этом стержень №1 удлинится на
величину.
УзелDпереместится в
положение.
Перемещение узлаDв новое
положение обозначим буквой.
Это перемещение узла D можно представить
состоящим из двух движений: сначала
стержень №2 удлинится на величинуи узел D попадет в положение,
а затем повернется, чтобы попасть в
положение. Если этого не произойдет, нарушится
принцип совместности деформаций.
Если этого не произойдет, нарушится
принцип совместности деформаций.
Теперь составим соотношение между удлинениями стержней №1 и №2. Для этого сначала выразим перемещение узла D через удлинение стержня №2:
,
а затем подставим это перемещение в уравнение, полученное из подобия треугольников АВи AD. Учитывая, что В=, а D=, имеем:
. (г)
Уравнение (г) включает в себя удлинения стержней №1 и №2 и представляет собой уравнение совместности деформаций. Преобразуем это уравнение к виду, удобному для решения. Выразим удлинения стержней через усилия, действующие в них, учитывая, что ,,,:
,
откуда с учетом того, что , получаем:
. (д)
5. Выражаем усилия в стержнях через внешнюю
силу
.
Для этого подставляемв уравнение (в), получим:
Выражаем усилия в стержнях через внешнюю
силу
.
Для этого подставляемв уравнение (в), получим:
,
откуда
; .
6. Вычисляем напряжения в стержнях №1 и №2, выразив их через силу :
; .
7. Большее из напряжений приравниваем допускаемому напряжению , откуда находим допускаемое значения для силы:
,
откуда
кН.
Анализируя результаты решения задач, приведенные в примерах 3.7, 3.8, можно отметить некоторые особенности расчета статически неопределимых систем:
недостающие для определения усилий уравнения могут быть получены только при помощи изучения совместности деформаций данной системы;
распределение усилий между элементами статически неопределимой системы зависит от соотношения между площадями, модулями упругости и длинами этих элементов;
чем
более жестким является данный элемент,
тем большую долю усилия он принимает
на себя.