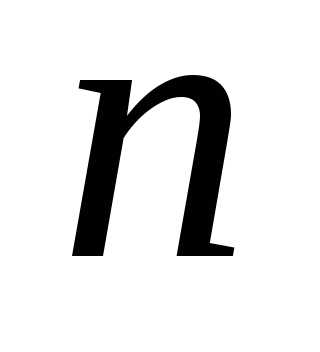Распределенная нагрузка
Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.
Размерность для линейной нагрузки — Н/м, для нагрузки распределенной по площади — Н/м2, для объемной (например при учете собственного веса элементов конструкции) — Н/м3.
Например, на рисунке 1.23, а приведена равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой
Q = q ∙ AB [Н],
приложенной в середине отрезка AB.
На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой
Q = qmax∙AB/2,
приложенной в точке C, причем AC = 2/3AB.
В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу
Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).
Рисунок 1.23
Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).
Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:
∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)
Рисунок 1.24
Проекция этой силы на ось Ox будет
∆Qx = q ∙ R ∙ ∆φ∙ cosφ. (1.15)
В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:
Qy = 0, т.е. Q = Qx, (1.16)
где АВ – хорда, стягивающая концы дуги.
Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м,2]. Если цилиндр рассечен по диаметру (рисунок 1.25), то равнодействующая этих сил равна F = q ∙ d ∙ h (d – внутренний диаметр) или
F = p ∙ 2R ∙ h.
Разрывающие баллон по диаметру усилия:
S1 = S2 = S;
2S = F;
S = p∙h∙R. (1.18)
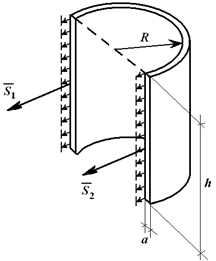
Рисунок 1.25
Если принять a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно
>> Уравнения равновесия системы сил
isopromat.ru
Распределенные нагрузки.
Теоретическая механика
Распределенные нагрузки
Как мы уже знаем, любая сила характеризуется тремя свойствами: модулем (скалярной размерностью), вектором (направлением в пространстве) и точкой приложения. Для того, чтобы иметь полное представление о характере и последствиях воздействия любой силы на тело или элемент конструкции, необходимо знать — какова величина этой силы, куда она направлена и к какой точке приложена.
В действительности сила не может быть приложена к точке, поскольку точка — безразмерная, бесконечно малая единица пространства, поэтому фактически силы воздействуют на очень малую площадку, размерами которой пренебрегают. Такие силы (приложенные к ничтожно малой площадке тела) называют сосредоточенными.
В реальности часто встречаются силы, приложенные не к точке, а к объему или поверхности тела, например сила тяжести, давления ветра, воды и т. п., т. е. нагрузку воспринимает не бесконечно малая площадка, а значительная площадь или объем тела. Такие силы называют распределенными.
Плоская система распределенных сил характеризуется ее интенсивностью, обычно обозначаемой латинской буквой q.
Интенсивность — это сила, приходящаяся на единицу длины (или площади) нагруженного участка.
Интенсивность в системе единиц СИ выражается в ньютонах на метр (Н/м) или, соответственно, в ньютонах на квадратный метр (для нагрузки, действующей на площадь).
Интенсивность воздействия силы на площадь характеризует такие физические понятия, как давление и напряжение. В плоской системе рассматривается интенсивность действия силы на единицу длины.
При решении задач статики распределенную нагрузку заменяют ее равнодействующей. Модуль равнодействующей равномерно распределенной нагрузки равен Q = ql (см. рисунок).
Равнодействующая равномерно распределенной нагрузки Q прикладывается в середине отрезка АВ.
Распределенная нагрузка, имеющая переменную интенсивность, называется неравномерно распределенной (рис. 2).
Примером такой нагрузки может служить меняющееся по высоте давление воды на плотину или снег, лежащий на крыше неровным слоем.
Определение точки С приложения равнодействующей неравномерно распределенной нагрузки производится путем геометрических расчетов и построений. Равнодействующая сила Q при таких нагрузках равна площади фигуры, охватываемой эпюрой нагрузки, а точка С приложения равнодействующей расположена в центре тяжести этой фигуры.
Нагрузки, распределенные по поверхности (по площади), характеризуются давлением, т. е. силой, приходящейся на единицу площади. В системе единиц СИ давление измеряется в Паскалях (Па) или ньютонах на квадратный метр (Н/м2).
***
Пример решения задачи с распределенной нагрузкой
Задача: Балка находится в равновесии под действием сосредоточенной силы F = 100 Н и равномерно распределенной нагрузки q = 60 Н/м (см. схему 3).
Необходимо определить реакцию RВ опоры В.
Решение.
Поскольку по условию задачи необходимо определить реакцию опоры В, составим уравнение моментов сил относительно опоры А, учитывая, что равномерно распределенную нагрузку можно заменить сосредоточенной силой:
Q = ql, где l = (10 — 5) метров — часть балки, к которой приложена распределенная нагрузка.
Точка приложения сосредоточенной силы Q расположена в середине той части балки, к которой приложена распределенная нагрузка; плечо этой силы относительно опоры А будет равно: h = (10 — 5)/2 = 2,5
Cоставляем уравнение моментов сил относительно опоры А из условия, что балка находится в состоянии равновесия (уравнение равновесия).
Учитываем знаки:
- сила RВ создает относительно точки А положительный момент, плечо которого равно 10м;
- сила F создает относительно точки А отрицательный момент, плечо которого равно 5 м;
- распределенная нагрузка q создает (посредством силы Q и плеча h) относительно точки А отрицательный момент.
Получаем уравнение равновесия балки, в котором лишь одна неизвестная величина (RВ):
ΣM = 10RВ — qlh — 5F = 10RВ — q(10-5)(10-5)/2 — 5F = 0, откуда находим искомую реакцию опоры RВ:
RВ = {q(10-5)(10-5)/2 + 5F}/10 = 125 Н
Задача решена.
***
Условия равновесия плоской системы сходящихся сил k-a-t.ru
Момент распределенной нагрузки
Вопрос: Как определить момент в точке балки, возникающий от распределенной нагрузки?
Ответ: При расчетах балок, в сопромате часто возникает задача определить изгибающий момент в сечениях балки вызванный действием равномерно распределенной нагрузки q.
В этом случае, как правило, удобнее пользоваться понятием равнодействующей силы Rq, которой можно заменить распределенную нагрузку.
Рассмотрим пример нахождения момента в произвольной точке C от равномерно распределенной между точками A и B нагрузки интенсивностью q.
Для определения момента нагрузки необходимо знать ее длину a и расстояние z от любого ее края до рассматриваемой точки.
Заменим распределенную нагрузку ее равнодействующей
Rq=qa
Как известно момент силы определяется произведением силы на плечо
M=Fl
В данном случае силой в вышеуказанном выражении является равнодействующая Rq.
Плечом этой силы является расстояние от точки C до равнодействующей нагрузки
l=a/2+z
Таким образом, момент нагрузки равен произведению интенсивности q нагрузки на ее длину a и на расстояние от ее середины до рассматриваемой точки a/2+z
MС=Rql=qa(a/2+z)
Для случая, когда точка лежит в пределах действия нагрузки, аналогично:
MС= Rql=qa(a/2-z)
Примечания:
- В случае действия неравномерно распределенной нагрузки ее интенсивность задается функцией.
- Для нагрузки, распределенной по площади (объему) при вычислении равнодействующей вместо длины надо подставлять площадь (объем) ее действия.
- Момент части распределенной нагрузки определяется аналогично.
Примеры решения задач >
Краткая теория >
isopromat.ru
Построение эпюры внутренних сил для стержня с продольно распределенной нагрузкой
Задача
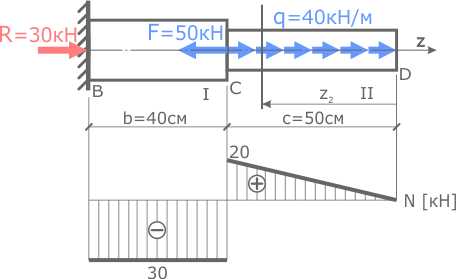
Рассчитать значения внутренних продольных сил N и построить их эпюру для стержня к которому приложены сосредоточенная сила и продольная равномерно распределенная нагрузка
для дальнейшего расчета на прочность.
Пример решения
Предыдущий пункт решения задачи:
Рассматриваемый стержень имеет два силовых участка, обозначим их цифрами I и II.
Для расчета внутренних сил на них воспользуемся методом сечений.
Начнем с первого силового участка BC.
Мысленно рассекаем участок в произвольном месте между сечениями B и C.
Выбираем для рассмотрения левую часть стержня, так как к ней приложено меньшее количество нагрузок.
Внутренняя сила на I силовом участке равна сумме внешних сил (с учетом правила знаков при растяжении-сжатии) приложенных к рассматриваемой отсеченной части стержня:
Так как на данном участке нет распределенной нагрузки, полученное значение NI будет одинаковым для всех сечений первого участка.
Переходим на второй силовой участок CD.
Проведя сечение,
рассматриваем правую часть стержня.
На данном участке есть распределенная нагрузка поэтому необходимо показать расстояние от границы участка до рассматриваемого сечения обозначив его переменной z2.
Интервал возможных значений переменной z2 лежит в пределах от 0 до 50см, т.е. 0 ≤ z2 ≤ 0,5м.
Выражение для расчета NII
В полученном выражении переменная z2 в первой степени, следовательно, зависимость линейная.
Рассчитаем значения внутренней силы NII на границах участка при z2=0 и z2=0,5м.
По полученным данным строим эпюру N.
На I участке в соответствии с выбранным масштабом откладываем вниз от базовой линии значение 30 кН и проводим горизонтальную линию в пределах участка.
На II участке было получено 2 значения. Переменная z2 откладывалась от правой границы участка (сечения D) поэтому под сечением D где z2=0 ставим точку на базовой линии.
Под сечением C где z2=0,5м откладываем значение 20кН.
Полученные точки соединяем прямой линией, проставляем знаки, заштриховываем и проверяем построенную эпюру.
Другие примеры решения задач >
isopromat.ru
1.6. Распределённая нагрузка
Поверхностные и объёмные силы
представляют собой нагрузку, распределённую
по некоторой поверхности или объёму.
Такая нагрузка задаётся интенсивностью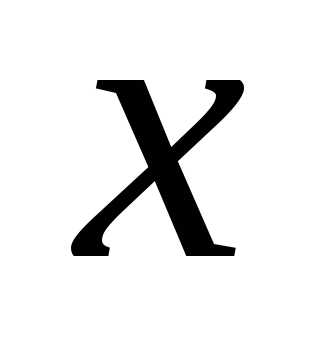 
,
которая представляет собой силу,
приходящуюся на единицу некоторого
объёма, или некоторой площади, или
некоторой длины.
Особое место при решении ряда
практически интересных задач занимает
случай плоской распределённой нагрузки,
приложенной по нормали к некоторой
балке. Если вдоль балки направить ось 
,
то интенсивность будет функцией
координаты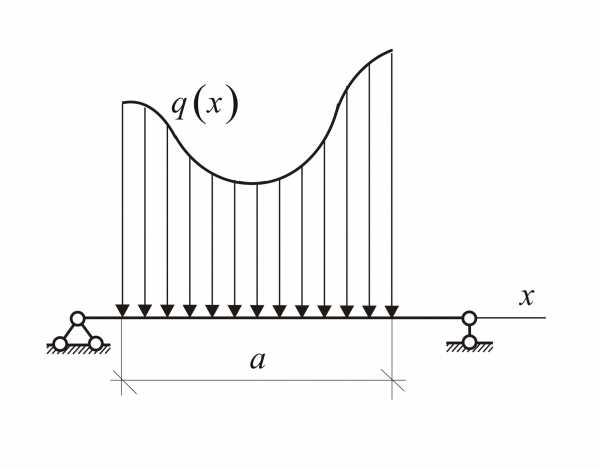 
и измеряется в Н/м. Интенсивность
представляет собой силу, приходящуюся
на единицу длины.
Плоская фигура, ограниченная балкой и графиком интенсивности нагрузки, называется эпюрой распределённой нагрузки (Рис. 1.28). Если по характеру решаемой задачи можно не учитывать деформации, т.е. можно считать тело абсолютно твёрдым, то распределённую нагрузку можно (и нужно) заменить равнодействующей.
|
| |
Рис. 1.28 | Рис. 1.29 | |
Разобьём балку на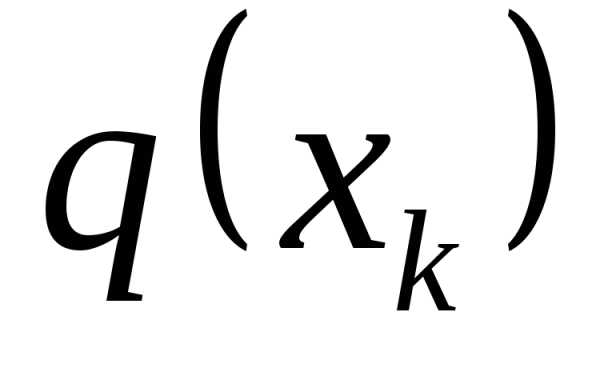 
отрезков длиной
,
на каждом из которых будем считать
интенсивность постоянной и равной 
,
где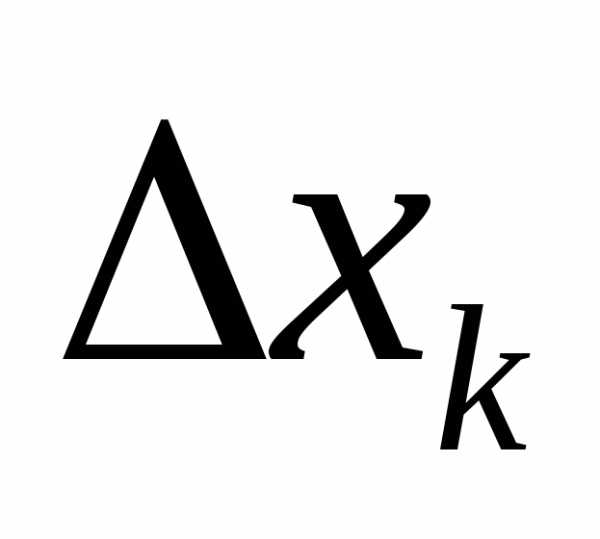 
–координата отрезка 
.
При этом кривая интенсивности заменяется
ломаной линией, а нагрузка, приходящаяся
на отрезок 
,
заменяется сосредоточенной силой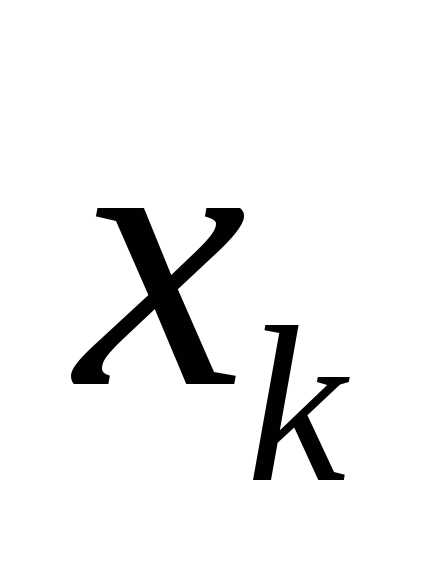 
,
приложенной в точке 
(Рис. 1.29). Полученная система параллельных
сил имеет равнодействующую, равную
сумме сил, действующих на каждый из
отрезков, приложенную в центре
параллельных сил.
Понятно, что такое представление
тем точнее описывает реальную ситуацию,
чем меньше отрезок 
,
т.е. чем больше число отрезков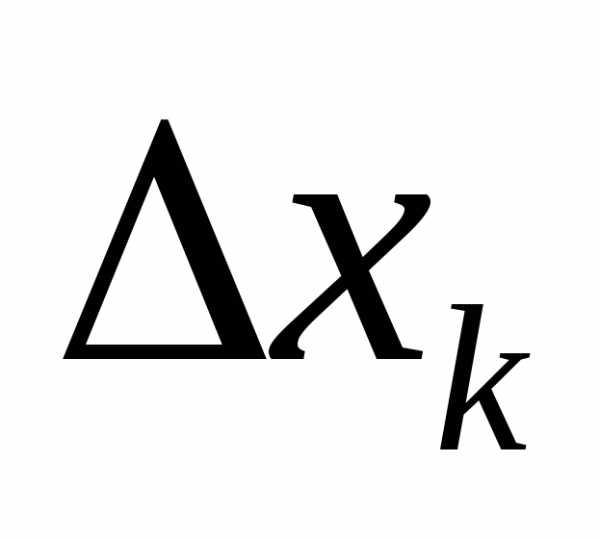 
.
Точный результат получаем, переходя к
пределу при длине отрезка 
,
стремящейся к нулю. Предел, получаемый
в результате описанной процедуры,
представляет собой интеграл. Таким
образом, для модуля равнодействующей
получаем:
Для определения координаты точки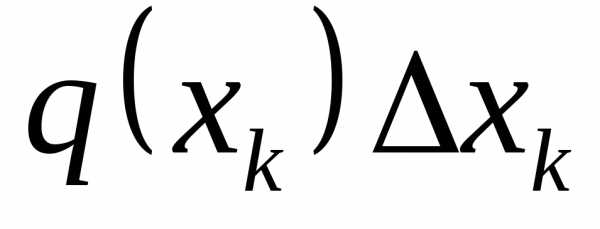 
приложения равнодействующей используем
теорему Вариньона:
если система сил имеет равнодействующую, то момент равнодействующей относительно любого центра (любой оси) равен сумме моментов всех сил системы относительно этого центра (этой оси)
Записывая эту теорему для системы сил 
в проекциях на ось 
и переходя к пределу при длине отрезков,
стремящейся к нулю, получаем:
Очевидно, модуль равнодействующей численно равен площади эпюры распределённой нагрузки, а точка её приложения совпадает с центром тяжести однородной пластины, имеющей форму эпюры распределённой нагрузки.
Отметим два часто встречающихся случая.
Равномерно распределённая нагрузка,(Рис. 1.30). Модуль равнодействующей и координата её точки приложения определяются по формулам:
В инженерной практике такая нагрузка встречается довольно часто. Равномерно распределённой в большинстве случаев можно считать весовую и ветровую нагрузку.
|
| |
Рис. 1.30 | Рис. 1.31 |
Линейно
распределённая нагрузка,
(Рис. 1.31). В этом случае:
В
частности, давление воды на вертикальную
стенку прямо пропорционально глубине 
.
Пример 1.5
Определить реакции опор 
и
балки, находящейся под действием двух
сосредоточенных сил и равномерно
распределённой нагрузки. Дано:
|
Рис. 1.32 |
Найдём равнодействующую распределённой нагрузки. Модуль равнодействующей равен
плечо силы 
относительно точки
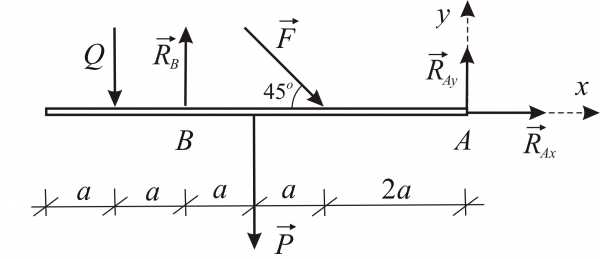равноРассмотрим равновесие балки. Силовая
схема представлена на Рис. 1.33.
|
Рис. 1.33 |
Условия равновесия в рассматриваемом случае имеют вид:
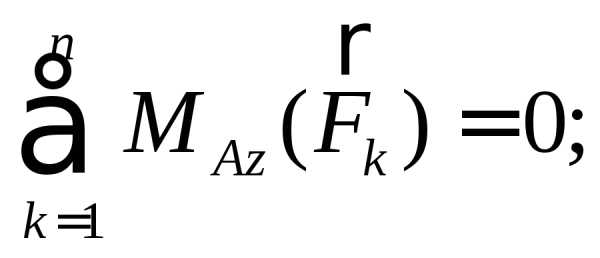
Пример 1.6
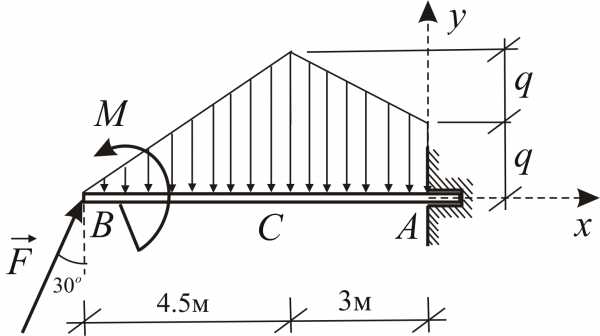
Определить реакцию заделки консольной балки, находящейся под действием сосредоточенной силы, пары сил и распределённой нагрузки (Рис. 1.34).
Дано:
Заменим распределённую нагрузку тремя сосредоточенными силами. Для этого разобъём эпюру распределённой нагрузки на два треугольника и прямоугольник. Находим
Силовая схема представлена на Рис. 1.35.
|
| |
Рис. 1.34 | Рис. 1.35 |
Вычислим
плечи равнодействующих относительно
оси 
Условия равновесия в рассматриваемом случае имеют вид:
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
1. Что называется интенсивностью распределённой нагрузки?
2. Как вычислить модуль равнодействующей распределённой нагрузки?
3. Как вычислить координату точки приложения равнодействующей распределённой
нагрузки?
4. Чему равен модуль и какова координата точки приложения равномерно распределённой нагрузки?
5. Чему равен модуль и какова координата точки приложения линейно распределённой нагрузки?
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 4.28; 4.29; 4.30; 4.33; 4.34.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА — теория и практика»: комплекты СР-2; СР-3.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ № 4-5
studfiles.net
Внешние силы
Все внешние силы (нагрузки), действующие на изучаемое тело, следует рассматривать как проявление взаимодействия его с окружающими телами, которое представляется в виде сил или пар сил (моментов).
Все внешние силы (нагрузки) могут рассматриваться как сосредоточенные или распределённые.
В природе сосредоточенных сил не бывает. Все реальные тела практически контактируют через небольшие площадки. Однако принцип Сен-Венана позволяет распределенную нагрузку заменить равнодействующей силой, что упрощает расчёт.
Сосредоточенные нагрузки выражаются в ньютонах [H] и обозначается буквой F.
Распределённые нагрузки обозначаются буквой q и они бывают:
- поверхностными (например, давление ветра, воды на стенку). Размерность [FL-2].
- объёмными. Их размерность [FL-3].
- распределенными по длине (например, силу тяжести стержня, учитывая небольшие размеры его поперечного сечения, рассматривают как распределённую нагрузку по длине). Размерность [FL-1].
Сосредоточенные и распределённые нагрузки могут быть как статическими, так и динамическими.
Статическими называются нагрузки, которые изменяют свою величину или точку приложения с очень небольшой скоростью, так что возникающими при этом ускорениями можно пренебречь.
Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью. Возникшие при этом силы инерции могут многократно превосходить те же нагрузки, приложенные статически.
Законы изменения нагрузок во времени могут иметь весьма сложный характер.
В сопротивлении материалов основным изучаемым элементом конструкции является брус – тело, у которого один из линейных размеров (длина) значительно превышает два других, определяющих поперечное сечение. При работе конструкции ее элементы воспринимают внешние силы и действие их передают друг другу.
Классификация внешних нагрузок
Внешние силы делятся на активные и реактивные (реакции связей). Активные связи принято называть нагрузками.
По способу приложения нагрузки бывают объемные и поверхностные, распределенные и сосредоточенные, по характеру изменения в процессе приложения – статические, динамические и повторно-переменные, по продолжительности действия – постоянные и временные.
Примеры решения задач >
Внутренние силовые факторы >
isopromat.ru
Нагрузки и воздействия
6. Сосредоточенная сила
Concentrated load
Равнодействующая поверхностных сил, распределенных по поверхности, размеры которой малы по сравнению с расстоянием до точки, в которой определяются компоненты напряженного и деформированного состояния.
7. Сплошная нагрузка
Distributed load. Continuous load
Нагрузка, точки приложения которой непрерывно заполняют данный отрезок или данную площадку.
8. Интенсивность нагрузки
Intensity of distributed load. Intensity of load
Предел отношения величины равнодействующей нагрузки, непрерывно распределенной по данной поверхности (или линии) к величине площади (или длине линии), если последняя стремится к нулю.
9. Равномерно распределенная нагрузка
Continuous load
Распределенная нагрузка постоянной интенсивности на единицу длины (площади поверхности).
10. Постоянная нагрузка
Dead load. Fixed load. Permanent load
Нагрузка, которая при расчете данной системы принимается действующей неизменно по величине и направлению.
11. Временная нагрузка
Live load. Varying load
Нагрузка, которая при расчете данного элемента системы может считаться действующей или отсутствующей в зависимости от ее значения для рассчитываемого элемента.
12. Подвижная нагрузка
Moving load. Travelling load. Rolling load. Live load
Нагрузка, которая может занимать различное положение на системе (например, вес поезда, автомобиля, трактора, мостового крана, скопления людей).
13. Статическая нагрузка
Statical load. Static load
Нагрузка, положение, направление и интенсивность которой принимаются при расчете не зависящими от
времени или изменяющимися столь медленно, что вызываемые ею силы инерции могут не вводиться в расчет.
14. Динамическая нагрузка
Dynamic load
Нагрузка, изменение величины, направления или положения которой происходит настолько быстро, что при расчете сооружения необходимо учитывать инерционные силы.
15. Повторно переменная нагрузка
Repeated-fluctuating load
Нагрузка, многократно изменяющая со временем значение или значение и направление.
16. Невыгоднейшее расчетное сочетание нагрузок
Unfavourable (position of) load
Совокупность постоянных и временных нагрузок, соответствующая максимальному положительному или наибольшему по абсолютной величине отрицательному значению вычисляемой величины (параметра).
17. Следящая нагрузка
Follower load
Нагрузка, направление которой зависит от деформации нагружаемой системы.
18. Несущая способность сооружения
Ultimate load carrying capacity. Holding power
Характеристика сооружения, которая выражается величиной нагрузки, отвечающей предельному состоянию сооружения по прочности.
19. Критическая нагрузка
Critical load
Наименьшая нагрузка, при которой происходит потеря устойчивости системы.
20. Критический параметр нагрузки
Critical load parameter
Значение параметра, характеризующего нагрузку, при которой происходит потеря устойчивости системы.
isopromat.ru