5. Определение перемещений пространственных систем
В пространственных стержневых системах в общем случае могут возникать шесть внутренних усилий. Поэтому формула вычисления перемещений содержит шесть компонент:
,
где индексом P обозначены усилия грузового состояния: – два изгибающих и крутящий моменты,– две поперечные и продольная силы; надчеркиванием обозначены соответствующие усилия единичного состояния;– моменты инерции относительно осейy, z и полярный момент инерции; – коэффициенты формы сечения.
Определение перемещений по этой формуле проводится как и при определении перемещений плоских стержневых систем. В пространственных рамах влиянием продольных и поперечных сил обычно пренебрегают и учитывают только первые три члена этой формулы, а в фермах учитывается только последний член.
6. Расчет пространственных рам методом сил
Степень статической неопределимости пространственной рамы определяется по формуле
,
где – число замкнутых контуров,– число удаленных связей.
Для ферм используется другая формула:
,
где – число стержней,– число опорных связей,– число узлов.
Основная система и канонические уравнения метода сил имеют тот же смысл и вид, как и для плоских рам. Но входящие в них коэффициенты определяются с учетом изгибающих моментов в двух плоскостях и крутящего момента в каждом элементе рамы.
Построение промежуточных и окончательных эпюр внутренних усилий и их проверка такие же, как и при расчете плоских рам.
В о п р о с ы
1. Какие внутренние усилия возникают в пространственных стержневых системах?
2. Чем отличается кинематический анализ пространственных систем от кинематического анализа плоских систем?
3. Какие методы используются при расчете пространственных ферм?
4. Какие особенности имеет определение перемещений и расчет методом сил пространственных систем по сравнению с плоскими?
Л е к ц и я 10 расчет статически неопределимых систем методом перемещений
Как уже знаем, при расчете статически неопределимых систем методом сил исключаются лишние связи, а за неизвестные принимаются силы (усилия) в этих связях. После их вычисления из канонических уравнений можно определять все остальные усилия, а также перемещения, напряжения и деформации системы.
Напряженно-деформированное состояние (НДС) статически неопределимых систем можно устанавливать и по-другому. В этом случае связи не исключаются, а делается наоборот – в систему вводятся дополнительные связи. Тогда за неизвестные принимаются перемещения во введенных связях, которые определяются из канонических уравнений. Поэтому этот метод называется методом перемещений
1. Неизвестные метода перемещений
Установим минимальное число узловых перемещений, необходимых для определения напряженно-деформированного состояния статически неопределимой стержневой системы.
С этой целью определим простейшие деформации некоторого стержня АВ стержневой системы, которые он получает при переходе в новое положение под воздействием внешней нагрузки (рис. (10.1 а). Данная задача упрощается, если стержень закрепить по обоим концам и, задавая его концам некоторые независимые перемещения, привести стержень к окончательному деформированному состоянию.

Рис. 10.1
Как следует из рисунков, для этого концам закрепленного стержня АВ необходимо последовательно задавать поступательные (линейные) перемещения и(рис. 10.1 б, в), угловые перемещенияи(рис. 10.1 г, д), а внутри стержня приложить внешнюю нагрузку (рис. 10.1 е).
При этом от поступательного перемещения всего стержня внутренние усилия и деформации не возникают (на рис. 10.1 б). Внутренние усилия и деформации от местной нагрузки, действующей в пределах закрепленного стержняАВ, можно найти отдельно. Значит, для определения НДС всего стержня достаточно знать три неизвестных перемещения – два угловых перемещения его концов ,и одно поступательное перемещение – взаимное смещение концов стержня. Поэтому степень кинематической неопределимости такого стержня равняется трем.
studfiles.net
Определение перемещений в раме с шарниром
Для рамы требуется определить угол поворота сечения 1 и горизонтальное перемещение сечения 2.
Дано: L=8 м, F=2 кН, q=1 кН/м, h=6 м, моменты инерции I1=I, I2=2I

1. Определяем опорные реакции и строим грузовую эпюру:
а) Определяем опорные реакции:
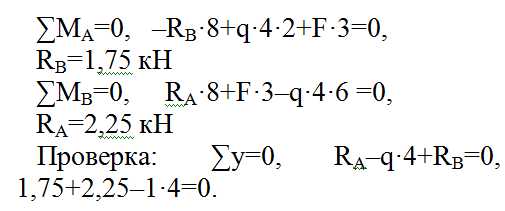
Проверка сошлась. Вертикальные реакции определены верно. Для определения горизонтальных реакций нужно использовать свойство шарнира, а именно — записать уравнение моментов относительно шарнира от всех сил, расположенных с одной стороны рамы.
Проверка сошлась, значит, горизонтальные реакции определены верно.
б) Строим грузовую эпюру — эпюру от заданной нагрузки. Грузовую эпюру будем строить на растянутых волокнах.
Разбиваем раму на участки. На каждом участке намечаем сечения в начале и конце участка, а на участках с распределенной нагрузкой дополнительное сечение в середине.
В каждом сечении определяем значение внутреннего изгибающего момента по правилу: изгибающий момент равен алгебраической сумме моментов всех внешних сил, расположенных с одной стороны от сечения, относительно центра этого сечения. Правило знаков для изгибающего момента: момент считается положительным, если он растягивает нижние волокна.Строим грузовую эпюру.
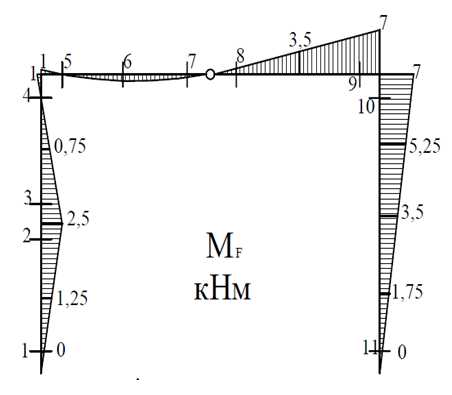
2.Определяем угол поворота сечения (1)
а) Для того, чтобы определить угол поворота указанного сечения, нужно зарисовать исходную раму без внешней нагрузки и к заданному сечению приложить единичный момент.
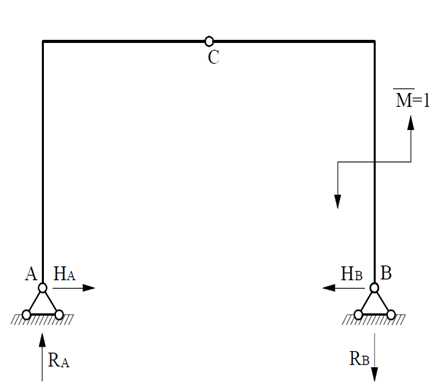
Сначала определяем реакции:
Строим единичную эпюру моментов.
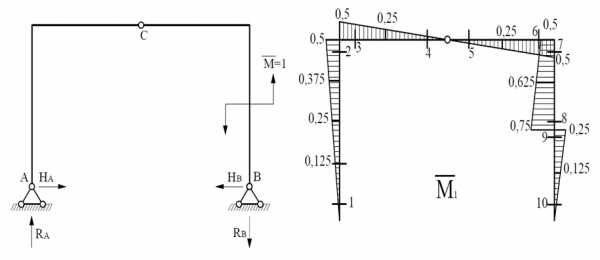

б) Определяем угол поворота по формуле Симпсона, подставив I1=I, I2=2I:
Знак « — » означает, что поворот сечения происходит против направления единичного момента, т.е. по часовой стрелке.
3. Определяем горизонтальное перемещение сечения (2).
а) Для того, чтобы определить горизонтальное перемещение в указанном сечении, нужно зарисовать исходную раму без внешней нагрузки и к заданному сечению приложить в горизонтальном направлении единичную силу.

Определяем реакции:
Строим единичную эпюру моментов
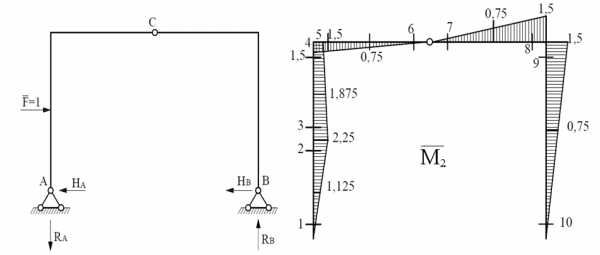
б) Определяем горизонтальное перемещение сечения (2) по формуле Симпсона:
Результат получился с «+», значит точка (2) перемещается по направлению единичной силы, т.е. вправо.
prosopromat.ru
РАСЧЕТ ПРОСТРАНСТВЕННОЙ РАМЫ — Энциклопедия по машиностроению XXL
Практически в большинстве случаев пространственной задачи используются или только три первых члена последней формулы (когда элементы системы работают преимущественно на изгиб и кручение, например при расчете пространственных рам и ломаных балок), или только четвертый член формулы (например, при расчете пространственных ферм). [c.439]Г о р б у н о в Б. Н., Расчет пространственных рам из тонкостенных стержней, Прикладная математика и механика , вып. 1, 1943. [c.188]
Г. К. Клейн, Применение способа распределения моментов к расчету пространственных рам, Вестник инженеров и техников , № 8, 1937.
Расчет рамных конструкций. Стержни пространственной рамы работают на изгиб, кручение, растяжение и сжатие стержни плоских рам при нагружении в плоскости работают на изгиб и осевую силу. Плоские рамы рассчитываются методами строительной механики [11], расчет пространственных рам лучше выполнять численными методами на ЭВМ (например, методом конечного элемента с использованием известных программ). [c.416]
РАСЧЕТ ПРОСТРАНСТВЕННОЙ РАМЫ. [c.43]
Расчет пространственных рам из тонкостенных стержней впервые в 1943 г. предложил Б. Н. Горбунов, опубликовав в Прикладной математике и механике соответствующую статью. [c.9]
Это обстоятельство существенно упрощает расчет плоских рам, нагруженных пространственной нагрузкой. Любую нагрузку можно разложить на составляющие в плоскости рамы и перпендикулярные к ней. Используя принцип независимости действия сил, можно рассчитать систему отдельно от нагрузок в плоскости рамы и от перпендикулярных к ней. [c.429]
В пособии изложены методы решения задач прикладной теории упругости, приведены расчеты плоской гибкой нити, сплошного стержня, тонкостенного стержня открытого профиля, тонких пластинок и оболочек, толстых плит, призматических пространственных рам, массивных тел и непрерывных сред. Каждая глава содержит общие положения, принятые рабочие гипотезы, расчетные уравнения на прочность, устойчивость и ко- [c.351]
Расчету призматических пространственных рам по методу [c.7]
РАСЧЕТ ПРИЗМАТИЧЕСКИХ ПРОСТРАНСТВЕННЫХ РАМ (МЕТОД В. 3. ВЛАСОВА) [c.330]
Теория расчета плоских рамных систем представляет частный случай теории расчета призматических пространственных рам, а [c.334]
Некоторые результаты расчета при 6 = 3 м приведены на рис. 125 а —эпюра поперечных изгибающих моментов в плоской раме б — эпюра поперечных изгибающих моментов для среднего поперечного сечения пространственной рамы при х= 0 м в —эпюра продольных нормальных напряжений для среднего поперечного сечения пространственной рамы. Штриховой линией на рис. 125, а и б показаны кривые эпюры от местной нагрузки.
Это обстоятельство существенно упрощает расчет плоских рам, нагруженных пространственной нагрузкой. Любую нагрузку можно разложить на составляющие в плоскости рамы и перпендикулярные к ней. Используя принцип независимости действия сил, можно рас- [c.455]
Расчету призматических пространственных рам по методу В. 3. Власова посвящена восьмая глава. [c.4]
Теория расчета плоских рамных систем представляет частный случай теории расчета призматических пространственных рам, а канонические уравнения метода перемещений являются частным случаем дифференциальных уравнений (8.9) [см. подчеркнутые члены второго уравнения (8.9)]. [c.243]
Строительная механика является теорией расчета на прочность, жесткость и устойчивость стержневых систем—плоских и пространственных ферм, балочных систем, арок, плоских и пространственных рам, подпорных стенок и т. д. В строительной механике используются все предпосылки сопротивления материалов, касающиеся свойств материалов, а также гипотезы сопротивления материалов. [c.4]
Белоус А. А. Колебания и статическая устойчивость рам. — В кн. Расчет пространственных конструкций. М. Изд-во литературы по строительству, 1965, вып. 3. [c.161]
Для расчета плоских и пространственных рам могут использоваться прямолинейные конечные элементы постоянного сечения, описываемые технической теорией бруса расчет жесткостных характеристик элементов этого типа рассмотрен в гл. 3 ( 3.4, 3.5). В общем случае пространственного нагружения элемент имеет 12 степеней свободы — три перемещения и три угла поворота в каждом из двух узлов i, / (см. рис. 3.8). Так же как и в случае статического нагружения, отнесем элемент к местной системе координат, направив ось х вдоль оси бруса, а оси у, z — по направлению главных осей инерции поперечного сечения. Будем снова разбивать узловые перемещения на четыре группы, образуя из них матрицы v , Vj,, Vg, v . Матрица [c.351]
Для плоско-пространственных рам, изображенных на соответствующих рисунках, определить внутренние силовые факторы в сечениях А. В расчетах принять поперечные сечения рам — круг диаметра d G = 0,4 J. [c.279]
Для изображенных на соответствующих рисунках пространственных рам определить вертикальное перемещение 5л сечения А или угол поворота 0 сечения В относительно оси Ох местной системы координат. В расчетах принять G = = 0,4Е, P = ql, М = ql . [c.294]
Так же, как и для плоских, для пространственных рам обычно напряжения и деформации, связанные с действием продольных и перерезывающих сил, малы по сравнению с напряжениями и деформациями от изгиба и кручения. Поэтому в расчете на прочность и при вычислении перемещений учитываются только последние. Исключение составляют лишь те специальные случаи, когда изгиб и кручение рамы происходят лишь вследствие деформаций растяжения-сжатия ее элементов. [c.276]
При расчете на прочность пространственных рам необходимо учитывать, что в их сечениях одновременно действуют нормальные и касательные напряжения. Эта проблема уже возникла ранее в примерах 9.3 и 9.4. Способы ее решения будут рассмотрены в гл. 11. [c.276]
В.9.12. Какие деформации преимущественно учитывают при расчете перемещений пространственных рам В какой форме записывается при этом интеграл Мора [c.287]
Для некоторых порталов (см. рис. III,3.2, а, в) предложены более простые методики расчета разложением на плоские рамы [0.21, 0.40, 0.58, 3], позволяющие довольно точно определить внутренние силовые факторы в плоскостях вертикальных рам. Для силового расчета и определения перемещений порталов можно применять универсальные программы расчета пространственных конструкций на ЭВМ. [c.469]
Белоус А. А., Колебания и статическая устойчивость плоских и пространственных рам, сборник Расчет пространственных конструкций , вып. 3, Стройиздат, 1955. [c.935]
А. А. Белоус [1.51 (1955) применил метод начальных параметров и метод деформаций к расчету колебаний балок плоских и пространственных рам в уточненной постановке, исходя из теории балки Тимошенко. Для п-оп собственной частоты шарнирно опертой балки получена формула [c.82]
При определении суммарных перемещений узлов ферм (8.10.7) часто учитывают лишь первый иктехрал, так как эти перемещения зависят в основном от растяжения (сжатия) стержней фермы. В расчетах пространственных рам основными являются второй, третий и четвертый интегралы, так как в этом случае преобладают перемещения, обусловленные кручением и изгибом. [c.78]
Ш. М. Гофман, Расчет плоских и пространственных рам способом группового последовачельного уравновешивания, Труды института сооружений АН Узб. ССР, выпуск 1, 1950. [c.225]
Расчеты свободных н вынужденных местных колебаний судовых конструкций выполняют с использованием схем однопролетных и неразрезных балок, плоских и пространственных рам, изогропных и ортотропных пластин, цилиндрических подкрепленных оболочек, ортогональных балочных решеток — перекрытий и некоторых других. Большинство из этих схем обычны для задач динамики сооружений, и соответствующие методы расчета приведены в работах [7, И, 16]. Некоторые особенности, характерные для судовых конструкций, проявляются при определении возмущающих сил, услови л закрепления элементов корпуса на опорах (опорном контуре), числовых характеристик демпфирования, а также при учете взаимодействия конструкций с жидкостью. [c.449]
В данное издание дополнительно включены разделы, посвященные перемещениям в стержнях большой кривизны и их устойчивости, учету упругих опор и оснований, расчету пространственных статически неопределимых рам, колебаниям стержневых систем, а также применению системы компьютерной математики Math AD для решения задач сопротивления материалов. Кроме того, значительно расширен материал, связанный с температурными деформациями и напряжениями. [c.2]
Каркас котлоагрегата состоит из пространственной многоэтажной рамы. При расчете такую раму расчленяют на плоские. При П-образной компоновке котлоагрегата получают четыре плоские рамы для радиационной части и столько же для конвективной. Влияние соединительных ригелей, расположевных между радиационной и конвективной частями котлоагрегата невелико и оно не учитывается. [c.75]
Железобетонное перекрытие (пол камеры под резервуаром) представляет собой круглую железобетонную плиту с круглым вырезом в центре для прохода на лестницу. Перекрытие рассчитывается на равномерно распределенную нагрузку, состоящую из собственного веса, веса настила, утепления и временной полезной нагрузки. Железобетон-н ы е колонны башни располагаются в плане по вершинам правильного многоугольника. Опорная конструкция башни из колонн, связанных ригелями, является жесткой пространственной рамой. Однак о в целях упрои(ения расчет м. б. произведен по методу, [c.211]
Бе лоус А, А, Колебания и статическая устойчивость плоских и пространственных рам, Б сб. Расчет пространственных конструкций, Вып, 3, М,, Госстройиздат,, 1965, 211—Й64 — РЖМех, 1956, № 10, 6923. [c.230]
В зазделе П при рассмотрении каркасов зданий даны подробные рекомендации к выбору наиболее простого метода расчета, поперечных рам и даны примеры таких расчётов. Расчеты каркасов даны применительно к рчсчленению их на плоские системы, но параллельно даны указания по учету пространственной работы каркаса. [c.13]
mash-xxl.info
Расчет статически неопределимых плоско-пространственных рам методом сил
При расчете пространственных систем, как и при расчете плоских, обычно в целях простоты расчета пренебрегают влиянием на перемещения внутренних сил Nz, Qx и Qy, поэтому при расчете пространственных систем чаще всего приходится строить эпюры Мх, Му и Mz от каждого основного неизвестного и от нагрузки, по которым определяются коэффициенты и свободные члены канонических уравнений.
Рис. 7
В плоской раме (рис. 7) основные неизвестные Х1, Х2, Х3, лежащие в плоскости рамы, вызывают перемещения только в этой плоскости, поэтому все побочные перемещения от этих сил Х1, Х2 и Х3 по направлению остальных основных неизвестных и Х4, Х5, Х6, как и взаимные их перемещения, равны нулю. Следовательно, канонические уравнения для таких систем независимо от нагрузки распадаются на две независимые группы. В одну из них будут входить неизвестные типа Х1, Х2 и Х3, а в другую— неизвестные типа Х4у Х5 и Х6. Если нагрузку также разложить на нагрузку, лежащую в плоскости рамы, и нагрузку, перпендикулярную ей, то нагрузка, лежащая в плоскости рамы, вызывает только основные неизвестные, расположенные в плоскости рамы (Х1, Х2 и Х3), а нагрузка, перпендикулярная плоскости рамы, вызывает неизвестные Х4, Х5 и Х6.
Пример . Построить эпюры изгибающих и крутящих моментов в раме (рис. 8, а), если сечения стержней круглые, E/G = 2,5; Г// = 2.
Основная система показана на рис. 8, б. По условию симметрии будем иметь одно неизвестное Х1 (изгибающий момент). Эпюры от Х1=1 показаны на рис. 8, в, а грузовые — на рис. 8, г. Каноническое уравнение:
δ11Х1 + Δ1Р = 0.
Коэффициент δ11 и свободный член Δ1Р при Т = 2I будут:
δ11 = = 2 =
Δ1Р = = – =– .
Следовательно:
13,5 Х1 – 15,75Р = 0, откуда Х1 = 1,167Р.
Окончательные эпюры показаны на рис. 8, д.
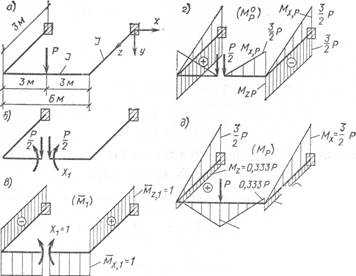
Рис. 8
Похожие статьи:
poznayka.org