Сопромат изгиб балки: Изгиб (деформация)

Содержание

Сопротивление материалов. Изгиб.

Сопротивление материалов

Основные понятия об изгибе

Деформация изгиба характеризуется потерей прямолинейности или первоначальной формы линией балки (ее осью) при приложении внешней нагрузки. При этом, в отличие от деформации сдвига, линия балки изменяет свою форму плавно.
Легко убедиться, что на сопротивляемость изгибу влияет не только площадь поперечного сечения балки (бруса, стержня и т. д.), но и геометрическая форма этого сечения.

Поскольку изгиб тела (балки, бруса и т. п.) осуществляется относительно какой-либо оси, на сопротивляемость изгибу влияет величина осевого момента инерции сечения тела относительно этой оси.
Для сравнения — при деформации кручения сечение тела подвергается закручиванию относительно полюса (точки), поэтому на сопротивление кручению оказывает влияние полярный момент инерции этого сечения.

На изгиб могут работать многие элементы конструкций – оси, валы, балки, зубья зубчатых колес, рычаги, тяги и т. д.

В сопротивлении материалов рассматривают несколько типов изгибов:
— в зависимости от характера внешней нагрузки, приложенной к брусу, различают чистый изгиб и поперечный изгиб;
— в зависимости от расположения плоскости действия изгибающей нагрузки относительно оси бруса — прямой изгиб и косой изгиб.

***

Чистый и поперечный изгиб балки

Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент (рис. 2).
Деформация чистого изгиба будет, например, иметь место, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил. Тогда в каждом сечении бруса будут действовать только изгибающие моменты.

Если же изгиб имеет место в результате приложения к брусу поперечной силы (рис. 3), то такой изгиб называется поперечным. В этом случае в каждом сечении бруса действует и поперечная сила, и изгибающий момент (кроме сечения, к которому приложена внешняя нагрузка).

Если брус имеет хоть одну ось симметрии, и плоскость действия нагрузок совпадает с ней, то имеет место прямой изгиб, если же это условие не выполняется, то имеет место косой изгиб.

При изучении деформации изгиба будем мысленно представлять себе, что балка (брус) состоит из бесчисленного количества продольных, параллельных оси волокон.
Чтобы наглядно представить деформацию прямого изгиба, проведем опыт с резиновым брусом, на котором нанесена сетка продольных и поперечных линий.
Подвергнув такой брус прямому изгибу, можно заметить, что (рис. 1):

— поперечные линии останутся при деформации прямыми, но повернутся под углом друг другу;
— сечения бруса расширятся в поперечном направлении на вогнутой стороне и сузятся на выпуклой стороне;

— продольные прямые линии искривятся.

Из этого опыта можно сделать вывод, что:

— при чистом изгибе справедлива гипотеза плоских сечений;
— волокна, лежащие на выпуклой стороне растягиваются, на вогнутой стороне – сжимаются, а на границе между ними лежит нейтральный слой волокон, которые только искривляются, не изменяя своей длины.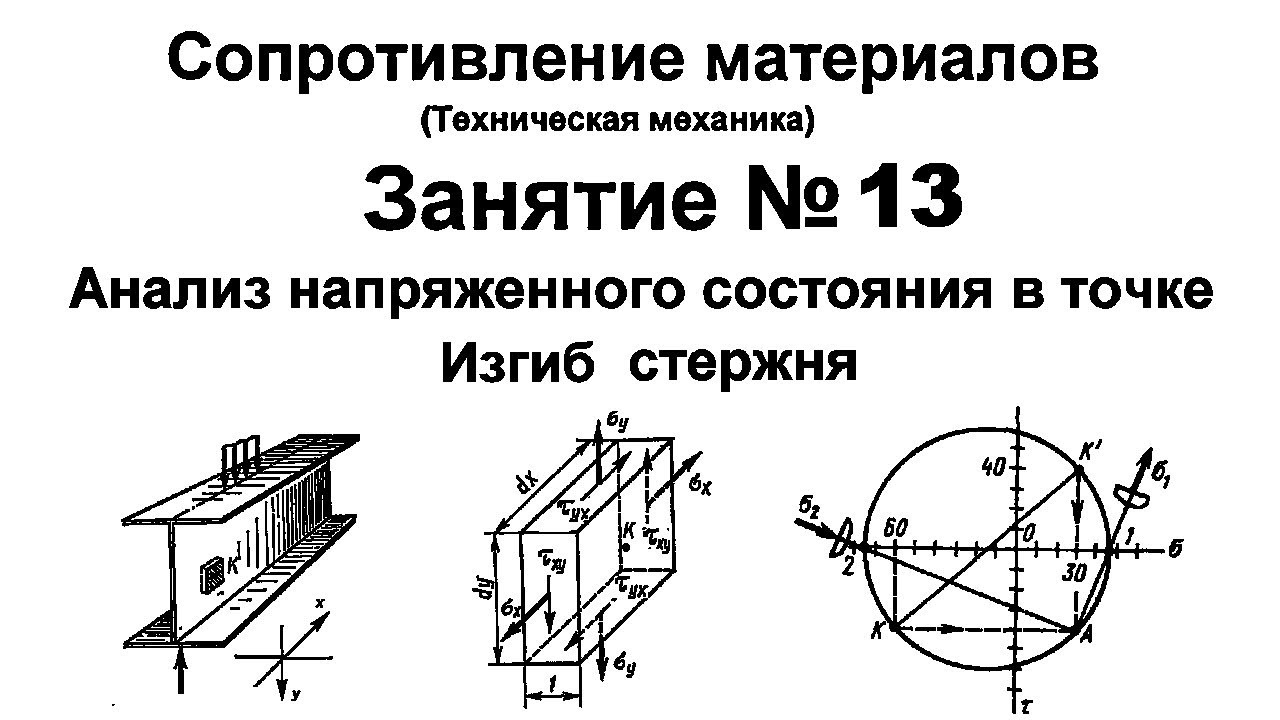

Полагая справедливой гипотезу о не надавливании волокон, можно утверждать, что при чистом изгибе в поперечном сечении бруса возникают только нормальные напряжения растяжения и сжатия, неравномерно распределенные по сечению.
Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью. Очевидно, что на нейтральной оси нормальные напряжения равны нулю.

***

Изгибающий момент и поперечная сила

Как известно из теоретической механики, опорные реакции балок определяют, составляя и решая уравнения равновесия статики для всей балки. При решении задач сопротивления материалов, и определении внутренних силовых факторов в брусьях, мы учитывали реакции связей наравне с внешними нагрузками, действующими на брусья.

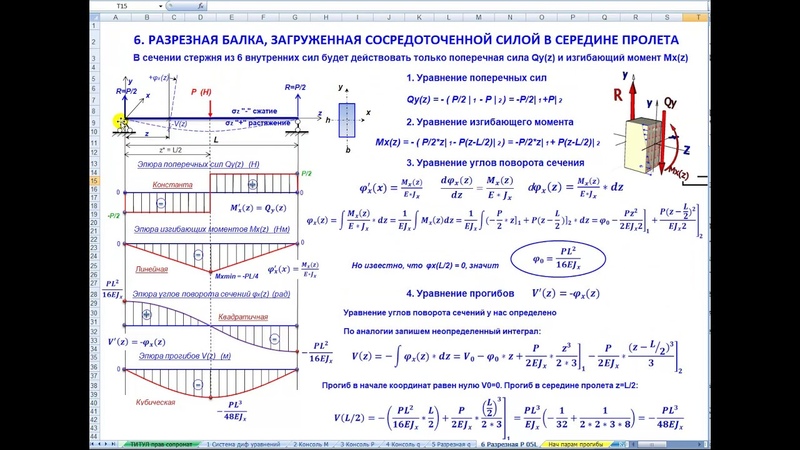
Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией – осью, к которой приложены активные и реактивные силы (нагрузки и реакции связей).

Рассмотрим два случая:

1. К балке приложены две равные и противоположные по знаку пары сил.
Рассматривая равновесие части балки, расположенной слева или справа от сечения 1-1 (рис. 2), видим, что во всех поперечных сечениях возникает только изгибающий момент М_и, равный внешнему моменту. Таким образом, это случай чистого изгиба.

Изгибающий момент есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки.

Обратим внимание на то, что изгибающий момент имеет разное направление для левой и правой частей балки. Это говорит о непригодности правила знаков статики при определении знака изгибающего момента.

2. К балке приложены активные и реактивные силы (нагрузки и реакции связей), перпендикулярные оси (рис. 3). Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать изгибающий момент М_и и поперечная сила Q.
Из этого следует, что в рассматриваемом случае в точках поперечных сечений действуют не только нормальные напряжения, соответствующие изгибающему моменту, но и касательные, соответствующие поперечной силе.

Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении балки.

Обратим внимание на то, что поперечная сила имеет противоположное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики при определении знака поперечной силы.

Изгиб, при котором в поперечном сечении балки действуют изгибающий момент и поперечная сила, называется поперечным.

У балки, находящейся в равновесии вод действием плоской системы сил, алгебраическая сумма моментов всех активных и реактивных сил относительно любой точки равна нулю; следовательно, сумма моментов внешних сил, действующих на балку левее сечения, численно равна сумме моментов всех внешних сил, действующих на балку правее сечения.
Таким образом, изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяжести сечения всех внешних сил, действующих на балку справа или слева от сечения

У балки, находящейся в равновесии под действием плоской системы сил, перпендикулярных оси (т. е. системы параллельных сил), алгебраическая сумма всех внешних сил равна нулю; следовательно сумма внешних сил, действующих на балку левее сечения, численно равна алгебраической сумме сил, действующих на балку правее сечения.
Таким образом, поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения.

Так как правила знаков статики неприемлемы для установления знаков изгибающего момента и поперечной силы, установим для них другие правила знаков, а именно: Если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот, если внешняя нагрузка стремится изогнуть балку выпуклостью вверх, то изгибающий момент в сечении считается отрицательным (

рис 4,a).

Если сумма внешних сил, лежащих по левую сторону от сечения, дает равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, если равнодействующая направлена вниз, то поперечная сила в сечении считается отрицательной; для части балки, расположенной справа от сечения, знаки поперечной силы будут противоположными (рис. 4,b). Пользуясь этими правилами, следует мысленно представлять себе сечение балки жестко защемлённым, а связи отброшенными и замененными реакциями.

Еще раз отметим, что для определения реакций связей пользуются правилами знаков статики, а для определения знаков изгибающего момента и поперечной силы – правилами знаков сопротивления материалов.
Правило знаков для изгибающих моментов иногда называют «правилом дождя», имея в виду, что в случае выпуклости вниз образуется воронка, в которой задерживается дождевая вода (знак положительный), и наоборот – если под действием нагрузок балка выгибается дугой вверх, вода на ней не задерживается (знак изгибающих моментов отрицательный).

***

Материалы раздела «Изгиб»:

Дифференциальные зависимости при изгибе. Теорема Журавского.
Напряжения и расчеты на прочность при изгибе.
Контрольная работа «Построение эпюр и расчеты на прочность при изгибе» (Word)

Деформация кручения

Главная страница

Страничка абитуриента

Дистанционное образование

Группа ТО-81
Группа М-81
Группа ТО-71

Специальности

Ветеринария
Механизация сельского хозяйства
Коммерция
Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

Инженерная графика
МДК.01.01. «Устройство автомобилей»
Карта раздела
Общее устройство автомобиля
Автомобильный двигатель
Трансмиссия автомобиля
Рулевое управление
Тормозная система
Подвеска
Колеса
Кузов
Электрооборудование автомобиля
Основы теории автомобиля
Основы технической диагностики
Основы гидравлики и теплотехники
Метрология и стандартизация
Сельскохозяйственные машины
Основы агрономии
Перевозка опасных грузов
Материаловедение
Менеджмент
Техническая механика

Советы дипломнику

Олимпиады и тесты

«Инженерная графика»
«Техническая механика»
«Двигатель и его системы»
«Шасси автомобиля»
«Электрооборудование автомобиля»

Правильные ответы на вопросы Теста № 10

№ вопроса	1	2	3	4	5	6	7	8	9	10
Правильный вариант ответа	3	1	3	2	3	2	2	1	2	3

РГЗ сопромат 2-2 — Косой изгиб балки

_{МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ}

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

«Национальный исследовательский ядерный университет «МИФИ»

Озерский технологический институт – филиал НИЯУ МИФИ

Кафедра: ТМ и МАХП

Расчётно-графическое задание № 2

По дисциплине «Сопротивление материалов»

Тема: «Косой изгиб балки».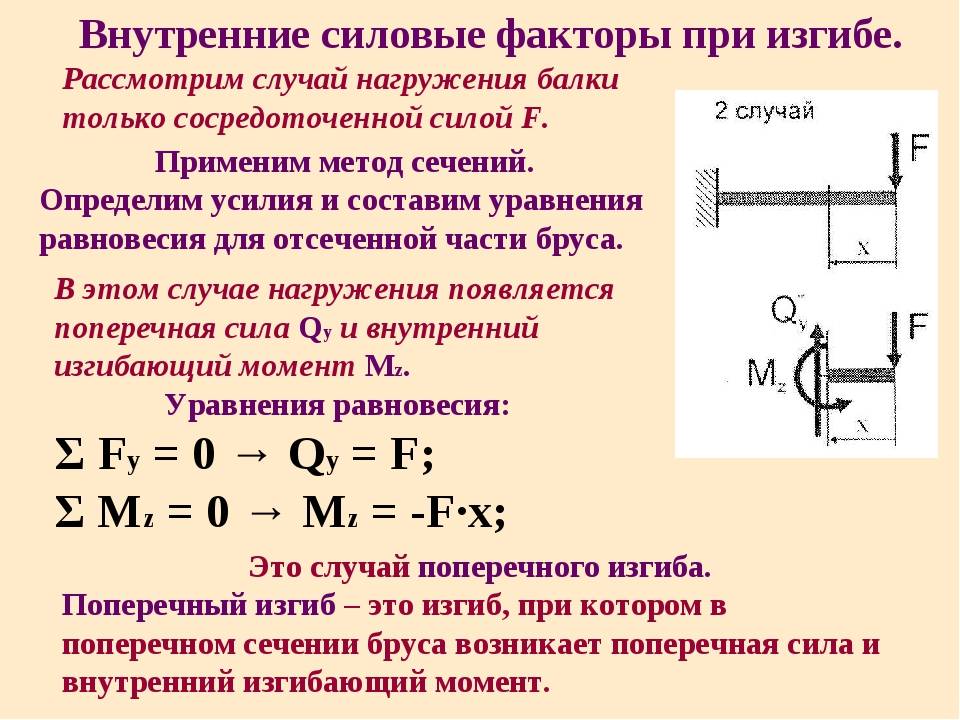

Выполнил студент группы	1ТМ-26Д	Сергеев П. С.

Проверил		Сосюрко В. Г.

Озёрск

2017

Для заданной схемы нагрузки стального профиля определить опасное сечение и наибольшее напряжение, возникающее в балке. Указать на чертеже в какой точке профиля возникает наибольшее напряжение и его знак. Построить эпюры изгибающих моментов. Чертёж балки и её профиль выполняется в произвольном масштабе.

Данные для расчёта представлены в таблице 1.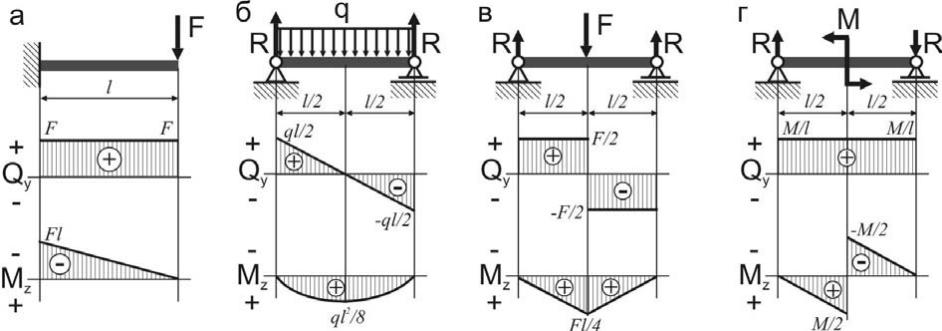 Конструкция изображена на схеме 1.

Таблица 1.
P₁, кН	P₂, кН	a, м	b, м	c, м	Сталь угловая неравнополочная Bb d, мм
4,5	5,5	1,4	3,2	1,8	16010010

Схема 1.

Определим реакции опор в плоскостях изгиба. Построим эпюры поперечных сил и изгибающих моментов.

Схема 2.

;

Схема 3.

;

Определим напряжения в опасных сечениях b-b и c-c.

; ; .

;

Схема 4.

;

Схема 5.

Максимальное растягивающее напряжение находится в точке между 4_c и 3_c. .

РойМех — Теория упругого изгиба

Суперпозиция…. Номенклатура…. Простой изгиб….

Прогиб…. Метод момента площади…. Составные балки. …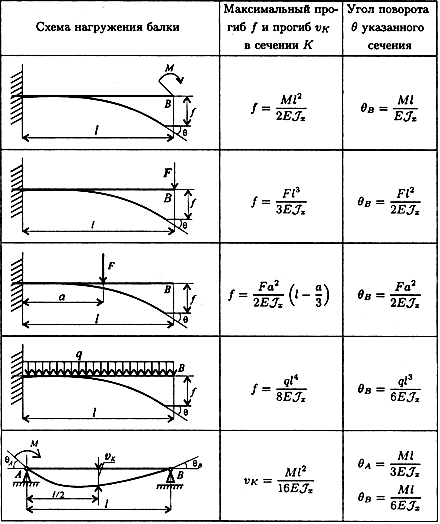

Введение

Напряжение, деформация, размер, кривизна, эластичность, все связаны, при определенных предположениях, по теории простого изгиба. Эта теория относится к изгибу балки в результате пары, приложенные к балке без учета перерезывающих сил.

Принцип суперпозиции

Принцип суперпозиции является одним из наиболее важных инструментов для решения проблемы нагрузки, позволяющие упростить очень сложные задачи проектирования.

Для балок, подвергающихся нескольким нагрузкам разных типов сила, изгибающий момент, наклон и прогиб могут быть найдены в любом месте путем суммирования эффекты из-за того, что каждая нагрузка действует отдельно на другие нагрузки.

Номенклатура

e = деформация
E = модуль Юнга = σ /e (Н/м ² )
y = расстояние поверхности от нейтральной поверхности (м).
R = Радиус нейтральной оси (м).
I = Момент инерции (м ⁴ — чаще см ⁴ )
Z = модуль сопротивления = I/y _max (м ³ — чаще см ³ )
F = Сила (Н )
x = расстояние вдоль балки
δ = прогиб (м)
θ = уклон (радианы)
σ = напряжение (Н/м ² )

Простая гибка

На прямой стержень из однородного материала действует только момент на одном конце и равный и противоположный момент на другом конце…

Предположения

Луч симметричен относительно Y-Y
Поперечные плоские сечения остаются плоскими и нормальными к продольным волокнам после изгиб (предположение Берулли)
Фиксированная зависимость между напряжением и деформацией (модуль Юнга) для материал балки одинаков для растяжения и сжатия ( σ = E.e )

Рассмотрим две секции, расположенные очень близко друг к другу (AB и CD).
После сгибания секции будут в точках A’B’ и C’D’ и перестанут быть параллельными.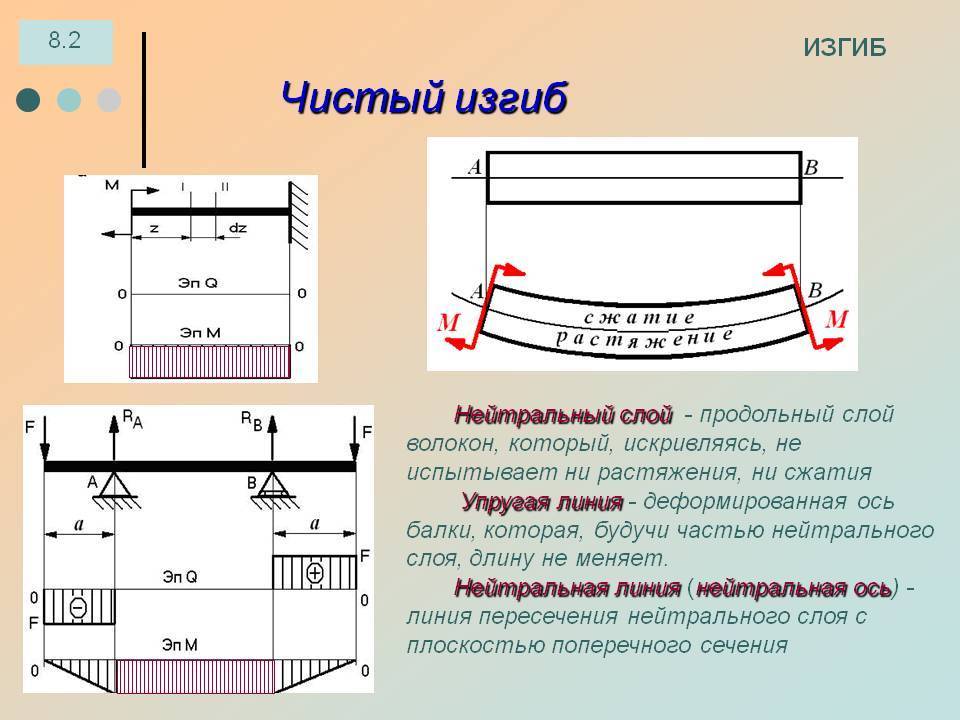 AC расширится до A’C’, а BD сожмется до B’D’
. Линия EF будет располагаться так, что ее длина не изменится. Эта поверхность называется нейтральной поверхностью, а ее пересечение с Z_Z называется нейтральной осью
. Линии развития A’B’ и C’D’ пересекаются в точке 0 под углом θ радиан, а радиус E’F’ = р
Пусть y будет расстоянием (E’G’) любого слоя H’G’, изначально параллельного EF. Тогда

H’G’/E’F’ = (R+y)θ /R θ = ( р+у)/р

А деформация e в слое H’G’ =

e = (H’G’- HG) / HG = (H’G’- HG) / EF = [(R+y)θ — R θ] /R θ = y /R

Принятое соотношение между напряжением и деформацией: σ=E.e Следовательно,

σ = E.e = E. y /R
σ / E = y / R

Следовательно, для проиллюстрированного примера растягивающее напряжение напрямую связано с расстоянием над нейтральной осью. Напряжение сжатия также напрямую связано с расстоянием ниже нейтральной оси. Предполагая, что E одинаково для отношения сжатия и растяжения одинаковы.

Поскольку балка находится в статическом равновесии и на нее действуют только моменты (нет вертикального сдвига силы) силы в сечении (AB) полностью продольные, а полные сжимающие силы должны уравновешивать общие растягивающие усилия. Внутренняя пара, возникающая в результате сумма ( σ.dA .y) по всему сечению должна равняться приложенному извне моменту.

Это может быть правильным только в том случае, если Σ(yδa) или Σ(y.z.δy) есть момент площади участок вокруг нейтральной оси. Это может быть ноль, только если ось проходит через центр тяжести (центроид) сечения.

Внутренняя пара, полученная из суммы ( σ.dA .y) по всему сечению, должна равен приложенному извне моменту. Поэтому пара сил, возникающих в результате напряжение на каждой площади, суммированное по всей площади, будет равно приложенному моменту

Из вышеизложенного вытекают следующие важные простые соотношения изгиба балки

Из вышеизложенного видно, что простая балка при изгибе создает максимальное напряжение на поверхности дальше от нейтральной оси. Для симметричных относительно Z-Z сечений максимальное сжимающее и растягивающие напряжения равны.

σ _макс = у _макс . М/Я

Коэффициенту I /y _max дается название раздела Modulus (Z) и, следовательно,

σ _макс. = M / Z

Значения Z приведены в таблицах, показывающих свойства стандартных стальных профилей

Прогиб балок

Ниже показана дуга нейтральной оси балки, подверженной изгибу.

Для малого угла dy/dx = tan θ = θ
Кривизна балки определяется как dθ /ds = 1/R
На рисунке δθ мало, а δx; практически = δs; т.е. ds/dx =1

Из этого простого приближения выводятся следующие соотношения.

Интегрирование между выбранными пределами.

Отклонение между пределами получается путем дальнейшего интегрирования.

Было доказано исх Сдвиг — Изгиб что dM/dx = S и dS/dx = -w = d ² M /dx
Где S = поперечная сила M — момент, а w — распределенная нагрузка на единицу длины балки. поэтому

Если w является постоянной или интегрируемой функцией от x, то это соотношение можно использовать для получить общие выражения для S, M, dy/dx или y путем последовательного интегрирования с константой интеграции добавляется на каждом этапе. Свойства опор или креплений можно использовать для определения констант. (x= 0 — просто поддерживается, dx/dy = 0 с фиксированным концом и т.д.)

Аналогично, если известно выражение для изгибающего момента, то наклон а прогиб можно получить в любой точке x однократным и двукратным интегрированием соотношения и применение подходящих констант интегрирования.

Функции сингулярности можно использовать для определения значений при загрузке не простой ссылки Функции сингулярности

Пример — Консольная балка

Рассмотрим консольную балку (однородного сечения) с одной сосредоточенной нагрузкой на конце. В фиксированный конец x = 0, dy = 0, dy/dx = 0

Из положения равновесия ..На опору действует момент сопротивления -FL и вертикальная направленная вверх сила F.
В любой точке x вдоль балки действует момент F(x — L) = M _x = EI d ² у/дх ²

Пример — свободно опертая балка

Рассмотрим свободно опертую балку одинакового сечения с одиночной нагрузкой F в центре. Луч будет отклоняться симметрично относительно центральной линии с нулевым наклоном (dy/dx) на центральной линии. Удобно выбирать начало координат на центральной линии.

Метод площади момента

Это метод определения изменения наклона или отклонения между двумя точками на луч. Это выражается в виде двух теорем…

Теорема 1
Если A и B две точки на балке, изменение угла (в радианах) между касательной в точке А, а касательная в точке В равна площади диаграммы изгибающих моментов между точками деленное на соответствующее значение EI (константа жесткости на изгиб).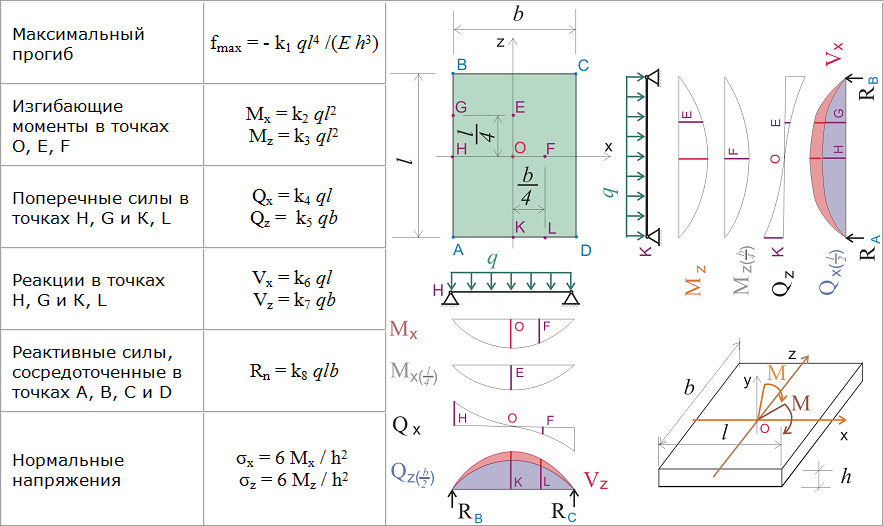

Теорема 2
Если A и B — две точки на балке, то смещение B относительно касательной балки в точке А равен моменту площади диаграммы изгибающих моментов между A и B относительно ординаты, проходящей через B, деленной на соответствующее значение EI (константа изгибной жесткости).

Примеры. Ниже приведены два простых примера для иллюстрации этих теорем.

Пример 1) Определите прогиб и наклон кантилевера, как показано на рисунке.

Изгибающий момент при A = M _A = -FL
Площадь диаграммы изгибающего момента A _M = -F.L ² /2
Расстояние до центра тяжести диаграммы BM от B= x _c = 2L/3
Отклонение B = y _b = A _M .x _c /EI = -F.L ³ /3EI
Наклон в точке B относительно тангенса при A = θ _б =A _M /EI = -FL ² /2EI

Пример 2) Определите центральный прогиб и торцевые уклоны свободно опертой балки, как показано на рисунке. .

E = 210 ГПа ……I = 834 см ⁴ …… EI = 1,7514. 10 ⁶ Н·м ²

А ₁ = 10 . 1,8 . 1,8/2 = 16,2 кН·м ²
А ₂ = 10 . 1,8 . 2 = 36 кНм ²
А ₃ = 10 . 1,8 . 2 = 36 кНм ²
А ₄ = 10 . 1,8 . 1,8/2 = 16,2 кН·м ²
x ₁ = центр тяжести A ₁ = (2/3) . 1,8 = 1,2 м
x ₂ = центр тяжести A ₂ = 1,8 + 1 = 2,8 м
x ₃ = центроид A ₃ = 1,8 + 1 = 2,8 м
x ₄ = центроид A _{4 9003 8 = (2 /3) . 1,8 = 1,2 м}

Наклон в точке A определяется площадью диаграммы моментов между A и C, деленной на EI.

θ _A = (A ₁ + A ₂ ) /EI = (16,2+36).10 ³ / (1,7514, 10 ⁶ ) 9000 9 = 0,029 рад = 1, 7 градусов

Отклонение в центре (С) равно отклонению точки А от линии, касательной к С.
Таким образом, должны быть учтены моменты относительно линии отклонения в точке A.

δ _C = (A _M .x _M ) /EI = (A ₁ x ₁ +A ₂ x _{2 90 038 ) / ЭИ = 120,24,10 ³ / ( 1,7514. 10 ⁶ )
= 0,0686м = 68,6мм}

Композитные балки

Балки, изготовленные более чем из одного материала, могут быть обработаны методом эквивалентной ширины, если максимальные напряжения в каждом из материалов находится в пределах соответствующего предела упругости материалов. Рассмотрим составную балку как показано ниже. Сталь имеет модуль упругости Е _S = 210,10 ³ Н/мм ² и алюминий имеет E _A = 78,10 ³ Н/мм ² .

Составная балка анализируется исходя из основного предположения, что плоские поверхности остаются плоскими при изгибе в пределах предела упругости. поэтому по всей глубине балки деформация (прогиб/исходная длина) постоянна, т.е. прогиб пропорционален расстоянию от нейтральная ось луча. Деформация равна (напряжение / модуль Юнга (E)) См. рисунок ниже

Теперь, чтобы получить эквивалентный раздел, который является всем алюминий размеры замещающего алюминия должны быть такими, чтобы механические свойства были эквивалентны к исходному материалу. Общая глубина преобразованного участка такая же, как у исходного участка. Результирующая деформация в любом элементе dA преобразованного сечения должен быть таким же, как в оригинальном разделе

Эквивалентная площадь преобразованного сечения на основе алюминия равна площади оригинальный стальной профиль x n _СА . Если глубина преобразованного сечения такая же, как и у исходного сечения, тогда ширина преобразованного алюминия сечение равно n _SA x ширина исходного стального сечения.

Эквивалентная площадь алюминиевой секции должна подвергаться той же деформации, что и исходная стальная секция, расположенная на одинаковом расстоянии от нейтральной оси сечения.