Сопротивление материалов

1. Общие сведения

Любая машина или конструкция помимо элементов, обеспечивающих своё функциональное назначение, имеет несущие конструкции, обеспечивающие прочность, жесткость и устойчивость (силовой каркас).

Сопротивление материалов – является наукой о прочности, жёсткости и устойчивости элементов конструкции.

1.1. Основные понятия и определения.

Работоспособность детали – это способность выполнять заданные функции, сохраняя эксплуатационные показатели в заданных нормативных пределах.

Работоспособность зависит от свойств материала.

В курсе «сопротивление материалов» рассматриваются три критерия работоспособности:

Прочность – способность детали выдерживать внешние нагрузки без разрушения.

Жесткость – способность детали сопротивляться изменению формы и размеров под действием внешних сил.

Устойчивость – способность конструкции (стержня) сопротивляться изменению формы при осевом сжатии.

1.2. Схематизация внешних нагрузок.

Силы, действующие на тело со стороны других тел, называются внешними нагрузками:

1) Сосредоточенные силы – это силы, действующие на площадку во много раз меньшую, чем вся рассматриваемая поверхность или сила, приложенная к точке.

2) Распределенные нагрузки.

Нагрузка, распределённая по длине (б) .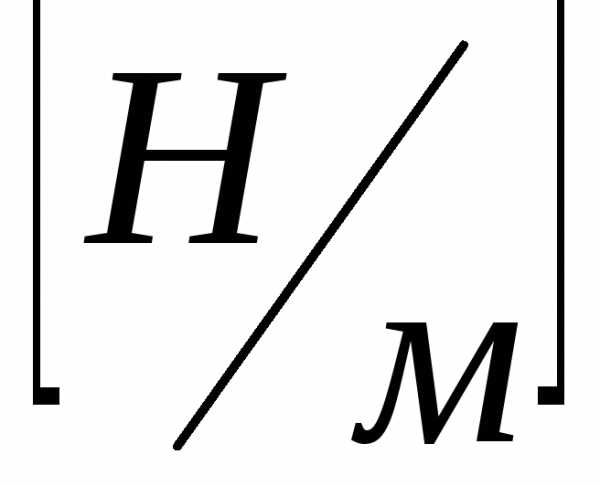

Для неравномерной нагрузки задаётся закон распределения нагрузки по длине (в) .

Нагрузка, распределенная по поверхности (а) (по площади или объёму

)

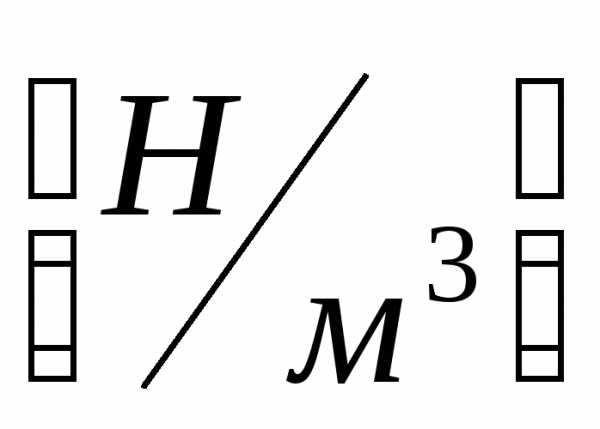
3) Изгибающий момент.

4) Крутящий момент.

1.3 Схематизация элементов конструкций

Для расчета конструкции ее упрощают, т.е. составляют расчетную схему.

Основными элементами расчетных схем являются:

1) Стержень (брус) – элемент конструкции, длина которого значительно превышает его поперечные размеры.

l >> b, h, d

2) Балка- элемент конструкции (стержень) работающий на изгиб.

3

Т_кр

Т_кр

) Вал – элемент конструкции (стержень), работающий на кручение.

4) Оболочка – элемент конструкции, длина и ширина которого много больше толщины.

5) Массивное тело – элемент конструкции, размеры которых сопоставимы друг с другом.

1.4. Типы опор, реакции связей

Опоры, подвижные (а), неподвижные (б), защемление (в)

а) б) в)

а) в шарнирно-подвижной опоре возникает только одна составляющая реакции – вертикальная ;

б) в шарнирно-неподвижной опоре возникает две составляющие реакции – вертикальная и горизонтальная;

в) в защемлении возникает три составляющие реакции – вертикальная , горизонтальная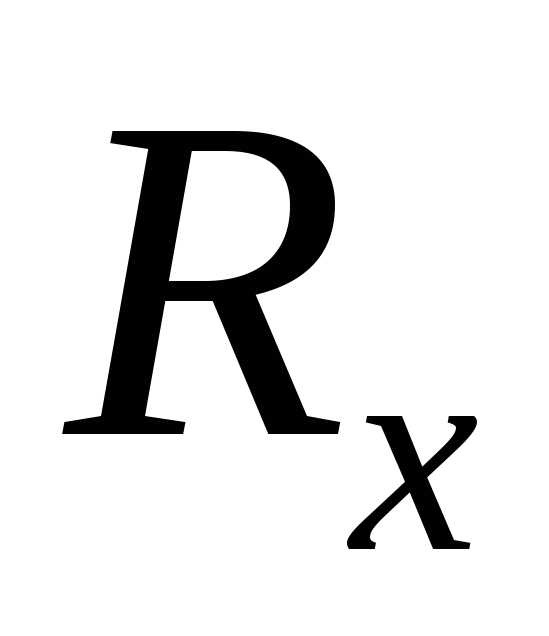и реактивный момент.

Реакции опор определяются уравнениями статики.

1.5 Деформация тел

Изменение формы тела или его размеров вследствие воздействия внешних сил или изменения температуры – называется деформацией.

Деформации могут быть упругие (исчезающие полностью после снятия нагрузки) и пластические (не восстанавливают форму и размеры после снятия нагрузки).

1.6. Гипотезы и допущения сопротивления материалов

Для упрощения расчетов, в сопротивлении материалов применяют ряд допущений и гипотез, полученных путём экспериментальных исследований и математического анализа.

1. Гипотеза о сплошном строении тела – предполагает, что материал полностью занимает объём тела, пустоты отсутствуют.

2. Об идеальной упругости материала: материал полностью восстанавливает свою форму и размеры после снятия нагрузки.

3. Гипотеза об однородности и изотропности материала – все частицы материала обладают одинаковыми свойствами, во всех направлениях свойства не меняются.

4. Гипотеза о плоских сечениях: сечения плоские и нормальные к оси бруса до деформации остаются такими же и после приложения нагрузки.

5. Гипотеза о малых перемещениях: перемещения или деформации малы по сравнению с размерами тела и не учитываются в расчётах на прочность.

6. Допущение о линейной зависимости сил и деформаций: деформация считается строго прямо пропорциональной приложенной нагрузке.

7. Принцип суперпозиции (принцип независимости действия сил): при действии на тело нескольких нагрузок приложенных в одной точке, они складываются друг с другом. То же самое происходит и с деформацией.

studfiles.net

Сопромат

Сопромат (сопротивление материалов) — наука об инженерных методах расчета на прочность, жесткость и устойчивость элементов сооружений и деталей машин.  Прочность — способность элементов сооружений или деталей машин выдерживать определенную нагрузку не разрушаясь. 

Жесткость — способность элементов сооружений или деталей машин противостоять внешним нагрузкам в отношении деформаций. 

Устойчивость — способность элементов сооружений или деталей машин сохранять первоначальную форму упругого равновесия при действии внешних нагрузок. 

 Учитывая большое разнообразие конструктивных форм элементов сооружений и деталей  машин в сопротивлении материалов рассматриваются четыре простых тела: брус, оболочка, пластина, массив.

Брус — тело, продольные размеры которого значительно превышают его поперечные размеры. Оболочка — тело, ограниченное криволинейными поверхностями, расположенными на близком расстоянии друг от друга. Пластинка — тело, ограниченное прямолинейными поверхностями расположенными на близком расстоянии друг от друга. Массив — тело, у которого все три размера одного порядка. 

 Решение основных задач сопромата начинается с выбора расчетной схемы. Выбор заключается в устранении второстепенных факторов, в схематизации рассматриваемого объекта. Основным расчетным объектом сопротивления материалов является брус.  Осью бруса называют линию, проходящую через центры тяжести всех последовательно проведенных поперечных сечений.  Поперечное сечение получается при рассечении бруса плоскостью, перпендикулярной к его оси.  Изменение размеров и формы тела под действием силовых факторов называется деформацией.  Деформации связаны с перемещениями точек, линий и плоскостей. Перемещения по прямой называются линейными. Перемещения, вызванные поворотом линий и плоскостей, называются угловыми. Линейная деформация имеет размерность длины, а угловая — размерность угла. Измеренная величина линейной деформации на данном участке называется абсолютной деформацией, а отношение абсолютной деформации к длине участка — относительной деформацией.  Деформации, полностью исчезающие после снятия нагрузки, называют упругими. Частично остающиеся деформации — пластическими. Свойство материалов полностью восстанавливать первоначальную форму при снятии нагрузок в сопротивлении материалов называется упругостью, а свойство накапливать остаточные деформации — пластичностью. Если внешние силы, действующие на брус, приводятся к силам по его оси, то это растяжение или сжатие. Брус, работающий на растяжение или сжатие, называется стержнем. Если внешние силы приводятся к паре сил, действующих в плоскости, перпендикулярной оси бруса, то это кручение. Брус, работающий на кручение, называется осью или валом.  Если внешние силы приводятся к паре сил, действующих в плоскости продольной оси бруса, то брус испытывает изгиб. Брус, работающий на изгиб, в сопромате называется балкой. Далее опишем основные допущения ( гипотезы), принимаемые в сопромате: 1. Гипотеза о сплошности материла. 2. Гипотеза об однородности и изотропности материала. 3. Гипотеза об идеальной упругости материала. 4. Гипотеза о малости деформаций. Она позволяет не учитывать их при рассмотрении условий равновесия. 5 Принцип независимости действия сил, состоящий в том, что упругую деформацию, вызванную многими силами, действующими одновременно, можно рассматривать как сумму упругих деформаций от каждой силы в отдельности. 6. Гипотеза плоских сечений. Плоские сечения, проведенные в теле до его деформации, остаются плоскими и при деформации.

Основные понятия в сопромате.

Задачи и методы сопромата.

Все элементы конструкции обладают прочностью и жесткостью.

Задачи сопромата: создание методов оценки прочности.

Сопромат характеризуется приближенными приемами расчета.

Расчетные схемы и модели.

Оценка прочности проводится по схеме (модели).

Модель – совокупность основных представлений от основного описания объекта.

Для одной и той же детали можно составить несколько подобных схем. В то же время для одной расчетной схемы можно найти различные детали схем материала, форм, нагружения и разгружения сил. 

Модели надежности.

Модели материала.

Материал бывает однородным, сплошным, непрерывным (можно применить математические формулы), изотропным.

Однородность материала – материал, по всему объему одинаков.

Расчетная модель материала обладает свойствами упругости, пластичности и ползучести.

Упругость – свойство материала восстанавливать форму.

Пластичность – свойство тела сохранять измененную форму.

Ползучесть – свойство тела изменять форму с течением времени (смола).

Модели формы.

Геометрическая форма тел очень сложна. Учесть в формулах все формы не возможно, поэтому их приводят к 4 схемам:

1.Стержень, брус.

2.Пластина.

3.Оболочка.

4.Массив.

Разновидности формы.

Стержень – форма детали, у которой один размер на порядок больше, чем два других.

Пластина – форма детали, у которой один размер меньше на порядок, чем два других.

Массив – все размеры разные, но отличаются меньше, чем на порядок.

Модели нагружения.

Сила – мера взаимодействия двух тел.

Сила бывает внешняя и внутренняя. Внешняя в сою очередь бывает сосредоточенной, распределенной и объемной.

Сосредоточенная – сила, приложенная на малой площади, которую можно считать точкой.

Распределенная – сила, действующая на значительной поверхности, размер которой нужно учитывать.

Объемная – сила, распределенная по всей массе тела.

Модели времени действия сил.

Различают

1. Статические

2. Переменные

a) Малоцикловые

b)   Многоцикловые (больше 100 тыс. изменений)

Модели разрушения.

Разрушение детали – изменение ее формы в плоть до разделения на части.

Изменение формы и разделение на части произойдет тогда, когда внутренние силы превысят силы сцепления отдельных частей материала.

Для суждения о прочности сравнивают внутренние силы с пределами прочности. Внутренние силы представляют собой силы межатомного взаимодействия возникающие при действии внешних сил.

Рассмотрим тело (а), находящееся в равновесии под действием внешних сил  мысленно рассечем это тело на 2 части плоскостью П и рассмотрим 1-у из них (б). Действие одной из них на другую следует заменить системой внутренних сил в сечении. Внутренние силы в сечениях частей тела всегда взаимны (действие равно противодействию). В сопромате изучаются тела находящиеся в равновесии.

Для нахождения равнодействующей (R) и момента (M) воспользуемся уравнениями равновесия.

Проектируем R и М на выбранные оси координат.

Отсеченная часть находится в равновесии

  

Возьмем систему координат xyz и разложим  и на составляющие части.

         

Тогда проекции  и М на эти оси называются внутренними силовыми факторами.

 — продольная сила,  — поперечные силы.

 — крутящий момент,   — изгибающие моменты.

Для вычисления внутренних сил. Факторов необходимо решить 6 уравнений равновесия.

Напряжение и деформация.

Напряжение – интенсивность внутренних сил. факторов.

– полное напряжение в точке.

Напряжение в точке

Касательные и нормальные напряжения.

Силу ΔR разложим на составляющие ΔN – нормальная и ΔQ – касательная силы.

σ – нормальное и τ – касательное напряжения.

                          

Напряжение имеет наименование силы деленной на площадь (Н/).

В системе СИ выражается в Паскалях (Па).

Связь напряжения с внутренними силовыми факторами.

    , где

N-продольная сила, вызывающая напряжение стержня

 — поперечные силы, вызывающие сдвиг.

 — крутящий момент – скручивание

 — изгибающие моменты – искривление продольной оси.

Если на тело действует сила, значит, оно деформируется. В сопромате все тела деформируются, но они крайне малы.

Центральное растяжение – сжатие.

Продольная сила.

Растяжение – вид деформации, при котором в поперечном сечении стержня возникает внутренняя продольная сила N, при этом длина увеличивается, а ширина уменьшается.

В условиях растяжения будет находиться стержень под действием осевых сил на краях (а). Равнодействующая системы равна F.

Для определения продольной внутренней силы N используют метод сечений.

Условимся считать эту силу положительной (т.е. присвоим знак «+»), если она растягивает стержень, и отрицательной – если сжимает – правило знаков.

Для определения N в произвольном сечении x стержня а) рассмотрим равновесие верхней отсеченной части б). Составляем уравнение равновесия , подставляя значения получим

-F+N=0

F=N

Знак «+» показывает, что стержень растянут.

Эпюра продольных сил.

Для суждения о прочности стержня нужно знать продольную силу в любой точке.

График (эпюру) изменения внутренних сил стоит на линии проведенной параллельно оси стержня. Каждая ордината эпюры равна N.

Участок – некоторая длина стержня, на котором отсутствует изменение площади или сил.

Пример.

Пусть стержень ОАВ нагружен силами  и имеет 2 участка ОА и АВ, на них выбраны сечения на расстоянии  и  от начала координат. В сечении  продольная сила      

в сечении  

Напряжения.

Сила N, приложенная в центре тяжести произвольного сечения стержня является равнодействующей внутренних сил, действующих на бесконечно малой площади dA поперечного сечения площади А и  . Тогда,

В пределах действия закона Гука ( ) плоские поперечные сечения стержня при деформации смещаются параллельно начальному положению, оставаясь плоскими (гипотеза плоских сечений), тогда норм. напряжение во всех точках сечения одинаково, т.е.  (гипотеза Бернулли) и тогда

При сжатии стержня напряжение имеют лишь другой (отрицательный) знак (нормальная сила направлена в тело стержня).

Деформация.

Стержень постоянного сечения площадью А под действием осевых растягивающих сил удлиняется на величину , где — длины стержня в деформированном и не деформированном состоянии. Это приращение длины называется полным или абсолютным удлинением.

Относительное удлинение – удлинение отнесенное к первоначальной длине стержня  назыв. линейной деформацией. Измеряется ε в %.

При растяжении (сжатии) возникает не только продольная, но и поперечная деформация стержня , где а – поперечный размер.

Отношение поперечной деформации к продольной  взятое по абсолютной величине, называетсякоэффициентом Пуассона.

Закон Гука. Удлинение стержня.

Между напряжением и малой деформацией существует линейная зависимость, называемая законом Гука. Для растяжения (сжатия) она имеет вид σ=Еε, где Е – коэффициент пропорциональности,модуль упругости.

Е – напряжение, которое вызывает деформацию .

Закон Гука для растяжения (сжатия) стержня.

Δl=Fe/EA=λF, где λ – коэффициент продольной податливости стержня.

ЕА – жесткость сечения стержня при растяжении.

Для стержня переменного (ступенчатого) сечения удлинение определяется по участкам (ступеням) и результаты суммируют алгебраически:

Диаграмм испытания материала.

В расчетах прочности стержня при растяжении и сжатии необходимо знать механич. Свойства материала, которые выявляются при испытаниях образцов на растяжение под нагрузкой. Испытание на растяжение позволяет судить о поведении материала и при сжатии, сдвиге, кручении и изгибе. График зависимости между растягивающей силой F и удлинением образца Δl называютдиаграммой растяжения.

Для исключения зависимости от размеров диаграмму перестаивают в координатах σ – ε.

Характеристики прочности и текучести.

Т.А – участок пропорциональности (закон сохранения Гука).

До т. С – текучесть материала.

Т. В – max значение.

Зоны:

ОА – упругости,

АД – пластичности,

ДВ – упрочения,

ВМ – местной текучести.

В зоне ОА справедлив закон Гука

Величина предела упругости близка к пределу пропорциональности.

Зона АД – зона общей пластичности. Для нее характерно существенное увеличение деформации (длины) образца без заметного увеличения нагрузки – площадка текучести (СД). Образование пластичной деформации вызвано сдвигом в кристаллической решетке.

Для оценки напряженности используют характеристику механ. свойств материала – предел текучести — напряжение, при котором в материале появляется заметное удлинение без увеличения напряжения.

Предел прочности.

Зона ДВ – зона упрочения; здесь удлинение образца возрастает более интенсивно с увеличением нагрузки по сравнению с зоной ОА. В т. В напряжение σ достигает максимума.

Если нагрузить образец в т. F, то при последующем нагружении материал приобретает способность воспринимать без остаточных деформаций воспринимать большие нагрузки.

Явление повышения упругих свойств материала в результате предварительного деформирования носит название наклепа.

Зону ВМ называют зоной местной текучести. Здесь удлинение образца происходит с уменьшением силы и сопровождается образованием местного сужения – шейки. Напряжение в поперечном сечении шейки возрастает. В т. М наступает разрушение образца. Максимальное напряжение на диаграмме, которое способен выдержать образец, называют пределом прочности  (временное сопротивление).

Пластичность и хрупкость.

Под пластичностью понимают способность материала получать большие остаточные деформации без разрушения.

Хрупкость —  способность материала разрушаться без образования заметных остаточных деформаций.

Допускаемые напряжения. Расчетные конструкции.

Условие прочности при растяжении запишется в виде , где [σ] – допускаемое напряжение, являющееся характеристикой конструкционного материала, которая зависит от принятого коэффициента запаса прочности n.

n – величина показывающая, во сколько раз предельное напряжение  для данного материала больше рабочих [σ]

Как правило, за предельное напряжение принимают предел текучести (прочности).

 

Сдвиг и кручение.

Основные вопросы:

1. Понятие сдвига

2. Закон Гука при сдвиге

3. Инженерные расчеты на сдвиг материала бруса

4. Понятие кручения бруса круглого сечения

5. Выражения касательных напряжений углов закручивания

6. Условие прочности и жесткости

7. Определение опасных сечений

8. Инженерные расчеты на кручение.

Внутренние силовые факторы и деформации. Сдвиг – вид деформации, когда в поперечном сечении стержня действует только перерезывающая сила, остальные силовые факторы – отсутствуют.Элементарные кубики искажаются, на боковых гранях возникает напряжение .

Схема сдвига. Закон Гука. Напряженное состояние, при к-м на гранях выделен. элемента возникает только касательные напряжение , называют чистым сдвигом.  а-абсолютный сдвиг, -угол, на к-й изменяются прямые углы элемента ,называют относительным сдвигом.

Уравнение равновесия отсеченной части , где G – модуль упругости, GA- жесткость при сдвиге  -з-н Гука при сдвиге,   

Расчет конструкций на сдвиг. Многие детали (склеенные, сваренные,…) подвержены сдвигу.

Условие прочности , — допускаемое напряжение на срез.

=(0,5…0,6) -для пластич. материалов

=(0,7…1,0) — для хрупких материалов

Кручение.

Кручение- вид деформации, при к-м действует только крутящий момент.

Внутренние силовые факторы. Чтобы построить эпюру, разбивают на участки, рассекая сечениями на расстояниях х1,х2,… Диаграмму, показывающую расраспределение значений крут. моментов по длине вала, называют эпюрой крутящих моментов. Правило знаков: момент, направленный против часовой стрелки- положителен, по стрелке- отриц.

Построение эпюры крутящих моментов. Ур-е равновесия  или -правая часть аналогично рассмат все сечения.

Вывод: в любом сечении вала действует крутящий момент, = сумме вращающих моментов, лежащих по одну сторону от этого сечения. Эпюра крутящих моментов — ступенчатая линия, к-я показывает степень нагружаемости каждого из участков вала.

Деформации при кручении. При кручении образующие цилиндра обращаются в винтовые линии, круглые и  плоские сечения сохраняют свою форму, поворот одного сечения относительно другого происходит на некоторый угол закручивания, расстояние между поперечными сечениями почти не меняется. Сечения, плоские до закручивания, остаются плоскими после закручивания, радиусы поперечных сечений при деформации остаются прямыми.

Кручение – результат сдвигов при взаимном повороте сечений.

Схема нагружения бруса.

,где -угол закручивания на единичной длине стержня.

— относит. угол закручивания.

Геометрия сдвига.

Значения касат. напряжений в точках сечения пропорциональны расст. её от оси стержня.

Момент кручения.

Напряжение при кручении.

-геометрич. характеристика- полярный момент инерции сечения.

-угол закручивания на ед. стержня. -полярный момент сопротивления сечения. 

Полярный момент инерции и сопротивления.

 -поляр. момент инерции.  ,    , для круглого сечения- 

Расчетные формулы. ,   ,  ,   ,  условие жесткости:

Расчеты на прочность и жесткость.

Условие прочности:  .Диаметр вала сплошного сечения

— угол закручивания- определяет жесткость.

Вал рассчитывают по 2 условиям и из найденных значений находят большее.

Изгиб.

Основные вопросы:

1. классификация изгибов

2. нагрузки и внутренние силовые факторы

3. построение эпюр нагрузок, правило знаков

4. нормальные напряжение при чистом изгибе

5. касательные напряжения при чистом изгибе

6. перемещение при изгибе

7. дифференциальное уравнение упругой линии балки

8. определение перемещений методом непосредственного интегрирования

Классификация изгибов. Изгиб – вид деформации, когда под действием внешних сил в поперечном сечении стержня (бруса) возникают изгибающие моменты.

Если изгибающий момент в сечении является единственным силовым фактором, а поперечные и нормальные силы отсутствуют, наз-ся чистым. Если в поперечных сечениях стержня наряду с изгибающими моментами действуют  и поперечные силы, изгиб наз-ся поперечным.

Иногда в поперечном стержне возникает несколько силовых факторов. Это сложное сопротивление. Расчеты стержней основываются на принципе независимости действия сил.

Опоры и их реакции. Для передачи нагрузок стержень должен быть зафиксирован относительно корпуса с помощью опор- устройств, воспринимающих внешние силы.

Различают 3 основных вида опор-  жесткое защемление: 1) заделка- а) исключает осевые , угловые смещения и воспринимает осевые силы и моментную нагрузку, 

2) шарнирно-неподвижная опора –б) ,- допускает поворот вокруг оси и не воспринимает момент,

3) шарнирно- подвижная опопра -в),-не допускает смещение стержня, только в направлении 1 из осей и передает нагрузку вдоль этой силы.

Опорные реакции. Под действием внеш. Нагрузок в местах закрепления стержня возникает опорная реакции. х находят из условий равновесия. Анализ внутренних сил начинается после определения реакции.

Внутренние силовые факторы. Стержень на 2-х опорах, нагруженный силами F. Из условия равновесия найдем опорные реакции:  . Под действием внеш. сил и опорных реакций стержень б) будет находиться в равновесии. Для определения внутренних силовых факторов в сечении m1-mi участка CD стержня мысленно разрежем на 2 части , рассмотрим равновесие левой в). Чтобы она была в равновесии, приложим к т. Сi неизвестные внутренние силовые факторы: нормальную силу Nx(xi), перерезывающую , изгибающий момент.

Правило знаков. Положит. изгибающий момент изгибает горизонтально расположенный стержень (балку ) выпуклостью вниз (а), а отриц. – выпуклостью вверх (б).

Положит. поперечная сила стремится сдвинуть левое сечение стержня вверх относительно правого или правое вниз относительно  левого (а). Отриц. поперечная сила имеет противоположное направление (б).

Определение силовых факторов. Перерезывающая сила в сечении стержня = сумме проекций на ось у всех внешних сил, действующих на мысленно отсеченную часть, т.е. . Изгибающий момент в сечении стержня равен сумме моментов внешних сил, действующих на отсеченную часть, взятых относительно центра тяжести рассматриваемого сечения, т.е.

.

Ур-я статики: , , (чистый изгиб). Если сделать сечение m2-m2 на участке АС и рассмотреть равновесие левой части, то найдем, что при  силовые факторы: (поперечный изгиб)

Схема чистого изгиба. Поля прилож. М продольной силы – дуги окружности, поперечного сечения остаются плоскими, т.е. гипотеза плоских сечений справедлива. При чистом изгибе волокна на выпуклой стороне растягиваются, на вогнутой — сжимаются. Существует слой, в котором удлинения отсутствует,  его называют нейтральным слоем — нейтральной линией.

Связь напряжений и внутренних факторов. Допускаем, стержень – совокупность растянутых и сжатых элементов стержней длинной l, которые свободно удлиняются и укорачиваются. Нормальные напряжения применяют постоянными по ширине сечения.

Статическая часть задачи. Условие равновесия между силовыми факторами:

 Условия б), в),г) удовлет-ся тождественно, условия а),е),д) имеют вид: .

Деформация волокон.  ,- относительное удлинение слоя.

Деформация некоторого слоя зависит от его координат z, отсчитываемой от нейтрального слоя. Используем з-н Гука: . Отношение  — постоянно для конкретного материала и конкретного случая изгиба. Поэтому напряжения — линейная функция координат z. Для нахождения величины нужно знать положение нейтрального слоя или радиус кривизны .

Нормальное напряжение при изгибе.

Из уравнений   а), д), е) с учетом к.

Из ур-я а), т.к. то — это статический момент площади поперечного сечения. Нейтральная ось является центральной осью. Из ур-я е)  получим  Это центробежный момент инерции, если он = 0 — оси главные, центральные. Из ур-я  д) :

 где . Расчетная формула полученна путем подстановки в последнюю зависимости  из формулы к.

Расчетные формулы.  

условие прочности:

Как следует из характеристики распределения, напряженные внутренние слои материала оказываются недогруженными.

Силовые факторы при поперечном изгибе. Гипотезы сопромата распространяются на поперечный изгиб.

Формула касательных напряжений. Выразим силы через нормальное напряжение, а напряжение — через изгибающие моменты, с учетом продольной силы, вызывающей касательное  напряжение получаем:

,    где А0- площадь отсеченной части. -статический момент отсеченной части. На поверхности в центре = max.

Характер перемещения при изгибе. При изгибе есть 2 типа перемещений: линейные и угловые .

,     при малых перемещениях.

Уравнение изогнутой оси.

— дифференциальное Ур-е изогнутой оси балки.

 

 

Основы направленного состояния материала.

Основные вопросы:

1. виды напряженного состояния

2. напряжения на наклонных площадках

3. закон парности касательных напряжений

4. главные площадки и главные напряжения

5. объемная деформация. Закон Гука

6. удельная потенциальная энергия

7. критерии пластичности и разрушения

8. эквивалентные напряжения

9. гипотезы прочности

Виды напряженного состояния. Оценка прочности детали – это совокупность напряженного состояния в «опасной» точки конструкции с пределом прочности материала. Такая оценка оказывается достаточно точной при одноосновном напряженном состоянии (растяжение, сжатие).

Однако многие элементы конструкции работают в условиях сложного напряженного состояния. Тогда совокупность напряжений в точке элемента сопоставляемыми с механическими характеристиками его материала, то есть вводится эквивалентное напряжение, т.е. напряжение в растянутом  образце при котором состояние равноопасно  с заданным.

studfiles.net

решение задач. Лекции. Кручение. Деформации и перемещения при кручении валов.

Меню сайта Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления. Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. + Полное расписанное решение! Теперь и для статически неопределимых балок! Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты

Базовый курс лекций по сопромату, теория, практика, задачи. ::Оглавление:: 2. Кручение. 2.3. Деформации и перемещения при кручении валов. Для вычисления деформаций вала при кручении воспользуемся формулой (2.7)           (2.17) Деформация вала на длине z (взаимный угол сечений) равна           (2.18) Если крутящий момент и величина GIp, называемая жесткостью вала при кручении, постоянны на всем участке интегрирования, то           (2.19) Аналогично, для вала длиной l получим           (2.20) Эта формула по своей структуре аналогична формуле для определения деформаций при растяжении — сжатии. Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания. Он равен           (2.21) Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого, т.е.           (2.22) Эта формула выражает условие жесткости вала при кручении. В этой формуле — допускаемый относительный угол закручивания в радианах на единицу длины вала. В большинстве случаев допускаемый относительный угол закручивания задают в градусах на 1 м длины, тогда из формулы (2.22) получим:           (2.23) Угол выбирают в зависимости от назначения вала и его размеров. Для валов средних размеров в «Справочнике машиностроителя» рекомендуется принимать допускаемый угол закручивания равным 0,5 градуса на 1 метр длины. Из условия (2.23) можно определить диаметр вала по заданной жесткости. Получаем           (2.24) ::Оглавление::

Сообщество Вход Решение задач Расчет редукторов Для Android (рекомендую) NEW Mobile Beam 2.0 Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME

www.sopromat.org

Сопротивление материалов. Основные понятия и определения

Основные определения

 

Сопротивление материалов — раздел физики, изучающий механические свойства различных материалов, используемых в строительстве и машиностроении

Сопротивление материалов позволяет определить прочность, жесткость и устойчивость элементов строительных конструкций и деталей машин, тем самым обеспечить долгую и надежную работу сооружений, машин и механизмов.

Объекты рассмотрения — твердые тела

Вещества и комбинации веществ, из которых состоят тела, и являются рассматриваемыми материалами. Все твердые тела по геометрической форме можно условно разделить на 3 группы:

1. Стержни — твердые тела, длина l которых значительно больше высоты h и ширины b.

Это можно выразить соотношением длины к высоте или ширине. Стержни можно условно разделить на 3 категории:

1.1. Стержни с соотношением l/h ≥ 10.

1.2. Стержни с соотношением 5 < l/h < 10.

1.3. Стержни с соотношением l/h ≤ 5. Чем меньше значение соотношения l/h или l/b, тем больше тело по своей геометрической форме приближается к пластине или массивному телу.

2. Пластины — тела, высота которых значительно меньше длины и ширины.

3. Массивные тела — тела, длина, ширина и высота которых сопоставимы.

Примечание: определение длины, ширины и высоты зависит от выбора системы координат. Например и балка перекрытия и колонна могут рассматриваться как стержни, а стена и плита перекрытия — как пластины.

Основной объект рассмотрения — стер­жень (балка, брус).

Так как высота и ширина стержня значительно меньше длины, то для решения множества задач на начальной стадии высотой и шириной стержня пренебрегают, а для расчетов используют только один параметр — длину стержня. Таким образом на чертежах стержень изображается как линия, имеющая некоторую длину l. Из курса геометрии нам известно, что линия может быть прямой, кривой, находящейся в одной плоскости, и кривой, для корректного описания которой нужно задавать координаты в трех плоскостях. То же можно сказать и о стержнях.

Ось стержня — линия, проходящая через центры тяжести поперечных сечений стержня.

Таким образом линия, изображающая стержень на чертежах, совпадает с осью стержня. Часто ось стержня называется упругой линией, нейтральной линией или нейтральной осью.

Поперечное сечение — сечение стержня в плоскости, перпендикулярной оси стержня.

Основными характеристиками поперечного сечения являются высота и ширина, а так как поперечное сечение перпендикулярно оси стержня, то высота и ширина поперечного сечения являются высотой и шириной стержня в рассматриваемом сечении. При решении некоторых строительных задач рассматриваются не только поперечные, но и наклонные сечения — сечения в плоскости, расположенной под некоторым углом к поперечному сечению или оси стержня. Для получения любого возможного сечения не нужна грубая физическая сила, а только сила мысли и немного пространственного воображения.

Расчет прочности — определение наименьших размеров поперечного сечения элементов конструкции

при которых исключается возможность разрушения конструкции при действии заданных нагрузок. Другими словами напряжения, возникающие в рассматриваемых поперечных сечениях, не должны превышать расчетного сопротивления материала.

Расчет жесткости — определение деформаций материала

возникающих под действием заданных нагрузок. Так как не существует материалов, имеющих бесконечно большую жесткость, то деформации материала конструкции приводят к изменению геометрической формы элементов конструкции, а значит и к перераспределению внутренних напряжений.

Устойчивость — состояние элементов конструкции

при котором изменение первоначальной геометрической формы под действием нагрузок и возникающего при этом перераспределения внутренних напряжений не приводит к разрушению конструкции.

Деформация — изменение геометрических размеров и первоначальной формы физического тела при действии сил.

Деформации рассматриваются как перемещение точек, линий и плоскостей.

Линейная деформация — перемещение рассматриваемой точки, линии или поперечного сечения относительно только одной из выбранных осей координат.

Линейная деформация измеряется в единицах длины.

Угловая деформация — перемещение, характеризуемое углом поворо­та рассматриваемой линии или поперечного сечения

относительно некоторой точки.

Абсолютная деформация — величина линейной де­формации

на рассматриваемом участке длины элемента конструкции.

Относительная деформация — отношение абсолютной деформации к длине

рассматриваемого участка.

Пластические (остаточные) деформации — изменения геометрических размеров и формы тела

остающиеся после снятия нагрузки.

Упругие деформации — деформации тела под действием нагрузок, не приводящие к остаточным деформациям после снятия нагрузок

Другими словами остаточные деформации, при упругой деформации равны нулю.

Упругость — свойство материала полностью восстанавливать первоначальную геометрическую форму тела

после снятия нагрузок.

Пластичность — свойство материала накапливать остаточные деформации

Все материалы обладают определенными упругими и пластичными свойствами. Например изготовление профилированного листа из листа металлопроката происходит в результате накопления остаточных деформаций. 

Сжатие или растяжение — такое воздействие на материал, при котором силы, действующие на стержень, направлены по оси или параллельно оси стержня.

Если силы направлены по оси, то такой элемент конструкции называют центрально сжатым или центрально растянутым. Если силы приложены на некотором расстоянии от оси, то такой элемент называют внецентренно сжатым или внецентренно растянутым, при этом расстояние от оси до точки приложения силы называется эксцентриситетом е.

Кручение — воздействие на материал пары сил, действующих в плоскости, перпендикулярной к оси стержня

т.е. в плоскости поперечного сечения

Изгиб — воздействие на материал пары сил, направленных в плоскости, проходящей через ось стержня.

т.е. в плоскости, перпендикулярной плоскости поперечного сечения.

Момент — создается любой парой сил, направленных не по одной прямой, а параллельно, а также любой силой, расположенной на некотором расстоянии от рассматриваемого сечения.

Моменты могут быть крутящими и изгибающими. Момент, возникающий при внецентренном растяжении или сжатии, является изгибающим.

Изотропный материал — материал, физико-механические свойства которого постоянны и одинаковы во всех направлениях

К изотропным материалам условно можно отнести металлы, камень, стекло.

Ортотропный материал — материал, физико-механические свойства которого постоянны, но не одинаковы в различных направлениях

Представителем такого материала является древесина.

Анизотропный материал — материал, не имеющий свойств изотропности или ортотропности

Свойства анизотропных материалов не являются предметом рассмотрения теории сопротивления материалов. Между тем не существует природных или искусственных материалов, имеющих идеальную упругость, изотропию или отротропию. Кроме того изготовить конструкцию идеальной геометрической формы практически невозможно. Это означает, что для точных расчетов необходимо учитывать все изменения геометрической формы, а также возможные отклонения от заданных физико-механических свойств. Однако в подавляющем большинстве случаев для обеспечения надежной работы строительной конструкции, машины или механизма достаточно выполнить приближенный (упрощенный) расчет. Выполняется такой расчет на основании следующих допущений.

 

Основные допущения, принимаемые в теории сопротивления материалов

 

1. Рассматриваемый материал является изотропным (или ортотропным) и идеально упругим.

2. Деформации материала пропорциональны приложенной нагрузке, не превышающей некоторой предельной величины, т.е рассматриваемые тела являются линейно-деформируемыми.

3. При составлении уравнений равновесия деформациями материала можно пренебречь, так как деформации рассматриваемых элементов значительно меньше геометрических размеров элементов. В данном случае не только значительно меньше длины, но также высоты и ширины.

4. При расчетах допускается использовать принцип независимости действия сил, т.е. упругую деформацию под действием нескольких сил можно рассматривать как сумму упругих деформаций от каждой отдельно взятой силы.

5. Предполагается, что сечения которые были плоскими до приложения нагрузок, остаются плоскими при деформациях материала.

 

Внешние и внутренние силы

 

Все силы, действующие на тело, можно условно разделить на внешние и внутренние. Условно потому, что силы тяжести, действующие на каждую частицу тела, находятся как бы внутри тела, а внутренние силы (силы взаимодействия между элементарными частицами вещества) действуют и до того, как к телу приложена какая-либо внешняя сила.

Потому внешние силы, вызывающие деформацию материала, чаще называют нагрузками, а разницу внутренних сил, возникающую при деформации — напряжениями или внутренними усилиями, подобно тому как в электротехнике напряжением называется разница потенциалов

Единицей измерения силы является Ньютон (Н) или килоНьютон (кН). Однако в технической литературе нередко встречается и другая единица — килограмм-сила (кгс) или тонно-сила (тс). Измерение силы в Ньютонах является более правильным. Так как сила есть произведение массы на ускорение, то тело массой в 1 кг создает нагрузку Q = mg = 1·9.81 м/с² = 9.81 кг·м/с² = 9.81 Н. Это означает, что при расчетах значения нагрузок вряд ли будут круглыми. И потому пользоваться при расчетах килограмм-силами или тонно-силами удобнее. Считается, что тело массой 1 кг создает нагрузку 1 кгс.

Внешние силы по характеру приложения можно разделить на четыре вида:

1. Объемные — действующие на все точки тела. Измеряются в Н/м³. 

2. Плоские (поверхностные) — распределенные на некоторой площади поверхности тела. Измеряются в Н/м².

3. Линейные (распределенные) — распределенные непрерывно по некоторой длине. Измеряются в Н/м.

Интенсивность нагрузки — это величина распределенной нагрузки, приложенной к единице объема, площади или длины.

Так как при расчетах изначально рассматривается ось стержня, не имеющая высоты и ширины, то объемные и плоские нагрузки часто приводятся к линейной. Это допускается делать без каких-либо поправочных коэффициентов, если интенсивность объемной или плоской нагрузки является постоянной.

4. Точечные (сосредоточенные) — приложенные в одной точке.

В природе точечных нагрузок не существует. Любая нагрузка прикладывается к некоторой площади, но если площадь приложения нагрузки, точнее длина приложения нагрузки после приведения плоской нагрузки к линейной, значительно меньше длины тела, то такую нагрузку можно условно рассматривать, как сосредоточенную в одной точке. Переход от сосредоточенной нагрузки к равномерно распределенной и наоборот осуществляется только с помощью соответствующих коэффициентов.

По времени действия нагрузки делятся на постоянные и временные

Постоянные нагрузки, например, собственный вес конструкции, действуют в течение всего срока службы. Временные нагрузки ограничены по времени действия.

По характеру изменения во времени нагрузки делятся на статические и динамические

Статические нагрузки прикладываются как бы постепенно, поэтому инертные силы, возникающие при движении инертных масс, при расчетах не учитываются. Динамические нагрузки прикладываются очень быстро и потому при расчетах влияние инертных сил необходимо учитывать.

Все вышеприведенные нагрузки рассматриваются как активные.

Напряжение — величина внутренней силы, приложенной к единице площади рассматриваемого сечения

Равнодействующую внутренних сил, действующую на рассматриваемую площадь, называют внутренним усилием.

Примечание: распределенные нагрузки как правило обозначаются литерой «q» вне зависимости от того, объемная, плоская или линейная нагрузка имеется в виду. Сосредоточенная нагрузка часто обозначается литерой «P», однако я предпочитаю обозначать сосредоточенную нагрузку литерой «Q», а литерой «P» — реактивные внутренние усилия, соответственно литерой «p» — реактивные напряжения.

 

Уравнения равновесия. Метод сечений

 

Так как рассматриваемое тело должно быть неподвижным в заданной системе координат, то все опоры тела можно заменить на реактивные силы — опорные реакции. Опорные реакции также рассматриваются как внешние силы. При этом для соблюдения равновесия (неподвижности рассматриваемого тела) сумма активных и реактивных сил, действующих на тело относительно любой координатной оси, должна быть равна нулю. На основании этого предположения составляются уравнения равновесия системы. Кроме того, если рассечь тело в любом месте, то чтобы тело по-прежнему оставалось в состоянии равновесия к полученному сечению нужно приложить некоторую внешнюю силу Q. Значение внешней силы определяется, исходя из условий равновесия. А так как сила действия равна силе противодействия, то считается, что внутренние усилия Р или напряжения р, возникающие в результате действия внешних сил (нагрузок) равны по значению нагрузкам, приложенным в рассматриваемом сечении и направлены в противоположную сторону. Такой метод расчета и называется методом сечений.

Примечание: Для решения статически неопределимых задач одних только уравнений равновесия и уравнения моментов недостаточно.

Рисунок 317.1

Так как напряжения, возникающие в рассматриваемых сечениях под действием внешних сил, редко бывают равномерно распределенными (не имеют постоянной интенсивности), то для решения задач сопротивления материалов важно знать не просто значение внутренних усилий, но также и значение напряжений в наиболее опасных точках сечения. Отношение внутреннего усилия ΔР, действующего на некоторой площади ΔF рассматриваемого сечения будет приближаться к некоторому пределу, если площадь ΔF будет стремиться к нулю (к точке А). Этот предел, как мы выяснили ранее, называется напряжением и определяет интенсивность внутренних усилий, действующих на рассматриваемую площадку в точке А. Напряжения могут быть различны не только в разных точках одного сечения, но и в одной и той же точке А, общей для различных сечений, т.е. сечений, рассекающих тело под различными углами.

Ось, перпендикулярная плоскости сечения, называется нормалью.

Полное напряжение в точке А, имеющей координаты (х, у, z) для сечения с нормалью n определяется по формуле:

(317.1)

где ΔР — элементарное внутреннее усилие, возникающее при отбрасывании части II тела и замене этой части элементарной внешней силой ΔQ, действующей на оставшуюся часть I для соблюдения условий равновесия.

Нормальное напряжение σ_n действует в направлении нормали

Если усилие ΔР не перпендикулярно рассматриваемой плоскости сечения (как на рисунке 317.1), то значение нормального напряжения можно определить по формуле:

(317.2)

Касательное напряжение т_n действует в плоскости сечения

Значение касательного напряжения можно определить по формуле:

(1.3)

Напряжения измеряются в Паскалях (Па) или МегаПаскалях (МПа), а также в кгс/см² или тс/см².

дальше

doctorlom.com

Виды деформации | ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Перейти к содержимому

• Введение
  • Задачи Сопромата
  • Основные понятия Сопромата
  • Основные допущения и гипотезы
• Материалы
  • Внутренние силы. Метод сечений
  • Напряжения
  • Механические и пластические свойства материалов
  • Напряженное и деформированное состояние в точке
  • Разрушения. Коэффициент запаса прочности
  • Критерии прочности
• Сопромат
  • Геометрические характеристики сечений
  • Растяжение — Сжатие
  • Теория напряженного и деформированного состояния в точке
  • Сдвиг
  • Кручение
  • Изгиб
  • Определение перемещений
  • Теории прочности
  • Метод сил
  • Сложное сопротивление
  • Устойчивость
  • Продольно-поперечный изгиб
  • Динамические нагрузки
  • Усталость
  • Теория накопления повреждений
  • Ползучесть и релаксация
• Задачи
  • Задачи на геометрические характеристики
  • Задачи на растяжение-сжатие
    • Статически неопределимые задачи. Р-С
    • Статически определимые задачи. Р-С
  • Задачи на кручение
    • Статически неопределимые задачи. Кручение
    • Статически определимые задачи. Кручение
  • Задачи на изгиб
    • Задачи на эпюры
    • Расчет на прочность
  • Задачи на определение перемещений
  • Задачи на напряженное и деформированное состояние в точке
  • Задачи на метод сил
  • Задачи на сложное сопротивление
  • Задачи на устойчивость
  • Задачи на динамические нагрузки
  • Задачи на переменные напряжения
  • Расчет вала
• История Сопромата
  • Об Истории
  • Великие учёные
  • Очерки из истории науки
    • Античная механика
    • Механика Средневековья
    • Механика эпохи Возрождения
    • Классическая механика
    • История механики в России
    • Развитие механики в Советском Союзе (СССР)
    • Отец русской авиации — Н.Е. Жуковский
    • К.Э. Циолковский. К звездам
    • А.Н. Крылов
    • И.В.Мещерский
• Студентам
  • Учиться без проблем
  • Формы занятий в ВУЗе
  • Конспектирование
  • Сессия, Экзамены
  • Про общежитие
  • Как устроиться на работу
• Вопросы и Ответы
  • Обозначения Сопромата
  • Вопросы
• Поиграем?
• Разное
• Прикладная механика
• Теория упругости
• Строительная механика
• Таблицы
• Словарь определений
• Сопромат в схемах
• Из В.И. Феодосьева
  • Десять лекций-бесед по сопротивлению материалов
  • Избранные задачи и вопросы по сопротивлению материалов
    • Растяжение, сжатие и кручение
    • Геометрические свойства сечений. Изгиб
    • Сложное напряженное состояние и теории прочности
    • Устойчивость
    • Разные вопросы и задачи
• Бегство от удивлений Г. Анфилова
  • Удивление падению
    • Камень и пушинка

Запись опубликована 02.01.2015 автором admin в рубрике Сопромат в схемах.

Навигация по записям

← Метод сечений Применение метода сечений →

Найти:

Рубрики

• А.Н. Крылов
• Античная механика
• Без рубрики
• В поисках покоя
• В прошлое путь закрыт
• Введение
• Вдоль мира
• Вдоль поверхности
• Вдоль пространства
• Великие учёные
• Внутренние силы. Метод сечений
• Вопросы
• Вопросы и Ответы
• Вопросы по механике
• Геометрические свойства сечений. Изгиб
• Геометрические характеристики сечений
• Говорят диаграммы
• Десять лекций-бесед по сопротивлению материалов
• Деформация изгиба
• Динамические нагрузки
• Задачи
• Задачи на геометрические характеристики
• Задачи на динамические нагрузки
• Задачи на изгиб
• Задачи на кручение
• Задачи на метод сил
• Задачи на напряженное и деформированное состояние в точке
• Задачи на определение перемещений
• Задачи на переменные напряжения
• Задачи на растяжение-сжатие
• Задачи на сложное сопротивление
• Задачи на устойчивость
• Задачи на эпюры
• Задачи по механике
• Задачи Сопромата
• Зоркий маятник
• И.В.Мещерский
• Избранные задачи и вопросы по сопротивлению материалов
• Изгиб
• История механики в России
• История Сопромата
• К.Э. Циолковский. К звездам
• Как изготовить тяжесть
• Как устроиться на работу
• Камень и пушинка
• Классическая механика
• Конспектирование
• Критерии прочности
• Кручение
• Лекции-беседы. Избранные вопросы и задачи В.И. Феодосьева
• Материалы
• Метод сил
• Механика Средневековья
• Механика эпохи Возрождения
• Механические и пластические свойства материалов
• Мир — взрыв
• Могущество механики
• На вращающемся стадионе
• На языке графиков
• Напряжения
• Напряженное и деформированное состояние в точке
• Об Истории
• Обозначения Сопромата
• Определение опорных реакций
• Определение перемещений
• Основные допущения и гипотезы
• Основные понятия и определения статики
• Основные понятия Сопромата
• Отец русской авиации — Н.Е. Жуковский
• Очерки из истории науки
• Пара сил и моменты сил
• Повиновение Эйнштейну
• Поиграем?
• Покаяние и напутствие
• Ползучесть и релаксация
• Постулаты Эйнштейна
• Почему падает камень
• Прикладная механика
• Про общежитие
• Продольно-поперечный изгиб
• Развитие механики в Советском Союзе (СССР)
• Разное
• Разные вопросы и задачи
• Разрушения. Коэффициент запаса прочности
• Растяжение — Сжатие
• Растяжение, сжатие и кручение
• Расчет вала
• Расчет на прочность
• Самый большой аквариум
• Сверхбыстрые приключения
• Свет и эфир
• Сдвиг
• Сейфы энергии
• Сессия, Экзамены
• Система произвольно расположенных сил
• Система сходящихся сил
• Следствия — после причин
• Словарь определений
• Сложное напряженное состояние и теории прочности
• Сложное сопротивление
• Сомнения и возражения
• Сопромат
• Сопромат в схемах
• Статически неопределимые задачи. Кручение
• Статически неопределимые задачи. Р-С
• Статически определимые задачи. Кручение
• Статически определимые задачи. Р-С
• Строительная механика
• Студентам
• Сюрпризы инерции
• Таблицы
• Теории прочности
• Теория накопления повреждений
• Теория напряженного и деформированного состояния в точке
• Теория упругости
• Усталость
• Устойчивость
• Устойчивость
• Учиться без проблем
• Формы занятий в ВУЗе
• Царица мира
• Что такое движение
• Что такое инерция
• Энергия, спрятанная в веществе

1777

prosopromat.ru

Перемещения при растяжении (сжатии)

Определение перемещений (деформаций) является важной задачей. По величине абсолютного перемещения можно судить о жесткости конструкции. Этот параметр является неотъемлемой частью любого инженерного расчета.

Студенты, как правило, оттачивают полученные теоретические знания на практике по разделу растяжение (сжатие) на брусьях различной формы. Поэтому рассказывать о методике определений перемещений сразу буду на примере брусьев.

Формула для определения перемещения:

В случае если брус имеет постоянную форму поперечного сечения, а также одинаковую величину продольной силы в поперечных сечениях,  хотя бы в пределах отдельных участков, то перемещение (удлинение/укорочение бруса) можно определить по формуле:

где N –продольная сила; l—первоначальная длина бруса, до нагружения; E – модуль упругости; A – площадь поперечного сечения.

Данная формула является следствием закона Гука.

Если поперечное сечение бруса не постоянное и меняется по определенному закону, то придется использовать формулу с интегралом:

Причем, сложность зачастую заключается не в решении интеграла, а в определении закона изменения поперечного сечения.

Тепловое расширение

Также, нужно знать, что перемещение зависит не только от приложенной нагрузки, но и от температуры. Понятно, что если речь идет о комнатной температуре, то и фактор этот нет смысла учитывать. А если брус работает в суровых условиях, при температуре, скажем, 600^оС, то перемещение следует вычислять по формуле:

где α — коэффициент линейного расширения.

ssopromat.ru