определение и формула — OneKu

Содержание статьи:

• Второй и третий законы Ньютона
• Сила реакции опоры
• Физическая причина появления силы N
• Как вычислять силу N
• Задача со стаканом на столе
• Задача с доской, двумя опорами и грузом

Статика — один из разделов современной физики, который изучает условия нахождения тел и систем в механическом равновесии. Для решения задач на равновесие важно знать, что такое сила реакции опоры. Данная статья посвящена подробному рассмотрению этого вопроса.

Второй и третий законы Ньютона

Прежде чем рассматривать определение силы реакции опоры, следует вспомнить о том, что вызывает движение тел.

Причиной нарушения механического равновесия является действие на тела внешних или внутренних сил. В результате этого действия тело приобретает определенное ускорение, которое вычисляется с помощью следующего равенства:

Вам будет интересно:Понятие о равноускоренном движении. Формулы перемещения и скорости. Равноускоренное вращение

F = m*a

Эта запись известна как второй закон Ньютона. Здесь сила F является результирующей всех действующих на тело сил.

Если одно тело воздействует с некоторой силой F1¯ на второе тело, то второе оказывает действие на первое с точно такой же по абсолютной величине силой F2¯, но она направлена в противоположном направлении, чем F1¯. То есть справедливо равенство:

Вам будет интересно:«Тлетворный» — это о разложении

F1¯ = -F2¯

Эта запись является математическим выражением для третьего ньютоновского закона.

При решении задач с использованием этого закона школьники часто допускают ошибку, сравнивая эти силы. Например, лошадь везет телегу, при этом лошадь на телегу и телега на лошадь оказывают одинаковые по модулю силы. Почему же тогда вся система движется? Ответ на этот вопрос можно правильно дать, если вспомнить, что обе названные силы приложены к разным телам, поэтому они друг друга не уравновешивают.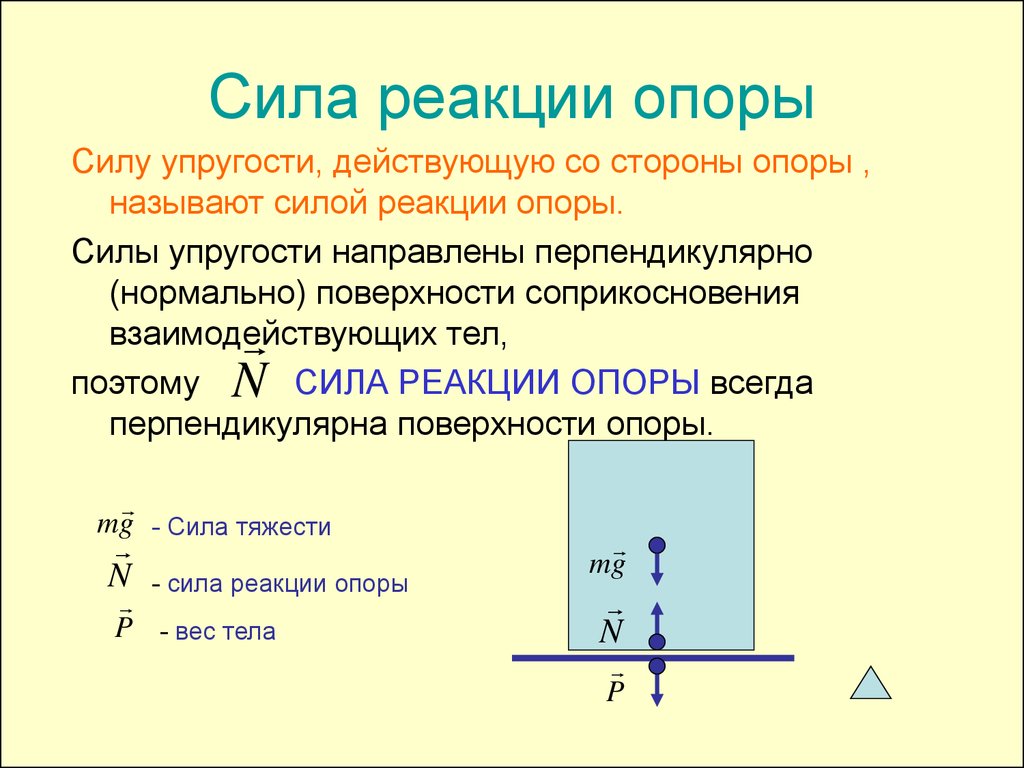

Сила реакции опоры

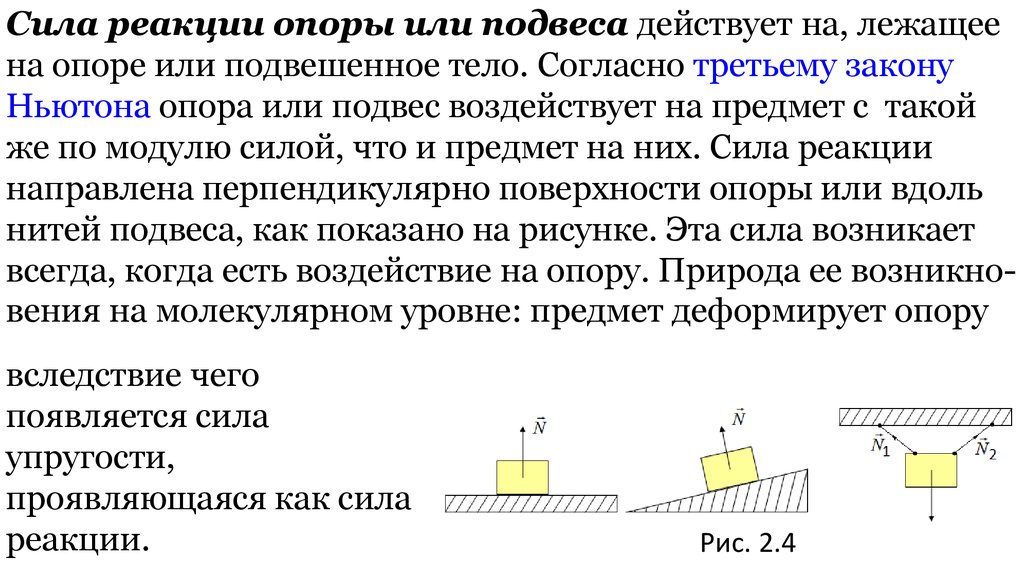
Сначала дадим физическое определение этой силы, а затем поясним на примере, как она действует. Итак, силой нормальной реакции опоры называется сила, которая действует на тело со стороны поверхности. Например, мы поставили стакан с водой на стол. Чтобы стакан не двигался с ускорением свободного падения вниз, стол воздействует на него с силой, которая уравновешивает силу тяжести. Это и есть реакция опоры. Ее обычно обозначают буквой N.

Сила N — это контактная величина. Если имеется контакт между телами, то она появляется всегда. В примере выше значение величины N равно по модулю весу тела. Тем не менее это равенство является лишь частным случаем. Реакция опоры и вес тела — это совершенно разные силы, имеющие различную природу. Равенство между ними нарушается всегда, когда изменяется угол наклона плоскости, появляются дополнительные действующие силы, или когда система движется ускоренно.

Сила N называется нормальной потому, что она всегда направлена перпендикулярно плоскости поверхности.

Если говорить о третьем законе Ньютона, то в примере выше со стаканом воды на столе вес тела и нормальная сила N не являются действием и противодействием, поскольку обе они приложены к одному телу (стакану с водой).

Физическая причина появления силы N

Как было выяснено выше, сила реакции опоры препятствует проникновению одних твердых тел в другие. Почему появляется эта сила? Причина заключается в деформации. Любые твердые тела под воздействием нагрузки деформируются сначала упруго. Сила упругости стремится восстановить прежнюю форму тела, поэтому она оказывает выталкивающее воздействие, что проявляется в виде реакции опоры.

Если рассматривать вопрос на атомном уровне, то появление величины N — это результат действия принципа Паули. При небольшом сближении атомов их электронные оболочки начинают перекрываться, что приводит к появлению силы отталкивания.

Многим может показаться странным, что стакан с водой способен деформировать стол, но это так. Деформация настолько мала, что невооруженным глазом ее невозможно наблюдать.

Как вычислять силу N?

Сразу следует сказать, что какой-то определенной формулы силы реакции опоры не существует. Тем не менее имеется методика, применяя которую, можно определить N для совершенно любой системы взаимодействующих тел.

Методика определения величины N заключается в следующем:

• сначала записывают второй закон Ньютона для данной системы, учитывая все действующие в ней силы;
• находят результирующую проекцию всех сил на направление действия реакции опоры;
• решение полученного уравнения Ньютона на отмеченное направление приведет к искомому значению N.

При составлении динамического уравнения следует внимательно и правильно расставлять знаки действующих сил.

Найти реакцию опоры можно также, если пользоваться не понятием сил, а понятием их моментов. Привлечение моментов сил справедливо и является удобным для систем, которые имеют точки или оси вращения.

Далее приведем два примера решения задач, в которых покажем, как пользоваться вторым ньютоновским законом и понятием момента силы для нахождения величины N.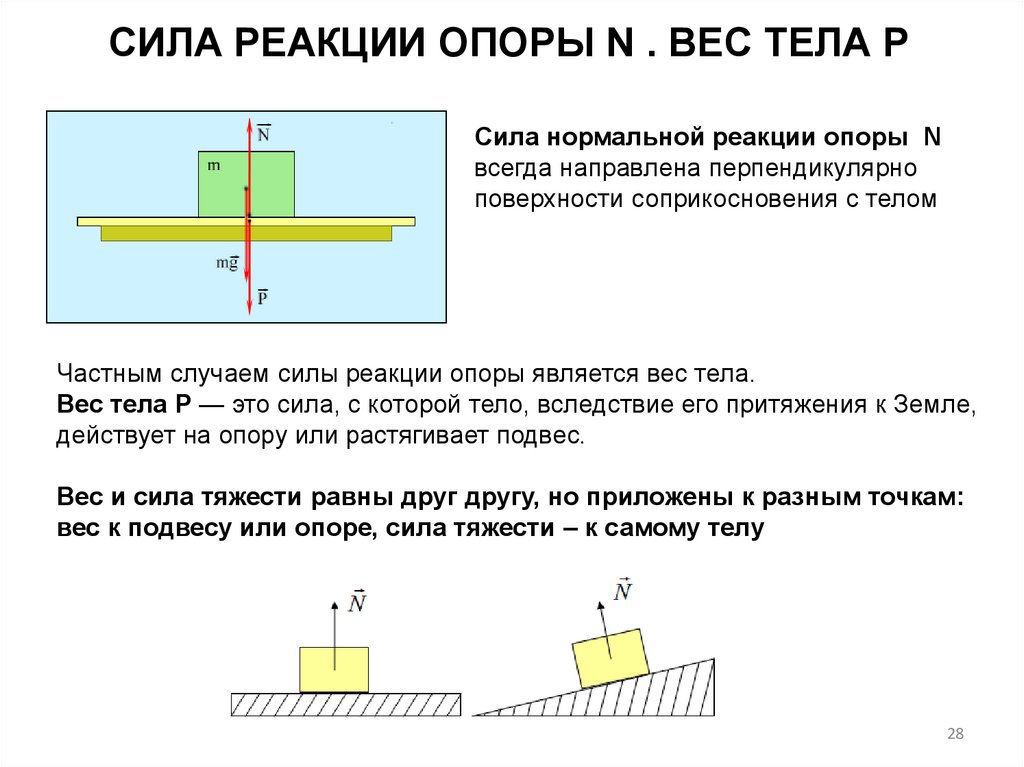

Задача со стаканом на столе

Выше уже был приведен этот пример. Предположим, что пластиковый стакан объемом 250 мл наполнен водой. Его поставили на стол, а сверху на стакан положили книгу массой 300 грамм. Чему равна сила реакции опоры стола?

Запишем динамическое уравнение. Имеем:

m*a = P1 + P2 — N

Здесь P1 и P2 — вес стакана с водой и книги соответственно. Поскольку система находится в равновесии, то a=0. Учитывая, что вес тела равен силе тяжести, а также пренебрегая массой пластикового стакана, получаем:

m1*g + m2*g — N = 0 =>

N = (m1 + m2)*g

Учитывая, что плотность воды равна 1 г/см3, и 1 мл равен 1 см3, получаем согласно выведенной формуле, что сила N равна 5,4 ньютона.

Задача с доской, двумя опорами и грузом

Доска, массой которой можно пренебречь, лежит на двух твердых опорах. Длина доски равна 2 метра. Чему будет равна сила реакции каждой опоры, если на эту доску посередине положить груз массой 3 кг?

Прежде чем переходить к решению задачи, следует ввести понятие момента силы.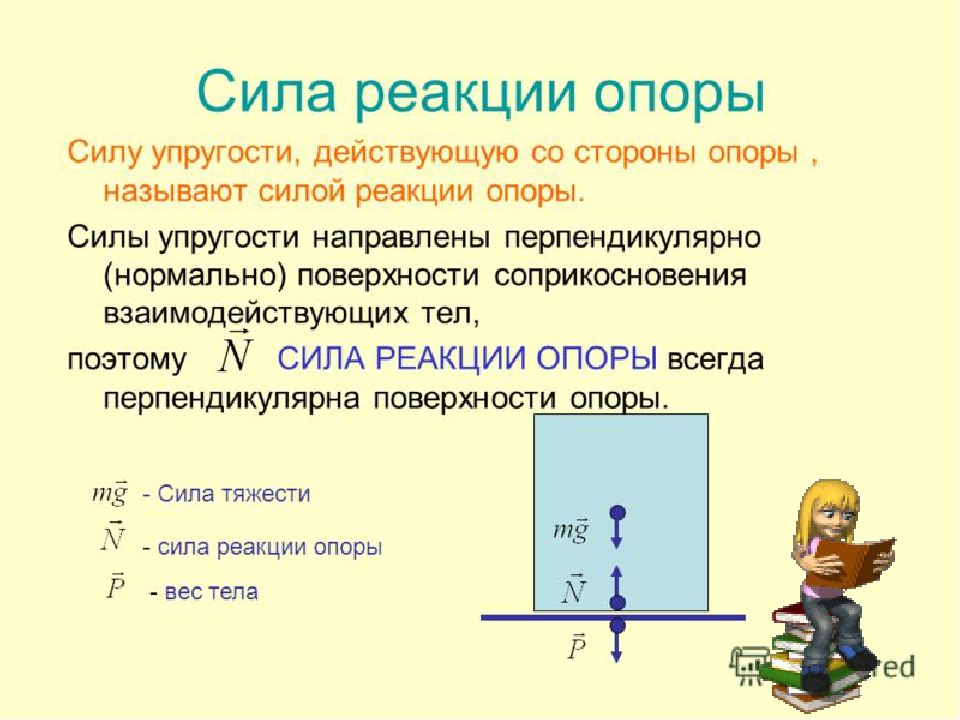 В физике этой величине соответствует произведение силы на длину рычага (расстояние от точки приложения силы до оси вращения). Система, имеющая ось вращения, будет находиться в равновесии, если суммарный момент сил равен нулю.

Возвращаясь к нашей задаче, вычислим суммарный момент сил относительно одной из опор (правой). Обозначим длину доски буквой L. Тогда момент силы тяжести груза будет равен:

M1 = -m*g*L/2

Здесь L/2 — рычаг действия силы тяжести. Знак минус появился потому, что момент M1 осуществляет вращение против часовой стрелки.

Момент силы реакции опоры будет равен:

M2 = N*L

Поскольку система находится в равновесии, то сумма моментов должна быть равной нулю. Получаем:

M1 + M2 = 0 =>

N*L + (-m*g*L/2) = 0 =>

N = m*g/2 = 3*9,81/2 = 14,7 Н

Заметим, что от длины доски сила N не зависит.

Учитывая симметричность расположения груза на доске относительно опор, сила реакции левой опоры также будет равна 14,7 Н.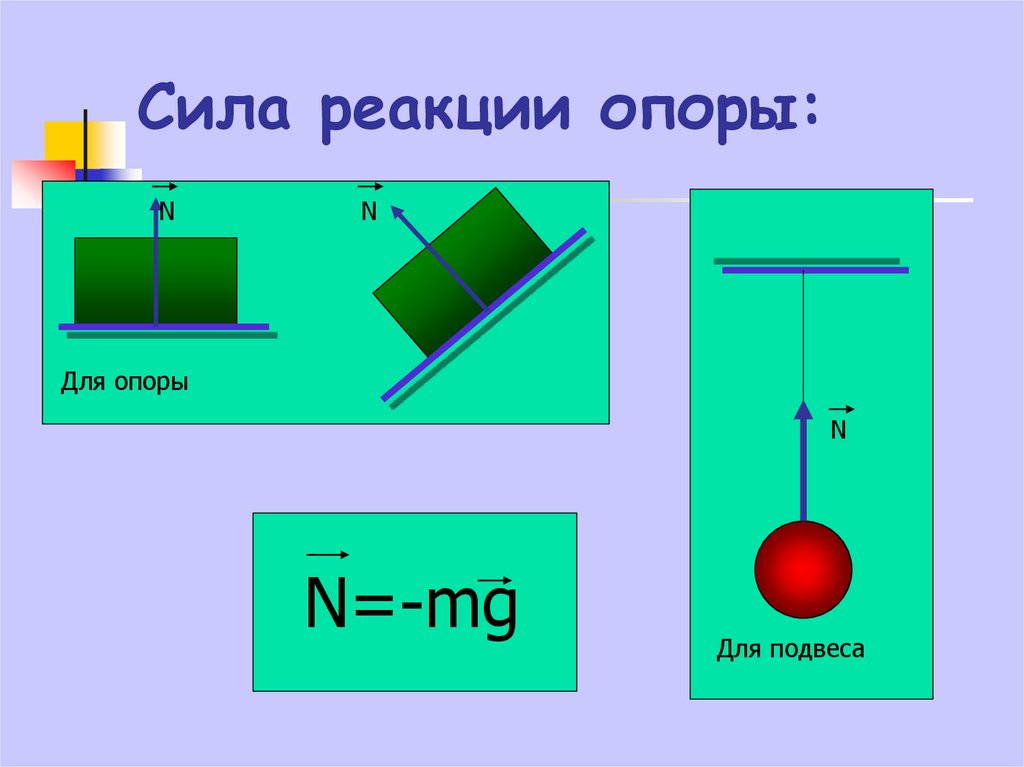

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

СИЛА РЕАКЦИИ НА ОСНОВЕ

СИЛА РЕАКЦИИ НА ОСНОВЕ

Силы наземного реагирования

Сила реакции земли равна по модулю и противоположна по направлению силы, с которой тело действует на опору поверхность через стопу.

	Вектор силы реакции опоры (GRFV) проходит вверх от стопы и вызывает движение в каждом суставе нижней конечности. Мы можем визуализировать GRFV, изучая лабораторные исследования нормальной походки, в которых используются силовые пластины для измерения трехмерной ориентации GRFV.

GRFV отличается от «линии гравитации», которая представляет собой вектор, проходящий вертикально от центра тяжести неподвижного тела. Вместо этого GRFV является «отражением произведения общей массы на ускорение всех сегментов тела и, следовательно, представляет собой сумму всех чистых мышечных и гравитационных сил, действующих в каждый момент времени в течение периода опоры» (Winter, 1984, p. .51).

	F=mg обозначает вектор, представляющий силу тяжести, действующую на объект. F=ma обозначает вектор, представляющий мгновенную сила инерции, действующая на объект. На этой диаграмме силы инерции ускоряют тело вниз и вправо. Вектор (F r ) равнодействующая или сумма сил гравитации и инерции.

При контакте с устойчивой поверхностью, такой как земля, вектор F _r представляет собой силу, которой противодействует сила реакции земли равной величины. Поскольку сила реакции земли равна и противоположна, линия приложения ее вектора такая же, как у F _r , и он оказывает такое же влияние на тело и его суставы.

GRFV сочетает в себе как действие гравитации на тело, так и эффекты движения тела и ускорения (изменения скорости) в трех плоскостях отсчета. Это делает GRFV особенно подходящим для изучения походки, во время которой различные массы тела подвергаются сложным ускорениям.

Сложное оборудование для анализа походки может генерировать видимый вектор силы на экране осциллографа и одновременно накладывать его на фотографию субъекта походки. Визуализация сил реакции опоры помогает нам понять их влияние на тело во время ходьбы и позволяет прогнозировать активность мышц с помощью простой модели:

М _мм = -М _ГРФ

Мы можем довольно точно предсказать активность мышц, если примем точку зрения, что сила реакции опоры (GRF) и мышцы (mm) создают равные и противоположные моменты (M) вокруг каждого сустава.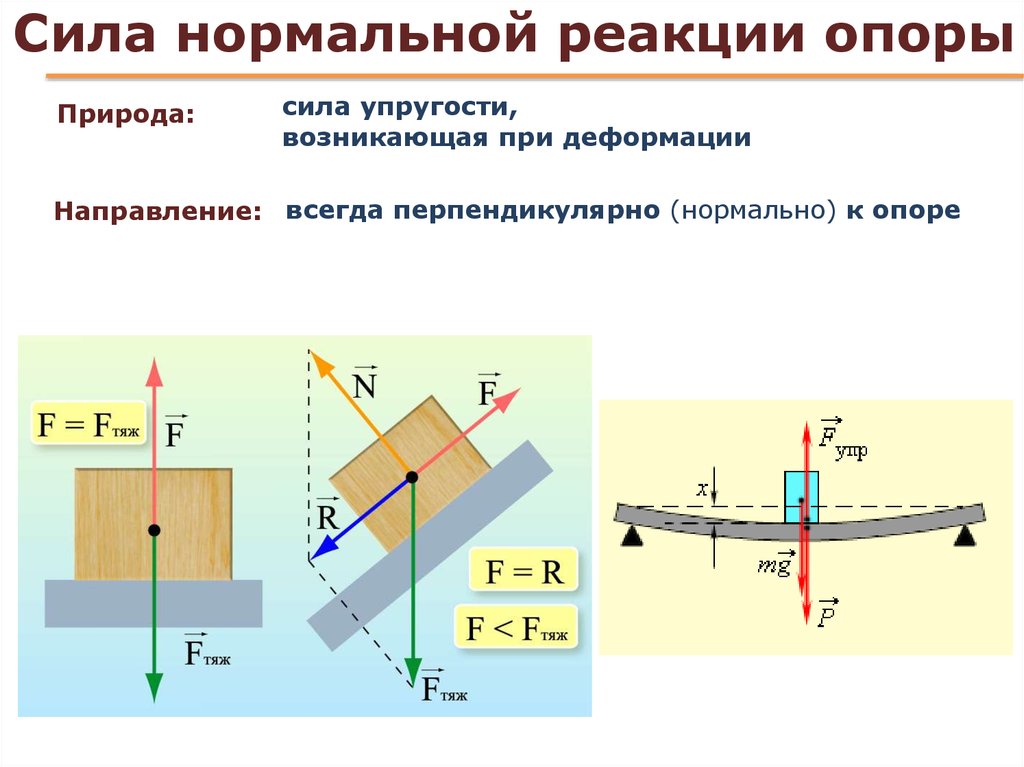

ВНИМАНИЕ: Реакция опоры — не единственная сила, действующая на суставы во время ходьбы. Вес и инерция движущегося сегмента влияет на дистальные и проксимальные сегменты. Движение верхней части ноги влияет на движение нижней части ноги. Эти совместные силы реакции могут иметь важное значение. Однако силы реакции суставов относительно невелики в нижних конечностях, по крайней мере, в фазе опоры. Поэтому клиницисты могут использовать положение GRFV само по себе, чтобы понять силы, которые человеческие мышцы должны контролировать во время фазы опоры при ходьбе.

Ссылки

Гронли, Дж. К., и Перри, Дж. (1984). Методы анализа походки. Физиотерапия, 63 , 1831-1838.

Winter, D. (1984) Кинематические и кинетические модели походки человека. Наука о движении человека, 3, 51-76.)

---

Последнее обновление 4 марта 2002 г. © Дэйв Томпсон PT

Правильный запрос сил реагирования в Abaqus

Что такое силы реагирования?

Реактивные силы проявляются телом при приложении к нему внешней силы. Например, если вы идете по улице, будет результирующая сила реакции со стороны улицы. Эта сила реакции имеет две составляющие. Во-первых, у нас есть вертикальная составляющая для поддержки силы вашего веса. Вторая – тангенциальная составляющая, трение. Итак, из этого примера становится очевидным, что эти силы присутствуют только в связанных узлах, а не в свободных. Здесь же Abaqus рассчитывает силы реакции.

Давайте рассмотрим два способа найти и нанести на график силы реакции, а также почему вы можете предпочесть один из них другому.

Настройка модели

В приведенной ниже модели показана явная симуляция жесткой сферы, подпрыгивающей на батуте. Мы смоделировали кровать батута, а также раму батута, используя элементы S4 . Что касается сферы, мы используем элементов R3D4

. Наконец, мы смоделировали пружины как элементов SPRINGA .

Ножки рамы батута зафиксированы во всех степенях свободы ( ИНКАСТРИРОВАННЫЕ ). Кроме того, основания всех семи опор рамы привязаны к опорной точке с помощью кинематического ограничения связи. Поскольку это испытание на падение, мы применим к твердой сфере начальную скорость 5 м/с. GIF показывает анимацию симуляции с цветовым полем, установленным на фон Мизес стресс.

Поскольку опоры рамы ограничены во всех степенях свободы, Abaqus будет рассчитывать силы реакции там и только там.

Существует два способа извлечения силы реакции:

1. Чтобы получить данные с лучшим разрешением и более высокой частотой дискретизации, вы можете запросить вывод истории силы реакции в контрольной точке, привязанной к ногам. Вы можете отрегулировать частоту для вывода с более высокой частотой дискретизации.
   • В Abaqus/CAE это делается с помощью Output > History Output Requests > Create , затем выбирая RF под Forces/Reactions
   • Во входном файле:

      *Вывод, история, временной интервал=0,0005
     
     *Вывод узла, nset=Set-1
     
     РФ1, РФ2, РФ3, РМ1, РМ2, РМ3 

     (Комплект-1 содержит указанную ранее опорную точку)

2. Если вы забыли запросить вывод истории, Abaqus по умолчанию выводит предварительно выбранные выходные переменные поля. После шага 4 (ниже) обязательно выберите опорный узел, привязанный к ножкам рамы батута. Вы можете найти это под Элементы/Узлы вкладка.

Нанесение на график сил реакции Результаты и обсуждение

Чтобы подчеркнуть разницу между двумя методами получения силы реакции, я наложил силу реакции из выходных данных истории, а также из выходных данных поля на один график. На этом графике показано усилие на опорах рамы, полученное из выходных данных истории. Период составляет 0,0005 секунды или частота дискретизации 2000 Гц, что дает 2000 точек. Кроме того, вы увидите ту же силу, полученную при гораздо более низкой частоте дискретизации из выходной переменной поля, показанной желтым цветом.

В диапазоне от 0,8 с до 1 с ясно, что сила из выходных данных истории хорошо выбрана, в то время как сила, полученная из выходных данных поля, выбрана недостаточно и не отражает полного поведения конструкции.

Регистрация силы реакции при высокой частоте дискретизации обычно касается только высокодинамичных систем.