23.4. Силы реакции опоры
Действие веса тела на опору встречает противодействие, которое называют реакцией опоры (или опорной реакцией).
Реакция опоры — это мера противодействия опоры действию на нее тела, находящегося с ней в контакте (в покое или движении). Она равна силе действия тела на опору, направлена в противоположную сторону и приложена к этому телу.
Обычно человек, находясь на горизонтальной опоре, испытывает противодействие своему весу. В этом случае опорная реакция, как и вес тела, направлена перпендикулярно к опоре. Это нормальная (или идеальная) реакция опоры. Если поверхность не плоская, то опорная реакция перпендикулярна к плоскости, касательной к точке опоры.
Когда вес статический,
то реакция опоры статическая; по величине
она равна статическому весу. Если человек
на опоре движется с ускорением,
направленным вверх, то к статическому
весу добавляется сила инерции и возникает
динамическая реакция о п о р ы (рис.
пассивная (реактивная). Она не может сама по себе вызвать положительные ускорения. Но без нее — если нет опоры, если не от чего оттолкнуться (или не к чему притянуться) — человек не может активно перемещаться.
Если отталкиваться от горизонтальной опоры не прямо вверх, то и сила давления на опору будет приложена не под прямым углом
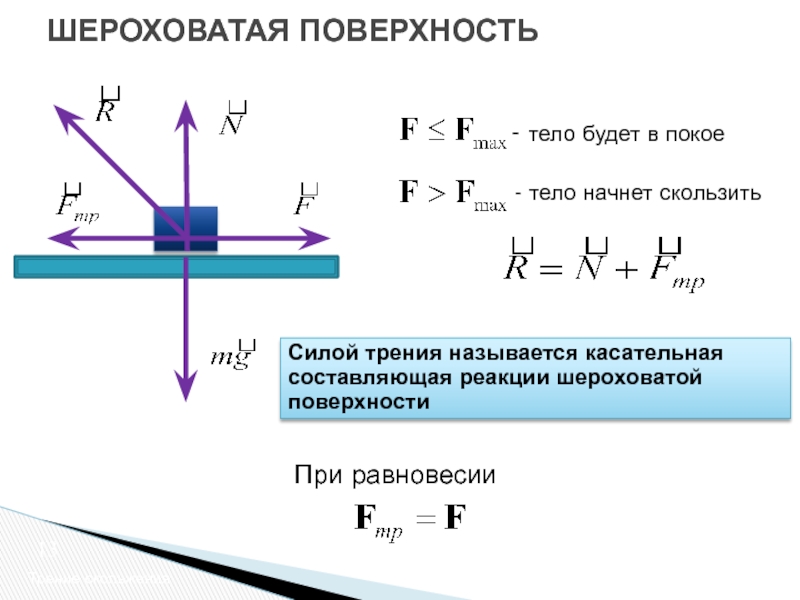
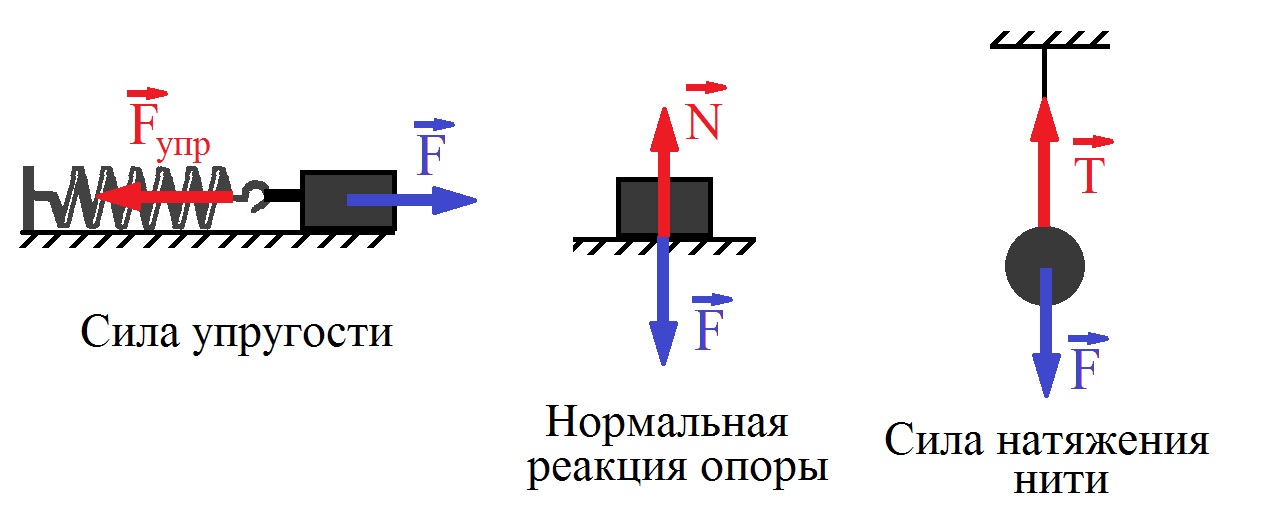
к ее поверхности. Тогда реакция опоры также не будет перпендикулярна к поверхности, ее можно разложить на н о р м а л ь н у ю и касательную составляющие. Когда соприкасающиеся поверхности ровные, без выступов, шипов и т. п. (асфальт, подошва ботинка), то касательная составляющая реакции опоры и есть сила трения.
Касательная реакция может быть обусловлена не только трением (как, например, между лыжей и снегом), но и другими взаимодействиями (например, шипы беговых туфель, вонзившиеся в дорожку).
Равнодействующая нормальной и касательной составляющих называется
о б щ е й реакцией
опоры. Она только при свободном неподвижном
положении над опорой (или под опорой)
проходит через ЦМ человека. Во время же
движений, отталкивания или амортизации
она обычно не проходит через ЦМ, образуя
относительно него момент.
Она только при свободном неподвижном
положении над опорой (или под опорой)
проходит через ЦМ человека. Во время же
движений, отталкивания или амортизации
она обычно не проходит через ЦМ, образуя
относительно него момент.
Спортсмену нередко приходится преодолевать сопротивление воздуха или воды. Среда, в которой движется человек, оказывает свое действие на его тело. Это действие может быть статическим (выталкивающая сила) и динамическим (лобовое сопротивление, нормальная реакция опоры).
Выталкивающая сила — это мера действия среды на погруженное в нее тело. Она измеряется весом вытесненного объема жидкости и направлена вверх.
Если выталкивающая сила (Q (рис. 36) больше силы тяжести тела (G), то тело всплывает. Если же сила тяжести тела больше выталкивающей силы, то оно тонет.
Лобовое сопротивление — это сила, с которой среда препятствует движению тела относительно нее. Величина лобового сопротивления (Rx) зависит от площади поперечного сечения тела, его обтекаемости, платности и вязкости среды, а также относительной скорости тела:
Изменяя площадь
поперечного сечения тела, можно изменить
и действие среды.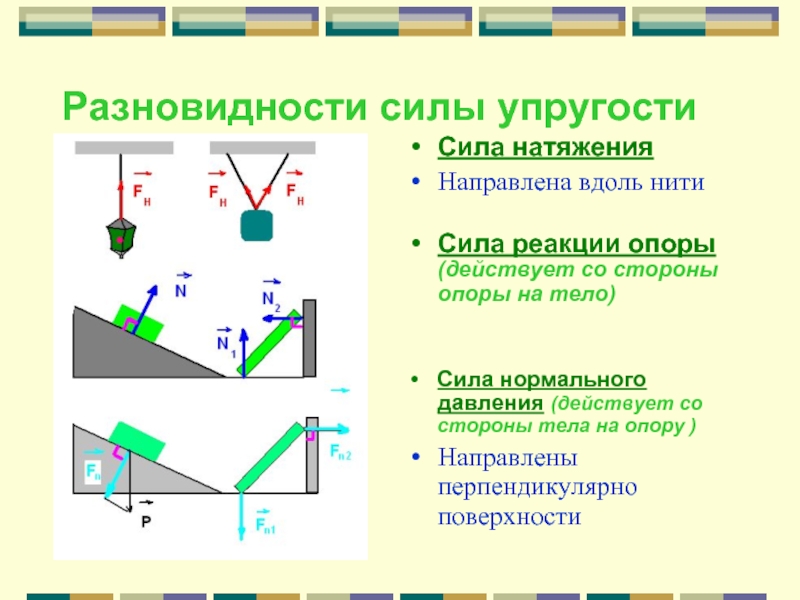 Так, у лыжника при
спуске с горы в высокой стойке
Так, у лыжника при
спуске с горы в высокой стойке
эта площадь почти в 3 раза больше, чем в низкой стойке. Значит, сопротивление воздуха при спуске можно изменять почти в 3 раза. Принимая в воде позы с лучшей обтекаемостью, нужно уменьшать сопротивление воды. Как известно, с увеличением скорости передвижения сопротивление воды или воздуха резко увеличивается (примерно пропорционально квадрату скорости).
Нормальная реакция среды — это сила, действующая со стороны среды на тело, расположенное под углом к направлению его движения. Она зависит от тех же факторов, что и лобовое сопротивление:
Нормальная реакция среды при гребке направлена перпендикулярно силе лобового сопротивления.
С нормальной
реакцией среды как с подъемной силой
приходится считаться (например, пловцу
во время продвижения по дистанции,
прыгуну на лыжах с трамплина во время
полета в воздухе).
Помогите решить / разобраться (Ф)
| wolf.ram |
| ||
04/06/10 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
wolf. ram ram |
| ||
04/06/10 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
wolf. ram ram |
| ||
04/06/10 |
| ||
| |||
| ukku |
| ||
20/04/11 |
| ||
| |||
| wolf.ram |
| ||
04/06/10 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
3.
 4 Реакции и опоры – инженерная механика: статика
4 Реакции и опоры – инженерная механика: статикаГлава 3: Основы твердого тела
Представьте себе луч, выходящий из стены. Какой вес может выдержать балка, прежде чем она оторвется или упадет со стены? Это зависит от способа крепления к стене. Мы моделируем эти ситуации реального мира, используя силы и моменты. Например, пешеходный переход в Гранд-Каньоне позволяет людям пройтись по Гранд-Каньону. Вы хотите быть уверены, что пешеходный переход устроен таким образом, что люди, находящиеся на нем, находятся в безопасности.
Мы называем пешеходную дорожку консольной балкой и превращаем реальную балку в двухмерную модель с ограничениями. Таким образом, мы можем использовать ту же терминологию, это фиксированное ограничение , предотвращающее горизонтальное движение, вертикальное движение и вращение.
Силы и моменты реакции — это то, как мы моделируем ограничения на конструкции. Это внешние силы. В этом курсе мы сосредоточимся на 3 различных типах ограничений, и каждый из них имеет разные силы реакции и моменты:
1. Фиксированный (без трения)
Фиксированный (без трения)
- Две силы реакции, действующие перпендикулярно в направлениях x и y.
- Прикрепленное ограничение, а затем показана диаграмма его свободного тела:
2. Фиксированный
- Две силы реакции, действующие перпендикулярно в направлениях x и y
- Момент, вращающийся вокруг фиксированного ограничения (обычно стены), используйте правило правой руки, чтобы найти его направление
- Это также называется консольной балкой.
- Фиксированное ограничение, а затем показано FBD
3. Ролик (есть несколько видов)
- Одиночная сила реакции, действующая в направлении Y
- Момент не создается
- Это также может быть земля, на которой стоит объект
- Показана свободная схема корпуса для катка
Обратите внимание, что фиксированное ограничение является наиболее ограничивающим, а ролик — наименее ограничивающим. Вы прикладываете силу, чтобы показать, как ограничение ограничивает движение. Ролик только удерживает объект от перемещения по вертикали, поэтому действует только 1 сила. Штифтовое ограничение не допускает горизонтального или вертикального движения, отсюда и две силы. Неподвижная балка ограничивает вертикальное перемещение, горизонтальное перемещение и вращение, поэтому есть момент и две силы. Обратите внимание, что это относится только к 2d ограничениям.
Вы прикладываете силу, чтобы показать, как ограничение ограничивает движение. Ролик только удерживает объект от перемещения по вертикали, поэтому действует только 1 сила. Штифтовое ограничение не допускает горизонтального или вертикального движения, отсюда и две силы. Неподвижная балка ограничивает вертикальное перемещение, горизонтальное перемещение и вращение, поэтому есть момент и две силы. Обратите внимание, что это относится только к 2d ограничениям.
Вот сводка, показывающая, какое движение разрешено ограничением этого типа:
Обычно силы реакции бывают следующими: закрепленная и фиксированная сила реакции вместе (1 сила реакции + 2 силы реакции = 3 ограничения) или неподвижная балка (2 силы реакции и 1 момент = 3 ограничения).
Показанная здесь информация предназначена для моделирования двухмерных ситуаций. В этом курсе статики мы не затрагиваем трехмерные задачи, разумеется, в трехмерном пространстве задействовано больше сил реакции и моментов, чем в двухмерном. В следующем разделе дается второе объяснение реакций и поддержки:
В следующем разделе дается второе объяснение реакций и поддержки:
3.4.1 Штифтовая или шарнирная опора
Штифтовая опора позволяет вращаться вокруг любой оси, но предотвращает движение в горизонтальном и вертикальном направлениях. Его идеализированное представление и реакции показаны в таблице 3.1:
3.4.2 Роликовая опора
Роликовая опора допускает вращение вокруг любой оси и перемещение (горизонтальное перемещение) в любом направлении, параллельном поверхности, на которую она опирается. Он сдерживает конструкцию от движения в вертикальном направлении. Идеализированное представление ролика и его реакции также показаны в таблице 3.1.
3.4.3 Кулисная опора
Характеристики качающейся опоры аналогичны характеристикам роликовой опоры. Его идеализированная форма изображена в таблице 3.1.
3.4.4 Звено
Звено имеет два шарнира, по одному на каждом конце. Он допускает движение во всех направлениях, кроме направления, параллельного его продольной оси, которая проходит через два шарнира.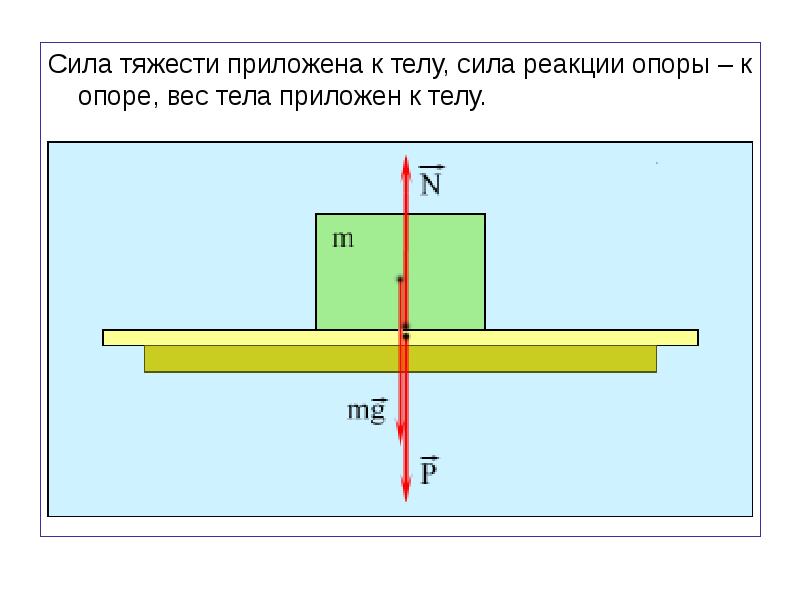 Другими словами, сила реакции звена направлена в направлении звена вдоль его продольной оси.
Другими словами, сила реакции звена направлена в направлении звена вдоль его продольной оси.
3.4.5 Фиксированная опора
Неподвижная опора препятствует вращению в любом направлении и предотвращает движение как в горизонтальном, так и в вертикальном направлениях.
Пример 1:
Пример 2 (A x Добавлено, даже если оно оказалось 0):
Пример 3:
Пример 4:
.
Источник: «Равновесные структуры, опорные реакции, детерминированность и устойчивость балок и рам» от LibreTexts под лицензией CC BY-NC-ND. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.03%3A_Equilibrium_Structures_Support_Reactions_Determinacy_and_Stability_of_Beams_and_Frames
В основном: Реактивные силы и моменты (или ограничения) показывают, как движение ограничено, здесь в двух измерениях.
Применение : Балка, прикрепленная к стене, имеет три способа ограничения движения: горизонтальное, вертикальное и вращательное.
Взгляд вперед: Каждый раз, когда мы моделируем сценарий, мы будем использовать силы реакции, чтобы показать, какой тип движения ограничивается. В главе 4 мы сможем рассчитать силы/моменты реакции.
Автор Гейла и Либби
изгиб — Какая сила создает реактивный момент в неподвижной опоре
$\begingroup$
Вопрос: Какая сила вызывает реактивный момент в неподвижном соединении?
Давайте рассмотрим очень простой пример: балка, один конец которой соединен неподвижной опорой со стеной.
Я так понимаю, что в точке А будет вертикальная сила реакции, горизонтальная сила реакции и момент реакции. Я так понимаю момент относительно оси всегда вызывается силой . Какая сила F вызывает реактивный момент?
В этом примере предположим, что F — это сила горизонтальной реакции. Из условия равновесия сил вдоль направления x получаем, что эта сила имеет нулевую величину и, следовательно, не может создавать реактивный момент.
Из условия равновесия сил вдоль направления x получаем, что эта сила имеет нулевую величину и, следовательно, не может создавать реактивный момент.
Допустим, F — вертикальная сила реакции. По-видимому, когда мы разрезаем балку в точке C и применяем условие равновесия моментов в точке C, мы должны включают как момент реакции, так и момент, создаваемый вертикальной силой реакции , что указывает на то, что момент, создаваемый вертикальной силой реакции, и момент реакции в точке A являются двумя разными моментами, вызванными разными силами.
Итак, в заключение, если момент в точке А не вызван ни вертикальной, ни горизонтальной силой реакции, то какой силой он вызван?
- моменты
- изгиб
$\endgroup$
4
$\begingroup$
Я интерпретировал ваш вопрос как 2 отдельных запроса.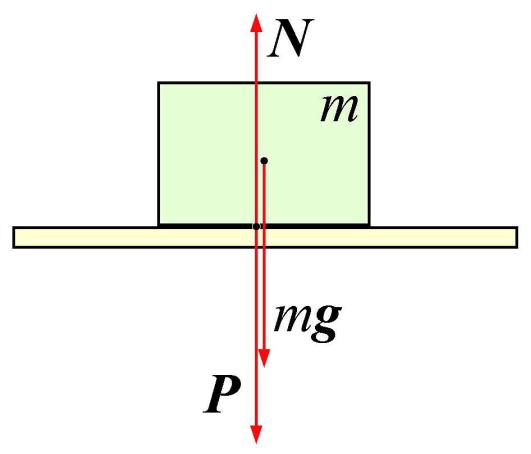
Какая фундаментальная физика заставляет неподвижную опору создавать момент вокруг центральной оси балки?
Как рассчитать внутренние силы в сечении «С» балки
Q1:
Вы можете представить, что балка крепится к стене с помощью клея. Когда луч пытается повернуться, луч будет вдавливаться в стену снизу и притягиваться к стене сверху клеем. Аналогичный процесс происходит, если балка прикручивается, приваривается или прикручивается к стене. Часть стенки внизу находится в состоянии «сжатия», и сжимаемый материал пытается расшириться до своего первоначального размера и, следовательно, помогает приложить силу, необходимую для вращения балки вокруг своей оси (момент).
Имейте в виду; >Чистая< сила в точке реакции в направлении х по-прежнему равна 0, потому что всасывание сверху и выталкивание снизу в сумме составляют ноль (0) ньютонов в направлении х.
Q2:
Вот окончательное решение для разреза сечения «С» на расстоянии 1 метра от балки. ПОЖАЛУЙСТА, имейте в виду, что вы должны убедиться, что вы полностью понимаете, как я рассчитал здесь все силы и моменты. По сути, вы хотите разрезать балку и убедиться, что сумма сил, воздействующих на (оба) балку (балки), и сумма моментов равна 0, как и для других задач статики. Опять же, новая точка разворота «фиксирована»
ПОЖАЛУЙСТА, имейте в виду, что вы должны убедиться, что вы полностью понимаете, как я рассчитал здесь все силы и моменты. По сути, вы хотите разрезать балку и убедиться, что сумма сил, воздействующих на (оба) балку (балки), и сумма моментов равна 0, как и для других задач статики. Опять же, новая точка разворота «фиксирована»
Внутренний момент балки на расстоянии 1 м от точки А равен 5 Н·м, поскольку при статическом равновесии:
$\Sigma Fx = 0; \Sigma F_y = 0 = F_{c_{y}} — 10(N)$
$\Sigma M = 0 = -10(N) * .5(m) + M_c$
$M_c = 5Nm$
$\endgroup$
7
$\begingroup$
момент в точке A представляет собой сумму вклада всех малых дифференциальных моментов dx по длине балки.
Его можно упростить как момент полной нагрузки, действующей в его ЦТ.
$$M_A=10N*2*1m=20Nm$$
Думаю, вы путаете момент свободного тела в случайной точке с моментом в точке A.
$\endgroup$
4
$\begingroup$
ИМХО вы путаете «момент силы относительно точки А», с «моментом реакции» который развивается при опоре конструкции, а точнее как они рассчитываются. Хотя они связаны, это не одно и то же.
Первое — очень фундаментальное понятие в физике. Момент силы равен произведению силы на расстояние точки от носителя силы (коллинеарная линия к силе).
Развивающийся реактивный момент создается конструкцией. Хотя в статике мы предполагаем жесткие конструкции (т. е. малые или несуществующие смещения), в реальной жизни все конструкции деформируются. Деформация конструкций может оказывать значительное влияние на конструкцию.
К чему я пытаюсь прийти, так это к тому, что «несущая конструкция, а также нагрузка определяют реакцию опоры».
Дополнительно по части вашего вопроса
По-видимому, когда мы разрезаем балку в точке C и применяем условие равновесия моментов в точке C, мы должны учитывать как момент реакции, так и момент, создаваемый вертикальной силой реакции, что указывает на то, что момент, создаваемый вертикальной силой реакции и момент реакции в точке А — это два разных момента, вызванных разными силами.

 2011, 13:37
2011, 13:37  04.2011, 13:51
04.2011, 13:51 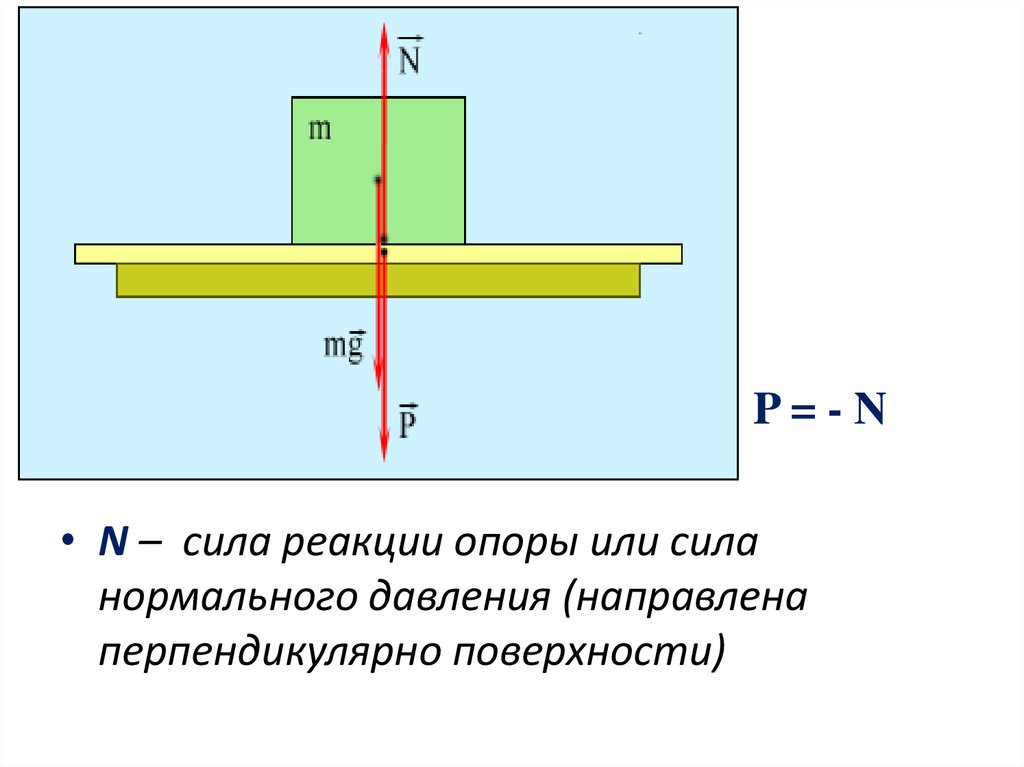 04.2011, 16:24
04.2011, 16:24  В данном случае сила взаимодействия равна силе реакции + сила трения. Сила взаимодействия между телами сонаправлена с , сила же реакции опоры такая же и соноправлена .
В данном случае сила взаимодействия равна силе реакции + сила трения. Сила взаимодействия между телами сонаправлена с , сила же реакции опоры такая же и соноправлена .