Костенко Н.А. Сопротивление материалов
Автор Костенко Н.А. «Сопротивление материалов» и другие ставили целью создать пособие, которое оказывает помощь при освоении практической части курса сопромата, в первую очередь студентам заочной формы обучения, однако также будет весьма полезно всем, изучающим науку о прочности. В связи с этим сознательно опущен углубленный анализ теории и выводы формул, а также некоторые вопросы, относительно редко возникающие перед инженером широкого профиля при решении практических задач. Среди них — расчет толстостенных цилиндров, вращающихся дисков и тонкостенных оболочек, теория контактных напряжений, расчет составных балок на изгиб, расчет балок на упругом основании, исследование моментов инерции плоских сечений с помощью кругов Мора, расчет на прочность при кручении тонкостенных валов открытого и закрытого профиля, расчет пластин и оболочек, учет собственного веса, расчеты за пределами упругости. Это тем более оправдано, что имеется много учебников по сопротивлению материалов с широким освещением теории и подробным выводом формул, на которые на данном пособии даются ссылки.
В то же время уделено огромное внимание изложению базовых понятий, анализу условий и гипотез сопротивления материалов, на которых можно использовать рассматриваемые методы расчета, а также практическим вопросам, трудно понимаемым студентами. Среди этих вопросов построение эпюр в пространственных и плоских рамах, определение знаков центробежных моментов, раскрытие статической неопределимости рам методом сил, расчеты при внецентренном растяжении — сжатии и косом изгибе, расчеты на прочность при колебаниях. Изложению материала сопутствует решение большого числа задач по всем темам курса, также и задач из контрольных работ.
Учитывая, что обучение студентов заочников всегда проходит в условиях дефицита времени, коллектив авторов стремился по возможности хорошо обучить студентов хотя бы одному методу решения конкретных задач. В пособии дается универсальный энергетический метод определения перемещений, который позволяет оценивать деформации при любых видах нагружения и не рассматривается, например, метод начальных параметров или метод непосредственного интегрирования.
С целью повышения обучающих возможностей учебника, а также обеспечения удобства в освоении новой информации в начале пособия, даны все имеющиеся в книге обозначения (язык прочности в символах), которые студенты обязаны знать, так как они лежат в основе прочностных расчетов всех специальных дисциплин.
Кроме того, рискуя быть обвиненными в «выхолащивании» курса, авторы сочли целесообразным дать в конце учебника таблицу основных формул сопротивления материалов под шуточной рубрикой «Запомни на всю оставшуюся жизнь!». Нам представляется, что этот материал, являясь «выжимкой» важнейшей информации, позволит еще раз укрупненно представить содержание курса, и его задачи, а также усвоить суть прочностного расчета, состоящую в том, что в двух частях основного условия прочности стоят независимые величины: в правой механические прочностные свойства материала, а в левой напряженное состояние объекта под нагрузкой. Используя эту информацию, студенту далее легко сосредоточиться на запоминании конкретных выражений (формул) для левой части условия прочности при разных видах нагружения.
Для студентов заочников эта концентрированная информация будет играть роль краткого справочника. Вопросы же инженерного приложения этой информации для решения конкретных задач подробно рассмотрены в пятнадцати главах пособия. В полной мере нашла отражение в пособии последняя концепция требований к общепрофессиональным дисциплинам для механических направлений и специальностей. В частности, всесторонне рассмотрены вопросы оценки прочности при циклических напряжениях, которые вызывают усталость материала. Учитывая также, что в последние десятилетия быстро развиваются новые, весьма перспективные направления в науке о прочности, прочностная надежность, механика разрушения, механика материалов, и в них уже разработаны инженерные методы расчета, мы сочли необходимым познакомить студентов с результатами работ в этих направлениях вплоть до решения практических задач.
Сопромат. Заочники. | Решебник. Контрольные курсовые работы Ижевск. Решение задач.
<в каталог
Задача 1.
Растяжение сжатие стержнейЗадача 2. Статически неопределимая стержневая конструкция.
Задача 3. Изгиб балок
Задача 4. Изгиб рам.
Задача 5. Кручение валов
Задача 6. Косой изгиб.
Задача 7. Совместное действие изгиба и кручения.
Задача 8. Расчет сжатых стержней на устойчивость.
Таблица с готовыми вариантами
Пример выполненной работы
Растяжение сжатие стержнейЗадача 1.
Для стержня (рис. 1) постоянного сечения следует:
№ строки | № схемы | Р, кН | а, м | Е, МПа |
1 | I | 30 | 1,1 | 1,2∙105 |
2 | II | 20 | 1,2 | 1,4∙105 |
3 | III | 25 | 1,3 | 1,5∙105 |
4 | IV | 30 | 1,4 | 1,6∙105 |
5 | V | 40 | 1,5 | 1,7∙105 |
6 | VI | 48 | 1,6 | 1,8∙105 |
7 | VII | 64 | 1,7 | 1,9∙105 |
8 | VIII | 80 | 1,8 | 2,0∙105 |
9 | IX | 90 | 1,9 | 2,1∙105 |
0 | X | 60 | 2,0 | 2,2∙105 |
| в | а | б | а |
1.
2. Выписать выражение наибольшего по модулю нормального напряжения σmax и из условия прочности определить необходимую площадь сечения F, приняв [σ]=160 МПа.
3. Определить перемещение сечения I-I.
4. Составить раскрытые выражения потенциальной энергии U в брусе.
Данные взять из таблицы 1.
Задача 2
Статически неопределимая стержневая конструкция.
Для системы, состоящей из абсолютно жесткого бруса и упругих стержней, требуется:
1. Определить усилия в стержнях, поддерживающих абсолютно жесткую балку (см. рисунок 2), от нагрузки Р.
2. Вычислить напряжения в стержнях от нагрузки Р.
3. Из условия прочности, определить необходимую площадь 
Материал стержней – сталь. Данные взять из таблицы
№ строки | № схемы | а, м | в, м | ℓ, м | Р, кН |
1 | I | 2,1 | 1,1 | 1,8 | 21 |
2 | II | 2,2 | 1,2 | 1,7 | 22 |
3 | III | 2,3 | 1,3 | 1,6 | 23 |
4 | IV | 2,4 | 1,4 | 1,5 | 24 |
5 | V | 2,5 | 1,5 | 1,4 | 25 |
6 | VI | 2,6 | 1,6 | 1,3 | 26 |
7 | VII | 2,7 | 1,7 | 1,2 | 27 |
8 | VIII | 2,8 | 1,8 | 1,1 | 28 |
9 | IX | 2,9 | 1,9 | 1,0 | 29 |
0 | X | 2,0 | 1,0 | 1,9 | 20 |
| в | а | б | в | в |
Задача 3
На рисунке 3 приведены схемы балок.
Требуется:
1. Построить эпюры изгибающих моментов и поперечных сил.
2. Подобрать сечение в виде прямоугольника (h=2b), приняв [σ]=160 МПа.
3. Построить эпюру нормальных напряжений в опасном сечении.
Данные взять из таблицы 3.
Принять интенсивность равномерно распределенной нагрузки q=6 кН/м.
№ строки | № схемы | а, м | Р, кН | М, кН∙м |
1 | I | 1,5 | 10 | 150 |
2 | II | 2,0 | 15 | 200 |
| 3 | III | 2,5 | 20 | 120 |
4 | IV | 3,0 | 25 | 100 |
5 | V | 3,5 | 30 | 300 |
6 | VI | 4,0 | 35 | 180 |
7 | VII | 4,5 | 40 | 60 |
8 | VIII | 5,0 | 45 | 240 |
9 | IX | 5,5 | 50 | 220 |
0 | X | 6,0 | 60 | 160 |
| в | а | б | в |
Задача 4
Изгиб рам.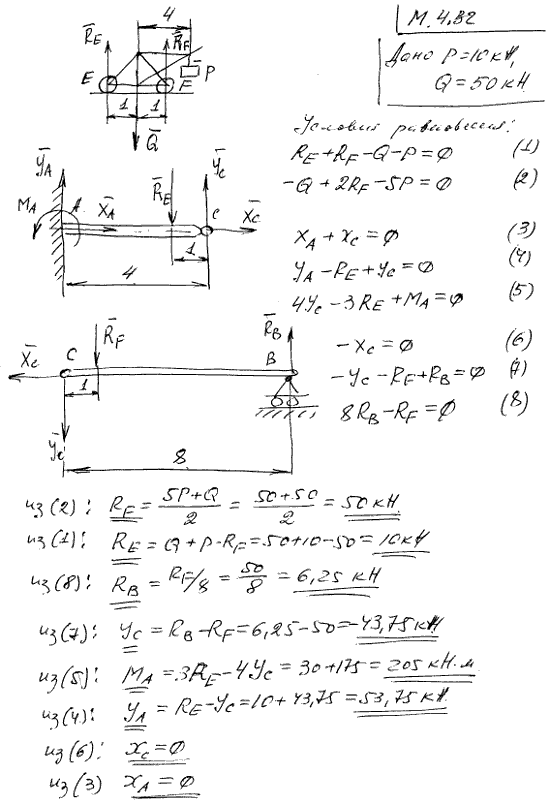
Для схемы рамы требуется:
1. Составить аналитические выражения изменения продольной силы Nx, поперечной силы Qy, изгибающего момента Mz.
2. Построить эпюры внутренних силовых факторов (э Nx, э Qy, э Mz).
3. По опасному сечению подобрать диаметр d поперечного сечения.
Исходные данные взять из таблицы.
№ строки | № схемы | с/a | P/qa | m/qa2 | a,м | q, кН/м |
1 | 1 | 1,2 | 0,6 | 0,2 | 0,5 | 6 |
2 | 2 | 1,4 | 0,5 | 0,4 | 1,0 | 8 |
3 | 3 | 1,6 | 0,8 | 0,6 | 1,5 | 10 |
4 | 4 | 1,8 | 1,2 | 0,8 | 2,0 | 12 |
5 | 5 | 2,0 | 1,5 | 1,0 | 2,5 | 14 |
6 | 6 | 1,2 | 1,6 | 0,2 | 1,5 | 16 |
7 | 7 | 1,4 | 1,0 | 0,4 | 2,0 | 12 |
8 | 8 | 1,6 | 1,8 | 0,6 | 1,0 | 10 |
9 | 9 | 1,8 | 2,4 | 0,8 | 2,5 | 8 |
0 | 0 | 2,0 | 2,0 | 1,0 | 0,5 | 6 |
| в | а | б | в | б | а |
Задача 5
Кручение валов.
На приводном валу (см. рис. 4) установлен ведущий шкив В и два рабочих 1 и 2, от которых последовательно берутся мощности: N1, N2 кВт. Требуется:
1. Построить эпюру крутящих моментов.
2. По заданным [τ] и [φ] определить необходимый диаметр сплошного вала и округлить его до ближайшей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200 (мм).
3. Построить эпюру углов закручивания вала.
Данные взять из таблицы 4.
№ строки | № схемы | а, м | в, м | с, м | N1, кВт | N2, кВт | n0, об/мин | [φ], град | [τ], МПа |
1 | I | 1,0 | 1,5 | 2,0 | 40 | 130 | 600 | 2 | 100 |
2 | II | 1,2 | 1,6 | 1,8 | 50 | 120 | 900 | 3 | 120 |
3 | III | 1,4 | 1,7 | 1,6 | 60 | 110 | 1200 | 4 | 140 |
4 | IV | 1,6 | 1,8 | 1,4 | 70 | 100 | 1500 | 3 | 160 |
5 | V | 1,8 | 2,0 | 1,2 | 80 | 90 | 1200 | 2 | 180 |
6 | VI | 2,0 | 1,8 | 1,4 | 90 | 80 | 900 | 3 | 200 |
7 | VII | 1,8 | 1,7 | 1,6 | 100 | 70 | 600 | 4 | 180 |
8 | VIII | 1,6 | 1,6 | 1,8 | 110 | 60 | 900 | 3 | 160 |
9 | IX | 1,4 | 1,5 | 2,0 | 120 | 50 | 1200 | 2 | 140 |
0 | X | 1,2 | 1,4 | 2,2 | 130 | 40 | 1500 | 4 | 120 |
| в | б | а | в | а | в | б | а | в |
Задача 6.
Косой изгиб.
Балка двутаврового профиля, повернутая на угол α относительно вертикали, загружена равномерно распределенной вертикальной нагрузкой q (рис. 6). Требуется:
1. Определить положение нулевой линии в опасном сечении.
2. Определить величину наибольшего нормального напряжения.
3. Вычертить опасное сечение балки и показать на нем нулевую линию, эпюру нормальных напряжений.
Данные взять из таблицы.
№ строки | q, кН/м | ℓ, м | α, град | № двутавра |
1 | 5,0 | 1,6 | 4 | 32 |
2 | 4,5 | 2,0 | 5 | 30 |
3 | 4,0 | 2,4 | 6 | 28 |
4 | 3,5 | 3,2 | 8 | 26 |
5 | 3,0 | 4,0 | 10 | 24 |
6 | 2,5 | 4,8 | 12 | 22 |
7 | 2,0 | 5,6 | 15 | 20 |
8 | 1,5 | 6,4 | 16 | 18 |
9 | 1,0 | 7,2 | 18 | 16 |
0 | 0,5 | 8,0 | 20 | 14 |
| в | б | в | а |
Задача 7.
Совместное действие изгиба и кручения.
На валу насажены зубчатые колеса. К колесам приложены окружные усилия Р1, Р2, Р3. Требуется:
1. Из условия равновесия ∑Мх=0 определить величину Р1 или Р3.
2. Определить крутящие моменты и построить эпюру крутящих моментов.
3. Определить силы, изгибающие вал в вертикальной и горизонтальной плоскости.
4. Построить эпюры изгибающих моментов от горизонтальных сил Му, и от вертикальных сил Мz.
5. При помощи эпюр найти опасное сечение и определить величину максимального расчетного момента.
6. Подобрать диаметр вала по III теории прочности – теории наибольших касательных напряжений.
Данные взять из таблицы.
№ строки | № схемы | Р1, кН | Р2, кН | Р3, кН | [σ], кН/см2 | а, см | b, см | Диаметры зубчатых колес, см | ||
D1 | D2 | D3 | ||||||||
1 | I | — | 6 | 10 | 10 | 40 | 50 | 40 | 40 | 20 |
2 | II | 8 | 5 | — | 9 | 50 | 40 | 50 | 40 | 20 |
3 | III | — | 7 | 9 | 10 | 40 | 30 | 40 | 30 | 30 |
4 | IV | 6 | 8 | — | 10 | 50 | 40 | 60 | 30 | 20 |
5 | V | — | 6 | 11 | 10 | 30 | 50 | 50 | 50 | 30 |
6 | VI | 5 | 8 | — | 9 | 20 | 30 | 30 | 30 | 20 |
7 | VII | — | 5 | 10 | 9 | 30 | 40 | 40 | 20 | 10 |
8 | VIII | 4 | 7 | — | 11 | 50 | 20 | 20 | 20 | 10 |
9 | IX | — | 6 | 11 | 10 | 30 | 50 | 30 | 30 | 20 |
0 | X | 8 | 6 | — | 9 | 40 | 30 | 50 | 20 | 10 |
| в | б | б | б | а | в | б | б | а | а |
Задача 8.