Реакция заделки — Энциклопедия по машиностроению XXL
Определить реакции заделки консольной балки, изображенной на рисунке и находящейся под действием сосредоточенной силы и пары сил. [c.39]Определить реакции заделки консольной балки, изображенной па рисунке и находящейся под действием равномерно распределенной нагрузки, сосредоточенной силы и пары сил. [c.39]
Определить реакции заделки консольной балки, изображенной на рисунке и находящейся под действием пары сил и распределенной нагрузки, изменяющейся по закону треугольника. [c.40]
Ответ X = —9 кН, У = 0, М = 40 кН м. 4.31(4.31). Определить реакцию заделки консольной балки, изображенной на рисунке и находящейся под действием сосредоточенной силы, пары сил и распределенной нагрузки, изменяющейся по закону треугольника и трапеции.

Решение. Реакцию заделки представляем в виде двух сил [c.134]
VI 1.25, а. Число неизвестных опорных реакций равно четырем три реакции заделки и одна реакция подвижной опоры. [c.197]
Задача. 21] Однородный брус АВ жестко заделан в стену, образуя с ней угол а=60° (рис. 59, а). Выступающая из стены часть бруса имеет длину 6=0,8 м и вес Р—100 Н. Внутри угла DAB лежит цилиндр весом Q=180 Н, касающийся бруса в точке , причем АЕ=а=0,3 м. Определить реакцию заделки. [c.51]
Реакция заделки слагается из сил Кд и пары с моментом т . [c.52]
А Ву Реакции заделки представляют собой [c.70]
Подъем бадьи вызывается парой внешних сил, действующей на барабан лебедки. Определить реакции заделки [c.293]
Сначала определим реакцию заделки, реактивный момент горизонтальную [c.316]
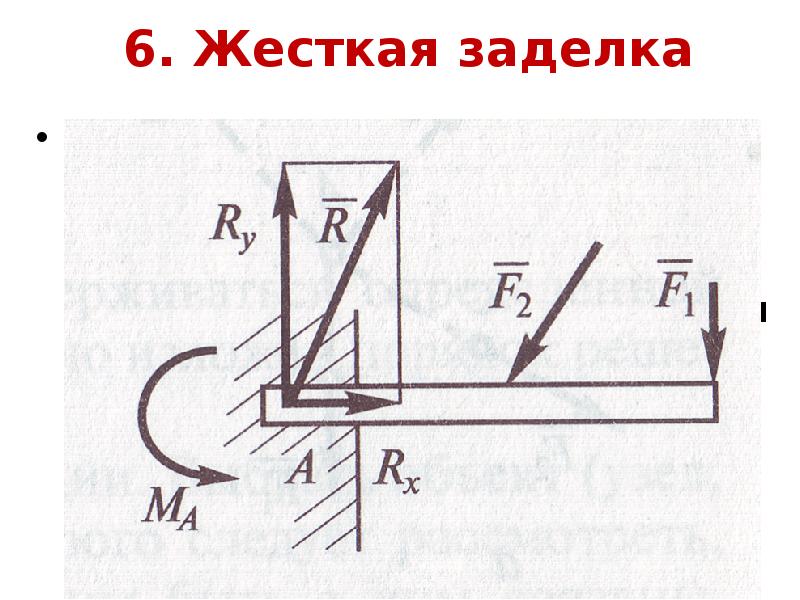
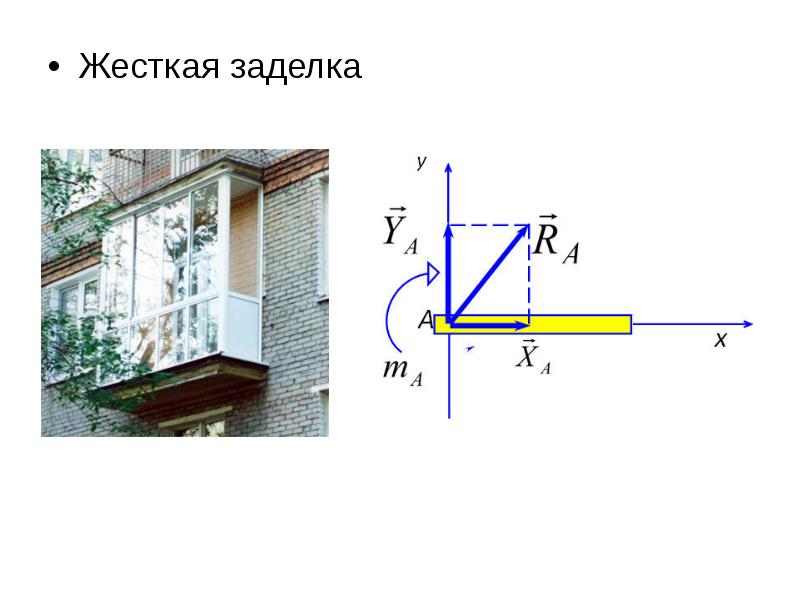
Если балка АВ, расположенная с приложенными к ней заданными силами F,, F ,. . . в плоскости кАу, закреплена концом А жестко, т. е. заделка в точке А препятствует как поступательному перемещению балки в любом направлении в плоскости хАу, так и вращательному движению вокруг оси Az, перпендикулярной к плоскости хАу, то реакция заделки эквивалентна силе R/i, приложенной в точке. 4, направление которой заранее неизвестно, и паре сил с моментом т, причем силу R А можно разложить на составляющие, направленные по осям л и у, т. е. Ra =Ха + Уд.
[c.22]
. . в плоскости кАу, закреплена концом А жестко, т. е. заделка в точке А препятствует как поступательному перемещению балки в любом направлении в плоскости хАу, так и вращательному движению вокруг оси Az, перпендикулярной к плоскости хАу, то реакция заделки эквивалентна силе R/i, приложенной в точке. 4, направление которой заранее неизвестно, и паре сил с моментом т, причем силу R А можно разложить на составляющие, направленные по осям л и у, т. е. Ra =Ха + Уд.
[c.22]
Определить реакции заделки. [c.173]
Пример 1.8. Жестко защемленная балка АВ нагружена силой Р= кН, как показано на рис. 1.56, а. Определить реакции заделки, если а=30°. [c.48]
Пример 1.15. Жестко заделанная балка длиной /=1,4м и квадратным поперечным сечением со стороной а=0,2 м нагружена, как показано на рис. 1.81, а, горизонтальной силой Д=2 кН и вертикальной равномерно распределенной нагрузкой интенсивностью д= кН/м. Определить реакции заделки.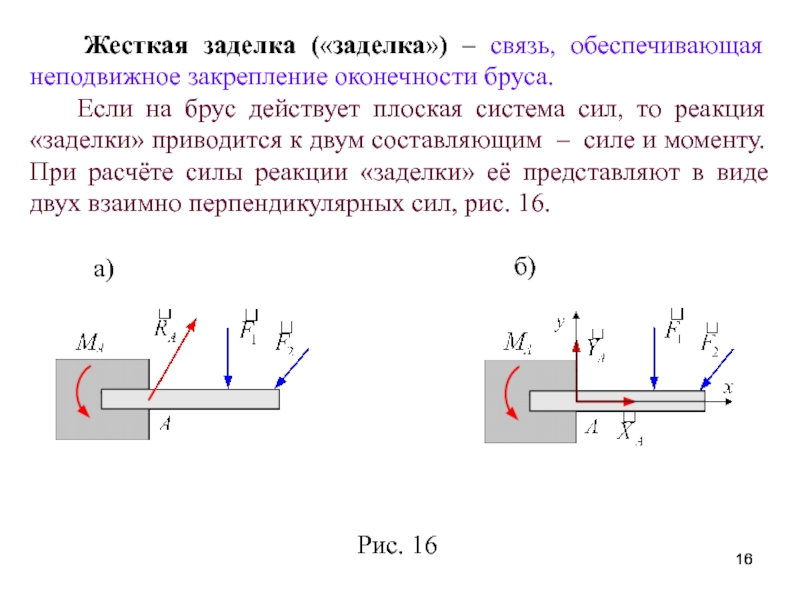
Разрежем брус по сечению 3—3 на участке СО. Отбросив верхнюю часть (отбрасываем каждый раз верхнюю часть потому, что реакция заделки в сечении О неизвестна), находим нормальную силу N3 в сечении 3—3 (рис. 2.12, г) [c.161]
На Г-образную раму AB , конец А которой жестко заделан, действует в плоскости рамы сила F. Определить реакции заделки Л. [c.24]
Решение. Если балка заделана в стену, то на заделанный конец балки действует система распределенных сил (реакций). Приведем их по методу Пуансо к точке А, заменим одной неизвестной реакцией заделки (с проекциями Х и К ) и одним неизвестным моментом заделки М. Эти три неизвестные определим из уравнений равновесия сил, действующих на балку. [c.88]
Реакции заделки в точке А в общем случае дают три неизвестных две составляющие силы но осям координат и момент пары сил одна неизвестная сила имеется в точке В.
 Таким образом, имеем четыре неизвестных, а независимых уравнений для их определения — только три. Систему следует расчленить (рис. 53), приложив к каждому телу в точке С силы действия одного тела на другое, которые равны численно, но противоположны но направлению.
[c.60]
Таким образом, имеем четыре неизвестных, а независимых уравнений для их определения — только три. Систему следует расчленить (рис. 53), приложив к каждому телу в точке С силы действия одного тела на другое, которые равны численно, но противоположны но направлению.
[c.60]Момент, реакции. .. заделки. Момент пары сил. .. в заделке. Освобождение. .. от заделки. [c.24]
Определить в кН вертикальную составляющую реакции заделки Л консольной балки, если сила натяжения троса F = 10 кН и угол а = 30°. (5,0)
Определить реакцию заделки, еслп P, = Pi — P, 7 = 2Я// q,= = (1/V/. [c.26]
Определить реакцию заделки. [c.26]
Определить реакцию заделки, если а = 00°, = 30°, / = 1 м. [c.27]
Горизонтальная балка заделана одним концом в стену, а на другом конце поддерживает подшипник вала. От веса г.ала, шкивов и подшипника балка испытывает вертикальную нагрузку Q, равнуго 1,2 кН. Пренебрегая весом балки и считая, что нагрузка О действует на расстоянии а = 0,75 м от стены, определить реакции заделки.
[c.26]
Пренебрегая весом балки и считая, что нагрузка О действует на расстоянии а = 0,75 м от стены, определить реакции заделки.
[c.26]
Пример 15. Горизонтальная балка АВ длиной /=1,2 м, поддсржиоающал балкой, заделана в стсну. На балку действует равномерно распределенная нагрузка ИПТСНС1ШН0СТИ q= 1,25 кН/м. Определить реакции заделки (рис. 98). [c.70]
Для определения реакций заделки воспользуемся уравнением возможных мощностеГ] [c.246]
Для определения вертикальной составляющей Уц реакции заделки отбросим связь, препятствующую вертикальному перемещению точки В, заменив жесткую заделку скользящей (вертикальными направляющими) и при южив реакцию Ку (рис. 182). [c.250]
Решение. Данная система состоит из двух тел балок АВ и ВС. Реакция наклонной плоскости направлена перпендикуляра к этой плоскости, а реакция заделки эквивалентна силе / д, приложенной в точке А, направление которой неизвестно, и паре сил с нeизвe тнымJwoмeнтoм т [см. рис. 16(10)]. Обозначая составляющие силы по координатным осям через Хд и составим три уравнения равновесия внешних сил, приложенных к данной системе уравнения проекций
[c.65]
рис. 16(10)]. Обозначая составляющие силы по координатным осям через Хд и составим три уравнения равновесия внешних сил, приложенных к данной системе уравнения проекций
[c.65]
Таким образом, если опорой тела является жеегкая заделка, то со стороны последней на тело дейсгвуют реакция заделки, которую можно заменить двумя взаимно перпендикулярными составляющими, и момент заделки.
Задача 84-14. Жестко заделанная у левого конца консольная балка АВ (рис. 109, а) нагружена равномерно раснрсдслснной нагрузкой интенсивностью г/ = 5 кН/.м, сосрсдогоченной силой / = 12 кН и моменто.м Г=20 кН м. Определить реакции заделки. [c.109]
Вьпле найдено, что 2 , = 0 значит реакция заделки В а перпендикулярна к оси X. Следовательно, [c.110]
На раму AB D в точке D действует сила F, лежащая в плоскости рамы. Определить реакции заделки А. [c.24]
Задача № 24 (№ 24.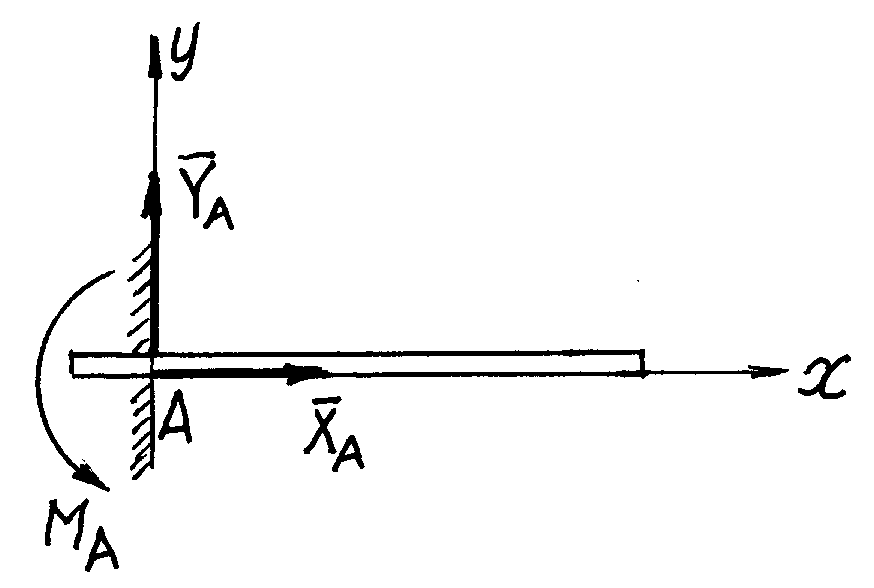 С. М. Т а р г. Краткий курс теоретической механикй. Фнзматгиз, 1958). Брус, вес которого Р = 100 кГ, приложен в точке С, жестко заделан в стену, образуя с ней угол а = 60° (рис. 60, а). Внутри угла ОЛВ лежит цилиндр весом Q= 180 кГ, касающийся брз са в точке Е, причем Л = 0,3, п и /4С = 0,4 м. Определить реакцию заделки.
[c.88]
С. М. Т а р г. Краткий курс теоретической механикй. Фнзматгиз, 1958). Брус, вес которого Р = 100 кГ, приложен в точке С, жестко заделан в стену, образуя с ней угол а = 60° (рис. 60, а). Внутри угла ОЛВ лежит цилиндр весом Q= 180 кГ, касающийся брз са в точке Е, причем Л = 0,3, п и /4С = 0,4 м. Определить реакцию заделки.
[c.88]
Чтобы определить реакцию заделки (X i, и М), надо составить три уравнения равновесия сил, действующих на брус, и, решив их, найти три неизвестные величины. Однако среди сил, действующих на брус, имеется еще одна неизвест- [c.88]
Фигурная балка OABD нахо щтся в равновесии. Определить составляющую в тоннах реакции заделки вдоль оси Oz, если дано ОЛ = , 1 м, ЛВ = 2 м, BD= 3,4 м. BD II Ох, сила F = 1 т и интенсивность распределенной нагрузки q — 2 т м. (4) [c.87]
Момент реакции заделки — Энциклопедия по машиностроению XXL
Момент, реакции.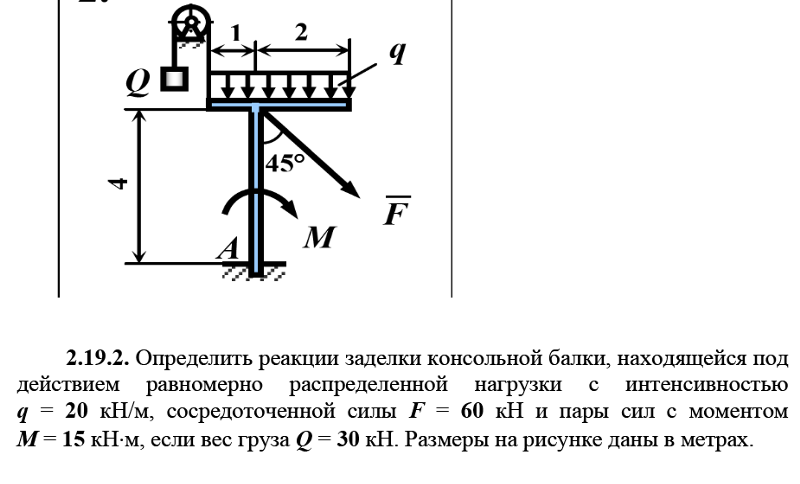 .. заделки. Момент пары сил. .. в заделке. Освобождение. .. от заделки.
[c.24]
.. заделки. Момент пары сил. .. в заделке. Освобождение. .. от заделки.
[c.24]На заделанную ось балки АС действуют со стороны поверхностей, на которые она опирается, неравномерно распределенные реакции этих поверхностей. Пользуясь теоремой Пуансо, их можно привести к одной точке (рис. 68, б) и заменить одной силой — реакцией / д, приложенной в точке А и равной главному вектору распределенных реакций, и одной парой с моментом М , равным главному моменту этих сил относительно точки А и называемым моментом реакции заделки. Нахождение неизвестной по модулю и по направлению реакции в свою очередь можно заменить нахождением алгебраических значений и У двух составляющих этой силы.
Каждому кинематическому ограничению соответствует некоторая реакция. Так, например, реакциями, соответствующими внешним ограничениям (1.2), являются вертикальные силы в сечениях л = 0 и л = / и момент в заделке в сечении х = 0.
 Заметим, что работа любой из этих реакций на произвольном кинематически допустимом смещении равна нулю. В дальнейшем предполагается, что все кинематические ограничения, наложенные на конструкцию, в этом смысле не могут быть источниками образования работы. Реакции, соответствующие внутренним ограничениям, будут рассмотрены в конце разд. 1.2.
[c.10]
Заметим, что работа любой из этих реакций на произвольном кинематически допустимом смещении равна нулю. В дальнейшем предполагается, что все кинематические ограничения, наложенные на конструкцию, в этом смысле не могут быть источниками образования работы. Реакции, соответствующие внутренним ограничениям, будут рассмотрены в конце разд. 1.2.
[c.10]Реакция заделки слагается из сил Кд и пары с моментом т . [c.52]
Сначала определяем реакцию и момент в заделке [c.147]
Сначала определим реакцию заделки, реактивный момент горизонтальную [c.316]
Определить реакции опор для того способа закрепления, при котором момент в заделке имеет наименьшее числовое значение. [c.5]
Если балка АВ, расположенная с приложенными к ней заданными силами F,, F ,. . . в плоскости кАу, закреплена концом А жестко, т. е. заделка в точке А препятствует как поступательному перемещению балки в любом направлении в плоскости хАу, так и вращательному движению вокруг оси Az, перпендикулярной к плоскости хАу, то реакция заделки эквивалентна силе R/i, приложенной в точке.
К балке АВ приложены две нагрузки — по всей длине равномерно распределена нагрузка Г нв точке В сила Мсв — переданное стержнем действие балки СВ (рис. 134, б). Обе эти нагрузки уравновешиваются вертикальной реакцией Ва и реактивным моментом Та заделки (реакция Ва заделки не отклонена от вертикали, так как в данном случае нет усилий, стремящихся сместить балку АВ в горизонтальном направлении). [c.134]
Решение. Если балка заделана в стену, то на заделанный конец балки действует система распределенных сил (реакций). Приведем их по методу Пуансо к точке А, заменим одной неизвестной реакцией заделки (с проекциями Х и К ) и одним неизвестным моментом заделки М. Эти три неизвестные определим из уравнений равновесия сил, действующих на балку. [c.88]
Таким образом, заделка, в отличие от шарнира, создает не только неизвестную по величине и направлению реакцию Ва, но еще и пару сил с неизвестным заранее моментом в заделке Ма (рис. 56, б).
[c.56]
56, б).
[c.56]
Величины реакции и момента в заделке определяются по формулам [c.349]
Реакции заделки в точке А в общем случае дают три неизвестных две составляющие силы но осям координат и момент пары сил одна неизвестная сила имеется в точке В. Таким образом, имеем четыре неизвестных, а независимых уравнений для их определения — только три. Систему следует расчленить (рис. 53), приложив к каждому телу в точке С силы действия одного тела на другое, которые равны численно, но противоположны но направлению. [c.60]
Для реакции и момента в заделке имеем [c.358]
Заделка создаёт неизвестную по величине и направлению реакцию и пару сил с неизвестным моментом в заделке. [c.24]
На рис. 2.62, а реактивный момент в заделке условно показан штриховой линией, что связано с тем, что одновременно показана и сама связь и ее реакция.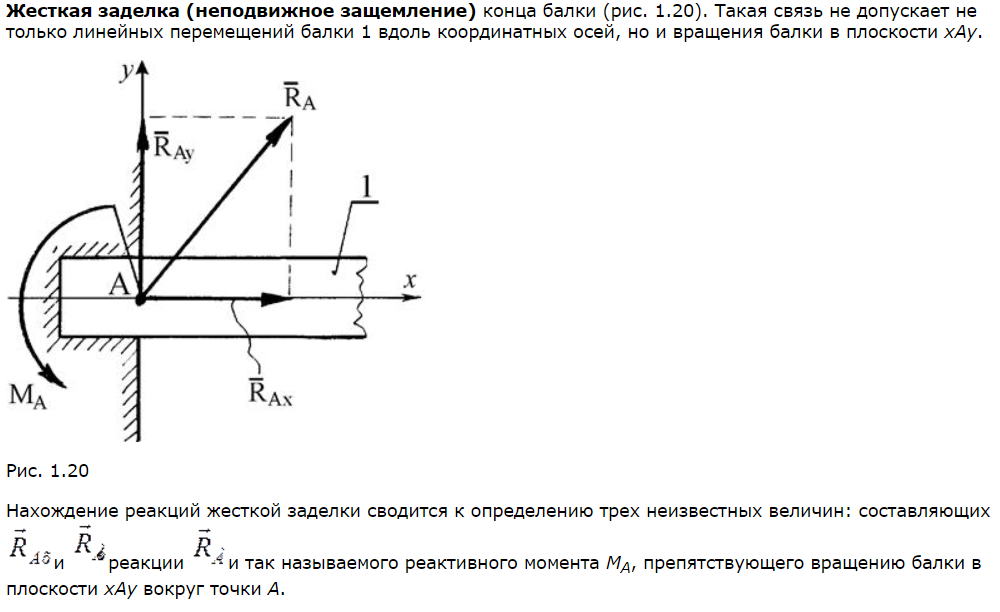 Реактивный момент Ша, как известно из теоретической механики, численно равен алгебраической сумме внешних активных моментов и направлен противоположно результирующему внешнему активному моменту.
[c.225]
Реактивный момент Ша, как известно из теоретической механики, численно равен алгебраической сумме внешних активных моментов и направлен противоположно результирующему внешнему активному моменту.
[c.225]
Определить реакции заделки. Размеры указаны на рис. 72, а. Решение. Балка АВ является тем телом, равновесие которого мы должны рассмотреть. К ней приложена сосредоточенная сила Р, пара сил с моментом т и силы, равномерно распределенные вдоль от- [c.102]
Таким образом, на сочлененную систему будут действовать заданные вертикальные силы К1, заданная пара с моментом т и реакции связей силы реакции Ха и У а и реактивная пара с моментом Ма заделки А, а также вертикальная реакция Ус шарнир но-подвижной опоры С. [c.116]
Для проверки правильности определения всех найденных значений реакций заделки составим уравнение моментов сил относительно шарнира D для левой части конструкции. [c.153]
Пример 4. 4. Балка АВ концом заделана в стену и нагружена силой Р, составляющей с ней угол а, и парой с моментом т. Найти реакцию заделки, если — Ра, а. = 30 (рис. 1.56, а). Массой балки АВ пренебречь.
[c.61]
4. Балка АВ концом заделана в стену и нагружена силой Р, составляющей с ней угол а, и парой с моментом т. Найти реакцию заделки, если — Ра, а. = 30 (рис. 1.56, а). Массой балки АВ пренебречь.
[c.61]
Для всех сечений будем на.ходить момент, оставляя часть балки левее се ю-нкя, т. е. построим эпюру со свободного конца, что даст воз.можность не вычислять реакцию и момент в заделке. Имеем [c.300]
Решение. Отбросим заделку, заменив ее реакциями, и рассмотрим равновесие балки. Реакции заделки представляют собой реактивную сипу П и реактивный момент т. Так как реактивный момент т может быть уравновешен только парой сил, то нагрузка Р и реакция К должны образовывать пару, следовательно, [c.36]
Переходим к определению реакции заделки В. Сначала найдем реактивный момент Мд. Для этого отбросим связь, препятствующую [c.277]
Решение. Для данного загружения балки реактивный момент будет равен тр = Р-(, а вертикальная реакция заделки А = Р.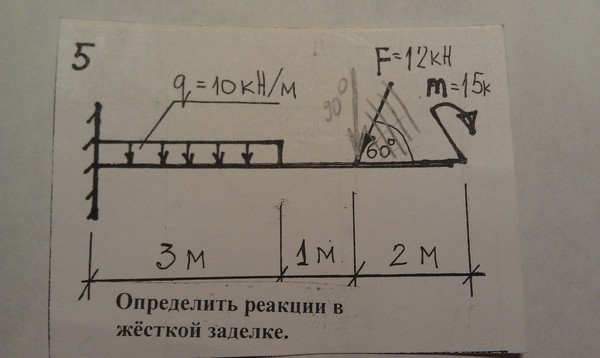 [c.205]
[c.205]
Левый из моментов (рис. 6.6) представляет собой реакцию заделки. [c.170]
Таким образом, заделка в отличие от гнарнира создает не только не известную по величине и направлению реакцию тю еще и пару сил с не известным заранее моментом в заделке (рис. 48, в). [c.60]
Решение. Применим к внешннм силам и силам инерции стержня А В слсдсгвия из принципа Даламбера в форме условий равновесия сил. Неизвестные реакцию и векгорный момент в заделке разложим по осям координат. [c.369]
Таким образом, наименьиши момент в заделке получается г.ри saf pen-яеиии бруса по схеме 6. Определим остальные опорные реакции для этой схемы [c.10]
Таким образом, если опорой тела является жеегкая заделка, то со стороны последней на тело дейсгвуют реакция заделки, которую можно заменить двумя взаимно перпендикулярными составляющими, и момент заделки. [c.101]
Задача 84-14.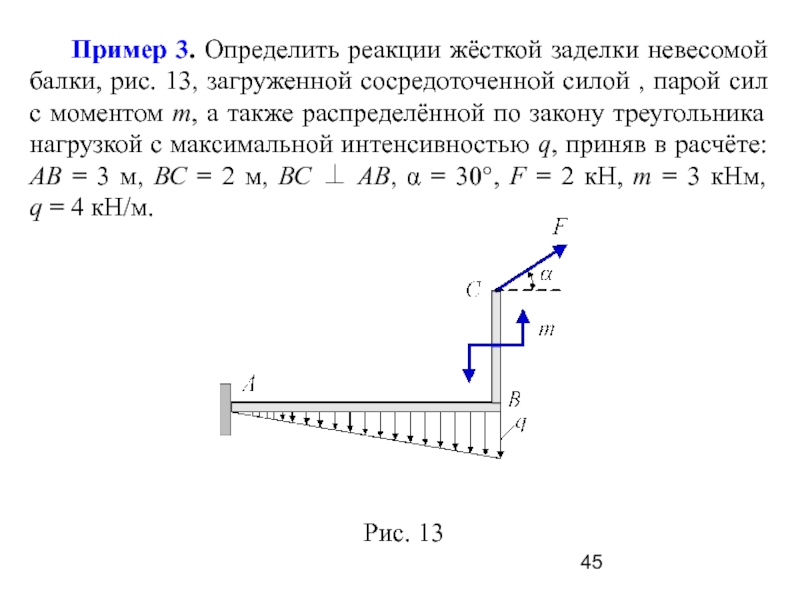 Жестко заделанная у левого конца консольная балка АВ (рис. 109, а) нагружена равномерно раснрсдслснной нагрузкой интенсивностью г/ = 5 кН/.м, сосрсдогоченной силой / = 12 кН и моменто.м Г=20 кН м. Определить реакции заделки.
[c.109]
Жестко заделанная у левого конца консольная балка АВ (рис. 109, а) нагружена равномерно раснрсдслснной нагрузкой интенсивностью г/ = 5 кН/.м, сосрсдогоченной силой / = 12 кН и моменто.м Г=20 кН м. Определить реакции заделки.
[c.109]
Реакции в заделке. Заделкой называется жесткое (неподвижное) соединение звеньев. Их взаимодействие сводится к силе и моменту реакции. На рис. 5.4,5 показана заделка в неподвижной стенке стержня, на который действует плоская система сил / 1 и РРеакцию удобно представить в виде двух составляющих и силы и реактивного момента М. [c.56]
Решение, Применим к внешним силам и силам инерции, действующим на стержень АВ, следствия из принципа Даламбера в форме шести условий равновесия. Неизвестные реакции Рд н векторный момент в заделке Мд разложим по осям координат. Если разбить весь стержень на элементарные участки одинаковой длины, то ускорения средни этих участков распределятся вдоль стержня по линепно.му закону (рнс. 261, б), так как ускорение каждой точки стержня
[c.348]
261, б), так как ускорение каждой точки стержня
[c.348]
Таким образом, заделка в отличие от шарнира со. даег не только неизвестную но величине и направлению реакцию Р а. но еще и пару сил с не известным заранее моментом в заделке А1 А (рис. 50, б). [c.57]
Условное изображение задвланной в стену балки, находящейся под дейстЕиегл плоской системы из сил Р и Q с реакциями заделки, приведено на рис. 2.11. Реакциями заделки в задачах на ПСС являются неизвестная сила Н и неизвестная пара сил с- моментом М — главный вектор и главный момент некоторой неизвестной системы сил ( ь действующей со стороны стены на заделанный конец балки. За центр приведения этой не-Рис. 2.11 известной СС принимается точка, где [c.50]
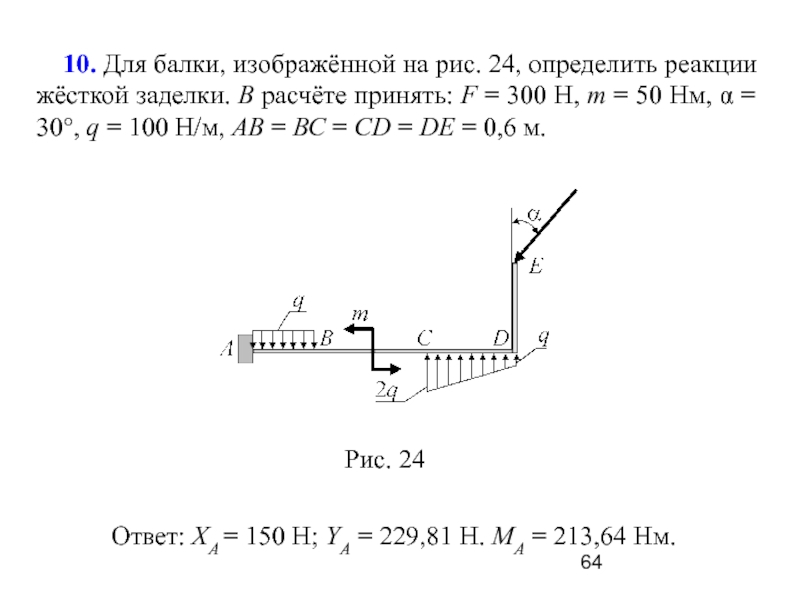
Определить реакции заделки в т.А Г-образной бажи, находящейся под действием сил F 10 кН. и F = 6 кН. пары сил с моментом [c.
 65]
65]Выясним, что представляет собой реакция такой связи. Для этого освободим балку от связи. Со стороны стены на защемленную часть балки действует некоторая совокуинссть сил, которую будем считать произвольной плоской системой снл (рис. 1.53, а). Приняв за центр приведения точку А, получим силу Яа и пару сил с моментом Ма (рис. 1.53,6). Эта совокупность силы и пары и представляет собой реакцию заделки. Поскольку ЯХ неизвестна по величине и во направлению, нахождение ее сво-дитея к определению двух составляющих Ха н Уа этой силы. [c.59]
Пример 4.7. Балка АВ, концом А заделанная в стенку, подвергается действию равно.мерно распределенной нагрузки ннтенсивнопн ) и пары с моментом т. Найти реакцию заделки, если АВ = 1,5 м, q — Ю кН/м, т = 1,25 кН-м (рис. 1,62, а). Силой тяжести балки пренебречь. [c.66]
Решение. Эпюри начинаем строить со свободного конца балки. Это ноз водит не определять реакцию и реактивный момент в заделке. [c.260]
[c.260]
В сечении на опорах перерезывающая сила и изгибающш момент численно равны опорной реакции и моменту в заделке или в onojje, если такой приложен. Если в шарнирной опоре не приложен сосредоточенный момент, то скачка изгибающего момента на эпюре не должно 6bm>. [c.27]
Определяем реакции в заделке. Предварительно произвольно направляем реащию и момент в заделке в противоположную сторону действия силы F и момента от этой си.аы. Составим уравнения равновесия — сумма проекций сил на ось у, сумм.а моментов относительно точки А должны быть равны нулю [c.27]
Уравнения равновесия удовлетворяются inpH отсутствии реакции и момента в заделке. [c.108]
Пример 2. Два стержня AD и ВС (рис. 221, а) соединены скользящим шарниром (ползуном) С. Опора.ми системы служат за- делка А и неподвижный шарн1ф В. На систему действуют сила Р = 20 кН, пара сил с моментом т = 60 кН-м и распределенная по закону треугольника нагрузка с максимальной интенсивностью = 20 кН/м.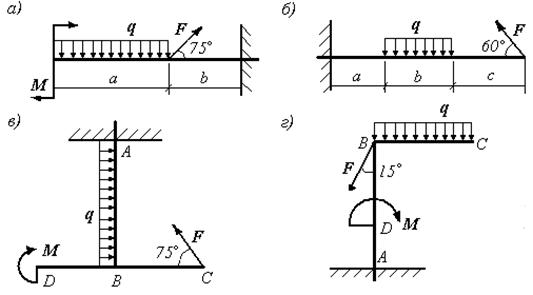 Размеры даны на с.хеме. Найти реакции заделки А, шарнира В и ползуна С.
[c.263]
Размеры даны на с.хеме. Найти реакции заделки А, шарнира В и ползуна С.
[c.263]
Соэффициенты при неизвестных г представляют собой реактивные моменты в заделках иди реакции в узловых стержнях основной системы, вызванные единичными смещениями. [c.524]
Домашнее задание №1
Домашнее задание №1Домашнее задание №1. Построение эпюр внутренних силовых факторов
Стр. 1, задача 1, растяжение-сжатие колонны
Данная задача была исключена из домашнего задания в 2016 году из-за сокращения программы курса. Тем не менее задачи на растяжение-сжатие я продолжаю рассматривать и на семинарах, и в данном руководстве, поскольку, во-первых, относительно простая тема позволяет лучше понять суть метода сечений и процедуру построения любых эпюр, а во-вторых, при выполнении и защите домашнего задания №2 строить эпюры для колонн все равно придётся.
Итак, вначале ищем реакцию заделки. Для этого складываем силы, вызывающие растяжение вблизи заделки и направленные, следовательно, вправо. Получается 2F + 3F = 5F. Далее, сила, взывающая сжатие, одна и равна F. Таким образом, «побеждают» растягивающие и создают в заделке силу 5F — F = 4F. Теперь можно идти слева направо, изображая скачки́ на эпюре там, где приложены силы. Причём силы, направленные вправо, создают растяжение (плюс) слева и сжатие (минус) справа, то есть скачок идет от плюса к минусу, то есть вниз.
Получается 2F + 3F = 5F. Далее, сила, взывающая сжатие, одна и равна F. Таким образом, «побеждают» растягивающие и создают в заделке силу 5F — F = 4F. Теперь можно идти слева направо, изображая скачки́ на эпюре там, где приложены силы. Причём силы, направленные вправо, создают растяжение (плюс) слева и сжатие (минус) справа, то есть скачок идет от плюса к минусу, то есть вниз.
Придя к правому торцу, мы встречаем силу, направленную влево. Рассуждая аналогично, приходим к выводу, что скачок должен выполняться вверх. Поскольку текущее (на третьем участке) значение нормальной силы равно –F, то мы приходим в нуль, что является проверкой решения.
Можно рассуждать и проще – на конце последнего участка усилие определяется силой, приложенной к торцу. Она равна F и является сжимающей, значит, порождающей отрицательное усилие того же модуля. То есть проверку можно закончить в точке приложения силы 2F.
Наконец, ещё проще не искать реакцию заделки и строить эпюру не слева направо, а в обратном направлении.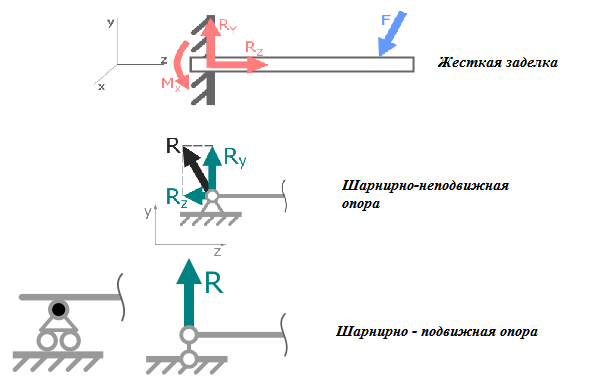 Правда, тогда мы лишаем себя проверки на левом конце, зато выигрываем время.
Правда, тогда мы лишаем себя проверки на левом конце, зато выигрываем время.
Стр. 2, задача 2, изгиб шарнирно опёртой балки
Решение выполнено внизу, эпюры изображены под расчетной схемой. К ним мы вернёмся позже.
Отбрасываем опоры, заменяем их реакциями {1}, {2}. Направления их выбираем, вообще говоря, произвольно, но можно постараться их предугадать – это позволит лучше понять «физику» задачи. В данном случае обе распределённые нагрузки направлены вниз, то есть, скорее всего, обе реакции (одна-то уж наверняка) направлены вверх. Елизавета Ильинична так и поступила.
Составляем сумму сил на вертикаль {3}. Пока в нём мало проку – одно уравнение содержит две неизвестных.
Теперь выберем точку для составления суммы моментов {4}. Разумеется, она может быть произвольной, но удобно выбирать точку приложения реакции – это позволит исключить её из уравнения. Елизавета Ильинична выбрала точку В. Произвольное правило знаков для моментов {5} не слишком удачно: гораздо удобнее выбирать направление так, чтобы неизвестная величина (в данном случае RD) вошла с минусом. Это позволит, перенеся её в правую часть, сменить её знак с минуса на желанный плюс и больше никаких знаков не менять.
Это позволит, перенеся её в правую часть, сменить её знак с минуса на желанный плюс и больше никаких знаков не менять.
Далее из {4} находим RD {6} и, подставляя её в {3}, определяем реакцию RВ {7}. Как и предполагалось, обе реакции оказались положительными.
Альтернативный способ составления уравнений равновесия в подобных задачах заключается в том, что составляют уравнения моментов относительно точек приложения реакций, а сумма на вертикаль не составляют вовсе. Это позволяет получить не систему второго порядка (в данном случае {3} и {4}), а два независимых уравнения относительно реакций. Недостаток способа – дробные величины плеч реакций. Не берусь безусловно порекомендовать ни тот, ни другой путь. Следует попробовать оба и выбрать понравившийся.
Есть и ещё (по крайней мере) один способ – для истинных гурманов. Особенно эффективен он, когда имеется лишь один участок распределённой нагрузки. Тогда уравнение моментов составляется относительно середины этого участка, тем самым слагаемые, связанные с распределённой нагрузкой, в уравнение не входят. К данной задаче, как видно, способ хоть и применим, но не ведёт к упрощению решения.
К данной задаче, как видно, способ хоть и применим, но не ведёт к упрощению решения.
Стр. 3, задача 2, продолжение
Изображаем безопорную расчётную схему {1}. На участке АВ выбираем произвольное сечение Е с текущей координатой zAB {2} и вводим неизвестные внутренние силовые факторы Qy {3} и Mx {4} c направлениями строго согласно правилам знаков. А вот произвольное направление положительного момента {5} на этот раз выбрано удачно, в чём мы убедимся ниже.
Составляем сумму сил на вертикаль {6}, выражаем искомую поперечную силу Qy и подставляем в него значения координаты в начале {7} и в конце {8} участка. Видно, что сила знак не меняет, значит, экстремума изгибающего момента на этом участке нет. Сумма моментов {9} составляется относительно текущей точки Е, что позволяет исключить из уравнения поперечную силу. С учетом выбранного правила знаков переносим неизвестный момент Mx в правую часть и без смены знаков получаем функцию момента относительно координаты. Подставляем в него начальное {10} и конечное {11} значения координаты и получаем моменты на краях участка.
Подставляем в него начальное {10} и конечное {11} значения координаты и получаем моменты на краях участка.
При рассмотрении участков от второго и далее удобно делать не одно, а два сечения. Первое из них находится на дифференциально малом расстоянии слева от (раньше, не доходя до) начала текущего участка {12}. Второе – текущее в точке К. В левое сечение переносим найденные в конце предыдущего участка значения силы и момента: сила получилась отрицательной {8} и, значит, на левом конце расчётной схемы по правилу знаков она направляется вниз {13}. Отрицательный момент {11} по той же причине направляется против часовой стрелки {14}.
На участке CD поперечная сила меняет знак с плюса {15} на минус {16}. Это значит, что момент достигает экстремума. Для его поиска левую часть уравнения для силы {17} приравниваем нулю и находим координату экстремума {18}. По давней традиции величины, относящиеся к экстремуму (координата и момент), обозначаются звездочкой. Составляем сумму моментов {19} и, выражая из него неизвестный момент (это уравнение Елизавета Ильинична не выписала отдельно, делая выкладки в уме), подставляем найденную в {18} координату экстремума.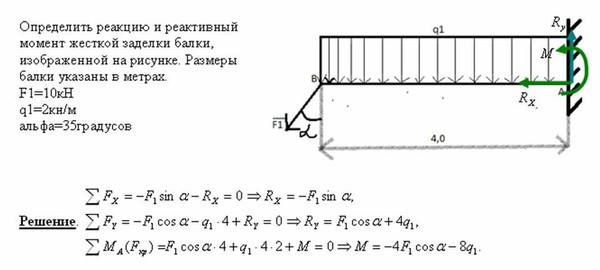 Точное значение экстремума {20} равно 5929/2592 q·l2. Погрешность указанного десятичного значения 2.3 q·l2 составляет 0.55%, так что отказ от громоздкой простой дроби выглядит вполне оправданным.
Точное значение экстремума {20} равно 5929/2592 q·l2. Погрешность указанного десятичного значения 2.3 q·l2 составляет 0.55%, так что отказ от громоздкой простой дроби выглядит вполне оправданным.
Эпюры поперечной силы {8} и изгибающего момента {9} показаны под расчетной схемой (Стр. 2), что очень удобно для визуальной проверки обеих эпюр.
Стр. 4, задача 3, изгиб шарнирно опёртой балки
Стр. 5, задача 3, продолжение
Стр. 6, задача 4, изгиб шарнирно опёртой балки
Стр. 7, задача 4, продолжение
Данные задачи решаются по тому же алгоритму и отдельных комментариев не требуют.
Стр. 8, задача 5, изгиб консольной балки
Здесь уместно обратить внимание на грамотный выбор Елизаветой Ильиничной направлений неизвестных реакций заделки.
Согласно правилам знаков, на левом конце расчётной схемы положительный момент направлен по часовой стрелке, а положительная сила – вверх. Внешние силовые факторы тех же направлений порождают положительные внутренние. Следовательно, если направить реакции именно так, то по их формальным знакам можно будет сразу судить о фактических знаках внутренних силовых факторов.
Следовательно, если направить реакции именно так, то по их формальным знакам можно будет сразу судить о фактических знаках внутренних силовых факторов.
Отбросив заделку, Елизавета Ильинична направила реактивный момент по часовой {1}, а реактивную силу {2} – вверх. Реакции получили такие знаки: сила – плюс {3}, момент – минус {4}. Именно такие знаки автоматически оказались на эпюрах – {5} и {6} соответственно.
Стр. 9, задача 5, продолжение
Стр. 10, задача 6, изгиб шарнирно опёртой балки с врезанным шарниром
Данная задача была включена в задание, можно сказать, в виде шутки, или, точнее, розыгрыша. Дело в том, что решается она за считанные секунды и не требует ни рисунков, ни формул. Тем не менее подавляющее большинство студентов подходят к ней со всей серьёзностью и ответственностью, расписывая все уравнения и делая сечения. Более того, некоторые умудряются ещё и ошибаться. Ниже я покажу, как можно потратить на решение ровно столько времени, сколько требуется для выполнения одного рисунка – эпюры моментов.
Предельная простота задачи определяется наличием шарнира, врезанного над средней опорой. Во врезанном шарнире момент всегда равен нулю. То есть мы сразу, во-первых, имеем одну точку эпюры над средней опорой. Во-вторых, расчётная схема разбивается на две независимых балки слева и справа от средней опоры. В-третьих, отпадает необходимость поиска не только реакции средней опоры, но и, как правило, реакций остальных опор.
Данная задача распадается на шарнирно опёртую балку АВ, нагруженную распределённой силой и моментом на левом конце, и на балку ВС с одним моментом на правом конце.
Начнем с участка АВ, а точнее, с момента. Согласно правилу знаков, ему будет отвечать отрицательный изгибающий момент в сечении А. Далее идёт парабола выпуклостью вверх, приходящая в сечении В, как мы уже знаем, в нуль. Поиск экстремума, правда, всё же требует определения реакции в опоре А, но без учёта участка ВС. Итак, составляя сумму моментов слева от врезанного шарнира, находим реакцию в опоре А – она равна 3/2 q·l и направлена вверх. Нетрудно догадаться, что вся эпюра поперечной силы на данном участке будет расположена сверху оси и её не пересечёт. Значит, и экстремума на участке АВ нет. Рисуем эпюру и переходим к участку ВС.
Нетрудно догадаться, что вся эпюра поперечной силы на данном участке будет расположена сверху оси и её не пересечёт. Значит, и экстремума на участке АВ нет. Рисуем эпюру и переходим к участку ВС.
А на нём и рассматривать-то нечего: слева нуль, справа +2 q·l2. Соединяем точки прямой и всё – эпюра построена, задача решена.
Стр. 11, задача 7, изгиб балки с двумя врезанными шарнирами
В расчётной схеме пять неизвестных: в сечении А момент и две силы, горизонтальная и вертикальная, и по одной реакции в сечениях С и Е. Исходя из суммы на горизонталь, сразу исключаем из рассмотрения все горизонтальные силы, как реактивные, так и внутренние. Остаются 4 неизвестных. Уравнений будет больше, а именно:
- Сумма сил на вертикаль;
- Сумма моментов всех внешних силовых факторов слева от шарнира В, относительно него же;
- То же, справа от В;
- То же, слева от D;
- То же, справа от D;
- Сумма всех моментов относительно произвольной точки.
То есть имеем шесть уравнений для четырёх неизвестных. Значит, четыре уравнения используем для поиска реакций, одно – для необязательной проверки, а одно оказывается линейной комбинацией всех остальных уравнений и, таким образом, лишним.
Елизавета Ильинична выбрала уравнения №№5, 3, 1 и 2 ({1}-{4}), соответственно. Порядок решения выглядит разумным – каждое уравнение даёт новую, ранее неизвестную, величину, с учётом предыдущих результатов. Реакция R4 вычисляется сразу {1}, что позволяет последовательно найти R3 {2}, затем R1 {3}, и, окончательно, R2 {4}.
Далее, не делая сечения и не рисуя отсечённый кусочек (точнее, выполняя эти действия мысленно) {5}, Елизавета Ильинична ищет координату экстремума {6} и его величину {7}, на участке АВ.
Остальные расчёты выполняются аналогично.
Стр. 12, задача 7, продолжение
Стр. 13, задача 8, плоская рама
Задача также решена исключительно в уме. Сперва составляем сумму моментов относительно неподвижного шарнира. Обе внешние силы дают по моменту Fl против часовой стрелки. Чтобы уравновесить конструкцию, реакция в подвижном шарнире с плечом l должна быть направлена вниз и равняться 2F. Сумма на горизонталь даёт нулевую горизонтальную реакцию в неподвижном шарнире. Вертикальная в нём же равна 2F и направлена вверх, хотя для построения эпюры она и не нужна.
Сперва составляем сумму моментов относительно неподвижного шарнира. Обе внешние силы дают по моменту Fl против часовой стрелки. Чтобы уравновесить конструкцию, реакция в подвижном шарнире с плечом l должна быть направлена вниз и равняться 2F. Сумма на горизонталь даёт нулевую горизонтальную реакцию в неподвижном шарнире. Вертикальная в нём же равна 2F и направлена вверх, хотя для построения эпюры она и не нужна.
Строим эпюру начиная, допустим, с правого верхнего угла. Вертикальная сила вызывает сжатие, а не изгиб, и может пока не учитываться. Горизонтальная сила сжимает левые (внутренние) слои и в правом нижнем углу даёт момент 2Fl. Из узла согласно правилу «с чем пришёл – с тем ушёл» мы уходим с тем же моментом, сжимающим те же внутренние слои. Но далее вертикальная сила заставляет эпюру момента идти вниз и прийти в нуль в левом нижнем углу. Задача решена.
Стр. 14, задача 9, плоская круговая рама
Постановка задачи {1}. Далее в уме находим реакции, составляя сперва сумму моментов относительно шарнира D.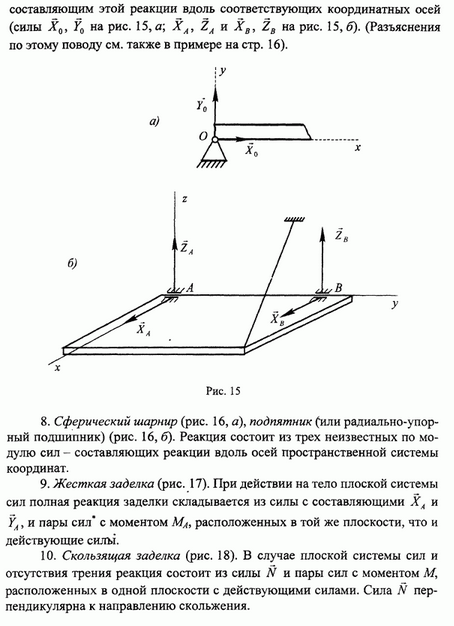 Обе внешних нагрузки дают момент Fr + 2F·r = 3Fr по часовой стрелке. Тогда сила в шарнире А с плечом r должна быть направленной вниз и быть равной 3F. Теперь из проекций на вертикаль и горизонталь находим реакции в самом шарнире D. Безопорная конструкция {2}.
Обе внешних нагрузки дают момент Fr + 2F·r = 3Fr по часовой стрелке. Тогда сила в шарнире А с плечом r должна быть направленной вниз и быть равной 3F. Теперь из проекций на вертикаль и горизонталь находим реакции в самом шарнире D. Безопорная конструкция {2}.
Стр. 15, задача 9, продолжение
Разбиваем раму на участки DC и CA. На первом из них {1} произвольно выбираем направление изгибающего момента и правило знаков (вновь, на мой взгляд, неудобное).
В начале участка СА сила 5F {2} – внутренняя, найденная в уме из равновесия участка DC, а сила 2F {3} – внешняя. В уравнение равновесия попадает их сумма, точнее, разность 3F вместе с внутренним моментом 5Fr, также найденным на предыдущем участке.
Углу 180° в выбранной системе координат соответствует сечение А. Момент получился отрицательным и равным по модулю Fr {5}. Согласно выбранному правилу знаков {6} отрицательным считается момент, сжимающий внешние слои рамы. Именно таков по модулю и направлению внешний момент в сечении А – проверка сошлась.
Именно таков по модулю и направлению внешний момент в сечении А – проверка сошлась.
Эпюра {3} показана на Стр. 14.
Стр. 16, задача 10, Т-образная плоская рама
Реакции заделки найдены на черновом рисунке внизу. Построение эпюры очевидно.
Две остальные задачи (всего их в то время было 12) посвящены плоскопространственной и пространственной рамам, соответственно. В настоящее время эти задачи исключены из домашнего задания и здесь не рассматриваются.
Нахождение опорных реакций 2 — Сопромат — Каталог статей
Теперь рассмотрим другую схему, где встретится жесткая заделка и изгибающий момент.
Вот такая вот балка. Конечно, для ее расчета на прочность, не обязательно находить реакции, возникающие в жесткой заделке, но сейчас мы рассматриваем именно их, а расчет на прочность нам не важен.
И так, как говорилось ранее, в жесткой заделке возникают три силы: горизонтальная Ha, вертикальная Ra и изгибающий момент Ма.
Распределенную нагрузку заменяем на Q, которое равно (Q=q*L) 2*3=6.
Как и в прошлом примере На равняется 0, т.к. кроме нее нет сил, которые дадут проекцию на ось Х.
Теперь нам нужно найти Ma и Ra.
Сначала найдем Ма, т.к. найти Ra первым мы не сможем.
Берем сумму моментов относительно точки А.
На и Ra не учитываются, так как они действуют в этой точке и у них нет плеча, но момент Ма действовать будет, несмотря на то, что он приложен в этой точке.
Смотрим, какие силы куда вращают конструкцию, если «гвоздь» забит в точке А и какие плечи будут у этих сил.
Ма – действует против часовой стрелки, плечи для моментов мы не берем., знак +
Q – вращает по часовой стрелке с плечом 2.5 (если не понятно, почему именно 2.5 — смотрите прошлый урок), знак —
F – против часовой стрелки с плечом равным 5, знак +
М – у нас против часовой стрелки и плеча у него нету, так как для моментов плечи не нужны, знак +
Чтобы не пропустить какую-либо силу, лучше рассматривать поочередно, слева направо (как у нас в примере) или справа налево.
Расписываем:
∑МА=0
Ma-Q*2.5+F*5+М=0
Подставляем значения
Ма-6*2,5+5*5+3=0
Ма-15+25+3=0
Ма=-13
Момент получился отрицательный, значит на чертеже мы обозначили его не в том направлении. Чтобы он был равен не -13, а 13, нужно изменить его, чтобы он поменял направление и стал действовать по часовой стрелке, но этого мы делать не будем и оставим все так.
Теперь нам надо найти Ra. И для этого мы распишем сумму моментов относительно любой другой точки.
Я возьму сумму моментов относительно точки В, т.к. я не хочу учитывать в сумме уравнений Q, которая действует в этой точке и момента не даст, ведь у нее не будет плеча.
Распишем силы и их плечи слева направо.
Ма – без плеча, действует против часовой стрелки, знак +
Ra – плечо равно 2,5 , конструкцию вращает по часовой стрелке, знак –
Q как мы уже сказали, не действует
F – плечо 2,5 , вращает против часовой стрелки, знак +
М – момент без плеча и вращается он против часовой стрелки, знак +
Расписываем:
∑МВ=0
Ма-Ra*2.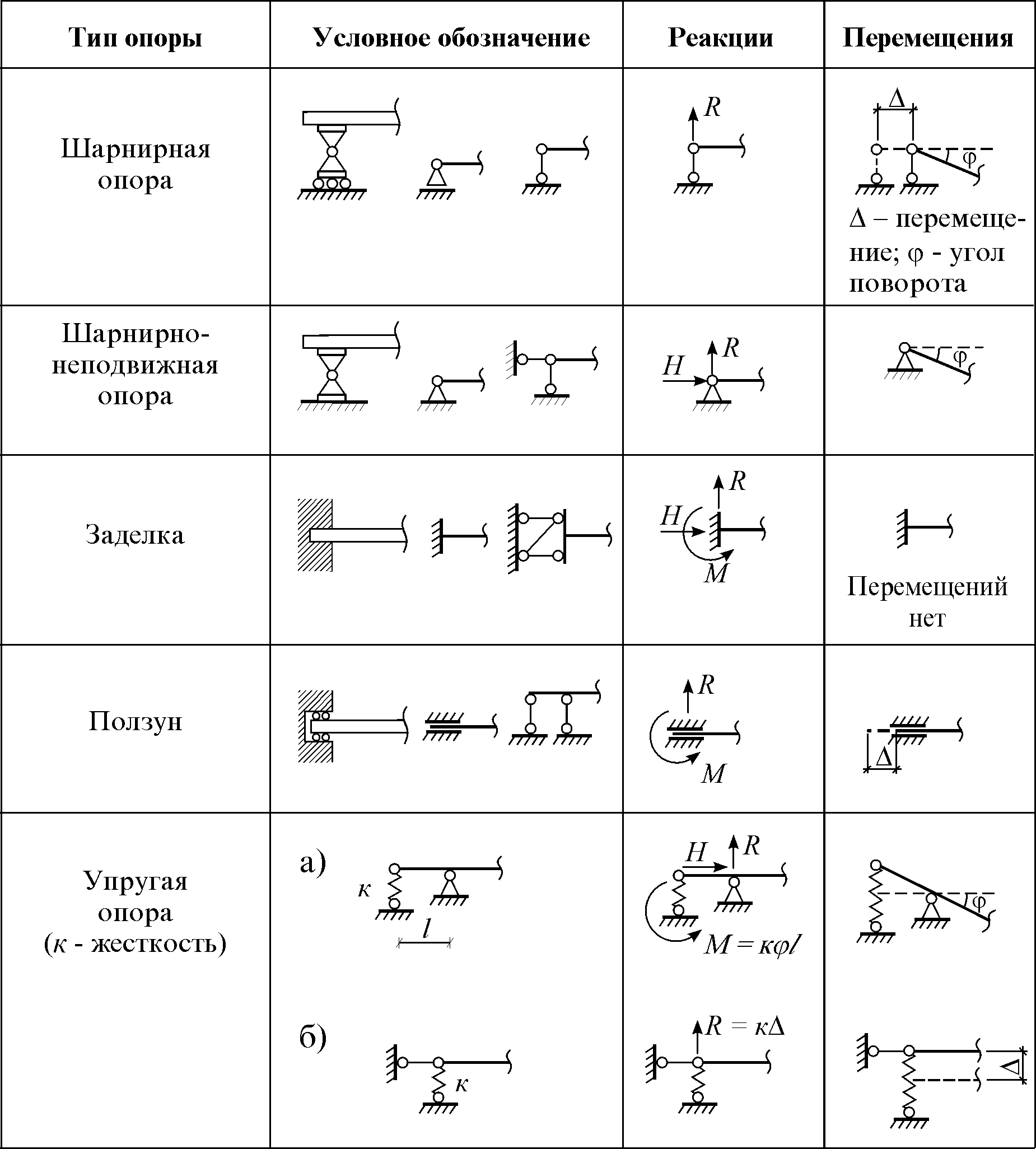 5+F*2.5+M=0
5+F*2.5+M=0
Подставляем значения:
-13-Ra*2.5+5*2.5+3=0
-13+12.5+3=Ra*2.5
2.5=Ra*2.5
Ra=1
И так, мы нашли все неизвестные нам силы.
Обычная проверка с суммой сил на какую-либо ось нам не подходит, так как есть момент Ма, его нам тоже необходимо проверить.
По этому опять расписываем сумму моментов относительно какой-нибудь оставшейся точки, например D
∑MD=0
М-F*3+Q*5.5-Ra*8+Ma=0
3-15+33-8+(-13)=0
0=0
Проверка выполнена, значит все найдено правильно.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie.
 Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie. - Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie
потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Предоставить доступ без файлов cookie
потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Герметик — обзор | ScienceDirect Topics
7.7 Выводы
Герметики играют решающую роль во многих различных машинах и конструкциях, защищая их от окружающей среды. Сшитые каучуки традиционно играли центральную роль в герметизации таких устройств и обычно обладают значительной устойчивостью ко многим различным химическим веществам, особенно когда в их составе используются специальные добавки. Примеры включают уплотнения двигателя, где главный коленчатый вал должен быть уплотнен кромкой, чтобы предотвратить просачивание масла.Манжетные уплотнения из витона широко используются в этой важной роли из-за их стойкости к маслу, теплу и высокому давлению. Уплотнения также играют важную роль в гидравлических системах, таких как тормозные контуры, и если они по какой-либо причине выходят из строя, водитель может потерять контроль над своим транспортным средством, если уплотнение выйдет из строя и мощность торможения будет потеряна. Усталость резиновых изделий может возникать по многим причинам, но является признаком недостаточной конструкции, неправильного выбора материала, размеров, устойчивости к гидравлическим жидкостям или плохого обслуживания. Это смертоносно по своим последствиям, потому что водитель не будет знать о какой-либо проблеме до последних стадий роста трещины, когда происходит утечка жидкости, за которой быстро следует полная потеря жидкости, когда трещина становится критической и растет до конца.
Сшитые каучуки традиционно играли центральную роль в герметизации таких устройств и обычно обладают значительной устойчивостью ко многим различным химическим веществам, особенно когда в их составе используются специальные добавки. Примеры включают уплотнения двигателя, где главный коленчатый вал должен быть уплотнен кромкой, чтобы предотвратить просачивание масла.Манжетные уплотнения из витона широко используются в этой важной роли из-за их стойкости к маслу, теплу и высокому давлению. Уплотнения также играют важную роль в гидравлических системах, таких как тормозные контуры, и если они по какой-либо причине выходят из строя, водитель может потерять контроль над своим транспортным средством, если уплотнение выйдет из строя и мощность торможения будет потеряна. Усталость резиновых изделий может возникать по многим причинам, но является признаком недостаточной конструкции, неправильного выбора материала, размеров, устойчивости к гидравлическим жидкостям или плохого обслуживания. Это смертоносно по своим последствиям, потому что водитель не будет знать о какой-либо проблеме до последних стадий роста трещины, когда происходит утечка жидкости, за которой быстро следует полная потеря жидкости, когда трещина становится критической и растет до конца.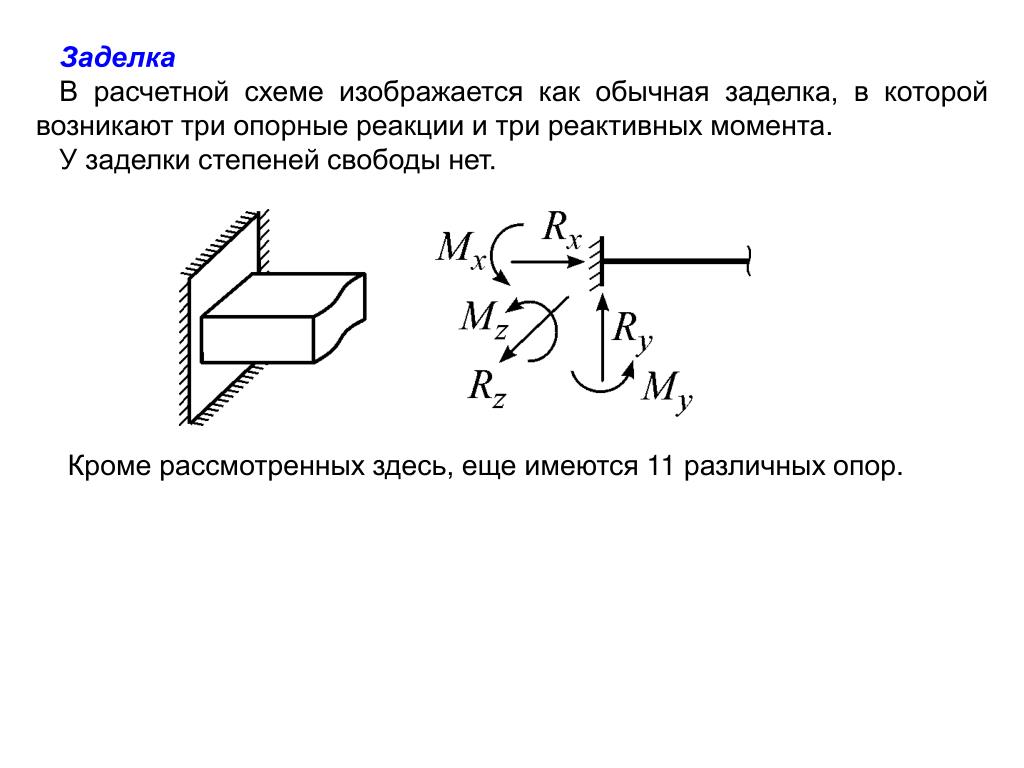
Каучуки обладают совершенно разными физическими свойствами, простым примером которых является устойчивость к отскоку (глава 1). Твердый полибутадиеновый мяч будет высоко подпрыгивать (около 75%), поскольку каучук обладает высокой эластичностью при 20 °C, в то время как мяч из натурального каучука будет подпрыгивать примерно на 60 % от первоначальной высоты, а бутиловый – только на 10 %. Но упругость сильно зависит от температуры и всегда падает с понижением температуры. В случае уплотнительных колец Viton падение упругости было критическим во время катастрофы Challenger в январе 1986 года и позволило пороховым газам выйти из ракеты-носителя во время старта.Более низкие, чем ожидалось, температуры воздуха охлаждали резину почти до температуры замерзания, и кольца не могли достаточно быстро реагировать на вибрации в монтажном соединении. Горячие газы выходили через крошечную щель, которая затем быстро увеличивалась по мере выгорания резины. В результате взрыва космический шаттл был сброшен в море, и все астронавты погибли.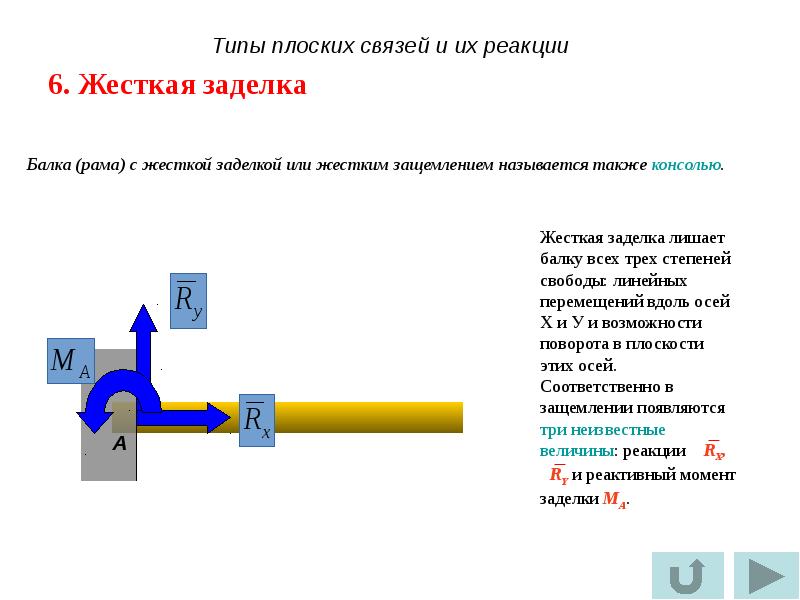 Проблема была понятна из предыдущих инцидентов, но НАСА и руководство Thiokol преодолели возражения, и последовала катастрофа. Дизайн теперь был изменен за счет большего количества уплотнительных колец, но почему это не было сделано до события, а не после?
Проблема была понятна из предыдущих инцидентов, но НАСА и руководство Thiokol преодолели возражения, и последовала катастрофа. Дизайн теперь был изменен за счет большего количества уплотнительных колец, но почему это не было сделано до события, а не после?
Резиновые уплотнения в пневматических системах имеют жизненно важное значение для нормальной работы, и когда в 2001 году на заводе по производству полупроводников в Японии начались отказы, пострадали многие блоки по производству микросхем, поскольку все они контролировались через одну и ту же линию и питались от одинаковая подача воздуха.Сначала внимание привлекла оксидированная мембрана NBR, но вскоре стало очевидно, что основной причиной проблем был озонолиз. ESEM-исследование треснувшего уплотнения показало, что трещины растут из двух острых внутренних углов, а поверхности излома обогащены атомарным кислородом. Независимый анализ воздушного потока выявил следы озона и оксидов азота, свидетельствующие об образовании электрического разряда.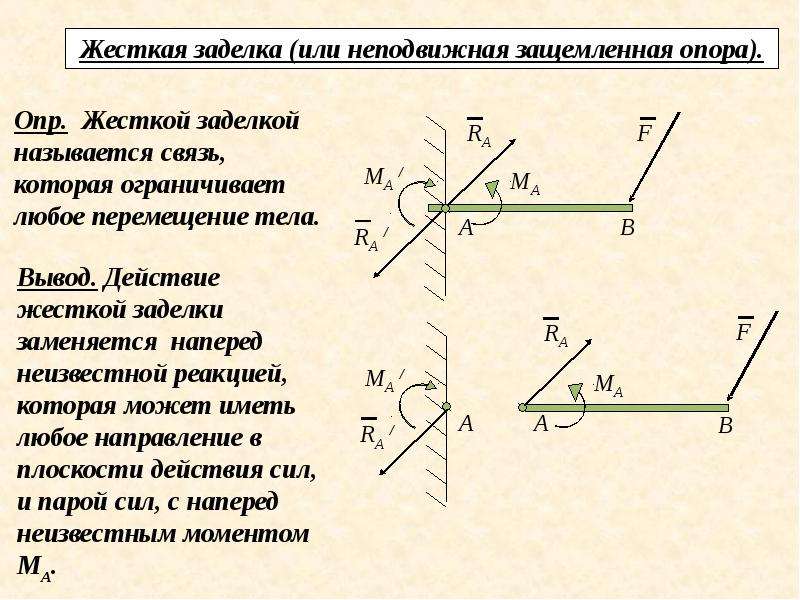 Вероятно, источником газов была новая конструкция компрессора, а фильтры в системе были не в состоянии поглощать такие загрязнения.Новые фильтры решили проблему. Другой крупный производитель пневматики предупредил о проблеме до того, как проблема возникла, но сообщение не было замечено и не было предпринято никаких действий. Изменения в оборудовании иногда могут привести к неожиданным последствиям и должны быть тщательно изучены перед внедрением.
Вероятно, источником газов была новая конструкция компрессора, а фильтры в системе были не в состоянии поглощать такие загрязнения.Новые фильтры решили проблему. Другой крупный производитель пневматики предупредил о проблеме до того, как проблема возникла, но сообщение не было замечено и не было предпринято никаких действий. Изменения в оборудовании иногда могут привести к неожиданным последствиям и должны быть тщательно изучены перед внедрением.
Замена обычных уплотнений на термопластичные каучуки также может привести к непредвиденным проблемам. Новые шайбы для систем центрального отопления были изготовлены из полиэфирного эластомера Hytrel и успешно использовались в кранах с горячей водой.Однако при использовании на радиаторах, где они постоянно подвергались воздействию высоких температур, они затвердевали в результате кристаллизации и последующего растрескивания. Уплотнения сжались и позволили образоваться утечкам. Первые сообщения об утечках произошли из общественных учреждений, которые поддерживали высокие температуры в своих помещениях.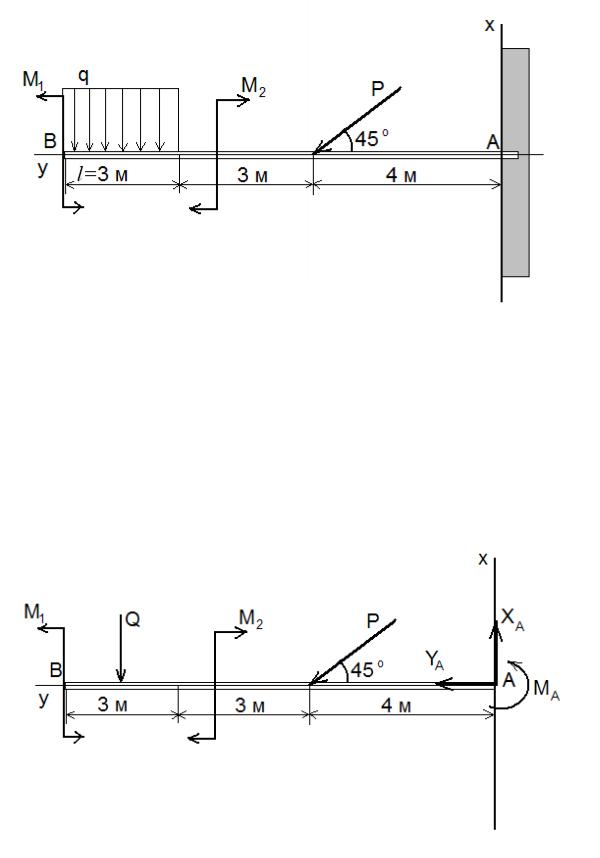 Техническая литература, имевшаяся до появления отказов, предупреждала о проблеме гидролиза, но не была замечена производителем. Перед внедрением должны были быть проведены испытания, чтобы убедиться, что материал может выдержать такое воздействие.Шайбы теперь отлиты из термостойкого и стойкого к гидролизу эластомера.
Техническая литература, имевшаяся до появления отказов, предупреждала о проблеме гидролиза, но не была замечена производителем. Перед внедрением должны были быть проведены испытания, чтобы убедиться, что материал может выдержать такое воздействие.Шайбы теперь отлиты из термостойкого и стойкого к гидролизу эластомера.
Использование мастик для герметизации строительных компонентов, таких как воздуховоды и остекление, широко распространено, но эти герметики должны быть устойчивы к окружающей среде. Многие новые материалы были разработаны с использованием термопластичных полимеров, пластификаторов и наполнителей. Некоторые из них использовались для герметизации воздуховодов в учебном здании пожарной команды, которые использовались для отвода синтетического дыма в выбранные части здания. Дым состоял из аэрозоля парафинового масла, а некоторые герметики были пластифицированы маслом, поэтому они разжижались, и уплотнения не работали.Это позволило маслу сконденсироваться на изоляции, вызвав настоящий пожар. Герметики должны быть проверены перед использованием. Были разработаны новые герметики с использованием полибутена, олигомера с низкой молекулярной массой, но при его использовании в качестве герметика для застекленных крыш в зданиях возникли проблемы. Проблема может быть вызвана преждевременным окислением.
Герметики должны быть проверены перед использованием. Были разработаны новые герметики с использованием полибутена, олигомера с низкой молекулярной массой, но при его использовании в качестве герметика для застекленных крыш в зданиях возникли проблемы. Проблема может быть вызвана преждевременным окислением.
Новые способы использования как традиционных, так и новых материалов всегда следует тестировать, подвергая эти материалы воздействию ожидаемых условий эксплуатации. И эти условия должны быть наихудшими из ожидаемых, цель, которую не всегда легко достичь на практике, как показала проблема озона на заводе полупроводников.Но в литературе имеется огромное количество информации, которая все чаще предоставляется из источников во всемирной паутине. Подобные проблемы могли быть обнаружены ранее при другом применении того же материала и могут дать представление о предполагаемом будущем использовании. Некоторые общие принципы также могут указать на возможные потенциальные ловушки, такие как высокая реакционная способность двойных связей в цепных молекулах, особенно в отношении окислительных процессов.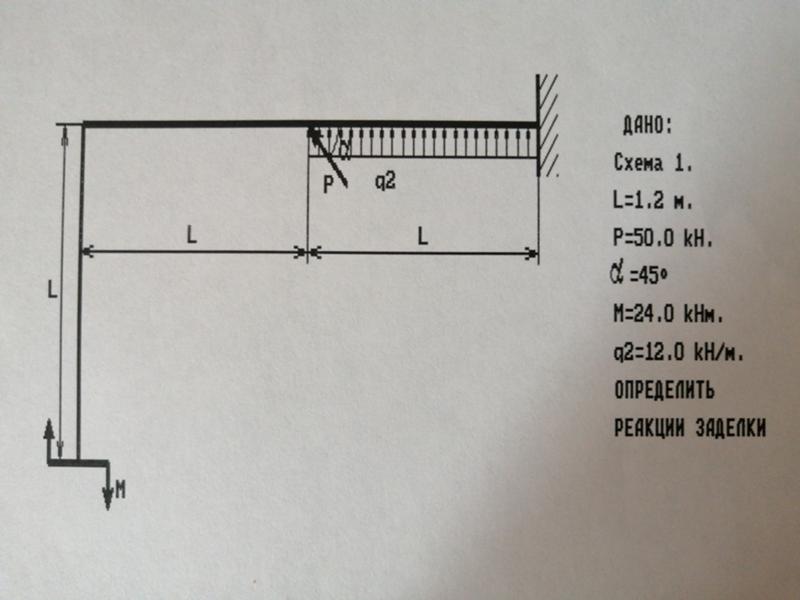 Сбои продуктов, однако, не получают широкого распространения, если только они уже не стали достоянием общественности в результате отзывов, судебных дел или предупреждений, опубликованных в технической прессе.При отсутствии таких предупреждений нет лучшего способа исследования целостности продукта, чем тщательно спланированное прямое тестирование.
Сбои продуктов, однако, не получают широкого распространения, если только они уже не стали достоянием общественности в результате отзывов, судебных дел или предупреждений, опубликованных в технической прессе.При отсутствии таких предупреждений нет лучшего способа исследования целостности продукта, чем тщательно спланированное прямое тестирование.
Но даже когда дело доходит до суда, среди некоторых экспертов часто возникает предвзятость, которая предоставляет клиентам мнение, которое они хотели бы услышать, а не истину по делу. Это, безусловно, произошло со стиральными машинами Hytrel, и в результате удлинился корпус и затраты на консультации других специалистов. Расследования должны быть независимыми, потому что никто не выигрывает от плохого и вводящего в заблуждение отчета, и менее всего те, кто инструктирует таких экспертов.Если есть фундаментальная проблема, она должна быть выявлена, проанализирована и предана гласности, чтобы не повторялись новые проблемы того же рода.
Реакция Твиттера на то, что Джален Хёртс сломал лодыжки защитникам «Сэйнтс» во время игры, закрывающей ТД
Джален Хёртс делает заявления каждую неделю, продолжая показывать руководству «Иглз», что он может быть квотербеком франшизы.
В воскресенье в сокрушительной победе над «Сэйнтс» «Хёртс» забил 3 быстрых тачдауна, доминируя над защитой «Нью-Орлеана» с рывком на 69 ярдов.
Последнее приземление стало гвоздем в крышку гроба, поскольку Hurts потряс защитника Saints Карла Грандерсона на пути к 24-ярдовому тачдауну, чтобы вывести Philadelphia со счетом 40-22.
Социальные сети отреагировали, и результаты были изумительными.
USA Today
21 ноября 2021 г.; Филадельфия, Пенсильвания, США; Квотербек «Филадельфии Иглз» Джален Хёртс (1) реагирует после своего приземления против «Нью-Орлеан Сэйнтс» в первом квартале на «Линкольн Файненшл Филд». Обязательный кредит: Билл Стрейхер-USA TODAY Sports
Какой восклицательный знак от Jalen Hurts!
6ABC
21 ноября 2021 г .; Филадельфия, Пенсильвания, США; Квотербек «Филадельфии Иглз» Джален Хертс (1) забивает тачдаун против «Нью-Орлеан Сэйнтс» в первой четверти на «Линкольн Файненшл Филд».Обязательный кредит: Эрик Хартлайн-USA TODAY Sports
Больно смешно
ESPN
История продолжается
14 ноября 2021 г . ; Денвер, Колорадо, США; Квотербек «Филадельфия Иглз» Джален Хертс (1) празднует победу над «Денвер Бронкос» на стадионе «Эмпауэр Филд» на Майл Хай. Обязательное указание: Рон Ченой — USA TODAY Sports
; Денвер, Колорадо, США; Квотербек «Филадельфия Иглз» Джален Хертс (1) празднует победу над «Денвер Бронкос» на стадионе «Эмпауэр Филд» на Майл Хай. Обязательное указание: Рон Ченой — USA TODAY Sports
Hurts снова доминирует над Saints
PFF
14 ноября 2021 г .; Денвер, Колорадо, США; Квотербек «Филадельфия Иглз» Джален Хертс (1) празднует победу над «Денвер Бронкос» на стадионе «Эмпауэр Филд» на Майл Хай.Обязательное указание: Рон Ченой — USA TODAY Sports
Hurts — новый КОРОЛЬ ФИЛЛИ
Philly Pod
Квотербек Philadelphia Eagles Джален Хертс (1) бросает мяч против Denver Broncos во время первой половины футбольного матча NFL, воскресенье, ноябрь 14 февраля 2021 года в Денвере. (AP Photo/David Zalubowski).
Если у вас установлено соответствующее программное обеспечение, вы можете загрузить данные о цитировании статей в менеджер цитирования по вашему выбору.Просто выберите программное обеспечение менеджера из списка ниже и нажмите «Загрузить».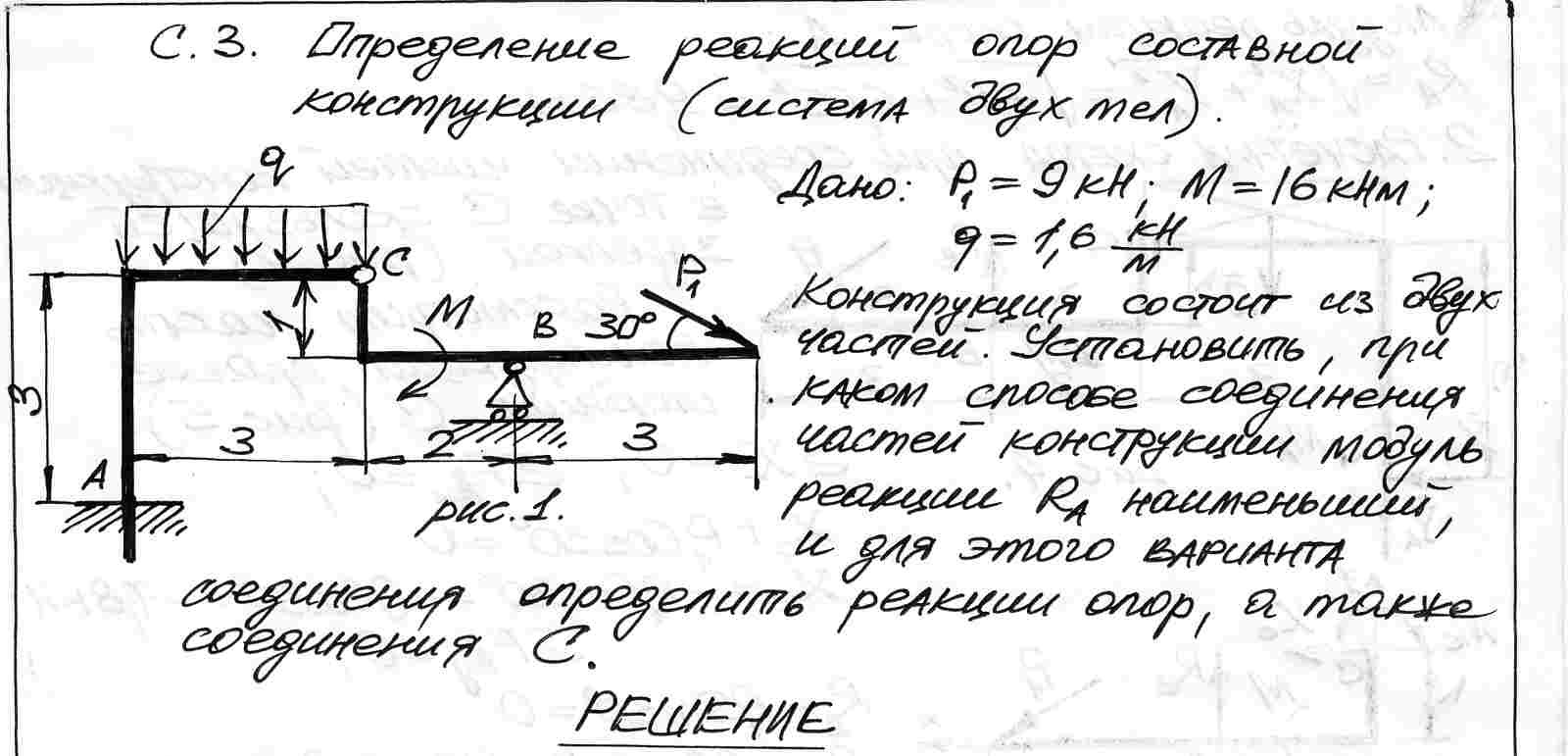
Цитируется по
1. Слуховая биология морских зайцев (Erignathus barbatus)
2. Тактика самонаведения тюленей Уэдделла в условиях антарктического припая
3.901 -внешнее поведение взрослых и молодых кольчатых нерп (Pusa hispida) в Беринговом и Чукотском морях
4. Регуляция сердечного ритма у ныряющих морских львов: правила блуждающего нерва
5. Земноводный слух у кольчатой нерпы ( Пуса гиспида ): подводные аудиограммы, аэроаудиограммы и измерения критических соотношений
6. Дыхание и физиология ныряния
7. Роль гликогена, глюкозы и лактата в активности нейронов при гипоксии в мозге хохлача (Cystophora cristata)
8. Земноводный слух у ларг ( Фока Ларга ): подводные аудиограммы, аэроаудиограммы и измерения критического соотношения
9. Биологический журнал физиологических параметров высших морских позвоночных
10. Дыхание и физиология ныряния
Дыхание и физиология ныряния
11. Влияние глубины на сердечные и поведенческие реакции двуногих бакланов ( Phalacrocorax auritus ) во время добровольного ныряния
12. Интеграция функции и экологии в исследованиях адаптации: исследование двигательной способности как модельной системы
13. Сколько времени должно длиться погружение? Простая модель принятия решений о корме ныряльщиками с задержкой дыхания в неоднородной среде
14. Частота сердечных сокращений и поведение морских котиков: значение для измерения полевой энергетики и млекопитающие
16. СЕЗОННЫЕ ДВИЖЕНИЯ И ПРЫЖКИ МОЛОДИЛЬНОСТИ БАЙКАЛЬСКИХ ТЮЛЕНЕЙ PHOCA SIBIRICA
17. Мышечный кровоток у ныряющих млекопитающих
18 Ненейронные расширения тактильной чувствительности
19. Маленькая видеокамера, прикрепленная к тюленю Уэдделла: новый способ наблюдения за поведением при нырянии Физиология поведения ластоногих
Реактивно-транспортное моделирование окислительно-восстановительных реакций и герметизации трещин во время экспериментов по гидравлическому стимулированию на руднике Хоумстейк, Южная Дакота COLLAB Site
Аннотация
Гидромеханические (ГМ) процессы в первую очередь контролируют распространение трещин в усовершенствованных геотермальных системах (EGS) и нетрадиционных резервуарах углеводородов. Следовательно, эксперименты и модели по стимуляции трещин редко учитывают геохимические эффекты. В рамках исследования ЭГС по геотермальной программе Министерства энергетики США подземные эксперименты, проведенные на руднике Хоумстейк в Южной Дакоте, включают закачку разбавленной «шахтной воды» в сульфидсодержащие богатые карбонатами метаосадки для образования трещин, мониторинга микросейсмичности, изображения удельного электрического сопротивления (ERT). и выполните трассировочное тестирование. После создания гидроразрывов закачка жидкости в течение нескольких дней или недель приводила к неожиданному повышению давления закачки.Учитывая окислительно-восстановительное неравновесие между закачиваемой насыщенной кислородом водой и содержащей сульфиды породой, для оценки эволюции проницаемости трещины необходимо учитывать реакции вода-порода. Трехмерная реактивно-транспортная модель дискретной трещины была построена для параллельного кода TReactMech, чтобы зафиксировать осаждение/растворение минералов (равновесное/кинетическое), изменения пористости-проницаемости и изменение давления.
Следовательно, эксперименты и модели по стимуляции трещин редко учитывают геохимические эффекты. В рамках исследования ЭГС по геотермальной программе Министерства энергетики США подземные эксперименты, проведенные на руднике Хоумстейк в Южной Дакоте, включают закачку разбавленной «шахтной воды» в сульфидсодержащие богатые карбонатами метаосадки для образования трещин, мониторинга микросейсмичности, изображения удельного электрического сопротивления (ERT). и выполните трассировочное тестирование. После создания гидроразрывов закачка жидкости в течение нескольких дней или недель приводила к неожиданному повышению давления закачки.Учитывая окислительно-восстановительное неравновесие между закачиваемой насыщенной кислородом водой и содержащей сульфиды породой, для оценки эволюции проницаемости трещины необходимо учитывать реакции вода-порода. Трехмерная реактивно-транспортная модель дискретной трещины была построена для параллельного кода TReactMech, чтобы зафиксировать осаждение/растворение минералов (равновесное/кинетическое), изменения пористости-проницаемости и изменение давления.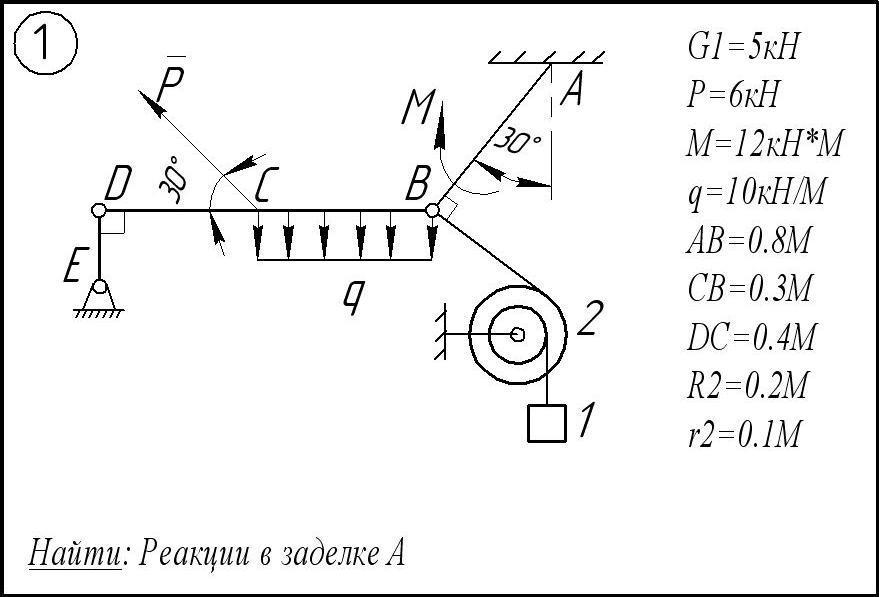 Поскольку окисление сульфидов может привести к повышению температуры, теплота реакции была связана с кондуктивным и адвективным переносом тепла.В инъекционных реакциях преобладали реакции окисления пирротина, выделения швертманнита в полосе менее 0,5 м от нагнетательной скважины, выделения кальцита на глубине от 1 до 2,5 м и некоторого количества ферригидрита вблизи фронта реакции (около 4 м). После 10 дней закачки пористость трещин снизилась более чем на 4% в зоне преобладания швертманнита. Это привело к падению проницаемости на 50%, если исходить из кубического закона, и к нелинейному увеличению давления на входе. Меньшая электропроводность и высокая реакционная способность шахтной воды позволили визуализировать и смоделировать фронт реакции с помощью ERT (рисунок).Смоделированные тепловые эффекты окисления сульфидов были небольшими, поскольку трещина была насыщена водой и растворенный кислород быстро расходовался. Полевые наблюдения показали некоторое закупоривание микробиологической активностью, однако без определения характеристик поверхности трещин степень закупоривания трещин биопленками неопределенна.
Поскольку окисление сульфидов может привести к повышению температуры, теплота реакции была связана с кондуктивным и адвективным переносом тепла.В инъекционных реакциях преобладали реакции окисления пирротина, выделения швертманнита в полосе менее 0,5 м от нагнетательной скважины, выделения кальцита на глубине от 1 до 2,5 м и некоторого количества ферригидрита вблизи фронта реакции (около 4 м). После 10 дней закачки пористость трещин снизилась более чем на 4% в зоне преобладания швертманнита. Это привело к падению проницаемости на 50%, если исходить из кубического закона, и к нелинейному увеличению давления на входе. Меньшая электропроводность и высокая реакционная способность шахтной воды позволили визуализировать и смоделировать фронт реакции с помощью ERT (рисунок).Смоделированные тепловые эффекты окисления сульфидов были небольшими, поскольку трещина была насыщена водой и растворенный кислород быстро расходовался. Полевые наблюдения показали некоторое закупоривание микробиологической активностью, однако без определения характеристик поверхности трещин степень закупоривания трещин биопленками неопределенна.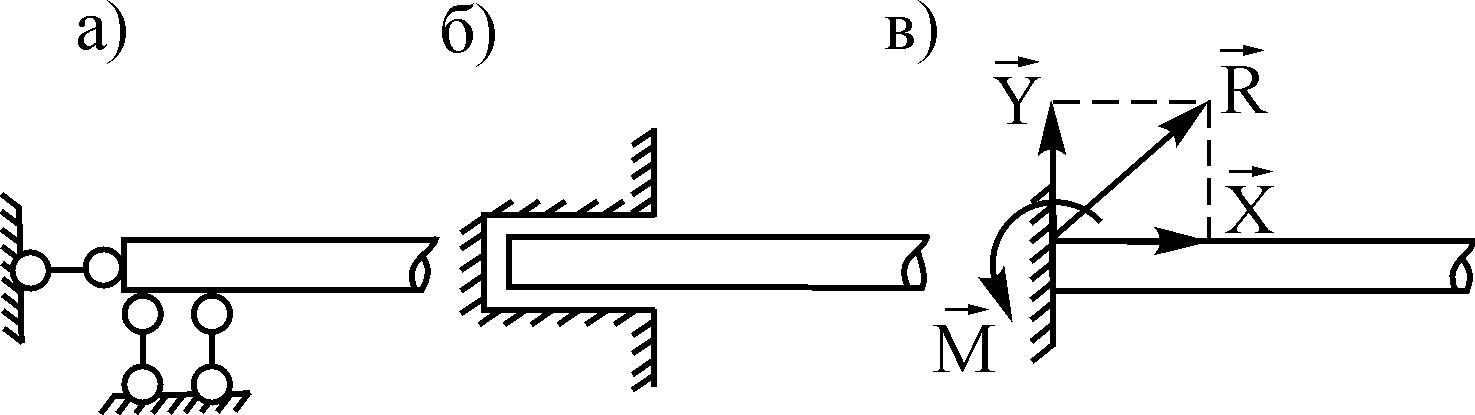 В заключение, апертура трещины и структура проницаемости могут быстро измениться после распространения трещины, что сильно отклоняется от предсказаний модели ГМ.
В заключение, апертура трещины и структура проницаемости могут быстро измениться после распространения трещины, что сильно отклоняется от предсказаний модели ГМ.
Реакция Ричарда Шермана и Тома Брэди на запечатывающий игру перехват Малкольма Батлера | Bleacher Report
Getty ImagesВсего через пару игр после того, как он стал жертвой одного из самых безумных розыгрышей в истории Суперкубка, защитник New England Patriots Малкольм Батлер придумал решающий перехват.
Когда «Сиэтл Сихокс» отставали со счетом 28–24 на последней минуте игры и столкнулись с вторым голом с 1-ярдовой линии Новой Англии, Батлер перепрыгнул через маршрут и отбил передачу квотербека «Сихокс» Рассела Уилсона на линии ворот. .
Перехват вызвал совершенно разные реакции со стороны защитника «Сихокс» Ричарда Шермана и квотербека «Пэтриотс» Тома Брэди:
Дэн Грациано @DanGrazianoESPNКэрролл говорит NBC, что последний звонок был «полностью моей ошибкой», что он назвал это, потому что северо-восток был на линии ворот персонал, а игра Батлера была «чудесной».
»
Дэн Грациано @DanGrazianoESPNКэрролл сказал NBC, что последний звонок был «полностью моей ошибкой», что он назвал это тем, что NE был на линии ворот, а игра Батлера была «чудесной».
Это была отличная игра. Батлером, чтобы придумать перехват, но многие задавались вопросом, почему «Сихоукс», у которых оставался один тайм-аут, не сообщили о бегущем назад Маршоне Линче, также известном как Beast Mode. полностью виноват», как он назвал это, потому что NE был в персонале на линии ворот, а игра Батлера была «чудесной».»
Бывший товарищ Линча по команде, ресивер «Детройт Лайонс» Голден Тейт, не понял, почему Beast Mode не получил мяч, когда на кону чемпионство:
Эль Флако @bomani_jonesсегодня вечером, они в чертова линия ворот с MARSHAWN LYNCH. и они бросили пас? usc не пробежал на 4-й и 2-й. это было ПЛОХО. Грациано:
Paracosm @WompWizard*привет, у нас есть Маршон Линч, лучший раннингбек в лиге, ТАК ДАВАЙТЕ ПРОПУСТИТЕ!!!*
[Vine, Twitter]
Склеивание и запайка
Термосварка
В то время как DuPont™ Tyvek® можно сплавить друг с другом, используя только тепло, получить прочные швы трудно.
Уплотнительные матрицыЭто связано с тем, что расплавление Tyvek® разрушает структуру волокна, снижая как гибкость, так и прочность на разрыв в области шва. Однако, если Tyvek® склеен сам с собой, следует использовать модели без антистатического покрытия и без обработки коронным разрядом (например, модели 1059B и 1073B). Это связано с тем, что молекулярная пленка оксида и антистатика на поверхности обработанных коронным разрядом/антистатических моделей приводит к неравномерному плавлению Tyvek®, что снижает прочность уплотнения.
с подпружиненной ограничительной пластиной успешно используются для термосварки.Однако предпочтительным методом является нанесение покрытия с более низкой температурой плавления, чем у Tyvek®. С таким покрытием можно достичь высокой прочности герметика с помощью горячего стержня или импульсного метода.
Диэлектрическое уплотнение
Tyvek®, как и полиэтиленовая пленка, не может быть диэлектрически герметизирован обычными методами.
Однако были разработаны коммерческие запатентованные процессы, которые позволяют диэлектрически герметизировать Tyvek® с помощью обычного радиочастотного оборудования.
Ультразвуковая сварка
Недавние разработки в области ультразвуковой сварки также продемонстрировали разрыв волокон при использовании большинства видов Tyvek® без складок, которые часто возникают при термосварке Tyvek®. Этот процесс также образует прочные швы на различных пластиковых пленках и нетканых материалах. Для получения дополнительной информации о герметизации, пожалуйста, свяжитесь с нами.
Склеивание
Для приклеивания Тайвек® к самому себе или к другим подложкам можно использовать ряд клеев.Как правило, предпочтительны клеи на водной основе, которые обеспечивают быстрое схватывание и быстрое высыхание. Однако первым шагом при выборе клея является определение того, как он будет реагировать с Tyvek®. Лабораторные испытания — лучший способ сделать это определение.

Натуральные клеи на основе крахмала, декстрина, казеина или побочных продуктов животного происхождения предпочтительнее клеев на синтетической основе. Синтетические клеи часто содержат материалы с низким молекулярным весом, которые могут действовать как растворители при повышенных температурах и вызывать набухание и образование складок.Горячий животный клей — отличный клей для приклеивания Tyvek® к картону. Синтетические решетки на водной основе также соединяют Tyvek® с самим собой и различными субстратами. Этилен/винилацетатные клеи особенно полезны, как и акриловые клеи, чувствительные к давлению. Однокомпонентные полиуретановые клеи на основе растворителей обеспечивают оптимальную адгезию (внахлестку и сдвигу), гибкость и водостойкость для приклеивания Tyvek® к самому себе и различным основаниям.
Технология клея-расплава была широко продемонстрирована в ряде применений, связанных с Tyvek®, включая изготовление влагопоглотителей, конвертов и медицинской упаковки.
