Лекция № 4 Растяжение (сжатие) прямого стержня
Определение внутренних сил в растягиваемых и сжимаемых стержнях.
напряжения при растяжении (сжатии) прямого стержня. Понятие о допускаемом напряжении.
Определение деформаций и перемещений. Закон Гука.
Опытное изучение свойств материалов.
Растяжение и сжатие – это простой и часто встречающийся случай напряженного состояния элементов конструкции и деталей машин.
В таких условиях работает буксировочный канат или трос подъемного механизма, колонна здания.
Чистое (центральное) растяжение или сжатие возникает в элементе конструкции, если внешняя нагрузка вызывает в нем только одно внутреннее усилие, которое сопротивляется этой внешней нагрузке, —
При определении значений внутренних нормальных сил, действующих в поперечных сечениях стержней, примем следующее правило знаков:
— нормальная сила положительна, если сопротивляется растяжению стержня;
— нормальная сила отрицательна – если сопротивляется сжатию.
Для определения значений внутренней нормальной силы в любом из поперечных сечений используется метод сечений.
Пусть прямой стержень постоянной толщиной в одном конце закреплен, а к его другому торцу приложена растягивающая его вдоль оси стержня внешняя сила F.
Какое по величине внутреннее продольное усилие возникает в некотором поперечном сечении стержня n—n?
Прежде всего, отметим, что под действием закрепления и внешней силы стержень растягивается (деформируется), но никуда не движется, т.е. остается в равновесии.
Удобно вначале мысленно «снять» со стержня закрепление. Заменим его влияние на стержень эквивалентно действующей внешней силой. Эта сила равна реакции закрепления.
Т.е. в закреплении возникает некоторое усилие, благодаря которому верхний край стержня остается неподвижным. Это усилие называют реакцией закрепления на внешнюю нагрузку, передающееся на это закрепление через деформируемый стержень.
Незакрепленный стержень, теперь уже под действием двух внешних воздействий: известной силы и неизвестной пока реакции также никуда не движется, т.е. находится в равновесии.
Определить величину реакции поможет математическая формулировка этого факта.
Проведем координатную ось Оz, для удобства совпадающую с осью стержня. Стержень никуда не движется под действием силы и реакции в частности, не движется и вдоль оси, потому что проекции этих внешних сил на ось уравновешивают друг друга.
Такого рода факт в механике формулируется уравнением общего равновесия стержня: суммарная проекция на ось Оz всех действующих на стержень внешних сил, равна нулю:
При построении уравнений общего равновесия механики принято использовать следующее правило знаков:
Проекция усилия на ось положительна, если ее направление совпадает с выбранным направлением этой оси;
И наоборот – проекция отрицательна, если направлена в противоположную сторону.
Эпюры – графики внутренних усилий, напряжений, перемещений, деформаций, возникающих в элементах конструкций и деталях машин под воздействием внешней нагрузки.
Напряжения при растяжении (сжатии) прямого стержня
Предположим, растягивающую брус внешнюю силу удалось распределить равномерно по его торцам.
Опыты показывают. Что в этом случае каждое продольное волокно бруса подвержено только растяжению и в любом его поперечном сечении внутренние силы действуют только по нормали к этим сечениям.
Поперечные сечения бруса, плоские до деформации, под действием внешних сил перемещаются параллельно своему начальному положению и остаются постоянными.
Растягивающие стержень внешние силы не всегда удается распределить по площади стержня равномерно.
Но опыты показывают, что поведение поперечных сечений растягиваемых стержней, расположенных на некотором расстоянии от места приложения внешней нагрузки, уже не зависит от способа приложения этих сил и всегда соответствует гипотезе плоских сечений.
При рассмотрении деформаций растяжения или сжатия, а также при рассмотрении последующих простых деформаций нами будет рассматриваться
Рассмотрим стержень, подверженный действию продольных сил
Если на поверхность призматического стержня нанести сетку линий параллельных и перпендикулярных оси стержня, и приложить к нему растягивающую силу, то можно убедиться в том, что линии сетки и после деформации останутся взаимно-перпендикулярными, но расстояние между ними изменятся.
Все горизонтальные линии, например, cd, переместятся вниз, оставаясь горизонтальными и прямыми.
Можно предположить, что и внутри стержня будет происходить то же самое, т.е. поперечные сечения стержня плоские и нормальные к его оси до деформации, останутся плоскими и нормальными к оси и после деформации. Эту гипотезу называют гипотезой плоских сечений (гипотезой Бернулли).
Продольная сила N есть равнодействующая нормальных напряжений в поперечном сечении:
поскольку , то
, отсюда
В частном случае, когда на стержень действует одна внешняя сила, из уравнения равновесия получим:
И вместо общей формулы получим частный вид формулы для растяжения:
Эти формулы справедливы и для сжатия, с той только разницей, что сжимающие напряжения считаются отрицательными.
Кроме того, сжатые стержни помимо расчета на прочность рассчитываются также и на устойчивость.
Очевидно, что эти напряжения в реальных условиях нельзя создавать больше или много меньше определенной величины. Поэтому вводится понятие
Определение деформаций и перемещений. Закон Гука.
Опыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии – наоборот.
Для многих материалов при нагружении до определенных пределов опыты показали следующую зависимость между относительным удлинением стержня и напряжением:
, где
— абсолютное удлинение стержня
— длина образца до деформации
— длина образца после деформации
Эта зависимость носит название закона Гука и формулируется следующим образом: линейные деформации прямо пропорциональны нормальным напряжениям.
— коэффициент, зависящий от материала, т.е. его способность сопротивляться деформированию. Он характеризует жесткость материала, т.е. его способность сопротивляться деформированию.
Для ст.3 .
Для других материалов значение можно найти в справочниках.
Имея ввиду, что для стержня постоянного сечения:
, а
Можно получить формулу для определения полного (абсолютного) удлинения (укорочения) стержня:
Между продольным удлинением и поперечным существует зависимость:
Здесь —коэффициент поперечной деформации (коэффициент Пуассона),который характеризует способность материала к поперечным деформациям.
При пользовании этой формулой удлинение считается положительным, а укорочение – отрицательным.
Для всех материалов .
Для стали при упругих деформациях можно принимать =0,3.
Зная можно определить полное поперечное сужение или расширение стержня:, где- поперечный размер стержня до деформации
— поперечный размер стержня после деформации.
В стержнях переменного сечения напряжения в поперечных сечениях можно считать распределенными равномерно (если угол конусности ) и определять их по той же формуле, что и для стержня постоянного сечения.
Для определения деформаций стержня переменного сечения, в поперечных сечениях которого действует продольная сила N, найдем сначала удлинение элемента длиной, которое является дифференциалом полного удлинения.
Согласно закону Гука, имеем:
Полное удлинение стержня получим, интегрируя выражение в пределах :
, если и- величины постоянные, то
Чтобы воспользоваться этой формулой, необходимо знать закон изменения в зависимости от.
Для ступенчатых стержней интегрирование заменяется суммирование, и полное изменение длины бруса определяется как алгебраическая сумма деформаций его отдельных частей, в пределах которых :
Например, для стержня изображенного на схеме, имеем:
Определим теперь удлинение стержня постоянного сечения под действием силы тяжести, которая представляет собой нагрузку, равномерно распределенную вдоль стержня.
Удельный вес материала обозначим через .
Рассмотрим деформацию элемента , выделенного на расстоянииот нижнего конца.
Удлинение элемента равно:
Интегрируя это выражение в пределах, получим
Это выражение можно представить в другом виде, если учесть, что сила тяжести бруса равна: или, тогда получим-формула по определению перемещения с учетом собственного веса при известной длине
Следовательно, удлинение бруса постоянного сечения от собственной силы тяжести в два раза меньше удлинения от действия силы, равной силе тяжести и приложенной к его концу.
Опытное изучение свойств материалов
Для изучения свойств материалов и установления значения предельных (по разрушению или по пластическим деформациям) производят испытания образцов материала вплоть до разрушения. По виду деформации различают испытания на растяжение, сжатие, кручение и изгиб.
Испытания производят при статической и ударной (испытание на усталость и выносливость) нагрузках на ГМС – 50.
Цель испытания на растяжение – определение механических характеристик материала.
При проведении испытания автоматически записывается диаграмма зависимости между растягивающей силой и удлинением образца.
Условия и порядок выполнения работы
Стальной стержень ступенчатого сечения находится под действием внешней силы и собственного веса.
Необходимо построить эпюры:
Площадь большего поперечного сечения стержня в 2 раза превышает меньшую.
studfiles.net
2. Центральное растяжение и сжатие стержней.
Основные определения и формулы
Центральное растяжение и сжатие прямого стержня вызывается действием осевых нагрузок, в состав которых входят сосредоточенные силы и распределенные нагрузки, характеризующиеся интенсивностью q. Приq=constнагрузка называется равномерно распределенной, равнодействующая которой равна произведениюqа, гдеа– длина участка распределения.
В поперечных сечениях стержня действуют только нормальные напряжения и одно внутреннее усилие – продольная сила N, определяемая с помощью метода сечений. При этом продольная сила равна сумме проекций на осьОхнагрузок, приложенных к одной из частей стержня (рис.2.1).
Р
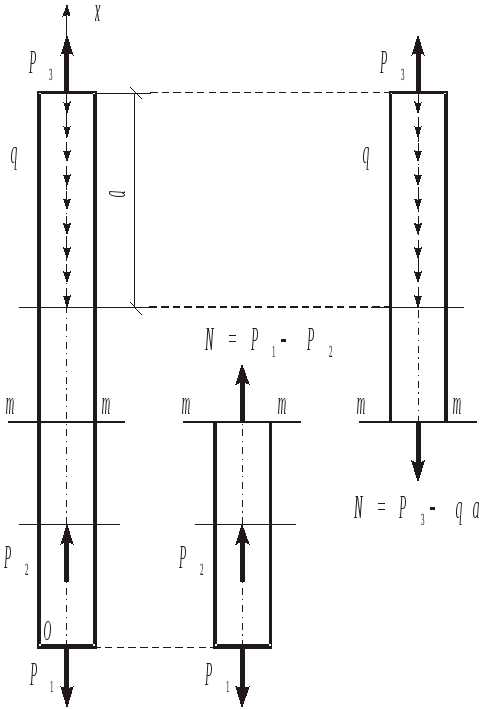
После определения продольных сил Nв характерных сечениях стержня можно построить график изменения этих сил по длине стержня (эпюруN). Для её построения используется дифференциальное соотношение
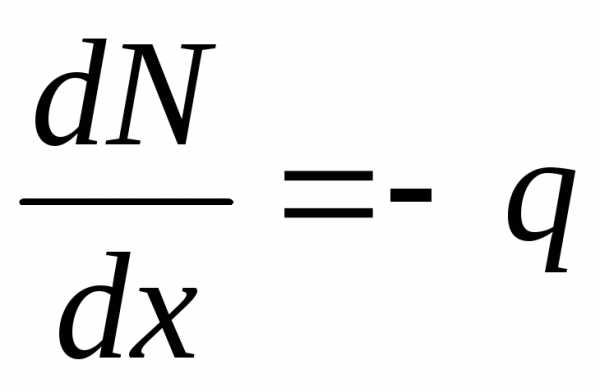 . (2.1)
. (2.1)
Нормальные напряжения одинаковы во всех точках поперечного сечения и определяются по формуле
Рис.2.1
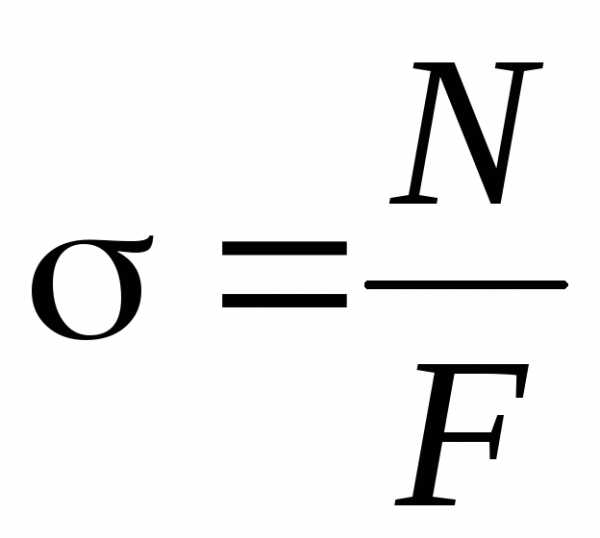 , (2.2)
, (2.2)где F– площадь поперечного сечения.
В системе СИ напряжения имеют размерность Па = Н/м2, МПа =
= 10–1кН/см2и др.
Относительная деформация стержня длиной lравна
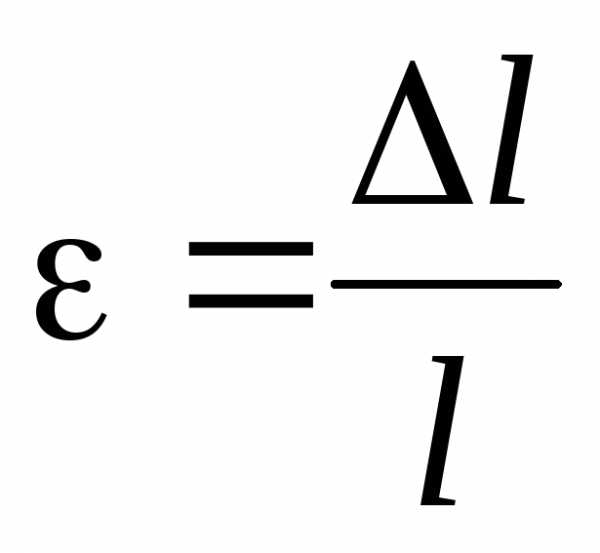 ,
(2.3)
,
(2.3)
где l– удлинение или укорочение стержня.
В пределах упругих деформаций справедливо линейное соотношение между напряжениями и деформациями, называемое законом Гука
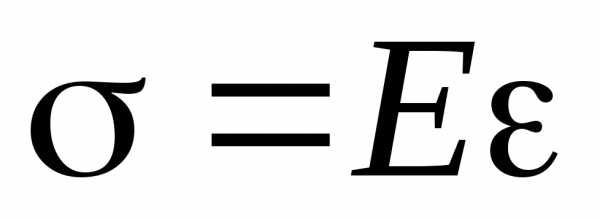 ,
(2.4)
,
(2.4)
где Е– модуль упругости материала.
Удлинение или укорочение стержня, закрепленного в начальном сечении х= 0, определяется по формуле
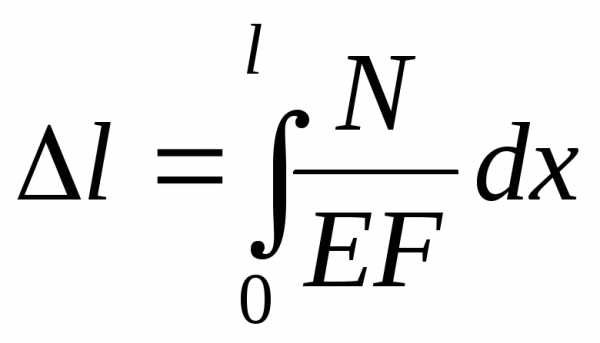 . (2.5)
. (2.5)
Для частного случая ЕF=constиN = constимеем
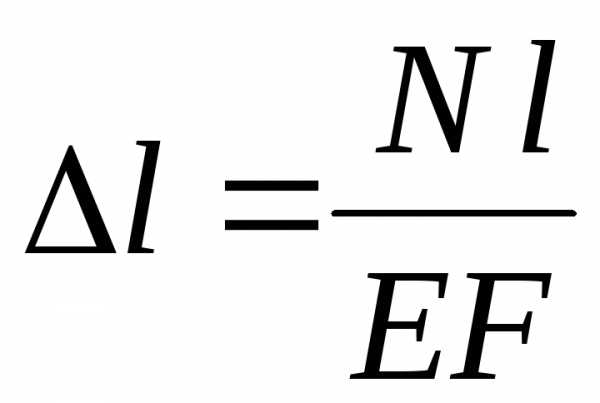 . (2.6)
. (2.6)
Для стержня с постоянной жесткостью ЕFпри произвольном законе изменения продольной силыNвеличинуlможно определить по формуле
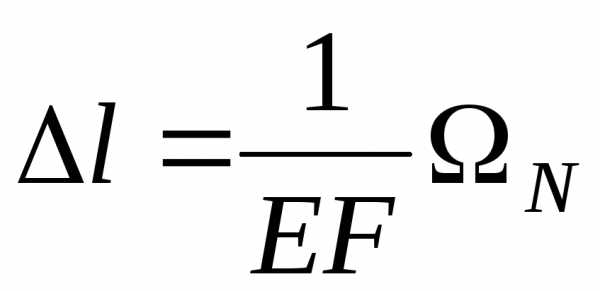 , (2.7)
, (2.7)
где N– площадь эпюрыNна рассматриваемом участке стержня.
Поперечные сечения стержня, оставаясь плоскими и перпендикулярными к оси, получают осевые перемещения u = u(x). Эпюра осевых перемещений строится после определения удлинений и укороченийlучастков стержня.
Если при определении продольных сил и опорных реакций уравнений равновесия недостаточно, то стержень или стержневая система называются статически неопределимыми. Для их расчета необходимо использовать условия деформации.
Расчет на прочность элементов строительных конструкций производится по методу предельных состояний. В поперечных сечениях стержня при центральном растяжении или сжатии должно выполняться условие прочности
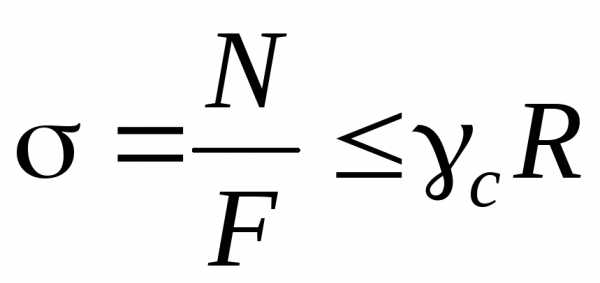 , (2.8)
, (2.8)
где R– расчетное сопротивление материала, характеризующее его прочность, ис– коэффициент условий работы. Величина продольной силыNвычисляется от действия расчетных нагрузок, определяемых с учетом коэффициента надежности по нагрузкамf . ЗначенияR,сиfприведены в соответствующих разделах СНиП.
Подбор сечения стержня производится по формуле
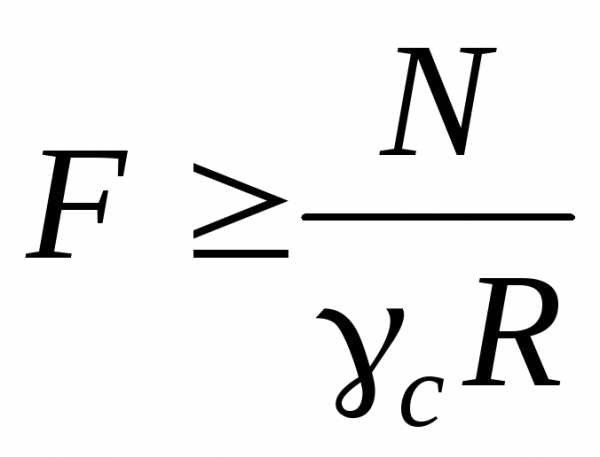 . (2.9)
. (2.9)
Расчет элементов машиностроительных конструкций производится по методу допускаемых напряжений. Условие прочности в этом случае записывается в виде
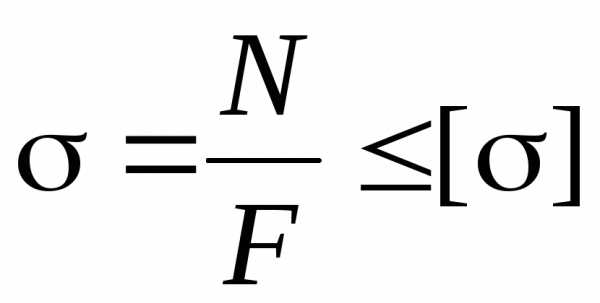 , (2.10)
, (2.10)
где 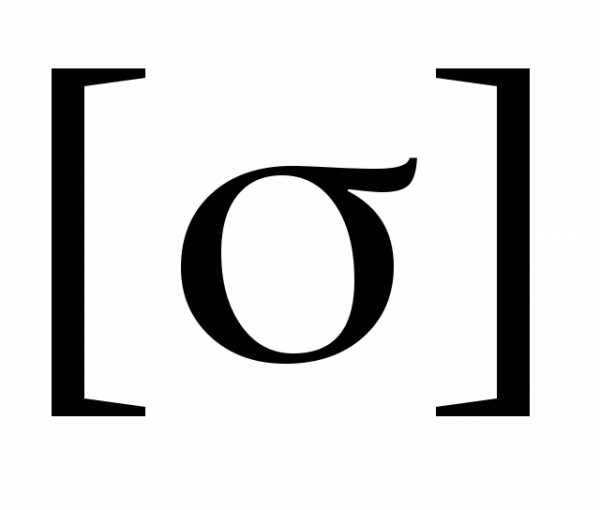 – допускаемое напряжение.
– допускаемое напряжение.
При расчете стержней и стержневых систем из пластичных материалов
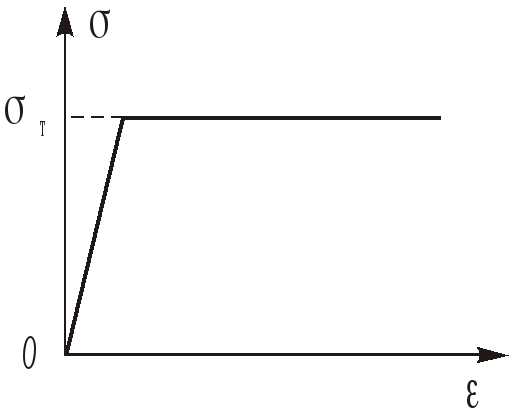
может быть использована упрощённая диаграмма зависимости =f(), например, диаграмма Прандтля (рис.2.2). Согласно этой диаграмме при достижении напряжениями предела текучеститдеформации неограниченно возрастают. При этом продольная сила в стержне принимает предельное значение (разрушающая сила)
З
Рис.2.2
а начало разрушения (предельное состояние) стержневой системы можно принять момент, когда напряжения в одном или нескольких стержнях достигнут предела текучести. При этом величина предельной нагрузкипредопределяется из уравнений равновесия. Допускаемая нагрузка определяется по формуле 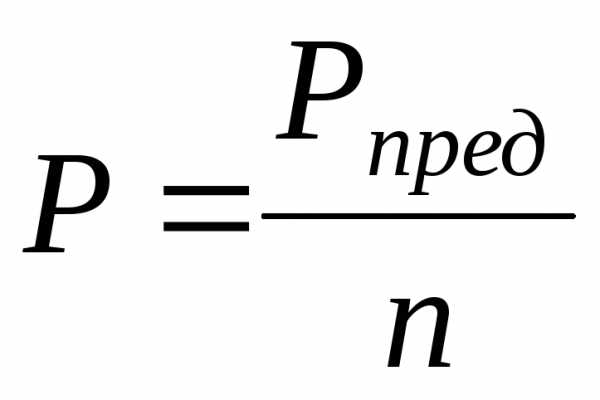 , (2.12)
, (2.12)
где n– коэффициент запаса прочности.
studfiles.net
1.2.2. Расчет статически неопределимой стержневой конструкции, работающей на растяжение-сжатие (задача № 5)
Условие задачи
Стержневая конструкция, состоящая из абсолютно жесткого диска и двух деформируемых стержней длиной l1иl2, соединенных шарнирами, подвержена действию силыF(рис. 1.11). Примем следующие исходные данные: м, м,,,м,м.
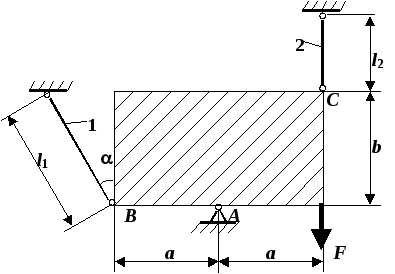
Рис. 1.11. Схема конструкции в задаче № 5
Задача состоит из трех частей:Часть 1.Расчет по упругой стадии деформации. В зависимости от исходных данных, выписанных из таблицы и являющихся индивидуальными для каждого студента, надо либо определить грузоподъемность конструкции, либо подобрать размеры поперечного сечения расчетом по допускаемым напряжениям.
Часть 2. Расчет по предельному пластическому состоянию. Требуется найти грузоподъемность (или подобрать сечения стержней) расчетом по предельному состоянию.
Часть 3.Определение дополнительных напряжений, связанных с изменением температуры наTили неточностью изготовленияодного из стержней. Допустим, что в рассматриваемой задаче стержень 1 охлаждается (T1 < 0), и найдем возникающие в стержнях конструкции температурные напряжения.
Решение
Прежде всего убедимся, что рассматриваемая конструкция является статически неопределимой. Сосчитаем число неизвестных: ими являются продольные силы в двух деформируемых стержнях и две опорные реакции в шарнирно неподвижной опоре в точке А.Таким образом, имеем 4 неизвестные, а число независимых уравнений статики для данной системы равно 3. Система является один раз статически неопределимой.
Часть 1.Для расчета конструкции по упругой стадии деформации необходимо составить три группы уравнений:
уравнения равновесия;
уравнения совместности деформаций;
физические уравнения (закон Гука).
Чтобы составить уравнения равновесия, нарисуем план сил. Для этого рассечем стержни и, отбросив части стержней, заменим их внутренними усилиями – продольными силами N1иN2(рис. 1.12,а). Важно, чтобы на плане сил направления усилий соответствовали плану перемещений. Для того, чтобы выяснить как направлены продольные силы в стержнях, нарисуем приближенный план перемещений (рис. 1.12,б), пользуясь принципами, описанными при решении задачи № 3. ТочкиВиСжесткого диска поворачиваются с радиусамиABиАСвокруг неподвижной точкиАна один и тот же уголи перемещаются по дугам, которые заменяем перпендикулярамииДля того, чтобы найти абсолютные деформации стержней, надо из точеки(новые положения узловВиС) опустить перпендикуляры на направления стержней. Как видно из рис. 1.12,бстержень 1 укорачивается на(выделенный жирным отрезок), и поэтому на плане сил усилиеN1показано сжимающим. Стержень 2 согласно плану перемещений удлиняется на, и на рис. 1.12,апродольная силаN2нарисована растягивающей.
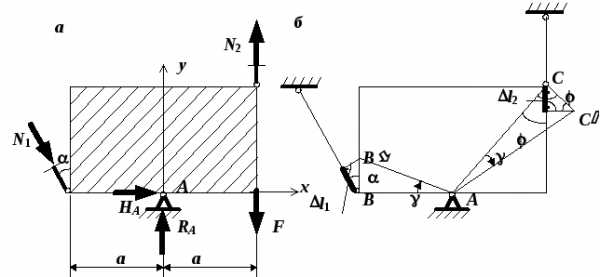
Рис. 1.12. К решению задачи № 5:
а – план сил от действия F;
б – план перемещений от действия F
Теперь составим три уравнения равновесия:;;
;;
;.
Запишем вторую группу уравнений – уравнения совместности деформаций. Поскольку данная система является один раз статически неопределимой, необходимо составить одно уравнение совместности деформаций. Это геометрическое уравнение, связывающее абсолютные деформации стержней, и его мы получим на основании плана перемещений. Из подобия треугольников ABBиACCна рис. 1.12,б. Связывая отрезкиBB иCCс деформациями стержнейии учитывая, чтоAB =a, а, получим уравнение совместности деформаций
.
Поскольку , то окончательно
.
Это уравнение показывает, во сколько
раз абсолютное удлинение второго стержня
больше абсолютного укорочения первого
стержня. При построении плана перемещений
в масштабе (что рекомендуется) результаты
вычислений можно проверить по рисунку,
измерив отрезки 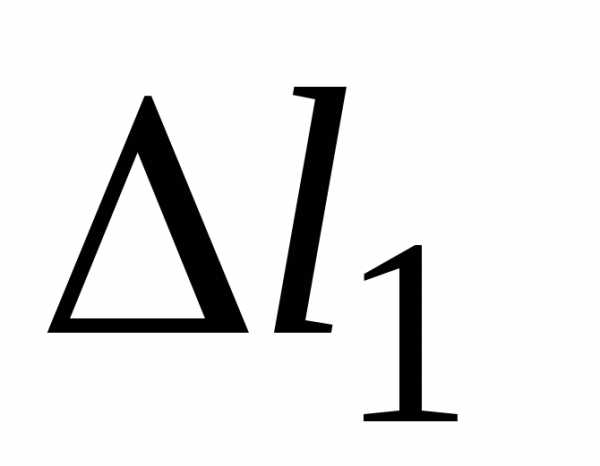 и
и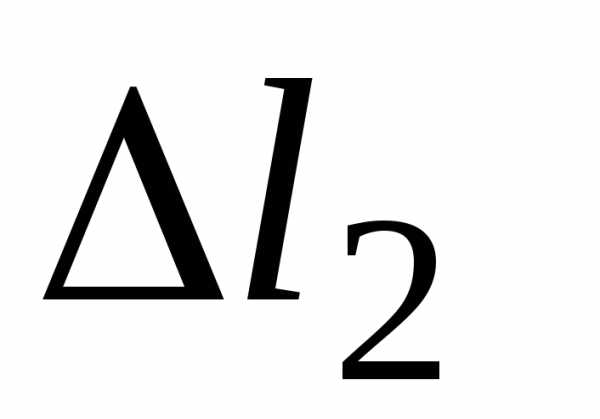 и найдя их отношение.
и найдя их отношение.
Теперь надо связать деформации стержней с внутренними усилиями. Предполагая, что материал подчиняется закону Гука (расчет по упругой стадии деформаций), запишем третью группу уравнений
и.
Мы получили полную систему уравнений для определения всех неизвестных (). Как правило, нас интересуют только продольные силы в стержнях, поэтому из уравнений равновесия при решении системы используется только последнее уравнение, в которое не входят опорные реакции. Решая полученную систему уравнений, найдем внутренние усилия в стержнях:
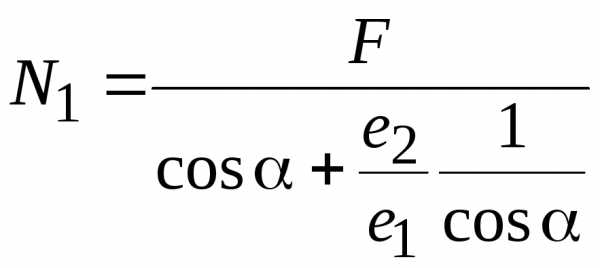 ;
;
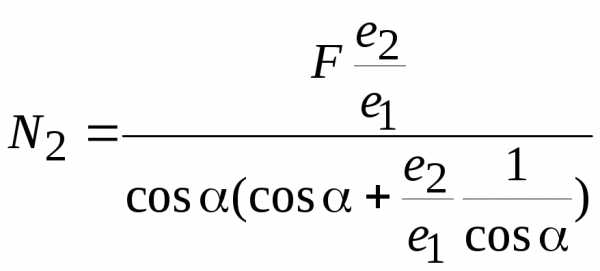 .
.
Здесь введено обозначение – погонная жесткостьi-го стержня.
Заметим, что, как видно из полученных формул, усилия зависят не только от величины нагрузки и геометрических размеров конструкции, как в статически определимых системах, но и от отношения погонных жесткостей стержней. Эта важная закономерность справедлива для любой статически неопределимой конструкции и позволяет влиять на распределение усилий в стержнях без изменения ее геометрической схемы. Для принятых в данной задаче исходных данных получим и.
Определив внутренние усилия в стержнях, находим напряжения и выбираем наиболее напряженный стержень. Из условия прочности этого (наиболее напряженного) стержня либо определяем допускаемую нагрузку, либо подбираем размеры поперечных сечений стержней (заданное отношение площадей сечения необходимо сохранить). Напряжения в стержнях ,. Из сравнения видно, что наиболее напряженным является стержень 2. Из условия прочности этого стержня
находим либо значение F, либоА1(А2по заданному отношению равноА1/2).
Для проверки рекомендуем после определения допускаемой нагрузки (либо размеров площадей сечения) еще раз найти напряжения в стержнях и убедиться в том, что условие прочности выполняется в обоих стержнях.
Часть 2.Сделаем расчет конструкции по предельному пластическому состоянию. Поскольку заданная система является один раз статически неопределимой, то в предельном состоянии должны потечь два стержня, то есть все деформируемые стержни конструкции. Для определения предельной нагрузки нарисуем план сил в предельном состоянии (рис. 1.13). Направления усилий снова должны соответствовать плану перемещений. Составим одно уравнение равновесия в предельном состоянии (такое уравнение, в которое не входят неизвестные опорные реакции):
;.
Из этого уравнения можно найти значение предельной нагрузки. Для конкретных исходных данных, использованных в первой части задачи, получим:
.
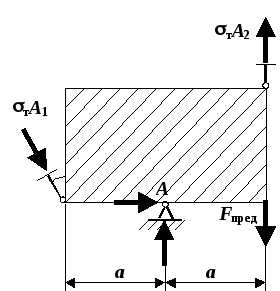
Рис. 1.13. План сил в предельном состоянии
Из условия прочности конструкции по предельному состояниюлибо находим значение допускаемой нагрузки, либо подбираем размерА1.Сравним величины допускаемых нагрузок, найденных разными методами для рассмотренного примера. Допускаемая нагрузка, определенная расчетом по упругой стадии деформации
,
оказалась меньше допускаемой нагрузки, полученной расчетом по предельному пластическому состоянию , на 56%.
Часть 3.Найдем дополнительные напряжения в стержнях конструкции, связанные с охлаждением стержня 1 наградусов. Предполагая, что в процессе деформации материал стержней остается упругим, расчет ведем по той же схеме, что и в первой части задачи, т. е. составляем три группы уравнений:
уравнения равновесия;
уравнения совместности деформаций;
физические уравнения.
Уравнения равновесия составляем по плану сил (рис. 1.14, а), уравнения совместности деформаций – по плану перемещений (рис. 1.14,б). План сил и план перемещений, как и раньше, должны соответствовать друг другу. Поясним особенности построения плана перемещений от температурного воздействия. Если бы конструкция была статически определимой, т. е. стержень 2 отсутствовал, то стержень 1 при охлаждении уменьшил бы свою длину на величину, жесткий диск повернулся бы на уголи узелВпереместился в положениеВ. Поскольку конструкция статически неопределима, то лишний стержень 2 препятствует такой деформации. В результате жесткий диск повернется только на угол, точкаВперейдет в положениеВ. Стержень 1 окажется растянутым на величину(выделенный жирным отрезок на плане перемещений рис. 1.14,б) и в нем возникнет растягивающее усилиеN1. В свою очередь стержень 2 в процессе деформации также будет растянут на величину продольной силойN2. В соответствии с планом перемещений на плане сил (см. рис. 1.14,а) оба стержня показаны растянутыми.
Рис. 1.14. К решению задачи № 5:
а – план сил от температурного воздействия;
б – план перемещений от температурного воздействия
Теперь запишем систему уравнений для определения внутренних усилий в заданной конструкции:уравнение равновесия
;;
уравнение совместности деформации 3
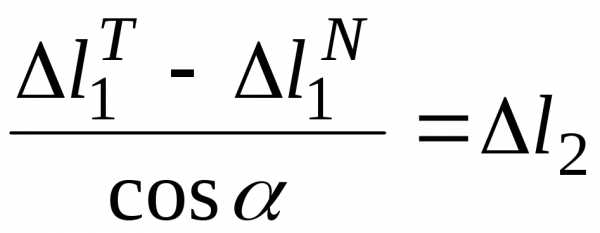
и физические уравнения
;;.
Решая эту систему уравнений, найдем усилия в стержнях системы, а далее по формуле (1.1) температурные напряжения. Заметим, что отрицательный знак используется только при построении плана перемещений (стержень укорачивается от действия температуры), при решении системы уравнений величинуследует принять положительной.
Примечание.Определение монтажных напряжений, связанных с неточностью изготовления одного из стержней, производится так же, как температурных напряжений. Например, если в рассмотренном примере стержень 1 будет изготовлен короче, чем требуется, на величину(эта величина в таблице исходных данных [4] задана отрицательной), то при сборке конструкции стержень 1 надо будет растянуть и при этом стержень 2 тоже растянется. На плане перемещений отрезокзаменим наи решение задачи будет справедливо, если в полученной системе уравнений всюду заменитьна заданную величину.(Отрицательный знакпри решении системы уравнений не учитывается.)
studfiles.net