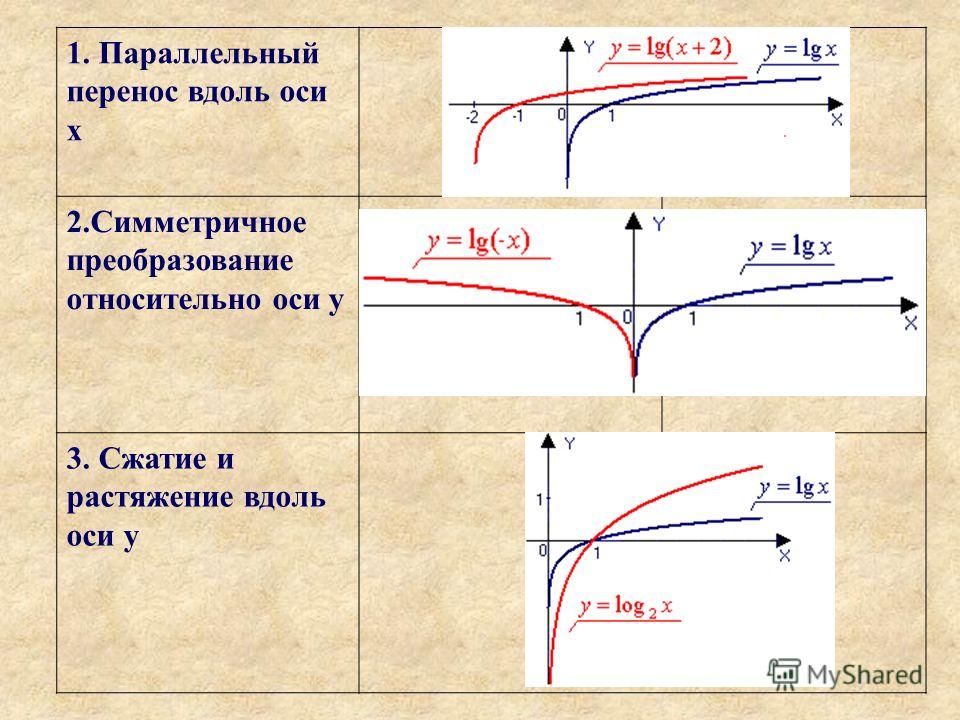
Растяжение и сжатие функции: Растяжение и сжатие графиков функций вдоль осей координат с примерами

2}{4} $

$y_2 = y_1 при x_2 = 2x_1$

График растягивается в 2 раза по оси OX

Гипербола:

$ y_1 = f(x) = \frac{4}{x}$

$y_2 = f \left(\frac{x}{2}\right) = \frac{4}{x/2} = \frac{8}{x}$

$ y_2 = y_1 при x_2 = 2x_1$

График растягивается в 2 раза по оси OX

Квадратный корень:

$y_1 = f(x) = \sqrt{x}$

$y_2 = f \left(\frac{x}{2}\right) = \sqrt{\frac{x}{2}}$

$y_2=y_1 при x_2 = 2x_1$

График растягивается в 2 раза по оси OX

Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)

Содержание

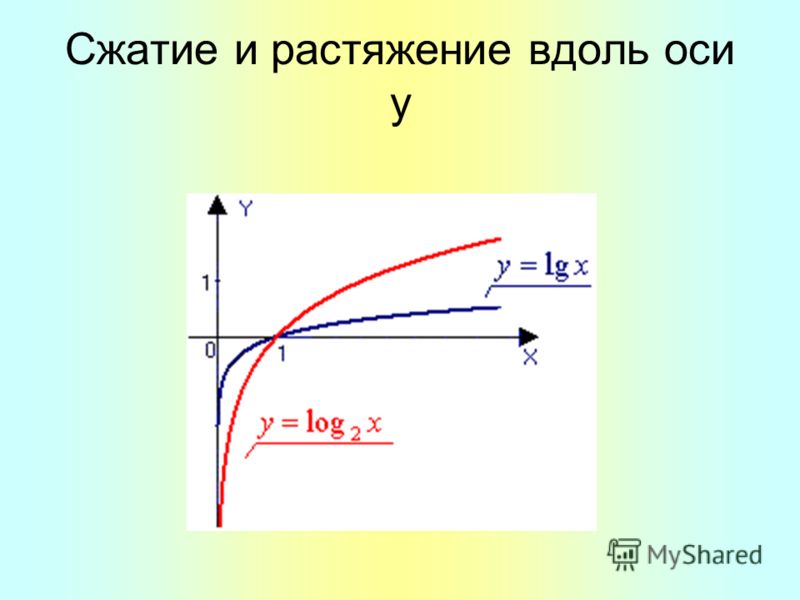
Растяжение и сжатие графика по оси OY

Сравним графики пар функций, которые в общем виде можно записать так:

$$ y_1 = f(x), \quad y_2 = Af(x) $$

где $A \gt 1$, произвольный положительный множитель.

Пусть A = 2. 2}{2}$

$y_2 = \frac{1}{2}y_1 при x_2 = x_1$

График сжимается в 2 раза по оси OY

Гипербола:

$ y_1 = f(x) = \frac{4}{x}$

$y_2 = \frac{1}{2}f(x) = \frac{2}{x}$

$ y_2 = \frac{1}{2}y_1 при x_2 = x_1$

График сжимается в 2 раза по оси OY

Квадратный корень:

$y_1 = f(x) = \sqrt{x}$

$y_2 = \frac{1}{2}f(x) = \frac{\sqrt{x}}{2}$

$y_2 = \frac{1}{2}y_1 при x_2 = x_1$

График сжимается в 2 раза по оси OY

Примеры

Пример 1. Постройте в одной координатной плоскости графики функций:

$$ y = \sqrt{x}, y = \sqrt{3x}, y = \sqrt{\frac{x}{3}}, y = 3\sqrt{x} $$

Сделайте выводы.

По сравнению с графиком $y = \sqrt{x}$:

график функции $y = \sqrt{3x}$ сжимается в 3 раза по оси OX(←)

график функции $y = \sqrt{\frac{x}{3}}$ растягивается в 3 раза по оси OX(→)
график функции $y = 3\sqrt{x}$ растягивается в 3 раза по оси OY(↑)

Пример 2*. 2+3x+2$:

график функции y = f(2x) сжимается в 2 раза по оси OX(→)
график функции $y = f \left(\frac{x}{2}\right)$ растягивается в 2 раза по оси OX(←)
график функции y = 2f(x) растягивается в 2 раза по оси OY(↑)

Рейтинг пользователей

за неделю

за неделю
один месяц
три месяца

Помогай другим

Отвечай на вопросы и получай ценные призы каждую неделю

См. подробности

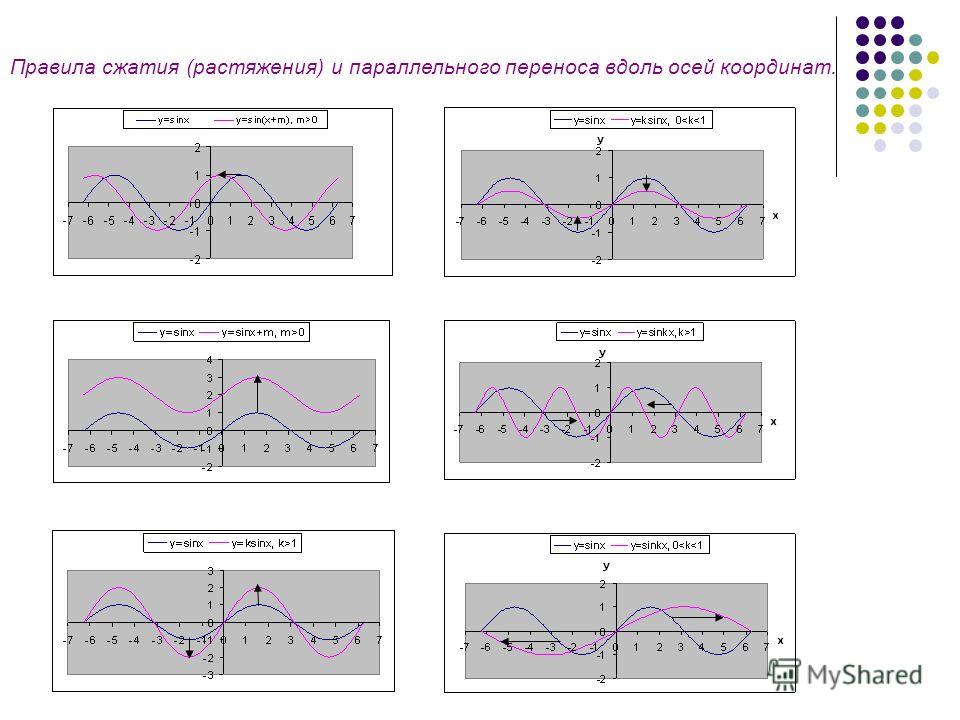
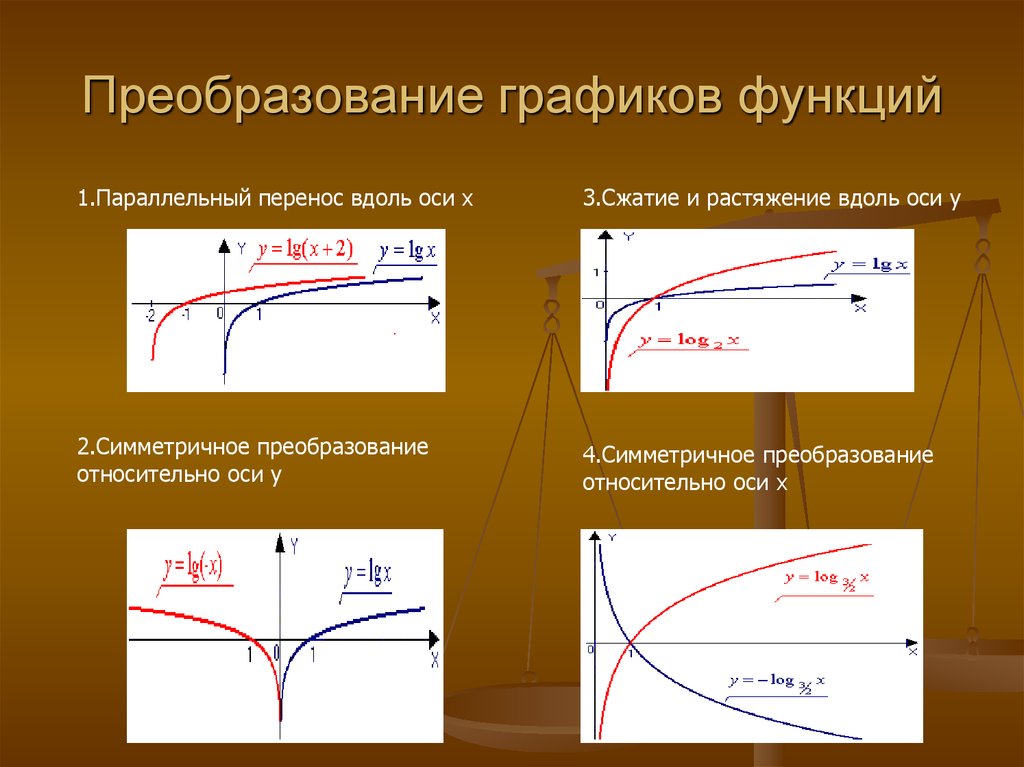
Растяжение и сжатие графиков. Параллельный перенос графиков функций

ЦЕЛИ: 1) рассмотреть графики функций y=f(x), y=kf(x), y=f(x)+n, y=f(x-m) и y=f(x-m)+n и их свойства, используя ПК и программу Advanced Grapher;

2)расширить представления о преобразованиях графиков более сложных функций;

3)способствовать развитию у учащихся навыков чтения графиков и построения графиков функций.

I. Новый материал – объяснительная лекция.

Графики функций широко используются в различных областях инженерных знаний, поэтому умение строить, “читать”, прогнозировать их “поведение” имеют огромную роль в практической деятельности инженерных работников, гидро, метеорологов и людей других “математических” специальностей.

Выясним, какая связь существует между графиками функций y = f(x) и y = kf(x), где k-число, не равное нулю.

Пусть графиком функции y = f(x), область определения которой- промежуток[-2;4],является кривая, изображённая на рис.1а f(x) = x(x-3)(x+1).

Рассмотрим сначала случай, когда k>1.Построим график функции y = kf(x), где k=2. Для этого расстояние каждой точки графика функций y = f(x) от оси X увеличим в 2раза, т.е.умножим её ординату на 2. Построение выполним с помощью программы Advanced Grapher, набрав формулу функции F₁с клавиатуры. Заметим, что точки с абсциссами 0; 3; -1, принадлежащие оси Х, останутся на месте, т.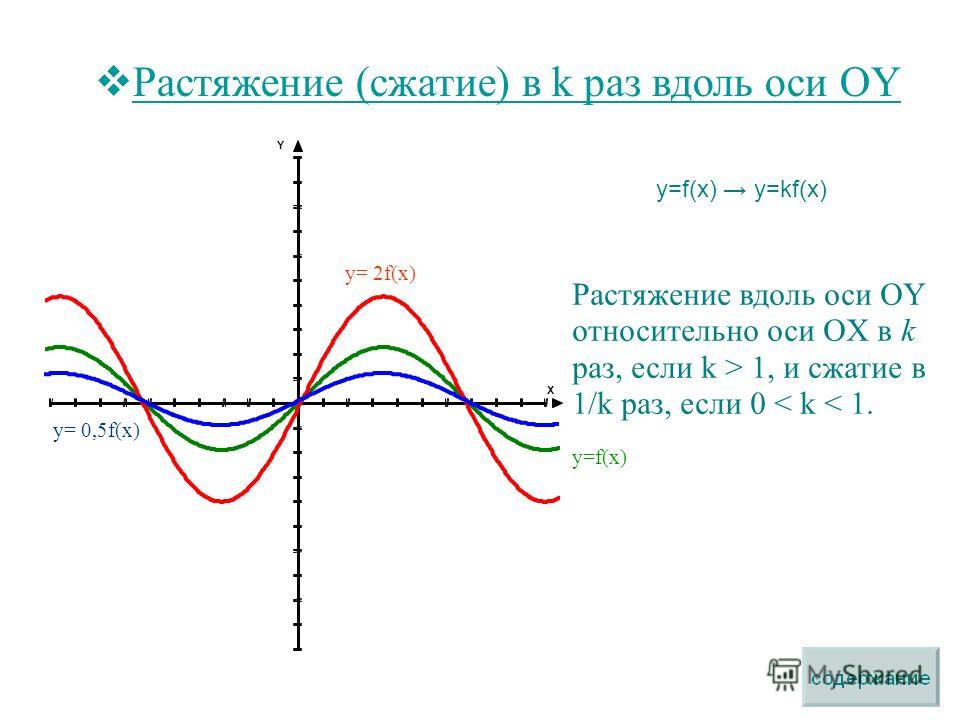 к.их ординаты равны нулю (0*2х = 0).Все остальные точки графиков у_1, и у, имеющие одинаковые абсциссы, будут лежать соответственно на перпендикулярах к оси Х, причём каждая точка графика функции у= 2f(x) будет находиться от оси Х на расстоянии в 2 раза большем, чем соответственная точка графика функции y = f(x). (рис. 1б).

Рассмотрим теперь случай, когда О < k < 1, например k =, и построим график функции y= kf (x), при k = , используя программу Advanced Grapher.

Опять же заметим, что точки с абсциссами -1; 0 и 3, принадлежащие оси Х, останутся на месте ( 0* = 0 ), а каждая точка графика функции y= f (x), будет находиться от оси Х на расстоянии в 2 раза меньшем, чем соответственная точка графика функции y = f(x) (рис.1в).

Делаем вывод о том, что график функции y = f(x) при k < 1 можно получить из графика функции y = f(x) растяжением от оси Х исходного графика в k раз, а при О < k < 1- сжатием к оси Х графика функции y = f(x) в раз.

И рассмотрим случай, когда k< 0. Ограничимся значением k = -1, т.е. выясним, как можно построить график функции y= -f(x), зная график функции y = f(x).

Задав с клавиатуры формулу графика y = -f(x) и получив соответствующее изображение на экране (рис. 1г), заметим, что каждой точке графика y, кроме точек с абсциссами -1; 0 и 3, соответствует точка графика y = f(x) с противоположной ординатой.

Соответственно делаем вывод, что график функции y = -f(x) можно получить с помощью симметрии относительно оси Х.

Аналогично, графики функций y = kf(x) и y = -kf(x) при любом k0 симметричны относительно оси Х.

Иначе говоря, чтобы построить график функции y = kf(x), где k < 0, можно сначала построить график функции y = -kf(x), где -k > 0, а затем отобразить его симметрично относительно оси Х.

Выясним, как связаны между собой графики функций y = f(x) и y = f(x)+n, где n –произвольное число.

Рассмотрим графики функций y = x, y = x — 4 , y= x-4, y = x+ , y= x- (рис. 2).

Рассматривать будем попарно графики функций у и у(рис.2а), у и y(рис.2б), у и y(рис.2в), у и y(рис.2г).

Моментальное построение графика каждой из выше указанных функций даст возможность сделать вывод, что график функции y = f(x) + n можно получить из графика функции y = f(x) с помощью сдвига вдоль оси Y на n единиц вверх, если n>0, или на единиц вниз, если n<0.

Выясним теперь, как связаны между собой графики функций y = f(x) и y = f(x-m), где m – произвольное число.

Рассмотрим графики функций y = (x-3), y = (x+2), y = (x), y = (x+).

Получаем рис.3 и делаем вывод, что график функции y = f(x) можно получить с помощью сдвига вдоль оси Х на m единиц вправо, если m>0, или на единиц влево, если m<0.

Из курса алгебры VII класса известно, что график функции y = x (парабола) симметричен относительно ось У.

Построим, используя программу Advanced Grapher, в одной системе координат графики функций y = x, у== x+2, y= (х-3) и y= (х-3) +2 ( рис.4).

Учащимся наглядно видно, что у параболы у== x+2 осью симметрии является ось У, а у параболы y= (х-3) — прямая х = 3. Графиком же функции y= (х-3) +2 является парабола с вершиной в точке (3;2) и осью симметрии её является прямая х = 3.

Из наглядного наблюдения учащиеся видят, что при построении графика функции у = (х-3) +2 нужно последовательно выполнить два параллельных переноса: один в направлении оси У на 2 единицы вверх, а другой в направлении оси Х на 3 единицы вправо.

Делаем вывод, что графиком функции вида у = (х-m) +n является парабола с вершиной в точке А(m;n) .А также обобщаем выше рассмотренные преобразования графиков и делаем вывод, что график функции y = f(x-m)+n может быть получен из графика функции y=f(x) в результате последовательно выполненных двух параллельных переносов: сдвига вдоль оси Х на m единиц и сдвига графика функции у = (х-m) вдоль оси У на n единиц.

II. Закрепление

У: Изобразите на координатной плоскости заданные точки и определите, используя обороты “выше на…” и “ниже…”, взаимное расположение соответствующих точек:

а) А(-1;7) и А₁(-1;10) б) В(2;7) и В₁(2;5) в) С (0;-6) и С₁(0;-5) г) Д (3;-4) и Д₁(3;-7) .

У: Как найти расстояние между точками, имеющими одинаковые ординаты? Закончите предложение: “Если точки имеют одинаковые ординаты, то расстояние между ними равно…”

Обучающая исследовательская работа.
(карточки-распечатки см. Приложение 1)

I вариант.

1. Заданы функции y = f(x) и y = f(x) + 2. заполните таблицу значений этих функций и сделайте вывод о взаимном расположении точек данных функций и их графиков:

X	1	2	4	6	7
y=f(x)	5	7	-5
y=f(x)+2				3	-11

Д: Любая точка графика y = f(x)+2 с абсциссой X находится на 2 единицы “выше”, чем точка графика y = f(x) с той же самой абсциссой; а график функции y = f(x)+2 можно получить из графика y = f(x) параллельным переносом вдоль оси ординат на 2 единицы “вверх”.

II вариант.

1. Заданы функции y = f(x) и y = f(x) – 3. заполните таблицу значений этих функций и сделайте вывод о взаимном расположении точек данных функций и их графиков:

X	0	1	3	5	9
y=f(x)	4	-6	5
y=f(x)-3				-3	0

Д: Любая точка графика y = f(x)-3 с абсциссой X находится на 3 единицы “ниже”, чем точка графика y = f(x) с той же самой абсциссой; а график функции y=f(x)-3 можно получить из графика y = f(x) параллельным переносом вдоль оси ординат на 3 единицы “вниз”.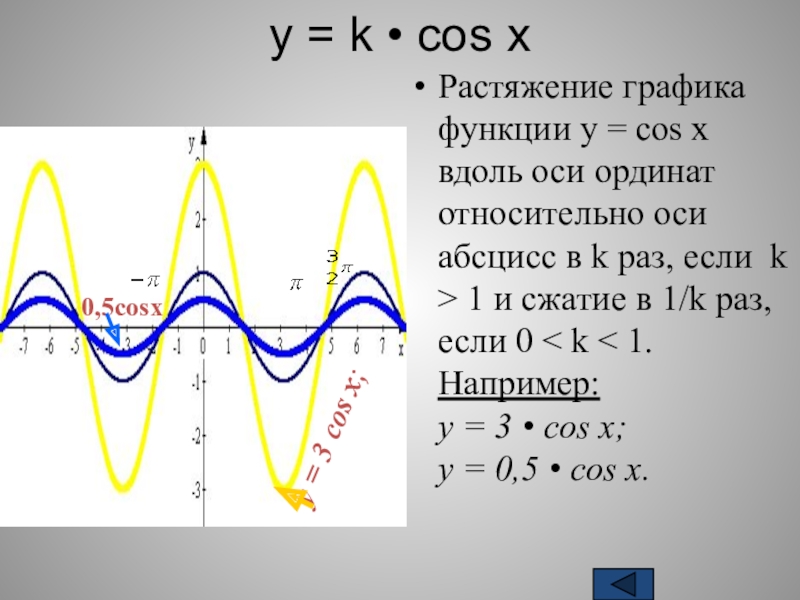

У: С помощью какого преобразования можно получить график функции y = f(x)+a, а0 из графика функции y = f(x).

Д: Обобщённый вывод (записать в тетрадь): График функции y₁= f(x)+a, а0 можно получить из графика функции y = f(x) параллельным переносом вдоль оси ординат на единиц “вниз”, если а<0, и на единиц “вверх”, если а>0.

У: Пусть даны графики функций y = f(x) и y = f(x)+7. Известно, что один из них проходит через начало координат. Определите точку пересечения другого графика с осью ординат.

Д: A (0;7) или А (0;-7).

У: Пусть даны графики функций y = f(x) и y = f(x)+c. Известно, что один из них проходит через точку А(-11;231) и другой через точку А (-11;132). Найдите все возможные значения С.

Д: 99 или -99.

I вариант.

2. Постройте графики функций, используя известный график y = kx:

a) y = x-4 ; б) у = x+1; в) у = 2 x-1.

II вариант.
2. Постройте графики функций, используя известный график y = kx:
а) у = -x+3; б) у = -0,5x+2; в) у = -2x-3.
3.
У: Изобразите на координатной плоскости заданные точки и определите, используя обороты “левее на …” и “правее на …” взаимное расположение следующих точек:
а) А (-1;7) и А (6;7) б) С (8;-6) и С (14;-6) в) В (2;3) и В (-2;3) г) Д (-13;_4) и Д (-3;-4).
У: Как найти расстояние между точками, имеющими одинаковые абсциссы? Закончите предложение: “Если точки имеют одинаковые абсциссы, то расстояние между ними равно…”
I, II вариант.
4. Заданы функции y=f(x), y= f(x+2) и y= f(x-3). Заполните таблицу значений этих функций:
У: Как взаимно расположены точки графиков функций y = f(x) и y = f(x+2)?
Каким образом можно получить график функции y= f(x+2) из графика функции y = f(x)?
Д: Любая точка графика y= f(x+2) с абсциссой х-2 находится на 2 единицы “левее”, чем точка графика y=f(x) с абсциссой х, а график функции y= f(x+2) можно получить из графика y = f(x), “сдвинув” его на 2 единицы влево вдоль оси абсцисс.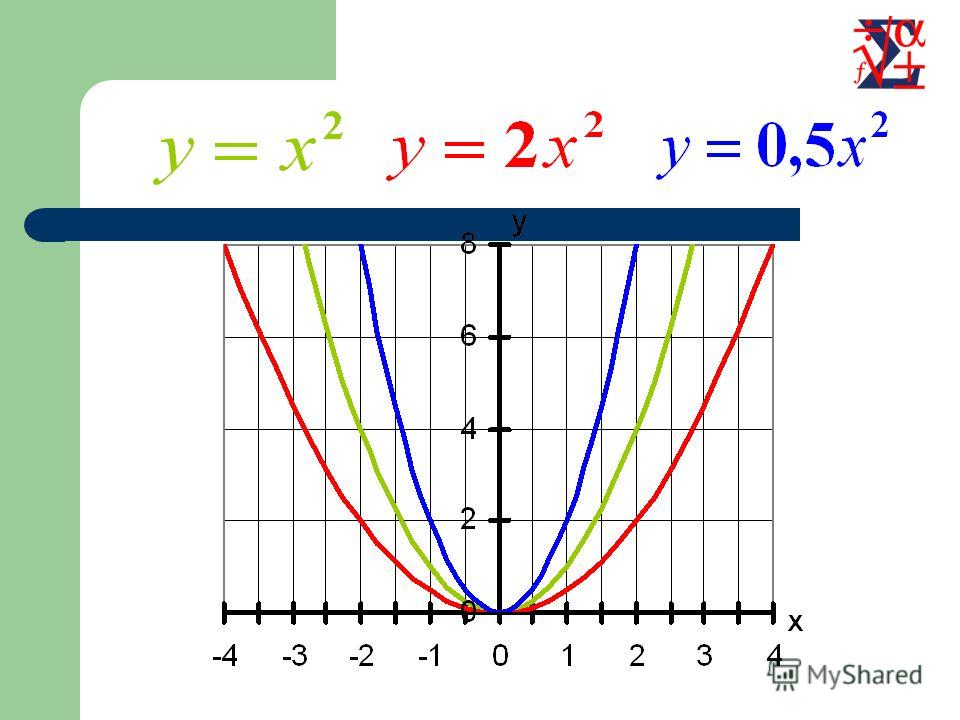
У: Как взаимно расположены точки графиков функций y = f(x) и y= f(x-3)?
Каким образом можно получить график функции y= f(x-3) из графика функции y = f(x)?
Д: Любая точка графика y= f(x-3) с абсциссой х+3 находится на 3 единицы “правее”, чем точка графика y = f(x) с абсциссой х, а график функции y= f(x-3) можно получить из графика функции y = f(x) “сдвинув” его на 3 единицы вправо вдоль оси абсцисс.
У: Попытайтесь сделать вывод о том как можно получить график функции y= f(x+а) из графика функции y = f(x)?
Д: График функции y= f(x+а) можно получить из графика функции y = f(x), “сдвинув” его на единиц вправо вдоль оси абсцисс, если а<0, и на единиц влево вдоль оси абсцисс, если а>0.
У: Пусть даны графики функций y = f(x) и y= f(x+7). Известно, что один из них проходит через начало координат. Какую точку пересечения графика с осью абсцисс можно указать наверняка?
Д: А(-7;0) и А (7;0).
У: Опишите как расположены относительно друг друга графики функций (задания 5-9 выполнены на карточках-распечатках, ответы в устной форме):
5. y = f(x-2) и y = f(x+7).
6. y = f(2x) и y = f(2x-4).
7. y = f(2x) и y = f(2x+1).
8. y = f(0,5x) и y = f(0,5x-4).
9. y = f() и . y = f(-1).
III . Лабораторно-исследовательская работа.
(все задания выполнены на карточках-распечатках, ответы см. в приложении 2)

I вариант.
10. Постройте графики функций, используя программу Advanced Grapher :
а) у = (x-4). б) у = (x+2).
11. Пусть дан график функции y=f(x). Как получить график функции y = f(x+3)-4?
12. Постройте графики функций, используя программу Advanced Grapher:
а) у = -4; б) у = (x+3)-4.

II вариант.
10. Постройте графики функций, используя программу Advanced Grapher :
а) у = 2(x-1), б) у = -(x+3).
11. Пусть дан график функции y=f(x). Как получить график функции y = f(x-5)+2?
12. Постройте графики функций, используя программу Advanced Grapher:
а) у =+2; б) у =(x-5)+2.

III вариант.
10. Постройте графики функций, используя программу Advanced Grapher :
а) у = -0,5(x-4); б) у = (2x-3).
11. Пусть дан график функции y = f(x). Как получить график функции y = f(x+1)+3?
12. Постройте графики функций, используя программу Advanced Grapher:
а) у =+3; б) у = (x+1)+3.

IV вариант.
10. Постройте графики функций, используя программу Advanced Grapher :
а) у = 4x+4х+1; б) у = —х-1.
11. Пусть дан график функции y=f(x). Как получить график функции y = f(x-2)-1?
12. Постройте графики функций, используя программу Advanced Grapher:
а) у =-1; б) у = (x-2)-1.
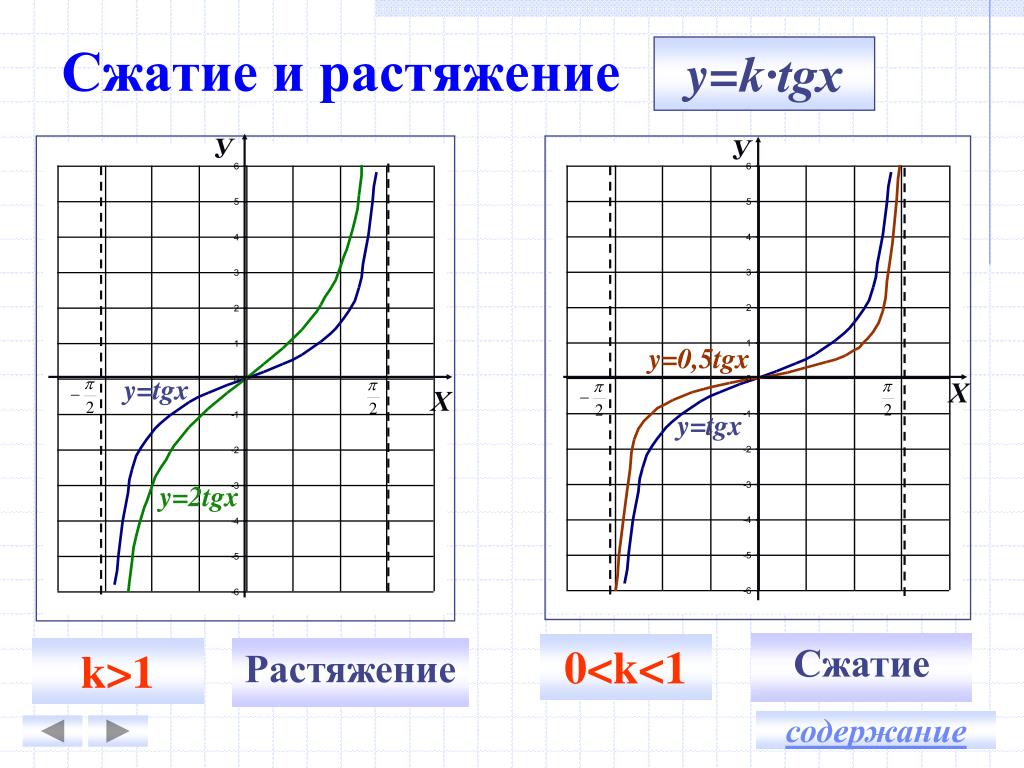
Горизонтальное и вертикальное растяжение/сжатие
Существует печатная версия этих уроков, если она будет вам полезна.
$y = f(x)$
$y = 2f(x)\,$
Вертикальное растяжение;
$y$-значения дублируются;
очков уходят дальше от $x$-ось
$y = f(x)$
$y = \frac{f(x)}{2}\,$
Вертикальная усадка;
$y$-значения уменьшаются вдвое;
очков становятся ближе к $x$-ось
Вертикальное растяжение/сжатие изменяет $y$-значения баллов.
Преобразования, влияющие на $y$-значения интуитивно понятны.
$y = f(x)$
$y = f(2x)\,$
Горизонтальная усадка;
$x$-значения делятся пополам;
очков становятся ближе к $y$-ось
$y = f(x)$
$y = f(\frac x2)$
Горизонтальное растяжение;
$x$-значения дублируются;
очков уходят дальше от $y$-ось
Горизонтальное растяжение/сжатие изменяет $x$-значения баллов.
Преобразования, влияющие на $x$-значения являются контринтуитивными.
Вертикальное/горизонтальное растяжение/сжатие обычно изменяет форму графика.
Урок Графические инструменты: Вертикальное и горизонтальное масштабирование в Учебная программа по алгебре II дает подробное обсуждение горизонтального и вертикального растяжения и сжатия. Ключевые понятия повторяются здесь.
Упражнения в этом уроке повторяют упражнения в Графические инструменты: Вертикальное и горизонтальное масштабирование .
Идеи относительно вертикального масштабирования (Растягивание/сжатие)
Точки на графике $\,y=f(x)\,$ имеют вид $\,\bigl(x,f(x)\bigr)\,.$
Точки на графике $\,y=3f(x)\,$ имеют вид $\,\bigl(x,3f(x)\bigr)\,. $
Таким образом, график $\,y=3f(x)\,$ находится путем взятия график $\,y=f(x)\,$ и умножение $y$-значения на $\,3\,.$ Это перемещает точки дальше от $x$-ось, что делает график более крутым.
Точки на графике $\,y=f(x)\,$ имеют вид $\,\bigl(x,f(x)\bigr)\,.$
Точки на графике $\,y=\frac13f(x)\,$ имеют вид $\,\bigl(x,\frac13f(x)\bigr)\,. $
Таким образом, график $\,y=\frac13f(x)\,$ найден взяв график $\,y=f(x)\,$ и умножение $y$-значения по $\,\frac13\,.$ Это перемещает точки ближе к $x$-ось, что делает график более плоским.
Преобразования с участием $\,y\,$ работают так, как вы ожидаете от них — они интуитивно понятны.
Вот мыслительный процесс, который вы должны использовать когда вам дан график $\,у=е(х)\,$ и спросил о графике $\,y=3f(x)\,$:
$$ \начать{выравнивать} \text{исходное уравнение:} &\quad y=f(x)\cr \text{новое уравнение:} &\quad y=3f(x) \end{выравнивание} $$
Интерпретация нового уравнения:
$$ \начать{собирать} \overset{\text{новые значения y}}{\overbrace{ \стойка\ \ у\ \ }} \overset{\text{являются}}{\overbrace{ \стойка\ \ =\ \ }} \overset{\text{три раза}\ \ }{\overbrace{ \ стойка \ \ 3 \ \ }} \overset{\text{предыдущие значения y}}{\overbrace{ \стойка\ \ f(x)\ \ }} \конец{собрать} $$
Резюме вертикального масштабирования
Пусть $\,k \gt 1\,. $ Начните с уравнения $\,y=f(x)\,.$ Умножьте предыдущее $y$-значения на $\,k\,$, что дает новое уравнение $\,y=kf(x)\,.$ $y$-значения умножаются на число больше $\,1\,$ чтобы они отошли подальше от $x$-ось. Это делает график более крутым, и называется вертикальным растяжением.
Пусть $\,0 \lt k \lt 1\,.$ Начните с уравнения $\,y=f(x)\,.$ Умножьте предыдущее $y$-значения на $\,k\,$, что дает новое уравнение $\,y=kf(x)\,. $ $y$-значения умножаются на число между $\,0\,$ и $\,1\,$ поэтому они приближаются к $x$-ось. Это делает график более плоским, и называется вертикальной усадкой.
В обоих случаях точка $\,(a,b)\,$ на графике $\,y=f(x)\,$ перемещается в точку $\,(a,kb)\,$ на графике $\,y=kf(x)\,.$
Этот тип преобразования формально называется вертикальное масштабирование (растяжение/сжатие) .
Идеи относительно горизонтального масштабирования (Растягивание/сжатие)
Точки на графике $\,y=f(x)\,$ имеют вид $\,\bigl(x,f(x)\bigr)\,. $
Точки на графике $\,y=f(3x)\,$ имеют вид $\,\bigl(x,f(3x)\bigr)\,.$
Как мы можем найти эти искомые точки $\,\bigl(x,f(3x)\bigr)\,$?
Во-первых, перейти к делу $\,\цвет{красный}{\bigl(3x\,\,f(3x)\bigr)}\,$ на графике $\,\color{red}{y=f(x)}\,.$
Эта точка имеет $y$-значение что мы хотим, но это неправильно $x$-значение. Значение $x$ этой точки $\,3x\,$ но желаемое $x$-значение просто $\,x\,.$
Таким образом, текущий $\color{purple}{x}$-значение необходимо разделить на $\,\color{фиолетовый}{3}\,$. $\color{purple}{y}$-значение остается такой же. Это дает желаемую точку $\,\color{green}{\bigl(x,f(3x)\bigr)}\,. $
Таким образом, график $\,y=f(3x)\,$ совпадает с графиком $\,y=f(x)\,$ за исключением того, что $x$-значения были разделены на $\,3\,$ (, а не , умноженное на $\,3\,$, как вы могли ожидать).
Обратите внимание, что разделение $x$-значения на $\,3\,$ перемещает их ближе к $y$-ось. Это называется горизонтальной усадкой.
Преобразования с участием $\,x\,$ НЕ работают так, как вы ожидаете, что они будут работать! Они противоречат интуиции — они противоречат вашей интуиции.
Вот мыслительный процесс, который вы должны использовать когда вам дан график $\,y=f(x)\,$ и спросил о графике $\,y=f(3x)\,$:
$$ \начать{выравнивать} \text{исходное уравнение:} &\quad y=f(x)\cr \text{новое уравнение:} &\quad y=f(3x) \end{выравнивание} $$
$$ \начать{собирать} \text{Интерпретация нового уравнения:}\cr\cr у = е( \overset{\text{заменить $x$ на $3x$}}{\overbrace{ \ \ 3x\ \ }} ) \конец{собрать} $$
Замена каждого $\,x\,$ на $\,3x\,$ в уравнении вызывает $x$-значения в графе ДЕЛИТЬСЯ на $\,3\,. $
Краткий обзор горизонтального масштабирования
Пусть $\,k\gt 1\,.$ Начните с уравнения $\,y=f(x)\,.$ Замените каждый $\,x\,$ на $\,kx\,$, чтобы дают новое уравнение $\,y=f(kx)\,.$ Это вызывает $x$-значения на графе, подлежащем ДЕЛЕНИЮ на $\,k\,$ который перемещает точки ближе к $y$-ось. Это называется горизонтальной усадкой. Точка $\,(a,b)\,$ на графике $\,y=f(x)\,$ перемещается в точку $\,(\frac{a}{k},b)\,$ на графике $\,y=f(kx)\,. $
Кроме того:
Пусть $\,k\gt 1\,.$ Начните с уравнения $\,y=f(x)\,.$ Замените каждый $\,x\,$ на $\,\frac{x}{k}\,$, чтобы задайте новое уравнение $\,y=f(\frac{x}{k})\,.$ Это вызывает $x$-значения на графе, который нужно УМНОЖИТЬ на $\,k\,$ который перемещает точки дальше от $y$-ось. Это называется горизонтальной растяжкой. Точка $\,(a,b)\,$ на графике $\,y=f(x)\,$ перемещается в точку $\,(ka,b)\,$ на графике $\,y=f(\frac{x}{k})\,. $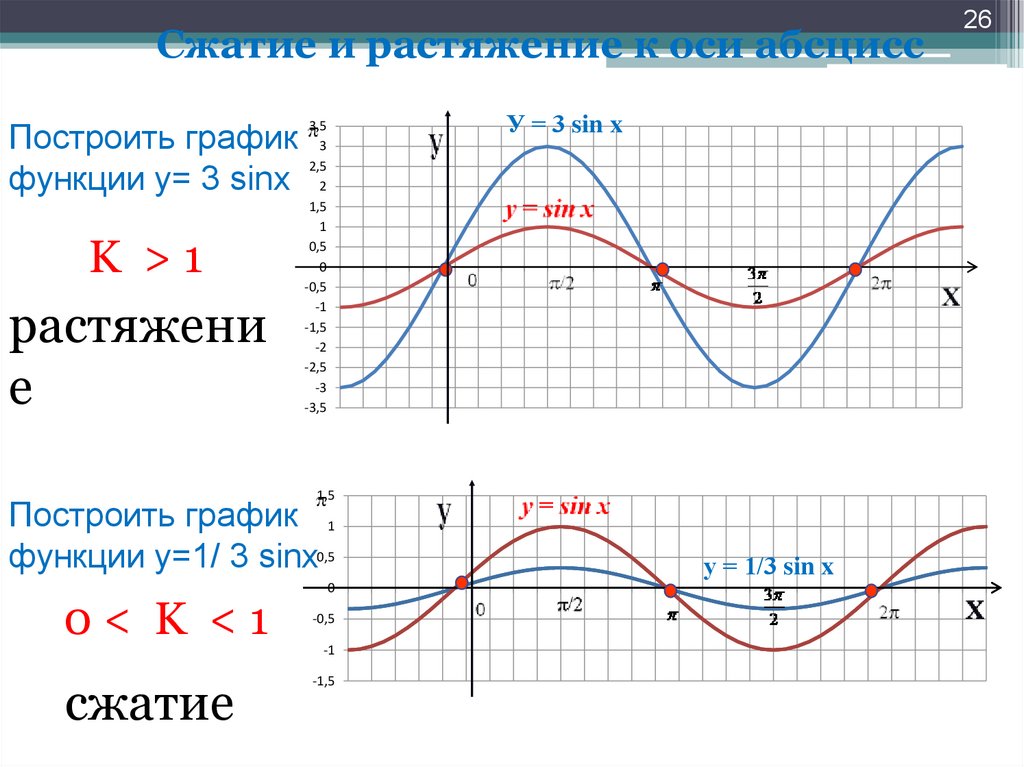
Этот тип преобразования формально называется масштабирование по горизонтали (растяжение/сжатие) .
Различные слова, используемые для разговора Преобразования с участием $\,y\,$ и $\,x\,$
Обратите внимание, что разных слова используются, когда речь идет о преобразованиях с участием $\,y\,$ и преобразования с участием $\,x\,.$
Для преобразований с участием $\,у\,$ (то есть преобразования, которые изменяют $y$-значения точек), мы говорим:
СДЕЛАЙТЕ ЭТО к предыдущему $y$-значение
Для преобразований с участием $\,х\,$ (то есть преобразования, которые изменяют $x$-значения точек), мы говорим:
ЗАМЕНИТЬ предыдущий $x$-значения по $\ldots$
Убедитесь, что вы видите разницу!
Вертикальное масштабирование:
Переход от $\,у=е(х)\,$ к $\,y = kf(x)\,$ для $\,k\gt 0$
Горизонтальное масштабирование:
Переход от $\,у = f(x)\,$ к $\,y = f(kx)\,$ для $\,k\gt 0$
Убедитесь, что вы видите разницу между (скажем) $\,у = 3f(x)\,$ и $\,y = f(3x)\,$!
В случае $\,y = 3f(x)\,$ $\,3\,$ находится «снаружи»: мы опускаем $\,x\,$ в ячейку $\,f\,$, получение соответствующего вывода, и , затем , умноженное на $\,3\,. $ Это вертикальная растяжка.
В случае $\,y = f(3x)\,$ $\,3\,$ находится «внутри»: мы умножаем $\,x\,$ на $\,3\,$ перед , опуская его в поле $\,f\,$. Это горизонтальная усадка.
Примеры
Вопрос: Начните с $\,y = f(x)\,.$ Сделайте вертикальную растяжку: $y$-значения на графике следует умножить на $\,2\,.$ Что такое новое уравнение?
Решение: Это трансформация, включающая $\,у\,$; это интуитивно понятно.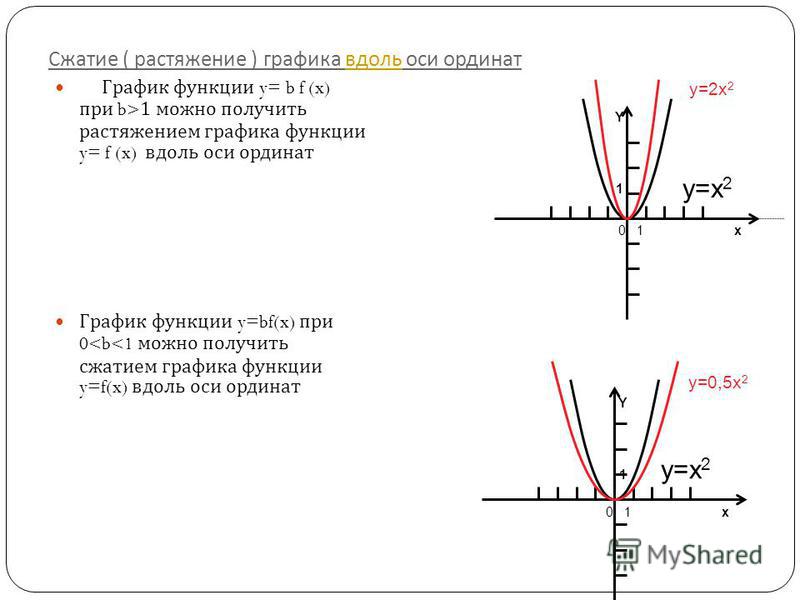 Вы должны умножить предыдущее $y$-значения на $\,2\,.$ Новое уравнение: $\,y = 2f(x)\,$
Вопрос: Начните с $\,y = f(x)\,.$ Сделайте горизонтальную растяжку: $x$-значения на графике должно быть умножено на $\,2\,.$ Что такое новое уравнение?
Решение: Это трансформация, включающая $\,х\,$; это нелогично. Вы должны заменить каждый $\,x\,$ в уравнении через $\,\frac{x}{2}\,.$ Новое уравнение: $\,y = f(\frac{x}{2})\,$ 93\,. 3\,$
Вопрос: Предположим, что $\,(a,b)\,$ — точка на графике $\,y = f(x)\,.$ Тогда какая точка находится на графике $\,y = f(\frac{x}{3})\,$?
Решение: Это трансформация, включающая $\,х\,$; это нелогично. Замена каждого $\,x\,$ на $\,\frac{x}{3}\,$ в уравнении вызывает $x$-значения на графике, который нужно умножить на $\,3\,.$ Таким образом, новая точка есть $\,(3a,b)\,.$
Концептуальная практика
БиоМатематика: Трансформация Графиков
Что такое вертикальное растяжение и сжатие?
В то время как переводы перемещают точки пересечения x и y базового графа, растягивание и сжатие эффективно растягивают базовый граф наружу или сжимают его внутрь, изменяя общие размеры базового графа без изменения его формы. Когда график растягивается или сжимается по вертикали, x — перехваты действуют как якоря и не меняются при преобразовании.
Определение
Для базовой функции f ( x ) и константы k > 0 функция, заданная как
г ( х ) = к ф ( х ),
можно нарисовать, растянув f ( x ) по вертикали с коэффициентом к если к > 1
или
путем уменьшения по вертикали f ( x ) с коэффициентом k
если 0 < k < 1.

Помните, что точки пересечения x не двигаются при вертикальном растяжении и сжатии. Другими словами, если f ( x ) = 0 для некоторого значения x , то k f ( x ) = 0 для того же значения x. Кроме того, вертикальное растяжение/сжатие в k раз означает, что точка ( x, y ) на графике f ( x ) трансформируется в точку ( x , ky ) на графике г ( х ).
Примеры вертикального растяжения и сжатия
Рассмотрим следующие базовые функции,
(1) ф ( х ) = х ² — 2,
(2) г ( x ) = sin ( x ).
Графическое представление функции (1), f ( x ), представляет собой параболу. Как вы думаете, граф
y ₁ ( x ) = 1/2 f ( x )
выглядит? Используя определение f ( x ), мы можем записать y ₁ ( x ) как,
y ₁ ( x ) = 1/2 f ( x ) = 1/2 ( x ² — 2) = 1/2 x ² — 1
На основании определения вертикальной усадки график y ₁ ( x ) должен выглядеть как график f ( x ), сжатый по вертикали в 1/2 раза. Посмотрите на графики f ( x ) и y ₁ ( x ).

Обратите внимание, что точки пересечения x не сдвинулись.
Функция (2), г ( x ), представляет собой синусоидальную функцию. Что бы график
г ₂ ( x ) = 6 г ( x )
похож? Используя наши знания о вертикальных растяжениях, график y ₂ ( x ) должен выглядеть как базовый граф g ( x ), растянутый по вертикали в 6 раз. Чтобы проверить это, мы можем написать y _{2 90 362 ( х ) как,}
у ₂ ( х ) = 6 г ( х ) = 6 sin ( х ),
построить таблицу значений и построить график новой функции.