Расход грунтовки по металлу на 1м2
Что бы краска держалась много лет на окрашенной поверхности, сначала ее нужно прогрунтовать. В наше время рынок грунтовок очень обширен, и в первую очередь они позволяют сэкономить. Грунтовочная смесь помогает предотвратить появление грибка, эрозии, бактерий а так же и экономят расход клеящих материалов. Количество используемой грунтовки всегда рассчитывается нормой, для каждого вида своя норма. Ее расход всегда оправдан ценой, как правило она ниже стоимости краски.
Расход грунтовки на 1м2 метала как правило зависит от таких факторов:
- Типа самой поверхности, которая потребует окраски.
- Норма растворимой порции которая задана производителем.
- От вида краски, клея и т.д.
- От климатических условий.
Специалисты для грунтование металла выбирают смесь без акрила. Поскольку акрил не предотвращает появления ржавления железа. Поверхность металла сначала нужно подготовить. На ней не должно бить ржавчины или отслаиваемого железа.
Для грунтование металла лучше всего подойдет эпоксидная грунтовка на основе смол. Она предназначена для железа и бетонных конструкций. По общим нормам трата грунтовки для отделки металла составит от 60 до 100 г. Это минимальный показатель среди всех обрамляемых поверхностей.
Грунтовка ГФ-021 (Самая популярная смесь для металла)
Жидкость «ГФ-021» представляет собой суспензию наполнителей и пигментов в лаке на алкидной основе с добавлением сиккатива, стабилизаторов и растворителей. Состав предназначен для металлических и деревянных оснований под покрытие различными эмалями.
Расход грунтовки ГФ-021 на 1м2 металла оговорен в стандарте и составляет 60-100 граммов на один слой.
Разумеется, при расчете количества грунта, необходимого для производства работ, не стоит забывать про пару тонкостей.
- Расход грунту по металлу ГФ-021 увеличивается при ее загустевании. Грунт волей-неволей ложится более толстым слоем.
- На пористых поверхностях он тоже возрастает: часть грунтования впитывается в основание.
Технические характеристики и расход грунтовочной смеси — таблица
| Цвет и текстура пленки. Внешний вид пленки | Красно-коричневый (серый, белый), полуглянцевая либо матовая текстура. Однородная, ровная, без расслоений и кратеров |
| Степень перетира | 40 мкм |
| Условная вязкость | 45 |
| Время высыхания до третьей степени при температуре 20?С | 12 часов |
| Эластичность при изгибе | 1 мм |
| Ударная прочность | 50 см |
| Твердость пленки | 0,35 |
| Адгезия пленки | не более 1 балла |
| Стойкость пленки к статическому жидкостному воздействию 20?С | |
| хлористого натрия/ минеральных масел | не менее 24/48 часов |
| плотность | 1,25-1,3 кг/л |
| Расход на один слой | 60-100 грамм на квадратный метр |
| Нелетучих веществ, % | 54-60 |
Надо четко понимать, что это довольно усредненные нормы расходов.
Нормы расхода теплоизоляции Броня. — Жидкая керамическая теплоизоляция Броня
СВЕРХТОНКИЕ ТЕПЛОИЗОЛЯЦИОННЫЕ ПОКРЫТИЯ «БРОНЯ» Расход материала в зависимости от условий нанесенияРасход теплоизоляционных покрытий серии «БРОНЯ» одинаков для всех модификаций и зависит от ряда факторов, среди которых ведущую роль играют способ нанесения и состояние поверхности, а также ряд других.
Лабораторный расход (т.е. без учета типа поверхности и способа нанесения) сверхтонких теплоизоляционных покрытий серии «БРОНЯ» составляет 1 литр на 1 м2 при толщине покрытия 1 мм.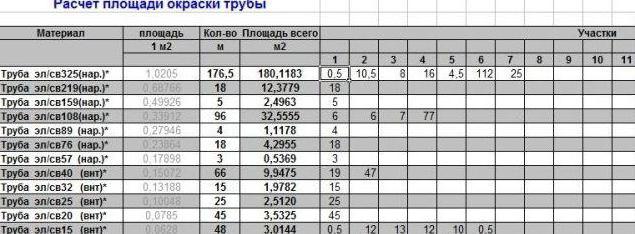
Фактический же расход материала отличается от лабораторного и мы рекомендуем в различных условиях прибавлять следующий перерасход (в % относительно лабораторного):
- При нанесении кистью на вертикальную металлическую поверхность в безветренную погоду — 3-5 %
- При нанесении кистью на вертикальную бетонную поверхность в безветренную погоду — 5-10%
- При нанесении безвоздушными распылителями на вертикальную металлическую поверхность в безветренную — 15-25%
- При нанесении безвоздушными распылителями на вертикальную бетонную поверхность в безветренную погоду — 35-45%
Следует также учитывать, что на перерасход влияют такие факторы как — диаметр трубопровода (в случае нанесения на трубы), степень шероховатости поверхности, способ нанесения на объект (альпинисты, с люльки, леса и пр.), степень подготовки маляра, погодные условия и пр.
При нанесении безвоздушными распылителями рекомендуем перед применением внимательно изучить инструкцию по подбору, настройке и работе с безвоздушными распылителями Graco: СКАЧАТЬ ИНСТРУКЦИЮ ПО РАБОТЕ С БЕЗВОЗДУШНЫМИ РАСПЫЛИТЕЛЯМИ
Обращаем внимание на необходимость соблюдения инструкций по работе с жидкими теплоизоляционными покрытиями серии «БРОНЯ».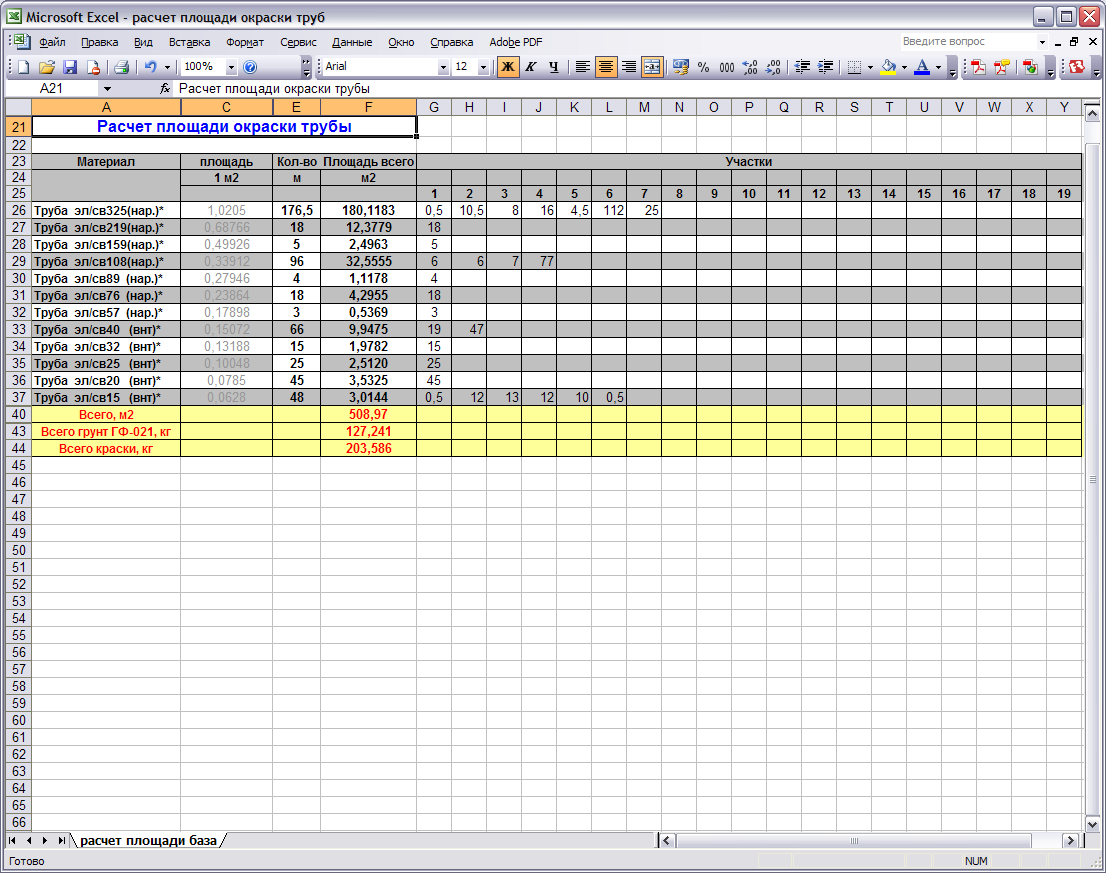
Инструкция Броня Классик
Инструкция Броня Фасад
В случае возникновения дополнительных вопросов — свяжитесь с нами или с нашим официальным представителем в Вашем регионе!
Расход порошковой краски при нанесении
Совершенство технологии порошковой покраски(покраска порошковой полимерной краской) заключается в достижении наилучшего качества полимерного покрытия при минимальной себестоимости порошковой окраски в полном соответствии с экологическими требованиями.
Доля, приходящаяся на порошковую краску в расчете себестоимости окраски квадратного метра при промышленном цикле занимает около 65 — 70%. Поэтому очень важно напылить полимерное покрытие, используя минимальный расход краски.
Как видно из расчетных формул, расходные нормы порошковой краски при нанесении зависят от различных факторов:
| • | Толщина пленки влияет на эксплуатационные качества полимерного покрытия, кроме того, она определяет расход порошковой краски, соответственно, важно его контролировать. Зависит от типа формируемой поверхности (структурированная либо гладкая), а так же от требуемых свойств полимерного покрытия (декоративное, защитное либо защитно-декоративное). Зависит от типа формируемой поверхности (структурированная либо гладкая), а так же от требуемых свойств полимерного покрытия (декоративное, защитное либо защитно-декоративное).Декоративное полимерное покрытие требует современные порошковые краски с хорошей укрывистостью, которые обеспечивают возможность окраски слоем толщиной 40 — 50 мкм. Защитно-декоративные полимерные покрытия предполагают оптимальную толщину покрытия 70 — 100 мкм. Защитные полимерные покрытия должны быть толщиной в пределах 90 — 130 мкм и более. |
| • | Фракционный (гранулометрический) состав. Распределение частиц порошковой краски по размеру может оказывать влияние на сыпучесть, характеристики покрытия и его внешний вид. Полимерное покрытие характеризуется размером частиц основной фракции, этот показатель отвечает за толщину нанесенного слоя. |
| • | Удельный вес краски. Чем краска «легче», тем она меньше расходуется при одной и той же толщине покрытия. В идеале, при удельном весе 1,2 гр/см3 и толщине покрытия 80 мкм можно достичь обещанного производителями порошковой краски расхода равного 100 гр/м2. Но, к сожалению, это только в идеале, на практике же для большинства производств эта цифра в среднем около 120 — 140 гр/м2. Чем краска «легче», тем она меньше расходуется при одной и той же толщине покрытия. В идеале, при удельном весе 1,2 гр/см3 и толщине покрытия 80 мкм можно достичь обещанного производителями порошковой краски расхода равного 100 гр/м2. Но, к сожалению, это только в идеале, на практике же для большинства производств эта цифра в среднем около 120 — 140 гр/м2. |
| • | Человеческий фактор. При всем совершенстве краскораспылителей остается влияние человеческого фактора при ручном нанесении порошковой краски. Таким образом полимерное покрытие получают толщиной, зависящей от концентрации порошка в факеле распылителя, времени прохода изделия через факел, а так же от степени зарядки и коэффициента осаждения краски. Высокая квалификация маляра может обеспечить существенное снижение расхода краски до 10 — 15%. |
| • | Форма и сложность окрашиваемых изделий. Равномерность толщины полимерного покрытия для плоских панелей либо сложных деталей будет отличаться, соответственно и показатели расхода краски будут абсолютно разными. Равномерность толщины полимерного покрытия для плоских панелей либо сложных деталей будет отличаться, соответственно и показатели расхода краски будут абсолютно разными. |
При выборе порошковой краски необходимо руководствоваться не только ценой, главное, чтобы полученное из нее полимерное покрытие в максимальной степени удовлетворяло требованиям потребителя — внешний вид, долговечность покрытия и гарантийный срок эксплуатации.
Производители порошковых красок имеют возможность в индивидуальном порядке с учетом всех требований и пожеланий к свойствам конечной продукции подобрать оптимальный состав краски для обеспечения наилучшей покрываемости и минимизации расходных норм при нанесении полимерного покрытия.
По материалам http://euroimpianti.com.ua/articles/rashod-kraski.html
|
Решения NCERT для математики класса 9 Глава 13 Площади и объемы
Решения NCERT для математики класса 9 Глава 13 Площади поверхности и объемы Пример 13.1 являются частью решений NCERT для математики класса 9. Здесь мы предоставили решения NCERT для класса 9 по математике, глава 13, площади поверхности и объемы, пример 13.1.
Решения NCERT для математики класса 9 Глава 13 Площади поверхностей и объемы Пример 13.1
Пример 13.1 Математика класса 9 Вопрос 1.Необходимо изготовить пластиковый ящик длиной 1,5 м, шириной 1,25 м и глубиной 65 см. Он открывается сверху. Пренебрегая толщиной пластикового листа, определите
(i) площадь листа, необходимую для изготовления коробки.
(ii) Стоимость листа для него, если лист размером 1 м2 стоит ₹20.
Решение:
(i) Здесь длина (l) = 1,5 м, ширина th(b) = 1,25 м
и высота (h) = 65 см = \(\frac { 65 }{ 100 }\) м = 0.
 65 м
65 м ∵ Открыт сверху.
∴ Площадь его поверхности
= [Площадь боковой поверхности] + [Площадь основания]
= [2(1 + b)h] + [lb]
= [2(1,50 + 1,25)0,65] м 2 + [1,50 x 1.25] M 2
= [2 x 2,75 x 0,65] m 2 + [1.875] m 2
= 3,575 м 2 + 1,875 м 2 = 5,45 м 2
∴ область листа, необходимого для изготовления коробки = 5,45 м 2
(ii) Стоимость 1 м 2 листа = рупий. 20
Стоимость 5.45 м 2 листа = рупий. (20 x 5,45)
= рупий. 109
Отсюда стоимость необходимого листа = руб. 109
Упр. 13.1 Класс 9 МатематикаВопрос 2.
Длина, ширина и высота комнаты равны 5 м, 4 м и 3 м соответственно. Найти стоимость побелки стен комнаты и потолка из расчета 17,50 руб. за м 2 .
Решение:
Длина комнаты (l) = 5 м
Ширина комнаты (b) = 4 м
Высота комнаты (h) = 3 м
Комната похожа на параллелепипед, четыре стенки которого (боковая поверхность) и потолок побелить.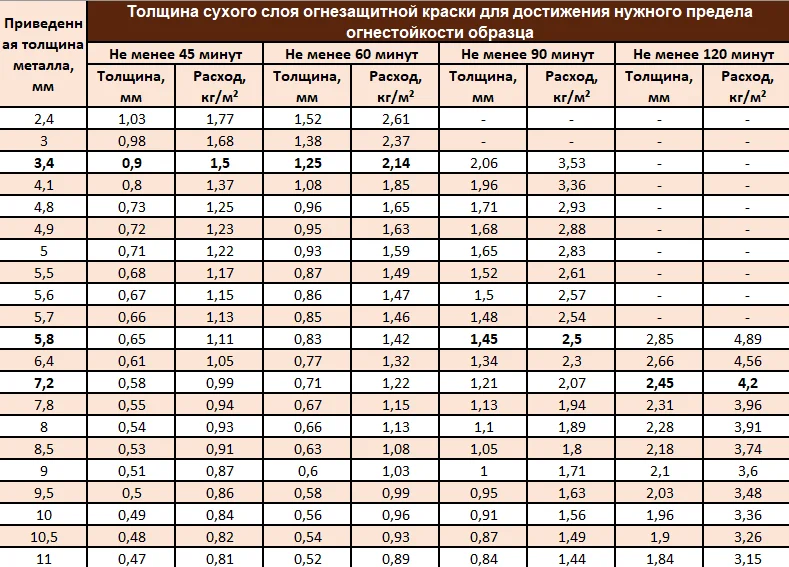
∴ Площадь побелки
= [Площадь боковой поверхности] + [Площадь потолка]
= [2(l + b)h] + [lxb]
= [2(5 + 4) x 3] м 2 + [5 x 4] м 2 = 54 м 2 + 20 м 2 = 74 м 2
Стоимость побелки 1 м2 площади = рупий. 7,50
∴ Стоимость побелки 74 м 2 площади = рупий. (7,50 х 74) = рупий. 555
Таким образом, необходимые затраты на стирку белья = руб. 555
Упр. 13.1 Класс 9 МатематикаВопрос 3.
Пол прямоугольного зала имеет периметр 250 м.Если стоимость покраски четырех стен из расчета 10 ₹ за м 2 составляет 15000 ₹, найдите высоту зала.
[Подсказка: площадь четырех стен = площадь боковой поверхности]
Решение:
Прямоугольный зал означает прямоугольный параллелепипед.
Пусть длина и ширина зала равны l и b соответственно.
∴ Периметр пола = 2(l + b)
⇒ 2(l + b) = 250 м
∵ Площадь четырех стен = Площадь боковой поверхности = 2(1 + b) xh, где h — высота пола. зал = 250 кв.м 2
зал = 250 кв.м 2
Стоимость покраски четырех стен
= рупий.(10 х 250 ч) = рупий. 2500h
⇒ 2500 h = 15000 ⇒ h = \(\frac { 15000 }{ 2500 }\) = 6
Таким образом, требуемая высота зала = 6 м
Решение:
Общая площадь, которую можно покрасить = 9,375 м 2
Здесь Длина кирпича (l) = 22,5 см
Ширина кирпича (b) = 10 см
Высота кирпича (h) = 7 .5 см
Так как кирпич похож на прямоугольный параллелепипед, то
Общая площадь поверхности кирпича = 2[lb + bh + hl]
= 2[(225 x 1(0) + (10 x 7,5) + (7,5 x 22,5 )] см 2
= 2[(225) + (75) + (168,75)] см 2
= 2[468,75] см 2 = 937,5 см 2 = \(.\frac5 } { 10000 }\) m 2
Пусть искомое количество кирпичей равно n
∴ Суммарная площадь поверхности n кирпичей = nx \(\frac { 937,5 }{ 10000 }\) m 2
Таким образом, искомое количество кирпичей = 100
Пример 13.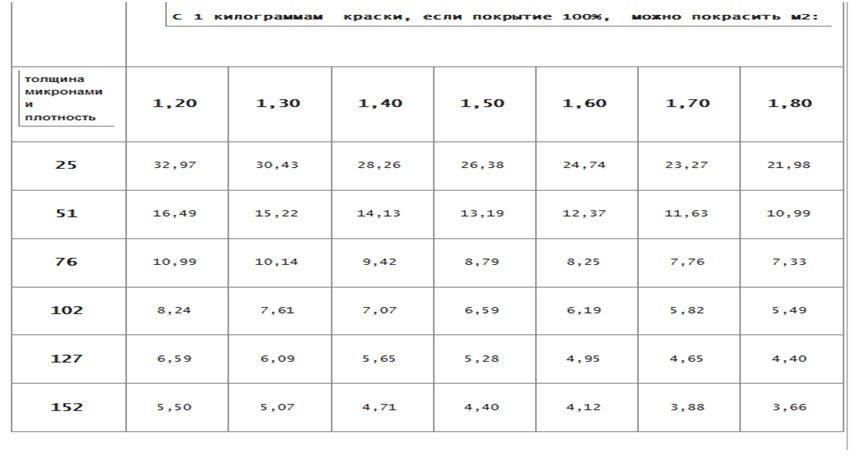 1 Класс 9 МатематикаВопрос 5.
1 Класс 9 МатематикаВопрос 5.
Кубическая коробка имеет каждое ребро по 10 см, а другая прямоугольная коробка имеет длину 12,5 см, ширину 10 см и высоту 8 см.
(i) У какого ящика площадь боковой поверхности больше и на сколько?
(ii) У какой коробки общая площадь поверхности меньше и на сколько?
Решение:
Для кубической коробки с ребром (a) = 10 см
Площадь боковой поверхности = 4a 2 = 4 x 10 2 см 2
= 400 см 2
Общая площадь поверхности 2 = 6 x 10 2 см 2
= 600 см 2
Для прямоугольной коробки с размерами
Длина (l) = 12.5 см,
Ширина (b) = 10 см,
Высота (h) = 8 см
∴ Площадь боковой поверхности = 2[l + b] xh = 2[12,5 + 10] x 8 см 2 = 360 см 2
Общая площадь поверхности = 2[lb + bh + hl]
= 2[(12,5 x 10) + (10 x 8) + (8 x 12,5)] см 2
= 2[125 + 80 + 100 ] см 2
= 2[305] см 2
= 610 см 2
(i) Кубический ящик имеет большую площадь боковой поверхности на (400 – 360) см 2 = 40 см 2 .
(ii) Общая площадь поверхности кубического ящика меньше кубического ящика на (610 – 600) см 2 = 10 см 2 .
Упр. 13.1 Класс 9 МатематикаВопрос 6.
Небольшая закрытая теплица (гербарий) сделана полностью из стеклянных панелей (включая основание), скрепленных лентой. Длина 30 см, ширина 25 см, высота 25 см.
(i) Какова площадь стекла?
(ii) Сколько ленты потребуется для всех 12 краев?
Решение:
Гербарий похож на прямоугольный параллелепипед.
Здесь длина (l) = 30 см,
ширина (b) = 25 см,
высота (h) = 25 см
(i) Площадь поверхности гербария (стекло)
= 2[lb + bh + hl]
= 2[(30×25) + (25×25) + (25×30)] см 2 – 2[750 + 625 + 750] см 2
= 2[2125] см 2
= 4250 см 2
Таким образом, необходимая площадь стекла = 4250 см 2
(ii) Общая длина 12 ребер = 4l + 4b + 4h
= 4(l + b + h)
= 4 (30 + 25 + 25) см
= 4 х 80 см = 320 см
Таким образом, необходимая длина ленты = 320 см
Пример 13. 1 Класс 9 МатематикаВопрос 7.
1 Класс 9 МатематикаВопрос 7.
Shanti Sweets Столл размещал заказ на изготовление картонных коробок для упаковки сладостей. Требовались коробки двух размеров. Больший из размеров 25 см х 20 см х 5 см и меньший из размеров 15 см х 12 см х 5 см. Для всех перекрытий требуется дополнительно 5% от общей площади поверхности. Если стоимость картона составляет 4 рубля за 1000 см², найдите стоимость картона, необходимого для производства 250 коробок каждого вида.
Решение:
Для большей коробки:
Длина (l) = 25 см,
Ширина (b) = 20 см,
Высота (h) = 5 см
Общая площадь поверхности коробки = 2 (lb + bh + hl)
= 2[(25 x 20) + (20 x 5) + (5 x t25)] см 2
= 2 [500 + 100 + 125] см 2
= 2[725] см 2
= 1450 см 2
Общая площадь 250 коробок = (250 x 1450) см 2 = 362500 см 2
Для меньшей коробки:
l = 15 см, b = 5 см см
Общая площадь поверхности коробки = 2 [lb + bh + hl]
= 2[(15 x 12) + (12 x 5) + (5 x 15)] см 2
= 2[180 + 60 + 75] см 2 = 2[315] см 2 = 630 см 2
∴ Общая площадь поверхности 250 коробок = (250 x 630) см площадь поверхности обоих типов коробок = 362500 см 2 +157500 см 2 = 520000 см 2 Площадь перекрытий = 5% от [общей площади]
= \( \frac { 5 }{ 100 }\) x 520000 см 2 = 26000 см 2
∴ Общая площадь требуемой поверхности картона = [Общая площадь поверхности 250 коробок каждого типа] + [Площадь нахлестов]
= 520000 см 2 + 26000 см 2 = 546000 см 2
∵ Стоимость 1000 см 2 картона = рупий. 4
4
∴ Стоимость 546000 см 2 картона
= рупий\(\frac { 4\times 546000}{1000}\) = рупий. 2184
Упражнение 13.1 Класс 9 МатематикаВопрос 8.
Парвин хотела сделать временное убежище для своей машины, соорудив коробчатую конструкцию из брезента, закрывающую все четыре стороны и верхнюю часть машины (с передней стороной как клапан, который можно свернуть). Предполагая, что поля сшивания очень малы и поэтому незначительны, сколько брезента потребуется для изготовления укрытия высотой 2.5 м, при размерах основания 4 м х 3 м?
Решение:
Здесь длина (l) = 4 м,
ширина (b) = 3 м
и высота (h) = 2,5 м
Структура похожа на прямоугольный параллелепипед.
∴ Площадь поверхности прямоугольного параллелепипеда без основания
= [Площадь боковой поверхности] + [Площадь потолка]
= [2(l + b)h] + [lb]
= [2(4 + 3) x 2.5] м 2 + [4 x 3] м 2
= 35 м 2 + 12 м 2 = 47 м 2
Таким образом, потребуется 47 м 2 9. 0016 брезента.Пример 13.1 площадь прямого кругового цилиндра высотой 14 см равна 88 см 2 . Найдите диаметр основания цилиндра.
0016 брезента.Пример 13.1 площадь прямого кругового цилиндра высотой 14 см равна 88 см 2 . Найдите диаметр основания цилиндра.
Решение:
Пусть r — радиус цилиндра.
Здесь высота (h) = 14 см и площадь криволинейной поверхности = 88 см xrx 14 = 88
⇒ r = \(\frac { 88\times 7 }{2\times 22\times 14 }\) = 1 см
∴ Диаметр = 2 xr = (2 x 1) см = 2 см
Пример 13.2 9 класс МатематикаВопрос 2.
Требуется изготовить закрытый цилиндрический резервуар высотой 1 м и диаметром основания 140 см из металлического листа. Сколько квадратных метров листа потребуется для того же?
Решение:
Здесь высота (h) = 1 м
Диаметр основания = 140 см = 1,40 м
Радиус (r) = \(\frac { 1,40 }{ 2 }\)m = 0,70 м
Общая площадь поверхности цилиндра = 2πr (h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 0,70(1 + 0,70)м 2
= 2 x 22 x 0,10 x 1,70 м 2
= 2 x 22 x \(\frac {10}{100}\) x \(\frac {170}{100}\)m 2
= \(\frac {748}{100}\)m 2 = 7. 48 м 2
48 м 2
Следовательно, необходимый лист = 7,48 м 2
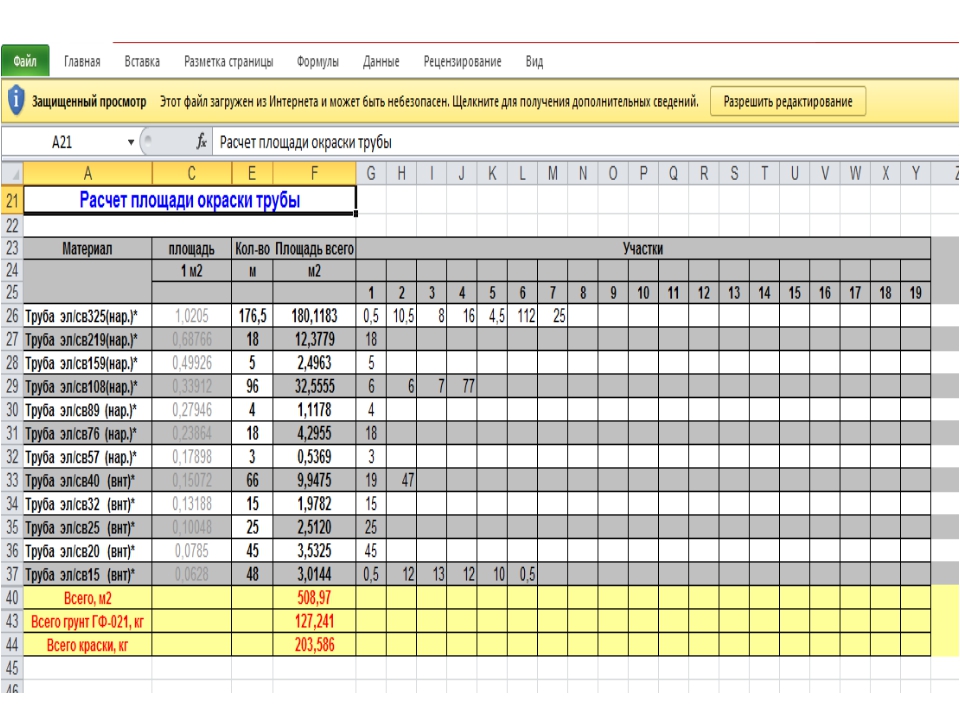
Длина металлической трубы 77 см. Внутренний диаметр поперечного сечения 4 см, внешний диаметр 4,4 см (см. рисунок). Найдите его
(i) площадь внутренней криволинейной поверхности.
(ii) площадь внешней изогнутой поверхности.
(iii) общая площадь поверхности.
Решение:
Длина металлической трубы = 77 см.
Имеет форму цилиндра.
∴ Высота цилиндра (h) = 77 см
Внутренний диаметр = 4 см
Внутренний радиус (r) = \(\frac { 4}{ 2 }\) см = 2 см
Внешний диаметр = 4.4 см
⇒ Внешний радиус (R) = \(\frac { 4,4 }{ 2 }\) см = 2,2 см
(i) Площадь внутренней изогнутой поверхности = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 2 x 77 см 2
= 2 x 22 x 2 x 11 см 2 = 968 см 2
(ii) Площадь внешней изогнутой поверхности = 2πRh
(iii) Общая площадь = [Площадь внутренней изогнутой поверхности] + [Площадь внешней изогнутой поверхности] + [Площадь двух круглых концов]
= [2πrh] + [2πRh] + 2[π(R 2 – r 2 )]
= [ 968 см 2 ] + [1064. 8 см 2 ]
8 см 2 ]
Упражнение 13.2 Класс 9 МатематикаВопрос 4.
Диаметр валика 84 см, длина 120 см. Чтобы выровнять игровую площадку, требуется 500 полных оборотов. Найдите площадь детской площадки в м 2 .
Решение:
Ролик имеет форму цилиндра диаметром = 84 см
⇒ Радиус ролика (r) = \(\frac { 84 }{ 2 }\) см = 42 см
Длина ролика ( h) = 120 см
Площадь кривизны ролика = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 42 x 120 см 2
= 2 x 22 x 6 x 120 см 2 = 31680 см 2
Теперь площадь площадки, выровненная за один оборот катка = 31680 см 2
= \(\frac { 31680 }{ 10000 }\)m 2
∴ Площадь площадка выровнена за 500
оборотов = 500 х \(\frac { 31680 }{ 10000 }\)м 2 = 1584м 2
Цилиндрический столб диаметром 50 см и высотой 3,5 м. Найти стоимость покраски криволинейной поверхности столба из расчета 12,50 руб.
 за м 2 .
за м 2 . Решение:
Диаметр столба = 50 см
∴ Радиус (r) = \(\frac { 50}{ 2 }\)m = 25 м = \(\frac { 1 }{ 4 }\)m
и высота (h) = 3,5 м
Площадь криволинейной поверхности стойки = 2πrh
∴ Площадь криволинейной поверхности, подлежащей окраске = \(\frac { 11}{ 2 }\)м 2
∴ Стоимость покраски 1 м 2 столба = рупий.12,50
∴ Стоимость покраски \(\frac { 11 }{ 2 }\) м 2 столба
= рупий. ( \ (\ frac { 11 }{ 2 } \) x 12,50 )
= рупий. 68,75.
Упражнение 13.2 Класс 9 МатематикаВопрос 6.
Площадь кривизны прямоугольного цилиндра составляет 4,4 м2. Найдите его высоту, если радиус основания цилиндра равен 0,7 м. Площадь криволинейной поверхности прямоугольного цилиндра равна 4,4 м2. Найдите его высоту, если радиус основания цилиндра равен 0,7 м.
Решение:
Радиус (r) = 0,7 м
Пусть высота цилиндра равна hm
Площадь криволинейной поверхности цилиндра = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x \(\frac { 7 }{ 10 }\) x hm 2
Но площадь криволинейной поверхности равна 4. 4 м 2 . [Дано]
4 м 2 . [Дано]
Упражнение 13.2 Класс 9 МатематикаВопрос 7.
Внутренний диаметр круглого колодца составляет 3,5 м. Глубина 10 м. Найдите
(i) площадь его внутренней криволинейной поверхности.
(ii) стоимость штукатурки этой криволинейной поверхности из расчета 40 ₹ за м 2 .
Решение:
Ганс Внутренний диаметр скважины = 3,5 м
Радиус скважины (r) = \(\frac { 3,5 }{ 2 }\)
Высота скважины (h) = 10 м
(i) Внутренний площадь изогнутой поверхности = 2πrh
(ii) Стоимость штукатурки за м 2 = рупий.40
∴ Общая стоимость оштукатуривания площади 110 м 2
= руб. (110 х 40) = рупий. 4400
В системе водяного отопления имеется цилиндрическая труба длиной 28 м и диаметром 5 см. Найдите полную излучающую поверхность в системе.
Решение:
долларов США Длина цилиндрической трубы (h) = 28 м
Диаметр трубы = 5 см
∴ Радиус (r) = \(\frac { 5 }{ 2 }\) cm = \(\frac { 5 }{ 200 }\) m
Площадь криволинейной поверхности цилиндра = 2πrh
Таким образом, общая излучающая поверхность равна 4.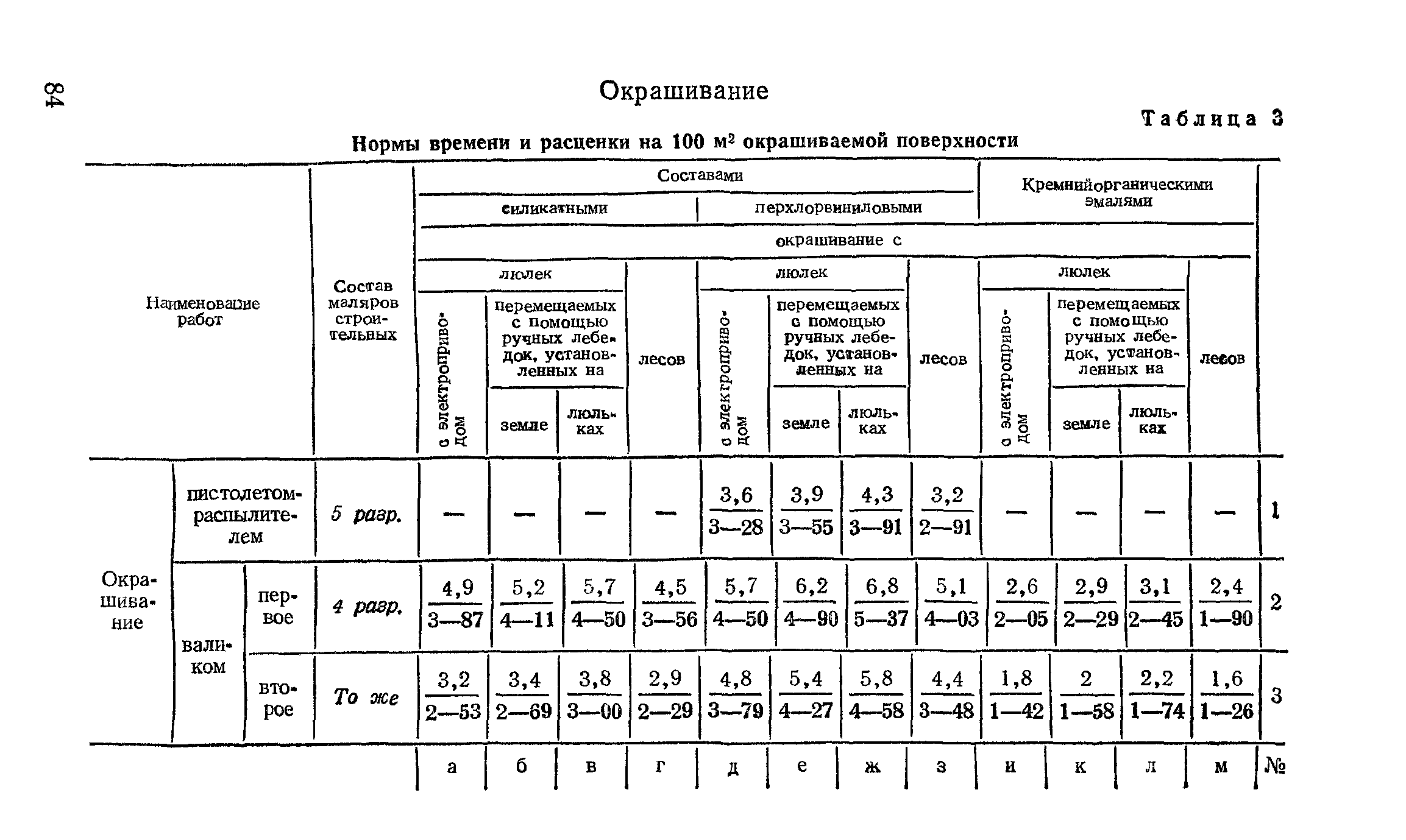 4 м 2 .
4 м 2 .
Упр. 13.2 Класс 9 МатематикаВопрос 9.
Найдите
(i) площадь боковой или криволинейной поверхности закрытого цилиндрического резервуара для хранения бензина диаметром 4,2 м и высотой 4,5 м.
(ii) сколько стали было фактически использовано, если \(\frac { 1 }{ 12 }\) фактически использованной стали было потрачено впустую при изготовлении резервуара.
Решение:
Накопительный бак имеет форму цилиндра.
∴ Диаметр резервуара = 4,2 м
⇒ Радиус (r) = \(\frac { 4,2 }{ 2 }\) = 2,1 м
Высота (h) = 4.5 м
Сейчас,
(i) Площадь боковой (или изогнутой) поверхности резервуара = 2πrh
= 2 x \(\frac { 22}{7}\) x 2,1 x 4,5 м 2
= 2 x 22 x 0,3 x 4,5 м 2 59,4 м 2
(ii) Общая площадь поверхности резервуара = 2πr(r + h)
= 2 x \(\frac { 22 }{ 7 }\) x 2,1( 2,1 + 4,5) м 2
= 44 x 0,3 x 6,6 м 2 = 87,13 м 2
Пусть фактическая площадь использованной стали равна xm 2
frac { 1 }{ 12 }\) xxm
= \(\frac { x }{ 12 }\)m 2
Площадь используемой стали = x – \(\frac { x }{ 12 }\) m 2
Таким образом, необходимая площадь стали, которая фактически использовалась, равна 95.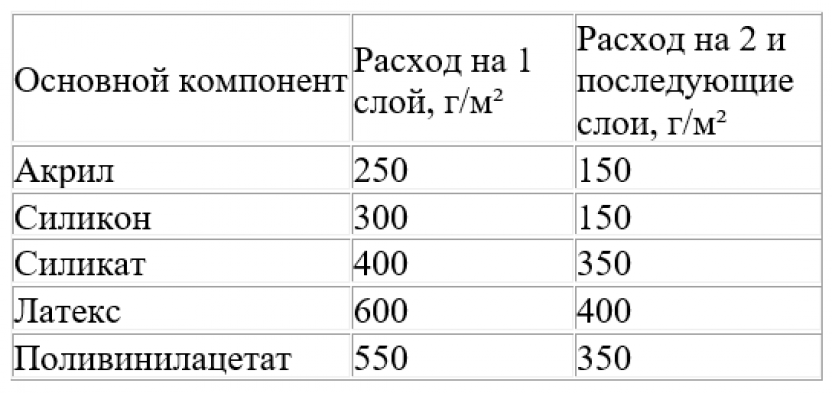 04 м 2 .
04 м 2 .
На рисунке вы видите каркас абажура. Его нужно обтянуть декоративной тканью. Рама имеет диаметр основания 20 см и высоту 30 см. Необходимо оставить запас в 2,5 см для загибания по верху и низу рамы. Найдите, сколько ткани потребуется для покрытия абажура.
Решение:
Абажур имеет форму цилиндра,
где радиус (r) = \(\frac { 20 }{ 2 }\) см = 10 см
и высота = 30 см.
Сверху и снизу рамки необходимо добавить поля по 2,5 см.
∴ Общая высота цилиндра, (h)
= 30 см + 2,5 см + 2,5 см = 35 см x 35 см 2
= 2200 см 2
Таким образом, необходимая площадь ткани = 2200 см для изготовления и декорирования подставки для ручек в форме цилиндра с основанием из картона.Каждый держатель для ручек должен был иметь радиус 3 см и высоту 10,5 см. Видьялая должна была снабжать конкурентов картоном. Если участников было 35, сколько картона нужно было купить для конкурса?
Решение:
Здесь подставки для ручек имеют форму цилиндра.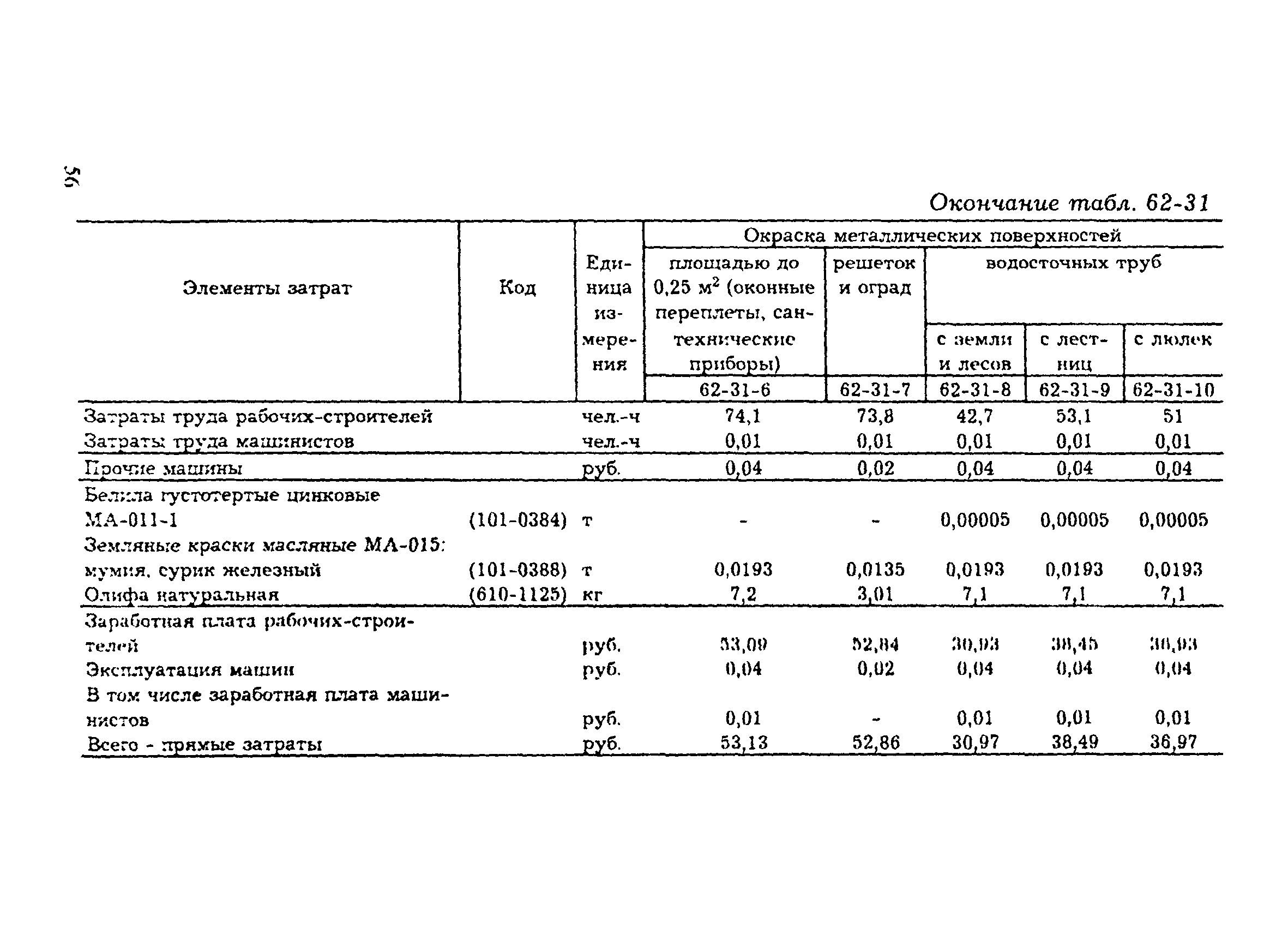
Радиус подставки для ручек (r) = 3 см
Высота подставки для ручек (h) = 10,5 см
Так как подставка для ручек должна быть открыта сверху.
Теперь площадь поверхности держателя для ручек = [Площадь боковой поверхности] + [Площадь основания]
= [2πrh] + [πr 2 ]
∴ Площадь поверхности 35 держателей для ручек
= 35 x \(\frac { 1584 }{ 7 }\) см 2 = 7920 см 2
Таким образом, потребовалось купить 7920 см 2 картона.
NCERT Solutions for Class 9 Math Chapter 13 Площади поверхностей и объемы Ex 13.3
Ex 13.3 Class 9 Math Question 1.
Диаметр основания конуса 10,5 см, а его наклонная высота 10 см. Найдите площадь его криволинейной поверхности.
Решение:
Здесь диаметр основания = 10,5 см
⇒ Радиус (r) = \(\frac { 10,5 }{ 2 }\) см
и высота наклона (l) = 10 см
Площадь криволинейной поверхности конуса = πrl
= \(\frac { 22 }{ 7 }\) x \(\frac { 10,5 }{ 2 }\) x 10 см 2
= 11 x 15 x 1 см 2 = 165 см 2
Пример 13.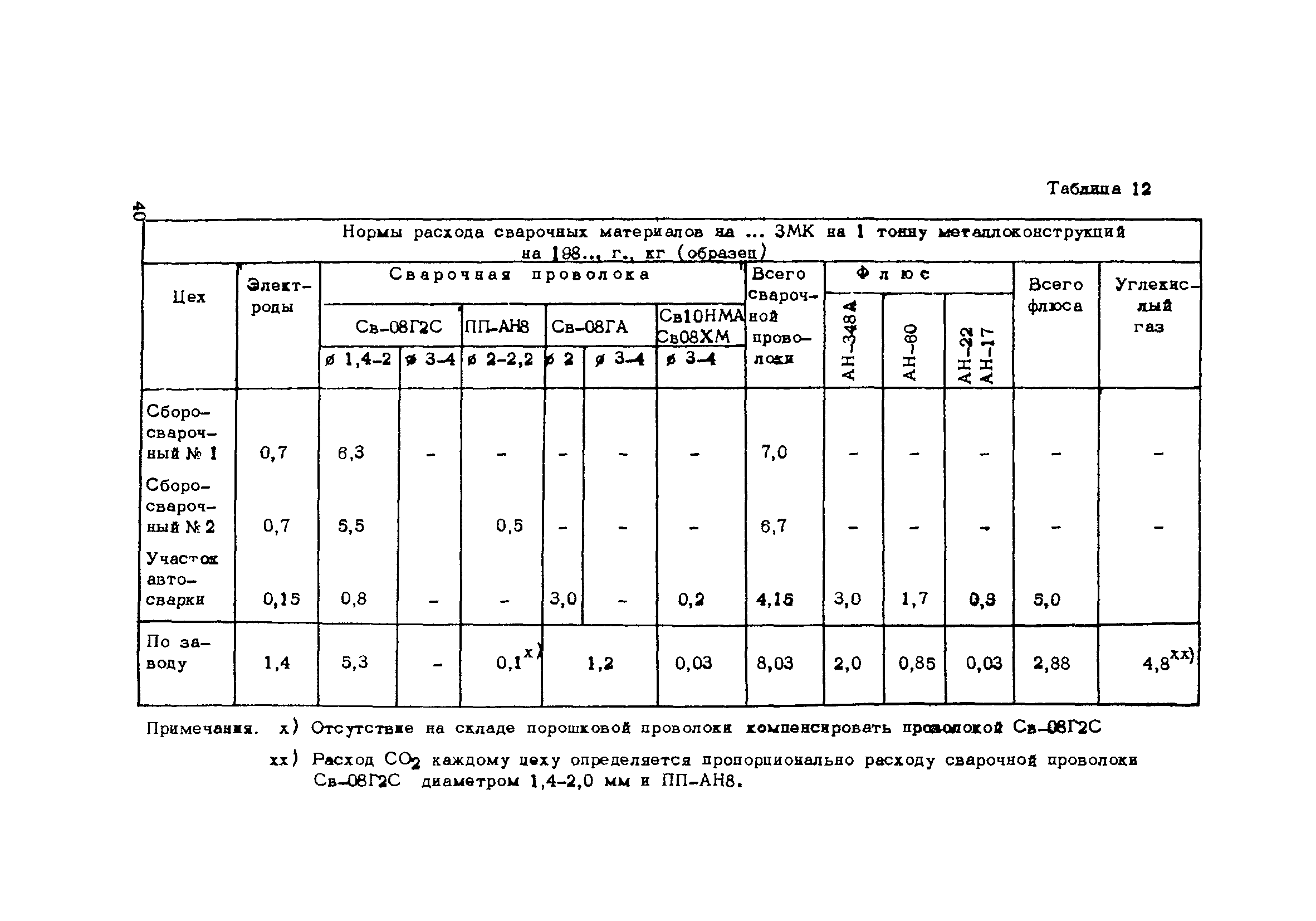 3 9 класс МатематикаВопрос 2.
3 9 класс МатематикаВопрос 2.
Найдите площадь полной поверхности конуса, если его наклонная высота 21 м, а диаметр основания 24 м.
Решение:
Здесь диаметр = 24 м 24
∴ Радиус (r) = \(\frac { 24}{ 2 }\) m = 12 м
и наклонная высота (l) = 21 м
∴ Общая площадь поверхности a конус = πr(r +1)
Упражнение 13.3 Класс 9 МатематикаВопрос 3.
Площадь криволинейной поверхности конуса составляет 308 см², а его наклонная высота составляет 14 см. Найдите
(i) радиус основания и
(ii) общую площадь поверхности конуса.
Решение:
Здесь площадь криволинейной поверхности = πrl = 308 см 2
Наклонная высота (l) = 14 см
(i) Пусть радиус основания равен ‘r’ см
∴ πrl = 308 ⇒ \( \frac { 22 }{ 7 }\) xrx 14 = 308
r = \(\frac { 308\times 7 }{ 22\times 14 }\) = 7 см
Таким образом, радиус конуса равен 7 см
( ii) Площадь основания = πr 2 = \(\frac { 22 }{ 7 }\) x 7 2 см 2 Пример 13. (ii) Площадь криволинейной поверхности конуса = πrl Пример 13.3 Класс 9 МатематикаВопрос 5. радиус основания 6м? Предположим, что дополнительная длина материала, которая потребуется для сшивания полей и потерь при раскрое, составляет примерно 20 см.{ 2 } }\) m 8 2 Пример 13.3, класс 9, математика, вопрос 6. = рупий. 384,336 = рупий. 384,34 (прибл.) Упр. 13.4 Класс 9 Математика Вопрос 1. (ii) Здесь r = 5,6 см (iii) Здесь r90 площадь сферы = 4πr 2 Упр. (ii) Здесь диаметр = 21 см (iii) Здесь диаметр = 3,5 м Упр. Найдите площадь полной поверхности полусферы радиусом 10 см. (Используйте π = 3,14) Упр. 13.4 Класс 9 МатематикаВопрос 4. Case II: когда радиус (R 2 ) = 14 см 2 Пример 13. Таким образом, искомый радиус сферы равен 3.5 см. Таким образом, требуемое соотношение = 1 : 16. ∴ Внешний радиус (R) [5,00 + 0251 см = 5,25 см 9 класс МатематикаВопрос 9. Решение: (ii) Для правильного кругового цилиндра Пример 13.5 Класс 9 Математика Вопрос 1. Пример 13.5 Класс 9 МатематикаВопрос 2. Упр. 13.5 Класс 9 МатематикаВопрос 3. Упражнение 13.5 Класс 9 МатематикаВопрос 4. Упр. 13. 6 емкость бака = 50000 литров Пр 13.5 Класс 9 МатематикаВопрос 6. ∴ Максимальное количество деревянных ящиков = 10667. Таким образом, искомое отношение = 4 : 1 Длина (l) = 2 км = 2000 м Пример 13.6 9 класс Математика Вопрос 1. Упр. 13.6 Класс 9 МатематикаВопрос 2. Упр. 13.6 Класс 9 МатематикаВопрос 3. (ii) Для цилиндрической упаковки Пример 13. Таким образом, радиус цилиндра = 3 см (ii) Объем цилиндра = πr 2 ч ∴ Площадь внутренней криволинейной поверхности сосуда (ii) Пусть r – радиус основания цилиндрического сосуда. Пусть r m — радиус основания сосуда. Теперь общая площадь поверхности цилиндрического сосуда Таким образом, необходимый металлический лист = 0,4708 м 2 . ∴ Радиус карандаша (R) = \(\frac { 7 } { 20 }\) см ∴ Объем дерева = [Объем карандаша] – [Объем графита] Таким образом, больнице необходимо ежедневно готовить 38,5 литров супа для 250 пациентов. Упр. 13.7 Класс 9 Математика Вопрос 1. Таким образом, необходимая вместимость конического сосуда равна 1.232 литра. ∴ Вместимость конического сосуда Таким образом, необходимая вместимость конического сосуда равна \(\frac { 11 }{ 35 }\) литров. Таким образом, необходимый радиус основания равен 10 см. Диаметр = 2 x радиус. Таким образом, емкость конической ямы составляет 38,5 кл. Упр. 13.7 Класс 9 МатематикаВопрос 6. Таким образом, необходимая высота 48 см. (ii) Пусть наклонная высота равна l см. (iii) Площадь криволинейной поверхности конуса = πrl Таким образом, мы имеем радиус основания образовавшегося конуса (r) = 5 см Таким образом, требуемое соотношение равно 5 : 12. Таким образом, требуемый объем = 86,625 м 3 Таким образом, необходимая площадь полотна составляет 99,825 м 2 . Таким образом, требуемый объем = 1437\(\frac { 1 }{ 3 }\)см 3 Таким образом, требуемый объем равен 1,05 м 3 (прибл.) Упр. Таким образом, отображаемое количество воды = 0,004851 м 3 . Плотность металла = 8,9 г на см 3 Таким образом, масса шара равна 345,39 г (приблизительно) Упражнение 13.8, класс 9, математика, вопрос 4. Упражнение 13.8 Класс 9 МатематикаВопрос 5. ∴ Внешний радиус (R) = 1 м + 0.01 м = 1,01 м Таким образом, требуемый объем используемого железа Упр. 2 Упражнение 13.8 Класс 9 МатематикаВопрос 8. Теперь объем воздуха внутри купола = объем полусферы Таким образом, требуемый объем воздуха внутри купола составляет 523,9 м 3 (приблизительно). Следовательно, радиус новой сферы равен 3r. Таким образом, S : S’ = 1 : 9 = 22,45833 мм 3 Решение: Решение: Следовательно, стоимость Требуется покраска = 1000 руб. 2784.25 Теперь уменьшите процент В изогнутой площади 60016 Мы надеемся, что решения NCERT для математики класса 9 Глава 13 Площади поверхности и объемы Пример 13. Стены и потолок несложно отделать так, чтобы краска не облезла, а поверхность долгие годы выглядела безупречно. Строители решают эту проблему с помощью инновационных составов, которые наносят на поверхности перед покраской, шпаклевкой и другими отделочными работами. применяются на всех этапах строительства и ремонта домов и квартир; ими обрабатывают поверхности из различных материалов, стены и полы. Этот важный технологический этап подготавливает основу для дальнейшей работы и выполняет следующие функции: Перед покупкой грунтовки необходимо правильно рассчитать необходимое количество материала. При проектировании следует учитывать ряд факторов, влияющих на количество потребляемой грунтовки . Оценив все факторы, можно рассчитать расход грунта на 1 м2 площади обрабатываемой поверхности. К основным нормам рекомендуется прибавить 10%, затем полученное число умножить на площадь стен или потолка. В результате получается количество литров, необходимое для работы. В продаже есть упаковки разного объема (самая распространенная – объем 5 литров). Сухие смеси продаются по весу, указанному в кг. Когда вы разделите общее количество литров на 5, вы получите количество канистр, которые вам нужно купить. При выборе грунтовки следует учитывать, что для разных видов работ и материалов основы используются разные составы.Есть решения для наружных и внутренних работ, а также универсальные продукты. Грунтовочные смеси различаются по типу связующего и дополнительным полезным добавкам, придающим изделиям особые свойства или требуемые характеристики. Грунтовки бывают следующих типов: Акриловые грунтовки универсальны. Они совместимы со многими отделочными материалами, нетоксичны и не имеют резкого запаха, что делает их пригодными для внутренних работ. Они также используются для отделки фасадов. Эти продукты подходят для всех оснований, кроме металла. На рынке строительной химии жесткая конкуренция, компании-производители борются за качество и лояльность покупателей. Российские бренды не уступают мировым лидерам по популярности и ассортименту, инновационным разработкам и техническим характеристикам продукции. Среди популярных продуктов для грунтования – российская марка «Нортекс-грунтовка». Этот состав на водной основе идеально подходит для использования с акриловыми красками и наносится на деревянные, кирпичные, гипсовые и каменные стены и полы.При отверждении укрепляет и увеличивает адгезию основного материала. Несомненными достоинствами смеси являются: Известный российскому покупателю бренд «Оптимист» выпускает универсальную композицию акрилового латекса с акриловым песком, бетоноконтакт, грунтовки глубокого проникновения, а также богатую палитру разнообразных красок.Широкий ассортимент и отличное качество позволяют продукции «Оптимист» занимать одну из лидирующих позиций на рынке строительной химии. Грунты этой марки проходят серьезные испытания на стендах в лабораториях предприятия, что позволяет контролировать качество продукции на всех этапах производства. Составы этой фирмы экологичны и универсальны, а также доступны по цене.Благодаря этим преимуществам они получают отличные отзывы от строителей и пользуются большой популярностью. Грунтовки «Старатели» зарекомендовали себя на рынке как качественные смеси с дополнительными полезными свойствами. Грунтовки этой марки можно использовать как внутри помещений, так и снаружи (для фасадных работ). Состав глубоко проникает в структуру основания, укрепляет ее, придавая материалу прочность и обеспыливая его. Гладкая водоотталкивающая пленка защищает поверхность даже во влажных условиях. Быстрое высыхание экономит время на ремонт. Антисептические свойства позволяют получить отличные результаты при обработке древесины. Также возможно нанесение его на подложки из других материалов. Покупатели отмечают отличные технические характеристики товара, хорошее соотношение цены и качества. Все эти средства можно найти в любом хозяйственном магазине или гипермаркете. Они расфасованы в тару разного объема, снабжены подробной инструкцией и полностью сертифицированы. Если все расчеты произведены, а грунт куплен, важно обработать основание, чтобы краска легла ровно и красиво, а покрытие надолго сохранило безупречный вид. Эту задачу можно решить, выполняя работы строго по технологии, а также с учетом рекомендаций опытных специалистов в данной области . При соблюдении всех рекомендаций загрунтованная поверхность будет прочной и защищенной от вредоносной микрофлоры, а краска, декоративная штукатурка, обои или лак лягут ровным, аккуратным слоем и долго будут прекрасно выглядеть. В следующем видео вы найдете секреты выбора материала и профессиональные советы по идеальной грунтовке. При проведении любых ремонтно-отделочных работ важное место занимает оштукатуривание поверхностей. Это делается для того, чтобы обеспечить ровную и гладкую поверхность. Для этого требуется смесь извести, песка и цемента.Одной из самых популярных в этом направлении является гипсовая штукатурка Rotband, позволяющая добиться высокого качества работы, не затрачивая лишних усилий. Rotband производится немецкой компанией Knauf. Его состав основан на гипсе, смешанном с минеральными добавками. Именно он является связующим. Перед смешиванием все компоненты измельчаются, что увеличивает площадь контакта и повышает сцепление как самих компонентов, так и материала с основой. После создания производимая штукатурная смесь Rotband произвела настоящий фурор на рынке строительных материалов. Обычные смеси были на основе цемента, тогда как Rotband изготавливался в основном из гипса. Вся продукция этой компании проходит серьезные лабораторные исследования, работы выполняются профессиональными специалистами на современном оборудовании, что гарантирует высокое качество товаров, которые должны быть сертифицированы и соответствовать всем стандартам качества. Пластырь экологически чистый, не содержит вредных химических веществ и не представляет вреда для здоровья потребителей. Если говорить о технических характеристиках, то в первую очередь следует отметить расход. В среднем она составляет около 5 килограммов на квадратный метр при толщине слоя 10 миллиметров. На 30 килограммов сухого состава потребуется около 20 литров воды. Пластырь довольно быстро затвердевает, поэтому рекомендуется использовать его максимально в течение получаса . Максимальная толщина слоя штукатурки: наносимая на стены — до 50 миллиметров, на потолок — до 15 миллиметров. Особенностью данного вида штукатурной смеси является то, что она абсолютно универсальна и не требует дальнейшей обработки, создавая ровную поверхность … В отличие от составов на основе цемента, сохнет не месяц, а всего 7 дней .Смесь способна пропускать воздух, что помогает избавиться от сырости в помещении, исключает появление грибка и плесени. Кроме того, он обладает водоудерживающими свойствами, что предохраняет готовый материал от трещин и расслаивания. Специалисты отмечают, что со штукатурной смесью этой марки могут работать как профессионалы, так и новички. В упаковке находится подробная инструкция, следуя которой вы сможете выполнить работу качественно, грамотно и без ошибок. Rotband имеет отличные отзывы потребителей, но есть некоторые нюансы в ее использовании. Во-первых, продукт находится в средней ценовой категории, а значит, на рынке есть гораздо более дешевые материалы. Кроме того, при нарушении технологии использования состав может давать небольшую усадку при высыхании. .Их можно использовать для работы с большим количеством поверхностей из бетона, газобетона, цемента, гипсокартона и других. Подходит для использования на кирпичной кладке. Материалы используются исключительно для внутренней отделки, наружные работы рекомендуется выполнять с использованием фасадных штукатурок, которые также имеются в наличии у производителя. После высыхания штукатурки на ровном основании можно клеить обои или наносить лакокрасочные составы. Перед приобретением смеси необходимо произвести максимально точный расчет ее расхода. Если штукатурная смесь наносится слоем в 1 см, ее расход должен составлять примерно от 8 до 10 килограммов на квадратный метр. При заданной толщине слоя упаковки весом 30 килограммов должно хватить примерно на 3 квадратных метра. Необходимо учитывать, что перед работой поверхность необходимо предварительно обработать, обезжирить, очистить от загрязнений и серьезных неровностей. Это поможет поддерживать расход смеси в заявленных пределах и не приведет к ее чрезмерному использованию. Применение грунтовки обязательно. После грунтовки сохнет в течение 12 часов . Если смесь нанести слоем в 1,5 сантиметра, расход на квадратный метр увеличится и составит уже около 12-15 килограммов. Специалисты рекомендуют наносить состав слоем около 10 миллиметров, но это необязательное условие. При необходимости толщину материала можно увеличить до 15 миллиметров на потолках и до 50 – на стенах. В случае, когда этого недостаточно, можно нанести еще один слой, но это делается после высыхания первого, который затем также необходимо прогрунтовать для повышения адгезии материалов. В первую очередь нужно подготовить инструменты, которые потребуются для дальнейшей работы. После этого можно приступать к подготовке поверхности, которую необходимо тщательно очистить и обезжирить, а также освободить от предыдущего покрытия во избежание появления отслоений и трещин. Одним из важнейших этапов подготовки фундамента является установка маяков. Профили маячков продаются в строительных магазинах. Они бывают размером 6 и 10 миллиметров, причем последний считается самым жестким. Маяки должны быть ровными и не иметь визуальных дефектов. Маяки нужно вырезать, определив их необходимую высоту, а затем вдавить в штукатурку на расстоянии 130-180 сантиметров друг от друга. Их выравнивают в одной плоскости, а затем в соответствии с ними распределяют смесь. Необходимо отремонтировать зазор между маяками и стеной. Количество элементов рассчитывается исходя из длины стены. О том, как правильно разводить состав Ротбанд, можно узнать из инструкции, которая в обязательном порядке находится на каждой упаковке со штукатуркой. Важна температура жидкости, так как если она будет слишком горячей, раствор схватится намного быстрее и вы можете не успеть разбить комочки, что негативно скажется на дальнейшей работе. Очень важно наносить состав с приличной скоростью, так как он довольно быстро начинает высыхать. Специалисты рекомендуют не разбавлять смесь в больших количествах.Для лучшего результата перемешивания можно использовать как строительный миксер, так и дрель со специальной насадкой. Консистенция гипса должна быть похожа на густую сметану. Для улучшения качеств состава после замешивания его нужно дать настояться 10 минут, затем снова перемешать, и только после этого приступать к работе. Рекомендуется обратить внимание, что в процессе оштукатуривания поверхностей его компоненты нельзя добавлять в состав, требуется готовить новый раствор. Наносить следует с помощью длинного и широкого шпателя. Необходимое количество смеси наносится в соответствии с маяками. Обрабатывать поверхность нужно, двигаясь снизу вверх .… Штукатурка может осесть под собственным весом, поэтому ее следует вытаскивать несколько раз. При необходимости создания рельефного слоя в работе используется строительная гребенка.Этот слой необходимо просушить, загрунтовать и еще раз нанести поверх него штукатурную смесь вторым слоем. Если основания выполнены из пенополистирола или цемента, то они требуют обязательной обработки, а нанесение штукатурки производить на армирующую сетку. Его также необходимо правильно установить. Делается это с помощью клея ПВА или тонкого слоя гипса, на который приклеивается элемент. По прошествии почти часа состав успел сильно затвердеть, но не успел высохнуть. В этот период можно приступать к выравниванию поверхности. С помощью металлической рейки сглаживают неровности и удаляют дефекты поверхности. Ямки и углубления также заполняются штукатурной смесью. На такой слой можно укладывать плитку. Если требуется поклейка обоев или использование лакокрасочных материалов, работа на этом не заканчивается.В этом случае нужно подождать еще 15 минут, а затем протереть штукатурку губкой или специальной теркой. Эту процедуру проводят после смачивания слоя штукатурной смеси небольшим количеством воды, которая впитается в него. Затем можно поклеить обои. Однако, если их цвета слишком светлые, рекомендуется покрыть штукатурку финишным составом. Это предотвратит просвечивание смеси сквозь полотна. При покраске стен, а также при отделке тонкими обоями базовый слой должен быть идеально гладким и ровным.С этой задачей легко справляется шпатлевка. Именно она устраняет мельчайшие дефекты и трещины, кроме того, использование этого состава способствует улучшению сцепления между основанием и отделочными материалами. Использование шпаклевки позволяет сократить расход клея для обоев и лакокрасочных материалов, а также позволяет предотвратить возможное осыпание штукатурки в дальнейшем. Время высыхания штукатурной смеси зависит от ряда факторов. Если необходимо максимально ускорить ее, целесообразно будет заранее предусмотреть хорошую вентиляцию в помещении, в котором проводятся работы. Нельзя забывать, что перед нанесением состава поверхность необходимо предварительно обработать грунтовкой . Полное высыхание штукатурки Rotband занимает около недели. Если слой очень толстый, а также в случае, когда их несколько, время высыхания может увеличиться до 14 дней. Не используйте для работы загрязненные инструменты и неочищенные емкости. После нанесения каждого слоя все аксессуары необходимо промыть под проточной чистой водой. Что касается условий работы, то в первую очередь необходимо соблюдать температурный режим. При этом температура в помещении, где проводится отделка, должна быть от +5 до +30 градусов, при этом оптимальной считается +25. При превышении этого показателя есть угроза того, что состав растрескается и начнет отваливаться с поверхности.Если, наоборот, температура ниже, раствор будет сохнуть гораздо дольше, чем должен. А также немаловажным фактором, влияющим на высыхание поверхности, является влажность в помещении. Как нетрудно догадаться, чем он больше, тем больше времени потребуется для полного высыхания покрытия .
= 22 x 7 см 2 = 154 см 2
и изогнутая поверхность площадь = 308 см 2 [Дано]
∴ Общая площадь поверхности конуса
= [Площадь криволинейной поверхности] + [Площадь основания] = 308 см 2 + 154 см 2
= 462 см 8  { 2 } }\) m = \(\sqrt { 576+100 }\) m = \(\sqrt { 676 }\) m = 26 м
{ 2 } }\) m = \(\sqrt { 576+100 }\) m = \(\sqrt { 676 }\) m = 26 м
Таким образом, необходимая наклонная высота палатки составляет 26 м.
∴ Требуемая площадь брезента
= \(\sqrt { 36+64 }\) m
= \(\sqrt { 100 }\)m = 10 м
Теперь площадь криволинейной поверхности = πrl
= 3,14 x 6 x 10 м 2
= \(\frac { 314 }{ 100 }\) x 6 x 10 м 2 = 1884 м 2
Таким образом, площадь брезента, необходимая для изготовления палатки = 188,4 м
Пусть длина брезента равна L м
Длина x Ширина = 188,4
⇒ L x 3 = 188,4 ⇒ L = \(\frac { 188,4 }{ 3 }\) = 62,8
Дополнительная длина брезента, необходимая для полей = 20 см = \(\frac {20}{100}\)m = 0. 2 м
2 м
Таким образом, необходимая общая длина брезента = 62,8 м + 0,2 м = 63 м
Наклонная высота и диаметр основания конической гробницы составляют 25 м и 14 м соответственно. Найти стоимость побелки его криволинейной поверхности из расчета 210 руб. за 100 м 2 .
Решение:
Здесь радиус основания (r) = \(\frac { 14 }{ 2 }\) m = 7 м
Наклонная высота (l) = 25 м
∴ Площадь криволинейной поверхности = πrl
= \(\frac { 22 }{ 7 }\) x 7 x 25 м 2 = 550 м 2
Стоимость побелки 100 м 2 площади = руб.{ 2 } }\)см
= \(\sqrt { 576+49 }\)см = \(\sqrt { 625 }\) см = 25 см
∴Площадь боковой поверхности = πrl = \(\frac { 22} { 7 }\) x 7 x 25 см 2 = 550 см 2
∴ Площадь боковой поверхности 10 крышек = 10 x 550 см 2
= 5500 см 2
лист = 5500 см 2 
Автобусная остановка отгораживает оставшуюся часть дороги с помощью 50 полых конусов из переработанного картона.Каждый конус имеет диаметр основания 40 см и высоту 1 м. Если нужно покрасить внешнюю сторону каждого из конусов, а стоимость покраски составляет 12 ₹ за м², сколько будет стоить покраска всех этих конусов? (Используйте π = 3,14 и возьмите \( \sqrt{104} \) = 1,02)
Решение:
Диаметр основания = 40 см
Таким образом, необходимая стоимость покраски составляет рупий. 384,34 (прибл.). Решения NCERT для математики класса 9 Глава 13 Площади поверхности и объемы Пример 13.4
Найдите площадь поверхности сферы радиусом
(i) 10,5 см
(ii) 5,6 см
(iii) 14 см
Решение:
(i) Здесь r = 10,5 см
Площадь поверхности сферы = 4πr 2
Площадь поверхности сферы = 4πr 2  13.4 Класс 9 МатематикаВопрос 2.
13.4 Класс 9 МатематикаВопрос 2.
Найдите площадь поверхности сферы диаметром
(i) 14 см
(ii) 21 см
(iii) 3.5 м
Решение:
(i) Здесь диаметр = 14 см
Решение:
Здесь радиус (r) = 10 см
Общая площадь поверхности полушария = 3πr 2
= 3 x 3,14 x 10 x 10 см 2 = 942 см 2
Радиус сферического воздушного шара увеличивается с 7 см до 14 см по мере накачивания в него воздуха. Найдите отношение площадей поверхности шара в обоих случаях.
Решение:
Найдите отношение площадей поверхности шара в двух случаях.
BSD Случай I: Когда радиус (r 1 ) = 7 см
Площадь поверхности = 4πr 1 2 = 4 x \(\frac { 22 }{ 7 }\) x (7) см 2
= 4 x 22 x 7 см 2 = 616 см 2
площадь поверхности = 4πR 2 2 = 4 х \(\frac { 22 }{ 7 }\) x (14) 2 см 2
= 4 x 22 x 14 x 2 см 2 = 2464 см 2
∴ Искомое отношение = \( \frac { 616 }{ 2464 }\) = \(\ frac { 1 }{ 4 }\) или 1 : 4 4 Математика 9 классВопрос 5.
4 Математика 9 классВопрос 5.
Полусферическая чаша из латуни имеет внутренний диаметр 10,5см. Найдите стоимость лужения его изнутри из расчета 16 ₹ за 100 см².
Решение:
Внутренний диаметр полусферической чаши = 10,5 см
Найдите радиус сферы, площадь поверхности которой равна 154 см².
Решение:
Пусть радиус сферы равен r см.
Площадь поверхности сферы = 4πr 2
∴ 4πr 2 = 154
Диаметр Луны составляет примерно одну четвертую диаметра Земли. Найдите отношение площадей их поверхностей.
Решение:
Пусть радиус Земли равен r.
∴ Радиус луны = \(\frac { r }{ 4 }\)
Площадь поверхности сферы = 4πr 2
Так как Земля, как и Луна, считается сферой.
Площадь поверхности земли = 4πr 2 
Чаша полусферической формы изготовлена из стали толщиной 0,25 см. Внутренний радиус чаши 5 см. Найдите площадь внешней криволинейной поверхности чаши.
Решение:
Внутренний радиус (r) = 5 см
Толщина = 0,25 см
Прямой круговой цилиндр окружает сферу радиусом r (см. рисунок). Найдите
(i) площадь поверхности сферы,
(ii) площадь криволинейной поверхности цилиндра,
(iii) отношение площадей, полученных в (i) и (ii).
(i) Для сферы радиус = r
∴ Площадь поверхности сферы = 4πR 2
Радиус цилиндра = радиус сферы
∴ Радиус цилиндра = r
Высота цилиндра = Диаметр сферы
∴ Высота цилиндра (h) 2r
Поскольку площадь криволинейной поверхности цилиндра = 2πrh
= 2πr(2r) = 4πr 2 Решения NCERT для математики класса 9 Глава 13 Площади поверхности и объемы Пример 13.
 5
5
Размеры спичечного коробка 4 см x 2,5 см x 1,5 см. Каков будет объем пакета, содержащего 12 таких коробок?
Решение:
Так как спичечный коробок имеет форму прямоугольного параллелепипеда.
Здесь длина (l) = 4 см, ширина (b) = 2,5 см
и высота (h) = 1,5 см
∴ Объем спичечного коробка = lxbxh
= 4 x 25 x 1,5 см 3
= 4 x \(\frac { 25 }{ 10 }\) x \(\frac { 15 }{ 10 }\)см 3
= 15 см 3
⇒ Объем 12 таких коробок = 12 x 15 см 3
= 180 см 3
Прямоугольный резервуар для воды имеет длину 6 м, ширину 5 м и глубину 4,5 м. Сколько литров воды он может вместить? ( 1 м 3 = 1000L)
Решение:
Длина (l) = 6 м, ширина (h) = 5 м и
глубина (h) = 4,5 м
∴ Вместимость = lxbxh = 6 x 5 x 4,5 м 3
= 6 x 5 x \(\frac { 45 }{ 10 }\)m = 3 x 45 м 3 = 135 м 3
∵ 1 м 3 = 1000 литров 2 0 9 5 м
⇒ 0 1 = 135000 литров
∴ Необходимое количество воды в баке = 135000 литров.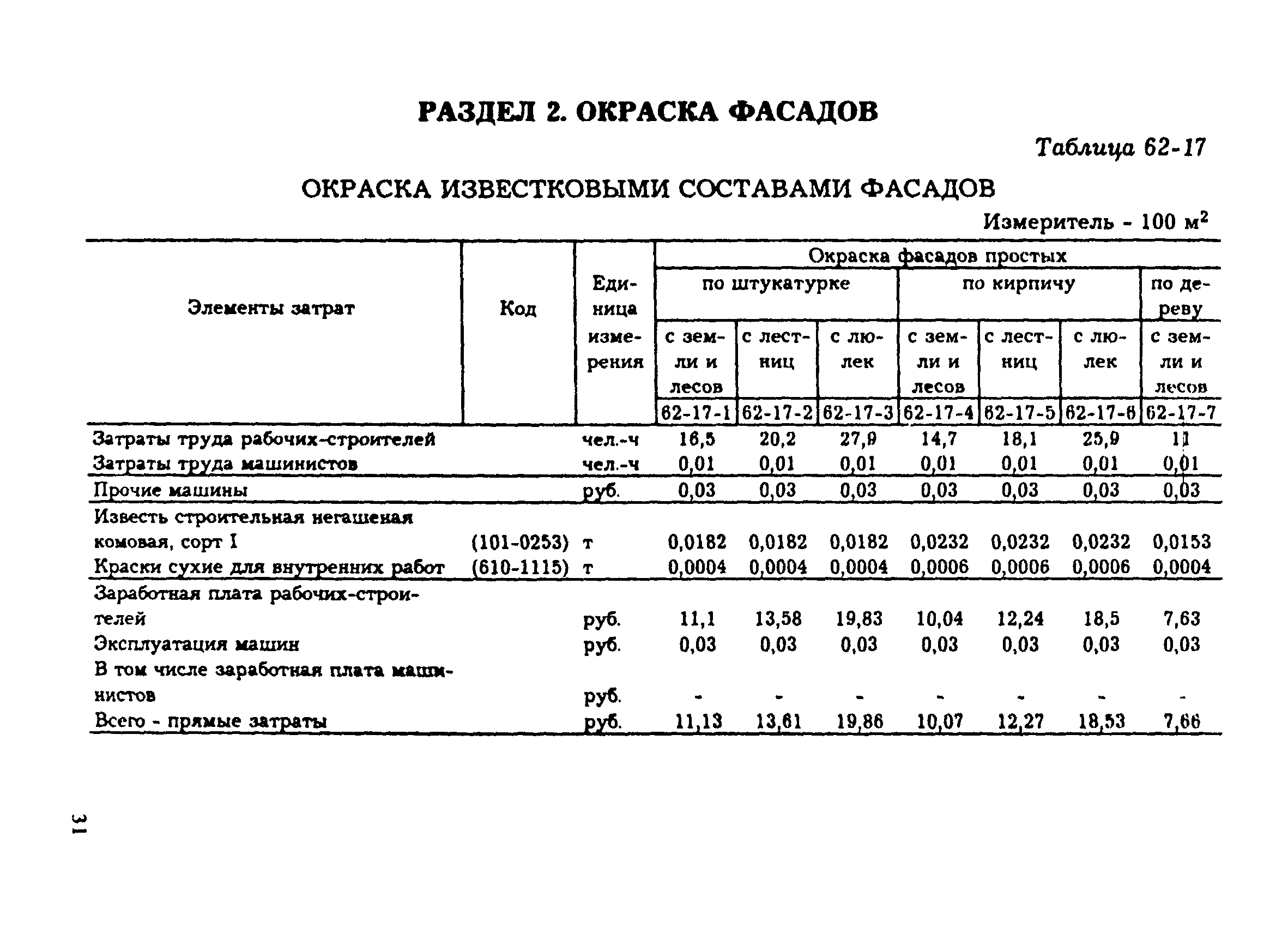
Сосуд прямоугольной формы имеет длину 10 м и ширину 8 м. Какой высоты его надо сделать, чтобы вместить 380 кубометров жидкости?
Решение:
Длина (l) = 10 м, ширина (b) = S м
Объем (V) = 380 м 3
Пусть высота прямоугольного сосуда равна «h».
Пр. 13.5 Класс 9 МатематикаОбъем кубовидного сосуда = lxbxh
⇒ 10 x 8 xhm 3 = 80h m 3
⇒ 80h = 380
⇒ h = 7.} } frac { 380 м
Таким образом, необходимая высота судна = 4.75 м
Найдите стоимость рытья прямоугольного котлована длиной 8 м, шириной 6 м и глубиной 3 м из расчета 30 ₹ за м³.
Решение:
Длина (i) = 8 м
Ширина (b) = 6 м
Глубина (h) = 3 м
∴ Объем прямоугольной ямы = lxbxh
= 8 x 6 x 3 м 3 = 144 м 3
Отсюда стоимость рытья котлована = рупий. (144 x 30)
= рупий. 4320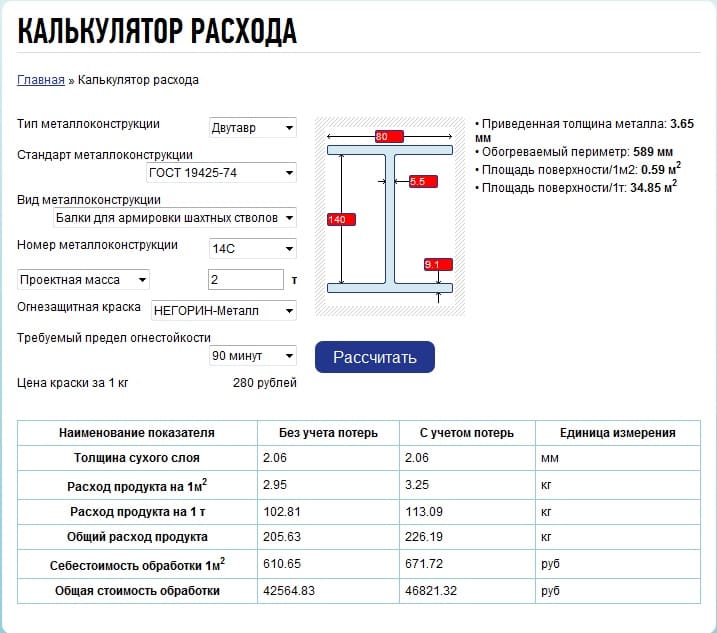 5 Класс 9 МатематикаВопрос 5.
5 Класс 9 МатематикаВопрос 5.
Емкость прямоугольного резервуара составляет 50000 литров воды.Найдите ширину резервуара, если его длина и глубина соответственно 2,5 м и 10 м.
Решение:
ira Длина резервуара (l) = 2,5 м
Глубина резервуара (h) = 10 м
Пусть ширина резервуара равна b м.
∴ Объем (емкость) бака = lxbxh
= 2,5 xbx 10 м 3
= \(\frac { 25}{ 10 }\) x 10 x bm 3
= 25bm 3
= 50 м 3 [ ∵ 1000 литров = 1 м 3 ]
∴ 25b = 50 ⇒ b = \(\frac { 50 }{ 25 }\) = 2
Таким образом, ширина бака = 2 м
Деревне с населением 4000 человек требуется 150 литров воды на душу населения в день. Он имеет резервуар размером 20 м х 15 м х 6 м. На сколько дней хватит воды в этом баке?
Решение:
fcWra Длина резервуара (l) = 20 м
Ширина резервуара (b) = 15 м
Высота резервуара (h) = 6 м
∴ Объем резервуара = lxbxh
= 20 x 15 x 6 м 3 = 1800 м 3
Т. к., 1 м 3 = 1000 литров
к., 1 м 3 = 1000 литров
∴ Емкость бака = 1800 х 1000 литров = 1800000 литров
Так как на душу населения требуется 150 литров воды в день.
∴ Количество воды, необходимое 4000 человек в день = 150 x 4000 литров
Пусть необходимое количество дней равно x
∴ 4000 x 150 xx = 1800000
⇒ x = \(\frac { 1800000 }{ 4000\times 150 } \) = 3
Таким образом, требуемое количество дней равно 3.
Спуск имеет размеры 40 м х 25 м х 10 м. Найдите максимальное количество деревянных ящиков размером 15 м х 125 м х 0,5 м каждый, которые можно хранить в нише.
Решение:
Объем спуска = 40 x 25 x 10 м 3
Объем деревянного ящика = 1.5 x 1,25 x 0,5 м 3
Твердый куб со стороной 12 см разделен на восемь кубов одинакового объема. Какой будет сторона нового куба? Кроме того, найдите отношение между их поверхностями.
Решение:
Сторона данного куба = 12 см
Объем данного куба = (сторона) 3 = (12) 3 см 3
Пусть сторона нового куба равна n
∴ Объем новый кубик = n 3
⇒ Объем 8 новых кубиков = 8n 3
Согласно вопросу,
8n 3 = (12) 3 = 12 x 12 x 12 0
0 = 12 x 12 x 12 0
0 0 (\frac { 12\times 12\times 12}{ 8 }\) = 6 x 6 x 6
⇒ n 3 = 6 3
⇒ n = 6
Таким образом, искомая сторона нового куба равна 6 см.
Теперь площадь поверхности данного куба = 6 x (сторона) 2 = 6 x 12 2 см 2 = 6 x 12 x 12 см 2
Площадь поверхности нового куба = 6 x 6 2 см 2
= 6 x 6 x 6 см 2
Теперь,
Решение:
Воду, текущую в реке, можно представить в виде прямоугольного параллелепипеда.
Ширина (b) = 40 м,
глубина (h) = 3 м
∴ Объем воды (объем образованного кубоида) = lxbxh
= 2000 x 40 x 3 м 3
Теперь, объем воды, протекающий за 1 час (60 минут) = 2000 x 40 x 3 м 3
Объем воды, который упадет за 1 минуту
= [2000 x 40 x 3] + 60 м 3
= 4000 м 3 Решения NCERT для математики класса 9 Глава 13 Площади поверхности и объемы Пример 13.6
Окружность основания цилиндрического сосуда 132 см, высота 25 см. Сколько литров воды он может вместить? (1000 см³ = 1 л.)
Решение:
Пусть радиус основания цилиндрического сосуда равен r см.
∴ Окружность основания = 2πr
⇒ 2πr = 132 [Диаметр = 132 см, (дано)]
= 2 x \(\frac { 22 }{ 7 }\) xr = 132
⇒ r = \(\frac { 132 x 7 }{ 2 x 22 }\) см = 21 см
Так как высота сосуда (h) = 25 см
Объем сосуда (h) = πr 2 h
= \(\frac { 22 }{ 7 }\) x (21) 2 x 25 см 3
= \(\frac { 22 }{ 7 }\) x 21 x 21 x 25 см 3
= 22 x 3 x 21 x 25 CM 3
= 34650 см
= 34650 см
= 34650 см 3
∵ Capaoty судна = объем VSEL
∴ емкость цилиндрического сосуда = 34650 см 3
с, с тех пор, 1000 см 3 = 1 литр
⇒ 34650 см 3 = \(\frac { 34650 }{ 1000 }\) литров = 34.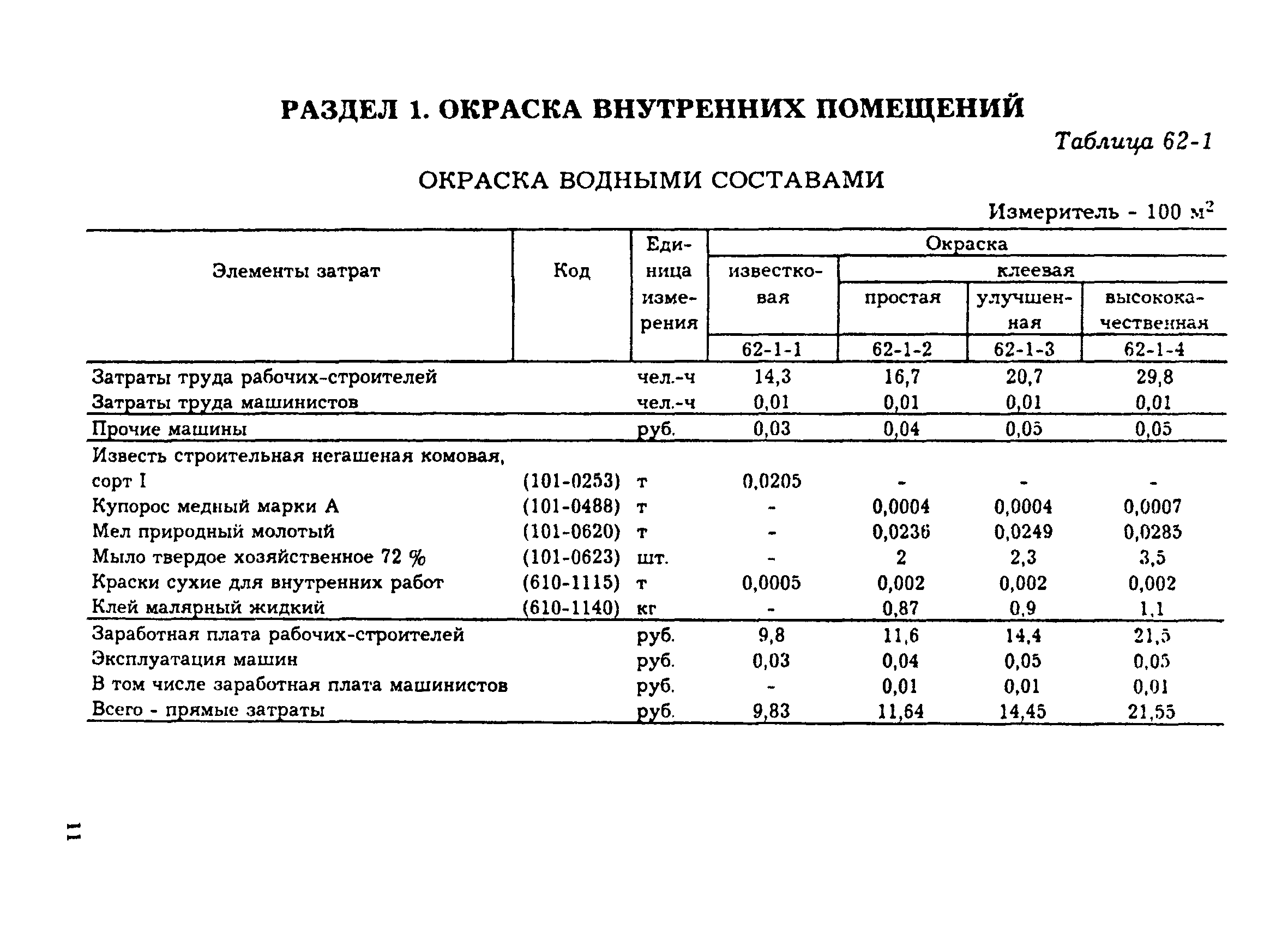 65 литров
65 литров
Таким образом, сосуд вмещает 34,65 литра воды.
Внутренний диаметр цилиндрической деревянной трубы составляет 24 см, а наружный диаметр — 28 см. Длина трубы 35см. Найдите массу трубы, если 1 см3 дерева имеет массу 0,6 г.
Решение:
Внутренний диаметр цилиндрической трубы = 24 см
⇒ Внутренний радиус трубы (r) = \(\frac { 24 }{ 2 }\)см = 12 см
Внешний диаметр трубы = 28 см
Внешний радиус длины трубы (R) = 14 см
Длина трубы (h) = 35 см
∴ Количество древесины в трубе = Внешний объем – Внутренний объем
= πR 2 ч – πr 2 ч
= πh ( R + r) (R – r)
[∵ a2 – b2 = (a + b)(a – b)]
= \(\frac { 22 }{ 7 }\) x 35 x (14+12) x (14 – 12)см 3
=22 x 5 x 26 x 2 см 3
Масса древесины в трубе = (Масса древесины в 1 см 3 древесины) x (Объем древесины в трубе труба)
= (0.6г) x (22 x 5 x 26 x 2)см 3
= \(\frac { 6}{10}\) x 22 x 10 x 26 г = 3432 г
= \(\frac { 3432 }{ 1000 }\) кг = 3,432 кг [∵ 1000 г = 1 кг]
Таким образом, требуемая масса трубы составляет 3,432 кг.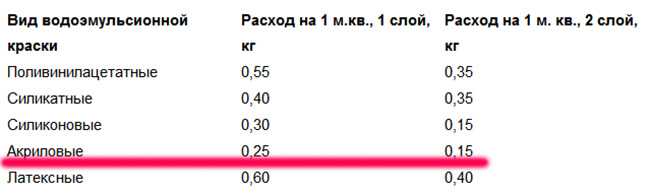
Безалкогольный напиток выпускается в двух упаковках
(i) жестяная банка с прямоугольным основанием длиной 5 см и шириной 4 см, высотой 15 см.
(ii) пластиковый цилиндр с круглым основанием диаметром 7 см и высотой 10 см. Какой контейнер имеет большую вместимость и на сколько?
Решение:
(i) Для прямоугольной упаковки,
Длина (l) = 5 см,
Ширина (b) = 4 см
Высота (h) = 15 см
Объем = lxbxh = 5 x 4 x 15 см 3 = 300 см 3
∴ Вместимость прямоугольной упаковки = 300 см 3
Диаметр основания = 7 см
∴ Радиус основания (r) = \(\frac { 7 }{ 2 }\) см
Высота (h) = 10 см
∴ Объем = πr 2 h = \(\frac { 22 }{ 7 }\) x (\(\frac { 7 }{ 2 }\ )) 2 x 10 см
= \(\frac { 22 }{ 7 }\) x \(\frac { 7 }{ 2 }\) x \(\ frac { 7 }{ 2 }\) x 10 см
= 11 x 7 x 5 см 3 = 385 см 3
∴ Вместимость цилиндрического пакета = 385 см 3
Таким образом, цилиндрический пакет имеет большую вместимость
на (385 – 300) см 3 85028 = 3 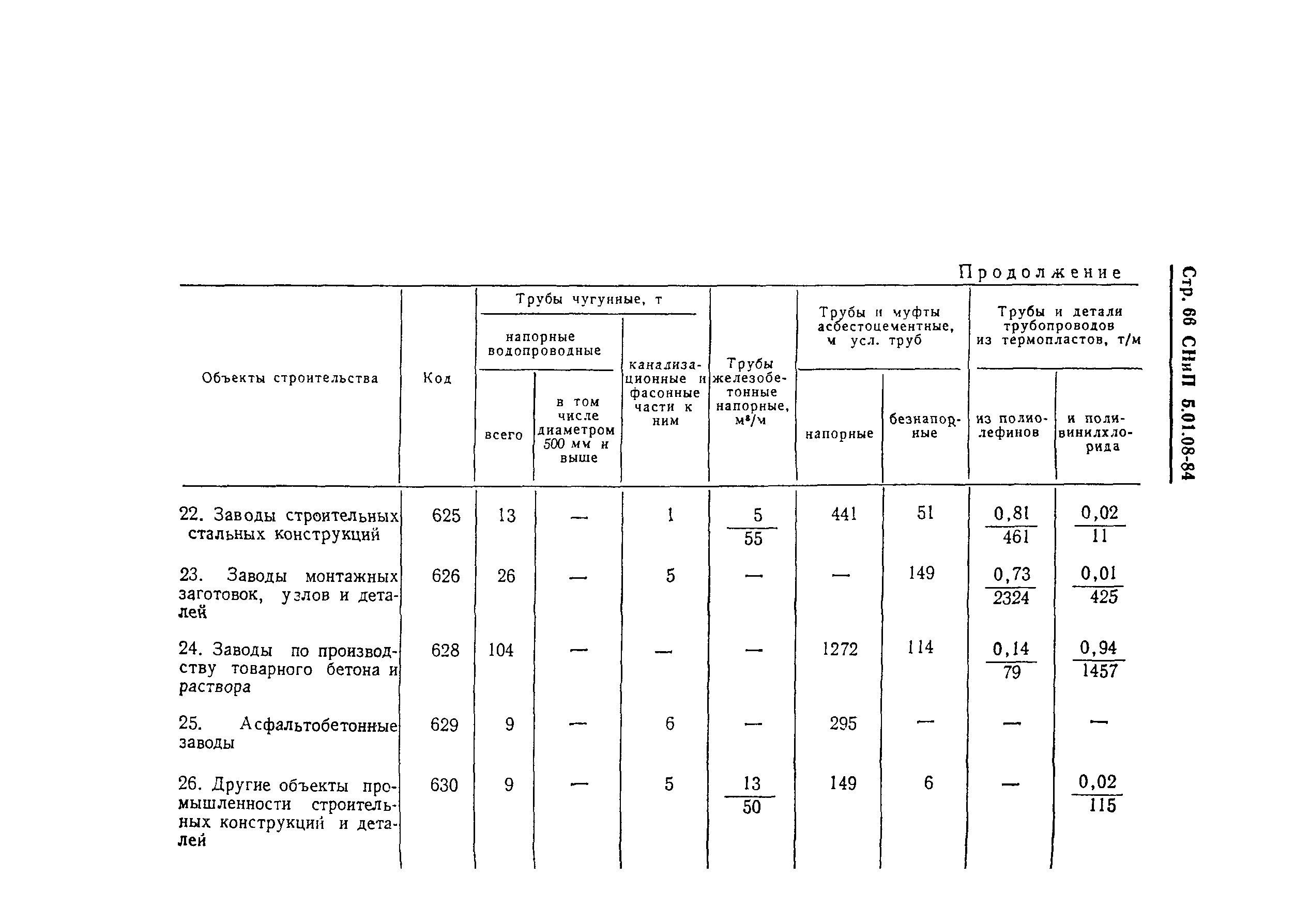 6 Математика 9 классаВопрос 4.
6 Математика 9 классаВопрос 4.
Если боковая поверхность цилиндра равна 94,2 см², а его высота 5 см, то найдите
(i) радиус его основания,
(ii) его объем. (Используйте π = 3,14)
Решение:
Высота цилиндра (h) = 5 см
Пусть радиус основания цилиндра равен «r».
Но боковая поверхность цилиндра 94,2 см 2 [дано]
2πrh = 94,2
⇒ Объем tlw данного цилиндра
= 3.14 (3) 2 x 5 см 3
= \(\frac { 314 }{ 100 }\) x 3 x 3 x 5 см 3
= \(\frac { 1413 }{ 10 }\) см = 141,3 см 3
Таким образом, требуемый объем = 141,3 см 3
Окраска внутренней изогнутой поверхности цилиндрического сосуда глубиной 10 м стоит 2200 фунтов стерлингов. Если стоимость покраски составляет 20 рупий за м², найдите
(i) площадь внутренней криволинейной поверхности сосуда,
(ii) радиус основания,
(iii) вместимость сосуда.
Решение:
(i) Общая стоимость покраски = рупий. 2200
Стоимость покраски площади л м 2 = руб. 20
Общая стоимость
= 110 м 2
Площадь кривизны цилиндра = 2πrh
Вместимость закрытого цилиндрического сосуда высотой 1 м составляет 15,4 литра. Сколько квадратных метров листового металла потребуется для его изготовления?
Решение:
Вместимость цилиндрического сосуда
= 15.4 литра = 15,4 x 1000 см 3 [1 литр = 10(x) см 3 ]
Грифельный карандаш состоит из деревянного цилиндра с твердым цилиндром из графита, заполненным внутри. Диаметр карандаша 7 мм, диаметр графита 1 мм. Если длина.длина карандаша 14 см, найдите объемы дерева и графита.
Диаметр карандаша 7 мм, диаметр графита 1 мм. Если длина.длина карандаша 14 см, найдите объемы дерева и графита.
Решение:
Поскольку, 10 мм = 1 см:
∴ 1 мм = \(\frac { 1 }{ 10 }\) см
Для графитового цилиндра,
Высота карандаша (h) = 14 см
Объем карандаша = πR 2 h
= 5,39 см 3 – 0,11 см 3
= 5,28 см 3
Таким образом, необходимый объем древесины = 5.28 см 3 .
Больному в больнице ежедневно дают суп в цилиндрической миске диаметром 7 см. Если миска наполнена супом на высоту 4 см, сколько супа должна ежедневно готовить больница, чтобы обслужить 250 пациентов?
Решение:
∵ Чаша имеет цилиндрическую форму, диаметр основания = 7 см
Решения NCERT для математики класса 9 Глава 13 Площади поверхности и объемы Пример 13.7
Найдите объем правильного круглого конуса с
(i) радиусом 6 см, высотой 7 см
(ii) радиусом 3,5 см, высотой 12 см
Решение:
(i) Здесь радиус конуса (r) = 6 см
Высота (h) = 7 см
Найдите вместимость в литрах конического сосуда с
(i) радиусом 7 см, наклонной высотой 25 см
(ii) высота 12 см, наклонная высота 13 см
Решение:
(i) Здесь радиус (r) = 7 см и наклонная высота (l) = 25 см
Высота конуса 15 см. Если его объем равен 1570 см³, найдите радиус основания. (Используйте π = 3,14)
(Используйте π = 3,14)
Решение:
Здесь высота конуса (h) = 15 см
Объем конуса = 1570 см 3
Пусть радиус основания равен r см.
Если объем прямого круглого конуса высотой 9 см равен 48 см³, найдите диаметр его основания.
Решение:
Объем конуса = 48 ит см 3
Высота конуса (h) = 9 см
Пусть r см радиус основания.
∴ Диаметр основания конуса = (2 x 4) см = 8 см.5 м это 12 м в глубину. Какова его емкость в килолитрах?
Решение:
Здесь диаметр конической ямы = 3,5 м
Радиус (r) = \(\frac { 3,5 }{ 2 }\) м = \(\frac { 35 }{ 20 }\)м,
Глубина (h) = 12 м
⇒ Объем (емкость) = \(\frac { 1 }{ 3 }\) πr 2 h
Объем прямого кругового конуса равен 9856 см 3 . Если диаметр основания равен 28 см, найдите
Если диаметр основания равен 28 см, найдите
(i) высота конуса
(ii) высота наклона конуса
(iii) площадь криволинейной поверхности конуса
Решение:
Объем конуса = 9856 см 3
Диаметр основания 28 см
Радиус основания (r) = \(\frac { 28 }{ 2 }\) = 14 см
⇒ l 2 = R 2 + H 2 + H 2
⇒ L 2 = 14 2 + 48 2 = 48 2 = 196 + 2304 = 2500
∴ l = 50
Таким образом, требуемая высота наклона = 50 см.
∴ Площадь криволинейной поверхности = \(\frac { 22 }{ 7 }\) x 14 x 50 см 2
= 2200 см 2
Таким образом, площадь криволинейной поверхности конуса 2200 см 2 .
Прямоугольный треугольник ABC со сторонами 5 см, 12 см и 13 см вращается вокруг стороны 12 см. Найдите объем полученного твердого тела.
Решение:
Стороны прямоугольного треугольника ABC равны 5 см, 12 см и 13 см.
Прямоугольный треугольник вращается вокруг стороны 12 см.
Высота (h) = 12 см
∴ Объем полученного таким образом конуса = \(\frac { 1 }{ 3 }\)πr 2 h
= \(\frac { 1 }{ 3 }\) x π x (5) 2 x 12см 3
= 100 π см 3
Таким образом, требуемый объем конуса равен 100πсм 3 .
Если треугольник ABC в вопросе 7 выше вращается вокруг стороны 5 см, то найдите объем полученного тела. Найдите также отношение объемов двух тел, полученных в вопросах 7 и 8.
Решение:
Так как прямоугольный треугольник вращается вокруг стороны 5 см.
∴ Высота полученного конуса (h) = 5 см
Радиус конуса (r) = 12 см
Решение:
Здесь ворох пшеницы имеет форму конуса с диаметром основания = 10,5 м
Теперь площадь холста для покрытия вороха должна быть равна к площади криволинейной поверхности конической кучи. Решения NCERT для математики класса 9 Глава 13 Площади поверхности и объемы Пример 13.8
Упр. 13.8 Класс 9 Математика Вопрос 1.
Найдите объем сферы, радиус которой равен
(i) 7 см
(ii) 0,63 см
Решение:
(i) Здесь радиус (r) = 7 см 13.8 Класс 9 МатематикаВопрос 2.
13.8 Класс 9 МатематикаВопрос 2.
Найдите количество воды, вытесненной твердым сферическим шаром диаметром
(i) 28 см
(ii) 0.21 м
Решение:
(i) Диаметр шара = 28 см
Радиус шара (r) см \(\frac { 28 }{ 2 }\)см = 14 см
Объем сферического шара = \(\ frac { 4 }{ 3 }\)πr 3
⇒ Радиус (r) = \(\ frac { 0,21 }{ 2 }\)m = \(\ frac { 21 }{ 200 }\)m
Диаметр металлического шара 4,2 см. Какова масса шарика, если плотность металла равна 8.9 г на см 3 ?
Решение:
Диаметр металлической приманки = 4,2 см
⇒ Радиус (r) = \(\frac { 4,2 }{ 2 }\) см = 2,1 см
Диаметр Луны составляет примерно одну четвертую диаметра земли. Какую часть объема Земли составляет объем Луны?
Решение:
Пусть диаметр Земли равен 2r.
⇒ Радиус Земли = \(\frac { 2r }{ 2 }\) = r
Поскольку диаметр Луны = \(\frac { 1 }{ 4 }\) (Диаметр Земли)
⇒ Радиус Луны = \(\frac { 1 }{ 4 }\)(Радиус Земли)
Радиус Луны = \(\frac { 1 }{ 4 }\) (r) = \(\frac { r }{ 4 }\)
∴ Объем земли = \(\frac { 4 }{ 3 }\)πr 3 и
Сколько литров молока может вместить полусферическая миска диаметром 10,5 см держит?
Решение:
Диаметр полусферической чаши = 10.5 см
⇒ Радиус полусферической чаши (r) = \(\frac { 10,5 }{ 2 }\)см = \(\frac { 105}{ 20 }\)см
Таким образом, вместимость чаша = 0,303 литра (прибл.)
Полусферический резервуар сделан из листа железа толщиной 1 см. Если внутренний радиус равен 1 м, то найдите объем железа, пошедшего на изготовление бака.
Решение:
Внутренний радиус (r) = 1 м
∵ Толщина = 1 см = \(\frac { 1}{ 100 }\)m = 0,01 м
= 0,06348 м 3 (приблизительно)
Решение:
Пусть r будет радиусом сферы.
∴Площадь его поверхности = 4πr 2
4πr 2 = 154 [Дано]
Купол здания имеет форму полусферы. Изнутри он был выбелен за 498 фунтов стерлингов.{ 2 }\)
Таким образом, необходимая площадь поверхности купола составляет 249,48 м 2 .
∴ Площадь внутренней поверхности купола = 2πr 2 
Двадцать семь твердых железных сфер, каждая с радиусом r и площадью поверхности S, расплавлены, чтобы сформировать сферу с площадью поверхности S’.Найдите
(i) радиус r’ новой сферы,
(ii) отношение S и S’.
Решение:
(i) Пусть радиус маленького шара равен r
∴ Его объем = \(\frac { 4 }{ 3 }\)πr 3
Объем 27 маленьких шаров 27 x [ \(\frac { 4 }{ 3 }\)πr 3 ]
Пусть радиус новой сферы равен r’
∴ Объем новой сферы = \(\frac { 4 }{ 3 }\)π(r’) 3
= S = 4πr 2 и S’ = 4π (3r) 2 [∵ r’ = 3r]
Капсула с лекарством имеет форму сферы диаметром 3,5 мм. Сколько лекарства (в миллиметрах 3 ) необходимо для заполнения этой капсулы?
Решение:
Диаметр сферической капсулы = 3,5 мм
⇒ Радиус сферической капсулы (r) = \(\frac {3,5}{2}\) мм = \(\frac {35}{20}\)мм
∴ Объем сферической капсулы = 4πr 3
= 22,46 мм 3 (приблизительно)
Таким образом, необходимое количество лекарства = 22. 46 мм 3 (прибл.)
46 мм 3 (прибл.) Решения NCERT для математики класса 9, глава 13 Площади поверхностей и объемы Ex 13.9
Ex 13.9, математика класса 9, вопрос 1.
Деревянная книжная полка имеет следующие внешние размеры:
Высота = 110 см, глубина = 25 см, Ширина = 85 см (см. рисунок). Толщина доски везде 5 см. Наружные поверхности должны быть отполированы, а внутренние поверхности должны быть окрашены. Если цена полировки — 20 пайз за см 2 , а цена полировки — 10 пайз за см 2 , найдите общие затраты, необходимые для полировки и покраски поверхности книжной полки.
Здесь длина (l) = 85 см,
ширина (b) = 25 см и высота (h) = 110 см
Площадь внешней поверхности = Площадь четырех лиц + Площадь спинки + Площадь переда
= [2 (110 + 85) x 25 + 110 x 85 + (110 x 5 x 2) + (75 x 5) x 4] см 2 = 21700 см 2
∴ Стоимость полировки внешних поверхностей = рупий. (21700 x \(\frac { 20}{100}\)) = рупий. 4340
4340
Площадь внутренней поверхности = площадь пяти граней 3 прямоугольных параллелепипедов размерами 75 см х 30 см х 20 см каждый размеры 75 см x 30 см x 20 см 3(2(75 x 30 + 30 x 20 + 75 x 20)) см 2 – 3 x (75 x 30) см 2
= 6(2250 + 600 + 1500) см 2 – 6750 см 2 = 19350 см 2
∴ Стоимость покраски внутренних поверхностей = руб.19350 х \(\frac { 10}{100 }\) = рупий. 1935
Hene, общие расходы = рупий. (4340 + 1935)
= рупий. 6275
Передняя составная стена дома украшена деревянными сферами диаметром 21 см, размещенными на небольших подставках, как показано на рисунке. Для этой цели используются восемь таких сфер, которые должны быть окрашены в серебристый цвет. Каждая опора представляет собой цилиндр радиусом 1,5 см и высотой 7 см и должна быть окрашена в черный цвет. Найдите стоимость необходимой краски, если серебряная краска стоит 25 пайсов за см 2 , а черная краска стоит 5 пайсов за см 2 .
Здесь диаметр сферы = 21 см
Радиус сферы (r) = \(\frac { 21}{ 2 }\) см
Площадь поверхности сферы = 4πr 2
∴ Площадь поверхности из 8 сфер
= 8 x 4 x \(\frac { 22 }{ 7 }\) x (\(\frac { 21 }{ 2 }\)) 2 см 2
Диаметр сферы уменьшился на 25%. На сколько процентов уменьшилась его криволинейная поверхность?
Решение:
Пусть диаметр сферы равен d.
После уменьшения диаметр сферы
= d – \(\frac { 25 }{ 100 }\) xd
= d – \(\frac { 1 }{ 4 }\)d = \(\frac { 3 } { 4 }\)d
Поскольку площадь поверхности сферы = 4πr 2 или π(2r) 2 или πd 2
Площадь поверхности сферы, когда диаметр сферы равен Ncert Solutions для класса 9 Maths
 1 помочь вам. Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 9, глава 13, площади поверхности и объемы, пример 13.1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
1 помочь вам. Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 9, глава 13, площади поверхности и объемы, пример 13.1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время. Расход грунтовки на 1 м2 стены: Грунт акриловый для внутренних работ, продукция Нортекс-праймер, норма расхода на 1 м2 для пола
Особенности
Грунтовки
ИзображениеИзображение
Норма расхода
Image Нормы расхода указаны на каждой упаковке любого вида грунтовки.Однако практика показывает, что нормы, установленные на испытательных стендах в лабораториях производителей, обычно меньше расхода в более сложных условиях реальной стройки.
Нормы расхода указаны на каждой упаковке любого вида грунтовки.Однако практика показывает, что нормы, установленные на испытательных стендах в лабораториях производителей, обычно меньше расхода в более сложных условиях реальной стройки. Вот средние нормы расхода различных составов для грунта, выраженные в литрах на 1 кв.м:
ImageImage
Область применения
 Разведенная смесь имеет консистенцию и цвет побелки, поэтому оставляет светлые разводы на темной основе.Этот материал прекрасно подходит для подготовки стен и потолка к отделке, хорошо ложится под обои, идеально сочетается с акриловыми красками.
Разведенная смесь имеет консистенцию и цвет побелки, поэтому оставляет светлые разводы на темной основе.Этот материал прекрасно подходит для подготовки стен и потолка к отделке, хорошо ложится под обои, идеально сочетается с акриловыми красками.
ImageImage Эпоксидная грунтовочная смесь на основе синтетических смол содержит антикоррозионные добавки и преобразователь ржавчины.Такие составы разработаны специально для обработки металлических поверхностей перед покраской и могут применяться даже при наличии ржавчины. Например, перед грунтованием ржавых труб следует лишь предварительно счистить с металла чешуйки и пыль с помощью жесткой щетки. Базовый расход такой грунтовки 60-100 мл на м2
ImageImage
ИмажеИажеИзображение Содержит фунгицидные и антисептические добавки, препятствующие биологическому повреждению и разрушению древесины.
Содержит фунгицидные и антисептические добавки, препятствующие биологическому повреждению и разрушению древесины. Производители
Изображение Солидная научная база позволяет инновационным разработкам находить практическое применение в новых рецептурах.
Солидная научная база позволяет инновационным разработкам находить практическое применение в новых рецептурах.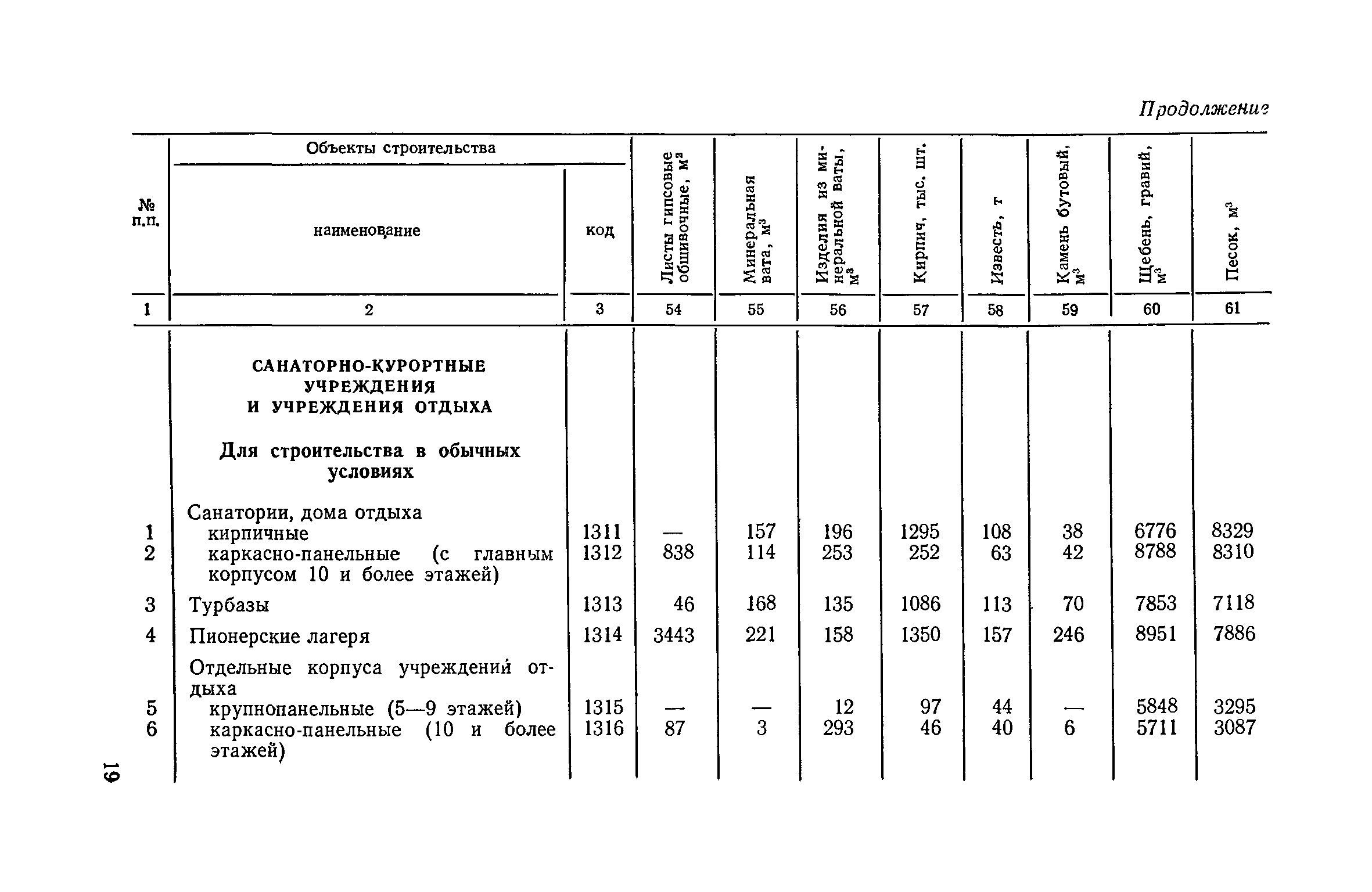
ИзображениеИзображение Советы и рекомендации
Image
ИзображениеИзображениеИзображение
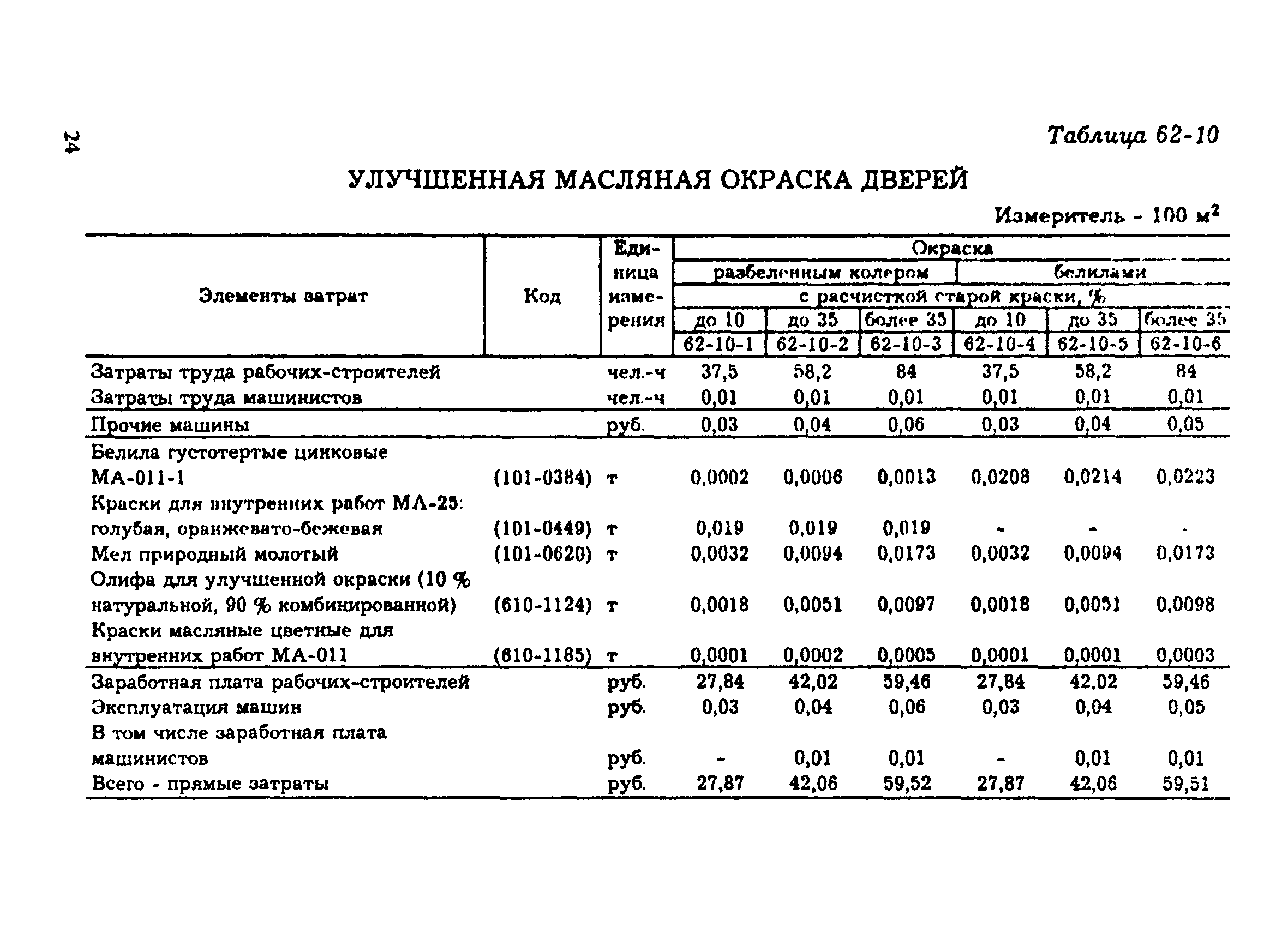
Штукатурка Ротбанд — Инструкция по применению: Расход на 1м2, Расчет количества штукатурной смеси Кнауф на 1м2 Стены
Особенности
Штукатурка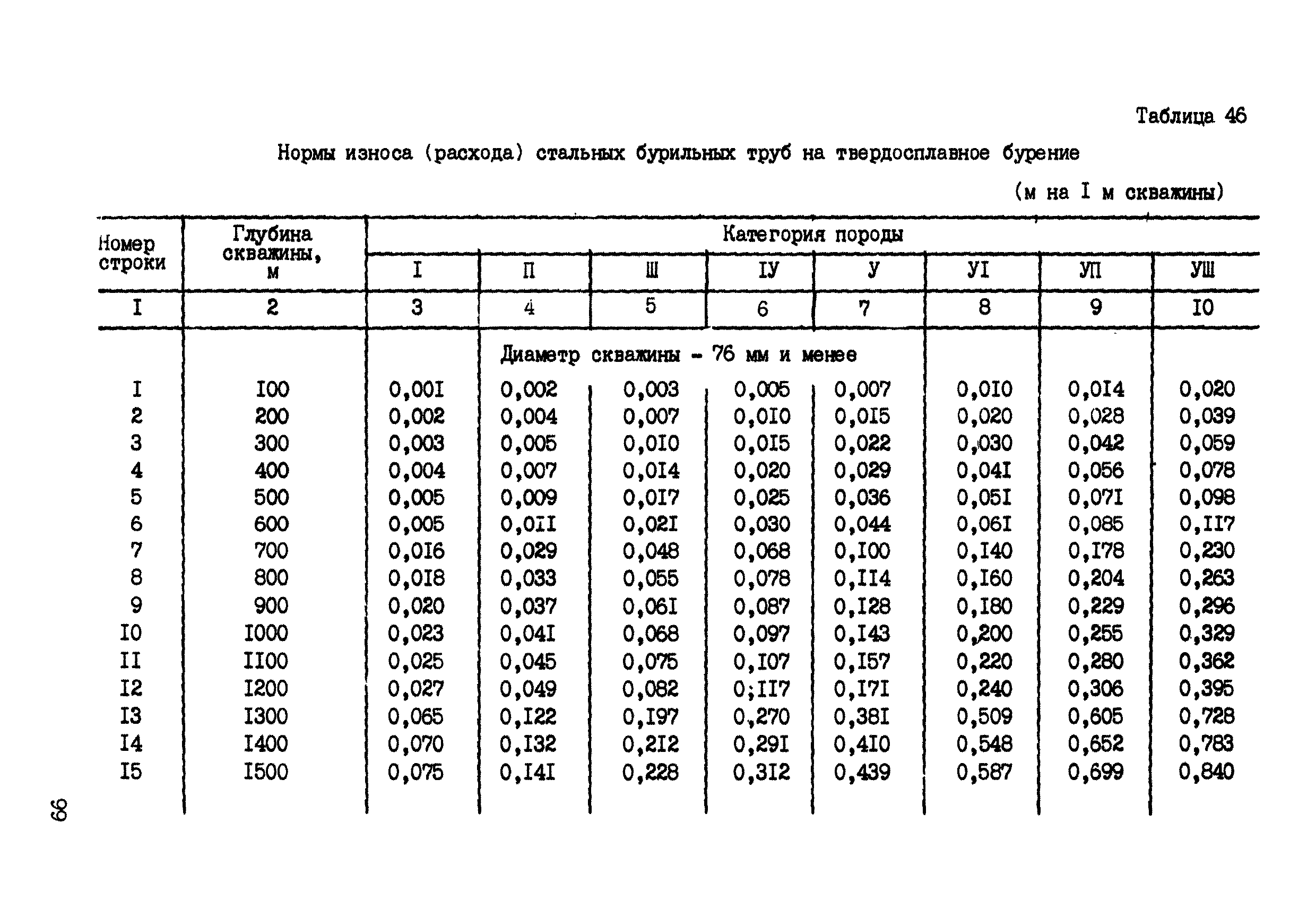 Это позволяло наносить состав в один слой, который затем выравнивался, а необходимость в последующих просто отпадала, в отличие от аналогов, выпускаемых другими компаниями.
Это позволяло наносить состав в один слой, который затем выравнивался, а необходимость в последующих просто отпадала, в отличие от аналогов, выпускаемых другими компаниями. Состав окончательно схватывается примерно через неделю, время полного застывания зависит от микроклимата в помещении, где выполняются работы. Прочность 2,5 МПа, плотность в твердом состоянии 950 кг/м3. Композиция расфасована в пакеты весом 5, 10, 25 и 30 килограмм, что удобно для потребителя. Хранится в закрытых пакетах 6 месяцев.
Состав окончательно схватывается примерно через неделю, время полного застывания зависит от микроклимата в помещении, где выполняются работы. Прочность 2,5 МПа, плотность в твердом состоянии 950 кг/м3. Композиция расфасована в пакеты весом 5, 10, 25 и 30 килограмм, что удобно для потребителя. Хранится в закрытых пакетах 6 месяцев.
Штукатурка ImageImageImage Кроме того, с помощью состава появляется возможность декорировать поверхности и экспериментировать с дизайном.
Кроме того, с помощью состава появляется возможность декорировать поверхности и экспериментировать с дизайном. Область применения
Довольно широко распространены штукатурные смеси Rotband Композиция выполняет три основные функции:
ИзображениеИзображениеИзображениеИзображение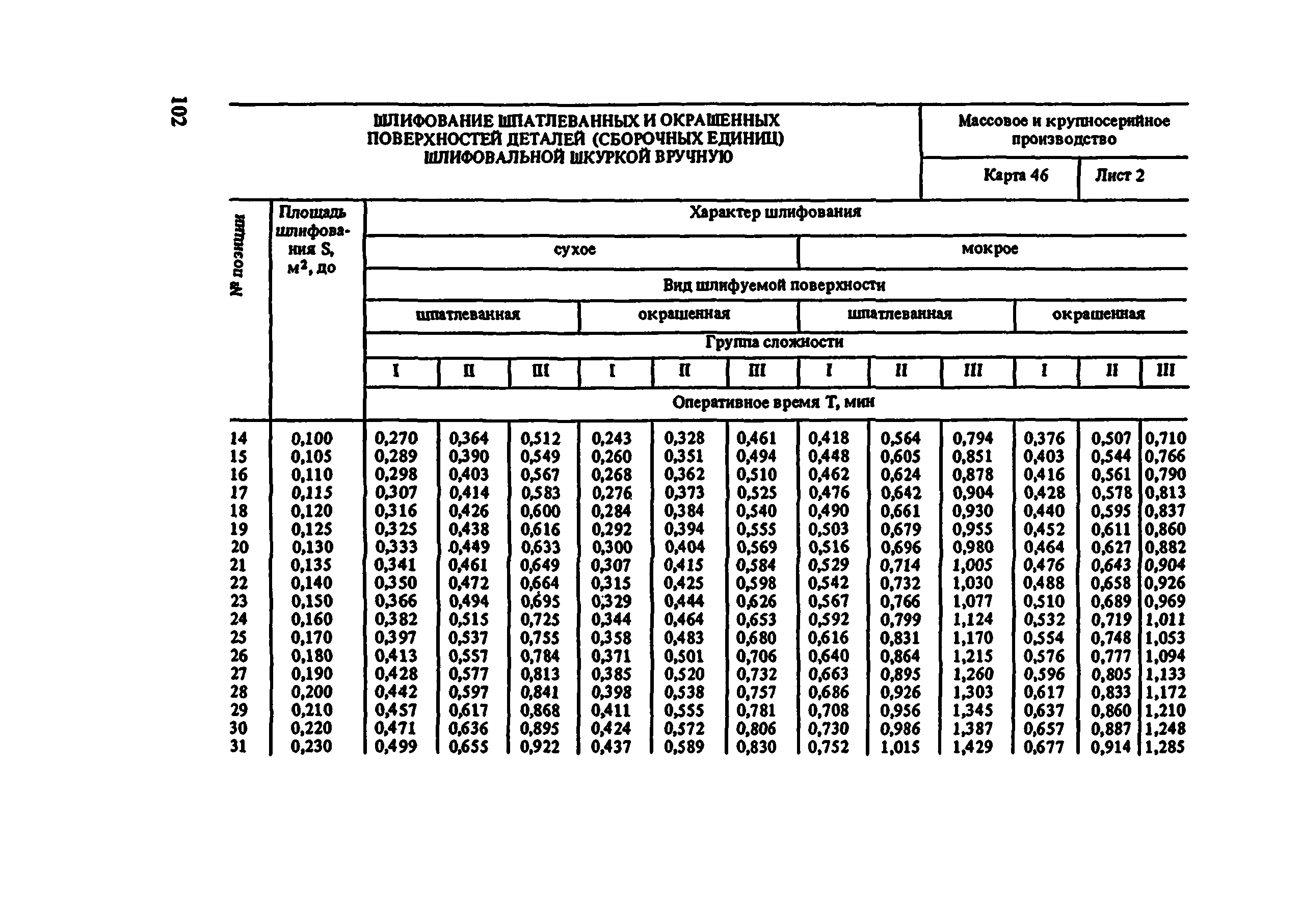
Расход на 1 м2
 В этой ситуации рекомендуется использовать гипсовую сетку для повышения качества работы. При правильном приготовлении смеси и соблюдении технологии нанесения одного слоя может хватить, и поверхность будет готова к оклейке обоями. Покраску производят после укладки финишного слоя материала.
В этой ситуации рекомендуется использовать гипсовую сетку для повышения качества работы. При правильном приготовлении смеси и соблюдении технологии нанесения одного слоя может хватить, и поверхность будет готова к оклейке обоями. Покраску производят после укладки финишного слоя материала.
ИзображениеИзображение Тонкости применения
 Черновой пол должен быть ровным, с минимумом неровностей и дефектов. Металлические основания необходимо обработать составами с антикоррозийным эффектом. Стену необходимо загрунтовать, а затем просушить .
Черновой пол должен быть ровным, с минимумом неровностей и дефектов. Металлические основания необходимо обработать составами с антикоррозийным эффектом. Стену необходимо загрунтовать, а затем просушить . Установка маяков
ImageImage Разведение
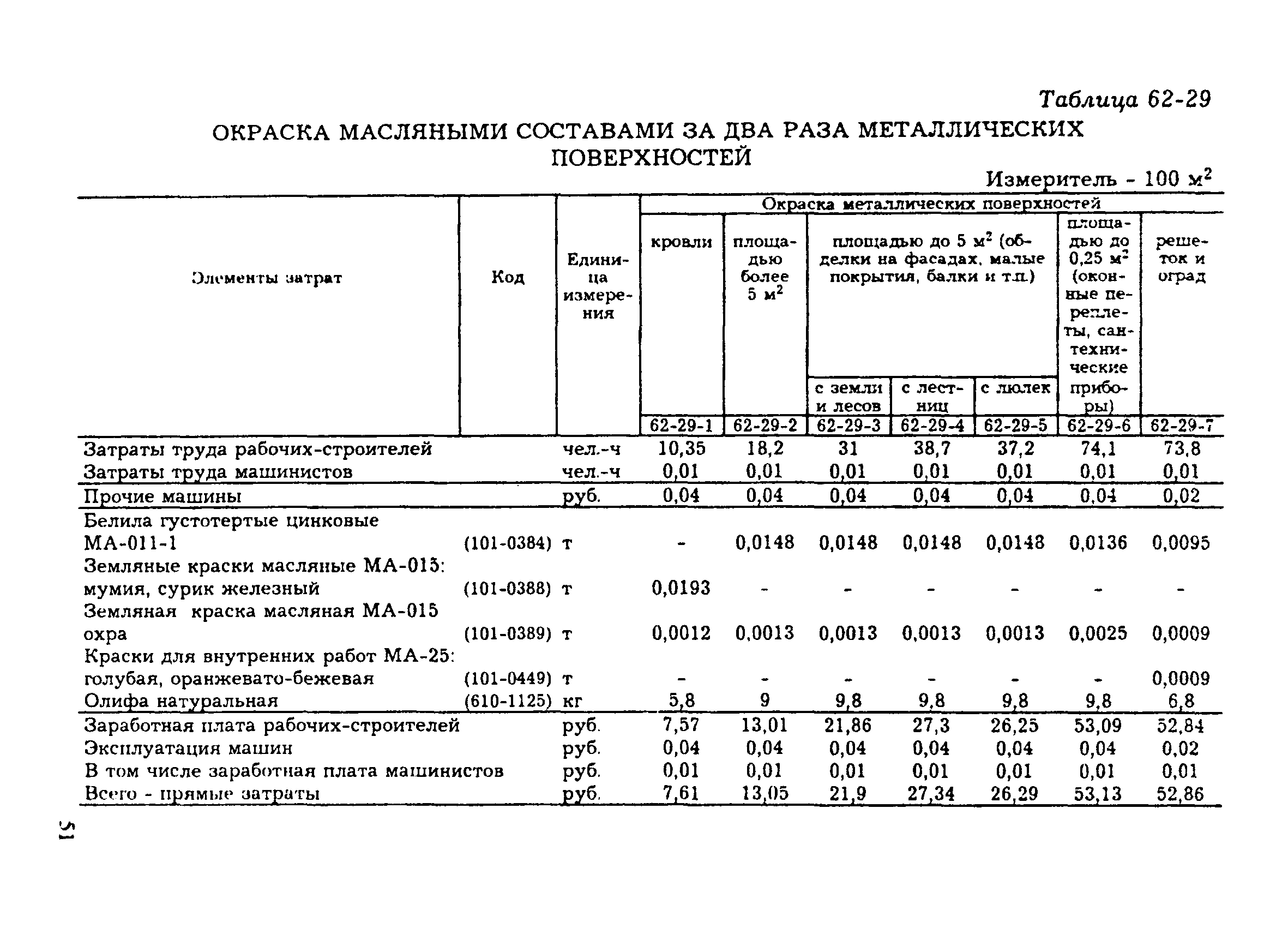 В целом механизм действия тот же. Пакет массой 30 кг необходимо развести в 18 литрах прохладной воды.
В целом механизм действия тот же. Пакет массой 30 кг необходимо развести в 18 литрах прохладной воды.
Image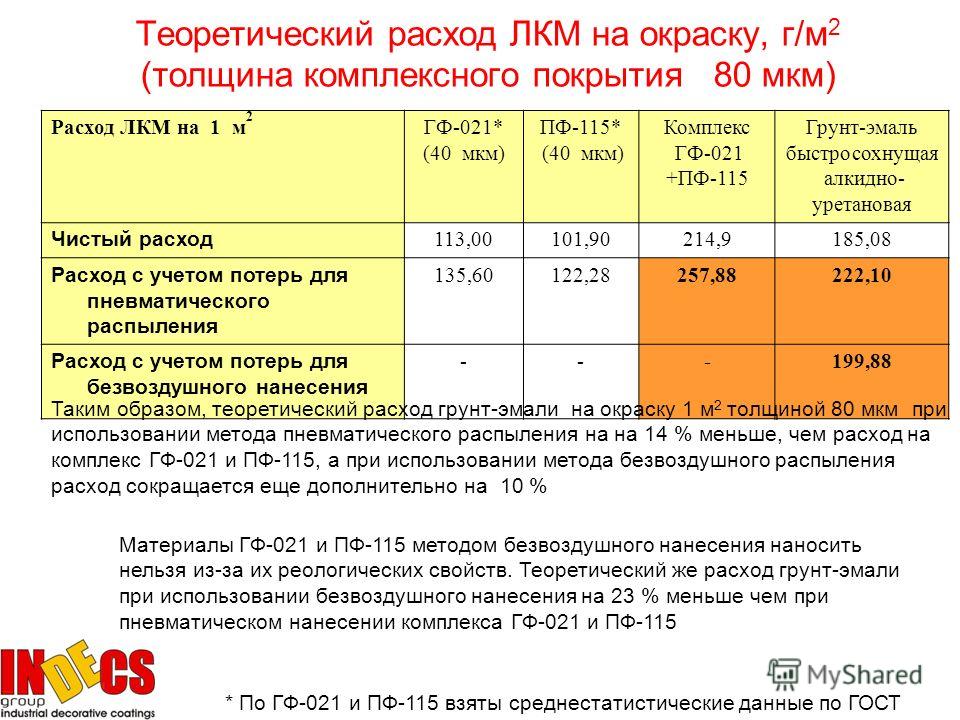 Температура в помещениях, где проводятся работы, должна быть не ниже +5 градусов и не выше +30 градусов.
Температура в помещениях, где проводятся работы, должна быть не ниже +5 градусов и не выше +30 градусов. Приложение
№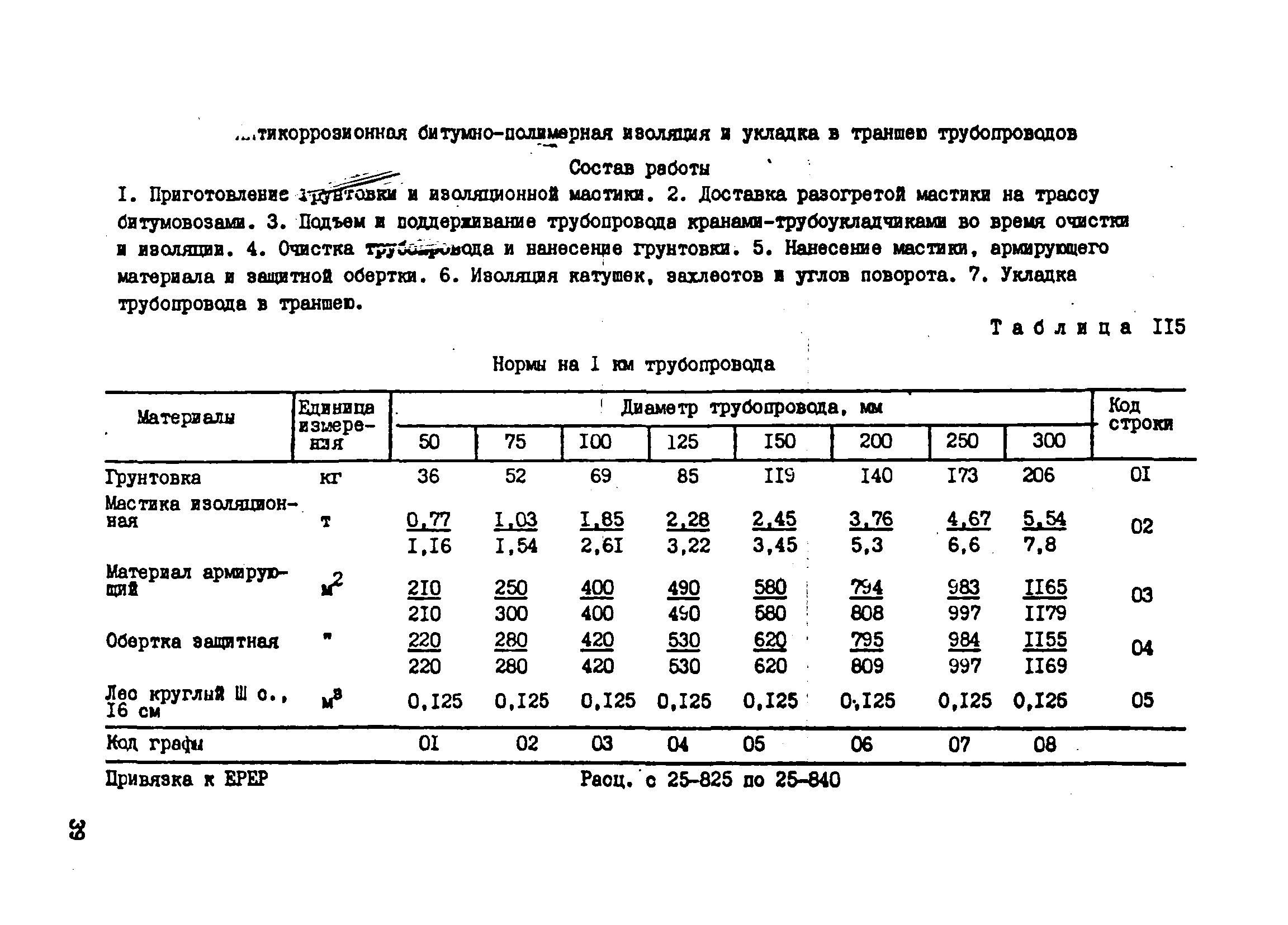 Сетку необходимо вдавить и тщательно загладить, затем оштукатурить, загрунтовать и высушить.Далее уже наносится штукатурная смесь Rotband.
Сетку необходимо вдавить и тщательно загладить, затем оштукатурить, загрунтовать и высушить.Далее уже наносится штукатурная смесь Rotband. Выравнивание
ImageImage
Советы и рекомендации
 Но это время индивидуально и зависит от микроклимата помещения, а также внешних условий. В любом случае максимальная толщина слоя штукатурной смеси должна быть не более 5 сантиметров.
Но это время индивидуально и зависит от микроклимата помещения, а также внешних условий. В любом случае максимальная толщина слоя штукатурной смеси должна быть не более 5 сантиметров.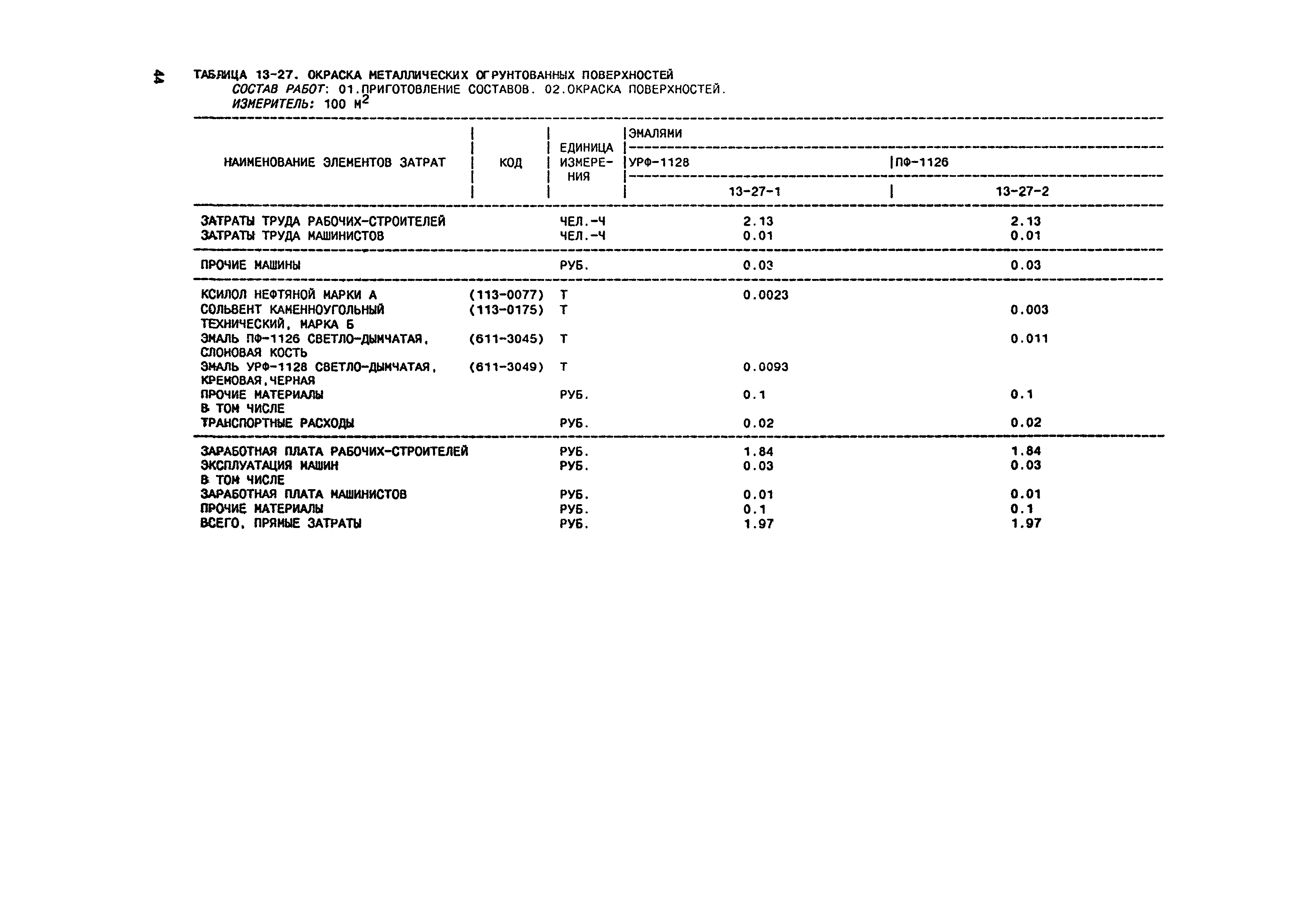
 Web.Mvc.Html.ChildActionExtensions.ActionHelper (HtmlHelper htmlHelper, String actionName, String controllerName, RouteValueDictionary routeValues, TextWriter textWriter) +573
System.Web.Mvc.Html.ChildActionExtensions.Action (HtmlHelper htmlHelper, String actionName, String controllerName, RouteValueDictionary routeValues) +113
ASP._Page_Views_Shared_PageNotFound_cshtml.Execute() в d:\Websites\Live Jotun.Com\Views\Shared\PageNotFound.cshtml:1
System.Web.WebPages.WebPageBase.Выполнить иерархию страниц () +252
System.Web.Mvc.WebViewPage.ExecutePageHierarchy() +148
System.Web.WebPages.StartPage.ExecutePageHierarchy() +86
System.Web.WebPages.WebPageBase.ExecutePageHierarchy(WebPageContext pageContext, модуль записи TextWriter, начальная страница WebPageRenderingBase) +107
System.Web.Mvc.ViewResultBase.ExecuteResult (контекст контроллера) +378
System.Web.Mvc.Async.<>c__DisplayClass21.
Web.Mvc.Html.ChildActionExtensions.ActionHelper (HtmlHelper htmlHelper, String actionName, String controllerName, RouteValueDictionary routeValues, TextWriter textWriter) +573
System.Web.Mvc.Html.ChildActionExtensions.Action (HtmlHelper htmlHelper, String actionName, String controllerName, RouteValueDictionary routeValues) +113
ASP._Page_Views_Shared_PageNotFound_cshtml.Execute() в d:\Websites\Live Jotun.Com\Views\Shared\PageNotFound.cshtml:1
System.Web.WebPages.WebPageBase.Выполнить иерархию страниц () +252
System.Web.Mvc.WebViewPage.ExecutePageHierarchy() +148
System.Web.WebPages.StartPage.ExecutePageHierarchy() +86
System.Web.WebPages.WebPageBase.ExecutePageHierarchy(WebPageContext pageContext, модуль записи TextWriter, начальная страница WebPageRenderingBase) +107
System.Web.Mvc.ViewResultBase.ExecuteResult (контекст контроллера) +378
System.Web.Mvc.Async.<>c__DisplayClass21. AsyncControllerActionInvoker.EndInvokeAction(IAsyncResult asyncResult) +38
System.Web.Mvc.Controller.
AsyncControllerActionInvoker.EndInvokeAction(IAsyncResult asyncResult) +38
System.Web.Mvc.Controller. ExecuteStep (шаг IExecutionStep, логическое значение и выполнено синхронно) +134
ExecuteStep (шаг IExecutionStep, логическое значение и выполнено синхронно) +134