Расчет железобетонной балки: Расчёт железобетонной балки

Содержание

Обзор существующих подходов к расчету железобетонных балок в условиях кручения с изгибом

Автор: Гусева Оксана Вячеславовна

Рубрика: Архитектура, дизайн и строительство

Опубликовано в Молодой учёный №50 (340) декабрь 2020 г.

Дата публикации: 12.12.2020 2020-12-12

Статья просмотрена: 113 раз

Скачать электронную версию

Скачать Часть 2 (pdf)

Библиографическое описание:

Гусева, О. В. Обзор существующих подходов к расчету железобетонных балок в условиях кручения с изгибом / О. В. Гусева. — Текст : непосредственный // Молодой ученый. — 2020. — № 50 (340). — С. 77-79. — URL: https://moluch.ru/archive/340/76556/ (дата обращения: 08.05.2023).

В статье рассматриваются принципы работы железобетонных балок в условиях кручения с изгибом. Представлен обзор существующих подходов к расчету данного напряженно-деформированного состояния конструкции. Особое внимание уделено подходам, представленным в нормативной документации разных стран.

Ключевые слова: кручение с изгибом, нормативная документация, расчет железобетонной балки.

В настоящее время исследования в области расчета строительных конструкций направлены преимущественно на оптимизацию существующих подходов, уменьшения материалоемкости, учет реальной работы конструкций в условиях сложных деформаций.

Одним из таких сложных напряженно-деформированных состояний является кручение с изгибом. Пространственная работа конструкций усложняет возможность точного аналитического расчета.

Наиболее часто кручению с изгибом подвергаются железобетонные балки. Зачастую крутящие моменты, возникающие в данных конструкциях, не учитываются в расчетах, поскольку возникающее кручение либо имеет небольшую величину, либо возникло в результате случайных эксцентриситетов, либо возникающие в балках усилия могут быть перераспределены на смежные конструкции. При расчетах данных элементов кручение рассматривают как вторичный фактор, который будет учтен коэффициентами запаса или будет воспринят поперечным армированием, которое было подобрано из условия восприятия поперечных сил.

Важно понимать, как работает балка в условиях кручения с изгибом, чтобы отличать ситуации, в которых кручением пренебрегать нельзя (краевые балки, балки с боковыми консолями).

Работа в области исследования кручения с изгибом ведется с начала прошлого столетия, ей занимались такие ученые, как Е.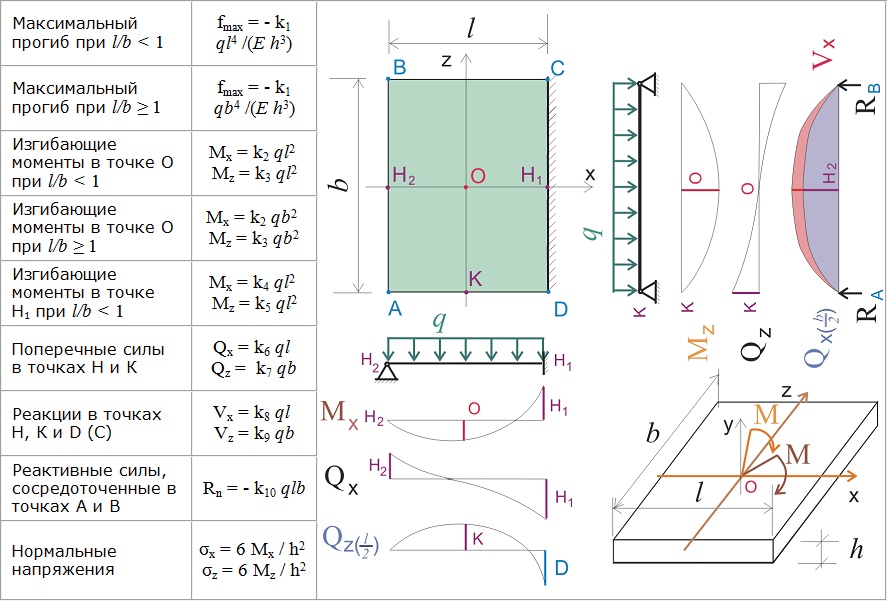 Мерш, Г. Коуэн, Э. Г. Ц. Бах и др. В нашей стране значительный вклад в развитие теорий расчета данного напряженно-деформированного состояния внесли А. А. Гвоздев и Н. Н. Лессиг. А. А. Гвоздев [1] разработал теорию предельного равновесия, на основании которой впоследствии Н. Н. Лессиг [2] были проведены экспериментальные исследования и выведены методы расчета прочности балок, работающих в условиях кручения с изгибом.

Разрушение балки происходит по пространственному сечению, что усложняет аналитический расчет. Механизм образования трещины представлен на рис.1. А. С. Залесовом [3] был предпринят подход с заменой пространственного сечения плоским диагональным, однако, данное упрощение не всегда находит подтверждение в экспериментальных исследованиях.

Рис. 1. Пространственная трещина в балке [8, с. 57]

Нормативная документация является базой для расчета строительных конструкций. Все сооружения, возводящиеся в любой стране, должны отвечать местным требованиям норм, рассчитываться по формулам, подходам, которые представлены в них. Рассмотрим, как в нормативной документации разных стран учитывается работа конструкций в условиях кручения с изгибом.

В СП 63.13330.2018 [4] учитывается работа конструкции в условиях кручения с изгибом по некоторому обобщенному закону. Расчет по прочности пространственных сечений с использованием кривых взаимодействий крутящих и изгибающих моментов производится по формуле (1):

(1)

где — крутящий момент от внешней нагрузки в пространственном сечении;

— предельный крутящий момент, воспринимаемый пространственным сечением;

— изгибающий момент от внешней нагрузки в нормальном сечении;

— предельный изгибающий момент, воспринимаемый нормальным сечением.

Формула расчета (1) может быть представлена в виде:

Или в виде кривой зависимости (Рис. 2).

Рис. 2. Кривая взаимодействия для элемента, работающего на кручение с изгибом. I — область обеспеченной прочности; II — область необеспеченной прочности

Если точка с координатами лежит в пределах области, ограниченной кривой и осями координат, то прочность сечения обеспечена, если за пределами данной области — прочность обеспечена не будет.

В основе подхода расчета по СП лежит принцип, по которому несущая способность балки на кручение уменьшается на величину, необходимую для восприятия изгибающего момента.

В индийских строительных нормах IS 456:2000 [7] также представлены формулы, которые учитывают связь двух силовых факторов. Продольное армирование подбирается из условия действия фиктивного изгибающего момента, который является функцией действующих в конструкции изгибающего и крутящего моментов.

где — изгибающий момент в поперечном сечении

где — это крутящий момент;

D — полная высота сечения балки;

b — это ширина балки.

В американских ACI 318–14 Building Code [5] и европейских строительных нормах EN 1992–1–1 [6] подбор армирования для восприятия изгибающего и крутящего моментов производится независимо друг от друга, сначала подбирается армирование для восприятия изгибных усилий, затем подбирается арматура для восприятия кручения (поперечная и продольная).

Затем продольная арматура для восприятия всех силовых факторов суммируется. Данный подход приводит к большим запасам прочности, что подтверждается экспериментальными исследованиями.

Литература:

1. Гвоздев, А. А. Расчет несущей способности по методу предельного равновесия / А. А. Гвоздев. — М.: Стройиздат, 1949. — 279 с.

2. Лессиг, Н. Н. Определение несущей способности железобетонных элементов прямоугольного сечения, работающих на изгиб с кручением. / Н. Н. Лессиг / Исследование прочности элементов железобетонных конструкций: сб. трудов НИИЖБ. — М.: НИИЖБ, 1959. — № 5.

3. Залесов, А. С. Расчет железобетонных конструкций по прочности, трещиностойкости и деформациям. / Залесов А. С., Кодыш Э. Н., Лемыш Л. Л., Никитин И. К. — М. Стройиздат., 1988 г. — 120 с.

4. СП 63.13330.2018. Бетонные и железобетонные конструкции. Основные положения. / Госстрой России. -М.: ГУП НИИЖБ, 2012.-155 с.

5. ACI 318–14 Building Code Requirements for Structural Concrete and Commentary, American Concrete Institute, 2014–524 с.

6. EN 1992–1–1:2004 Eurocode 2: Design of concrete structures — Part 1–1: General rules and rules for buildings — Brussels, 2004–227 с.

7. IS 456 (2000): Plain and Reinforced Concrete — Code of Practice (Fourth Revision) — New Delhi, 2000–114 с.

8. Elfgren, L. Reinforced Concrete Beams Loaded in Combined Torsion, Bending and Shear. A study of the ultimate load-carrying capacity / L. Elfgren. — Göteborg: Division of Concrete Structures, 1972–233 с.

Основные термины (генерируются автоматически): условие кручения, крутящий момент, нормативная документация, пространственное сечение, изгиб, изгибающий момент, кручение, ACI, внешняя нагрузка, нормальное сечение.

Ключевые слова

нормативная документация, кручение с изгибом, расчет железобетонной балки

кручение с изгибом, нормативная документация, расчет железобетонной балки

Расчет железобетонной балки.

Прямоугольная балка

Похожие презентации:

Творческий проект «Умный дом»

Грузоподъемные машины. (Лекция 4.1.2)

Основы архитектуры и строительных конструкций. Основы проектирования

Лакокрасочные материалы. Виды, состав

Металлические конструкции

Виды кранов

Общие сведения о кранах

Классификация крыш и покрытий

Фундамент. Классификация фундаментов

Свайные фундаменты. Классификация. (Лекция 6)

1. Расчет железобетонной балки

Прямоугольная балка

2. Расчет балки. Итог расчета

3. Расчет балки. Нормы

СП 63.13330.2012
Бетонные и железобетонные
конструкции.
Основные положения.
Актуализированная редакция СНиП
52-01-2003 (с Изменениями N 1, 2,
3)

4. Расчет балки. Нормы

ПОСОБИЕ
по проектированию
бетонных и
железобетонных
конструкций из тяжелых
и легких бетонов без
предварительного
напряжения арматуры
(к СНиП 2.

03.01-84)

5. Расчет балки 1 группа предельных состояний

• Расчет прочности нормального
сечения
• Расчет прочности наклонных
сечений:
– Конструирование каркаса
– Обеспечение прочности по наклонной
трещине
– Расчет прочности сжатой полосы
между наклонными трещинами

6. Расчет балки 2 группа предельных состояний

7. Расчет балки. Нормы

8. Расчет балки. Нормы

9. Расчет балки. Нормы

10. Расчет балки. Нормы

Коэффициент условия работы бетона по п. 6.1.12:

11. Расчет балки. Шаг 1

12. Расчет балки. Шаг 1

13. Расчет балки. Шаг 1

14. Расчет балки. Шаг 1

Усилия определяются по правилам
строительной механики.
Для равномерно распределенной
нагрузки:

15. Расчет балки. Шаг 1

16. Расчет балки. Шаг 2

17. Расчет балки. Шаг 2

• Задаем характеристики
материалов:
– Класс бетона по прочности
(Сопротивление бетону на сжатие)
– Класс продольной арматуры
(Сопротивления растяжению и
сжатию арматуры)
• Геометрические размеры сечения
(высота и ширина)

18.

Расчет балки. Шаг 2• Задаемся величиной а –
расстояние от крайнего
растянутого волокна бетона до
центра тяжести арматуры (3-5 см)
• Определяем рабочую высоту
бетона:

19. Расчет балки. Шаг 3

• Находим значение коэффициент А0:
• Он не должен превышать граничного
значения А0R (табл. 18 Пособия)
• Иначе изменить материалы или
геометрию сечения (если не возможно,
то считают как балку с двойной
арматурой)

20. Расчет балки. Шаг 3

21. Расчет балки. Шаг 4

• По величине коэффициента А0 по
таблице 20 Пособия определяем
коэффициенты

22. Расчет балки. Шаг 4

23. Расчет балки. Шаг 5

• Определяем требуемую площадь
арматуры по любой из формул:

24. Расчет балки. Шаг 6

• Задаем количество стержней и
определяем диаметр арматуры
(Сортамент арматуры):

25. Расчет балки. Шаг 6

26. Расчет балки. Шаг 7

• Определяем процент
армирования сечения

27. Расчет балки.

Шаг 8• Определяем диаметр
поперечных стержней:

28. Расчет балки. Шаг 9

• Определяем диаметр
поперечных стержней:

29. Расчет балки. Шаг 10

• Назначаем защитный слой
бетона:

30. Расчет балки. Шаг 10

• Минимальные значения
защитного слоя (СП
63.13330.2012):

31. Расчет балки. Конструирование

32. Расчет балки. Наклонные сечения

33. Наклонные сечения. Шаг 1

Принимаем шаг поперечного
армирования:
— на приопорных участках
S не более h/2 и не более 150 мм
S не более h/3 и не более 500 мм
— на остальных участках
S не более 3/4h и не более 500 мм
Поперечные стержни не требуются

34. Наклонные сечения. Шаг 2

Проверка выполнения условия:
Если условие выполняется, то
дальнейшего расчета не требуется –
бетон выдерживает поперечную силу

35. Наклонные сечения. Шаг 3

Усилие в поперечных
стержнях:

36. Наклонные сечения. Шаг 4

Находят значение С0:
Его принимают не более

37.

Наклонные сечения. Шаг 5Уточняют поперечную силу,
которую воспринимает бетон:
Если
расчет
, то продолжают

38. Наклонные сечения. Шаг 6

Определяем поперечную
силу, воспринимаемую
поперечными стержнями:

39. Наклонные сечения. Шаг 7

Проверяем условие:
Если выполняется – прочность обеспечена.
Если не выполняется – меняем
бетон, шаг поперечных стержней,
диаметр поперечных стержней или
сечение элемента => производим
расчет заново

40. Наклонные сечения. Шаг 7

Проверяем условие:
Если выполняется – прочность
обеспечена.
Если не выполняется – меняем
бетон или сечение элемента =>
производим расчет заново

41. Наклонные сечения. Шаг 7

42. Ширина раскрытия трещин. Шаг 1

43. Ширина раскрытия трещин. Шаг 1

44. Ширина раскрытия трещин. Шаг 1

45. Прогиб элемента. Шаг 1

English Русский Правила

Конструкция железобетонной балки | Расчет армирования балки

Обычный человек может оценивать подкрепление как единичную сумму.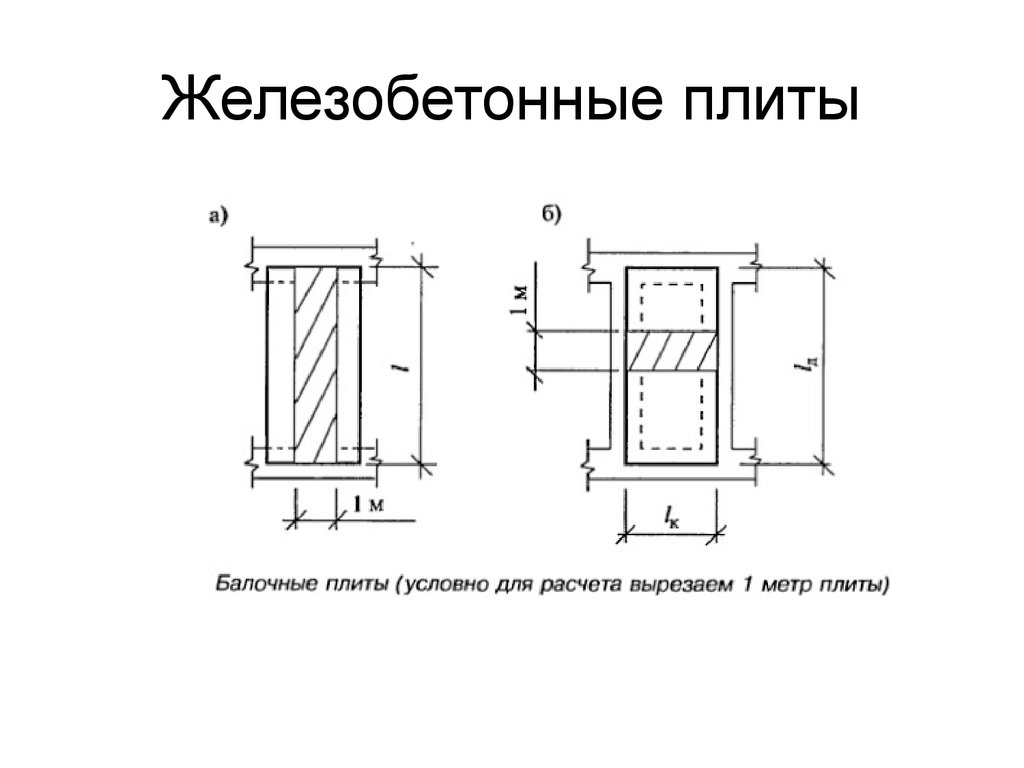 Мы видим, что многие люди оценивают подкрепление как уровень твердого объема, например, 2% или 1,5% твердого объема. В любом случае, как специалист по разработке, вы не должны измерять количество арматуры в процентах от объема твердого тела. Вы должны оценить это, как показано на основном чертеже.

Оценить количество арматуры просто. Все, что вам нужно, чтобы получить длину резки для каждого вида стержня в балке. В этом посте мы поговорим о том, как оценить арматуру балки по чертежу. Мы будем использовать стандартные идеалы в качестве вспомогательного чертежа балки.

Инструкции по расчету арматуры балки

Для оценки армирования балки сначала необходимо понять, какие типы стержней доступны в балке. Из идеального плана мы обнаружили сопутствующую информацию:

– 2D20
• Хомут, S1 – D10 @ 4″ c/c

Вам также потребуется сопроводительная информация для оценки арматуры балки:

• Прозрачная крышка для усиления
• Длина внахлест
• Длина изгиба

Вы можете получить эту информацию из общего листа примечаний вспомогательного чертежа. Итак, теперь у нас достаточно информации для измерения арматуры балки. Как насчет того, чтобы начать оценку?

Верхний продольный стержень (T)
Примените соответствующую формулу, чтобы получить длину обрезки верхнего продольного стержня.
Длина резки верхнего продольного стержня,
= Длина балки – 2 × прозрачная крышка + 2 × длина изгиба – 2 × длина вычета изгиба + длина нахлеста

Сейчас, Длина балки: 20″ + (22′-8″) + 20″ + (8′-4″) + 20″ = 36′ (сверху)
Прозрачное покрытие: 1½»
Длина изгиба: 12D = 12 × 20 = 240 мм, состояние 9½»
Длина вычета изгиба: Длина вычета изгиба для изгиба 90° эквивалентна многократному диаметру стержня = 2 × 20 мм = 40 мм = 1½»

Таким образом, длина реза верхнего продольного стержня составляет
= 36′ – 2 × 1½ дюйма + 2 × 9½ – 2 × 1½ дюйма + 0,
= 37′-1″.

На приведенном выше рисунке показаны три количества верхнего продольного стержня. Итак, полная длина верхнего продольного стержня равна

= 3 × (37′-1″)
= 111′-3″.

Мы знаем, что полная длина усиливающего стержня составляет около 40 футов. Длина верхнего продольного стержня, который мы оцениваем, не превосходит длину запасного стержня. Таким образом, вам не нужно включать длину круга.

Базовый продольный стержень (B)
Рецепт расчета длины реза базового продольного стержня аналогичен уравнению для верхнего продольного стержня. Таким образом, длина дополнительно эквивалентна T1. Это 37′-1″.
Таким образом, абсолютная длина стержня B1 составляет
= количество стержней B1 × длина резки стержня B1
= 3 × (37′-1″)
= 111′-3″.

Дополнительный верхний стержень на опоре 1 (Et1)
Расчет длины обрезки дополнительной верхней стержни выполняется по следующему уравнению:
Длина обрезки Et1 = длина в развернутом виде от опоры + ширина опоры – чистое покрытие + длина изгиба – длина вычета изгиба
Расширенный длина от опоры: 7′-5″
Ширина опоры: 20″
Прозрачная крышка: 1½″
Длина изгиба: 9½″
Длина вычета изгиба: 1½″

Таким образом, длина резки Et1 равна
= (7′-5″) + 20″ – 1½ дюйма + 9½ дюйма – 1½ дюйма
= 9′-7½ дюйма

На чертеже показаны два количества стержня Et1. Таким образом, абсолютная длина Et1 равна
= 2 × (9′-7½»)
19′-3″

Дополнительный верхний стержень на опоре 2 (Et2)
Длина в расширенном состоянии от опоры: 7′-5″
Ширина опоры: ширина опоры для Et2 должна быть шириной опоры 2 + расстояние между опорами 2 и опорой 3 + ширина опоры3 = 20″ + (8′-4″) + 20″ = 11′-8″
Прозрачная крышка: 1½»
Длина изгиба: 9½»
Длина отвода: 1½»

Таким образом, длина резки Et2 = (7′-5″) + (11′-8″) – 1½ дюйма + 9½ дюйма – 1½ дюйма
= 19′-7½ дюйма

Общая длина Et2 = 2 × (19′-7½»)
= 39′-3″

Дополнительная нижняя балка (Eb)
Длина обрезки дополнительной базовой балки составляет,
= Расстояние между опорами – 2 × расстояние между дополнительной базовой балкой и ближайшей опорой
= (22′-8″) – 2 × (2′ -10″)
= 17′

Абсолютная длина дополнительного базового стержня:
= 2 × 17′ (на рисунке выше показаны 2 стержня для Eb)
= 34′

Хомут (S1)
Для оценки хомута необходимо вычислить необходимое количество хомутов для балки и длину отрезка стержня для хомута.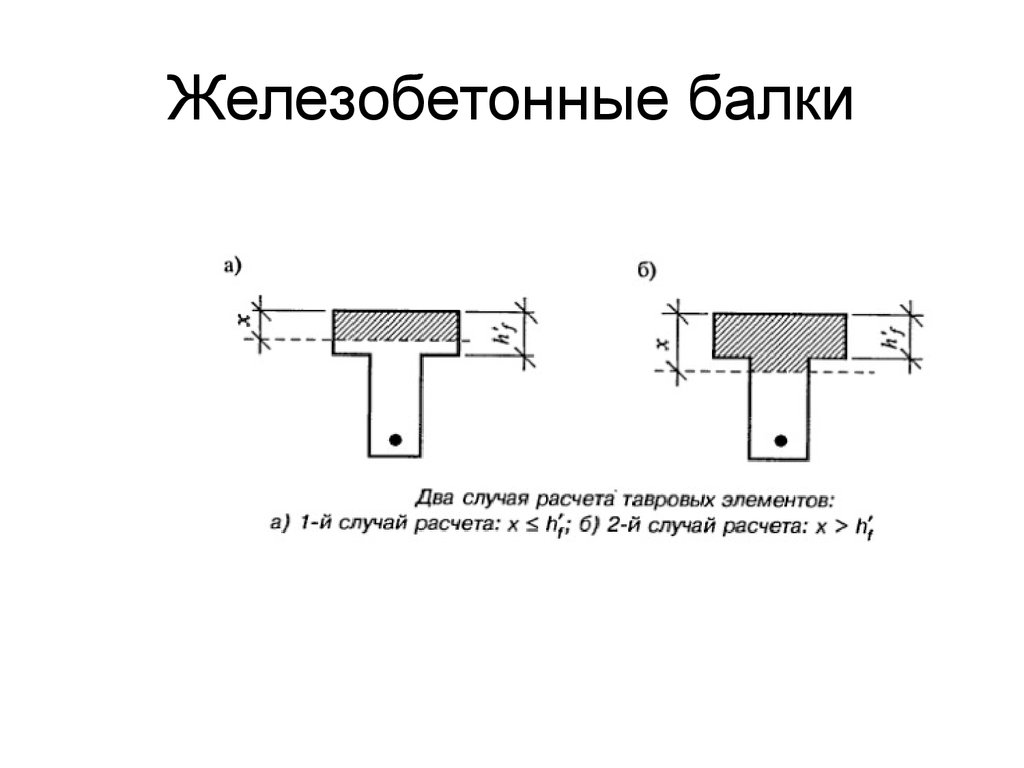
Количество хомутов: необходимое количество хомутов для первого ряда,
= (22′-8″)/4″ +1 = 69 + 1 = 70 шт.
Необходимое количество хомутов для второго диапазона,
= (8′-4″)/4″ + 1 = 25 + 1 = 26 ед.
Общее количество стремян = 70 + 26 = 96 шт.

Уравнение для расчета длины отрезка стержня стремени:
= 2 × (a+b) + 24D (для малого барабана 135°)

Где,
a = длина длинной стороны хомута
b = длина короткой стороны хомута
D = диаметр стержня хомута

Следовательно, длина реза стержня составляет
= 2 × (21″+9″) + 24 × 10
= 69½ дюйма (240 мм = 9½ дюйма)
= 5′-9½ дюйма

Общая длина стержней для всех хомутов,
= 96 × (5′-9½»)
= 556′

Рандаун: общее количество укрепляющих стержней, которое мы оценили для балки до этого момента —

• Пруток ø 20 мм
• T = 111′-3″
• B = 111′-3″
• Et1 = 19′-3″
• Et2 = 19′-7½»
• Eb = 34′

Таким образом, абсолютный стержень ø 20 мм равен
= 111′-3″ + 111′-3″ + 19′-3″ + 19′-7½″ + 34′ = 296′.
стержень ø 10 мм,
S1 = 556 футов

Как бы то ни было, арматура стальная оценивается на рынке в килограммах. Итак, вам нужно изменить длину стержня на килограммы. Удельный вес стержня ø 10 мм составляет 0,188 кг/фут, а стержня ø 20 мм — 0,75 кг/фут. Итак, арматура, необходимая для нашей модельной балки,

• стержень ø 20 мм = 296 футов × 0,75 = 222 кг.
• стержень ø 10 мм = 556 × 0,188 = 105 кг.

Примечание : Когда вам нужно купить арматурный стержень для балки, вы должны добавить 5% больше к расчетной сумме в качестве потерь.

Вот оно! У вас есть количество подкрепления в вашем луче.

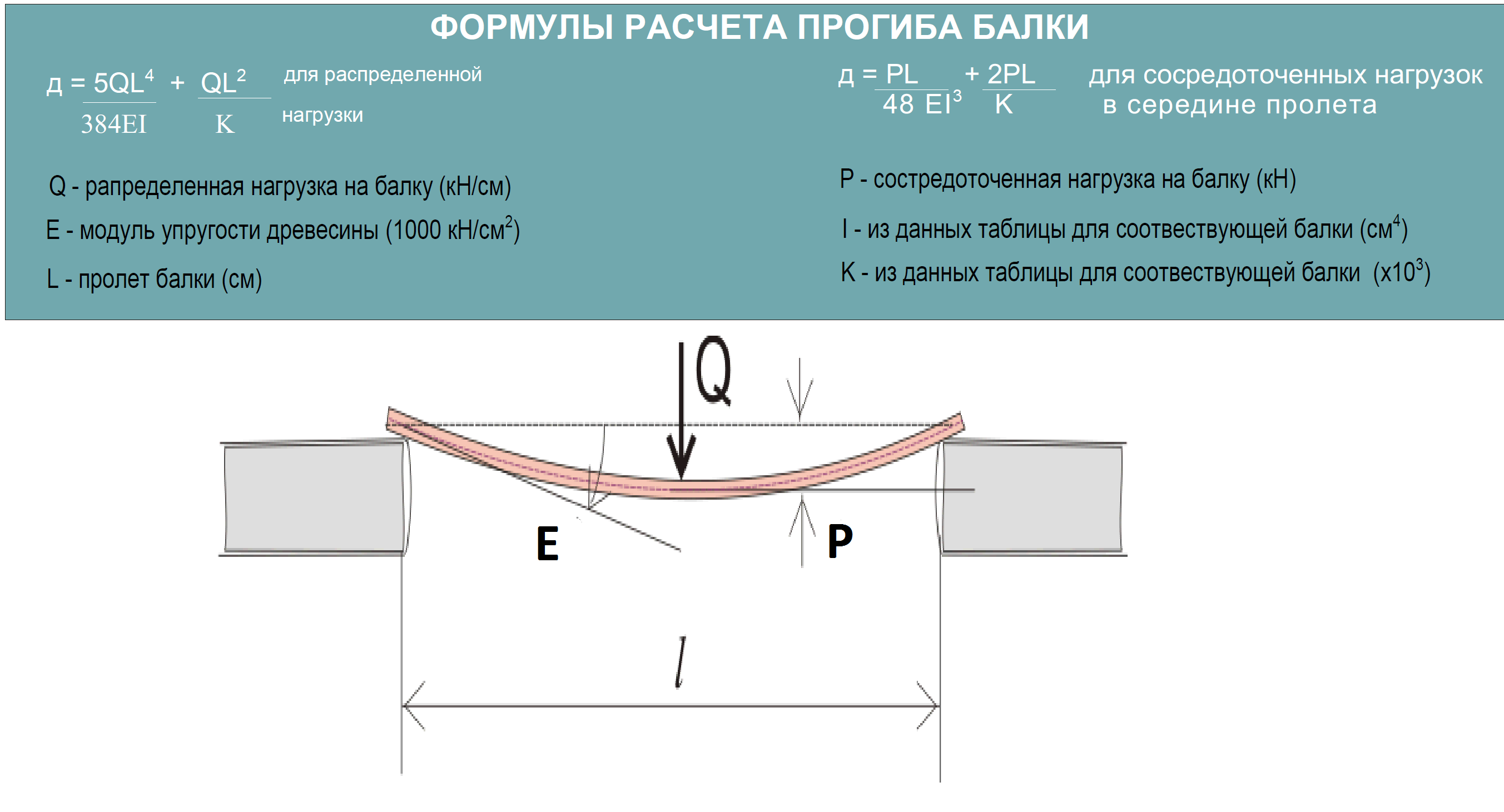
Расчет прогиба железобетонной балки

Главная | Общая информация | Список расчетов | Отзывы

Расчет прогиба железобетонной тавровой балки

Предположения и требования

Рассчитано в соответствии с Eurocode2 (EN1992-1-1:2004).