2.5. Расчет фундамента на устойчивость против опрокидывания и

сдвига

Устойчивость конструкций против опрокидывания следует рассчитывать по формуле

,

где и – моменты соответственно опрокидывающих и удерживающих сил относительно оси возможного поворота (опрокидывания) конструкции, проходящий по крайним точкам опирания, кН·м;

–коэффициент условий работы, принимаемый при проверке конструкции, опирающихся на отдельные опоры, для стадии строительства равным 0,95; для стадии постоянной эксплуатации равным 1,0; при проверке сечений бетонных конструкций и фундаментов на скальных основаниях, равным 0,9; на нескальных основаниях – 0,8;

–коэффициент надежности по назначению сооружения, принимаемый равным 1,1 при расчетах для стадии постоянной эксплуатации и 1,0 при расчетах для стадии строительства.

Опрокидывающие силы следует принимать с коэффициентом надежности по нагрузке, большим единицы.

Удерживающие силы следует принимать с коэффициентом надежности по нагрузке для постоянных нагрузок < 1, для временной вертикальной подвижной нагрузки от подвижного состава железных дорог, метрополитена и трамвая=1.

При расчете фундаментов опор мостов на устойчивость против сдвига по основанию сила стремится сдвинуть фундамент, а сила трения его о грунт(по подошве фундамента) сопротивляется сдвигу. Силаравна

,

где – коэффициент трения фундамента по грунту.

В соответствии с требованиями СНиП 2.05.03 –84 устойчивость конструкций против сдвига (скольжения) следует рассчитывать по формуле

,

где – сдвигающая сила, кН, равная сумме проекций сдвигающих сил на направление возможного сдвига;

–коэффициент условий работы, принимаемый равным 0,9;

–коэффициент надежности по назначению сооружения, принимае

мый равным 1,1;

–удерживающая сила, кН, равная сумме проекций удерживающих сил на направление возможного сдвига.

Сдвигающие силы следует принимать с коэффициентом надежности по нагрузке, большим единицы, а удерживающие силы – с коэффициентом надежности по нагрузке, указанные выше.

В качестве удерживающей горизонтальной силы, создаваемой грунтом, допускается принимать силу, значение которой не превышает активного давления грунта.

При расчете фундамента на сдвиг принимают следующие значении коэффициентов трения кладки по грунту:

Таблица 2.5.1. — Значении коэффициентов трения

Грунты
Глины во влажном состоянии	0,29
Глины в сухом состоянии	0,30
Суглинки и супеси	0,30
Гравийные и галечниковые	0,50
Пески	0,40
Скальные с омыливающейся поверхностью (глинистые сланцы, известняки и т. п.)	0,25
Скальные с неомыливающейся поверхностью	0,6

Пример 2.5.1.Определить устойчивость фундамента опоры моста против опрокидывания, если дано: вертикальная сила =7704 кН; момент опрокидывающих сил=2190 кН·м.Размеры фундамента и другие характеристики приведены на рис.5.

Рис.5. Схема к расчету фундамента на устойчивость против опрокидывания

Решение. Устойчивость конструкций против опрокидывания следует рассчитывать по формуле

.

кН·м

Принимаем и.

Тогда .

Следовательно, проверка на устойчивость против опрокидывания обеспечена.

Пример 2.5.2. Определить устойчивость фундамента опоры моста, опирающейся на глину, против сдвига, если дано: вертикальная сила =7704 кН; момент опрокидывающих сил=2190 кН·м.Размеры фундамента и другие характеристики приведены на рис.5.

Решение. Устойчивость конструкций против сдвига (скольжения) следует рассчитывать по формуле

.

Принимаем и. Из табл.2.5.1. значение коэффициента принимаем равным 0,3.

Тогда удерживающая сила будет равна

кН.

Сдвигающую силу определим по формуле

кН.

кН.

Так как728 < 1891,следовательно, устойчивость фундамента против сдвига по подошве обеспечена.

Расчет отдельно стоящих фундаментов в SCAD office

Инженер, столкнувшийся с расчетом каркаса здания, одним из несущих элементов которого является колонна, придет к необходимости расчета отдельно стоящего фундамента. Для расчета в вычислительном комплексе SCAD разработчики предусмотрели практически полный функционал для определения несущей способности по всем критериям проверки фундамента.

Итак, выполнив построение каркаса, например, металлического потребуется расчет отдельно стоящих фундаментов. Для этого в вычислительном комплексе SCAD необходимо указать узлы, закрепленные от смещения по заданным направлениям и углам поворота (именно в этих узлах можно выполнить расчет реакции опор). Анализу подвергаются чаще всего вертикальная реакция, горизонтальная и момент в плоскости работы конструкции. Вычислительный комплекс SCAD выводит реакции для всех узлов, отмеченных пользователем, как правило, рассматривается три комбинации нагрузок для:

Rz_макс, Rx_соотв, Ruy_соотв

Rz_соотв, Rx_макс, Ruy_соотв

Rz_соотв, Rx_соотв, Ruy_макс

Максимальные значения при большой загруженности схемы визуально определить непросто, можно воспользоваться инструментом «документирование», где с помощью вывода таблицы всех значений из вычислительного комплекса SCAD в MS Excel фильтруется нужные ячейки чисел.

Полученные комбинации значения необходимо далее использовать при расчете отдельно стоящего фундамента. Расчет отдельно стоящих фундаментов можно выполнять и вручную, для этого производятся вычисления давления под подошвой фундамента.

Ввиду возникающего момента, давление получается неравномерным. Вычисление краевых значений производится по формуле

где:

• N – сумма вертикальных нагрузок на фундамент, тс
• A – площадь фундамента, м2
• M — момент от равнодействующей всех нагрузок, действующих по подошве фундамента
• W — момент сопротивления площади подошвы фундамента, м³ (для ленточного фундамента длина сечения 1м) , где b – ширина фундамента.

Следующим этапом расчета отдельно стоящего фундамента становится определение расчетного сопротивления грунта. Вычисления производятся по СП 22.13330.2011 «Основания зданий и сооружений», формула 5.

7. Для расчета нужны инженерно-геологические изыскания слоев грунта рассматриваемой площадки строительства (или непосредственно под отдельно стоящем фундаменте).

Вычисления расчетного сопротивления грунта для отдельно стоящего фундамента можно также производить с помощью программы ЗАПРОС (сателлита вычислительного комплекса SCAD). В программе реализован расчет по СП 22.13330.2011 «Основания зданий и сооружений».

Получившееся значение R должно быть обязательно больше значения давления P. В противном случае требуется уменьшение давления на грунт, например, увеличением площади отдельно стоящего фундамента. Площадь фундамента и момент сопротивления сечения фундамента находятся в знаменателе формулы нахождения давления P, что и заставляет снижать показатель давления.

При расчете отдельно стоящего фундамента нельзя также забывать и о расчете фундаментной плиты на продавливание и вычисления несущей способности. Фундаментная плита по несущей способности рассчитывается как двух консольная балка, нагрузка на которую равна давлению на грунт (III закон Ньютона). Результатом расчета становится установка рабочей «нижней» арматуры сечения плиты.

Усилие на плиту от колонны приходит весьма существенное, поэтому при расчете на продавливание может возникнуть необходимость установки дополнительных ступеней отдельно стоящего фундамента.

Продавливание, как и расчет двух консольной балки, может выполнить программа АРБАТ (сателлита вычислительного комплекса SCAD).

При выполнении всего вышеописанного алгоритма можно считать расчет отдельно стоящего фундамента выполненным.

Теперь вернемся к схеме каркаса здания. Любой фундамент на грунтовом основании (кроме скального) проседает под действием той или иной нагрузки. Полученная дополнительная деформация схемы способствует изменению перераспределению усилий уже в элементах схемы. Отсюда появляется необходимость в некоторых случаях (наиболее ответственных) устанавливать не жесткое защемление, а упругую связь, в месте примыкания колонны к отдельно стоящему фундаменту.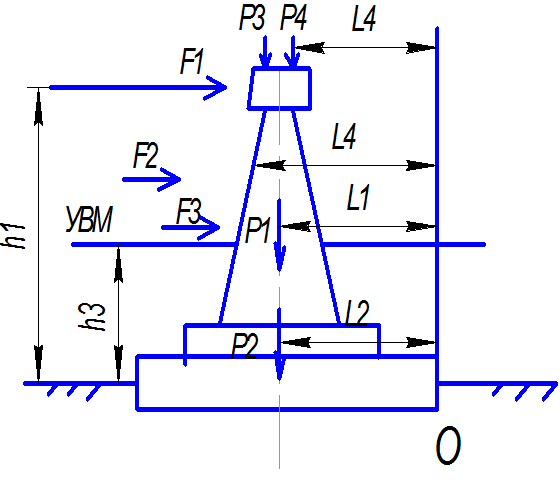 Вычислительный комплекс SCAD не вычисляет автоматически жесткость упругой связи, но можно эту операцию выполнить вручную. Жесткость упругой связи при вертикальном смещении равна отношению несущей способности отдеьлно стоящего фундамента к его осадке, полученное значение измеряется в т/м. Осадка может быть вычислена с помощью программы ЗАПРОС (сателлита вычислительного комплекса SCAD).

Произведя расчет отдельно стоящих фундаментов мы получаем более точную картину деформации здания, а значит и более точные усилия в конченых элементах.

Итак, с помощь вычислительного комплекса SCAD пользователь сможет выполнить требуемый расчет отдельно стоящих фундаментов, подобрать необходимую площадь основания, выполнить расчет на продавливание, определить крен здания, а также учесть перераспределение усилий в зависимости полученной осадки конструкции.

Скачать пример из задачи

Как рассчитать опрокидывающий момент фундамента? – idswater.com

idswater. com

Найдите все, что вам нужно

6 мая 2020 г. Выкл. К idswater

Как рассчитать опрокидывающий момент фундамента?

3. Рассчитайте общий опрокидывающий момент M, измеренный в нижней части фундамента. M/S или обычно завершается вычислением эксцентриситета, который равен M, деленному на P. Если e превышает длину фундамента, деленную на 6, то M/S превышает P/A.

Как рассчитать конструкцию фундамента?

Расчет изолированного фундамента

1. ВВЕДЕНИЕ. Фундаменты – это уложенные на грунт основания, на которых возводится сооружение.
2. РАСПРЕДЕЛЕНИЕ ФУНДАМЕНТА ДЛЯ КОЛОННЫ:
3. Столбец Б:
4. Проверка на изгибающий момент:
5. Проверка одностороннего сдвига.
6. Проверка на двусторонний сдвиг.
7. Проверка нагрузки на подшипник.
8. Проверка длины проявления.

Какой коэффициент опрокидывания?

Коэффициент безопасности при опрокидывании (OSF) представляет собой сумму моментов сопротивления, деленную на сумму моментов опрокидывания. Большинство кодов требует, чтобы этот коэффициент был больше 1,5.

Какие существуют типы фундаментов?

Различные типы фундаментов, используемых в строительстве, описаны ниже:

• Непрерывный фундамент стены. Фундамент, который поддерживает длинную каменную кладку или стену из железобетона, известен как сплошной фундамент.
• Изолированное основание.
• Комбинированный фундамент.
• Ленточный фундамент.
• Ременная опора.
• Основание плота.
• Свайный фундамент.

Как рассчитать вес фундамента?

Как рассчитать размер фундамента

1. Определите ширину и длину цементной плиты в дюймах.
2. Разделите ширину на 12, чтобы преобразовать ее в футы.
3. Разделите длину на 12, чтобы преобразовать ее в футы.
4. Определите глубину или толщину фундамента в дюймах.
5. Умножьте ширину на длину, а затем на глубину.

Сколько существует типов фундаментов?

Существует четыре типа мелкозаглубленного фундамента: Отдельный фундамент или изолированный фундамент.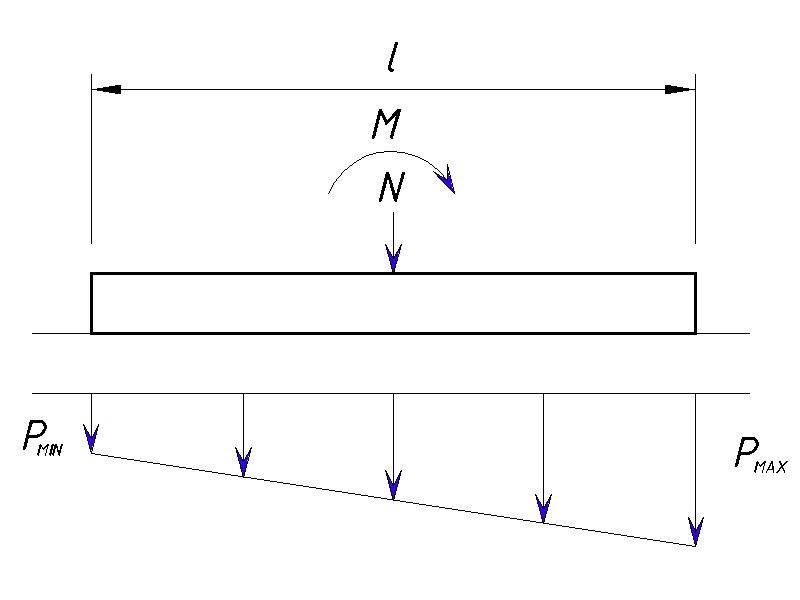 Комбинированное основание. Ленточный фундамент.

Как не перевернуть момент?

Способность стены сопротивляться опрокидыванию рассчитывается аналогично опрокидывающему моменту путем размещения суммы веса стены на расстоянии от общей точки опрокидывания. Этот вес на расстоянии создает момент, а именно момент сопротивления.

Как рассчитать опрокидывающий момент ветра?

Приложенная сила ветра сосредоточена на середине высоты стойки, поэтому опрокидывающий момент равен высоте стойки плюс половина высоты стойки.

Что нужно знать об опрокидывающихся фундаментах?

опрокидывание = P x e Комбинированные фундаменты Конструкция комбинированного фундамента требует, чтобы центр тяжести площади был как можно ближе к равнодействующей двух нагрузок на колонны для равномерного давления и осадки. Подпорные стены При проектировании подпорных стен необходимо учитывать опрокидывание, осадку, скольжение и опорное давление. Вода в

Каков процесс проектирования фундамента?

Конструкция подошвенного фундамента основана на сочетании нескольких процессов, в том числе:

Почему фундамент должен быть устойчивым?

Фундамент должен иметь достаточную способность сопротивляться скольжению, вызванному любыми горизонтальными нагрузками. Фундамент должен быть достаточно устойчивым, чтобы выдерживать опрокидывающие нагрузки. Опрокидывающие нагрузки обычно вызываются горизонтальными нагрузками, приложенными над основанием фундамента.

Как выбирается геометрия фундамента?

Традиционно геометрия фундамента или наголовника сваи выбирается с учетом нефакторизованных нагрузок. Затем выполняется структурный расчет фундамента с использованием расчета прочности в соответствии с ACI 318. Комитет ACI 336 находится в процессе разработки методологии завершения расчета всего фундамента с использованием метода расчета прочности.

КатегорияТенденции

фундаментов при двухосном изгибе — База знаний ClearCalcs

При проектировании бетонных фундаментов определить их прочностную часть довольно просто, используя основные принципы расчета бетона. Однако найти нагрузки для проектирования фундамента может быть намного сложнее, особенно в случае, когда изгиб происходит одновременно в направлениях X и Y. В этой статье подробно рассказывается о том, как ClearCalcs выполняет эти расчеты, и как вы можете сделать то же самое вручную, если вы чувствуете себя авантюрно.

Во-первых, давайте установим четыре основных измерения, от которых будут зависеть остальные наши расчеты. Наши размеры в плане фундамента определяются шириной $B$, параллельной оси X, и длиной $L$, параллельной оси Y.

Соотношение между моментом и осевой нагрузкой лучше всего определяется эксцентриситетом нагрузки, определяемым следующим образом:

$$ e_x = \frac{\left|M_x\right|}{P} \text{ и } e_y = \frac{\left|M_y\right|}{P} $$

Обратите внимание, что для простоты расчетов мы берем абсолютные значения моментов, а это значит, что равнодействующая сила всегда будет в первом квадранте.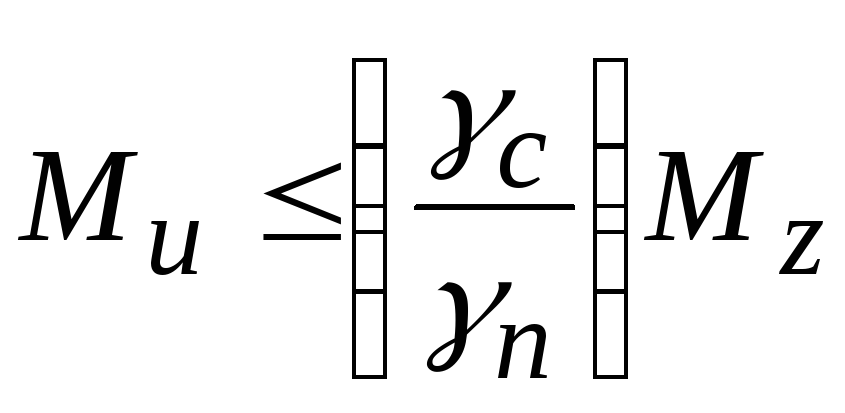 Из-за симметрии значения, которые мы получаем ниже, будут одинаковыми независимо от того, в каком квадранте это происходит.

Расчет несущей способности почвы

Все эти уравнения предоставлены Джоном Беллосом и Николаосом Бакасом в их статье, доступной здесь, и были независимо проверены нашей командой. Они основаны на первых принципах статики и удовлетворяют равновесию сил и моментов для всех случаев. Условные обозначения, которые мы используем, немного отличаются от бумажных, но уравнения остаются прежними.

Зоны эксцентриситета

Самая трудная часть определения распределения напряжения заключается в том, что, поскольку грунт не может сопротивляться подъему за счет растяжения, при больших эксцентриситетах некоторые части фундамента могут отрываться от земли и не нести никакой нагрузки. Форма области, все еще несущей нагрузку, будет варьироваться в зависимости от эксцентриситета нагрузки и будет соответствовать одной из пяти форм, показанных ниже. 92}}\right) \Big/\left(1 +4\dfrac{e_y}{B}\right)$$ и $e_y\leq \dfrac{B}{4}$ 5 $e_x\gt \dfrac{L}{4}$ и $e_y\gt \dfrac{B}{4}$

Эти уравнения могут быть легко усваиваемы компьютером, но их очень трудно рассмотреть, особенно для зон 2–4. На основе показанных выше пределов эксцентриситета мы можем нанести на карту пять различных зон, где: если эксцентриситет нагрузки попадает в эту область, форма нагруженной области будет соответствовать формам, показанным выше. Эта карта зон эксцентриситета позволяет намного легче увидеть, где падает эксцентриситет. Мы сгенерировали эту карту с помощью графического онлайн-калькулятора Desmos — смотрите здесь!

Зоны 3, 4 и 5 простираются довольно далеко от центра фундамента — в частности, коэффициент безопасности опрокидывания всегда будет очень низким, если эксцентриситет находится в зоне 5, и конструкция будет далеко не эффективной.

Профиль давления подшипника

Как только мы определили зону эксцентриситета, мы знаем форму, которую примет наша опорная зона. На данный момент нам нужно определить его. В своей статье Беллос и Бакас определяют площадь опоры с помощью трех точек — максимальное опорное давление ($q_{max}$) и две точки пересечения линии нулевого давления (нейтральная ось основания) с осями, образованными два верхних правых края фундамента ($x_n$ и $y_n$). Перехваты могут быть снаружи фундамента (низкий эксцентриситет) или внутри (высокий эксцентриситет).

Этот метод оказывается весьма удобным позже, когда придет время найти нагрузки на фундамент от опорного давления, как будет показано позже. Три параметра, $q_{max}$, $x_n$ и $y_n$, определены в разделах ниже. Они были получены Bellos & Bakas с использованием принципов равновесия и статики.

Получив свойства профиля подшипника, мы можем сравнить максимальное давление подшипника с нашим допустимым давлением подшипника. От этого будут зависеть размеры фундамента в плане. Как только эти размеры определены, мы переходим к определению поперечных и моментных нагрузок на критический участок фундамента, которые мы рассмотрим в следующем разделе.

Зона 1

Это зона с наименьшим эксцентриситетом, где все основание испытывает сжатие. Перехваты даны:

$$ x_n = L\times \dfrac{1+6\frac{e_x}{L}+6\frac{e_y}{B}}{12 \frac{e_x}{L}} $$

и

$$ y_n = B\times \dfrac{1+6\frac{e_x}{L}+6\frac{e_y}{B}}{12 \frac{e_y}{B}} $$

Максимальное давление подшипника:

$$ q_{max} = \frac{P}{BL}\times \left(1+6\frac{e_x}{L}+6\frac{e_y}{B}\right) $$ 92}}\right) }{\frac{1}{2}-\frac{e_x}{L}} $$

Зона 5

Это, пожалуй, самая простая для расчета зона, и эти уравнения легко вывести графически, используя свойства тетраэдров. Нахождение перехватов:

$$ x_n = 4 L \left(\frac{1}{2}-\frac{e_x}{L}\right) $$

и

$$ y_n = 4B\left(\frac{1}{2} — \frac{e_y}{B}\right) $$

Также встречается максимальное давление в подшипниках:

$$ q_{max} = \frac{P}{BL} \times \frac{3} {8 \left(\frac{1}{2}-\frac{e_x}{L}\right)\left (\frac{1}{2} — \frac{e_y}{B}\right)} $$

Нагрузки на фундамент

Определение нагрузок, действующих на бетонное основание, является следующим шагом в нашем проекте. Он используется для определения толщины основания и необходимой арматуры. Общая основа процедуры заключается в том, что мы должны найти объем под профилем опорного давления, чтобы найти полную поперечную нагрузку, и его центр тяжести, чтобы найти изгибающий момент.

В большинстве программных пакетов используется двойное или тройное интегрирование, которое выполняется численно.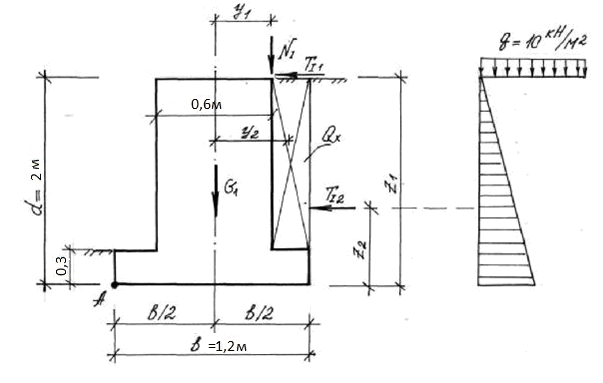 Это, однако, относительно медленно и, что более важно, очень «черный ящик», чего мы стараемся избегать, насколько это возможно. Таким образом, мы разработали собственный метод определения поперечных и моментных нагрузок на фундамент, который мы объясним ниже.

Использование тетраэдров для представления профиля опорного давления

Если мы посмотрим на несущий профиль ниже, то ясно увидим, что перед нами тетраэдр (tet) высотой $q_{max}$ и размером основания $x_n \times y_n$.

Это частный случай тройника с тремя прямыми углами в одной вершине — он называется треугольным тетраэдром . Его объем и центроид легко найти:

$$ \begin{align} Q &= \frac{1}{6}x_ny_nq_{max}\\ \bar{x} &= \frac{x_n}{4} \\ \bar{y} &= \ frac{y_n}{4} \end{aligned} $$

Проблема возникает, когда наш тетраэдр выходит за пределы ширины основания или критического сечения, которое мы определяем как расстояние $a$ от края основания. Внезапно наш хорошо определенный тет оказывается нарезанным, и эти простые свойства не так хорошо применимы. В этом случае нам нужно разбить наш tet на разные компоненты, как показано ниже:

Теперь мы можем видеть, что у нас есть до четырех различных отдельных тетов, которые также являются треугольными, помеченными от A до D. Tet A содержит как B, C, так и D, тогда как Tet B и Tet C содержат Tet D. Это становится важным, когда мы находим наши опорные нагрузки позже. Их свойства зависят от профиля несущего давления грунта, размеров основания и положения критического сечения, которое обычно отличается для сдвига и момента.

Для ножниц:

$$ a = \frac{L}{2}-\frac{\ell}{2}-d $$

И на момент:

$$ a = \frac{L}{2}-\frac{\ell}{2} $$

Где $\ell$ — длина столбца.

Тет А

Найти его проще всего — это идеальный набор, который мы определили выше. Единственное отличие состоит в том, что теперь мы определяем наш центроид по его расстоянию от критического сечения, тогда как ранее он определялся по его расстоянию от края фундамента.

93 \end{выровнено} $$

Чтобы найти наш центр тяжести, мы знаем, что он находится на расстоянии одной четверти длины тета от края основания. Таким образом, центроид около критического сечения:

$$ \bar{y}_B = a- \frac{x_n}{4y_n}\left(y_n -B\right) $$

Тет С

Этот тет связан с меньшим значением $e_x$. Он появляется, когда:

$$ x_n \gt a $$

В этом случае длину найти легко, а вот для нахождения ширины и высоты воспользуемся подобными треугольниками. Получаем наш объем: 93 \end{выровнено} $$

Мы находим центроид около критического сечения, но в данном случае он находится ниже критического сечения, поэтому мы добавляем знак минус:

$$ \bar{y}_C = — \frac{x_n — a}{4} = \frac{a-x_n}{4} $$

Тет Д

Этот tet проявляется только в случаях малых эксцентриситетов, когда длина Tet B больше, чем расстояние до критического сечения:

$$ x_n\left(1-\frac{B}{y_n}\right) >a $$

Это, безусловно, труднее всего найти, так как он застрял внутри как Tet B, так и Tet C.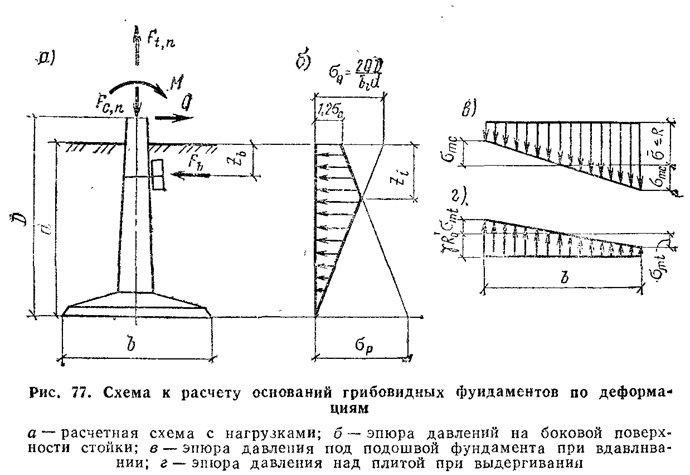 Но это также означает, что мы можем использовать некоторые из их свойств, чтобы облегчить себе жизнь. Для объема: 9{\text{Высота}} \\ &=\frac{q_{max}}{6} \left(\frac{y_n}{x_n}\left(x_n -a\right)-B\right) \left( \frac{x_n}{y_n}\left(y_n -B\right)-a\right) \left(1-\frac{a}{x_n} -\frac{B}{y_n}\right) \\ \ конец {выровнено} $$

Нахождение центроида, который также находится ниже критического сечения:

$$ \bar{y}_D = — \frac{\frac{x_n}{y_n}\left(y_n -B\right)-a}{4} = \frac{a-\frac{x_n}{y_n }\left(y_n -B\right)}{4} $$

Определение фактических нагрузок на фундамент

Теперь, когда у нас есть свойства всех наших множеств, мы можем вернуться к нахождению поперечных и моментных нагрузок. На самом деле это самая простая часть — сдвиг — это просто комбинация объемов, а момент — это комбинация объемов, умноженных на их моментные плечи! Возвращаем нашу диаграмму:

Мы можем составить общее уравнение, чтобы найти сдвиг:

$$ \begin{align} V_{u}&=Q_A-(Q_B-Q_D)-(Q_C-Q_D)-Q_D \\ &= Q_A -Q_B-Q_C+Q_D \end{align} $$

И на момент:

$$ M_u = Q_A \bar{y}_A -Q_B \bar{y}_B -Q_C \bar{y}_C + Q_D \bar{y}_D $$

В зависимости от значений $x_n$ и $y_n$ некоторые из множеств могут исчезнуть, и в этом случае связанные с ними члены удаляются из предыдущих уравнений.