Расчет статически определимых систем с использованием поэтажных схем
Строительство и архитектура \ Строительные конструкции
Страницы работы
5 страниц (Word-файл)
Посмотреть все страницы
Скачать файл
Содержание работы
Многие балочные и рамные статически определимые системы содержат промежуточные шарниры. Для определения опорных реакций в такой системе можно составить три уравнения статики, а также уравнения моментов относительно шарниров. В итоге количество совместно решаемых уравнений будет равно числу искомых реакций плюс число промежуточных шарниров.
Однако указанный способ расчета является слишком громоздким. Поэтому сложные системы стремятся расчленить на простые элементы и рассмотреть их отдельно.
Основные и дополнительные диски. В структуре многих статически определимых систем,
содержащих шарниры, можно выделить основные и дополнительные элементы (диски,
балки, рамы).
Основные диски прикреплены к земле неподвижно (например, при помощи заделки или двух шарнирных опор). Удаление из сооружения основного диска приводит к изменяемости системы. В общем случае основными элементами могут быть не только отдельные стержни, но и геометрически неизменяемые и неподвижные системы.
Дополнительные (присоединенные) диски прикреплены шарнирами к основным дискам, а также могут опираться на землю. Разновидностью дополнительных являются подвесные диски, прикрепленные к двум основным или дополнительным дискам двумя шарнирами. Дополнительные диски самостоятельно использоваться не могут, так как без основных дисков они геометрически изменяемы.
Поэтажные схемы.
Для наглядности расчетная схема конструкции, содержащей основные,
дополнительные и подвесные элементы, изображается в виде поэтажной схемы (схемы взаимодействия).
Естественно, предварительно надо убедиться в геометрической неизменяемости
системы, для чего проводится кинематический анализ.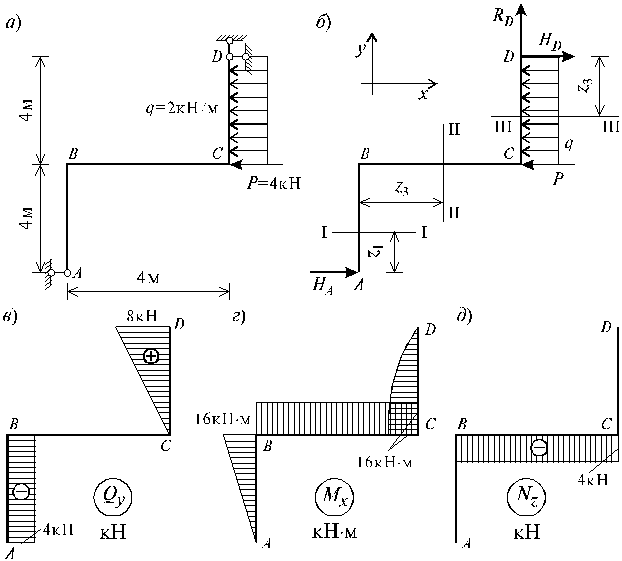
При составлении поэтажной схемы используются следующие принципы:
§ основные диски считаются I этажом;
§ дополнительные и подвесные диски могут быть II, III, … этажами;
§ каждый из шарниров, соединяющих основные и дополнительные диски, заменяется шарнирно неподвижной опорой;
§ один из шарниров, присоединяющих подвесной диск, заменяется шарнирно неподвижной опорой, другой – шарнирно подвижной; при этом в опору нижележащего диска добавляется один стержень;
§ полученная поэтажная схема и каждый ее элемент в отдельности должны быть геометрически неизменяемыми.
На рисунке 3.3 изображена двухпролетная статически определимая рама и ее поэтажная схема. Средняя часть рамы геометрически неизменяема и неподвижна, поэтому она является основным диском.
Рисунок 3.3 | Крайние элементы опираются на основной диск и на
землю, следовательно, это дополнительные диски. На рисунке 3.4, а, б показаны многопролетные балки двух типов и их поэтажные схемы. Основные балки прикреплены к основанию либо с помощью двух шарнирных опор, либо посредством заделки. Дополнительные балки имеют шарнирное соединение с землей, подвесная – только с основными балками. Анализируя поэтажные схемы и их элементы в отдельности, убеждаемся, что все они геометрически неизменяемы. |
Рисунок
Далее можно исследовать каждый элемент поэтажной схемы отдельно. Расчет начинается с верхних этажей, на которые действует только заданная нагрузка. Затем рассчитываются нижние этажи, на которые, кроме приложенной нагрузки, действуют силы в виде опорных давлений верхних этажей. Эпюры внутренних усилий обычно строятся на одной базе для всей системы.
Пример 1 Требуется рассчитать статически определимую раму, которая состоит из двух
элементов АВ и СD, соединенных шарниром. Расчетная схема рамы показана
на рисунке 3.5, а.
Расчетная схема рамы показана
на рисунке 3.5, а.
Рисунок 3.5
Составим поэтажную схему рамы. В ее структуре выделим основную часть АВ, прикрепленную к земле неподвижно (I этаж), и дополнительную CD, присоединенную к основной с помощью шарнира С (II этаж). При этом шарнир С заменим шарнирно-неподвижной опорой (рисунок 3.5, б).
Далее разделим раму на две части, которые будем рассчитывать отдельно (рисунок 3.6). К основной раме кроме заданных нагрузок приложим еще две силы, равные соответствующим опорным реакциям дополнительной рамы. Точки приложения сил и узлы пронумеруем от 1 до 4. Определим величину угла α. Так как tg α =
Расчет дополнительной рамы CD. Определим опорные реакции, для этого составим уравнения равновесия
∑МC = 0: НD · 2a – q · 2a · a = 0;
∑Z = 0: –HC + HD = 0; ∑Y = 0: VC – q · 2a = 0,
Рисунок | откуда HC = qa; VC = 2qa; HD = qa. Для проверки составим уравнение ∑МD = 0: q · 2a · a – VC · 2a + HC · 2a = = 2qa2 – 2qa · 2a + qa · 2a = 0. Проверка выполняется. Далее определим внутренние усилия. При вычислении моментов в скобках будем указывать растянутые волокна. |
Участок D-4. МD = 0, M4 = HDa = qa2 (лев.), QD—4 = –HD = – qa, ND—4 = 0.
Участок С-4 (рисунок 3.7, а). MC = 0, M4 = qa
Рисунок 3. | Из равновесия левой части (∑Y‘ = 0) QC = –HC sin α + VC cos α = = –qa · 0,447 + 2qa · 0,894 = 1,341qa; (∑Z‘ = 0) NC = HC cos α + VC sin α = = qa · 0,894 + 2qa · 0,447 = 1,788qa. Из равновесия правой части (∑Y‘ = 0) Q4 = –HD sin α = –qa · 0,447 = –0,447qa; (∑Z‘ = 0) N4 = HD cos α = qa · 0,894 = 0,894 qa.По полученным данным для рамы CD строим эпюры
(рисунок 3.8). Эпюра Q пересекает ось на некотором расстоянии z‘0 от точки С, следовательно, здесь будет
максимальный момент (рисунок 3. z‘0 = = 1,68 а. |
Максимальный момент
Mmax = VC z‘0 cos α – HC · z‘0 sin α – q· 0,5 · (z‘0 cos α)2 = 2qa· 1,68 a · 0,894 –
– qa· 1,68 a · 0,447 – q· 0,5 · (1,68 a · 0,894)2 = 1,125qa2.
Расчет основной рамы АВ. Определим опорные реакции, для этого составим уравнения равновесия
∑МВ = 0: VB · 3a – P · 3a – HC · 2a – VC · 3a = 0;
∑МA = 0: VA · 3a – P · 3a – HC · 2a = 0; ∑Z = 0: –HA + HC + P = 0,
откуда
VA = 1,667 qa; VB
= 3,667qa; HA = 2qa.
Для проверки составим уравнение ∑Y = 0:
VB – VA – VC = 3,667 qa –1,667 qa – 2qa = 0.
Проверка выполняется.
Далее определим внутренние усилия.
Участок A-1. МA = 0, M1 = HA· 3a = 2qa · 3a = 6qa2 (прав.),
QA-1 = HA = 2qa, NA-1 = VA = (5/3)qa.
Участок 1-2. M1 = 6qa2 (ниж.), M2 = HC· a = qa · a = qa2 (ниж.),
Q1-2 = –VA = –1,667qa, N1-2 = HA = 2qa.
Участок 2-3. М2 = qa2 (лев. ), M3 = 0,
), M3 = 0,
Q2-3 = –HС = –qa, N
Участок В-3. МВ = M3 = 0, QВ-3 = 0, NВ-3 = –VВ = –3,667qa.
По полученным данным строим эпюры (см. рисунок 3.8). ý
Рисунок 3.8
Таким образом, поэтажная схема делает более понятной работу сложной системы и упрощает ее расчет. Пример расчета многопролетной балки с использованием поэтажной схемы будет рассмотрен далее.
Похожие материалы
Информация о работе
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
 Даля 166
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Безделев В.В., Дмитриева Т.Л. Расчет статически неопределимых рам методом сил . Методическое пособие для студентов строительных специальностей
Практикум- формат doc
- размер 1.46 МБ
- добавлен 21 декабря 2010 г.
Иркутск: Издательство ИрГТУ. – 2002, 34 с.
Содержит указания по расчету статически неопределимых систем
методом сил. Дан пример расчета рамы. Вычисления произведены в
среде MathCad 2000. Контроль расчета выполнен с использованием
системы COMPASS.
Дан пример расчета рамы. Вычисления произведены в
среде MathCad 2000. Контроль расчета выполнен с использованием
системы COMPASS.
Смотрите также
Практикум- формат doc
- размер 547.89 КБ
- добавлен 21 декабря 2010 г.
Иркутск: Изд-во ИрГТУ. –2004, 25 с. Содержит методические указания по решению статически неопределимых арок методом сил. Содержание: Основные термины и определения Теоретические сведения Общий ход расчета Бесшарнирная арка Двухшарнирная арка Пример расчета двухшарнирной арки с затяжкой Расчет арки в среде MathСAD Особенности расчета арок в программной системеCOMPASS Сравнение результатов расчета Приложение №1 Приложение №2 Список литературы
- формат djvu
- размер 7.97 МБ
- добавлен
24 марта 2011 г.

Учебное пособие. М.: Стройиздат, 1965. — 406 с. В книге компактно и полно изложены различные применяющиеся на практике методы расчета статически неопределимых рам (метод сил, метод перемещений, смешанный метод, методы трех и четырех моментов, метод моментных фокусов, метод угловых фокусов, приближенные методы расчета). Книга построена следующим образом. В первой главе даны общие понятия и основные теоремы о деформациях упругих систем. Каждому ме…
- формат djvu
- размер 2.23 МБ
- добавлен 18 октября 2010 г.
Учеб. пособие, 2009. 168 с. Изложены методы строительной механики для расчета статически неопределимых несущих систем вагонов. Излагаются особенности анализа напряженного состояния и устойчивости несущих элементов вагонов. Пособие может быть полезно студентам строительных и машиностроительных специальностей и инженерам.
- формат doc
- размер 52.94 МБ
- добавлен 04 июня 2011 г.
Расчет статически неопределимых рам методом сил. Расчет статически неопределимых рам методом перемещений. Самарский государственный Архитектурно-строительный университет. специальность — ПГС (заочное отделение), 4 курс, выполнено в word, 23 страницы.
- формат doc
- размер 2.37 МБ
- добавлен 07 сентября 2009 г.
М.: Изд-во, РУДН, 2004г. Для студентов 3-го курса специальности «Строительство». Подготовлено на кафедре сопротивления материалов. Содержание. Основные понятия и положения. Кинематический анализ сооружений. Расчет статически определимых сооружений. Учет подвижной статической нагрузки. Загрузка линий влияния. Линии влияния при узловом действии нагрузки. Плоские статически определимые фермы. Построение линий влияния усилий в стержнях ферм. Расчет…
Учет подвижной статической нагрузки. Загрузка линий влияния. Линии влияния при узловом действии нагрузки. Плоские статически определимые фермы. Построение линий влияния усилий в стержнях ферм. Расчет…
- формат pdf
- размер 1 МБ
- добавлен 15 апреля 2011 г.
Пособие содержит теоретические сведения и основные положения расчета статически неопределимых систем методом сил, перемещений, смешанным и комбинированным способами при силовых, температурных и кинематических воздействиях. Многочисленные примеры расчета сопровождаются необходимыми пояснениями к решению и включают задания для самоконтроля работы. Учебное пособие предназначено для студентов строительных специальностей, изучающих общий курс строител…
- формат djvu
- размер 16.2 МБ
- добавлен
24 октября 2009 г.
Основы расчета статически определимых и статически неопределимых стержневых систем на статическую и динамическую нагрузки и на устойчивость, а также основы приближенного расчета подпорных стенок. М.: Стройиздат, 1960 г. – 516 с. 1. Кинематический анализ сооружений 2. Графические методы строительной механики и веревочный многоугольник 3. Общая теория линий влияния и примеры их применения 4. Общие свойства статически определимых систем 5. Трехшарн…
- формат pdf
- размер 19.81 МБ
- добавлен 09 августа 2011 г.
Учебное пособие для вузов.- М.: Высш. школа, 1982 г.- 400 с. Изложенный в книге курс: строительной механики рассчитан на три семестра обучения и включает спецкурс, предусмотренный учебной программой Минвуза СССР для строительных специальностей вузов. В отличие от прежних учебников в нем значительно сокращена традиционная часть, относящаяся к расчету статически определимых систем и к классическим методам расчета рам. Взамен расширены новые разделы…
Взамен расширены новые разделы…
- формат djvu
- размер 270.68 КБ
- добавлен 06 января 2011 г.
Иркутск: Издательство ИрГТУ — 2000 г. — 32 стр. Описание: Приведены теоретические сведения о расчете гибких сжато-изогнутых статически определимых и статически неопределимых стержней с учетом деформированной схемы. Рассмотрены примеры определения перемещений и возникающих дополнительных усилий для наиболее распространенных расчетных схем и условий загружения гибкого стержня, рекомендуемые для аудиторных и самостоятельных занятий. Лекции предназн…
- формат djvu
- размер 953.98 КБ
- добавлен 07 апреля 2010 г.
Одесса: 2001г. -155с. Методы построения эпюр в статически определимых и статически неопределимых системах для студентов механических специальностей, Книга состоит из 4 глав, в которых достаточно подробно рассматриваются методы построения эпюр внутренних силовых факторов статически определимых и статически неопределимых стержневых системах. Книга снабжена большим количеством примеров.
Книга снабжена большим количеством примеров.
3.3: Определенность и устойчивость балок и рам
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 42953
- Рене Альдерлистен
- Делфтский технологический университет через TU Delft Open
Перед выбором аналитического метода важно установить определенность и устойчивость структуры. Детерминированная структура — это структура, неизвестная внешняя реакция или внутренние элементы которой могут быть определены только с помощью условий равновесия. Неопределенной конструкцией является такая, неизвестные силы которой не могут быть определены только условиями статического равновесия и потребуют, кроме того, рассмотрения условий совместимости различных частей конструкции для ее полного анализа. Кроме того, структуры должны быть стабильными, чтобы иметь возможность выполнять свои желаемые функции. Конструкция считается устойчивой, если она сохраняет свою геометрическую форму при воздействии внешних сил.
Кроме того, структуры должны быть стабильными, чтобы иметь возможность выполнять свои желаемые функции. Конструкция считается устойчивой, если она сохраняет свою геометрическую форму при воздействии внешних сил.
Формулы устойчивости и детерминированности балок и рам
Условия определенности, неопределенности и неустойчивости балок и рам можно сформулировать следующим образом: \[\begin{array}{l} 3 m+r<3 j+C \text { Структура статически неустойчивая} \\ 3 m+r=3 j+C \text { Структура статически определимая}\\ 3 m+r>3 j+C \text { Структура статически неопределимая} \end{array }\]
где
- \(r\) = количество опорных реакций.
- \(C\) = уравнения условий (два уравнения для одного внутреннего ролика и одно уравнение для каждого внутреннего штифта).
- \(м\) = количество участников.
- \(j\) = количество суставов.
\(Таблица 3.1\). Виды опор.
Альтернативная формулировка для определения и устойчивости балок и рам
\[\begin{array}{l} r+F_{i}<3 m \text { Конструкция статически неустойчива}\\ r+F_{i }=3 m \text { Структура статически определимая}\\ r+F_{i}>3 m \text { Структура статически неопределимая} \end{массив}\]
где
- \(r\) = количество реакций поддержки.
- \(F_{i}\) = количество сил реакции, передаваемых внутренним шарниром или внутренним роликом.
- \(м\) = количество участников.
Пример 3.1
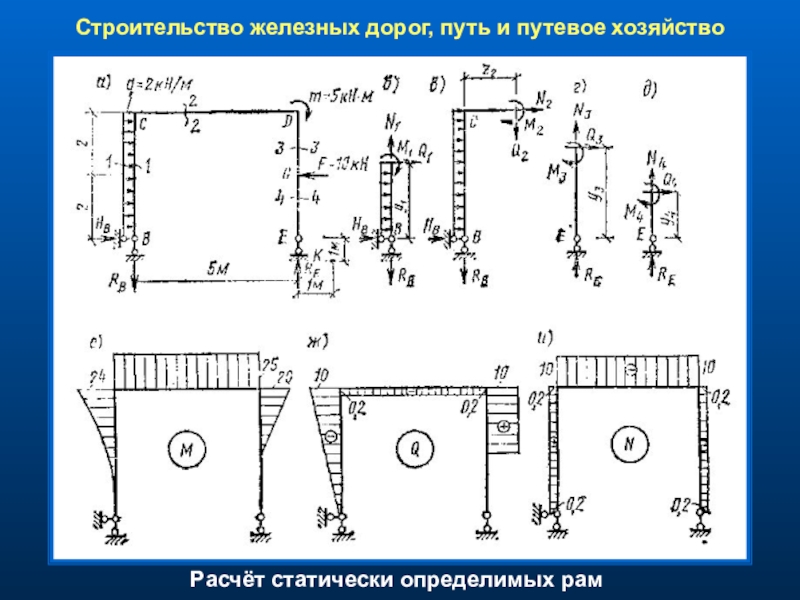
Классифицируйте балки, показанные на рис. 3.1–рис. 3.5, как стабильные, детерминированные или недетерминированные, и при необходимости укажите степень неопределенности.
\(рис. 3.1\). Луч.
Решение
Сначала нарисуйте диаграмму свободного тела каждой балки. Чтобы определить классификацию, примените уравнение 3.3 или уравнение 3.4. 9{\circ}\).
\(рис. 3.5\). Луч.
Решение
Используя уравнение 3.3, \(r = 5\), \(m = 5\), \(c = 2\), \(j = 6\). Применение уравнения приводит к \(3(5) + 5 = 3(6) + 2\) или \(20 = 20\). Следовательно, балка статически определима.
Используя уравнение 3.4, \(r = 5\), \(m = 3\), \(F_{i} = 4\). Применение уравнения приводит к \(5 + 4 > 3(3)\) или \(9 = 9\). Следовательно, балка статически определима.
Пример 3. 2
2
Классифицируйте кадры, показанные на рисунках с рис. 3.6 по рис. 3.8, как стабильные или нестабильные, а также определенные или неопределенные. Если неопределенно, укажите степень неопределенности.
\(рис. 3.6\). Рамка.
Решение
Используя уравнение 3.3, \(r = 3\), \(m = 3\), \(c = 0\), \(j = 4\). Применение уравнения приводит к \(3(3) + 3 = 3(4) + 0\) или \(12 = 12\). Следовательно, рама статически определима.
Используя уравнение 3.4, \(r = 3\), \(m = 1\), \(F_{i} = 0\). Применение уравнения приводит к \(3 + 0 = (3)(1)\) или \(3 = 3\). Следовательно, рама статически определима.
Примечание. При использовании уравнения 3.3 для классификации рамы рама должна быть разобрана в местах соединений, чтобы правильно определить количество элементов. 9{\circ}\).
Примечание. При использовании уравнения 3.4 для классификации рамы с замкнутой петлей, как указано здесь, петля должна быть разрезана методом разреза, и при анализе следует учитывать внутренние реакции в разрезе.
Эта страница под заголовком 3.3: Определенность и стабильность балок и рам распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Рене Альдерлистеном (TU Delft Open) через исходный контент, который был отредактирован к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Рене Альдерлистен
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- источник@https://textbooks.
 open.tudelft.nl/textbooks/catalog/book/15
open.tudelft.nl/textbooks/catalog/book/15
- источник@https://textbooks.
Статическая детерминированность жестких рам
1.1 Введение
Конструкция устойчива, когда она поддерживает баланс силы и момента. В результате мы знаем, что из статики, если структура должна быть в равновесии;
∑Fy = 0; ∑Fx = 0; ∑Mi = 0; ——————- (1.1)
Где;
∑Fy = сумма вертикальных сил
∑Fx = сумма горизонтальных сил
∑M i = сумма моментов составляющих сил, действующих в плоскости x-y, проходящей через точку i .
Если количество ограничений в конструкции позволяет использовать уравнение статики (уравнение 1.1) для анализа конструкции, говорят, что конструкция является статически определимой. В противном случае оно статически неопределимо, и для анализа используется дополнительное уравнение, полученное из соотношения нагрузка-деформация. Для записей, есть два хорошо известных подхода к анализу неопределенных структур, и они есть;
1. Методы гибкости – когда конструкция анализируется с учетом неизвестных сил
Методы гибкости – когда конструкция анализируется с учетом неизвестных сил
2. Методы жесткости – когда конструкция анализируется с учетом неизвестных перемещений
Конструкция может быть неопределенной из-за избыточных компонентов реакции и/или избыточных члены. Обратите внимание, что избыточная реакция или элемент на самом деле не являются необходимыми для удовлетворения минимальных требований стабильности и статического равновесия. Однако в структурах желательна избыточность, потому что они являются более дешевой альтернативой детерминированным структурам. Степень неопределенности (обозначаемая в этом посте как RD) равна количеству неизвестных составляющих сил/внешних реакций, которые превышают уравнения равновесия, доступные для их решения.
1.2 Определение жестких рам
В жестких рамах приложенная система нагрузок передается на опоры за счет создания осевых нагрузок, поперечных сил и изгибающих моментов в элементах. Поскольку для статического равновесия требуются три компонента реакции, общее число неизвестных равно;
U = (3 × m) + r ————— (1. 2)
2)
Поскольку у нас есть три уравнения равновесия, мы имеем (3 × n) уравнений, следовательно;
RD = (3m + r) – 3n – s ————— (1,3)
Где;
m = количество стержней
r = количество опорных реакций
n = количество узлов
S = количество особых условий (например, внутренний шарнир)
Другое уравнение, которое можно использовать для расчета степени неопределенности в рамах:
RD = R – e – S ———— (1.4)
Где;
R = количество опорных реакций
e = количество уравнений равновесия (т.е. 3)
S = количество особых условий (например, внутренний шарнир)
Всякий раз;
RD = 0 (структура статически определима и устойчива)
RD < 0 (структура неустойчива)
RD > 0 (структура статически неопределима)
1.3 Решенные примеры
В кадрах, показанных ниже, классифицируйте следующие кадры как
Решение
Используя уравнение 1.3
RD = (3m + r) – 3n – s
(a) m = 6, r = 6, n = 7, s = 1
RD = [3(6) + 6] – 3(7) – 1 = 2, Следовательно, репер неопределен до 2-го порядка
(б) m = 5, r = 5, n = 6, s = 2
RD = [3(5) + 5] – 3(6) – 2 = 0, Следовательно, система статически определима
( в) m = 4, r = 4, n = 5, s = 1
RD = [3(4) + 5] – 3(6) – 1 = 0, Следовательно, репер статически определим
(d) m = 3, r = 5, n = 4, s = 0
RD = [3(5) + 5] – 3(4) – 0 = 2, Следовательно, репер статически неопределим 2-го порядка
(e) m = 4, r = 5, n = 5, s = 1
RD = [3(4) + 5] – 3(5) – 1 = 1, Следовательно, репер статически неопределим в 1-м порядке
(е) m = 3, r = 3, n = 4, s = 1
RD = [3(3) + 3] – 3(4) – 1 = -1, Следовательно, система неустойчива
Альтернативно, используя уравнение 1.

 7
7 7, б). Найдем величину z‘0 из подобия треугольников:
7, б). Найдем величину z‘0 из подобия треугольников: