1.2 Расчет статически определимых многопролетных балок на неподвижную и подвижную нагрузки
Многопролетные статически определимые балки представляют собой протяженные балочные конструкции, перекрывающие несколько пролетов и состоящие из простых балок, соединенных между собой шарнирами (рис. 1.14).
Особенность расчета подобных стержневых конструкций заключается в расчленении многопролетной балки в шарнирных соединениях на отдельные простые балки, расчет которых осуществляется по методам сопротивления материалов.
В этом случае составляется поэтажная схема балки, в которой определяются основная (несущая) и вспомогательные балки, опирающиеся на несущую балку, имеющую три связи с землей.
На рис. 1.15, а показана поэтажная схема многопролетной балки, приведенной на рис. 1.14, а. Несущей балкой здесь является балка АС, которая остается неподвижной при удалении других вспомогательных балок СЕ и Е

Статический расчет (расчет на неподвижную нагрузку) начинается с верхней балки. Следующая вспомогательная балка рассматривается под воздействием своей внешней нагрузки и реакции в опорном шарнире и т. д.
Верхняя балка ЕF нагружена активной силой Р, следующая балка СЕ нагружена только реакцией Rе, возникающей в шарнире Е. Аналогично, балка АС будет нагружена только реакцией Rс.
При расчете на подвижную нагрузку наиболее удобным способом построения линий влияния в многопролетных балках является кинематический способ. В качестве иллюстрации на рис. 1.16 приведены линии влияния реакции RА, поперечных сил и моментов в сечении «n» справа от опоры D.
Пример
1. 2. Для
заданной статически определимой
многопролетной балки (рис. 1.17, а)
необходимо, используя поэтажную схему
балки, построить эпюры внутренних
усилий. Построить линии влияния реакций RA и RB,
линии влияния М и Q в сечениях n (слева от
опоры В)
и в сечении m.
Вычислить по ним внутренние усилия и
сравнить со значениями, полученными
при построении эпюр.
Построить линии влияния реакций RA и RB,
линии влияния М и Q в сечениях n (слева от
опоры В)
и в сечении m.
Вычислить по ним внутренние усилия и
сравнить со значениями, полученными
при построении эпюр.
Решение. 1. Для построения поэтажной схемы многопролетной балки проводим анализ заданной стержневой системы., которая состоит их двух простых балок АС и СD. Балка АС, имеющая три связи с землей, является основной (несущей), а балки СD вспомогательная. В соответствии с этим и строим поэтажную схему (рис. 1.17, б).
2. Для статического расчета построения эпюр внутренних усилий рассмотрим каждую балку. Начинаем расчет с верхней вспомогательной балки
mD = 0, q∙4∙1 — Rc∙3 = 0,
RC = 40/3 кН.
mC = 0, Rd∙3 — q∙4∙2 = 0.
RD = 80/3 кН.
Проверка: y = 0.
RD q∙4 + RC = 80/3 40 + 40/3 = 0.
Вычисляем по участкам внутренние усилия.
1й участок. 0 < x1 < 1 м.
Q1 = q∙x1Qx=0 = 0, Qx=1 = 10 кН.
M1 = — q∙x12/2, Mx=0 = 0, Mx=1 = 5 кНм,
Mx=0. 5 = 1.25 кНм
5 = 1.25 кНм
2-й участок. 0<x2<3 м.
Q2 = RC — q∙x2, Qx=0 = 13.3 кН, Qx=3 = — 16,7 кН, Qm
M2 = R∙сx2 — q∙x22/2, Мх=0 = 0, Мх=3 = — 5 кНм.
На участке CD поперечная сила Q меняет знак. Q2 = Rc — q∙x0 = 0,
х0 = Rc/q = 1.33 м и
Мх=1,33 = 13,3∙1,33 —
10∙1,33∙0,67 = 8,89 кНм.
Мm= Мх=1 = 13,3∙1 — 10∙1∙0,5 = 8,3 кНм
По полученным значениям строим эпюры М и Q для балки DЕ (рис. 1.18).
Рассмотрим теперь балку AC (рис. 1.19), которая находится под воздействием реакции со стороны балки CDRС. Реакция RС должна быть направлена в сторону, обратную направлению этой же реакции, приложенной к балке CD, поскольку при совмещении балок в шарнире C эти реакции должны быть взаимно уравновешены. Проводим статический расчет балки AC.
Определяем опорные реакции.
mA = 0. RВ∙2 – RС∙4 = 0.
RВ = 80/3 = 26.
mB = 0. – RС∙2 + RА∙2 = 0.
RА = 13.3 кН.
Проверка реакций. y=0.
RА + RВ RС = 13.3 + 26,7 13.3 = 0.
Вычисляем по участкам внутренние усилия.
3-й участок. 0 < x3 < 2 м.
Q3 = Rc 13.3 кН.
M3 = Rcx3. Мх=0 = 0, Мх=2 = 26,7 кНм.
4-й участок. 0 < x4 < 2 м.
Q 4 = RА = — 13. 3 кН.
3 кН.
M4 = RАx4, Мх=0 = 0, Мх=2 = 26,7 кНм.
По полученным значениям строим эпюры Q и М в простой балке (рис. 1.19).
Совместим все построенные эпюры внутренних усилий вдоль многопролетной балки в едином масштабе (рис. 1.17, в, г) и проведем окончательную проверку на соответствие их заданной нагрузке.
3. Строим линии влияния двух реакций RА и RС и поперечной силы и изгибающего момента для сечений m и n. Построение линий влияния будем проводить кинематическим способом.
Так, при построении линии влияния реакции
 Это единичное перемещение приведет к
повороту консольной балки АС вокруг опоры В.
Шарнир С опустится вниз и повернет балку СD вокруг опоры D Полученная в результате схема перемещений
и дает вид линии влияния этой реакции.
Аналогично получена линия влияния RС путем вертикального смещения опоры С вверх на единицу.
Это единичное перемещение приведет к
повороту консольной балки АС вокруг опоры В.
Шарнир С опустится вниз и повернет балку СD вокруг опоры D Полученная в результате схема перемещений
и дает вид линии влияния этой реакции.
Аналогично получена линия влияния RС путем вертикального смещения опоры С вверх на единицу.При построении линий влияния Q и М необходимо убрать связи, воспринимающие поперечную силу и изгибающий момент. То есть, для построения линии влияния Q в сечении n нам необходимо в этом сечении дать торцам взаимное вертикальное смещение на единицу. Отметим, что если торцы стержней параллельны, то параллельны друг другу левый и правый стержни целиком. Аналогично поступаем и с сечением m при построении линии влияния Qm.
Врезав
поочередно в сечениях n и m шарниры и задав единичное угловое
смещение получаем эпюры возможных
перемещений, дающих вид линий влияния Мm и Мn (рис. 1.20).
1.20).
4. Подсчитаем значения внутренних усилий в заданных сечениях по линиям влияния. Для этого нам необходимо интенсивность распределенной нагрузки q умножить на площадь, очерченную линией влияния под нагрузкой. При перемножении используем следующие правила знаков: нагрузки, направленные вниз и ординаты линий влияния и площади, расположенные выше осевой линии положительны.
Qm =
Мn = q∙( — 0,523 + 0.512/3) = 10∙(-3 + 1/3)= 26.7 кНм.
Qn = q∙(- 0,5∙1∙3 + 0,5∙1∙1/3) = 10∙(-3/2 + 1/6)= — 13.3 кН,
Mm = q∙(0,52/3∙3 — 0.511/3) = 10∙(1 — 1/6)= 8.3 кНм.
Значения внутренних
усилий, полученные по линиям влияния,
совпадают со значениями расчета на
постоянную нагрузку.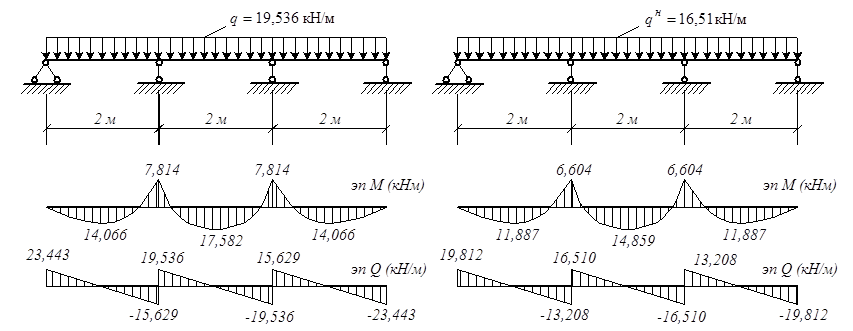
Пример 1.3. Для заданной статически определимой многопролетной балки (рис. 1.21, а) необходимо, используя поэтажную схему балки, построить эпюры внутренних усилий. Построить линии влияния двух опорных реакций и линии влияния М и Q в сечениях m и n. Вычислить по ним внутренние усилия и сравнить со значениями, полученными при построении эпюр. В расчетах принять d = 1,5 м, Р = 45 кН, q = 6 кН/м.
Решение. 1. Для построения поэтажной схемы многопролетной балки проводим анализ заданной стержневой системы, которая состоит их трех простых балок АВ, ВD и DЕ . При этом видно, что консольная балка АВ, имеющая три связи с землей, является основной (несущей), а балки ВD и DЕ вспомогательными. В соответствии с этим и строим поэтажную схему, представив балку АВ как опорную (рис. 1.8, б).
2. Для статического
расчета
построения эпюр внутренних усилий
рассмотрим каждую балку отдельно.
Начинаем расчет с верхней вспомогательной
балки DЕ (рис. 1.22).
Определяем опорные реакции.
Для статического
расчета
построения эпюр внутренних усилий
рассмотрим каждую балку отдельно.
Начинаем расчет с верхней вспомогательной
балки DЕ (рис. 1.22).
Определяем опорные реакции.
mD = 0, P∙2d+RE∙3d = 0, RE = 30 кН.
mE=0, — RD∙3d + P∙d = 0. RD = 15 кН.
Проверка:
y = 0. RD P + RE =15 45 + 30 = 0.
Вычисляем по участкам внутренние усилия.
1й участок. 0 < x1 < 1,5 м.
Q1 = Rе, Qx=0 = Qx=1,5 =
30 кН.
M1 = Rex1, Mx=0 = 0, Mx=1,5 = 45 кНм.
2-й участок. 0 <x2 <3 м.
Q2 = RD, Qx=0 = Qx=3 = 15 кН;
M2 = Rdx2, Мх=0 = 0, Мх=3 = 45 кНм.
По полученным значениям строим эпюры М и Q для балки DЕ (рис. 1.22).
Рассмотрим
теперь балку ВD (рис. 1.23), которая находится под воздействием
реакции со стороны балки DE RD.
Реакция RD должна быть направлена в сторону,
обратную направлению этой же реакции,
приложенной к балке DЕ,
поскольку при совмещении балок в шарнире D эти реакции должны быть взаимно
уравновешены. Проводим статический
расчет балки ВD.
Проводим статический
расчет балки ВD.
mB = 0. RC∙2d – RD∙3d = 0.
RC = 22,5 кН.
mС = 0. – RB∙2d – RD∙d = 0.
RB = 7,5 кН.
Знак минус у реакции RBозначает, что она направлена в обратную сторону. Направим ее вниз, зачеркнув первоначально выбранное направление и в дальнейших расчетах значение реакции RBбудем принимать положительным.
Проверка реакций. y=0.
RB + RC RD =
7,5 + 22,5
15 = 0.
Вычисляем по участкам внутренние усилия.
3-й участок. 0<x3<1,5 м.
Q3 = RD, Qx=0 = Qx=1,5 = 15 кН.
M3 = RDx3. Мх=0 = 0, Мх=3 = 22,5 кНм.
4-й участок. 0 < x4 < 3 м.
Q4 = RB, Qx=0 =Qx=3 = 21,5 кН.
M4 = RBx4, Мх=0 = 0, Мх=3 =
22,5 кНм.
По полученным значениям строим эпюры Q и М во второй простой балке (рис. 1.23).
Консольная балка АВ нагружена распределенной нагрузкой и реакцией RBсо стороны балки ВD, направленной вверх (рис. 1.24). В данном случае при вычислении внутренних усилий можно обойтись без определения реакций, рассматривая правую часть балки.
5-й участок. 0 < x5 < 6 м.
Q5 = q∙x5 RB,
Qx=0 = 7, ∙5 кН, Qx=6 = 28,5 кН,
M5 = RB∙x5 q∙x2/2,
Мх=0=0, Мх=3=4,5 кНм,
Мх=6=63
кНм.
Поскольку Q на 5-м участке меняет знак, найдем координату х0, при которой:
Q5 = q∙x0 RB = 0,
тогда х0 = 7,5/6 = 1,25 м.
Мх=1,25 = 4,7 кНм.
Эпюры М и Q для основной балки показаны на рис. 1.24.
Совместим все построенные эпюры внутренних усилий вдоль многопролетной балки в едином масштабе (рис. 1.21, в, г) и проведем окончательную проверку на соответствие их заданной нагрузке.
3. Строим линии влияния двух реакций RA и RC и поперечной силы и изгибающего момента для сечений m и n (рис. 1 25). Построение линий влияния будем проводить кинематическим способом.
Так,
при построении линии влияния реакции
вертикальной RА убираем связь, препятствующую вертикальному
смещению опоры, и даем единичное смещение
этой опоры по направлению RА.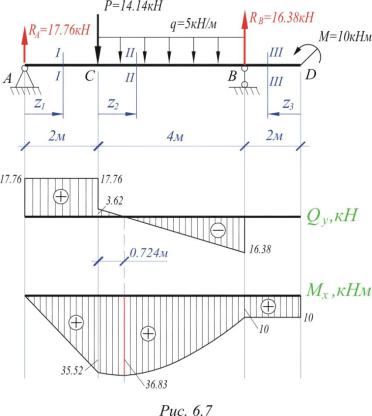 Поскольку опора А – заделка, которая при воздействии
малой поперечной силы не перемещается,
то единичное перемещение приведет к
перемещению консольной балки АВ параллельно самой себе. Полученная в
результате схема перемещений и дает
вид линии влияния этой реакции RА.
Аналогично получена линия влияния RС путем вертикального смещения опоры С на единицу (рис. 1.25,в).
Поскольку опора А – заделка, которая при воздействии
малой поперечной силы не перемещается,
то единичное перемещение приведет к
перемещению консольной балки АВ параллельно самой себе. Полученная в
результате схема перемещений и дает
вид линии влияния этой реакции RА.
Аналогично получена линия влияния RС путем вертикального смещения опоры С на единицу (рис. 1.25,в).
При построении линий влияния Q и М необходимо убрать связи, воспринимающие поперечную силу и изгибающий момент. То есть для построения линии влияния Q в сечении m нам необходимо в этом сечении дать торцам взаимное вертикальное смещение на единицу (рис. 1.25, г). Отметим, что если торцы стержней параллельны, то параллельны друг другу левый и правый стержни целиком. Аналогично поступаем и с сечением n при построении линии влияния Qn (рис. 1.25, е)
Врезав
поочередно в сечениях m и n шарниры и задав единичное угловое
смещение получаем эпюры возможных
перемещений, дающих вид линий влияния Мm и Мn (рис. 1.25, д, ж).
1.25, д, ж).
. Подсчитаем значения внутренних усилий в заданных сечениях по линиям влияния. Для этого нам необходимо силу Р умножать на ординаты соответствующих линий влияния, а интенсивность распределенной нагрузки q на площадь, очерченную линией влияния под нагрузкой q. При перемножении используем следующие правила знаков: нагрузки, направленные вниз, ординаты линий влияния и площади, расположенные выше осевой линии положительны.
Qm = P∙0,167 + q∙12d = 7,5 + 18 = 10,5 кН,
Мm = Р∙d/3 q(0,52d2d) = 22,5 27 = 4,5 кНм.
Qn = P∙2/3 = 30 кН (Сила Р находится слева от сечения n, поэтому умножили ее на левую ординату л.в. Qn).
Mn = P∙2d/3
= 45 кНм.
Значения внутренних усилий, полученные по линиям влияния, совпадают со значениями расчета на постоянную нагрузку.
Расчет статически определимой многопролетной балки
Статически определимые многопролетные шарнирно-консольные балки (ШКБ).
Задача. Построить эпюры Q и M для статически определимой многопролетной балки (ШКБ).
- Проверим статическую определимость балки по формуле: n=Соп—Ш-3
где n – степень статической определимости,
Соп – количество неизвестных опорных реакций,
Ш — количество шарниров,
3 – количество уравнений статики.
Балка опирается на одну шарнирно неподвижную опору (2 опорные реакции) и на три шарнирно подвижных опоры (в каждой по одной опорной реакции). Таким образом: Соп = 2+3=5. Балка имеет два шарнира, значит, Ш=2
Таким образом: Соп = 2+3=5. Балка имеет два шарнира, значит, Ш=2
Тогда n=5-2-3=0. Балка является статически определимой.
- Строим этажную схему балки, для этого заменяем шарниры шарнирно неподвижными опорами.
Шарнир – это место стыка балок, и, если посмотреть на балку с этой точки зрения, то многопролетную балку можно представить в виде трех отдельных балок.
Обозначим опоры на этажной схеме буквами.
Балки, которые опираются только на свои опоры, называются основными. Балки, которые опираются на другие балки, называются подвесными. Балка СD – основная, остальные – подвесные.
Расчет начинаем с балок верхних этажей, т. е. с подвесных. Влияние верхних этажей на нижние передается с помощью реакций с обратным знаком.
е. с подвесных. Влияние верхних этажей на нижние передается с помощью реакций с обратным знаком.
3. Расчет балок.
Каждую балку рассматриваем отдельно, строим для нее эпюры Q и М. Начинаем с подвесной балки АВ.
Определяем реакции RА, RВ.
Наносим реакции на схему.
Строим Эп Q методом сечений.
Строим Эп М методом характерных точек.
В точке, где Q=0 на балке обозначим точку К – это точка, в которой М имеет экстремум. Определим положение т.К, для этого приравниваем уравнение для Q2 к 0, а размер z заменим на х.
Рассмотрим еще одну подвесную балку – балку ЕР.
Балка ЕР относится к простым балкам, эпюры для которых известны.
Теперь рассчитываем основную балку СD. В точках В и Е передаем на балку СD с верхних этажей реакции RВи RЕ, направленные в обратную сторону.
Рассчитываем реакции балки СD.
Наносим реакции на схему.
Строим эпюру Q методом сечений.
Строим эпюру М методом характерных точек.
Точку L поставим дополнительно в середине левой консоли – она загружена равномерно распределенной нагрузкой, и для построения параболической кривой требуется дополнительная точка.
Строим эпюру М.
Строим эпюры Q и М для всей многопролетной балки, при этом не допускаем переломов на эпюре М. Задача решена.
Метод распределения моментов
– рабочие примеры
доктора Шона Кэрролла
|
Опубликовано: 23 июля 2022 г.
|
Учебник
В этом уроке мы рассмотрим метод распределения моментов. Это отличный метод для быстрого определения эпюр поперечной силы и изгибающего момента для неопределенных балочных и рамных конструкций . В этом уроке мы сосредоточимся на применении метода распределения моментов к балкам.
Мы начнем с четкого понимания этапов процедуры, а затем применим то, что узнали, к более сложному рабочему примеру в конце. Если вы предпочитаете посмотреть, как я объясняю решение, вы можете посмотреть видео ниже.
Этот учебник основан на моем курсе Неопределенные конструкции и метод распределения моментов . После того, как вы закончите этот учебник, вы можете продолжить обучение.
После того, как вы закончите этот учебник, вы можете продолжить обучение.
Если вы читаете это, я предполагаю, что вы уже умеете рисовать диаграммы поперечной силы и изгибающего момента для статически определимых балок. Если нет, сначала пройдите этот урок.
1.0 Введение в метод распределения моментов
Начнем с суммирования основных особенностей метода распределения моментов; метод направлен на определение изгибающих моментов во внутренних соединениях посредством итеративного процесса применения балансирующих и перераспределяющих моментов.
Итерации продолжаются, последовательно уменьшая дисбаланс моментов, пока не будет достигнуто равновесие моментов во всех соединениях конструкции. Когда эти внутренние моменты установлены, пролетные моменты, поперечные силы и опорные реакции определяются с использованием диаграмм свободного тела и простой статики.
Начнем с фиксации всех внутренних соединений от проворачивания. Это часто называют блокировкой конструкции . В многопролетной балке это приводит к ряду сегментов балки, изолированных друг от друга замковыми соединениями. Далее определяем изгибающие моменты, возникающие в каждом замковом соединении в результате нагрузки на каждый сегмент балки. Как правило, в каждом суставе будет моментный дисбаланс. В этот момент мы вступаем в итеративный процесс балансировки моментов; на каждый сустав по очереди мы:
В многопролетной балке это приводит к ряду сегментов балки, изолированных друг от друга замковыми соединениями. Далее определяем изгибающие моменты, возникающие в каждом замковом соединении в результате нагрузки на каждый сегмент балки. Как правило, в каждом суставе будет моментный дисбаланс. В этот момент мы вступаем в итеративный процесс балансировки моментов; на каждый сустав по очереди мы:
- применить уравновешивающий момент для устранения дисбаланса
- распределить уравновешивающий момент между элементами, сходящимися в стыке, пропорционально их жесткости на изгиб
- переносят более 50% распределенного момента на другой конец каждого из элементов, встречающихся в стыке — при условии, что соседний шарнир способен выдерживать моменты — мы поясним это ниже)
Этот переносной момент снова разбалансирует соединения в конструкции. Это означает, что нам нужно повторить процесс балансировки и распределения. Этот процесс повторяется снова и снова, однако с каждой итерацией моментные диспропорции в структуре становятся все меньше и меньше.
Как обычно, единственный реальный способ понять это — посмотреть на это в действии, поэтому давайте рассмотрим простой пример.
2.0 Простой пример
Рассмотрим простую двухпролетную неразрезную недетерминированную балку на рис. 1 ниже. Этот пучок является статически неопределимым, поскольку имеется более трех неизвестных реакций. Таким образом, мы не можем определить их значения только с помощью 3 уравнений статики. Это делает структуру первым кандидатом для анализа распределения моментов.
Рис. 1. Двухпролетная неразрезная балка неопределенного сечения. 2.1 Блокировка стыков от проворачиванияПервым шагом является блокировка любого стыка, который еще не зафиксирован от проворачивания, в данном случае это стык B. Теперь конструкция состоит из двух изолированных пролетов, AB и BC с нагрузкой на один пролет не влияет на другой.
Рис. 2. Балка со всеми соединениями, зафиксированными от вращения. Далее мы можем определить моменты, возникающие в каждом замковом соединении из-за пролетной нагрузки в каждом сегменте балки. Самый быстрый способ сделать это — использовать таблицы моментов неподвижных концов. Приведена таблица общих моментов на неподвижных концах, рис. 3.
Самый быстрый способ сделать это — использовать таблицы моментов неподвижных концов. Приведена таблица общих моментов на неподвижных концах, рис. 3.
Мы видим, что в этом случае суставные моменты, возникающие из-за нагрузки между AB, равны . Совместные моменты, вызванные нагрузкой на BC, равны . Другой способ представить моменты на неподвижных концах состоит в том, что это реактивные моменты, возникающие на неподвижных концах в ответ на приложенную нагрузку.
Рис. 4. Моменты на неподвижных концах, возникающие в заблокированных соединениях. 2.2 Балансировка сустава Если мы теперь сосредоточимся на суставе B, мы увидим дисбаланс момента из-за движения по часовой стрелке от AB и против часовой стрелки от BC. Если мы теперь представим себе освобождение этого сустава, теоретически он испытает результирующий момент против часовой стрелки . В ответ на это мы добавим уравновешивающий момент по часовой стрелке для устранения дисбаланса моментов, рис. 5.
5.
При добавлении уравновешивающего момента к шарниру он должен быть распределен между всеми элементами, которые сходятся в соединении. Это распределение выполняется пропорционально изгибной жесткости элементов, встречающихся в стыке. Подробнее о том, как определяются эти жесткости, мы поговорим ниже, а пока просто предположим, что отрезок балки AB в два раза жестче отрезка BC.
Это будет означать, что уравновешивающий момент распределяется между AB и BC в соотношении 2:1. Итак, в член AB и в BC. В результате сустав теперь уравновешен моментами уравновешивания друг друга по обе стороны от сустава.
Рис. 6. Распределение уравновешивающего момента. 2.4 Переносной момент Мы еще не закончили, последним шагом будет распространение переносного момента на противоположные концы каждого сегмента балки. Поскольку конструкция имеет фиксированные опоры в точках А и С, мы не можем применить уравновешивающие моменты в точке В без соответствующего момента, развивающегося на внешних опорах.
Поскольку конструкция имеет фиксированные опоры в точках А и С, мы не можем применить уравновешивающие моменты в точке В без соответствующего момента, развивающегося на внешних опорах.
Поскольку опоры полностью закреплены, уравновешивающие моменты будут перенесены, рис. 7. Если бы A или B были штифтовой или роликовой опорой, которая не оказывает сопротивления вращению, переносящие моменты были бы равны нулю.
Рис. 7. Переносные моменты.Теперь мы можем суммировать конечные моменты в каждом соединении, рис. 8. Это было относительно простое распределение, требующее только одной итерации балансировки. Для конструкций с более чем одним внутренним замковым соединением требуется несколько итераций балансировки — мы увидим пример этого ниже.
Рис. 8. Суммирование окончательных моментов соединения конструкции. Для более сложных структур с несколькими итерациями мы можем использовать таблицу, чтобы отслеживать анализ. A simple table tracking this analysis is shown below, Table 1.
| Joint | A | B | B | C | |||||||||||||||||||||||||||||||||||||||||||||||||
| Member | АВ | ВА | ВС | CB | |||||||||||||||||||||||||||||||||||||||||||||||||
| Distribution Factor | 0.66 | 0.33 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| Fixed-end moments | -100 | 100 | -208.3 | 208.3 | |||||||||||||||||||||||||||||||||||||||||||||||||
| Distribution | 72.2 | 36.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| . Перенос | .0014-63.9 КНМ | 172,2 КНМ | -172,2 КНМ | 226,4 КНМ |
| Joint | A | B | B | C |
| Member | AB | BA | BC | CB |
| Distribution Factor | 0.56 | 0.44 | ||
| Fixed-end moments | -100 | 100 | -208.3 | 208.3 |
| Distribution | (0.56×108.3) = 60.65 | (0.44×108.3)= 47.65 | ||
| Carry-over | 30.33 | 23.83 | ||
| Final | -69,67 КНМ | 160,65 КНМ | -160,65 КНМ | 232. 13 КН 13 КН |
4.0 Реакции, поперечные силы и изгибающие моменты
Наш анализ выявил изгибающие моменты в каждом соединении. Но чтобы завершить анализ и построить диаграммы поперечной силы и изгибающего момента, нам еще предстоит проделать большую работу.
К счастью, недостающую информацию можно легко получить с помощью простой статики и диаграмм свободного тела. Рассмотрим диаграмму свободного тела сегмента балки АВ, рис. 10.9.0003 Рис. 10. Диаграмма свободного тела сегмента балки AB.
Здесь у нас есть два неизвестных, поперечные силы в точках A и B. Мы можем определить поперечную силу непосредственно слева от B, вычислив сумму моментов относительно A. Будем считать, что моменты по часовой стрелке положительны.
(7)
(8)
(9)
Далее мы можем оценить сумму вертикальных сил, чтобы определить .
(10)
(11)
(12)
Поскольку на сегмент балки действует одноточечная нагрузка, мы знаем, что будет пиковый момент под точечной нагрузкой, и что момент будет линейно изменяться между этим пик и два опорных момента.
Точно так же мы знаем, что диаграмма поперечной силы будет состоять из двух горизонтальных прямых линий. На этом этапе процесса вам необходимо иметь хорошее представление об основах построения диаграмм поперечной силы и изгибающего момента — просмотрите этот учебник сейчас, если это необходимо.
Мы можем определить внутренний изгибающий момент под точечной нагрузкой, сделав разрез в конструкции в этом месте, чтобы выявить внутренний момент, , рис. 11.
рис. моменты о резке урожайности,(13)
(14)
(15)
Теперь мы можем повторить этот процесс для сегмента балки BC, рис. 12.
Рис. 12. Схема свободного тела сегмента балки BC.Сначала вычисляем сумму моментов относительно B.
(16)
(17)
(18)
Теперь вычисляем сумму сил в вертикальном направлении.
(19)
(20)
(21)
На этот сегмент балки действует равномерно распределенная нагрузка (UDL), что означает, что поперечная сила будет линейно изменяться слева и справа.
Максимальный момент будет там, где поперечная сила равна нулю. Таким образом, чтобы определить это расстояние справа от B, мы можем разделить сдвиг слева на скорость, с которой он уменьшается, из-за UDL,
(22)
Здесь мы можем сделать наш разрез чтобы выявить максимальный пролетный момент, рис. 13
Рис. 13. Диаграмма свободного тела сегмента балки с указанием местоположения максимального момента.Оценка суммы моментов относительно места разреза,
(23)
(24)
(25)
Теперь у нас есть вся информация, необходимая для построения полных диаграмм поперечной силы и изгибающего момента для этой балки, рис. 14.
Рис. График сил и изгибающих моментов. В этом пошаговом руководстве по анализу продемонстрирован полный метод распределения моментов. Теперь вы должны хорошо понимать различные этапы и осознавать потенциал, который предлагает этот метод для ручного анализа как балочных, так и рамных конструкций. В следующем разделе мы рассмотрим немного более сложный пример балки, который потребует от нас реализации решения, состоящего из нескольких итераций.
5.0 Метод распределения моментов: многократный рабочий пример
Для этого примера рассмотрим многопролетную неразрезную балку, показанную ниже, рис. 15. Мы снова будем считать, что для этой балки постоянна. На этом примере мы увидим, что с относительно сложным пролетом и расположением нагрузки можно довольно быстро справиться, используя процесс распределения моментов.
При некоторой практике обработка может стать очень упорядоченной и несколько шаблонной для реализации. Вы можете продолжить чтение решения или посмотреть видео с полным решением ниже.
Рис. 15. Многопролетная неразрезная балка. 5.1 Жесткости элементов Основываясь на предыдущем обсуждении жесткостей элементов, мы можем утверждать следующее: сегмент DE, так как в этот сегмент не будет передаваться уравновешивающий момент. Это потому, что мы уже знаем, каким будет последний момент в этом месте из-за того, что это консоль.
Это потому, что мы уже знаем, каким будет последний момент в этом месте из-за того, что это консоль.
Рассчитываем коэффициенты распределения для каждого внутреннего шарнира обычным способом, опять же особо отмечая, что уравновешивающий момент не будет распределяться на DE и, следовательно, коэффициент распределения для DC будет равен 1.
(29 )
(30)
(31)
(32)
(33)
(34)
5,3 Моменты с фиксированным кондиционеромРассмотрение сегмента AB First, Fig 16, фиксированные моменты. получаются как,
(35)
(36)
Рис. 16. Моменты на неподвижных концах, отрезок AB.Затем мы можем оценить сегмент балки BC, рис. 17.
(37)
(38)
Рис. 17. Моменты на неподвижных концах, сегмент BC. При расчете моментов на концах отрезка CD фиксируем соединение C как обычно. Однако, поскольку балка может свободно вращаться справа от D, т. е. она не ограничена из-за того, что она является консолью справа от D, мы оставляем это соединение закрепленным. Таким образом, момент на неподвижном конце рассчитывается для модели консоли с подпиранием, рис. 18.9.0003
е. она не ограничена из-за того, что она является консолью справа от D, мы оставляем это соединение закрепленным. Таким образом, момент на неподвижном конце рассчитывается для модели консоли с подпиранием, рис. 18.9.0003
(39)
(40)
Рис. 18. Моменты на неподвижных концах, сегмент CD.Наконец, мы можем определить моменты на неподвижных концах в точках DE и ED, которые на самом деле представляют собой просто консольные моменты, оцениваемые из простой статики.
(41)
(42)
5.4 Распределение моментовТеперь, когда мы установили всю входную информацию, мы можем построить таблицу распределения моментов и обработать распределение, Таблица 3. В отличие от нашего предыдущего примера , так как эта конструкция имеет несколько внутренних соединений, нам потребуется выполнить несколько итераций балансировки и распределения, чтобы постепенно уменьшить дисбаланс моментов на каждой опоре.
Первые четыре строки таблицы содержат всю информацию о структуре и загрузке, которую мы только что определили. После этого мы:
После этого мы:
- Определение момента дисбаланса в каждом соединении и расчет балансирующего момента для распределения на каждый элемент на основе коэффициентов распределения.
- После того, как все шарниры сбалансированы, мы переносим уравновешивающий момент на соседние заблокированные суставы. Обратите внимание еще раз, что к постоянному току не применяется переносной момент, поскольку консольный момент в этом месте уже определен.
- Переносные моменты снова разбалансировали суставы, поэтому нам нужно определить новый уравновешивающий момент для каждого шарнира, поэтому мы возвращаемся к первому шагу и повторяем процесс.
Этот процесс продолжается до тех пор, пока прилагаемые уравновешивающие моменты не станут достаточно малыми. Практически мы можем прекратить балансировку, как только моменты уменьшатся примерно до 1 или 2 процентов от начальных моментов фиксированного конца. Это оставляет нам сбалансированные внутренние суставы.
| Соединение | A | B | B | C | C | D | D | E | |||||||||||||||||||||||||||||||||||||||||||||
| Member | AB | BA | до н. э. э. | CB | CD | DC | DE | ED | |||||||||||||||||||||||||||||||||||||||||||||
| Дистрибутивные коэффициенты | 393 | 3393 | | | | .0096 | 0.57 | 0.47 | 0.53 | 1 | 0 | | ||||||||||||||||||||||||||||||||||||||||||
| Fixed-end Moments | -53.3 | 53.3 | 66.7 | -33.3 | -10 | 0 | — 50 | 50 | |||||||||||||||||||||||||||||||||||||||||||||
| Распределение | (-120) -51,6 | (-120) -68,4 | (43,317) -68,4 | (43,31717 20,317 -68,4 | (43,317) 20,317 00
|
 Это было просто для того, чтобы мы могли проработать анализ от начала до конца, не отвлекаясь.
Это было просто для того, чтобы мы могли проработать анализ от начала до конца, не отвлекаясь. 9. Жесткости элементов балки на основе вращательной фиксации на опорах.
9. Жесткости элементов балки на основе вращательной фиксации на опорах.
 8
8

 com. Я надеюсь, что вы нашли этот урок полезным. Проведя 10 лет в качестве преподавателя в университете по проектированию конструкций, я запустила DegreeTutors.com, чтобы помочь большему количеству людей понять инженерию и получить такое же удовольствие от ее изучения, как и я. Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей.
com. Я надеюсь, что вы нашли этот урок полезным. Проведя 10 лет в качестве преподавателя в университете по проектированию конструкций, я запустила DegreeTutors.com, чтобы помочь большему количеству людей понять инженерию и получить такое же удовольствие от ее изучения, как и я. Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей. Неограниченный доступ к инструментам онлайн-анализа. 🛠️
Неограниченный доступ к инструментам онлайн-анализа. 🛠️ Результаты показали, что нормальное напряжение и напряжение сдвига сосуществуют в поперечном сечении многопролетной сплошной глубокой балки, а это означает, что напряжение сдвига может вызвать деформацию поперечного сечения, в то время как нормальное напряжение может привести к тому, что сечение будет параллельным экструзия нейтрального слоя. Кроме того, мы случайно обнаружили, что с увеличением высоты балки постепенно увеличивается влияние деформации потери устойчивости и деформации выдавливания на изгиб балки. Новый метод расчета, обеспечиваемый устоявшейся механической моделью многопролетной неразрезной глубокой балки, расширил возможности метода расчета традиционной неразрезной глубокой балки.
Результаты показали, что нормальное напряжение и напряжение сдвига сосуществуют в поперечном сечении многопролетной сплошной глубокой балки, а это означает, что напряжение сдвига может вызвать деформацию поперечного сечения, в то время как нормальное напряжение может привести к тому, что сечение будет параллельным экструзия нейтрального слоя. Кроме того, мы случайно обнаружили, что с увеличением высоты балки постепенно увеличивается влияние деформации потери устойчивости и деформации выдавливания на изгиб балки. Новый метод расчета, обеспечиваемый устоявшейся механической моделью многопролетной неразрезной глубокой балки, расширил возможности метода расчета традиционной неразрезной глубокой балки. С увеличением высоты балки деформация сдвига и деформация выдавливания все больше влияют на изгиб балки, но влияние деформации выдавливания намного меньше, чем деформации сдвига.
С увеличением высоты балки деформация сдвига и деформация выдавливания все больше влияют на изгиб балки, но влияние деформации выдавливания намного меньше, чем деформации сдвига.

 закон глубокого луча.
закон глубокого луча. Затем средние опоры глубокой балки были удалены, и эквивалентные вертикальные силы были приложены к местам расположения средних опор, чтобы убедиться, что места расположения средних опор не имеют вертикального смещения, как показано на рисунке 2.
Затем средние опоры глубокой балки были удалены, и эквивалентные вертикальные силы были приложены к местам расположения средних опор, чтобы убедиться, что места расположения средних опор не имеют вертикального смещения, как показано на рисунке 2.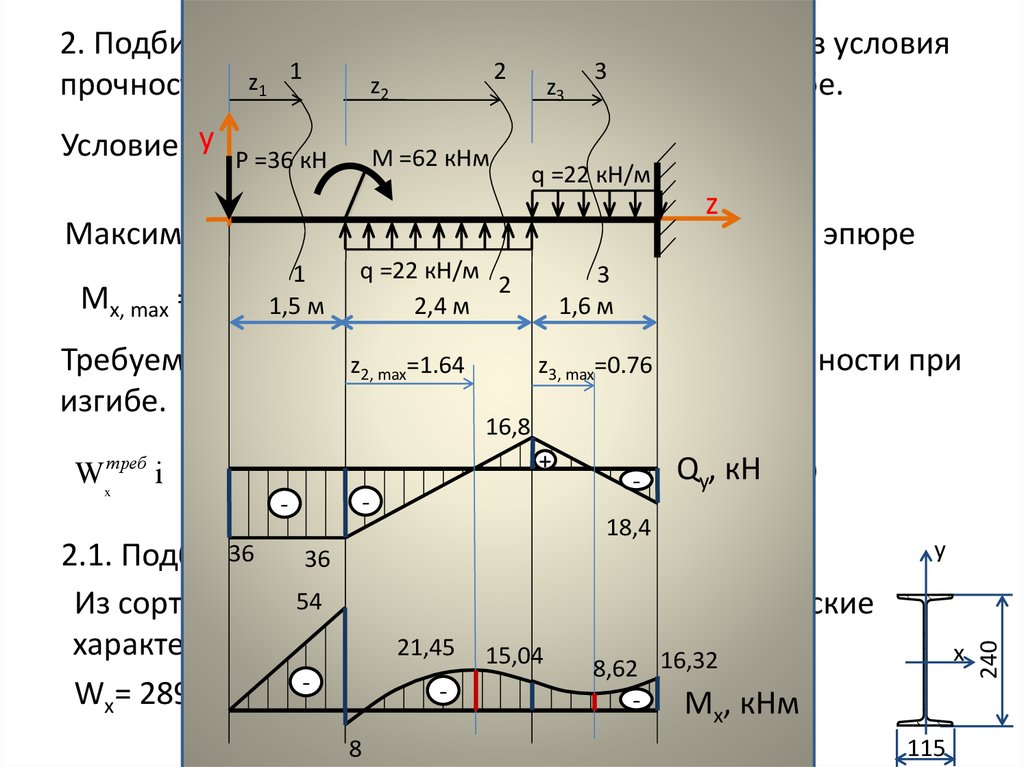 (6)Решение уравнения состояния балки 1-го этажа. Подставляя (6) в (4), мы можем получить следующее:
Очевидно, что матрица коэффициентов в (8) переведена в матрицу постоянных коэффициентов; предполагать Тогда (8) упрощается до По методу матричной экспоненты решение (10) получается Предполагать Тогда (11) упрощается до При , (13) преобразуется в где () — значение координаты верха балки 1-го этажа, — значение координаты низа балки 1-го этажа (равно общей высоте балки 1-го этажа), — вектор-столбец перемещений и составляющих напряжений в месте , и является вектор-столбцом компонентов смещения и напряжения в месте .
(6)Решение уравнения состояния балки 1-го этажа. Подставляя (6) в (4), мы можем получить следующее:
Очевидно, что матрица коэффициентов в (8) переведена в матрицу постоянных коэффициентов; предполагать Тогда (8) упрощается до По методу матричной экспоненты решение (10) получается Предполагать Тогда (11) упрощается до При , (13) преобразуется в где () — значение координаты верха балки 1-го этажа, — значение координаты низа балки 1-го этажа (равно общей высоте балки 1-го этажа), — вектор-столбец перемещений и составляющих напряжений в месте , и является вектор-столбцом компонентов смещения и напряжения в месте . 5. Обсуждение разрешимости уравнения модели
5. Обсуждение разрешимости уравнения модели где – координата направления сосредоточенной силы на верхней поверхности балки, а .
где – координата направления сосредоточенной силы на верхней поверхности балки, а .
 На рис. 6(б) показано распределение напряжения сдвига по высоте балки (так как на рис. 6(а) показано расположение наблюдаемых поперечных сечений). Совершенно очевидно, что теоретические результаты согласуются с результатами ANSYS, а касательное напряжение на верхней и нижней поверхности конструкции отсутствует, что согласуется с фактом.
На рис. 6(б) показано распределение напряжения сдвига по высоте балки (так как на рис. 6(а) показано расположение наблюдаемых поперечных сечений). Совершенно очевидно, что теоретические результаты согласуются с результатами ANSYS, а касательное напряжение на верхней и нижней поверхности конструкции отсутствует, что согласуется с фактом. Причина в том, что в поперечном сечении балки есть напряжение сдвига и нормальное напряжение, и напряжение сдвига может привести к деформации поперечного сечения, в то время как нормальное напряжение может привести к сечению, параллельному экструзии нейтрального слоя. .
Причина в том, что в поперечном сечении балки есть напряжение сдвига и нормальное напряжение, и напряжение сдвига может привести к деформации поперечного сечения, в то время как нормальное напряжение может привести к сечению, параллельному экструзии нейтрального слоя. . На рис. 9 показаны кривые деформации вертикального сжатия в различных точках средней секции опоры. Чем выше высота балки, тем больше деформации вертикального сжатия различных точек в средней части опоры, а чем ниже высота балки, тем меньше деформации вертикального сжатия. С увеличением высоты балки деформации вертикального сжатия все больше влияют на деформацию изгиба многопролетной неразрезной глубокой балки.
На рис. 9 показаны кривые деформации вертикального сжатия в различных точках средней секции опоры. Чем выше высота балки, тем больше деформации вертикального сжатия различных точек в средней части опоры, а чем ниже высота балки, тем меньше деформации вертикального сжатия. С увеличением высоты балки деформации вертикального сжатия все больше влияют на деформацию изгиба многопролетной неразрезной глубокой балки.
 Р. Каупер, «Коэффициент сдвига в теории балки Тимошенко», Журнал прикладной механики , том. 33, нет. 2, с. 335–340, 1966.
Р. Каупер, «Коэффициент сдвига в теории балки Тимошенко», Журнал прикладной механики , том. 33, нет. 2, с. 335–340, 1966. 77, нет. 3, стр. 440–444, 1981.
77, нет. 3, стр. 440–444, 1981. Ф. Ван, «Анализ напряжения свободно поддерживаемых глубоких балок», Журнал Чэндуского университета науки и технологий , том. 70, нет. 3, стр. 70–76, 1993 (китайский).
Ф. Ван, «Анализ напряжения свободно поддерживаемых глубоких балок», Журнал Чэндуского университета науки и технологий , том. 70, нет. 3, стр. 70–76, 1993 (китайский). 9, стр. 40–46, 1995 (китайский).
9, стр. 40–46, 1995 (китайский).