Нагрузка, выдерживаемая швеллером
Нагрузка, выдерживаемая швеллером
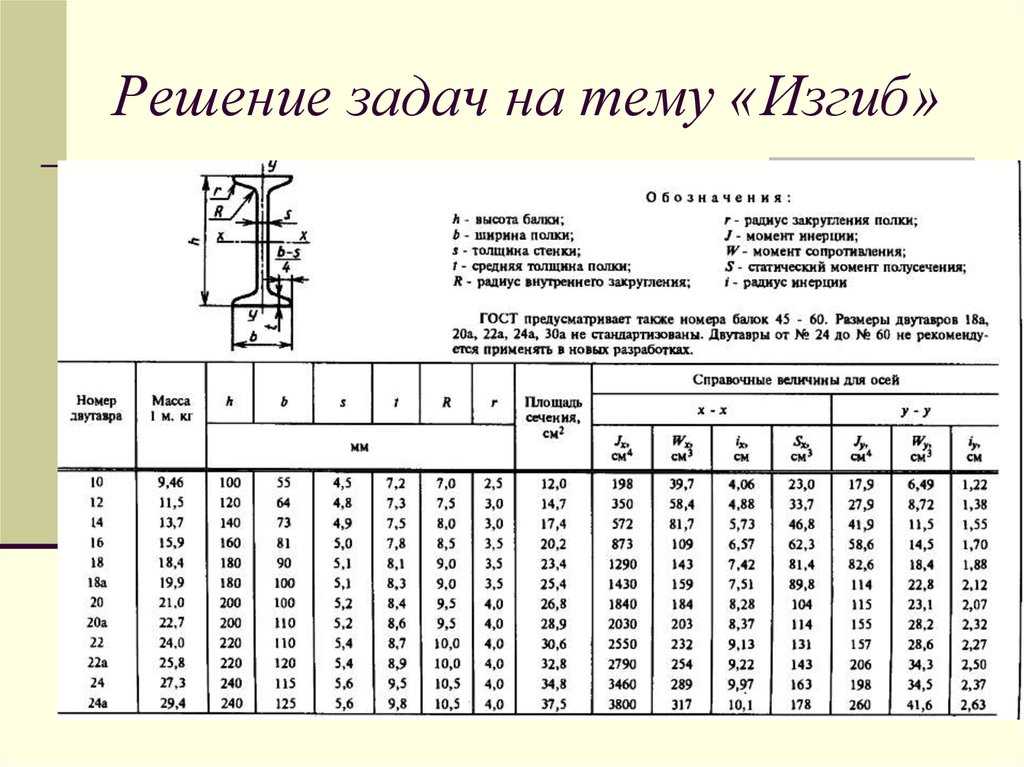
Швеллер – вид металлопроката, который в своем сечении напоминает букву «П». В своей конструкции изделие имеет перемычку и полки, которые могут отходить от основы под углом. Высотой швеллера принято считать высоту его полок. Получают этот вид металлопроката путем горячей прокатки на сортовых станках. Применяют его в строительстве, так как швеллер выдерживает высокие нагрузки, а также обладает сопротивлением и жесткостью.
Классификация и маркировка швеллеров
Для швеллеров существуют несколько классификаций и маркировок, которые описывают особенности конкретного проката. Существует две группы изделий:
- горячекатаная продукция;
- гнутая.
Первый профиль обладает большим запасом прочности, что позволяет применять его в качестве несущих конструкций. Второй тип имеет изгиб полок, что уменьшает допустимую нагрузку на изделие, но облегченная масса и дешевизна товара делают его предпочтительнее для создания опорных конструкций.
Также принято различать швеллеры по уровню точности:
- «А» – высокая;
- «Б» – повышенная;
- «В» – обычная.
Эти показатели применяют для обозначения точности изготовления изделия.
Помимо высоты, в каждом профиле принято выделять другие показатели, которые влияют на габариты изделия:
- ширина полки – расстояние от внешнего угла полки до конца грани. Размер может варьироваться 35-115 мм;
- толщина балки;
- толщина полки.
Отдельно в характеристике швеллера описывается его длина. Все швеллеры можно распределить на три группы по этому параметру:
- мерной;
- кратной мерной;
- немерной длины;
Также встречаются буквенные обозначения В маркировке швеллера различают следующие их значения:
- «У» – угловое изделие. Указывает на изгиб полок друг к другу. Уклон составляет 4-10%;
- «П» – полки, по отношению друг к другу находятся параллельно;
- «Л» – облегченное изделие;
- «Э» – выполнен из экономичных материалов.
 К этой группе относят изделия с параллельными полками;
К этой группе относят изделия с параллельными полками; - «С» – специальная партия. Выполняют на заказ с нестандартными наклонами граней.
Также встречается маркировка Ст1-4, которая обозначает марку стали, из которой изготовлена продукция.
Номенклатура изделий с равными и гнутыми полками имеет определенные различия.
Представим типичную расшифровку горячекатаной марки с ровными полками:
- В первую очередь принято писать вид изделия, в нашем случае – швеллер.
- Следующей идет цифра, указывающая высоту полки в сантиметрах, к примеру, 21.
- Затем указывают конструктивные особенности проката («У», «П», «Л» и т.д.)
- После обозначения особых характеристик указывают точность проката и ГОСТ, согласно которому он выполнен.
В итоге получаем:
Швеллер 21П-Б ГОСТ, что означает изделие с высотой стенки 210 мм с параллельными полками, повышенной точности, выполненная по указанному ГОСТу.
Далее через дробь указывают марку и степень раскисления, которые применялись в изготовлении.
21П-Б ГОСТ/Ст3сп ГОСТ. В данном случае указана сталь третьей марки, степень раскисления – «спокойная».
Угловой профиль также имеет свои особенности, которые сказываются на маркировке. Так, ГОСТ имеет значение 8278-83 для равнополочного изделия и 8281-80 для неравнополочного. В обозначении указывают:
- высоту * ширину полки * толщину заготовки. Эти показатели указываются в милиметрах;
- точность изготовления;
- ГОСТ.
Вторая часть дроби не отличается от изделий с равными полками.
Маркировка в итоге выглядит так:
100х50х4Б ГОСТ/Ст3сп ГОСТ, что означает соотношение высоты, ширины полки и толщины изделия в 100-50-4 миллиметра, повышенную точность и изготовление согласно указанному ГОСТу/сталь третьей марки, степень раскисления «спокойная».
Максимальный прогиб для швеллера
Максимально допустимый прогиб – это показатель, который рассчитывается преимущественно при строительстве перекрытий и несущих конструкций. Для вычисления максимально допустимого прогиба применяют коэффициент 5/384, который затем умножают на следующую дробь:
- числитель указывает нагрузку, которая действует на балку – её умножают на четверть длины изделия;
- знаменатель – значение продольной упругости умножают на момент инерции.
Расчёт нагрузки
В зависимости от способа применения профиль может испытывать различные виды нагрузок. Чтобы точно подобрать швеллер, способный выдержать нужную нагрузку, необходимо знать основные её группы:
- А – равномерная нагрузка, которую принято называть «подъездный козырек». Применяют балки, которые имеют жесткие заделки. Пространство между швеллерами заполняют железобетоном;
- В – равномерная нагрузка при установке балок межэтажных перекрытий. К данной группе относят однопролетные балки;
- С – нагрузка по типу балконных плит. Применяют шарнирно-опертые балки, которые имеют две точки опоры с консолью, а основная часть вынесена непосредственно за пределы конструкции. Момент нагрузки между балками распределяется равномерно;
- D – нагрузка перекрытия. Применяют шарнирно-опертые балки, на которых сконцентрирована одна сила;
- F – нагрузка, которая по своему виду напоминает группу «А», только вместо железобетона применяют металлические листы с большим показателем жесткости.
После того как выбран необходимый вид нагрузки, можно приступить к её расчету. Расчет нагрузки на швеллер проводится последовательно и выглядит следующим образом:
- Коэффициент надежности по нагрузке умножается на всю нагрузку, которая направлена на балку. Под всей нагрузкой подразумевают расчетную вместе нормативной.
- Полученный результат умножается на шаг швеллеров.
- Производится подсчет максимального изгибающего момента. Для этого необходимо расчетную нагрузку умножить на длину балки в квадрате. Полученное значение измеряется в кНм.
- Вычисляется момент сопротивления. Для этого максимальный изгибающий момент умножается на коэффициент условий работы. Эти значения находятся в числителе, а в знаменателе указывается коэффициент пластических деформаций.
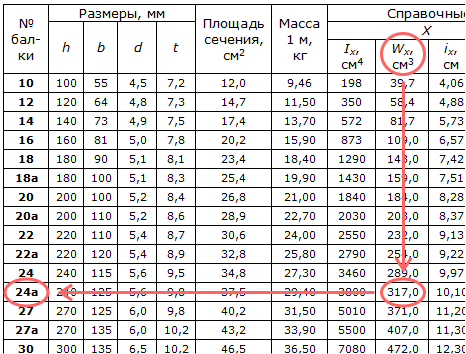
Полученное значение указывает на необходимое сечение швеллера в кубических сантиметрах, при этом стоит учитывать, что номер швеллера должен быть несколько больше полученного числа.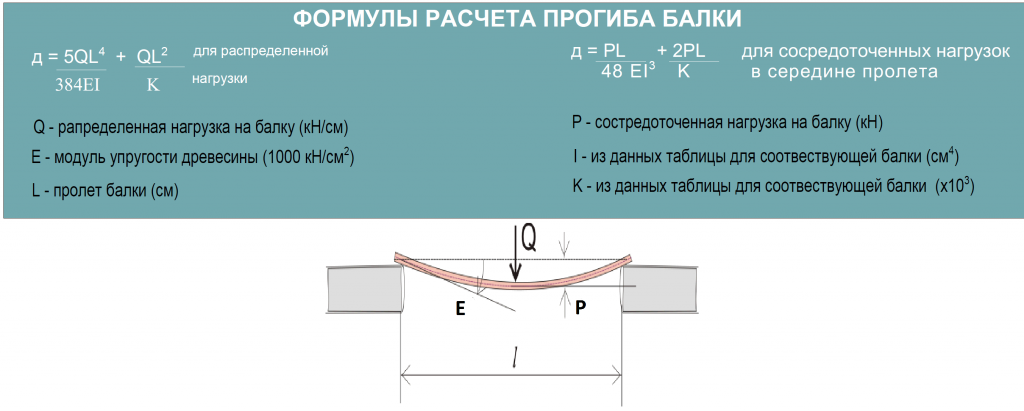
Все постоянные значения необходимо брать из ГОСТа. В качестве примера возьмем швеллер 10П из стали 09Г2С.
Исходные постоянные значения для него:
- предел текучести для 09Г2С составляет 345 МПа;
- момент сопротивления балки по оси Х – 34,9 сантиметров кубических, по оси Y – 7,37 сантиметров кубических.
Изгибающий момент получаем умножением момента сопротивления балки по оси Х на предел текучести для 09Г2С. Получаем 34,9 * 345 = 12040,5 Нм. Таким же образом умножаем момент сопротивления балки по оси Y на предел текучести для 09Г2С и получаем 7,37 * 345 = 2542,65 Нм.
Коэффициент пластических деформаций равен 8 – отсюда вычисляем расчетную нагрузку по каждой оси:
- вертикальная: 8 * 12040,5/102 = 96,3 кгс/м;
- горизонтальная: 8 * 2542,65/102 = 20,3 кгс/м.
Отсюда видим, что в данных условиях несущая способность балки практически в 5 раз больше по вертикали, чем по горизонтали.
Задача на подбор сечения и проверку прочности.
 Касательное напряжение и энергетический критерий прочности
Касательное напряжение и энергетический критерий прочностиПроектный и проверочный расчеты. Для балки с построенными эпюрами внутренних усилий подобрать сечение в виде двух швеллеров из условия прочности по нормальным напряжениям. Проверить прочность балки, используя условие прочности по касательным напряжениям и энергетический критерий прочности. Дано:
Покажем балку с построенными эпюрами Q и М
Согласно эпюре изгибающих моментов опасным является сечение С, в котором МС=Мmax=48,3кНм.
Условие прочности по нормальным напряжениям для данной балки имеет вид σmax=MC/WX≤σadm. Требуется подобрать сечение из двух швеллеров.
Определим необходимое расчетное значение осевого момента сопротивления сечения:
Для сечения в виде двух швеллеров согласно сортаменту прокатной стали принимаем два швеллера №20а, момент инерции каждого швеллера Ix=1670см4, тогда осевой момент сопротивления всего сечения:
Перенапряжение (недонапряжение) в опасных точках посчитаем по формуле: Тогда получим недонапряжение:
Теперь проверим прочность балки, исходя из условия прочности по касательным напряжениям.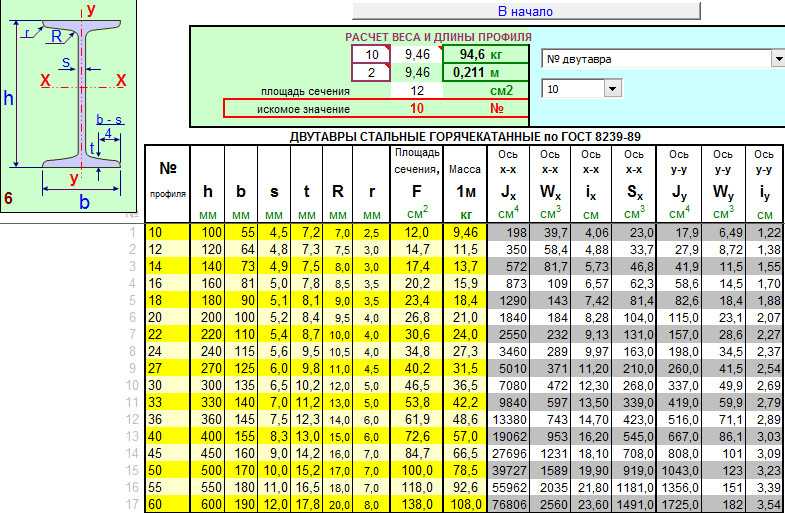 Согласно эпюре поперечных сил опасными являются сечения на участке ВС и сечение D. Как видно из эпюры, Qmax=48,9 кН.
Согласно эпюре поперечных сил опасными являются сечения на участке ВС и сечение D. Как видно из эпюры, Qmax=48,9 кН.
Условие прочности по касательным напряжениям имеет вид:
Для швеллера №20 а: статический момент площади Sx1=95,9 см3, момент инерции сечения Ix1=1670 см4, толщина стенки d1=5,2 мм, средняя толщина полки t1=9,7 мм, высота швеллера h1=20 см, ширина полки b1=8 см.
Для поперечного сечения из двух швеллеров:
Sx= 2Sx1=2·95,9=191,8 см3,
Ix=2Ix1=2·1670=3340 см4,
b=2d1=2·0,52=1,04 см.
Определяем значение максимального касательного напряжения:
τmax=48,9·103·191,8·10−6/3340·10−8·1,04·10−2=27МПа.
Как видно, τmax <τadm (27МПа<75МПа).
Следовательно, условие прочности выполняется.
Проверяем прочность балки по энергетическому критерию.
Из рассмотрения эпюр Q и М следует, что опасным является сечение С, в котором действуют MC=Mmax=48,3 кНм и QC=Qmax=48,9 кН.
Проведем анализ напряженного состояния в точках сечения С
Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Определим нормальные и касательные напряжения на нескольких уровнях (отмечены на схеме сечения)
Уровень 1-1: y1-1=h1/2=20/2=10см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 2−2: y2-2=h1/2−t1=20/2−0,97=9,03см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 3−3: y3-3=h1/2−t1=20/2−0,97=9,03см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 4−4: y4-4=0.
Нормальные и касательные напряжения:(в середине нормальные напряжения равны нулю, касательные максимальны, их находили в проверке прочности по касательным напряжениям)
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 5−5:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 6−6:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 7−7:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
В соответствии с выполненными расчетами эпюры напряжений σ, τ, σ1, σ3, τmax и τmin представлены на рис. Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Анализ этих эпюр показывает, что в сечении балки опасными являются точки на уровне 3-3 (или 5-5), в которых:
Используя энергетический критерий прочности, получим
Из сравнения эквивалентного и допускаемого напряжений следует, что условие прочности также выполняется
(135,3 МПа<150 МПа).
Руководство по расчету допусков на изгиб и уменьшения изгиба
Гибка с ЧПУ открывает новый мир возможностей при лазерной резке листового металла. Мы хотим сделать эти возможности достижимыми, поэтому мы создали Калькулятор изгиба, который вычисляет для вас сложный допуск на изгиб и значение вычета изгиба. В этом видео и статье рассказывается, как мы проводим эти расчеты, чтобы вы точно знали, что происходит, когда вы заказываете гнутые детали из листового металла.
Видеоруководство по расчету допусков на изгиб и уменьшению изгиба
Примечание: вам будет легче понять содержание этого видео и статьи, если вы смотрели наше предыдущее видео о К-факторе в гибке.
Знакомство с калькулятором гибки
Следуйте видео и расшифровке ниже, открыв калькулятор гибки SendCutSend и самостоятельно введя значения.
В нашем калькуляторе гибки вы можете ввести желаемый материал, а также единицы измерения, используемые в вашем проекте (дюймы или миллиметры). Вы также можете ввести фланцы. В этом примере мы ввели два фланца и сделали нашу базовую длину равной 2 дюймам. Мы сделали фланец R1 6 дюймов с 9под углом 0° вверх, а фланец R2 2 дюйма под углом 90° вверх.
Прокручивая страницу вниз, вы увидите, что для вашей части есть вид сверху и сбоку. На виде сбоку вы можете видеть, что наш образец детали представляет собой изгиб С-образного канала.
Если вы прокрутите немного вниз, вы увидите желаемую длину и измененную длину. Это два разных размера из-за расчетного допуска на изгиб и уменьшения изгиба.
Это два разных размера из-за расчетного допуска на изгиб и уменьшения изгиба.
Наконец, «Дополнительные сведения», которые вы можете увидеть, включают тип материала, К-фактор, радиус изгиба и толщину. Калькулятор изгиба использует эти значения в дополнение к толщине материала для расчета допуска на изгиб и уменьшения изгиба.
Фоновые вычисления
Давайте посмотрим, что на самом деле делает этот калькулятор в фоновом режиме. Это проще всего понять на примере.
В нашем примере у нас есть два фланца высотой 2 дюйма с основанием шириной 6 дюймов, поэтому всего у него два изгиба. Эта деталь будет вырезана лазером из алюминия 5052 толщиной 0,080 дюйма. Он будет иметь радиус изгиба 0,125 дюйма, К-фактор 0,4, а два угла изгиба будут составлять 90°. Что мы должны учитывать, так это то, что если мы сгладим этот изгиб, у нас получится плоская часть длиной 10 дюймов.
Однако из-за растяжения и сжатия на вершине изгиба, если мы согнем 10-дюймовую плоскую часть, чтобы получить две 2-дюймовые полки, полки в конечном итоге будут немного выше 2 дюймов. Материаловедение, стоящее за этим, рассматривается в нашем последнем видео о гибке «Что такое К-фактор в гибке?» В конечном счете, однако, у нас есть силы растяжения и сжатия, которые удлиняют материал, растягивая его, как эластичную ленту. Это приводит к изменению размеров вашей детали после гибки.
Материаловедение, стоящее за этим, рассматривается в нашем последнем видео о гибке «Что такое К-фактор в гибке?» В конечном счете, однако, у нас есть силы растяжения и сжатия, которые удлиняют материал, растягивая его, как эластичную ленту. Это приводит к изменению размеров вашей детали после гибки.
Мы исправим это с помощью вычисления, называемого «вычет изгиба». Это будет сумма, которую нам нужно вычесть из размеров детали, чтобы получить правильные точки изгиба и правильно измерить фланец. Но прежде чем мы сможем вычислить вычет изгиба, мы должны вычислить допуск изгиба. Допуск на изгиб — это фактическое измерение растянутой нейтральной оси, которая представляет собой невидимую линию, проходящую через центр материала.
Чтобы рассчитать допуск на изгиб, нам нужно знать коэффициент К, который вы также можете найти в нашем калькуляторе гибки для используемого вами материала. Мы будем использовать это уравнение для расчета припуска на изгиб:
Припуск на изгиб = Угол (Π/180) (Радиус изгиба + Коэффициент K (Толщина))
Возьмите это уравнение и подставьте свои собственные значения для угла, радиуса изгиба и К-фактор.
Когда мы делаем это для нашего примера, мы получаем значение 0,2466”. 0,2466 дюйма — это измерение нейтральной оси по всему изгибу.
Теперь, когда мы знаем, какой длины будет этот изгиб после того, как он был «растянут», мы можем вычислить вычет изгиба. Вычет изгиба говорит нам, какую часть длины нам нужно удалить (вычесть) из детали, чтобы поставить линии изгиба в нужном месте. Чтобы вычислить вычет изгиба, нам нужны радиус изгиба, толщина, угол изгиба и допуск изгиба, которые мы только что вычислили:
Вычет изгиба = 2(Радиус изгиба+Толщина)·tan(Угол/2)-Допуск изгиба
Если мы подставим эти значения из нашего примера, мы получим 0,1634”.
Как применить вычитание сгиба к детали, чтобы линии сгиба находились в правильном месте?
В нашем примере с 6-дюймовым основанием и двумя 2-дюймовыми фланцами нам нужно будет вычесть половину вычета изгиба (0,0817 дюйма) с обеих 2-дюймовых сторон и полный вычет изгиба (0,1634 дюйма) из 6-дюймового основания.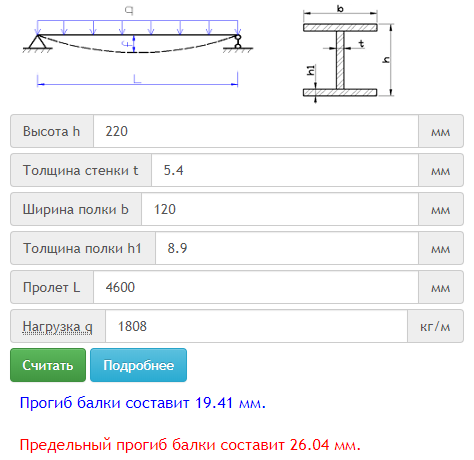 Это сократит общую длину плоской части. Когда мы действительно сгибаем деталь, «растяжение» материала добавит размер вычета изгиба обратно к общей длине детали, что позволит нам получить правильные размеры фланца и основания.
Это сократит общую длину плоской части. Когда мы действительно сгибаем деталь, «растяжение» материала добавит размер вычета изгиба обратно к общей длине детали, что позволит нам получить правильные размеры фланца и основания.
Мы упростили вам задачу, поэтому вам не нужно вычислять это вручную, прежде чем загрузить свою часть. Как мы уже говорили, если вы зайдете в наш калькулятор изгиба на веб-сайте и введете туда правильные значения, вы увидите рассчитанные для вас значения вычета изгиба и сможете соответствующим образом изменить размеры файла проекта. Если вы используете программное обеспечение САПР, иногда вы можете ввести значения К-фактора и радиуса изгиба непосредственно в программное обеспечение, и оно даст вам те же уменьшенные значения. Это зависит только от того, какое программное обеспечение вы используете.
Заключение
Наши прецизионные процессы лазерной резки и гибки с ЧПУ упрощают получение высокоточных разрезов и гибов в пределах +/-0,005″ и 1° соответственно. Мы по-прежнему хотим, чтобы вы знали, что мы делаем в нашем цехе для обработки ваших деталей в соответствии со спецификацией, поэтому мы постоянно добавляем в наш список статей, подобных этой. Если у вас есть какие-либо другие вопросы о гибке, обработке или механической обработке, лучше всего начать с этих статей и наших руководств.
Мы по-прежнему хотим, чтобы вы знали, что мы делаем в нашем цехе для обработки ваших деталей в соответствии со спецификацией, поэтому мы постоянно добавляем в наш список статей, подобных этой. Если у вас есть какие-либо другие вопросы о гибке, обработке или механической обработке, лучше всего начать с этих статей и наших руководств.
Или, если вы уже сейчас готовы к резке, обработке и отправке гнутых деталей из листового металла в течение нескольких дней, загрузите свой файл в наше приложение и получите мгновенное предложение уже сегодня!
Машиностроение. Поведение сборного С-образного канала при изгибе
Задавать вопрос
спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 766 раз
$\begingroup$
Я анализирую сборный С-образный профиль на изгиб (2 точечные нагрузки по 1200 Н каждая на расстоянии 30 см симметрично от CL). Фланцы изготовлены из другого материала, чем стенка, они также имеют другую толщину. Эти два материала имеют очень разные упругие и прочностные свойства. Предположим, что соединение между полками и стенкой идеальное.
Фланцы изготовлены из другого материала, чем стенка, они также имеют другую толщину. Эти два материала имеют очень разные упругие и прочностные свойства. Предположим, что соединение между полками и стенкой идеальное.
До сих пор я использовал трюк с «эквивалентным сечением», чтобы преобразовать размеры полок, как если бы они были сделаны из материала 2, и найти напряжения как в стенке, так и в полках, после этого я провел МКЭ балки. и напряжения очень близки к тому, что предсказывает теория.
Следующим и самым сложным этапом анализа является определение прогиба балки под действием изгибающей нагрузки. Хотя трюк с «эквивалентным сечением» помогает найти максимальные напряжения, я не уверен, что его можно использовать для определения фактического прогиба. Кроме того, мне нужно вычислить центр сдвига 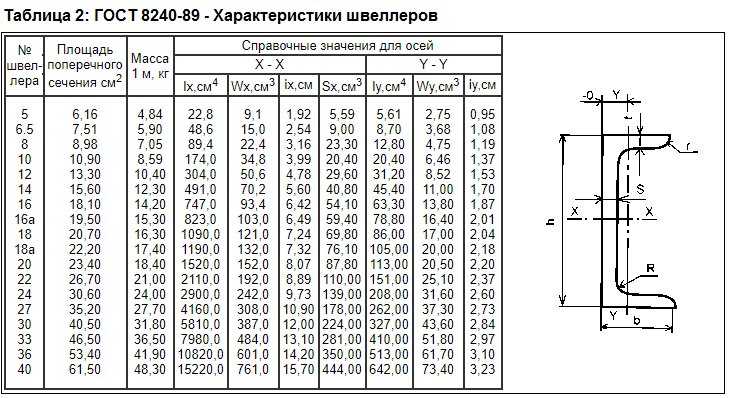 Хотя формулы Рорка для напряжения и деформации дают представление о том, как рассчитать напряжения сдвига при кручении в С-образных каналах, они обычно предполагают однородные свойства материала, что не относится к этому каналу. Материалы намного слабее на сдвиг, чем на растяжение/сжатие, так что это на самом деле моя главная проблема.
Хотя формулы Рорка для напряжения и деформации дают представление о том, как рассчитать напряжения сдвига при кручении в С-образных каналах, они обычно предполагают однородные свойства материала, что не относится к этому каналу. Материалы намного слабее на сдвиг, чем на растяжение/сжатие, так что это на самом деле моя главная проблема.
Может ли кто-нибудь порекомендовать какие-либо ресурсы, инструменты или приемы для решения этой проблемы? У меня есть доступ к книгам по механике материалов моего колледжа, и даже в расширенном издании я не смог найти ничего, что могло бы мне помочь. Теоретически я мог бы просто использовать программное обеспечение FEA для этого раздела, но мне не с чем сверять результаты, и я всегда предпочитаю иметь хотя бы приблизительное аналитическое число для перепроверки.
Любая помощь будет принята с благодарностью. Спасибо, ребята.
- машиностроение
- расчет конструкций
- напряжения
- механика твердого тела
$\endgroup$
3
$\begingroup$
Предполагая, что ваш эскиз был нарисован в масштабе, вручную вычислить положение центра сдвига будет непросто.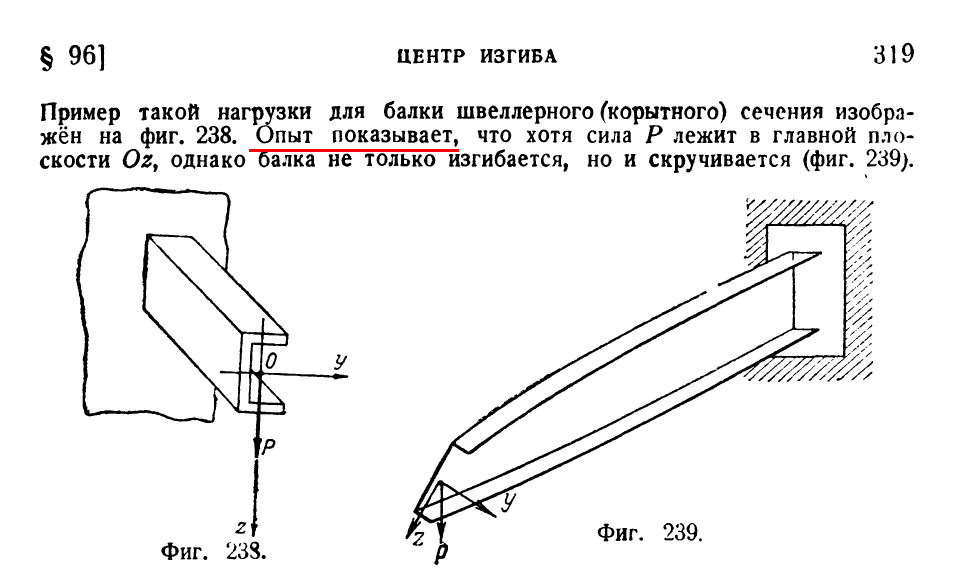
Если вам нужно точное местоположение центра сдвига, вам в значительной степени придется использовать МКЭ с 3D-элементами. Сдвиговое течение в поперечном сечении с толстыми стенками — слишком сложная тема, чтобы заморачиваться ею.
Для расчета приблизительного местоположения с использованием аппроксимации тонкостенного поперечного сечения можно использовать следующий подход: преобразованное сечение, что очень похоже на использование эквивалентного сечения, но не совсем. То есть вы выбираете один материал в качестве эталонного материала (например, номер 2) и умножаете вклад другого материала (в данном случае 1) на отношение E для двух материалов. Разница в том, что вы не настраиваете ширину или толщину материала 1. Преобразованное сечение не имеет геометрического представления в виде сечения одного материала.
Предположим, что поперечное сечение нагружено чистым сдвигом, т.