Соединения Расчет шпонок — Энциклопедия по машиностроению XXL
При расчете указанных коэффициентов крепежные детали, детали соединений трубопроводов, шпонки, прокладки, лампочки, [c.58]
Расчет шпоночных соединений. Рассчитывают шпонку как наиболее слабую деталь соединения. Размеры стандартных шпонок подобраны из условия прочности на смятие, поэтому основным расчетом их является проверочный расчет на смятие. [c.297]
Расчет шпоночных соединений. Сечение шпонки подбирают по диаметру вала d длину — обычно на 5—10 мм короче ступицы закрепляемой детали соединение проверяют на смятие. [c.373]
Рассмотренные типы шпоночных соединений стандартизованы. Размеры сечения Ь и /г) клиновой и призматической шпонок выбирают по ГОСТам в зависимости от диаметра вала, а длину назначают по размеру ступицы, насаживаемой на вал детали, и проверяют расчетом на прочность.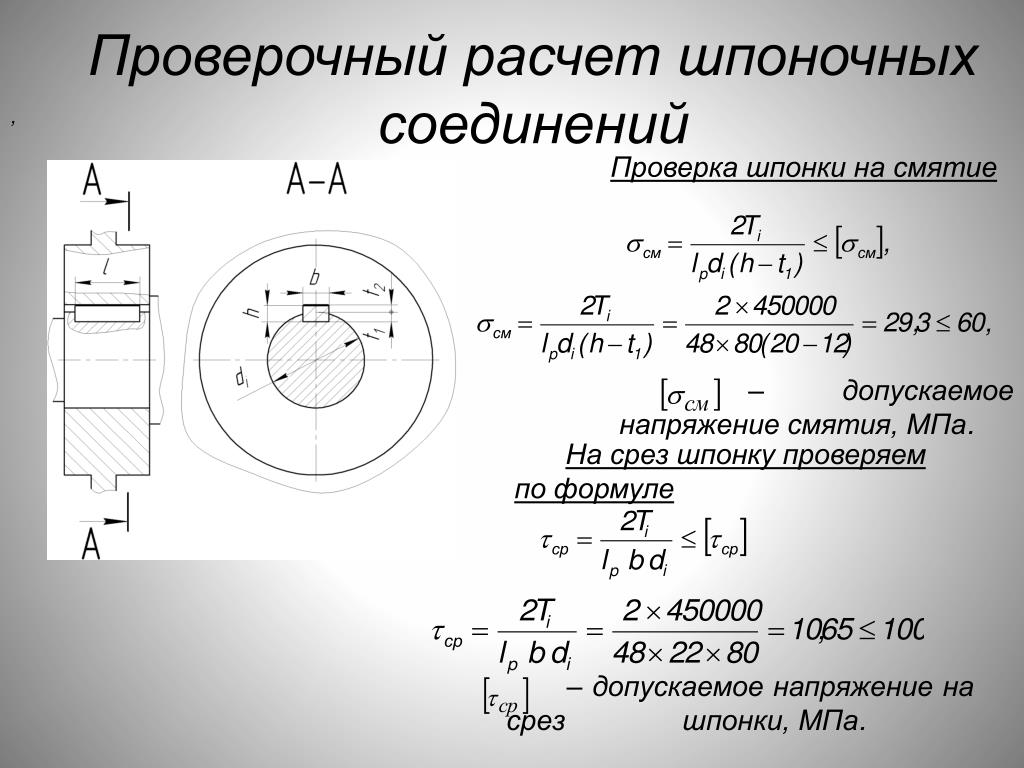
Ограничимся рассмотрением расчета соединений призматическими шпонками. [c.395]
Ограничимся рассмотрением расчета соединений призматическими шпонками. Размеры 6 и /г принимают по ГОСТ 8788—68 в зависимости от rf длину шпонки I — по длине ступицы с округлением до ближайшего стандартного значения по ГОСТ 8789—68. [c.419]
Расчет шпоночных соединений. Рассчитывают шпонку как наиболее слабую деталь соединения. Размеры [c.97]
Основным критерием работоспособности шпоночных соединений является прочность. Шпонки выбирают по таблицам ГОСТов в зависимости от диаметра вала, а затем соединения проверяют на прочность.
При расчете одноступенчатых коробок скоростей результаты расчета шпоночных и шлицевых соединений на прочность и жесткость сразу же выдаются на печать. При расчете многоступенчатых коробок это явно нерационально, так как интерес представляет расчет при максимальных моментах. Поэтому, хотя расчет шпонок производится на всех ступенях, результаты печатаются лишь один раз для расчета при наихудших условиях. Анализ работы шпонок на всех ступенях и организация печати производится блоками 9—14.
При Прочностном расчете шпонок определяют наибольшие крутящие моменты, передаваемые шпоночным соединением, исходя из допускаемых напряжений на смятие
[c. 541]
541]
Если условие (7.13) не соблюдается, соединение усиливают шпонкой. Расчет шпоночного соединения выполняют по полному моменту нагрузки Т [см. формулу (6.1)]. Влияние посадки на конус учитывают, как и в посадках с натягом, при выборе допускаемых напряжений [асм]. [c.114]
Расчет соединений со шпонками других типов см. в работе 10.531. [c.233]
Шпонки выбирают по таблицам стандарта в зависимости от диаметра вала, а затем соединение проверяют на прочность. Размеры шпонок и пазов подобраны так, что прочность их на срез и изгиб обеспечена, если выполнено условие прочности на смятие, поэтому основной расчет шпоночных соединений -расчет на смятие. [c.51]
Нагрузки от дисков, шкивов, зубчатых колес и других деталей также передаются на валы через площадки контакта. Распределение давлений (напряжений) в зонах контакта зависит от ряда конструктивных и технологических факторов (см. гл. 29), а расчетное определение этих давлений в соединениях и передачах связано со значительными математическими трудностями. В приближенных расчетах валов обычно не учитывают распределение нагрузок по длине зубьев зубчатых колес и шлицевых соединений, вдоль шпонок, вкладышей подшипников скольжения и других деталей, и при составлении расчетной схемы вала эти давления обычно заменяют эквивалентными сосредоточенными силами, приложенными в середине площадки (площадок) контакта 1,
[c.131]
В приближенных расчетах валов обычно не учитывают распределение нагрузок по длине зубьев зубчатых колес и шлицевых соединений, вдоль шпонок, вкладышей подшипников скольжения и других деталей, и при составлении расчетной схемы вала эти давления обычно заменяют эквивалентными сосредоточенными силами, приложенными в середине площадки (площадок) контакта 1,
[c.131]
Если условие (7.15) не соблюдается, соединение усиливают шпонкой — см. пример расчета. Расчет шпоночного соединения выполняют по полному моменту нагрузки Т [формула (6.6)] Влияние посадки на конус учитывают при выборе допускаемых напряжений которые принимают такими же, как для прессовых посадок (стр. 96).
Напишите формулу для расчета на смятие соединения призматической шпонкой и объясните значения величин, входящих в эту формулу. [c.305]
Размеры шпонок и пазов в ГОСТах подобраны из условия прочности на смятие, поэтому основной проверочный расчет шпоночных соединений — расчет на смятие. Проверку шпонок на срез в большинстве случаев не производят.
[c.44]
Проверку шпонок на срез в большинстве случаев не производят.
[c.44]
Проверочный расчет шпоночного соединения. Расчет производят обычно на напряжения смятия, поскольку напряжения среза (в призматических и сегментных шпонках) при соотношении размеров Ь и /г, предусмотренных стандартом, менее опасны (рис. 50). [c.58]
Шпоночные и шлицевые соединения. Для соединений призматическими шпонками основным является условный расчет на смятие [c.61]
При расчете указанных коэффициентов крепежные детали, детали соединений трубопроводов, шпонки, прокладки, лампочки, слесарно-сборочный инструмент и другие подобные детали не учитывают их учитывают отдельно. [c.312]
Расчет соединений, имеющих шпонки со скругленными торцами, производят по рабочей длине 1 (рис. 245, а) без учета округлений. [c.289]
Длину ступицы обычно делают больше длины шпонки на 6…10 мм. Если но результатам расчета шпоночного соединения длина ступицы получается 1,5г/, го шпоночное соединение следует заменить шлицевым или соединением с натягом.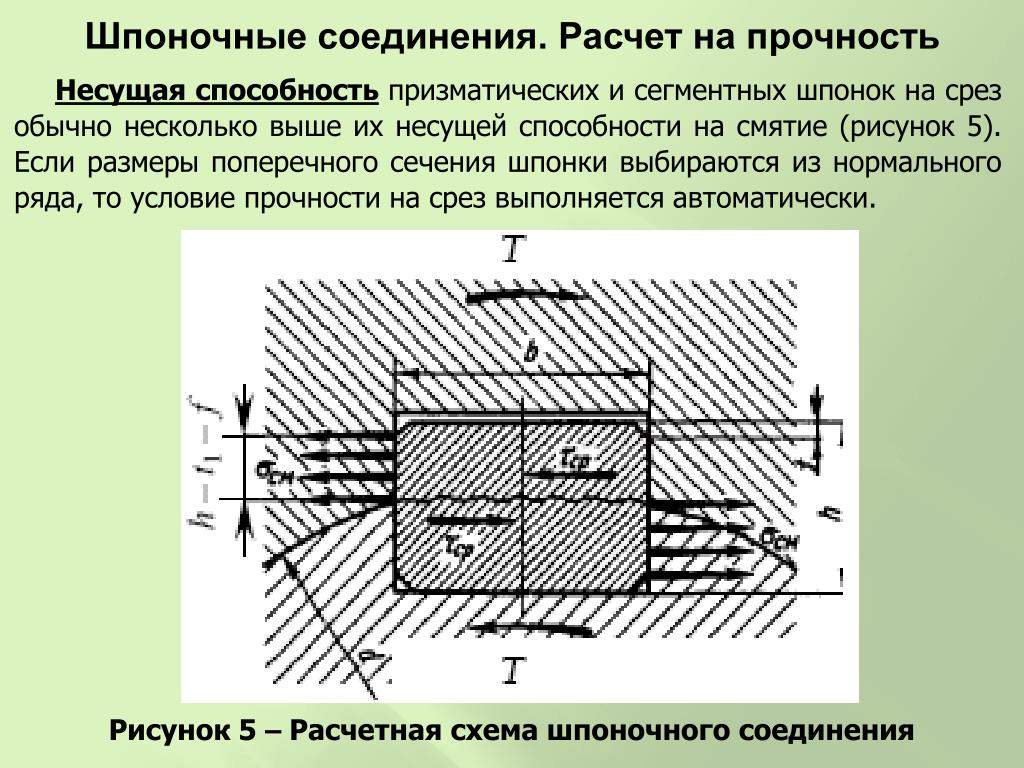 1 ис 5.1
[c.91]
1 ис 5.1
[c.91]
Расчет шпоночных соединений. Для передачи вращающего момента 7″= 55,5 10 Нмм со шкива на вал червяка применим шпоночное соединение. По табл. 19.11 для диаметра вала 30 мм /) = 8,0 мм, й = 7 мм, 1=4 мм. Длина шпонки /=32 мм, рабочая длина /р = /—/> = 32 — 8 = 24 мм. Расчетные напряжения смятия [c.240]
Призматические шпонки имеют прямоугольное сечение концы скругленные (рис. 6.1, а) или плоские (рис. 6.1, б). Стандарт предусматривает для каждого диаметра вала определенные размеры поперечного сечения шпонки. Поэтому при проектных расчетах размеры А и А берут из табл. 24.29 и определяют расчетную длину 1р шпонки. Длину 1= 1р + Ь шпонки со скругленными или / = /р с плоскими торцами выбирают из стандартного ряда (табл. 24.29). Длину ступицы назначают на 8… 10 мм больше длины шпонки. Если по результатам расчета шпоночного соединения получают длину ступицы а 1,5Д то вместо шпоночного целесообразнее применить шлицевое соединение или соединение с натягом.
 [c.77]
[c.77]Допущение о равномерности распределения касательных напряжений по сечению весьма условно. Однако это допущение во многих случаях себя оправдывает и поэтому в инженерной практике им широко пользуются при расчете болтов, заклепочных соединений, шпонок, сварных соединений и других деталей. [c.196]
Расчет соединения ведут, исходя из работы одной шпонки, так как каждая шпонка передает момент в одну сторону. [c.130]
Если соединение передает вращающий момент Т при диаметре вала с1, то длина шпонки I определяется из расчета на смятие по формуле [c.381]
Аналогично, при громадном разнообразии машин все они состоят из отдельных деталей, т. е. простейших частей, изготовляемых без применения сборочных операций. При этом многие из деталей встречаются в самых различных машинах вне зависимости от их назначения и конструкции. Такие детали принято называть деталями общего назначения. Это детали, служащие для соединения частей машин, — болты, винты, штифты, шпонки и т.
Расчет шлицевых соединений. Размеры зубьев аналогично шпонкам выбирают ио [c.391]
Расчет ненапряженных шпоночных соединений. Основными критериями работоспособности ненапряженных шпоночных соединений являются прочность шпонки на срез и прочность соединения на смятие. Расчеты на срез и смятие основаны на предположении, что соответствующие напряжения распределены по сечениям равномерно. Расчетная формула на срез шпонки (рис. 3.27) имеет вид
[c. 52]
52]
Размеры стандартных призматических и сегментных шпонок установлены в зависимости от диаметра вала по з словию прочности шпонки на срез, поэтому основным для таких соединений является проверочный расчет на смятие, а расчет на срез необходим лишь для нестандартных шпонок и особо ответственных конструкций. Если требуется определить длину призматической шпонки, то ее также определяют из расчета на смятие. Обычно длина призматической шпонки должна быть на 3—10 мм меньше длины ступицы, насаженной на вал детали. [c.53]
Подбор и проверочный расчет шпоношого соединения. Для передачи крутящего момента от коинческогс колеса иа муфту применим призматическую шпонку со скругленными торцами по СТ СЭВ 189—75 (табл. 4,1). Примем диаметр соединения полумуфт с зубчатыми колесами 2, и Zi d = 55 мм (см, рлс. 8,15). Выписываем из указанного стандарта размеры сечения шпонки и пазов (мм)
Выбор и проверочный расчет шпоноч foro соединения. Для передачи крутящего момента от III вала па i V вал применим две призматические шпонки (рис. 8.20) со скэуглеиными торцами но СТ СЭВ 189—75 (см. табл. 4.1). По диаметру вала d = 36 мм принимаем размеры сечения шпонки и пазов (мм) 6=10 /i—=8 Л = 5 2 = 3,3 г,(апм = 0,25 Гианб —0,4.
[c.327]
Для передачи крутящего момента от III вала па i V вал применим две призматические шпонки (рис. 8.20) со скэуглеиными торцами но СТ СЭВ 189—75 (см. табл. 4.1). По диаметру вала d = 36 мм принимаем размеры сечения шпонки и пазов (мм) 6=10 /i—=8 Л = 5 2 = 3,3 г,(апм = 0,25 Гианб —0,4.
[c.327]
Расчет и выбор переходных посадок. Переходные посадки H/j Н/к, И/ш, Н/п используют в неподвижных разъемных соединениях для центрирования сменных деталей пли деталей, которые при необходимости могут передвигаться вдоль вала. Эти посадки характеризуются малыми зазорами и натягами, что, как правило, позволяет собирать детали при небольших усилиях (вручную или с помош,ью молотка). Для гарантии неподвижности одной детали относительно друго11 соединения дополнительно кренят шпонками, стопорными винтами и другими крепежными средствами. [c.220]
Расчет и выбор посадок с натягом. Посадки с патягом предназначены в основном для получения неподвижных неразъемных соединений без дополнительного крепления деталей. Иногда для повышения надежности соединения дополнительно используют шпонки, штифты и другие средства креилення, как, например, при крепле-ппи маховика на коническом конце коленчатого вала двигателя. Относительная неподвижность деталей обеспечивается силами сцепления (трения), возникающими на контактирующих поверхностях вследствие их деформации, создаваемой натягом при сборке соединения. Благодаря надежности и простоте конструкции деталей и сборк1г соединений эти посадки применяют во всех отраслях машиностроения (например, при сборке осей с колесами на железнодорожном транспорте, венцов со ступицами червячных колес, втулок с валами, составных коленчатых валов, вкладышей подшипников скольжения с корпусами и т. д.).
[c.222]
Иногда для повышения надежности соединения дополнительно используют шпонки, штифты и другие средства креилення, как, например, при крепле-ппи маховика на коническом конце коленчатого вала двигателя. Относительная неподвижность деталей обеспечивается силами сцепления (трения), возникающими на контактирующих поверхностях вследствие их деформации, создаваемой натягом при сборке соединения. Благодаря надежности и простоте конструкции деталей и сборк1г соединений эти посадки применяют во всех отраслях машиностроения (например, при сборке осей с колесами на железнодорожном транспорте, венцов со ступицами червячных колес, втулок с валами, составных коленчатых валов, вкладышей подшипников скольжения с корпусами и т. д.).
[c.222]
В зависимости от взаимного расположения полей допусков посадки могут быть (рис. 3.4) с зазором (а), переходные (б) и с натягом (в). Посадки назначают из расчета или опыта, имеющегося в данной отрасли. Посадки с зазоро.м обычно применяют в подвижных соединениях (например, подшипниках скольжения) и в неподвижных, если надо обеспечить легкую сборку и разборку.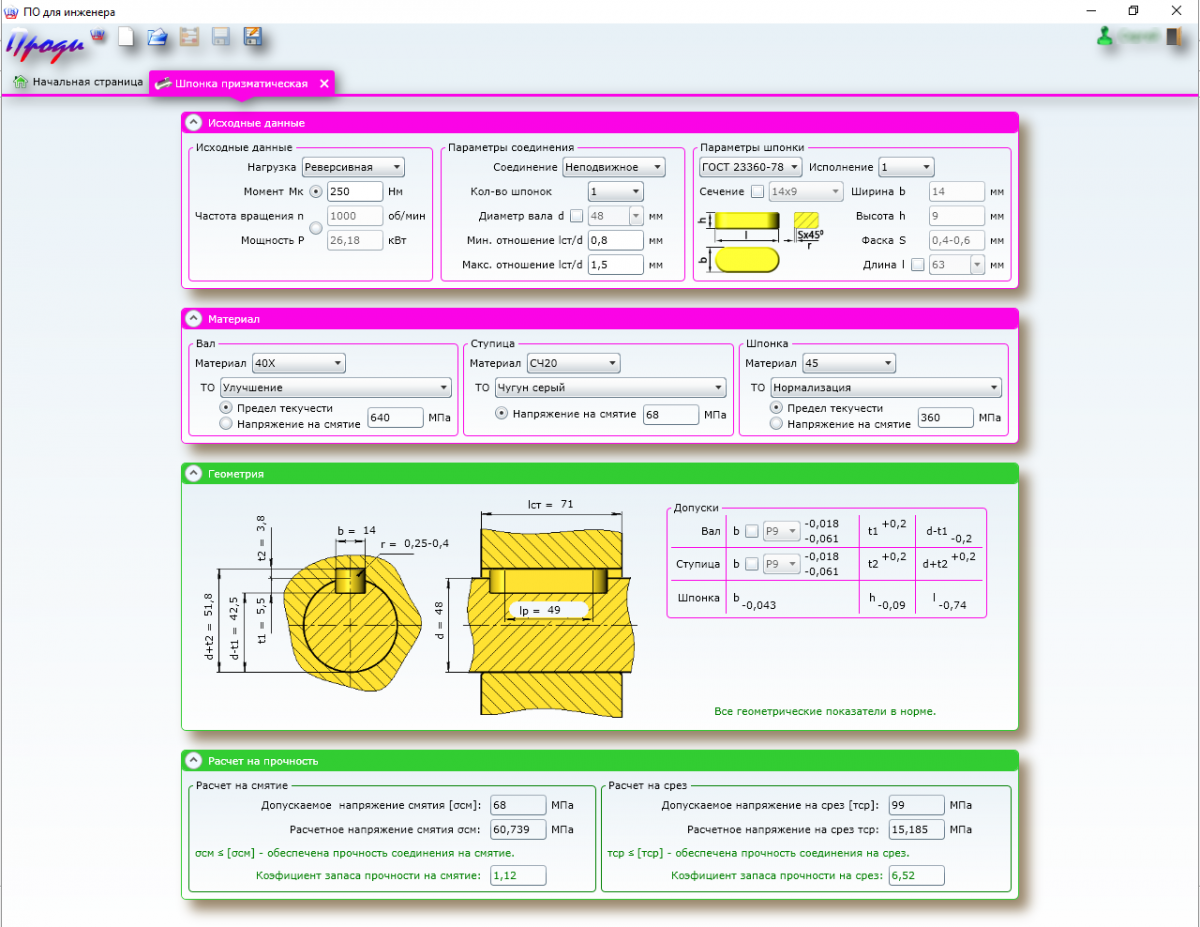 Переходные используют в неподвижных соединениях, требующих повторных сборок и разборок с применением дополнительных креиле-ний (шпонок, резьбовых деталей и т. д.). Посадки с натягом применяют в неподвижных соединениях. Поскольку посадка образуется сочетание.м полей допусков отверстия и вала, на чертежах ее обозначают в виде дроби, причем в числителе указывают обозначение поля допуска отверстия, а в знаменателе— вала, например 01ОЯ7/К6.
[c.265]
Переходные используют в неподвижных соединениях, требующих повторных сборок и разборок с применением дополнительных креиле-ний (шпонок, резьбовых деталей и т. д.). Посадки с натягом применяют в неподвижных соединениях. Поскольку посадка образуется сочетание.м полей допусков отверстия и вала, на чертежах ее обозначают в виде дроби, причем в числителе указывают обозначение поля допуска отверстия, а в знаменателе— вала, например 01ОЯ7/К6.
[c.265]
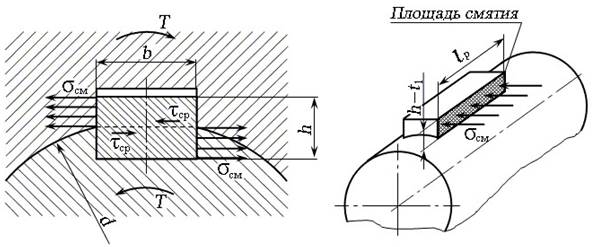
Критерием работоспособности крепежного штифтового соединения является прочность. В соединении (рис. 3.32, в) диаметр штифта можно определить из расчета его на срез по двум поперечным сечениям в соединении, показанном на рис. 3.32, г, диаметр и длина / круглой шпонки определяются из расчета на сре3 по диаметральному сечению (один из размеров задается, например, d = 0,25d , где d — диаметр вала), а затем проверяют соединение на смятие, причем условная площадь смятия равна половине площади диаметрального сечения круглой шпонки.
 [c.61]
[c.61]Проверочный расчет шпоночных соединений
Опубликовано 01 Окт 2013
Механика | 22 комментария
Одной из самых распространенных, простых и дешевых деталей соединения вала со ступицей зубчатого колеса, шкива, маховика является призматическая шпонка. Клиновые, сегментные и цилиндрические шпонки применяются на практике гораздо реже. Хотя приходилось встречать…
…при ремонтных работах все вышеперечисленные типы шпонок, при проектировании новых машин я и мои коллеги применяли исключительно шпоночное соединение с призматической шпонкой, как наиболее технологичное из всех вышеназванных.
Основной задачей, которую выполняет шпоночное соединение, является передача крутящего момента от ступицы валу или от вала ступице. Материалом для изготовления шпонок на практике чаще всего являются Сталь45 и Сталь40Х с временным сопротивлением разрыву более 550…600 МПа.
Шпоночное соединение с призматическими шпонками регламентировано ГОСТ23360-78, а с призматическими высокими шпонками — ГОСТ10748-79.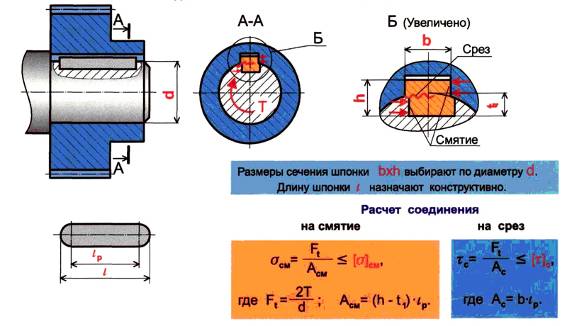 В этих двух ГОСТах даны размеры и допуски на изготовление, как самих шпонок, так и пазов в валу и ступице. ГОСТы можно свободно найти в Интернете и скачать. Они понадобятся в нашей дальнейшей работе. «Выжимки» из этих ГОСТов есть в любом справочнике конструктора-машиностроителя.
В этих двух ГОСТах даны размеры и допуски на изготовление, как самих шпонок, так и пазов в валу и ступице. ГОСТы можно свободно найти в Интернете и скачать. Они понадобятся в нашей дальнейшей работе. «Выжимки» из этих ГОСТов есть в любом справочнике конструктора-машиностроителя.
Предварительно сечение призматической шпонки выбирается по диаметру вала! Длина шпонки назначается из конструктивных и прочностных соображений.
Блок: 1/7 | Кол-во символов: 1382
Источник: http://al-vo.ru/mekhanika/raschet-shponochnogo-soedineniya.html
Шпоночное соединение. Проверочный расчет в Excel
Этот простой расчет можно быстро выполнить в программе MS Excel или в программе OOo Calc.
В ячейки со светло-бирюзовой заливкой пишем исходные данные, в том числе данные, выбранные пользователем по таблицам ГОСТов.
В ячейках со светло-желтой заливкой считываем результаты расчетов.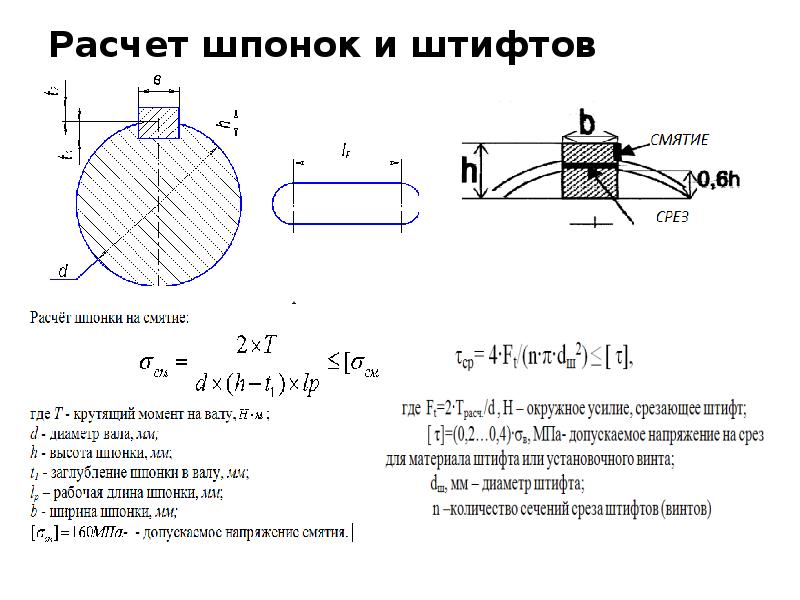
Синий шрифт – это исходные данные.
Красный шрифт – это результаты расчетов.
Еще раз напоминаю, что в итоговом файле с программой в примечаниях ко всем ячейкам столбца D помещены пояснения — как и откуда взяты или по каким формулам рассчитаны все значения в таблице!!!
Начинаем по пунктам выполнять алгоритм расчета на примере конкретного соединения. Расчетная схема представлена на рисунке внизу этого текста. Скриншот окна программы расположен сразу после исходных данных.
Блок: 2/7 | Кол-во символов: 806
Источник: http://al-vo.ru/mekhanika/raschet-shponochnogo-soedineniya.html
ШПОНКИ ПРИЗМАТИЧЕСКИЕ
Принятые обозначения:
— наибольший допускаемый вращающий момент, Н·м;
l — рабочая длина шпонки, мм;
d — диаметр вала, мм;
b и h — ширина и толщина шпонки, мм;
К — выступ шпонки от шпоночного паза;
— допускаемое напряжение смятия, МПа;
— допускаемое напряжение среза, МПа.
При расчете принимают нагружение шпонки по длине равномерным.
Шпонки рассчитывают на смятие, а в особо ответственных случаях проверяют на срез.
Рабочие грани проверяют на смятие, а сечение С — С — на срез.
Условие прочности на смятие:
= 0,5·d·K·l··10-3
Условие прочности сечения С — С на срез:
= 0,5·(d+K)·b·l··10-3
В случае установки двух противоположно расположенных шпонок вводят поправочный коэффициент 0,75.
Блок: 2/5 | Кол-во символов: 745
Источник: https://alexfl.pro/inform/inform_raschet1.html
Шпонки призматические ГОСТ 23360-78
| Диаметр вала d | Сечение шпонки bхh | Глубина паза | K=h-t | |
| Вала t | Втулки t1 | |||
| Св. 6 до 8 | 2×2 | 1.2 | 1.0 | 0.8 |
| 8 — 10 | 3×3 | 1. 8 8 | 1.4 | 1.2 |
| 10 — 12 12 — 17 17 — 22 | 4×4 5×5 6×6 | 2.5 3.0 3.5 | 1.8 2.3 2.8 | 1.5 2.0 2.5 |
| 22 — 30 30 — 38 | 7×7 8×7 | 4.0 5.0 | 3.3 3.3 | 3.7 3.7 |
| 10×8 | 5.0 | 3.3 | 3.0 | |
| Св. 38 до 44 44 — 50 50 — 58 58 — 65 | 12×8 | 5.0 | 3.3 | 3.0 |
| 14×9 | 5.5 | 3.8 | 3.5 | |
| 16×10 | 6.0 | 4.3 | 4.0 | |
| 18×11 | 7.0 | 4.4 | 4.0 | |
| Св. 65 до 75 | 20×12 | 7.5 | 4.9 | 4.5 |
| 75 — 85 | 22×14 | 9.0 | 5.4 | 5.0 |
| 85 — 95 | 24×14 25×14 | 9.0 | 5. 4 4 | 5.0 |
| 95-110 | 28×16 | 10.0 | 6.4 | 6 |
| 110 — 130 130 — 150 150 — 170 170 — 200 200 — 230 | 32×18 36×20 40×22 45×25 50×28 | 11.0 12.0 13.0 15.0 17.0 | 7.4 8.4 9.4 10.4 11.4 | 7.0 8.0 9.0 10.0 11.0 |
| 230 — 260 260 — 290 | 56×32 63×32 | 20.0 20.0 | 12.4 12.4 | 12.0 12.0 |
| 290 — 330 330 — 380 | 70×35 80×40 | 22.0 25.0 | 11.4 15.4 | 13.0 15.0 |
| 280 — 440 440 — 500 | 90×45 100×50 | 28.0 31.0 | 17.4 19.5 | 17.0 19.0 |
Расчет сегментных шпонок.
Призматические шпонки рассчитывают на смятие, а в особо ответственных случаях проверяют на срез. При расчете принимают нагружение шпонки по длине равномерно.
При расчете принимают нагружение шпонки по длине равномерно.
где — наибольший допускаемый крутящий момент, H м;
Мкр — крутящий момент на валу, Н м;
l — рабочая длина шпонки, мм;
d — диаметр вала, мм;
b и h — ширина и высота шпонки, мм;
К — выступ шпонки от шпоночного паза, мм;
— допускаемое напряжение на срез, МПа;
— допускаемое напряжение на смятие, МПа;
В случае установки двух противоположно расположенных шпонок вводят поправочный коэффициент 0,75.
В машиностроении принимают
= (0,3 … 0,5) σт — для неподвижных соединений
и = (0,1 … 0,2 )σт — для подвижных соединений,
где σт — предел текучести материала шпонки.
Блок: 2/2 | Кол-во символов: 1742
Источник: https://kataltim.ru/chponka.php
ШПОНКИ ТОРЦОВЫЕ
Торцовая шпонка — это призматическая шпонка, поставленная в плоскость стыка, например, при фланцевом соединении концов двух валов.
Узкая грань шпонки подвергается смятию; продольное сечение шпонки, плоскость которого совпадает с плоскостью стыка валов, испытывает напряжение среза (сдвига).
Условие прочности на смятие:
Блок: 4/5 | Кол-во символов: 344
Источник: https://alexfl.pro/inform/inform_raschet1.html
Несколько итоговых замечаний:
1. Расчеты на срез можно не выполнять, так как смятие всегда наступит раньше для любых шпонок по ГОСТ23360-78 и ГОСТ10748-79.
2. Если одна шпонка не выдерживает нагрузки, то можно поставить две через 180˚ друг от друга. При этом нагрузочная способность соединения возрастет по данным разных авторов в 1,5…2,0 раза.
3. Значения допустимых напряжений смятия у разных авторов существенно разнятся:
При стальной ступице и спокойной нагрузке =100…150 МПа
При стальной ступице и колебаниях нагрузки =75…120 Мпа
При стальной ступице и ударной нагрузке =50…90 Мпа
При чугунной ступице и спокойной нагрузке =50…75 Мпа
При чугунной ступице и колебаниях нагрузки =40…60 Мпа
Для неподвижных соединений =(0,3…0,5)*
Для подвижных соединений =(0,1…0,2)*
Для поверхности с твердостью меньше 240HB = 150 МПа
Для поверхности с твердостью 270…300HB = 250 МПа (???!!!.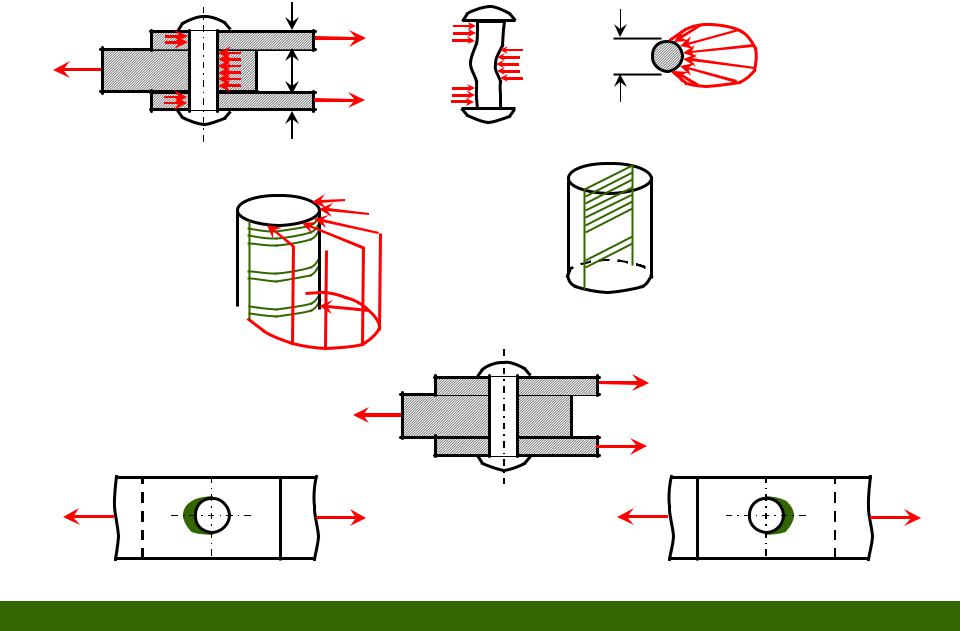 .)
.)
На практике для неподвижных соединений валов со стальными ступицами при колебаниях нагрузки и отсутствии сильных ударов я успешно применял в расчетах =90 Мпа. При этом твердость поверхностей шпонки, вала, и иногда ступицы задавал около 300 HB (28…32 HRC). Наверное, перестраховывался.
4. При разработке рабочего чертежа ступенчатого вала старайтесь расположить шпоночные пазы в одной плоскости и выполнить их одной ширины (даже вопреки рекомендациям ГОСТов). При соблюдении вышесказанного пазы на фрезерном станке будут сделаны за одну установку и без смены инструмента – за что технолог и фрезеровщик вам скажут спасибо!
5. Если внимательно посмотреть на расчетные формулы, то можно заметить, что площадь поверхности смятия и площадь поверхности среза считаются по некорректным формулам! Не учитываются фаски кромок и радиусы скруглений шпонки. Не правильно считается высота, а значит и площадь выступающей из вала боковой поверхности шпонки – не учитывается «спад» окружности. Однако все это не имеет существенного значения и влияния на результат из-за глобальной неопределенности, о которой мы говорили в пункте 3 итоговых замечаний…
Однако все это не имеет существенного значения и влияния на результат из-за глобальной неопределенности, о которой мы говорили в пункте 3 итоговых замечаний…
Для получения информации о выходе новых статей и для скачивания рабочих файлов программ прошу вас на анонсы в окне, расположенном в конце статьи или в окне вверху страницы.
Готов ответить на ваши вопросы и выслушать на статью, уважаемые читатели!!!
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
Ссылка на скачивание файла: raschet-shponki (xls 39,0 KB).
Другие статьи автора блога
На главную
Блок: 5/7 | Кол-во символов: 2468
Источник: http://al-vo.ru/mekhanika/raschet-shponochnogo-soedineniya.html
Количество использованных доноров: 4
Информация по каждому донору:
- http://al-vo.
 ru/mekhanika/raschet-shponochnogo-soedineniya.html: использовано 3 блоков из 7, кол-во символов 4656 (48%)
ru/mekhanika/raschet-shponochnogo-soedineniya.html: использовано 3 блоков из 7, кол-во символов 4656 (48%) - https://alexfl.pro/inform/inform_raschet1.html: использовано 3 блоков из 5, кол-во символов 1342 (14%)
- https://studbooks.net/1540594/tovarovedenie/proverochnyy_raschet_shponochnyh_soedineniy: использовано 1 блоков из 3, кол-во символов 1982 (20%)
- https://kataltim.ru/chponka.php: использовано 1 блоков из 2, кол-во символов 1742 (18%)
Расчет на прочность соединений с призматическими шпонками
Характеристика шпоночных соединений
Шпонка представляет собой продолговатую деталь, которая вставляется в паз, вырезанный в валу. Они имеют в разрезе разную форму и делятся:
- призматические;
- круглые;
- сегментные;
- тангенциальные;
- клиновые.
По исполнению различают ненапряженные и напряженные соединения.
Призматические шпонки устанавливаются с легким натягом. Аналогично собирают сегментное соединение. Происходит центрирование без монтажных напряжений. Такие соединения относят к ненапряженным.
Происходит центрирование без монтажных напряжений. Такие соединения относят к ненапряженным.
При установке клиновых шпонок и из разновидности — тангенциальных, требуется точно подогнать размер. Делается большой монтажный натяг при запрессовке втулки и возникает осевое смещение. Соединения называют напряженными.
Ступица имеет сквозную выборку по отверстию и надевается на выступающую из вала шпонку.
Прочность шпоночного соединения рассчитывают:
- на срез;
- на смятие.
Обычно расчет ведется на смятие шпонки, поскольку разрушение начнется с него. Срез шпонки возможен только в случаях, когда напряжение сконцентрировано по линии соприкосновения вала и ступицы при неправильной подгонке шпонок. Если сечение детали значительно меньше ее высоты, он может срезаться. Это используют, когда нужен предохранительный механизм от перегрузок. Менять детали зубчатого зацепления дорого и долго, проще переставить шпонку.
Выбор шпонки для расчета осуществляется по диаметру вала подбором соответствующих ему соединительных деталей.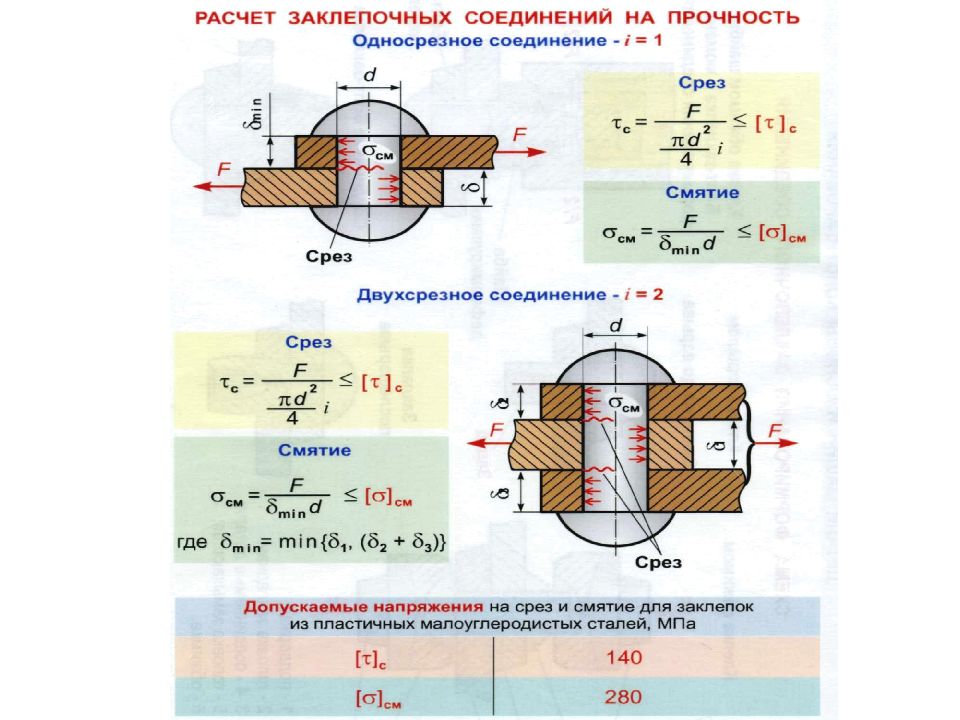 Длина вычисляется по нагрузке, чтобы она ее выдержала. Все детали имеют стандартные размеры, и выбираются по таблице округлением до большей, чем расчетная деталь.
Длина вычисляется по нагрузке, чтобы она ее выдержала. Все детали имеют стандартные размеры, и выбираются по таблице округлением до большей, чем расчетная деталь.
На смятие расчет делается по формуле:
[Mкр max] = 0,5DKLδсм
Где: Mкр max – максимальный крутящий момент, допустимый на валу;
D – диаметр вала, соответственно 0,5 d его радиус;
K – высота выступающей из паза вала части шпонки ;
L – длина;
δсм – допускаемое напряжение при смятии.
Откуда расчетный размер длины шпонки высчитывается по формуле:
L = Mкр/0,5DKδсм
Где Mкр – крутящий момент вала.
Подбор детали нужного размера делается по таблице нормализованных длин для шпонок. Значение округляется до ближайшего размера. Например, в результате расчета получили расчетную длину 16,6. 16 мм будет мало, следующее значение 18 мм подходит.
Проверка правильности расчета делается на срез, по формуле:
[Mкр max] = 0,5(D+K)bL[τср ]
Где: τср – допустимое значение на срез.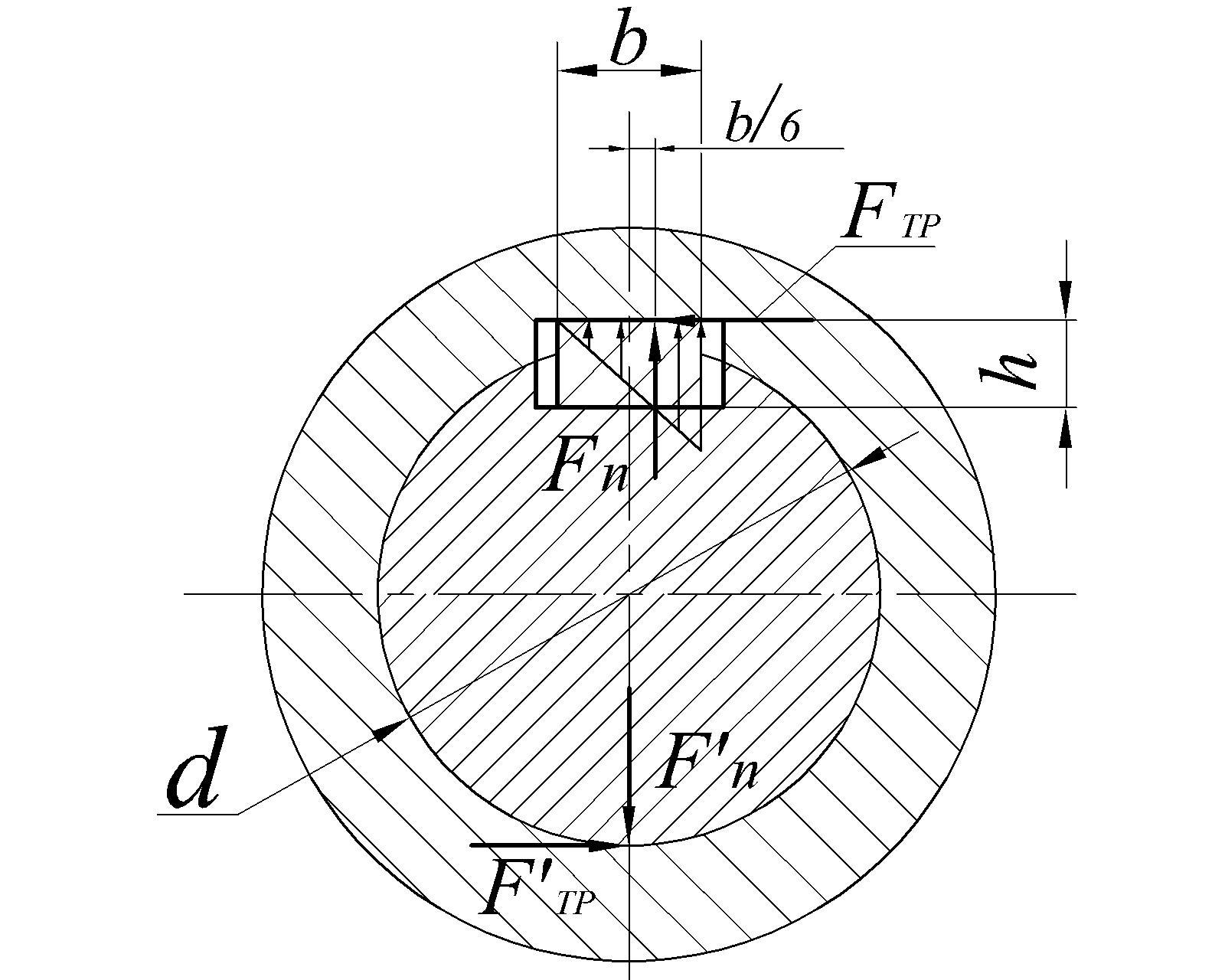
Минимальная расчетная длина детали на срез проверяется по формуле:
L = Mкр/0,5(D+K)b[τср ]
Расчетная длина по второй формуле должна быть больше. Сравнением 2 чисел определяется нагруженность соединения.
При больших нагрузках ступица может оказаться короче расчетной длины шпонки. В этом случае устанавливается 2 детали. Надо учитывать погрешность изготовления деталей и неравномерно распределенную нагрузку. Расчетный коэффициент нагрузки при 2 соединениях 0,75.
Пазы делаются под углом 180° и располагаются напротив. Для упрощения технологии обработки, рекомендуется на разных диаметрах одного вала фрезеровать одинаковые пазы. Операция проводится с одной установки и инструмент не выходит из оси.
Основные разновидности
Для соединения валов и ступиц используются сегментные шпонки двух разновидностей:
- нормальные, представляющие собой целый сегмент;
- низкие, изготавливаемые в виде срезанного сегмента.
Шпонки последнего типа применяются при сборке деталей достаточно редко.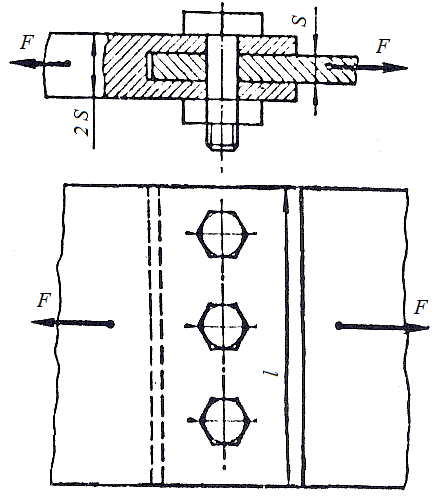 Согласно нормативам, использоваться они могут только по обоюдному согласию производителя и потребителя. Применяются срезанные шпонки обычно просто для фиксации деталей узла. То есть используются они в соединениях при неподвижной посадке тогда, когда крутящий момент передается только за счет силы трения.
Согласно нормативам, использоваться они могут только по обоюдному согласию производителя и потребителя. Применяются срезанные шпонки обычно просто для фиксации деталей узла. То есть используются они в соединениях при неподвижной посадке тогда, когда крутящий момент передается только за счет силы трения.
Алгоритм расчета
Расчет шпонки по исходным данным можно сделать с помощью компьютерных программ. Наиболее простые, и удобные в пользовании: MS Excel и OOo Calc. Программа включает в себя расчетные формулы, содержит все нормализованные размеры на валы, ступицы и шпонки.
Для выполнения алгоритма расчета используем пример с реальными цифрами. Их следует заносить в строгой последовательности в раздел с синими надписями значений. Проставлять цифры следует в свободную колонку между условными обозначениями из формул и единицами измерения. Например:
- Крутящий момент на валу – 300 Н/м.
- Диаметр вала – 45 мм.
- Глубина паза на валу – 5,5 мм.
- Высота шпонки – 9 мм.
 Выбирается по справочной таблице, которая имеется в программе.
Выбирается по справочной таблице, которая имеется в программе. - Ширина шпонки – 14 мм.
- Длину шпонки – 63 мм.
- Вариант исполнения – 1. С прямыми углами, или закругленными торцами с одной или двух сторон. Выбираем с полукруглыми торцами. По классификации они обозначаются 1.
- Величина допускаемого при смятии напряжения – 90 Мпа.
- Напряжение среза – 54 Мпа. Значение берется как 60% от величины смятия.
Результаты расчетов программа выдает в той же таблице, только ниже, это действующие величины напряжений смятия и среза, нагруженность соединения по этим напряжениям.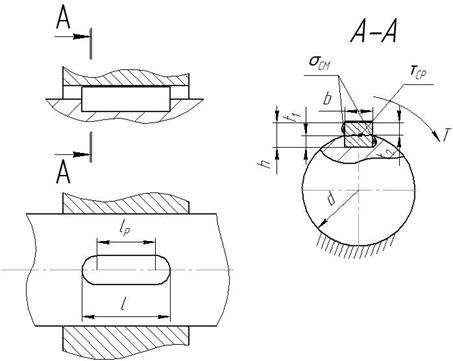
В таблице приведены результаты расчета на компьютерной программе MS Excel.
| Название показателя | Формула расчета | Полученное значение |
| Напряжение смятия действующее | δсм=2*T/(d*(h-t1)*Lp) | 77,7 МПа |
| Напряжение действующее среза | δсм=2*T/(d*(h-t1)*Lp) | 19,4 Мпа |
| Нагруженность по напряжению смятия | sсм=δсм/{δсм} | 86,40% |
| Нагруженность по срезу | Sср=TСР/{Tср} | 36,00% |
Расчет на смятие и срез производится приблизительный, поскольку не учитывается целый ряд факторов, влияющих на фактический размер нагрузки:
- неравномерное соединение по всей плоскости;
- наличие фасок на детали, уменьшающих площадь;
- не прилегание на скругленных торцах втулки на зубчатом колесе.
На практике обычно делают расчет на смятие, поскольку эта сила воздействия значительно превышает давление на срез. При разрушении в результате перегрузок, происходит деформация поверхности соприкосновения деталей, потом шпонка срезается. При расчете механизмов, результат умножается на коэффициент прочности. Для каждого вида машин он разный.
При расчете механизмов, результат умножается на коэффициент прочности. Для каждого вида машин он разный.
Программы подходят и для расчета круглых шпонок. Площадь воздействия и сечение берутся по аналогии с призматическими, рассчитываются через радиус.
Сопряжения
Собираются узлы с использованием сегментных шпонок с учетом нормативов, предусмотренных ГОСТ 24071. Основным назначением элементов этого типа является предотвращение проворачивания детали на валу. В сопряжении при этом участвуют три поверхности:
- пазы на валу;
- пазы во втулке;
- поверхность самой шпонки.
Соединения сегментные шпонки образуют ненапряженные. При этом работают они, как и обычные призматические, боковыми гранями. Используют сегментные элементы чаще всего в неподвижных соединениях. При этом последние могут быть:
- нормальными;
- плотными.
ГОСТ допускает также свободное соединение сегментной шпонки со втулкой и валом. Используются такие детали обычно только в узлах с небольшим диаметром сопряжения — до 38 мм.
Призматические шпонки
Простые в исполнении и сборке призматические шпонки широко применяются в зубчатых зацеплениях и других узлах, передающих крутящий момент. В поперечном оси сечении они имеют форму прямоугольника. С торцов могут быть закругленными.
Изготавливаются из проката среднеуглеродистых сталей Ст 45 и Ст 40х. После строжки с припуском проходят нормализацию или закалку для получения твердости 300-320 Hb. Чистовой размер доводится шлифовкой, иногда прямо на сборке по фактическому размеру паза. Крепится плотно в пазах вала. Прилегание рабочей поверхности втулки может выполняться без натяга.
Расчет призматической шпонки делается на смятие по площади, выступающей с вала детали. Перепроверяется на срез по размеру ширины шпонки в случае работы с динамическими нагрузками и при вибрации.
В узлах, работающих на улице, в условиях пыли и переменных нагрузок шпонки могут не запрессовываться туго в паз, а прикручиваться.
Из какого материала изготавливают
Делают сегментные шпонки по ГОСТ 8786-68, из стали, предназначенной именно для таких деталей.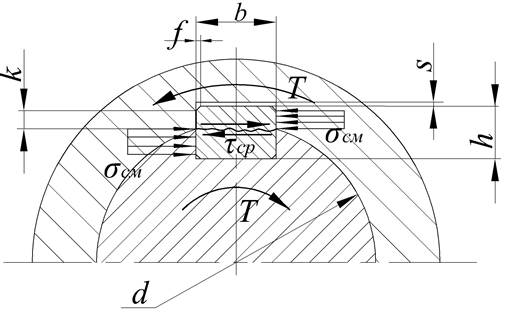 Также иногда для производства этих элементов используются и другие марки подобного материала. При этом по ГОСТ, для изготовления шпонок такой разновидности допускается применять исключительно среднеуглеродистые стали с временным разрывом не менее [σ]≥ 600 МПа МН/м2. Это может быть, например, материал марок Ст 6, 45 или 50.
Также иногда для производства этих элементов используются и другие марки подобного материала. При этом по ГОСТ, для изготовления шпонок такой разновидности допускается применять исключительно среднеуглеродистые стали с временным разрывом не менее [σ]≥ 600 МПа МН/м2. Это может быть, например, материал марок Ст 6, 45 или 50.
Соблюдаются такие нормативы при производстве сегментных шпонок в обязательном порядке. При этом заготовки, предназначенные для изготовления таких деталей, обычно еще и подвергаются улучшающей термической обработке. Выполняя эту процедуру, помимо всего прочего, учитывают и то, что твердость поверхности шпонок в конечном итоге должна быть все же ниже такого же параметра самих сопрягаемых элементов узла.
Под обычные шпонки пазы в валах делают простыми фрезами. Под сегментные элементы канавки вырезают с помощью дисковых инструментов. Используют для пазов шпонок исключительно фрезы, изготовленные с соблюдением определенных нормативов ГОСТ.
Сегментные
Шпонки, представляющие собой фрагменты окружности, называют сегментными. Они имеют полукруглый низ. Иногда для уменьшения их глубины, часть полукруга срезают.
Они имеют полукруглый низ. Иногда для уменьшения их глубины, часть полукруга срезают.
Расчет сегментной шпонки производится аналогично призматической, поскольку толщина и рабочая поверхность – высота выступающей части, работают в одинаковых условиях.
Заготовкой под обработку служит поковка. При малых нагрузках могут изготавливаться из круглого проката, но тогда нагрузка идет вдоль волокон стали и при динамических нагрузках большого значения деталь может срезаться.
Как выбирают допустимые напряжения
Этот параметр зависит в первую очередь от характера нагрузки и условий работы соединения. При использовании стальных валов допустимое напряжение будет составлять:
- для стальных ступиц в неподвижных соединениях — 130…200 МПа;
- для ступиц из чугуна или стальных литых в неподвижных соединениях — 80…100 МПа;
- в подвижных безнагрузочных соединениях для ступиц из стали — 20…40 МПа.
Большие значения при сборке узлов во внимание принимают при постоянной нагрузке. При ударной же или переменной за основу берут меньшие параметры. При реверсивной нагрузке допустимый показатель снижают в 1.5 раза. На срез же шпонок предельные показатели напряжения принимают за 70…100 МПа. При этом, как и в первом случае, при постоянной нагрузке за основу берут больший параметр.
При ударной же или переменной за основу берут меньшие параметры. При реверсивной нагрузке допустимый показатель снижают в 1.5 раза. На срез же шпонок предельные показатели напряжения принимают за 70…100 МПа. При этом, как и в первом случае, при постоянной нагрузке за основу берут больший параметр.
26 Общие сведения о шпоночных соединениях
Общие сведения о шпоночных соединениях.
Шпоночное соединение относится к разъемным, служат для передачи крутящего момента от вала к ступице (или от ступицы к валу).
Выполняется механическим способом с помощью специальных соединительных деталей, устанавливаемых в пазах вала и ступицы – шпонок.
Шпоночные соединения делят на 2 группы:
· Напряженные (с помощью клиновых шпонок), в настоящее время не применяются;
· Ненапряженные (с помощью призматических или сегментных шпонок), в настоящее время применяются в основном в мелкосерийном производстве при невысоких скоростях вращения.
Достоинства:
Простота изготовления и низкая стоимость.
Недостатки:
Рекомендуемые файлы
1. Возможен перекос шпонки под нагрузкой (особенно призматические шпонки).
2. Трудность обеспечения взаимозаменяемости (необходима ручная подгонка).
3. Является концентратором напряжения.
4. Трудность обеспечения соосности вала и ступицы.
Призматические шпонки.
Имеют прямоугольное сечение, могут иметь плоские или скругленные края.
lшп b
h
r = b/2
lp
Для стандартных шпонок : .
Если d<20 мм, то шпонки в сечении квадратные.
Если d>100, то высота меньше, чем длина.
Шпоночное соединение можно показать двумя способами:
1.
d
2. D10/h9 – подвижное
соединение (посадка с
t2 зазором)
Js9/h9- неподвижное и
t1 h Нереверсивное (переходная)
b P9/h9- неподвижная
реверсивная
Шпонки на вал и на ступицу сажаются по посадке:
P9/h9- с натягом между валом и шпонкой.
Недостаток:
Возможен перенос шпонки под нагрузкой из-за ее неглубокой посадки на вал.
Сегментные шпонки.
Являются разновидностью призматической.
R
Достоинства:
Засчет более глубокой посадки в паз вала не перекашивается под нагрузкой. Однако, сильно ослабляется вал, поэтому их применяют при небольших моментах и диаметрах валов d<40 мм.
Критерии работоспособности и расчет шпоночных соединений.
Основные причины выхода из строя шпоночных соединений:
1. смятие боковых поверхностей шпонок или пазов вала и ступицы;
2. срез шпонки.
Т.о. основными критериями работоспособности шпоночных соединений являются прочность по напряжениям смятия и прочность по напряжениям среза.
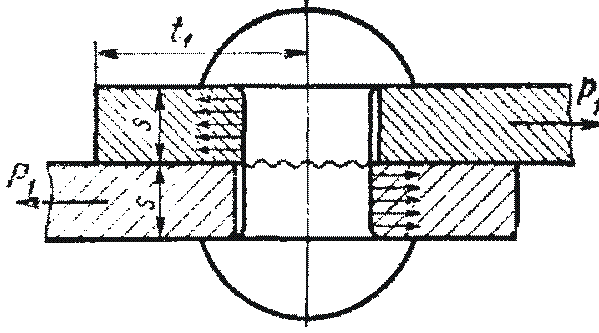
Нарисуем схему взаимодействия и эпюры напряжений, возникающих в соединении:
sсм1 Реальное распределение
t1 t h sсм2
d b
Напряжения смятия:
Т.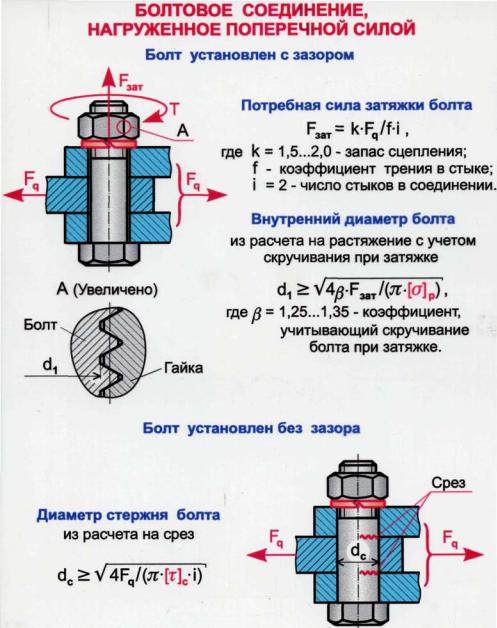 к. для стандартных шпонок t1>h — t1 , поэтому площадь смятия (1) меньше площади смятия (2) ( sсм1>sсм2 — для одинаковых материалов шпонки, вала и ступицы).
к. для стандартных шпонок t1>h — t1 , поэтому площадь смятия (1) меньше площади смятия (2) ( sсм1>sсм2 — для одинаковых материалов шпонки, вала и ступицы).
Поэтому расчет шпонки на смятие проводится по формуле:
(1)
Напряжения среза:
(2)
Покажем, что даже при напряжение среза .
Умножим выражение (1) на b и разделим на b:
(3)
Учитывая, что ,а , перепишем (3) в виде:
, если , а в стандарте .
Условие прочности на срез стандартных шпонок обеспечено при стандартизации , поэтому при расчетах стандартных шпонок необходима проверка только по напряжениям смятия.
Допускаемое напряжение на смятие:
Меньшее значение (80,150) для ступиц из чугуна, а большее (150,200) – из стали.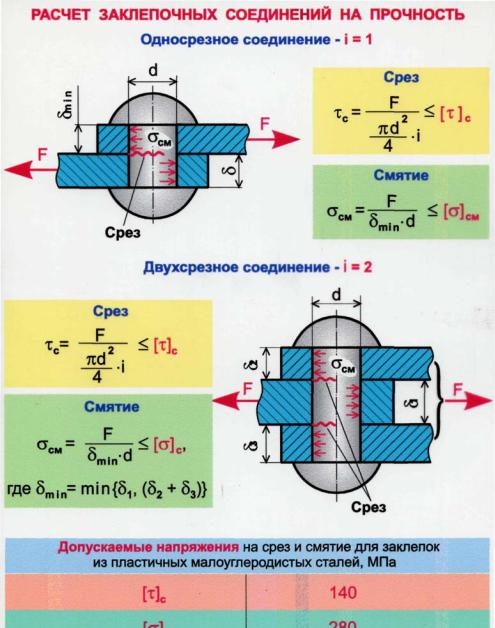
При ударной нагрузке напряжения смятия уменьшаются в 2 раза.
Конструирование шпоночных соединений.
lст
1¸2мм
1
2
1-H7/d11-зазор
Рекомендуем посмотреть лекцию «Предисловие автора».
2-H7/p6- прямозубые цилиндрические передачи,
H7/r6- косозубые цилиндрические и конические,
H7/s6- червячные передачи.
Если шпоночное соединение не проходит по напряжениям смятия (), то необходимо увеличить длину ступицы, но не более чем .
Если и теперь шпонка не проходит, то переходим к шлицевому соединению.
Условные расчеты на прочность — презентация онлайн
1. Условные расчеты на прочность
Основные расчетныезависимости
• Конструкции современных машин содержат
различные соединительные элементы, в частности
винты, штифты, заклепки и т.п.
• Данные виды конструкций не относятся к
стержневым и, поэтому, не могут быть рассчитаны
методами сопротивления материалов (с
использованием гипотезы плоских сечений).
• Расчет на прочность данного вида конструкций
основан на формулах, полученных в результате
эмпирических исследований: испытания до
разрушения на срез, смятие и разрыв. Результаты
таких испытаний показывают хорошую
воспроизводимость результатов
Определить размеры заклепочного соединения
4. Рассмотрим основные виды разрушения
9. Пример расчета заклепочного соединения.
Дано:P 50 кН
[ ] 100 МПа
[ ]cp 80 МПа
[ ] 100 МПа
[ ]cм 200 МПа
Определить размеры соединения
Определим диаметр заклепок из условия прочности на срез
P
cp
[ ]cp
Scp
d 2
Scp
2 4 2 d 2
4
P
50 10 3
d
9,97 мм
2 [ ]cp
2 80
Принимаем
d 10 мм
Определим толщину соединяемых листов
из расчета на прочность на смятие
P
cм
[ ]cм
Scм
Scм d t 3 3dt
P
50 10 3
t
8,33 мм
3d[ ]cм 3 0,01 200
t 9 мм
Принимаем
Определим толщину накладок из условия прочности на смятие
cм
P
[ ]cм
Scм
Scм d t1 3 2 6dt
P
50 10 3
t1
8,17 мм
6d [ ]cм 6 0,01 200
Принимаем
t1 8,5 мм
Определим длину l соединяемой пластины
из условия прочности на срез
cp
P
[ ]cp
Scp
Scp 2 d l 3 6dl
P
50 10 3
l
10,4 мм
6 d [ ]cр 6 0,01 80
Принимаем
l 11 мм
Определим длину l1 накладки
Scp 4 d l1 3 12dl
P
cp
[ ]cp
Scp
P
50 10 3
l1
5,2 мм
12 d [ ]cр 12 0,01 80
Принимаем
l1 6 мм
Определим размер b из условия прочности при разрыве
P
S (b d ) l 3 3(b d )l
[ ]
S
P
P
[ ]
b
3d
(b 3d )l
[ ]l
13.
 Пример расчета шпоночного соединения Дано:
Пример расчета шпоночного соединения Дано:P 50 кН
[ ] 50МПа
[ ]cp 80 МПа
[ ]cм 200 МПа
[ ] 50МПа
[ D] ?, [b] ?, [h] ?
Определим диаметр вала из условия прочности на кручение
T
8PD
max
[ ]
3
Wp 0, 2 D
8P
D
0, 2[ ]
8P
8 50 10 3
[ D]
20 см
0, 2[ ]
0, 2 [50]
Определим усилие, действующее на шпонку
Pш
2 M 2 8PD
16P
D
D
Определим длину шпонки из условия прочности на срез
P
16 P
cp шп
[ ]cp
Scp 6b b
8P
8 50 10 3
[b]
4,08 мм
3[ ]cp
3 80
Определим высоту шпонки из условия прочности на смятие
см
Pшп 16P 2
[ ]см
Sсм
6b h
16 P
16 50 10 3
[ h]
2,7 мм
3 b [ ]см
3 5 200
15. Расчет штифта
d2Дано:
P 50 кН
h
[ ]cp 80 МПа
d1
H
[ ]cм 200 МПа
[ ] 100 МПа
F
[d1 ] ?, [d 2 ] ?, [h] ?, [ H ] ?
dиз
1 условия прочности на растяжение.
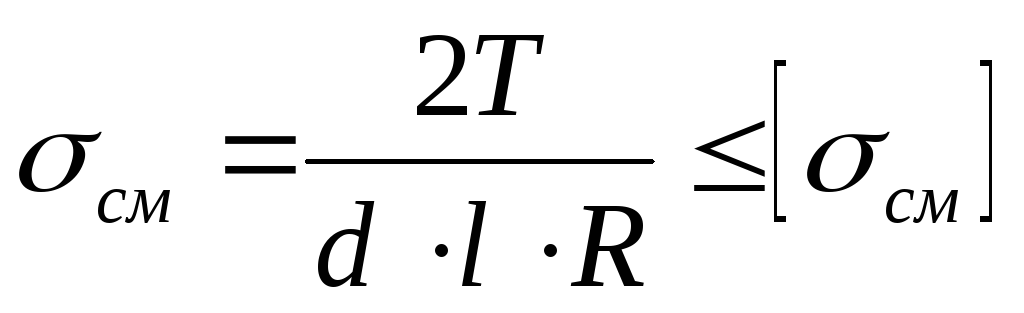
Определим диаметр
P 4P
2 [ ]
S d1
откуда
Определим диаметр
4P
4 50 10 3
d1
2,52 10 2 м
[ ]
3,14 100
d1 3 10 2 м
из условия прочности на смятие
P
P 4
см
[ ]см
2
2
Sсм (d2 d1 )
откуда
3
4
P
4
50
10
d 22
d12
(3 10 2 )2 3,1 10 2 м
[ ]см
200
Определим размеры
P
P
cp
[ ]cp
Scp d 2 h
P
P
cp
[ ]cp
Scp d 2 H
и
из условия прочности на срез
откуда
откуда
d2 4 10 2 м
P
50 10 3
h
8 мм
d 2 [ ]ср 3,14 3 10 2 50
P
50 10 3
H
8,5 мм
2
d 2 [ ]ср 3,14 4 10 50
Сила затонувшего ключа
Сила затонувшего ключа
Рис. 1 Силы, действующие на утопленный ключШпонка, соединяющая вал и ступицу, показана на рис. 1.
Пусть T = крутящий момент, передаваемый валом,
F = тангенциальная сила, действующая по окружности вала,
d = Диаметр вала,
l = длина ключа,
w = ширина ключа.
t = толщина шпонки и
τ и σc = напряжения сдвига и сдавливания материала ключа.
Небольшое рассмотрение покажет, что из-за мощности, передаваемой валом, шпонка может выйти из строя из-за сдвига или раздавливания.
С учетом сдвига шпонки тангенциальная сила сдвига, действующая по окружности вала,
F = площадь сопротивления сдвигу × напряжение сдвига = l × w × τ
∴ Крутящий момент, передаваемый валом,
T = F × d/2 = l × w × τ × d/2 ……….(i)
С учетом сдавливания шпонки тангенциальная сдавливающая сила, действующая по окружности вала,
F = площадь сопротивления раздавливанию × напряжение раздавливания = l × t × σc / 2
∴ Крутящий момент, передаваемый валом,
T = F × d/2 = l × t × σc / 2 × d/2 ……….(ii)
Ключ одинаково прочен на срез и раздавливание, если
l × w × τ × d/2 = l × t × σc / 2 × d /2 (‘.’ Из уравнений (i) и (ii))
вт/т = σс/2τ ………. (iii)
Допустимое напряжение сдавливания для обычного материала ключа как минимум в два раза превышает допустимое напряжение сдвига. Следовательно, из уравнения (iii) имеем w = t. Другими словами, четырехгранный ключ одинаково силен при срезании и раздавливании.
Следовательно, из уравнения (iii) имеем w = t. Другими словами, четырехгранный ключ одинаково силен при срезании и раздавливании.
Чтобы найти длину шпонки для передачи полной мощности вала, прочность шпонки на сдвиг равна прочности вала на сдвиг при кручении.2/w × τ] = πd/ t × τ1/τ = 1,571 d × τ1/τ … (Принимая w = d/4) ………. (vi)
Если материал шпонки такой же, как у вала, то τ = τ1.
∴ l = 1,571 d … [Из уравнения (vi)]
Справочник Учебник проектирования машин Р.С. Хурми и Дж.К. Гупта
%PDF-1.4
%
308 0 объект
>
эндообъект
внешняя ссылка
308 170
0000000016 00000 н
0000003770 00000 н
0000003945 00000 н
0000004101 00000 н
0000004165 00000 н
0000004362 00000 н
0000006817 00000 н
0000006992 00000 н
0000007076 00000 н
0000007173 00000 н
0000007259 00000 н
0000007379 00000 н
0000007450 00000 н
0000007553 00000 н
0000007625 00000 н
0000007728 00000 н
0000007799 00000 н
0000007972 00000 н
0000008043 00000 н
0000008199 00000 н
0000008271 00000 н
0000008346 00000 н
0000008418 00000 н
0000008588 00000 н
0000008659 00000 н
0000008734 00000 н
0000008806 00000 н
0000008923 00000 н
0000008995 00000 н
0000009085 00000 н
0000009175 00000 н
0000009247 00000 н
0000009319 00000 н
0000009444 00000 н
0000009516 00000 н
0000009672 00000 н
0000009742 00000 н
0000009913 00000 н
0000009983 00000 н
0000010073 00000 н
0000010163 00000 н
0000010234 00000 н
0000010339 00000 н
0000010409 00000 н
0000010514 00000 н
0000010585 00000 н
0000010656 00000 н
0000010820 00000 н
0000010891 00000 н
0000010967 00000 н
0000011038 00000 н
0000011163 00000 н
0000011234 00000 н
0000011309 00000 н
0000011380 00000 н
0000011518 00000 н
0000011587 00000 н
0000011701 00000 н
0000011772 00000 н
0000011889 00000 н
0000011959 00000 н
0000012122 00000 н
0000012192 00000 н
0000012319 00000 н
0000012390 00000 н
0000012464 00000 н
0000012535 00000 н
0000012682 00000 н
0000012752 00000 н
0000012902 00000 н
0000012973 00000 н
0000013047 00000 н
0000013118 00000 н
0000013270 00000 н
0000013341 00000 н
0000013415 00000 н
0000013486 00000 н
0000013637 00000 н
0000013707 00000 н
0000013783 00000 н
0000013853 00000 н
0000014002 00000 н
0000014073 00000 н
0000014147 00000 н
0000014217 00000 н
0000014329 00000 н
0000014399 00000 н
0000014488 00000 н
0000014577 00000 н
0000014648 00000 н
0000014753 00000 н
0000014822 00000 н
0000014936 00000 н
0000015006 00000 н
0000015110 00000 н
0000015179 00000 н
0000015249 00000 н
0000015320 00000 н
0000015391 00000 н
0000015438 00000 н
0000015660 00000 н
0000015971 00000 н
0000016332 00000 н
0000016882 00000 н
0000017104 00000 н
0000017145 00000 н
0000017197 00000 н
0000017249 00000 н
0000017774 00000 н
0000020453 00000 н
0000021050 00000 н
0000021129 00000 н
0000022962 00000 н
0000025212 00000 н
0000025322 00000 н
0000025543 00000 н
0000025854 00000 н
0000026215 00000 н
0000026765 00000 н
0000026987 00000 н
0000027028 00000 н
0000027080 00000 н
0000027132 00000 н
0000027657 00000 н
0000030336 00000 н
0000030933 00000 н
0000031012 00000 н
0000032845 00000 н
0000035095 00000 н
0000035205 00000 н
0000035425 00000 н
0000035729 00000 н
0000036082 00000 н
0000036614 00000 н
0000036721 00000 н
0000036762 00000 н
0000039441 00000 н
0000039519 00000 н
0000039799 00000 н
0000042857 00000 н
0000043071 00000 н
0000043244 00000 н
0000043930 00000 н
0000044146 00000 н
0000044366 00000 н
0000044657 00000 н
0000044879 00000 н
0000045093 00000 н
0000045314 00000 н
0000045381 00000 н
0000045719 00000 н
0000045775 00000 н
0000045956 00000 н
0000046174 00000 н
0000046680 00000 н
0000046897 00000 н
0000047454 00000 н
0000049662 00000 н
0000050379 00000 н
0000050592 00000 н
0000050671 00000 н
0000051537 00000 н
0000051587 00000 н
0000051644 00000 н
0000051693 00000 н
0000051742 00000 н
0000051799 00000 н
0000054407 00000 н
0000004400 00000 н
0000006794 00000 н
трейлер
]
>>
startxref
0
%%EOF
309 0 объект
>
эндообъект
310 0 объект
A]-:t:m\\[\\&A\r-)
/U (jE~~D4{SG}\)C8E. evHҮw5h,boNS»bئ2$d
evHҮw5h,boNS»bئ2$d
РЕШЕНО:’Q3.Разработайте прямоугольную шпонку для вала диаметром 50мм. Напряжения сдвига и раздавливания материала шпонки составляют 42 МПа и 70 МПа.’
Стенограмма видео
этот вопрос, мы собираемся найти максимальное количество имплантатов. Да, местность. А главный мой плавательный план она подняла на главные напряжения у сосны А. На валу. А этот рисунок представляет собой свободную схему тела вала. А это схема свободного тела вала в поперечном сечении.A. Таким образом, из этого рисунка мы можем, что это означает интернет-силы и моменты uh в точке A. Итак, когда сигма падает в направлении переменного тока, равна нулю и равна F. И сила сигмы в Y. Направление равно нулю, мы равны P над два. И когда суммарный момент равен нулю. м. ржанка четыре. И исходя из этого мы можем рассчитать нормальную гонку, которая выше A плюс несовершеннолетние EMC. О, я мм. И это сила выдоха, которую я имею в виду под Землей, потому что это сжимающая сила и А.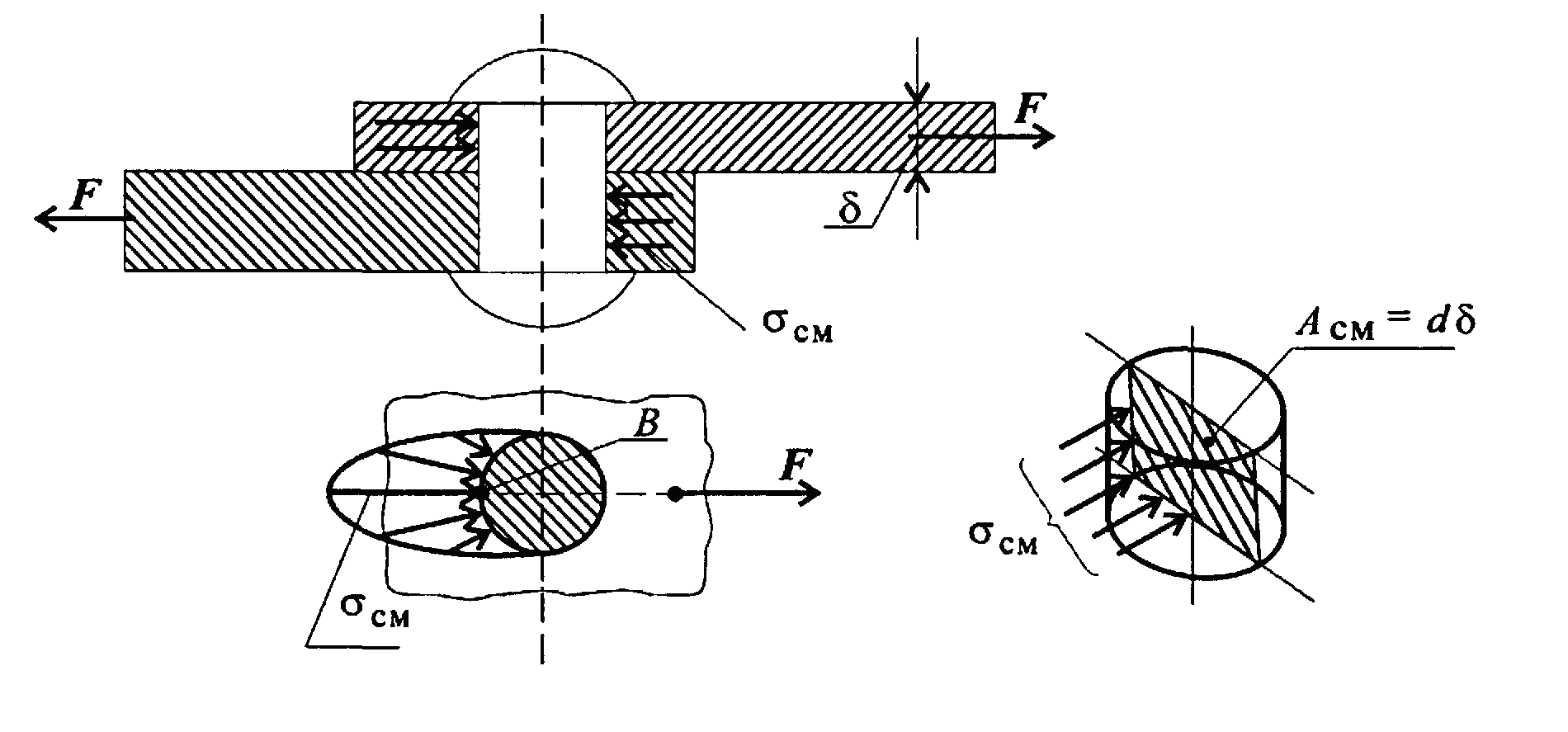 Это диаметр на площадь круга, повредившего А.Д. М. с. п. л. 0. 4 см. радиус стержня. А я момент инициатор притирки. Теперь у нас будет то, что нет, гм, Австралии. Это будет четыре или два квадрата P. L. O. D минус F. Теперь об этом. Э-э, потому что точка A. находится на краю стержня, поэтому Q. A. равна нулю. И что может башня А. Которую мы убьем А. Или И. Т. Равно нулю. Так что значит на .8 есть только и почти всегда. Что это за значение. Нет, у вас есть это напряжение в X. Направление равно сигме, которое является этим значением. А поскольку в Y нет ударения.Направление, потому что нет силы в нарушение. Так что пот в нарушении будет равен нулю. А также в этом году стресс в плане ХУ. Таким образом, директор клянется, что сигма равна одной сигме, яйцам и сигме равна сигме Y, то есть генеральному директору. Так что это 1? Итак, это наш первый ответ, а следующий — максимально простой. Она была одета, Мы можем найти это с помощью этого уравнения, Было всего шесть, и из этого мы получим, что это будет равно нашему квадратному пирогу два P.
Это диаметр на площадь круга, повредившего А.Д. М. с. п. л. 0. 4 см. радиус стержня. А я момент инициатор притирки. Теперь у нас будет то, что нет, гм, Австралии. Это будет четыре или два квадрата P. L. O. D минус F. Теперь об этом. Э-э, потому что точка A. находится на краю стержня, поэтому Q. A. равна нулю. И что может башня А. Которую мы убьем А. Или И. Т. Равно нулю. Так что значит на .8 есть только и почти всегда. Что это за значение. Нет, у вас есть это напряжение в X. Направление равно сигме, которое является этим значением. А поскольку в Y нет ударения.Направление, потому что нет силы в нарушение. Так что пот в нарушении будет равен нулю. А также в этом году стресс в плане ХУ. Таким образом, директор клянется, что сигма равна одной сигме, яйцам и сигме равна сигме Y, то есть генеральному директору. Так что это 1? Итак, это наш первый ответ, а следующий — максимально простой. Она была одета, Мы можем найти это с помощью этого уравнения, Было всего шесть, и из этого мы получим, что это будет равно нашему квадратному пирогу два P. L. Или d минус F. И это ответы.
L. Или d минус F. И это ответы.
Численный анализ характеристик сдвига и дробления частиц в кольцевой системе сдвига с использованием PFC2D
Abstract
Характеристики сдвига и дробления частиц плоскости разрушения (или поверхности сдвига) при катастрофических движениях массы исследуются с помощью устройства кольцевого сдвига, которое обычно используется из-за его пригодности для больших деформаций. Основываясь на результатах предыдущих экспериментов с отходами из заброшенных месторождений шахт, мы использовали простую численную модель, основанную на испытании на кольцевой сдвиг с использованием кода потока частиц (PFC 2D ).Мы исследовали дренаж, нормальное напряжение и зависящие от скорости сдвига характеристики сдвига оползневых материалов. Для скоростей сдвига 0,1 и 100 мм/с и нормального напряжения (NS) 25 кПа численные результаты хорошо согласуются с результатами, полученными из экспериментальных результатов. Разница между экспериментальными и численными результатами остаточного напряжения сдвига составила примерно 0,4 кПа для NS, равного 25 кПа, и 0,9 кПа для NS, равного 100 кПа, как для осушенного, так и для недренированного состояния. Кроме того, мы исследовали эффект дробления частиц при сдвиге, используя концепцию работы трения в PFC.Мы рассчитали работу трения как при пиковых, так и при остаточных напряжениях сдвига, а затем использовали результаты в качестве критериев разрушения в численном анализе. Пиковая работа трения и остаточные напряжения сдвига находились в диапазоне от 303 кПа·с до 2579 кПа·с для данного дренажа и условий нормального напряжения. Эти результаты показали, что комковатые частицы были частично раздроблены при пиковом напряжении сдвига, а дальнейшее дробление частиц по отношению к получению более мелких частиц при сдвиге регистрировалось при остаточном напряжении сдвига в плоскости сдвига.
Кроме того, мы исследовали эффект дробления частиц при сдвиге, используя концепцию работы трения в PFC.Мы рассчитали работу трения как при пиковых, так и при остаточных напряжениях сдвига, а затем использовали результаты в качестве критериев разрушения в численном анализе. Пиковая работа трения и остаточные напряжения сдвига находились в диапазоне от 303 кПа·с до 2579 кПа·с для данного дренажа и условий нормального напряжения. Эти результаты показали, что комковатые частицы были частично раздроблены при пиковом напряжении сдвига, а дальнейшее дробление частиц по отношению к получению более мелких частиц при сдвиге регистрировалось при остаточном напряжении сдвига в плоскости сдвига.
Ключевые слова: остаточное напряжение сдвига, дробление частиц, испытание на кольцевой сдвиг, код потока частиц (PFC 2D ), работа трения
1. Введение порча имущества в городах. После начала обрушения откоса движения растекающейся массы сильно связаны с характеристиками трения на этапах движения.
 В частности, оценка остаточного напряжения сдвига имеет решающее значение, когда ожидается значительное распространение движений массы после начала обрушения откоса.Для безопасности экосистем интенсивно изучались быстро движущиеся вниз массы, включающие почву, горные породы, воду или их комбинации [1,2,3,4,5]. Оценка процессов разрушения и послеаварийных процессов при быстрых оползнях требует глубоких знаний различных научных дисциплин, таких как геоморфология, геомеханика, гидравлика и реология, для прогнозирования, предотвращения и стабилизации массовых движений. Кроме того, напряжение сдвига является важным механическим параметром, необходимым для понимания мобилизации оползня.Для исследования характеристик сдвига геоматериалов были проведены различные испытания на сдвиг [6,7,8,9,10,11,12,13,14,15,16,17,18]. Прочность на сдвиг гранулированных материалов по-прежнему сложно определить как экспериментальными, так и численными методами.
В частности, оценка остаточного напряжения сдвига имеет решающее значение, когда ожидается значительное распространение движений массы после начала обрушения откоса.Для безопасности экосистем интенсивно изучались быстро движущиеся вниз массы, включающие почву, горные породы, воду или их комбинации [1,2,3,4,5]. Оценка процессов разрушения и послеаварийных процессов при быстрых оползнях требует глубоких знаний различных научных дисциплин, таких как геоморфология, геомеханика, гидравлика и реология, для прогнозирования, предотвращения и стабилизации массовых движений. Кроме того, напряжение сдвига является важным механическим параметром, необходимым для понимания мобилизации оползня.Для исследования характеристик сдвига геоматериалов были проведены различные испытания на сдвиг [6,7,8,9,10,11,12,13,14,15,16,17,18]. Прочность на сдвиг гранулированных материалов по-прежнему сложно определить как экспериментальными, так и численными методами. Багерзаде-Халхали и Миргасеми [6] исследовали прочность крупнозернистых грунтов на прямой сдвиг с помощью экспериментального и численного анализа при различных нормальных напряжениях. Они обнаружили, что характеристики крупнозернистого грунта менялись от деформационного упрочнения до размягчения в зависимости от продолжительности сдвига по мере увеличения нормального напряжения, а угол внутреннего трения уменьшался с увеличением уровня напряжения.Кабалар и др. [7] провели трехосные и циклические испытания для оценки прочности различных песков с учетом влияния формы частиц. Они обнаружили, что щебневые пески, добытые в северной части Кипра, обладают значительно большей прочностью, чем пески, полученные из Газиантепа, из-за различной формы частиц песка. Они также утверждали, что степени сферичности и округлости частиц увеличивают прочность песка и могут уменьшить его объемную деформацию.Вышеупомянутые экспериментальные тесты демонстрируют ограничения в оценке общих характеристик сдвига при движении различных масс. Наиболее широко используемыми испытаниями на сдвиг являются испытания на прямой сдвиг, трехосный сдвиг и кольцевой сдвиг; каждый из них имеет преимущества и ограничения.
Они обнаружили, что характеристики крупнозернистого грунта менялись от деформационного упрочнения до размягчения в зависимости от продолжительности сдвига по мере увеличения нормального напряжения, а угол внутреннего трения уменьшался с увеличением уровня напряжения.Кабалар и др. [7] провели трехосные и циклические испытания для оценки прочности различных песков с учетом влияния формы частиц. Они обнаружили, что щебневые пески, добытые в северной части Кипра, обладают значительно большей прочностью, чем пески, полученные из Газиантепа, из-за различной формы частиц песка. Они также утверждали, что степени сферичности и округлости частиц увеличивают прочность песка и могут уменьшить его объемную деформацию.Вышеупомянутые экспериментальные тесты демонстрируют ограничения в оценке общих характеристик сдвига при движении различных масс. Наиболее широко используемыми испытаниями на сдвиг являются испытания на прямой сдвиг, трехосный сдвиг и кольцевой сдвиг; каждый из них имеет преимущества и ограничения. В отличие от других испытаний на сдвиг, испытание на кольцевой сдвиг может измерять напряжение сдвига при большом смещении [18]. Кроме того, он выполняется с помощью передового оборудования, способного контролировать уплотнение, дренаж и скорость сдвига в статических и динамических условиях.Численный анализ часто используется как способ преодоления ограничений лабораторных экспериментов.
В отличие от других испытаний на сдвиг, испытание на кольцевой сдвиг может измерять напряжение сдвига при большом смещении [18]. Кроме того, он выполняется с помощью передового оборудования, способного контролировать уплотнение, дренаж и скорость сдвига в статических и динамических условиях.Численный анализ часто используется как способ преодоления ограничений лабораторных экспериментов.
Lobo-Guerrero и Vallejo [19] предложили метод дискретных элементов для моделирования эволюции дробления сахарных частиц, подвергнутых испытанию на кольцевой сдвиг; они использовали код потока частиц в двух измерениях (PFC 2D ). Периодическое движение частиц в кольцевом аппарате сдвига моделировалось двумя параллельными периодическими границами и двумя пилообразными стандартными границами; они были сделаны с несколькими кромками для моделирования поверхности сдвига.Они обнаружили, что остаточный коэффициент сахарных материалов оставался постоянным, несмотря на дробление частиц. Однако при объединении границ периодического пространства и стандартных границ могут возникать ошибочные вычисления напряжений, поскольку периодическое пространство несовместимо со стандартной границей в PFC [20]. Кроме того, шероховатая поверхность сдвига с кратными краями отрицательно влияет на отклик частиц и расчет напряжения, особенно для частиц, распределенных по углам.Кроме того, ни периодическое пространство, ни стандартный граничный метод не учитывают взаимодействия между компонентами машины и частицами.
Кроме того, шероховатая поверхность сдвига с кратными краями отрицательно влияет на отклик частиц и расчет напряжения, особенно для частиц, распределенных по углам.Кроме того, ни периодическое пространство, ни стандартный граничный метод не учитывают взаимодействия между компонентами машины и частицами.
Необходима более точная и эффективная оценка характеристик кольцевого сдвига высокоподвижных оползневых материалов с использованием PFC 2D . Чтобы смоделировать испытание на кольцевой сдвиг, мы использовали общую границу, которая имеет решающее значение и полезна для моделирования взаимодействия между гранулированными материалами и компонентами машины. Мы смоделировали дробление частиц, используя метод комков и технику фрикционной работы из PFC 2D .Численные результаты подтвердили результаты, полученные из экспериментов с кольцевым сдвигом. Напряжение сдвига рассчитывали с учетом четырех различных скоростей сдвига (0,01, 0,1, 1 и 100 мм/с), условий дренирования и нормальных напряжений в диапазоне от 20 до 150 кПа. Метод дискретных элементов в PFC 2D требует контактных моделей, учитывающих микромеханические свойства гранулированных материалов. Механические свойства материала, полученные экспериментально, принимаются за макромеханические свойства и рассчитываются с использованием микромеханических свойств методом проб и ошибок в PFC 2D [20].Полученные микросвойства можно использовать для разработки поведения отходов при сдвиге в условиях опасности оползней с использованием ПФУ.
Метод дискретных элементов в PFC 2D требует контактных моделей, учитывающих микромеханические свойства гранулированных материалов. Механические свойства материала, полученные экспериментально, принимаются за макромеханические свойства и рассчитываются с использованием микромеханических свойств методом проб и ошибок в PFC 2D [20].Полученные микросвойства можно использовать для разработки поведения отходов при сдвиге в условиях опасности оползней с использованием ПФУ.
2. Материалы и методы
2.1. Материалы
Отходы были получены из столичного города Пусан, Корея. Они взяты из месторождений шахты Имги, где оползень происходит из-за интенсивных осадков [21,22,23]. В оползневом материале преобладают рассыпчатые и угловатые зерна, сложенные пиритом, каолинитом, серицитом, пирофиллитом и кварцем.Образец, использованный для лабораторных испытаний на сдвиговое кольцо, состоял из 35% гравия, 63% песка и 2% других мелких материалов (т. е. мелких частиц, которые составляют более 50% почвы, проходят через сито 0,075 мм). Таким образом, пробу почвы можно рассматривать как крупнозернистые отложения. Пористость, отношение объема пустот к общему объему грунта, составляет примерно 40 %. Эти отходы относятся к категории гравийно-песчаных почв. Их средний диаметр, эффективный размер зерна и коэффициент однородности равны 1,5 мм, 0.3 мм и 5 мм соответственно. Используемые материалы очень похожи на типичные материалы для оползней, встречающиеся в Корее. обобщает геотехнические свойства используемых материалов. Эта работа больше фокусируется на численном анализе; более подробную информацию о подготовке образцов и свойствах материалов можно найти в [21].
Таким образом, пробу почвы можно рассматривать как крупнозернистые отложения. Пористость, отношение объема пустот к общему объему грунта, составляет примерно 40 %. Эти отходы относятся к категории гравийно-песчаных почв. Их средний диаметр, эффективный размер зерна и коэффициент однородности равны 1,5 мм, 0.3 мм и 5 мм соответственно. Используемые материалы очень похожи на типичные материалы для оползней, встречающиеся в Корее. обобщает геотехнические свойства используемых материалов. Эта работа больше фокусируется на численном анализе; более подробную информацию о подготовке образцов и свойствах материалов можно найти в [21].
Таблица 1
Физические свойства отходов.
| Удельная гравитация | Содержание воды (%) | Общая единица Вес (T / M 3 ) | Лимит жидкости (% ) | Пористость (%) | USCS | |
|---|---|---|---|---|---|---|
2. 63 63 | 6,9 | 1,7 | 1,59 | 24,5 | 39,5 | СМ |
Испытание на кольцевой сдвиг подходит для исследования характеристик сдвига оползней, поскольку оно дает несколько преимуществ и позволяет измерять сдвиг при большом смещении; его также можно использовать для исследования механических характеристик поверхностей скольжения из-за больших сдвиговых перемещений [14]. Мы провели лабораторные испытания на кольцевой сдвиг с помощью прибора для кольцевого сдвига, разработанного в Корейском институте геолого-геофизических исследований и минеральных ресурсов (KIGAM). Эта машина может количественно моделировать консолидацию, дренаж и скорость сдвига в условиях статической и динамической нагрузки. Наружный и внутренний диаметры и высота коробки сдвига кольцевого аппарата сдвига КИГАМ составляли 250, 110 и 75 мм соответственно. Коробка сдвига состоит из верхней и нижней коробок, как показано на рис. Во время испытания кольца на сдвиг верхняя коробка фиксируется, а нижняя вращается. Поверхность сдвига хорошо видна после испытаний (б). Оползни могут иметь разную форму и размер.Нормальное напряжение можно рассматривать на основе толщины грунта, где наблюдается поверхность сдвига. Скорость сдвига важна для определения прочности на сдвиг по отношению к скорости движения оползня. Существует множество типов оползней, скорость которых варьируется от очень медленной до очень быстрой. Дренаж является одним из важных условий инициации оползня, так как он напрямую связан с формированием порового давления воды на поверхности сдвига (или движением оползня). Состояние дренирования может быть применено для условий отсутствия порового давления воды; таким образом, его можно использовать для воспроизведения очень медленных оползней, таких как ползучее движение богатых глиной оползней (например,г.
Эта машина может количественно моделировать консолидацию, дренаж и скорость сдвига в условиях статической и динамической нагрузки. Наружный и внутренний диаметры и высота коробки сдвига кольцевого аппарата сдвига КИГАМ составляли 250, 110 и 75 мм соответственно. Коробка сдвига состоит из верхней и нижней коробок, как показано на рис. Во время испытания кольца на сдвиг верхняя коробка фиксируется, а нижняя вращается. Поверхность сдвига хорошо видна после испытаний (б). Оползни могут иметь разную форму и размер.Нормальное напряжение можно рассматривать на основе толщины грунта, где наблюдается поверхность сдвига. Скорость сдвига важна для определения прочности на сдвиг по отношению к скорости движения оползня. Существует множество типов оползней, скорость которых варьируется от очень медленной до очень быстрой. Дренаж является одним из важных условий инициации оползня, так как он напрямую связан с формированием порового давления воды на поверхности сдвига (или движением оползня). Состояние дренирования может быть применено для условий отсутствия порового давления воды; таким образом, его можно использовать для воспроизведения очень медленных оползней, таких как ползучее движение богатых глиной оползней (например,г. , несколько сантиметров в год). В экспериментальной программе клапан, расположенный в кольцевой коробке сдвига, открыт; таким образом, вода может свободно перемещаться во время сдвига. Поровое давление воды не возникает. Однако недренированные условия специально используются при относительно быстром возникновении оползня (например, выше 1,8 м/ч). Те же самые граничные условия используются в численном анализе, как подробно описано в следующем разделе. Мы экспериментально измерили нормальные напряжения, вертикальное перемещение от линейного регулируемого дифференциального трансформатора, поровое давление и крутящие моменты.В экспериментальных испытаниях учитывались следующие параметры: нормальное напряжение, условия дренажа и скорость сдвига, как показано на рис. Подробности лабораторных экспериментов можно найти в [21].
, несколько сантиметров в год). В экспериментальной программе клапан, расположенный в кольцевой коробке сдвига, открыт; таким образом, вода может свободно перемещаться во время сдвига. Поровое давление воды не возникает. Однако недренированные условия специально используются при относительно быстром возникновении оползня (например, выше 1,8 м/ч). Те же самые граничные условия используются в численном анализе, как подробно описано в следующем разделе. Мы экспериментально измерили нормальные напряжения, вертикальное перемещение от линейного регулируемого дифференциального трансформатора, поровое давление и крутящие моменты.В экспериментальных испытаниях учитывались следующие параметры: нормальное напряжение, условия дренажа и скорость сдвига, как показано на рис. Подробности лабораторных экспериментов можно найти в [21].
Схематическое изображение кольцевой коробки сдвига и поверхности сдвига после испытаний: ( a ) конфигурация кольцевой коробки сдвига и ( b ) наблюдение поверхности сдвига после испытаний.
Таблица 2
| Условия испытаний | Скорость (мм/с) | Нормальное напряжение (кПа) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Без жидкости 9.19401 0.1 1 100 | 20 | 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60148 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60148 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100 | 9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 150148 8 | 3.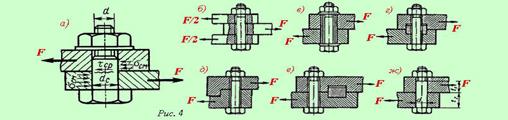 Числовая модель Числовая модель3.1 . Описание метода дискретных элементов в PFC2D и методе сгустков Код потока частиц (PFC 2D ), разработанный Кандаллом, представляет собой программное обеспечение на основе метода дискретных элементов (DEM), предназначенное для моделирования движения и взаимодействия нагруженных зернистые сборки.Кандалл и его коллеги [24, 25, 26] являются одними из передовых исследователей, применивших метод дискретных элементов к движению зернистых сборок. Гранулярная сборка состоит из различных частиц, которые смещаются независимо друг от друга, а взаимодействие между частицами происходит только в точках контакта или границах раздела. Предположения PFC следующие: частицы считаются твердыми телами; метод мягкого контакта характеризует частицы в точках контакта, где им разрешено перекрываться; контакт между частицами может быть определен связями; форма частиц либо круглая, либо сферическая, с единичной толщиной; величина перекрытия связана с силой контакта законом сила–перемещение [20]; перекрытие мало по сравнению с размером частиц. Un= RA+RB-d контакт частица-частица Rb-d патрик-граница контакт (1) где RA и RB — радиусы соприкасающихся частиц. Rb и d — радиус частицы в контакте со стенкой (границей) и расстояние между центрами частиц соответственно. Кроме того, процесс расчета включает альтернативное применение формулы сила-перемещение в точках контакта и второго закона Ньютона к твердым телам.Таким образом, движение каждого твердого тела за счет контакта и приложенных к нему сил определяется вторым законом Ньютона; кроме того, обновление контактных сил, вычисленных по относительному движению при каждом контакте, регулируется законом сила-смещение. Этот закон применяется как для контактов частица-частица, так и для контакта частица-стенка (т.е. граница модели). Вычислительная схема представляет собой пошаговый алгоритм, который состоит из многократного применения закона движения к каждой частице, закона силы-смещения к каждому контакту и постоянного обновления положения стенок, как показано на рис. Расчетная схема метода дискретных элементов (DEM) в PFC 2D. В прошлые десятилетия частицы, генерируемые любой гранулированной сборкой, были просто круглыми или сферическими; однако с помощью современной ЦМР можно создать общую форму частиц, используя две или более круглых или сферических частиц [28,29,30]. Процесс создания частицы любой формы называется методом сгущения или кластеризации [27]. Частица, созданная в зернистой сборке, может представлять собой сгусток из двух, трех или четырех частиц, в зависимости от количества образующих его частиц.Например, чтобы смоделировать сборку гранул, содержащую треугольные или квадратные частицы или зерна более естественной формы, нужно всего лишь скомбинировать несколько предопределенных простых частиц для создания желаемой формы частиц. Создание частиц треугольной или квадратной формы показано на рисунках а, б. Контактная модель определяется только между частицами сгустка. Иллюстрация формирования комков: ( a ) Треугольная частица, состоящая из девяти перекрывающихся круглых частиц и ( b ) Квадратная частица, состоящая из 15 перекрывающихся круглых частиц. 3.2. Процедура моделирования Поскольку чрезвычайно сложно измерить микромеханические свойства материалов грунта и горных пород в лабораторных экспериментах, в которых можно измерить только макромеханические свойства материалов, микромеханические свойства синтетических материалов в PFC 2D можно использовать для получения макромеханических свойств сыпучих материалов методом проб и ошибок [20]. Мы выполнили моделирование кольцевого сдвига, чтобы исследовать влияние нормального напряжения и скорости сдвига на напряжение сдвига. Метод комков, как показано в коде потока частиц PFC 2D , использовался для создания гранулированных систем ().Сгустки частиц были созданы с пятью круглыми частицами (а) и случайным распределением размеров в сборке. Материал для цементации частиц, который связывал комковатые частицы, был настроен на параллельную связь (b, c). Поскольку в PFC 2D отсутствует жидкостная связь на контакте между соприкасающимися частицами, как осушенные, так и недренированные условия были смоделированы с использованием параллельной связи между комковатыми частицами, и процесс калибровки может быть использован для получения макросвойств [20]. Слипшиеся частицы и сборка: ( a ) слипшиеся частицы, ( b ) идеализация параллельных связей между частицами, ( c ) параллельное соединение связей между слипшимися частицами и ( d ) слипшиеся частицы в кольцевом блоке сдвига. Таблица 3 Свойства синтетического материала.
Наши результаты показали, что напряжение сдвига увеличивается, когда увеличивается нормальное напряжение и скорость сдвига. 4. Результаты и обсуждение Мы использовали ряд численных моделей для исследования влияния нормального напряжения и скорости сдвига на напряжение сдвига. Микросвойства, разработанные в PFC, позволяют моделировать макромеханические свойства, полученные в результате лабораторных экспериментов, с использованием процедуры проб и ошибок. В этом исследовании рассматриваются три основных макросвойства: модуль упругости, пиковое напряжение и остаточное напряжение.После того, как материалы были созданы в соответствии с процедурой генезиса материала с использованием микромеханических свойств, перечисленных в , мы неоднократно проводили численные испытания на кольцевой сдвиг. 4.1. Напряжение сдвига и время сдвига Мы сравнили экспериментальные и численные результаты для характеристик напряжения сдвига в течение 300 с в кольцевой системе сдвига для данного дренажа и условий нормального напряжения.Чтобы изучить влияние дренажа и нормального напряжения на напряжение сдвига, мы построили кривые зависимости напряжения сдвига от времени сдвига при скорости сдвига 0,1 мм/с; нормальное напряжение было постоянным во время каждого теста (). Кривая зависимости напряжения сдвига от времени в кольцевой системе сдвига: ( a , b ) нормальное напряжение 25 кПа и ( c , d ) нормальное напряжение 100 кПа. Внезапное падение напряжения сдвига появилось как для экспериментальных, так и для расчетных кривых после того, как было найдено пиковое напряжение сдвига. Независимо от нормального уровня напряжения и условий дренажа, материалы, оцененные здесь, продемонстрировали способность к размягчению при деформации (). Для нормального напряжения 25 кПа расчетное и экспериментальное время достижения пикового напряжения отличались на 1.1 с для неосушенного состояния и 8,5 с для осушенного состояния. Для нормального напряжения 100 кПа расчетное и измеренное время, необходимое для достижения пикового напряжения, отличалось на 5,7 с для недренированного состояния и на 0,9 с для осушенного состояния. Эти различия могут быть связаны с разницей в схеме шага по времени, используемой для расчета напряжения сдвига в PFC 2D [20]. Кроме того, показано остаточное напряжение сдвига, вызванное сопротивлением слипшихся частиц после падения пикового напряжения сдвига.Это сопротивление обусловлено трением между частицами и эффектом блокировки между частицами комков. Таким образом, численный анализ является эффективным способом объяснения перегруппировки частиц по отношению к снижению прочности на сдвиг. Стабилизация достигается за 150–300 с как в осушенном, так и в недренированном состоянии при различных нормальных напряжениях. Форма частиц комков также имеет решающее значение для создания некоторого сопротивления после падения пикового напряжения. Мы предположили, что остаточное напряжение сдвига представляет собой напряжение сдвига, измеренное в течение периода стабилизации, следующего за внезапным падением пикового напряжения сдвига.В зернистой сборке после снижения пикового напряжения сдвига произошло постепенное дробление комковатой частицы. Для нормального напряжения 25 кПа разница в остаточном напряжении сдвига между экспериментальным и численным анализом составила 0,4 кПа как для осушенных, так и для недренированных условий (а, б). 4.2. Напряжение сдвига и скорость сдвига Влияние скорости сдвига на напряжение сдвига гораздо более специфично, чем влияние дренирования и нормальных напряжений. Мы исследовали характеристики сдвига материалов отходов в зависимости от скорости сдвига по отношению к значениям пикового и остаточного напряжения сдвига. показано влияние скорости сдвига на пиковое и остаточное касательное напряжение при различных дренажных и нормальных напряжениях.В целом напряжение сдвига увеличивается с увеличением скорости сдвига для всех данных условий (). При нормальном напряжении 25 кПа в осушенном состоянии для скоростей сдвига 0,01, 0,1, 1 и 100 мм/с разница пикового напряжения сдвига между экспериментальным и численным анализом составила 0,1, 0,3, 0,1 и 0,7 кПа. Пиковое и остаточное напряжение сдвига как функция скорости сдвига: ( a , b ) в осушенном состоянии и ( c , d ) в недренированном состоянии. Таблица 4Сравнение пиковых и остаточных касательных напряжений в зависимости от нормального напряжения.
Для нормального напряжения 25 кПа при недруженном состоянии при скорость сдвига 0,1 мм/с, численное пиковое напряжение сдвига было аналогично полученному экспериментально; при скорости сдвига 0.01, 1 и 100 мм/с разница пиковых значений напряжения сдвига, полученных экспериментально и численно, составила 0,2, 0,1 и 1,8 кПа соответственно; остаточные касательные напряжения различались на 1,5, 0,4, 0,6 и 2,2 кПа соответственно. При нормальном напряжении 100 кПа в недренированных условиях при скоростях сдвига 0,01, 0,1 и 1 мм/с как по численным, так и по экспериментальным оценкам были получены аналогичные пиковые напряжения сдвига; при скорости сдвига 100 мм/с разница в пиковом напряжении сдвига между экспериментом и численным анализом равнялась 0. 4.3. Напряжение сдвига и нормальное напряжение представляет влияние нормального напряжения на напряжение сдвига в осушенном и недренированном состоянии, полученное с помощью численного и экспериментального анализа. Скорость сдвига (0.1 мм/с) использовали для изучения влияния нормального напряжения на напряжение сдвига. Для нормального напряжения 20, 40, 60, 80, 100 и 150 кПа в осушенном состоянии значения, полученные для разницы пикового напряжения сдвига между экспериментальным и численным анализом, составили 0,2, 0,1, 0,1, 0,1, 0,3, и 0,2 кПа соответственно. При нормальном напряжении 80 кПа экспериментальное остаточное напряжение сдвига было аналогично полученному в результате численного анализа; при нормальном напряжении 20, 40, 60, 100 и 150 кПа остаточные касательные напряжения отличались на 0. Напряжение сдвига по сравнению с нормальным напряжением: ( a ) осушенное и ( b ) недренированное состояние. В недренированном состоянии грунта разница пикового напряжения сдвига между экспериментальным и численным расчетами составила 0,1, 0,1, 0,1, 0,4, 0,2 и 0,9 кПа при нормальных напряжениях 20, 40, 60, 80, 100, и 150 кПа соответственно. Для нормального напряжения 20, 40, 60, 80 и 150 кПа разница между экспериментальным и расчетным остаточным напряжением сдвига равнялась 0.1, 0,6, 0,1, 0,7 и 0,1 кПа соответственно. Эти результаты показывают, что напряжение сдвига увеличивается по мере увеличения нормального напряжения. Аналогичные результаты были получены и рядом других исследователей [31]. Эти экспериментальные и численные результаты находятся в хорошем согласии. В частности, остаточные касательные напряжения, полученные в результате экспериментального и численного анализа, очень похожи друг на друга; однако пиковое напряжение сдвига в дренированном состоянии постепенно увеличивается с нормальным напряжением и почти в три раза выше, чем у аналога. 4.4. Характеристики дробления частиц Получить информацию о микромеханике дробления частиц в лабораторных экспериментах очень сложно. Однако это препятствие можно преодолеть, моделируя дробление частиц методом дискретных элементов. Различные формы частиц могут быть созданы с помощью двух или более отдельных частиц с использованием логики комков; генерируемые частицы рассматриваются как твердые тела. Механизмы дробления возникают из-за двух различных механизмов: истирания и перенапряжения.Истирание происходит за счет трения, когда частица трется о другую частицу и постепенно истирается или ломается. Перенапряжение возникает, когда в комковой частице образуется трещина, которая распадается на две или более меньших частиц по мере расширения трещины [19,32,33]; эта трещина создается чрезмерным приложением сил, включая сжимающие, растягивающие и диаметральные силы. В данной работе мы использовали механизм истирания для имитации дробления частиц комков. Предыдущие исследования моделировали дробление частиц в системе на основе экспериментальных данных по дроблению одной частицы.Во многих случаях дробление частиц в зернистой системе часто может происходить одновременно. В этом исследовании дробление частиц моделировалось с использованием энергии, рассеиваемой фрикционным скольжением в точках контакта между частицами. Эта энергия называется работой трения [20]. Как упоминалось ранее, остаточное напряжение сдвига поддерживалось постоянным благодаря сопротивлению трения между частицами комков. Дробление частиц происходит, когда между частицами создается необходимая работа трения; эта величина работы трения использовалась для оценки процесса дробления частиц в нашей гранулированной сборке.представлена работа трения и развитие зоны сдвига в кольцевых испытаниях на сдвиг. Для лабораторного эксперимента энергия трения принималась за площадь под кривыми зависимости напряжения сдвига от времени после достижения пикового напряжения сдвига (а). Энергия трения и зона сдвига в кольцевом испытании на сдвиг: ( a ) отношение напряжения сдвига к деформации для определения пикового и остаточного напряжения сдвига и ( b ) зона сдвига в кольцевой коробке сдвига. Для моделирования ЦМР разрешалось дробление комков до тех пор, пока в системе зернистой сборки не будет достигнута необходимая энергия трения в зависимости от скорости сдвига. Работа трения Wf рассчитывается как [27]: где Nc, Fis и ΔDisslip. – количество контактов, среднее усилие сдвига и приращение смещения скольжения соответственно на контакте за текущий временной шаг. Приращение смещения скольжения, произведенное за временной шаг Δt, определяется как: где Vis — относительное сдвиговое движение при контакте, которое рассчитывается как: ) где x˙i∅j и ω3∅j — поступательная и вращательная скорости объекта ∅j соответственно.Они выражаются следующим образом: ∅1, ∅2= A, B частица − контакт частиц b, w частица − граничный контакт (5) и ti=−n2, n1 (n1 и n2 — единичные векторы нормали). Энергия трения является важным механическим свойством гранулированных материалов. В этом исследовании изучается взаимосвязь времени трения между работой и сдвигом. Энергия трения и время сдвига зависят от дренажа и нормального состояния напряжения. Раздробление комковатой частицы разрешалось после того, как системы зернистой сборки достигли соответствующей работы трения при пиковых и остаточных напряжениях сдвига. показывает постепенное возникновение дробления частиц комков при пиковом и остаточном напряжении сдвига. Синие стрелки указывают, где на границе кольца возник механизм постепенного дробления; дробление комковатой частицы происходит в основном на поверхности сдвига на внешней границе кольца. Разрушение комков частиц при: ( a ) пиковом напряжении сдвига и ( b ) остаточном напряжении сдвига. Стрелки указывают на постепенное возникновение дробления комков частиц. 5. Выводы В этом исследовании была разработана простая численная модель кольцевого сдвига для исследования характеристик сдвига и измельчения гранулированных материалов. Пиковые и остаточные напряжения сдвига сильно зависят от изменений нормального напряжения, скорости сдвига и условий дренирования.Как и ожидалось, напряжение сдвига увеличивается с увеличением нормального напряжения и скорости сдвига, независимо от условий дренирования. Явление дробления частиц при кольцевом испытании на сдвиг анализируется с помощью ЦМР, поскольку оно напрямую влияет на напряжение сдвига. Используя концепцию фрикционной работы в PFC 2D , в PFC был реализован новый язык FISH для моделирования дробления комков частиц как при пиковых, так и при остаточных напряжениях сдвига. Типы шпонок, функция и расчет напряженияШпонка представляет собой кусок мягкой стали, вставленный между валом и ступицей, чтобы соединить их вместе, чтобы предотвратить относительное движение между ними . Он всегда вставляется параллельно оси вала. Шпонки выпускаются как временные крепления и подвергаются значительным сдавливающим и срезающим напряжениям. Типы ключей: Назначение клавиш Есть две основные функции шпонок, когда они используются для блокировки трансмиссионного вала. Основная функция заключается в ограничении относительного вращательного движения и осевого перемещения между валом и элементом машины. Также доступны некоторые специальные типы шпонок, например шпоночные и шлицевые, шпонки, допускающие осевое перемещение между ними. 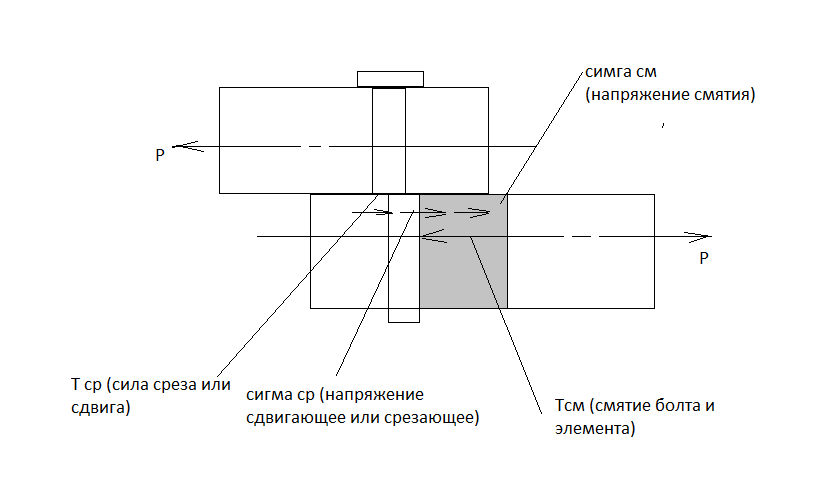 Вторая функция ключа заключается в передаче крутящего момента от вращающегося вала к поворотному элементу машины. Один и тот же ключ работает для передачи крутящего момента в обоих направлениях; от вала к элементу машины или от элемента машины к валу. Напряжения сдвига и сжатия в шпонке рассчитываются с использованием следующих уравнений: Разрушение шпонок при сдвиге Напряжение сдвига является причиной этого типа отказа ключа.Действительно, при вращении вала и элемента машины, например ступицы, каждый элемент оказывает на шпонку равную и противоположную силу. Эти противоположные силы создают напряжение сдвига по радиусу вала. Затем ключ начинает деформироваться и через некоторое время выходит из строя. Предельное напряжение зависит от прочности материала ключа и угловой скорости вращения. Вы можете рассчитать поперечную силу, приложенную к шпонке, используя приведенную ниже формулу.  Разрушение ключа Напряжения сдвига и сжатия в шпонке рассчитываются по следующим уравнениям: Напряжение сдвига, Ss = 2T/DWL Где, Напряжение сжатия, Sc = 2T/DhL Где, Экспериментальное исследование поведения сдвига на границе между крупнозернистым песком и бетоном при высоких нагрузках Сдвиг на границе между грунтом и конструкцией является горячей темой исследований. 1. Введение Взаимодействие породно-грунтового массива и структуры широко распространено в подземном строительстве. Из-за разницы в жесткости между конструкцией и грунтом такие проблемы, как нелинейность, большая деформация и локальная неоднородность [1], приводят к очень сложному сдвиговому поведению на границе раздела [2]. Испытание на сдвиг является простейшим методом исследования механических свойств этой поверхности раздела [3]. С тех пор, как Потенди [4] принял аппарат прямого сдвига, многие исследователи изучали характеристики грунта и поверхности раздела.Зонг-Зе и др. [5] провели крупномасштабные испытания на прямой сдвиг на границе между грунтом и бетоном и указали, что они скользят неравномерно. Ху и Пу [6] провели испытание песка на сдвиг с использованием усовершенствованного аппарата прямого сдвига и проанализировали деформационный механизм разрушения при сдвиге на границе раздела. Для эффективной обработки поврежденных подземных сооружений и научного проектирования новых подземных сооружений необходимо изучить поведение сдвига на границе между подземным сооружением и окружающим скальным грунтом. Анализ сил и расчет деформаций подземной конструкции служат основой для выбора влияющих факторов. Potyondy [4] изучал механические свойства при сдвиге на различных поверхностях между песком, глиной, связным гранулированным грунтом и сталью, бетоном и деревом посредством сотен прямых испытаний на сдвиг.Экспериментальное исследование, проведенное Фахаряном и Эвгином [12], показывает, что изменение объема и отношение тангенциального напряжения к деформации на границе между песком и конструкцией тесно связаны с траекторией напряжения и нормальной жесткостью. Ян и др. В связи с тем, что существующие проекты развиваются в направлении более высоких и глубоких направлений, например, Пиндиншань, Хуайнань и Фэнфэн, которые имеют глубину более 600 м, а средняя глубина новых шахт составляет 500 м, необходимо срочно развивать исследование поведения сдвига и влияющих факторов поверхности раздела грунт-конструкция в условиях высокого напряжения[18–23]. Гуо и др. [24] разработали простое устройство для испытания на сдвиг для проведения простого испытания на сдвиг на границе раздела между насыщенным песком и конструкцией и проанализировали конститутивную модель интерфейса и изменение тенденции жесткости интерфейса на сдвиг в условиях высокого напряжения. В ходе этого исследования система испытания горных пород RMT-150B была специально модифицирована для проведения испытаний на сдвиг при высоком напряжении при четырех различных факторах: нормальное напряжение, содержание влаги, базальная твердость и шероховатость; во время испытания контролировались соответствующие напряжение сдвига и сдвиговое смещение, объемная деформация и сдвиговое смещение, а также дробление частиц на поверхности раздела. 2. Система и метод тестирования2.1. Испытательная система Существующие инструменты прямого сдвига могут выдерживать относительно небольшие вертикальные нагрузки, но трудно удовлетворить требованиям к высокому нормальному напряжению.Таким образом, система механики горных пород РМТ-150Б была модифицирована путем специальной разработки и обработки таких аксессуаров, как коробка прямого сдвига и уменьшение сопротивления для плиты. Модифицированная испытательная система может выдерживать вертикальную нагрузку 1000 кН, поперечную нагрузку 500 кН и максимальный сдвигающий ход 20 мм. Верхняя коробка сдвига представляет собой стальной цилиндр с внутренним диаметром 124 мм и размером бетонного основания. (a) Аппарат прямого сдвига (b) Блок сдвига (a) Аппарат прямого сдвига (b) Блок сдвига 2.2. Определение экспериментальных факторов2.2.1. Шероховатость и твердость бетонного основания Основание представляет собой бетонную панель с искусственно изготовленной стандартной призматической формой с одинаковой высотой и шириной на шероховатой стороне. Бетонные основания с четырьмя значениями прочности C20, C30, C40 и C50 изготавливаются в соответствии с соотношениями смесей, указанными в литературе [33–36]. Твердость бетонного основания может быть непосредственно выражена значением отскока, измеренным в ходе испытания на отскок. Значение прочности четырех протестированных бетонных оснований составляет 28.1, 33.9, 38.1 и 41.9. 2.2.2. Подготовка крупного песка Размер частиц и характеристические параметры крупного песка приведены в таблице 1, максимальная плотность крупного песка в сухом состоянии составляет 1,9 г/см 3 , а кривая распределения частиц по размерам показана на рисунке 3.
2 9,26122 9,26127 Определение нормального напряжения Когда глубина подземного проекта превышает 100 м, горизонтальное давление на грунт [35] в глубоком и толстом слое грунта составляет:
где – глубина заглубления расчетной точки, м, – расчетный коэффициент в пределах от 0. В настоящее время глубина подземной инженерии в основном находится в диапазоне 50~500 м. Так, в данной работе погребенные глубины установлены как 100 м, 200 м, 300 м и 400 м, а соответствующий коэффициент равен 0,2. Нормальное напряжение интерфейса рассчитывается как 2 МПа, 4 МПа, 6 МПа и 8 МПа с использованием уравнения (1). 2.3. Схема испытанийВыбираются четыре фактора, влияющие на сдвиговые характеристики границ раздела при высоких нагрузках, включая базовую твердость бетона, шероховатость поверхности, нормальное напряжение и влажность почвы, и рассчитываются 4 уровня каждого влияющего фактора, как показано в таблице. 2.
Перед проведением испытания на сдвиг образец крупнозернистого песка сначала нагружали в вертикальном направлении со скоростью 0,5 кН/с; затем осуществляли консолидацию при определенной нормальной нагрузке со скоростью 0,0025 мм/мин; примерно через 3 мин консолидация стала стабильной; испытание на сдвиг начиналось со скорости 0.02 мм/с при постоянной нормальной нагрузке. Когда кривая сдвигового напряжения-перемещения становилась плоской или сдвиговое смещение достигало 12 мм, испытание заканчивали. В то же время регистрировались касательное напряжение, относительное сдвиговое смещение и нормальное смещение образца границы раздела. 3. Результаты и анализ испытаний на сдвиг3.1. Кривая сдвигового напряжения-смещенияКривая сдвигового напряжения-смещения на границе между крупнозернистым песком и конструкцией под высоким напряжением показана на рисунке 4. Можно видеть, что при различной базальной твердости бетона кривая сдвигового напряжения-перемещения была одинаковой, и нормальное напряжение оказало очевидное влияние на кривую. Прочность на сдвиг и жесткость на сдвиг увеличились с нормальным напряжением. Когда нормальное напряжение составляло 2 МПа, кривая сдвигового напряжения-смещения демонстрировала идеальные пластические свойства. Когда нормальное напряжение было больше или равно 4 МПа, поскольку раздробленные крупные частицы песка были относительно стабильными, а коэффициент пустотности почти не менялся, когда нормальное напряжение составляло 2 МПа, кривая показала явление деформационного упрочнения.В соответствии с принципом связи между плотностью и прочностью на сдвиг [36] прочность на сдвиг стремится к устойчивому значению. 3.2. Регрессионный анализ данных испытанийНелинейная гиперболическая модель может быть преобразована в модель линейной регрессии [37], где сдвиговое смещение, и параметры регрессии модели. Трансформированная гиперболическая линейная модель регрессии была использована для выполнения регрессионных анализа на тестовых данных сдвига, как показано в таблице 3.
можно увидеть, что факторы, влияющие на предельную прочность на сдвигу в порядке убывания, являются нормальным стрессом, базальной твердостью, содержанием влаги и шероховатость.Оптимальной комбинацией испытаний является A4B4C4D1, в которой предельная сдвиговая жесткость границы между крупнозернистым песком и бетоном была наибольшей при нормальном напряжении 8 МПа; комбинация: шероховатость 0,332, содержание влаги 0% и базовая твердость 41,9. По рисунку 8 путем визуального анализа экспериментальных данных было установлено, что начальная сдвиговая жесткость нелинейно увеличивалась с увеличением нормального напряжения; это связано с тем, что на начальной стадии сдвига энергия сдвига пропорциональна нормальному давлению.Однако при различном нормальном напряжении регулировка угла трения поверхности раздела и дробление крупных частиц песка различны, что приводит к нелинейному увеличению нормального напряжения и начальной жесткости при сдвиге. С увеличением влажности начальная сдвиговая жесткость сначала увеличивалась, а затем уменьшалась, а минимальное значение было обнаружено при влажности от 8% до 16%. Из-за низкой прочности сухого песка на раздавливание были увеличены плотность крупного песка и сопротивление сдвигу между крупным песком и структурой бетона.По мере увеличения влажности водная пленка между почвенными частицами появлялась «адсорбционной». Водяная пленка между частицами выдерживала часть силы, и прочность крупного песка на раздавливание постепенно увеличивалась, уменьшая степень дробления частиц. Однако при дальнейшем увеличении влажности «адсорбционный» эффект водной пленки постепенно уменьшался и исчезал. В это время прочность крупного песка на раздавливание постепенно снижалась [45], а значит, существовала оптимальная влажность, и прочность на раздавливание достигала максимального значения.В литературе [46] указано, что при одном и том же нормальном напряжении на скелетной кривой при разной влажности существовала критическая влажность, которая оказалась равной 11,2 %. Прочность на сдвиг увеличивалась с увеличением твердости основания; шероховатость поверхности мало влияла на предельное напряжение сдвига, которое незначительно увеличивалось с увеличением шероховатости. 4.3. Визуальный анализ дробления частиц на границе разделаДля определения оптимального уровня, оптимального сочетания и приоритетного порядка начальной прочности на сдвиг был проведен диапазонный анализ данных испытаний ортогональной таблицы.Результаты анализа отображаются в таблице 7.
Согласно Таблице 7, можно увидеть, что степень влияния факторов на предельная прочность на сдвиг в порядке убывания — это нормальное напряжение, базальная твердость, влажность и шероховатость.Оптимальное сочетание теста — A4B1C1D3, что означает нормальное напряжение 8 МПа, шероховатость 0,083, влажность 16% и базовую твердость 28,1. Разрушение частиц на границе между крупным песком и бетоном является наиболее серьезным. Согласно рис. 10 видно, что относительное дробление частиц бетона увеличивается с увеличением нормального напряжения. Когда нормальное напряжение составляло 4 МПа-8 МПа, относительное приращение нормального напряжения при дроблении было значительно больше, чем при 2МПа-4 МПа.Что касается сухого песка с влажностью 0 %, то его относительная скорость дробления частиц была выше, чем у песка с влажностью 8 %. При влажности 16% пик дробления возникал, а затем ослабевал; частицы постепенно разрушались с увеличением шероховатости поверхности и базальной твердости, и все они имели тенденцию к уменьшению. При анализе вышеуказанных факторов метод напряжения влияет на начальную прочность на сдвиг, предельную прочность на сдвиг и скорость разрушения частиц; самый большой глубоко заглубленный в почву и инженерный интерфейс бетона должен полностью учитывать влияние глубины залегания, для вертикальной стены шахты с глубокими сваями и других проектов, необходимых от грубой степени бетонной поверхности, чтобы отрегулировать предел прочности на сдвиг интерфейса и избежать неравномерности оседание пластового грунта, приводящее к экструзионному повреждению конструкции. 5. Выводы(1)Разработано устройство для испытания интерфейса на сдвиг при высоких напряжениях. Можно получить, что предел прочности на сдвиг при высоком напряжении увеличивается с увеличением нормального напряжения, а сдвиговая жесткость интерфейса увеличивается с сдвиговым смещением; когда нормальное напряжение составляло 2 МПа, кривая сдвигового напряжения-сдвигового смещения представляла идеальную пластичность. Когда нормальное напряжение было больше или равно 4 МПа, кривая показывала характеристики деформационного упрочнения.Как кривая сдвигового напряжения-смещения при сдвиге, так и кривая объемной деформации-сдвига-смещения могут быть описаны с использованием гиперболической модели (2). Начальная жесткость при сдвиге крупнозернистого песка и поверхности раздела показали линейную зависимость от нормального напряжения; начальная сдвиговая жесткость демонстрировала очевидную тенденцию к увеличению с увеличением шероховатости поверхности раздела и базовой твердости. При сочетании нормального напряжения 8 МПа, шероховатости 0,083, влажности 24% и базовой твердости 38.1, предел прочности при сдвиге границы раздела между крупнозернистым песком и бетоном достиг максимума. . Вслед за шероховатостью интерфейса степень влияния содержания влаги была немного больше, чем прочность бетонного интерфейса. При нормальном напряжении 8 МПа шероховатость 0,332, влажность 0% и базовая твердость 41.9, предельная жесткость на сдвиг поверхности раздела между крупнозернистым песком и бетоном достигает наивысшего значения (4). Относительная скорость дробления крупнозернистого песка увеличивается с увеличением нормального напряжения, а взаимосвязь между относительным дроблением и нормальным напряжением представляет собой нелинейное увеличение. в проеме вверх. Нормальное напряжение оказало наиболее очевидное влияние на сопротивление поверхности раздела при сдвиге, за которым следовала шероховатость интерфейса. Твердость и влажность подложки оказали более слабое влияние на разрушение при сдвиге интерфейса конструкции Доступность данныхДанные, использованные для подтверждения результатов исследования, можно получить у соответствующего автора по запросу. Конфликт интересовАвторы заявляют об отсутствии конфликта интересов. БлагодарностиИсследовательская работа, описанная в этой статье, была поддержана проектом Национального фонда естественных наук Китая (51778215) и ключевыми проектами Департамента науки и технологий провинции Хэнань (152102210318). Анализ болтовых соединений | Механический калькуляторПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения.Пожалуйста, включите JavaScript. Болтовое соединение является одним из наиболее распространенных методов соединения. Другие распространенные методы соединения включают заклепки, сварку, запрессовку, штифты, шпонки и клеи. Основные компоненты болтового соединения включают в себя резьбовое соединение, а также соединяемые детали (зажимные детали ). Болтовое соединение работает, вызывая начальную зажимную силу («предварительную нагрузку») на соединение путем вкручивания крепежного элемента либо в гайку, либо в резьбу, нарезанную на одной из частей.Эта предварительная нагрузка гарантирует, что зажатые детали останутся в контакте и сжатии в течение всего срока службы соединения. Шайбы обычно используются в соединении и служат многим целям. Они сводят к минимуму погружение головки болта и гайки в зажимаемые детали и облегчают затяжку. Поскольку отверстия под болты могут иметь острые края или заусенцы, для защиты галтели под головкой болта от царапин используются шайбы, поскольку это критическая область, которая может выйти из строя. Шайбы также служат для распределения предварительного натяга и приложенного усилия по большей площади как на головке болта, так и на торцах зажимаемых деталей.Это снижает нагрузку на подшипник, помогает предотвратить проскальзывание и помогает предотвратить повреждение поверхности зажатых деталей. Содержимое Размеры резьбыПри анализе соединения необходимо знать характерные размеры как наружной, так и внутренней резьбы. Размер резьбы указывается на основе номинального (наибольшего) диаметра и либо количества витков на дюйм (для унифицированных дюймовых резьб), либо шага (для метрических резьб).Размеры резьбы для крупной и мелкой резьбы можно найти в таблицах, расположенных в любом стандартном справочнике по проектированию станков, а также в таблицах размеров резьбы в Приложении. Шаг, P — расстояние между витками. Когда шаг измеряется в дюймах, он связан с числом витков на дюйм, TPI, следующим образом: ТПИ = 1/П Размеры резьбы (внутренняя и внешняя резьба):
В таблицах ниже приведены уравнения для некоторых интересующих размеров профиля резьбы как для унифицированной дюймовой резьбы, так и для метрической резьбы ISO.В случае метрической резьбы профиль резьбы основан на параметре H, высоте основного треугольника. Значение H связано с шагом резьбы P соотношением: Внешняя резьба (болт) Размеры:
Размеры внутренней резьбы:
Внешняя резьба (болт) Участки: В приведенных выше таблицах единицы измерения США указаны в дюймах, а метрические единицы — в миллиметрах. Предварительная нагрузкаБолты устанавливаются с предварительным натягом, который обеспечивает зажатие и сжатие элементов соединения в течение всего срока службы соединения. Предварительная нагрузка также важна для суставов с циклически прикладываемой нагрузкой. Предварительная нагрузка увеличит среднее напряжение, но снизит переменное напряжение. Значения предварительной загрузкиПреднатяг обычно указывается в процентах от предела текучести материала болта при растяжении, S ty .Чтобы рассчитать усилие предварительной нагрузки в процентах от предела текучести, используйте: F PL = % yld · S ty A t где % yld — процент текучести при предварительной нагрузке, S ty — предел текучести, а A t — площадь растягивающего напряжения. Как правило, усилие предварительного натяжения должно быть не меньше максимального растягивающего усилия, которое будет приложено к соединению. Это гарантирует, что зажатые детали всегда остаются в контакте и сжимаются.Поскольку часть силы растяжения, приложенной к соединению, будет уменьшать сжатие в зажатых частях, соединение разъединится при значении приложенной силы, несколько превышающем предварительную нагрузку. Это будет обсуждаться в следующем разделе. Поскольку сила растяжения, которая будет приложена к соединению, определяет требуемую предварительную нагрузку, максимальная полезность болта достигается за счет его предварительной нагрузки до максимально возможного значения. Пластичность материала болта определяет, насколько близко к пределу текучести болт может быть предварительно нагружен.Шигли и Линдебург рекомендуют следующие (консервативные) значения предварительной нагрузки: где F пруф — пробная нагрузка крепежного изделия. Соотношение между пробной нагрузкой и пробной прочностью S пруф : F пруф = S пруф A t По Шигли предел текучести примерно равен 85% предела текучести при растяжении, S ty . На основе доказательства S = 0.85·S ty , рекомендуемое усилие предварительного натяга в зависимости от предела текучести составляет: Учитывая, что приведенные выше значения являются консервативными, общее эмпирическое правило заключается в том, чтобы предварительно натянуть крепежный элемент до 2/3 предела текучести (т. е. % 90 303 yld 90 304 = 66,7%). Расслабление предварительной нагрузкиСуществует много факторов, которые могут привести к «расслаблению» или потере предварительного натяга, применяемого во время установки. Колебания температуры приведут к расширению и сжатию соединительных элементов и могут привести к увеличению или уменьшению силы предварительного натяга в зависимости от относительного удлинения и укорочения между крепежным элементом и зажатыми частями.Если предварительная нагрузка достигается за счет приложения крутящего момента к болту или гайке, то это приведет к скручиванию крепежной детали, что увеличит натяжение болта и, следовательно, усилие предварительной нагрузки. Со временем это кручение рассеется и вызовет ослабление силы предварительной нагрузки. Другие факторы, которые способствуют релаксации предварительной нагрузки, включают заделку и ползучесть. Ослабление предварительной нагрузки можно уменьшить за счет использования механизмов фиксации резьбы, включая фиксирующие клеи, стопорные гайки, стопорные шайбы, стопорную проволоку и стопорные шарики/пластыри.Barrett предлагает всестороннее описание механизмов блокировки резьбы. Согласно Справочнику по машинному оборудованию, ослабление предварительной нагрузки происходит в течение нескольких часов после установки, и, как правило, допустимой потери предварительной нагрузки в размере около 10% достаточно. Неопределенность предварительной нагрузкиТочность предварительной нагрузки, применяемой во время установки, сильно зависит от используемого метода затяжки. Следующая таблица взята из Barrett, из MIL-HDBK-60 и из Machinery’s Handbook:
Крутящий момент для получения предварительной нагрузкиВо многих распространенных методах затяжки усилие предварительного натяга достигается за счет приложения крутящего момента к гайке или головке болта.При затягивании крепежа с помощью динамометрического ключа, который является одним из самых простых и распространенных методов, крепеж считается затянутым надлежащим образом после достижения указанного крутящего момента. В этом случае необходимо определить величину крутящего момента, необходимую для достижения требуемой силы предварительного натяга в болте. Этот крутящий момент рассчитывается с использованием: T = K T d ном. F PL где d nom — номинальный диаметр болта, а F PL — сила предварительного натяга болта.K T – коэффициент крутящего момента, который рассчитывается по формуле: где r t — средний радиус резьбы (эффективное место, в котором действует трение в резьбе), r c — средний радиус буртика (эффективное место, в котором действует трение о поверхность подшипника), f t — коэффициент трения между поверхностями резьбы, f c — коэффициент трения между поверхностями буртика (опорной поверхности), λ — угол опережения, α — половинный угол резьбы ( α = 30°, согласно ASME B1.1, 10.1б). Барретт приводит хорошую таблицу коэффициентов трения. Значение для r t рассчитывается как половина среднего диаметра болта, который является средним значением малого диаметра и номинального диаметра: Площадь буртика — это площадь опорной поверхности детали, которая вращается во время установки (либо гайки, либо головки болта). Ширина под ключ гайки обычно в 1,5 раза больше номинального диаметра. В этом случае средний радиус воротника рассчитывается как: Угол опережения, λ, рассчитывается по формуле: где l — ход за оборот (= 1/TPI). Shigley предоставляет таблицу коэффициентов крутящего момента в зависимости от состояния болта, которая была адаптирована, как показано ниже. Если состояние болта неизвестно, для K T рекомендуется значение 0,2.
Из-за множества переменных, влияющих на значение коэффициента крутящего момента, любой метод затяжки, который косвенно измеряет усилие предварительного натяга через значение крутящего момента, по своей сути будет неточным. Именно по этой причине существует такая большая неопределенность в точности предварительного натяга при использовании динамометрического ключа. Ознакомьтесь с нашим калькулятором болтовых соединений, основанным на методологии, описанной здесь.
Жесткость суставовШарнир можно рассматривать как набор пружин. Части рукоятки действуют как набор последовательно соединенных пружин, а рукоятка и болт действуют как параллельные пружины. Соединение можно смоделировать, как показано ниже. Обратите внимание, что в соединении, показанном ниже, в захвате только 2 детали; однако количество частей не ограничено двумя, и каждая часть в соединении будет представлена пружиной. Каждая пружина на рисунке выше имеет жесткость: , где A — площадь, E — модуль упругости материала, а L — длина. Жесткость болтаКогда соединение собрано правильно, весь стержень болта будет находиться в захвате вместе с резьбой некоторой длины. Жесткость хвостовика определяется: где A nom — номинальная площадь болта, E болт — модуль упругости материала болта, а L стержень — длина стержня болта. Жесткость резьбовой части рукоятки определяется по формуле: где A t — площадь растягивающего напряжения, а L thd.g — длина резьбовой части в захвате. Стержень и резьбовая часть болта будут последовательно действовать как пружины, так что эффективная жесткость части болта в рукоятке определяется выражением: В соответствии с ASME B18.2.1 номинальная длина резьбы болтов дюймовой серии определяется по формуле: Длину стержня болта можно найти по: L хвостовик = L − L thd Длина резьбы в захвате находится по формуле: L тыс. руб.г = L г − L хвостовик , где L г — длина рукоятки. Жесткость захватаЖесткость захвата рассчитывается на основе упрощенного метода конуса давления, представленного Шигли. Этот метод прогнозирует распределение давления по всей толщине захвата. Конус давления для соединения можно представить на диаграмме ниже. Часть детали внутри конуса давления называется усеченным конусом .Каждая часть захвата будет содержать либо 1, либо 2 усеченных конуса. Жесткость отдельного усеченного конуса определяется выражением: где d — внутренний диаметр усеченного конуса, D — наименьшее значение внешнего диаметра усеченного конуса, t — толщина усеченного конуса, E — модуль упругости материала, α — угол конуса давления. Шигли рекомендует значение 30° для α. Высота прижимного конуса зависит от длины захвата, L g , которая представляет собой суммарную толщину деталей, зажимаемых в соединении (см. рисунок выше).В соединении с гайкой нажимной конус начинается под головкой болта и заканчивается под гайкой. Диаметры усеченного конуса в этом случае легко определить по диаметрам опорных поверхностей. В резьбовом соединении конус давления начинается под головкой болта и заканчивается в резьбовой части последней пластины. Согласно Шигли, эффективная толщина захвата конечной пластины определяется как: L’ г.п2 = мин(т, д ном ) / 2 где t — толщина пластины, а d nom — номинальный диаметр болта.Диаметр усеченного конуса на конце конуса давления принимается равным 1,5·d nom . Жесткость захвата рассчитывается с учетом того, что усеченные конусы действуют как последовательно соединенные пружины: Упрощение жесткости захватаШигли приводит уравнение, которое вычисляет правильную жесткость захвата при условии, что каждая часть захвата имеет одинаковый модуль упругости . Пока это условие выполняется, тогда жесткость сцепления, рассчитанная с использованием приведенного ниже упрощенного уравнения, будет такой же, как и рассчитанная с использованием полной процедуры, в которой каждый усеченный конус рассматривается отдельно: В приведенном выше уравнении E — модуль упругости материала рукоятки, L g — длина рукоятки, α — угол усеченного конуса (30°), d bh — диаметр опорной поверхности под головкой болта, d — внутренний диаметр усеченного конуса.Значением d может быть либо номинальный диаметр болта (для более приблизительного результата), либо диаметр отверстия в самой центральной части соединения (для более реалистичного результата). Еще более упрощенное уравнение для жесткости захвата можно найти, если предположить, что диаметр головки болта на 50 процентов больше номинального диаметра болта (т. е. d bh = 1,5 · d nom ): Ознакомьтесь с нашим калькулятором болтовых соединений, основанным на методологии, описанной здесь.
Нагрузка на болт в зависимости от приложенной нагрузкиПреднатяг удлиняет болт и сжимает зажатые детали. Когда к соединению прикладывается растягивающая нагрузка, некоторая часть приложенной нагрузки уменьшает сжатие в зажатых частях, а другая часть дополнительно удлиняет болт.Часть приложенной нагрузки, которую несет болт, зависит от относительной жесткости болта и зажатых частей. Эта относительная жесткость известна как постоянная соединения C: Ниже представлена репрезентативная диаграмма нагрузки на болты в зависимости от приложенной нагрузки на соединение: На приведенном выше рисунке по оси X отложена растягивающая нагрузка, приложенная к соединению, а по оси Y отложена растягивающая нагрузка, существующая в болте. Когда приложенная нагрузка равна нулю, растягивающая нагрузка на болт равна силе предварительной нагрузки.Когда к соединению прикладывается нагрузка, часть приложенной нагрузки действует на уменьшение сжатия в зажатых частях, а часть приложенной нагрузки действует на увеличение натяжения болта. Линия нагрузки на болт имеет постоянный наклон, равный постоянной соединения C. Кривая номинальной нагрузки на болт показана толстой сплошной синей линией. Две более светлые синие линии, идущие параллельно номинальной кривой, представляют собой кривые минимальной и максимальной нагрузки на болт. Минимальная кривая учитывает неопределенность предварительного натяга из-за способа установки, а также релаксацию предварительного натяга.Максимальная кривая учитывает неопределенность предварительной нагрузки. На приведенных выше кривых использовалась неопределенность предварительного натяга ±25 % (соответствующая установке с помощью динамометрического ключа) вместе с ослаблением предварительного натяга на 10 %. Еще одна кривая, которую следует отметить на рисунке выше, — это линия нагрузки при растяжении болта, показанная горизонтальной красной пунктирной линией. Эта линия указывает значение растягивающей нагрузки на болт, которая приведет к текучести. Эта линия учитывает сдвиг и изгиб, поэтому любая сила сдвига или изгибающие моменты, действующие на болт, опустят эту линию. Совместное разделениеКолено кривой на приведенной выше диаграмме нагрузки на болт показывает точку, в которой соединение разделяется. В этот момент приложенная нагрузка достаточна для разделения деталей в соединении (все сжатие в зажатых деталях снято), и после этого момента любая нагрузка, приложенная к соединению, полностью воспринимается болтом. Сила, вызывающая отрыв сустава, находится по формуле: Обратите внимание, что усилие разделения всегда будет несколько выше, чем усилие предварительного натяга. Разделение соединения является критерием отказа, и соединение должно быть спроектировано таким образом, чтобы оно не отделялось во время эксплуатации. Коэффициент запаса прочности при разделении находится по формуле: Силы на болтеСуммарное растягивающее усилие на болте обусловлено двумя составляющими: усилием предварительного натяжения и приложенной растягивающей нагрузкой. Значения этих компонентов для каждой части кривой нагрузки на болт находятся по формуле:
Общая растягивающая сила на болте представляет собой сумму натяжения из-за предварительного натяга и натяжения из-за приложенной нагрузки, как определено из таблицы выше: F b.t = F b.PL + Ф б.т. приложение Другой способ выразить общую растягивающую силу на болте: Сила сдвига, действующая на болт, равна нагрузке сдвига, приложенной к соединению: F b.s = F s.app Изгибающий момент может возникнуть в болте, если между пластинами есть зазор (например, из-за прокладки) или если в соединении используются длинные прокладки: М б = Ф б.с а/2 где а — плечо момента.Более подробное обсуждение изгибающего момента на болте дано в Приложении. Расчет приложенных силЭта ссылка на анализ болтового соединения предполагает, что усилия растяжения и сдвига, приложенные к соединению, известны. Обсуждение того, как рассчитать силы растяжения и сдвига, действующие на отдельные болтовые соединения в массиве болтов, приведено в нашем справочнике по распределению усилий в массиве болтов. Напряжение болтаНапряжения в болте рассчитываются по уравнениям, приведенным в таблице ниже:
где A t — площадь растягивающего напряжения, а A s — площадь сдвига (либо номинальная площадь, если плоскость сдвига находится в хвостовике, либо меньшая площадь, если плоскость сдвига находится в резьбе). Мы видим, что напряжение изгиба зависит от диаметра d, который представляет собой либо номинальный диаметр, если максимальный момент приходится на хвостовик, либо меньший диаметр, если максимальный момент приходится на резьбу. Если рассматривать болт как неподвижную направляющую балку (как обсуждается в Приложении), то мы видим, что максимальный момент будет возникать при граничных условиях болта, расположенных под головкой и в начале внутренней резьбы . Поскольку максимальный момент возникает в резьбе, для расчета напряжения изгиба следует использовать меньший диаметр болта. Напряжение по Мизесу рассчитывается по формуле: В приведенном выше уравнении n представляет собой коэффициент нагрузки, который применяется к напряжениям растяжения, изгиба и сдвига, но не применяется к напряжению предварительной нагрузки. Коэффициент нагрузки связан с коэффициентом безопасности, с той разницей, что это коэффициент, который применяется к нагрузкам или напряжениям, чтобы гарантировать, что напряжение болта остается ниже допустимого напряжения. Коэффициент безопасности можно найти итеративно, найдя значение коэффициента нагрузки, при котором напряжение по Мизесу равно допустимому напряжению: Ознакомьтесь с нашим калькулятором болтовых соединений, основанным на методологии, описанной здесь.
Резьбонарезные ножницыСрез резьбы является важным видом отказа для болтового соединения, и это происходит, когда резьба срезается либо с болта ( срез внешней резьбы ), либо с гайки или резьбовой части ( срез внутренней резьбы ). Между резьбой болта и внутренней резьбой должно быть достаточное зацепление, чтобы болт не выдержал растяжения до того, как резьба срежется.Это обеспечит развитие полной прочности болта (и, следовательно, отсутствие «потеря прочности» болта), и позволит избежать задачи сверления и повторного нарезания внутренней резьбы. Срез резьбы следует учитывать как для внешней (болтовой) резьбы, так и для внутренней резьбы. Длина резьбового соединенияДлина зацепления резьбы является доминирующим фактором, определяющим, будет ли резьба разрушаться при сдвиге. Эмпирическое правило заключается в том, что длина зацепления, равная диаметру болта, обычно достаточна для защиты от сдвига резьбы.Однако для обеспечения безопасности всегда следует выполнять расчеты на сдвиг в соответствии со следующими разделами. В болтовом соединении с гайкой, если болт выступает за конец гайки, длину резьбового зацепления можно оценить по высоте гайки, h гайка . В действительности будет некоторая потеря зацепления из-за снятия фаски вокруг резьбового отверстия в гайке. В резьбовом соединении глубина резьбы в конечной части должна быть равна минимальной толщине резьбовой части, t p , или номинальному диаметру болта, d nom , поэтому длина зацепления резьбы может быть оценивается как минимальное из этих значений.Обратите внимание, что эти оценки не учитывают фаски на конце болта или вокруг резьбового отверстия в детали. Оценки длины зацепления резьбы в болтовом соединении резюмируются следующим уравнением. Затем это значение L E следует использовать для расчета коэффициентов запаса прочности на сдвиг внешней и внутренней резьбы. Наружные резьбонарезные ножницыПлощадь среза резьбы для наружной резьбы определяют по цилиндрическому участку высотой, равной длине зацепления резьбы, L E , и диаметром, равным делительному диаметру, d п.доб . Согласно FED-STD-h38/2B площадь среза резьбы для наружной резьбы рассчитывается по формуле: Напряжение сдвига во внешней резьбе рассчитывается по формуле: где F b.t — полное растягивающее усилие, действующее на болт, с учетом предварительного натяга и части приложенной растягивающей нагрузки, воспринимаемой болтом. Коэффициент запаса прочности при сдвиге наружной резьбы по отношению к пределу текучести при сдвиге S sy материала резьбы рассчитывается по формуле: Предел текучести при сдвиге обычно оценивается как 0.577·С ти . Значение 0,577 соответствует обратной величине √3 члена критерия отказа фон Мизеса. См. Barrett для получения более подробной информации об оценках допустимого сдвига. Ножницы для внутренней резьбыСдвиг внутренней резьбы рассчитывается аналогично сдвигу внешней резьбы. Согласно FED-STD-h38/2B площадь среза внутренней резьбы рассчитывается по формуле: где d p.int — делительный диаметр внутренней резьбы, а L E — длина зацепления резьбы, которая рассчитывается так же, как и для сдвига наружной резьбы. Напряжение сдвига во внутренней резьбе рассчитывается по формуле: Коэффициент запаса прочности при сдвиге внутренней резьбы по отношению к пределу текучести материала резьбы при сдвиге рассчитывается по формуле: Напряжения зажатой деталиРазрушение зажатых деталей необходимо исследовать при анализе болтового соединения. Существует несколько основных механизмов отказа зажатых деталей, которые описаны в следующих разделах. ПротянутьСила растяжения, приложенная к соединению, будет действовать так, чтобы протягивать части над местом приложения силы друг через друга.На рисунке ниже головка болта протягивает шайбу 1, шайба 1 протягивает пластину 1, шайба 2 протягивает пластину 2, а гайка протягивает шайбу 2. Соответствующие уравнения:
В таблице выше d o — наружный диаметр протягиваемой детали, t p — толщина рассматриваемой детали, F t.app — приложенное растягивающее усилие, а S sy — предел текучести при сдвиге материала рассматриваемой детали. Предел текучести при сдвиге обычно можно оценить как 0,577·S ty . Значение 0,577 соответствует обратной величине √3 члена критерия отказа фон Мизеса. См. Barrett для получения более подробной информации об оценках допустимого сдвига. ПодшипникСила предварительного натяга будет действовать таким образом, чтобы каждая деталь опиралась на соседние детали.Например, на предыдущем рисунке головка болта и шайба 1 будут упираться друг в друга, как и шайба 1 и пластина 1.
В приведенной выше таблице d o.min — минимальный наружный диаметр двух деталей, опирающихся друг на друга, d h — диаметр сквозного отверстия рассматриваемой детали, а S на — предел текучести подшипника. прочность рассматриваемой детали.Предел текучести подшипника обычно можно оценить как 1,5·S ty . См. Barrett для получения более подробной информации об оценках допустимых пеленгов. F медведь — сила подшипника. Величина несущей силы на поверхности зависит от положения этой поверхности по отношению к месту приложения растягивающей силы в соединении. На предыдущем рисунке поверхность 3 находится внутри мест приложения растягивающей силы, поэтому эта поверхность не испытывает увеличения из-за приложенной силы.Однако все поверхности 1, 2, 4 и 5 находятся за пределами мест приложения силы и испытывают увеличение. Если опорная поверхность находится внутри мест приложения силы, то максимальная опорная сила, воздействующая на поверхность, представляет собой просто силу предварительного натяга. Если опорная поверхность находится за пределами мест приложения силы, то опорная сила увеличивается на приложенную силу, и максимальная опорная сила, воздействующая на эту поверхность, равна растягивающей силе в болте. Подшипник штифтаЕсли соединение нагружено сдвигом, то болт может быть прижат к внутренним стенкам сквозных отверстий в защемленных деталях.
В приведенной выше таблице d nom — номинальный диаметр болта, t p — толщина детали, F s.app — приложенная сила сдвига, а S на — предел текучести материала подшипника. Предел текучести подшипника обычно можно оценить как 1.5·S ty . См. Barrett для получения более подробной информации об оценках допустимых пеленгов. PDH Classroom предлагает курс повышения квалификации на основе этой справочной страницы по анализу болтовых соединений. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE. Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание! ПриложениеРазмеры оборудования: унифицированная дюймовая резьбаРазмеры крепежа: метрическая резьбаМаксимальный изгибающий момент на болтеМаксимальный изгибающий момент болта определяется по формуле: М б = Ф с а/2 , где F s — приложенная сила сдвига, а — плечо момента. Болт можно смоделировать как фиксированную направляющую балку (т. е. балку с фиксированным граничным условием на одном конце и управляемым граничным условием на другом конце). В приведенной ниже модели левый конец болта зафиксирован (все степени свободы фиксированы), а правый конец направляется (вращение и перемещение по оси x фиксированы, но могут перемещаться по оси y). К правому концу приложена поперечная сила в 100 фунтов силы. Диаграмма свободного тела (FBD) и деформированная сетка для этого случая показаны ниже.Если бы приведенная выше модель была консольной балкой, момент из-за приложенной силы полностью воспринимался бы одним закрепленным концом. Однако, поскольку модель зафиксирована от вращения с обоих концов, момент распределяется между двумя концами болта. Диаграмма момента сдвига для этого случая показана ниже: Подпишитесь, чтобы время от времени получать обновления о последних улучшениях: Каталожные номераОбщие каталожные номера:
Технические характеристики и стандарты:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Он обозначает относительное смещение контакта в нормальном направлении. Уравнение перекрытия имеет вид:
Он обозначает относительное смещение контакта в нормальном направлении. Уравнение перекрытия имеет вид: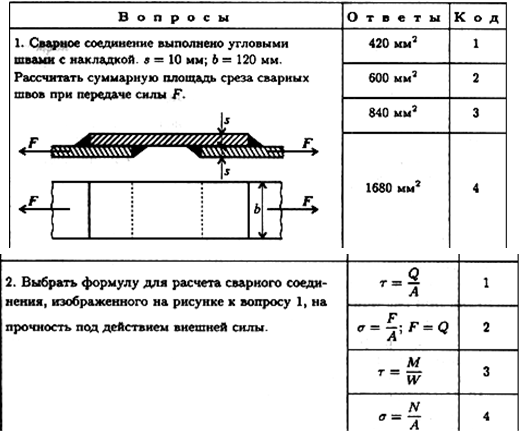 Подробное описание DEM в PFC можно найти в [27].
Подробное описание DEM в PFC можно найти в [27].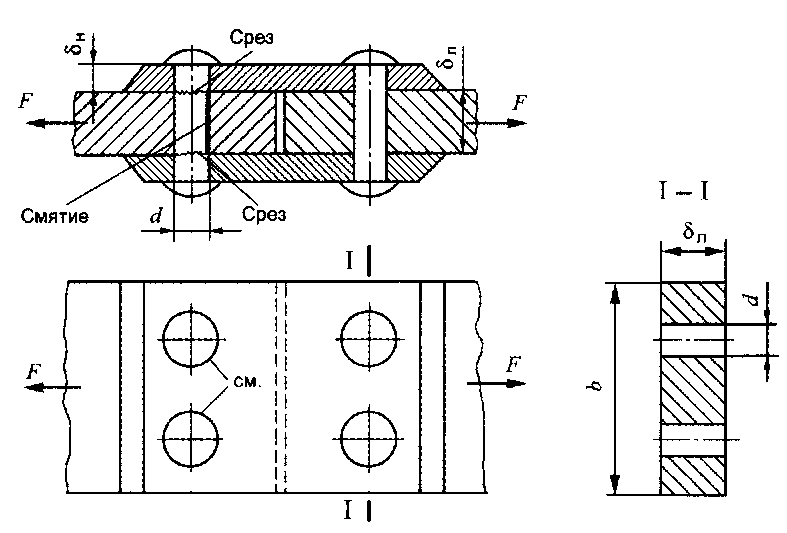 Модель контактной жесткости, модель проскальзывания и разделения и модель сцепления — это три разные модели контакта, предоставляемые PFC. Модели связи делятся на два типа: модели контактной связи могут просто создавать силу, и модели параллельной связи, которые могут создавать как силу, так и момент.Здесь мы использовали параллельную связь в качестве цементирующего материала между частицами комков, поскольку она обеспечивает эффективное вращательное движение частиц в зернистой системе.
Модель контактной жесткости, модель проскальзывания и разделения и модель сцепления — это три разные модели контакта, предоставляемые PFC. Модели связи делятся на два типа: модели контактной связи могут просто создавать силу, и модели параллельной связи, которые могут создавать как силу, так и момент.Здесь мы использовали параллельную связь в качестве цементирующего материала между частицами комков, поскольку она обеспечивает эффективное вращательное движение частиц в зернистой системе. Хотя моделирование ЦМР не может учитывать столько же частиц, сколько используется в экспериментальной выборке, оно гарантирует хорошее приближение [20]. PFC 2D версии 4.0 поддерживает до 100 000 частиц для одной гранулированной сборки. В этом исследовании для сокращения времени вычислений было использовано 6830 частиц для моделирования теста на кольцевой сдвиг.
Хотя моделирование ЦМР не может учитывать столько же частиц, сколько используется в экспериментальной выборке, оно гарантирует хорошее приближение [20]. PFC 2D версии 4.0 поддерживает до 100 000 частиц для одной гранулированной сборки. В этом исследовании для сокращения времени вычислений было использовано 6830 частиц для моделирования теста на кольцевой сдвиг. Микромеханические свойства материала Lac du Bonnet [20] использовались для моделирования отходов.представляет свойства материалов системы сборки частиц комков. Различные нормальные напряжения были установлены в сборке с использованием процедуры установки начального напряжения. После установки нормального напряжения была создана кольцеобразная граница с использованием общего механизма стенки (d). Предполагалось, что верхняя часть кольцевой коробки сдвига будет имитировать трехмерный эксперимент по сдвигу кольца. Кольцевая коробка сдвига вращалась путем приложения к внешней границе скоростей вращения (т.е. 0,01, 0,1, 1 и 100 мм/с).
Микромеханические свойства материала Lac du Bonnet [20] использовались для моделирования отходов.представляет свойства материалов системы сборки частиц комков. Различные нормальные напряжения были установлены в сборке с использованием процедуры установки начального напряжения. После установки нормального напряжения была создана кольцеобразная граница с использованием общего механизма стенки (d). Предполагалось, что верхняя часть кольцевой коробки сдвига будет имитировать трехмерный эксперимент по сдвигу кольца. Кольцевая коробка сдвига вращалась путем приложения к внешней границе скоростей вращения (т.е. 0,01, 0,1, 1 и 100 мм/с).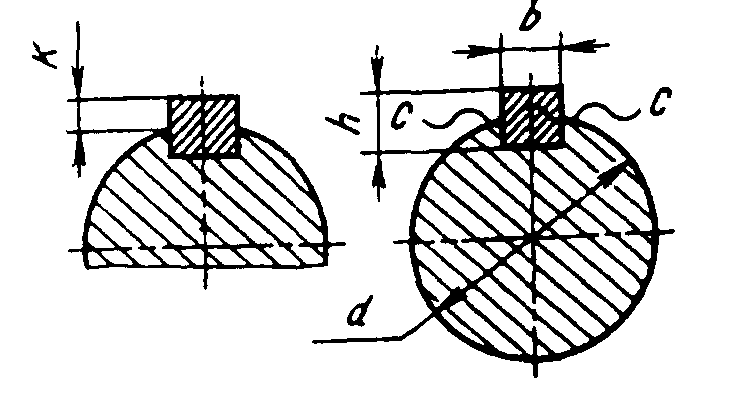
 Угловая скорость сдвига создает центробежную силу на частицах. Материалы испытывают при нормальном напряжении 20, 40, 60, 80, 100 и 150 кПа. Материал был создан в кольцеобразном сосуде для получения изотропной и хорошо связанной гранулированной сборки при заданном нормальном напряжении.Чтобы выполнить точное моделирование кольцевого сдвига, сборка сгустков частиц была создана с использованием процедуры генезиса материала [20].
Угловая скорость сдвига создает центробежную силу на частицах. Материалы испытывают при нормальном напряжении 20, 40, 60, 80, 100 и 150 кПа. Материал был создан в кольцеобразном сосуде для получения изотропной и хорошо связанной гранулированной сборки при заданном нормальном напряжении.Чтобы выполнить точное моделирование кольцевого сдвига, сборка сгустков частиц была создана с использованием процедуры генезиса материала [20].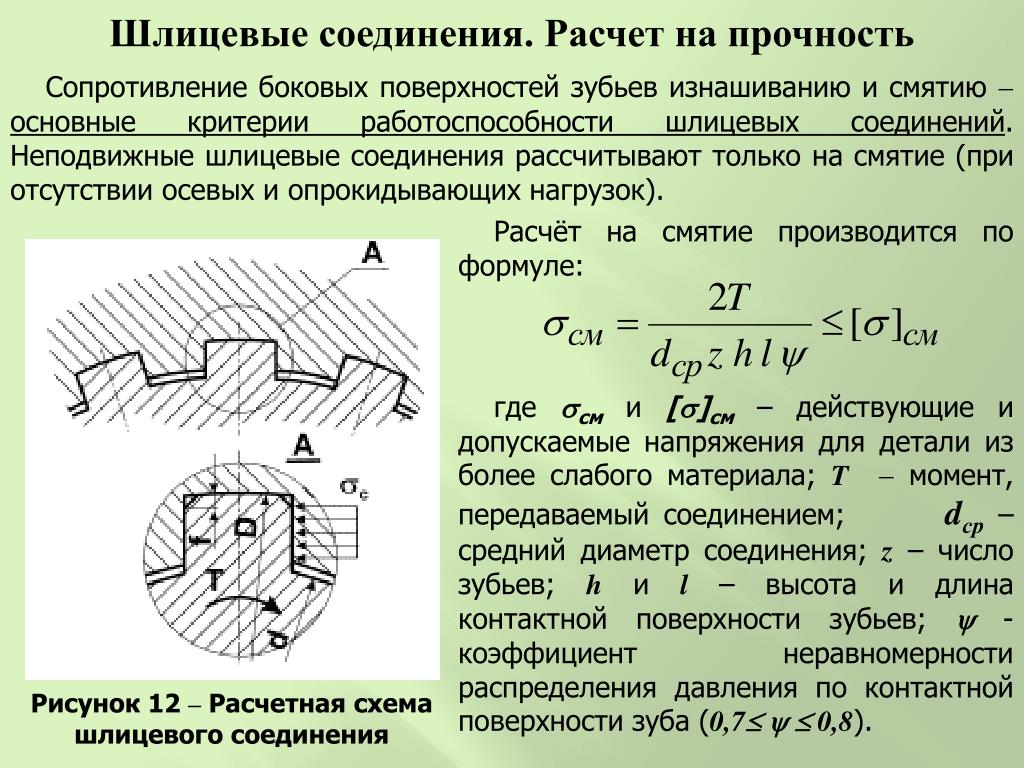 Затем полученные численные значения напрямую сравнивали с экспериментальными результатами путем сопоставления макромеханических свойств. Чтобы воспроизвести соответствующее поведение отходов, мы определили соответствующие микросвойства с помощью процесса калибровки, в котором реакция синтетического материала напрямую сравнивается с измеренной реакцией материалов отходов.Результаты, полученные экспериментально, сравнивались с результатами, полученными с помощью численного моделирования. На основании результатов исследования выделяются следующие моменты: (а) время сдвига, (б) скорость сдвига, (в) нормальное напряжение и (г) явление дробления во время сдвига.
Затем полученные численные значения напрямую сравнивали с экспериментальными результатами путем сопоставления макромеханических свойств. Чтобы воспроизвести соответствующее поведение отходов, мы определили соответствующие микросвойства с помощью процесса калибровки, в котором реакция синтетического материала напрямую сравнивается с измеренной реакцией материалов отходов.Результаты, полученные экспериментально, сравнивались с результатами, полученными с помощью численного моделирования. На основании результатов исследования выделяются следующие моменты: (а) время сдвига, (б) скорость сдвига, (в) нормальное напряжение и (г) явление дробления во время сдвига.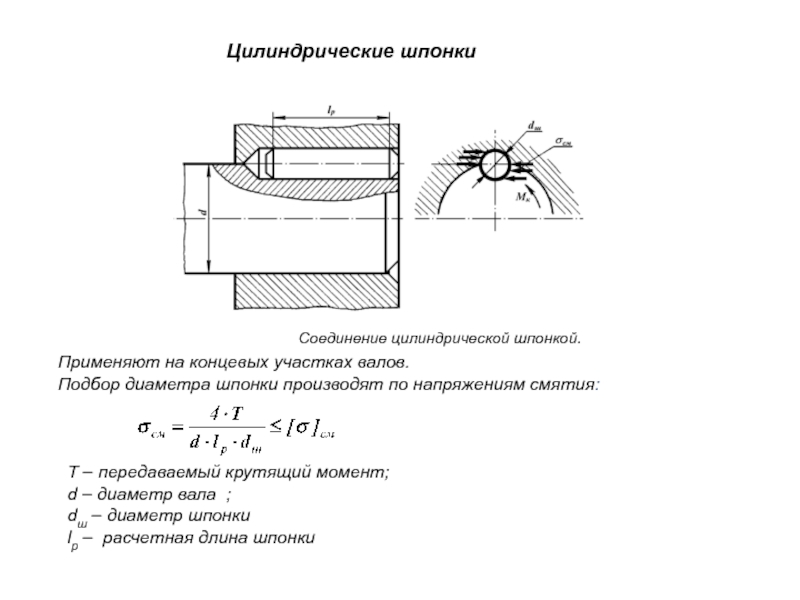 Существует четкое пиковое значение зависимости напряжения сдвига от времени независимо от условий дренирования. При нормальном напряжении 25 кПа экспериментальные и численные оценки выявили разницу наклона 0,81 и 0,28 кПа/с в осушенном и недренированном состоянии соответственно; в то время как для нормального напряжения 100 кПа разница наклона между экспериментальной и расчетной кривыми была равна 0.56 и 0,39 кПа/с в осушенном и неосушенном состоянии соответственно. Кроме того, в недренированном состоянии численные и экспериментальные результаты показали аналогичные значения пикового напряжения 10,1 и 13,7 кПа при нормальном напряжении 25 и 100 кПа соответственно; пиковая разница напряжений 0,3 кПа была получена в осушенном состоянии как для нормальных напряжений 25, так и для 100 кПа. Эти результаты показывают, что экспериментальные и численные результаты как для осушенного, так и для недренированного состояния хорошо согласуются.
Существует четкое пиковое значение зависимости напряжения сдвига от времени независимо от условий дренирования. При нормальном напряжении 25 кПа экспериментальные и численные оценки выявили разницу наклона 0,81 и 0,28 кПа/с в осушенном и недренированном состоянии соответственно; в то время как для нормального напряжения 100 кПа разница наклона между экспериментальной и расчетной кривыми была равна 0.56 и 0,39 кПа/с в осушенном и неосушенном состоянии соответственно. Кроме того, в недренированном состоянии численные и экспериментальные результаты показали аналогичные значения пикового напряжения 10,1 и 13,7 кПа при нормальном напряжении 25 и 100 кПа соответственно; пиковая разница напряжений 0,3 кПа была получена в осушенном состоянии как для нормальных напряжений 25, так и для 100 кПа. Эти результаты показывают, что экспериментальные и численные результаты как для осушенного, так и для недренированного состояния хорошо согласуются.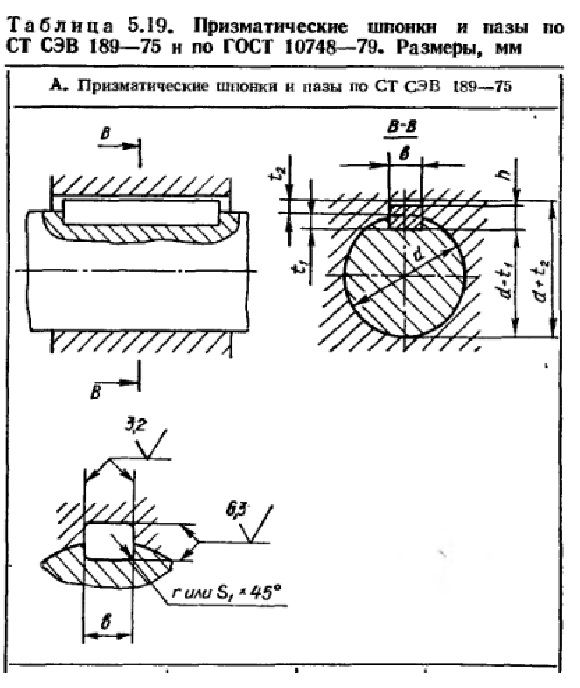 ( a , c ) в осушенном и (b , d ) недренированном состоянии при одинаковой скорости сдвига 0,1 мм/с.
( a , c ) в осушенном и (b , d ) недренированном состоянии при одинаковой скорости сдвига 0,1 мм/с.
 Для нормального напряжения 100 кПа остаточное напряжение сдвига, полученное экспериментально и численно, отличалось на 0,7 кПа и 0,9 кПа для осушенных и неосушенных условий соответственно (c, d). В результате, чем больше нормальное напряжение, тем больше разница.Эти результаты показывают, что значения остаточного напряжения сдвига, полученные нами экспериментально и численно, хорошо согласуются.
Для нормального напряжения 100 кПа остаточное напряжение сдвига, полученное экспериментально и численно, отличалось на 0,7 кПа и 0,9 кПа для осушенных и неосушенных условий соответственно (c, d). В результате, чем больше нормальное напряжение, тем больше разница.Эти результаты показывают, что значения остаточного напряжения сдвига, полученные нами экспериментально и численно, хорошо согласуются. , соответственно; остаточные касательные напряжения различались на 1, 0,4, 0,5 и 1,7 кПа соответственно. Для нормального напряжения 100 кПа в осушенном состоянии при скорости сдвига 0.01 мм/с экспериментальное значение пикового напряжения сдвига находилось в аналогичном диапазоне по сравнению с полученным в результате численного анализа; при скоростях сдвига 0,1, 1 и 100 мм/с разница пикового напряжения сдвига между экспериментальными и численными оценками составила 0,3, 0,2 и 0,3 кПа соответственно. Похоже, что на напряжение сдвига не сильно влияет низкая скорость сдвига (т.е. 0,01 мм/с) в используемом кольцевом аппарате сдвига. При этом остаточные напряжения сдвига различались на 0,4, 0,7, 1 и 2,3 кПа при скоростях сдвига 0.01, 0,1, 1 и 100 мм/с соответственно (а, б).
, соответственно; остаточные касательные напряжения различались на 1, 0,4, 0,5 и 1,7 кПа соответственно. Для нормального напряжения 100 кПа в осушенном состоянии при скорости сдвига 0.01 мм/с экспериментальное значение пикового напряжения сдвига находилось в аналогичном диапазоне по сравнению с полученным в результате численного анализа; при скоростях сдвига 0,1, 1 и 100 мм/с разница пикового напряжения сдвига между экспериментальными и численными оценками составила 0,3, 0,2 и 0,3 кПа соответственно. Похоже, что на напряжение сдвига не сильно влияет низкая скорость сдвига (т.е. 0,01 мм/с) в используемом кольцевом аппарате сдвига. При этом остаточные напряжения сдвига различались на 0,4, 0,7, 1 и 2,3 кПа при скоростях сдвига 0.01, 0,1, 1 и 100 мм/с соответственно (а, б).
 21
21  1 кПа. Остаточные напряжения сдвига различались на 1,23, 0,9, 1,9 и 3 кПа при скоростях сдвига 0,01, 0,1, 1 и 100 мм/с соответственно (в, г). Эти результаты показывают, что напряжение сдвига увеличивается с увеличением скорости сдвига. Аналогичные результаты были получены Fukuoka et al. [31].
1 кПа. Остаточные напряжения сдвига различались на 1,23, 0,9, 1,9 и 3 кПа при скоростях сдвига 0,01, 0,1, 1 и 100 мм/с соответственно (в, г). Эти результаты показывают, что напряжение сдвига увеличивается с увеличением скорости сдвига. Аналогичные результаты были получены Fukuoka et al. [31].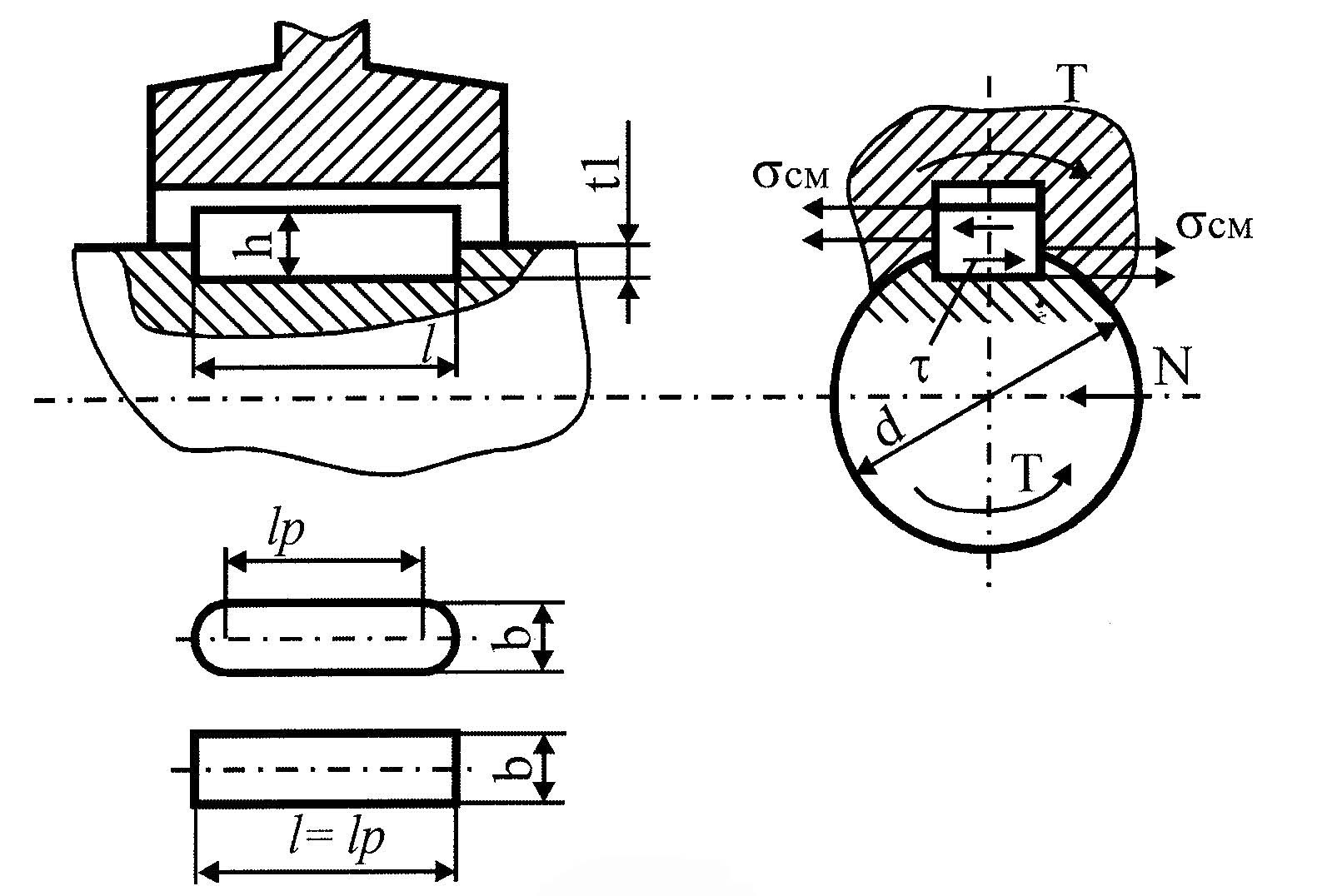 8, 0,1, 0,1, 0,7 и 0,1 кПа соответственно.
8, 0,1, 0,1, 0,7 и 0,1 кПа соответственно. Это может быть связано с тем, что в осушенном состоянии происходит более сильное взаимодействие между частицами, что приводит к более высокому сопротивлению сдвигу. В недренированном состоянии вода может играть важную роль в процессе дробления и разрушения гранулированного материала. Кажется, что смазывающий эффект мелких частиц может проявляться в недренированном состоянии. Как упоминалось ранее, после внезапного и резкого падения пикового напряжения сдвига характеристики сдвига после разрушения были исследованы с использованием остаточного напряжения сдвига.Эта фаза в основном характеризуется механизмом дробления частиц, который обсуждается в следующем разделе.
Это может быть связано с тем, что в осушенном состоянии происходит более сильное взаимодействие между частицами, что приводит к более высокому сопротивлению сдвигу. В недренированном состоянии вода может играть важную роль в процессе дробления и разрушения гранулированного материала. Кажется, что смазывающий эффект мелких частиц может проявляться в недренированном состоянии. Как упоминалось ранее, после внезапного и резкого падения пикового напряжения сдвига характеристики сдвига после разрушения были исследованы с использованием остаточного напряжения сдвига.Эта фаза в основном характеризуется механизмом дробления частиц, который обсуждается в следующем разделе. В методе дискретных элементов дробление гранулированного материала определяется как отрыв одной или нескольких частиц от комковатой частицы. Таким образом, для осуществления дробления частиц требуется один или несколько критериев. Комковатая частица может быть частично или полностью разрушена, когда удовлетворяются критерии дробления. Для этого была реализована определяемая пользователем функция с использованием языка FISH в PFC 2D .
В методе дискретных элементов дробление гранулированного материала определяется как отрыв одной или нескольких частиц от комковатой частицы. Таким образом, для осуществления дробления частиц требуется один или несколько критериев. Комковатая частица может быть частично или полностью разрушена, когда удовлетворяются критерии дробления. Для этого была реализована определяемая пользователем функция с использованием языка FISH в PFC 2D .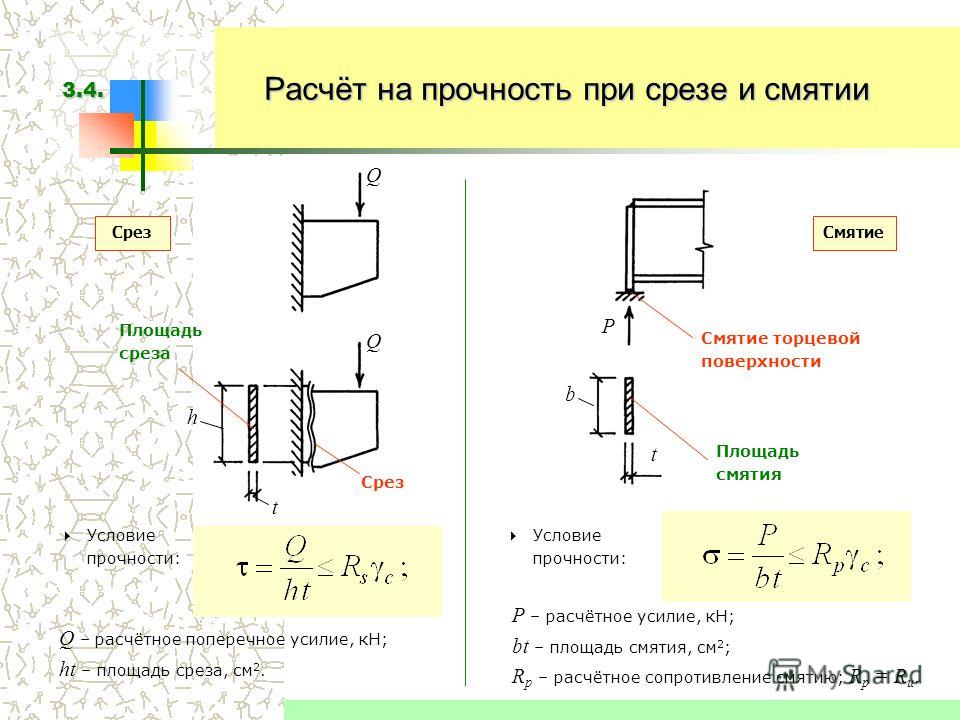
 Прогрессирующее развитие зоны сдвига связано со снижением касательного напряжения при оползнях. Это можно проиллюстрировать в кольцевой коробке сдвига (b). По сравнению с начальным состоянием сдвига зона сдвига во время сдвига становится все больше и больше. Сдвиг может привести к образованию более мелких частиц в зоне сдвига и снижению прочности на сдвиг (т.е., поведение при размягчении деформации) во время сдвига. Согласно результатам предыдущих исследований, крупные частицы могут концентрироваться в центре кольцевой коробки сдвига, мелкие частицы могут скапливаться в основном в нижней части кольцевой коробки сдвига из-за вертикального движения, возникающего при сдвиге [2,15,31]. Кроме того, для мелкозернистых отложений поверхность сдвига очень тонкая (например, менее 1 мм толщиной), а для крупнозернистых отложений поверхность сдвига увеличивается со временем сдвига [2,31,34].
Прогрессирующее развитие зоны сдвига связано со снижением касательного напряжения при оползнях. Это можно проиллюстрировать в кольцевой коробке сдвига (b). По сравнению с начальным состоянием сдвига зона сдвига во время сдвига становится все больше и больше. Сдвиг может привести к образованию более мелких частиц в зоне сдвига и снижению прочности на сдвиг (т.е., поведение при размягчении деформации) во время сдвига. Согласно результатам предыдущих исследований, крупные частицы могут концентрироваться в центре кольцевой коробки сдвига, мелкие частицы могут скапливаться в основном в нижней части кольцевой коробки сдвига из-за вертикального движения, возникающего при сдвиге [2,15,31]. Кроме того, для мелкозернистых отложений поверхность сдвига очень тонкая (например, менее 1 мм толщиной), а для крупнозернистых отложений поверхность сдвига увеличивается со временем сдвига [2,31,34].
 представляет изменение работы трения, рассчитанное по измеренному напряжению сдвига и временной реакции при постоянной скорости (т. е. 0,1 мм/с) для различных условий дренажа и нормального напряжения; D-NS25 и UD-NS25 обозначают осушенное и недренированное состояние при нормальном напряжении 25 кПа соответственно.Работа трения линейно возрастает со временем. Работа трения, полученная при пиковом напряжении сдвига, составила 303, 190, 220 и 155 кПа·с для D-NS100, UD-NS100, D-NS25 и UD-NS25 соответственно. Работа трения при остаточном напряжении сдвига составила 2579, 2418, 2280 и 1387 кПа·с для Д-НС100, УД-НС100, Д-НС25 и УД-НС25 соответственно. Интересно, что можно видеть, что энергия трения гораздо более чувствительна в условиях нормального напряжения, чем в условиях дренажа. По сравнению с другими, существует большая разница в энергии трения в конце испытаний (т.е., 300 с) при нормальном напряжении 25 кПа в недренированном состоянии. Общее время сдвига (т.е. 300 с) может быть одним из ограничений в этом исследовании.
представляет изменение работы трения, рассчитанное по измеренному напряжению сдвига и временной реакции при постоянной скорости (т. е. 0,1 мм/с) для различных условий дренажа и нормального напряжения; D-NS25 и UD-NS25 обозначают осушенное и недренированное состояние при нормальном напряжении 25 кПа соответственно.Работа трения линейно возрастает со временем. Работа трения, полученная при пиковом напряжении сдвига, составила 303, 190, 220 и 155 кПа·с для D-NS100, UD-NS100, D-NS25 и UD-NS25 соответственно. Работа трения при остаточном напряжении сдвига составила 2579, 2418, 2280 и 1387 кПа·с для Д-НС100, УД-НС100, Д-НС25 и УД-НС25 соответственно. Интересно, что можно видеть, что энергия трения гораздо более чувствительна в условиях нормального напряжения, чем в условиях дренажа. По сравнению с другими, существует большая разница в энергии трения в конце испытаний (т.е., 300 с) при нормальном напряжении 25 кПа в недренированном состоянии. Общее время сдвига (т.е. 300 с) может быть одним из ограничений в этом исследовании. Тем не менее, считается достаточным понять характеристики сдвига и разрушения оползневых материалов в отношении инициирования обрушения склона. Условие нормального напряжения 25 кПа указывает на относительно малую толщину грунта. Его толщина в поле составляет около 1 метра. Вода свободно перемещается по почвенной матрице в дренированных условиях; однако в недренированном состоянии вода, захваченная в зоне сдвига или вокруг нее из-за инфильтрации воды во время или после сильного ливня, может привести к внезапному снижению прочности на сдвиг и вызвать высокую подвижность оползневых материалов.
Тем не менее, считается достаточным понять характеристики сдвига и разрушения оползневых материалов в отношении инициирования обрушения склона. Условие нормального напряжения 25 кПа указывает на относительно малую толщину грунта. Его толщина в поле составляет около 1 метра. Вода свободно перемещается по почвенной матрице в дренированных условиях; однако в недренированном состоянии вода, захваченная в зоне сдвига или вокруг нее из-за инфильтрации воды во время или после сильного ливня, может привести к внезапному снижению прочности на сдвиг и вызвать высокую подвижность оползневых материалов. Результаты показали, что комковатые частицы были частично раздроблены при пиковом напряжении сдвига, т. е. одна частица была отделена от исходной комковатой частицы (а). Площадь сдвига с пиковым значением составляет примерно 5–7 % от общей (см. ). Большее дробление частиц происходило в состоянии остаточного напряжения сдвига (b) из-за значительной работы трения, то есть продолжалось постепенное дробление. Для данного смещения сдвига (или времени) количество частиц составляет примерно 10–16 при пиковом напряжении сдвига (а), но примерно 15–19 при остаточном напряжении сдвига (б), когда мы выбираем конкретную часть и внимательно смотрим в верхней и нижней частях кольцевой коробки сдвига.Раздавливание или истирание комковатой частицы, состоящей из нескольких частиц при максимальном напряжении сдвига, постепенно истирается по мере увеличения работы трения; дробление происходило в основном вблизи границы сдвига из-за не только напряжения сдвига, но и напряжения сжатия, а также диаметральных и центробежных сил, создаваемых в системе зернистой сборки сдвигаемого кольца.
Результаты показали, что комковатые частицы были частично раздроблены при пиковом напряжении сдвига, т. е. одна частица была отделена от исходной комковатой частицы (а). Площадь сдвига с пиковым значением составляет примерно 5–7 % от общей (см. ). Большее дробление частиц происходило в состоянии остаточного напряжения сдвига (b) из-за значительной работы трения, то есть продолжалось постепенное дробление. Для данного смещения сдвига (или времени) количество частиц составляет примерно 10–16 при пиковом напряжении сдвига (а), но примерно 15–19 при остаточном напряжении сдвига (б), когда мы выбираем конкретную часть и внимательно смотрим в верхней и нижней частях кольцевой коробки сдвига.Раздавливание или истирание комковатой частицы, состоящей из нескольких частиц при максимальном напряжении сдвига, постепенно истирается по мере увеличения работы трения; дробление происходило в основном вблизи границы сдвига из-за не только напряжения сдвига, но и напряжения сжатия, а также диаметральных и центробежных сил, создаваемых в системе зернистой сборки сдвигаемого кольца. Сжимающее напряжение возникает в основном из-за приложенного нормального напряжения, тогда как диаметральные и центробежные силы создаются между частицами комков за счет поступательных и вращательных скоростей в системе сборки гранул.Другие исследователи также обнаружили, что дробление частиц происходило в основном на поверхности сдвига [35].
Сжимающее напряжение возникает в основном из-за приложенного нормального напряжения, тогда как диаметральные и центробежные силы создаются между частицами комков за счет поступательных и вращательных скоростей в системе сборки гранул.Другие исследователи также обнаружили, что дробление частиц происходило в основном на поверхности сдвига [35]. В целом наблюдается очень хорошее совпадение экспериментальных и численных результатов. Как для дренированных, так и для недренированных условий напряжение сдвига быстро достигает пикового значения, а затем резко падает, после чего следует период колебаний перед стабилизацией (т. Это может быть связано с возникновением комковатой перестройки и дробления частиц при сдвиге.Кроме того, различия в пиковых и остаточных напряжениях сдвига намного больше в осушенном состоянии, чем в недренированном состоянии. Другими словами, можно ожидать, что при низком нормальном напряжении и недренированном состоянии почва может быть подвижна гораздо легче, чем в противоположном случае.
В целом наблюдается очень хорошее совпадение экспериментальных и численных результатов. Как для дренированных, так и для недренированных условий напряжение сдвига быстро достигает пикового значения, а затем резко падает, после чего следует период колебаний перед стабилизацией (т. Это может быть связано с возникновением комковатой перестройки и дробления частиц при сдвиге.Кроме того, различия в пиковых и остаточных напряжениях сдвига намного больше в осушенном состоянии, чем в недренированном состоянии. Другими словами, можно ожидать, что при низком нормальном напряжении и недренированном состоянии почва может быть подвижна гораздо легче, чем в противоположном случае. Поскольку работа трения монотонно возрастает, работа трения при остаточном напряжении сдвига больше, чем полученная при пиковом напряжении сдвига. Следовательно, комковатые частицы были частично раздроблены при максимальном напряжении сдвига, т. е. одна частица была отделена от исходной комковатой частицы, состоящей из пяти частиц; кроме того, произошло большее дробление (и было визуализировано) в состоянии остаточного напряжения сдвига из-за значительной работы трения. Это объясняет прогрессивный механизм дробления при моделировании испытания на кольцевой сдвиг с помощью ЦМР.Разрушение (или истирание) комковатой частицы, состоящей из четырех частиц, при максимальном сдвиговом напряжении прогрессировало по мере увеличения работы трения. Из-за ограниченного сдвига дробление частиц сгустков в основном происходило вблизи границы внешнего кольца. В будущих исследованиях характеристики сдвига и дробления в течение длительного периода времени сдвига должны быть исследованы с помощью трехмерного анализа.
Поскольку работа трения монотонно возрастает, работа трения при остаточном напряжении сдвига больше, чем полученная при пиковом напряжении сдвига. Следовательно, комковатые частицы были частично раздроблены при максимальном напряжении сдвига, т. е. одна частица была отделена от исходной комковатой частицы, состоящей из пяти частиц; кроме того, произошло большее дробление (и было визуализировано) в состоянии остаточного напряжения сдвига из-за значительной работы трения. Это объясняет прогрессивный механизм дробления при моделировании испытания на кольцевой сдвиг с помощью ЦМР.Разрушение (или истирание) комковатой частицы, состоящей из четырех частиц, при максимальном сдвиговом напряжении прогрессировало по мере увеличения работы трения. Из-за ограниченного сдвига дробление частиц сгустков в основном происходило вблизи границы внешнего кольца. В будущих исследованиях характеристики сдвига и дробления в течение длительного периода времени сдвига должны быть исследованы с помощью трехмерного анализа.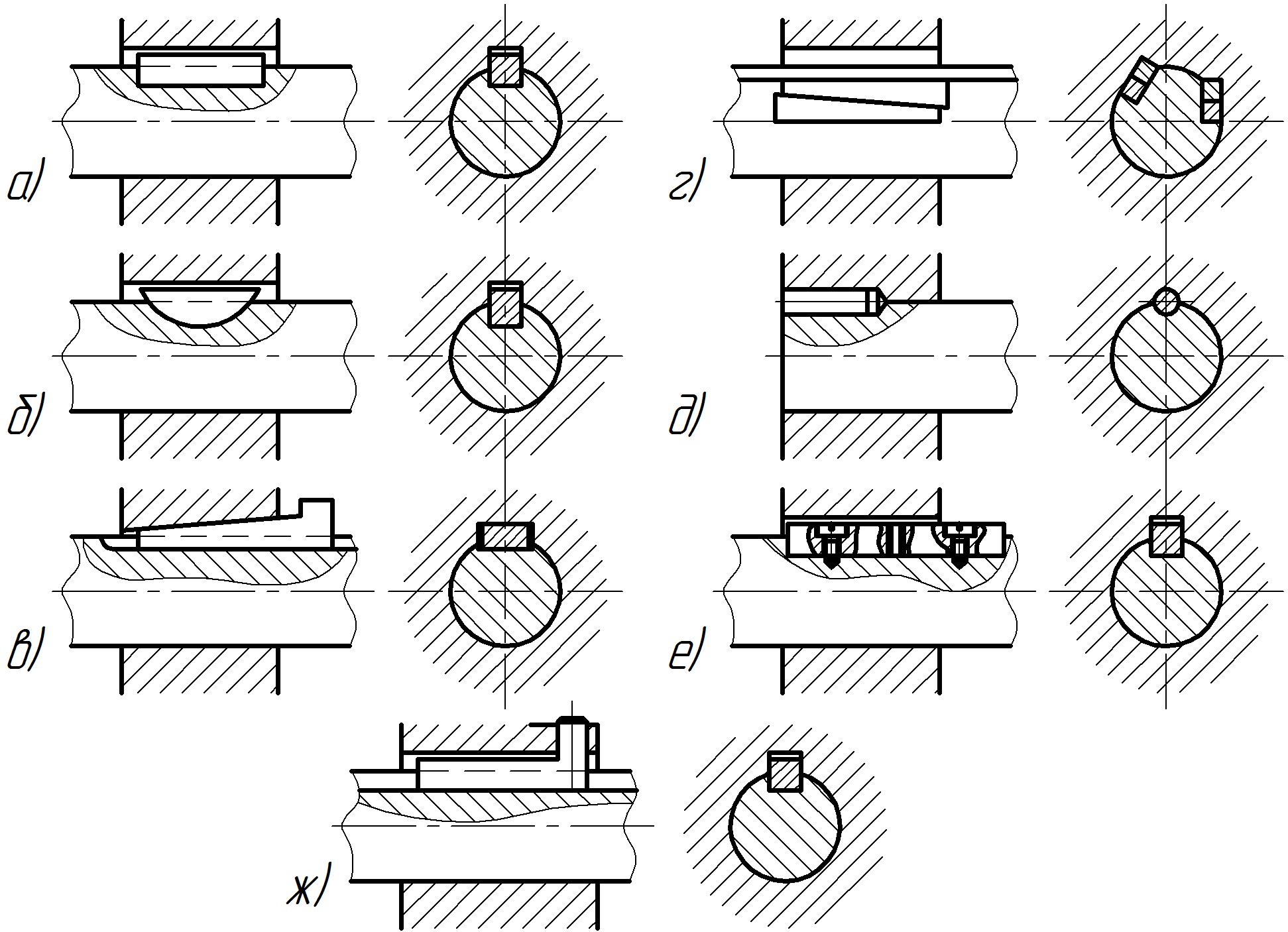
 На основе системы РМТ-150Б была проведена серия высоконапряженных прямых испытаний на крупнозернистом песке в условиях различной влажности и бетонных основаниях с различной шероховатостью и твердостью. Результаты показали, что кривая сдвигового напряжения-смещения и объемная кривая деформации-смещения границы раздела под высоким напряжением могут быть аппроксимированы гиперболической моделью; предельная прочность на сдвиг и начальная жесткость на сдвиг интерфейса увеличивались с нормальным напряжением, в то время как жесткость на сдвиг уменьшалась с сдвиговым смещением.Скорость дробления крупных частиц песка на поверхности раздела увеличивается с нормальным напряжением. После анализа диапазона факторов, влияющих на поведение интерфейса при сдвиге, было показано, что для предела прочности при сдвиге их последовательностью степени влияния являются нормальное напряжение, шероховатость интерфейса, влажность и твердость бетонного основания; для начальной прочности на сдвиг последовательностью было нормальное напряжение, содержание влаги, шероховатость поверхности и базальная твердость.
На основе системы РМТ-150Б была проведена серия высоконапряженных прямых испытаний на крупнозернистом песке в условиях различной влажности и бетонных основаниях с различной шероховатостью и твердостью. Результаты показали, что кривая сдвигового напряжения-смещения и объемная кривая деформации-смещения границы раздела под высоким напряжением могут быть аппроксимированы гиперболической моделью; предельная прочность на сдвиг и начальная жесткость на сдвиг интерфейса увеличивались с нормальным напряжением, в то время как жесткость на сдвиг уменьшалась с сдвиговым смещением.Скорость дробления крупных частиц песка на поверхности раздела увеличивается с нормальным напряжением. После анализа диапазона факторов, влияющих на поведение интерфейса при сдвиге, было показано, что для предела прочности при сдвиге их последовательностью степени влияния являются нормальное напряжение, шероховатость интерфейса, влажность и твердость бетонного основания; для начальной прочности на сдвиг последовательностью было нормальное напряжение, содержание влаги, шероховатость поверхности и базальная твердость.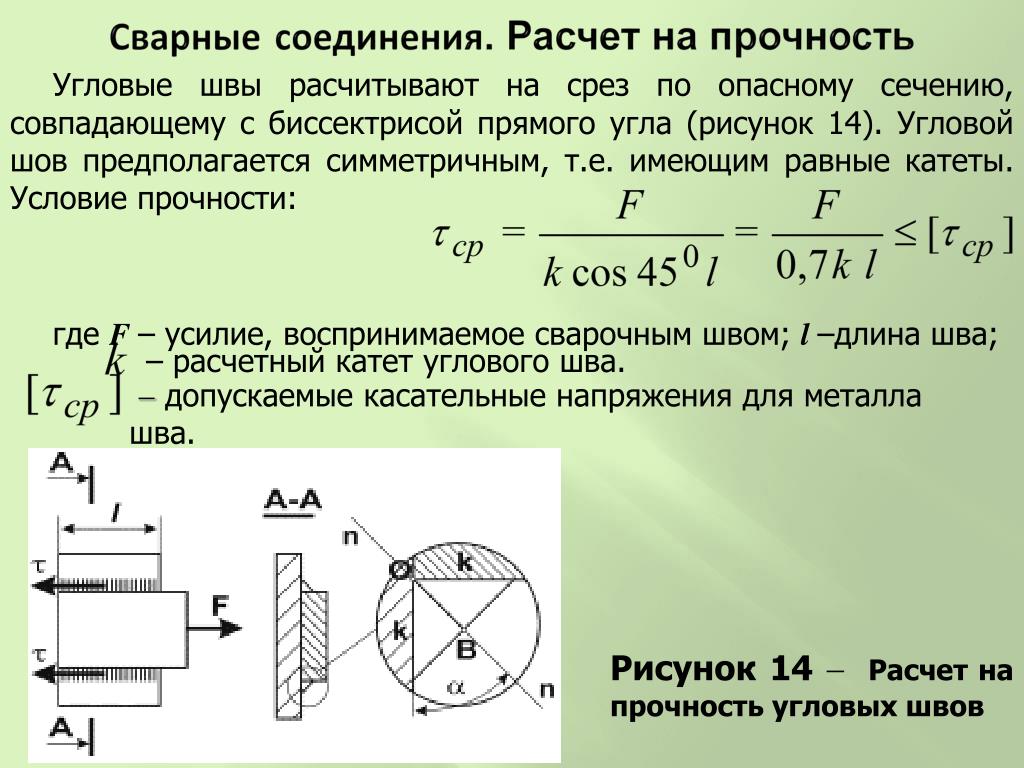 Что касается сухого песка, то возможность относительного дробления частиц была выше, чем у песка влажностью 8 %, а пик дробления приходился на влажность 16 %.
Что касается сухого песка, то возможность относительного дробления частиц была выше, чем у песка влажностью 8 %, а пик дробления приходился на влажность 16 %. Сьютс и др. [7], Таха и Фолл [8], Ван и др. [9], Сяо и Лю [10], а также Фархади и Лашкари [11] использовали прямые испытания на сдвиг для изучения механических свойств поверхности раздела грунт-конструкция.
Сьютс и др. [7], Таха и Фолл [8], Ван и др. [9], Сяо и Лю [10], а также Фархади и Лашкари [11] использовали прямые испытания на сдвиг для изучения механических свойств поверхности раздела грунт-конструкция.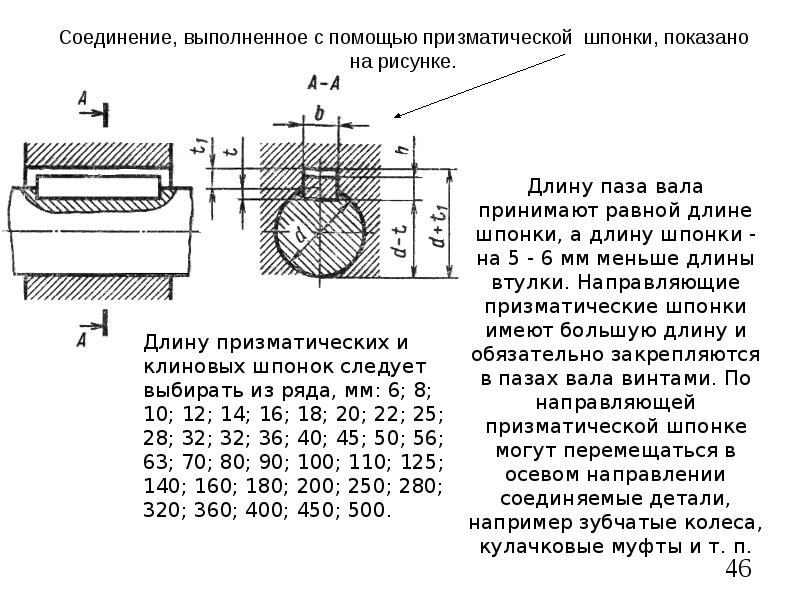 [13] проанализировали трение георешетки с точки зрения нескольких аспектов, таких как метод испытаний, метод нагрузки, краевой эффект и эффект размера испытательной коробки, толщина наполнителя, степень уплотнения и характеристики состояния зажима арматуры, влияющие на факторы. Чен и др.[14] использовали крупномасштабный аппарат прямого сдвига для проведения испытаний на прямой сдвиг на границе раздела образцов красной глины и бетона и количественно проанализировали влияние шероховатости на разрушение при сдвиге и деформацию интерфейса и обсудили механизм влияния шероховатости. Алие и др. [15] провели испытания на прямой сдвиг на границе между сферическим песком и геотекстилем. Тест показал, что форма частиц влияет как на пиковое значение, так и на угол остаточного трения. Джи и др.[16] проанализировали влияние температуры замерзания, шероховатости контактной поверхности и наличия крупных или мелких заполнителей на характеристики сдвига с помощью прямого испытания на сдвиг границы раздела мерзлый грунт-бетон.
[13] проанализировали трение георешетки с точки зрения нескольких аспектов, таких как метод испытаний, метод нагрузки, краевой эффект и эффект размера испытательной коробки, толщина наполнителя, степень уплотнения и характеристики состояния зажима арматуры, влияющие на факторы. Чен и др.[14] использовали крупномасштабный аппарат прямого сдвига для проведения испытаний на прямой сдвиг на границе раздела образцов красной глины и бетона и количественно проанализировали влияние шероховатости на разрушение при сдвиге и деформацию интерфейса и обсудили механизм влияния шероховатости. Алие и др. [15] провели испытания на прямой сдвиг на границе между сферическим песком и геотекстилем. Тест показал, что форма частиц влияет как на пиковое значение, так и на угол остаточного трения. Джи и др.[16] проанализировали влияние температуры замерзания, шероховатости контактной поверхности и наличия крупных или мелких заполнителей на характеристики сдвига с помощью прямого испытания на сдвиг границы раздела мерзлый грунт-бетон.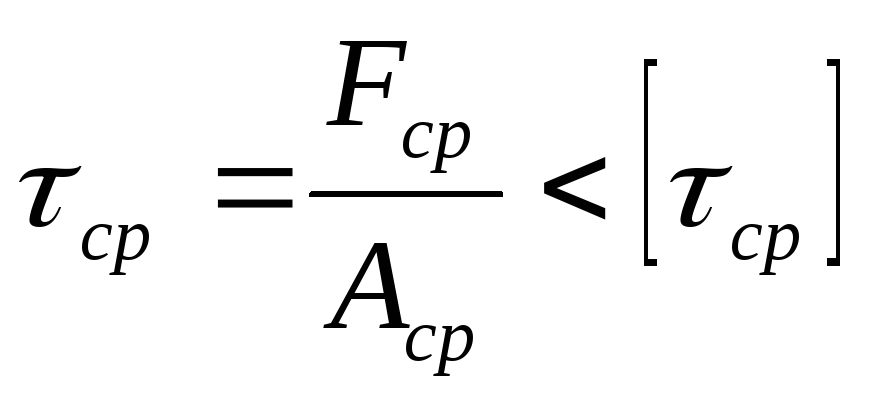 Ли и др. [17] проверили влияние температуры на механические свойства границы раздела ворс-красная глина с помощью испытаний на прямой сдвиг при контролируемой температуре в помещении и указали, что прочность на сдвиг границы раздела ворс-красная глина немного увеличивается с повышением температуры. Упомянутое выше исследование способствовало изучению взаимодействия между грунтом и конструкцией и углубило понимание механических характеристик взаимодействия сдвига.
Ли и др. [17] проверили влияние температуры на механические свойства границы раздела ворс-красная глина с помощью испытаний на прямой сдвиг при контролируемой температуре в помещении и указали, что прочность на сдвиг границы раздела ворс-красная глина немного увеличивается с повышением температуры. Упомянутое выше исследование способствовало изучению взаимодействия между грунтом и конструкцией и углубило понимание механических характеристик взаимодействия сдвига. Лю и др. [25, 26] использовали инструмент прямого сдвига высокого давления для изучения взаимосвязи между пиковой прочностью, остаточной прочностью и нормальным напряжением интерфейса различных структур. Лу [27] использовал прибор с высоким остаточным напряжением при нормальном напряжении для систематического изучения характеристик сдвига границы раздела грунт-конструкция с различной шероховатостью. В настоящее время изучение механики сдвига и деформационных характеристик поверхности раздела между грунтом и конструкцией при высоких напряжениях ограничено; эволюция состояния интерфейса, такая как разрушение частиц в процессе разрушения при сдвиге, редко участвовала [28–31].Между тем влияние относительного масштаба частиц грунта и морфологии поверхности структурной поверхности рассматривалось редко, а понимание механизма сдвиговой прочности границы раздела еще недостаточно.
Лю и др. [25, 26] использовали инструмент прямого сдвига высокого давления для изучения взаимосвязи между пиковой прочностью, остаточной прочностью и нормальным напряжением интерфейса различных структур. Лу [27] использовал прибор с высоким остаточным напряжением при нормальном напряжении для систематического изучения характеристик сдвига границы раздела грунт-конструкция с различной шероховатостью. В настоящее время изучение механики сдвига и деформационных характеристик поверхности раздела между грунтом и конструкцией при высоких напряжениях ограничено; эволюция состояния интерфейса, такая как разрушение частиц в процессе разрушения при сдвиге, редко участвовала [28–31].Между тем влияние относительного масштаба частиц грунта и морфологии поверхности структурной поверхности рассматривалось редко, а понимание механизма сдвиговой прочности границы раздела еще недостаточно. После анализа результатов испытаний с использованием метода интуитивного анализа ожидается, что влияние этих четырех факторов на предел прочности при сдвиге, начальную жесткость при сдвиге, остаточную объемную деформацию, начальную объемную деформацию и относительную скорость дробления частиц послужит ориентиром для изучения механика сдвига и дробление частиц интерфейса.
После анализа результатов испытаний с использованием метода интуитивного анализа ожидается, что влияние этих четырех факторов на предел прочности при сдвиге, начальную жесткость при сдвиге, остаточную объемную деформацию, начальную объемную деформацию и относительную скорость дробления частиц послужит ориентиром для изучения механика сдвига и дробление частиц интерфейса. Результат испытаний показывает, что максимальное нормальное напряжение может достигать более 10 МПа. Устройство также имеет функции автоматической загрузки, сбора данных в реальном времени и автоматического построения графиков.Гидравлическая система с сервоуправлением может применять вертикальные и горизонтальные нагрузки. Между нижней секционной коробкой и основным оборудованием установлен ролик, уменьшающий трение, для повышения точности регистрации напряжения сдвига. Модифицированная испытательная система показана на рисунке 1.
Результат испытаний показывает, что максимальное нормальное напряжение может достигать более 10 МПа. Устройство также имеет функции автоматической загрузки, сбора данных в реальном времени и автоматического построения графиков.Гидравлическая система с сервоуправлением может применять вертикальные и горизонтальные нагрузки. Между нижней секционной коробкой и основным оборудованием установлен ролик, уменьшающий трение, для повышения точности регистрации напряжения сдвига. Модифицированная испытательная система показана на рисунке 1. Ширина равна 0 мм, 2 мм, 3 мм и 4 мм, а угол основания равнобедренной трапециевидной призмы составляет 45°, как показано на рисунке 2. методом [32], многократно распределяя крупнозернистый песок по поверхности коньковой конструкции, высыпая песок в лоток после соскабливания и выравнивания и покрывая песок градуированным цилиндром на 100 мл 3 раза.Отношение среднего значения объема песка к площади поверхности конструкции определяется как шероховатость поверхности раздела. Измеренная шероховатость составляет 0, 0,133, 0,249 и 0,332.
Ширина равна 0 мм, 2 мм, 3 мм и 4 мм, а угол основания равнобедренной трапециевидной призмы составляет 45°, как показано на рисунке 2. методом [32], многократно распределяя крупнозернистый песок по поверхности коньковой конструкции, высыпая песок в лоток после соскабливания и выравнивания и покрывая песок градуированным цилиндром на 100 мл 3 раза.Отношение среднего значения объема песка к площади поверхности конструкции определяется как шероховатость поверхности раздела. Измеренная шероховатость составляет 0, 0,133, 0,249 и 0,332. Содержание влаги песка составляет 0%, 8%, 16% и 24% соответственно. Конкретная процедура подготовки выглядит следующим образом: взвесьте и поместите 1000 г высушенного крупнозернистого песка на лоток, а затем распылите воду 0 г, 80 г, 160 г и 240 г для приготовления образца песка.
Содержание влаги песка составляет 0%, 8%, 16% и 24% соответственно. Конкретная процедура подготовки выглядит следующим образом: взвесьте и поместите 1000 г высушенного крупнозернистого песка на лоток, а затем распылите воду 0 г, 80 г, 160 г и 240 г для приготовления образца песка. от 01 до 0,02.
от 01 до 0,02.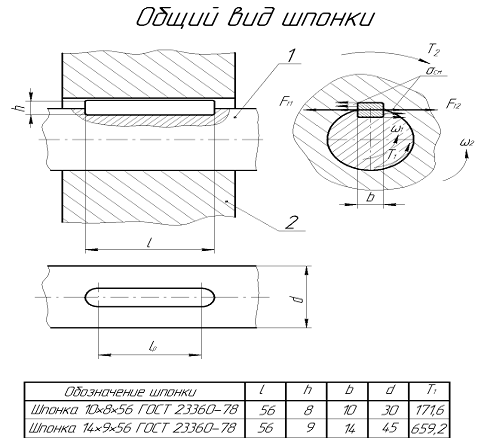 083 (B1)
083 (B1)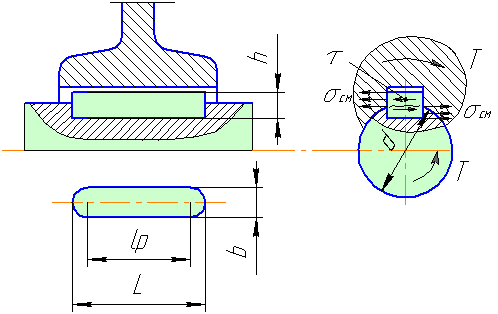
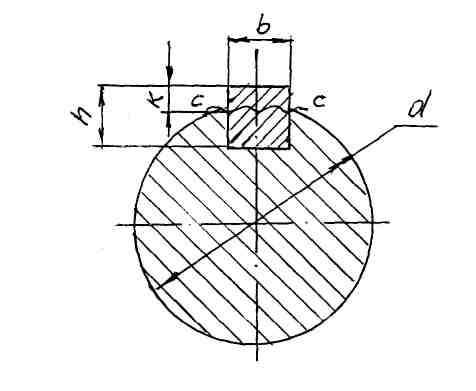 Когда нормальное напряжение было больше или равно 4 МПа, с увеличением смещения при сдвиге, плотности и прочности на сдвиг, а также уменьшением коэффициента пустотности количество разбитых частиц песка увеличивалось. В испытании на прямой сдвиг при высоком напряжении соотношение между напряжением сдвига и смещением не соответствовало форме гиперболической модели, и на начальную жесткость интерфейса при сдвиге влияли различные факторы, касающиеся интерфейса.
Когда нормальное напряжение было больше или равно 4 МПа, с увеличением смещения при сдвиге, плотности и прочности на сдвиг, а также уменьшением коэффициента пустотности количество разбитых частиц песка увеличивалось. В испытании на прямой сдвиг при высоком напряжении соотношение между напряжением сдвига и смещением не соответствовало форме гиперболической модели, и на начальную жесткость интерфейса при сдвиге влияли различные факторы, касающиеся интерфейса.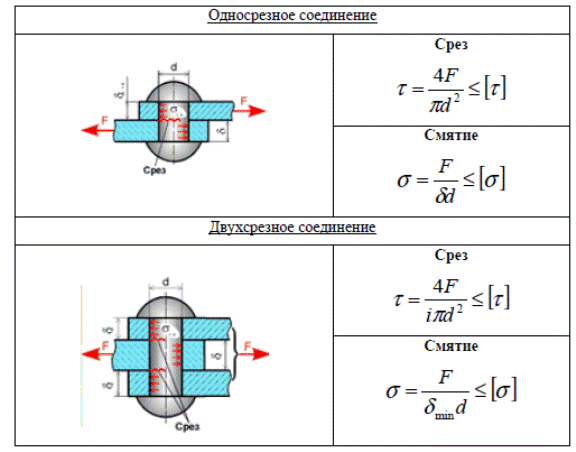 689
689 284
284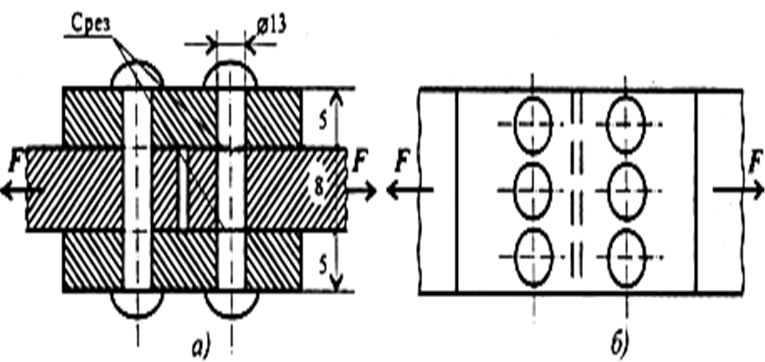 Конечная прочность на сдвиг и начальная жесткость сдвига интерфейса под высоким стрессом перечислена в таблице 5.
Конечная прочность на сдвиг и начальная жесткость сдвига интерфейса под высоким стрессом перечислена в таблице 5. 604
604 492
492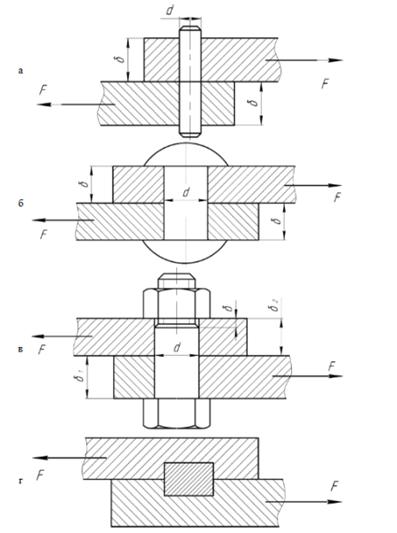 3. Механизм дробления частицы на границе раздела и определение толщины зоны сдвига
3. Механизм дробления частицы на границе раздела и определение толщины зоны сдвига Таким образом, когда прочность на сдвиг самой частицы была меньше, чем сила зажима, частицы будут разрушаться при сдвиге под действием противовращательной силы. Лю и Лу [38] указали, что напряжение сдвига является важным фактором, определяющим дробление частиц. Частица и интерфейс в основном существуют в виде точечного контакта. Чем выше нормальное напряжение, чем ближе зацеп между частицами и границей раздела, тем труднее частицам скользить и катиться, что приводит к увеличению разрушения частиц при горизонтальном сдвиге.
Таким образом, когда прочность на сдвиг самой частицы была меньше, чем сила зажима, частицы будут разрушаться при сдвиге под действием противовращательной силы. Лю и Лу [38] указали, что напряжение сдвига является важным фактором, определяющим дробление частиц. Частица и интерфейс в основном существуют в виде точечного контакта. Чем выше нормальное напряжение, чем ближе зацеп между частицами и границей раздела, тем труднее частицам скользить и катиться, что приводит к увеличению разрушения частиц при горизонтальном сдвиге. Ван и др. [41] проанализировали метод двумерных дискретных элементов и обнаружили, что максимальная толщина зоны сдвига на границе раздела составляет (8-10) d50. Наблюдая под микроскопом испытание на прямой сдвиг, Чжан [42] обнаружил, что толщина крупнозернистого грунта и зоны структурного сдвига составляет около (5-6) d50; шероховатость конструкционной панели и нормальное напряжение мало повлияли на толщину зоны сдвига. В данной работе, чтобы гарантировать качество данного исследования, толщина межфазной зоны сдвига была установлена как максимальное значение (10) d50.Средний размер частиц крупнозернистого песка, использованного в испытании на сдвиг на границе раздела сред, был равен 0,5 мм, а соответствующая толщина полосы сдвига на поверхности была установлена равной 4,30 мм при высоком напряжении. Чтобы обеспечить постоянство толщины отбора проб, были спроектированы верхний и нижний короба сдвига, которые могут быть встроены, как показано на рисунке 5. Нижняя часть нижнего ящика сдвига находится в контакте с поверхностью бетона, а его высота соответствует толщина выбранной полосы сдвига.
Ван и др. [41] проанализировали метод двумерных дискретных элементов и обнаружили, что максимальная толщина зоны сдвига на границе раздела составляет (8-10) d50. Наблюдая под микроскопом испытание на прямой сдвиг, Чжан [42] обнаружил, что толщина крупнозернистого грунта и зоны структурного сдвига составляет около (5-6) d50; шероховатость конструкционной панели и нормальное напряжение мало повлияли на толщину зоны сдвига. В данной работе, чтобы гарантировать качество данного исследования, толщина межфазной зоны сдвига была установлена как максимальное значение (10) d50.Средний размер частиц крупнозернистого песка, использованного в испытании на сдвиг на границе раздела сред, был равен 0,5 мм, а соответствующая толщина полосы сдвига на поверхности была установлена равной 4,30 мм при высоком напряжении. Чтобы обеспечить постоянство толщины отбора проб, были спроектированы верхний и нижний короба сдвига, которые могут быть встроены, как показано на рисунке 5. Нижняя часть нижнего ящика сдвига находится в контакте с поверхностью бетона, а его высота соответствует толщина выбранной полосы сдвига.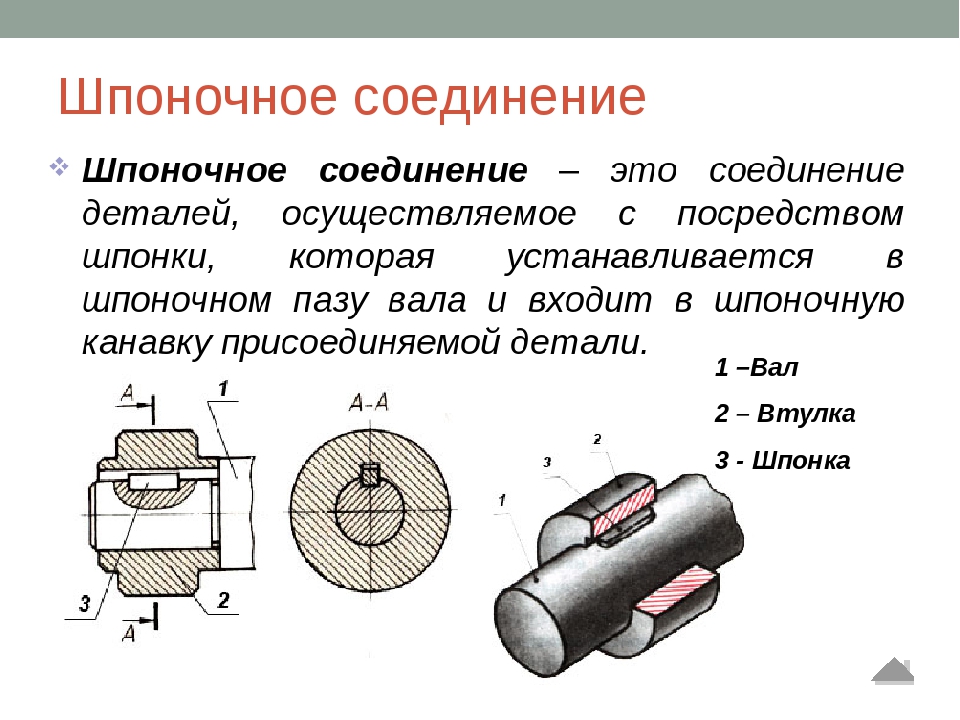 Верхнюю коробку сдвига можно полностью снять для выполнения сглаживания, отбора проб и просеивания.
Верхнюю коробку сдвига можно полностью снять для выполнения сглаживания, отбора проб и просеивания.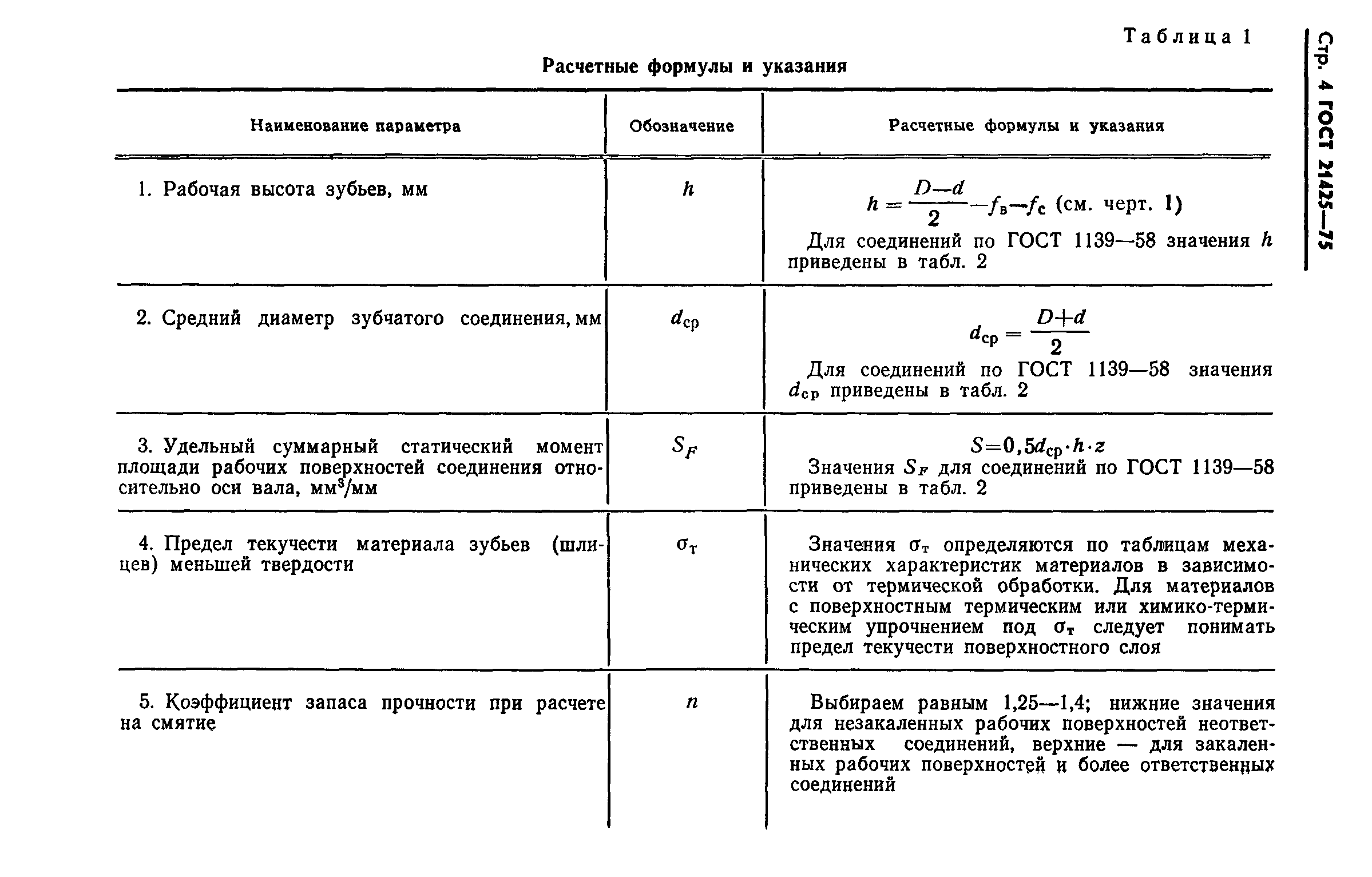 можно использовать в качестве показателя для оценки дробления частиц, и можно обсудить некоторые проблемы дробления частиц.
можно использовать в качестве показателя для оценки дробления частиц, и можно обсудить некоторые проблемы дробления частиц. По сравнению с влажностью, базальной твердостью и шероховатостью влияние нормального напряжения было более значительным.(2) Когда содержание влаги составляло 0%, относительное дробление частиц быстро увеличивалось при нормальном напряжении; при одном и том же нормальном напряжении относительная скорость дробления частиц сначала увеличивалась, а затем уменьшалась с увеличением влажности; наиболее сильное дробление частиц появлялось при скорости 16%. При дальнейшем увеличении содержания влаги относительное дробление частиц уменьшалось. (3) Влияние базовой твердости и шероховатости поверхности на дробление частиц было относительно дискретным.
По сравнению с влажностью, базальной твердостью и шероховатостью влияние нормального напряжения было более значительным.(2) Когда содержание влаги составляло 0%, относительное дробление частиц быстро увеличивалось при нормальном напряжении; при одном и том же нормальном напряжении относительная скорость дробления частиц сначала увеличивалась, а затем уменьшалась с увеличением влажности; наиболее сильное дробление частиц появлялось при скорости 16%. При дальнейшем увеличении содержания влаги относительное дробление частиц уменьшалось. (3) Влияние базовой твердости и шероховатости поверхности на дробление частиц было относительно дискретным.