Расчет однопролетной балки переменного сечения по норме Еврокод 3

В следующей статье описывается расчет однопролетной балки, подвергаемой изгибу и сжатию, которая выполняется в соответствии с EN 1993-1-1 в дополнительном модуле RF-STEEL EC3. Da der Träger als gevouteter Querschnitt ausgeführt ist und es sich damit nicht um ein gleichförmiges Bauteil handelt, ist der Nachweis entweder nach dem Allgemeinen Verfahren nach Abs. 6.3.4 EN 1993-1-1 zu führen oder mittels Theorie II. Ordnung. Оба варианта будут объяснены и сравнены, а для расчета по методу второго порядка доступен дополнительный формат расчета с использованием метода частичных внутренних сил (PIFM). Поэтому расчет делится на три этапа:

Конструктивная система и нагрузки

Сварной двутавр из стали марки С235 имеет следующие размеры в мм:
Высота = 500/300
Ширина = 200
Толщина стенки = 14
Толщина полки = 14
Толщина шва = 4

Pисунок 01 — Конструктивная система и нагрузки

Расчет по общему методу 6.

3.4 EN 1993-1-1

Расчет балки выполняется в модуле RF-/STEEL EC3 как расчет блока стержней. Поскольку блоки стержней по умолчанию рассчитываются в модуле RF-/STEEL EC3 по общему методу, дальнейшие настройки не требуются. In Maske «1.7 Knotenlager» und dem damit verbundenen Ausschnittsfenster können die Randbedingungen des Stabsatzes sehr gut kontrolliert werden. Кроме того, здесь можно проверить ориентацию местной системы координат. Местную систему координат можно активировать, щелкнув соответствующую кнопку под изображением частичного вида. Как видно из граничных условий узловых опор, в расчете по общему методу существуют степени свободы, которые характеризуют разрушение плоскости рамы. В данном примере узловые опоры определяются как боковые и торсионные заделки. Предустановленные опоры уже соответствуют данному типу опор, так что можно сразу начать расчет.

Pисунок 02 — Ввод узловых опор

Расчет по общей методике выполнен и дает результат 0,97. Критический коэффициент α_{cr, op} равен 1,647.

Pисунок 03 — таблица результатов

Тип отказа можно проверить в отдельном окне частичного просмотра, которое можно открыть, щелкнув по кнопке [Формы колебаний] справа от максимального расчетного соотношения.

Pисунок 04 — Собственная форма

Pисунок 05 — Графическое отображение результатов

Расчет по методу второго порядка с помощью модуля RF-/STEEL Warping Torsion

Чтобы сравнить результаты расчета по общему методу с расчетом по методу второго порядка, необходимо продублировать расчетный случай, нажав на кнопку «Файл» → «Копировать случай». Теперь новый расчетный случай можно скорректировать для расчета по методу второго порядка. Расчет по методу второго порядка с учетом депланации выполняется как расчет на эквивалентные напряжения и его можно выбрать в «Подробности» → «Кручение с депланацией».

Этот метод расчета доступен только для блоков стержней. Как и в первом расчетном случае, необходимо проверить и отрегулировать узловые опоры. Как видно в окне для ввода узловых опор, расширение модуля RF-/STEEL Warping Torsion учитывает не только четыре, а семь степеней свободы. В нашем примере важно обеспечить концы стержней в направлении X свободными опорами; в противном случае осевая сила не будет применена к компоненту.

Pисунок 06 — Ввод узловых опор

Для последующего расчета важно не только ввести узловые опоры, но и, в частности, задать несовершенство. Ее можно найти, например, в национальном приложении к норме EN 1993-1-1. В таблице NA.2 представлена соответствующая информация для данного примера: e

0/1 = 1/300 применяется для сварного двутавра с h/b> 2. Это значение необходимо удвоить, если коэффициент гибкости находится в диапазоне от 0,7 до 1,3. Коэффициент гибкости можно задать с помощью значения λ_{cr, op} в первом расчетном случае по общему методу. В нашем примере предварительно задано значение 1/300. Наконец, можно приступить к расчету.

Pисунок 07 — Определение несовершенства

Расчет выполнен, результат равен 0,90. Критическое значение потери устойчивости равно 1,651.

Pисунок 08 — таблица результатов

Pисунок 09 — Графическое отображение результатов

Расчет по методу второго порядка с применением модуля RF-/STEEL Warping Torsion и RF-/STEEL Plasticity

Для более эффективного расчета доступно расширение RF-/STEEL Plasticity дополнительного модуля RF-/STEEL EC3. Он позволяет анализировать внутренние силы по методу второго порядка из расчета кручения с депланацией с помощью метода частичных внутренних сил по Киндману для расчета устойчивости блока стержней или по симплекс-методу для общих сечений.

После копирования второго расчетного случая, можно активировать пластический расчет в «Подробности» → «Пластичность». При копировании второго расчетного случая уже были адаптированы правильные узловые опоры. Однако необходимо проверить и исправить несовершенство. В таблице NA.2 указано значение 1/200 для пластического расчета сварного двутавра с h/b> 2.

Pисунок 10 — Определение несовершенства

Теперь можно приступить к расчету.

Pисунок 11 — таблица результатов

Pисунок 12 — Графическое отображение результатов

Заключение

Для конических конструктивных элементов в модуле RF-/STEEL EC3 доступны два метода расчета. В дополнение к интегрированному общему методу по гл. 6.3.4 из EN 1993-1-1, можно выполнить расчет по методу второго порядка, включая учет коробления в расширении модуля RF-/STEEL Warping Torsion. Кроме того, расчет на кручение при депланации можно применить и к другим ситуациям сечений и нагрузок.

Для более эффективного расчета можно в дополнение к расчету на кручение с депланацией выполнить пластический расчет по методу частичных внутренних сил (PIFM) или по симплекс-методу в расширении модуля RF-/STEEL Plasticity.

Литература

[1]	DIN EN 1993-1-1: 2010-12 с NA: 2015-08

Расчет металлической балки на прогиб: учимся составлять формулы

Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Разновидности балок, применяемых в строительстве

Современная стройиндустрия при возведении сооружений промышленного и жилого назначения, практикует использование стержневых систем различного сечения, формы и длины, изготовленных из различных материалов.

Наиболее большее распространение получили стальные и деревянные изделия. В зависимости от используемого материала, определение значения прогиба имеет свои нюансы, связанные со структурой и однородностью материала.

Деревянные

Современное малоэтажное строительство индивидуальных домов и загородных коттеджей практикует широкое использование лаг, изготовленных из хвойных и твердых пород древесины.

В основном, деревянные изделия, работающие на изгиб, применяются для обустройства напольных и потолочных перекрытий. Именно эти элементы конструкции испытают наибольшее действие поперечных нагрузок, взывающих наибольший прогиб.

Стрела прогиба деревянной лаги зависит:

1. От материала (породы древесины), который использовался при изготовлении балки.
2. От геометрических характеристик и формы попечённого сечения расчетного объекта.
3. От совокупного действия различного вида нагрузок.

Критерий допустимости прогиба балки учитывает два фактора:

1. Соответствие реального прогиба предельно допустимым значениям.
2. Возможность эксплуатации конструкции при наличии расчетного прогиба.

Стальные

Имеют более сложное сечение, которое может быть составным, выполненным из нескольких видов металлического проката. При расчете металлоконструкций, помимо определения жесткости самого объекта его элементов, часто появляется необходимость определения прочностных характеристик соединений.

Обычно, соединение отдельных элементов стальной металлоконструкции проводится:

1. С использованием электросварки.
2. Путем применения резьбовых (шпилечных, болтовых и винтовых) соединений.
3. Соединением заклепками.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

• в опорах прогибы равны нулю;
• в жесткой заделке прогиб и угол поворота сечения равен нулю.

Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.

Построение эпюр Q и М

Подробный пример построения эпюр поперечных сил Q и изгибающих моментов M для балки

Видео про расчет значений Q и M для построения эпюр:

В пролете балки 0 ≤ z2 ≤ l

QII= — RB+ qz2= -52+30∙z2 QII(z=0)= -52 кН QII(z=l)= -52+30∙4=68 кН

MII=RB∙z2-qz22/2=52z2-30∙z22/2 MII (z=0)= 0 MII (z=l)= -32 кНм

На консоли l ≤ z1≤ (l+a)

QI= — RB+ ql — RA=-52+30∙4-108=-40 кН

MI=RB z1-ql(z1-l/2)+RA(z1-l)=52z1-30∙4(z1-4/2)+108(z1-4) MI (z=l)= -32 кНм MI (z=l+a)= 0

По этим данным построены эпюры Q и М.

Короткое видео о том, как надо строить эпюры:

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:

Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

\[ { V }_{ A }=0\quad при\quad x=0 \]

\[ { V }_{ B }=0\quad при\quad x=8м \]

Записываем уравнение метода начальных параметров для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=… \]

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]

Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки.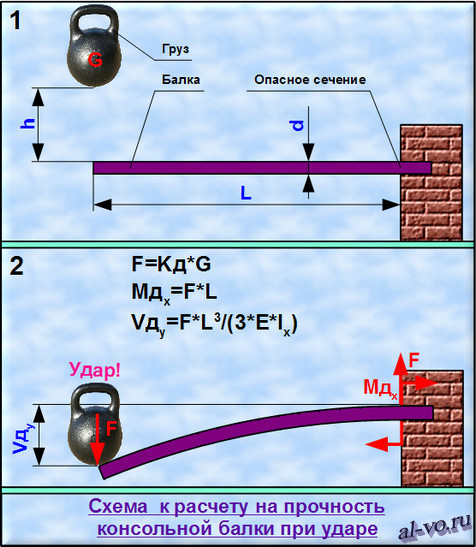 { 3 } }{ E{ I }_{ z } } \]

Упрощенный расчет (по готовым формулам)

Расчет производится по формулам расчетной схемы 2.1 для шарнирной балки.

1.1 Определение опорных реакций:

А = B = ql/2 = 3.2·4.6/2 = 7.36 кН (671.1)

Соответственно максимальная поперечная сила, действующая в поперечных сечениях балки будет «Q» = 7.36 кН. Действовать эта поперечная сила будет на опорах балки

1.2. Определение максимального изгибающего момента:

Максимальный изгибающий момент будет действовать посредине пролета балки и он составит:

М = ql2/8 = 3.2·4.62/8 = 8,464 кНм (671.2)

1.3. Подбор сечения балки:

3.1 Для деревянной балки с расчетным сопротивлением R = 13 МПа (13000 кПа) требуемый момент сопротивления составит:

Wтр = M/R = 8.464/13000 = 0.000651077 м3 (651.077 см3) (671.3.1)

Как правило поперечные сечения деревянных балок имеют прямоугольную форму. Момент сопротивления прямоугольного сечения определяется по следующей формуле:

W = bh3/6 (671. 3.2)

Дальше возможны различные варианты, например при высоте сечения балки h = 20 см требуемая ширина сечения составит не менее:

b = 6W/h3 = 6·651.77/202 = 9.77 см (671.3.3)

По сортаменту таким требованиям удовлетворяет балка с сечением 20х10 см.

Если поперечное сечение деревянной балки имеет форму, отличную от прямоугольной или квадратной, то для определения момента сопротивления можно воспользоваться одной из следующих формул, а при особо сложной форме сечения сначала определить момент инерции, а потом уже момент сопротивления.

3.2 Для стальной балки с расчетным сопротивлением R = 245 Мпа (245000) кПа) требуемый момент сопротивления составляет:

Wтр = M/R = 8.464/245000 = 3.45·10-5 м3 (34.5 см3) (658.3.7)

Далее требуемое сечение подбирается по одному из сортаментов.

Ну а подбор сечения ж/б балки — это отдельная большая тема.

1.4. Проверка по касательным напряжениям (для деревянной балки):

Расчетное сопротивление скалыванию вдоль волокон (для древесины второго сорта) Rск = 1. 6 МПа.

Для прямоугольного сечения максимальные касательные напряжения определяются по следующей формуле:

т = 1.5″Q»/bh = 1.5·7.36/(0.1·0.2) = 552 кПа (0.552 МПа) < 1.6 МПа (671.4)

Требование по касательным напряжениям соблюдено.

Для сечений другой формы значение касательных напряжений определяется по формуле Журавского.

Стандартные стальные профили в дополнительной проверке по касательным напряжениям как правило не нуждаются.

1.5. Определение прогиба:

Для деревянной балки сечением 20х10 см момент инерции составит:

I = Wh/2 = 666.66·20/2 = 6666.6 см4 (0.00006666 м4) (671.5.1)

Модуль упругости древесины составляет Е = 1·104 МПа (107 кПа)

f = 5Ql4/(384EI) = 0.02798 м (2.798 см) (671.5.2)

В данном случае прогиб составляет 1/164 от длины пролета балки.

Вот собственно и весь упрощенный расчет.

Калькулятор модуля упругости

| Elastic and Plastic

Этот инструмент вычисляет модуль сопротивления сечения , одно из наиболее важных геометрических свойств при расчете балок, подвергаемых изгибу. Кроме того, он вычисляет нейтральную ось и момент инерции площади наиболее распространенных структурных профилей (если вам нужен только момент инерции, проверьте наш калькулятор момента инерции)

Формулы для модуля сечения прямоугольника или круга относительно легко вычислить. Тем не менее, при работе с сложной геометрии, такой как тройник, швеллер или двутавровая балка , калькулятор может сэкономить время и помочь нам избежать ошибок.

В следующих разделах мы обсудим два типа модуля сечения, как рассчитать модуль сечения по моменту инерции, а также представим формулы модуля сечения прямоугольника и многих других распространенных форм.

Как рассчитать модуль сопротивления по моменту инерции

Модуль сопротивления используется инженерами для быстрого прогнозирования максимального напряжения, которое изгибающий момент вызовет на балку. Уравнение для максимального абсолютного значения напряжения в балке, подвергнутой изгибу:

σm=McI\sigma_m = \frac{Mc}{I}σm​=IMc​

, где:

• σm\sigma_mσm​ — максимальное абсолютное значение напряжения в конкретном сечении балки;
• МММ — Изгибающий момент, которому подвергается балка в этом сечении;
• ccc — наибольшее расстояние от нейтральной оси до поверхности элемента; и
• III — Второй момент площади (также известный как момент инерции площади) относительно нейтральной оси сечения (также рассчитывается этим инструментом).

Например, в круге наибольшее расстояние равно радиусу, а в прямоугольнике оно равно половине высоты.

Поскольку отношение I/cI/cI/c зависит только от геометрических характеристик, из него можно определить новое геометрическое свойство, называемое модулем сечения, обозначаемое буквой SSS:

S=IcS = \frac{I }{c}S=cI​

Как и второй момент площади, это новое геометрическое свойство доступно во многих таблицах и калькуляторах, но если вы хотите знать, как рассчитать модуль сечения по моменту инерции, просто разделите III по ccc, и вы его получите.

Наконец, мы можем связать модуль сечения с напряжением и моментом:

σm=MS\sigma_m = \frac{M}{S}σm​=SM​

🙋 Вам знакомо это соотношение? Это соотношение эквивалентно уравнению осевого напряжения: σ=FA\sigma = \frac{F}{A}σ=AF​. Изгибающий момент аналогичен осевой силе, а модуль упругости аналогичен площади поперечного сечения. Вы можете использовать наш калькулятор напряжения для расчета осевого напряжения.

Учитывайте эти соображения при расчете момента сопротивления и максимальных напряжений:

• Мы получаем изгибающий момент посредством статического или структурного анализа балки.
• Чтобы получить модуль сечения , мы можем использовать таблицы для предопределенных структурных элементов, но этот калькулятор является лучшим вариантом, если вы имеете дело с нестандартной геометрией.
• Если мы рассматриваем балку с однородным сечением (как обычно), место максимального напряжения будет в точке максимального изгибающего момента. Если это не так, σm\sigma_mσm может находиться в другом месте.
• Предыдущие формулы применимы к материалам, которые демонстрируют упругие свойства и подчиняются закону Гука. Когда есть пластическая деформация вместо упругой деформации, нам нужно использовать модуль пластического сечения.

Модуль пластического сечения: сверх модуля упругого сечения

Предыдущие уравнения не применяются, когда мы подвергаем материал балки напряжениям , превышающим предел текучести , поскольку они предполагают, что напряжение и деформация связаны линейно. В этом случае мы должны использовать модуль пластического сечения. Подобно модулю упругого сечения НДС, его пластический аналог обеспечивает связь между напряжением и моментом:

Mp=ZσYM_p = Z\sigma_YMp​=ZσY​

, где:

• MpM_pMp​ — пластический момент сечения;
• ZZZ — Модуль пластического сечения; и
• σY\sigma_YσY​ — Предел текучести материала стержня.

Пластический момент относится к моменту, необходимому для того, чтобы вызвать пластическую деформацию по всей поперечной площади сечения элемента.

Полезность последнего уравнения заключается в том, что мы можем предсказать изгибающий момент, который вызовет пластическую деформацию, просто зная предел текучести и модуль пластического сечения .

Следующий рисунок лучше описывает то, что мы имеем в виду, когда говорим о пластических моментах:

Графическое изображение распределения напряжения изгиба при пластической деформации. Мы предполагаем идеальную модель пластичности; следовательно, фактическое распределение напряжений не такое однородное.

Чтобы произошла пластическая деформация, мы должны вызвать некоторое напряжение , равное пределу текучести материала . Как вы можете заметить, переход от упругости к пластичности не является равномерным по всему элементу, так как некоторые области достигают предела текучести раньше других.

Как только все сечения достигают предела текучести, во всем этом сечении происходит пластическая деформация. Изгибающий момент, необходимый для достижения этого, называется пластическим моментом .

Формулы модуля сечения для прямоугольного сечения и других форм

В следующей таблице мы приводим формулы модуля сечения для прямоугольного сечения и многих других профилей ( прокрутите таблицу вбок, чтобы увидеть все уравнения ):

94)Ix​=Iy​=4π​(R4−Ri4​)
Sx=Sy=IxycS_x = S_y =\frac{I_x}{y_c}Sx​=Sy​=yc​Ix​​

🔎 Вас интересует расчет прогибов вместо напряжений? У нас есть калькулятор отклонения луча.

Каковы единицы второго момента площади?

Момент секунд единиц площади равен мм⁴ или м⁴ в Международной системе единиц и in⁴ в обычных единицах США. С другой стороны, единицы модуля упругого сечения равны мм³ , м³ и дюймов³ .

FAQ

Как рассчитать момент сопротивления сваи?

To calculate the section modulus of a pipe pile of thickness t and radius R , use the section modulus formula for a very thin annulus:

S = π R ² t или выполните следующие действия:

1. Измерьте радиус R и толщину t трубной сваи.
2. Умножьте число π на квадрат радиуса.
3. Умножьте последний результат на толщину.
4. Вот оно! Вы также можете использовать наш калькулятор модуля сечения и сделать это быстрее.

Если труба не очень тонкая, ее можно рассчитать с помощью нашего калькулятора модуля упругости .

Каковы единицы измерения модуля упругости сечения?

Единицы модуля упругости сечения равны мм³ или м³ в Международной системе единиц и дюймов³ в общепринятых единицах США. Любопытно, что это одни и те же единицы объема.

Каковы размеры балки W6 x 12?

Размеры W6 x 12 :

• Площадь: 3,55 дюйма²;
• Отделение: 6,03 дюйма;
• Ширина фланца: 4,00 дюйма;
• Толщина фланца: 0,280 дюйма; и
• Толщина стенки: 0,230 дюйма

Кроме того, его второй момент площади относительно горизонтальной центральной оси составляет 22,1 дюйма⁴, а модуль упругого сечения относительно той же оси составляет 7,31 дюйма³.

Какова формула модуля сечения для прямоугольного сечения?

Формула модуля упругости сечения прямоугольника: S = bd ²/6 , где:

• S — модуль сечения;
• b — высота прямоугольника; и
• d — Основание или ширина прямоугольника.

Учтите, что модуль этого сечения относится к горизонтальной центральной оси.

Мы можем вывести формулу модуля сечения для прямоугольного сечения, разделив его второй момент площади ( bh ³/12) на максимальное расстояние от нейтральной оси ( h /2 ):

S = (bh ³/12)/( h /2) = bh ²/6

Какова формула модуля сечения для квадратного сечения?

Формула модуля упругости сечения квадрата: S = a ³/6 , где:

• S — модуль сечения; и
• a — длина любой из сторон квадрата;

Мы можем вывести формулу модуля сечения для квадратного сечения, разделив его второй момент площади ( a ⁴/12 ) на максимальное расстояние от нейтральной оси ( a /2 ):

S = ( a ⁴/12)/( a 293 = 396 a ³/6

Как рассчитать модуль упругости двутаврового сечения?

Для вычисления модуля пластиковой секции IS-сечения , используйте формулы:

• Zₓ = 0,25 D ² T ᵥᵥ + BT (D + T) 4444449 444449 44444449 4449 4 46444444449 4 4644444444449 444449 4444449 4 40004444444444477 449 4449 444449 4 4064449 4 4 . 0022
• Zᵧ = 0,5 b ² t + 0,25 dtᵥᵥ ²

, где:

• Zₓ — Модуль пластического сечения относительно горизонтальной пластической нейтральной оси;
• Zᵧ — Модуль пластического сечения относительно вертикальной пластиковой нейтральной оси;
• d — длина стенки;
• t ᵥᵥ — Толщина стенки; 93.

  Существует два типа модулей сечения: модуль упругого сечения и модуль пластического сечения. Модуль упругости сечения применяется к конструкциям, которые находятся в пределах предела упругости материала, что является наиболее распространенным случаем. Часто «модуль упругости сечения» называют просто «модуль сечения».

  Модуль сопротивления сечения используется в проектировании конструкций для расчета изгибающего момента, который приводит к деформации балки, по следующему уравнению:

  где

  • S = момент сопротивления
  • σ _y = предел текучести материала

  Балки при изгибе испытывают напряжения как растяжения, так и сжатия.

  Калькуляторы модуля упругости

  Используйте приведенные ниже калькуляторы для расчета модулей упругости сечения обычных форм, таких как прямоугольники, двутавровые балки, круги, трубы, полые прямоугольники и c-образные каналы, которые подвергаются изгибу. Постоянные единицы необходимы для каждого калькулятора, чтобы получить правильные результаты.

  Калькулятор модуля сечения прямоугольника

  Уравнение для расчета модуля упругости сечения прямоугольника:

  где

  • b = ширина сечения
  • h = высота секции
  Калькулятор модуля упругости двутавровой балки

  Модуль упругости двутавровой балки рассчитывается по следующей формуле:

  где

  B = ширина полки0022
  • H = высота двутавровой балки
  • b = ширина полки минус ширина стенки
  • h = высота стенки
  Секция модуля раздела калькулятора кругового калькулятора

  Приведенное ниже уравнение используется для расчета модуля эластичной секции круга:

  , где

  d = диаметр круга

  a Hollow Circle Calculator

  Формула для расчета модуля упругости сечения трубы приведена ниже:

  где

  • d1 = внутренний диаметр = 2 x внутренний радиус
  • d2 = внешний диаметр = 2 x внешний радиус
  Калькулятор модуля сечения полого прямоугольника

  Модуль упругого сечения полого прямоугольника можно определить по следующей формуле:

• H = внешняя высота
• b = внутренняя (полая) ширина
• h = внутренняя (полая) высота

Калькулятор модуля упругости С-образного канала

Модуль упругого сечения С-образного канала рассчитывается по следующей формуле:

, где

• B2 = ширина полки
• H = общая высота
• b = ширина полки минус толщина стенки
• h = высота стенки

Какова формула модуля сечения?

Общая формула для модуля упругости поперечного сечения:

где

I = момент инерции площади (или второй момент площади)

y = расстояние от нейтральной оси до внешнего края балка

Каков требуемый модуль сопротивления сечения?

Требуемый модуль упругости можно рассчитать, если известны изгибающий момент и предел текучести материала. Рассмотрим следующий пример:

Балка из стали A36 должна быть подвергнута нагрузке в 120 000 фунтов силы на дюйм. Рассчитайте требуемый модуль сопротивления с коэффициентом запаса 2.

Преобразуйте уравнение из начала этого поста в следующий вид:

Допустимое напряжение в стали

A36 равно пределу текучести 36 000 фунтов на квадратный дюйм. Таким образом, требуемый модуль сопротивления сечения для достижения коэффициента запаса прочности 2 при изгибе рассчитывается, как показано ниже:

Для этого примера задачи требуемый модуль сопротивления составляет 6,67 дюйма3.

Как найти момент сопротивления неправильной формы?

Даже если форма не имеет предопределенного уравнения модуля сечения, все равно можно рассчитать модуль ее сечения.

Напомним, что модуль сопротивления равен I/y, где I — момент инерции площади. Определение момента инерции:

, где

дА = площадь элемента площади поперечного сечения неправильной формы

l = перпендикулярное расстояние от элемента до нейтральной оси, проходящей через центр тяжести

Таким образом, модуль сечения неправильной формы может быть определен как высокий уровень точности для неправильной формы. По этой причине в таких случаях обычно используют специализированное программное обеспечение для расчета модуля сечения.

В чем разница между модулем упругости и модулем упругости?

Когда используется термин модуль упругости, он обычно относится к модулю упругости. Это наиболее распространенное использование, поскольку оно имеет дело с материалами, которые находятся в пределах своего предела упругости или имеют напряжения меньше, чем предел текучести.

Модуль пластического сечения, однако, используется, когда материалу позволяют текучесть и пластическая деформация. Очень редко секции допускают текучесть, поэтому модуль пластического сечения используется редко.

В чем разница между моментом инерции и модулем сечения?

Термин «момент инерции» используется в двух случаях:

• Момент инерции площади: геометрическое свойство поперечного сечения (также известное как второй момент площади)
• Момент инерции массы или полярный момент инерции: сопротивление массы изменению скорости вращения

Модуль упругости и момент инерции площади тесно связаны между собой, поскольку оба они являются свойствами площади поперечного сечения балки.

Момент инерции площади можно использовать для расчета напряжения в балке из-за приложенного изгибающего момента на любом расстоянии от нейтральной оси с помощью следующего уравнения:

где σ — напряжение в балке, y — расстояние от нейтральной оси, проходящей через центр тяжести, а I — момент инерции площади.

Поскольку напряжение максимально на самом дальнем расстоянии от нейтральной оси, модуль сечения объединяет момент инерции площади и максимальное расстояние от нейтральной оси в один член:

Таким образом, уравнение для максимального напряжения изгиба принимает вид :

Модуль сечения и 92.

Как увеличить модуль сопротивления?

Модуль упругости можно увеличить вместе с площадью поперечного сечения, хотя некоторые методы более эффективны, чем другие. Возьмем, к примеру, прямоугольное поперечное сечение, модуль сечения которого определяется следующим уравнением:

Удвоение ширины прямоугольника b увеличит модуль сечения в 2 раза.