симметричная задача на примере балки с двумя опорами

Расчет реакций относится к разделу физики с названием «Статика», которая рассматривает структуру и системы, находящиеся в покое.

Силой реакции опоры называется усилие противодействия опоры действующему на нее объекту, при этом она равна по модулю и противоположна по направлению усилию, с которым объект действует на опору, согласно третьему закону Ньютона.

Система между некоторой структурой и опорой, которая препятствует линейному или угловому перемещению этой структуры, называется системой опоры. Существует несколько типов опор:

• Шарнир (валик) — опора первого порядка, ограничивающая смещение в пространстве в одном измерении и обладающее реакцией опоры перпендикулярной основанию.
• Плоская опора — опора второго порядка, которая ограничивает перемещение в пространстве в двух измерениях (горизонтальном и вертикальном) и разрешает только движение вращения структуры.

Расчет равновесных систем связан с вычислением результирующего динамического момента. В ньютоновской (классической) механике момент силы определяется как векторное произведение усилия, действующего на опору, на вектор, образованный между точкой опоры и точкой приложения этого усилия. Момент силы также называют динамическим моментом или просто моментом.

Далее в статье приводится пример расчета реакции для наиболее распространенной задачи: балки с двумя опорами.

Содержание:

• Решение задачи о реакции опоры балки
  • Первый способ: через моменты
  • Второй способ: через силы
• Видео

Решение задачи о реакции опоры балки

Как было сказано выше, балка с двумя опорами является типичной и наиболее простой задачей статики. Задача состоит в расчете реакций в точках А и В ввиду действующих на балку усилий.

Знание этих величин необходимо для правильного понимания диаграмм моментов и диаграмм сил данной системы, и является важной частью статики в школьных и университетских курсах.

Существует компьютерная программа SkyCiv, которая предоставляет мощный инструмент по расчету таких реакций для различных равновесных систем.

Возвращаясь к поставленной выше задаче, напомним, что основным ее условием является статическое состояние, то есть отсутствие каких-либо линейных перемещений и вращений объектов. В простой физике последний факт означает, что сумма векторов всех усилий равна нулю (то есть сумма усилий, направленных вверх, равна таковым, направленным вниз). Вторым условием равновесия системы является равенство нулю динамических моментов, приложенных относительно определенной точки опоры.

Чтобы определить реакции подпорок балки, следуйте нижеизложенным двум способам решения задачи:

• используя равенство нулю суммы динамических моментов;
• используя равенство нулю суммы действующих усилий.

Первый способ: через моменты

Для начала нужно положить, что сумма всех моментов относительно точки реакции равна нулю, то есть ΣMi = 0, где Мi — момент усилия. Расчет таких моментов для нашей задачи очень прост, и состоит в перемножении действующих усилий на расстояния от точки их приложения до точки реакции.

Будем считать, что наша балка имеет длину 4 метра и расположена на двух подпорках А и В. Посредине балки вертикально вниз действует усилие в 20 кН, и нужно рассчитать реакции каждой подпорки, то есть Ay и By . Описанная задача представлена на рисунке.

Например, рассчитаем сумму всех динамических моментов относительно точки реакции В, учитывая ее равенство нулю в равновесии. Выбор точки В, относительно которой будет проводиться расчет, является произвольным, точно так же можно выбрать точку А. Таким образом, просуммируем все динамические моменты относительно точки В, полагая эту сумму равной нулю:

ΣMв = 0 = 20*2 — A y * 4 ==> A y = 10 кН.

Отметим, что в формуле выше мы выбрали положительное направление для моментов, действующих против часовой стрелки, и отрицательное направление для моментов, действующих по часовой стрелке. Такой выбор знаков моментом является наиболее общим, однако, вы можете выбрать и наоборот. Необходимо помнить, что всегда нужно использовать одно и то же соглашение на знак моментов, начиная сначала и следуя ему на протяжении всего решения конкретной задачи.

Таким образом, мы получили нашу первую формулу, из которой определили силу реакции опоры в точке А. Аналогичная формула запишется для определения реакции в точке В. В нашем случае, ввиду симметричности действующего вертикально вниз усилия в 20 кН относительно точек подпорок, реакция в точке В будет равна таковой в точке А, то есть 10 кН.

Второй способ: через силы

Для существования равновесия сумма всех вертикальных сил должна быть равна нулю, то есть ΣF y = 0, где индекс Y определяет конкретную вертикальную силу в системе. Помните, что в данном случае мы должны включать в расчет все действующие в системе силы. Принимая во внимание последний факт, проводим суммирование всех вертикальных сил, в итоге получаем следующую формулу:

ΣF y = 0 = A y + В y — 20 кН, откуда 0 = 10 кН + В y — 20 кН, и В y = 10 кН.

Так же, как и в случае моментов сил, силы являются векторными величинами и имеют знак, здесь мы приняли за положительные силы те, которые действуют вверх, и за отрицательные те, которые действуют вниз. Выбор знака остается за вами, однако, напоминаем, что этот выбор не должен изменяться в процессе решения задачи. Отметим, что в формуле выше мы использовали результат, полученный в предыдущем пункте, когда вычислили силу реакции Ay.

Таким образом, мы решили, поставленную в начале этого параграфа задачу о расчете сил реакций опоры балки, используя при этом две системы уравнений, уравнения момента силы и уравнения силы, и получили ответы: силы реакции в точках А и В равны между собой и составляют 10 кН. Напоминаем, что физический смысл полученного равенства заключается в том, что действующая на балку внешняя сила приложена точно посередине балки. В случае ее приложения в другой точке, приведенные формулы также будут действительны и процесс расчета остается тем же самым.

Видео

Эта видеоподборка поможет вам лучше разобраться в теме и закрепить полученные знания.

Определение реакций опор

Схема нагружения быстроходного вала.

Горизонтальная плоскость XOZ:

Знак минус говорит о том, что сила направлена в противоположную сторону.

Проверка:

Строим эпюру изгибающих моментов в характерных точках относительно оси Х:

Вертикальная плоскость YOZ:

Проверка:

Строим эпюру изгибающих моментов в характерных точках от носитель оси Y:

Строим эпюру крутящих моментов:

Определяем суммарные реакции опор для расчета подшипников

Схема нагружения тихоходного вала.

Горизонтальная плоскость XOZ [3]:

Знак минус говорит о том, что сила направлена в противоположную сторону.

Проверка:

Строим эпюру изгибающих моментов в характерных точках относительно оси Х:

Вертикальная плоскость YOZ:

Знак минус говорит о том, что сила направлена в противоположную сторону.

Проверка:

Строим эпюру изгибающих моментов в характерных точках от носитель оси Y:

Строим эпюру крутящих моментов:

Определяем суммарные реакции опор для расчета подшипников

Предварительно назначенный подшипник для быстроходного вала роликовые конические однорядные средней серии №7304А [3].

Таблица 4.1 – Размеры и характеристика выбранного подшипника.

№	d, мм	D, мм	B, мм	Cr, кН	C0, кН	е	Y
7304	20	52	15	31,9	20	0,30	2,00

Определяем осевые составляющие

(4. 10)

(4.11)

Так как и , находим осевые силы нагружающие подшипники по следующим формулам

(4.12)

Отношение для опоры А

(4.13)

Что меньше е=0,30 и для опоры А Х=1 Y=0.

Отношение для опоры В

(4.14)

Что больше е=0,30 и для опоры В Х=0,4 Y=2,03.

Эквивалентные динамические нагрузки при коэффициенте динамичности нагрузки для всех типов редукторов К_Б=1,5 и температурном коэффициенте К_Т=1, т. к. t_раб.<100^оС [3].

Опора А

(4.15)

Опора В

(4.16)

Расчетный ресурс более нагруженного подшипника опоры В, при обычных условиях нагружения а

23=0,6.

(4.17)

где

(4.18)

Подшипник 7304A пригоден, т.к. расчетный ресурс больше требуемого .

Предварительно назначенный подшипник для тихоходного вала легкой серии №7207А.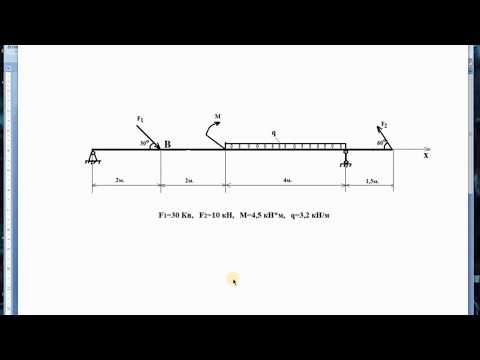

Таблица 4.2 – Размеры и характеристика выбранных подшипников.

№

d, мм

D, мм

B, мм

Cr, кН

C0, кН

е

Y

Продолжение таблицы 4.2

7207А

35

72

17

58,3

40,0

0,37

1,60

Определяем осевые составляющие [3]

(4. 19)

(4.20)

Так как и , находим осевые силы нагружающие подшипники по следующим формулам

(4.21)

Отношение для опоры С

(4.22)

Что меньше е=0,37 и для опоры А Х=1 Y=0.

Отношение для опоры D

(4.23)

Что больше е=0,37 и для опоры В Х=0,4 Y=1,62.

Эквивалентные динамические нагрузки при коэффициенте динамичности нагрузки для всех типов редукторов К_Б=1,5 и температурном коэффициенте К_Т=1, т. к. t_раб.<100^оС.

Опора C

(4.24)

Опора D

(4.25)

Расчетный ресурс более нагруженного подшипника опоры В, при обычных условиях нагружения а₂₃=0,6.

(4.26)

Подшипник 7304A пригоден, т.к. расчетный ресурс больше требуемого .

Механика для людей — Расчет реакций поддержки в кадре

Сочинения и письменные задания, выполненные для вас

Получите помощь с любым заданием — от школьного эссе до докторской диссертации

Расчет реакций поддержки в статически обнаруживаемая рама

Пример определения реакций в опорах плоской рамы, нагруженной силой, моментом и распределенной нагрузкой.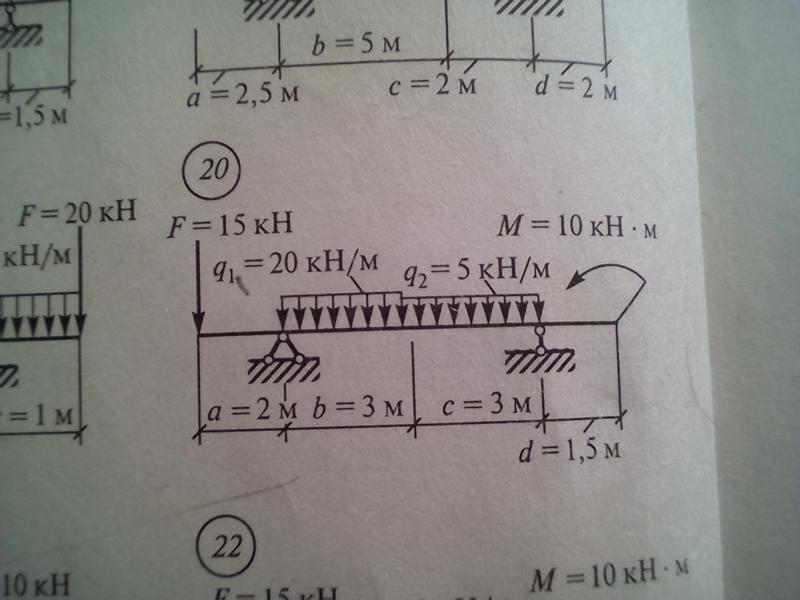

под действием нагрузки системы:

размер а=3м.

Расчет реакции

Перед началом решения задачи численные данные нагрузок переносим на расчетную схему и обозначаем характерные точки (сечения) рамы буквами А, В, С, Г и E.

Опорные реакции рамы будем определять из условия равновесия плоской системы сил.

Наш краткий видеоурок по расчету реакций балочных опор:

В шарнирно-неподвижной опоре (точка А) могут возникать две составляющие реакции — горизонтальная Н _А и вертикальная R _А , а в шарнирно-подвижной опоре (точка А) только одна реакция — вертикальная R _В .

О реакциях в шарнирных опорах

На данном этапе решения эти реакции могут быть направлены произвольно, например:

Для нахождения трех неизвестных сил нужны три уравнения статики: два уравнения суммы моментов относительно контрольных точек и суммы проекций всех сил на горизонтальную ось X, которая должна быть равна нулю.

Записываем их:

Из каждого уравнения выражаем и находим соответствующее значение опорной реакции:

Знак «-» реакции R _B указывает на то, что произвольно выбранное направление оказалось неверным, и его необходимо перенаправить в обратную сторону, при этом поменяв знак на положительный.

В задачах такого рода после расчета реакций в опорах настоятельно рекомендуется проверять полученные значения, так как даже небольшая ошибка в дальнейших расчетах может привести к неверному результату.

Проверка реакции

Проведем арифметическую проверку реакций, записав сумму моментов относительно, например, середины поперечины CD (точка К):

Тождество выполнено, значит реакции выполнены определены правильно.

После расчета и проверки опорных реакций можно приступать к построению диаграмм факторов внутренних сил в рамах.

Эссе и письменные задания для вас

Получите помощь с любым заданием — от школьного сочинения до кандидатской диссертации

3.4: Расчет опорных реакций для плоских конструкций

Опорные реакции для статически определимых и устойчивых конструкций на плоскости определяются с помощью уравнений равновесие. Процедура расчета описана ниже.

Процедура расчета опорных реакций

• Нарисуйте диаграмму конструкции в свободном теле, указав все неизвестные реакции с помощью стрелочной диаграммы.
• Проверьте устойчивость и определенность конструкции, используя уравнение 3.3 или 3.4. Если структура классифицируется как детерминированная, приступайте к анализу.
• Определите неизвестные реакции, применяя три уравнения равновесия. Если расчетная реакция приводит к отрицательному ответу, первоначально предполагаемое направление неизвестной реакции, как показано стрелкой на диаграмме свободного тела, неверно и должно быть исправлено, чтобы показать противоположное направление. После внесения поправки величина силы должна быть указана в виде положительного числа в скорректированном наконечнике стрелки на диаграмме свободного тела 9.0079

Пример 3.3

На консольную балку действует равномерно распределенная нагрузка и наклонная сосредоточенная нагрузка, как показано на рис.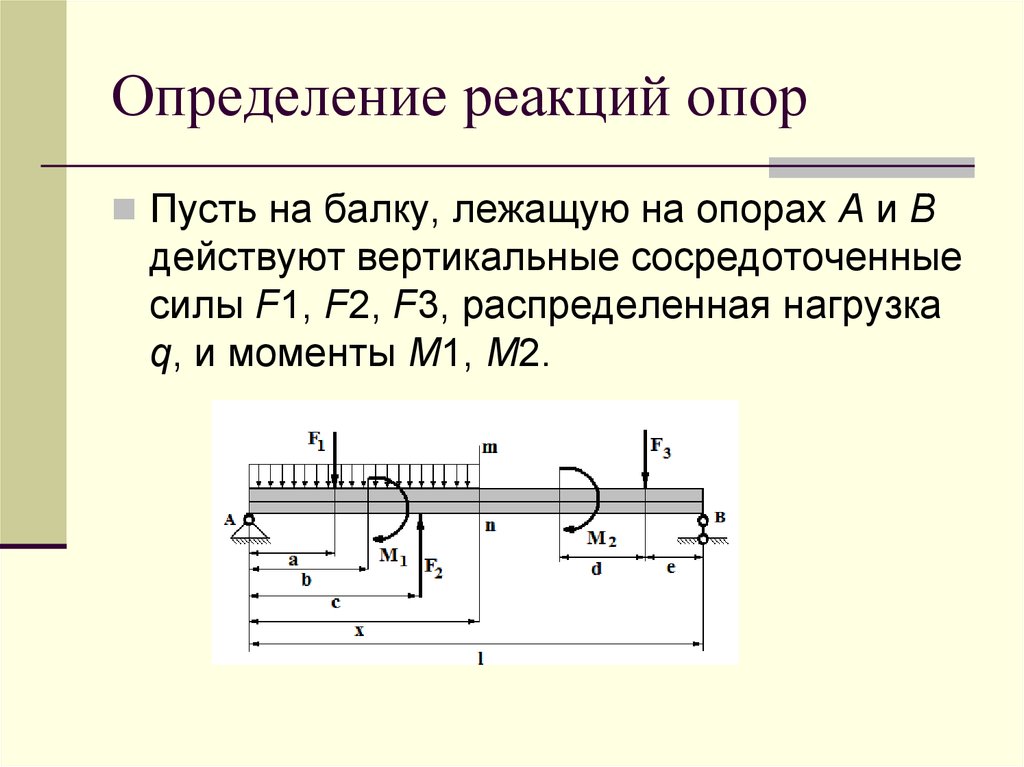 3.9а. Определить реакции на опоре A .

\(рис. 3.9\). Балка

Решение

Диаграмма свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.9b. Опорные реакции, как показано на диаграмме свободного тела, равны \(A_{y \prime}\) \(A_{y \prime}\) и \(M\).

Расчет реакций. Перед расчетом опорных реакций распределенную нагрузку следует заменить единой равнодействующей силой, а наклонную нагрузку разложить на вертикальную и горизонтальную составляющие. Величина равнодействующей силы равна площади под прямоугольной нагрузкой и действует через центр тяжести прямоугольника. Как видно на рис. 3.9c, \(P=[(4 \mathrm{kN} / \mathrm{m})(2 \mathrm{m})]\), и его расположение находится в центре тяжести прямоугольной нагрузки \ (=\left[\left(\frac{1}{2}\right)(2 \mathrm{m})\right]\). Применение уравнений статического равновесия дает следующее: 9{\ circ} — (4 \ times 2) = 0 \\ A_ {y} = 23,45 \ mathrm {kN} \\ \ rightarrow + \ sum \ mathrm {F} _ {\ mathrm {x}} = 0 \\ \ mathrm{A}_{\mathrm{x}}=0 \end{array} \quad \begin{array}{c} A_{y}=23,45 \mathrm{kN} \uparrow \\ \mathrm{A}_ {\ mathrm {х}} = 0 \ конец {массив} \)

Пример 3. 4

Простая балка длиной 12 футов несет равномерно распределенную нагрузку в 2 тысячи фунтов на фут по всему пролету и сосредоточенную нагрузку в 8 тысяч фунтов в середине пролета, как показано на рис. 3.10a. Определить реакции в опорах \(A\) и \(B\) балки.

\(рис. 3.10\). Простой луч.

Решение

Диаграмма свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.10b.

Расчет реакций. Распределенная нагрузка сначала заменяется единой равнодействующей силой, как показано на рис. 3.10c. Величина равнодействующей силы равна площади прямоугольного нагружения (распределенная сила). Таким образом, \(P=[(2 \mathrm{k} / \mathrm{ft})(12 \mathrm{ft})]\), и его расположение находится в центре тяжести прямоугольной нагрузки \(=\left[ \left(\frac{1}{2}\right)(12 \mathrm{ft})\right]\) Поскольку в этом примере нагрузка симметрична, реакции на обоих концах балки равны, и их можно определить с помощью уравнений статического равновесия и принципа суперпозиции следующим образом:

\(\begin{array}{l} +\стрелка вверх \sum F_{y}=0 \\ A_{y}=B_{y}=\left(\frac{2 \times 12}{2}\ справа)+\frac{2}{2}=13 \mathrm{kips} \\
+\стрелка вправо \sum \mathrm{F}_{\mathrm{x}}=0 \\ \mathrm{A}_{ \mathrm{x}}=0 \end{array} \quad \begin{array}{l} A_{y}=B_{y}=13 \mathrm{kips} \uparrow \\ \mathrm{A}_{ \mathrm{x}}=0 \end{массив}\)

Пример 3. 5

Балка с выступом подвергается переменной нагрузке, как показано на рис. 3.11а. Определить реакции на опорах \(A\) и \(B\).

\(рис. 3.11\). Балка с навесом.

Решение

Диаграмма свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.11b.

Расчет реакций. Обратите внимание, что распределенная нагрузка в балке треугольная. Распределенная нагрузка сначала заменяется единой равнодействующей силой, как показано на рис. 3.11c. Величина единой равнодействующей силы равна площади под треугольным нагружением. Таким образом, \(\rho=\left(\frac{1}{2}\right)(6 \mathrm{m})(10 \mathrm{kN} / \mathrm{m})\), а его центроид равен в центре загрузки (6м). Применение уравнений равновесия дает следующее:

\(\begin{array}{l} \curvearrowleft+\sum M_{A}=0 \\ -\left(\frac{1}{2}\right)(10)(6)(3)+3 B=0 \\ B_{y}=30 \mathrm{kN} \quad \quad B_{y}=30 \mathrm{kN} \\ \uparrow+\sum F_{y}=0 \\ 30+A_{y }-\left(\frac{1}{2}\right)(6)(10)=0 \quad \mathrm{A}_{\mathrm{y}}=0\\ \rightarrow+\sum \mathrm{ F} _ {\ mathrm {x}} = 0 \\ \ mathrm {A} _ {\ mathrm {x}} = 0 \ quad \ quad \ mathrm {A} _ {\ mathrm {x}} = 0 \ end {массив}\)

Пример 3. 6

Балка с выступающими концами выдерживает три сосредоточенные нагрузки в 12 тысяч фунтов, 14 тысяч фунтов и 16 тысяч фунтов и момент 100 тысяч фунтов на фут, как показано на рисунке 3.12a. Определить реакции на опорах А и В .

\(рис. 3.12\). Брус с выступающими концами.

Решение

Диаграмма свободного тела. Диаграмма свободного тела балки показана на рисунке 3.12b.

Расчет реакций. Применение уравнений равновесия дает следующее:

\(\begin{array}{l} +\curvearrowleft M_{A}=0 \\ -100+12(2)-14(2)-16(8)+ 4 B_{y}=0 \\ B_{y}=58 \text { тыс.фунтов } \quad \quad B_{y}=58 \text { тыс.фунтов } \uparrow \\ +\uparrow \sum F_{y}=0 \\ 58+A_{y}-12-14-16=0 \quad A_{y} = 26 \text { тысяч фунтов } \uparrow\\ +\rightarrow \sum F_{x}=0 \\ A_{x} =0 \quad \quad A_{x} \end{массив}\)

Пример 3.7

Составная балка подвергается нагрузкам, показанным на рис. 3.13а. Найти опорные реакции в точках \(A\) и \(B\) балки.

\(рис. 3.13\). Составной луч.

Решение

Диаграмма свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.13b.

Идентификация основных и дополнительных структур. Для правильного анализа составной структуры необходимо идентифицировать основные и дополнительные части структуры для правильного понимания их взаимодействия. Взаимодействие этих частей показано на рис. 3.13c. Первичная конструкция — это часть составной конструкции, которая может выдерживать приложенную внешнюю нагрузку без помощи дополнительной конструкции. С другой стороны, дополнительная конструкция является частью составной конструкции, которая зависит от основной конструкции для поддержки приложенной внешней нагрузки. Для данной структуры часть \(AC\) является первичной структурой, а часть \(CB\) является дополнительной структурой.

Расчет реакций. Анализ сложной структуры всегда должен начинаться с анализа дополнительной структуры, поскольку дополнительная структура поддерживается первичной структурой. Используя уравнения равновесия, опорные реакции балки определяются следующим образом:

Расчет комплементарной конструкции \(CB\) .

Расчет опорной реакции. Диаграмма изолированного свободного тела комплементарной структуры показана на рис. 3.13c. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), которая равна площади прямоугольной нагрузки, как показано на рис. 3.13d и рис. 3.13e. Применяя уравнения равновесия и учитывая, что из-за симметрии нагрузки опорные реакции в точке C и B равны по величине, дает следующее:

\(\begin{array}{l} +\стрелка вверх \sum F_{y}=0 \\ B_{y}=C_{y} =\frac{10(7)}{2}=35 \mathrm{кН} \quad B_{y}=\mathrm{C}_{y}=\frac{10(7)}{2}=35 \ mathrm{k} \end{array}\)

Анализ первичной структуры \(AC\) .

Расчет опорной реакции. Заметим, что до расчета реакций реакция в точке \(С\) дополнительной структуры прикладывается к основной структуре в качестве нагрузки. Величина приложенной нагрузки такая же, как и у комплементарной конструкции, но противоположна по направлению. Применение уравнений равновесия предполагает следующее: \(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ -25(2)-35(4)+M_{A}=0 \ \
M_{A}=190 \mathrm{kN} \cdot \mathrm{m} \quad M_{A}=190 \mathrm{kN} \cdot \mathrm{m} \curvearrowleft \\ +\uparrow \sum F_{ y}=0 \\ \mathrm{A}_{\mathrm{y}}-25-35=0 \\ \mathrm{A}_{\mathrm{y}}=60 \mathrm{kN} \quad \ mathrm{A}_{\mathrm{y}}=60\mathrm{kN} \uparrow\\ +\rightarrow\sum\mathrm{F}_{\mathrm{x}}=0 \\ \mathrm{A} _ {\ mathrm {x}} = 0 \ quad \ mathrm {A} _ {\ mathrm {x}} = 0 \ конец {массив} \)

Пример 3.8

Найдите реакции опор \(A\), \(C\) и \(E\) составной балки, несущей равномерно распределенную нагрузку 10 тысяч фунтов/фут по всей длине, как показано на рис. 3.14a.

Рис. 3.14. Составной луч.

Решение

Диаграмма свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3. 14b.

Идентификация основных и дополнительных структур. Диаграмма взаимодействия для данной структуры показана на рис. 3.14в. AB является основной структурой, а BD и DE являются дополнительными структурами.

Расчет реакций.

Анализ дополнительной структуры \(DE\) .

Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рис. 3.14c. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)) равной площади прямоугольной нагрузки, как показано на рис. 3.14d. Применяя уравнения равновесия и отмечая, что из-за симметрии нагрузки опорные реакции в точках \(D\) и \(E\) равны по величине, можно сделать следующее:

\(\begin{array}{ l} +\стрелка вверх \sum F_{y}=0 \\ D_{y}=E_{y}=\frac{10(8)}{2}=40 \mathrm{kips} \quad E_{y}= 40 \mathrm{kips} \uparrow \end{массив}\)

Анализ дополнительной структуры \(BD\) .

Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рисунке 3. 14e. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади прямоугольной нагрузки, как показано на рис. 3.14f. Нагрузка от комплементарной конструкции приложена в точке \(D\). Применение уравнений равновесия предполагает следующее:

\(\begin{array}{l} +\curvearrowleft \sum M_{B}=0 \\ -10(8)\left(\frac{8}{2} \right)-40(8)+4 C_{y}=0 \\ C_{y}=160 \text { тысяч фунтов } \quad C_{y}=160 \text { тысяч фунтов } \uparrow \\ +\uparrow \ сумма F_{y}=0 \\ 160-B_{y}-10(8)-40=0 \\ B_{y}=40 \text { тыс.фунтов } \end{array}\)

Анализ первичной структуры \(AB\) .

Расчет опорной реакции. Заметим, что до расчета реакций равномерная нагрузка заменяется единой равнодействующей силой, а реакция в точке \(B\) дополнительной конструкции прикладывается к основной конструкции как нагрузка. Применение требования равновесия дает следующее:

\(\begin{array}{l} \quad+\curvearrowleft \sum M_{A}=0 \\ \mathrm{M}-10(10)\left(\frac{ 10}{2}\right)+40(10)=0 \\ M_{A}=100 \mathrm{kips} . \mathrm{ft} \quad \quad M_{A}=100 \mathrm{kips} . \mathrm{ft} \curvearrowleft \\ +\uparrow \sum F_{y}=0 \\ A_{y}-10(10)+40=0 \\ A_{\mathrm{y}}=60 \mathrm{ тысяч фунтов} \quad \quad A _{\mathrm{y}}=60 \mathrm{kips} \uparrow\\ +\rightarrow \sum \mathrm{F}_{\mathrm{x}}=0 \\ A_{x }=0 \quad \quad A_{x}=0 \end{массив}\)

Пример 3.9

Найдите реакции опор \(A\), \(B\), \(E\) и \(F\) нагруженной составной балки, как показано на рис. 3.15a.

\(рис. 3.15\). Составной луч.

Решение

Диаграмма свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.15b.

Идентификация основной и дополнительной структуры. Диаграмма взаимодействия для данной структуры показана на рис. 3.15в. \(CD\) является дополнительной структурой, а \(AC\) и \(DF\) являются первичными структурами.

Расчет реакций.

Анализ дополнительной структуры \(CD\) .

Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рис. 3.15c. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади прямоугольной нагрузки, как показано на рис. 3.15d. Применяя уравнения равновесия и отмечая, что из-за симметрии в нагружении опорные реакции в точках \(C\) и \(D\) равны по величине, можно сделать следующее:0005

\(\begin{array}{l} +\стрелка вверх \sum F_{y}=0 \\ C_{y}=D_{y}=\frac{10(4)}{2}=20 \mathrm {kN} \end{array}\)

Анализ первичной структуры \(AC\) .

Расчет опорной реакции. Обратите внимание, что реакция в \(AC\) комплементарной структуры применяется как направленная вниз сила той же величины в той же точке первичной структуры. Применение уравнения равновесия предполагает следующее:

\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ -24(2)-20(5.5)+4 B_{y} =0\В_{у}=39.5 \mathrm{kN} \quad \quad B_{y}=39,5 \mathrm{kN} \uparrow\\ +\uparrow \sum F_{y}=0 \\ \mathrm{A}_{y}+39,5 -24-20=0 \\ A_{y}=4,5 \mathrm{kN} \quad \quad A_{y}=4,5 \mathrm{kN} \стрелка вверх\\ +\стрелка вправо \sum \mathrm{F}_{ \mathrm{x}}=0 \\ A_{x}=0 \quad \quad A_{x} = 0 \end{array}\)

Анализ первичной структуры \(DF\) .

Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рис. 3.15f. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади треугольной нагрузки, как показано на рис. 3.15g. Применяя уравнения равновесия и отмечая, что опорная реакция в точке \(D\) дополнительной конструкции действует как нагрузка на основную конструкцию, можно сделать следующее:0005

\(\begin{array}{l} +\curvearrowleft \sum M_{F} =0 \\ -20+\left(\frac{1}{2} \times 8 \times 10\right)\left (\frac{2}{3} \times 8\right)+20(8)-4 E_{y}=0 \\ E_{y}=88,33 \mathrm{kN} \quad E_{y}=88,33 \ mathrm{kN} \uparrow \\ +\uparrow \sum F_{y}=0 \\ F_{y}+88,33-\left(\frac{1}{2} \times 8 \times 10\right)-20 =0 \\ F_{y}=28,33 \mathrm{kN} \quad F_{y}=28,33 \mathrm{kN}стрелка вверх \end{array}\)

Пример 3.10

Определение реакции опор A и D кадра, показанного на рис. 3.16а.

\(рис. 3.16\). Рамка.

Решение

Диаграмма свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.16b.

Расчет реакций. Распределенные нагрузки в колонне \(AB\) и балке \(BC\) сначала заменяются одиночными результирующими силами, определяемыми как площадь их соответствующего оттенка нагрузки, как показано на рисунке 3.16c. Применение условий равновесия предполагает следующее:

\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ D_{y}(6)-\left(\frac{1}{2}\right)(6) (3)(3)-(2)(8)(4)=0 \\ D_{y}=15,7 \text { тыс.фунтов } \quad D_{y}=15,7 \mathrm{kips} \uparrow \\ +\ стрелка вверх \sum F_{y}=0 \\ \mathrm{A}_{y}+15,17-3(6)=0 \\ A_{y}=2,830 \mathrm{kips} \quad A_{y}=2,830 \mathrm{kips} \uparrow \\ +\rightarrow \sum \mathrm{F}_{\mathrm{x}}=0 \\ -\mathrm{A}_{x}+(2 \times 8)=0 \\ A_{x}=16 \mathrm{kips} \quad A_{x}=16 \mathrm{kips} \leftarrow \end{массив}\)

 

Пример 3.11

Жесткая рама нагружена, как показано на рис. 3.17а. Определить реакции на опоре \(D\).

\(рис. 3.17\). Жесткая рама.

Решение

Диаграмма свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.17b.

Расчет реакций. Распределенная нагрузка в части AB рамы сначала заменяется единой равнодействующей силой, как показано на рисунке 3.17c. Применение уравнений равновесия позволяет сделать следующее:

\(\begin{align} &+\curvearrowleft \sum M_{D}=0\\ &-M_{D}-16(8)+(4 \times 14)\left(\frac{14}{ 2}\right)-10(10)=0\\ &M_{D}=164 \text { тысяч фунтов } \mathrm{ft} \quad M_{D}=164 \text { тысяч фунтов } \mathrm{ft} \curvearrowright \mathrm{A}\\ &+\uparrow \sum F_{y}=0\\ &D_{y}-4(14)-10=0\\ &D_{y}=66 \text { тысяч фунтов } \ quad D_{y}=66 \text {kips} \uparrow\\ &+\rightarrow \sum\mathrm{F}_{\mathrm{x}}=0\\ &-D_{x}+16=0\ \ &D_{x}=16 \text { тысяч фунтов } \quad D_{x}=16 \text { тысяч фунтов } \leftarrow \end{aligned}\)

 

Пример 3.12

Найдите реакции на опорах E и F рамы, показанной на рис.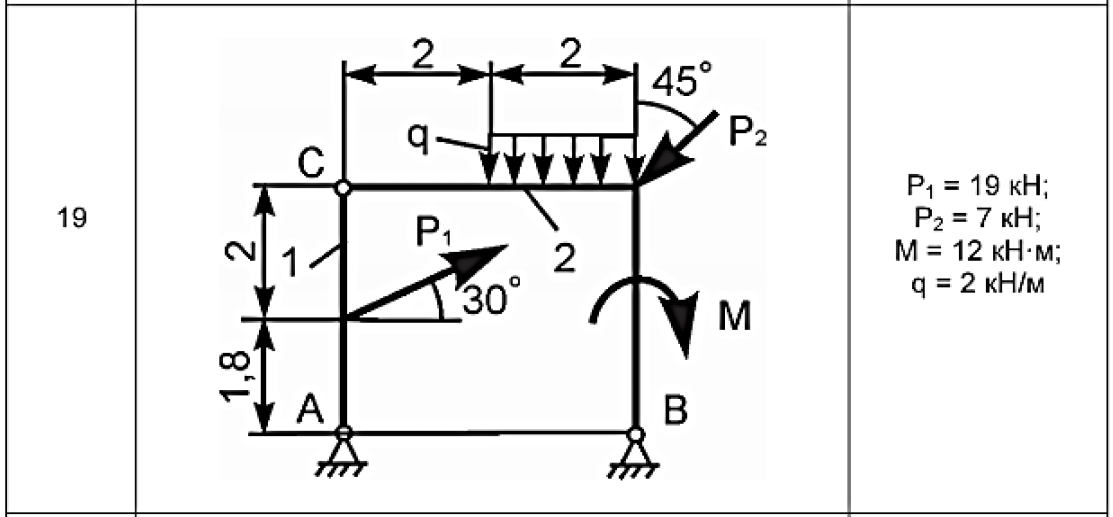 3.18а.

\(рис. 3.18\). Рамка.

Решение

Диаграмма свободного тела. Схема свободного тела рамы показана на рисунке 3.18b.

Расчет реакций. Распределенные нагрузки сначала заменяются единичными равнодействующими силами, как показано на рис. 3.18c. Применение уравнений статического равновесия позволяет сделать следующее:

\(\begin{array}{l} +\curvearrowleft \sum M_{E}=0 \\ \left(\frac{1}{2} \times 4 \times 8\right)\left(\frac {1}{3} \times 4\right)-(4\times 7)\left(\frac{7}{2}\right)-\left(\frac{1}{2} \times 4 \times 8\right)\left(\frac{7}{2}+\frac{1}{3} \times 4\right)+7 F_{y}=0 \\ F_{y}=22 \mathrm{kN } \quad F_{y}=22 \mathrm{kN} \uparrow \\ +\uparrow \sum F_{y}=0 \\ E_{y}+22-2\left(\frac{1}{2} \times 4 \times 8\right)-4(7)=0 \\ E_{y}=38 \mathrm{kN} \quad E_{y}=38 \mathrm{kN} \uparrow \\ +\rightarrow \ сумма \mathrm{F}_{\mathrm{x}}=0 \\ E_{x}=0 \quad E_{x}=0 \end{массив}\)

Пример 3.13

Определите реакции опоры A жесткой рамы, показанной на рис. 3.19а.

\(рис. 3.19\). Жесткая рама.

Решение

Диаграмма свободного тела. Схема свободного тела рамы показана на рисунке 3.19b.

Расчет реакций. Распределенная нагрузка в столбце \(AB\) сначала заменяется одной равнодействующей силой, как показано на рис. 3.19c. Применение уравнений статического равновесия позволяет сделать следующее:

\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ -M_{A}-20(3)-\left(\frac{1}{2} \times 10 \times 10\right)\left(\frac{1}{3} \times 10\right)=0 \\ M_{A}=-226,67 \mathrm{kN} \cdot \mathrm{m} \quad \quad M_{A}=226,67 \mathrm{kN} \cdot \mathrm{m} \curvearrowleft \\ +\uparrow \sum F_{y}=0 \\ A_{y}-20=0 \\ A_{y}= 20 \mathrm{kN} \quad \quad A_{y}=20 \mathrm{kN} \uparrow\\ +\rightarrow \sum F_{x}=0 \\ -A_{x}+\left(\frac{ 1}{2} \times 10 \times 10\right)=0 \\ A_{x}=50 \mathrm{kN} \quad \quad A_{x}=50 \mathrm{kN} \leftarrow \end{array }\)

Пример 3.14

Определите реакции на опорах \(A\) и \(E\) рамы, шарнирно закрепленной в точке \(C\), как показано на рис. 3.20a.

\(рис. 3.20\). Рамка.

Решение

Диаграмма свободного тела. Схема свободного тела рамы показана на рисунке 3.20b.

Расчет реакций. Реакции в составной раме рассчитываются с учетом диаграмм свободного тела как всей рамы, так и ее части. Перед расчетом реакций распределенную нагрузку в колонне заменяют единой равнодействующей силой. Вертикальные реакции в \(Е\) и \(А\) и горизонтальные реакции в \(А\) находятся путем применения уравнений статического равновесия и рассмотрения диаграммы свободного тела всей рамы. Горизонтальная реакция в \(E\) находится при рассмотрении части \(CDE\) диаграммы свободного тела.

\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ 8 E_{y}-(2 \times 10)\left(\frac{10}{2}\right )-10(4)=0 \\ E_{y}=17.5 \text { тыс.фунтов } \quad \quad E_{y}=17.5 \mathrm{kips} \uparrow \\ +\uparrow \sum F_{y}= 0 \\ A_{y}+17,5-10=0 \\ A_{y}=-7,5 \text { тысяч фунтов } \quad \quad A_{y}=7,5 \text { тысяч фунтов } \downarrow \end{array}\ )

Знак минус означает, что первоначально предполагаемое направление \(A_{y}\) было неверным. Следовательно, \(A_{y}\) действует вниз, а не вверх, как первоначально предполагалось. Это должно быть исправлено при последующем анализе.

Чтобы определить \(E_{x}\), рассмотрим момент сил в элементе \(CDE\) относительно шарнира.

\(\begin{array}{l} \curvearrowleft +\sum M_{C}=0 \\ 17,5(4)-10 E_{x}=0 \\ E_{x}=7 \text { тысяч фунтов } \quad \quad E_{x}=7 \text { тыс.фунтов } \leftarrow \\ +\rightarrow \sum F_{x}=0 \\ -A_{x}-7+2 \times 10=0 \\ A_{ x}=13 \text { тысяч фунтов } \quad \quad A_{x}=13 \text { тысяч фунтов } \leftarrow \end{массив}\)

Пример 3.15

Найдите реакции в опорах \(A\) и \(B\) нагруженной рамы на рис. 3.21а. Рама шарнирно закреплена в точке \(D\).

\(рис. 3.21\). Загруженный кадр.

Решение

Диаграмма свободного тела. Схема свободного тела рамы показана на рисунке 3.21b.

Расчет реакций. Распределенная нагрузка в столбце \(AC\) сначала заменяется единой результирующей силой путем нахождения области нагрузки, как показано на рис. 3.21. Реакция в точке \(B\) вычисляется путем принятия момента сил в части \(DB\) рамы относительно штифта в точке \(D\), а остальные реакции определяются путем применения других условий равновесия.

\(\begin{align} &+\curvearrowleft \sum M_{D}=0\\ &B_{y}(0)-15(4)=0\\ &B_{y}=0\\ &+n \sum M_{A}=0\\ &M_{A}+6 \times 0-\left(\frac{1}{2} \times 8 \times 20\right)\left(\frac{1}{3) } \times 8\right)-12(3)+15(4)=0\\ &M_{A}=189,33 \mathrm{kN} \cdot \mathrm{m} \quad M_{A}=189,33 \mathrm{ кН} \cdot \mathrm{m} \curvearrowright\\ &+\стрелка вверх \sum F_{y}=0\\ &A_{y}+0-12=0\\ &A_{y}=-12 \mathrm{kN } \quad A_{y}=12 \downarrow \end{aligned}\)

Знак минус означает, что первоначально предполагаемое направление A _y неверно. Следовательно, A _y действует вниз, а не вверх, как предполагалось изначально. Это должно быть исправлено при последующем анализе.

\(\begin{array}{l} +\стрелка вправо \сумма F_{x}=0 \\ -A_{x}-15+\left(\frac{1}{2} \times 8 \times 20 \right)=0 \\ A_{x}=65 \mathrm{kN} \quad \quad A_{x}=65 \mathrm{kN} \rightarrow \end{array}\)

Краткое изложение главы

Условия статического равновесия: Конструкция находится в состоянии статического равновесия, если равнодействующая всех действующих на нее сил и моментов равна нулю. Математически это выражается следующим образом:

\(\Сигма F=0\) \(\Сигма M=0\)

Для тела на плоскости существуют следующие три уравнения равновесия:

\(\Sigma F_{X}=0\) \(\Sigma F_{Y}=0\)∑ \(\Sigma M_{0}=0\)

Типы опор: Различные символические представления используются для моделирования различных типов опор для конструкций. Ролик используется для моделирования опоры, которая препятствует вертикальному движению конструкции, но допускает горизонтальное перемещение и вращение. Штифт используется для моделирования опоры, которая предотвращает горизонтальные и вертикальные перемещения, но допускает вращение. Неподвижная опора моделирует опору, предотвращающую горизонтальные и вертикальные перемещения и повороты.

Детерминированность, неопределенность и устойчивость структур: Структура является детерминированной, если число неизвестных реакций равно числу статических равновесий. Таким образом, для определения опор такой конструкции достаточно уравнений статического равновесия. С другой стороны, статически неопределимая структура — это структура, в которой количество неизвестных реакций превышает уравнения равновесия. Для анализа неопределенной конструкции нужны дополнительные уравнения, и эти уравнения можно получить, рассматривая совместность конструкции. Неопределенные конструкции иногда необходимы, когда необходимо уменьшить размеры элементов или увеличить жесткость элементов. Стабильная структура — это структура, в которой опорные реакции не параллельны и не параллельны друг другу. Формулировки устойчивости и определенности балок и шпангоутов следующие:

Балки и рамы:	\(3 m+r<3 j+C\) Структура неустойчива
	\(3 m+r=3 j+C\) Структура детерминированная
	\(3 m+r>3 j+C\)Структура не определена

Практические задачи

3. 1 Классифицируйте конструкции, показанные на рисунках P3.1a–P3.1p, как статически определимые или неопределимые, а также статически устойчивые или неустойчивые. Если неопределенно, укажите степень неопределенности.

\(Рис. П3.1\). Структурная классификация.

3.2. Определите опорные реакции для балок, показанных на рис. P3.2–рис. P3.12.

\(Рис. П3.2\). Луч.

\(Рис. П3.3\). Луч.

\(Рис. П3.4\). Луч.

\(Рис. П3.5\). Луч.

\(Рис. П3.6\). Луч.

\(Рис. П3.7\). Луч.

\(Рис. П3.8\). Луч.

\(Рис. П3.9\). Луч.

\(Рис. П3.10\). Луч.

\(Рис. П3.11\). Луч.

\(Рис. П3.12\). Луч.

3.3. Определите опорные реакции для рам, показанных на рис. P3.13–рис. P3.20.

\(Рис. П3.13\). Рамка.

\(Рис. П3.14\). Рамка.

\(Рис. П3.15\). Рамка.

\(Рис. П3.16\). Рамка.

\(Рис. 3.17\). Рамка.

\(Рис. 3.18\). Рамка.

\(Рис. 3.19\). Рамка.

\(Рис. 3.20\). Рамка.

3.4 Определите опорные реакции для ферм, показанных на рис. P3.21–рис. P3.27.

\(Рис. П3.21\). Ферма.

\(Рис. П3.22\). Ферма.

\(Рис. П3.23\). Ферма.

\(Рис. П3.24\). Ферма.

\(рис. П3.25\). Ферма.

\(рис. П3.26\). Ферма.

\(Рис. П3.27\). Ферма.

 

---

Эта страница под названием 3.4: Расчет опорных реакций для плоских конструкций распространяется по лицензии CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Рене Альдерлистеном (TU Delft Open) с помощью исходного содержимого, которое было отредактировано. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.